A unified theory of electron-rich and electron-deficient multicenter bonds in molecules and solids: a change of paradigms

Abstract

Here, we propose a multicenter bond theory that addresses the origin and mechanisms behind the formation of electron-rich multicenter bonds (ERMBs) and electron-deficient multicenter bonds (EDMBs), with special emphasis on molecules and solids primarily composed of electron-rich elements. We show that both types of multicenter bonds have the same origin, but a different mechanism of formation upon increasing electronic density; e.g. upon reduction, increase of pressure, or chemical substitution of elements by their heavier analogs. In addition to our recent demonstration of the formation of EDMBs in electron-rich systems, such as pnictogens, chalcogens, and chalcogenides related to phase change materials (see H. H. Osman et al., J. Mater. Chem. C, 2024, 12, 10447–10474), here we present other examples of solids with electron-rich elements forming EDMBs and ERMBs. We conclude that EDMBs can occur not only as three-center–two-electron (3c–2e) bonds in molecules but also as linear or quasi-linear two-center–one-electron (2c–1e) bonds in extended solids. In addition, we propose that pure ERMBs can only occur as linear or quasi-linear three-center–four-electron (3c–4e) bonds. All these claims suppose a change of paradigms regarding the current understanding of ERMBs and EDMBs. To understand the formation of ERMBs and EDMBs in electron-rich elements, we show some of the simplest geometries of linear EDMBs and ERMBs along one (1D), two (2D), and three (3D) dimensions that can be found in the hypercoordinated multicenter units of molecules and solids with electron-rich elements and propose a new way of notation of these hypercoordinated units. Finally, we show that both types of multicenter bonds, in general, do not violate the doublet/octet rule.

---

1. Introduction

The nature of the chemical bonding in the crystalline phases of phase change materials (PCMs) has been debated for over 70 years due to their extraordinary properties. In recent works,^1,2 it has been proposed that the octahedrally-coordinated α-Po and β-Po phases observed in pnictogens and chalcogens, as well as the crystalline phases of PCMs, feature the old electron-deficient multicent bond (EDMB). This bond is the generalized version of the three-center–two-electron (3c–2e) bond proposed by Rundle and Longuet-Higgins in the 1950s^3–6 and it is known to be typically present in materials with electron-deficient elements (hydrogen and elements of groups 1, 2, and 13), such as the hydrogenonium ion H₃⁺, elemental boron, boranes, and BaAl₄ among others.^7–10 Noteworthy, W. Lipscomb was awarded the Nobel Prize in Chemistry in 1976 for the explanation of boranes with the use of 3c–2e bonds.¹¹

The electron-deficient character of the bonds in the octahedrally-coordinated α-Po and β-Po phases of group-15 and -16 elements has been evidenced by the small value of the charge density at the bond critical point and the electron localization function (ELF) between two bonded atoms as well as by the number of electrons shared between two atoms (ES) obtained from quantum mechanical calculations.^1,2 This last magnitude is calculated as two times the delocalization index (DI) obtained from the quantum theory of atoms in molecules (QTAIM) as already done in previous works.^12–15 It has also been shown that the ES values combined with the renormalized number of electrons transferred between two atoms (ET), typically calculated as the Bader charge of the cation divided by the nominal oxidation state of the cation, can be used in a two-dimensional (2D) ES vs. ET map (Fig. 1) to identify the different types of bonds in materials.^12–15 Importantly, the density-based ES vs. ET map has been demonstrated to be equivalent to an orbital-based map, where the ES value is calculated as two times the integrated crystal orbital bond index (ICOBI), and the ET value is calculated as the normalized Löwdin charge.^15,16 In this context, we have also provided the orbital-based ES vs. ET map in Fig. S1 in the ESI† to complement the density-based map. Although both maps provide the same information, some examples are located better on one map than on the other. Consequently, we believe that the ES vs. ET map, or any other equivalent map, could help to locate the different kinds of bonds in different regions of the map. In particular, we are going to show that it can be used to distinguish between the two known types of multicenter bonds, the EDMB and the electron-rich multicenter bond (ERMB) from the classical covalent, ionic, and metallic bonds.

Fig. 1 2D map with the number of electrons shared (ES) vs. the normalized number of electrons transferred (ET) showing the chemical bond classification in materials. The red, black, and blue regions correspond to the classical covalent, ionic, and metallic bonds, respectively. In addition, the map shows the orange and green regions of materials with electron-rich multicenter bonds (ERMBs) and electron-deficient multicenter bonds (EDMBs), respectively. Circles correspond to materials studied in previous studies.¹⁴ Pnictogens and chalcogens studied in a previous work at different pressures² are shown as open squares. As observed, the structures of pnictogens and chalcogens with octahedral coordination are located in the green region of EDMBs as well as PCMs, such as GeTe, SnTe, and PbS.

The ERMB, also known as the hypervalent bond,¹⁷ is the generalized version of the three-center–four electron (3c–4e) bond proposed by Rundle and Pimentel in the 1950s.^18,19 This bond has been assumed to be typically present in materials with electron-rich elements (elements of groups 15 to 18), such as hypervalent molecules I₃⁻, XeF₂, XeF₄, XeF₆, simple cubic (sc) Sb, and several Zintl phases, such as Li₂Sb, BaZnSb₂, TlTe.²⁰ It must be mentioned that the very existence of ERMBs has been questioned in several works.^21,22

According to the ES and ET values in Fig. 1, covalent bonds with a bond order of 1 (red region in Fig. 1) extend from pure covalent bonds (ET = 0 and ES ≈ 2) to iono-covalent bonds or polar covalent bonds (ET ≈ 0.65 and ES ≈ 0.9).^2,14 In contrast, EDMBs in the octahedrally-coordinated α-Po and β-Po phases of pnictogens and chalcogens (also with ET = 0) as well as PCMs (ET ≠ 0), such as β-GeTe, SnTe, and PbS, extend along the same range of ET values, but are characterized by much smaller values of ES (ES ≈ 1) (green region in Fig. 1 and Fig. S1, ESI†). Note that EDMBs are characterized by having a bond order of 0.5 since they are longer than covalent bonds. We will show later that a similar situation is found for a molecule with EDMBs, such as diborane (B₂H₆),²³ whose central B–H bonds are also located in the green region of Fig. 1 and Fig. S1 (ESI†).

Similar to EDMBs, ERMBs are longer than covalent bonds and were supposed to have a bond order of 0.5 according to the Pimentel model;^18,19 however, ERMBs are typically shorter than EDMBs and feature a bond order higher than those of EDMBs, as has been recently shown for polyiodides.²⁴ However, the ES values of ERMBs are larger than those of iono-covalent bonds of similar polarity (similar value of ET). This result allows us to locate ERMBs in the orange region of Fig. 1 and Fig. S1 (ESI†), as we will show later for molecules with ERMBs, such as [FHF]⁻ and XeF₂, and for solids, such as CsI₃, whose H–F, Xe–F, and I–I bonds, respectively, are in good agreement with recent findings in hypervalent molecules.¹⁵

The EDMB model for PCMs proposed in ref. 1 and 2 is in contrast to the two previous bond models for PCMs: the hypervalent and metavalent bond models. The hypervalent bond model considers that the crystalline phases of PCMs, which feature hypercoordinated electron-rich elements, are characterized by the ERMBs; however, this does not agree with the position of bonds in PCMs in the ES vs. ET map. On the other hand, the metavalent bond model considers that the crystalline phases of PCMs are characterized by a new bond type, the metavalent bond, which is a two-center–one-electron (2c–1e); i.e., an electron-deficient bond, whose position in the ES vs. ET map is similar to that of the position of the EDMBs. Noteworthy, the supporters of the metavalent bond model for PCMs do not consider the multicenter character of the bond in PCMs although they do not discard that it can have a multicenter character.^{13–15,25,26} In recent works, we have stressed that if the multicenter character is added to the electron-deficient nature of the metavalent bond, then the metavalent bond becomes naturally the EDMB.^1,2,27

It must be clarified that the proponents of the metavalent bond model have not clarified the position of EDMBs in the 2D ES vs. ET map. Instead, the authors of ref. 1 and 2 claim that the new metavalent bond is nothing else but the old EDMB. Therefore, the properties of the EDMB are those that have been attributed to the new metavalent bond: (i) hypercoordination (violation of the 8 − N rule); in other words, a higher atomic coordination than that expected for compounds with covalent ppσ-bonds that obey the 8 − N rule, (ii) relatively low band gaps and shiny metallic luster, (iii) moderate electrical conductivity, (iv) extremely high optical dielectric constants and Born effective charges, (v) low-frequency optical phonons and high Grüneisen parameters, (vi) low thermal conductivity, (vii) brittleness (due to the directional character of EDMBs), and (viii) high probability of multiple emission events in laser-assisted field evaporation measurements (due to the softer character of EMDBs than that of the covalent ones).‡

In ref. 1 and 2, it has been also shown that the octahedrally-coordinated α-Po and β-Po phases of pnictogens (As, Sb, Bi) and chalcogens (Se, Te) at high pressure (HP) feature linear EDMBs formed by a mechanism that transforms the primary covalent bond and the secondary weak non-covalent bond (present in the low-coordinated phases of these elements at room pressure (RP)) into EDMBs at HP. It was commented that the mechanism of EDMB formation is different from that of ERMB formation; however, these two mechanisms were not discussed in considerable detail in those works.

The present work is the second part of the manuscript already sent for publication on December 2023,¹ which we have decided to split into two parts (ref. 2 and this work) for the sake of clarity. This work presents a unified multicenter bond theory which is aimed at discussing at length the similitudes and differences between ERMBs and EDMBs, mainly in electron-rich elements; the common origin and different formation mechanisms of both multicenter bonds; the geometries of the hypercoordinated units of electron-rich elements with both types of multicenter bonds; and the compliance of the doublet/octet rule, in general, in the atoms participating in both ERMBs and EDMBs. To facilitate the understanding and differentiation of both kinds of multicenter bonds in electron-rich elements, we provide and discuss the crystalline structures of different molecules and solids with different bond types (even a solid with a mixture of both EDMBs and ERMBs in a single element, i.e., homoatomic bonds, within the same crystalline structure). The clear distinction between ERMBs and EDMBs will help us to explain the structures and properties found in many important technological materials, including PCMs, thermoelectrical and photovoltaic materials, Zintl phases, intermetallics, polyhalides, and cluster compounds at RP as well as the structures and properties found in several polyhalogen anions and the atomic/polymeric phases of nitrogen and hydrogen at HP.

To achieve this, we have performed first-principles simulations based on density functional theory (DFT) for several materials (further details are provided in the ESI†). In particular, a comparison of the experimental and simulated structural data of the different materials studied in this work is provided in Table S1 of the ESI.† The theoretical bonding descriptors between two atoms are provided for density- (Table S2 of the ESI†) and orbital-based methods (Table S3 of the ESI†). In particular, the density-based method using QTAIM¹² allows us to obtain the Bader atomic charges as well as ES and ET values using the CRITIC2 program,²⁸ while the orbital-based method allows us to obtain the Löwdin charges and ES and ET values using the LOBSTER program.²⁹ Hereon, the different values of bonding descriptors in different materials will be noted as X.X [X.X] as obtained from CRITIC2 [LOBSTER] program and these values can be found in Table S2 [Table S3, ESI†]. Note that the ES and ET values obtained from CRITIC2 and LOBSTER are different; however, in general, they provide similar information if we compare Fig. 1 and Fig. S1 (ESI†), as already shown in previous works.^2,16,25 Therefore, it can be concluded that our results on ES and ET values obtained from DFT simulations are robust since they do not depend on density- or orbital-based methods as long as DFT simulations are considered to be valid for the description of the studied systems.

Here we want also to notice that the distinction of the different types of multicenter bonds (ERMBs and EDMBs) from iono-covalent bonds is mainly done by taking into account the different bond lengths of multicenter and iono-covalent bonds and with the use of ES and ET values. Note that multicenter bond indices for solids have not been well developed yet. In this context, it must be mentioned that despite multicenter bond indices have been calculated for molecules since 1990,^22,30–32 and extended to aromatic molecules,^33,34 multicenter bond indices for solids have been barely explored since the results are not so clear with correlated wavefunctions³⁵ and are not available in the CRITIC2 code yet. A multicenter bond index for solids has been proposed in LOBSTER, the integrated crystal orbital bond index for three centers, ICOBI(3c);³⁶ however, its validation for solids, like PCMs is doubtful,³⁷ as already discussed in ref. 2.

2. Origin and mechanism of formation of ERMBs and EDMBs

Multicenter bonds, either electron-deficient or electron-rich, are bonds extended beyond two centers. Therefore, the simplest multicenter bond is necessarily the three-center bond as found in trimers. Consequently, the origin of multicenter bonds in trimers, either electron-rich, like in I₃⁻, or electron-deficient, like in H₃⁺, must come from the interaction of primary bonds, like intramolecular bonds in I₂ and H₂ molecules, and secondary non-covalent bonds, like intermolecular bonds between I₂ and I⁻ and between H₂ and H⁺. The formation of three-center bonds requires a trans influence between both the primary and secondary bonds; that is, a perturbation of the primary bond (typically resulting in lengthening and weakening) as the secondary bond shortens and strengthens. In the end, the original primary and secondary bonds (both are two-center interactions) tend to be equal in length and strength (provided that they are formed by the same elements, such as in I₃⁻ and H₃⁺) to give rise to the multicenter (three-center) bond in the trimer.

Examples of the formation of 3c–4e bonds in trimers coming from the interaction between primary and secondary bonds were already provided in 1998 by Landrum and Hoffmann, who realized that the formation of linear ERMBs in trimers with central Sb and Te atoms was promoted when the primary bond length of the trimer was above a certain value.³⁸ These data were further analyzed by Lubchenko and coworkers, who stated more clearly that the formation of ERMBs was promoted with the decrease of the trimer mean bond length as the mass density increases.³⁹ The same tendency to form ERMBs as the trimer total length decreases was found in the formation of ERMBs in I₃⁻ trimers in different compounds by Savastano,⁴⁰ who revised the old work of Money-Slater.⁴¹ In all these papers, it was shown that both primary and secondary bonds tend to equalize when the ERMB is formed. In addition, Papoian and Hoffmann suggested that ERMB formation could also be induced by reduction, i.e., providing electrons to the system.²⁰ Altogether, these data suggest that the formation of ERMBs by equalization of original short primary and long secondary bonds is promoted when the electronic density increases.

On the other hand, it has been recently concluded that EDMB formation in pnictogens and chalcogens can be also induced by pressure and by atomic substitution by heavier elements in a group;²i.e., two mechanisms that also lead to an increase in electronic density. It must be stressed that a similar conclusion was provided by Grochala et al., who considered that pressure promoted the formation of multicenter bonds.⁴² Consequently, we can tentatively conclude that, in general, the formation of multicenter bonds is promoted by any means that leads to an increase in the electronic density (either by pressure, substitution by heavier elements, or reduction). Conversely, it can be also concluded that multicenter bonds split into a primary and a secondary bond when the electronic density goes below a given value (induced either by decreasing pressure, substitution by lighter elements, or oxidation); a sentence that is in line with the results of Lubchenko and coworkers.³⁹

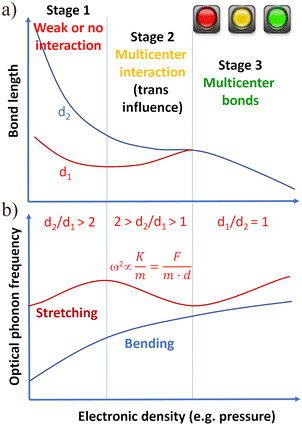
To illustrate the general simplest process of multicenter bond formation on increasing electronic density, we present a scheme of how multicenter bonds can be formed from initial primary bonds and secondary interactions/bondings via a gradual process with three stages (see Fig. 2). The evolution of the distances of a primary strong bond (d₁) and a relatively weak secondary interaction (d₂) is shown in Fig. 2a, while the evolution of the optical phonon frequencies of a material that develops a multicenter bond with increase of the electronic density is shown in Fig. 2b.

Fig. 2 General behavior of the (a) bond lengths and (b) optical phonon frequencies of a material with a primary and a secondary bond, which are linked by a trans influence, and therefore lead to the multicenter bond formation upon the increase of the electronic density; e.g. upon reduction, increase of pressure, or chemical substitution of an element by a heavier analog.

Let us first comment on the evolution of bond lengths with increasing electronic density during the formation process of multicenter bonds (Fig. 2a). In the first stage of multicenter bond formation, the ratio between the distances of the secondary interaction and the primary bond is so large (typically d₂/d₁ > 2) that both bonds/interactions are not linked; i.e., the strong primary bond (typically of iono-covalent nature) is not affected by the presence of the weak secondary interaction (typically being a non-covalent interaction of electrostatic nature). In the second stage, the ratio between the distances of the secondary and primary bonds are comparable (typically 1 < d₂/d₁ < 2) due to the considerable shortening of the secondary bond length (now the secondary interaction can be considered a bond) as the electronic density increases. In this stage, the secondary bond perturbs (trans influence) the primary bond, so both bonds tend to a similar (sometimes equal) value of bond length as the electronic density increases. The trans influence is a well-known phenomenon in Chemistry§ by which the primary bond length typically increases at the expense of the decrease of secondary bond length and it has been documented in a number of papers during the formation of ERMBs^24–26,38 and EDMBs.^1,2 In the third stage, beyond a critical electronic density, both bonds become equal or almost equal in bond length (typically d₂/d₁ < 1.05) and strength and behave similarly upon an increase in electronic density. When this behavior occurs, a multicenter bond has been formed.

It must be stressed that the presence of three stages during the formation of EDMBs was clearly shown in ref. 1 and 2 and that the same number of stages was noted during the formation of 3c–4e bonds in several systems, e.g. in [FHF]⁻ or HF₂⁻,⁴³ and during the breaking of 3c–4e bonds; e.g. the C–C≡N of acetonitrile during a S_N2 reaction.⁴⁴ The observation of these three stages in the formation of multicenter bonds contrasts with the results of several works that suggested that it would be difficult to distinguish between the scenario with primary and secondary bonds and the scenario with multicenter bonds.^38,39,45

The three stages of the multicenter bond formation process are also reflected in the evolution of the vibrational modes of the materials with increasing electronic density (see Fig. 2b). In the first stage, the increase in electronic density leads to a normal increase in the optical phonon frequencies of both high-frequency stretching phonons and low-frequency bending phonons (the last ones derived from the acoustic phonons of the Brillouin zone edge due to folding of the Brillouin zone). In the second stage, the trans influence leads to an anomalous softening of the stretching phonons. This softening can be understood if we consider that the square of the frequency of stretching phonons is proportional to the bond force constant per unit length, K, and inversely proportional to the mass, m, of the linked atoms or equivalently proportional to the bond force constant, F, and inversely proportional m, and bond length, d, of the linked atoms (see equation in Fig. 2). Therefore, the anomalous increase in the primary bond length (in addition to the loss of charge of the primary bond in the mechanism of EDMB formation (see Fig. 3d–f) explains the softening of the stretching phonons related to the primary bond. Finally, in the third stage, there is a re-hardening of the stretching phonons due to the normal behavior of the bond distance and charge density of the multicenter bonds.^1,2

Fig. 3 (a)–(c) Schematics of the mechanism of a 3c–4e bond formation in a system with three electron-rich atoms (A, B, and C) as the electronic density increases. (d)–(f) Schematics of the mechanism of a 3c–2e bond formation in a system with three electron-rich atoms (A, B, and C) as the electronic density increases. At low electronic densities (a) and (d), A and B atoms are assumed to be linked by a primary iono-covalent bond and B and C atoms are linked by a secondary non-covalent interaction/bond in which a LEP is involved.

We want to stress that the different behavior of the frequency of acoustic and bending phonons compared to that of stretching phonons as a function of pressure (i.e., one process that allows increasing the electronic density) during the whole process of formation of EDMBs has been already discussed regarding the bonding present in PCMs.^1,2,46 We also want to note that the behavior described in Fig. 2b is a general one and does not consider phonon anharmonic interactions or electron–phonon interactions that can make each system evolve in a particular way. It is noteworthy that the three-stage process in the multicenter bond formation is consistent with the distribution of the electronic charge of atoms in three spheres: the core, valence, and van der Waals spheres, and the penetration indices of these spheres as discussed by Echeverría and Álvarez.^47,48 In particular, the three-stage formation process of multicenter bonds with the penetration of the valence spheres is commented on Fig. S2 of the ESI† concerning the formation of the I₃⁻ anion from the original I₂ and I⁻ entities, which is discussed in the next section.

All in all, the aim of Fig. 2 is to show that both ERMBs and EDMBs have a common origin; i.e., the existence of a primary bond and a secondary interaction that are linked by the trans influence, and also a similar formation process. Most specifically, Fig. 2 shows the simplest way of forming ERMBs and EDMBs; i.e., via a second-order (or even higher-order) phase transition in which there is a progressive and gradual transformation of the primary bond and the secondary interaction into multicenter bonds via an intermediate stage characterized by the occurrence of secondary bonds and a trans influence process that involves a charge reorganization in both bonds. Note that the above description does not preclude the possible formation of ERMBs and EDMBs upon increase of electronic density via a reconstructive (first-order) phase transition in which stage 2 can be bypassed.

At this point, it is important to stress that the mechanisms of ERMB and EDMB formation are different.^1,2 The mechanism of ERMB formation has been schematized in ref. 45 and 49, while the mechanism of EDMB formation has been schematized in ref. 1 and 2. Fig. 3 schematically shows the two mechanisms of multicenter bond formation for three electron-rich atoms (A, B, and C) as the electronic density increases. Since we only use three atoms for simplicity, Fig. 3a–c illustrates the formation of an ERMB (3c–4e bond), while Fig. 3d–f illustrates the formation of an EDMB (3c–2e bond). We make this comment because we will later address the case of 2c–1e EDMBs extended to more than three centers (a case that we will show cannot occur in ERMBs), so Fig. 3d–f is a simplified version of the real situation in extended systems with a 2c–1e ERMBs.

Let us start with the ERMB formation mechanism

The formation of a 3c–4e bond was addressed by Lee and Elliott,^45,49 who proposed that the two non-bonding electrons of the stereochemically active LEP of atom C (Fig. 3a) become more and more aligned with the A–B bond as the electronic density increases; i.e., there is a LEP reorientation along the B–C direction (Fig. 3b). This process goes on until the three atoms (A, B, and C) are fully (or almost fully) aligned once the A–B–C 3c–4e bond is formed (Fig. 3c). In this process, the non-bonding electrons of the LEP in Fig. 3a transform in a progressive way in bonding electrons in Fig. 3c as the electronic density increases. The secondary non-covalent interaction that leads to the ERMB formation is traditionally considered to be caused by the interaction of the LEP (donor or Lewis base) of atom C and the anti-bonding orbital (σ*, acceptor or Lewis acid) associated with the primary ionocovalent ppσ-bond between A and B atoms. Typically, there are two models of this donor–acceptor secondary interaction,⁵⁰ the charge transfer (LEP-σ*) model, also noted as n → σ* model,⁵¹ and the σ-hole bond model.^52,53 The LEP-σ* bond model considers that the LEP charge is transferred to σ* as the electronic density increases, while the σ-hole bond model considers that there is no charge transfer from the LEP to σ* and that there is only an electrostatic interaction between an electronegative (nucleophilic) region, the LEP, and the electropositive (electrophilic) region, known as the σ-hole, situated at the end of the iono-covalent bond. This last model considers that there is no charge transfer but only a charge shift and polarization. In any case, both models account for the formation of the ERMBs and it is commonly believed that the σ-hole bond model represents best the initial stages of ERMB formation while the LEP-σ* bond model represents the final stages of ERMB formation. We must also note that, in the last years, the formation of ERMBs in hypercoordinated structures has also been understood as the delocalization of electrons of LEPs into bonding or anti-bonding orbitals according to the “increased-valence” theory.⁵⁴ Therefore, it is clear, as we propose, that ERMB formation involves the transformation of non-bonding electrons in LEPs into bonding electrons in the ERMB as shown in Fig. 3a–c.

Let us continue now with the EDMB formation mechanism

As suggested by Manjón and coworkers for the formation of 3c–2e (also applied to extended 2c–1e bonds),^1,2 the non-bonding electrons of the stereoactive LEP of atom C (Fig. 3d) in general do not participate in bonding as the electronic density increases. In this scenario, the LEP becomes distorted, depopulated, and delocalized as the electronic density increases (despite a part of the LEP is reoriented along the B–C direction of the secondary bond, Fig. 3e). In this way, the LEP (if there exists as in electron-rich elements) progressively loses its stereoactivity until the three atoms (A, B, and C) are fully (or almost fully) aligned once the A–B–C 3c–2e bond is formed (Fig. 3f). Along this process, the non-bonding electrons of the LEP, in general, remain non-bonded and the charge needed to form the new B–C bond (of the A–B–C 3c–2e bond) comes from the primary iono-covalent A–B bond (see curved arrow in Fig. 3e). In other words, there is a net charge transfer from the iono-covalent A–B bond to the newly formed B–C bond as the electronic density increases until the charges of both A–B and B–C bonds equalize and the multicenter A–B–C 3c–2e bond is formed.

It must be stressed that the secondary interactions that lead to the EDMB formation cannot be explained either with the LEP-σ* bond model or with the σ-hole bond model since these two models do not consider a charge transfer from the primary bond to the secondary interaction. On the other hand, it must be mentioned that the mechanism of EDMB formation might be explained with the “increased-valence” theory,⁵⁴ which accounts for the electron delocalization of non-bonding electrons from LEPs, provided that the theory is extended to include the delocalization of bonding electrons from bonding electron pairs (BEPs), i.e., those present in iono-covalent bonds.

We want to note that the mechanism we have proposed for the formation of EDMBs in electron-rich elements in Fig. 3d–f, in which LEPs do not participate, in general, in the formation of the secondary and multicenter bond, is consistent with the formation of EDMBs in electron-deficient elements since electron-deficient elements do not have LEPs that can participate in secondary and multicenter bonds. Therefore, the LEPs play a major role in the formation of secondary and multicenter bonds in ERMBs (see Fig. 3a–c), while LEPs play a minor role in the formation of secondary and multicenter bonds in EDMBs (see Fig. 3d–f).

We want to close this general description of multicenter bond origin and formation by stating that the two different mechanisms of ERMB and EDMB formation are reflected in the different evolution of the ES and ET values for the primary and secondary bonds/interactions as the electronic density increases (see Fig. S3 of the ESI†). During the formation of both ERMBs and EDMBs, the ES and ET values tend to equalize in both cases; however, their final values are completely different in ERMBs and EDMBs. On the one hand, ES values should be between 1.4 and 1.9 in ERMBs while they are typically around 1.0 in EDMBs. On the other hand, ET values can be considered to increase during the ERMB formation and be more or less constant or have a small change during the EDMB formation.

3. Examples of the mechanisms of ERMB and EDMB formation

In this section, we show examples that illustrate the mechanisms of ERMB and EDMB formation. The two mechanisms can be illustrated by the formation of two well-known entities, the 3c–4e bonds in I₃⁻ polyanion and the 3c–2e bonds in diborane (B₂H₆) molecule, as schematized in Fig. 4a and b, respectively. Note that we have used in those figures the formalism of the σ-hole bond model in both cases to account for the electrostatic interaction that is present at the initial stage (stage 1 in Fig. 2) of ERMB and EDMB formation in both systems, despite the σ-hole bond model cannot account for the charge transfer occurring in stage 2 of the EDMB formation, as previously discussed.

Fig. 4 Scheme of the formation mechanism of (a) I₃⁻ polyanion and (b) B₂H₆ molecule using the formalism of the σ-hole bond model for secondary bonds. The charge transfer from the primary covalent bond towards the secondary bond in (b) is plotted with an arrow. (c) and (d) Schemes of the pressure-induced polymerization of HF and I₂ molecules which leads to an infinite zigzag chain with quasi-ERMBs. (e) and (f) Schemes of the pressure-induced polymerization of H and I atoms which leads to an infinite linear chain with EDMBs. Here we show some details on bond distances, Bader atomic charges, ET, and ES of various bonds in I₃⁻ and B₂H₆ that can be found in Table S2 (ESI†). LEPs are depicted on the right side of (d) and (f) to illustrate the total electron distribution in the infinite chains with multicenter bonds in electron-rich elements.

I₃⁻ polyanion

The ERMB formation in the I₃⁻ polyanion can be considered as the result of the approach of an I⁻ ion to an I₂ molecule as the electronic density increases (Fig. 4a).^40,50,55 As they approach, a trans influence of the secondary bond between the I₂ molecule and the I⁻ ion into the covalent bond of the I₂ molecule occurs. As already commented, the ERMB formation in I₃⁻ can be understood in the light of the three current bond models. According to the donor–acceptor charge-transfer model, a charge transfer from the donor unit (I⁻) to the acceptor unit (the anti-bonding orbital of the covalent bond in I₂) occurs as they approach each other. In other words, the anti-bonding orbital of the covalent bond of the I₂ molecule is populated due to the charge transfer from the LEP of the I⁻ ion. This trans influence occurs until both the intramolecular I–I distance of the I₂ molecule and the intermolecular I–I distance between the I⁻ ion and one of the I atoms in the I₂ molecule become almost equal.^40,56 Alternatively, the mechanism of ERMB formation can be understood in the light of the σ-hole bond model of secondary bonds. In this model, the negatively charged I⁻ ion (nucleophile) is attracted to the electropositive (electrophile) region known as the σ-hole, which is situated at the end of the I–I covalent bond within the I₂ molecule. Contrary to the charge-transfer model, when the electrophilic and nucleophilic entities approach each other, there is no outright transfer of charge from the donor to the acceptor unit. Instead, a polarization of charges occurs within the I₂ molecule due to the trans influence caused by the proximity of the I⁻ ion.

Specifically, as the I⁻ ion approaches the closer I atom of the I₂ molecule (now it becomes the central I atom of the I₃⁻ polyanion), the I⁻ ion shares part of its charge with the central I atom. This sharing induces a shift of part of the charge of the central I atom towards the other I atom of the I₂ molecule, which is positioned opposite to the I⁻ ion, so a symmetric (− + −) charge configuration is observed in the 3c–4e bond. This mechanism of ERMB formation explains the more electronegative external parts of this multicenter bond, as originally proposed by Rundle and Pimentel,^18,19 and also the large values of the normalized number of electrons transferred (ET) of molecules with ERMBs, such as XeF₂, CF₃, and SF₄.²⁵ In fact, the values of ES (above 1.6) and ET (0.45, obtained as the difference in Bader charges between the central and external atoms, see all details in Table S2, ESI†) for the I–I bond in the I₃⁻ ion (see Fig. 4a) allow us to locate this bond in the orange region of Fig. 1 corresponding to the ERMB, like XeF₂. The same description is found when the values of the bonding descriptors are obtained from orbital-based methods (see Fig. S1 and Table S3, ESI†). Therefore, there is an equivalence of both ES vs. ET maps obtained from density-based (Fig. 1) and orbital-based (Fig. S1, ESI†) methodologies. Finally, the third model suggests that the formation of hypercoordinated structures with ERMBs can be understood within the “increased-valence” theory as caused by the delocalization of electrons of LEPs into bonding or anti-bonding orbitals.⁵⁴ In this context, we think that the σ-hole bond model and the “increased-valence” models seem to be more appropriate than the charge-transfer model to describe the ERMB formation. Therefore, we conclude that the ERMB formation does not involve a charge transfer between the primary and secondary bonds, unlike in EDMBs.² In other words, the primary bond in the ERMB does not lose charge, thus resulting in a rather large ES value compared to EDMBs, as found for I₃⁻ and XeF₂ (see ref. 25 and Tables S2 and S3, ESI†). It is the delocalization of non-bonding electrons at LEPs into the secondary bond which provides the charge for the formation of the ERMB as shown in Fig. 3a–c.

In connection with the formation of ERMBs in I₃⁻ it may be worth pointing out that it has been suggested that the charge shift mechanism during the ERMB formation in trimers that leads to the symmetric (− + −) charge configuration in the 3c–4e bond avoids the central atom of the three-center entity to severely violate the octet rule.^52,56–59 Indeed, the shift of charge to the external parts of a hypervalent trimer, such as I₃⁻, results in an 8 + 2 charge of the central atom (see Fig. 5). This means that, excluding the first electronic sphere of core electrons (dark blue sphere in Fig. 5), in a first approximation we can consider that the central atom avoids violating the octet rule since the second electronic sphere (light blue in Fig. 5), corresponding to the valence electrons, only contains 8 electrons. Only when the third electronic sphere (light red in Fig. 5) is included, there is an apparent violation of the octet rule since this sphere contains 2 electrons.

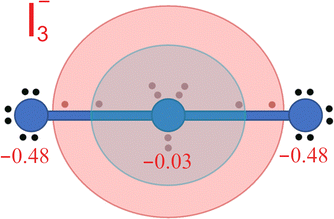Fig. 5 Schematic distribution of the 22 electrons of the I₃⁻ polyanion depicted in Fig. 4 when the Bader charges (in red) are considered. Since external atoms have a more negative charge than the central atom, the two electrons present at each collinear I–I bond can be considered to be shifted towards the external atoms. Therefore, electrons around the central atom can be distributed in three spheres. The internal core sphere (dark blue), the intermediate valence sphere (light blue), and the external van der Waals sphere (light red) are shown. ERMB in I₃⁻ can be interpreted as if 8 electrons were allocated at the valence sphere and 2 electrons were allocated at the van der Waals sphere. In this way, it can be considered that the octet rule is not violated in ERMBs since there are no more than 8 electrons in the valence sphere.

It is important to note that Echeverría and Álvarez have recently justified the distribution of the electronic charge in different spheres as mentioned in the previous paragraph. These authors have ordered the different spheres in order of decreasing electron density and named them core, valence, and van der Waals spheres.^47,48 They have used the different spheres to introduce the concept of penetration index to understand the chemical bonding between the strong iono-covalent bonds and the weak van der Waals interactions, including hydrogen bonds and secondary non-covalent interactions present in materials that lead to the formation of ERMBs and EDMBs, such as those of HF₂⁻ and B₂H₆, respectively. In this context, the large bond length of ERMBs formed by the two largest spheres depicted in Fig. 5 can be understood as the sum of the valence sphere (typical of the iono-covalent bonds^47,48) and an additional small van der Waals sphere (typically with a radius 0.2–0.4 Å larger than the valence sphere). In such a way, the central atom of an ERMB would always have 8 electrons in the valence sphere, thus satisfying the octet rule, and the additional charge would be located at the additional van der Waals sphere, thus avoiding the violation of the octet rule.

A similar procedure allows us to explain the linear ERMB formation and charge distribution in other 1D linear molecules, such as XeF₂ and HF₂⁻, in 2D molecules, such as XeF₄, and even in 3D molecules, such as SF₆ and XeF₆. We propose that the electronic configuration of the central atom in XeF₄ and XeF₆ can be thought to be 8 + 4 and 8 + 6, respectively.⁶⁰ Therefore, Fig. 5 can be extended in 2D and 3D to explain how electrons are distributed in the different electronic spheres in XeF₄ and XeF₆ molecules so that the central Xe atom avoids the violation of the octet rule, because only 8 electrons are in the valence sphere while the rest are occupying the outer van der Waals sphere.

Once introduced the concepts of the core, valence, and van der Waals spheres,^47,48 the three-stage mechanism of ERMB formation in the I₃⁻ anion can be understood with the use of the valence sphere, as described in Fig. S2 (ESI†). It can be observed that the multicenter interaction (stage 2) starts when d₂/d₁ = 2 in the formation of ERMBs, such as in the I₃⁻ anion and the [FHF]⁻ molecule, as discussed in the ESI.†

B₂H₆ molecule

Now that the formation of ERMBs has been clarified, we will deal with the EDMB formation in the B₂H₆ molecule (Fig. 4b), which can be considered as a two-proton attack on the B–B bond of the B₂H₄²⁻ unit,⁶¹ but it can also be seen as two borane (BH₃) molecules with three covalent B–H bonds that interact together via secondary interactions in a dimerization process.^62,63 According to the σ-hole bond model of secondary interactions, a σ-hole appears at the end of each atom involved in the covalent B–H bond and it becomes attracted by the large negative electrostatic potential at the bond critical point of one of the B–H bonds of the neighbor BH₃ molecule. Consequently, the two BH₃ molecules approach each other in such a way that there are two simultaneous trans influences of two new intermolecular B–H bonds into two intramolecular B–H bonds (see Fig. 4b). As a result, there must be a charge transfer of electrons from the two intramolecular bonds towards the two intermolecular bonds (note that neither B nor H atoms have LEPs that could provide the charge needed to form the two new intermolecular bonds). This charge transfer or electron donation from the intramolecular bonds towards the intermolecular ones leads to the transformation of two covalent B–H bonds (plus their associated weak secondary intermolecular B⋯H bonds) into two B–H–B 3c–2e bonds, as suggested by Walsh.⁶⁴ The charge transfer ends when both the intramolecular and intermolecular bonds become equal and the two B–H–B 3c–2e bonds are formed in the center of B₂H₆ (with all central B–H distances having the same length).

The diborane molecule has four, short, external, iono-covalent B–H bonds (d = 2.238 Å) and four, long, central B–H bonds (d = 2.478 Å) which form part of the two B–H–B 3c–2e EDMBs. The larger B–H bond length within the EDMBs than the iono-covalent B–H bond is explained by the trans influence process and accounts for the 0.5 bond order of the B–H bond in the EDMB in contrast with the ca. 1.0 bond order of the iono-covalent B–H bond in BH₃ (see Tables S2 and S3, ESI†). The two simultaneous trans influences lead to the formation of two supported 3c–2e bonds.¹⁰ These EDMBs are favored because of the filling of the empty sp³ orbital of the two B atoms, so the B atoms in B₂H₆ reach a more stable tetrahedral geometry than the planar trigonal geometry of the BH₃ molecules (see the molecular orbitals in Fig. S4 of the ESI†).⁶³ Moreover, the octet rule is accomplished for the B atom in B₂H₆, unlike in the isolated BH₃ molecules, if we take into account for each B atom not only the four electrons of the two iono-covalent B–H bonds but also the two electrons of each B–H–B 3c–2e bond, as recently proposed.⁶² Note that the 3c–2e bond can be considered within the valence bond theory as a bond in which two electrons resonate between two covalent bonds so that there is one electron in each bond when an average in time is considered.⁷

The fundamental point here is that the mechanism of EDMB formation in B₂H₆ is the same as that of EDMB formation in the octahedrally-coordinated phases of group-15 and -16 elements, as shown in ref. 1 and 2. In both cases, there is a charge transfer from the primary covalent bond to the secondary non-covalent bond that softens and enlarges the primary covalent bond as shown in Fig. 3d–f. The loss of charge of the primary covalent bond is the reason for the small value of ES in EDMBs once they are formed. The ES value of an EDMB is expected to be smaller than the ES value of an iono-covalent bond of similar polarity (similar ET value) as shown in the green region of EDMBs in Fig. 1. In particular, we have obtained that the ES value of each B–H bond within the 3c–2e EDMB to be 0.68 [0.60]. Moreover, the Bader [Löwdin] charge of the different atoms is B^1.80+[1.65+], central H^{0.63−[0.59−]}, and external H^{0.59−[0.47−]}. Since the Bader [Löwdin] charge of the central H atoms is −0.63 [−0.59], this quantity in absolute value is taken as the ET value for every B–H bond within the EDMB. These ES and ET values allow us to locate the central B–H bond as an EDMB in the green region of Fig. 1 and Fig. S1 (ESI†), as mentioned in the introduction. In this molecule, the Bader [Löwdin] charge of B and H atoms are +1.94 [+1.72] and −0.61 [−0.57]. The ET and ES values of the terminal B–H bonds are taken as 0.61[0.57] and 1.25[0.95], which allows us to classify these bonds as iono-covalent ones according to Fig. 1 and Fig. S1 (ESI†), as expected. Note that the short iono-covalent B–H bond has a value of ca. 1.18 Å which is similar to that experimentally obtained.⁶⁵ Curiously, both the ES and ET values of the EDMB in B₂H₆ are similar to those obtained in lead halide perovskites, such as CsPbI₃.^25,66 Therefore, our results for B₂H₆ suggest that all EDMBs are located in the green region of Fig. 1 and Fig. S1 (ESI†).

Again, the concepts of the core, valence, and van der Waals spheres can help us now to see that the multicenter interaction (stage 2) starts when d₂/d₁ = 2 not only in the formation of ERMBs, such as in the I₃⁻ anion and the [FHF]⁻ molecule, as discussed in the ESI,† but also in the formation of EDMBs. We do not have information regarding the EDMB formation in B₂H₆, but we have information regarding hydrogen (H₂) under compression.^67–70 A discussion on the formation of pressure-induced EDMBs in this system can be found in Section S2.3 of the ESI.†

Since stage 2, when multicenter interaction starts, is crucial to understand the formation of both types of multicenter bonds from mere electrostatic secondary interactions in stage 1, we can make the following statement regarding the formation chemical bonds in general: “it is important to stress that electrostatics (or its extension to electromagnetism), which can be used to describe supramolecular interactions of van der Waals type when d₂/d₁ > 2, is not enough to describe the stronger chemical bonds because it only provides a first approximation to the problem. In stronger chemical bonds, such as covalent bonds and multicenter bonds, electrons are so close in real space (closeness measured in terms of the atomic Bohr radius and now in terms of the valence sphere^47,48) that quantum mechanics plays a role, as we have shown in stage 2 of the formation of multicenter bonds. Therefore, chemical bonds should be explained with the Schrödinger equation and even this is not always enough. It is well known that properties of materials with heavy elements (with main quantum numbers n = 5 and 6, in which valence electrons travel at a fraction of the speed of light) need relativity to be properly explained. Consequently, we conclude that, in the last term, strong chemical bonds should be explained with the Dirac equation that implements the spin–orbit interaction, which also takes into account magnetic interactions. In other words, chemical bonds must be explained within the realm of quantum electrodynamics; i.e., the theory that comprises electromagnetism, quantum mechanics, and relativity.⁷¹ This is the reason why more and more sophisticated computer simulations performing these complex theoretical calculations, mainly developed in the last half a century, have provided us with an ever-increasing power to understand chemical bonds and materials properties in more and more detail.”

It must be noted that the mechanisms of ERMB and EDMB formation in I₃⁻ and B₂H₆ discussed in this section show only part of the full formation mechanism proposed in Fig. 2 since these examples focus on stage 2 (trans influence). This is the stage in which the two mechanisms of multicenter bond formation differ. Now we will provide other examples that illustrate a more complete picture of the mechanism of ERMB and EDMB formation from stage 1 upon increasing the electron density. In most of the examples below, the electron density increases by increasing thermodynamic pressure.

Regarding the ERMB formation, an example of pressure-induced ERMB formation is the pressure-induced hydrogen bond symmetrization due to the formation of infinite zigzag X–H–X chains in hydrogen halides HX (X = F, Cl, Br, I).^72–77 HX are simple diatomic molecules forming molecular solids in which a hydrogen bond is found in the condensed state. It has been demonstrated that, at certain conditions of pressure and temperature, a Cmc2₁ phase (with infinite zigzag chains showing asymmetric X–H⋯X bonds) shows a pressure-induced second-order phase transition to a Cmcm phase (with infinite zigzag chains showing symmetric X–H–X bonds) in several HX compounds, as schematized in Fig. 4c for HF. As pressure increases, there is a decrease in the separation of the HX molecules on the left side of Fig. 4c, so both intramolecular and intermolecular bond lengths tend to equalize forming the zigzag chain on the right side of Fig. 4c.^72–77 This is a pressure-induced polymerization process in which the X–H–X bonds are ERMBs as illustrated on the right side of Fig. 4c.

Following Zhang et al.,⁷⁷ we have performed simulations of HF that have confirmed the multicenter nature of the X–H–X bonds in the zigzag chain of the Cmcm phase. Simulations for HF show a larger bond length (about 0.2 Å longer) for the H–F bond in the 3c–4e ERMBs at the phase transition pressure (19 GPa) in the Cmcm phase than the covalent H–F bonds present in the molecular Cmc2₁ phase of HF at RP (see Table S2, ESI†). This result is similar to that found in previous simulations.^72–77 The equalization of the short H–F and long H–F bonds as pressure increases and the larger H–F bond length at the Cmcm phase than the short covalent H–F bond at Cmc2₁ phase evidence the trans influence occurring during the compression of the Cmc2₁ phase of HF and the multicenter character of the H–F bond in the Cmcm phase.^72–77 The ES and ET values of the covalent H–F bond in the Cmc2₁ phase and of the H–F ERMB in the Cmcm phase (see Tables S2 and S3, ESI†) allow us to plot them in Fig. 1 and Fig. S1 (ESI†). Curiously, the ES and ET values of the H–F bonds in the Cmcm phase (see Tables S2, S3 and Fig. S1, ESI† and Fig. 1) suggest that these bonds are closer to EDMBs than to the ERMBs of the F–H–F bonds in the HF₂⁻ molecule (see Fig. 1). The reason for the decrease of the ES value of the F–H ERMB in the zigzag chain with respect to the isolated HF₂⁻ molecule is that molecules with ERMBs longer than 3 centers become more and more electron-deficient as the number of bonds increase.^27,39 This will be discussed further in Section 6. The transformation from a covalent H–F bond plus a secondary hydrogen H···F bond in the Cmc2₁ phase to an F–H–F ERMB in the Cmcm phase can be seen when the 3D isosurfaces of the ELF are plotted (see Fig. S5 of the ESI†). The toroidal isosurface, corresponding to the three LEPs of F atoms, transforms into a cushew-like isosurface corresponding to two LEPs of F atoms since the electrons of one LEP of F atoms now take part in the ERMB in the Cmcm phase. In summary, the symmetric zigzag chain in HX compounds can be considered as a zigzag concatenation of linear 3c–4e ERMBs that already tend to become EDMBs; i.e., they are not pure ERMBs as those of the isolated X–H–X trimers.

Furthermore, the vibrational modes measured and calculated confirm our claims for the multicenter bond formation in the Cmcm phase of HX compounds.^72–77 While low-frequency phonons have a positive pressure dependence, high-frequency phonons show an anomalous softening in the Cmc2₁ phase. Instead, all the phonons exhibit a normal positive pressure coefficient when the Cmcm phase is formed.^72–77 Therefore, the example of HF clearly exemplifies the general features observed in Fig. 2 regarding the formation of ERMBs from the structural and vibrational points of view. This example of pressure-induced ERMB formation complements the examples of pressure-induced EDMB formation previously reported in ref. 1 and 2 that will be summarized later.

At this point, we want to comment that the pressure-induced formation of infinite zigzag chains in HX compounds is similar to the imaginary example of pressure-induced ERMB formation due to the polymerization of molecular iodine, as schematized in Fig. 4d. This example has been recently simulated and discussed due to its relationship with the pressure-induced phase transitions in elemental iodine.⁷⁸ In solid I₂, both intramolecular and intermolecular bond lengths tend to equalize as pressure increases, thus forming the infinite zigzag chain (see Fig. 4d). This can be considered as a zigzag concatenation of linear 3c–4e ERMBs, as those of the linear I₃⁻ trimer. As for the case of the symmetric zigzag chain in HX compounds, the symmetric zigzag iodine chain in Fig. 4d consists of linked 3c–4e ERMBs that are about 0.2 Å longer than the covalent bonds present in the diiodine molecule⁷⁸ due to the trans influence. This comment agrees with our previous suggestion that there is a different bond type in the infinite linear and zigzag iodine chains (Fig. 4d and f).²⁷ As already found for HX compounds in the Cmcm phase, our ES and ET calculations for the symmetric phase of the infinite zigzag iodine chain suggest that the ERMBs in the chain are not pure unlike in the linear I₃⁻ trimer as can be seen from its place in Fig. 1 and Fig. S1 (ESI†).

Additionally, we can provide one example of ERMB formation due to a reduction of a system (injection of electrons in the system), which also leads to an increase in the electron density of the system. In a recent work on linear 1D-iodine structures encapsulated in single-wall carbon nanotubes, it was shown that the encapsulated iodine atoms tend to form linear I₅⁻ units and that electron injection in the nanotubes promotes the transformation of the linear I₅⁻ units into I₃⁻ units.⁷⁹ We propose that this transformation can be understood as the reaction 3I₅⁻ + 2e⁻ → 5I₃⁻. It has been already stated regarding Fig. 4a and 5 that I₃⁻ units are characterized by an ERMB. In addition, it has recently been discussed that linear I₅⁻ units do not show ERMBs and are slightly stable linear polyiodide units since isolated I₅⁻ units tend to be V- or L-shaped.^24,27 Therefore, the transformation of the linear I₅⁻ units into I₃⁻ units upon reduction constitutes a clear example of reduction-induced ERMB formation.

On the other hand, examples of pressure-induced EDMB formation from intermolecular, secondary bonds occur in pnictogens and chalcogens,^1,2 in the formation of polymeric CO₂ phases,⁸⁰ and in the atomic/polymeric phases of elemental nitrogen⁴² and hydrogen.^67–70 The pressure-induced EDMB formation in these systems has recently been discussed.^1,2 For instance, it has been shown that stage 1 in elemental As occurs between RP and 16 GPa. Above this pressure, the trans influence of stage 2 leads to an increase in the primary bond length until both primary and secondary bond distances equalize above 25 GPa (stage 3).^1,2 The behavior of bond distances, vibrational modes, and the ES value in elemental As as pressure increases (schematized in Fig. 2 and Fig. S3, ESI†) can be nicely seen in ref. 1 and 2. However, the most extreme case of pressure-induced EDMB formation likely corresponds to H₂,^67–70 in which a normal decrease of both intramolecular H–H and intermolecular H···H bond lengths occurs below 100 GPa (stage 1). This is followed by an anomalous increase (decrease) of the intramolecular (intermolecular) bond distance in H₂ as pressure increases above 100 GPa due to the trans influence (stage 2). This anomalous increase of the primary bond distance is accompanied by the charge transfer from the intramolecular covalent bonds to the intermolecular non-covalent bonds that ends once both bond distances equalize, and each bond in the atomic/polymeric phase has a single electron per atom pair, i.e., once all H–H bonds become 2c–1e bonds (stage 3), as has been demonstrated in ref. 70. Noteworthy, the charge transfer in elemental hydrogen from the intramolecular covalent bond towards the intermolecular non-covalent bond is out of any doubt since the two electrons of the H₂ molecule at RP are between the two H atoms of the H₂ molecule and there is only one electron per H atom (no LEPs involved). Therefore, it seems that the atomic/polymeric phase (stage 3) of elemental hydrogen, which is supposed to exist above 500 GPa and discussed in ref. 1 and 2, is likely characterized by interacting or multicenter 2c–1e EDMBs that can be considered as extended 3c–2e bonds. Note that the mechanism of EDMB formation shown in Fig. 3d–f is also valid for electron-deficient elements, such as H and B, if the LEP is removed from that figure, as already commented.

The aforementioned stages of the pressure-induced EDMB formation in As and H₂ cannot only be related to the equalization of primary and secondary bond distances, as shown in Fig. 2a; they can also be traced by the behavior of the optical phonon frequencies, as shown in Fig. 2b. In elemental As, there is an anomalous decrease of the stretching phonon frequency from 0 to 25 GPa and an increase above this pressure. These features have been attributed to the weakening (strengthening) of the primary (secondary) bonds and the equalization of both bonds above 25 GPa.^1,2 In H₂, the first increase and posterior decrease of the phonon frequencies in the region near 100 GPa has been attributed to the weakening (strengthening) of the intramolecular (intermolecular) interaction,⁷⁸ which clearly can be ascribed to the charge transfer (trans influence) from the intramolecular bonds to the intermolecular bonds, as already commented in ref. 70.

Noteworthy, the case of EDMB formation in elemental hydrogen at HP is similar to the case of the infinite linear chain of hydrogen atoms (Fig. 4e), which in turn is similar to the case of the infinite linear chain of iodine atoms (Fig. 4f). The only possible electron distribution shown in Fig. 4e and f, when the VSEPR theory is considered,⁸¹ clearly shows that these two examples of hydrogen and iodine polymerization show EDMBs in both electron-deficient and electron-rich elements, respectively, i.e., in elements without LEPs and with LEPs, respectively. In both cases, the intramolecular bond of the hydrogen (H₂) and iodine (I₂) molecules at low pressure loses its covalent character as a 2c–2e bond upon polymerization when the molecules approach each other at increasing pressure. The trans influence of the secondary intermolecular bond into the primary intramolecular bond (as both tend to equalize distances with increasing pressure) forces a charge transfer from the primary bond towards the secondary bond that results in a final electron-deficient 2c–1e bond, irrespective of the electron-deficient or electron-rich character of the bonded elements, thus resulting in the formation of EDMBs in the infinite linear atomic chains.

To conclude this section, we want to stress that the different mechanisms of ERMB and EDMB formation presented in this section and the ES and ET values found for different compounds with ERMBs and EDMBs allow us to reaffirm our conclusions in ref. 1 and 2; i.e., that bonds in crystalline PCMs and the octahedrally-coordinated A_h and A_i phases of group-15 and -16 elements are indeed EDMBs. These EDMBs are similar to those of boranes and also similar to those occurring in elemental nitrogen and hydrogen at HP once intermolecular and intramolecular bonds equalize. Therefore, we can conclude that EDMBs can be observed in materials with both electron-deficient and electron-rich elements. This is a change of paradigm since EDMBs were supposed not to exist in electron-rich elements and will be further discussed in Section 6. The EDMB formation is characterized by the coexistence of localized and delocalized electrons and is an intermediate step between iono-covalent bonding, with fully localized electrons, and metallic bonding, with fully delocalized electrons. This explains the intermediate position of the EDMB between the covalent and metallic bonds in the ES vs. ET maps in Fig. 1 and Fig. S1 (ESI†).

It should be stressed that our view of EDMBs and their position in the ES vs. ET maps is consistent with the well-known progressive delocalization of electrons as pressure increases until the metallic bond is reached at enough HP.^39,42 It is significant that the occurrence of EDMBs under compression, as in the A_h and A_i phases of group-15 and -16 elements, in atomic/polymeric nitrogen and hydrogen, and, in general, in all materials at HP, agrees with the already expressed general view that all elements, irrespective of their valence electrons, should show multicenter bonds (it should be interpreted in many cases as EDMBs) at HP.^39,82 Note that pressure tends to increase atomic coordination in all materials, thus all atoms, sooner or later above a given atomic coordination, will fall short in electrons to share two electrons with neighbor atoms.⁴² Therefore, all the new bonds in those pressure-induced hypercoordinated atoms will have to share necessarily less than two electrons per atomic pair until full electron delocalization, typical of metallic bonding, is finally attained at very HP, even in hydrogen.⁸³

All in all, in this section we have shown, using the examples of the I₃⁻ and B₂H₆ molecules, the examples of EDMBs in pnictogens and chalcogens of ref. 1 and 2, and the examples of ERMBs in the symmetric zigzag chains of HF and I₂, that the mechanisms of ERMB and EDMB formation are different and that the ES and ET values allow us to distinguish between EDMBs and ERMBs thanks to the ES vs. ET maps obtained either with density-based or orbital-based methods. Our different ES values for ERMBs and EDMBs agree with recent works that have shown the different ES values for molecules with ERMBs (XeF₂, ClF₃, and SF₄) and for solids with EDMBs (octahedrally coordinated crystalline phases of pnictogens, chalcogens, and PCMs).^2,25

4. ERMBs and EDMBs in materials with electron-rich elements

To prove the change in paradigm related to multicenter bonds in electron-rich elements, we provide in this section examples of materials made of electron-rich elements in which there are linear ERMBs and EDMBs in 1D, 2D, and 3D. In particular, we are going to comment on examples that were previously assumed to be ERMBs²⁰ and they are indeed EDMBs. As done in the previous section, to evidence the presence of the two kinds of multicenter bonds and to distinguish between them, we will evaluate the bond distances, the Bader [Löwdin] atomic charges, as well as the ES and ET values between two atoms in the different bonds present in these systems (see data in Tables S2 and S3, ESI†).

As aforementioned, EDMBs and ERMBs have been considered until now to be present only in molecules and solids with electron-deficient and electron-rich elements, respectively.⁸⁴ However, it is curious that hypervalent bonds (or ERMBs) in 1D, 2D, and 3D present in solids with electron-rich elements, such as Li₂Sb, BaZnSb₂, and sc-Sb, respectively, have been traditionally considered to share less than two electrons between two atoms.²⁰ In other words, the assumed ERMBs in these solids have been considered to be 2c–1e bonds according to the Pimentel model,^18,19 like the EDMBs of B₂H₆ and sc-Po.

Despite assuming that the bonds in sc-Sb, isostructural to sc-Po,⁸⁴ are 2c–1e bonds, these bonds have not been considered to be EDMBs but ERMBs,²⁰ being the only distinction between ERMBs and EDMBs the assumption that ERMBs and EDMBs are found in molecules and solids with electron-rich and electron-deficient elements, respectively.⁸⁴ This argument to distinguish between EDMBs and ERMBs is at odds with the number of electrons shared (ES) and the renormalized number of electrons transferred (ET) between two atoms for these two types of multicenter bonds according to Fig. 1 and Fig. S1 (ESI†), as we have reasoned in the previous section.

In a recent work,²⁷ we have mentioned that part of the misunderstanding in distinguishing between ERMBs and EDMBs comes from the simple molecular diagram used to understand 3c–2e EDMBs and 3c–4e ERMBs; i.e., the Pimentel three-level model.^18,19 According to this diagram (see Fig. 1 in ref. 27), it is thought that the two electrons occupying the non-bonding orbital in 3c–4e bonds belong exclusively to the external atoms and are not even partially shared with the central atom. However, this reasoning results in a contradiction of the hypervalent model because if those electrons are not shared with the central atom, then there is no violation of the octet rule for the central atom of the trimer and there should be no hypervalency. On the contrary, if it is assumed that there is a violation of the octet rule that leads to hypervalency then it must be assumed that these electrons are fully shared with the central atom, so the molecular diagram is not valid and the ERMBs cannot be considered as 2c–1e bonds. The contradiction can be solved if we consider that ERMBs are not 2c–1e bonds and that the classical molecular diagram of Fig. 1 in ref. 27 is not valid to understand 3c–4e bonds. This is because the electrons of the non-bonding orbital are partially shared (not fully shared) with the central atom in a trimer as the rather large ES values of ERMBs suggest. Note that the partial sharing of these electrons explains the smaller ES value in ERMBs than in covalent bonds, the larger ES value in ERMBs than in EDMBs (since ERMBs are not 2c–1e bonds unlike EDMBs), and the lack of a severe violation of the octet rule for the central atom in the ERMB (since the extra electrons in 3c–4e bonds with respect to 3c–2e bonds are only partially shared with the central atom as if they would be in a secondary electronic valence sphere, the van der Waals sphere,^47,48 as explained for the I₃⁻ anion in Fig. 5).

4.1. Solids with ERMBs

In this subsection, we provide examples of different materials with electron-rich elements and well-known ERMBs. Examples of 1D ERMBs are the I₃⁻ polyanion (Fig. 4a and 5) alone or inside solid CsI₃, the HF₂⁻ polyanion, and the XeF₂ molecule. Examples of 2D ERMBs are the XeF₄ molecule and the planar Te₅²⁻ molecules in solid Cs₂Te₅. Examples of 3D ERMBs are the SF₆ and XeF₆ molecules and the square TeI₆²⁻ molecules in solid Cs₂TeI₆. Since 3c–4e ERMBs in molecules with electron-rich elements have been thoroughly discussed in the literature, we will focus here only on the three mentioned solids. The crystalline structures of these solids (CsI₃, Cs₂Te₅, and Cs₂TeI₆) are shown in Fig. 6 and the relevant data are provided in Tables S1–S3 (ESI†).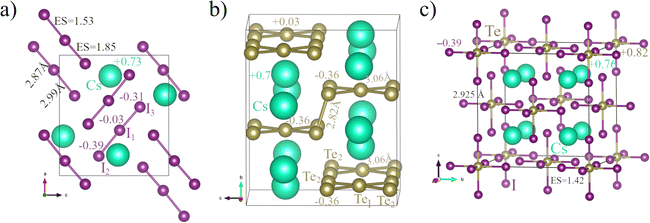

Fig. 6 The crystal structure of solids (a) CsI₃, (b) Cs₂Te₅, and (c) Cs₂TeI₆. These solids show molecular units with 3c–4e bonds (ERMBs) in 1D, 2D, and 3D. In CsI₃, I₁, I₂, and I₃ atoms correspond to three independent 4c sites. In Cs₂Te₅, Te₁ and Te₂ atoms correspond to Te(4c) and Te(16h) atoms, respectively. Details on bond distances and Bader atomic charges are illustrated here and also summarized in Table S2 (ESI†).

As can be seen in Fig. 6 and Tables S2 and S3 (ESI†), the I₃⁻, Te₅²⁻, and TeI₆²⁻ molecules in CsI₃, Cs₂Te₅, and Cs₂TeI₆ exhibit ERMBs with larger Bader [Löwdin] charges in the external atoms than in the central atom of the 3c–4e bonds and larger values of ES in the corresponding two-center bonds within the molecule with ERMBs than those found in the corresponding two-center bonds in solids with EDMBs for similar ET values.^2,25 Consequently, ERMBs in these solids are located at the orange color region of Fig. 1 and Fig. S1 (ESI†) slightly above the red region of covalent bonds and much above the green region of EDMBs. These results for solids agree with the results we have previously shown for I₃⁻, HF₂⁻, and XeF₂ molecules with ERMBs and with previous simulations on similar molecules (XeF₂, ClF₃, and SF₄).²⁵

Let us comment in more detail on the results of ERMBs in the aforementioned solids. In CsI₃ (Fig. 6a), all the I–I bonds are more than 0.1 Å larger than the covalent I–I bond in the Cmca phase of elemental iodine at RP.⁸⁵ The ES and ET values of all the I–I bonds in CsI₃ are similar to those in the I₃⁻ polyanion (see Tables S2 and S3, ESI†), so they can be classified as ERMBs and are located close to the I₃⁻ polyanion in the ES vs. ET map (see Fig. 1 and Fig. S1, ESI†). For the I₃⁻ polyanion (alone or in CsI₃), the ET value is taken as the difference in the Bader [Löwdin] charge between the terminal and the central I atoms of the I₃⁻ polyanion (note that the charge of the central atom must be divided between the two terminal atoms). Similarly, all the I–Te–I 3c–4e bonds in Cs₂TeI₆ (Fig. 6c) show I–Te bond distances of 2.925 Å, which are much larger than iono-covalent I–Te bonds with an average bond distance of ca. 2.74 Å in monoclinic TeI₄.⁸⁶ Note that the I–Te bond in Cs₂TeI₆ exhibits ES and ET values of 1.42 [0.94] and 0.52 [0.34], respectively, so they can be classified as ERMBs and are plotted correspondingly in Fig. 1 and Fig. S1 (ESI†). These values are in contrast with the ES and ET values of ca. 1.90 [1.4] and 0.15 [0.13] that correspond to iono-covalent I–Te bonds in monoclinic TeI₄ with calculated distances ca. 2.77 Å (see Table S2, ESI†). We want to stress that obtaining the ET value in ternary compounds could be very challenging because it could be difficult to know between which atoms the electronic charge has been transferred. For Cs₂TeI₆, we have taken as ET the absolute value of the difference in Bader [Löwdin] charge between the external I atom and the central Te atoms of the TeI₆²⁻ polyanion (taking into account that the charge of the central atom must be divided between the six terminal atoms).

A different case occurs for Cs₂Te₅ (Fig. 6b). This solid contains two distinct types of Te–Te bonds. The Te(16h)–Te(16h) bonds mainly along the b-axis are short (d = 2.82 Å) and have ES = 2.2 [1.65] and ET = 0 [0], so they can be classified as pure covalent bonds. On the other hand, the long Te(4c)–Te(16h) bonds (d = 3.06 Å) within the planar Te₅²⁻ array extended in the ac plane have ES = 1.43 [0.94] and ET = 0.39 [0.33], so they can be classified as ERMBs. It must be noted that the molecular compounds with ERMBs usually have large bandgaps, like in CsI₃⁸⁷ and Cs₂TeI₆;⁸⁸ however, low bandgaps and relatively high electrical conductivity were reported in Cs₂Te₅ along the layer plane (likely due to the zigzag connectivity of ERMBs and covalent bonds along the layer plane).⁸⁹

In the above solids, it can be considered that the ERMB formation in the I₃⁻, Te₅²⁻, and TeI₆²⁻ molecules is promoted by the increase in their electron densities, which is caused by the reduction of these systems due to the donation of electrons from the Cs atoms. In other words, Cs atoms give their electrons to the I₃, Te₅, and TeI₆ polyanions to form nominal I₃⁻, Te₅²⁻, and TeI₆²⁻ molecular units. These molecular units exhibit 3c–4e ERMBs in 1D, 2D, and 3D (in which the central atom is hypercoordinated) and are linked to Cs atoms by ionic bonds. This view is consistent with the Bader [Löwdin] atomic charge expressed as a superindex in the three compounds; e.g. CsI₃ at RP has Cs^0.73+[0.65+]. Note that in the I₃⁻ units of CsI₃ at RP there are two slightly different I–I bonds (one short and one long) that tend to form two equal ERMBs at HP;⁹⁰i.e., equal bonds as shown by the linear array of the I₃⁻ polyanion in Fig. 4a. A similar case occurs for Cs₂Te₅ (see Fig. 6b) with two Cs^0.70+[0.67+] atoms giving their charges to the five Te atoms of the Te₅ molecule to form the Te₅²⁻ polyanion. In this case, there are two independent Te atoms in the Te₅²⁻ polyanion that show two different negative charges with the charge of the external Te atoms being larger than that of the central Te atom, as expected for 3c–4e bonds. In particular, Te(4c) and Te(16h) atoms are Te^0.03+[0.01+] and Te^{0.36−[0.34−]}, respectively. The different atomic charges of the central (positive) and external (negative) Te atoms in the planar Te₅ array are consistent with the ERMB nature of these bonds in 2D. Finally, the Bader [Löwdin] atomic charges in Cs₂TeI₆ are: Cs^0.76+[0.63+], Te^0.82+[0.68+], and I^{0.39−[0.32−]}. This means that the TeI₆²⁻ units (see Fig. 6c) have a central Te atom that also gives almost one electron to the terminal I atoms to form ERMBs in 3D. Therefore, as expected for linear 3c–4e ERMBs (in this case in three perpendicular directions), the terminal I atoms have a larger electronic charge, so this cubic TeI₆²⁻ unit behaves as a pseudo-SbI₆³⁻ unit that is isoelectronic to XeF₆. Note that the central atoms of the 3c–4e bonds (e.g. Te(4c) in Cs₂Te₅ and Te in Cs₂TeI₆) have positive Bader [Löwdin] charges, so they behave as cations.

In brief, the three mentioned solids in this subsection are Zintl phases that can be understood on the light of the Zintl–Klemm concept by which atoms can exchange electronic charge irrespective of their electronegativity or electron affinity values.^20,91,92 The charge donated by Cs atoms is accepted by the polyanions in such a way that Cs atoms are linked to the polyanions via ionic bonds while there are homonuclear or homoatomic bonds (bonds between the same atomic species, Te–Te and I–I) and heteronuclear or hetereoatomic bonds (bonds between different atomic species, Te–I) some of them being ERMBs inside the polyanions.

4.2. Solids with EDMBs

Let us discuss the formation of EDMBs in 1D, 2D, and 3D in solids with electron-rich elements. Here we are going to present the solids with EDMBs in two main categories: solids with homopolar (or homonuclear or homoatomic) EDMBs (Fig. 7) and solids with heteropolar (or heteronuclear or heteroatomic) EDMBs (Fig. 8). In the first category, we will comment on the formation of (i) 1D EDMBs in the infinite linear Sb chains in Li₂Sb, (ii) 2D EDMBs in the square planar array of Sb atoms in solid BaZnSb₂, and (iii) 3D EDMBs in the octahedrally-coordinated phases of pnictogens and chalcogens, such as the sc phase of Po (α-Po) at RP, which is isostructural to the HP phases sc-As and sc-Sb. In the second category, we will comment on the formation of (i) 1D EDMBs in TeO₂ at RP (also the cases of SbPO₄, and Sc₂Si₂O₇ at RP are discussed in the ESI†), (ii) 2D EDMBs in the Cmcm phase of SnSe at HP (also of GeSe at HP), which is isostructural to the low-pressure phase of InBr, InI, and TlI, and (iii) 3D EDMBs in the rocksalt (rs) phase of β-GeTe at HP, isostructural to PbS, PbSe, and PbTe at RP.

Fig. 7 The crystal structure of solids (a) Li₂Sb, (b) BaZnSb₂, and (c) sc-Po (α-Po). These solids show hypercoordinated units with EDMBs in 1D, 2D, and 3D. In Li₂Sb, Sb₁ and Sb₂ atoms correspond to Sb(1b) and Sb(2c) atoms, respectively. In BaZnSb₂, Sb₁ and Sb₂ atoms correspond to Sb(4c) and Sb(4e) atoms, respectively. In Li₂Sb, Sb atoms form hypercoordinated units with 1D EDMBs and a linear geometry as that of Fig. 10a. In BaZnSb₂, Sb atoms form hypercoordinated units with 2D EDMBs and a square planar geometry as in Fig. 10b. In sc-Po, Po atoms form hypercoordinated units with 3D EDMBs and a cubic geometry as that of Fig. 10c. Details on bond distances, Bader atomic charges, ET, and ES of various bonds are illustrated here and summarized in Table S2 of the ESI.†

Fig. 8 The crystal structure of solids (a) TeO₂, (b) Cmcm-type SnSe, and (c) β-GeTe. These solids show heteropolar 1D, 2D, and 3D EDMBs, respectively. TeO₂ shows hypercoordinated units with a see-saw geometry as that of Fig. 10a. Cmcm-type SnSe shows hypercoordinated units with a square pyramidal geometry as in Fig. 10b. β-GeTe shows hypercoordinated units with a cubic geometry as that of Fig. 10c. Details on bond distances, Bader atomic charges, ET, and ES of various bonds are illustrated here and summarized in Table S2 of the ESI.†

4.2.1. Homopolar EDMBs. Homopolar EDMBs are characterized by being EDMBs with ET = 0, so they are typically formed by a single element; i.e., they are usually homoatomic bonds. A clear example is the case of bonds between atoms that occupy the same Wyckoff site. The first example of solid with homopolar EDMBs we are going to comment is solid sc-Po (α-Po), isostructural to sc-As and sc-Sb, in which 3D EDMBs are observed (Fig. 7c).^1,2 In sc-Po, Po–Po EDMBs occur in the three spatial directions with ES (ET) ≈ 1 (0) at RP (see Fig. 1). The formation of EDMBs in sc-Po at RP and in sc-As and sc-Sb at HP as well as in the rhombohedral (rh) phase of Po (β-Po) at RP and of rh-Se and rh-Te at HP have been thoroughly discussed in ref. 1 and 2. Note that the rhombohedral β-Po phase is a slightly distorted modification of the cubic α-Po phase which has been found in all chalcogens at different pressures. Noteworthy, our results are contrary to a previous work in which the α-Po phase and the same phase in the other pnictogens (sc-Sb) were previously assumed to exhibit 3D ERBMs.²⁰

The second example of homopolar EDMB is the solid BaZnSb₂ (Fig. 7b) in which 2D EDMBs can be observed. This is an intermetallic compound that was also previously considered to feature 2D Sb₁–Sb₁ ERBMs.²⁰ We find, in a similar way as for α-Po (and β-Po),^1,2 that the infinite square planar array of Sb₁ atoms in BaZnSb₂ features Sb₁–Sb₁ bonds with ES = 1.16 [0.8] and ET = 0 [0]. The important point here is that these ES and ET values are closer to those of EDMBs in α-Po, crystalline PCMs, such as β-GeTe and SnTe, and B₂H₆ than to those of ERMBs (see Fig. 1 and Fig. S1, ESI†).¶ Note that the Sb₁–Sb₁ bond distance in BaZnSb₂ at RP (d = 3.24 Å) is of the same order as that of the Sb–Sb bonds reported in sc-Sb at RP (d = 3.16 Å)⁹³ and much larger than the more covalent Sb–Sb bond distance of Sb in the A7 phase at RP (d = 2.96 Å).^1,2 Therefore, we conclude that Sb₁–Sb₁ bonds in BaZnSb₂ at RP are EDMBs with a half or partial bond order. It is important to mention that our claim for EDMBs between Sb₁ atoms of the square planar Sb array in BaZnSb₂ is supported by Jeitschko and coworkers, who also suggested the presence of EDMBs with 0.5 bond order in As–As and Sb–Sb bonds in the square planar array of isostructural intermetallic compounds ACuAs₂ and AAgSb₂ (A = rare earth and uranium).⁹⁴ Moreover, our claim for the presence of EDMBs in BaZnSb₂ is also supported by Nesper, who suggested that Bi–Bi bonds at the square planar array of Bi atoms in the Zintl phase of LiBi are 2c–1e bonds with 0.5 bond order.⁹⁵ Our results for pnictogens and chalcogens^1,2 and our current theory of multicenter bond formation provide a clear explanation for the results of these two works.

The third example we have chosen is solid Li₂Sb, in which EDMBs are found in 1D (Fig. 7a). This compound crystallizes in space group no. 189⁹⁶ and have two independent Sb atoms located at 1b and 2c sites. Again, as for the cases of sc-Sb and BaZnSb₂, both Sb₁–Sb₁ and Sb₂–Sb₂ bonds of Li₂Sb (d = 3.260 Å in both cases) were previously assumed to be 1D ERMBs.²⁰ However, the ES and ET values for the two types of Sb–Sb bonds in Li₂Sb at RP are 1.41 [0.7] and 0 [0], respectively. These values allow us to locate these Sb–Sb bonds in the green region of EDMBs in Fig. 1 and Fig. S1 (ESI†). Note that Sb–Sb bonds in Li₂Sb are even longer than the EDMBs commented in the previous paragraph for BaZnSb₂ and sc-Sb at RP. Therefore, we conclude tentatively that the Sb–Sb bonds in Li₂Sb are EDMBs and not ERMBs unlike previously assumed.²⁰ Our results are thus consistent with the suggestion of 2c–1e bonds present in the 1D infinite linear Sb chains in U₂TiSb₃ and isostructural antimonides by Jeitschko and coworkers.⁹⁷

To close this subsection, we want to comment that the Sb–Sb EDMBs in the studied solids sc-Sb (3D), BaZnSb₂ (2D), and Li₂Sb (1D) have ES values of around 1.0 [0.9], 1.2 [0.8], and 1.4 [0.7], respectively. In other words, the ES values of the Sb–Sb bonds increase as we move from 3D to 1D. At present, we do not yet definitely know the cause of this deviation, but we think that the reason could be related to the Bader [Löwdin] charge of the Sb atoms in those bonds. These charges for Sb atoms are 0 [0], −0.6 [−0.8], and −1.63 [−1.0] for sc-Sb, BaZnSb₂, and Li₂Sb, respectively. This means that while Sb atoms in sc-Sb behave as neutral Sb atoms (Sb⁰), the Sb₁ atoms in the Zintl compound BaZnSb₂ (ideally Sb⁻) behave as pseudo-Te atoms, and the Sb atoms in the Zintl compound Li₂Sb (ideally Sb²⁻) behave as a pseudo-I atoms. In other words, the larger the atomic charge of the Sb atom the larger the ES value. A possible explanation for this behavior is the difficulty of the nucleus of Sb to retain close to the nucleus the extra electronic charge given by the most electropositive atoms, so this extra electronic charge is more shared with the neighbor atoms thus leading to a larger ES value. Another possible explanation is that this trend is related to the electron count: in 3D systems (sc-Sb), each Sb atom participates in three EDMBs (six 2c–1e bonds), requiring three electrons for bonding. In 2D systems (BaZnSb₂), each Sb atom participates in two EDMBs (four 2c–1e bonds), thus requiring fewer electrons (ideally two) for bonding. Finally, in 1D systems (Li₂Sb), even fewer electrons (ideally one) are required to form one EDMB (two 2c–1e bonds). Therefore, the availability of electrons in Sb atoms for bonding through EDMBs is larger as the dimensionality of the EDMB decreases – although the extra electrons that do not take part in EDMBs are assumed to form part of LEPs and consequently not to participate in bonding –, so perhaps a small contribution of these extra electrons is reflected in the ES of the EDMBs.

4.2.2. Heteropolar EDMBs. Heteropolar EDMBs are characterized by being EDMBs with ET ≠ 0, so they are typically formed by two different elements; i.e., they usually constitute heteroatomic bonds. The first example we are going to comment on is that of β-GeTe, a crystalline PCM in which 3D EDMBs formed by Ge and Te can be observed (Fig. 8c). In β-GeTe at 5 GPa,⁹⁸ Ge and Te atoms occupy the 4a and 4b Wyckoff sites of the rs structure and all Ge–Te bonds (d = 2.892 Å) have a calculated ES and ET values of 1.16 [1.11] and 0.18 [0.09]. Here the ET value is calculated by dividing the absolute Bader [Löwdin] charge of Ge or Te atoms by the absolute nominal charge of Ge and Te atoms (2) since both Ge and Te atoms have the same atomic multiplicity.|| According to the ES and ET values, Ge–Te bonds, which are considered as metavalent bonds by Wuttig and collaborators,^2,14 can be classified as EDMBs (see Fig. 1 and Fig. S1, ESI†). Note that we get a value of density-based ET slightly smaller than that obtained by Wuttig and coworkers (∼0.23).^2,14 It is also interesting to note that the EDMBs in β-GeTe are dative (or coordinative) EDMBs in a similar way as there are covalent and dative covalent bonds. This means that in β-GeTe, unlike in sc-As, in which all As atoms contribute equally to the EDMB, Te atoms contribute more to the EDMB than Ge atoms because Te atoms have more valence electrons than Ge atoms. Note that GeTe is isoelectronic to As since both are 10-electron materials. In order to establish 3D EDMBs in sc-As, each As atom contributes with three p-type electrons (one along each direction) since the two s-type electrons are non-bonding (forming part of an inactive LEP). In β-GeTe, the two s-type electrons of Ge and Te are also non-bonding (forming part of inactive LEPs), so there are two p-type electrons in Ge and four p-type electrons in Te to form 3D EDMBs. This means that Ge lacks one p-type electron to form an EDMB along one direction while Te has one extra p-type electron to form an EDMB. As a result, Te gives its extra electron to Ge to form the EDMB along one direction, so on average both Ge and Te have three p-type electrons, like As. This allows both atoms to form EDMBs along the three perpendicular directions. In other words, dative or coordinative EDMBs occur in β-GeTe.

The second example we want to show is the layered orthorhombic Cmcm (also noted as Bbmm) phase of both GeSe and SnSe at HP (see Fig. 8b).^99–101 Both GeSe and SnSe crystallize in the layered orthorhombic Pnma phase at RP. In the Pnma structure, both Ge (Sn) and Se atoms are threefold coordinated via dative iono-covalent bonds, whereas in the Cmcm phase all atoms are fivefold coordinated. The Cmcm phase of these compounds at HP is isostructural to that of InBr, InI, and TlI at RP.¹⁰² It has been reported that there are two different covalent bonds in the Pnma phase of SnSe and GeSe, and that both bonds evolve differently under compression: the bond almost perpendicular to the layers (axial bond) and the two equivalent bonds almost parallel to the layers (equatorial bonds).^99–101 Whereas the axial bond evolves as a normal iono-covalent bond since the bond length decreases under compression and its related high-frequency vibrational modes show a positive pressure coefficient, the equatorial bonds show anomalous behavior under compression with an increase of the bond length and a softening of related vibrational modes at HP. Our simulations of SnSe at HP reproduce nicely the behavior of bond lengths experimentally reported (see Fig. S6 in ESI†).⁹⁹ The different behavior of both iono-covalent bonds at the Pnma phase can be understood if we consider that the axial bond remains as a short iono-covalent bond when the Cmcm phase is attained at HP whereas the equatorial bonds suffer a trans influence that ends with the formation of two long EDMBs in the layer plane. In other words, in the Cmcm phase of SnSe and GeSe, the quasi-linear 2D EDMBs can be observed perpendicular to the b-axis (see Fig. 8b). The iono-covalent (EDMB) nature of the axial (equatorial) bonds at the Cmcm phase of SnSe are confirmed by our ES and ET values (see Table S2 and Fig. S6, ESI†) according to the location in Fig. 1 and Fig. S1 (ESI†). A detailed explanation of the ES and ET values of the Cmcm phase of SnSe at 10 GPa and its comparison with the Cmcm phase of TlI at RP is provided in Section 2.7 of the ESI.†

The third example we want to comment on is the solid paratellurite (α-TeO₂), in which quasi-linear 1D Te–O EDMBs are formed. In paratellurite at RP, Te and O atoms are at 4a and 8b sites, respectively. Each Te atom is fourfold coordinated to O atoms with two short (d = 1.919 Å) and two long (d = 2.087 Å) Te–O bonds in a see-saw geometry (note that Te⁴⁺ has a single LEP) derived from the trigonal bipyramidal geometry (Fig. 8a).¹⁰³ The two short (long) bonds have ES = 1.64 [1.5] (1.06 [0.9]) and both have ET = 0.29 [0.23]. Note that to calculate the ET value for the Te–O bonds we have to take the Bader [Löwdin] charge of the Te atom and divide it by the nominal valence of Te (+4). In addition, this value must be divided by the atomic multiplicity ratio between Te and O atoms (2), which is the average number of O atoms to which the electrons of Te atoms are transferred. Note that, equivalently, the ET value can be calculated by taking the absolute Bader [Löwdin] charge of the O atom and dividing it by the nominal valence of O (−2) and also by the multiplicity ratio between Te and O (2). The first procedure can be used more frequently since there are usually more anions than cations in many materials; however, the last procedure can be used when there is more than one single cation providing charge to a single anion. With the ES and ET values we can see that the short Te–O bonds can be considered iono-covalent bonds, while the long Te–O bonds are EDMBs (see Fig. 1 and Fig. S1, ESI†). Note that the smaller ES value of the long bonds than of the short bonds (both with same ET value) necessarily implies that, if the two short bonds are iono-covalent, the two long bonds must be EDMBs since ERMBs are expected to have larger values of ES than the iono-covalent bonds for a given ET as seen in Fig. 1 and Fig. S1 (ESI†). Support to our conclusions about the bonds in paratellurite comes from the compounds BaTeO₃¹⁰⁴ and CoTeO₃.¹⁰⁵ In both compounds, Te atoms are linked to three O atoms with only one type (iono-covalent) of short Te–O bonds and with lengths of the order of 1.86–1.88 Å and 1.90–1.92 Å, respectively. These bonds have similar bond lengths to those of short iono-covalent bonds in α-TeO₂, thus giving support to the EDMB nature of the long Te–O bonds in paratellurite.

An additional example of quasi-linear 1D EDMB is that formed by Sb and O bonds in SbPO₄ (see explanation in Section S2.8 of the ESI† regarding Fig. S7a).¹⁰⁶ At this point, it is interesting to comment that the calculation of ET values in heteronuclear bonds is easy for binary compounds with a single Wyckoff site for each element and the same multiplicity, such as in β-GeTe or SnSe. In this case, the charge lost by one atom is the charge gained by the other and the normalized number of transferred electrons can be readily calculated by the Bader [Löwdin] charge divided by the nominal atomic valence. However, it is more complex to calculate ET when the charge is gained or lost by more than one element, as already commented. We have shown the cases of TeO₂ where the charge of each Te atom is transferred to two O atoms and the case of a ternary compound (SbPO₄) in which the charge of two atoms Sb and P is transferred to two O atoms on average. In these complex cases, the normalized ET value must be calculated by additionally dividing the previous value (Bader [Löwdin] charge divided by the nominal valence) by the multiplicity ratio between the donor and acceptor atoms. In this way, the different bond types could be reasonably located in Fig. 1 and Fig. S1 (ESI†).

Up to this point, we have suggested that ERMBs and EDMBs can be found in molecules and solids with electron-rich elements, like As, Sb, Te, and I. In fact, EDMBs have also been recently suggested to occur in iodates at different pressures.¹⁰⁷ However, we must mention that we are not the first authors to propose that EDMBs could be observed in electron-rich elements. Vegas and collaborators already suggested that 3c–2e bonds should be present in the linear Si–C–Si bond of the carbocation [Si₂(CH₃)₇]⁺, in the linear Si–O–Si bonds of hexamethyldisiloxane, (H₃C)₃–Si–O–Si–(CH₃)₃, as well as in the linear Si–O–Si bonds within the [O₃Si–O–SiO₃]⁶⁻ polyanion in solid Sc₂Si₂O₇ silicate.^92,108 In addition, it must be mentioned that electron-deficient bonds have been proposed to exist in several large C–C bonds, such as those present in carboranes and hydrocarbons,^65,109 in large O–O bonds in H₂O₂, and in weak F–F bonds in F₂. Some of these bonds were classified as proto-covalent, charge-shift bonds, and electron-deficient covalent bonds.^110–113 However, there is a large confusion regarding these systems and the notation of their bondings since charge-shift bonds have been clearly shown to be related to ERMBs (which are not electron-deficient bonds), like XeF₂.¹¹⁴ Note also that relatively strong secondary bonds between different molecules, in which LEPs are involved in a dative or donor way as we propose for ERMBs, have been also classified as dative or coordinate covalent bonds.^115,116 To illustrate one of the above examples, we have performed calculations for monoclinic Sc₂Si₂O₇ at RP (see explanation in Section S2.8 of the ESI† regarding Fig. S7b) and found two types of Si–O bonds within the [O₃Si–O–SiO₃]⁶⁻ polyanion. The terminal (central) heteropolar Si–O bonds of the [O₃Si–O–SiO₃]⁶⁻ polyanion can be classified as iono-covalent bonds (EDMBs), thus confirming the suggestion of Vegas and collaborators.^92,108

To finish this section, it must be stressed that the presence of EDMBs in Zintl phases, intermetallic compounds, and cluster compounds of main-group elements (with homonuclear bonds) is consistent with the well-known brittle and shiny metallic properties attributed to them.^91,92,117 Note that EDMBs are directional bonds, due to the existence of partially localized electrons,^1,2 which leads to brittle behavior. At the same time, EDMBs have partially delocalized electrons,^1,2 which results in a shiny metallic aspect and moderate electrical conductivity, as expected for incipient metals (assumed to feature the new metavalent bond by Wuttig and collaborators).^{13–15,25,26} Additionally, it must be also noticed that the formation of EDMBs in electron-rich elements should be no surprise since ERMBs can also be found in electron-deficient elements; e.g. hydrogen can form a 3c–4e ERMB with F atoms in the [FHF]⁻ or HF₂⁻ anion (cataloged as a hydrogen bond by IUPAC).^19,50,55,118 as we have already stated in Sections 2 and 3.

5. TlTe: simultaneous presence of ERMBs and EDMBs at RP

Further examples of molecules and solids with electron-rich elements and EDMBs will be provided in future works; however, regarding the different geometries and properties of ERMBs and EDMBs, we consider important to comment here a last and paradigmatic example that will help us to distinguish between both kinds of multicenter bonds. Noteworthy, the crystalline structure of solid TlTe at room conditions exhibits simultaneously both ERMBs and EDMBs.

First of all, it must be mentioned that the structure of this solid was mentioned by Böttcher⁹¹ and by Papoian and Hoffmann,²⁰ but no satisfactory explanation for its crystalline structure was given to our knowledge. According to the most recent work of Papoian and Hoffmann, the structure can be understood on the light of the Zintl–Klemm concept by considering that each Tl atom donates one electron to each Te atom so the Te atoms become pseudo-I atoms, thus leading to the formation of homonuclear ERMBs between the Te atoms.²⁰ In contrast, we are going to show that, despite we agree that this is a Zintl compound in which the Tl atom donates charge to the Te atoms, the interpretation of all the Te–Te bonds as ERMBs is not correct. A hint that goes against the conclusion of Papoian and Hoffmann is that, despite its simple formula unit, the crystalline structure of TlTe is rather complex since it features one independent Tl atom and three independent Te atoms, so it is expected that the three different Te atoms have different atomic charges which could lead to the formation of different types of chemical bonds.

The tetragonal crystalline structure of TlTe¹¹⁹ shown in Fig. 9 has four independent atoms at the following Wyckoff sites: Tl(16k), Te₁(8h), Te₂(4b), and Te₃(4a). All Te atoms can be considered to be linked forming linear homonuclear Te–Te–Te bonds; however, we are going to show that these bonds are different (EDMBs and ERMBs) depending on the type of Te and the different electronic charges. Our ab initio simulations yield the following Bader [Löwdin] charges: Tl^0.32+[0.09+], Te₁^{0.41−[0.14−]}, Te₂^{0.05−[0.06−]}, and Te₃^{0.39−[0.11−]}. As observed, there is a considerable difference between the Bader and Löwdin charges; however, the Bader and Löwdin charges of the Tl and Te atoms do fit with the multiplicities of all atoms. As we have done for paratellurite, the charge of Te atoms must be divided by the appropriate multiplicity ratio between the Te atom multiplicity and the multiplicity of Tl atom (16) to get the charge of Tl. For instance, the Bader charge of Tl (+0.32) can be obtained as the sum of all the renormalized Bader charges of the Te atoms ((−0.41/2) + (−0.05/4) + (−0.39/4) = −0.315) if we consider that the dividing factors of the Bader charges of the Te atoms are the multiplicity ratios (16/8 = 2, 16/4 = 4, and 16/4 = 4, respectively) to be applied to the Te atoms (at 8h, 4b, and 4a Wyckoff sites, respectively).

Fig. 9 Details of the crystalline structure of TlTe. Te₁, Te₂, and Te₃ atoms correspond to Te(8h), Te(4b), and Te(4a) atoms, respectively. Te(4a) and Te(8h) atoms form EDMBs and ERMBs, respectively, with the linear geometry of Fig. 10a. Te(4d) atoms form ERMBs and EDMBs in perpendicular directions that correspond to the square planar geometry of Fig. 10b. Details on bond distances, Bader atomic charges, ET, and ES of various bonds are illustrated here and summarized in Table S2 of the ESI.†

According to our calculations, bonds between Te₃ atoms are the easiest to understand since these atoms show twofold coordination by forming infinite linear tellurium chains along the c-axis. The Te₃–Te₃ bond distance is 3.09 Å (simulated value of 3.05 Å) and its calculated ES (ET) value is 1.04 [0.65] (0 [0]). Therefore, the large value of this Te₃–Te₃ bond distance, when compared to the more covalent Te–Te bond distance of 2.84 Å in the A8 phase of Te at RP, and the small ES value (close to 1.0) indicates that the Te₃–Te₃ bonds of the infinite linear tellurium chain are EDMBs (see Te₃–Te₃ bonds in Fig. 1 and Fig. S1, ESI†). These EDMBs are similar to those found in the infinite linear iodine chain (Fig. 4c). This can be understood if we consider that Te₃ atoms (with a Bader charge of −0.39) behave as pseudo-I atoms, as initially assumed by Papoian and Hoffmann,²⁰ since they accept the charge donated by Tl atoms. However, they do not form ERMBs, unlike it was previously assumed,²⁰ but EDMBs, like in the infinite linear iodine chain.^24,27

A different case is that of fourfold coordinated Te₂ atoms. Our calculations show that they behave as pure Te atoms because they do not accept electronic charge from the Tl atoms (Bader charge of −0.05), unlike the assumption of Papoian and Hoffmann. Te₂ atoms show two types of bonds. On the one hand, Te₂ atoms also form infinite linear tellurium chains along the c-axis, like Te₃ atoms, and with the same Te₂–Te₂ bond distance as Te₃–Te₃ bonds. The ES (ET) value for the Te₂–Te₂ bond is 1.04 [0.65] (0 [0]), much like the Te₃–Te₃ bond. Therefore, the Te₂–Te₂ bonds can also be classified as EDMBs, like the Te₃–Te₃ bonds. On the other hand, Te₂ atoms also form two bonds with adjacent Te₁ atoms that are perpendicular to the infinite linear tellurium chain. Therefore, the infinite linear Te₂ chain along the c-axis can be considered as a crosswise stacking of linear triatomic Te₁–Te₂–Te₁ fragments. The experimental (simulated) Te₁–Te₂ bond distance is 3.01 Å (2.99 Å) and exhibits a calculated ES (ET) value of 1.4 [0.88] (0.36 [0.08]). Note that the ET value is calculated as the difference between the electronic charges of the Te₂ and Te₁ atoms. Due to the large Te₁–Te₂ bond distance and the larger values of ES and ET than the Te₃–Te₃ and Te₂–Te₂ bonds, the Te₁–Te₂ bond within the linear Te₁–Te₂–Te₁ trimer can be classified as an ERMB, indeed the linear triatomic Te₁–Te₂–Te₁ fragment is a 3c–4e bond (see Te₁–Te₂ bond in Fig. 1). This result is consistent with the different Bader charges of the central and external atoms of this linear trimer and the accumulation of the electronic charge in the external atoms of the trimer (see Fig. 9).

We must note that our calculations of Löwdin charges and ES values with LOBSTER lead to a classification of the Te₁–Te₂–Te₁ bond as an EDMB (see Fig. S1, ESI†). We think that the wrong classification of this bond by LOBSTER comes from the small Löwdin charge (∼−0.14) attributed to the Te₁ and Te₃ atoms, which is related to the small Löwdin charge (∼+0.09) attributed to the Tl atom. The anomalously small positive charge of Tl atoms given by LOBSTER is in contradiction with the original view that TlTe is a Zintl phase in which Tl atoms give their electrons to Te atoms in order to form the homonuclear bonds experimentally found in the structure and that is consistent with the already discussed pseudo-I character of Te₃ atoms.

We have demonstrated the case of TlTe, where density-based calculations show better agreement with experimental data than orbital-based calculations. This example complements previous cases, such as Sc₂Si₂O₇, where the opposite trend is observed. The reasons behind why some examples are better described by density-based methods while others align more closely with orbital-based methods remain unclear. These differences may stem from the inherent limitations of these methods in capturing the complexity of the multicenter bonds studied here. Nevertheless, we can confidently conclude that, in general, both density-based and orbital-based methods exhibit consistent trends (see Fig. 1 and Fig. S1, ESI†), underscoring the robustness of our results regardless of the method employed.

In brief, the tetragonal structure of TlTe at RP exhibits two types of Te–Te bonds: ERMBs and EDMBs. While EDMBs extend along more than three bonds forming infinite linear chains of Te₃ and Te₂ atoms along the c-axis, ERMBs only extend along three centers forming finite linear triatomic Te₁–Te₂–Te₁ fragments or trimers perpendicular to the c-axis. Both EDMBs and ERMBs in TlTe are longer than covalent Te–Te atoms, thus explaining the confusion in distinguishing between both types of multicenter bonds. However, ERMBs and EDMBs can be distinguished because ERMBs are finite (we will show in the next section that all pure ERMBs are indeed 3c–4e bonds), have external atoms bearing much larger electronic charge than the central atom, and the ES (also ET) values of ERMBs are usually larger than those of EDMBs and comparable or even larger than those of iono-covalent bonds. Moreover, ERMBs are usually slightly shorter than EDMBs. In TlTe, Te–Te EDMBs are of the order of 3.05 Å, while ERMBs are of the order of 2.99 Å. The larger bond length of EDMBs than of ERMBs is consistent with the smaller ES value for EDMBs than for ERMBs and accounts for the smaller bond order of EDMBs than of ERMBs. In other words, the smaller the number of electrons shared between two atoms is, the longer the bond and the smaller the bond order, as expected from Pauling's formula for bond order.²⁴

Due to the different ES and ET values in ERMBs and EDMBs, both multicenter bonds are expected to exhibit different properties. In this context, we can briefly comment that at relatively low pressures AX₃ compounds (A = Na, K, Rb, Cs; X = Cl, Br, I) crystallize in phases showing finite linear X–X–X ERMBs, as we have shown for CsI₃ at RP in the previous section; however, AX₃ compounds undergo a phase transition at HP to a phase with infinite linear X–X–X bonds as those of Fig. 4f. In fact, a recent report has highlighted the different nature and properties of the two different types of bonds in AX₃ compounds.¹²⁰ These different properties can be understood if the infinite linear atomic bonds (typically found in the Pm3̄n phase) of AX₃ compounds are EDMBs as we have already suggested in this work.¹²⁰ More detailed work on these compounds to show the pressure-induced EDMB formation from original ERMBs is in progress.¹²¹

6. A change of paradigms

The above examples have led us to propose that the paradigm that EDMBs can be found only in electron-deficient elements (not in electron-rich elements) is not valid anymore. Moreover, we have shown examples in which EDMBs are 3c–2e bonds, such as B₂H₆ and Sc₂Si₂O₇, and examples in which EDMBs are infinitely extended 2c–1e bonds. In addition, we have found an extensive number of examples among molecules and solids that justify that ERMBs are found only in three-center molecules in different directions, such as in 1D (I₃⁻, [FHF]⁻, XeF₂, and I₃⁻ in CsI₃), in 2D (XeF₄ and Te₅²⁻ in Cs₂Te₅), and in 3D (SF₆, XeF₆, and TeI₆²⁻ in Cs₂TeI₆). Besides, we have reasoned that ERMBs do not show a flagrant violation of the doublet/octet rule. Under this light, we tentatively propose four new paradigms:

(1) EDMBs and ERMBs can be found in molecules and solids made of electron-rich elements.

(2) EDMBs, present in either electron-rich or electron-deficient elements, are found as 3c–2e bonds or as infinitely extended 2c–1e bonds.

(3) Pure ERMBs can be formed only in linear or quasi-linear three-center molecules. This means that all ERMBs are 3c–4e bonds extended either in one, two, or three dimensions. Corollary: multicenter bonds extended to more than three centers in one dimension, either in a linear or a zigzag way, cannot be pure ERMBs and tend to form EDMBs.

(4) EDMBs and ERMBs do not violate, in general, the doublet/octet rule.

Since the first two paradigms are clear from the examples analyzed in ref. 1 and 2 and in the previous sections, we are going to provide in this section additional arguments to support the third paradigm. We will show that the lack of linear ERMBs longer than three centers is supported by symmetry and energy arguments and that angular or zigzag ERMBs are not pure ERMBs. The fourth paradigm will be discussed in Section 8.

6.1. Energy arguments

Lubchenko and coworkers have tentatively proposed a rule about a two-center localized molecular orbital that states:³⁹ “in a stable (or metastable) molecule, the bonding localized molecular orbitals should be two-center and cover each nearest neighbor bond. Conversely, when the molecule is not fully covered by two-center localized molecular orbitals, the molecule is subject to structural instability”. In other words, a system with n centers and (n + 1) bonding electrons is stable if there are enough electrons to fill (n − 1) localized molecular orbitals. This can be translated into the equation n + 1 = 2(n − 1), whose only solution is n = 3.³⁹

This result shows that the 3c–4e (n = 3) bond is the only stable molecule with n centers and n + 1 bonding electrons and allows explaining the large number of linear three-center molecules with four electrons experimentally found in 1D, 2D, and 3D,³⁹ and commented in the previous sections. It must be stated that the energy argument agrees with simulations that prove that linear polyiodide anions with n atoms and n + 1 bonding electrons that are longer than three centers; i.e., longer than I₃⁻, have different bond lengths along the chain and are either directly unstable or weak and easily perturbed.^24,122

6.2. Symmetry arguments

According to Lubchenko and coworkers,³⁹ multicenter bonds become electron deficient for any linear molecule longer than three centers. We have recently extended this reasoning to linear and angular polyiodides^24,27 thanks to ab initio calculations.¹²² Moreover, the geometry of different polyiodides has been recently discussed. The preference of angular geometries for polyiodides longer than three centers has been justified as a way to reinforce the chains when weak EDMBs occur in linear polyiodides longer than three centers.²⁴

As an example, we show in Fig. 4c–f the possible polymerization of the H₂ and I₂ molecules in infinite linear and zigzag chains. The infinite linear iodine chain in Fig. 4f is a clear example of EDMB (extended 2c–1e bond) similar to the infinite linear hydrogen chain in Fig. 4e. The only difference between the two infinite linear chains is that, unlike in the infinite linear hydrogen chain, the I atoms in the infinite linear iodine chain each I atom exhibits six non-bonding electrons, corresponding to three LEPs, distributed around each I atom in the plane perpendicular to the 2c–1e bonds, which are in a linear p-type configuration. Note that the six electrons of the LEPs in the infinite linear iodine chain can be thought to form a sp² configuration in the plane perpendicular to the 2c–1e bonds thus resulting in a total bipyramidal geometry (symmetry requirements show that the six electrons are distributed forming a toroid when ELF isosurfaces are plotted (see toroidal ELF in HF in Fig. S5a, ESI†).

The bonding in the infinite linear chains of H and I atoms is different from that in the infinite zigzag chain of H and F atoms (Fig. 4c) and the infinite zigzag iodine chain (Fig. 4d), as already commented in ref. 24 and 27. The infinite zigzag chains show ERMBs because terminal atoms of the linear branches do not have six non-bonding electrons but only four; i.e., two LEPs instead of three. This means that terminal halogen atoms have three bonding electrons that contribute to the formation of 3c–4e bonds in both HF and I zigzag chains. As already commented, these zigzag chains can be understood as a concatenation of 3c–4e ERMBs.^24,27 This result agrees with the view of Dronskowski and coworkers for the infinite zigzag iodine chain.⁸⁵ Therefore, we conclude that the different symmetry of the two infinite atomic chains in Fig. 4c–f results in a different bond type. While the infinite linear atomic chain bears EDMBs, the infinite zigzag chain bears ERMBs.

The above examples prove that the comparison of bonding in PCMs, like β-GeTe, and in polyiodides (in general) done in ref. 85 is not valid since the type of bonding in polyiodides depends on the geometry and size of the polyiodide chain.^24,27 Noteworthy, the infinite linear iodine chains have been experimentally observed in AX₃ compounds (A = Na, K, Rb, Cs; X = Cl, Br, I).¹²⁰ These halides have the same kind of bonds that occur in the nominally assumed Sb²⁻ atoms in Li₂Sb and Te₃⁻ atoms in TlTe, as already discussed. This is not surprising since these charged atoms can be considered pseudo-I atoms within the Zintl–Klemm perspective. Contrarily, the ERMBs shown in Fig. 4d for the infinite zigzag iodine chain have been observed in iodine at HP⁸⁵ and also occur in Te⁻ atoms (again pseudo-I atoms) in UTe₅.⁹¹

It is important to stress that the ERMBs occurring in the infinite zigzag atomic chains that result from the coalescence or concatenation of 3c–4e bonds are not pure ERMBs, unlike those of the isolated molecules with linear 3c–4e bonds. This conclusion is supported by our calculations. For instance, the ES value of the F–H bond in the F–H–F 3c–4e bond of the HF₂⁻ molecule is much larger than that of the F–H bond in the F–H–F bond in the Cmcm HP phase of HF at 20 GPa (i.e., when solid HF exhibits infinite zigzag chains of H and F atoms as that shown in Fig. 4c), despite both bonds can be classified as ERMBs. The reason is that the concatenation of 3c–4e bonds even in a zigzag form leads to an increase in the bond length of the two-center bonds within ERMB (with respect to the pure 3c–4e bond) and to a loss of shared electrons in line with Pauling's formula for bond order as recently justified for polyiodides.⁶⁴ Consequently, ERMBs in infinite zigzag atomic chains are not pure ERMBs and can be considered as weakened ERMBs in the sense that they tend to become EDMBs as the length of the bonds increases with the increase of atoms in the chain beyond three centers.

A possible explanation for the decrease of the ES value in concatenated 3c–4e bonds in HF with respect to pure isolated 3c–4e bonds in HF²⁻ could be due to the reduction in the number of electrons available for bonding in solid HF with respect to HF²⁻. This reduction arises from the stoichiometry of the system: in solid HF there is a 1 : 1 ratio of H and F atoms that has fewer electrons for bonding compared to isolated HF²⁻ ions with a 1 : 2 stoichiometry. In both cases, four electrons are expected to participate in the bonding of three atoms and the rest of electrons are considered to be part of LEPs; however, the smaller number of electrons in LEPs in HF than in HF²⁻ ions, could lead to a smaller ES value in HF than in HF²⁻ if those extra electrons participate with a small contribution to the bonding. This argument is the same as the electron count hypothesis previously commented in Section 4.2.1.

Other examples of materials in which symmetry plays a role are crystalline solids, e.g. BaZnSb₂ and sc-Po, since the translational symmetry is the main one in crystalline solids. As already mentioned, all Sb atoms of the planar array in BaZnSb₂ are at 4c sites, so they are all equivalent and must have the same Bader [Löwdin] charge (−0.6 [−0.82]). Similarly, all Po atoms in sc-Po are located in the 4a Wyckoff position, so all atoms are equivalent and must have the same charge as already found in ref. 1 and 2. In both compounds, Sb–Sb and Po–Po bonds have ET = 0, so ERMBs cannot be found simply because ERMBs are characterized by relatively high ET values. Therefore, symmetry prevents ERMBs from occurring in homonuclear bonds of atoms occupying the same Wyckoff position in solids. In other words, we have already reasoned that the central atom of a trimer has always a more positive charge than the external atoms within a 3c–4e bond due to the different Wyckoff sites for the central and terminal atoms of the trimer. Consequently, the translational symmetry in solids makes it impossible for the central atom of a given or chosen trimer to shift electronic charge to the terminal parts of the unit provided that all atoms of the trimer have the same Wyckoff site. This symmetry argument makes it impossible to establish ERMBs in an infinite linear atomic chain with all atoms having the same Wyckoff site, as in the infinite linear chain of H and I atoms.

A good example of the impossibility of ERMBs to be formed in infinite linear molecules, even when these molecules have atoms at different Wyckoff sites with different electronic charges, is the crystalline rs phase of PCMs; e.g. IV–VI chalcogenides, such as β-GeTe (Fig. 8c). In β-GeTe, Ge and Te are located at 4a and 4b sites and have Bader [Löwdin] charges of +0.36 [+0.18] and −0.36 [−0.18], respectively. Since Ge and Te occupy different Wyckoff sites in β-GeTe, the impossibility commented in the above paragraph does not apply and we could a priori assume that a 3c–4e ERMB could be possible along three perpendicular axes around the Ge atom with positive Bader [Löwdin] charge and a Te^δ−–Ge^δ+–Te^δ− configuration (according to our previous reasoning of (− + −) charge distribution in the I₃⁻ molecule). However, a 3c–4e ERMB cannot be possible around the Te atom with negative Bader [Löwdin] charge and Ge^δ+–Te^δ−–Ge^δ+ configuration. Note that this configuration would result in a (+ − +) charge distribution that has not been observed in any 3c–4e molecule yet. The reason is that this charge configuration will concentrate the charge at the central atom of the trimer, and this will lead to a flagrant violation of the octet rule; a situation that tends to be avoided in Nature,⁵⁷ and that does not occur in 3c–4e bonds as we have shown in Fig. 5. On the other hand, no five-center bond with Te^δ−–Ge^δ+–Te^δ−–Ge^δ+–Te^δ− configuration or larger ERMBs with equal Ge–Te bond distances could be possible, as already discussed for polyiodides.²⁴ A similar linear five-atom configuration is observed in the linear I₅⁻ molecule which is only slightly stable¹²² and is not observed isolated but only in confined spaces like in nanotubes.⁷⁹ It must be stressed that the linear I₅⁻ molecule does not show ERMBs as recently discussed,^24,122 since this molecule can be understood as a system composed of two external I₂ molecules weakly linked to a central I⁻ anion, as shown by their different I–I bond distances. Only angular V- or L-shape I₅⁻ molecules (i.e., showing a zigzag geometry), with ERMBs in a configuration similar to that of Fig. 4c and d, are stable as already discussed.^24,122

Regarding the possibility of linear molecules with ERMBs larger than three centers (4c–6e, 5c–6e, 5c–8e, etc.), we have to stress that they have been thoroughly studied,^54,85,123 but it must be clarified that these linear molecules do not have the equal or nearly equal bond distances as those observed in 3c–4e ERMBs, as already discussed for the linear I₄⁻, I₄²⁻, and I₅⁻ polyanions, and in EDMBs (either in 3c–2e bonds or in general in extended 2c–1e bonds).^24,122 In any case, we want to stress that the issue is different in molecules, even inside solids, where several symmetry restrictions must not be obeyed.

It must be noted that there are ways to overcome the limitation of the extension of ERMBs to three centers and extend ERMBs to infinite in one or more dimensions. One example of the infinite extension of ERMBs in 2D is found in Cs₂Te₅ (Fig. 6b). In this solid, terminal Te₂ atoms in planar Te₅²⁻ molecular units form short pure covalent Te₂–Te₂ bonds that are almost perpendicular to the planar Te₅²⁻ molecular units with Te₂–Te₁–Te₂ ERMBs. The covalent bonds link the planar Te₅²⁻ molecular units in two directions.¹²⁴ In other words, since ERMBs cannot be extended beyond three centers, the alternation of covalent bonds and ERMBs in a zigzag way is a way to extend ERMBs in different directions. A similar example is the recent finding of Ru–Ru–Ru trimers featuring 3c–4e bonds in the low-temperature monoclinic phase of crystalline RuP.¹²⁵ In this solid, the central and external Ru atoms of the trimer occupy different 4e Wyckoff sites so the Ru–Ru–Ru trimers can be extended along one direction forming zigzag-like ladders because the external Ru atoms form covalent-like Ru–Ru bonds almost perpendicular to the direction of the 3c–4e bonds. These two examples are similar to the polymerized infinite zigzag chains schematized in Fig. 4c and d that also show linked 3c–4e bonds due to the change of direction to avoid the previously mentioned restrictions for the formation of ERMBs. In summary, we consider that ERMBs with equal bond distances are not possible in linear molecules of more than three atoms inside crystalline solids. Consequently, infinite linear multicenter bonds in crystalline solids cannot be ERMBs and must be necessarily EDMBs.

As a final comment regarding the difference between ERMBs and EDMBs, we want to comment that it could be argued against our claim for the formation of linear EDMBs in the octahedral phases of pnictogens and chalcogens and crystalline PCMs² that linear 3c–2e EDMBs are rare in molecules,¹²⁶ whereas linear 3c–4e ERMBs are common in molecules.⁵⁴ In this regard, it must be emphasized that two types of 3c–2e bonds are known: supported and unsupported 3c–2e bonds.¹⁰ It has been commented that the 3c–2e bonds of H₃⁺ and B₂H₆ are of the supported type and tend to be bent, while the B–H–B and Al–H–Al 3c–2e bonds in B₂H₇⁻ and Al₂H₇⁻ molecules are of the unsupported type.¹⁰ It has been proposed that these unsupported 3c–2e bonds can be either bent or linear: bent in the absence of a crystal lattice and linear when the crystal lattice is present; i.e., when a translational symmetry is imposed.^127,128 Therefore, the existence of linear unsupported EDMBs in crystalline solids can also be justified due to the presence of the translational symmetry of the crystal lattice. This argument is in line with the symmetry arguments mentioned in this section.

Moreover, in this comparison between ERMBs and EDMBs, we consider that there is an anti-symmetry between ERMBs and EDMBs. The infinite extension of ERMBs along one direction, which occurs thanks to the formation of infinite zigzag chains as a concatenation of 3c–4e bonds, has its anti-symmetrical counterpart in EDMBs since the infinite extension of EDMBs along one direction occurs thanks to the formation of infinite linear chains with 2c–1e bonds, which can be considered a concatenation of 3c–2e bonds. Curiously, 3c–4e bonds, which are linear or quasi-linear, become extended by forming infinite zigzag chains, whereas 3c–2e bonds, which are typically non-linear, become extended by forming infinite linear chains. Therefore, the 2c–1e EDMBs in the infinite linear atomic chains in the octahedrally-coordinated phases of pnictogens, chalcogens, PCMs, and in the twofold-coordinated phases of H (Fig. 4c) and halogens (Fig. 4d)²⁴ can be considered as the equivalent to the weakened ERMBs in the infinite zigzag atomic chains in HX compounds (X = F, Cl, Br, I) and in polyhalogens.²⁴ This concept will be developed in more detail in a forthcoming article.

7. Hypercoordinated units in ERMBs and EDMBs

In this section, we want to make a pertinent observation about the hypercoordinated multicenter units with different geometries that have been experimentally observed upon the formation of both ERMBs and EDMBs in electron-rich elements; units whose geometries go beyond those of the classical geometries of iono-covalent bonds.

As already stated, electron-rich elements participating in hypercoordinated multicenter units have been traditionally associated with the presence of ERMBs or hypervalent 3c–4e bonds. In the literature, the concept of hypervalent molecules of main-group elements has been related with the violation of the 8 − N rule for atomic coordination, where N is the total number of valence s and p electrons and 8 − N indicates the number of covalent 2c–2e bonds to be formed to complete the octet.^129–131 In other words, hypervalent molecules show elements with a larger atomic coordination (hypercoordination) than expected if all bonds were considered single covalent 2c–2e bonds.

Frequently, the violation of the 8 − N rule has been interpreted (see ref. 60 and 132) as if these hypercoordinated molecules, with assumed 2c–2e bonds, would have also violated the Lewis–Langmuir doublet/octet rule;^133,134i.e., it has been considered that the central atom of a 3c–4e bond is surrounded by more than the two (eight) atoms allowed for s (s + p) orbitals. However, as we have already discussed regarding Fig. 5, several works have suggested that hypervalent molecules, such as XeF₂ or I₃⁻, do not violate the doublet/octet rule.^{57,58,135–141} Although there is still a doubt whether there is a violation of the octet rule for hypervalent molecules of the second kind (PF₅ and SF₆) and not for those of the first kind (XeF₂ or I₃⁻).^142,143 Moreover, it has been proposed that the terms “hypervalence” and “hypervalent” should be sent to the graveyard and replaced by more convenient terms, like “hypercoordinated” or “hypobound”.^{57,60,135–141}

Recent works by Grabowski on molecules have discussed the formation of hypervalent units driven by various non-covalent interactions in secondary bonds, including hydrogen, triel, tetrel, pnictogen, chalcogen, and halogen bonds. Grabowski has pointed out that the mechanism of formation of these secondary bonds is the same in all of them and related to the σ-hole model.^58,144 Moreover, it has been suggested that the hypervalent units formed by secondary bonds, leading to 3c–4e ERMBs in molecules follow the rules of the VSEPR model.^49,81,132

Unfortunately, the linear ERMBs have not been clearly distinguished in the diagrams of the hypervalent units in previous works in our opinion;^{49,58,132,144} so we have plotted in Fig. 10 some of the simplest hypercoordinated units with ERMBs according to the VSEPR model⁸¹ with a special emphasis on the location of the linear multicenter bonds (green bonds). As a matter of example of ERMBs, the XeF₂ molecule, and I₃⁻ ion in CsI₃ exhibit the linear geometry of Fig. 10a, the XeF₄ molecule shows the square planar geometry of Fig. 10b, and the TeI₆ molecule in Cs₂TeI₆ features the cubic geometry of Fig. 10c.

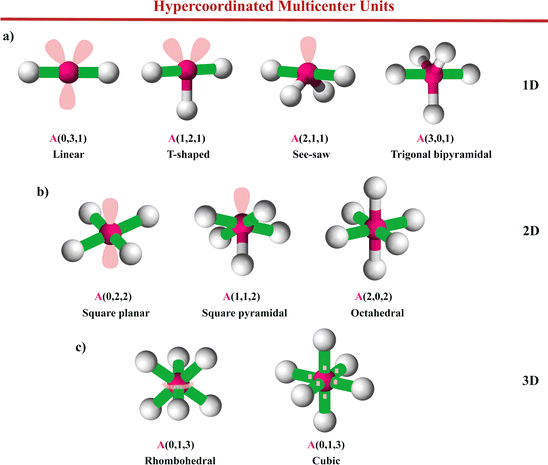Fig. 10 Hypercoordinated multicenter units around a central electron-rich A atom (pink color) showing the simplest linear three-center bonds in (a) one (1D), (b) two (2D), and (c) three (3D) dimensions. Each unit around the A atom is defined by three numbers enclosed in parentheses, A(C, E, M), denoting the number of iono-covalent bonds (C), LEPs (E), and linear multicenter bonds (M) that are depicted in white-pink, light pink, and green color, respectively. These units are typical of molecular units with electron-rich multicenter bonds (ERMBs) that specifically correspond to 3c–4e bonds. These units have been observed in molecules, such as I₃⁻, XeF₂, XeF₄, and SF₆, and solids, such as CsI₃, Cs₂Te₅, TlTe, and Cs₂TeI₆. However, these 1D, 2D, and 3D units extended indefinitely also appear in solids with electron-deficient multicenter bonds (EDMBs), such as the A_h and A_i phases of group-15 and -16 elements,² in IV–VI and V₂–VI₃ PCMs, such as β-GeTe and Bi₂Te₃, and in other solids, e.g. Li₂Sb, TlTe, and BaZnSb₂. In (c), the light pink halo (squares) indicates the presence of a stereochemically weakly active (inactive) LEP in the rhombohedral (cubic) geometries, as it happens in the A_i (A_h) phases of group-16 (group-15) elements (see ref. 2).

The replot of the simplest hypercoordinated units with linear ERMBs of Fig. 10 is also interesting for EDMBs since we have shown in this work and in previous ones^1,2 that those hypercoordinated multicenter units are also observed in EDMBs in which electron-rich elements participate. Notice that the linear three-center geometries in Fig. 10 (in most cases related to the presence of LEPs in electron-rich elements) are in general different from those found in EDMBs of electron-deficient elements, which have no LEPs.¹²⁶ Notably, the 3D EDMBs of the A_h phase of α-Po show the cubic geometry of Fig. 10c and the A_i phase of β-Po shows the rhombohedral geometry of Fig. 10c.^1,2 Similarly, the cubic geometry of Fig. 10c has been observed in 3D EDMBs of PCMs with rs structure, such as β-GeTe, SnTe, PbS, PbSe, and PbTe, and the rhombohedral geometry of Fig. 10c has been observed in 3D EDMBs of PCMs with tetradymite-like structure, such as α-Bi₂Se₃, β-As₂Te₃, α-Sb₂Te₃, and α-Bi₂Te₃. On the other hand, the 1D Sb–Sb (Te–Te) EDMBs of the infinite linear atomic chains in Li₂Sb (TlTe) show the linear geometry of Fig. 10a and the 1D Te–O EDMBs and the covalent bonds of TeO₂ show the see-saw geometry of Fig. 10a. The 2D Sb–Sb EDMBs of the planar Sb array in BaZnSb₂ (Fig. 7b) and the mixture of 2D Te–Te ERMBs and EDMBs of Te(4b) in TlTe exhibit the square planar geometry of Fig. 10b, while the 2D Sn–Se EDMBs and the covalent bond in Cmcm-type SnSe (Fig. 8b) exhibit the square pyramidal geometry of Fig. 10b. This last reasoning also applies to isostructural InBr, InI, and TlI.

In view of these results, we conclude that the hypercoordinated multicenter units shown in Fig. 10 represent some of the simplest linear multicenter bonds that comply with VSEPR rules, regardless of whether they are ERMBs (3c–4e) or EDMBs (3c–2e or extended 2c–1e). In the hypercoordinated units, multicenter bonds can be directed in 1D, 2D, and 3D, alone or in combination with LEPs and iono-covalent bonds, which are noted as E and C, respectively in Fig. 10. Therefore, our work shows that linear hypercoordinated multicenter units such as those shown in Fig. 10 occur for both ERMBs and EDMBs in molecules and solids made of electron-rich elements.

We must note in passing that no “hypervalency” occurs in multicenter bonds. It was assumed that the atomic hypercoordination was caused because the atom was acting with a valence higher than expected (hence the term “hypervalency”);¹⁷e.g. Ge and Te atoms in β-GeTe have 2⁺ and 2⁻ valence, respectively, but both atoms exhibit a sixfold coordination (hypercoordination) as if they would act with a valence 6⁺ and 6⁻, respectively. However, there is no hypervalency since the hypercoordinated atoms do not show a valency beyond their maximum allowed values. Note that the atom valency is defined as the capacity of the atom to share one electron in each formed covalent bond; since the bonds in hypercoordinated units are not all covalent bonds, but there are multicenter bonds, the assumed hypervalency is not correct. Consequently, we suggest, in agreement with previous works,^{57,60,135–141} that the terms “hypervalency” and “hypervalent” should be replaced by “hypercoordination” and “hypercoordinated”, as shown in Fig. 10, because atomic hypercoordination means the presence of multicenter bonds in the involved atom. We note that the terms “hypobonding” or “hypobonded” can complement “hypercoordination” and “hypercoordinated” when describing multicenter bonds. In this context, an atom is said to form a “hypobond” when the bond involves fewer electrons shared than in a pure covalent bond, as is characteristic of multicenter bonding.

It must be stressed that the formation of hypercoordinated multicenter units corresponding to 3c–4e ERMBs is clearly illustrated in Fig. 10, as ERMBs cannot extend beyond three centers. However, the formation of hypercoordinated multicenter units corresponding to 2c–1e EDMBs that are extended beyond three centers (along 1D, 2D, or 3D) in solids could lead to misinterpretation of Fig. 3d–f and 10 since in these figures the bonds are represented only for three-center molecules. In this context, it must be understood that the formation of extended 2c–1e EDMBs (along 1D, 2D, or 3D) is similar to the mechanism shown in Fig. 3d–f and the geometries of Fig. 10 but extended infinitely in the corresponding directions. For instance, in As-I phase (A7 structure) the primary covalent As–As bond is almost linearly linked by secondary bonds to two As atoms of neighbor layers (As⋯As–As⋯As) along one direction;² thus, the trans influence of the two As⋯As secondary bonds on the primary covalent As–As bond is on both sides of the central As₂ molecule. Moreover, since each As atom in the A7 phase of As participates in three, almost perpendicular primary As–As bonds, this picture should be extended in the three, almost perpendicular directions. In this way, the A_h structure of the As-II(sc-As) phase at HP is formed by extended 3D EDMBs² (not by 3c–4e bonds as previously assumed²⁰), unlike what Fig. 3d–f and 10 could initially suggest due to their limited schematic view. The polymerization reactions schematized in Fig. 4e and f help us to illustrate the extension of EDMBs shown in Fig. 3d–f and 10 in one direction.

Now that we have demonstrated that the geometries of hypercoordinated units present in Fig. 10 can be found in both ERMBs and EDMBs in electron-rich elements, we propose a new notation for these hypercoordinated multicenter units. Our notation is different from that used by Crabtree⁵⁰ and Grabowski,⁵⁸ who use the number of ligands, L, which can be understood as the number of bonds, but do not distinguish between ERMBs and EDMBs (note that previous diagrams considered only ERMBs⁵⁸). Here we propose that the hypercoordinated multicenter units of Fig. 10 might be noted as A(C, E, M), where A refers to the symbol of the hypercoordinated central atom A, while the numbers C, E, and M correspond to the number of iono-covalent bonds, LEPs, and linear multicenter bonds (both ERMBs of EDMBs), respectively.

To illustrate the application of our notation with various compounds exhibiting EDMBs, we can cite: (i) the A(0,3,1) unit of chains of Sb atoms in Li₂Sb⁹⁶ and of Te(4a) atoms in TlTe;¹⁰³ (ii) the A(1,2,1) unit of O atom in SbOF (see Fig. S8a of the ESI†);¹⁴⁵ (iii) the A(2,1,1) unit of Te atoms in TeO₂¹⁰³ and of Sb atoms in SbOF;¹⁴⁵ (iii) the A(3,0,1) units of P atoms in TiPO₄-V at 48 GPa (see Fig. S8b of the ESI†);¹⁴⁶ (iv) the square planar A(0,2,2) unit of Sb atoms at the planar array in BaZnSb₂ or of Te(4b) in TlTe;¹⁰³ (v) the square pyramidal A(1,1,2) units present around Sn (Tl) and Se (I) atoms in Cmcm-type SnSe (TlI);¹⁰² and (vi) the rhombohedral and cubic A(0,1,3) units of the A_h and A_i phases in group-15 and -16 elements as well as of many PCMs of IV–VI and V₂–VI₃ families with rs and tetradymite-like structures, respectively,² including crystalline GST, the reference material for phase change electronic storage.

As we have mentioned, the geometries in Fig. 10 are different from those of EDMBs found in electron-deficient elements; however, we would like to add that a similar geometry to that of the linear geometry in Fig. 10a would be found for the case of the infinite linear hydrogen bond (see Fig. 4e). This could be considered a A(0,0,1) unit (not shown in Fig. 10 but is similar to the A(0,3,1) unit without the three LEPs). The A(0,0,1) unit of hydrogen could also correspond to the type of bond in the atomic/polymeric hydrogen at HP,⁷⁰ in which H–H bonds form a ring instead of an infinite linear atomic chain.

8. Is the doublet/octet rule violated in the hypercoordinated units of ERMBs and EDMBs?

In Fig. 5 we have already discussed that the central atom in ERMBs, such as those in HF₂⁻, XeF₂, and I₃⁻, does not flagrantly violate the doublet/octet rule; however, we would like to conclude this paper with a broader discussion on whether the central A atom in the hypercoordinated multicenter A(C, E, M) units of Fig. 10 violates or not the doublet/octet rule when M is either an ERMB or an EDMB.

To verify whether the doublet/octet rule is satisfied or not, we can consider, as a first approximation, that: (i) each iono-covalent bond contains two electrons (the bonding electron pair); (ii) each LEP contains two electrons (the non-bonding electron pair); and (iii) each multicenter bond is characterized by partially sharing two electrons between every two atoms (ERMB) or only one electron between every two atoms (EDMB). In this way, we can easily check that, in general, the A(C, E, M) units of Fig. 10 for EDMBs seem to verify the octet rule, although some cases need further discussion. The verification of the octet rule is not so clear for ERMBs,⁶⁰ despite Grabowski has reasoned that the formation of the hypercoordinated units in molecules with 3c–4e ERMBs is connected with the mechanism of the σ-hole model to uphold the doublet rule for alkali and alkaline earth metals and the octet rule in main-group elements.^57,58 Let us comment here in more detail on the possible violation of the doublet/octet rule in both ERMBs and EDMBs.

Regarding ERMBs, we have already commented in Section 2, when talking about the electron distribution in hypercoordinated XeF₂, XeF₄, and XeF₆ molecules, that the octet rule is not severely violated, unlike proposed in ref. 60, since it can be considered that this violation of the octet rule occurs in a second approximation and not in a first approximation. The reason is that it can be considered that there are only 8 electrons in the valence electron sphere close to the central Xe atom and 2, 4, and 6 additional electrons in the van der Waals electron sphere (at longer distance from the central Xe atom) in XeF₂, XeF₄, and XeF₆, respectively.⁶⁰ In any case, there is still a doubt whether there is a violation of the octet rule for hypervalent molecules of the second kind (PF₅ and SF₆) and not for those of the first kind (XeF₂ or I₃⁻).^142,143 In this regard, we consider that all pure ERMBs (either of first or second kind) are 3c–4e bonds, so the reasoning of Fig. 5 regarding I₃⁻ can be applied to every pure ERMB in 1D, 2D or 3D to verify that the doublet/octet rule is in general satisfied as a first approximation.

Regarding EDMBs, it has been suggested that the octet rule is being satisfied in molecules⁶² and the same is expected in solids. Taking into account the above considerations, eight electrons seem to surround each A atom in hypercoordinated units with only one EDMB (1D geometry), such as in the A(0,3,1), A(1,2,1), A(2,1,1), and A(3,0,1) units of Fig. 10a. The same occurs for the units with two EDMBs (2D geometry), the A(0,2,2), A(1,1,2), and A(2,0,2) units of Fig. 10b, and for the units with three EDMBs (3D geometry), such as the cubic A(0,1,3) units of Fig. 10c.

A clear example of the validity of the octet rule for EDMBs with the geometry of the A(0,1,3) unit is the A_h phase of pnictogens, e.g. the sc-As phase.² Since pnictogens have two s-type and three p-type valence electrons, the A_h phase features two s-type electrons forming part of the inactive LEP (they are distributed into six lobes, as shown by pink regions in the cubic A(0,1,3) unit of Fig. 10c), while the three p-type electrons participate in the three mutually perpendicular EDMBs. Therefore, the central A atom of the cubic A(0,1,3) units has eight valence electrons, thus satisfying the octet rule. It must be emphasized that this result is contrary to the previous assumption that hypercoordinated units in the crystalline phases of PCMs, such as β-GeTe (isoelectronic to sc-As), led to a violation of the octet rule.¹³² The same reasoning would apply to consider the validity of the doublet rule for H, when it forms EDMBs at HP. In particular, polymeric H (⋯H–H–H⋯) either in ring form at HP⁷⁰ or in the infinite linear chain of Fig. 4e could be considered to form hypercoordinated A(0,0,1) units (with no LEPs) with only one EDMB (1D geometry). Therefore, two electrons surround each H atom, thus satisfying the doublet rule. It can be observed that the EDMBs of I atoms in the infinite linear iodine chain (Fig. 4f) lead I atoms to obey the octet rule.

In summary, assuming that each iono-covalent bond, each LEP, and each EDMB, accounts for two electrons in multicenter hypercoordinated A(C, E, M) units, the doublet and octet rules are satisfied for the central A atom if we consider the equation 2(C + E + M) = 2 or 8. For the octet rule, it has to be satisfied that C + E + M = 4. This is exactly the condition satisfied by all the A(C, E, M) units of Fig. 10. For the doublet rule (case of H), it has to be satisfied that C + M = 1 since H has no LEP (E = 0). In this context, H has only three bonding possibilities to satisfy the doublet rule, either it has a covalent bond (C = 1, M = 0), as in H₂, an ERMB (C = 0, M = 1), as in HF₂⁻, or an EDMB (C = 0, M = 1), as it is expected to occur in atomic/polymeric hydrogen at HP.

Interestingly, the octet rule seems to be violated in the hypercoordinated units with EDMBs for group-16 elements, e.g. the cubic and rhombohedral A(0,1,3) units of α-Po and β-Po.^1,2 In this case, in addition to the six p-type electrons of the three EDMBs around each central A atom (three coming from the central A atom), one has to count the three additional electrons of the A atom (two s-type electrons corresponding to the LEP plus the extra p electron in chalcogens compared to pnictogens). This extra electron is distributed either among the six lobes of the cubic A(0,1,3) unit (see light pink cubes in Fig. 10c) typical of α-Po or in the toroidal halo of the rhombohedral A(0,1,3) unit (see light pink monosynaptic toroidal in Fig. 10c) typical of β-Po. Therefore, a total number of nine electrons seems to be around each hypercoordinated EDMB unit for octahedrally-coordinated chalcogens, thus violating the octet rule.

Perhaps the violation of the octet rule in the hypercoordinated (octahedrally coordinated) units with EDMBs for group-16 elements in the A_h and A_i phases is only apparent. A study of the prevalence of the cubic vs. the rhombohedral units in AF₆E molecules with ERMBs, where A is the central atom, F is the ligand atom, and E is the LEP, has concluded that both the cubic O_h symmetry, like that of the cubic unit of Fig. 10c, or the C_3v symmetry, like that of the rhombohedral unit of Fig. 10c, in AF₆E molecules, such as XeF₆, are very close in energy.¹⁴¹ The predominance of one geometry over the other seems to be related to a very fine balance between ligand–ligand repulsions and the energy gained by the expansion of the two non-bonding electrons of the LEP in the valence shell. This balance has been suggested to mainly depend on the atomic radii ratio between the central atom and the ligands. Interestingly, the small energy difference between the two configurations for AF₆E molecules with ERMBs is similar to the one we have found between the two polymorphs of Po at 0 K, which explains that β-Po tends to α-Po above 2 GPa.² With the above considerations, it could be speculated that, similarly to the case of AF₆E molecules with ERMBs,¹⁴⁷ the cubic and rhombohedral configurations of the two phases of Po at RP likely occur because of the fine balance of the two aforementioned energy terms (which certainly will depend on the temperature and pressure conditions).

Regarding the violation of the octet rule, it has also been suggested in the same work of AF₆E molecules with ERMBs, that the non-bonding electrons (being part of LEPs) in the AF₆E molecules could behave as a mixture of valence-core electrons so on average they contribute with only one valence electron; i.e., one of the two electrons of the s-type LEP could be considered part of the core.¹⁴⁷ Therefore, it could also be speculated that the three non-bonding electrons of chalcogens in the A_h and A_i phases likely behave as in AF₆E molecules with ERMBs, so that on average they contribute with only two valence electrons, that summed to the other six p-type electrons of the three EDMBs would make the central atom to satisfy the octet rule. This hypothesis of the mixture of valence-core electrons for s-type electrons can be justified in the A_h and A_i phases of chalcogens due to the large energy difference between s and p states in chalcogens.¹⁴⁸ In summary, this reasoning could be a possible explanation for the fulfilment of the octet rule in both the cubic and rhombohedral geometries with EDMBs in the A_h and A_i phases of chalcogens. Moreover, this reasoning could provide an answer to the question, posed by Papoian and Hoffmann²⁰ and already commented in our previous work,² about how could it be possible the existence of the cubic α-Po phase taking into account the electron counting rule suggested by Papoian and Hoffmann for the formation of multicenter bonds.²⁰ Note that we have already commented that the electron counting rule of Papoain and Hoffmann for the formation of multicenter bonds is correct.² However, they applied it incorrectly to explain the bonds in many Zintl phases. They interpreted all multicenter bonds in materials of electron-rich elements as ERMBs; a feature that we have shown in this work and in ref. 2 to be incorrect because some of them are EDMBs.

To close this section, it is important to stress that the already commented rocksalt structure of β-GeTe at HP, the orthorhombic Cmcm structure of SnSe at HP and TlI at RP, and the paratellurite (α-TeO₂) structure at RP, would constitute examples of the violation of the octet rule if we discard the presence of EDMBs, as it has been repeatedly suggested.²⁰ The rocksalt structure of β-GeTe shows Ge and Te atoms with sixfold coordination. This means that if all were single covalent bonds, a total of 12 valence electrons (6 bonds × 2 electrons per bond) would lead to a flagrant violation of the octet rule in addition to hypervalence, as already discussed. If we assume that they are ERMBs, as Hoffmann and his collaborators suggest,^20,85 they would also violate the octet rule since there are ca. 1.5 electrons shared in any ERMB (6 bonds × 1.5 electrons per bond = 9 electrons). Only considering that they are EDMBs one gets a total of 8 valence electrons around Ge and Te atoms as it should be to complete the octet (6 bonds × 1 electrons per bond = 6 electrons plus the two electrons from the inactive s-type LEP). Similarly, the Cmcm structure of SnSe at HP with fivefold coordination for Sn and Se atoms cannot be understood without the participation of EDMBs. Note that if all bonds were single covalent bonds a total 12 valence electrons would be around each Sn and Se atom (5 bonds × 2 electrons per bond = 10 electrons plus 2 electrons from the LEP which accounts for the layered structure of SnSe). Therefore, both Sn ans Se atoms would strongly violate the octet rule. The same would occur if the four bonds of SnSe in the layer plane were considered ERMBs since 10 electrons would be around each Sn and Se atom (4 bonds × 1.5 electrons per bond = 6 electrons plus two electrons from the covalent bond and two electrons from the LEP). On the other hand, metallic bonds cannot be invoked to explain the structure and properties of β-GeTe and SnSe at HP. In particular, the layered Cmcm structure of SnSe and the relatively strong directionality of the bonds within the layers are incompatible with the presence of non-directed metallic bonds but are compatible with the presence of directed EDMBs. The mystery for SnSe can be solved if we consider that each atom has 4 valence electrons in the direction perpendicular to the layers (coming from one iono-covalent bond and one LEP) plus 4 valence electrons in the layer plane (corresponding to each of the 4 2c–1e bonds that form the 2D EDMBs).

Similar arguments can be invoked to explain the structure and properties of paratellurite, in which Te atoms are fourfold coordinated to O atoms. If the four bonds were single covalent, there would be 4 bonds × 2 electrons per bond = 8 electrons, which added to the two electrons from the LEP present in Te that result in a trigonal bipyramidal geometry, leads to a total of 10 valence electrons around Te atoms. The mystery here is solved if we consider that two collinear Te–O bonds are EDMBs and provide 2 electrons in total and not 4, thus resulting in the 8 valence electrons around the Te atoms. Therefore, our results explain why there are two short and two long bonds in α-TeO₂ without the need to invoke the existence of a thermal variation in bond lengths.¹⁴⁹ In summary, we conclude that the doublet/octet rule is not violated, in general, in multicenter bonds. Moreover, the doublet/octet rule and the VSEPR theory are fundamental tools to realize that both ERMBs and EDMBs can be naturally integrated in a unified theory of multicenter bonding.

9. Conclusions

ERMBs and EDMBs are two types of multicenter bonds that are relatively well known in molecules but remain poorly studied in solids. We have shown that both ERMBs and EDMBs can occur in molecules and solids made of electron-rich elements. In our recent work,² it has been shown that the octahedrally-coordinated phases of α-Po and β-Po in pnictogens and chalcogens, respectively, and typically found at HP, are characterized by EDMBs; a result that can be extrapolated to the crystalline phases of PCMs, such as β-GeTe. Such a result is in contrast to the previous metavalent bond model for PCMs, which considers that PCMs feature 2c–1e bonds, and to the previous hypervalent bond model for PCMs, which considers that crystalline PCMs are characterized by ERMBs (also known as hypervalent bonds or hyperbonds).

In this work, which is a continuation of ref. 2, we have addressed the nature of EDMB and ERMBs in several molecules and solids, most of them having electron-rich elements. We have shown that ERMBs and EDMBs have the same origin; i.e., they come from a mixture of primary iono-covalent bonds and secondary non-covalent bonds, and a similar formation mechanism, which consists of three stages; however, they differ in the electronic charge reorganization at stage 2. The non-bonding electrons of the stereochemically active LEP become bonding electrons when the ERMB is formed thus providing the two electrons needed for the new bond. Contrarily, the non-bonding electrons of the stereochemically active LEP tend to remain as non-bonding delocalized electrons in a weakly stereochemically active or even inactive LEP when the EDMB is formed and the charge needed for the new bond mainly comes from the primary iono-covalent bond.

Both ERMBs and EDMBs are usually longer (by more than 0.2 Å) than the covalent bond. We have clarified that quantum mechanical calculations, leading to the 2D ES vs. ET map, can help distinguishing both EDMBs and ERMBs since the two kinds of multicenter bonds are located at different positions with respect to the classical ionic, covalent, and metallic bonds.

The ERMB is a multicenter bond that can be considered the extension of the single polar covalent (2c–2e) bond to three centers, giving rise to the well-known 3c–4e bond. We have shown that the ERMB has less than two electrons shared between two atoms, but it is not a 2c–1e bond, like the EDMB. In other words, the EDMB has approximately half the electronic charge of a pure single covalent (2c–2e) bond. The simplest EDMB is the 3c–2e bond typical of boranes, although it can be also found as extended 2c–1e bonds in solids.

We have provided several examples of electron-rich systems that exhibit ERMBs, all of which involve 3c–4e bonds. We have also shown that several compounds made of electron-rich elements, such as Li₂Sb, BaZnSb₂, and α-Po, feature indeed homopolar EDMBs in 1D, 2D, and 3D, respectively, despite they were previously assumed to exhibit ERMBs.²⁰ Also examples of heteropolar EDMBs in β-GeTe, SnSe, TeO₂, ScSi₂O₇, and SbPO₄ as well as a paradigmatic example with simultaneous homopolar ERMBs and EDMBs (TlTe) have been discussed.

We have shown that all EDMBs fall in the same region of the ES vs. ET map than the central B–H bonds of the B₂H₆ molecule. We have reasoned that the bonds found in atomic/polymeric hydrogen at HP must be EDMBs since the mechanism of strengthening of the secondary, intermolecular bonds is the same for hydrogen, B₂H₆, pnictogens, chalcogens, halides, and crystalline PCMs, such as β-GeTe. All these materials have been shown to feature extended EDMBs of unsupported type at certain pressures.

We have provided the simplest geometries of linear or quasi-linear hypercoordinated multicenter units (both with ERMBs and EDMBs) around a central electron-rich A element. These units do not obey the 8 − N rule, have geometries compatible with the VSEPR model, and are not hypervalent despite being formed by electron-rich elements. We suggest that the “hypervalent” units should be renamed as “hypercoordinated multicenter units”. Besides, we have proposed a new notation (A(C,E,M)) to classify hypercoordinated units that include multicenter bonds which is based on the number of iono-covalent bonds, LEPs, and multicenter bonds (either ERMBs or EDMBs).

We have justified that in extended solids hypercoordination of electron-rich elements with linear or quasi-linear bonds is only possible for EDMBs since ERMBs can only appear in three-center molecular units (even in solids) as 3c–4e bonds due to energy and symmetry restrictions. ERMBs cannot form linear bonds longer than three centers without severely violating the octet rule for the internal atoms of the molecule. Extension of ERMBs along one direction usually needs to alternate ERMBs (alone or in combination with other types of bonds) in a zigzag configuration due to the impossibility of doing it in a linear configuration. This limitation does not hold for 3c–2e EDMBs, which extend to infinite as colinear 2c–1e bonds.

Finally, we have reasoned about the violation of the doublet/octet rule for the central A atom in hypercoordinated multicenter units (mainly those formed by electron-rich elements). We have shown that, in general, the doublet/octet rule is satisfied around the central A atom for hypercoordinated units with EDMBs. For hypercoordinated units with ERMBs, the central A atom seems to obey the octet rule as a first approximation and to violate the octet rule only in a second approximation. This is justified by the distribution of atomic electrons in concentric electronic (core, valence, and van der Waals) spheres.

All the results summarized here have allowed us to tentatively propose four new paradigms:

(1) EDMBs and ERMBs can be found in molecules and solids made of electron-rich elements.

(2) EDMBs, present in either electron-rich or electron-deficient elements, are found as 3c–2e bonds or as infinitely extended 2c–1e bonds.

(3) Pure ERMBs can be formed only in linear or quasi-linear three-center molecules. This means that all ERMBs are 3c–4e bonds extended either in one, two, or three dimensions. Corollary: multicenter bonds extended to more than three centers in one dimension, either in a linear or a zigzag way, cannot be ERMBs and tend to form EDMBs.

(4) EDMBs and ERMBs do not violate, in general, the doublet/octet rule.

In summary, we have presented in this work a novel unified theory of multicenter bonding that is consistent with the VSEPR rules and the doublet/octet rules and that has challenged several paradigms related to the ERMBs and EDMBs. For this reason, we consider that the results of this work have very far-reaching consequences for the broad scientific community, not only for supramolecular chemists but also for condensed matter scientists, since the clear distinction between ERMBs and EDMBs we have provided here will allow explaining the structures (and also the properties) found in many materials from simple elements to complex materials, such as PCMs, highly efficient thermoelectrics, topological insulators, superconductors, highly efficient photovoltaic materials, Zintl phases, intermetallics, and cluster compounds at RP, as well as in atomic/polymeric nitrogen and hydrogen at HP. This understanding will open the door for a better understanding of the chemical bonding mechanisms in the above-commented advanced materials for improving their performance. In summary, we hope that this work will promote further work to understand ERMBs and EDMBs in solids and their associated exceptional property portfolio.

Data availability

The data supporting this article has been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This publication is financed by Spanish Ministerio de Ciencia e Innovación and the Agencia Estatal de Investigación MCIN/AEI/10.13039/501100011033 as part of the project MALTA Consolider Team network (RED2022-134388-T), and I + D + i projects PID2022-138076NB-C42/C44 co-financed by EU FEDER funds, by project PROMETEO CIPROM/2021/075 (GREENMAT) financed by Generalitat Valenciana and co-financed by EU FEDER. This study also forms part of the Advanced Materials programme supported by MCIN with funding from European Union NextGenerationEU (PRTR-C17.I1) and by Generalitat Valenciana through project MFA/2022/025 (ARCANGEL). We would like to express our gratitude to A. Otero-de-la-Roza, J. Contreras-García, Á. Lobato, F. Izquierdo, M. Savastano, and Á. Vegas for their insightful and engaging discussions on our findings. Their input and feedback greatly enriched the development of this article. More specifically, A. Otero-de-la-Roza has assisted us with the CRITIC2 code; Á. Lobato and J. Contreras-García called our attention to the parallelism between the mechanism of EDMB formation and the bond formation in the atomic/polymeric phases of nitrogen and hydrogen, respectively; Á. Lobato and F. Izquierdo are acknowledged by collaborating in the study of multicenter bonds in AX₃ compounds; Á. Vegas draw our attention to various systems, including Sc₂Si₂O₇; and M. Savastano is acknowledged for his collaboration on the study of polyiodides and for suggesting us the works of J. Echeverría and S. Álvarez.

References

1. H. H. Osman, A. Otero-de-la-Roza, P. Rodríguez-Hernández, A. Muñoz and F. J. Manjón DOI:10.26434/chemrxiv-2023-pv66p-v2.
2. H. H. Osman, A. Otero-de-la-Roza, P. Rodríguez-Hernández, A. Muñoz and F. J. Manjón, J. Mater. Chem. C, 2024, 12, 10447–10474.
3. R. E. Rundle, J. Am. Chem. Soc., 1947, 69, 1327–1331.
4. R. E. Rundle, J. Chem. Phys., 1949, 17, 671–675.
5. R. E. Rundle, J. Phys. Chem., 1957, 61, 45–50.
6. H. C. Longuet-Higgins, Quarterly Reviews, Chemical Society, 1957, 11, 121–133.
7. L. Pauling, The Nature of the Chemical Bond and the Structure of Molecules and Crys- tals: an Introduction to Modern Structural Chemistry, Cornell Univ. Press, Ithaca, New York, 1960.
8. K. Wade, Electron deficient compounds, Nelson, London, 1971.
9. C. Zheng and R. Hoffmann, Z. Naturforsch. B, 1986, 41, 292–320.
10. R. L. DeKock and W. B. Bosma, J. Chem. Educ., 1988, 65, 194.
11. W. M. Lipscomb, The Boranes and their Relatives.
12. R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press, Oxford, 1990.
13. J.-Y. Raty, M. Schumacher, P. Golub, V. L. Deringer, C. Gatti and M. Wuttig, Adv. Mater., 2019, 31, 1806280.
14. Y. Cheng, O. Cojocaru-Mirédin, J. Keutgen, Y. Yu, M. Küpers, M. Schumacher, P. Golub, J.-Y. Raty, R. Dronskowski and M. Wuttig, Adv. Mater., 2019, 31, 1904316.
15. M. Wuttig, C. Schön, D. Kim, P. Golub, C. Gatti, J. Raty, B. J. Kooi, Á. M. Pendás, R. Arora and U. Waghmare, Adv. Sci., 2023, 35, 2308578.
16. P. C. Müller, S. R. Elliott, R. Dronskowski and R. O. Jones, J. Phys.: Condens. Matter, 2024, 36, 325706.
17. J. I. Musher, Angew. Chem., Int. Ed. Engl., 1969, 8, 54–68.
18. R. J. Hach and R. E. Rundle, J. Am. Chem. Soc., 1951, 73, 4321–4324.
19. G. C. Pimentel, J. Chem. Phys., 1951, 19, 446–448.
20. G. A. Papoian and R. Hoffmann, Angew. Chem., Int. Ed., 2000, 39, 2408–2448.
21. B. Silvi, J. Mol. Struct., 2002, 614, 3–10.
22. R. Ponec, G. Yuzhakov and D. L. Cooper, Theor. Chem. Acc., 2004, 112, 419–430.
23. I. Mayer, J. Mol. Struct.:THEOCHEM, 1989, 186, 43–52.
24. M. Savastano, H. H. Osman, Á. Vegas and F. J. Manjón, Chem. Commun., 2024, 60, 12677–12689.
25. M. Wuttig, C.-F. Schön, J. Lötfering, P. Golub, C. Gatti and J.-Y. Raty, Adv. Mater., 2023, 35, 2208485.
26. M. Wuttig, V. L. Deringer, X. Gonze, C. Bichara and J.-Y. Raty, Adv. Mater., 2018, 30, 1803777.
27. F. J. Manjón, H. H. Osman, M. Savastano and Á. Vegas, Materials, 2024, 17, 2840.
28. A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
29. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
30. M. Giambiagi, M. S. de Giambiagi and K. C. Mundim, Struct. Chem., 1990, 1, 423–427.
31. M. S. De Giambiagi, M. Giambiagi and M. De Souza Fortes, J. Mol. Struct.:THEOCHEM, 1997, 391, 141–150.
32. R. Ponec and I. Mayer, J. Phys. Chem. A, 1997, 101, 1738–1741.
33. P. Bultinck, R. Ponec and S. Van Damme, J. Phys. Org. Chem., 2005, 18, 706–718.
34. E. Matito, Phys. Chem. Chem. Phys., 2016, 18, 11839–11846.
35. F. Feixas, M. Solà, J. M. Barroso, J. M. Ugalde and E. Matito, J. Chem. Theory Comput., 2014, 10, 3055–3065.
36. P. C. Müller, C. Ertural, J. Hempelmann and R. Dronskowski, J. Phys. Chem. C, 2021, 125, 7959–7970.
37. J. Hempelmann, P. C. Müller, C. Ertural and R. Dronskowski, Angew. Chem., Int. Ed., 2022, 61, e202115778.
38. G. A. Landrum and R. Hoffmann, Angew. Chem., Int. Ed., 1998, 37, 1887–1890.
39. J. C. Golden, V. Ho and V. Lubchenko, J. Chem. Phys., 2017, 146, 174502.
40. M. Savastano, Dalton Trans., 2021, 50, 1142–1165.
41. R. C. L. Money-Slater, Acta Crystallogr., 1959, 12, 187–196.
42. W. Grochala, R. Hoffmann, J. Feng and N. W. Ashcroft, Angew. Chem., Int. Ed., 2007, 46, 3620–3642.
43. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
44. R. M. Lobayan, R. C. Bochicchio and A. D. Marturet, J. Mol. Graphics Modell., 2022, 112, 108121.
45. T. H. Lee and S. R. Elliott, Adv. Mater., 2020, 32, 2000340.
46. J.-P. Gaspard, Phys. Status Solidi RRL, 2022, 16, 2200111.
47. J. Echeverría and S. Alvarez, Chem. Sci., 2023, 14, 11647–11688.
48. J. Echeverría and S. Alvarez, Chem. Sci., 2024, 15, 12166–12168.
49. T. H. Lee and S. R. Elliott, Phys. Status Solidi RRL, 2021, 15, 2000516.
50. R. H. Crabtree, Chem. Soc. Rev., 2017, 46, 1720–1729.
51. H. A. Bent, Chem. Rev., 1968, 68, 587–648.
52. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
53. J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038.
54. R. D. Harcourt, Bonding in Electron-Rich Molecules, Springer International Publishing, 2016.
55. G. A. Landrum, N. Goldberg and R. Hoffmann, J. Chem. Soc., Dalton Trans., 1997, 3605.
56. N. W. Alcock, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1972, vol. 15, pp. 1–58.
57. S. J. Grabowski, Phys. Chem. Chem. Phys., 2017, 19, 29742–29759.
58. S. J. Grabowski, Molecules, 2021, 26, 4939.
59. G. Parkin, J. Chem. Educ., 2023, 100, 4644–4652.
60. S. Noury, B. Silvi and R. J. Gillespie, Inorg. Chem., 2002, 41, 2164–2172.
61. K. S. Pitzer, J. Am. Chem. Soc., 1945, 67, 1126–1132.
62. G. Parkin, J. Chem. Educ., 2019, 96, 2467–2475.
63. G. R. Eaton, Found. Chem., 2023, 25, 285–298.
64. A. D. Walsh, J. Chem. Soc., 1947, 89–92.
65. T. Shimajiri, S. Kawaguchi, T. Suzuki and Y. Ishigaki, Nature, 2024, 634, 347–351.
66. M. Wuttig, C.-F. Schön, M. Schumacher, J. Robertson, P. Golub, E. Bousquet, C. Gatti and J.-Y. Raty, Adv. Funct. Mater., 2022, 32, 2110166.
67. V. Labet, P. Gonzalez-Morelos, R. Hoffmann and N. W. Ashcroft, J. Chem. Phys., 2012, 136, 074501.
68. V. Labet, R. Hoffmann and N. W. Ashcroft, J. Chem. Phys., 2012, 136, 074502.
69. V. Labet, R. Hoffmann and N. W. Ashcroft, J. Chem. Phys., 2012, 136, 074503.
70. V. Riffet, V. Labet and J. Contreras-García, Phys. Chem. Chem. Phys., 2017, 19, 26381–26395.
71. H. Nakatsuji, Acc. Chem. Res., 2012, 45, 1480–1490.
72. P. G. Johannsen, W. Helle and W. B. Holzapfel, J. Phys. Colloq., 1984, 45, C8-199–C8-201.
73. A. Ikram, B. H. Torrie and B. M. Powell, Mol. Phys., 1993, 79, 1037–1049.
74. T. Kume, T. Tsuji, S. Sasaki and H. Shimizu, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, 8149–8151.
75. E. Katoh, H. Yamawaki, H. Fujihisa, M. Sakashita and K. Aoki, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 11244–11250.
76. D. Duan, F. Tian, Z. He, X. Meng, L. Wang, C. Chen, X. Zhao, B. Liu and T. Cui, J. Chem. Phys., 2010, 133, 074509.
77. L. Zhang, Y. Wang, X. Zhang and Y. Ma, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 014108.
78. H. Mao and R. J. Hemley, Rev. Mod. Phys., 1994, 66, 671–692.
79. A. A. Tonkikh, D. V. Rybkovskiy and E. D. Obraztsova, J. Phys. Chem. C, 2023, 127, 3005–3012.
80. J. Contreras-García, Á. M. Pendás, B. Silvi and J. M. Recio, J. Phys. Chem. B, 2009, 113(4), 1068–1073.
81. R. J. Gillespie, Coord. Chem. Rev., 2008, 252, 1315–1327.
82. R. Hoffmann, Solids and surfaces: A chemist's view of bonding in extended structures, Wiley-VCH, 1988.
83. E. Wigner and H. B. Huntington, J. Chem. Phys., 1935, 3, 764–770.
84. R. Hoffmann, (Cornell University, Ithaca, NY, USA). Private communication.
85. J. Hempelmann, P. C. Müller, L. Reitz and R. Dronskowski, Inorg. Chem., 2023, 62, 20162–20171.
86. P. Schneiderhan, P. Schmidt, M. Ströbele, C. P. Romao and H.-J. Meyer, Cryst. Growth Des., 2020, 20, 3780–3784.
87. S. Wei, J. Wang, S. Deng, S. Zhang and Q. Li, Sci. Rep., 2015, 5, 14393.
88. I. Vázquez-Fernández, S. Mariotti, O. S. Hutter, M. Birkett, T. D. Veal, T. D. C. Hobson, L. J. Phillips, L. Danos, P. K. Nayak, H. J. Snaith, W. Xie, M. P. Sherburne, M. Asta and K. Durose, Chem. Mater., 2020, 32, 6676–6684.
89. A. Ruth, K. Németh, K. C. Harkay, J. Z. Terdik, L. Spentzouris and J. Terry, J. Appl. Phys., 2013, 113, 183703.
90. T. Porȩba, S. Racioppi, G. Garbarino, W. Morgenroth and M. Mezouar, Inorg. Chem., 2022, 61, 10977–10985.
91. P. Böttcher, Angew. Chem., Int. Ed. Engl., 1988, 27, 759–772.
92. Á. Vegas, Structural Models of Inorganic Crystals, Universitat Politècnica de València, 1st edn, 2018.
93. D. Akhtar, V. D. Vankar, K. L. Goel and T. C. Chopra, J. Mater. Sci., 1979, 14, 988–994.
94. M. Brylak, M. H. Möller and W. Jeitschko, J. Solid State Chem., 1995, 115, 305–308.
95. R. Nesper, Prog. Solid State Chem., 1990, 20, 1–45.
96. R. Gérardin and J. Aubry, C. R. Acad. Sci., Ser. C: Sci. Chim., 1974, 278, 1097–1098.
97. M. Brylak and W. Jeitschko, Z. Naturforsch., B, 1994, 49, 747–752.
98. Y. Wang, K. Wang, Y. Ma, M. Zhou, H. Wang and G. Liu, J. Phys.:Condens. Matter, 2021, 33, 355403.
99. I. Loa, R. J. Husband, R. A. Downie, S. R. Popuri and J.-W. G. Bos, J. Phys.:Condens. Matter, 2015, 27, 072202.
100. M. Xu, S. Jakobs, R. Mazzarello, J.-Y. Cho, Z. Yang, H. Hollermann, D. Shang, X. Miao, Z. Yu, L. Wang and M. Wuttig, J. Phys. Chem. C, 2017, 121, 25447–25454.
101. I. Efthimiopoulos, M. Berg, A. Bande, L. Puskar, E. Ritter, W. Xu, A. Marcelli, M. Ortolani, M. Harms, J. Müller, S. Speziale, M. Koch-Müller, Y. Liu, L.-D. Zhao and U. Schade, Phys. Chem. Chem. Phys., 2019, 21, 8663–8678.
102. L. Helmholz, Z. Kristallogr. – Cryst. Mater., 1936, 95, 129–137.
103. J. Leciejewicz, Z. Kristallogr., 1961, 116, 345–353.
104. F. Folger, Z. Anorg. Allg. Chem., 1975, 411, 111–117.
105. K. Kohn, K. Inoue, O. Horie and S.-I. Akimoto, J. Solid State Chem., 1976, 18, 27–37.
106. A. L. de J. Pereira, D. Santamaría-Pérez, R. Vilaplana, D. Errandonea, C. Popescu, E. L. da Silva, J. A. Sans, J. Rodríguez-Carvajal, A. Muñoz, P. Rodríguez-Hernández, A. Mujica, S. E. Radescu, A. Beltrán, A. Otero-de-la-Roza, M. Nalin, M. Mollar and F. J. Manjón, Inorg. Chem., 2020, 59, 287–307.
107. D. Errandonea, H. H. Osman, R. Turnbull, D. Diaz-Anichtchenko, A. Liang, J. Sanchez-Martin, C. Popescu, D. Jiang, H. Song, Y. Wang and F. J. Manjon, Mater. Today Adv., 2024, 22, 100495.
108. Á. Vegas, R. Notario, E. Chamorro, P. Pérez and J. F. Liebman, Acta Crystallogr., 2013, 69, 163–175.
109. R. N. Grimes, Carboranes, Academic Press, 3rd edn, 2016.
110. R. Llusar, A. Beltrán, J. Andrés, S. Noury and B. Silvi, J. Comput. Chem., 1999, 20, 1455–1592.
111. S. Shaik, D. Danovich, B. Silvi, D. L. Lauvergnat and P. C. Hiberty, Chem. – Eur. J., 2005, 11, 6358–6371.
112. Y. Yang, J. Phys. Chem. A, 2012, 116, 10150–10159.
113. S. Shaik, D. Danovich, J. M. Galbraith, B. Braïda, W. Wu and P. C. Hiberty, Angew. Chem., Int. Ed., 2020, 59, 984–1001.
114. B. Braïda and P. C. Hiberty, Nat. Chem., 2013, 5, 417–422.
115. J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548.
116. P. Politzer and J. S. Murray, Theor. Chem. Acc., 2012, 131, 1114.
117. H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1981, 20, 33–51.
118. S. Grabowski, Crystals, 2015, 6, 3.
119. K. Stöwe, J. Solid State Chem., 2000, 149, 123–132.
120. Y. Yin, A. Aslandukova, N. Jena, F. Trybel, I. A. Abrikosov, B. Winkler, S. Khandarkhaeva, T. Fedotenko, E. Bykova, D. Laniel, M. Bykov, A. Aslandukov, F. I. Akbar, K. Glazyrin, G. Garbarino, C. Giacobbe, E. L. Bright, Z. Jia, L. Dubrovinsky and N. Dubrovinskaia, JACS Au, 2023, 3, 1634–1641.
121. E. Bandiello, A. Lobato, F. Izquierdo, H. H. Osman, A. Muñoz, P. Rodríguez-Hernández, and F. J. Manjón, to be published.
122. L. J. Sæthre, O. Gropen, J. Sletten, T. Pedersen, L. B. Zinner, F. Lehrich, C. J. Nielsen, D. L. Powell and M. Trætteberg, Acta Chem. Scand., 1988, 42a, 16–26.
123. S. Hayashi, T. Nishide and W. Nakanishi, Heteroat. Chem., 2018, 29, 1–12.
124. P. Boettcher and U. Kretschmann, Z. Anorg. Allg. Chem., 1982, 491, 39–46.
125. D. Hirai, K. Kojima, N. Katayama, M. Kawamura, D. Nishio-Hamane and Z. Hiroi, J. Am. Chem. Soc., 2022, 144, 17857–17864.
126. S. P. Gnanasekar and E. Arunan, Aust. J. Chem., 2020, 73, 767–774.
127. K. Raghavachari, P. von R. Schleyer and G. W. Spitznagel, J. Am. Chem. Soc., 1983, 105, 5917–5918.
128. A. M. Sapse and L. Osorio, Inorg. Chem., 1984, 23, 627–628.
129. H. G. Grimm and A. Sommerfeld, Z. Phys., 1926, 36, 36–59.
130. W. Hume-Rothery, London, Edinburgh Dublin Philos. Mag. J. Sci., 1930, 9, 65–80.
131. W. B. Pearson, Acta Crystallogr., 1964, 17, 1–15.
132. T. H. Lee and S. R. Elliott, Nat. Commun., 2022, 13, 1458.
133. G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762–785.
134. I. Langmuir, J. Am. Chem. Soc., 1919, 41, 1543–1559.
135. P. von R. Schleyer, Chem. Eng. News, 1984, 62, 4.
136. L. Suidan, J. K. Badenhoop, E. D. Glendening and F. Weinhold, J. Chem. Educ., 1995, 72, 583.
137. O. J. Curnow, J. Chem. Educ., 1998, 75, 910.
138. W. B. Jensen, J. Chem. Educ., 2006, 83, 1751.
139. J. M. Galbraith, J. Chem. Educ., 2007, 84, 783.
140. B. A. Jackson, J. Harshman and E. Miliordos, J. Chem. Educ., 2020, 97, 3638–3646.
141. N. C. Norman and P. G. Pringle, Chemistry, 2022, 4, 1226–1249.
142. M. Häser, J. Am. Chem. Soc., 1996, 118, 7311–7325.
143. M. Kaupp, The Chemical Bond, John Wiley & Sons, Ltd, 2014, pp. 1–24.
144. S. J. Grabowski, Science, 2022, 4, 17.
145. A. Åström and S. Andersson, J. Solid State Chem., 1973, 6, 191–194.
146. M. Bykov, E. Bykova, M. Hanfland, H. Liermann, R. K. Kremer, R. Glaum, L. Dubrovinsky and S. van Smaalen, Angew. Chem., Int. Ed., 2016, 55, 15053–15057.
147. J. Pilmé, E. A. Robinson and R. J. Gillespie, Inorg. Chem., 2006, 45, 6198–6204.
148. S. Deng, J. Köhler and A. Simon, Angew. Chem., Int. Ed., 2006, 45, 599–602.
149. E. R. Barney, A. C. Hannon and D. Holland, J. Phys. Chem. C, 2012, 116, 3707–3718.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc04441j

‡ The properties of a solid should not be confused with those of its bonds. Solid properties emerge from the collective behavior of bonds in the structure. In solids with a single bond type, like rocksalt-type PCMs, solid properties may reflect bond properties. However, in solids with multiple bond types, such as B₂H₆, the solid's properties result from the combined response of all bonds, making it difficult to directly infer individual bond properties.

§ Notice that it would be more appropriate to say that the primary and secondary bonds mutually influence each other during the formation of a multicenter bond. This is a consequence of Newton's third law which states that for every action there is an equal and opposite reaction. Therefore, in any interaction between two objects A and B, the “action” and “reaction” refer to forces, so if object A exerts a force on object B, then object B exerts an equal amount of force on object A in the opposite direction. However, the weak secondary bond evolves as expected during the formation of a multicenter bond (it increases in strength and decreases in bond length when the multicenter interaction starts in stage 2), while the strong primary bond evolves in an unexpected or anomalous way during the formation of a multicenter bond since it decreases in strength and increases in length in stage 2. Therefore, in this manuscript, we prefer to say that the secondary bond influences the primary bond as has been understood for decades in the chemical bond terminology of supramolecular interactions. We hope that maintaining this terminology would lead chemists to a better understanding of the process of formation of multicenter bonds despite being true that in any interaction there is a mutual influence as expected from Newton's third law. Notice that our point of view is similar to the one we commonly use for the fall of an object in a gravitational field. For instance, we say that a small object falls to the Earth and not that the object and the Earth fall towards the center of mass of the compound system (object + Earth). As usual, if the change of the center of gravity of the object is much larger than the change of the center of gravity of the Earth in their travel towards the center of mass of the compound system, we use to say that the object falls to the Earth (although we all implicitly know that both object and Earth fall or attract to each other).

¶ Note that in the I4/mmm structure of BaZnSb₂ there are two different Wyckoff sites for Sb atoms (4c and 4e sites). Each independent Sb atom has a different charge. All Sb atoms in the square planar array occupy the 4c sites, so ET = 0 for Sb(4c)–Sb(4c) bonds.

|| In this work atomic multiplicity refers to crystallographic multiplicity. In crystallography, the atom multiplicity is the number of the Wyckoff site of an atom. This is different from the chemical multiplicity which is the number of possible orientations of the total spin relative to the total orbital angular momentum.

---