Variation in the zero-point energy difference via electrostatic interactions in Co(II)-Cltpy-based spin-crossover molecular materials†‡
Mousumi
Dutta
a,
Ajana
Dutta§
b,
Prabir
Ghosh§¶
*c,
Shubhankar
Maiti§
a,
Laurentiu
Stoleriu
d,
Cristian
Enachescu
d and
Pradip
Chakraborty
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Kharagpur, Kharagpur-721302, India. E-mail: pradipc@chem.iitkgp.ac.in
bDepartment of Physics, Indian Institute of Technology Kharagpur, Kharagpur-721302, India
cDepartment of Mechanical Engineering, Indian Institute of Technology Kharagpur, Kharagpur-721302, India. E-mail: prabir.chem@gmail.com
dFaculty of Physics, Al. I. Cuza University, 700506 Iasi, Romania
First published on 24th October 2024
Abstract
Herein, newly synthesized Co(II)-Cltpy-based spin-crossover molecular materials composed of ClO4−, BF4−, PF6−, and CF3SO3− are systematically investigated, emphasizing their structure–property interplay. The multi-faceted character of the ligand 4′-chloro-2,2′:6′,2′′-terpyridine (Cltpy) causes the Co(II)-based molecular materials to show electronical behavior crucial to spin crossover involving crystallographic packing and disparity in the zero-point energy difference, ΔE0HL, through electrostatic interactions mediated by their cationic and anionic moieties as well as other dipolar and quadrupolar moieties. All crystalline coordination networks were found to be phase-pure, well-crystallized, and geometrically constrained, subsequently demonstrating fascinating crystal packing along with a gradual, incomplete temperature-dependent magnetic response and negligible elastic interactions among the Co(II)-spin-crossover centers. The ClO4− and PF6− analogs showed comparatively strong intra-chain and inter-chain interactions, resulting in substantially strong effective crystal fields experienced by the Co(II)-spin-crossover centers. This indicated large positive values of ΔE0HL and their distribution with considerable stabilization of the low-spin state over the high-spin state at higher temperatures, indicating an identical magnetic response close to the pure low-spin state. Alternatively, the BF4− analog demonstrated comparatively weak intra-chain interactions without having any inter-chain interactions, resulting in moderately weak effective crystal fields around the Co(II)-spin-crossover centers. This signified negative values of ΔE0HL and their distribution towards stabilization of the high-spin state over the low-spin state, as exhibited by the enhanced magnetic response up to room temperature. In the case of the CF3SO3− analog, discrete molecular moieties were observed without any intra- and inter-molecular interactions, which was attributed to its weakest effective crystal-field strength among all the compounds reported herein, essentially signifying moderately large negative values of ΔE0HL and their distribution towards stabilization of the high-spin state over the low-spin state, as indicated by the rapid increase in the magnetic response to the greatest extent. Further, the EPR data of the reported compounds at 8 K showed an excellent fingerprint for the formation of the LS Co(II). The significant variation in the polarity of the individual counter anions played a vital role in the alteration of the crystal packing, along with varying intra-, inter-molecular, and electrostatic interactions. The experimental results were further integrated with the newly developed physically interpreted theoretical model (electrostatic-mechanoelastic model) to highlight the role of electrostatic interactions in combination with the alteration in the crystallographic packing for successfully reproducing the experimental magnetic behavior.
Introduction
Electronically switchable inorganic materials have emerged as attractive candidates due to their fascinating and novel features originating at the molecular level, which further integrate different functionalities (i.e., multifunctionality) and exhibit various stimuli-responsive properties in different structural forms and dimensions.1–5 Among them, spin-crossover molecular materials form one of the most exciting subclasses, which involve stimuli-responsive (for instance, temperature, pressure, wavelength-selective electromagnetic radiation, and electric or magnetic field) reversible rearrangement of the d-electrons between the high-spin (HS, S = 2, paramagnetic) and low-spin (LS, S = 0, diamagnetic) configurations. This yields the maximum and minimum number of unpaired electrons, respectively, distributed in the t2g (non-bonding) and (antibonding) set of d-orbitals split in a pseudo-octahedral ligand coordination environment.6–14 The thermal switching between the HS and LS states is highly sensitive to tuning the local ligand fields and essentially determined by the zero-point energy difference (ZPE), ΔE0HL, between the HS and LS manifolds and their inhomogeneous distribution.8,15–17 Additionally, in crystalline solids, the finite and non-stochastic short-range nearest-neighbor interactions among the spin-crossover active centers in superposition with the long-range elastic/magnetic interactions (i.e., mediated by electron–phonon/spin-phonon coupling and propagates via significant volume change in the ligand coordination spheres) lead to macroscopic communication across the lattice (known as cooperativity), and also tremendously influence the thermal spin-crossover behavior.5,18–24 The various aspects of the thermal spin-crossover behavior and cooperativity have been studied using different experimental techniques, for instance, structural characterization through single crystal and powder X-ray diffraction, magnetic susceptibility measurements, optical, and Mössbauer and EPR spectroscopy.12,25–29 In addition, they are also well-understood within the framework of different theoretical models developed over the past few decades.
(antibonding) set of d-orbitals split in a pseudo-octahedral ligand coordination environment.6–14 The thermal switching between the HS and LS states is highly sensitive to tuning the local ligand fields and essentially determined by the zero-point energy difference (ZPE), ΔE0HL, between the HS and LS manifolds and their inhomogeneous distribution.8,15–17 Additionally, in crystalline solids, the finite and non-stochastic short-range nearest-neighbor interactions among the spin-crossover active centers in superposition with the long-range elastic/magnetic interactions (i.e., mediated by electron–phonon/spin-phonon coupling and propagates via significant volume change in the ligand coordination spheres) lead to macroscopic communication across the lattice (known as cooperativity), and also tremendously influence the thermal spin-crossover behavior.5,18–24 The various aspects of the thermal spin-crossover behavior and cooperativity have been studied using different experimental techniques, for instance, structural characterization through single crystal and powder X-ray diffraction, magnetic susceptibility measurements, optical, and Mössbauer and EPR spectroscopy.12,25–29 In addition, they are also well-understood within the framework of different theoretical models developed over the past few decades.
To date, the experimental results obtained for spin-crossover systems have been mainly explained by using either mean field or Ising type models. However, mean field models are only suitable for bulk materials and cannot describe properties at the nanoscale, and thus they are not well adapted for systems, which are important for applications in nanodevices. Alternatively, Ising models are not realistic, and they only describe interactions in a very basic manner;30 therefore, a new class of models, namely elastic models, has been introduced.31 These models, in which the interactions are considered to originate from the difference between the volumes of the high spin and low-spin species, successfully reproduce macroscopic features such as thermal transition, photoexcitation and ultra-fast dynamics,18,19,21,32–35 together with microscopic aspects such as cluster nucleation from corners features of spin-crossover compounds.36,37
In this case, it is also important to mention that other recently performed DFT studies also successfully explained the cooperativity, crystal packing and counterion/solvent-induced effects in spin-crossover materials.19,38–40 The mechanoelastic model is primarily based on the ball-spring concept, where the spin-crossover active centers are represented by rigid, hard spheres and connected by springs in 2D or 3D, which can be elongated or compressed during thermal spin state switching. The elongation or compression occurs via a volume change in the spheres, instantaneously yielding elastic forces to the nearby springs, which eventually result in infinite possibilities of the local switching events among the spin-crossover centers. Also, the variation in the short- and long-range interactions are ascribed to the changes in the elastic spring constants.32–35,41–43
Herein, we used a newly developed modified version of the mechanoelastic model, in which besides the elastic interaction, we considered the electrostatic repulsion between charged entities in the system, thus adapting the mechanoelastic model designed initially for neutral systems to samples containing centers of net electrostatic charges. We call this new variant of our model the electrostatic-mechanoelastic model.
In spin-crossover solids, one of the most convenient ways to alter the local ligand field (hence, ΔE0HL and its variation via inhomogeneous distribution), and consequently the thermal spin state switching behavior is by varying the electrostatic interactions between the spin-crossover cations and anions, involving an alteration in the crystal packing. One of these efforts can be executed experimentally by varying the counter anions, while keeping the spin-crossover cationic moieties unaltered.44–48 Additionally, from a theoretical standpoint, one can understand this behavior based on the various electrostatic interactions applied to spin-crossover solids, i.e., by demonstrating an electrostatic-mechanoelastic model, representing an exciting variation of the mechanoelastic model considering electrostatic interactions.
N-containing ligands are the most suitable and extensively studied considering the appropriate ligand fields for tuning the stimuli-responsive spin-crossover behavior. Among them, 2,2′:6′,2′′-terpyridine-based ligand scaffolds form a fascinating subclass owing to their strong π-acceptor character, intrinsic ability to tune their structural and substituent diversity, and easy availability (either commercially or synthetically) with a wide range of applications.49–56 Concerning the substituent diversity, in particular the 4′-position offers a unique position with a wide variety and considerable inductive influence, where the diversity in crystal packing (occurs via different non-covalent interactions, such as H-bonding and π–π interactions) becomes evident depending on the nature of the 4′-substituent.50,54,57,58 In this regard, 4′-chloro-2,2′:6′,2′′-terpyridine (Cltpy) is particularly suitable, in contrast with some recent studies,50,54,58,59 for highlighting the role of the electron-withdrawing Cl-group (also serves as an additional hydrogen-bond acceptor) together with the strong π-acceptor character of the terpy-scaffold and π–π interactions via terpy in the crystallographic packing and their subsequent influence on the thermal spin-crossover behavior in newly synthesized Co(II)-Cltpy-based spin-crossover networks with different counter anions and presence of other dipolar and quadrupolar moieties in connection with the variation in the electrostatic interactions, which is lacking in the literature.
Particularly, Co(II)-based spin-crossover molecular materials were chosen in the present study given that the variation in the Co(II)–N(ligand) average bond lengths (∼0.1 Å, hence, molecular volume) and entropy difference (i.e., the spin degeneracy ratio, ΔSspin = 5.8 J K−1 mol−1, and also the ratio between electronic degeneracy and vibrational densities of state) between the S = 3/2 (i.e., t52ge2g configuration with 4T1 ground state, HS) and S = 1/2 (i.e., t62ge1g configuration with 2E ground state, LS) states is comparatively smaller than that of Fe(III) (∼0.15 Å with ΔSspin = 9.13 J K−1 mol−1) and Fe(II) (∼0.2 Å with ΔSspin = 13.38 J K−1 mol−1).17,27,48,60–62 Also, Co(II)-systems are highly sensitive to the local environment fluctuation (i.e., ΔE0HL and its variation via inhomogeneous distribution), crucially depending on the alteration in their crystal packing involving counter anions or lattice solvents.47,48,54,62,63 Furthermore, they are highly susceptible to the Jahn–Teller effect, although the cooperativity effects of elastic/magnetic origin are often marginal or absent with a few exceptions.17,60,64 In particular, Co(II)-terpy-based systems are unique (compared to Co(II)-bpy, which is a classic HS complex) in terms of their coordination motif (includes strong dependency on the second coordination sphere, i.e., counter anions or lattice solvents) and diversity in electronic structures and geometry.47,48,56,58,65,66 This involves an anisotropic bond-length variation, which occurs via the strengthened Jahn–Teller effect and responsible for the stabilization of the LS state, and eventually much less explored compared to Fe(II) and Fe(III).17,27,54,61,67 Accordingly, herein, we report the variation in the zero-point energy difference, ΔE0HL, probed via the variation in the thermal spin-crossover behavior (i.e., focusing on the structure–property interplay) in newly synthesized Co(II)-Cltpy-based spin-crossover molecular materials with different counter anions, including ClO4−, BF4−, PF6− and CF3SO3−. The experimental aspects of the structure–property interplay were illustrated by performing single crystal and powder-XRD, FTIR spectroscopy, HRMS, SQUID magnetic susceptibility and EPR measurements. The experimental results were further integrated with a newly developed modified version of the mechanoelastic model (i.e., an electrostatic-mechanoelastic model) to highlight the role of crystal packing (and its alteration with different counter anions) and its subsequent influence on the thermal spin-crossover behavior discussed within the framework of physically-interpreted electrostatic interactions (i.e., by varying the ratio between the positive and negative average electrostatic interactions), which is reported for the first time to the best of our knowledge for Co(II)-based spin-crossover molecular materials.
Experimental
Syntheses of [Co(Cltpy)2]X2, where X: ClO4− (1), BF4− (2), PF6− (3), CF3SO3− (4); Cltpy: 4′-chloro-2,2′:6′,2′′-terpyridine
Synthesis of [Co(Cltpy)2](ClO4)2 (compound 1)
Briefly, 0.092 g (0.25 mmol) of Co(ClO4)2·6H2O was added to 10 mL of methanol, and 0.135 g (0.50 mmol) of Cltpy was added to 15 mL of methanol. These two solutions were mixed and refluxed with stirring for 1 h, and subsequently cooled to room temperature. A reddish brown-colored precipitate was obtained, which was filtered and successively dried in an oven at 60 °C. To grow single crystals of compound 1, a concentrated CH3CN solution (served as the solvent) of the resultant powder material was prepared and layered carefully with diethyl ether (served as the antisolvent) in a 15 mL vial. The vial was kept undisturbed under ambient conditions for the crystallization. After approximately two weeks, compound 1 was obtained as dark red-colored crystals via the liquid-to-liquid slow diffusion process (yield: 0.175 g, 88%).Synthesis of [Co(Cltpy)2](BF4)2 (compound 2)
Compound 2 was synthesized by following an experimental protocol similar to that for compound 1, except that CoCl2·6H2O (0.06 g, 0.25 mmol) and NaBF4 (0.028 g, 0.25 mmol) were used instead. Reddish-brown-colored crystals of compound 2 were obtained via the liquid-to-liquid slow diffusion process. Specifically, a CH3CN solution (solvent) of compound 2 was layered with dichloromethane (antisolvent) in a 15 mL vial and the crystals were grown over a period of two weeks and collected (yield: 0.172 g, 90%).Synthesis of [Co(Cltpy)2](PF6)2 (compound 3)
Compound 3 was synthesized following a strategy similar to that for compound 1, except that CoCl2·6H2O (0.06 g, 0.25 mmol) and KPF6 (0.046 g, 0.25 mmol) were used instead. The liquid-to-liquid slow diffusion process was used, where a CH3CN solution (solvent) of compound 3 was layered with dichloromethane (antisolvent) in a 15 mL vial. Dark-brown-colored crystals were grown over three weeks and collected (yield: 0.192 g, 87%).Synthesis of [Co(Cltpy)2](CF3SO3)2 (compound 4)
Compound 4 was synthesized using a protocol similar to that for compound 1, except that cobalt(II) trifluoromethanesulfonate (0.089 g, 1 mmol) was used instead. Over the period of about three weeks, dark-brown-colored crystals were grown via the liquid-to-liquid slow diffusion process with a CH3CN (solvent): Et2O (antisolvent) combination and collected (yield: 0.192 g, 86%).Structural characterization
Single-crystal X-ray diffraction (SCXRD)
For all the compounds, good-quality and large single crystals were chosen under a StereoZoom optical microscope (Leica Model No. S9E) for the single-crystal X-ray diffraction measurements. The data collection for compound 1 (CCDC No. 2330712, 2330713‡), compound 2 (CCDC No. 2330714, 2330715‡), compound 3 (CCDC No. 2330716, 2330717‡), and compound 4 (CCDC No. 2330718‡) was performed on a Bruker, D8 Quest diffractometer equipped with a PHOTON II detector and monochromatic Mo-Kα X-radiation (λ = 0.71073 Å). The data collection was performed for all compounds at 295 and 100 K. The single-crystal diffraction data were collected using the standard omega scan technique and scaled, reduced, and integrated using the APEX-III software.68 The structure solution was carried out using the direct method using SHELXS-2014, and the refinement was executed by full-matrix least-squares with SHELXL-2018, refining on F2.69,70 All atoms except hydrogen were refined anisotropically. Hydrogen atoms were included in the refinement process following the riding model. All the single crystal data reported in the present work have been deposited in the Cambridge Crystallographic Data Center, and the CCDC deposition numbers are mentioned above (2330712–2330718‡) as well as in the crystallographic table (see below, Tables 1–3). The dimensions of the crystals are mentioned in the CIF files, which are 0.21 × 0.18 × 0.12 mm3 (compound 1), 0.30 × 0.27 × 0.23 mm3 (compound 2), 0.19 × 0.12 × 0.09 mm3 (compound 3) and 0.28 × 0.23 × 0.18 mm3 (compound 4).| CCDC No. | 1a | 1b | 2a | 2b |
|---|---|---|---|---|
| 2330712 | 2330713 | 2330714 | 2330715 | |
| Chemical formula | C30H20Cl4CoN6O8 | C30H20Cl4CoN6O8 | C30H20B2Cl2CoF8N6 | C30H20B2Cl2CoF8N6 |
| Formula mass | 793.25 | 793.25 | 767.97 | 767.97 |
| T [K] | 100(2) | 295(2) | 100(2) | 295(2) |
| Radiation, λ [Å] | 0.71073 | 0.71073 | 0.71073 | 0.71073 |
| Crystal system | Monoclinic | Monoclinic | Monoclinic | Monoclinic |
| Space group | C c | C c | C c | C c |
| Z | 4 | 4 | 4 | 4 |
| a (Å) | 12.7957(3) | 12.828(4) | 12.6907(4) | 12.676(2) |
| b (Å) | 12.1417(3) | 12.411(4) | 12.1730(4) | 12.390(2) |
| c (Å) | 19.8429(4) | 20.224(5) | 19.6560(6) | 19.919(3) |
| β (°) | 98.7320(10) | 97.874(18) | 98.327(2) | 97.368(11) |
| V (Å3) | 3047.09(12) | 3189.4(16) | 3004.52(17) | 3102.5(9) |
| ρ calcd (g cm−3) | 1.729 | 1.652 | 1.698 | 1.644 |
| μ (mm−1) | 0.979 | 0.935 | 0.834 | 0.808 |
| F(000) | 1604 | 1604 | 1540 | 1540 |
| 2θ range (°) for data collection | 4.154 to 80.54 | 4.066 to 80.6 | 4.66 to 54.294 | 4.124 to 80.706 |
| Completeness | 100% | 100% | 99.9% | 100% |
| Index range, h, k, l | −23 ≤ h ≥ 23 | −23 ≤ h ≥ 22 | −16 ≤ h ≥ 15 | −22 ≤ h ≥ 22 |
| −22 ≤ k ≥ 22 | −22 ≤ k ≥ 22 | −15 ≤ k ≥ 15 | −22 ≤ k ≥ 22 | |
| −36 ≤ l ≥ 36 | −36 ≤ l ≥ 36 | −25 ≤ l ≥ 25 | −36 ≤ l ≥ 36 | |
| Measured reflections | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 374 374 |
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 721 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 314 314 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 368 |
| Independent reflections | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987 987 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056 |
6382 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 412 412 |
| Restraints/parameters | 3/432 | 3/469 | 2/432 | 2/491 |
| Goodness-of-fit on F2 | 1.053 | 0.920 | 1.058 | 0.903 |
| R int | 0.0715 | 0.1267 | 0.0340 | 0.1320 |
| R 1, wR2 [I > 2σ(I)] | 0.0440, 0.0983 | 0.0635, 0.1292 | 0.0356, 0.0925 | 0.0613, 0.1302 |
| R 1, wR2 [all data] | 0.0604, 0.1048 | 0.1714, 0.1660 | 0.0365, 0.0928 | 0.1655, 0.1687 |
| Largest diff. peak/hole [e Å−3] | 1.05/−1.20 | 0.42/−0.40 | 1.06/−0.82 | 0.41/−0.45 |
| 3a | 3b | 4a | ||
|---|---|---|---|---|
| CCDC No. | 2330716 | 2330717 | CCDC No. | 2330718 |
| Chemical formula | C30H20Cl2CoF12N6P2 | C30H20Cl2CoF12N6P2 | Chemical formula | C32H20Cl2CoF6N6O6S2 |
| Formula mass | 884.29 | 884.29 | Formula mass | 892.49 |
| T [K] | 100(2) | 295(2) | T [K] | 100(2) |
| Radiation, λ [Å] | 0.71073 | 0.71073 | Radiation, λ [Å] | 0.71073 |
| Crystal system | Tetragonal | Tetragonal | Crystal system | Monoclinic |
| Space group |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c 21c |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c 21c |
Space group | C c |
| Z | 2 | 2 | Z | 4 |
| a = b (Å) | 8.9233(2) | 9.0260(14) | a (Å) | 13.1635(7) |
| — | — | b (Å) | 13.1720(7) | |
| c (Å) | 20.1704(6) | 20.444(5) | c (Å) | 19.6197(10) |
| — | — | — | β (°) | 90.674(3) |
| V (Å3) | 1606.07(9) | 1665.6(6) | V (Å3) | 3401.6(3) |
| ρ calcd (g cm−3) | 1.829 | 1.763 | ρ calcd (g cm−3) | 1.743 |
| μ (mm−1) | 0.906 | 0.874 | μ (mm−1) | 0.874 |
| F(000) | 882 | 882 | F(000) | 1796 |
| 2θ range (°) for data collection | 4.038 to 80.718 | 3.984 to 49.984 | θ range (°) for data collection | 4.152 to 80.808 |
| Completeness | 99.3% | 99.8% | Completeness | 100% |
| Index range, h, k, l | −16 ≤ h ≥ 16 | −10 ≤ h ≥ 10 | Index range, h, k, l | −23 ≤ h ≥ 23 |
| −23 ≤ k ≥ 23 | ||||
| −16 ≤ k ≥ 16 | −10 ≤ k ≥ 10 | −35 ≤ l ≥ 35 | ||
| −36 ≤ l ≥ 36 | −24 ≤ l ≥ 24 | |||
| Measured reflections | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 917 917 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121 121 |
Measured reflections | 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 320 |
| Independent reflections | 5079 | 1474 | Independent reflections | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 327 |
| Restraints/parameters | 0/123 | 0/123 | Restraints/parameters | 2/497 |
| Goodness-of-fit on F2 | 1.018 | 1.060 | Goodness-of-fit on F2 | 1.028 |
| R int | 0.0693 | 0.0908 | R int | 0.1086 |
| R 1, wR2 [I > 2σ(I)] | 0.0274, 0.0649 | 0.0258, 0.0605 | R 1, wR2 [I > 2σ(I)] | 0.0540, 0.1169 |
| R 1, wR2 [all data] | 0.0400, 0.0705 | 0.0312, 0.0618 | R 1, wR2 [all data] | 0.0965, 0.1323 |
| Largest diff. peak/hole [e Å−3] | 0.34/−0.63 | 0.18/−0.24 | Largest diff. peak/hole [e Å−3] | 0.50/−0.61 |
| 1a | 1b | 2a | 2b | 3a | 3b | 4a | |
|---|---|---|---|---|---|---|---|
| Temp. [K] | 100(2) | 295(2) | 100(2) | 295(2) | 100(2) | 295(2) | 100(2) |
| V [Å3] | 3047.09(12) | 3189.4(16) | 3004.52(17) | 3102.5(9) | 1606.07(9) | 1665.6(6) | 3401.6(3) |
| Bond lengths [Å] | |||||||
| CoII1–N1 | 1.996(2) | 2.072(4) | 1.999(4) | 2.135(3) | 2.094(11) | 2.127(2) | 2.088(3) |
| CoII1–N2 | 1.873(19) | 1.956(4) | 1.870(4) | 1.944(4) | 1.899(13) | 1.961(3) | 1.897(3) |
| CoII1–N3 | 1.989(2) | 2.081(4) | 1.995(4) | 2.128(4) | — | — | 2.082(3) |
| CoII1–N4 | 2.173(19) | 2.159(4) | 2.157(4) | 2.057(4) | — | — | 2.084(3) |
| CoII1–N5 | 1.936(19) | 1.980(4) | 1.933(4) | 1.929(4) | — | — | 1.897(3) |
| CoII1–N6 | 2.165(2) | 2.148(4) | 2.170(4) | 2.071(4) | — | — | 2.083(3) |
| Co II –N (Avg) | 2.022(19) | 2.066(4) | 2.021(4) | 2.044(4) | 1.996(13) | 2.044(3) | 2.022(3) |
| Bite angles (°) | |||||||
| ∠N1 Co1 N2 | 81.11(8) | 79.13(16) | 81.42(16) | 78.76(15) | 79.85(3) | 78.34(7) | 80.05(12) |
Powder X-ray diffraction (PXRD)
Powder X-ray diffraction (PXRD) measurements were performed to confirm the phase purity and crystallinity. Specifically, the single crystals were crushed into homogeneous bulk polycrystalline powdered samples. The powder X-ray diffraction measurements for all the as-synthesized compounds (i.e., compounds 1–4) were performed at room temperature on a Bruker D8 Advance diffractometer using a Cu-Kα radiation source in the angular range of 5° ≤ 2θ ≤ 60°, at a scan rate of 0.15° min−1. X’PERT HIGH SCORE PLUS (version 4.8) was used to analyze the PXRD patterns.71 Le Bail profile refinements were carried out in JANA2006.72 The background was estimated using a Legendre polynomial function containing 30 coefficients, and the peak shape parameters such as GU, GV, GW, LX, and LY were refined using the pseudo-Voigt function. Subsequently, the lattice parameters were obtained.Results and discussion
Scheme 1 shows the chemical structure of the 4′-chloro-2,2′:6′,2′′-terpyridine (Cltpy) ligand. The basic architecture of the ligand is based on a terpyridine-scaffold with the 4′-position occupied by the Cl atom, which is considered an important member of the terpy-family.50,73 The basic coordination motif of the ligand is tridentate (as shown by the arrows in Scheme 1), and therefore the first coordination sphere formed by two of these ligands is pseudo-octahedral with constrained geometry provided by the ligand backbone. The strong π-acceptor character of the terpy-scaffold is further accompanied by the electron-withdrawing character of the Cl-substituent with an additional possibility for another non-covalent and H-bonding acceptor through Cl and π–π interactions via terpy. Moreover, the electron-withdrawing character of the Cl-substituent also influences the σ-donor ability of the N-sites of the terpy-scaffolds. Therefore, from an electronic structure/effect standpoint, the ligand itself has multiple facets, which crucially contribute to the spin-crossover behavior of the Co(II)-based molecular materials involving crystal packing and the variation in the electrostatic interactions mediated by the cationic and anionic moieties and other dipolar and quadrupolar moieties present. | ||
| Scheme 1 Structural motif of the 4′-chloro-2,2′:6′,2′′-terpyridine (Cltpy) ligand with the coordination sites shown by arrows. | ||
FTIR
Fig. S1 (see ESI‡) shows the Fourier-transform infrared (FTIR) spectra of all the as-synthesized compounds (i.e., compounds 1–4), which are in complete agreement with the desired molecular species formed under the above-mentioned experimental conditions. The following bands shown in Fig. S1 (ESI‡) undoubtedly confirm their formation: compound 1: Co–N (νStr.) at ∼571 cm−1 (m) and Cl–O (νStr.) at ∼613 cm−1 (m) and 1077 cm−1 (s); compound 2: Co–N (νStr.) at ∼571 cm−1 (m) and B–F (νStr.) at ∼1045 cm−1 (s); compound 3: Co–N (νStr.) at ∼561 cm−1 (s) and P–F (νStr.) at ∼822 cm−1 (s) and 785 cm−1 (m) and compound 4: Co–N (νStr.) at ∼571 cm−1 (s), C–F (of –CF3) (νStr.) at ∼1256 cm−1 (s) and S–O (of –SO3) (νStr.) at ∼1140 cm−1 (s). As is known, the stimuli-responsive spin-crossover behavior is highly sensitive to the presence of lattice solvent and varies drastically to establish systematic structure–property interplay only with the different counter anions. Thus, all the Co(II)-spin-crossover molecular materials (i.e., compounds 1–4) reported herein were dehydrated and free from any lattice solvent.High-resolution mass spectrometry
The newly synthesized Co(II)-spin-crossover molecular materials (i.e., compounds 1–4) exhibit expected monocationic high-resolution mass spectra (in +ve mode, as shown in Fig. S2, ESI‡) in acetonitrile, where the monocationic species is formed upon the loss of one counter anion from each molecular moiety with the m/z of 692.98 for ClO4− (compound 1), 681.04 for BF4− (compound 2), 739.00 for PF6− (compound 3), and 742.99 for CF3SO3− (compound 4)]. The calculated average masses of the monocationic species are in excellent agreement with the experimentally observed high-resolution masses of all the reported compounds. Although the dicationic masses (i.e., M2+/2) of all the synthesized compounds are the same, due to the presence of different counter anions, their monocationic masses are different, as illustrated in Fig. S2 (ESI‡).Crystallographic studies
Single-crystal X-ray diffraction (SCXRD)
The relevant dataset obtained from the single-crystal structural analysis containing all the necessary structural refinement parameters for compounds 1–4 are listed in Tables 1 and 2, and selected bond lengths and bond angles are shown in Table 3. For convenience, the notation ‘a’ and ‘b’ mentioned in the text and figure caption below represent the structure solution and refinement for compounds 1–4 performed at 100 K and 295 K, respectively.Structure of [Co(Cltpy)2](ClO4)2
At both temperatures, compound 1 [i.e., 1a (CCDC No. 2330712‡) and 1b (CCDC No. 2330713‡)] is revealed as a mononuclear complex without any lattice solvent. This compound crystallizes in a monoclinic crystal system with the Cc space group at both temperatures (i.e., 100 K and 295 K). No change in symmetry was observed between these two temperatures, implying the absence of any first-order crystallographic phase transition down to 100 K. Fig. 1 illustrates the asymmetric unit of compound 1 at 100 K (denoted as 1a). At both temperatures (i.e., 100 K and 295 K), the asymmetric unit contains one Co(II) atom, which is adopted in a constrained octahedral coordination geometry (as mentioned above) surrounded by two tridentate Cltpy ligands. Thus, the Co(II) center is bound to six nitrogen donor atoms from the two Cltpy ligand scaffolds. The two ligands are conformationally attached to the metal center in a bis-tridentate fac fashion, resulting in a tetragonally distorted [CoN6] (i.e., compressed) octahedron. Moreover, each mononuclear species of [Co(Cltpy)2]2+ is associated with two ClO4− anions, which not only maintain the overall charge of the compound but also play a pivotal role in its crystal packing, inter-molecular interactions, and structural modulation via the variation in electrostatic interactions. Among them, one of the ClO4− anions is disordered in its two oxygen positions with an occupancy factor of 44% and 56%. Upon growing the entire structure, it forms 1D chain-like stacked crystal packing patterns, showing both intra-chain and inter-chain interactions (as shown in Fig. S3 and discussed below, ESI‡).For a better understanding of the other relevant structural parameters at 100 and 295 K, selected bond lengths and angles are listed in Tables 1 and 3. The average Co–N bond distances are 2.022 (19) Å and 2.066 (4) Å at 100 K and 295 K, respectively. This variation (i.e., by 0.044 Å) in the average metal–ligand bond length is too large for thermal contraction alone, somewhat collectively responsible for the thermal contraction (minor contribution) and thermal spin-crossover behavior (major contribution), and eventually serves as the first indication of the thermal spin-crossover phenomenon. However, the magnitude of this variation clearly indicates partial thermal spin-crossover between 295 K and 100 K and is well mapped with the magnetic susceptibility measurements discussed later. It is important to note that the axial or distal Co–N(2) and Co–N(5) bond distances involving the pyridine rings (an average of 1.905 (19) Å and 1.968 (4) Å at 100 K and 295 K, respectively) are shorter than the Co-N(1), N(3), N(4), and N(6) equatorial or central bond distances (an average of 2.081 (19) Å and 2.115 (4) Å at 100 K and 295 K, respectively). This indicates the tetragonally compressed octahedral geometry of the first coordination sphere, and in the HS state at 295 K, the coordination sphere is comparatively less distorted than in the LS state at 100 K [i.e., the manifestation of the Jahn–Teller effect].17,74 In the case of compound 1, the bite angle of ∠N1–Co1–N2 is found to be 81.11(8)° at 100 K and 79.13(16)° at 295 K (see Table 3), significantly deviating from 90°, which further supports the distortion from a regular octahedral geometry. Similarly, the other bite angles also deviate from the ideal octahedral geometry (see CCDC No. 2330712, 2330713‡).
Structure of [Co(Cltpy)2](BF4)2
A suitable reddish-brown-colored single crystal of compound 2 [i.e., 2a (CCDC No. 2330714‡) and 2b (CCDC No. 2330715‡)] was chosen for X-ray diffraction, and the data was collected at two different temperatures of 100 K (marked as 2a) and 295 K (marked as 2b). With the same ligand (Cltpy) backbone and only varying the counter anion from ClO4− to BF4−, compound 2 possesses the same asymmetric unit (shown in Fig. 2) as compound 1 in the absence of any lattice solvent. Compared to compound 1, compound 2 is also obtained as a mononuclear complex, which belongs to a monoclinic crystal system with the identical Cc space group at the two different experimental temperatures mentioned above. However, its crystallographic packing is different, as reflected by its different unit cell parameters mentioned in Table 1. Moreover, similar to compound 1, its asymmetric unit consists of one Co(II) surrounded by two tridentate Cltpy ligand moieties bonded through their N-donating sites. The cationic complex exists in an fac conformation, which causes the cationic moiety to be present in a tetragonally compressed [CoN6] octahedron. The two BF4− anions present in each mononuclear unit maintain the overall charge of the molecular entity, and also play a significant role in the crystallographic packing, intermolecular, and other electrostatic interactions. Similar to compound 1, between the two BF4− anions present in compound 2, one BF4− anion is also disordered in its two fluorine positions with occupancy factors of 46% and 54%. Additionally, the fluorine atoms are likely involved in the H-bonding interactions with the terpy-embraces of the [Co(Cltpy)2]2+ moiety. Upon growing the entire structure, it forms 1D chain-like crystal packing patterns, showing only intra-chain interactions (as shown in Fig. S4 and discussed below, ESI‡).Selected bond lengths and angles are listed below (Table 3) at two different temperatures. The average Co–N bond distances are 2.021(4) Å at 100 K and 2.044(4) Å at 295 K, respectively. As discussed above, this shortening in the average Co(II)–N bond length is also responsible for the partial thermal spin-crossover behavior and is well mapped with the magnetic susceptibility data discussed later. It is essential to note that the axial or distal Co–N(2) and Co–N(5) bond distances involving the pyridine rings (avg. 1.902 (4) Å and 1.936 (4) Å at 100 K and 295 K, respectively) are shorter than the Co–N(1), N(3), N(4), and N(6) equatorial or central bond distances (avg. 2.080 (4) Å and 2.098 (4) Å at 100 K and 295 K, respectively). This geometrically confirms the tetragonally compressed octahedral first coordination sphere as a result of the Jahn–Teller effect with comparatively less distorted HS state at 295 K than the LS state at 100 K.17,74 Similar to compound 1, the bite angle of ∠N1–Co1–N2 is 81.42(16)° at 100 K, and 78.76(15)° at 295 K (Table 3) and the other angles (see CCDC No. 2330714, 2330715‡) of compound 2 significantly deviate from the ideal octahedral geometry, further supporting the geometrical distortion. Furthermore, the identical symmetry retained at both temperatures establishes the absence of any crystallographic phase transition upon cooling or heating.
Structure of [Co(Cltpy)2](PF6)2 [3]
Changing the non-coordinating anion to PF6− (shown in Fig. 3 for compound 3) within the same embrace of [Co(Cltpy)2]2+ resulted in the formation of a single crystal with mononuclear and unsolvated lattice, [Co(Cltpy)2](PF6)2. Although the fundamental structural aspects of compound 3 were reported earlier,57 the role of the non-coordinating counter ion PF6− (together with other anions, such as ClO4−, BF4− and CF3SO3− reported herein) in its crystallographic packing and its subsequent effect on the thermal spin-crossover behavior argued experimentally and theoretically within the framework of electrostatic interactions is novel and reported for the first time herein. The single-crystal XRD data of compound 3 was recorded, solved, and refined at 100 K (i.e., 3a, CCDC No. 2330716‡) and 295 K (i.e., 3b, CCDC No. 2330717‡) (also shown in Table 2). Unlike other counter ion analogs discussed herein, at both temperatures, compound 3 crystallizes in the tetragonal space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c. Accordingly, in Fig. 3 (inset), the coordination environment around the Co(II) center is shown as the asymmetric unit, where ¼th of the molecule is displayed. Upon growing the entire structure, it forms 1D chain-like stacked crystal packing patterns (as also seen for compound 1 mentioned above), showing both intra-chain and inter-chain interactions (as shown in Fig. S5 and discussed below, ESI‡). At both temperatures, similar to compounds 1 and 2, compound 3 retains its exact crystal symmetry, implying the absence of symmetry breaking (i.e., absence of first-order crystallographic phase transition) upon cooling or heating. At 100 K and 295 K, selected bond lengths and bond angles are listed in the table below (Table 3). The average Co–N bond distances are 1.996 (13) Å at 100 K and 2.044 (3) Å at 295 K. As previously mentioned for compounds 1 and 2, this shortening in the average Co(II)–N bond length for compound 3 indicates partial thermal spin-crossover and is well-correlated with the magnetic susceptibility data discussed below.
21c. Accordingly, in Fig. 3 (inset), the coordination environment around the Co(II) center is shown as the asymmetric unit, where ¼th of the molecule is displayed. Upon growing the entire structure, it forms 1D chain-like stacked crystal packing patterns (as also seen for compound 1 mentioned above), showing both intra-chain and inter-chain interactions (as shown in Fig. S5 and discussed below, ESI‡). At both temperatures, similar to compounds 1 and 2, compound 3 retains its exact crystal symmetry, implying the absence of symmetry breaking (i.e., absence of first-order crystallographic phase transition) upon cooling or heating. At 100 K and 295 K, selected bond lengths and bond angles are listed in the table below (Table 3). The average Co–N bond distances are 1.996 (13) Å at 100 K and 2.044 (3) Å at 295 K. As previously mentioned for compounds 1 and 2, this shortening in the average Co(II)–N bond length for compound 3 indicates partial thermal spin-crossover and is well-correlated with the magnetic susceptibility data discussed below.
 | ||
| Fig. 3 Complete structural motif of compound 3 at 100 K. Inset: Asymmetric unit of compound 3 at 100 K (3a, CCDC No. 2330716‡). | ||
Structure of [Co(Cltpy)2](CF3SO3)2 [4]
A suitable single-crystal of compound 4 was chosen for the X-ray diffraction measurement, and the data is recorded at two different temperatures, i.e., 100 K (4a, CCDC No. 2330718‡) (shown in Table 2) and 295 K (4b). At 100 K, the structure was fully solved and refined with an excellent R-factor. However, the room temperature data shows a high degree of disorder, and as a result, the corresponding structural data could not be modeled. At 100 K, compound 4 is obtained as a mononuclear Co(II) complex, [Co(Cltpy)2](CF3SO3)2, with a similar structure to compounds 1 and 2. At this temperature, compound 4 crystallizes in a monoclinic crystal system (with space group Cc). Upon changing the counter anion to CF3SO3−, the crystallographic packing becomes different and can be understood based on the variation in the unit cell parameters mentioned in Table 2. The coordination environment around the Co(II) center is displayed in the asymmetric unit shown in Fig. 4. At 100 K, the asymmetric unit consists of one Co(II) atom that is bonded with the N-donor end of the two tridentate Cltpy ligands existing in a fac conformation, which forces the cationic moiety to adopt a tetragonally compressed octahedral geometry in the absence of any disorder in the structure. Upon growing the entire structure, it forms unique crystal packing with discrete individual molecular moieties without any intra- and inter-chain molecular interactions (as shown in Fig. S6 and discussed below, ESI‡). The average Co–N bond distance is 2.022 (3) Å at 100 K. The axial or distal Co–N(2) and Co–N(5) bond distances of the pyridine rings (an average of 1.897 (3) Å at 100 K) are shorter than the Co–N(1), N(3), N(4), and N(6) equatorial or central bond distances to the pyridine rings (an average of 2.084 (3) Å at 100 K), confirming the tetragonally compressed octahedral geometry of the first coordination sphere (i.e., the Jahn–Teller distortion). Moreover, the bite angle of ∠N1–Co1–N2 is 80.05(12)°, while other bite angles at 100 K (listed in Table 3 and CCDC No. 2330718‡) of compound 4 also significantly deviate from 90° (i.e., ideal octahedral geometry), further supporting the geometrical distortion from the regular octahedron.To further highlight their importance and gain insight into the various non-covalent interactions present in the reported coordination networks with different counter anions in connection with the crystallographic packing, Fig. S3–S6 (ESI‡) show the crystal packing patterns for compounds 1–4, respectively, where the relevant distances between the cationic and anionic moieties including other dipolar and quadrupolar components present are clearly illustrated. In the case of compound 1 (i.e., ClO4−) and compound 3 (i.e., PF6−), 1D chain-like stacked crystal packing patterns are formed upon growing the unit cells, where the intra-chain interactions among the Co(II)-Cltpy spin-crossover active cationic scaffolds are exhibited by the comparatively strong H-bonding interactions mediated via the ClO4−/PF6− counter anions (i.e., occurs between C–H⋯O–Cl/C–H⋯F–P with an average interaction length of ∼2.3 Å, as shown in the Fig. S3 and S5 for compound 1 and 3, respectively, ESI‡) and are effectively understood in terms of the dipolar electrostatic interactions between the cationic and anionic moieties present. Alternatively, the inter-chain interactions among the cationic moieties are further stabilized via various non-covalent π⋯π and CH⋯π interactions involving the terpy moieties and other dipolar and quadrupolar moieties (with an average interaction length of ∼3.5 Å, as shown in Fig. S3 and S5 (ESI‡) for compound 1 and 3, respectively), resulting effective strong 3D interactions between the cationic and anionic moieties combining both intra- and inter-chain interactions. Consequently, the effective crystal fields (which can be understood in terms of the superposition of the primary covalent and secondary non-covalent interactions originating from the first and second coordination spheres, respectively) experienced by the Co(II) ions are substantial, resulting in ΔE0HL and its distribution being large positive values (where the LS manifolds are comparatively more stable than the corresponding HS manifolds). Thereby, the LS state is stabilized to a large extent and is well mapped with the magnetic susceptibility behavior discussed below.
Alternatively, compound 2 (i.e., BF4−) shows a distinct 1D chain-like crystal packing pattern (shown in Fig. S4, ESI‡), involving only intra-chain interactions among the in-plane spin-crossover active Co(II)-Cltpy scaffolds mediated by the comparatively weak H-bonding interactions between C–H⋯F–B due to the larger average interaction length (i.e., more than 2.6 Å, as shown in the Fig. S4, ESI‡). The comparatively weak nature (unlike O–Cl and F–P in compounds 1 and 3, respectively) of the H-bonding is possibly attributed to the efficient back-bonding [i.e., F(2p) → B(2p), but absent in the case of O(2p)–Cl(3p) and F(2p)–P(3p)], resulting in inefficient dipolar electrostatic interactions between the cationic scaffolds and anionic moieties present in the crystal packing. Conversely, inter-chain interactions among the cationic moieties are absent due to the perpendicular (i.e., out-of-plane) arrangement of the other Co(II)-Cltpy scaffolds. Consequently, the aforementioned effective crystal fields experienced by the Co(II) ions are moderately weak, resulting in ΔE0HL and its distribution being negative values (where the HS manifolds are more stable than the corresponding LS manifolds). Thereby, the HS state is stabilized to a moderate extent and is well-matched with the magnetic susceptibility behavior discussed later.
Finally, compound 4 (i.e., CF3SO3−) distinctly shows a different crystal packing (shown in Fig. S6, ESI‡), where unlike compounds 1, 2, and 3, no intra- and inter-chain molecular interactions are present. Instead, discrete individual molecular moieties are observed, which result in the weakest aforementioned effective crystal-field strength among the four compounds, signifying ΔE0HL and its distribution towards moderately large negative values (where the HS manifolds are more stable than the corresponding LS manifolds). Thereby, the HS state is stabilized to a large extent and is well-correlated with the magnetic susceptibility behavior discussed later.
Therefore, the overall variation in the crystallographic packing largely influences the various intra- and inter-molecular interactions (occurs via H-bonding and CH–π and π–π interactions), which can be effectively understood in terms of electrostatic interactions mediated by the cationic and anionic moieties, including other dipolar and quadrupolar moieties in combination with the significant variation in the polarity of the counter anions (i.e., ClO4−, BF4−, PF6−, and CF3SO3−). Also, the extent of their dipolar interactions during crystallographic packing collectively regulates the thermal spin switching behavior via the variation in the zero-point energy difference, ΔE0HL, and its inhomogeneous distribution (i.e. structure–property interplay).
Powder X-ray diffraction (PXRD)
To investigate the phase purity and crystallinity of the synthesized bulk powdered materials, laboratory PXRD data was collected for polycrystalline bulk samples of compounds 1–4. Fig. 5 shows the room temperature PXRD data of the powdered bulk samples (i.e., compounds 1–4) and their comparison with the individual simulated patterns obtained from the single-crystal XRD data. Indexing of the experimental powder patterns was carried out using the HighScore Plus software (version 4.8), and the major peaks are illustrated in Fig. 5. According to Fig. 5, it is evident that for each compound, its experimental powder pattern well-matches with the simulated pattern and well-crystallized, as indicated by the presence of distinct Bragg peaks. Subsequently, Le Bail profile refinement of the powder-XRD data was carried out using the JANA 2006 software, considering the structural models obtained from the single-crystal data for each compound (i.e., compounds 1–4). In the case of compounds 1 and 2, Le Bail profile refinement was performed on a monoclinic crystal system with the Cc space group (Z = 4), employing the room temperature cell parameters obtained from single-crystal XRD, for instance, a = 12.828(4) Å, b = 12.411(4) Å, c = 20.224(5) Å, β = 97.874(18)° (for compound 1) and a = 12.676(2) Å, b = 12.390(2) Å, c = 19.919(3) Å and β = 97.368(11)° (for compound 2). The refined cell parameters are a = 12.7686(3) Å, b = 12.3473(3) Å, c = 20.1339(10) Å, β = 97.8424(3)° (for compound 1) and a = 12.6723(6) Å, b = 12.3921(6) Å, c = 19.8961(15) Å and β = 97.2732(6)° (for compound 2). Fig. S7 in the ESI‡ shows the fitted profile of compound 1 (Rp = 0.87, Rwp = 1.35, and χ2 = 1.50) and compound 2 (Rp = 0.66, Rwp = 0.91, and χ2 = 1.21). In the case of compound 3, the refinement was carried out using a tetragonal crystal system with the P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c (Z = 2) space group, applying the room temperature cell parameters obtained from single-crystal XRD, such as a = b = 9.026(14) Å and c = 20.444(5) Å and the refined cell parameters are a = b = 9.0287(1) Å and c = 20.4853(5) Å. Additionally, the fitted profile of compound 3 (Rp = 0.96, Rwp = 1.68, χ2 = 2.51) is presented in Fig. S7 in the ESI.‡
21c (Z = 2) space group, applying the room temperature cell parameters obtained from single-crystal XRD, such as a = b = 9.026(14) Å and c = 20.444(5) Å and the refined cell parameters are a = b = 9.0287(1) Å and c = 20.4853(5) Å. Additionally, the fitted profile of compound 3 (Rp = 0.96, Rwp = 1.68, χ2 = 2.51) is presented in Fig. S7 in the ESI.‡
In the case of compounds 1–3, we employed their room temperature structural models for the powder-XRD refinement. On the contrary, for compound 4, we applied the low-temperature single-crystal data for the PXRD profile refinement given that we could not obtain a meaningful structure at room temperature due to its high degree of disorder. The cell parameters used for the refinement in a monoclinic crystal system with the Cc space group are a = 13.1635(7) Å, b = 13.172(7) Å, c = 19.6197(10) Å and β = 90.674(3)°. The refined cell parameters are a = 13.2964(7) Å, b = 13.3015(6) Å, c = 19.7614(10) Å and β = 90.9801(4)°. The fitted profile of compound 4 (Rp = 0.91, Rwp = 1.56, and χ2 = 2.33) is shown in Fig. S7 in the ESI.‡
After performing all the refinement procedures, the experimental, calculated, and difference powder-XRD profiles are illustrated in Fig. S7 in the ESI.‡ The changes in the unit cell parameters for all the compounds (i.e., compounds 1–4) were obtained by following the profile refinement of the individual compounds, where the observed and calculated patterns are in excellent agreement, unequivocally indicating the phase purity of compounds 1–4. This is further reflected by the excellent χ2 (GOF) value of each compound (i.e., compounds 1–4). The details of the fitted profiles and resulting refined cell parameters are listed in Table 4. Additionally, the powder-XRD data represents a collective average over many crystallites of different sizes with random orientations, while the single-crystal data are collected and measured for a large crystallite, resulting in an experimental variation in the lattice parameters, as observed between the single-crystal XRD and powder-XRD data mentioned herein.
| Compound | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Crystal system | Monoclinic | Monoclinic | Tetragonal | Monoclinic |
| Space group | C c | C c |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c 21c |
C c |
| Refined cell parameters | a = 12.7686(3) Å | a = 12.6723(6) Å | a = b = 9.0287(1) Å | a = 13.2964(7) |
| b = 12.3473(3) Å | b = 12.3921(6) Å | c = 20.4853(5) Å | b = 13.3015(6) | |
| c = 20.1339(10) Å | c = 19.8961(15) Å | α = β = γ = 90° | c = 19.7614(10) | |
| β = 97.8424(3)° | β = 97.2732(6)° | β = 90.9801(4) | ||
| R p | 0.87 | 0.66 | 0.96 | 0.91 |
| R wp | 1.35 | 0.91 | 1.68 | 1.56 |
| χ 2 | 1.50 | 1.21 | 2.51 | 2.33 |
Magnetic properties
The magnetic behavior of compounds 1–4 is illustrated in Fig. 6 and represented as the temperature dependence of the product of molar magnetic susceptibility (χM) and temperature (T). In the case of all the compounds, their χMT values are temperature dependent, showing gradual thermal spin-crossover between 10 and 295 K. However, the nature of the magnetic curves changes with a variation in the counter anions present outside the first coordination sphere of [Co(Cltpy)2]2+ (i.e., ClO4−, BF4−, PF6−, and CF3SO3−, respectively).45,46,75,76 The gradual variation of the magnetic susceptibility as a function of temperature in connection with the thermal spin-crossover behavior is often understood by (a) the small variation in the metal–ligand bond length between the HS and LS states, (b) the small variation in the change in enthalpy, ΔH0HL, and entropy, ΔS0HL, and (c) the smaller electronic degeneracy ratio and small difference in the vibrational frequencies between the HS and LS manifolds, leading to smaller vibrational densities of states and smaller range in the ligand-field strength for which SCO is expected.17,27,48,62 Altogether, they result in negligible elastic interactions among the Co(II)-SCO centers, which is attributed to the gradual nature of the spin-crossover behavior without showing any pronounced cooperative character, except where the lowering in symmetry due to significant Jahn–Teller distortion in the LS state leads to cooperativity.17,77 Moreover, due to the smaller range in the ligand-field strength, the thermal spin-crossover behavior is highly sensitive to the fluctuation in the local environment (thus, ΔE0HL and its variation) involving the variation in the nature of counter anions and any solvent molecules present in the lattice (i.e., variation in the second coordination sphere). In contrast to Fe(II)-based HS or SCO molecular materials,48,60,67 where the HS state is favored mainly at higher temperatures due to the significant contribution of the configurational entropy (i.e., ΔS0HL is large), leading to negligible LS population at the higher temperature, for Co(II)-based SCO molecular materials, the absence of a large entropic variation (i.e., due to small ratio of the spin/orbital degeneracy and vibrational densities of states triggering small differences in the electronic properties between the HS and LS states) leads to various degrees of LS population (by varying the zero-point energy difference, ΔE0HL) even at higher temperature, as observed for compounds 1–4 in Fig. 6. | ||
| Fig. 6 Product of molar magnetic susceptibility and temperature plotted as a function of temperature between 10 K and 295 K for compounds 1–4. | ||
Compounds 1 and 3 show almost identical magnetic behavior irrespective of the different counter anions present and reach the minimum χMT value of 0.43 cm3 mol−1 K between 10 and 150 K, indicating a fully thermally relaxed LS state, and therefore the occurrence of this plateau is due to the thermal stabilization of the 2E (LS) state. Above 150 K, the χMT values increase slowly and gradually and reach the value of 1.26 cm3 mol−1 K at 295 K, which is much lower than the spin-only contribution (i.e., 1.90 cm3 mol−1 K) of the 4T1 HS state of Co(II), implying that both compounds 1 and 3 undergo incomplete thermal spin transition with a large fraction of LS population at 295 K. Alternatively, for compounds 2 and 4, the changes in the magnetic susceptibility values are more pronounced (i.e., shows strong temperature dependence), but gradual upon cooling and heating between 295 K and 10 K. At 10 K, upon cooling, compounds 2 and 4 reach the minimum χMT values of 0.51 and 0.57 cm3 mol−1 K respectively, indicating that all their Co(II) centers are in the LS state. On heating, their magnetic susceptibility increases rapidly and exponentially and reaches the value of 2.23 and 2.81 cm3 mol−1 K, respectively, at 295 K (i.e., significantly higher than the spin-only contribution), indicating an entropy-driven thermal population transfer to the 4T1 (HS) states of the Co(II) center. The enhanced magnetic susceptibility values in the HS state are in in good agreement with the earlier reports56,78–82 and attributed to the significant orbital contribution to the magnetic moment with additional possibilities for first-order and second-order spin–orbit coupling process (occurs via considerable configuration interactions in the 4T1 (HS) states between the ground (t52ge2g) and excited (t42ge3g) state configurations) in these pseudo-octahedral Co(II)-based spin-crossover molecular materials, together with the electrostatic interactions between the cationic and anionic moieties, crystal packing and high sensitivity to the crystal-field fluctuation, local structural alteration and accompanying distortion, and ion disorder.65,74
Comparing the temperature-dependent magnetic behavior of all the compounds, it is important to note that compounds 1 and 3 have a much stronger tendency to stabilize the LS state than compounds 2 and 4 simply by tuning the ΔE0HL, resulting in a shift in the spin transition temperature (T1/2) towards a higher temperature by a large extent. Thus, upon varying the counter anions, these Co(II)-based spin-crossover molecular materials become progressively LS stabilized and the variation in ΔE0HL and its inhomogeneous distribution towards positive values follows the order of PF6− ≈ ClO4− > BF4− > CF3SO3−. As discussed above, this behavior is also well-argued and well mapped with the variation in crystallographic packing and its subsequent influence. Moreover, the initial sloppy nature of the magnetic curves for compounds 2 and 4 below 150 K (tentatively similar to other earlier reports17,47,83,84) is tentatively assigned to the spin–orbit coupling in combination with the high sensitivity to the crystal-field fluctuation, resulting in a small spin-split energy, local structural alteration, and accompanying distortion experienced by the Co(II)-SCO centers, which strongly influences the temperature-dependent variation in ΔH0HL and ΔS0HL.85 However, the exact origin of this behavior is unknown at the moment and is subject to future research. The following model section further highlights the role of electrostatic interactions in combination with the crystal packing and reproduces the experimental magnetic behavior successfully within the framework of an electrostatic-mechanoelastic model, i.e., the mechanoelastic model argued based on electrostatic consideration.
EPR spectroscopy
Compounds 1–4 all exhibit anisotropic metal-based EPR spectra (shown in Fig. 7) in the solid state (i.e., powder form) at 8 K. Compound 3 shows fully resolved hyperfine splitting with eight lines (2nI + 1, n = 1, and I = 7/2) originating from the interaction between the electron spin of Co(II) and the spin of the 59Co(I = 7/2) nucleus.86 However, compounds 1, 2, and 4 display partially resolved hyperfine splitting. The peak near 1635 Gauss corresponds to the g-tensor of 4.245 in all the compounds due to the background. The 〈g〉 in the range of 2.070–2.119 is consistent with the LS Co(II) center present in all the reported compounds. The 〈g〉 deviates from the free electron value of 2.0023. A high Δg and large hyperfine spectra (Table S1 and Fig. 7, ESI‡) indicate metal-based spectra.17,87 The rhombic nature of the EPR spectrum suggests that the LS Co(II) center presents a distorted octahedral geometry in all the compounds, as further supported by the different Co(II)–N distances, N–Co(II)–N angles (shown in Tables 1–4) and magnetic orbitals, which are an admixture of dx2–y2 and dz2 orbitals.47Model
The mechanoelastic model has been used to explain several experimentally observed behaviors of spin-crossover materials at different time scales ranging from quasistatic magnetic processes, such as hysteresis, to femtosecond effects due to the propagation of elastic perturbations, and under different external stimuli such as pressure, temperature, and light excitation, in both 2D and 3D configurations.34,36,42,88,89This model describes the samples as networks of spring-connected spheres, where the spheres depict the spin-crossover molecules and the springs represent the bonds between them. The low-spin (LS) and the high-spin (HS) states of each molecule are characterized by different radii of the associated sphere, with the radius of a high-spin sphere being 10% greater than that of the low-spin radius.
Overall, the model has two main stages, as follows:
-in the first stage, we start from known values of physical parameters such as temperature and local pressure acting on each molecule, and then we estimate which molecules switch their state by using a set of two probabilities (switching probability from LS to HS and from HS to LS) characteristic to each molecule i, as follows:
where τ is a normalization factor, D marks the energy difference between the LS and HS states, T is the sample temperature, kB
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g gives the entropy difference between the states, Ea is the HS state activation energy and p(i) is the local pressure force acting on the ith spin-crossover center, while κ is a constant scaling factor, which controls the local pressure effect on the probabilities.
g gives the entropy difference between the states, Ea is the HS state activation energy and p(i) is the local pressure force acting on the ith spin-crossover center, while κ is a constant scaling factor, which controls the local pressure effect on the probabilities.
The probabilities are checked using a Monte Carlo approach and this first step ends when all the molecules have been verified once and all their radii have been updated.
-The second stage is solving the differential equations of motion for the entire sample to find the equilibrium position of each molecule considering the radius changes dictated by the first stage, as follows:
Going through these two stages represents one time-step of the model.
The systems described herein have as a particularity the presence of net electrostatic charges, which bring new interaction between the molecules. Thus, besides the already described elastic interactions, which are included as local mechanical pressure terms acting on each molecule due to its position relative to its neighbors, we also consider a new pressure term originating from the electrostatic interactions between each molecule and all the other positive and negative electrostatic charges in the sample.
To study the effect of this type of interactions on the spin-crossover systems in the framework of a new variant of our model, the electrostatic-mechanoelastic model, we depicted the samples as networks of 9900 spheres, with each sphere experiencing a local elastic interaction term and a supplementary interaction term, as follows:
| p(i) = p(i)elastic + p(i)electrostatic |
Although the pressure term that originates from the elastic interactions, p(i)elastic, is permanently updated as a function of the radii and positions of the neighbors, the p(i)electrostatic term is considered to be constant and independent of the spin state or temperature due to its origins in the electrostatic long-range interactions.
Although the sample as a whole is electrostatically neutral, this constant interaction term was chosen to be positive for 50% of the molecules and negative for the other 50%, while to account for different inhomogeneities, the values of the positive and negative interactions are normally distributed.
We considered three cases to account for three different relative local conditions including the average positive interaction is larger, equal, or smaller than the absolute average negative interaction value, as depicted by the histograms in Fig. 8.
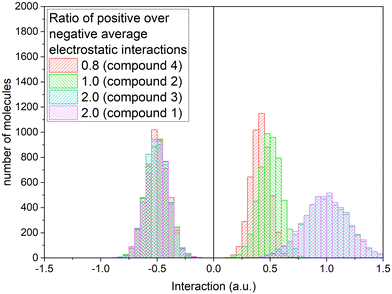 | ||
| Fig. 8 Histograms of the electrostatic interaction terms for three values of the ratio between the average positive interactions over the average negative interactions. | ||
With these constant interaction terms assigned to each molecule, the evolution of the systems with a change in temperature is represented in Fig. 9, showing the increasing LS stabilization effect due to the increase in the ratio between the positive and negative electrostatic interactions, i.e., highest for PF6− (compound 3) and ClO4− (compound 1) analogs and progressively decreases towards BF4− (compound 2) and the minimum for CF3SO3− (compound 4) analog. Therefore, the given ratio mentioned here directly governs the variation in ΔE0HL and its inhomogeneous distribution. Moreover, the deviation observed between the experimental and simulated curves is qualitatively attributed to the assumption that at low temperatures, both ΔH0HL and ΔS0HL are considered essentially temperature independent; however, in practice, these thermodynamic parameters are strongly temperature dependent, which is possibly due to the spin–orbit coupling in combination with the high sensitivity in the ligand-field fluctuation, resulting in a small spin-split energy, local structural alteration, and accompanying distortion experienced by the Co(II)-SCO centers.
Conclusions
The newly synthesized Co(II)-Cltpy-based spin-crossover molecular materials with different counter anions including ClO4−, BF4−, PF6− and CF3SO3− are phase pure, well-crystallized, geometrically constrained, and demonstrate fascinating crystal packing patterns. Furthermore, they provided insight into the various non-covalent interactions in combination with the significant variation in the polarity of the counter anions. The ClO4− and PF6− analogs showed a comparatively potent combination of intra-chain H-bonding and inter-chain π⋯π and CH⋯π interactions, which strongly influence the effective crystal-field strengths around the Co(II)-spin-crossover centers. This results in the significant stabilization of the low-spin manifolds over the high-spin ones with large positive values of ΔE0HL and their distribution. Alternatively, the BF4− analog exhibited comparatively weak intra-chain H-bonding interactions without showing any inter-chain molecular interactions, resulting in a moderately weak effective crystal field around the Co(II)-centers, which indicates negative values of ΔE0HL and their distribution with the stabilization of the high-spin population over low-spin. In contrast, the CF3SO3− analog showed discrete molecular entities without exhibiting intra- and inter-chain molecular interactions, causing the weakest effective crystal-field strength around the Co(II)-centers among the compounds. Eventually, it exhibited stabilization of the high-spin over the low-spin states to a large extent, accompanying moderately large negative values of ΔE0HL and their distribution. Similarly, the enhanced magnetic response for the BF4− and CF3SO3− analogs was attributed to the significant orbital contribution to the magnetic moment for the largely stabilized high-spin states with additional possibilities for first-order and second-order spin–orbit coupling. Alternatively, for the ClO4− and PF6− analogs, their much lower magnetic response indicated considerable stabilization of the low-spin state at a higher temperature by varying ΔE0HL and its distribution towards positive values. Overall, the gradual and incomplete temperature-dependent magnetic response and negligible elastic interactions among the Co(II)-spin-crossover centers, was attributed to the slight variation in the metal–ligand bond length and change in enthalpy and entropy between the two spin-manifolds, together with the contribution from the smaller electronic degeneracy ratio and vibrational densities of states. The EPR data of the reported spin-crossover molecular materials at 8 K further showed excellent agreement with the formation of the desired LS Co(II) moieties with characteristic fingerprints. Further, the physically-interpreted electrostatic-mechanoelastic model was implemented for the first time to highlight the role of electrostatic interactions (i.e., the ratio between the positive and negative average electrostatic interactions) in combination with the alteration in the crystallographic packing among these coordination networks for successfully reproducing the experimental magnetic behavior. Therefore, the combined experimental and the electrostatic-mechanoelastic model studies notably establish a promising variation of the structure–property interplay in the newly synthesized Co(II)-based spin-crossover molecular materials reported to date.Author contributions
MD performed all the new materials syntheses, data collection, characterizations, magnetic data analysis and writing of the manuscript; AD performed all the PXRD data analysis and manuscript writing; PG performed all the SCXRD and EPR data analysis and manuscript writing; SM assisted with the syntheses, crystal growth and data collection; LS and CE performed the electrostatic-mechanoelastic model simulation and the corresponding data analysis and writing the model section of the manuscript. The entire manuscript was structured, edited and finalized with contributions from all authors. The entire project was conceived and supervised by PC and finally, the manuscript was edited, and finalized by PC. All the authors approved the final version of the manuscript for publication.Data availability
The data supporting this article have been included as part of the ESI.‡Conflicts of interest
All authors declare no conflicts of interest.Acknowledgements
Prof. Malcolm Halcrow, Department of Chemistry, University of Leeds, UK is gratefully acknowledged for providing the ligand. M. D. and S. M. gratefully acknowledge IIT Kharagpur for their research fellowship. We acknowledge Department of Chemistry, IIT Kharagpur, for the single-crystal XRD, Powder-XRD, FTIR and HRMS facilities. P. G. acknowledges the financial support from SERB NPDF (Grant No. PDF/2021/004430/CS). A. D. acknowledges the financial support from CSIR RA (Grant No. 09/0081 (18484)/2024-EMR-I). P. C. sincerely acknowledges the financial support from SERB (Grant no. ECR/2018/000923) and IIT Kharagpur (Grant no. IIT/SRIC/CY/ENE/2018-19/194). We also acknowledge the SQUID-VSM magnetometer and EPR facility at the Central Research Facility, IIT Kharagpur. Finally, we sincerely thank Dr D. Banerjee, Department of Physics, IIT Kharagpur, Dr S. Mandal, and Dr S. Mishra, Department of Chemistry, IIT Kharagpur for the helpful discussion.References
- A. B. Gaspar, V. Ksenofontov, M. Seredyuk and P. Gütlich, Coord. Chem. Rev., 2005, 249, 2661–2676 CrossRef CAS.
- D. Maspoch, D. Ruiz-Molina and J. Veciana, Chem. Soc. Rev., 2007, 36, 770–818 RSC.
- H. Phan, S. M. Benjamin, E. Steven, J. S. Brooks and M. Shatruk, Angew. Chem., 2015, 127, 837–841 CrossRef.
- J. Ge, Z. Chen, L. Zhang, X. Liang, J. Su, M. Kurmoo and J. Zuo, Angew. Chem., 2019, 131, 8881–8885 CrossRef.
- A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313–3335 RSC.
- O. Sato, Nat. Chem., 2016, 8, 644–656 CrossRef CAS PubMed.
- ed. P. Gütlich and H. A. Goodwin, Spin crossover in transition metal compounds, Springer, Berlin, New York, 2004 Search PubMed.
- P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054 CrossRef.
- A. Hauser, Chem. Phys. Lett., 1986, 124, 543–548 CrossRef CAS.
- Y.-S. Meng and T. Liu, Acc. Chem. Res., 2019, 52, 1369–1379 CrossRef CAS PubMed.
- K. S. Kumar and M. Ruben, Angew. Chem., Int. Ed., 2021, 60, 7502–7521 CrossRef CAS PubMed.
- P. Gütlich, A. B. Gaspar and Y. Garcia, Beilstein J. Org. Chem., 2013, 9, 342–391 CrossRef.
- A. Šagátová, B. Brachňaková and I. Šalitroš, Acta Chim. Slov., 2023, 16, 22–40 CrossRef.
- J.-F. Létard, J. Mater. Chem., 2006, 16, 2550–2559 RSC.
- X. Li, D. Zhang, Y. Qian, W. Liu, C. Mathonière, R. Clérac and X. Bao, J. Am. Chem. Soc., 2023, 145, 9564–9570 CrossRef CAS.
- M. Halcrow, Crystals, 2016, 6, 58 CrossRef.
- I. Krivokapic, M. Zerara, M. L. Daku, A. Vargas, C. Enachescu, C. Ambrus, P. Tregenna-Piggott, N. Amstutz, E. Krausz and A. Hauser, Coord. Chem. Rev., 2007, 251, 364–378 CrossRef CAS.
- H. Spiering, K. Boukheddaden, J. Linares and F. Varret, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 184106 CrossRef.
- H. Banerjee, M. Kumar and T. Saha-Dasgupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 174433 CrossRef.
- Y.-F. Deng, Y.-N. Wang, X.-H. Zhao and Y.-Z. Zhang, Dalton Trans., 2024, 53, 699–705 RSC.
- M. Nishino, K. Boukheddaden, Y. Konishi and S. Miyashita, Phys. Rev. Lett., 2007, 98, 247203 CrossRef PubMed.
- N. Willenbacher and H. Spiering, J. Phys. C: Solid State Phys., 1988, 21, 1423–1439 CrossRef.
- S. Brooker, Chem. Soc. Rev., 2015, 44, 2880–2892 RSC.
- H. Shahed, N. Sharma, M. Angst, J. Voigt, J. Perßon, P. Prakash, K. W. Törnroos, D. Chernyshov, H. Gildenast, M. Ohl, G. Saffarini, A. Grzechnik and K. Friese, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2023, 79, 354–367 CrossRef CAS PubMed.
- M. J. Wallis, A. R. Craze, H. Zenno, R. Tokunaga, T. Taira, H. Min, M. M. Bhadbhade, S. K. Bhattacharyya, R. Tian, A. M. Rich, S. Hayami, J. K. Clegg, C. E. Marjo, L. F. Lindoy and F. Li, J. Mater. Chem. C, 2023, 11, 8908–8918 RSC.
- M. Grzywa, R. Röβ-Ohlenroth, C. Muschielok, H. Oberhofer, A. Błachowski, J. Żukrowski, D. Vieweg, H.-A. K. Von Nidda and D. Volkmer, Inorg. Chem., 2020, 59, 10501–10511 CrossRef CAS.
- C. Enachescu, I. Krivokapic, M. Zerara, J. A. Real, N. Amstutz and A. Hauser, Inorg. Chim. Acta, 2007, 360, 3945–3950 CrossRef CAS.
- P. Chakraborty, C. Enachescu, C. Walder, R. Bronisz and A. Hauser, Inorg. Chem., 2012, 51, 9714–9722 CrossRef CAS PubMed.
- S. Ou, C. Wu, Z. Fan, J. Chen, H. Tian and X. Bao, Cryst. Growth Des., 2023, 23, 3275–3283 CrossRef CAS.
- C. Enachescu and W. Nicolazzi, C. R. Chim, 2018, 21, 1179–1195 CrossRef CAS.
- R. Traiche, H. Oubouchou and K. Boukheddaden, Crystals, 2023, 13, 937 CrossRef CAS.
- C. Enachescu, M. Nishino, S. Miyashita, A. Hauser, A. Stancu and L. Stoleriu, EPL, 2010, 91, 27003 CrossRef.
- C. Enachescu and A. Hauser, Phys. Chem. Chem. Phys., 2016, 18, 20591–20599 RSC.
- L. Stoleriu, P. Chakraborty, A. Hauser, A. Stancu and C. Enachescu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 134102 CrossRef.
- H. Spiering, E. Meissner, H. Köppen, E. W. Müller and P. Gütlich, Chem. Phys., 1982, 68, 65–71 CrossRef CAS.
- L. Stoleriu, M. Nishino, S. Miyashita, A. Stancu, A. Hauser and C. Enachescu, Phys. Rev. B, 2017, 96, 064115 CrossRef.
- M. Nishino, C. Enachescu, S. Miyashita, P. A. Rikvold, K. Boukheddaden and F. Varret, Sci. Rep., 2011, 1, 162 CrossRef CAS PubMed.
- S. Vela and H. Paulsen, Inorg. Chem., 2018, 57, 9478–9488 CrossRef CAS.
- H. Paulsen, Magnetochemistry, 2016, 2, 14 CrossRef.
- L. Kreutzburg, C. Hübner and H. Paulsen, Materials, 2017, 10, 172 CrossRef PubMed.
- C. Enachescu, M. Nishino, S. Miyashita, L. Stoleriu and A. Stancu, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 054114 CrossRef.
- C. Enachescu, L. Stoleriu, A. Stancu and A. Hauser, Phys. Rev. Lett., 2009, 102, 257204 CrossRef PubMed.
- C. Enachescu, L. Stoleriu, A. Stancu and A. Hauser, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 104114 CrossRef.
- Y.-H. Luo, G.-J. Wen, L.-S. Gu, M.-N. Wang and B.-W. Sun, Polyhedron, 2017, 121, 101–106 CrossRef CAS.
- J. A. Kitchen, N. G. White, G. N. L. Jameson, J. L. Tallon and S. Brooker, Inorg. Chem., 2011, 50, 4586–4597 CrossRef CAS PubMed.
- M. Yamada, H. Hagiwara, H. Torigoe, N. Matsumoto, M. Kojima, F. Dahan, J. Tuchagues, N. Re and S. Iijima, Chem. - Eur. J., 2006, 12, 4536–4549 CrossRef CAS.
- P. Nielsen, H. Toftlund, A. D. Bond, J. F. Boas, J. R. Pilbrow, G. R. Hanson, C. Noble, M. J. Riley, S. M. Neville, B. Moubaraki and K. S. Murray, Inorg. Chem., 2009, 48, 7033–7047 CrossRef CAS PubMed.
- A. B. Gaspar, M. C. Muñoz, V. Niel and J. A. Real, Inorg. Chem., 2001, 40, 9–10 CrossRef CAS PubMed.
- C. Wei, Y. He, X. Shi and Z. Song, Coord. Chem. Rev., 2019, 385, 1–19 CrossRef CAS PubMed.
- J. Chambers, B. Eaves, D. Parker, R. Claxton, P. S. Ray and S. J. Slattery, Inorg. Chim. Acta, 2006, 359, 2400–2406 CrossRef CAS.
- H. Hofmeier and U. S. Schubert, Chem. Soc. Rev., 2004, 33, 373–399 RSC.
- D. J. Hathcock, K. Stone, J. Madden and S. J. Slattery, Inorg. Chim. Acta, 1998, 282, 131–135 CrossRef CAS.
- G. A. Bhat, A. Rajendran and R. Murugavel, Eur. J. Inorg. Chem., 2018, 795–804 CrossRef.
- S. Hayami, Y. Komatsu, T. Shimizu, H. Kamihata and Y. H. Lee, Coord. Chem. Rev., 2011, 255, 1981–1990 CrossRef CAS.
- S. Hayami, M. Nakaya, H. Ohmagari, A. S. Alao, M. Nakamura, R. Ohtani, R. Yamaguchi, T. Kuroda-Sowa and J. K. Clegg, Dalton Trans., 2015, 44, 9345–9348 RSC.
- F. Kobayashi, Y. Komatsumaru, R. Akiyoshi, M. Nakamura, Y. Zhang, L. F. Lindoy and S. Hayami, Inorg. Chem., 2020, 59, 16843–16852 CrossRef CAS PubMed.
- E. C. Constable, K. Harris, C. E. Housecroft, M. Neuburger and J. A. Zampese, CrystEngComm, 2010, 12, 2949–2961 RSC.
- D. Shao, Z. Ruan, J. Dong, L. Huang, M. You, J. Yang and L. Shi, J. Mol. Struct., 2023, 1294, 136548 CrossRef CAS.
- G. Zhang, J. Tan, Y. Z. Zhang, C. Ta, S. Sanchez, S.-Y. Cheng, J. A. Golen and A. L. Rheingold, Inorg. Chim. Acta, 2015, 435, 147–152 CrossRef CAS.
- H. A. Goodwin, Spin Crossover in Transition Metal Compounds II, Topics in Current Chemistry, Springer, Berlin, Heidelberg, 2004, vol. 234, pp. 23–47 Search PubMed.
- P. Thuery, J. Zarembowitch, A. Michalowicz and O. Kahn, Inorg. Chem., 1987, 26, 851–855 CrossRef CAS.
- S. Hayami, Y. Shigeyoshi, M. Akita, K. Inoue, K. Kato, K. Osaka, M. Takata, R. Kawajiri, T. Mitani and Y. Maeda, Angew. Chem., Int. Ed., 2005, 44, 4899–4903 CrossRef CAS.
- H. Zenno, F. Kobayashi, M. Nakamura, Y. Sekine, L. F. Lindoy and S. Hayami, Dalton Trans., 2021, 50, 7843–7853 RSC.
- D. Shao, L. Shi, F.-X. Shen, X.-Q. Wei, O. Sato and X.-Y. Wang, Inorg. Chem., 2019, 58, 11589–11598 CrossRef CAS PubMed.
- R. Sieber, S. Decurtins, H. Stoeckli-Evans, C. Wilson, D. Yufit, J. A. K. Howard, S. C. Capelli and A. Hauser, Chem. – Eur. J., 2000, 6, 361–368 CrossRef CAS.
- M. Nakaya, R. Ohtani, J. W. Shin, M. Nakamura, L. F. Lindoy and S. Hayami, Dalton Trans., 2018, 47, 13809–13814 RSC.
- P. Guionneau, M. Marchivie, G. Bravic, J.-F. Létard and D. Chasseau, J. Mater. Chem., 2002, 12, 2546–2551 RSC.
- APEX Suite of Crystallographic Software, APEX 3 Version 2015-5.2, Bruker AXS Inc., Bruker, Madison, Wisconsin, USA, 2015 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2008, 64, 112–122 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- T. Degen, M. Sadki, E. Bron, U. König and G. Nénert, Powder Diffr., 2014, 29, S13–S18 CrossRef CAS.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr. - Cryst. Mater., 2014, 229, 345–352 CrossRef.
- J. E. Beves, E. C. Constable, C. E. Housecroft, M. Neuburger and S. Schaffner, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, o2497–o2498 CrossRef CAS.
- B. N. Figgis and J. Lewis, Prog. Inorg. Chem., 1964, 6, 37–239 CAS.
- W. Huang, W. You, L. Wang and C. Yao, Inorg. Chim. Acta, 2009, 362, 2127–2135 CrossRef CAS.
- S. Zhao, H. Zhou, C. Qin, H. Zhang, Y. Li, M. Yamashita and S. Wang, Chem. - Eur. J., 2023, 29, e202300554 CrossRef CAS.
- S. Klokishner and S. M. Ostrovsky, Magnetochemistry, 2020, 6, 62 CrossRef CAS.
- Y. Guo, X. L. Yang, R. J. Wei, L.-S. Zheng and J. Tao, Inorg. Chem., 2015, 54, 7670–7672 CrossRef CAS.
- S. Ostrovskya, Z. Tomkowicz and W. Haasea, Coord. Chem. Rev., 2009, 253, 2363–2375 CrossRef.
- B. P. Yang, A. V. Prosvirin, Y. Q. Guo and J. G. Mao, Inorg. Chem., 2008, 47, 1453–1459 CrossRef CAS.
- A. V. Palii, S. M. Ostrovsky, S. I. Klokishner, O. S. Reu, Z. M. Sun, A. V. Prosvirin, H. H. Zhao, J. G. Mao and K. R. Dunbar, J. Phys. Chem. A, 2006, 110, 14003–14012 CrossRef CAS PubMed.
- G. Agusti, C. Bartual, V. Martinez, F. J. Munoz-Lara, A. B. Gaspar, M. Carmen Munoz and J. A. Real, New J. Chem., 2009, 33, 1262–1267 RSC.
- A. Galet, A. B. Gaspar, M. C. Munoz and J. A. Real, Inorg. Chem., 2006, 45, 4413–4422 CrossRef CAS PubMed.
- R. Rabelo, L. Toma, M. Julve, F. Lloret, J. Pasán, D. Cangussu, R. Ruiz-García and J. Cano, Dalton Trans., 2024, 53, 5507–5520 RSC.
- M. Nath, S. Joshi and S. Mishra, Phys. Chem. Chem. Phys., 2024, 26, 15405–15416 RSC.
- M. Nößler, R. Jäger, D. Hunger, M. Reimann, T. Bens, N. I. Neuman, A. Singha Hazari, M. Kaupp, J. Van Slageren and B. Sarkar, Eur. J. Inorg. Chem., 2023, e202300091 CrossRef.
- S. Kremer, W. Henke and D. Reinen, Inorg. Chem., 1982, 21, 3013–3022 CrossRef CAS.
- R. Bertoni, M. Lorenc, H. Cailleau, A. Tissot, J. Laisney, M.-L. Boillot, L. Stoleriu, A. Stancu, C. Enachescu and E. Collet, Nat. Mater., 2016, 15, 606–610 CrossRef CAS PubMed.
- A.-I. Popa, L. Stoleriu and C. Enachescu, J. Appl. Phys., 2021, 129, 131101 CrossRef CAS.
Footnotes |
| † This paper is dedicated to the loving memory of our dear friend and esteemed colleague, Cristian Enachescu, whose invaluable contributions to the field of spin transition materials have left an indelible mark. His work encompassed everything from the quasistatic processes, such as hysteresis, to the ultra-fast effects. His legacy will endure as a testament to his dedication and brilliance. |
| ‡ Electronic supplementary information (ESI) available. CCDC 2330712–2330718. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4tc02203c |
| § Contributed equally to this work. |
| ¶ Current address: Centre for Interdisciplinary Science, JIS Institute of Advanced Studies and Research (JISIASR) Kolkata, JIS University, GP Block, Sector-5, Salt Lake, Kolkata-700091, West Bengal, India. |
| This journal is © The Royal Society of Chemistry 2025 |









