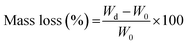DOI:
10.1039/D5TB00456J
(Paper)
J. Mater. Chem. B, 2025,
13, 6456-6468
Engineering long-term controlled drug release from biodegradable devices 3D printed with vat polymerization†
Received
28th February 2025
, Accepted 6th May 2025
First published on 7th May 2025
Abstract
Vat polymerization (VP) 3D printing with biodegradable resins has recently emerged as a potential method to fabricate patient specific drug delivery devices. The unique advantage of VP printing is the ability to print complex geometries with high resolution and intricate details that can offer a high level of control of drug release kinetics. However, non-degrading and slow-degrading photoreactive resins are often used to print these devices as fast degradation of the device can lead to uncontrolled drug release rates. Therefore, drug release from these devices often tends to be Fickian or diffusion-controlled in that drug release gradually decreases over time. Some studies have shown that device degradation could be an advantage in controlled release, but there is currently no fundamental understanding on how it can be utilized to control long-term drug release from 3D-printed devices. In this study, we employ VP 3D printing of relatively fast degrading polyester resins loaded with surrogate drug rhodamine b (RhB) as a model system to investigate the role of degradation in achieving controlled drug release. Degradation of the resulting devices was modified by varying key geometric parameters such as surface area to volume ratio, strut beam size, and pore size and the effect of these parameters on the release on RhB was determined. The results revealed that print geometry affected the degradation of devices, and long-term controlled release of RhB could be achieved by modifying print geometry. It was also implied that onset of degradation-controlled release could be a crucial factor in achieving constant drug release. The insights obtained from these studies provide a better understanding of how 3D printing with biodegradable resins can be applied towards the engineering of long-term controlled release from clinically relevant devices.
Introduction
In the past century, innovations in modern pharmaceutical technologies as well as advances in biotechnology have led to a new class of drugs that have significantly improved the lives of patients and reduced the number of deaths caused by disease. Examples of this can be seen from development of drugs to combat cancer to the rise of vaccine technologies.1,2 Conventionally, drugs have been administered via the oral or intravenous route. Oral dosage forms are generally preferred since they are usually painless, uncomplicated, and self-administered. However, many drugs administered orally are degraded within the gastrointestinal tract or are not adsorbed in sufficient quantities to be effective due to first pass metabolism in the liver.3 Therefore, repeated dosing is often required to maintain the drug concentration within a desired therapeutic window. While the intravenous route does increase the bioavailability of drugs in the system, it can often cause discomfort to the patient, requires a healthcare provider, and can lead to drug overdose.4
One aspect of drug-related research is improving upon the disadvantages of conventional drug delivery by fabricating devices that deliver drugs at a controlled rate at the target site as precisely as possible to achieve maximum efficacy and safety.5,6 This controlled release is often in the form of constant and sustained release over time, thereby maintaining drug concentrations within the therapeutic window for an extended period of time. Additive manufacturing, or three-dimensional (3D) printing with polymers has emerged as a promising way to fabricate these controlled drug delivery devices as it offers a layer-by-layer approach to fabricate devices with a high degree of controllability. Through careful design and modification of geometric parameters such as surface area, porosity, pore size and internal structures, and considering material properties and print resolution, one can tailor the drug release characteristics to meet specific therapeutic needs.7–9 This has been demonstrated with melt-based 3D-printing techniques.10–12 Furthermore, biodegradable polyesters have been used to 3D print these devices as they do not require surgical intervention for removal after they have served their purpose.13–15 However, there are some disadvantages of using melt-based 3D printing techniques in that the drugs can be degraded at the relatively high temperatures (i.e., ∼170–280 °C) needed to process the devices can degrade the incorporated drug.
Vat polymerization (VP) techniques such as stereolithography and digital light projection (DLP), utilize light instead of heat to 3D print objects.16–18 In the VP printing process, a build platform is submerged in a vat of liquid photoreactive polymer resin, and ultraviolet (UV) light is used to cure a layer of the resin. The platform moves upward or downward, depending on the printer's design, allowing the next layer to be cured onto the previous one to create the solid 3D object or geometry. This technique provides more versatility than melt based 3D printing technologies in that they offer the ability to produce devices with high resolution and intricate detail. Therefore, specific geometries with a high degree of controllability can be fabricated.19 Furthermore, drug delivery devices fabricated with VP can be produced at room temperature, avoiding the risk of thermal drug degradation. Additionally, biodegradable photoreactive polyesters can be used to print these devices (Fig. 1(a)). Due to these advantages, there have been several investigations in utilizing VP to fabricate controlled release devices.20–26 However, the geometries in these studies are often printed with non-degradable or poly(caprolactone) (PCL) based photoreactive resins which have a relatively slow degrading rate. As a result, the release profiles obtained from these devices often follow Fickian diffusion kinetics in that the concentration of drug released gradually decreases over time.27,28 These diffusion-controlled devices printed from non-degradable or slow degrading polymers are often preferred because degradation can lead to inconsistent or uneven drug release, in that a secondary accelerated phase of drug release is often observed leading to biphasic or triphasic release profiles, which may not meet the therapeutic needs of the patient.29–32 Furthermore, it is often easier to describe the drug release behavior through mathematical models as degradation adds a level of complexity to the models due to drug diffusivity changing over time as the polymer matrix degrades. However, the applicability of these diffusion-controlled devices in long-term controlled release applications is limited as they are often limited to drugs with large therapeutic windows.
 |
| | Fig. 1 (a) Hydrolytic degradation of photo-crosslinked polyesters. (b) Schematic describing drug release over time from hydrolytically degradable devices. | |
Despite the disadvantages of polymer degradation in achieving controlled drug release, it can also be an advantage because as the drug loaded device degrades, drug diffusivity and release increase (Fig. 1(b)). Therefore, degradation could compensate for the reduction in drug release observed in Fickian systems. This has been shown with drug loaded poly(lactic-co-glycolic acid) (PLGA) microspheres.33,34 Although PLGA microspheres often exhibit catastrophic bulk hydrolytic degradation, which could lead uncontrolled drug release rates, the degradation was controlled by modifying the microsphere size. PLGA degrades through hydrolysis and by modifying microsphere size or surface area to volume ratio, the rate of water penetration into the bulk or acidic degradation byproducts out of the bulk is also modified. The thereby alters the degradation rate of the polymer and offers a lever for control of degradation. However, a disadvantage of this method is the difficulty in fabricating uniform microspheres. In another study, Amsden et al., fabricated photo crosslinked drug delivery devices from fast degrading photoreactive biodegradable polyesters composed of lactide, caprolactone, trimethylene carbonate monomers.35 By ranging the ratios of these monomers and the degradation rate of the resulting polymer network, they were able to obtain nearly constant and sustained release of model drug triamcinolone. While this shows promise for controlled release applications, due to the limitations of the fabrication process, a simple 1 mm cylindrical geometry was chosen as the device. 3D-printing can be used to fabricate more complex geometries, and there have been some studies in utilizing 3D printing with fast degradable materials to deliver controlled release. For example, Yang et al., 3D printed PCL-chitosan based drug delivery implants and evaluated the release of model drug ibuprofen from different complex geometries.36 While they saw controlled and sustained release of ibuprofen from some of the printed structures, the length of release was only 120 min undermining its applicability for long term release. This is also seen in a study done by King et al. in their use of DLP 3D-printing with fast degrading salicylic acid photopolymers for sustained release of model drugs Nile blue and fluorescein.37 While this presents a novel approach to control drug release, the length of release only approximately 7 d. Therefore, an in-depth analysis on the role of degradation in achieving long-term controlled release was not done.
The aim of this study is to bridge this gap by providing a systemic investigation on the role of degradation in achieving long-term controlled release from 3D-printed devices through the modification of device geometry. Here, we exceed prior studies by utilizing VP-3D printing with a fast-degrading photo-reactive polymer resin to achieve long-term controlled release of the small molecule drug surrogate rhodamine b (RhB). First, simple cylinders with different surface area to volume (SA/V) ratios were 3D-printed and the release RhB from the cylinders were measured. Different mathematical models were then fit to the release data to examine and understand how the interplay of drug diffusion and device degradation impacted controlled release of RhB. The results obtained were then translated to more complex geometries and the effect of different geometric parameters such as SA/V ratio, strut beam length, and pore size on the controlled release behavior of RhB were examined.
Materials and methods
Photoset® resin (linear triblock methacrylated polymer of poly(caprolactone), poly(glycolide), poly(trimethylenecarbonate)) and was provided by poly-Med, Inc (Anderson, SC). Rhodamine B (RhB), isopropanol (IPA), acetone, phosphate buffer saline (PBS), and dichloromethane (DCM, 99.8%) were purchased from Sigma-Aldrich.
Preparation of rhodamine B (RhB) loaded formulation
Resin formulations were prepared by adding RhB to the photoset resin at 0.2 wt%. 2 mm yttrium beads were added to the mixture at 50 wt%. The formulation was then mixed in a centrifugal mixer (DAC 150.1 FVZ-K speed mixer, FlakTek, Landrum, SC, USA) at 2500 rpm for 1 min and 3000 rpm for 1 min.
Working curves to determine print parameters
DLP-VP printing parameters for the RhB loaded resin was obtained with working curve measurements based on Jacob's fundamental working curve equation:38| |  | (1) |
where Cd is the depth of a cured resin or height of a polymerized resin, Emax is the incident energy dosage per area (a product of light irradiance and exposure time), Ec is the critical energy dosage needed for polymerization, and Dp is the “depth of penetration” of light into the resin, which is the depth at which light is attenuated to 1/e (i.e. 37%) of incident light irradiance.
In the working curve process, the RhB loaded resin was loaded on a 50 mm × 64 mm × 0.17 mm glass side. A hollow film of cross-linked polydimethylsiloxane (PDMS) with a depth of 4.5 mm was placed around the edges of the slide to contain the resin. The loaded slide was placed directly on the build window of the DLP-VP printer (Kudo 3D Micro, MicroSLA, Dublin, CA, USA) and the resin was exposed to UV light at an irradiance of 45 mW cm−2 to form a crosslinked grid of 5 mm × 5 mm square cells at a range of exposure times. Following light exposure, residual resin was removed and cleaned with a Kimwipe. The cure depth of the square cells in the grid was measured with a 3D optical profilometer (VR5000, Keyance, Itasaca, IL). A semi-log plot of cure depth as a function of exposure time (energy dosage) was created. Following this, a logarithmic regression was performed to create a best-fit model to predict the exposure time necessary to cure a 30 μm layer height during the prints. Working curve values (Ec, Dp, and 30 μm exposure time) obtained for the non-loaded and RhB loaded resin is shown is Table S1 (ESI†).
Assessment of geometric limitations and print accuracy of RhB loaded resin
To assess the geometric limitations and print accuracy of the RhB loaded resin, a custom test model was designed in SolidWorks SP3.1 (Dassault Systèmes, Vélizy-Villacoublay, France) comprising of solid cylinders with a range of beam diameters (0.1 to 3 mm) and hollow cylinders with a range of pore-sizes (2.8 to 0.4 mm). The test models were printed (n = 3) using parameters estimated from the working curve process described prior at the same irradiance with a layer height of 30 μm. After printing, excess resin was removed from the printed models using a Kimwipe. The printed models were then washed with 40 mL of 70/30 IPA/acetone for 2 min, then IPA for 2 min. This cycle was repeated two more times. After the solvent washes, the surface solvent was removed by exposing the device to a compressed air stream for 5 s. The samples were then scanned, and the beam diameter and pore sizes were measured using a 3D optical profilometer (Keyence VR5000). The accuracy of the beam diameter and pore size of the prints were calculated relative to the design dimensions on the model.
Design and fabrication of solid and lattice cylindrical drug delivery devices
To study the effects of device geometry on the release of RhB, models with different geometric parameters were designed and 3D-printed. First, solid cylinders with diameters of 6 mm, 3 mm and 1 mm and heights of 12 mm were designed on SolidWorks to serve as a simple evaluation of the effect of surface to volume (SA/V) ratio on the release of RhB (diameter series). Following this, more complex cylindrical geometries were generated with lattice software generator Altair Sulis (Altair Engineering, Troy, Michigan, USA). Three series of lattice architectures were designed. In the first series (unit cell series), the effect of strut length was evaluated by creating a cylindrical gyroid lattice structure that is 6 mm by 12 mm cylinder with unit cell sizes 4 mm, 2 mm, and 1 mm. The pore-size of this series was kept the same at 1.6 mm. In the second series (lattice type series), the unit cell size was held constant at 3 mm, but the unit cell type changed from gyroid type to primitive or Fisher Koch to create different lattice types. The cylindrical part geometry was held constant at 6 mm × 12 mm. In the third series (pore size series), the effect of pore-size was evaluated by creating a cylindrical gyroid lattice structure with the same part geometry but keeping the unit cells size constant and varying the pore-size at 2.45 mm. 1.6 mm, and 0.75 mm. Geometric parameters were calculated using the CAD model (Fig. S1 and Tables S2–S5, ESI†). All structures were printed with 30 um layer height using the DLP-VP MicroSLA printer at same irradiance and parameters used to print the test models. After printing, excess resin was removed from the samples using a Kimwipe. The lattice samples were cleaned with compressed air for 1 min to remove any residual resin trapped in the pores. Afterwards, the samples were post cured for 200 s under a UV spot lamp (Bluewave 200, Dymax, Torrington, CT, USA) at the same print irradiance.
In vitro drug release studies
For in vitro drug release studies, samples were immersed in 20 mL on 0.01 M PBS (pH 7.4). However, for the diameter series the same SA/V ratio to release medium was used in the study to account for differences in the loading of the cylinders. Therefore, the 6 mm was immersed in 20 mL of PBS, while the 3 mm and 1 mm cylinders were placed in 10 mL and 4 mL of PBS, respectively. The samples were placed in an incubating shaker (Innova 4300, New Brunswick Scientific, Edison, NJ, USA) at 37 °C under constant oscillation at 50 rpm. At each designated time point, 1 mL of the release medium was collected, and the absorbance was measured using a UV/Vis spectrophotometer (Lambda 365+, PerkinElmer, Waltham, MA, USA). The amount of drug released at each timepoint was quantified by extrapolating against a standard curve on known concentrations in PBS using the UV/Vis spectrophotometer. At this point, the remainder of the release medium was removed and replenished before placing the samples back in the incubating shaker. The cumulative release (%) was calculated using the equation shown below:| |  | (2) |
where Ct is the amount of drug released at time t, Ct−1 is the amount of drug released before time t, and C0 is the initial amount of drug.
In vitro degradation studies
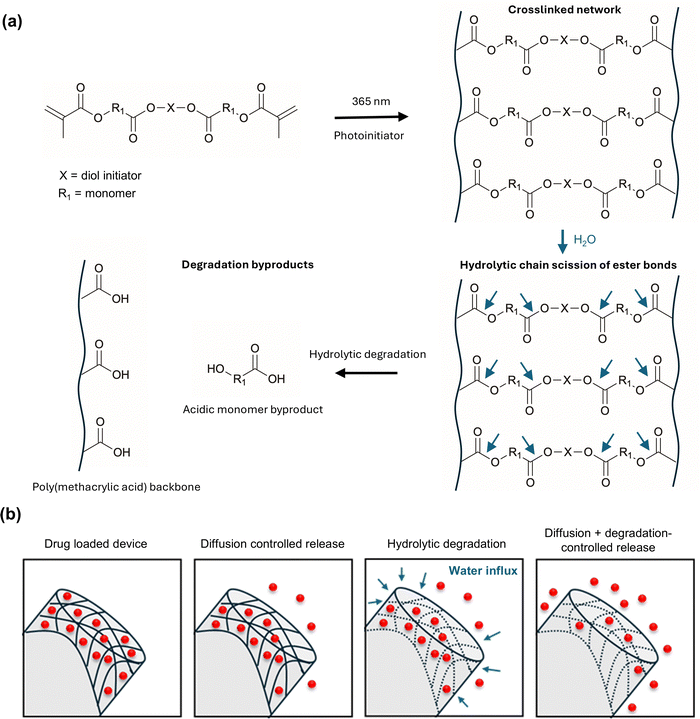
To examine the degradation behavior of the samples, an in vitro degradation study was performed using a protocol based on ASTM F1635-16: Standard Test Method for in vitro Degradation Testing of Hydrolytically Degradable Polymer Resins and Fabricated Forms for Surgical Implants. Briefly, the samples were pre-weighed (W0) and added to a 50 mL centrifuge tube. 20 mL of phosphate buffer solution (100 nM) at pH 7.4 with 0.01% (w/v) sodium azide was added to the centrifuge tubes. The samples were placed in an incubated shaker (Innova 4300) at 37 °C under oscillation at 50 rpm for the duration of the study. The buffer was replaced weekly to account for pH changes during degradation. At each desired timepoint, the cylinders were removed from the buffer (n = 3) and the wet weight (Ww) was recorded. The samples were then dried under vacuum to a constant dry weight (Wd). The mass loss and due to degradation were determined using the following equation:| | 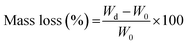 | (3) |
Gel fraction
To determine gel content of the samples, they (n = 3) were first placed in a 20 mL glass scintillation vial and the initial weight was obtained (W0). 10 mL of DCM was added to the vials and the vials were placed under constant oscillation (Innova 4300) at room temperature for 7 d. Afterwards, the samples were removed from DCM, the surface solvent was removed by gently blotting the surface with a Kimwipe. The swollen solvent was then transferred to a tared and capped vial. The samples were then dried under vacuum at room temperature for 3 d and the dry weight was recorded (Wd). The gel fraction of the samples was determined according to the following equation:| |  | (4) |
Results and discussion
Assessment of print accuracy of RhB loaded photoreactive resin
One of the advantages of using VP in biomedical applications is that devices with complex and intricate geometries can be fabricated with high precision and accuracy. In drug delivery, there are additional advantages in that drug delivery devices can be fabricated to provide precise control of drug release to suit a desired release profile. In VP, the accuracy of a print is determined by the printer's light source and resin properties. DLP 3D printers like the one used in this study utilize projector or LCD screens as the light source and the x–y resolution of a print is determined by the pixel size of the illuminated image. On the other hand, resin properties also play a role in print resolution, in that the resin used should have a low depth of light penetration (as close to the layer thickness of the 3D printing process) and suitable polymerization kinetics that allow for controlled reactivity on the x and y plane limiting propagation out of the pixel of irradiation.39,40 Therefore, to fabricate intricate geometries with high precision and accuracy, there must be an understanding of the composition and properties of the material as well as the capabilities of the VP printer being used. The DLP printer (Micro, MicroSLA) used in these studies has a pixel size resolution of 25 μm indicating that very intricate and complex geometries can be manufactured. However, the depth of penetration measured for the RhB loaded resin was approximately 360 μm which could limit the resolution of printed parts that can be achieved (Table S1, ESI†).39,40
To investigate the role of print geometry on drug release, the geometric limitations and print accuracy that can be achieved by the print formulation must first be assessed. A test model was designed to assess the capability of a RhB loaded photoreactive resin to print defined architectures (Fig. 2(a)).41,42 Two geometric parameters were evaluated (beam diameter and pore-size) by measuring the outer diameter or inner diameter of different sized solid and hollow cylinders showcased on the test model (Fig. 2(b)). The print accuracy was calculated by comparing the measured dimensions to the theoretical dimensions of the cylinders. Fig. 2(c) and (d) show the print accuracy of solid cylinders (beam diameter) and hollow cylinders (pore size), respectively. Measurements of the solid cylinders showed that the RhB resin formulation were capable of printing solid cylinders with beam diameters up to 0.4 mm with print accuracy >95% for all solid cylinders printed. This represents the apparent minimum feature size that can be printed with the parameters (light intensity, exposure time, and layer height) for the subsequent print geometries used in this work. Interestingly, no target diameters below 0.2 mm survived the printing process. These cylinders most likely delaminated from the print stage as the forces imparted during the layer-by-layer printing process were too large to maintain adhesion to the print stage. However, this can be resolved by including support structures in the model. Measurements of the hollow cylinders also showed that the RhB resin formulation were capable of printing pore sizes up to 0.4 mm. However, the print accuracy starts to decrease after 0.8 mm (<95%) with the 0.6 mm and 0.4 mm showing print accuracy of less than 90%. This was most likely due to the overcuring in the x- and y-plane of the cylinders which can be mitigated by adding a higher concentration UV absorbers or dyes.43,44 This was avoided as it could affect the spectroscopic measurement of RhB in the release studies. All geometries investigated in this work, however, were above the geometric limitation of the printed formulation used to 3D print them.
 |
| | Fig. 2 Mean accuracy of printed parts from target dimensions in test model. (a) Test model comprising of solid cylindrical beams with diameters ranging from 3 mm to 0.1 mm and hollow beams with pore sizes ranging from 2.8 mm to 0.4 mm. (b) Representative VR measurements of target dimensions. (c) Percent accuracy of solid beam diameter (n = 3). (d) Percent accuracy of hallow beam pore size (n = 3). Error bars represent one standard deviation. | |
Effect of SA/V on RhB release from 3D printed cylindrical devices (diameter series)
Modifying the SA/V ratio of a polymeric drug delivery device is a well-known approach to tailor release kinetics.7,8,45 Drug release from a polymeric device is typically through diffusion through the polymer matrix or network and changing the SA/V of a device alters the diffusion distance of the drug which affects release. There have been some investigations on the effect of SA/V ratio on the release of small molecule drugs from devices 3D printed with VP. Typically, it has been shown that increasing the SA/V ratio of a device or part translates to an increase in drug release as the drug has less distance to travel in the matrix or network of the device. However, these studies have been done with non-degradable silicone resins or slow degrading PCL based resin formulations, which yield relatively slow degrading devices. Therefore, the effect of degradation on drug release was not investigated. Furthermore, while drug release was modified, controlled or constant release was seldomly achieved. In this study, we assessed how modifying SA/V ratio affects the release of RhB from drug delivery devices 3D printed with relatively fast degrading Photoset photoreactive resin.40,46 To determine the effect of SA/V on release, RhB loaded cylinders were printed with a height of 12 mm and diameter of 6 mm, 3 mm, or 1 mm. Visible light images of the fabricated cylinders are shown in Fig. 3(a). As expected, decreasing the diameter of the cylinder increases the SA/V ratio (Fig. 3(b)). The SA/V ratios obtained from measurements of the cylindrical models were 4.2 mm−1, 1.5 mm−1, and 0.8 mm−1 for the 1 mm, 3 mm, and 6 mm cylinders, respectively.
 |
| | Fig. 3
In vitro release from diameter series. (a) Images of cylinders. (b) Drug loading and SA/V ratios of cylinders with different diameters. Comparison of actual and predicted RhB release from (c) 6 mm, (d) 3 mm, and (e) 1 mm cylinders. The predicted drug release if assuming simple radial diffusion from the cylinders and that the drug release profiles follow a simple diffusion model. (f) Total amount of RhB released from cylinders (n = 3). Error bars represent one standard deviation. | |
Fig. 3(c)–(e) shows the cumulative release of RhB from the cylinders as measured using a UV/Vis spectrophotometer. The 1 mm cylinder showed higher release rates followed by the 3 mm, and 6 mm cylinders. At 56 d days, more than 60% of the RhB has been released compared to 20% and 10% for the 3 mm and 6 mm cylinders, respectively. This was expected and attributed to the increase in SA/V ratio as discussed prior. The release of RhB did plateau at approximately 70%. This was first attributed to degradation of the drug during printing. However, extraction studies of the 6 mm cylinders show that actual drug loading was very close to the theoretical drug loading (Table S6, ESI†). Therefore, this is most likely not the case. It can however be reasoned that for a diffusion dominant drug release mechanism, drug release will reach an equilibrium which could serve as an explanation for the plateau. The study was not expanded past 112 d due to difficulties running the release study as the 3 mm and 6 mm had undergone significant degradation and interfered with UV/Vis absorbance measurements. Therefore, it is expected that further degradation of the cylinders could lead to a second burst in release.
Drug release mechanism of RhB from diameter series
Mathematical models are often used to describe the mechanism of drug release from a polymeric device. This mechanism can depend on several factors such as drug diffusivity, the intrinsic and/or extrinsic properties of the material, and environmental conditions like pH and temperature. For a one-dimensional radial release from a cylindrical device under sink conditions, with constant drug diffusivity, the solution for Ficks second law can be used to describe drug release over time with the following equation| |  | (5) |
where Mt is the cumulative release of the drug release at a given time, M0 is the initial mass of the drug within the device, D is the drug diffusion coefficient in the polymer network, r is radius of the cylinder, t is the time, and αn are the positive roots of the zero-order Bessel function J0(rαn) = 0. An alternative solution highlighted by Siepmann and Siepmann47 useful for short-time and long-time behavior is given as| |  | (6) |
| |  | (7) |
For mass fractions less than 25%, the contribution of the second term on the right side of eqn (6) is negligible and the mass fraction can therefore be expressed as
| |  | (8) |
The diffusion coefficient of RhB within the polymer network was estimated by fitting eqn (8) to the cumulative release data obtained from the 3 mm cylinder up to 56 d using Matlab (Fig. S2 and Table S7, ESI†). The diffusion coefficient was calculated to be 3.1 × 10−11 cm2 s−1 with a 95% confidence interval of ±0.2 × 10−11. Eqn (6) and (7) was used to predict the release profile expected from a monolithic cylindrical device with the same radius as the cylinders used in diameter series with the calculated diffusion coefficient. The plot of the predicted release curves obtained from the diameter series are shown in Fig. 3(c)–(e). The predicted curves provide good agreement to actual release curves initially but begin to deviate over time. This was attributed to the degradation of the cylinders over time with the difference in release kinetics most likely due to differences in degradation behaviors of the cylinders. Degradation of biodegradable polyesters occur mainly via hydrolysis, a process in which water causes the cleavage of ester bonds in the polymer chain, generating acidic oligomers or monomers as byproducts and is typically quantified by measuring molecular weight reduction or mass loss over time.48,49 The release data was fit to the semi-empirical equation Korsmeyer–Peppas kinetic model (eqn (9)) to the first 60% of RhB release to estimate the role of degradation in release.10,36,50–55
| |  | (9) |
where
Mt/
M0 is the fraction of drug released at time
t and
k is a constant incorporating the structural and geometric characteristics of the device under investigation. In the Korsmeyer–Peppas model, the diffusional exponent
n is an important indicator of the mechanism of drug release. For a cylindrical geometry, the value
n ≤ 0.45 indicates a Fickian diffusion-controlled mechanism whereas
n ≥ 0.89 indicates drug release dominated by a degradation mechanism. For values 0.45 <
n < 0.89, the release is described as anomalous, implying a combination of diffusion and degradation contributes to the release of the drug. As seen in Fig. S3 (ESI
†), the release exponent n was less than 0.45 for the 1 mm, 3 mm, and 6 mm cylinders up to 35 d, 56 d, and 84 d respectively, indicating that the release up to these timepoints was diffusion controlled. However, the release starts to deviate from diffusion-controlled release (
n > 0.45), at approximately 47 d for the 1 mm cylinder, 65 d for the 3 mm, and 89 d for the 6 mm (
Fig. 4). This also matches when we start to see this deviation of the actual release from the predicted release. The difference in deviation time of the different cylinders is attributed to the onset of degradation as a rate limiting mechanism of release. This onset of degradation-controlled release in the 1 mm cylinder is faster than the 3 mm and 6 mm cylinders. This is likely due to faster release of acidic degradation byproducts formed during the chain scission of the ester bonds in the 1 mm cylinder as a result of the higher SA/V ratio whereas the degradation byproducts accumulate in the bulk of the 3 mm and 6 mm cylinders.
34 This is confirmed by visual inspection of the cylinders at 84 d showing that the 6 mm and 3 mm cylinders degraded significantly more than the 1 mm cylinder (Fig. S4, ESI
†). This increase in degradation is most likely the reason for the accelerated phase of RhB observed at 56 d from the 3 mm cylinder and 84 d from the 6 mm cylinder.
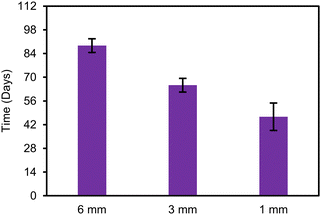 |
| | Fig. 4 Timepoint of deviation from diffusion-controlled release (n > 0.45 in Korsmeyer–Peppas model) in diameter series (n = 3). Error bars represent one standard deviation. | |
The release data obtained up to the plateau was fitted to a zero-order kinetic model (eqn (10)) to evaluate controlled release with a higher fit or R2 value corresponding to more constant or controlled release.56,57
| |  | (10) |
where
k0 is the zero-order release constant. The 1 mm cylinder showed the most significant fit to the zero-order kinetic model with an
R2 of 0.98 followed by the 3 mm and 6 mm cylinders with
R2 values of 0.90 and 0.64, respectively (Fig. S5, ESI
†). Therefore, the 1 mm cylinder offers the likeliest pathway for RhB release at a constant release rate. This could indicate that the onset degradation is important in the zero-order kinetic release as degradation could compensate for the reduction in diffusion pathlength over time observed in Fickian (slow or non-degrading) systems. As the device degrades, there is an increase in pathway through the polymer network, hence diffusivity of RhB and subsequent release rate from the device increases. Therefore, we propose that having the ability to modify the onset of degradation-controlled release by adjusting print geometry could serve as an advantage in the goal of achieving long term constant and controller release.
Release of RhB from 3D printed lattice structures (unit cell series)
While the zero-order release kinetics of RhB observed from the 1 mm cylinder presents a promising approach for long term-controlled delivery, there was a large difference in the total amounts of RhB released in the cylinders. As seen in Fig. 3(f), the total amount of RhB released from the 1 mm cylinder was 100-fold less than the 3 mm cylinder and 500-fold less than the 6 mm cylinder. This difference in amount release was expected as the difference in volume, hence drug loading between the cylinders was large. This would present a challenge in implementing this approach to modify drug release in that tuning release profile would also result in different drug release dosages which can be harmful to the patient. However, VP 3D printing enables the flexibility to design and fabricate more complex structures that can maintain the zero-order kinetic advantages of the 1 mm cylinder with increased drug loading. In this study, we use lattice structures to demonstrate this. Lattice structures are 3D open-celled porous structures that are topologically ordered and formed of repeatable units. They are often used in biomedical applications to improve the mechanical properties of devices. There are several open sources unit cell types that have been designed and are available to create lattice structures.58,59 In this study Altair Sulis, a lattice generator software, was used to design 6 mm × 12 mm cylindrical lattices with a gyroid unit cell array. The gyroid lattice structures were designed with three different unit cell sizes (4 mm, 3 mm, or 2 mm) to generate devices with three different SA/V ratios (Fig. 5(a)). The parts were fabricated with 0.2 wt% RhB loaded Photoset resin and showed a smaller difference in mass, thus RhB loading, compared to the diameter series (Fig. 5(b)). Furthermore, it was shown that decreasing the unit cell size increases the SA/V ratio with the 4 mm, 3 mm, and 2 mm unit cell with SA/V ratios of 1.95 mm−1, 2.87 mm−1, and 5.43 mm−1, respectively (Fig. 5(c)). This highlights the versatility of VP as we were successfully able to design devices with comparable SA/V ratios as the diameter series, but small differences in drug loading.
 |
| | Fig. 5 Characterization of unit cell series. (a) CAD models of lattice devices. (b) Visible light photographs of 4 mm, 3 mm, and 2 mm unit cell gyroid lattices, from left to right. (c) Drug loading and SA/V ratio of different lattices. (d) Cumulative release of RhB from unit cells series compared to 6 mm solid cylinder (n = 3). Error bars represent one standard deviation. | |
A release study was then conducted to determine the effect of lattice unit cell size on release. To ensure the RhB release was due to the differences in SA/V ratio, not due to differences in the polymer network as an effect of printing or posturing, a gel fraction study was conducted. It was shown that there was no significant difference in the gel content of the lattices indicating that the polymer networks were similar at the molecular level (Fig. S6, ESI†). Fig. 5(d) shows the cumulative release of RhB from the 3D-printed lattices. An initial burst release was observed in all the samples, which was expected as drugs on the surface of the printed lattices rapidly release but this was followed sustained release. Similar to the diameter series, the 2 mm unit cell gyroid lattice structure, which has the highest SA/V ratio, exhibited faster RhB release over 112 d. This was followed by the 3 mm unit cell lattice, then the 4 mm unit cell lattice. Furthermore, visible light images of the lattices during release indicate that there were degradation differences between the lattices as seen in the diameter series (Fig. 6(a)–(c)). Like the 1 mm cylinder, the 2 mm unit cell lattice exhibited less degradation than the 3 mm and 4 mm unit cell lattices. The 4 mm unit cell lattice showed the highest degree of degradation. Quantification of mass loss over time also corroborates this as the 4 mm unit cell lattice showed the highest mass loss over 112 d while the 2 mm unit cell mm showed the lowest mass loss (Fig. 6(d)). This again was attributed to the acid accumulation effect observed in bulk hydrolysis. As shown in the diameter series, to achieve controlled RhB release a balance between RhB diffusivity and network degradation should be achieved. To determine the effect of lattice unit cell size on controlled RhB release, the release data was fitted to a zero-order kinetic model. Results showed that the 3 mm unit cell lattice had the highest kinetic fit with an R2 value of 0.97 followed by the 4 mm and 2 mm unit cell lattices with R2 values of 0.95 and 0.86, respectively (Table 1). This indicates that the 3 mm unit cell provided a good balance between initial RhB diffusivity and onset of the secondary accelerated phase induced by network degradation when compared to the 2 mm and 4 mm unit cell lattices. These results highlight the advantages of vat polymerization with fast degrading resins can offer in controlled release applications.
 |
| | Fig. 6 Visible light images of RhB loaded unit cell lattices at (a) 56 d, (b) 70 d, and (c) 84 d of release. (d) Mass loss over time of unit cell series. Error bars represent one standard deviation. | |
Table 1 Zero order kinetic fit of unit cell series and lattice type series
| Lattice |
R
2
|
| 4 mm gyroid |
0.95 |
| 3 mm gyroid |
0.97 |
| 2 mm gyroid |
0.86 |
| 3 mm primitive |
0.97 |
| 3 mm Fisher–Koch |
0.93 |
Effect of unit cell type on RhB release from lattice structures (lattice type series)
To further demonstrate the utility of vat polymerization with fast degrading resins in controlled delivery applications, an alternative approach to create lattice structures with different SA/V ratios was investigated. In this approach, the unit cell type was changed from the gyroid unit cell to a primitive or Fisher Koch unit cell to generate a 6 mm × 12 mm cylindrical lattice structure (Fig. 7(a)). The unit cell size was kept constant at 3 mm. The SA/V ratios of the models were measured, and the Fisher–Koch lattice structure was shown to have the highest SA/V ratio at 4.58 mm−1, followed by the gyroid lattice structure at 2.87 mm−1 and the primitive lattice structure at 1.95 mm−1 (Fig. 7(c)). The models were 3D-printed with 0.2 wt% RhB loaded resin (Fig. 7(b)) and the cumulative release of RhB was evaluated (Fig. 7(d)). Interestingly, the primitive and gyroid lattices showed similar release profiles even though the gyroid lattice has a higher SA/V ratio. However, both lattices had strut beam lengths of 1.4 mm which could indicate that strut length has a higher impact on release behavior than SA/V ratio. Furthermore, it was expected that Fisher–Koch lattice would show the highest release rate since it has the highest SA/V ratio. However, the release profile obtained was substantially lower than that observed with the primitive and gyroid lattices. We hypothesized that this could be due to poor wetting effects of the smaller pore size obtained with the Fisher–Koch lattice. Furthermore, fitting the data to a zero-order kinetic model showed that the gyroid and primitive lattices showed the highest kinetic fits with R2 values of 0.97 compared to the Fisher–Koch lattice with an R2 value of 0.93 (Table 1).
 |
| | Fig. 7 Characterization of lattice type series. (a) CAD models of lattice devices. (b) Visible light photographs of 3 mm unit cell primitive, gyroid, and Fisher–Koch lattices, from left to right. (c) Drug loading and SA/V ratio of different lattices. (d) Cumulative release of RhB from lattice type series (n = 3). Error bars represent one standard deviation. | |
Effect of pore size on RhB release from lattice structures (pore size series)
To investigate the effect of pore size on RhB release from lattice structures, gyroid lattices with pore sizes of 2.5 mm, 1.6 mm and 0.75 mm were designed and 3D-printed (Fig. 8(a) and (b)). The strut beam length of the lattice structures was fixed and constrained in the 6 mm × 12 mm cylindrical geometry. The SA/V was also held constant (Fig. 8(c)). Fig. 8(d) shows the cumulative release of RhB from 3D-printed lattices. The release profiles obtained from the lattice series were similar to those obtained from the lattice type series in that RhB release from the 0.75 mm pore size was a lot slower than the 2.5 mm and 1.6 mm pore sizes. Furthermore, the 2.5 mm and 1.6 mm showed similar release profiles. This result confirmed the hypothesis that pore size has effect on release from the lattice structures and provides an explanation from the slower release observed with the Fisher–Koch lattice observed prior. This is not unexpected as pore size has been shown to be a strong determinant in release. This phenomenon has also been observed by the Kyobula et al. in their study on the thermal inkjet-printed beeswax tablets with honeycomb pores.10 This indicates that below a certain pore size, the release of RhB is reduced and the controlled release obtained by changing the SA/V or device architecture can be disrupted. These results as well as results obtained from the lattice type series highlight that controlling drug release by altering SA/V is much more complex in practice and geometric parameters should be thoroughly examined and taken into consideration during the design of controlled drug delivery devices.
 |
| | Fig. 8 Characterization of pore-size series. (a) CAD models of lattice devices. (b) Visible light photographs of 0.75 mm, 1.6 mm, and 2.5 mm pore size gyroid lattices, from left to right. (c) Drug loading and SA/V ratio of different lattices. (d) Cumulative release of RhB from pore-size series (n = 3). Error bars represent one standard deviation. | |
Conclusions
Drug loaded structures with complex geometries were fabricated using VP 3D printing with biodegradable resins as the printing material and rhodamine B (RhB) as the model drug. The effect of different geometric parameters including SA/V ratio, strut beam length, and pore size on release behavior was assessed. It was shown that long-term controlled release could be achieved by varying the geometric parameters. This was attributed to the interplay of diffusion of the drug and degradation of structures, both of which are influenced by print geometry. Furthermore, the Korsmeyer–Peppas model was used to show that the onset of degradation-controlled release as a drug release mechanism could play an important role in achieving controlled release. This study not only provides an understanding of how print geometry can be modified to achieve controlled release but also showcases 3D printing with biodegradable devices as a platform to enable controlled treatment regimes.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors would like to thank Poly-Med, Inc. for supporting this research. The authors would also like to thank Dr Debra Tindall and Dr Mohsen Esmaeili for scientific discussions as well as Alex Wong for help with creating the test model.
References
- A. K. Mitra, V. Agrahari, A. Mandal, K. Cholkar, C. Natarajan, S. Shah, M. Joseph, H. M. Trinh, R. Vaishya, X. Yang, Y. Hao, V. Khurana and D. Pal, J. Controlled Release, 2015, 219, 248–268 CrossRef CAS.
- Y. Wang, Z. Zhang, J. Luo, X. Han, Y. Wei and X. Wei, Molecular Cancer, 2021, 20, 33 CrossRef CAS.
- S. V. Sastry, J. R. Nyshadham and J. A. Fix, Pharm. Sci. Technol. Today, 2000, 3, 138–145 CrossRef CAS PubMed.
- S. H. Yalkowsky, J. F. Krzyzaniak and G. H. Ward, J. Pharm. Sci., 1998, 87, 787–796 CrossRef CAS PubMed.
- T. M. Allen and P. R. Cullis, Science, 1979, 2004(303), 1818–1822 Search PubMed.
- R. Langer, Chem. Eng. Commun., 1980, 6, 1–48 CrossRef CAS.
- S. A. Chew, M. A. Arriaga and V. A. Hinojosa, J. Biomed. Mater. Res., Part A, 2016, 104, 1202–1211 CrossRef CAS.
- A. Goyanes, P. Robles Martinez, A. Buanz, A. W. Basit and S. Gaisford, Int. J. Pharm., 2015, 494, 657–663 CrossRef CAS PubMed.
- A. Goyanes, J. Wang, A. Buanz, R. Martínez-Pacheco, R. Telford, S. Gaisford and A. W. Basit, Mol. Pharmaceutics, 2015, 12, 4077–4084 CrossRef CAS.
- M. Kyobula, A. Adedeji, M. R. Alexander, E. Saleh, R. Wildman, I. Ashcroft, P. R. Gellert and C. J. Roberts, J. Controlled Release, 2017, 261, 207–215 CrossRef CAS.
- B. Zhang, J. Nasereddin, T. McDonagh, D. von Zeppelin, A. Gleadall, F. Alqahtani, R. Bibb, P. Belton and S. Qi, Int. J. Pharm., 2021, 604, 120626 CrossRef CAS.
- A. Lion, R. D. Wildman, M. R. Alexander and C. J. Roberts, Pharmaceutics, 2021, 13, 1679 CrossRef CAS PubMed.
- H. G. Yi, Y. J. Choi, K. S. Kang, J. M. Hong, R. G. Pati, M. N. Park, I. K. Shim, C. M. Lee, S. C. Kim and D. W. Cho, J. Controlled Release, 2016, 238, 231–241 CrossRef CAS PubMed.
- S. A. Stewart, J. Domínguez-Robles, V. J. McIlorum, E. Mancuso, D. A. Lamprou, R. F. Donnelly and E. Larrañeta, Pharmaceutics, 2020, 12, 105 CrossRef CAS PubMed.
- B. Zhang, A. Gleadall, P. Belton, T. Mcdonagh, R. Bibb and S. Qi, Addit. Manuf., 2021, 46, 102196 CAS.
-
C. W. Hull, US Pat. preprint, 4575330, 1986 Search PubMed.
- J. Huang, Q. Qin and J. Wang, Processes, 2020, 8, 1138 CrossRef CAS.
- X. Xu, A. Awad, P. Robles-Martinez, S. Gaisford, A. Goyanes and A. W. Basit, J. Controlled Release, 2021, 329, 743–757, DOI:10.1016/j.jconrel.2020.10.008 , preprint.
- M. Asadi-Eydivand, T. C. Brown and A. Bagheri, ACS Appl. Polym. Mater., 2022, 4, 4940–4948 CrossRef CAS.
- X. Xu, A. Goyanes, S. J. Trenfield, L. Diaz-Gomez, C. Alvarez-Lorenzo, S. Gaisford and A. W. Basit, Mater. Sci. Eng., C, 2021, 120, 111773 CrossRef CAS PubMed.
- S. Asikainen, B. Van Bochove and J. V. Seppala, Biomed. Phys. Eng. Express, 2019, 5, 025008 CrossRef.
- C. J. Bloomquist, M. B. Mecham, M. D. Paradzinsky, R. Janusziewicz, S. B. Warner, J. C. Luft, S. J. Mecham, A. Z. Wang and J. M. DeSimone, J. Controlled Release, 2018, 278, 9–23 CrossRef CAS PubMed.
- R. Janusziewicz, R. Shrivastava, D. K. Dahl, I. C. Young, M. Bis, A. N. Whitesell and S. R. Benhabbour, Mater. Today Chem., 2022, 24, 100978 CrossRef CAS.
- A. Bagheri, M. Asadi-Eydivand, A. A. Rosser, C. M. Fellows and T. C. Brown, Adv. Eng. Mater., 2023, 25, 1438–1656 CrossRef.
- H. J. B. Chua, A. A. Rosser, C. M. Fellows, T. C. Brown and A. Bagheri, ACS Appl. Polym. Mater., 2024, 6, 10853–10864 CrossRef CAS.
- A. Triacca, G. Pitzanti, E. Mathew, B. Conti, R. Dorati and D. A. Lamprou, Int. J. Pharm., 2022, 616, 121529 CrossRef CAS PubMed.
- K. A. Davis and K. S. Anseth, Crit. Rev. Ther. Drug Carrier Syst., 2002, 19, 385–424 CrossRef CAS.
- G. Acharya and K. Park, Adv. Drug Delivery Rev., 2006, 58, 387–401 CrossRef CAS PubMed.
- C. Li, C. Guo, V. Fitzpatrick, A. Ibrahim, M. J. Zwierstra, P. Hanna, A. Lechtig, A. Nazarian, S. J. Lin and D. L. Kaplan, Nat. Rev., 2020, 5, 61–81 Search PubMed , preprint.
- S. K. Prajapati, A. Jain, A. Jain and S. Jain, Eur. Polym. J., 2019, 120, 109191 CrossRef CAS.
- Y. Xu, C. Kim, D. M. Saylor and D. Koo, J. Biomed. Mater. Res., Part B, 2017, 105, 1692–1716 CrossRef CAS PubMed.
- B. van Bochove and D. W. Grijpma, J. Biomater. Sci., Polym. Ed., 2019, 30(2), 77–106 CrossRef CAS.
- C. Raman, C. Berkland, K. Kim and D. W. Pack, J. Controlled Release, 2005, 103, 149–158 CrossRef CAS PubMed.
- C. Berkland, K. Kim and D. W. Pack, PLG Microsphere Size Controls Drug Release Rate through Several Competing Factors, Pharm. Res., 2003, 20(7), 1055–1062 CrossRef CAS.
- B. G. Amsden and D. Marecak, Mol. Pharmaceutics, 2016, 13, 3004–3012 CrossRef CAS.
- Y. Yang, H. Wu, Q. Fu, X. Xie, Y. Song, M. Xu and J. Li, Mater. Des., 2022, 214, 110394 CrossRef CAS.
- O. King, M. M. Pérez-Madrigal, E. R. Murphy, A. A. R. Hmayed, A. P. Dove and A. C. Weems, Biomacromolecules, 2023, 24, 4680–4694 CrossRef CAS.
-
J. F. Paul, Fundamentals of Stereolithography, 1992 Search PubMed.
- A. Salas, M. Zanatta, V. Sans and I. Roppolo, ChemTexts, 2023, 9, 4 CrossRef.
- H. Busari, O. T. Mefford and M. A. Vaughn, ACS Appl. Polym. Mater., 2025, 7, 467–477 CrossRef CAS.
- L. Jaksa, D. Pahr, G. Kronreif and A. Lorenz, Inventions, 2022, 7, 35 CrossRef.
- A. Nulty, BDJ Open, 2022, 8, 14 CrossRef PubMed.
- J. H. Lee, R. K. Prud’homme and I. A. Aksay, J. Mater. Res., 2001, 16, 3536–3544 CrossRef CAS.
- H. Gong, M. Beauchamp, S. Perry, A. T. Woolley and G. P. Nordin, RSC Adv., 2015, 5, 106621 RSC.
- T. D. Reynolds, S. A. Mitchell and K. M. Balwinski, Drug Dev. Ind. Pharm., 2002, 28, 457–466 Search PubMed.
-
M. M. Stanford, PhD thesis, Clemson University, 2023.
- J. Siepmann and F. Siepmann, J. Controlled Release, 2012, 161, 351–362 CrossRef CAS PubMed.
- L. N. Woodard and M. A. Grunlan, ACS Macro Lett., 2018, 7(8), 976–982 CrossRef CAS PubMed.
- L. S. Nair and C. T. Laurencin, Prog. Polym. Sci., 2007, 32, 762–798 CrossRef CAS.
- S. Dash, P. M. Murthy, L. Nath and P. Chowdhury, Acta Pol. Pharm., 2010, 67, 217–223 CAS.
-
M. L. Bruschi, Strategies to Modify the Drug Release from Pharmaceutical Systems, Woodhead Publishing, 2015, pp. 63–86 Search PubMed.
- R. W. Korsmeyer, R. Gurny, E. Doelker, P. Buri and N. A. Peppas, Int. J. Pharm., 1983, 15, 25–35 Search PubMed.
- Y. Gao, J. Zuo, N. Bou-Chacra, T. D. J. A. Pinto, S. D. Clas, R. B. Walker and R. Löbenberg, BioMed Research Intl., 2013, 2013, 136590 Search PubMed.
- W. Zhu, J. Long and M. Shi, Materials, 2023, 16, 3282 CrossRef CAS PubMed.
- G. Gorkem Buyukgoz, D. Soffer, J. Defendre, G. M. Pizzano and R. N. Davé, Int. J. Pharm., 2020, 591, 119987 CrossRef CAS PubMed.
- S. A. Khaled, J. C. Burley, M. R. Alexander, J. Yang and C. J. Roberts, Int. J. Pharm., 2015, 494, 643–650 CrossRef CAS.
-
T. T. T. Trang, M. Mariatti, H. Y. Badrul, K. Masakazu, X. T. T. Nguyen and A. A. H. Zuratul, Drug Release Profile Study of Gentamicin Encapsulated Poly(lactic Acid) Microspheres for Drug Delivery, 2019, vol. 17 Search PubMed.
- S. AlMahri, R. Santiago, D. W. Lee, H. Ramos, H. Alabdouli, M. Alteneiji, Z. Guan, W. Cantwell and M. Alves, Addit. Manuf., 2021, 46, 102220 CAS.
- M. Martorelli, A. Gloria, C. Bignardi, M. Calì and S. Maietta, J. Healthc. Eng., 2021, 2021, 1 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *bcd and
M. Aaron
Vaughn
*ac
*bcd and
M. Aaron
Vaughn
*ac