Atomistic characterization of hydration-dependent fuel cell ionomer nanostructure: validation by vibrational spectroscopy

Abstract

The development of Nafion alternatives for fuel cells and electrolyzers requires a fundamental understanding of hydration-dependent ion-exchange site acid/base chemistry. We present here reactive force field (ReaxFF) molecular dynamics (MD) simulations of Nafion at varying molar water/ion-exchange-site ratios (λ), which we correlate to our experimental and density functional theory-based vibrational spectra. ReaxFF describes the formation and breaking of covalent bonds, enabling simulations of proton exchange between sulfonic acid/sulfonate groups and water/hydronium. Our MD simulations determine the λ-dependent equilibrium proportions of protonated and deprotonated sites. We find that protonated sites persist across all λ from 0 to 20, challenging the widely accepted notion that all sites are ionized above a threshold λ value (e.g., 3 or 4). Our simulations generate hundreds of realistic exchange site environments, the characterization of which are based on 6 Å radii sulfur-centered ‘inner-spheres’. These inner- and outer-sphere regions elucidate an interplay of stereoelectronic factors that influence protonation states, including the number of inner-sphere waters (Λ). Our simulations produce broad λ-dependent distributions of Λ values, representing non-uniform exchange site hydration. Moreover, we demonstrate that these distributions are specific to both protonated and deprotonated sites, with significant overlap between the two distributions for all non-zero λ. These distributions underpin the IR spectra of hydrated membranes, with each exchange site contributing an IR spectrum characteristic of its protonation state and Λ. We expect that these nanostructural characterizations of Nafion exchange sites will contribute to the development of new ionomers.

---

1 Introduction

Clean hydrogen technologies underpin long-term strategies established by the Paris Agreement.^1,2 Efficacious use of clean hydrogen relies on infrastructure spanning production, storage, delivery, and consumption of the fuel which generates electricity and clean water as byproducts. The primary and terminal stages are accomplished by electrolyzers and fuel cells, respectively. Polymer electrolyte membrane (PEM) electrolyzers and fuel cells are low-temperature (∼80 °C) devices with over half a century of development.^3–6 PEMs are solid-state ionomer membranes that also serve as separators of anode and cathode reactant streams, enabling compact system integration for rapid response to load demand changes.^6–8

Nafion is a benchmark perfluorinated sulfonic acid (PFSA) ionomer with superior chemical-mechanical stability and high protonic conductivity (Fig. 1).^9–11 PFSAs feature polytetrafluoroethylene (PTFE) backbones with randomly grafted perfluoroether sidechains, each terminated by a superacidic sulfonic acid group (i.e., the proton exchange site). The PTFE backbone provides structural integrity and resistance to thermochemical degradation, while the exchange sites promote the sorption^12–16 and retention of water required for proton transport via diffusion (vehicular) and Grotthuss (hopping or shuttling) mechanisms.^17–21 The contrasting backbone and exchange site polarities give rise to a dynamic multiphase morphology driven by an interplay of electrostatic (hydration of ionic sites) and mechanical (deformation of backbone) force minimizations.^10,14,22 Hydration dependent forces balance the distribution of hydrophobic (semicrystalline), hydrophilic (interphasial), and water-rich domains.^9,10,23–25 Despite decades of investigation, a consensus on hydration-dependent size, shape, and interconnectivity of domains remains elusive.^15,22,26,27

Fig. 1 General perfluorinated sulfonic acid structure (top left) and physical parameters of Nafion membranes (bottom left). Snapshot of hydrated molecular dynamics Nafion cell (top right).

Exceptional detail of hydration-dependent exchange site environments have been derived from analyses of IR and confocal Raman spectra, correlated to density functional theory (DFT) calculated normal modes and molecular dynamics (MD) simulations (Fig. 2a and b).^8,28–35 Eigenvector normal mode animations^36,37 guide vibrational group mode assignments, involving major contributions by multiple functional groups with intimately (mechanically) coupled^38–40 internal coordinates.^8,28–35 For example, the PFSA fingerprint region hosts a set of group modes primarily attributed to the mechanically coupled exchange site and its nearest ether link (Table 1).^{8,28–35,37,40–46} These group modes are specific to either the proton associated (i.e., α) or proton dissociated (i.e., β) exchange site states (Fig. 2c). All sites are protonated (i.e., α-sites) in exhaustively dehydrated§ PFSAs (blue spectra) and contribute to high and low frequency α-bands (i.e., α_HF and α_LF, respectively). Nearly all sites are deprotonated (i.e., β) in the fully hydrated state (red spectra) and contribute to high and low frequency β-bands (i.e., β_HF and β_LF, respectively). At partial hydration states (purple spectra), in situ,^{8,29,35,47–50} ex situ,^{29,30,35,51,52} and operando³¹ hydration-dependent spectra show the coexistence of α- and β-bands. A video of the simultaneous evolution of α-bands and the disappearance of β-bands during Nafion dehydration (corresponds to Nafion column of Fig. 2b) is available (ESI Video†). Doubly protonated exchange sites^19,53–55 (i.e., –SO₃H₂⁺) are assumed not to be statistically significant (Section 3.2.2) and are therefore not considered in this work.

Fig. 2 Operando and ex situ vibrational spectra. (a) Potential dependent Raman spectra of 25 wt% Nafion cathode catalyst (Fe-N_x/C + Pt under O₂), adapted with permission from Kendrick et al.³¹ 2016 under Creative Commons Attribution 4.0 License. (b) Hydration-state dependent PFSA membrane transmission spectra, adapted with permission from Loupe et al.⁸ Copyright 2020 American Chemical Society. (c) α- and β-site Newman projections.

Table 1 Vibrational group mode assignments for Nafion 212 transmission FTIR bands and corresponding DFT-calculated normal modes (X3LYP/6-311G**++), adapted with permission from Loupe et al.⁸ copyright 2020 American Chemical Society. Eigenvector animations for each normal mode are available^8 a

Frequency (cm^−1)		Label	Group mode assignment (dominant contributors in bold)
FTIR	DFT
a νs: symmetric stretching; νas: asymmetric stretching; HF: high-frequency; LF: low-frequency.
1414	1405
1058	1059
969	983
910	786

---

PFSA hydration is often specified by the overall water/SO₃(H) ratio, λ.⁵⁶ The exchange site-specific local water content, Λ,¶ represents the number of water molecules within a designated radial boundary (‘inner-sphere’) surrounding each exchange site.^8,33 Ab initio studies show that exchange site protonation states are Λ-dependent.^{8,29,30,33,35,47,53,57–67} For example, DFT geometry optimizations show that dissociation of an isolated RSO₃H molecule requires at least three waters of solvation (i.e., Λ_d = 3).^{47,53,60–63,66,67} In contrast, classical MD (CMD) simulations require a priori designation of protonation states, as their empirical force fields do not accommodate dynamic proton transfer reactions.^64,65 Accordingly, Nafion is typically modeled with a minimum λ value of 3,^68–84 with the assumption that all exchange sites are β for λ ≥ 3.^{68–78,80–88} This approach implies a uniform Λ distribution, contrary to an evolving number of works suggesting non-uniform water content^{8,40,64,79,89–91} and our recent CMD study|| showing a wide Λ distribution for all simulated non-zero λ cells.⁸ This approach also presupposes that DFT-optimized Λ environments are sufficiently realistic and applicable to MD-modeled exchange site environments. This paper addresses the validity of this presumption.

Sengupta and Lyulin demonstrated the profound morphological impact of a priori designated protonation levels (i.e., α-site/β-site ratios) in Nafion CMD simulations.⁷⁹ Their work stimulated us to perform reactive force field (ReaxFF)-based MD simulations, which explicitly accommodates modeling of proton dissociation and association processes without requiring a priori knowledge of protonation levels.⁹² ReaxFF offers a unique balance between accuracy and computational expense,⁹³ enabling simulations of systems with up to a million atoms for much larger length and time scales than those modeled with empirical valence bond^20,94–98 and ab initio MD simulations.^21,42,99,100

In Section 3.1, DFT-calculated normal modes of Nafion repeat units are correlated to acquired spectra by visualization of eigenvector animations. In Section 3.2, ReaxFF MD simulations of Nafion cells with λ values ranging from 0 to 20 are presented. Each hydrated simulation produces equilibrium proportions of α- and β-sites. In Section 3.2.3, stereoelectronic factors that affect exchange site protonation states are discussed. To our knowledge, this is the first report of ReaxFF modeling of proton exchange between ion-exchange sites and water within an ionomer membrane.

The following premises underpin the approach adopted in this work. Given that Λ_α and Λ_β represent the number of inner-sphere water molecules for protonated (α) and deprotonated (β) sites, respectively:

• Premise I – for any overall ionomer water content λ, there are characteristic Λ_α and Λ_β distributions. The total frequency of each distribution (i.e., the sum of all Λ_α and Λ_β number frequencies) is λ-dependent.

• Premise II – the fingerprint region of any membrane spectrum can be interpreted as the convolution of either:

(a) The site-spectrum of every exchange site environment (each characterized by some Λ_α or Λ_β).

(b) Two subspectra:¹⁰¹ an α-subspectrum (convolution of all Λ_α site-spectra) and a β-subspectrum (convolution of all Λ_β site-spectra).

• Premise III – the IR spectrum of an ionomer membrane is characteristic of its overall water content λ.

The Fig. 2b spectra exemplify the premises: Any dry membrane spectrum (blue) has no β-subspectrum component; any fully hydrated membrane spectrum (red) has a negligible α-subspectrum component; any partially hydrated spectrum (purple) is a convolution of an α-subspectrum and β-subspectrum.

2 Methods

2.1 DFT calculations

Unrestricted hybrid DFT (PBE0-D3/LACV3P**++) was used for all quantum mechanics (QM) calculations including geometry optimization and IR vibrational normal mode analysis (i.e., frequency analysis). Calculations were performed in Jaguar (v. 12.1, ©Schrödinger, LLC, New York, NY, 2024) and executed on a high-performance computing cluster (Discovery cluster, Holyoke, MA) accessed through Northeastern University. The D3 semi-empirical correction¹⁰² was paired with the PBE0 hybrid functional^103–105 to account for long-range van der Waals attraction interactions. Polarization (i.e., “**”)¹⁰⁶ and diffuse (i.e., “++”)¹⁰⁷ functions were added to the triple-ζ Gaussian-type basis set LACV3P.**

Three Nafion ‘component models’ (perfluorinated dimethyl ether, triflic acid, and triflate) and three Nafion monomer models (1-mer-sbb, 1-mer-CH₃, and 1-mer-CF₃) were the model compounds¹⁰¹ considered (Fig. S1-1; ESI†). The component models represent minimal ionomer fragments, making them useful for elucidating individual functional group contributions to ionomer vibrational normal modes (ESI-S1†).⁸ All models were optimized without an external dielectric medium or implicit solvent.^30,35 QM calculations were performed on incrementally hydrated 1-mer-CF₃ as previously reported for triflic acid.^8,30,35

2.2 MD simulations

2.2.1 System setup and equilibration. Nafion membranes were modeled using 32 10-mer chains (i.e., 320 total exchange sites per simulation cell) at nine hydration levels: λ = 0, 1, 2, 3, 5, 7, 10, 15, 20 (Fig. 3). Each monomer has 14 –CF₂– units followed by a single sidechain and an additional CF₂ unit. Oligomer backbones are capped with fluorine atoms. All exchange sites are protonated (and remain so) during the non-reactive equilibration stage. The above results in 692 atoms per oligomer and 22144 Nafion atoms per cell. The total number of atoms per cell varies from 22144 (λ = 0) to 41344 (λ = 20). Initial cell structures were generated using Packmol.¹⁰⁸

Fig. 3 Nafion oligomer for molecular dynamics simulations (top) and table of specified number of atoms, cell dimensions, and densities (bottom).

All cells were first relaxed by steepest-descent energy minimization, followed by a 10 ps NVT^17,109 simulation at 10 K to generate initial velocities. All cell densities were then set to an initial 1.8 g cm⁻³ (N117 at λ = 15 is ∼1.75 g cm⁻³)¹⁶ before undergoing the following 1.6 ns annealing procedure: 1a) heating from 10 K to 400 K over 150 ps; 1b) 100 ps equilibration at 400 K; 2a) cooling to 300 K over 50 ps; 2b) 100 ps equilibration; 2c) heating to 400 K over 50 ps; 2d) 100 ps equilibration; 2e) three repetitions of steps 2a–2d; 3a) cooling to 300 K over 50 ps; 3b) 100 ps equilibration. The cells were then equilibrated for another 10 ns at 300 K.

The universal force field¹¹⁰ was employed for the non-reactive simulations using LAMMPS.^111,112 The equations of motion were integrated using the Verlet algorithm¹¹³ (1.0 fs time step). Electrostatic interactions were calculated with the particle–particle particle–mesh method.¹¹⁴

2.2.2 ReaxFF MD simulations. ReaxFF, developed by Goddard and co-workers, describes bond formation and breaking in terms of a bond energy and bond order versus distance relation, which allows bond order changes within MD simulations.⁹² ReaxFF partitions the total system energy (E_system) into bonded and nonbonded terms (eqn (1)).

E_system = E_bonded + E_nonbonded (1)

Bonded terms include bond, over-coordination penalty (over), under-coordination stability (under), lone-pair (lp), valence angle (val), and torsion (tor) energies. Nonbonded terms include Coulombic (Coul), van der Waals (vdW), and hydrogen bond (HB) energies (eqn (2)).

E_system = (E_bond + E_over + E_under + E_lp + E_val + E_tor) + (E_Coul + E_vdW + E_HB) (2)

ReaxFF determines bonded interactions among all atoms in the system using the bond order (BO) concept, where BOs are expressed as a continuous function of interatomic distance. Contributions from σ, π, and ππ bonds are calculated as follows:

where BO^σ_ij, BO^π_ij, and BO^ππ_ij are the partial contributions of σ, π, and ππ bonds, respectively, between atoms i and j (r_ij is the distance between i and j). The σ, π, and ππ bond radii are r^σ₀, r^π₀, and r^ππ₀, respectively. The p_bo terms are empirical parameters fitted against reference QM results (or sometimes Experimental data). The nonbonded terms (i.e., Coul, vdW, and HB) are calculated between every pair of atoms regardless of their connectivity. The QEq charge equilibration method¹¹⁵ was used for electrostatic interactions. A more comprehensive review of ReaxFF is described elsewhere.⁹³

If all charges are allowed to respond to the forces and electric fields, the proper dielectric constant is 1. Accordingly, our DFT calculations of model compounds employ a dielectric constant of 1 (Section 2.1). Typical force fields use fixed point charges and hence, should have a non-unit dielectric constant, but the correct value is generally unknown. UFF and ReaxFF allow charges to fluctuate according to the QEq charge equilibration model. Thus, the proper dielectric constant is 1, just as for QM. Applying macroscopic dielectric constants to atomistically modeled environments is not justified.

In this study, ReaxFF was trained to capture the correct qualitative trends in reactivity and proton dynamics in hydrated polymeric systems, based on QM data for triflic acid in the presence of one to five explicit water molecules. ReaxFF-minimized structures show that proton transfer occurs when three or more water molecules are present, in good agreement with QM results (Fig. S2-1; ESI†).^{47,53,60–63,66,67}

ReaxFF MD (RMD) simulations were conducted on all classically equilibrated cells (Section 2.2.1) to simulate proton exchange between Nafion and water. The cells were relaxed by steepest-descent energy minimization, followed by a 10 ps NVT simulation at 10 K. The cells were then heated to 300 K over 50 ps. ReaxFF simulations were conducted for 2 ns under NPT¹⁷ conditions (300 K and 1 atm), during which the cell densities were monitored (Fig. S2-2; ESI†).

RMD simulations were performed using LAMMPS (0.5 fs time step). RMD structure files corresponding to snapshots at 2 ns are available (ESI PDB files†). Molecular surfaces were generated in Maestro (version 13.3, ©Schrödinger, LLC, New York, NY, 2023). Closed Connolly surfaces with a 1.4 Å probe radius were applied to various atom groupings.

3 Results and discussion

3.1 DFT calculated Nafion monomer vibrational normal modes

We have reported extensive frequency analyses (at the X3LYP/6-311G**++ level) of dry (i.e., Λ = 0) RSO₃(H) models (e.g., 1-mer-CH₃; Fig. 4a).^{8,29–31,33–35} These include group mode assignments (Table 1) correlated to hydration-dependent PFSA vibrational bands (Fig. 2a and b). Assignments are based on the visualization of eigenvector normal mode animations (ESI Videos†).^{8,30,36,37,40} Excellent agreement was found between X3LYP 1-mer-CH₃ frequencies and corresponding IR†† band frequencies (Fig. 4b). The calculated frequencies are within ∼1% of experimental values, except for α_LF, which is 14% lower than the observed 910 cm⁻¹ band. Frequency errors are often attributed to scaling factors (varies with functional and basis set) and the choice of chemical repeat unit.^28,35,101

Fig. 4 Theoretical and experimental Nafion vibrational group mode analyses: (a) model monomer structures; (b) effect of functional and backbone capping groups on calculated frequencies (columns 1-3). Animations for all listed 1-mer-CF₃ normal modes (column 3) are available (ESI†). X3LYP-based frequencies (column 3), FTIR band frequencies (column 4), and NR212 spectra are adapted with permission from Loupe et al.⁸ Copyright 2020 American Chemical Society.

Yamaguchi and Ohira evaluated several hybrid functional and basis set combinations for PFSA sidechain models, finding that PBE0/6-311G(d) offers the best balance of accuracy and computational time.³⁷ Thus, we performed frequency analyses with the PBE0-D3 hybrid functional,^103–105 which accounts for long-range interactions,¹⁰² and the same basis set as previously reported^{8,29–31,33–35} (Section 2.1). The 1-mer-CH₃ α_LF value improves by ∼6% and the β_LF value improves slightly with PBE0-D3 (Fig. 4b). All other listed modes increase in error. The insensitivity of the Nafion side chain (NSC)‡‡ band to state-of-hydration^8,30,35 (band is fixed at 983 cm⁻¹) is better captured with PBE0-D3. Yet, the X3LYP NSC values are much closer to the observed band. Thus, for 1-mer-CH₃, neither functional clearly outperforms the other, deeming both suitable for frequency analysis.

Historically, the 1-mer-CH₃ model was used to avoid “computational interference” with the sidechain –CF₃ group.^8,29,33–35 Replacing methyl groups with –CF₃ groups (1-mer-CF₃; Fig. 4a), however, has a negligible effect on the PBE0-D3 frequencies (Fig. 4b). Notably, the NSC group modes (dominated by sidechain –CF₃ and COC–B motions) are unaffected by the backbone capping groups, as their large separation from the COC–B group prevents significant coupling of their motions.

The exceptional accuracy of the X3LYP-calculated dry 1-mer-CH₃ β_HF frequency (1059 cm⁻¹; Fig. 4b) is fortuitous given that β-sites are formed and stabilized in the presence of water.^47,53 In comparison, the PBE0-D3 β_HF frequency for all monomer models are 26 cm⁻¹ less than the observed 1058 cm⁻¹ band. Hydration of the 1-mer-CF₃ β-site greatly reduces the PBE0-D3 β_HF frequency error ((Table S1-2†): β_HF increases to 1049 cm⁻¹ at Λ_d (i.e., Λ = 3); β_HF is 1052 ± 1.5 cm⁻¹ between Λ = 3 and Λ = 15. As Λ increases, the local permittivity around the β-site should approach that of hydrated membrane β-sites,^10,116 allowing for a more realistic β_HF group mode calculation.

DFT-calculated exchange site environments are typically derived from a limited landscape of energy-minimized structures,⁵⁷ lacking both the structural complexity and site-to-site variation inherent in real ionomer repeat units.¹⁰¹ Thousands of realistic exchange site environments are accessed with a lower level of theory like MD, as discussed below (Section 3.2).

QM-calculated IR spectra of all model compounds (ESI-S1†) and normal mode animations for component models and 1-mer-CF₃ are available (ESI Videos†).

3.2 Nafion ReaxFF MD simulations

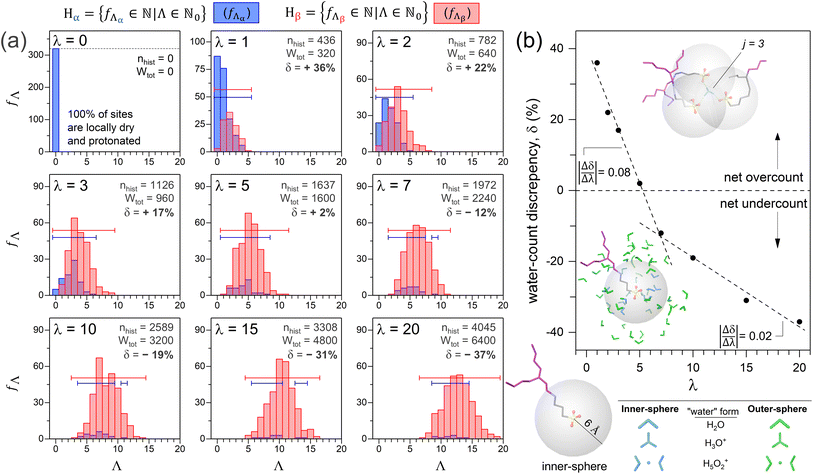
RMD simulations of nine Nafion cells were performed at λ values ranging from 0 to 20. Trajectories of protonation levels versus time established a standard simulation duration of 2 ns (Fig. S2-3; ESI†). In this section, ‘water’ includes all water molecules whether they are neutral or are part of a protonated hydration complex (i.e., hydronium, Zundel, Eigen, etc.),^21,73 unless otherwise specified. A standard sulfur-centered radial cutoff distance (b) of 6 ŧ§ defines an ‘inner-sphere’ and ‘outer-sphere’ boundary in this work. The integer number of inner-sphere waters is Λ. Each DFT and RMD-generated exchange site environment will be referred to by its protonation state (i.e., α or β) and a numerical subscript representing the site's Λ value (e.g., β₁₄ denotes an ionized exchange site with 14 inner-sphere waters).

3.2.1 Inner-sphere and outer-sphere waters. For real and theoretical ionomer samples, W_tot is the total number of waters (eqn (4)):where N_A is Avogadro's number, m_dry is the dry mass, and N_S is the total number of sulfur atoms. For both the RMD simulations and our previous all-classical simulations, N_S is 320.⁸ Every exchange site has an integer Λ value representing inner-sphere water oxygens. Waters contributing to multiple Λ (i.e., multiple sulfur-spheres) are “bridge”⁸⁴ waters. Waters that contribute to single sulfur-spheres are “non-bridge” waters. The sum of all inner-sphere waters (W_IS) and all outer-sphere waters (W_OS) is W_tot (eqn (5)).

W_tot = W_IS + W_OS (5)

Fig. 5a shows histograms of Λ number frequencies (f_Λ) versus Λ for the nine simulated cells, where f_Λ values range from 0 to N_S. Thus, the range of f_Λ values can formally be defined by the set, {f_Λ ∈ [Doublestruck N]₀|f_Λ ≤ N_S}. The histogram color coding is discussed later (Section 3.2.2). The sum of the f_Λ by Λ products is the MD cell's histogram number, n_hist (eqn (6)).

Fig. 5 Inner- and outer-sphere water content versus λ. (a) Overlapping histograms of f_Λ versus Λ, for nine λ values. Blue and red histograms correspond to protonated and deprotonated exchange sites, respectively. (b) Water-count discrepancy, δ, versus λ. Structural examples contributing to δ are inset: (top) pronated bridge-water overcounted twice (i.e., j = 3): and (bottom) non-bridge inner-sphere waters (light blue) and undercounted outer-sphere waters (green).

The upper limit p is the maximum Λ value recorded for a Λ distribution, which depends on b and λ (e.g., p is 19 for λ = 20; Fig. 5a). The domain of Λ is formally, {Λ ∈ [Doublestruck N]₀|Λ ≤ p}. If there are no bridge waters, n_hist equals W_IS. The presence of bridge waters breaks the equality and thus contributes towards a net overcount (n_over) of W_IS (eqn (7)).

W_IS = n_hist − n_over (7)

Bridge-waters within j inner-spheres are overcounted j − 1 time(s), where j is 2 or larger. The domain of j is formally,{j ∈ [Doublestruck N]|j ≥ 2}. The number of bridge waters occupying j spheres is f_j. The sum of f_j by j − 1 products is n_over (eqn (8)).

The upper limit q is the maximum number of inner-spheres that a water resides in, which, similar to p, depends on b and λ (q is either 4 and 5 across the nine λ systems, Table S2-1; ESI†). A more descriptive W_IS definition is now obtained by substitution of eqn (6) and (8) into eqn (7) (eqn (9)).

A full expression for W_tot is established by substitution of eqn (9) into eqn (5) (eqn 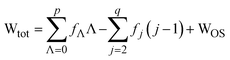(10)).

The water-count discrepancy (δ) represents the amount by which n_hist is an overcount (δ > 0) or undercount (δ < 0) of W_tot, relative to W_tot (eqn (11)).

Alternatively, δ may be recast in terms of n_over and W_OS (total number of over- and under-counts, respectively) by substitution of eqn (5) and (7) into eqn (11) (eqn (12)).

Eqn (4)–(12) are summarized as a two-dimensional conceptual illustration (Fig. S2-4; ESI†).

Fig. 5b shows δ versus λ for the simulations of the eight hydrated systems. There are two linear segments with slopes of −0.08 (between λ = 1 and λ = 7) and −0.02 (between λ = 7 and λ = 20) that intersect at λ₇. The steeper segment results from a reduction of overlapping sulfur-spheres (i.e., n_over decreases), concurrent with the emergence of a water-rich phase (i.e., W_OS increases). For very low λ, waters are predominantly inner-sphere¹⁰ and bridge exchange sites. Fig. 6 depicts bridge waters as light blue spheroids bridging yellow trefoils (exchange sites). Protonated bridge waters, or “hydronium-mediated bridges”, have been reported in CMD simulations of Nafion, Aquivion, and a perfluorinated phosphoric acid by Jang and coworkers.^69,83 The λ = 0 and λ = 2 cell cross-sectional surfaces both show a greater extent of clustered exchange sites than that of λ = 20, consistent with reports of stronger S–S pairwise correlations with decreasing λ.^{69,71,76–78,83,84,87} At λ = 5, while n_over is counterbalanced by W_OS, there remain bridge waters that impact the slope up until the intersection at λ = 7. The shallower slope is attributed almost exclusively to the progressive increase of outer sphere waters (i.e., W_OS increases while n_over is negligible). Outer-sphere waters (green) are either bulk-like (i.e., clustered) or isolated (Fig. 6). The hydration-dependent growth of a three-phase nanomorphology is illustrated in Fig. S2-5 (ESI†).

Fig. 6 Colored Connolly surfaces applied to atom groupings from λ = 0, 2, and 20 MD cells. Inner-sphere waters (light blue) are either bridge (overcounted) or non-bridge. Outer-sphere waters (green) are either isolated or bulk-like (both are undercounted).

3.2.2 Λ_α and Λ_β distributions. The λ = 0 cell (i.e., W_tot = 0) has 320 locally dry exchange sites (i.e., f₀ = 320), corresponding to the single Λ = 0 bar in Fig. 5a. All sites remained protonated throughout the simulation period (Fig. S2-3; ESI†), consistent with no autoprotolysis products (i.e., –SO₃H₂⁺ and –SO₃⁻).^19,53–55 A solvent autoprotolysis constant (K_ap), depends on the solvent equivalent weight, density, and dielectric constant (κ).¹¹⁷ Although K_ap for Nafion is not reported, it is likely negligible because of its low κ (κ ≈ 4 for λ = 1),¹¹⁶ high equivalent weight, and low anhydrous ionic conductivity.^118,119 Even for sulfuric acid, which has a high κ (κ ≈ 100; K_ap = 2.4 × 10⁻⁴ at 25 °C)^120,121 and low equivalent weight, only three H₃O₄⁺ ions are expected at equilibrium in a λ = 0 cell volume (ESI-S3†). In a transmission FTIR study of ‘dry’ Nafion, Buzzoni et al. attributed a weak intensity 1060 cm⁻¹ band (β_HF) to –SO₃⁻ groups formed via autoprotolysis.¹²² This is unlikely given the above discussion of sulfuric acid. In an ATR-FTIR study of ‘dry’ Nafion by Negro et al., the 1060 cm⁻¹ band is attributed to –SO₃⁻ groups persisting due to residual membrane water.¹²³ Whatever the acquisition technique, complete absence of the 1060 cm⁻¹ band requires maintenance of a completely dry atmosphere during measurement.²⁹ Loupe et al. describes in detail the challenges of obtaining completely dry PFSA spectra in an ATR configuration.⁸

All non-zero λ cells result in α-site and β-site Λ distributions, visualized as blue and red histograms, respectively (Fig. 5a). Each histogram is represented as a numerical set, with each element corresponding to a single bar. For example, each blue histogram is represented by the set H_α (eqn (13)).

H_α = {f_Λα ∈ [Doublestruck N]|Λ ∈ [Doublestruck N]₀} (13)

Each H_α element corresponds to a blue bar, representing non-zero frequencies of α-sites with specific Λ values (f_Λα). The number of f_Λα elements (i.e., number of blue bars) is the cardinality of H_α, |H_α| (Table 2). The sum of f_Λα over all Λ represents the total number of α-sites in the cell (N_Sα; eqn (14)).

Table 2 Cardinality of H_α, H_β, and the union of both sets versus λ for the nine simulated Nafion cells

---

Similarly, each red histogram is represented as the set, H_β (eqn (15)).

H_β = {f_Λβ ∈ [Doublestruck N]|Λ ∈ [Doublestruck N]₀} (15)

Each H_β element corresponds to a red bar, representing non-zero frequencies of β-sites with specific Λ values (f_Λβ). The number of f_Λβ elements is the cardinality of H_β, |H_β| (Table 2). The sum of f_Λβ over all Λ is the total number of β-sites for the cell (N_Sβ, eqn (16)).

The sum of N_Sα and N_Sβ is N_S (eqn (17) and (18)).

The sum of corresponding f_Λα and f_Λβ values is f_Λ, which represents the number of exchange sites with a given Λ, independent of protonation state. The rightmost expression of eqn (17) is then simplified to represent the sum of every Fig. 5a histogram bar, independent of its color (eqn (18)).

Fig. 7 shows N_Sα versus λ. According to eqn (14), the value of each bar is the sum of all blue histogram bars from Fig. 5a, for the corresponding λ. Thus, the exponential decay of N_Sα versus λ represents the diminishing significance of blue histograms with λ, and a sharp decrease in the proportion of α-sites with increasing water content. The persistence of α-sites across all λ contradicts the widely adopted notion that all exchange sites are ionized for λ ≥ 3.^{68–78,80–87} Our finding concurs with Sengupta and Lyulin's report of α-sites at high λ.⁷⁹

Fig. 7 –SO₃H counts versus λ after 2 ns of ReaxFF.

All eight hydrated cells result in overlapping histograms across variable Λ intervals (Fig. 5a). For λ₁, both H_α and H_β span Λ values from 0 to 5 (i.e., |H_α| = |H_β| = 6). With increasing λ, both histograms shift towards higher Λ, signifying a growing number of inner-sphere waters for every exchange site. Consequently, the proportion of locally dry sites (i.e., f₀/N_S) diminishes from 100% to 2% between λ = 0 and λ = 3. For λ = 5 and beyond, all exchange sites are hydrated by at least one water. It is noteworthy that the absence of Λ = 0 sites starting at λ = 5, coincides with the equality of over- and undercounted waters (i.e., δ ≈ 0 at λ = 5, Fig. 5b).

Table 2 shows that |H_β| generally increases with λ, reflecting a growing variety of β-site Λ values with hydration. This is consistent with a 3-mer Aquivion model, which shows an increasing preference for non-uniform hydration as λ increases.⁸⁹ In contrast, |H_α| remains roughly the same across all non-zero λ. The number of Λ values over which H_α and H_β overlap also show little variation with λ (Fig. 5a). The tails of the α histograms, on the high Λ side, never overlap with the β histograms beyond λ = 1, indicating that sites with the largest Λ values in any cell are always ionized.

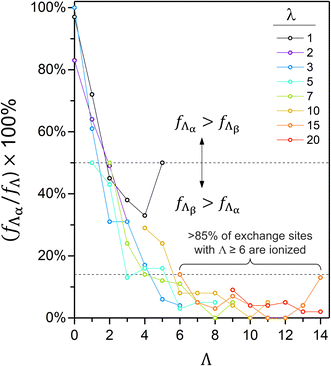
For any non-zero λ, the proportion of α-sites with a given Λ generally decreases with increasing Λ (i.e., f_Λα/f_Λ; Fig. 8). In the λ = 3 cell, for example, f_Λα/f_Λ decreases from 61% to 4% as Λ increases from 1 to 6. In every hydrated cell, f_Λα/f_Λ is generally less than 15% if Λ is at least 6. The negative correlation between f_Λα/f_Λ and Λ is consistent with reports of an increased ionization propensity for CF₃SO₃H (i.e., triflic acid) and CF₃CF₂SO₃H as Λ increases.^47,53

Fig. 8 Proportion of protonated (i.e., α) exchange sites versus Λ for all λ > 0 cells.

3.2.3 ReaxFF MD exchange site environments. Our RMD simulations model the spatial and temporal heterogeneity of 320 exchange sites per λ (Section 3.2.1 and 3.2.2), where each site is embedded in a realistic environment with up to ∼40 000 surrounding atoms. The coexistence of α- and β-sites with identical Λ values in all hydrated simulation cells (Fig. 8) suggests that additional variables beyond Λ influence protonation states. The interplay of three stereoelectronic variables is identified through visualization of inner- and outer-sphere environments (Fig. 9): (i) the local number density of polar and non-polar fragments, (ii) the spatial arrangement of water, polymer fragments, and ions, and (iii) long-range electrostatic effects.

Fig. 9 DFT and ReaxFF MD generated exchange site inner-sphere environments. The number of non-SO₃H inner-sphere atoms is N_np (np stands for nonpolar). Not all outer-sphere atoms (purple) are shown. Atom colors: hydrogen (white), carbon (grey), non-hydronium oxygen (red), hydronium oxygen (blue), fluorine (green), sulfur (yellow). An animated version of this figure is available (ESI†).

The ionization propensity (i.e., acidity) of exchange sites is primarily influenced by the identity and number density of inner-sphere atoms (variable i). Exchange site acidity is expected to increase with Λ (water molecules are highly polar) and decrease with the number density of non-polar fragments within the inner-sphere (e.g., CF₂ and COC groups). We chose to enumerate the latter parameter by the number of non-SO₃(H) Nafion atoms (N_np). Consider, the sixteen 1-mer-CF₃ monomer models geometry-optimized with DFT, each with a unique Λ ranging from 0 to 15 (Fig. S1-6; ESI-S1†). Since the monomer N_np values vary minimally (Fig. S1-7b; ESI†), their acidities primarily depend on Λ, leading to the establishment of a Λ dissociation threshold (Λ_d = 3): the exchange site is α for Λ < 3 and β for Λ ≥ 3 (Fig. S1-6; ESI†). In contrast, the RMD-modeled inner-spheres exhibit larger and more diverse N_np values that vary independently of Λ, precluding the establishment of a Λ_d (Fig. 9). The RMD inner-sphere structural diversity is facilitated by the abundant presence of polymer fragments from neighboring monomers, with minimal disruption to native³⁴ backbone dihedral angles.^{17,37,57,58,124}

The spatial arrangement of water, polymer atoms, and ions (variable ii) is also expected to influence exchange site protonation states. Consider the two arbitrarily selected α₅ and β₅ sites from the λ = 5 cell (Fig. 9). The α₅ site proton is partially stabilized by its nearest ether linkage, rather than by a water molecule. Moreover, the α₅ site is directly hydrated by only a single water, while the four remaining waters contribute to the stabilization of a neighboring β-site and two other protons. In contrast, the β₅ site has a much smaller N_np, lacks excess charge carriers, and is directly hydrated by two waters. The λ = 2 cell hosts a nearly equal number of α₂ and β₂ sites (Fig. 8). Despite the selected β₂ site (Fig. 9) having a large N_np, two nearby exchange sites contribute to stabilizing the dissociated proton (the proton serves as a hydronium-mediated bridge^69,83 between three exchange sites). Similarly, Paddison and Elliot report that the number of waters required to cause exchange site ionization is less than three when exchange sites are nearby one another.^57,58 The inclusion of a high dielectric constant continuum solvation model has also been shown to decrease the number of waters required for ionization.⁶¹ Meanwhile, the selected α₂ site proton lacks any direct interaction with water, causing it to remain associated. These observations from arbitrarily selected exchange sites highlight how the highly variable spatial arrangement of inner-sphere species influence proton association and dissociation.

Finally, the exertion of long-range electrostatic forces (variable iii) on RMD sites should not be excluded as a variable that influences protonation states. While these forces may be individually insignificant compared to shorter-range Coulombic interactions, the MD cells contain significantly more atoms contributing to them than the 1-mer-CF₃ complexes. The overall water content (i.e., λ) is expected to impact the long-range forces exerted on any exchange site.

4 Conclusion

This is the first report on ReaxFF modeling of proton exchange between water molecules and ion-exchange sites within an MD framework. MD simulations were performed on the perfluorinated sulfonic acid (PFSA) ionomer Nafion at λ values ranging from 0 to 20. Over each 2 ns simulation, proton exchange between initially protonated exchange sites (sulfonic acid groups) and water molecules resulted in λ-dependent equilibrium proportions of protonated sites (α, i.e., sulfonic acid) and deprotonated sites (β, i.e., sulfonate ion). An exponential decrease in the proportion of α-sites was observed with increasing λ. Notably, we found that α-sites persist across all λ cells, challenging the notion that all exchange sites are ionized above a fixed λ threshold.^{68,70–78,80–88} Exchange sites are hydrated non-uniformly, as demonstrated by λ-dependent distributions of Λ values, representing the number of waters within sulfur-centered ‘inner-spheres’ with 6 Å radii.^{8,40,64,79,89–91} For lower λ cells, the majority of waters reside either within a single exchange site inner-sphere (‘non-bridge’ waters) or multiple inner-spheres (‘bridge’ waters). As λ increases, the proportion of bridge waters decreases, due to the separation of sulfonate groups,^{69,71,76–78,83,84,87} concurrent with the evolution of a water-rich phase composed of outer-sphere waters.

Distributions of α- and β-site Λ values (Λ_α and Λ_β distributions, respectively) with significant overlap were observed. Examination of inner-spheres revealed the complex interplay of three stereoelectronic variables affecting protonation state: (i) the local number density of polar and non-polar fragments, (ii) the spatial arrangement of water, polymer fragments, and ions, and (iii) long-range electrostatic effects. We assert that each exchange site environment yields a characteristic IR spectrum (premise II),⁸ and that our Λ_α and Λ_β distributions form the basis for any observed IR spectrum (premises I, III).

Taken together, our study focuses on the intrinsic behavior of proton-exchanged Nafion, particularly the interactions between –SO₃H groups and water molecules. By modeling simplified H⁺/H₃O⁺ environments, we systematically explored hydration-dependent proton transfer dynamics, hydrogen-bond structures, and the microstructural organization driven by the acidic side chains. We acknowledge that in real PEM environments, contaminants such as alkali metal cations can influence the acid–base equilibrium and local hydration structure through ionic screening or competitive interactions. While this study aims to isolate and understand the fundamental interactions between –SO₃H groups and water molecules, we reported on the hydration-dependent spectroscopy of metal ion-exchanged Nafion (K⁺, Na⁺, Li⁺, Ca²⁺, Cd²⁺, Ni²⁺, and Al³⁺).^29,33 Future work can correlate our spectroscopic findings with ReaxFF simulations of metal ion-exchanged Nafion to better understand the impact of external cations.

Intense efforts are focused on the development of environmentally friendly polymer electrolytes that offer high proton conductivity, low gas permeability, and improved water-retention at elevated temperatures. Our methodology is not only applicable to any ionomer, but also to any molecular system undergoing solvation-dependent chemical changes.

Data availability

A collection of files supporting this article are available as part of the ESI:† vibrational normal mode animations of model compounds, PDB files of RMD cells, RMD data analysis files, and supporting figures with corresponding discussion. The ESI document provides a description of each supporting file (ESI†).

Author contributions

D. J. D.: conceptualization, data curation, formal analysis, methodology, visualization, and writing – original draft and editing. M. Y. Y.: data curation, formal analysis, investigation, software, writing – MD methods, and writing – review & editing. N. D.: data curation, investigation, supervision, writing – DFT methods, and writing – review & editing. S. S. J.: supervision and writing – review & editing. W. A. G.: conceptualization, project administration, resources, supervision, and writing – review & editing. E. S. S.: conceptualization, funding acquisition, project administration, resources, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors acknowledge financial support from A3 Global (grant code G0007820) and Northeastern University. The ReaxFF work used Expanse at San Diego Supercomputer Center through allocation DMR160114 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #2137603, #2138259, #2138286, #2138296, and #2138307.

References

1. United States Department of Energy, US National Clean Hydrogen Strategy and Roadmap, 2023.
2. United States Department of State; United States Executive Office of the President, The Long-Term Strategy of the United States: Pathways to Net-Zero Greenhouse Gas Emissions by 2050, 2021.
3. M. El-Shafie, Hydrogen Production by Water Electrolysis Technologies: A Review, Results Eng, 2023, 20(September), 101426,  DOI:10.1016/j.rineng.2023.101426.
4. J. Miyake and K. Miyatake, Fluorine-Free Sulfonated Aromatic Polymers as Proton Exchange Membranes, Polym. J., 2017, 49(6), 487–495,  DOI:10.1038/pj.2017.11.
5. M. Adamski, N. Peressin and S. Holdcroft, On the Evolution of Sulfonated Polyphenylenes as Proton Exchange Membranes for Fuel Cells, Mater. Adv., 2021, 2(15), 4966–5005,  10.1039/D1MA00511A.
6. M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, A Comprehensive Review on PEM Water Electrolysis, Int. J. Hydrogen Energy, 2013, 38(12), 4901–4934,  DOI:10.1016/j.ijhydene.2013.01.151.
7. United States Department of Energy, Comparison of Fuel Cell Technologies, https://www.energy.gov/eere/fuelcells/comparison-fuel-cell-technologies, accessed Mar 7, 2024.
8. N. Loupe, K. Abu-Hakmeh, S. Gao, L. Gonzalez, M. Ingargiola, K. Mathiowetz, R. Cruse, J. Doan, A. Schide, I. Salas, N. Dimakis, S. S. Jang, W. A. Goddard and E. S. Smotkin, Group Vibrational Mode Assignments as a Broadly Applicable Tool for Characterizing Ionomer Membrane Structure as a Function of Degree of Hydration, Chem. Mater., 2020, 32(5), 1828–1843,  DOI:10.1021/acs.chemmater.9b04037.
9. K. A. Mauritz and R. B. Moore, State of Understanding of Nafion, Chem. Rev., 2004, 104(10), 4535–4586,  DOI:10.1021/cr0207123.
10. A. Kusoglu and A. Z. Weber, New Insights into Perfluorinated Sulfonic-Acid Ionomers, Chem. Rev., 2017, 117(3), 987–1104,  DOI:10.1021/acs.chemrev.6b00159.
11. K.-D. Kreuer, Ion Conducting Membranes for Fuel Cells and Other Electrochemical Devices, Chem. Mater., 2014, 26(1), 361–380,  DOI:10.1021/cm402742u.
12. A. R. Crothers, A. Kusoglu, C. J. Radke and A. Z. Weber, Influence of Mesoscale Interactions on Proton, Water, and Electrokinetic Transport in Solvent-Filled Membranes: Theory and Simulation, Langmuir, 2022, 38(34), 10351–10728,  DOI:10.1021/acs.langmuir.2c00706.
13. M. Soniat and F. A. Houle, How the Hydrophobic Interface between a Perfluorosulfonic Acid Polymer and Water Vapor Controls Membrane Hydration, ACS Appl. Polym. Mater., 2022, 4(5), 2960–4046,  DOI:10.1021/acsapm.1c01805.
14. M. Fumagalli, S. Lyonnard, G. Prajapati, Q. Berrod, L. Porcar, A. Guillermo and G. Gebel, Fast Water Diffusion and Long-Term Polymer Reorganization during Nafion Membrane Hydration Evidenced by Time-Resolved Small-Angle Neutron Scattering, J. Phys. Chem. B, 2015, 119(23), 7068–7076,  DOI:10.1021/acs.jpcb.5b01220.
15. G. S. Hwang, D. Y. Parkinson, A. Kusoglu, A. A. MacDowell and A. Z. Weber, Understanding Water Uptake and Transport in Nafion Using X-Ray Microtomography, ACS Macro Lett., 2013, 2(4), 288–291,  DOI:10.1021/mz300651a.
16. D. R. Morris and X. Sun, Water-Sorption and Transport Properties of Nafion 117 H, J. Appl. Polym., 1993, 50(8), 1445–1452.
17. J. A. Elliott and S. J. Paddison, Modelling of Morphology and Proton Transport in PFSA Membranes, Phys. Chem. Chem. Phys., 2007, 9(21), 2602–2618,  10.1039/b701234a.
18. H. Rivera, J. S. Lawton, D. E. Budil and E. S. Smotkin, Effect of Sorbed Methanol, Current, and Temperature on Multicomponent Transport in Nafion-Based Direct Methanol Fuel Cells, J. Phys. Chem. B, 2008, 112(29), 8542–8548,  DOI:10.1021/jp803158h.
19. K. Sagarik, M. Phonyiem, C. Lao-ngam and S. Chaiwongwattana, Mechanisms of Proton Transfer in Nafion®: Elementary Reactions at the Sulfonic Acid Groups, Phys. Chem. Chem. Phys., 2008, 10(15), 2098,  10.1039/b718480h.
20. S. Feng and G. A. Voth, Proton Solvation and Transport in Hydrated Nafion, J. Phys. Chem. B, 2011, 115(19), 5903–5912,  DOI:10.1021/jp2002194.
21. R. Devanathan, N. Idupulapati, M. D. Baer, C. J. Mundy and M. Dupuis, Ab Initio Molecular Dynamics Simulation of Proton Hopping in a Model Polymer Membrane, J. Phys. Chem. B, 2013, 117(51), 16522–16529,  DOI:10.1021/jp410229u.
22. A. Kusoglu, S. Savagatrup, K. T. Clark and A. Z. Weber, Role of Mechanical Factors in Controlling the Structure–Function Relationship of PFSA Ionomers, Macromolecules, 2012, 45(18), 7467–7476,  DOI:10.1021/ma301419s.
23. P. V. Komarov, I. N. Veselov, P. P. Chu and P. G. Khalatur, Mesoscale Simulation of Polymer Electrolyte Membranes Based on Sulfonated Poly(Ether Ether Ketone) and Nafion, Soft Matter, 2010, 6(16), 3939–3956,  10.1039/b921369d.
24. M. Laporta, M. Pegoraro and L. Zanderighi, Perfluorosulfonated Membrane (Nafion): FT-IR Study of the State of Water with Increasing Humidity, Phys. Chem. Chem. Phys., 1999, 1(19), 4619–4628,  10.1039/a904460d.
25. H. L. Yeager and A. Steck, Cation and Water Diffusion in Nafion Ion Exchange Membranes: Influence of Polymer Structure, J. Electrochem. Soc., 1981, 128(9), 1880–1884,  DOI:10.1149/1.2127757.
26. F. I. Allen, L. R. Comolli, A. Kusoglu, M. A. Modestino, A. M. Minor and A. Z. Weber, Morphology of Hydrated As-Cast Nafion Revealed through Cryo Electron Tomography, ACS Macro Lett., 2015, 4(1), 1–5,  DOI:10.1021/mz500606h.
27. S. Rongpipi, J. M. Chan, A. Bird, G. Freychet, A. Kusoglu and G. M. Su, Revealing Mesoscale Ionomer Membrane Structure by Tender Resonant X-Ray Scattering, ACS Appl. Polym. Mater., 2024, 6(23), 14115–14123,  DOI:10.1021/acsapm.4c00286.
28. J. Doan, E. Kingston, I. Kendrick, K. Anderson, N. Dimakis, P. Knauth, M. L. Di Vona and E. S. Smotkin, Theoretical and Experimental Infrared Spectra of Hydrated and Dehydrated Sulfonated Poly(Ether Ether Ketone), Polymer, 2014, 55(18), 4671–4676,  DOI:10.1016/j.polymer.2014.07.011.
29. J. Doan, N. E. Navarro, D. Kumari, K. Anderson, E. Kingston, C. Johnson, A. Vong, N. Dimakis and E. S. Smotkin, Symmetry-Based IR Group Modes as Dynamic Probes of Nafion Ion Exchange Site Structure, Polymer, 2015, 73, 34–41,  DOI:10.1016/j.polymer.2015.07.017.
30. M. Webber, N. Dimakis, D. Kumari, M. Fuccillo and E. S. Smotkin, Mechanically Coupled Internal Coordinates of Ionomer Vibrational Modes, Macromolecules, 2010, 43(13), 5500–5502,  DOI:10.1021/ma100915u.
31. I. Kendrick, J. Fore, J. Doan, N. Loupe, A. Vong, N. Dimakis, M. Diem and E. S. Smotkin, Operando Raman Micro-Spectroscopy of Polymer Electrolyte Fuel Cells, J. Electrochem. Soc., 2016, 163(4), H3152–H3159,  DOI:10.1149/2.0211604jes.
32. K. Anderson, E. Kingston, J. Romeo, J. Doan, N. Loupe, N. Dimakis and E. S. Smotkin, Infrared Spectroscopy of Ion-Induced Cross-Linked Sulfonated Poly(Ether Ether Ketone), Polymer, 2016, 93, 65–71,  DOI:10.1016/j.polymer.2016.04.015.
33. N. Loupe, N. Nasirova, J. Doan, D. Valdez, M. Furlani, N. Dimakis and E. S. Smotkin, DFT - Experimental IR Spectroscopy of Lithiated Single Ion Conducting Perfluorinated Sulfonated Ionomers: Ion Induced Polarization Band Broadening, J. Electroanal. Chem., 2017, 800, 176–183,  DOI:10.1016/j.jelechem.2017.02.041.
34. I. Kendrick, D. Kumari, A. Yakaboski, N. Dimakis and E. S. Smotkin, Elucidating the Ionomer-Electrified Metal Interface, J. Am. Chem. Soc., 2010, 132(49), 17611–17616,  DOI:10.1021/ja1081487.
35. I. Kendrick, A. Yakaboski, E. Kingston, J. Doan, N. Dimakis and E. S. Smotkin, Theoretical and Experimental Infrared Spectra of Hydrated and Dehydrated Nafion, J. Polym. Sci., Part B: Polym. Phys., 2013, 51(18), 1329–1334,  DOI:10.1002/polb.23348.
36. E. Kraka, M. Quintano, H. W. La Force, J. J. Antonio and M. Freindorf, The Local Vibrational Mode Theory and Its Place in the Vibrational Spectroscopy Arena, J. Phys. Chem. A, 2022, 126(47), 8781–8798,  DOI:10.1021/acs.jpca.2c05962.
37. M. Yamaguchi and A. Ohira, Vibrational Analysis of Side Chain Model Compounds of Perfluorinated Alkyl Sulfonic Acid Ionomers, J. Phys. Chem. A, 2012, 116(44), 10850–10863,  DOI:10.1021/jp308663c.
38. A. Moran and S. Mukamel, The Origin of Vibrational Mode Couplings in Various Secondary Structural Motifs of Polypeptides, Proc. Natl. Acad. Sci. U. S. A., 2004, 101(2), 506–510,  DOI:10.1073/pnas.2533089100.
39. E. Kraka, W. Zou and Y. Tao, Decoding Chemical Information from Vibrational Spectroscopy Data: Local Vibrational Mode Theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10(5), 1–34,  DOI:10.1002/wcms.1480.
40. N. J. Silva, D. Tunega, C. Korzeniewski, H. Lischka and A. J. A. Aquino, Microhydration of Polymer Electrolyte Membranes: A Comparison of Hydrogen-Bonding Networks and Spectral Properties of Nafion and Bis[(Perfluoroalkyl)Sulfonyl] Imide, J. Phys. Chem. B, 2019, 123(46), 9899–9911,  DOI:10.1021/acs.jpcb.9b07815.
41. Y. Liang, J. P. Kitt, S. D. Minteer, J. M. Harris and C. Korzeniewski, Vibrational Spectroscopic Monitoring of the Gelation Transition in Nafion Ionomer Dispersions, Appl. Spectrosc., 2021, 75(4), 376–384,  DOI:10.1177/0003702820949129.
42. M. A. Barique, E. Tsuchida, A. Ohira and K. Tashiro, Effect of Elevated Temperatures on the States of Water and Their Correlation with the Proton Conductivity of Nafion, ACS Omega, 2018, 3(1), 349–360,  DOI:10.1021/acsomega.7b01765.
43. R. K. Singh, K. Kunimatsu, K. Miyatake and T. Tsuneda, Experimental and Theoretical Infrared Spectroscopic Study on Hydrated Nafion Membrane, Macromolecules, 2016, 49(17), 6621–6629,  DOI:10.1021/acs.macromol.6b00999.
44. C. K. Byun, T. Parker, C. Liang, I. Kendrick, N. Dimakis, E. S. Smotkin, L. M. Jin, D. Zhuang, D. D. Desmarteau, S. E. Creager and C. Korzeniewski, Thermal Processing as a Means to Prepare Durable, Submicron Thickness Ionomer Films for Study by Transmission Infrared Spectroscopy, Anal. Chem., 2012, 84(19), 8127–8132,  DOI:10.1021/ac301662f.
45. M. Danilczuk, L. Lin, S. Schlick, S. J. Hamrock and M. S. Schaberg, Understanding the Fingerprint Region in the Infra-Red Spectra of Perfluorinated Ionomer Membranes and Corresponding Model Compounds: Experiments and Theoretical Calculations, J. Power Sources, 2011, 196(20), 8216–8224,  DOI:10.1016/j.jpowsour.2011.05.067.
46. D. S. Warren and A. J. McQuillan, Infrared Spectroscopic and DFT Vibrational Mode Study of Perfluoro(2-Ethoxyethane) Sulfonic Acid (PES), a Model Nafion Side-Chain Molecule, J. Phys. Chem. B, 2008, 112(34), 10535–10543,  DOI:10.1021/jp801838n.
47. T. Shimoaka, C. Wakai, T. Sakabe, S. Yamazaki and T. Hasegawa, Hydration Structure of Strongly Bound Water on the Sulfonic Acid Group in a Nafion Membrane Studied by Infrared Spectroscopy and Quantum Chemical Calculation, Phys. Chem. Chem. Phys., 2015, 17(14), 8843–8849,  10.1039/c5cp00567a.
48. M. Ludvigsson, J. Lindgren and J. Tegenfeldt, FTIR Study of Water in Cast Nafion Films, Electrochim. Acta, 2000, 45(14), 2267–2271,  DOI:10.1016/S0013-4686(99)00438-7.
49. S. D. Bernardina, J.-B. Brubach, Q. Berrod, A. Guillermo, P. Judeinstein, P. Roy and S. Lyonnard, Mechanism of Ionization, Hydration, and Intermolecular H-Bonding in Proton Conducting Nanostructured Ionomers, J. Phys. Chem. C, 2014, 118(44), 25468–25479,  DOI:10.1021/jp5074818.
50. K. Feng, L. Hou, B. Tang and P. Wu, Does Thermal Treatment Merely Make a H2O-Saturated Nafion Membrane Lose Its Absorbed Water at High Temperature?, Phys. Chem. Chem. Phys., 2015, 17(14), 9106–9115,  10.1039/c5cp00203f.
51. R. Basnayake, G. R. Peterson, D. J. Casadonte and C. Korzeniewski, Hydration and Interfacial Water in Nafion Membrane Probed by Transmission Infrared Spectroscopy, J. Phys. Chem. B, 2006, 110(47), 23938–23943,  DOI:10.1021/jp064121i.
52. J. Ostrowska and A. Narebska, Infrared Study of Hydration and Association of Functional Groups in a Perfluorinated Nafion Membrane, Part 1, Colloid Polym. Sci., 1983, 261(2), 93–98,  DOI:10.1007/BF01410686.
53. V.-A. Glezakou, M. Dupuis and C. J. Mundy, Acid/Base Equilibria in Clusters and Their Role in Proton Exchange Membranes: Computational Insight, Phys. Chem. Chem. Phys., 2007, 9(43), 5752,  10.1039/b709752b.
54. M. Phonyiem, S. Chaiwongwattana, C. Lao-ngam and K. Sagarik, Proton Transfer Reactions and Dynamics of Sulfonic Acid Group in Nafion®, Phys. Chem. Chem. Phys., 2011, 13(23), 10923–10939,  10.1039/c1cp20469f.
55. S. J. Paddison, K. D. Kreuer and J. Maier, About the Choice of the Protogenic Group in Polymer Electrolyte Membranes: Ab Initio Modelling of Sulfonic Acid, Phosphonic Acid, and Imidazole Functionalized Alkanes, Phys. Chem. Chem. Phys., 2006, 8(39), 4530–4542,  10.1039/b611221h.
56. T. E. Springer, T. A. Zawodzinski and S. Gottesfeld, Polymer Electrolyte Fuel Cell Model, J. Electrochem. Soc., 1991, 138(8), 2334–2342,  DOI:10.1149/1.2085971.
57. S. J. Paddison and J. A. Elliott, On the Consequences of Side Chain Flexibility and Backbone Conformation on Hydration and Proton Dissociation in Perfluorosulfonic Acid Membranes, Phys. Chem. Chem. Phys., 2006, 8(18), 2193–2203,  10.1039/b602188c.
58. S. J. Paddison and J. A. Elliott, Molecular Modeling of the Short-Side-Chain Perfluorosulfonic Acid Membrane, J. Phys. Chem. A, 2005, 109(33), 7583–7593,  DOI:10.1021/jp0524734.
59. M. A. Ilhan and E. Spohr, Ab Initio Molecular Dynamics of Proton Networks in Narrow Polymer Electrolyte Pores, J. Phys. Condens. Matter, 2011, 23(23), 234104,  DOI:10.1088/0953-8984/23/23/234104.
60. H. Sakai and T. Tokumasu, Reaction Analysis for Deprotonation of the Sulfonic Group of Perfluorosulfonic Acid Molecules at Low Hydration Levels, J. Phys. Chem. A, 2014, 118(1), 275–282,  DOI:10.1021/jp409781s.
61. F. Sepehr and S. J. Paddison, Primary Hydration and Proton Transfer of Electrolyte Acids: An Ab Initio Study, Solid State Ionics, 2017, 306, 2–12,  DOI:10.1016/j.ssi.2017.03.013.
62. S. Singh, T. Taketsugu and R. K. Singh, Hydration, Prediction of the PKa, and Infrared Spectroscopic Study of Sulfonated Polybenzophenone (SPK) Block-Copolymer Hydrocarbon Membranes and Comparisons with Nafion, ACS Omega, 2021, 6(48), 32739–32748,  DOI:10.1021/acsomega.1c04484.
63. R. K. Singh, T. Tsuneda, K. Miyatake and M. Watanabe, Theoretical Investigation of Local Proton Conductance in the Proton Exchange Membranes, Chem. Phys. Lett., 2014, 608, 11–16,  DOI:10.1016/j.cplett.2014.05.076.
64. T. Zelovich, K. I. Winey and M. E. Tuckerman, Hydronium Ion Diffusion in Model Proton Exchange Membranes at Low Hydration: Insights from Ab Initio Molecular Dynamics, J. Mater. Chem. A, 2021, 9(4), 2448–2458,  10.1039/d0ta10565a.
65. B. F. Habenicht, S. J. Paddison and M. E. Tuckerman, The Effects of the Hydrophobic Environment on Proton Mobility in Perfluorosulfonic Acid Systems: An Ab Initio Molecular Dynamics Study, J. Mater. Chem., 2010, 20(30), 6342–6351,  10.1039/c0jm00253d.
66. C. Wang, J. K. Clark, M. Kumar and S. J. Paddison, An Ab Initio Study of the Primary Hydration and Proton Transfer of CF 3SO3H and CF3O(CF2) 2SO3H: Effects of the Hybrid Functional and Inclusion of Diffuse Functions, Solid State Ionics, 2011, 199–200(1), 6–13,  DOI:10.1016/j.ssi.2011.07.002.
67. S. J. Paddison, The Modeling of Molecular Structure and Ion Transport in Sulfonic Acid Based Ionomer Membranes, J. New Mater. Electrochem. Syst., 2001, 4, 197–207.
68. T. Flottat, B. Latour, F. Goujon, P. Hauret and P. Malfreyt, Investigating Percolation and Clustering Effects on Aquivion and Nafion Membranes at the Molecular Scale, Int. J. Hydrogen Energy, 2023, 48(85), 33283–33296,  DOI:10.1016/j.ijhydene.2023.05.086.
69. R. Lawler, C. Caliendo, H. Ju, J. Y. Kim, S. W. Lee and S. S. Jang, Effect of the Side-Chain Length in Perfluorinated Sulfonic and Phosphoric Acid-Based Membranes on Nanophase Segregation and Transport: A Molecular Dynamics Simulation Approach, J. Phys. Chem. B, 2020, 124(8), 1571–1580,  DOI:10.1021/acs.jpcb.9b10408.
70. S. S. Jang, V. Molinero, T. Çaǧin and W. A. Goddard, Nanophase-Segregation and Transport in Nafion 117 from Molecular Dynamics Simulations: Effect of Monomeric Sequence, J. Phys. Chem. B, 2004, 108(10), 3149–3157,  DOI:10.1021/jp036842c.
71. A. T. Kuo, W. Shinoda and S. Okazaki, Molecular Dynamics Study of the Morphology of Hydrated Perfluorosulfonic Acid Polymer Membranes, J. Phys. Chem. C, 2016, 120(45), 25832–25842,  DOI:10.1021/acs.jpcc.6b08015.
72. D. W. M. Hofmann, L. Kuleshova, B. D'Aguanno, V. D. Noto, E. Negro, F. Conti and M. Vittadello, Investigation of Water Structure in Nafion Membranes by Infrared Spectroscopy and Molecular Dynamics Simulation, J. Phys. Chem. B, 2009, 113(3), 632–639,  DOI:10.1021/jp806761h.
73. R. Wang, S. Liu, L. Wang, M. Li and C. Gao, Understanding of Nanophase Separation and Hydrophilic Morphology in Nafion and SPEEK Membranes: A Combined Experimental and Theoretical Studies, Nanomaterials, 2019, 9(6), 869,  DOI:10.3390/nano9060869.
74. Y. Zhao, Q. Gao, X. Xu, C. Ma, Q. He, Y. Min and S. Zhao, Compromise Mechanism of Proton Transfer in Crown Ether-Based Biomimetic Proton Exchange Membranes: Insights from Molecular Dynamics Simulations, Elsevier B.V., 2025, vol. 715,  DOI:10.1016/j.memsci.2024.123456.
75. S. Akbari, M. T. Hamed Mosavian, F. Moosavi and A. Ahmadpour, Elucidating the Morphological Aspects and Proton Dynamics in a Hybrid Perfluorosulfonic Acid Membrane for Medium-Temperature Fuel Cell Applications, Phys. Chem. Chem. Phys., 2018, 20(47), 29778–29789,  10.1039/C8CP05377D.
76. S. Cui, J. Liu, M. E. Selvan, S. J. Paddison, D. J. Keffer and B. J. Edwards, Comparison of the Hydration and Diffusion of Protons in Perfluorosulfonic Acid Membranes with Molecular Dynamics Simulations, J. Phys. Chem. B, 2008, 112(42), 13273–13284,  DOI:10.1021/jp8039803.
77. S. Cui, J. Liu, M. E. Selvan, D. J. Keffer, B. J. Edwards and W. V. Steele, A Molecular Dynamics Study of a Nafion Polyelectrolyte Membrane and the Aqueous Phase Structure for Proton Transport, J. Phys. Chem. B, 2007, 111(9), 2208–2218,  DOI:10.1021/jp066388n.
78. A. Venkatnathan, R. Devanathan and M. Dupuis, Atomistic Simulations of Hydrated Nafion and Temperature Effects on Hydronium Ion Mobility, J. Phys. Chem. B, 2007, 111(25), 7234–7244,  DOI:10.1021/jp0700276.
79. S. Sengupta and A. V. Lyulin, Molecular Modeling of Structure and Dynamics of Nafion Protonation States, J. Phys. Chem. B, 2019, 123(31), 6882–6891,  DOI:10.1021/acs.jpcb.9b04534.
80. D. W. M. Hofmann, L. Kuleshova and B. D'Aguanno, Molecular Dynamics Simulation of Hydrated Nafion with a Reactive Force Field for Water, J. Mol. Model., 2008, 14(3), 225–235,  DOI:10.1007/s00894-007-0265-9.
81. R. Cui, S. Li, C. Yu and Y. Zhou, The Evolution of Hydrogen Bond Network in Nafion via Molecular Dynamics Simulation, Macromolecules, 2023, 56(4), 1688–1703,  DOI:10.1021/acs.macromol.2c02106.
82. A. Rahbari, R. Hartkamp, O. A. Moultos, A. Bos, L. J. P. van den Broeke, M. Ramdin, D. Dubbeldam, A. V. Lyulin and T. J. H. Vlugt, Electro-Osmotic Drag and Thermodynamic Properties of Water in Hydrated Nafion Membranes from Molecular Dynamics, J. Phys. Chem. C, 2022, 126(18), 8121–8133,  DOI:10.1021/acs.jpcc.2c01226.
83. M. Bazaid, Y. Huang, W. A. Goddard and S. S. Jang, Proton Transport through Interfaces in Nanophase-Separation of Hydrated Aquivion Membrane: Molecular Dynamics Simulation Approach, Colloids Surf. A Physicochem. Eng. Asp., 2023, 676, 1–11,  DOI:10.1016/j.colsurfa.2023.132187.
84. S. Urata, J. Irisawa, A. Takada, W. Shinoda, S. Tsuzuki and M. Mikami, Molecular Dynamics Simulation of Swollen Membrane of Perfluorinated Ionomer, J. Phys. Chem. B, 2005, 109(9), 4269–4278,  DOI:10.1021/jp046434o.
85. R. Devanathan, A. Venkatnathan and M. Dupuis, Atomistic Simulation of Nafion Membrane. 2. Dynamics of Water Molecules and Hydronium Ions, J. Phys. Chem. B, 2007, 111(45), 13006–13013,  DOI:10.1021/jp0761057.
86. R. Devanathan, A. Venkatnathan, R. Rousseau, M. Dupuis, T. Frigato, W. Gu and V. Helms, Atomistic Simulation of Water Percolation and Proton Hopping in Nafion Fuel Cell Membrane, J. Phys. Chem. B, 2010, 114(43), 13681–13690,  DOI:10.1021/jp103398b.
87. R. Devanathan, A. Venkatnathan and M. Dupuis, Atomistic Simulation of Nafion Membrane: I. Effect of Hydration on Membrane Nanostructure, J. Phys. Chem. B, 2007, 111(28), 8069–8079,  DOI:10.1021/jp0726992.
88. A. V. Lyulin, S. Sengupta, A. Varughese, P. Komarov and A. Venkatnathan, Effect of Annealing on Structure and Diffusion in Hydrated Nafion Membranes, ACS Appl. Polym. Mater., 2020, 2(11), 5058–5066,  DOI:10.1021/acsapm.0c00875.
89. S. J. Paddison and J. A. Elliott, Selective Hydration of the ‘Short-Side-Chain’ Perfluorosulfonic Acid Membrane. An ONIOM Study, Solid State Ionics, 2007, 178(7–10), 561–567,  DOI:10.1016/j.ssi.2007.01.007.
90. M. Wang, K. W. Feindel, S. H. Bergens and R. E. Wasylishen, In Situ Quantification of the In-Plane Water Content in the Nafion® Membrane of an Operating Polymer-Electrolyte Membrane Fuel Cell Using 1H Micro-Magnetic Resonance Imaging Experiments, J. Power Sources, 2010, 195(21), 7316–7322,  DOI:10.1016/j.jpowsour.2010.05.029.
91. Z. Peng, V. Badets, P. Huguet, A. Morin, P. Schott, T. B. H. Tran, M. Porozhnyy, V. Nikonenko and S. Deabate, Operando μ -Raman Study of the Actual Water Content of Perfluorosulfonic Acid Membranes in the Fuel Cell, J. Power Sources, 2017, 356, 200–211,  DOI:10.1016/j.jpowsour.2017.04.095.
92. A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105(41), 9396–9409,  DOI:10.1021/jp004368u.
93. T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. Van Duin, The ReaxFF Reactive Force-Field: Development, Applications and Future Directions, npj Comput. Mater., 2016, 2, 15011,  DOI:10.1038/npjcompumats.2015.11.
94. T. Mabuchi and T. Tokumasu, Molecular Dynamics Simulation of Proton Transport in Polymer Electrolyte Membrane, J. Nanosci. Nanotechnol., 2015, 15(4), 2958–2963,  DOI:10.1166/jnn.2015.9647.
95. T. Mabuchi and T. Tokumasu, Relationship between Proton Transport and Morphology of Perfluorosulfonic Acid Membranes: A Reactive Molecular Dynamics Approach, J. Phys. Chem. B, 2018, 122(22), 5922–5932,  DOI:10.1021/acs.jpcb.8b02318.
96. M. K. Petersen and G. A. Voth, Characterization of the Solvation and Transport of the Hydrated Proton in the Perfluorosulfonic Acid Membrane Nafion, J. Phys. Chem. B, 2006, 110(37), 18594–18600,  DOI:10.1021/jp062719k.
97. D. Seeliger, C. Hartnig and E. Spohr, Aqueous Pore Structure and Proton Dynamics in Solvated Nafion Membranes, Electrochim. Acta, 2005, 50(21), 4234–4240,  DOI:10.1016/j.electacta.2005.03.071.
98. Y.-L. S. Tse, A. M. Herring, K. Kim and G. A. Voth, Molecular Dynamics Simulations of Proton Transport in 3M and Nafion Perfluorosulfonic Acid Membranes, J. Phys. Chem. C, 2013, 117(16), 8079–8091,  DOI:10.1021/jp400693g.
99. Y. K. Choe, E. Tsuchida, T. Ikeshoji, S. Yamakawa and S. A. Hyodo, Nature of Water Transport and Electro-Osmosis in Nafion: Insights from First-Principles Molecular Dynamics Simulations under an Electric Field, J. Phys. Chem. B, 2008, 112(37), 11586–11594,  DOI:10.1021/jp8041878.
100. Y. K. Choe, E. Tsuchida, T. Ikeshoji, S. Yamakawa and S. A. Hyodo, Nature of Proton Dynamics in a Polymer Electrolyte Membrane, Nafion: A First-Principles Molecular Dynamics Study, Phys. Chem. Chem. Phys., 2009, 11(20), 3892–3899,  10.1039/b819535h.
101. D. I. Bower and W. F. Maddams, The Vibrational Spectroscopy of Polymers, Cambridge University Press, Cambridge, 1989.
102. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344.
103. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
104. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78(7), 1396,  DOI:10.1103/PhysRevLett.78.1396.
105. C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110(13), 6158–6170,  DOI:10.1063/1.478522.
106. M. J. Frisch, J. A. Pople and J. S. Binkley, Self-Consistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets, J. Chem. Phys., 1984, 80(7), 3265–3269,  DOI:10.1063/1.447079.
107. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient Diffuse Function-augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-row Elements, Li–F, J. Comput. Chem., 1983, 4(3), 294–301,  DOI:10.1002/jcc.540040303.
108. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, Packmol: A Package for Building Initial Configurations for Molecular Dynamics Simulations, J. Comput. Chem., 2009, 30(13), 2157–2164,  DOI:10.1002/jcc.21224.
109. R. Devanathan, N. Idupulapati, M. D. Baer, C. J. Mundy and M. Dupuis, Ab Initio Molecular Dynamics Simulation of Proton Hopping in a Model Polymer Membrane, J. Phys. Chem. B, 2013, 117(51), 16522–16529,  DOI:10.1021/jp410229u.
110. A. K. Rappé, C. J. Casewit, K. S. Colwell, I. Goddard and W. M. Skiff, UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations, J. Am. Chem. Soc., 1992, 114(25), 10024–10035,  DOI:10.1021/ja00051a040.
111. S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19,  DOI:10.1006/jcph.1995.1039.
112. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales, Comput. Phys. Commun., 2022, 271, 108171,  DOI:10.1016/j.cpc.2021.108171.
113. L. Verlet, Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules, Phys. Rev., 1967, 159(98), 98–103,  DOI:10.1103/PhysRev.159.98.
114. R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, McGraw-Hill International Book Company, New York, 1981.
115. A. K. Rappe and I. Goddard, Charge Equilibration for Molecular Dynamics Simulations, J. Phys. Chem., 1991, 95(8), 3358–3363,  DOI:10.1021/j100161a070.
116. S. J. Paddison, D. W. Reagor and T. A. Zawodzinski Jr, High Frequency Dielectric Studies of Hydrated Nafion, J. Electroanal. Chem., 1998, 459(1), 91–97,  DOI:10.1016/S0022-0728(98)00321-0.
117. H. A. Laitinen and W. E. Harris, Chemical Analysis, ed. R. H. Summersgill and S. L. Langman, McGraw-Hill, Inc., New York, 2nd edn, 1975.
118. M. B. Herath, S. E. Creager, A. Kitaygorodskiy and D. D. DesMarteau, Perfluoroalkyl Phosphonic and Phosphinic Acids as Proton Conductors for Anhydrous Proton-Exchange Membranes, ChemPhysChem, 2010, 11(13), 2871–2878,  DOI:10.1002/cphc.201000184.
119. M. Schuster, T. Rager, A. Noda, K. D. Kreuer and J. Maier, About the Choice of the Protogenic Group in PEM Separator Materials for Intermediate Temperature, Low Humidity Operation: A Critical Comparison of Sulfonic Acid, Phosphonic Acid and Imidazole Functionalized Model Compounds, Fuel Cells, 2005, 5(3), 355–365,  DOI:10.1002/fuce.200400059.
120. P. A. H. Wyatt, Sulphuric Acid Autoprotolysis and the Theory of Dissociated Solvents, Trans. Faraday Soc., 1969, 65, 585–590,  10.1039/tf9696500585.
121. R. H. Flowers, R. J. Gillespie and E. A. Robinson, The Sulphuric Acid Solvent System: Part I. Acid-base Reactions, Can. J. Chem., 1960, 38(8), 1363–1370,  DOI:10.1139/v60-190.
122. R. Buzzoni, S. Bordiga, G. Ricchiardi, G. Spoto and A. Zecchina, Interaction of H2O, CH3OH, (CH3)2O, CH3CN, and Pyridine with the Superacid Perfluorosulfonic Membrane Nafion: An IR and Raman Study, J. Phys. Chem., 1995, 99(31), 11937–11951,  DOI:10.1021/j100031a023.
123. E. Negro, M. Vittadello, K. Vezzù, S. J. Paddison and V. Di Noto, The Influence of the Cationic Form and Degree of Hydration on the Structure of Nafion™, Solid State Ionics, 2013, 252, 84–92,  DOI:10.1016/j.ssi.2013.09.017.
124. A. Vishnyakov and A. V. Neimark, Molecular Dynamics Simulation of Nafion Oligomer Solvation in Equimolar Methanol−Water Mixture, J. Phys. Chem. B, 2001, 105(32), 7830–7834,  DOI:10.1021/jp004082p.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta03973h

‡ Co-first authors.

§ Total dehydration of ionomers requires a rigorous drying procedure as described by Doan et al.²⁹

¶ The symbol, Λ, is read as ‘lambda local’. The symbol replaces λ_site³³ and λ_local,⁸ both introduced by Loupe et al.

|| All exchange sites were a priori designated β and all Λ ≤ Λ_d sites were assumed to represent α-sites.

** LACV3P is identical to 6-311G for atoms lighter than K.

†† Transmission FTIR of Nafion 212 (NR212; see Fig. 1 for membrane specifications).

‡‡ NSC group modes are dominated by δ_u(CF₃) (see ESI Videos†).

§§ The arbitrarily chosen 6 Å cutoff boundary contains all 1-mer-CF₃ hydration waters (Fig. S1-6; ESI†).

---