A highly moisture-stable ferroelectric ammonium phosphate salt showing piezoelectric energy harvesting and rotation sensing applications

Abstract

Ferroelectric phosphate-based materials are known for their biocompatibility, dipole switching, and high thermal stability. In this context, we report a novel organic ferroelectric material, diisopropylammonium bis(4-nitrophenyl) phosphate (DIPA·BNPP), crystallizing in the monoclinic C₂ space group. DIPA·BNPP exhibits a high second harmonic generation (SHG) efficiency 2.5 times higher than that of potassium dihydrogen phosphate (KDP). The ferroelectric nature of DIPA·BNPP was confirmed by the observation of a rectangular P–E hysteresis loop, which gave a saturated polarization value of 6.82 μC cm⁻². The ferroelectric polar domains of DIPA·BNPP, along with the bias-dependent amplitude butterfly and phase hysteresis loops, were visualized by piezoresponse force microscopy (PFM). Furthermore, the polydimethyl siloxane (PDMS) composites of DIPA·BNPP enabled the fabrication of humidity-resistant piezoelectric nanogenerators (PENGs) with energy harvesting and mechanical–electrical sensing capabilities. The top-performing 10 wt% DIPA·BNPP-PDMS device achieved a peak output voltage of 9.5 V and a charge storage efficiency of 81.8%, successfully powering 53 LEDs. Additionally, its rapid response time of 18.5 ms enables precise rotation sensing capabilities, suggesting potential applications in motion monitoring, such as revolution per minute (RPM) counting. We also present a unique and refined method for obtaining the output work efficiency (OWE) parameter, which quantifies the ratio of harvested electrical energy to the maximum elastic energy stored in the composite device, taking into consideration several key parameters during the PENG measurements. For the 10 wt% DIPA·BNPP-PDMS composite, an OWE of 13.1% was achieved, highlighting both its current performance and potential for optimization. This metric provides a standardized approach for evaluating PENGs, addressing a critical gap in assessing mechanical-to-electrical energy conversion efficiency.

---

Introduction

The discovery of ferroelectricity in Rochelle salt and potassium dihydrogen phosphate (KDP) has inspired the development of molecular ferroelectric materials with switchable spontaneous polarization.^1,2 These ferroelectric substances, characterized by their adherence to polar point groups, have found extensive utility in a diverse array of electronic applications, encompassing field-effect transistors (FETs), transducers, photovoltaic systems, memory devices, self-powered portable electronics, etc.^3–8 Earlier research in this domain was predominantly focused on ceramic materials composed of inorganic oxides such as lead zirconate (PZT) and barium titanate (BTO), but the presence of heavy elements, such as Pb, spurred the study on molecular and polymeric ferroelectrics. This transition led to the development of a plethora of organic ferro- and piezoelectric materials, which offered a multitude of advantages, including lightweight nature, facile synthesis, mechanical flexibility, cost-effectiveness, environmental sustainability, and biocompatibility.^9–16 Amongst these, the diisopropylammonium (DIPA) family of salts has garnered significant attention due to their propensity to form noncentrosymmetric assemblies exhibiting high spontaneous polarization and low dielectric loss.¹⁷ Notably, the charge-separated halide salts of DIPA, including chloride (DIPAC), bromide (DIPAB), and iodide (DIPAI), have demonstrated exceptional ferroelectric polarizations.^18–21 Furthermore, alternative combinations of DIPA cations with ClO₄²⁻, and also complex anions such as MnBr₄²⁻ and CdBr₄²⁻ have been investigated, revealing substantial ferroelectric polarization characteristics (Scheme 1a–c). ^22–24 Notwithstanding the remarkable capacity of DIPA cations to stabilize polar ferroelectric phases, numerous compounds within this family are plagued by issues pertaining to their structural and environmental stability, primarily stemming from the nature of their counter anions. For instance, DIPAX (X = Cl, Br, I), DIPA(CdBr₄) and DIPA(MnBr₄) exhibit sensitivity to moisture due to the presence of halide-containing anions.²⁵ Moreover, many of these compounds manifest multiple polymorphic phases, which may coexist or undergo transitions in response to subtle environmental fluctuations, such as variations in temperature or humidity.^26–32 The mere absorption of moisture by these materials can result in the degradation of ferroelectric properties or an increase in dielectric losses, thereby compromising their viability for long-term applications. Consequently, there exists a pressing need for DIPA salts incorporating bulky and halogen-free anions to achieve high-performance organic ferroelectrics with enhanced T_c and stability.³³

Scheme 1 (a) Strategy to design diisopropylamine-based two-component ferroelectrics. (b) DIPA-derived ferroelectrics known for spherical anions. (c) DIPA-based ferroelectrics known for multi-atomic and metal-containing anions. (d) Synthetic scheme for the preparation of the ferroelectric DIPA·BNPP compound reported in this work.

Phosphates and organo-phosphates have gained attention due to their exceptional properties, including high flexibility, proton conductivity, elevated dielectric constants, remarkable ferroelectricity, and biocompatibility.^34–38 These attributes render phosphate-containing organic materials particularly attractive for the fabrication of advanced electronic devices with environmentally benign characteristics.^39–42 The dimensions of the phosphate anion and the resultant molecular distortion play pivotal roles in optimizing ferroelectric characteristics and phase transition kinetics in such materials.⁴³ Organophosphate anions exhibit the ability to retain their properties at elevated temperatures, thereby expanding the temperature range for ferroelectric applications. In light of these considerations, we present a charge-separated molecular ferroelectric, diisopropyl ammonium bis(4-nitrophenyl) phosphate, with the chemical formula (ⁱPr₂NH₂)·[PO₂(O-C₆H₄-^pNO₂)₂] (DIPA·BNPP) (Scheme 1d).

The two-component DIPA·BNPP system exhibited strong second-order nonlinear optical properties, manifesting a second-harmonic generation (SHG) efficiency 2.5 times that of the standard potassium dihydrogen phosphate (KDP). The ferroelectric P–E hysteresis loop analyses revealed a substantial saturation polarization (P_s) of 6.82 μC cm⁻², indicative of the material's robust ferroelectric nature. The ferro- and piezoelectric characteristics of DIPA·BNPP were further corroborated through piezoresponse force microscopy (PFM) measurements, which yielded the characteristic amplitude-bias “butterfly” and phase-bias hysteresis loops. Additionally, the piezoelectric nanogenerator (PENG) devices were fabricated by integrating DIPA·BNPP with polydimethylsiloxane (PDMS). These measurements resulted in the 10 wt% DIPA·BNPP-PDMS device emerging as the superior performer, generating the highest peak-to-peak voltage (V_PP) of 9.5 V for the 10 wt% DIPA·BNPP-PDMS composite device. The responsivity and sensitivity of the champion 10 wt% device were calculated to be 625 VMPa⁻¹ and 0.604 VN⁻¹, respectively. The device's efficacy was further validated through capacitor charging and LED flash lighting experiments, demonstrating its practical energy harvesting capabilities. Leveraging the remarkable responsivity and performance of the champion 10 wt% DIPA·BNPP-PDMS device, its utility as a sensor for motor rotation speed (measured in revolutions per minute, RPM) was demonstrated, utilizing the device's output voltage as the input signal. This practical application underscores the potential of two-component ammonium phosphate salts in advancing sensor technology. Moreover, one of the challenges in standardizing the performance of the PENGs is the lack of a universal method for evaluating their efficiencies. In this effort, this study introduces a novel metric for assessing energy harvesting efficiency, named as the output work efficiency (OWE) parameter. This parameter is defined as the ratio of harvested electrical energy as output work done (W_e) per second to the maximum elastic energy as input work done (W_d) per second within the device. For the top-performing 10 wt% DIPA·BNPP-PDMS device, an OWE of 13.1% was found, providing a quantitative measure of its energy conversion capabilities, and establishing a potential benchmark for future piezoelectric nanogenerator designs.

Results and discussion

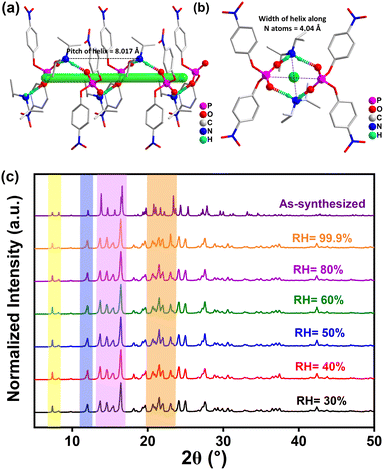
The two-component DIPA·BNPP salt was synthesized by adding an equimolar amount of diisopropylamine to the protonated form of bis(4-nitrophenyl) phosphate in a water–methanol medium (Fig. S1, ESI†). The resulting solution was filtered and left to crystallize, yielding pale-yellow crystals of DIPA·BNPP. The bulk purity of DIPA·BNPP was determined using infrared spectroscopy and nuclear magnetic resonance (NMR) spectroscopy (¹H, ¹³C, and ³¹P) (Fig. S2–S4, ESI†). Single-crystal X-ray diffraction (SCXRD) analyses at 150 K and 298 K confirmed that DIPA·BNPP crystallizes in the polar non-centrosymmetric monoclinic space group C₂ at both temperatures (Table S1, ESI†). The asymmetric unit consists of one BNPP anion and one DIPA cation, as shown in Fig. 1a. The distance between the centroids of the cation and anion (the pnictogen N and P atoms) in the asymmetric unit is 4.092 Å. The tetrahedral angles around the ammonium center are distorted and consistent with that of other known organic salts of DIPA. Notably, the H-N-H fragment exhibits the smallest angle of 106.7°, while the C–N–C angle is the largest at 117.20°. Intermediate angles of approximately 108° are found for the C-N-H fragments. Likewise, the phosphate anion exhibits distorted tetrahedral geometry, with angles ranging from 102.47° to 122.43°. These angles were found to vary marginally with temperature (Table S2, ESI†). The nitrate groups within the BNPP moiety exhibit positional disorder at both 150 K and 298 K. At 150 K, additional disorder was observed in one of the phenyl groups of the DIPA cation, with an alternative orientation of the benzene ring. However, this disorder was not detected at 298 K, likely due to either thermal averaging or limitations in resolving the atomic positions at higher temperatures. Despite these localized structural disorders, the overall polar order and symmetry of the crystal lattice were preserved at both temperatures, indicating that the disorder does not significantly disrupt the long-range polar arrangement of the crystal.

Fig. 1 (a) Formation of a 1D-helical chain structure in DIPA·BNPP mediated by hydrogen bonding interactions along the b-axis. (b) Top-view of the helical assembly along the c-axis. (c) Humidity dependent PXRD profiles of DIPA·BNPP showing its high moisture stability.

The crystal structure of DIPA·BNPP shows the formation of a 1D-helical H-bonded network along the polar b-axis, mediated by strong N–H⋯O interactions (Fig. S5, ESI†). The two amino protons of the DIPA cation interact with the oxygen atoms of two adjacent BNPP anions, while the two terminal oxygen atoms of each BNPP anion connect with protons from two DIPA cations, forming a helical single-stranded structure (Fig. 1a and b). The pitch of the helix is determined to be 8.017 Å, while the width of the helix is measured to be 4.04 Å (twice the distance from the N-atom to the principal axis) and 5.14 Å (twice the distance from the P-atom to the principal axis), respectively (Fig. S6, ESI†). The helical chirality was confirmed by the circular dichroism (CD) analysis in the solid state (Fig. S7, ESI†). The packing diagram of DIPA·BNPP reveals additional structural features along the crystallographic a- and c-directions. The view along the a-axis shows the formation of a criss-cross arrangement for the BNPP anions, while the view along the c-axis indicates an ABAB-type arrangement of the DIPA (A) and BNPP (B) moieties (Fig. S8, ESI†). Dipole interactions at the atomic level arise from electrostatic forces, which are strongly influenced by both the relative orientation of dipoles and the distance between opposite charges. Furthermore, the Mulliken charge distribution offers a quantitative understanding of electron density distribution and charge transfer processes, both of which directly influence dipole moments and the strength of dipole–dipole interactions (Fig. S9, Tables S3, and S4, ESI†). Such interactions can result in the cooperative alignment of dipoles within polar materials, giving rise to macroscopic polarization. A detailed Hirshfeld surface analysis⁴⁴ of DIPA·BNPP was carried out at 298 K, identifying several key interactions (Fig. S10, ESI†). Notably, the H⋯O/O⋯H interactions contribute 46.6% of the total intermolecular interactions (Fig. S11–S13 and Table S5, ESI†).

The bulk purity of the sample was determined by powder X-ray diffraction (PXRD) analysis (Fig. S14, ESI†). Thermogravimetric analysis (TGA) of DIPA·BNPP revealed its stability up to 495 K, while the differential thermal analysis (DTA) curve exhibited anomaly peaks at 448 K and 587 K, corresponding to its melting and decomposition points, respectively (Fig. S15, ESI†). Additionally, differential scanning calorimetry (DSC) analysis conducted between 240 K and 430 K revealed no anomalies during the heating and cooling cycles (Fig. S16, ESI†). To track potential phase transitions, we performed variable-temperature single-crystal X-ray diffraction (VT-SCXRD) measurements on DIPA·BNPP in the temperature range of 100 K to 400 K (Fig. S17 and S18, ESI†). These studies revealed no apparent changes in the lattice parameters, albeit with a marginal change in the beta-angle and slight volume expansion at around 330 K, attributed to thermal expansions in the unit cell.^45,46 Similarly, the variable-temperature powder X-ray diffraction (VT-PXRD) profiles of DIPA·BNPP showed no emergence of new peaks or shifts in peak positions across the entire temperature range, confirming phase stability at all measured temperatures (Fig. S19,† ESI†). To evaluate the moisture stability of DIPA·BNPP, we conducted humidity-dependent PXRD measurements under varying relative humidity (RH) conditions. The PXRD profiles showed no observable peak shifts across the tested humidity range, confirming that DIPA·BNPP remains stable at RH levels as high as 99.9% (Fig. 1c). The appearance of a few unresolved peaks in DIPA·BNPP after 24 hours of exposure to 99.9% humidity suggests that water interacts with the surface or localized regions of the crystal, likely due to the presence of phosphate and ammonium groups. However, this does not affect the crystal stability (Fig. S20, ESI†). The elemental composition of DIPA·BNPP was confirmed by FE-SEM-based energy-dispersive X-ray spectroscopy (EDXS) and X-ray photoelectron spectroscopy (XPS) analyses (Fig. S21 and S22, ESI†). The XPS spectrum shows characteristic peaks due to C 1s, N 1s and P 2p electrons present in DIPA·BNPP.

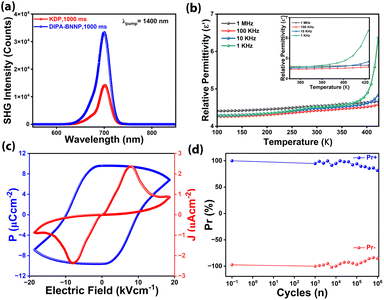
The acentric structure of DIPA·BNPP was further verified by the Kurtz–Perry (Graja) powder method.⁴⁷ Size-graded samples of DIPA·BNPP and KDP were subjected to 1400 nm femtosecond laser pulses to yield second-harmonic generation (SHG) responses. Analysis of SHG signal integral intensities indicated that DIPA·BNPP exhibits a high SHG efficiency of 2.5 relative to KDP (Fig. 2a). The SHG efficiency of DIPA·BNPP surpasses those of previously reported phosphate-based minerals such as PbZn(PO₄)F and NH₄H₂PO₄ (ADP), approaching that of KTiOPO₄ (KTP).^48–51 Notably, DIPA·BNPP is the first metal-free phosphate salt to demonstrate a higher SHG efficiency than KDP. The optical band gap of DIPA·BNPP was determined by solid-state UV/vis absorption spectroscopy on the powder sample (Fig. S23, ESI†). The spectral profile and Tauc plot reveal an optical band gap (E_g) of approximately 3.02 eV, comparable to those observed for several ferroelectric oxides and organic–inorganic hybrid ferroelectrics.⁵²

Fig. 2 (a) The spectra of the SHG response of DIPA·BNPP with respect to the reference KDP. (b)Temperature-dependent relative permittivity of DIPA·BNPP. (c) The P–E hysteresis loop and leakage current density plot of DIPA·BNPP. (d) Fatigue profile data of DIPA·BNPP up to 10⁶ cycles.

Furthermore, the dielectric properties of DIPA·BNPP were studied through frequency (f) and temperature (T) dependent permittivity measurements on compacted pellets. The experiment was conducted over the temperature range of 100 K to 413 K, and the data were analyzed over the frequency range of 1 kHz to 1 MHz. The real part of the dielectric permittivity (ε′) vs. T profiles exhibited a consistent increase in permittivity with increasing temperature, showing no heat anomalies (Fig. 2b). However, the dielectric permittivity remained nearly constant from 150 K to 298 K, suggesting the preservation of polar symmetry and structural stability throughout this range. These results confirm that DIPA·BNPP remains in the same polar phase, with no evidence of dipole reorientation or symmetry breaking within this temperature range. This behaviour can be attributed to the enhanced thermal activation of dipoles, resulting in greater polarization at higher temperatures. A similar trend was observed in the ε′ vs. f profiles, with permittivity values increasing at lower frequencies due to the contribution of all types of polarization mechanisms (electronic, ionic, dipolar, and interfacial) in these frequency ranges (Fig. S24,† ESI†).^53–55 The relative permittivity of DIPA·BNPP was found to be 4.51 at 1 kHz and 298 K. The temperature and frequency-dependent dielectric loss factors (tan δ) followed almost increasing trends, indicating energy dissipation associated with the polarization process (Fig. S25, ESI†). However, no significant heat anomalies were observed in the tan δ profiles, implying that thermal effects primarily influence permittivity without introducing substantial dielectric loss instability.

The molecular symmetry (C2) of DIPA·BNPP falls under the category of polar point groups capable of demonstrating ferroelectric characteristics. Polarization vs. electric field (P–E) loop measurements were performed at room temperature on a drop-casted thin film sample of DIPA·BNPP on a conducting indium tin oxide (ITO) coated glass substrate. These measurements yielded a rectangular hysteresis loop with a remnant polarization value (P_r) of 9.59 μC cm⁻² and a coercive field (E_c) of 19 kV cm⁻¹ (Fig. 2c). The polarization observed in DIPA·BNPP can be traced back to its stable charge-separated structure facilitated by the BNPP anion and DIPA cation, and their helical H-bonded 1-D structure along the polar b-axis. The observed remanent polarization (P_r) value of 9.59 μC cm⁻² that is higher than the saturation polarization (P_s) value of 6.82 μC cm⁻² can be attributed to several factors. Notably, organic ferroelectrics mostly rely on relatively weak intermolecular interactions to exhibit long-range order. The observation of higher P_r than P_s in them could likely be due to field-dependent relaxation effects. Similar trends, with higher P_r values compared to P_s, have been observed in previously reported molecular ferroelectrics.^56,57 The leakage current density plot measured along the P–E loop trace exhibits low leakage, with peaks that coincide with E_c, confirming the ferroelectric nature of the obtained loop. Ferroelectric fatigue measurements were conducted up to 10⁶ cycles, confirming the retention of ferroelectric behavior in DIPA·BNPP (Fig. 2d).

To investigate the polar domain structure in DIPA·BNPP, we conducted vertical piezoresponse force microscopy (VPFM) experiments on a single crystal grown on an ITO-coated glass plate. Fig. 3a and b present the respective amplitude and phase images of DIPA·BNPP, acquired from an active area of 10 × 10 μm². A uniform stripe-line domain structure was observed in the PFM images of the crystal. The bright and dark color contrasts in the amplitude image indicate varying strengths of piezoresponse in each domain, while the color tones in the phase image represent different domain orientations. Switching spectroscopy PFM (SS-PFM) was conducted on a fixed point of the topographic surface of the DIPA·BNPP crystal by applying an external bias of 60 V at the cantilever tip (Fig. 3c). Fig. 3d shows the characteristic amplitude “butterfly” loop showcasing its piezoelectricity and a rectangular phase hysteresis loop evidencing a 180-degree domain switching in DIPA·BNPP. The observed shift towards the negative axis in phase-bias hysteresis and amplitude-bias butterfly curves could be due to internal biases or built-in electric fields caused by defects and charge trapping at the film surface.^58–61

Fig. 3 PFM analysis of DIPA·BNPP showing (a) its vertical amplitude and (b) phase images. (c) The visualization of a single crystal of DIPA·BNPP on the drop-cast thin film along with the PFM tip and its 3D-topography image. (d) The SS-PFM spectroscopy derived amplitude-butterfly and phase-hysteresis loops as a function of voltage bias at a single point on the DIPA·BNPP film substrate.

The direct piezoelectric coefficient (d₃₃) of DIPA·BNPP was obtained using the Berlincourt method. A maximum d₃₃ of 7.9 pCN⁻¹ was obtained from a compacted pellet of DIPA·BNPP (Fig. S26, ESI†). The piezoelectric voltage constant (g₃₃) of DIPA·BNPP was calculated using the correlation between the absolute permittivity ε_r × ε₀ and piezoelectric constant (d₃₃), as described by the equation g₃₃ = d₃₃/ε₃₃. The absolute permittivity is found to be 39.93 pF m⁻¹. The obtained piezoelectric voltage constant was 0.198 VmN⁻¹, and the transduction coefficient (d₃₃×g₃₃) was calculated to be 1.563 × 10⁻¹² m³ J⁻¹, demonstrating a good electromechanical conversion efficiency of DIPA·BNPP. The electrostrictive coefficient for DIPA·BNPP is determined to be 1.45 m⁴ C⁻², comparable to that of PVDF and other recently reported high-performance electrostrictive organic and hybrid materials. Materials with a high piezoelectric voltage and electrostrictive coefficient are highly sought after for electromechanical applications (conversion of mechanical energy to electrical energy), which prompted us to explore the potential of DIPA·BNPP for PENG applications.

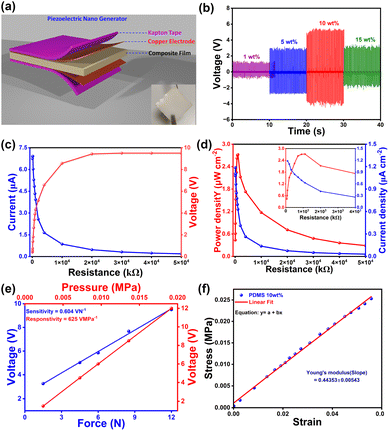
To create a flexible piezoelectric material, we prepared polymer composites with different weight percentages (1, 5, 10, and 15 wt%) of DIPA·BNPP in PDMS, a non-piezoelectric polymer, and tested its stability inside the polymer matrix (Fig. S27, ESI†). All polymer composites were thoroughly characterized by PXRD analysis (Fig. S28, ESI†). To prepare the devices, the composite films were sandwiched between two copper strips that serve as the top and bottom electrodes. The whole assembly was subsequently wrapped with Kapton tape to avoid environmental interference (Fig. 4a). Piezoelectric energy harvesting experiments were conducted using a home-built impact setup, where the PENG device under collision force was connected to a Keithley digital multimeter (model: DMM 7510 7 1/2) via copper wires attached to the surface of the copper electrodes. The peak-to-peak voltages and currents increased with the concentration of DIPA·BNPP in the PDMS composite films, ranging from 1 wt% to 10 wt%. The peak-to-peak voltage and current values reached a maximum of 9.5 V and 7.7 μA, respectively, for the 10 wt% DIPA·BNPP-PDMS composites under an optimized mechanical force of 12 N and an operating frequency of 8 Hz (Fig. S29 and S30, ESI†). The 10 wt% DIPA·BNPP-PDMS device exhibited the highest peak-to-peak output voltage of 9.5 V (forward) and 8.87 V (reverse). Polarity-switching by reversing electrode connections confirmed the intrinsic piezoelectric response, as evidenced by signals of nearly equal magnitude and opposite polarity. The slight voltage reduction in the reverse configuration (Fig. S31, ESI†) is attributed to minor interfacial asymmetries. The cycling stability of the 10 wt% DIPA·BNPP-PDMS device was tested after approximately 3 months under a 12 N force for up to 1200 cycles (Fig. S32, ESI†). In contrast, the recorded lower output voltage for 15 wt% DIPA·BNPP-PDMS, compared to the 10 wt% DIPA·BNPP-PDMS device, indicates a reduction in long-range dipole–dipole interactions among the ferroelectric particles. Typically, increasing the concentration of ferroelectric or piezoelectric particles in a composite generally leads to enhanced mechanical stiffness and a higher total dipole moment. This is attributed to improved stress transfer efficiency between the active particles and the polymer matrix, facilitating a more uniform mechanical load distribution and polarization within the composite structure. This, in turn, could result in a higher voltage output. However, achieving a noticeable enhancement at resonance requires an optimal minimum concentration, which, in our device architecture, is observed to be 10 wt% DIPA·BNPP-PDMS. Higher particle agglomeration occurs beyond this concentration (15 wt% DIPA·BNPP-PDMS), as observed from the FESEM images (Fig. S33, ESI†). The enhanced performance observed at the 10 wt% DIPA·BNPP-PDMS composition can be attributed to a combination of factors involving percolation behavior and atomic-level interactions within the composite system. As the concentration of piezoelectric particles increases, the increased interface area between the particles and the surrounding matrix enhances the Maxwell–Wagner–Sillars (MWS) polarisation, improving dielectric permittivity.^62,63 However, at low concentrations, the particles are more dispersed, resulting in a smaller interface area and a limited collective response to an applied electric field. While there is some increase in polarization at the interfaces, the overall effect on the material's dielectric properties is limited due to the insufficient particle distribution. Beyond a threshold concentration, say 10 wt% in this case, particle aggregation occurs, which increases permittivity but also leads to field concentration and reduced dipole mobility. These effects hinder the material's overall performance by distorting the electric field and limiting charge response.

Fig. 4 (a) Schematic diagram showing the architecture of a composite PENG device. The inset images show the flexibility of the 10 wt% DIPA·BNPP-PDMS film. (b) Comparative voltage performance of all composite devices of DIPA·BNPP with a shifted relative time axis. (c) The current and voltage profiles of the 10 wt% DIPA·BNPP-PDMS composite device under different external load resistances. (d) The current density and power density values of the 10 wt% DIPA·BNPP-PDMS composite device under different external load resistances. The inset shows the profiles at lower resistances. (e) The voltage vs. force and voltage vs. pressure plots of the 10 wt% DIPA·BNPP-PDMS device. (f) The stress vs. strain graph of the 10 wt% DIPA·BNPP composite film at lower strain percentages.

To identify the optimal impedance matching for maximum efficiency, the electrical output responses (voltage, current density, and power density) of the best-performing device (10 wt%) were measured using a range of resistors from 60 kΩ to 50 MΩ. The output voltage increased gradually with higher resistance values while the corresponding currents decreased (Fig. 4c). The maximum power density achieved was 2.72 μW cm⁻² at a threshold load resistance of 0.9 MΩ (Fig. 4d). Similarly, a high current density of 1.2 μA cm⁻² was achieved at the minimum load resistance of 100 kΩ (Fig. 4d inset). The observed power density values of the 10 wt% DIPA·BNPP-PDMS device are among the highest reported for organic and organic–inorganic hybrid composite piezoelectric energy harvesting devices (Tables S6 and S7, ESI†).

To further evaluate the sensitivity and responsivity of the 10 wt% DIPA·BNPP device, we systematically performed the force-determination measurement (details are given in Supporting Discussion 1 and Fig. S34, ESI†). We have conducted force-dependent measurements at various forces of 1.5, 4.5, 6, 8.5, and 12 N with corresponding pressures of 0.0024, 0.0072, 0.0096, 0.0136, and 0.0192 MPa, respectively (Fig. S35, ESI†). The slopes of the graphs of voltage vs. force and voltage vs. pressure yield the sensitivity and responsivity of the device, respectively (Fig. 4e). The champion 10 wt% PENG device demonstrated a sensitivity of 0.604 VN⁻¹ and a responsivity of 625 VMPa⁻¹. This indicates the device's ability to detect subtle force changes and efficiently convert them into electrical signals for application as force sensors.

In the field of piezoelectric energy harvesting, several metrics describe PENG device performance: peak-to-peak voltage and current, power and current density, threshold load resistance, etc. While these parameters are used for comparing various functional aspects of devices, for composite PENG devices, there is no clear-cut parameter that could evaluate how efficiently the applied mechanical energy is converted into electrical energy. This is a significant knowledge gap, as information about the intrinsic conversion efficiency could be used to assess the potential for improvements in both molecular design and functional device architecture. Using the 10 wt% DIPA·BNPP-PDMS champion device as an example, we provide a simple method for evaluating the output work efficiency (OWE) metric of a PENG device.

When an external force is applied to polymer composite devices, the generated mechanical energy is stored within the material as elastic energy and plays a crucial role in its piezoelectric energy harvesting potential.^64,65 This stored elastic energy can be quantified by conducting stress–strain measurements and extracting Young's modulus of the composite (Fig. 4f and S36, ESI†).⁶⁶ Upon subjecting the 10 wt% DIPA·BNPP-PDMS polymer composite film to a force of 12 N (at a pressure of 0.0192 MPa), the maximum elastic energy stored, defined as the input work done per second W_d (where the subscript d signifies the deformation of the device), was determined to be 3.70 × 10⁻² J s⁻¹. This signifies the considerable capacity of the device to store mechanical energy under optimized conditions. Similarly, by estimating the output voltage and current values for a one-second period (Fig. S37, ESI†), the maximum electrical energy (defined as the output work done per second, W_e) of the 10 wt% DIPA·BNPP-PDMS device was calculated to be 4.84 × 10⁻³ J s⁻¹ (the subscript e in W_e signifies electrical output). For full details pertaining to these calculations, kindly refer to Supporting Discussion 2 in the ESI† (page numbers S25–S27). This value provides insight into the effectiveness of the piezoelectric energy harvesting process within the device. From the ratio of these two work energy terms (W_e/W_d), the OWE parameter of the 10 wt% DIPA·BNPP-PDMS device was computed to be 13.1%. Although there are few methods to evaluate the efficiencies of the PENG devices, this method provides a simple and straightforward approach for obtaining work efficiency based on the input and output energies directly extracted from the impact setup (Table S6, ESI†). It should be noted that the provided method for calculating the OWE parameter is mostly reliable for composite devices such as DIPA·BNPP-PDMS and not for the neat piezoelectric crystals, as the applied force acts uniformly on the whole device. Hence, there is currently limited data available for performing device efficiency comparisons (Table S8, ESI†).

To test the energy storage capacity of the device, we connected a full-wave bridge rectifier circuit and a storage capacitor (with a capacitance of 22 μF) in parallel to the 10 wt% DIPA·BNPP-PDMS device. The maximum stored output charge across the 22 μF capacitor was calculated to be 171.1 μC in 550 s (Fig. 5a). The stored voltage (V) and stored energy were calculated to be 8 V and 6.92 mJ, respectively. The charge storage efficiency of the device at 550 s was found to be 81.8%. The voltage stored in the system is substantial, providing sufficient power to illuminate LEDs effectively (Fig. S38, ESI†). In a successful demonstration, we showcased the utility of this stored energy by achieving a bright glow of light for up to 53 LEDs (Video 1, ESI†). This result highlights the practical application and efficiency of the energy storage system based on the DIPA·BNPP-PDMS composite for powering miniature electronic devices.

Fig. 5 (a) The graph of charge storage by using the 22 μF capacitor, and the inset image shows the demonstration of flash lighting of 53 LEDs. (b) Voltage and energy vs. time profile during charging of a 22 μF capacitor. (c) Schematic representation of an RPM sensor based on DIPA·BNPP.

In our investigation, we evaluated the positive and negative response times, as well as the relaxation time, for the 10 wt% polymer composite device. Notably, the response time is smaller than the relaxation time due to the elasticity of the PDMS polymer (Fig. S37, ESI†). The total time for one full cycle of the signal (both positive and negative response) is 18.5 ms, indicating that the device can generate 54 electrical signals per second. This demonstrates the rapid and efficient signal processing capability of the 10 wt% device. Its quick response time and high signal generation rate could, therefore, be suitable for applications such as real-time rotations per minute (RPM) sensors. A model RPM sensor device was prepared using a brushless direct current (BLDC) motor with its probing arm in contact with the 10 wt% device (Fig. 5c and Video 2, ESI†). The continuous output voltage signal generated from the 10 wt% device was received in a microcontroller, which processes the data in RPM units (Supporting Discussion 3†). The measured RPM value of 142 matches well with the rated value of the commercial BLDC motor, signifying the precise nature of the DIPA·BNPP-PDMS sensor (Fig. S39, ESI†).

Conclusion

The main outputs from the present work are threefold: related to material design, functional aspects, and methodology. Material-wise, we have successfully synthesized an ammonium phosphate-based molecular ferroelectric, DIPA·BNPP, that exhibits a P_s of 6.82 μC cm⁻² at room temperature. Unlike previously reported diisopropyl ammonium-based organic salts, DIPA·BNPP displays no phase transitions up to its melting point (451 K). This can be attributed to the presence of a bulky phosphate anion in the system. The intrinsic noncentrosymmetry of this material is reflected in the 2.5-fold higher SHG efficiency of DIPA·BNPP relative to that of the reference KDP sample. The PFM studies performed on the crystal of DIPA·BNPP further support its ferro- and piezoelectric properties. In turn, the demonstrated functionalities of the DIPA·BNPP-PDMS composite device showcase its remarkable versatility and practical applicability in energy harvesting and sensing applications. The device exhibits excellent energy storage capabilities, achieving a charge storage efficiency of 81.8% with the ability to store 6.92 mJ of energy and generate up to 8 V across a storage capacitor. This performance translates into real-world applications, as evidenced by the successful powering of multiple LEDs. Beyond energy harvesting, the composite device displays technologically relevant dynamic response characteristics, with a complete signal cycle time of 18.5 ms, thus enabling the generation of 54 electrical signals per second. This rapid response capability has been successfully leveraged in the development of a precise RPM sensor, where the device accurately measured motor rotation speeds. The dual functionality of efficient energy harvesting and precise sensing capabilities positions this material system as a promising candidate for self-powered sensor applications, particularly in scenarios requiring both energy autonomy and real-time monitoring capabilities. Finally, this work also introduces a novel methodological approach for evaluating and comparing piezoelectric nanogenerator efficiency through the OWE parameter. This metric, derived from the formal ratio of harvested electrical energy to maximum elastic energy stored in the device, potentially addresses a significant gap in the field of piezoelectric energy harvesting. While existing metrics such as peak-to-peak voltage and current, power and current density provide valuable insights into device performance, they do not directly assess the efficiency of mechanical-to-electrical energy conversion. The OWE parameter, quantified at 13.1% for the top-performing 10 wt% DIPA·BNPP-PDMS composite, therefore offers a standardized method for comparing different piezoelectric nanogenerators and identifying potential areas for improvement in both molecular design and functional device architecture. Although current data for device comparisons are limited, the high OWE value observed in this study indicates substantial room for enhancing the conversion efficiency of stored elastic energy into electrical energy for harvesting applications. This new metric also paves the way for more informed research efforts in the field of piezoelectric energy harvesting applications.

Data availability

Experimental details, supplementary data, synthesis, and characterization of the compounds are included in ESI.† Crystallographic data have been submitted to CCDC under 2421897 and 2421898.

Author contributions

R. B. and V. K. designed the project. V. K. prepared the samples and performed the measurements. V. K. and R. B. performed the piezoelectric energy harvesting measurements and analysis; A. G. and K. S. performed the stress-train measurement. J. K. Z. performed non-linear optical and d₃₃ studies; V. K., N. P. and R. B. wrote the original manuscript. S. S., A. S. K., S. D., and J. K. Z. reviewed and edited the manuscript. R. B. directed the project. All the authors discussed the results and contributed sincerely to the preparation of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

R. B. thanks SERB, India, via Grant No. CRG/2023/000582 and SERB, India, for the Science and Technology Award for Research (STAR) via Grant No. STR/2021/000016. J. K. Z. acknowledges support from the Wroclaw University of Science and Technology and Academia Iuvenum. We thank Mr Aditya Raj for helping in creating the animated video. The authors thank Vijay Krushna Mistari and acknowledge the BIO-AFM (BSBE)–IRCC BIO Atomic Force Microscopy (BIO-AFM) Central Facility of I.I.T. Bombay for providing the PFM facility.

References

1. J. Valasek, Phys. Rev., 1921, 17, 475.
2. G. Busch and P. Scherrer, Naturwissenschaften, 1935, 23, 737.
3. J. J. Brondijk, K. Asadi, P. W. Blom and D. M. De Leeuw, J. Polym. Sci., Part B:Polym. Phys., 2012, 50, 47–54.
4. A. Petritz, E. Karner-Petritz, T. Uemura, P. Schäffner, T. Araki, B. Stadlober and T. Sekitani, Nat. Commun., 2021, 12, 2399.
5. S. Hannah, A. Davidson, I. Glesk, D. Uttamchandani, R. Dahiya and H. Gleskova, Org. Electron., 2018, 56, 170–177.
6. A. S. Dahiya, F. Morini, S. Boubenia, K. Nadaud, D. Alquier and G. Poulin-Vittrant, Adv. Mater. Technol., 2018, 3, 1700249.
7. H. Lu, J. Du, C. Yu, X. Wang, Y. Gao, W. Xu, A. Liu, X. Lu and Y. Chen, Macromol. Res., 2020, 28, 573–579.
8. A. R. Akbashev, V. M. Fridkin and J. E. Spanier, Nanoscale Ferroelectr. Multiferroics, 2016, 26, 830–850.
9. H. D. Megaw, Nature, 1945, 155, 484–485.
10. W.-Q. Liao, D. Zhao, Y.-Y. Tang, Y. Zhang, P.-F. Li, P.-P. Shi, X.-G. Chen, Y.-M. You and R.-G. Xiong, Science, 2019, 363, 1206–1210.
11. H.-Y. Zhang, Y.-Y. Tang, Z.-X. Gu, P. Wang, X.-G. Chen, H.-P. Lv, P.-F. Li, Q. Jiang, N. Gu and S. Ren, Science, 2024, 383, 1492–1498.
12. L. W. Martin and A. M. Rappe, Nat. Rev. Mater., 2016, 2, 1–14.
13. T. Vijayakanth, D. J. Liptrot, E. Gazit, R. Boomishankar and C. R. Bowen, Adv. Funct. Mater., 2022, 32, 2109492.
14. N. Leblanc, N. Mercier, L. Zorina, S. Simonov, P. Auban-Senzier and C. Pasquier, J. Am. Chem. Soc., 2011, 133, 14924–14927.
15. A. Ghosh, S. Menon, S. Biswas, S. Sahoo, A. Dey, R. Boomishankar, J. K. Zaręba, U. V. Waghmare and T. K. Maji, Adv. Funct. Mater., 2025, 2502787.
16. Q. Gu, X. Lu, C. Chen, X. Wang, F. Kang, Y. Y. Li, Q. Xu, J. Lu, Y. Han and W. Qin, Angew. Chem., Int. Ed., 2024, 63, e202409708.
17. Q. Pan, Z.-X. Gu, R.-J. Zhou, Z.-J. Feng, Y.-A. Xiong, T.-T. Sha, Y.-M. You and R.-G. Xiong, Chem. Soc. Rev., 2024, 53, 5781–5861.
18. D.-W. Fu, H.-L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang, X.-Y. Chen, G. Giovannetti, M. Capone and J. Li, Science, 2013, 339, 425–428.
19. D.-W. Fu, W. Zhang, H.-L. Cai, J.-Z. Ge, Y. Zhang and R.-G. Xiong, Adv. Mater., 2011, 23, 5658–5662.
20. R. K. Saripalli, D. Swain, S. Prasad, H. Nhalil, H. L. Bhat, T. N. Guru Row and S. Elizabeth, J. Appl. Phys., 2017, 121, 114101.
21. A. Piecha-Bisiorek, A. Gągor, D. Isakov, P. Zieliński, M. Gałązka and R. Jakubas, Inorg. Chem. Front., 2017, 4, 553–558.
22. K. Gao, M. Gu, X. Qiu, X. Ying, H.-Y. Ye, Y. Zhang, J. Sun, X. Meng, F. Zhang and D. Wu, J. Mater. Chem. C, 2014, 2, 9957–9963.
23. C. Jiang, N. Zhong, C. Luo, H. Lin, Y. Zhang, H. Peng and C.-G. Duan, Chem. Commun., 2017, 53, 5954–5957.
24. M. Rok, P. Starynowicz, A. Cizman, J. K. Zareba, A. Piecha-Bisiorek, G. y. Bator and R. Jakubas, Inorg. chem., 2020, 59, 11986–11994.
25. C. Housecroft, E. Catherine and A. G. Sharpe, Inorganic Chemistry, Pearson Hall, 2005.
26. S. Pongiappan and S. Karuppannan, J. Phys. Chem. Solids, 2021, 153, 110008.
27. P. Prince, J. Miller, F. Fronczek and R. Gandour, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 1990, 46, 336–338.
28. P. C. J. Effendy, C. J. Kepert, L. M. Louis, T. C. Morien, B. W. Skelton and A. H. White, Z. fur Anorg. Allg. Chem., 2006, 632, 1312–1325.
29. S. Bajorat and G. J. Reiss, Acta Crystallogr., Sect. E:Struct. Rep. Online, 2007, 63, o3144.
30. M. Haberecht, H.-W. Lerner and M. Bolte, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 2002, 58, o555–o557.
31. H. Yadav, N. Sinha, S. Goel, A. Hussain and B. Kumar, J. Appl. Crystallogr., 2016, 49, 2053–2062.
32. G. Kociok-Köhn, B. Lungwitz and A. C. Filippou, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 1996, 52, 2309–2311.
33. Z.-H. Wei, Z.-T. Jiang, X.-X. Zhang, M.-L. Li, Y.-Y. Tang, X.-G. Chen, H. Cai and R.-G. Xiong, J. Am. Chem. Soc., 2020, 142, 1995–2000.
34. A. Y. Teterina, O. Baranov, P. Mikheeva, M. Gol'dberg, S. Barinov and V. Komlev, Polym. Sci., Ser. D, 2021, 14, 265–268.
35. J. Florián, M. Štrajbl and A. Warshel, J. Am. Chem. Soc., 1998, 120, 7959–7966.
36. Y. Yoshii, N. Hoshino, T. Takeda and T. Akutagawa, J. Phys. Chem. C, 2015, 119, 20845–20854.
37. Z.-S. Cai, S. Uchikawa, N. Hoshino, T. Takeda, L.-M. Zheng, S.-i. Noro, T. Nakamura and T. Akutagawa, J. Phys. Chem. B, 2016, 120, 6761–6770.
38. P.-F. Wang, S.-S. Bao, X.-D. Huang, T. Akutagawa and L.-M. Zheng, Chem. Commun., 2018, 54, 6276–6279.
39. B. Chandanshive, D. Dyondi, V. R. Ajgaonkar, R. Banerjee and D. Khushalani, J. Mater. Chem., 2010, 20, 6923–6928.
40. P. Sharma, S. Rana, K. C. Barick, C. Kumar, H. G. Salunke and P. A. Hassan, New J. Chem., 2014, 38, 5500–5508.
41. A. Islam and P. X.-L. Feng, in Fundamentals and Applications of Phosphorus Nanomaterials, ACS Publications, 2019, pp. 179–194.
42. J. Wu, R. Xu, M. Shao, L. Zhao, W. Xu and Y. Guo, ACS Appl. Nano Mater., 2024, 7, 11022–11036.
43. Z. S. Cai, N. Hoshino, S. S. Bao, J. Jia, T. Akutagawa and L. M. Zheng, Chem.–Eur. J., 2018, 24, 13495–13503.
44. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
45. K. K. Rao, AIP Conf. Proc., 1974, 17, 219–230.
46. R. S. Krishnan, R. Srinivasan and S. Devanarayanan, Pergamon, 1979, 12, 54–104.
47. S. Kurtz and T. Perry, J. Appl. Phys., 1968, 39, 3798–3813.
48. M. Wen, H. Wu, H. Yu and X. Wu, J. Solid State Chem., 2020, 286, 121276.
49. X.-B. Li, C.-L. Hu, F. Kong and J.-G. Mao, Chem. Front., 2023, 10, 2268–2275.
50. L. Le Xuan, C. Zhou, A. Slablab, D. Chauvat, C. Tard, S. Perruchas, T. Gacoin, P. Villeval, J.-F. Roch and X. L. Le, Small, 2008, 4, 1332–1336.
51. L.-K. Su and B.-S. Hsu, Nature, 1968, 220, 780–781.
52. J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi, 1966, 15, 627–637.
53. X. Wu, X. Chen, Q. Zhang and D. Q. Tan, Energy Storage Mater., 2022, 44, 29–47.
54. S. Sikiru, N. Yahya, H. Soleimani, A. M. Ali and Y. Afeez, J. Mol. Liq., 2020, 318, 114039.
55. S. Singh, A. Kaur, P. Kaur and L. Singh, ACS Omega, 2023, 8, 25623–25638.
56. K. D. Kim, Y. B. Lee, S. H. Lee, I. S. Lee, S. K. Ryoo, S. Byun, J. H. Lee, H. Kim, H. W. Park and C. S. Hwang, Adv. Electron. Mater., 2023, 9, 2201142.
57. A. K. Srivastava, P. Divya, B. Praveenkumar and R. Boomishankar, Chem. Mater., 2015, 27, 5222–5229.
58. S. V. Kalinin and A. Gruverman, Scanning Probe Microscopy: Electrical and Electromechanical Phenomena at the Nanoscale, 2007.
59. K. P. Kelley, Y. Ren, A. N. Morozovska, E. A. Eliseev, Y. Ehara, H. Funakubo, T. Giamarchi, N. Balke, R. K. Vasudevan and Y. Cao, ACS Nano, 2020, 14, 10569–10577.
60. X. Wang, B. Li, X. Zhong, Y. Zhang, J. Wang and Y. Zhou, J. Appl. Phys., 2012, 112, 114103.
61. P. Zubko, D. Jung and J. Scott, J. Appl. Phys., 2006, 100, 114112.
62. K. Y. Lee, D. Kim, J. H. Lee, T. Y. Kim, M. K. Gupta and S. W. Kim, Adv. Funct. Mater., 2014, 24, 37–43.
63. M. Arous, H. Hammami, M. Lagache and A. Kallel, J. Non-Cryst. Solids, 2007, 353, 4428–4431.
64. Z. L. Wang and J. Song, Science, 2006, 312, 242–246.
65. F. Beer, E. Johnston, J. DeWolf and D. Mazurek, Mechanics, MeGraw-Hill, New York, 7^th edn, 2015.
66. S. Xu, Y. Qin, C. Xu, Y. Wei, R. Yang and Z. Wang, Nat. Nanotechnol., 2010, 5, 366.

---

Footnote

† Electronic supplementary information (ESI) available: CCDC 2421897 and 2421898. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5ta01846c

---