Pivotal role of Sb vacancies in quaternary half-Heusler thermoelectrics

Abstract

Half-Heusler compounds are promising high-temperature thermoelectric materials due to their high figure of merit and excellent mechanical properties. The capability of the Heusler structure to accommodate a large variety of different elements allows for a vast phase space of substitutions and compositions. The quaternary half-Heuslers (also known as “double half-Heuslers”) with 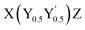stoichiometry have sparked particular interest as a route to lower the lattice thermal conductivity and enhance thermoelectric performance. Here, we unveil the pivotal role of intrinsic defects, namely Sb vacancies, in nominally stoichiometric X(Ni_0.5Fe_0.5)Sb quaternary half-Heuslers, where X = Ti, Zr, Hf. Sb vacancies naturally occur during synthesis and can switch the conduction behavior from intrinsic n-type to p-type. To control the formation of Sb vacancies, we developed a sophisticated synthesis method, which we argue will be crucial for rational design of n- and p-type quaternary half-Heusler thermoelectrics.

---

1 Introduction

The rising global demand for energy, coupled with pressing environmental challenges, highlights the crucial need for sustainable and eco-friendly energy sources. Thermoelectric (TE) materials and devices are interesting for those purposes as they realize direct conversion of heat into electricity via the Seebeck effect, which can be leveraged to enhance energy efficiency. From a material science perspective, the conversion efficiency of a TE device is determined by a dimensionless figure of merit, defined as zT = α²σT/κ, with α being the Seebeck coefficient, σ the electrical conductivity, T the absolute temperature, and κ the thermal conductivity, including both electronic and lattice contributions (κ = κ_el + κ_lat).¹ Due to the correlated and intertwined nature of these transport properties, enhancing zT poses an outstanding challenge.

Among various semiconducting material families investigated over the past decades, half-Heusler phases, with the general formula XYZ (F4̄3m space group), represent a large family of compounds with promising TE properties.^2,3 In general, their crystal structure and chemical bonding strongly correlate with the valence electron count (VEC), which determines electronic structure and stability. The Zintl–Klemm concept helps rationalize the valence electron rule, considering that the most electropositive X element transfers its electrons to the more electronegative Y and Z elements, forming d¹⁰ and s²p⁶ closed shell ions, making 18 valence electron half-Heusler compounds particularly stable semiconductors.⁴ Altering the valence electron count (VEC ≶ 18) typically disrupts the semiconducting ground state, causing the compounds to become metallic.⁵ Despite significant advancements in 18-electrons half-Heuslers,^6,7 their high lattice thermal conductivity κ_lat remains a major barrier to further improvements in their zT.

To overcome these limitations, Anand et al. proposed that an increase in structural complexity can be realized by combining two half-Heusler compounds with VEC = 17 and 19 to obtain an effective 18 valence electrons per formula unit, ⁸ To validate this approach, they compared the widely studied half-Heusler compound TiCoSb (VEC = 18) with the valence balanced quaternary half-Heusler alloy Ti(Fe_0.5Ni_0.5)Sb (VEC = (17 + 19)/2 = 18) derived from the two parent compounds TiFeSb (VEC = 17) and TiNiSb (VEC = 19). A twofold reduction in κ_lat was achieved for Ti(Fe_0.5Ni_0.5)Sb compared to TiCoSb due to enhanced phonon scattering while a high Seebeck coefficient and semiconducting ground state were retained. Since then, such compounds have garnered significant interest in the community as they open a whole new phase space of potentially interesting thermoelectric materials. The above-mentioned approach has often been referred to as “double half-Heuslers” in the literature. However, as Rogl et al. point out, this description is not without problems from a structural chemistry perspective.¹⁶ Instead, in this work, we prefer to use the more general and correct term - quaternary half-Heuslers. Despite the growing interest, the properties of these systems, particularly those reported for isovalent X(Fe_0.5Ni_0.5)Sb, where X represents Ti, Zr, or Hf, vary dramatically (Fig. 1), hindering further progress in enhancing zT. In their initial study, Anand et al. identified Ti(Fe_0.5Ni_0.5)Sb as a p-type semiconductor with α ≈ 300 μV K⁻¹, whereas subsequent studies reported significantly smaller values (α ≈ 120 μV K⁻¹) and even a change of the conduction type (from p- to n-type) for the samples with the same nominal composition^8,9,12,14,17 (Fig. 1). Similar ambiguity with respect to the conduction type exists in the Zr analogue Zr(Fe_0.5Ni_0.5)Sb.^12,13

Fig. 1 Range of variations in the maximum Seebeck coefficient values among X(Fe_0.5Ni_0.5)Sb compounds (X = Ti, Zr, or Hf) reported previously^8–15 and values obtained in this work (colored symbols).

Here, we unveil that the origin of this discrepancy can be understood by considering the pivotal role of point defects, such as vacancies and antisites, often encountered in Heusler compounds.^18–20 Such defects can directly affect the charge carrier concentration and carrier scattering,^21,22 and their formation is strongly influenced by the synthesis conditions.^19,23 Arc melting is one of the most common synthesis routes for Heusler compounds. Precise control of stoichiometry, however, is a well-known key challenge. In Sb-containing half-Heuslers and quaternary half-Heuslers, for instance, arc melting usually involves poorly controlled evaporation of Sb. To compensate for Sb losses, excess Sb (typically 2 to 10 wt%) may be added prior to the melt synthesis. However, the chemical composition is difficult to control precisely and inevitable small compositional differences, sometimes barely detectable by conventional analyses, can lead to fundamentally different transport properties.

In this work, we developed a sophisticated synthesis route to enable a higher degree of control over the stoichiometry and elucidate the phase formation mechanism in detail. Consequently, we identify the key experimental knobs to systematically tune the Sb vacancy formation in X(Fe_0.5Ni_0.5)Sb (X = Ti, Zr, or Hf), and find that, following this careful synthesis procedure, Ti(Fe_0.5Ni_0.5)Sb and Zr(Fe_0.5Ni_0.5)Sb exhibit intrinsic n-type conductivity. In contrast, the unavoidable formation of Sb vacancies in Hf(Fe_0.5Ni_0.5)Sb during phase formation makes it intrinsically p-type. These observations underscore the importance of precise control over the synthesis conditions to tailor the TE performance of quaternary half-Heuslers. Furthermore, we demonstrate that Ti(Fe_0.5Ni_0.5)Sb can be switched from n- to p-type, merely by changing the annealing conditions. This peculiar ability to switch the conduction type is particularly advantageous for the design of TE modules, as it enables the use of a single material for both p- and n-type legs, thereby mitigating device failures arising from mismatched thermal expansion coefficients and other compatibility challenges.

2 Results and discussion

2.1 Phase formation

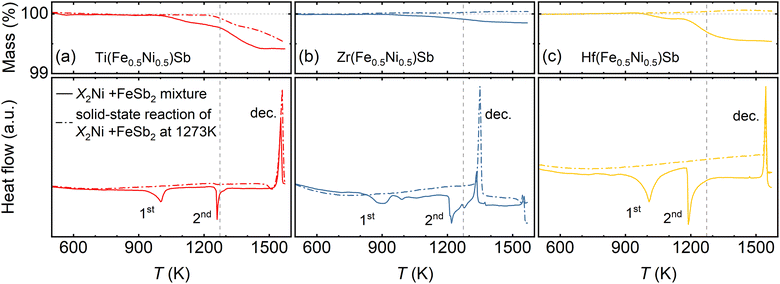
To minimize Sb losses and improve control over its stoichiometry during the synthesis of X(Fe_0.5Ni_0.5)Sb (X = Ti, Zr, or Hf), we initially synthesized the master alloys FeSb₂ and X₂Ni (X = Ti, Zr, or Hf) and used them as starting materials, as described in detail in Section 4. To investigate the phase formation mechanism of X(Fe_0.5Ni_0.5)Sb, we employed differential scanning calorimetry (DSC), thermogravimetric analysis (TGA), powder X-ray diffraction (XRD), and energy-dispersive X-ray spectroscopy (EDX) on two different powder mixtures of FeSb₂ and X₂Ni. The first one represented a stoichiometric mixture of FeSb₂ and X₂Ni powders (solid lines in Fig. 2), while the second mixture represented X(Fe_0.5Ni_0.5)Sb (Fig. S1†), obtained via a solid-state reaction between FeSb₂ and X₂Ni at 1273 K (dashed lines in Fig. 2).

Fig. 2 Differential scanning calorimetry (DSC) and thermogravimetric analysis (TGA) results for X(Fe_0.5Ni_0.5)Sb with X representing (a) Ti, (b) Zr, and (c) Hf. The upper panels show a mass loss, while the lower panels display heat flow during heating of a stoichiometric mixture of X₂Ni (X = Ti, Zr, Hf) and FeSb₂ (solid curves) and same mixture after solid-state reaction at 1273 K (dashed curves). The “1st” (≈1000 K) and “2nd” (≈1250 K) exothermic peaks correspond to sequential phase formation reactions, while the “dec.” peak at higher temperatures indicates the decomposition. Note that decomposition of Zr(Fe_0.5Ni_0.5)Sb happens at noticeably lower temperature (≈1350 K) compared to that of Ti(Fe_0.5Ni_0.5)Sb and Hf(Fe_0.5Ni_0.5)Sb (≈1550 K). Vertical dashed lines represent the temperature at which all the bulk samples were synthesized, sinter and annealed after SPS.

Upon heating the stoichiometrically mixed FeSb₂ and X₂Ni master alloys, we observed two endothermic peaks in the DSC curves for all samples (solid lines in Fig. 2). We attribute the first peak (”1st”, Fig. 2), observed in the range of 850–1000 K, to the initial formation of the half-Heusler phase (space group F4̄3m), as confirmed by the XRD (Fig. S1†). However, EDX analysis reveals that the majority of the grains within the powder particles exhibit noticeable deviations in the Fe/Ni ratio, and the sample contains secondary phases such as XFe_0.5Sb and XNi_0.5Sb (Fig. S1†). The second endothermic peak (“2nd”, Fig. 2) at the range of 1150–1250 K indicates the reaction between ternary intermediates formed in the first step and results in single-phase X(Fe_0.5Ni_0.5)Sb quaternary half-Heusler, as verified by XRD and EDX analysis of the master alloy mixture annealed at 1273 K for 5 days (Fig. S1†). Overall, according to the DSC/TGA, XRD, and EDX results, the complete quaternary half-Heusler phase formation mechanism can be proposed as follows (see Fig. S1† for more details):

According to our data, the minimum temperature required for the formation of the pristine half-Heusler phase must be at more than 1250 K, e.g., 1273 K (Fig. 2). However, at this temperature, all samples exhibited mass loss, which was most pronounced in Hf(Fe_0.5Ni_0.5)Sb (≈0.4 wt%). EDX analysis, in turn, revealed that a thin metallic layer formed on the walls of the quartz tube during the solid-state reaction between FeSb₂ and X₂Ni at 1273 K corresponds to pure Sb. This confirms that Sb loss is unavoidable even during solid-state reaction and appears to be the main reason for the variations in the reported Seebeck coefficient values and conduction behavior of X(Fe_0.5Ni_0.5)Sb (X = Ti, Zr, Hf) quaternary half-Heusler compounds (Fig. 1). For example, significant Sb loss in Hf(Fe_0.5Ni_0.5)Sb inevitably results in p-type conduction behavior, while the smaller Sb loss in Ti(Fe_0.5Ni_0.5)Sb and Zr(Fe_0.5Ni_0.5)Sb allows it to retain n-type conduction as will be shown later. Moreover, since Sb loss increases with temperature, it should, in principle, be possible to switch the conduction type of X(Fe_0.5Ni_0.5)Sb (X = Ti, Zr) by annealing at temperatures above 1273 K, e.g., 1373 K. However, the decomposition of Zr(Fe_0.5Ni_0.5)Sb occurs at a much lower temperature (≈1350 K) compared to that of Ti(Fe_0.5Ni_0.5)Sb and Hf(Fe_0.5Ni_0.5)Sb (≈1550 K). This hinders the possibility of switching Zr(Fe_0.5Ni_0.5)Sb from n- to p-type solely by processing conditions, unlike in the case of Ti(Fe_0.5Ni_0.5)Sb.

Investigations of decomposition of X(Fe_0.5Ni_0.5)Sb samples after solid-state reaction at 1273 K (as indicated by dashed lines in Fig. 2) revealed that the Hf- and Zr-based compounds exhibit minimal mass loss and decomposition temperature remain the same. In contrast, Ti(Fe_0.5Ni_0.5)Sb shows additional Sb loss beginning above 1250 K, reaching approximately 0.4 wt% at 1573 K. This feature opens the possibility for additional control over the Sb content in Ti-based quaternary half-Heuslers, which, in turn, allows tuning of the conduction type from n- to p-type, as demonstrated and discussed below.

2.2 Microstructure and elemental composition

The relative density of all samples exceeds 97% of the theoretical density. The average grain sizes for the X(Fe_0.5Ni_0.5)Sb samples are approximately 13.1 μm (X = Ti), 9.4 μm (X = Zr), and 8.7 μm (X = Hf), respectively (Fig. 3b–d). Additional annealing of Ti(Fe_0.5Ni_0.5)Sb at 1373 K (Fig. 3a) did not result in significant changes of the grain size.

Fig. 3 SEM micrographs captured in electron channeling contrast mode and corresponding box plots of elemental composition distribution across different grains estimated from EDX of (a) annealed Ti(Fe_0.5Ni_0.5)Sb and (b)–(d) X(Fe_0.5Ni_0.5)Sb (X = Ti, Zr, and Hf) samples, respectively. The upper parts of box plots demonstrate Fe and Ni distribution across different grains. Average element composition obtained from ICP-OES and EDX displayed under each SEM image and box plot, respectively.

The interquartile range obtained by EDX for all constituting elements of X(Fe_0.5Ni_0.5)Sb consistently aligns with the nominal stoichiometry (Fig. 3, right panel). However, as expected, a slight Sb deficiency was observed in all compositions except for Zr(Fe_0.5Ni_0.5)Sb. To precisely determine the average chemical composition, we performed ICP-OES analysis, which confirmed the EDX findings by revealing an actual Sb deficiency of approximately 0.3–0.4 at% in Ti(Fe_0.5Ni_0.5)Sb and Zr(Fe_0.5Ni_0.5)Sb and ≈0.9 at% in Hf(Fe_0.5Ni_0.5)Sb and annealed Ti(Fe_0.5Ni_0.5)Sb (Fig. 3 and Table S2†).

Additionally, the comparison of EDX spectra reveals distinguishable variation in the K_α line intensities for Fe and Ni across different grains of each sample (Fig. 3 right panel, Fig. S2†). Although the peaks of the Gaussian distribution for Fe and Ni align well with the nominal values, the tails of the distributions exceed 1 at% for all investigated compounds. This suggests that variations in the Fe/Ni ratio between the grains cannot be completely ruled out.

2.3 Crystal structure

All obtained samples crystallize in the face-centered cubic MgAgAs-type half-Heusler crystal structure with the F4̄3m space group. No secondary phases were detected (Fig. 4a). The lattice parameter a strongly depends on the X element (X = Ti, Zr or Hf) at 4a site; a increases when Ti is replaced by Zr, most likely due to a larger atomic radius of Zr (160 pm) compared to that of Ti (147 pm) (Fig. 4b). However, replacing Zr (160 pm) with Hf (159 pm) results in a decrease of a, a trend that cannot be explained solely by atomic size differences. Interestingly, a similar trend has also been observed in other XCoSb (X = Ti, Zr or Hf) half-Heuslers.²⁴

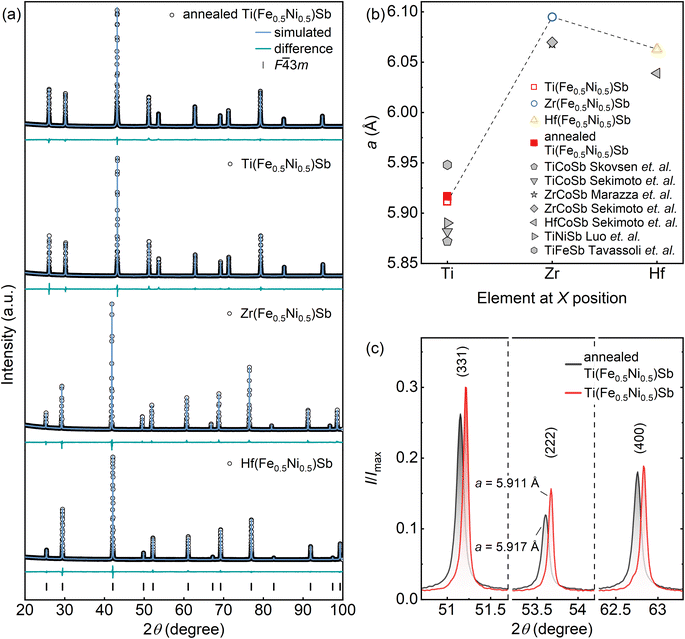Fig. 4 (a) Rietveld refinements of X-ray powder diffraction patterns of annealed Ti(Fe_0.5Ni_0.5)Sb and X(Fe_0.5Ni_0.5)Sb (X = Ti, Zr, Hf) samples, respectively. Positions of Bragg's reflections for the reference half-Heusler phase (F4̄3m space group) are indicated by black ticks at the bottom. Experimental data, simulated patterns, and the difference profiles are shown (black, blue, and green, respectively). Corresponding R-factors values of the refinement can be found in the ESI (Table S3†). (b) Calculated lattice parameters for annealed Ti(Fe_0.5Ni_0.5)Sb and X(Fe_0.5Ni_0.5)Sb (X = Ti, Zr, Hf), compared with reference values for other Sb-based half-Heusler compounds reported in the literature.^24–28 (c) Comparison of relative intensities in the XRD patterns of Ti(Fe_0.5Ni_0.5)Sb (red) and annealed Ti(Fe_0.5Ni_0.5)Sb (black) samples, highlighting changes attributed to Sb vacancy formation, as evidenced by the shift in lattice parameter a and variations in peak intensity ratios for (331), (222), and (400) reflections.

Quaternary half-Heuslers are commonly compared with their ternary analogs XYZ with the same VEC = 18.^8,9,29 In the case of X(Fe_0.5Ni_0.5)Sb, both the crystal and electronic structures are expected to resemble those of XCoSb.⁸ However, a comparison of the lattice parameter of X(Fe_0.5Ni_0.5)Sb with values reported in the literature for XCoSb reveals significant differences.^24,25 The substitution of Co by an equiatomic mixture of Fe and Ni at the Y-site does not yield similar lattice parameter values to XCoSb, as the majority of reported a values are noticeably lower. This, instead, may be caused by differences in chemical bonding³⁰ as it has been shown that covalent interactions in T’TE-type compounds contribute significantly more to the total energy of the system than Coulomb interactions for details see ref. 31. Further analysis reveals that the lattice parameter (Fig. 4b) of Ti(Fe_0.5Ni_0.5)Sb (a = 5.91146(3) Å) lies between those of TiFeSb (a = 5.9480 Å)²⁷ and TiNiSb (a = 5.8903 Å).²⁸ This additionally supports the hypothesis that the investigated quaternary half-Heuslers are more likely a solid solution of the two ternary half-Heuslers³² rather than a distinct new phase.⁸

Refinement of the crystal structures for Ti(Fe_0.5Ni_0.5)Sb and Zr(Fe_0.5Ni_0.5)Sb with different site occupancy, based on powder X-ray diffraction data, indicates that the smallest R-factor is obtained when the atomic sites 4a_X, 4b_Y, and 4c_Z are modeled as fully occupied (Table S3†). However, refinements for Hf(Fe_0.5Ni_0.5)Sb reveal increased displacement parameter values for the Sb position, highlighting the probability of reduced Sb occupancy at this site aligning with EDX/ICP-OES findings. Therefore, the site occupancy factor (SOF) for Sb was refined to be 0.96. This approach resulted in lower R-factor values and physically reasonable atomic displacement parameter values (Table S3†), indicating that under controlled synthesis conditions, Sb vacancies in X(Fe_0.5Ni_0.5)Sb compounds can be minimized. Nonetheless, the Hf-based quaternary half-Heusler compound inherently forms with Sb deficiency.

The comparison of diffraction patterns reveals clear differences between Ti(Fe_0.5Ni_0.5)Sb and annealed Ti(Fe_0.5Ni_0.5)Sb (Fig. 4c). For the annealed sample, the peak positions shifted toward lower diffraction angles, indicating an increase of the lattice parameter (from 5.91146(3) Å to 5.91657(2) Å) and the corresponding intensity ratio (I₃₃₁ + I₂₂₂)/I₄₄₀ compared to the non-annealed sample. Rietveld refinement, in turn, yielded a SOF = 0.95 for annealed Ti(Fe_0.5Ni_0.5)Sb, revealing Sb vacancy in this sample. This confirms the feasibility of fine-tuning the stoichiometry, conduction type, and maximum Seebeck coefficient value in Ti(Fe_0.5Ni_0.5)Sb solely through careful control of synthesis parameters.

Summarizing, the consistency between the EDX and ICP-OES-derived chemical compositions and the site occupancies refined through Rietveld analysis revealed that X(Fe_0.5Ni_0.5)Sb (X = Ti, Zr, or Hf) quaternary half-Heuslers naturally tend to form Sb vacancies during synthesis or annealing processes. However, our developed synthesis route provides a means to minimize vacancy formation, allowing for a more precise control over the thermoelectric transport properties.

2.4 Transport properties

In previously published data, Ti(Fe_0.5Ni_0.5)Sb was reported as a p-type semiconductor with α_max values ranging from 120 to 300 μV K⁻¹.^8,9 Later, the same composition was reported as an n-type semiconductor with α_max = −200 μV K⁻¹.^11,17 Literature data for Zr(Fe_0.5Ni_0.5)Sb vary from α_max −15 to 85 μV K⁻¹.^12,13 In our study, the Ti(Fe_0.5Ni_0.5)Sb and Zr(Fe_0.5Ni_0.5)Sb samples were identified as non-degenerate n-type semiconductors, with α_max reaching up to −350 μV K⁻¹ and −200 μV K⁻¹, respectively (Fig. 5a). To understand these observed deviations, one must consider the synthesis procedures. In several studies we reviewed, arc melting was used to prepare X(Fe_0.5Ni_0.5)Sb samples.^8,11,12,17 Liu et al. used ball-milling⁹ to synthesize Ti(Fe_0.5Ni_0.5)Sb. Both methods inevitably induce defects, due to uncontrollable Sb evaporation during arc melting and structural disorder from long-term ball-milling, which complicates investigations of their intrinsic properties. In the case of Zr(Fe_0.5Ni_0.5)Sb, uncontrollable synthesis conditions during arc melting inevitably lead to partial decomposition of the desired phase and, as a consequence, only modest α values.^12,13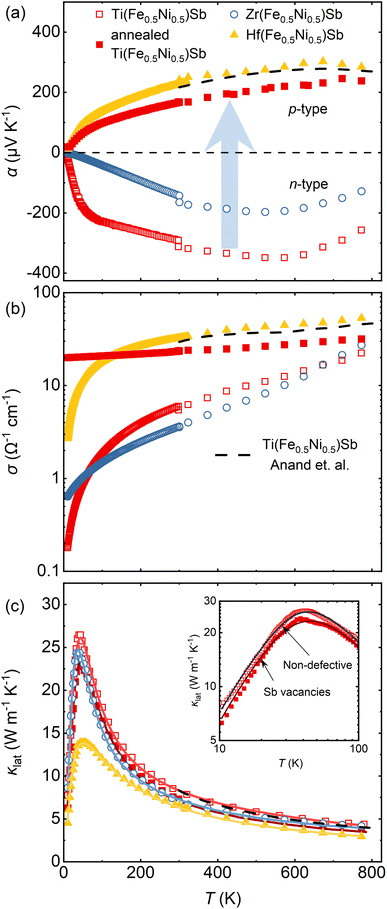

Fig. 5 Temperature dependence of (a) Seebeck coefficient α, (b) electrical conductivity σ, and (c) lattice thermal conductivity κ_lat of X(Fe_0.5Ni_0.5)Sb samples (X = Ti, Zr, and Hf) and the annealed Ti(Fe_0.5Ni_0.5)Sb sample, respectively. Both samples, annealed Ti(Fe_0.5Ni_0.5)Sb and Hf(Fe_0.5Ni_0.5)Sb, with evident Sb vacancies demonstrate p-type conductivity. Solid lines represent the fitting by the modified Debye-Callaway model,³³ dashed line represent κ_lat of Ti(Fe_0.5Ni_0.5)Sb synthesized via arc melting from.⁸ The inset in (c) shows κ_lat(T) in a log–log scale, highlighting the reduction in κ_lat of Ti(Fe_0.5Ni_0.5)Sb after annealing at 1373 K due to induced Sb vacancy formation.

Hf(Fe_0.5Ni_0.5)Sb and annealed Ti(Fe_0.5Ni_0.5)Sb samples, with the highest concentration of Sb vacancies, are identified as non-degenerate p-type semiconductors, with α_max of 300 μV K⁻¹ and 250 μV K⁻¹, respectively. From a VEC perspective, deficiency of Sb decreases the VEC compared to the nominal 18 electrons per unit cell in the pristine material, lowering E_F towards the valence band. The most pronounced realization of this concept is observed in the Ti(Fe_0.5Ni_0.5)Sb sample without annealing, which demonstrates n-type behavior as the chemical composition closely approximates the nominal one. Formation of Sb vacancies during annealing reduces the VEC, leading to p-type conduction behavior in annealed Ti(Fe_0.5Ni_0.5)Sb. On the other hand, the formation of Hf(Fe_0.5Ni_0.5)Sb inherently comes along with the formation of Sb vacancies that determine its conduction type. This intrinsic doping mechanism is also reflected in the electrical conductivity (Fig. 5b), which increases by about one to two orders of magnitude in the samples, for which substantial formation of Sb vacancies was identified. The effect on the thermal conductivity (Fig. 5c), however, is much more subtle (compare Ti(Fe_0.5Ni_0.5)Sb versus annealed Ti(Fe_0.5Ni_0.5)Sb), suggesting that the effect of the Sb vacancies is especially dramatic with respect to the electronic transport properties.

To assess whether the sizeable differences in the temperature-dependent Seebeck coefficient between Zr- and Ti/Hf-based compounds can be accounted for by differences in the electronic structure, we performed density functional theory calculations of the ground state electronic structure. The unfolded band structures along with the atom-projected partial and total densities of states are plotted in Fig. 6. It can be seen that all compounds share a similar semiconducting ground state with a band gap ranging from 0.8–0.9 eV. Thus, the most obvious explanation for the change in thermoelectric properties is the variation of the Fermi level caused by the different concentration of defects. The shift of the stoichiometry and VEC due to the formation of Sb vacancies pushes the Fermi level from the conduction band bottom towards the valence band top, thus changing the conduction type from n-type to p-type.

Fig. 6 Unfolded electronic band structure and corresponding total and partial density of states (DOS) for X(Fe_0.5Ni_0.5)Sb samples, with X representing (a) Ti, (b) Zr, and (c) Hf, respectively. The horizontal dashed lines indicate the Fermi level E_F, formation of Sb vacancies tune E_F from the conduction band to the valence band.

All measured X(Fe_0.5Ni_0.5)Sb samples exhibit a semiconducting temperature dependence of σ (Fig. 5b), i.e., the electrical conductivity increases with temperature. Similar to the Seebeck coefficient, a clear difference is observed between non-defective n-type (Ti- and Zr-based) samples and p-type (Hf-based and annealed Ti-based) samples with Sb vacancies. Since only the p-type samples demonstrate an enhancement in σ, it suggests that the presence of Sb vacancies increases hole charge carrier concentration, thereby improving σ at low to mid-range temperatures. At higher temperatures, where bipolar conduction becomes significant, both electrons and holes contribute to charge transport, resulting in similar σ values across all samples. The unusual low-temperature behavior of σ will be discussed in Chapter 2.5.

The lattice thermal conductivity κ_lat (Fig. 5c) is a dominant part of total thermal conductivity in all investigated samples since the κ_e contribution accounts for less than 3% owing to relatively low σ values. The Debye–Callaway model modified by Slack³³ reveals that for X(Fe_0.5Ni_0.5)Sb materials (where X = Ti, Zr, or Hf), normal scattering dominates in the low-temperature region which is responsible for observed κ_lat peak. At elevated temperatures, Umklapp, point defect, and phonon-electron scattering processes become dominant due to their high crystallinity, as evidenced in the crystal structure section and also consistent with a recently published study for other half-Heusler materials.^34–36 The Hf(Fe_0.5Ni_0.5)Sb and annealed Ti(Fe_0.5Ni_0.5)Sb samples demonstrate noticeably higher contribution from point defect scattering additionally revealing the presence of Sb vacancies (Table S4†).

2.5 Features of low-temperature transport

At low temperatures, α(T) and σ(T) decrease rapidly, clearly indicating a changing scattering mechanism. Notably, attempts to model the electrical transport using diffusive charge transport (e.g., the two-band model) failed to accurately describe the low-temperature behavior (Fig. S3†).³⁷ Among the potential mechanisms considered, the Kondo effect, Mott's variable range hopping (VRH), and the phonon drag effect emerge as the most plausible phenomena commonly observed in half-Heusler compounds.^35,38

Magnetic field-dependent measurements of σ and α revealed no field dependence, ruling out the Kondo effect (see Fig. S4†). Fitting revealed that ln(1/σ) proportional to T^−0.2 suggests scattering mechanism similar to VRH (T^−0.25).³⁹ However, the VRH model failed to explain Seebeck coefficient behavior, as it predicts α = 0 at 8 K, which is physically inappropriate. Furthermore, crystal structure analyses revealed that all obtained compounds are well-crystallized and lack significant atomic disorder, making the presence of VRH unlikely. On the other hand, the peak in lattice thermal conductivity (Fig. 5c) occurs in the temperature range where σ and α exhibit a noticeable change in slope. This observation suggests that the temperature dependence of σ and α may be influenced by the phonon drag effect, where the mean free paths of phonons become comparable to charge carriers, introducing an additional scattering mechanism below 50 K. In the case of annealed Ti(Fe_0.5Ni_0.5)Sb, most likely that the Sb vacancies shift the Fermi level into the valence band noticeably increasing holes concentration (as can be noted from relatively high σ) minimize the impact of electron scattering on long-wavelength phonon resulting in weak σ and α temperature dependence. A more detailed discussion of the phonon drag effect is provided in the ESI.†

3 Conclusions

Summarizing, we revealed that the phase formation process of quaternary half-Heusler follows two stages, ultimately leading to the formation of single-phase half-Heusler compounds. We found that Ti- and Hf-based quaternary half-Heuslers are particularly sensitive to synthesis temperatures and annealing above 1250 K, which promotes the formation of Sb vacancies. The Zr-based compounds hardly form any vacancies but decompose around 1340 K. Experimentally and theoretically, it has been established that non-defective X(Fe_0.5Ni_0.5)Sb materials are non-degenerate n-type semiconductors. However, the presence of Sb vacancies in Ti- and Hf-based materials induces a transition to non-degenerate p-type conduction behavior. Our work resolves the ambiguity of literature reports on the conduction type of the compounds and highlights the importance of preventing Sb vacancy formation for rational design of n-type quaternary half-Heusler thermoelectrics.

4 Materials and methods

4.1 Synthesis

As starting materials, we used a Ti rod (99.99 mass%), Zr rod (99.99 mass%), Hf ingot (99.9 mass%, with 1.2 at% of Zr), Fe ingot (99.995 mass%), Ni ingot (99.99 mass%), and Sb shot (99.999 mass%), all produced by Rare Metallic Co. (Japan). Due to the significant difference in the melting points of the elements, master alloys FeSb₂ and X₂Ni (X = Ti, Zr, or Hf) were initially synthesized and used as precursors. FeSb₂ was prepared by the melting of Fe and Sb in an evacuated carbon-coated quartz ampule for 24 h at 1323 K. The obtained product was ground into fine powder inside a glovebox, cold-pressed, and subsequently sealed in a quartz ampoule for a second annealing step at 873 K for 7 days, followed by quenching in cold water. The master alloy X₂Ni was prepared by arc melting under an Ar atmosphere, followed by hand-crushing inside a glovebox.

X₂Ni and FeSb₂ master alloys were weighed according to the stoichiometric ratio and subsequently mixed in a stainless-steel jar in a shaker mill (8000D Mixer/Mill, SPEX SamplePrep, USA) with a powder/ball ratio of 2 : 1 for 30 minutes. Afterward, the resulting powder was cold-pressed, sealed in a quartz tube, and annealed for 5 days at 1273 K, followed by quenching in cold water. The powder, after solid-state reaction, was densified by spark plasma sintering (Dr Sinter-1080, Fuji-SPS, Japan) in a ∅10 mm graphite die under uniaxial pressure of 50 MPa at 1273 K for 10 min, under Ar atmosphere, with a heating rate of 100 K min⁻¹. Finally, to homogenize chemical composition and remove residual stress, all fabricated specimens were annealed for three days at 1273 K under vacuum and quenched. To demonstrate the switchability of the Ti(Fe_0.5Ni_0.5)Sb sample from n- to p-type, the obtained bulk sample was additionally annealed for three days at 1373 K following the same procedure.

This synthesis approach enables precise control over the chemical composition and provides detailed insight into the phase formation process, a level of control unattainable with other methods such as arc melting or mechanical alloying.

4.2 Materials characterization

For phase identification, powder X-ray diffraction (XRD) using a θ/2θ Bragg–Brentano diffractometer (SmartLab3, Rigaku Corporation, Japan) was used. The measurements covered an angular range from 10° to 130° with a CuKα₁ radiation source (λ = 1.54056 Å), a step width of 0.02°, and a scan speed of 1° per min. For data evaluation and crystal structure refinement, the program package WinCSD was employed.⁴⁰

The microstructure and elemental composition of the obtained samples were investigated by scanning electron microscopy and energy-dispersive X-ray spectroscopy (EDX) using an ultra-high resolution HRSEM (SU8230 Hitachi, Japan) equipped with an EDX detector (X-Max^N Horiba, Japan). The EDX spectra were collected with an acceleration voltage of 25 keV, reaching 5 × 10⁶ counts per spectrum. Electron Channeling Contrast Imaging (ECCI) with a photo-diode BSE detector was applied to enhance grain structure representation. This method not only identifies variations in the local average atomic number but also discerns differences in grain orientation.⁴¹

Precise average elemental composition was determined by inductively coupled plasma-optical emission spectrometry (ICP-OES) using a 5800 ICP-OES spectrometer (Agilent, USA). Approximately 10 mg of the crushed bulk sample was decomposed in a 100 mL PFA beaker using 10 mL of aqua regia and 1–3 mL of HF by heating. The cooled residue was filtered (type 5C), and the filtrate was diluted to 250 mL with Milli-Q water. The residue and filter paper were ashed in an alumina crucible, fused with 0.25 g Na₂CO₃ and 0.75 g Na₂O₂, and the cooled melt was dissolved in Milli-Q water and 10 mL of HCl (1 : 1), then diluted to 100 mL. The filtrate was analyzed by radial viewing and emission intensity ratio method (20 mg L⁻¹ Mn: 257.610 nm, on-line addition), while the residue solution was measured by axial viewing and emission intensity method.

Thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) were performed using a simultaneous thermogravimetry analyzer (449 F1 Jupiter Netzsch, Germany). The phase formation mechanism was investigated using ∼0.1 g of a stoichiometric mixture of FeSb₂ and X₂Ni (X = Ti, Zr, Hf) master alloys (dashed curves in Fig. 2) placed in Al₂O₃ crucibles under a 6N argon stream, with a heating rate of 10 K min⁻¹ from 400 K to 1573 K. To confirm the thermal stability of the samples, mixtures of FeSb₂ and X₂Ni after solid-state reaction at 1273 K (solid curves in Fig. 2) were also subjected to the DSC-TGA analysis in the same conditions.

4.3 Transport properties measurements

Temperature dependencies of the electrical conductivity σ and the Seebeck coefficient α were simultaneously measured along the radial direction perpendicular to the pressure direction in the SPS of bar-shaped samples with dimensions of 10 mm × 3 mm × 1.5 mm by the four-probe method in the commercial set-up ZEM 3 (Advance-Riko, Japan). The temperature dependence of total thermal conductivity κ was calculated using the formula κ = χ × C_p × d, where χ is the thermal diffusivity determined from thermal diffusivity measurements by a laser flash method (LFA 457 MicroFlash, Netzsch, Germany), C_p is the specific heat capacity estimated using the comparison method with a standard sample (pyroceram-9606), and d is the bulk density determined using the Archimedes method. To minimize errors from the emissivity and reflectivity of the material to infrared radiation, the samples were covered with a thin layer of graphite. The lattice thermal conductivity (κ_lat) was calculated through κ_lat = κ − κ_e, where κ_e = σLT according to the Wiedemann–Franz law, with the Lorenz number derived from the measured Seebeck coefficient values.⁴²

Low-temperature σ, α, and κ were measured using a physical property measurement system (PPMS, Quantum Design, USA) from 10 to 300 K under a magnetic field of 7 T and without field. The magnetic field, electric current, and temperature gradient were all parallel to each other. Magnetization measurements were performed from 2 to 300 K using a superconducting quantum interference device magnetometer (MPMS, Quantum Design, USA).

4.4 Electronic structure calculations

The supercell DFT calculations for the quaternary half-Heusler compounds were performed using the Vienna ab initio simulation package (VASP).^43–48 To incorporate the partial substitution of Fe and Ni atoms at the 4c site, 2 × 2 × 2 supercells containing 24 atoms were constructed. The calculations were performed using the Perdew–Burke–Enzerhof generalized gradient approximation (GGA-PBE) exchange-correlation functional.⁴⁹

The crystal structures were relaxed in terms of total volumes and individual atomic positions, which is crucial for accommodating possible local distortions caused by the Fe and Ni substitution at the 4c site. For structural relaxation, a grid with a k-point spacing of 0.08 Å⁻¹ was employed to sample the Brillouin zone. A finer k-point mesh with a spacing of 0.04 Å⁻¹ was used for the self-consistent calculations of the electronic structure to minimize fluctuations in the density of states. The partial occupancies for each orbital were determined using the tetrahedron method with Bloch corrections. The optimal energy cutoff for the plane-wave basis set was determined through convergence tests on several supercells to be 450 eV.

To obtain the band structures of the respective supercells, the band structures were unfolded using the b4vasp tool.^50–52b4vasp utilizes robust algorithms in unfolding the band structure, effectively mapping the complex bands from the supercell back to the simpler Brillouin zone of the primitive cell. In the representation of the unfolded band structure, the color gradient depicts the spectral wave function A(k, E), which describes the probability density of finding an electron with a particular crystal momentum k and energy E. The methodology follows the principles outlined in ref. 50 and 52.

Data availability

The data that support the findings of this study are available from the corresponding author upon request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JST Mirai JPMJMI19A1 and JST SPRING JPMJSP2124 supported this work. Yu. G. acknowledges National Institute for Materials Science (NIMS, Japan) for financial support. The authors would like to acknowledge NIMS Nanofabrication Facility (NIMS, Japan) for SEM analysis and Material Analysis Station (NIMS, Japan) for the XRD and ICP-OES analysis. I.S. thanks Jean-François Halet (University of Rennes) and Cédric Bourges (University of Limoges) for fruitful and stimulating discussions.

References

1. A. F. Ioffe, Semiconductor Thermoelements, and Thermoelectric Cooling, Infosearch, London, 1957.
2. C. Felser and A. Hirohata, Heusler Alloys: Properties, Growth, Applications, Springer International Publishing, 2015.
3. W. Li, S. Ghosh, N. Liu and B. Poudel, Joule, 2024, 8, 1274–1311.
4. W. G. Zeier, J. Schmitt, G. Hautier, U. Aydemir, Z. M. Gibbs, C. Felser and G. J. Snyder, Nat. Rev. Mater., 2016, 1, 1–10.
5. T. Graf, C. Felser and S. S. Parkin, Prog. Solid State Chem., 2011, 39, 1–50.
6. M. Schwall and B. Balke, Phys. Chem. Chem. Phys., 2013, 15, 1868–1872.
7. H. Zhu, R. He, J. Mao, Q. Zhu, C. Li, J. Sun, W. Ren, Y. Wang, Z. Liu, Z. Tang, A. Sotnikov, Z. Wang, D. Broido, D. J. Singh, G. Chen, K. Nielsch and Z. Ren, Nat. Commun., 2018, 9, 2497.
8. S. Anand, M. Wood, Y. Xia, C. Wolverton and G. J. Snyder, Joule, 2019, 3, 1226–1238.
9. Z. Liu, S. Guo, Y. Wu, J. Mao, Q. Zhu, H. Zhu, Y. Pei, J. Sui, Y. Zhang and Z. Ren, Adv. Funct. Mater., 2019, 29, 1905044.
10. R. Hasan, Y. Gu, S. Y. Kim, D. W. Chun and K. H. Lee, Inorg. Chem. Front., 2023, 10, 5662–5667.
11. N. Li, H. Zhu, W. He, B. Zhang, W. Cui, Z.-Y. Hu, X. Sang, X. Lu, G. Wang and X. Zhou, J. Mater. Chem. C, 2020, 8, 3156–3164.
12. J. N. Kahiu, S. K. Kihoi, H. Kim, U. S. Shenoy, D. K. Bhat and H. S. Lee, ACS Appl. Energy Mater., 2023, 6, 4305–4316.
13. K. Dipanjan, L. Surafel Shiferaw, M. Shriparna, F. Olu Emmanuel, N. Ravishankar and C. Kamanio, J. Alloys Compd., 2022, 908, 164604.
14. M. A. Hassan, E. Chernyshova, E. Argunov, A. Khanina, D. Karpenkov, M. Seredina, F. Bochkanov, S. K. Elshamndy, M. Gorshenkov, A. Voronin, V. Khovaylo and A. El-Khouly, Phys. Scr., 2023, 98, 085913.
15. K. Imasato, P. Sauerschnig, M. Miyata, T. Ishida, A. Yamamoto and M. Ohta, J. Mater. Chem. C, 2025, 13(5), 2154–2164.
16. G. Rogl and P. F. Rogl, Crystals, 2023, 13, 1152.
17. R. Hasan, T. Park, S.-i. Kim, H.-S. Kim, S. Jo and K. H. Lee, Adv. Energy Sustainability Res., 2022, 3, 2100206.
18. W. G. Zeier, S. Anand, L. Huang, R. He, H. Zhang, Z. Ren, C. Wolverton and G. J. Snyder, Chem. Mater., 2017, 29, 1210–1217.
19. F. Garmroudi, M. Parzer, A. Riss, A. V. Ruban, S. Khmelevskyi, M. Reticcioli, M. Knopf, H. Michor, A. Pustogow, T. Mori and E. Bauer, Nat. Commun., 2022, 13, 3599.
20. W. Li, B. Poudel, R. A. Kishore, A. Nozariasbmarz, N. Liu, Y. Zhang and S. Priya, Adv. Mater., 2023, 35, 2210407.
21. Q. Ren, C. Fu, Q. Qiu, S. Dai, Z. Liu, T. Masuda, S. Asai, M. Hagihala, S. Lee, S. Torri, T. Kamiyama, L. He, X. Tong, C. Felser, D. Singh, T. Zhu, J. Yang and J. Ma, Nat. Commun., 2020, 11, 3142.
22. F. Garmroudi, M. Parzer, A. Riss, A. Pustogow, T. Mori and E. Bauer, Phys. Rev. B, 2023, 107, L081108.
23. L. Borgsmiller, D. Zavanelli and G. J. Snyder, Phys. Rev. X, 2022, 1, 022001.
24. T. Sekimoto, K. Kurosaki, H. Muta and S. Yamanaka, Mater. Trans., 2006, 47, 1445–1448.
25. I. Skovsen, L. Bjerg, M. Christensen, E. Nishibori, B. Balke, C. Felser and B. B. Iversen, Dalton Trans., 2010, 39, 10154–10159.
26. R. Marazza, R. Ferro and G. Rambaldi, J. Less-Common Met., 1975, 39, 341–345.
27. A. Tavassoli, A. Grytsiv, G. Rogl, V. Romaka, H. Michor, M. Reissner, E. Bauer, M. Zehetbauer and P. Rogl, Dalton Trans., 2018, 47, 879–897.
28. F. Luo, J. Wang, C. Zhu, X. He, S. Zhang, J. Wang, H. Liu and Z. Sun, J. Mater. Chem. A, 2022, 10, 9655–9669.
29. Q. Wang, X. Xie, S. Li, Z. Zhang, X. Li, H. Yao, C. Chen, F. Cao, J. Sui, X. Liu and Q. Zhang, J. Mater., 2021, 7, 756–765.
30. F. Wagner, D. Bende and Y. Grin, Dalton Trans., 2016, 45, 3236–3243.
31. D. Bende, Y. Grin and F. R. Wagner, Chem.–Eur. J., 2014, 20, 9702–9708.
32. J. Toboła, L. Jodin, P. Pecheur, H. Scherrer, G. Venturini, B. Malaman and S. Kaprzyk, Phys. Rev. B, 2001, 64, 155103.
33. C. J. Glassbrenner and G. A. Slack, Phys. Rev., 1964, 134, A1058–A1069.
34. A. Petersen, S. Bhattacharya, T. M. Tritt and S. J. Poon, J. Appl. Phys., 2015, 117, 035706.
35. A. Tavassoli, F. Failamani, A. Grytsiv, G. Rogl, P. Heinrich, H. Müller, E. Bauer, M. Zehetbauer and P. Rogl, Acta Mater., 2017, 135, 263–276.
36. M. Zhou, L. Chen, W. Zhang and C. Feng, J. Appl. Phys., 2005, 98, 013708.
37. M. Parzer, A. Riss, F. Garmroudi, J. de Boor, T. Mori and E. Bauer, arXiv, 2024, preprint, arXiv:2409.06261,  DOI:10.48550/arXiv.2409.06261.
38. G. Rogl, P. Sauerschnig, Z. Rykavets, V. Romaka, P. Heinrich, B. Hinterleitner, A. Grytsiv, E. Bauer and P. Rogl, Acta Mater., 2017, 131, 336–348.
39. N. F. Mott, Adv. Phys., 1967, 16, 49–144.
40. L. Akselrud and Y. Grin, J. Appl. Crystallogr., 2014, 47, 803–805.
41. J. I. Goldstein, D. E. Newbury, J. R. Michael, N. W. Ritchie, J. H. J. Scott and D. C. Joy, Scanning Electron Microscopy and X-Ray Microanalysis, Springer, 2017.
42. H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506.
43. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
44. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
45. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558.
46. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
47. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169.
48. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
50. M. Reticcioli, G. Profeta, C. Franchini and A. Continenza, Phys. Rev. B, 2017, 95, 214510.
51. D. Dirnberger, G. Kresse, C. Franchini and M. Reticcioli, bands4vasp Post-Processing Package, https://github.com/QuantumMaterialsModelling/bands4vasp, 2021, accessed: 2022-08-18.
52. D. Dirnberger, G. Kresse, C. Franchini and M. Reticcioli, J. Phys. Chem. C, 2021, 125, 12921–12928.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta01437a

---