DOI:
10.1039/D5TA01306B
(Paper)
J. Mater. Chem. A, 2025,
13, 23012-23018
Methods for accurate and rapid determination of purity of battery-grade silicon†
Received
17th February 2025
, Accepted 9th June 2025
First published on 23rd June 2025
Abstract
With high lithiation capacity, silicon is set to replace graphite as the active anode material in the next generation of lithium ion batteries. Si produced from various routes can contain proportions of oxide, both as a surface layer and in the bulk material. Accurate determination of Si purity is vital for anode formulation and performance testing. While there are many methods used for measuring the purity of Si, most of them are laborious, time-/resource-intensive or do not account for surface and bulk compositions. Here, we present two fast, simple and calibrated methods for the accurate determination of Si purity by using the thermogravimetric method or X-ray diffraction. The results show that by simply measuring pure Si and pure silica samples, a theoretical calibration curve can be developed for both methods, which shows excellent predictability of Si purity in real samples. Furthermore, we show that the thermal analysis was able to account for the dehydration of silica that was previously not noticed. With the increasing demand for Si for battery anodes and wider applications, this work represents a significant advance in rapidly and accurately quantifying Si purity.
Introduction
Silicon has a theoretical lithiation capacity around ten times higher than that of graphite (∼3500 and 372 mA h g−1, respectively); therefore, despite significant challenges, Si has been adopted as a replacement for graphite as the active anode material in the next generation of lithium ion batteries.1–8 Current research on Si-based battery anodes includes both metallurgical5 and synthesised Si.1,4,6,9 Furthermore, Si is also valuable in other applications such as hydrogen production and storage and carbon dioxide utilisation.10 Si materials have a natural surface oxide layer, and the thickness and composition are known to affect their performance.11 Many methods of producing silicon either start with silica (e.g. metallothermic reduction12) or are susceptible to silicon oxidation during formation (silane gas based Si coatings/nanostructures).13–15 Further oxidation can take place during downstream processing, leading to varied proportions of SiO2/SiOx,11,16–18 both on the surface and bulk. Therefore, accurate determination of the composition is vital for calculating Si active material content in the anode, for example.
There are several methods for determining the oxygen content in Si (see Table S1† for a summary); for example, Nilssen et al. utilised elemental analysis to obtain concentrations of oxygen (O) by total combustion.5 In these methods, a sample is heated in a graphite crucible, and any oxygen present in the sample reacts with the crucible to form carbon dioxide, which is detected in the carrier gas by infrared absorption. While this method is commonly used for analysing the purity of ceramics and metals, it is suitable for detecting extremely small impurities (∼ppm levels, ≪1 wt%).19 Hence, in the context of Si, they are limited to surface oxide determination and unsuitable for determining the bulk composition of oxide in Si (which can be ≫1 wt%). Dressler et al. used buoyancy measurements to analyse the oxygen content in Si based materials. Si from the samples was reacted with KOH to produce potassium silicates and hydrogen gas. The volume of hydrogen produced was used to quantify the content of pure silicon. The remaining amount of the sample (attributed to oxygen) was used to calculate oxygen content.20 The authors found that this method was not accurate when compared with benchmark methods and hence has limited use. This is because it is impractical to consume or access all available Si due to equilibrium limitations and potential encapsulation of Si within oxide, respectively. As a result, this method is laborious, time consuming and semi-quantitative at best.
Shallenberger developed a method to quantify oxygen content in thin silicon films by using the Si 2p peak from X-ray Photoelectron Spectroscopy (XPS).21 That study showed that extensive calibration using the distribution of the five valence states of Si, followed by rigorous validation using standards, is required and using a ratio of selected peak intensities is not sufficient. While XPS provides highly accurate measurement and can elucidate details of the chemical state of Si on the surface, it is limited to thin surface layers (penetration depth < 10 nm), and hence XPS is not suitable for quantifying the bulk purity of Si powders that are not thin films. Indeed, when studying micron sized Si/SiO2 fibres, Yamamoto et al. were able to use XPS only to identify the presence of oxide on the surface but unable to quantify the oxygen content in the bulk of the sample.3 Larbi et al. used X-Ray Diffraction (XRD) coupled with Rietveld quantitative crystal phase analysis to study the purity of the Si product obtained from the magnesiothermic reduction of silica.22 XRD analysis is based on quantifying crystalline products alone and assigning any remainder/unaccounted matter as amorphous without direct measurement of any unreacted amorphous silica precursor, which can lead to serious inaccuracies. Hence, such XRD-based quantification cannot provide true yields and purity of Si. It has been shown in other materials that a Pawley method using pseudo Voigt peaks can be used for quantifying amorphous phases directly;23 however, it is subjective due to arbitrary assignment of the peak (or an amorphous hump) without any benchmarking against known compounds,24 resulting in only semi-quantitative information at best. Thermogravimetric (TG) methods have been used for characterizing the purity of Si and can be carried out in a furnace with no requirement for specialist analytical instrumentation. Nöske et al. performed TG analysis (TGA) under nitrogen at elevated temperatures, followed the conversion of Si to Si3N4 and used the corresponding mass gain to determine the Si content.18 TGA under oxygenated conditions at elevated temperatures has also been commonly used where the oxidation of Si to SiO2 also results in mass gain that can be converted to molar composition.1,3,17 An assumption is made that the total mass gain in the sample during TGA is the addition of oxygen from the oxidation of Si. This is then used to calculate the moles of oxygen (nO2), which is also the moles of Si (nSi), and Si mol% obtained by using eqn (1).
| |  | (1) |
However, this method does not account for the mass change contributions from SiO2 and the potential non-linear nature of the mass change for different molar compositions of Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2. TGA is typically used under the assumption that the mass gain is linear with the proportion of Si and that the drying of chemisorbed water and oxidation of Si are the only contributing processes. However, there is also likely a mass loss by SiO2, which can be attributed to the dehydration/condensation of Si–OH groups. Therefore, the overall mass change detected by TGA is a balance between the weight gain from the oxidation of Si and the weight loss from the dehydration of Si–OH and is likely to be dependent of the Si mol%.
SiO2. TGA is typically used under the assumption that the mass gain is linear with the proportion of Si and that the drying of chemisorbed water and oxidation of Si are the only contributing processes. However, there is also likely a mass loss by SiO2, which can be attributed to the dehydration/condensation of Si–OH groups. Therefore, the overall mass change detected by TGA is a balance between the weight gain from the oxidation of Si and the weight loss from the dehydration of Si–OH and is likely to be dependent of the Si mol%.
Given the common use of TGA and XRD, here we focus on developing reliable and simple methods for quantifying Si purity using two independent methods – one based on thermal treatment and the other based on XRD. Firstly, in order to address the ambiguity in TGA data interpretation, in this paper, we systematically analyse the potential mass changes from different mixtures of silica and silicon. We use this information to develop a simple, theoretical calibration curve, without needing a full set of experimental data, relating the mass changes observed in TGA and the purity of Si. This method is then validated against a full set of experimental results. Secondly, we focused on XRD-based quantification of Si purity because TGA is laborious and time consuming; however, as noted above, XRD has not been used to account for the amorphous silica phase arising from the precursor or formed during the synthesis and purification process. Upon validation of the XRD-based method, finally, we compare both these methods in terms of their accuracy and practicality for determining Si purity.
Experimental
Materials
Sorbosil™ AC35, purity 98.8%; loss at 1000 °C: 8.3%, sample received from PQ Corporation, was used as the SiO2 reference material. 50 nm silicon powder, crystalline, 98%, laser synthesized from the vapour phase purchased from Thermo Scientific Chemicals, was used as the Si reference material. Reagents were dried at 120 °C under vacuum before use.
TGA
To create a theoretical calibration curve, Si powder and SiO2 were dried under vacuum at 120 °C for 24 hours to remove chemisorbed water. After drying, Si and SiO2 were analysed separately by TGA on a PerkinElmer TGA 4000 in air, from 25 to 950 °C at a rate of 10 °C min−1, and holding at the maximum temperature for 8 hours, before cooling at 10 °C min−1 to 25 °C. Once there was no change in mass, this was taken as the final measured mass change. The data were used to construct a “theoretical” calibration curve by using just the pure Si and pure silica data and mathematically constructing their mixtures.
Next, for the validation of this theoretical calibration, (real) mixtures of Si and SiO2 were prepared and TGA was performed to produce an “experimental” calibration. In order for the study to be comparable, Si and SiO2 were dried beforehand, under vacuum at 120 °C for 24 hours. For each sample, masses were recorded to 5 d.p. of (1) the empty crucible, (2) after adding Si, (3) after adding SiO2, and (4) after heating. The masses of the two constituents were randomly selected and used to determine the molar ratios in each sample. Pure samples with only Si or SiO2 were also included in the study as controls. Lids with holes were placed on to the crucibles to aid oxidation yet ensuring that the solids are not lost with the flowing gas. The crucibles were inserted into the centre of a Carbolite tube furnace, heated in air from room temperature to 950 °C at a rate of 10 °C min−1, and held at the maximum temperature for 24 hours, before uncontrolled cooling to room temperature. Then, the lids were removed and each crucible with the sample was reweighed to define the absolute mass change and converted to % mass change.
XRD
Powder XRD patterns of pure Si, pure silica and their mixtures were collected using a Panalytical Aeris diffractometer with a Cu X-ray source, a Ni Kβ incident beam filter, a PIXcel1D detector and <0.04° 2θ resolution. Patterns were collected over the 2θ range of 10–100° in rotating scanning mode. Binary mixtures of Si and SiO2 were mixed well and ground with a pestle and mortar beforehand. Diffractograms were analysed in OriginPro, using the Integration Gadget tool to extract the peak height intensities at 23° and 28.5° 2θ, and the ratio of these is the peak intensity ratio, PIR. Theoretical peak height intensities were calculated from diffractograms of pure Si and SiO2 to create a calibration curve. An assumption was made that I28.5° Si − I28.5° silica and I23° silica − I23° Si are proportional to nSi and nsilica, respectively. This method conveniently avoids values of zero for calculations of theoretical PIRs.
Results and discussion
TGA calibration
TGA of pure Si and SiO2 was conducted separately in air to obtain the mass change of each (Fig. 1); these mass changes (Δm) were taken as the possible limits for a given SiOx sample. Si showed a mass increase due to oxidation that plateaued at 74% (ΔmSi). Despite being thoroughly dried, the TGA of SiO2 resulted in an 8% mass loss (ΔmSiO2). As chemisorbed water was removed before analysis, the mass loss was attributed to the dehydration of silanol (Si–OH) groups. This was further supported by Attenuated Total Reflection Fourier Transform Infrared Spectroscopy (ATR-FTIR) analysis shown in the ESI.†
 |
| | Fig. 1 TGA of pure Si (50 nm) and SiO2 (Sorbosil), conducted in air. | |
These mass changes of pure Si and SiO2 were used to calculate Δm expected for theoretical Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 mixtures (created arbitrarily) with varying masses of Si (mSi) and silica (mSiO2) using eqn (2) (see Table 1).
SiO2 mixtures (created arbitrarily) with varying masses of Si (mSi) and silica (mSiO2) using eqn (2) (see Table 1).
| | | Δm = ΔmSi − ΔmSiO2 = 73.95% of mSi − 8.38% of mSiO2 | (2) |
Table 1 Theoretical mixtures and their mass changes calculated using eqn (2) and data from Fig. 1
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 (mass% or mole%) SiO2 (mass% or mole%) |
Mass gain from Si (%) |
Mass loss from SiO2 (%) |
Expected mass change (%) |
m
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mSiO2 mSiO2 |
n
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nSiO2 nSiO2 |
ΔmSi |
ΔmSiO2 |
Δm |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
74.0 |
0.0 |
74.0 |
87.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12.5 12.5 |
94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
64.7 |
1.0 |
63.7 |
75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 25 |
87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 13 |
55.5 |
2.1 |
53.4 |
62.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37.5 37.5 |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 22 |
46.2 |
3.1 |
43.1 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 32 |
37.0 |
4.2 |
32.8 |
37.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62.5 62.5 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 44 |
27.7 |
5.2 |
22.5 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 75 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
18.5 |
6.3 |
12.2 |
12.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 87.5 87.5 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77 77 |
9.2 |
7.3 |
1.9 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
0.0 |
8.4 |
−8.4 |
From these calculated mass changes, a theoretical calibration curve was created to show the expected/theoretical Δm of samples with different Si mol% (Fig. 2, black squares). An exponential fit was used to describe the relationship. From this theoretical calibration, the mass change of any sample measured by TGA can be converted to the true Si mol%.
 |
| | Fig. 2 TGA-based calibration. Black squares: theoretical calibration curve plotted from data calculated using eqn (2) (also shown in Table 1). Red circles: experimentally measured mass change for Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 mixtures (also listed in Table 2), with error bars in red on pure Si and SiO2. Blue triangles: experimentally measured mass changes, converted to Si mol% using “uncalibrated” eqn (1), with error bars in blue on pure Si and SiO2. Each dataset was fitted with an exponential equation (shown as lines and equations noted on the plot), with R2 > 0.99. SiO2 mixtures (also listed in Table 2), with error bars in red on pure Si and SiO2. Blue triangles: experimentally measured mass changes, converted to Si mol% using “uncalibrated” eqn (1), with error bars in blue on pure Si and SiO2. Each dataset was fitted with an exponential equation (shown as lines and equations noted on the plot), with R2 > 0.99. | |
Evaluating the accuracy of the theoretical TGA calibration
To test the accuracy of the theoretical calibration curve as shown in Fig. 2 (black squares), TGA was performed on mixtures of Si and SiO2, of known quantities. The molar ratios of Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 in each sample were determined from the initial masses, to give Si mol%, and their corresponding % mass change (Table 2). These were plotted (red circles) on the same axes as the calibration curve shown in Fig. 2. These experimental data represent an experimental calibration curve and are in excellent agreement with the theoretical calibration curve (only ∼4% offset in the y-axis). Furthermore, uncalibrated experimental data were also calculated where all mass changes were solely attributed to the oxidation of Si (calculated viaeqn (1), data shown in Table 2). The results shown in Fig. 2 (blue triangles) highlight that without accounting for weight loss from silica dehydration, a significant underestimation of Si purity is achieved, of the order of 25–30 Si mol%, leading to even negative Si mol% erroneously.
SiO2 in each sample were determined from the initial masses, to give Si mol%, and their corresponding % mass change (Table 2). These were plotted (red circles) on the same axes as the calibration curve shown in Fig. 2. These experimental data represent an experimental calibration curve and are in excellent agreement with the theoretical calibration curve (only ∼4% offset in the y-axis). Furthermore, uncalibrated experimental data were also calculated where all mass changes were solely attributed to the oxidation of Si (calculated viaeqn (1), data shown in Table 2). The results shown in Fig. 2 (blue triangles) highlight that without accounting for weight loss from silica dehydration, a significant underestimation of Si purity is achieved, of the order of 25–30 Si mol%, leading to even negative Si mol% erroneously.
Table 2 TGA experimental data showing Si purity of the samples used and the corresponding % mass changes recorded by TGA for a range of compositions of Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2. Si purity was calculated using either eqn (1) (“uncalibrated”)a or using the theoretical calibrationb from Fig. 2
SiO2. Si purity was calculated using either eqn (1) (“uncalibrated”)a or using the theoretical calibrationb from Fig. 2
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 SiO2 |
Mass change, Δm (%) |
Si contenta (mol%) |
Si contentb (mol%) |
n
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nSiO2 nSiO2 |
|
Calculated from eqn (1).
Calculated from theoretical calibration shown in Fig. 2.
|
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
67.9 ± 2.5 |
76.0 ± 1.7 |
96.5 ± 1.7 |
95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
60.7 |
70.9 |
91.6 |
84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
45.9 |
59.1 |
80.2 |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 22 |
37.4 |
51.1 |
72.5 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 27 |
33.0 |
46.5 |
68.2 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 28 |
33.5 |
47.1 |
68.7 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 31 |
27.7 |
40.7 |
62.6 |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
23.5 |
35.7 |
57.7 |
53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 47 |
15.3 |
24.9 |
46.9 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
7.8 |
13.5 |
35.1 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64 64 |
4.3 |
7.8 |
28.9 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66 66 |
2.5 |
4.6 |
25.3 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69 69 |
0.9 ± 0.2 |
1.6 ± 0.3 |
21.9 ± 0.4 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 90 |
−7.6 |
−15.5 |
0.8 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
−12.2 ± 1.2 |
−26.1 ± 2.9 |
−14.4 ± 4.5 |
The theoretical calibration and its validation using experimental data have the following implications. Firstly, given the excellent agreement between the theoretical and experimental data, it is clear that simply measuring TGA data for pure silica and pure silicon can provide a fairly accurate estimate of the purity of “real” samples, yet rapidly, without having to measure multiple samples to create a full experimental calibration. Secondly, these results highlight the importance of accounting for the weight loss of silica, which has not been discussed in previous literature. This weight loss in silica is likely to arise from the dehydration of silanol groups that could form during the synthesis and/or post-synthetic processing. Together, these results show that we have developed and validated a simple and rapid method for accurately quantifying Si purity. While this method is suitable for silicon nanoparticles and porous silicon, we have noticed that when using larger silicon structures (e.g. microparticles), the full oxidation requires extended periods and may not always be achieved due to diffusion limitations.
XRD calibration
It is possible that a quicker and less labour intensive method using XRD analysis can also be used to quantify the purity of Si. In order to explore this, SiO2 is identified by a broad amorphous signal at 23° 2θ and Si was identified by the dominant peak of the Si (111) plane at 28.5° 2θ. Previous reports have only focused on crystalline peaks as discussed above, but that analysis omits the presence of amorphous silica from the purity calculations, leading to overestimations. Here, we sought to explore the possibility of using the amorphous silica signal from XRD to test whether the ratio of the silica and silicon signal intensities enables a quick examination of the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 composition. Similar to the TGA study, we first created a theoretical calibration. Pure Si and SiO2 were analysed separately by XRD, and the peak intensities at 23° 2θ (I23° Si and I23° silica) and 28.5° 2θ (I28.5° Si and I28.5° silica) of each were recorded (Fig. 3). Using these measured values, peak intensities at 23° and 28.5° were calculated for theoretical mixtures of silica and silicon using eqn (3) and (4) as shown in Fig. 3. These were used to calculate the expected or theoretical peak intensity ratios (PIRs) in theoretical Si
SiO2 composition. Similar to the TGA study, we first created a theoretical calibration. Pure Si and SiO2 were analysed separately by XRD, and the peak intensities at 23° 2θ (I23° Si and I23° silica) and 28.5° 2θ (I28.5° Si and I28.5° silica) of each were recorded (Fig. 3). Using these measured values, peak intensities at 23° and 28.5° were calculated for theoretical mixtures of silica and silicon using eqn (3) and (4) as shown in Fig. 3. These were used to calculate the expected or theoretical peak intensity ratios (PIRs) in theoretical Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 mixtures using eqn (5) (data shown in Table 3). The PIR results were then used to develop a theoretical calibration (based on XRD), as shown in Fig. 4a (black squares).
SiO2 mixtures using eqn (5) (data shown in Table 3). The PIR results were then used to develop a theoretical calibration (based on XRD), as shown in Fig. 4a (black squares).| | | I28.5° = nSi × (I28.5° Si − I28.5° silica) + I28.5° silica | (3) |
| | | I23° = nsilica × (I23° silica − I23° Si) + I23° Si | (4) |
| |  | (5) |
 |
| | Fig. 3 XRD diffractograms of pure Si and SiO2, and the use of peak intensities of both taken at 23° and 28.5° for calculating the peak intensity ratio (PIR). | |
Table 3 Theoretical mixtures and their XRD intensities and ratio calculated using eqn (3)–(5)
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 SiO2 |
I
28.5°
(a.u.) |
I
23°
(a.u.) |
Expected PIRc |
n
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nSiO2 nSiO2 |
|
Calculated using eqn (3).
Calculated using eqn (4).
Calculated using eqn (5).
Experimental values from measuring pure silica and pure silicon samples.
|
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
6669d |
669d |
9.97 |
94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
6327 |
773 |
8.18 |
87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 13 |
5933 |
894 |
6.64 |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 22 |
5473 |
1034 |
5.29 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 32 |
4930 |
1200 |
4.11 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 44 |
4278 |
1399 |
3.06 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
3482 |
1642 |
2.12 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77 77 |
2487 |
1946 |
1.28 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1209d |
2336d |
0.52 |
 |
| | Fig. 4 (a) XRD-based calibration. Black squares: theoretical calibration of Si mol% vs. expected XRD PIR (data from Table 3). Red circles: experimental PIR vs. Si mol%. Lines show exponential fits with R2 > 0.99. (b) Stacked XRD diffractograms of Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 samples; numbers represent molar ratios. Peak intensities taken at 23° (amorphous SiO2) and 28.5° (Si) are shown by dashed and dotted lines, respectively. (c) and (d) Overlaid diffractograms at 23° and 28.5° respectively, with colours matching those in (b). SiO2 samples; numbers represent molar ratios. Peak intensities taken at 23° (amorphous SiO2) and 28.5° (Si) are shown by dashed and dotted lines, respectively. (c) and (d) Overlaid diffractograms at 23° and 28.5° respectively, with colours matching those in (b). | |
Evaluating the accuracy of the theoretical XRD calibration curve
In order to compare and validate the theoretical calibration with experimental measurements, XRD was performed on mixtures of Si and SiO2 of known quantities and their respective PIRs were plotted against Si mol% to give an experimental calibration (Fig. 4a, red circles). These experimental data are in excellent agreement with the theoretical calibration curve, which confirms that the method used herein based on ratios of intensities of amorphous silica and crystalline silicon obtained from XRD provides a good way for estimating Si purity. Furthermore, similar to the TGA-based approach described above, the theoretical data based on only two sample measurements provide a simple and quick way of determining the purity of Si. It is noted that using peak intensity from essentially an amorphous silica “hump” can add uncertainties; however, this method provides a rapid way for quantifying Si purity in the final products. However, as the XRD peak intensity depends on electronic density of a given sample, this XRD-based method will require that the calibrations are performed on samples or standards with densities similar to the samples of interest. For example, using a non-porous microparticulate silicon sample (highly dense) for calibration will provide erroneous results if the calibration is applied for the estimation of Si purity of highly porous or nanoparticulate (low density) materials.
In order to gauge the accuracies of both methods, measured data from both the TGA and XRD were converted to Si content using the theoretical calibrations and compared with the actual Si content (see Tables S2 and S3, and Fig. S2†). We find that both methods are quite accurate at Si contents higher than 40% (less than 5% and 3% deviations for TGA and XRD methods, respectively, see Fig. S2†); however, at low Si content, the accuracies decrease. Since high purity Si is needed for battery anodes (typically >80%), these methods provide excellent accuracies in that range. Finally, the experimental calibrations using real samples obtained from both the TGA- and XRD-based methods were compared (Fig. 5). We can see that the peak ratios measured from XRD and the weight changes measured from TGA for the same samples demonstrated a strong linear relationship. This further validates that these two methods are in excellent agreement, and both methods are effective. Furthermore, the excellent correlation between the TGA and XRD results highlights that a lengthy TGA-based method is not always needed, at least for screening purposes.
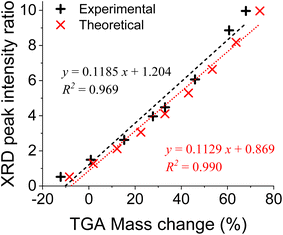 |
| | Fig. 5 A comparison between TGA-based and XRD-based results obtained from both theoretical calibrations and measurements of real mixtures of silica and silicon. | |
Conclusions
We developed two independent and simple theoretical calibration methods based on TGA and XRD to analyse the composition of Si and to provide a more accurate determination of SiO2 content in Si samples, which is vital for the use of Si in battery anodes. The TGA method accounts for the non-linear mass change for different compositions of Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2, arising from weight loss from silica. The TGA-based theoretical curve was derived from analysis of two samples only: pure Si and SiO2. This technique negates the need for extensive, time-consuming experimental calibration using a large number of samples/mixtures. Furthermore, this method is superior to current methods that use TGA but overlook the mass loss from silica dehydration. Furthermore, it is quicker and less labour intensive than obtaining an experimental calibration curve. Similarly, an XRD-based method was developed. The validity of the methods reported here were assessed by (a) comparing directly with their corresponding experimental calibration curves and (b) comparison with each other. There were excellent agreements in all cases: XRD theoretical and experimental data were particularly well aligned, and TGA theoretical data showed only a small overestimation of 4% mass change compared with experimental data. Furthermore, TGA and XRD results were linearly correlated with each other and both showed excellent accuracies, especially at high Si purity that is typically needed in anodes. This indicates that, despite using the amorphous silica peak signal, XRD data can be used as a reliable way for the determination of Si purity. Furthermore, the significance of these findings can be realised considering the fact that porous silicon, which has been considered as the holy-grail for battery anodes, (photo)catalysis and beyond, is more likely to contain oxide, especially given its synthesis routes.10,12,25 Accurate determination of Si purity is therefore highly valuable to researchers from other broader fields.
SiO2, arising from weight loss from silica. The TGA-based theoretical curve was derived from analysis of two samples only: pure Si and SiO2. This technique negates the need for extensive, time-consuming experimental calibration using a large number of samples/mixtures. Furthermore, this method is superior to current methods that use TGA but overlook the mass loss from silica dehydration. Furthermore, it is quicker and less labour intensive than obtaining an experimental calibration curve. Similarly, an XRD-based method was developed. The validity of the methods reported here were assessed by (a) comparing directly with their corresponding experimental calibration curves and (b) comparison with each other. There were excellent agreements in all cases: XRD theoretical and experimental data were particularly well aligned, and TGA theoretical data showed only a small overestimation of 4% mass change compared with experimental data. Furthermore, TGA and XRD results were linearly correlated with each other and both showed excellent accuracies, especially at high Si purity that is typically needed in anodes. This indicates that, despite using the amorphous silica peak signal, XRD data can be used as a reliable way for the determination of Si purity. Furthermore, the significance of these findings can be realised considering the fact that porous silicon, which has been considered as the holy-grail for battery anodes, (photo)catalysis and beyond, is more likely to contain oxide, especially given its synthesis routes.10,12,25 Accurate determination of Si purity is therefore highly valuable to researchers from other broader fields.
Data availability
The data supporting this article have been included in the article.
Author contributions
GC performed the investigations and data analysis and prepared the original draft. Both authors conceptualised this research and developed the methodology together. SP obtained the funding, supervised the work, reviewed and edited the manuscript and helped with the data analysis.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors thank the Faraday Institution for funding this work through the Seed (FIRG041) and Industry Sprint (FIRG068) projects. We thank Dr James McGregor (University of Sheffield) for the ATR-FTIR analysis.
References
- J. E. Entwistle, G. Beaucage and S. V. Patwardhan, Mechanistic understanding of pore evolution enables high performance mesoporous silicon production for lithium-ion batteries, J. Mater. Chem. A, 2020, 8, 4938–4949 RSC
 .
.
- D. Leblanc, P. Hovington, C. Kim, A. Guerfi, D. Bélanger and K. Zaghib, Silicon as anode for high-energy lithium ion batteries: From molten ingot to nanoparticles, J. Power Sources, 2015, 299, 529–536 CrossRef CAS
 .
.
- M. Yamamoto, M. Takatsu, R. Okuno, A. Kato and M. Takahashi, Nanoporous silicon fiber networks in a composite anode for all-solid-state batteries with superior cycling performance, Sci. Rep., 2023, 13, 17051 CrossRef CAS PubMed
 .
.
- Y. Li, Q. Li, J. Chai, Y. Wang, J. Du, Z. Chen, Y. Rui, L. Jiang and B. Tang, Si-based Anode Lithium-Ion Batteries: A Comprehensive Review of Recent Progress, ACS Mater. Lett., 2023, 5, 2948–2970 CrossRef CAS
 .
.
- B. E. Nilssen, B. R. Henriksen and R. A. Kleiv, The distribution of oxygen in submicron silicon powders produced by ultrafine grinding, Powder Technol., 2023, 427, 118657 CrossRef CAS
 .
.
- X. Zhao and V.-P. Lehto, Challenges and prospects of nanosized silicon anodes in lithium-ion batteries, Nanotechnology, 2021, 32, 042002 CrossRef CAS PubMed
 .
.
- A. Franco Gonzalez, N.-H. Yang and R.-S. Liu, Silicon Anode Design for Lithium-Ion Batteries: Progress and Perspectives, J. Phys. Chem. C, 2017, 121, 27775–27787 CrossRef CAS
 .
.
- Y. Jin, B. Zhu, Z. Lu, N. Liu and J. Zhu, Challenges and Recent Progress in the Development of Si Anodes for Lithium-Ion Battery, Adv. Energy Mater., 2017, 7, 1700715 CrossRef
 .
.
- K. A. Hays, B. Armstrong and G. M. Veith, Ending the Chase for a Perfect Binder: Role of Surface Chemistry Variation and its Influence on Silicon Anodes, ChemElectroChem, 2020, 7, 3790–3797 CrossRef CAS
 .
.
- M. Yan, S. Martell, S. V. Patwardhan and M. Dasog, Key developments in magnesiothermic reduction of silica: insights into reactivity and future prospects, Chem. Sci., 2024, 15, 15954–15967 RSC
 .
.
- L. Zhang, Y. Liu, B. Key, S. E. Trask, Z. Yang and W. Lu, Silicon Nanoparticles: Stability in Aqueous Slurries and the Optimization of the Oxide Layer Thickness for Optimal Electrochemical Performance, ACS Appl. Mater. Interfaces, 2017, 9, 32727–32736 CrossRef CAS PubMed
 .
.
- J. Entwistle, A. Rennie and S. Patwardhan, A review of magnesiothermic reduction of silica to porous silicon for lithium-ion battery applications and beyond, J. Mater. Chem. A, 2018, 6, 18344–18356 RSC
 .
.
- W. Wang and P. N. Kumta, Nanostructured Hybrid Silicon/Carbon Nanotube Heterostructures: Reversible High-Capacity Lithium-Ion Anodes, ACS Nano, 2010, 4, 2233–2241 CrossRef CAS PubMed
 .
.
- L.-F. Cui, Y. Yang, C.-M. Hsu and Y. Cui, Carbon–Silicon Core–Shell Nanowires as High Capacity Electrode for Lithium Ion Batteries, Nano Lett., 2009, 9, 3370–3374 CrossRef CAS PubMed
 .
.
- M. Salah, P. Murphy, C. Hall, C. Francis, R. Kerr and M. Fabretto, Pure silicon thin-film anodes for lithium-ion batteries: A review, J. Power Sources, 2019, 414, 48–67 CrossRef CAS
 .
.
- F. Erogbogbo, T. Lin, P. M. Tucciarone, K. M. LaJoie, L. Lai, G. D. Patki, P. N. Prasad and M. T. Swihart, On-Demand Hydrogen Generation using Nanosilicon: Splitting Water without Light, Heat, or Electricity, Nano Lett., 2013, 13, 451–456 CrossRef CAS PubMed
 .
.
- A. Touidjine, M. Morcrette, M. Courty, C. Davoisne, M. Lejeune, N. Mariage, W. Porcher and D. Larcher, Partially Oxidized Silicon Particles for Stable Aqueous Slurries and Practical Large-Scale Making of Si-Based Electrodes, J. Electrochem. Soc., 2015, 162, A1466 CrossRef CAS
 .
.
- M. Nöske, S. Breitung-Faes and A. Kwade, Electrostatic Stabilization and Characterization of Fine Ground Silicon Particles in Ethanol, Silicon, 2019, 11, 3001–3010 CrossRef
 .
.
- C. Kramer, P. Ried, S. Mahn, S. Richter, N. Langhammer and H. Kipphardt, Design and application of a versatile gas calibration for non-metal determination by carrier gas hot extraction, Anal. Methods, 2015, 7, 5468–5475 RSC
 .
.
- R. A. Dressler and J. R. Dahn, KOH Based Method for the Determination of Oxygen Content in Ball Milled SiOx Material, J. Electrochem. Soc., 2021, 168, 010515 CrossRef CAS
 .
.
- J. R. Shallenberger, Determination of chemistry and microstructure in SiOx (0.1<x<0.8) films by x-ray photoelectron spectroscopy, J. Vac. Sci. Technol., A, 1996, 14, 693–698 CrossRef CAS
 .
.
- K. K. Larbi, M. Barati and A. McLean, Reduction behaviour of rice husk ash for preparation of high purity silicon, Can. Metall. Q., 2011, 50, 341–349 CrossRef CAS
 .
.
- G. V. P. Bhagath Singh and K. V. L. Subramaniam, Quantitative XRD study of amorphous phase in alkali activated low calcium siliceous fly ash, Constr. Build. Mater., 2016, 124, 139–147 CrossRef CAS
 .
.
- A. Le Bail, Whole powder pattern decomposition methods and applications: A retrospection, Powder Diffr., 2005, 20, 316–326 CrossRef CAS
 .
.
-
Silicon as anode material: Is it “the next big thing”?, https://futurebatterylab.com/silicon-as-anode-material-is-it-the-next-big-thing, 2023 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Siddharth V.
Patwardhan
and
Siddharth V.
Patwardhan
 *
*

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2. TGA is typically used under the assumption that the mass gain is linear with the proportion of Si and that the drying of chemisorbed water and oxidation of Si are the only contributing processes. However, there is also likely a mass loss by SiO2, which can be attributed to the dehydration/condensation of Si–OH groups. Therefore, the overall mass change detected by TGA is a balance between the weight gain from the oxidation of Si and the weight loss from the dehydration of Si–OH and is likely to be dependent of the Si mol%.
SiO2. TGA is typically used under the assumption that the mass gain is linear with the proportion of Si and that the drying of chemisorbed water and oxidation of Si are the only contributing processes. However, there is also likely a mass loss by SiO2, which can be attributed to the dehydration/condensation of Si–OH groups. Therefore, the overall mass change detected by TGA is a balance between the weight gain from the oxidation of Si and the weight loss from the dehydration of Si–OH and is likely to be dependent of the Si mol%.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 mixtures (created arbitrarily) with varying masses of Si (mSi) and silica (mSiO2) using eqn (2) (see Table 1).
SiO2 mixtures (created arbitrarily) with varying masses of Si (mSi) and silica (mSiO2) using eqn (2) (see Table 1).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 (mass% or mole%)
SiO2 (mass% or mole%)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mSiO2
mSiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nSiO2
nSiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12.5
12.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37.5
37.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62.5
62.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44
44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75
75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 87.5
87.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77
77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 mixtures (also listed in Table 2), with error bars in red on pure Si and SiO2. Blue triangles: experimentally measured mass changes, converted to Si mol% using “uncalibrated” eqn (1), with error bars in blue on pure Si and SiO2. Each dataset was fitted with an exponential equation (shown as lines and equations noted on the plot), with R2 > 0.99.
SiO2 mixtures (also listed in Table 2), with error bars in red on pure Si and SiO2. Blue triangles: experimentally measured mass changes, converted to Si mol% using “uncalibrated” eqn (1), with error bars in blue on pure Si and SiO2. Each dataset was fitted with an exponential equation (shown as lines and equations noted on the plot), with R2 > 0.99.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 in each sample were determined from the initial masses, to give Si mol%, and their corresponding % mass change (Table 2). These were plotted (red circles) on the same axes as the calibration curve shown in Fig. 2. These experimental data represent an experimental calibration curve and are in excellent agreement with the theoretical calibration curve (only ∼4% offset in the y-axis). Furthermore, uncalibrated experimental data were also calculated where all mass changes were solely attributed to the oxidation of Si (calculated viaeqn (1), data shown in Table 2). The results shown in Fig. 2 (blue triangles) highlight that without accounting for weight loss from silica dehydration, a significant underestimation of Si purity is achieved, of the order of 25–30 Si mol%, leading to even negative Si mol% erroneously.
SiO2 in each sample were determined from the initial masses, to give Si mol%, and their corresponding % mass change (Table 2). These were plotted (red circles) on the same axes as the calibration curve shown in Fig. 2. These experimental data represent an experimental calibration curve and are in excellent agreement with the theoretical calibration curve (only ∼4% offset in the y-axis). Furthermore, uncalibrated experimental data were also calculated where all mass changes were solely attributed to the oxidation of Si (calculated viaeqn (1), data shown in Table 2). The results shown in Fig. 2 (blue triangles) highlight that without accounting for weight loss from silica dehydration, a significant underestimation of Si purity is achieved, of the order of 25–30 Si mol%, leading to even negative Si mol% erroneously.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2. Si purity was calculated using either eqn (1) (“uncalibrated”)a or using the theoretical calibrationb from Fig. 2
SiO2. Si purity was calculated using either eqn (1) (“uncalibrated”)a or using the theoretical calibrationb from Fig. 2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2
SiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nSiO2
nSiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60
60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90
90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 composition. Similar to the TGA study, we first created a theoretical calibration. Pure Si and SiO2 were analysed separately by XRD, and the peak intensities at 23° 2θ (I23° Si and I23° silica) and 28.5° 2θ (I28.5° Si and I28.5° silica) of each were recorded (Fig. 3). Using these measured values, peak intensities at 23° and 28.5° were calculated for theoretical mixtures of silica and silicon using eqn (3) and (4) as shown in Fig. 3. These were used to calculate the expected or theoretical peak intensity ratios (PIRs) in theoretical Si
SiO2 composition. Similar to the TGA study, we first created a theoretical calibration. Pure Si and SiO2 were analysed separately by XRD, and the peak intensities at 23° 2θ (I23° Si and I23° silica) and 28.5° 2θ (I28.5° Si and I28.5° silica) of each were recorded (Fig. 3). Using these measured values, peak intensities at 23° and 28.5° were calculated for theoretical mixtures of silica and silicon using eqn (3) and (4) as shown in Fig. 3. These were used to calculate the expected or theoretical peak intensity ratios (PIRs) in theoretical Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 mixtures using eqn (5) (data shown in Table 3). The PIR results were then used to develop a theoretical calibration (based on XRD), as shown in Fig. 4a (black squares).
SiO2 mixtures using eqn (5) (data shown in Table 3). The PIR results were then used to develop a theoretical calibration (based on XRD), as shown in Fig. 4a (black squares).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2
SiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nSiO2
nSiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44
44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77
77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 samples; numbers represent molar ratios. Peak intensities taken at 23° (amorphous SiO2) and 28.5° (Si) are shown by dashed and dotted lines, respectively. (c) and (d) Overlaid diffractograms at 23° and 28.5° respectively, with colours matching those in (b).
SiO2 samples; numbers represent molar ratios. Peak intensities taken at 23° (amorphous SiO2) and 28.5° (Si) are shown by dashed and dotted lines, respectively. (c) and (d) Overlaid diffractograms at 23° and 28.5° respectively, with colours matching those in (b).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2, arising from weight loss from silica. The TGA-based theoretical curve was derived from analysis of two samples only: pure Si and SiO2. This technique negates the need for extensive, time-consuming experimental calibration using a large number of samples/mixtures. Furthermore, this method is superior to current methods that use TGA but overlook the mass loss from silica dehydration. Furthermore, it is quicker and less labour intensive than obtaining an experimental calibration curve. Similarly, an XRD-based method was developed. The validity of the methods reported here were assessed by (a) comparing directly with their corresponding experimental calibration curves and (b) comparison with each other. There were excellent agreements in all cases: XRD theoretical and experimental data were particularly well aligned, and TGA theoretical data showed only a small overestimation of 4% mass change compared with experimental data. Furthermore, TGA and XRD results were linearly correlated with each other and both showed excellent accuracies, especially at high Si purity that is typically needed in anodes. This indicates that, despite using the amorphous silica peak signal, XRD data can be used as a reliable way for the determination of Si purity. Furthermore, the significance of these findings can be realised considering the fact that porous silicon, which has been considered as the holy-grail for battery anodes, (photo)catalysis and beyond, is more likely to contain oxide, especially given its synthesis routes.10,12,25 Accurate determination of Si purity is therefore highly valuable to researchers from other broader fields.
SiO2, arising from weight loss from silica. The TGA-based theoretical curve was derived from analysis of two samples only: pure Si and SiO2. This technique negates the need for extensive, time-consuming experimental calibration using a large number of samples/mixtures. Furthermore, this method is superior to current methods that use TGA but overlook the mass loss from silica dehydration. Furthermore, it is quicker and less labour intensive than obtaining an experimental calibration curve. Similarly, an XRD-based method was developed. The validity of the methods reported here were assessed by (a) comparing directly with their corresponding experimental calibration curves and (b) comparison with each other. There were excellent agreements in all cases: XRD theoretical and experimental data were particularly well aligned, and TGA theoretical data showed only a small overestimation of 4% mass change compared with experimental data. Furthermore, TGA and XRD results were linearly correlated with each other and both showed excellent accuracies, especially at high Si purity that is typically needed in anodes. This indicates that, despite using the amorphous silica peak signal, XRD data can be used as a reliable way for the determination of Si purity. Furthermore, the significance of these findings can be realised considering the fact that porous silicon, which has been considered as the holy-grail for battery anodes, (photo)catalysis and beyond, is more likely to contain oxide, especially given its synthesis routes.10,12,25 Accurate determination of Si purity is therefore highly valuable to researchers from other broader fields.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

