Thermodynamic insights into the Ba–S system for the formation of BaZrS₃ perovskites and other Ba sulfides

Abstract

BaZrS₃ stands out as one of the most extensively researched chalcogenide perovskites. Unlike its halide counterpart, this Pb-free alternative boasts superior intrinsic chemical stability. Notably, all three chemical elements are among the 20 most abundant elements in Earth's crust. With a band gap of approximately 1.8 eV, it is theoretically well suited to augment Si in tandem cells. Additionally, BaZrS₃ exhibits one of the highest band-edge absorption levels among all known solar cell materials and maintains stability in air up to 400 °C. However, the synthesis of BaZrS₃ thin films—essential for typical optoelectronic devices—remains a challenge. The primary obstacle lies in the elevated process temperatures required for achieving a high degree of crystallinity, potentially hindering integration into tandem photovoltaic devices. Nonetheless, the formation of high-order Ba polysulfides as intermediate phases can notably decrease the growth temperature of BaZrS₃. The purpose of the present work is to produce a pressure-temperature phase diagram for the Ba–S system, defining the domains of stability of binary Ba sulfides. By independently varying the temperatures of the sample and the S vapor source, an experimental phase diagram is initially constructed. Then a first-principles thermodynamic model for the sulfurisation of Ba is built and the theoretical results are compared with the experimental results. Good agreement is found for the BaS₂–BaS₃ transition, while the discrepancy observed for the BaS₂–BaS transition is attributed to equipment limitations. In the process, the easily overlooked roles of thermal gradients and thermal transport in the flow reactor are also highlighted. The insights gleaned are relevant to general thin-film sulfurisation systems, where achieving and maintaining a controlled high partial vapor pressure of S present greater challenges compared to solid-state chemistry. This study offers valuable thermodynamic guidance for the synthesis of a wide range of Ba sulfides and is of particular relevance for the formation of BaZrS₃ perovskites at moderate temperature.

---

Introduction

Si-based solar cells have long been the cornerstone of the photovoltaic (PV) market. Continuous improvements in both mass production and research have brought them so close to the physical limits of performance that a step change can now only be achieved through innovative new materials or device design. One promising approach involves stacking a wide gap subcell atop a Si-based device, with the top cell being more efficient at converting the short wavelength band of the solar spectrum.¹ Pb-halide perovskites are among the most promising materials for top cell absorbers, having disrupted the research community due to their low cost, ease of processing, and high performance.^2,3 However, their poor long-term stability remains a significant obstacle to mass production.^3,4 Additionally, societal acceptance of the presence of toxic Pb in solar modules is still questionable. Consequently, the research community has begun investigating Pb-free and more stable alternatives, such as chalcogenide perovskites.⁵ Among the many compounds belonging to this class, BaZrS₃ has emerged as particularly promising for PV applications.⁵ Its band gap is approximately 1.8 eV, a value nearly ideal for a top subcell to augment Si.^6,7 Additionally, its absorption coefficient is remarkably high, exceeding 10⁵ cm⁻¹ near the band edge.^6,8 BaZrS₃ has also demonstrated stability in air up to at least 400 °C.^9,10 Last but not least, all three constituents—Ba, Zr, and S—rank among the 20 most abundant elements in Earth's crust, further highlighting the potential of this chalcogenide perovskite as an outstanding and sustainable solar cell absorber candidate. However, the challenging synthesis of BaZrS₃ thin films, essential for typical optoelectronic devices, has thus far prevented the fabrication of solid-state solar cells. Only proof-of-concept photoelectrochemical devices have been reported so far.¹¹ One major hurdle has been the high formation temperature (T). Early work on thin films required processes with a peak T exceeding 900 °C to achieve a satisfactory degree of crystallinity.^12,13 Such T is incompatible with common metals or transparent conductive oxides, which usually form the back contact of a solar cell. Attempts have been made to fabricate thin films of colloidal BaZrS₃ nanoparticles at low T.^14,15 However, the resulting material exhibited poor uniformity and limited thickness in these early studies. The first successful synthesis of BaZrS₃ thin films on conductive substrates was published in 2022.¹⁶ By maintaining the process T below 600 °C, the authors successfully grew the perovskite with a high degree of grain quality on a Mo layer through the sulfurization of metal precursor films. It was speculated that BaS₃ might have served as an intermediate phase that facilitated the formation of the perovskite at moderate T. The crucial role of this high-order Ba polysulfide was later confirmed by a notable study by Yang et al. aimed at understanding the low-T growth mechanism of chalcogenide perovskite powders.¹⁷ They investigated the solid-state reaction between BaS₃ and ZrS₂ precursors in sealed ampoules, identifying two distinct regimes in the formation mechanism. Below 540 °C, the reaction was diffusion limited and proceeded slowly. However, above 540 °C, a liquid flux accelerated the process, overcoming mass-transport limitations and promoting grain growth, leading to higher precursor conversion rates and improved crystallinity. The authors identified this liquid flux as BaS₃, seeing its melting at 540 °C. Similarly, Vincent et al. observed a transition at 525 °C between these two regimes in the formation of BaZrS₃ thin films by solution processing in the presence of excess S vapor.¹⁸ As in the study by Yang et al., they attributed the accelerated reaction to a liquid flux, although they identified it as BaS_x with x > 3. A closer examination of the T-composition phase diagram for the Ba–S system (Fig. 1) reveals that such a liquid phase exists in this T range only for an S concentration close to 80 at% and above. Liquid stoichiometric BaS₃ is indeed present only above 660 °C, undergoing a peritectic transformation as T decreases. This suggests that the order of the liquid polysulfide must be greater than 3.0 at lower T. In a related study, Sasaki et al. investigated the low-T topochemical insertion of Fe and Ni in BaS₃ and BaS₂ to form BaFe₂S₃ and BaNiS₂, respectively.¹⁹ They described the reaction as a thermo-assisted solid-state intercalation process, in which no molten species are involved. This mechanism suggests that the transition metal progressively diffuses into the precursor from the surface to the bulk with a concurrent cleavage of S–S bonds. The low-energy reaction at T ≤ 340 °C was claimed possible because the structural transformation could occur without destructive reorganization of the precursor framework. Despite the different structure of BaZrS₃, it has not yet been investigated whether a similar mechanism might be involved in the formation of this chalcogenide perovskite at moderate T. Specifically, it would be valuable to explore whether BaS₂ offers any advantages over BaS in this context.

Fig. 1 T-Composition phase diagram for the Ba–S system. Digitized from Vincent et al.¹⁸

Besides the scattered reports mentioned above, however, there is no systematic study tracking how adjusting the partial pressure of S (p_S) leads to different Ba–S phases. The purpose of the present work is to produce a p_S–T phase diagram for the Ba–S system, defining the domains of stability of the binary phases.

Results and discussion

Control of p_S in the sulfurization furnace

As discussed in the Introduction, high-order Ba polysulfides are anticipated to play a key role in the formation of BaZrS₃ at moderate T, making it compatible with typical thin-film solar cell processing. The aims of this work are (a) to produce conditions under which each sulfide phase can form and (b) to define the p_S required in each case, by combining experiments and theory. For these purposes, a custom-made tube furnace was used for sulfurization in this study, as well as in previous work.¹⁶ A photo and a schematic diagram of the setup are shown in Fig. 2. The furnace was specifically designed to enable rapid heating and cooling of both the sample and the S source. Using two sliding rods, independent T control is achieved by positioning the sample and the S source at a chosen point within the quartz tube (ca. 1.5 m in length), which maintains a T gradient ranging from ca. 25 °C in the load lock to 400–600 °C in the heating block. When the S source is placed at a defined position with temperature T_S in the sealed (rather than pumped) furnace, the S powder begins to evaporate and the S vapor is transported by convection and diffusion throughout the furnace, gradually filling the tube. The S vapor that reaches the cold zones can condense on the inner walls of the quartz tube. It is then assumed that p_S approaches the saturated vapor pressure in the local thermodynamic quasi-equilibrium with the condensed phase, i.e. the evaporation rate of the source is greater than the rate of S vapor loss due to condensation. Under this assumption, the S vapor pressure curve from published experimental data is then used to convert T_S to p_S (see Fig. S4†).²⁰ Condensation is assumed to mainly promote further evaporation from the source to maintain equilibrium. It implies that the higher the condensation rate in the cold zones, the higher the evaporation rate of the S source, and the shorter the time before the (finite) S source is depleted.

Fig. 2 (a) Photo and (b) schematic diagram of the custom-made tube furnace used for sulfurization.

To provide scope for obtaining high p_S/long sulfurization times, the effect of two parameters on the T gradient—and thus on the condensation rate—across the quartz tube was investigated. The first is the total pressure in the furnace (p_T), mainly determined by the background gas, Ar. The second is the degree of insulation of the cold zones, modified by wrapping parts of the quartz tube with insulation tape. To quantify these effects, three thermocouples were placed on the outer walls of the quartz tube (under the insulation tape if present) at different positions between the heating block and the load lock to record the T gradient, as shown in Fig. 2b. The distance between the thermocouples was 5 cm. Fig. 3 illustrates the recorded T profiles in four distinct situations: three without additional insulation (at p_T of 15, 400, and 82 000 Pa) and one with insulating wraps applied to the cold zones (at a p_T of 400 Pa). The T of the heating block was set to 600 °C in all four cases.

Fig. 3 T gradient across the cold zone of the quartz tube under different p_T. The positions of the thermocouples are illustrated in Fig. 2b. In one case, part of the cold zone was wrapped in insulation tape. Data points for 15 and 400 Pa nearly overlap.

Fig. 3 clearly indicates that the higher the p_T, the hotter the quartz tube. Although the difference between 15 and 400 Pa (unwrapped) was minimal, at 82 000 Pa, the temperature rose considerably. This effect is attributed to a larger concentration of Ar atoms, resulting in faster heat conduction away from the hot zone to the rest of the tube. The largest effect was however caused by the insulation tape, which clearly reduced heat dissipation to the surrounding air. Overall, both an increased p_T and an improved insulation reduced the extent of the cold parts of the furnace. This reduction is expected to decrease S condensation and sustain higher p_S levels for longer durations, thereby extending the time available for reactions to proceed. For the subsequent study on the formation of binary Ba sulfides, insulation tape was therefore always applied on the quartz tube. p_T was maintained at 400 Pa to avoid overheating of the quartz–metal seals at the tube ends.

Experimental p_S–T phase diagram

The mapping of phase transitions was carried out using similar BaS₂ samples produced beforehand by sulfurization of sputtered metal layers, as described in the Experimental section. These precursors were then sulfurized again by varying the T of both the S source (T_S) and the sample (T_sample), yielding different phase mixtures. Grazing Incidence X-ray Diffraction (GI-XRD) was used for phase identification, demonstrating that the entire relevant p_S range can be covered, and the patterns of three representative samples—in which either BaS, BaS₂, or BaS₃ predominates—are presented in Fig. 4 together with their respective reference patterns from the literature.^21–23 These specific samples were sulfurized with T_S and T_sample of 100 and 488 °C, 165 and 548 °C, and 230 and 430 °C, respectively. Only one Ba sulfide phase was detected in each of these three samples. However, several peaks possibly belonging to BaSO₃ were observed in the sample with BaS,²⁴ while some of the additional peaks in the sample with BaS₂ match well with the BaSO_4. reference.²⁵ The sample with BaS₃ seems to be the purest among the three sulfides, with only one minor peak belonging to an impurity, possibly BaO.²⁶ This observation is encouraging, as the trisulfide is indeed the most promising intermediate phase among the three for the synthesis of BaZrS₃ at moderate T, as discussed in the Introduction. The O contributing to these impurities is expected to be introduced either during the transfer of the precursors from the sputtering chamber to the furnace or from the residual atmosphere within the quartz tube during sulfurization. Like typical tube furnaces, this setup is not a high-vacuum system but operates at a base pressure of approximately 1 Pa, which may result in sufficient residual O being present.

Fig. 4 GI-XRD patterns of representative samples in which either BaS, BaS₂, or BaS₃ predominates, together with their relative reference patterns.^21–23 Peaks belonging to BaSO₃ or BaSO₄ impurities are marked with an asterisk.^24,25

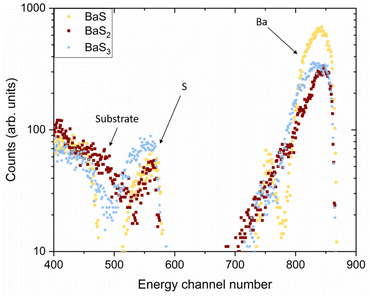
To assess the elemental composition, Rutherford Backscattering Spectrometry (RBS) was performed on the same three samples. The raw data are presented in Fig. 5. The peaks around energy channels 560 and 840 correspond to S and Ba, respectively. Fig. S1–S3† also show the simulated spectra used to calculate the [Ba] : [S] ratios in the samples containing BaS, BaS₂, or BaS₃, which are estimated to be 1 : 1, 1 : 1.5, and 1 : 2.7, respectively. These values only account for S and Ba coexisting at the same film depth. For instance, Ba that has diffused into the substrate without any accompanying S is excluded from the analysis. RBS does not, however, discern chemical bonds, e.g. whether Ba is in the form of an oxide, sulfide, sulfite, or sulfate. As XRD did detect the presence of such secondary phases, an estimated S-deficient ratio is therefore expected for the binary sulfides. It can be concluded that the XRD and RBS results are consistent, showing that the higher the ratio of [S] to [Ba], the higher the order of the polysulfide.

Fig. 5 Raw data from RBS measurements. Yellow dots, red squares, and blue stars represent representative samples in which either BaS, BaS₂, or BaS₃ is the predominant phase, respectively. The peaks around energy channels 560 and 840 correspond to S and Ba, respectively. Counts below energy channel 500 originate from the substrate.

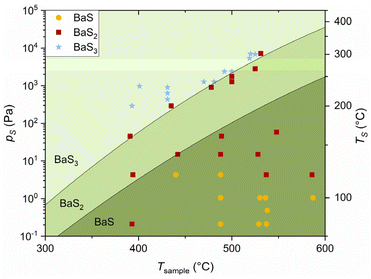
To construct the experimental p_S–T phase diagram, 38 processes with different combinations of T_S and T_sample were carried out. Under a given set of reaction conditions, the presence of BaS or BaS₃ alongside BaS₂ was interpreted as evidence of partial conversion of BaS₂ to the respective phase. Consequently, such samples were classified as BaS or BaS₃ in the phase diagram presented in Fig. 6. The incomplete conversion observed may be attributed to the limited reaction time, which is discussed in the Experimental section.

Fig. 6 Experimental p_S–T phase diagram for the Ba–S system. Following the sulfurization of BaS₂ precursors, the graph indicates whether some BaS or BaS₃ formed or if no phase transformation occurred. The shaded areas indicate the estimated regions of stability for the different phases. The measured T_S was mapped to a p_S equivalent assuming that saturation was reached.

For the first time, the actual (albeit approximate) values for p_S needed to stabilize BaS and BaS₃ have been defined. At 500 °C, for instance, they are ca. <10 and >2000 Pa, respectively. The behavior illustrated in Fig. 6 aligns with expectations, as three distinct stability domains are observed for BaS, BaS₂ and BaS₃, with the higher-order sulfides requiring higher p_S and/or lower T_sample to form. As T_sample increases, the higher entropy S vapor state becomes thermodynamically favorable through the −T_S term in free energy, driving the order reduction of stable Ba sulfides according to the following chemical reaction:

BaS_x → BaS_(x−1) + S (g)

This shift can be counteracted through the +P_V term by supplying more S vapor to the reaction, thereby increasing p_S. The interplay between these two contributions, rigorously described elsewhere,²⁷ leads to the typical anticorrelation between T and p observed at boundaries in phase diagrams. This behavior is evident for the BaS₂–BaS₃ transition. On the other hand, the transition between BaS and BaS₂ appears to depend on T_sample only up to ca. 440 °C, beyond which the trend seems to slightly reverse—an unexpected outcome. A potential explanation for this anomaly could be the unaccounted contribution of background S. Although the furnace was prebaked before every run, outgassing of residual S condensed on the inner walls of the quartz tube could also contribute to p_S. This effect would become significant at high furnace T and low T_S, as the contribution of background S becomes comparable to that of the primary source.

First-principles thermodynamic model

A first-principles model was implemented to provide further insight into the chemical thermodynamics of the Ba–S system in equilibrium with S vapor. This model uses Density Functional Theory (DFT) with the meta-GGA exchange–correlation functional (SCAN)²⁸ and first-principles lattice dynamics to predict the Gibbs free energy of each competing solid-state phase in the Ba–S system. To describe the S vapor, an analytic expression for chemical potential was applied.²⁹ In contrast to previously published work following this method,²⁷ the vapor model was referenced to S in the solid α-phase using an experimentally measured value for the sublimation enthalpy (12.552 kJ mol⁻¹).³⁰ This approach is expected to produce a more accurate description, as SCAN is optimized for application to condensed matter. The resulting phase diagram is shown in Fig. 7.

Fig. 7 Predicted p_S–T phase diagram for the Ba–S system. Colored regions indicate which material is most stable at a given T_sample and p_S. The overlapped scatter points correspond to experimental data. The measured T_S was mapped to a p_S equivalent, assuming that saturation was reached.

As expected, the required p_S to form the S-rich binaries BaS₂ and BaS₃ increases with increasing T_sample. At high T_sample, all three phases can be accessed with increasing p_S, in line with what is found experimentally. At T_sample below 400 °C, only BaS₂ and BaS₃ are accessible, again in line with experiments. For comparison, the experimental data points are presented together with the computed phase diagrams in Fig. 7. Excellent agreement is found between the experimentally identified BaS₂ to BaS₃ transition and the computational prediction, especially in the high T_sample/p_S range. The BaS–BaS₂ transition does not agree nearly as well. Possible reasons for this discrepancy, relating to the difficulty of controlling low p_S in our furnace, are explained in the previous section. In this case, the theory-derived result is suggested as the best guide. The overall good agreement between calculations and experiments lends support to the initial assumption, i.e., the saturation p_S is reached inside the custom-made furnace and the S vapor pressure curve can therefore be used to convert T_S to p_S (see Fig. S4†).²⁰

Implications for the synthesis of BaZrS₃

Researchers can use the phase diagram constructed here to guide the synthesis of a wide range of Ba sulfides (e.g. BaHfS₃, BaTiS₃, BaCu₄S₃, or Ba₂SnS₄) in various types of open or closed reactors. This section, however, highlights the implications of the present findings for BaZrS₃, contextualizing them within the framework of previous studies. It is of particular interest to determine whether and how BaS, BaS₂ and BaS₃ (or BaS_x>3) can influence the formation of BaZrS₃, especially at moderate T.

In an early investigation,¹² amorphous Ba–Zr–S precursors were annealed in the absence of additional S supply at a T ranging from 650 to 1000 °C. Extrapolating the results shown in Fig. 6, the expected binary Ba sulfide to have formed as an intermediate phase is therefore BaS, which is not anticipated to have any accelerating effect on BaZrS₃ formation. Indeed, the optimal T in terms of photoluminescence and XRD was around 900 °C, with the Full Width at Half Maximum (FWHM) of the main diffraction peak (121) being 0.41°. In later work, on the other hand, the sample was heated at ca. 590 °C, while S vapor was provided with a T_S varied from 105 to 165 °C.¹⁶ The crystallinity of these films was comparable to those synthesized earlier, at least in terms of FWHM of the main XRD peak (121), which was as low as 0.39°, despite the substantially lower growth T. A proposed explanation for this difference was the formation of BaS₃ as an intermediate phase. According to the new results presented here, however, BaS₂ is expected to be the binary Ba sulfide that formed as an intermediate phase under those conditions. To confirm this hypothesis, a BaS₂ sample was sulfurized in the present work using the same process conditions as in a previous paper.¹⁶ The only difference between the two approaches is the presence of an Ar flow in the original investigation. The sole phase detected by XRD after sulfurization was BaS₂ in this work. It follows that in the earlier study, BaS₃ was likely not the reason for the improved crystallization, and it is therefore possible that BaS₂ also has some beneficial effect on the growth kinetics. The investigation by Sasaki et al. supports this hypothesis, where the accelerated reaction was associated with the presence of S–S bonds, which are found not only in BaS₃, but also in BaS₂.¹⁹ Using similar tube furnaces, the advantages of BaS₃ over BaS₂ in the formation of BaZrS₃ remain to be investigated and quantified. The p_S–T phase diagram constructed here can now be used in the future as a guide for synthesis in a flow reactor of many Ba sulfides, including BaZrS₃.

It should be noted that, in the present study, the maximum T_S was limited by the capacity of the carrier vessel. Above 300 °C, the S powder completely evaporated before reaching the target T_S. This limitation impeded the formation of BaS₃ with the sample at 530 °C or above. Although a T_sample as low as 525 °C has already been reported to switch the BaZrS₃ formation from a diffusion-limited to an accelerated-growth regime,¹⁸ it would be of interest to synthesize BaZrS₃ at higher T_sample and compare the film quality. The challenge in a flow reactor, as opposed to sealed ampoules, is to keep a sufficiently high p_S to ensure the formation of BaS₃ for a long time. If BaS₃ does turn out to be advantageous for low-T growth of chalcogenide perovskites, then reactor design for high p_S will need to be prioritized.

Experimental section and methods

Sample preparation

BaS₂ films were prepared on either quartz, sapphire, or Si/SiO_x substrates. A Kurt J. Lesker sputtering system, with a base pressure (p_b) of the order of 10⁻⁵ Pa, was used for the subsequent depositions, which were carried out in an Ar atmosphere (purity of the source: 99.9997%) at 0.57 Pa. The diameter of all targets was 7.62 cm (3 inches). The purity of the Zr and Ba targets was 99.7% (excluding Hf) and 99.5%, respectively. The metallic targets were manufactured by Plasmaterials, Inc. To prevent Ba from reacting with Si during sulfurization, a Zr thin film was initially deposited atop the substrates. The target was powered by pulsed DC for 4 min with a power density of 1.21 W cm⁻². Then Ba was sputtered in radio frequency mode for 50 min with 0.81 W cm⁻². Finally, a ca. 7 nm SnS capping layer was deposited in situ atop the Ba film to prevent excessive oxidation of the as-sputtered metal films during transfer from the sputtering chamber to the sulfurization furnace. The SnS target (Pioneer Materials, Inc.) was powered by pulsed direct current for 60 s with a power density of 0.55 W cm⁻². The sample was rotated during all the depositions.

A custom-made tube furnace (see Fig. 2), with a volume of ca. 15 L and a p_b of ca. 1 Pa, was employed for sulfurization. The initial Ba precursors, capped with SnS, underwent a first sulfurization at ca. 600 °C for 20 min to form BaS₂. GI-XRD was performed to confirm that this binary Ba sulfide was the predominant phase. Choosing BaS₂ as the starting material ensured that the thin films would undergo at most one phase transition to form either BaS or BaS₃. Choosing a different starting phase would have resulted in some samples undergoing multiple phase transitions, potentially requiring a higher thermal budget and a longer sulfurization duration. However, given the finite S source, this would have further constrained the accessible temperature range. The resulting thin films were then sulfurized a second time to construct the p_S–T phase diagram. When BaS₂ remained the main phase, some samples were used multiple times. Before beginning the sulfurization process, the T of the heating block was set and it was ensured that all sections of the furnace reached a stable T—including the cold zones—by monitoring the signal given by several thermocouples attached to different points of the furnace. The sample was placed onto an open graphite holder, while S powder (Alfa Aesar, Puratronic, 99.9995% purity) was loaded into a separate small vessel. Both were simultaneously inserted into a load lock, which was then pumped to remove air traces before starting sulfurization. The S source was pushed towards the hot zone of the furnace with the aid of a rod and a vacuum feedthrough. T_S—and therewith p_S—was controlled by sliding the S-containing vessel closer to (or farther away from) the heating block and maintained within ±2 °C from the set temperature. The sample was transferred into the hot zone of the furnace using a second rod and a second vacuum feedthrough. To obtain BaS, the S powder was usually inserted before the sample, and the sulfurization time was 20 min. To obtain BaS₃, the sample was normally inserted first, and the sulfurization time had to be reduced to avoid exhaustion of the S source before completion of the sulfurization process. Depending on the reaction rate, such a scenario could reverse the phase transformation towards the end of the sulfurization period as p_S decreases below the transition threshold. For the highest p_S, both the sample and the S source were immediately pulled out as soon as the desired T_S was reached. Finally, both the sample and the S source were gradually pulled away from the heating zone into the load lock and allowed to cool to below 50 °C before unloading.

Characterization

GI-XRD was performed using an Empyrean setup. The K_α2 component and the background were computationally subtracted from the raw diffraction patterns using HighScore Plus software by PANalytical.³¹

RBS was performed using the 5 MV NEC-5SDH-2 tandem accelerator at Uppsala University. The probing beam consisted of 2 MeV ⁴He⁺ impinging on the sample at a polar angle of 5° with respect to the surface normal. Backscattered ions were detected at a polar angle of 170° relative to the path of the beam. The azimuth angle of the sample was randomly adjusted within a 2° interval during measurement to average out possible ion channeling effects. The RBS spectra were fitted with the SIMNRA software package.³²

Computational methods

Classical thermodynamics was used to evaluate the stability of competing phases in the Ba–S system. A spontaneous reaction occurs at T and p_T when the change in Gibbs free energy ΔG of the reaction is negative. ΔG consists of the entropy and enthalpy contributions and can be determined through the balance of chemical potentials. For solid materials, atomic displacements from equilibrium were assumed harmonic and solids were considered incompressible. The resulting parameters for the chemical potential of solids are total energy, crystal volume, zero point energy, vibrational entropy and heat capacity. These values were taken from previously published work, which used density functional theory with the SCAN meta-GGA exchange–correlation functional and first-principles lattice dynamics.²⁷ For the chemical potential of S vapor, an analytic expression parameterized by Jackson et al. was adopted.²⁹ This expression is particularly convenient because it accounts for the coexistence of 13 S allotropes. Although based primarily on first-principles data, it also includes an empirical correction to calculated phonon frequencies. To reference this model to first-principles data for S in the solid α-phase, an experimental value of 12.552 kJ mol⁻¹ was used for S sublimation enthalpy at 298 K and 10⁵ Pa.³⁰ To map the measured T_S to an equivalent p_S, published experimental data from West and Menzies were used (see Fig. S4†).²⁰

Conclusions

High-order Ba polysulfides as intermediate phases are expected to significantly decrease the formation temperature of BaZrS₃. In this work, both an experimental and a theoretical pressure–temperature phase diagram for the Ba–S system were constructed. To achieve this, both the temperature of the sample and the S source were varied independently, and the thin films were characterized by XRD and RBS. It was possible to fabricate thin films of BaS, BaS₂, and BaS₃ and define the process conditions required to form these compounds. As expected, it was found that the sulfur temperature required to form BaS₃ increases with increasing sample temperature. On the other hand, the transition from BaS₂ to BaS does not appear to depend on the sample temperature above 440 °C, which was attributed to equipment limitations. A first-principles thermodynamic model was also built to provide further insight into the chemical thermodynamics. The theoretical model agrees well with the experimental results for the BaS₂–BaS₃ transition. However, it predicts that the BaS₂–BaS transition should indeed occur at higher partial vapor pressures of S for increasing sample temperature, deviating from the experiments. In this case, the theory-derived results are recommended as the best guide. This work gives thermodynamic insights into the Ba–S system and offers valuable guidance for synthesizing a variety of Ba sulfides (with a particular focus on BaZrS₃ perovskites) in a general thin film flow reactor, where achieving high partial vapor pressures of S presents a greater challenge compared to the conditions attainable in sealed ampoules commonly used in solid-state research. These results can be used to improve the growth of BaZrS₃ thin films and other Ba sulfides, thereby advancing the investigation of such material systems in device applications.

Data availability

Data are available from the authors upon request.

Author contributions

Corrado Comparotto: conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, and writing – original draft. Lucy Whalley: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, validation, visualization, and writing – review & editing. Kostiantyn Sopiha: conceptualization, methodology, validation, and writing – review & editing. Robert J. W. Frost: investigation, data curation, formal analysis, validation, and writing – review & editing. Tomas Kubart: supervision and writing – review & editing. Jonathan J. S. Scragg: conceptualization, funding acquisition, methodology, project administration, resources, supervision, validation, and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the Swedish Research Council (2017-04336) and the strategic research area STandUP for Energy for funding this research. The Swedish Research Council is also acknowledged for supporting the operation of the accelerator employed for ion beam analysis (contract VR-RFI-2019_00191). Myfab Uppsala is acknowledged for providing facilities and experimental support. Myfab is funded by the Swedish Research Council (2019-00207) as a national research infrastructure. This work used the Oswald High-Performance Computing Facility operated by Northumbria University (UK). Through our membership in the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/X035859), this work used the ARCHER2 UK National Supercomputing Service. This article is based upon work from COST Action Research and International Networking on Emerging Inorganic Chalcogenides for Photovoltaics (RENEW-PV), CA21148, supported by COST (European Cooperation in Science and Technology).

References

1. J. Werner, B. Niesen and C. Ballif, Adv. Mater. Interfaces, 2018, 5, 1700731.
2. T. J. Jacobsson, A. Hultqvist, A. García-Fernández, A. Anand, A. Al-Ashouri, A. Hagfeldt, A. Crovetto, A. Abate, A. G. Ricciardulli, A. Vijayan, A. Kulkarni, A. Y. Anderson, B. P. Darwich, B. Yang, B. L. Coles, C. A. R. Perini, C. Rehermann, D. Ramirez, D. Fairen-Jimenez, D. Di Girolamo, D. Jia, E. Avila, E. J. Juarez-Perez, F. Baumann, F. Mathies, G. S. A. González, G. Boschloo, G. Nasti, G. Paramasivam, G. Martínez-Denegri, H. Näsström, H. Michaels, H. Köbler, H. Wu, I. Benesperi, M. I. Dar, I. Bayrak Pehlivan, I. E. Gould, J. N. Vagott, J. Dagar, J. Kettle, J. Yang, J. Li, J. A. Smith, J. Pascual, J. J. Jerónimo-Rendón, J. F. Montoya, J.-P. Correa-Baena, J. Qiu, J. Wang, K. Sveinbjörnsson, K. Hirselandt, K. Dey, K. Frohna, L. Mathies, L. A. Castriotta, M. H. Aldamasy, M. Vasquez-Montoya, M. A. Ruiz-Preciado, M. A. Flatken, M. V. Khenkin, M. Grischek, M. Kedia, M. Saliba, M. Anaya, M. Veldhoen, N. Arora, O. Shargaieva, O. Maus, O. S. Game, O. Yudilevich, P. Fassl, Q. Zhou, R. Betancur, R. Munir, R. Patidar, S. D. Stranks, S. Alam, S. Kar, T. Unold, T. Abzieher, T. Edvinsson, T. W. David, U. W. Paetzold, W. Zia, W. Fu, W. Zuo, V. R. F. Schröder, W. Tress, X. Zhang, Y.-H. Chiang, Z. Iqbal, Z. Xie and E. Unger, Nat. Energy, 2021, 7, 107–115.
3. C. Yang, W. Hu, J. Liu, C. Han, Q. Gao, A. Mei, Y. Zhou, F. Guo and H. Han, Light:Sci. Appl., 2024, 13, 227.
4. T. A. Berhe, W.-N. Su, C.-H. Chen, C.-J. Pan, J.-H. Cheng, H.-M. Chen, M.-C. Tsai, L.-Y. Chen, A. A. Dubale and B.-J. Hwang, Energy Environ. Sci., 2016, 9, 323–356.
5. K. V. Sopiha, C. Comparotto, J. A. Márquez and J. J. S. Scragg, Adv. Opt. Mater., 2022, 10, 2101704.
6. Y. Nishigaki, T. Nagai, M. Nishiwaki, T. Aizawa, M. Kozawa, K. Hanzawa, Y. Kato, H. Sai, H. Hiramatsu, H. Hosono and H. Fujiwara, Sol. RRL, 2020, 4, 1900555.
7. T. Gupta, D. Ghoshal, A. Yoshimura, S. Basu, P. K. Chow, A. S. Lakhnot, J. Pandey, J. M. Warrender, H. Efstathiadis, A. Soni, E. Osei-Agyemang, G. Balasubramanian, S. Zhang, S.-F. Shi, T.-M. Lu, V. Meunier and N. Koratkar, Adv. Funct. Mater., 2020, 30, 2001387.
8. X. Wei, H. Hui, C. Zhao, C. Deng, M. Han, Z. Yu, A. Sheng, P. Roy, A. Chen, J. Lin, D. F. Watson, Y.-Y. Sun, T. Thomay, S. Yang, Q. Jia, S. Zhang and H. Zeng, Nano Energy, 2020, 68, 104317.
9. J. Xu, Y. Fan, W. Tian, L. Ye, Y. Zhang, Y. Tian, Y. Han and Z. Shi, J. Solid State Chem., 2022, 307, 122872.
10. S. Niu, J. Milam-Guerrero, Y. Zhou, K. Ye, B. Zhao, B. C. Melot and J. Ravichandran, J. Mater. Res., 2018, 33, 4135–4143.
11. P. Dallas, K. Gkini, A. Kaltzoglou, L. Givalou, M. Konstantakou, S. Orfanoudakis, N. Boukos, E. Sakellis, P. Tsipas, A. Kalafatis, A. G. Karydas, A. Lagogiannis, P. Falaras, V. Psycharis and T. Stergiopoulos, Mater. Today Commun., 2024, 39, 108608.
12. C. Comparotto, A. Davydova, T. Ericson, L. Riekehr, M. V. Moro, T. Kubart and J. Scragg, ACS Appl. Energy Mater., 2020, 3, 2762–2770.
13. Z. Yu, X. Wei, Y. Zheng, H. Hui, M. Bian, S. Dhole, J.-H. Seo, Y.-Y. Sun, Q. Jia, S. Zhang, S. Yang and H. Zeng, Nano Energy, 2021, 85, 105959.
14. V. K. Ravi, S. H. Yu, P. K. Rajput, C. Nayak, D. Bhattacharyya, D. S. Chung and A. Nag, Nanoscale, 2021, 13, 1616–1623.
15. R. Yang, A. D. Jess, C. Fai and C. J. Hages, J. Am. Chem. Soc., 2022, 144, 15928–15931.
16. C. Comparotto, P. Ström, O. Donzel-Gargand, T. Kubart and J. J. S. Scragg, ACS Appl. Energy Mater., 2022, 5, 6335–6343.
17. R. Yang, J. Nelson, C. Fai, H. A. Yetkin, C. Werner, M. Tervil, A. D. Jess, P. J. Dale and C. J. Hages, Chem. Mater., 2023, 35, 4743–4750.
18. K. C. Vincent, S. Agarwal, J. W. Turnley and R. Agrawal, Adv. Energy Sustainability Res., 2023, 4, 2300010.
19. S. Sasaki, M. Lesault, E. Grange, E. Janod, B. Corraze, S. Cadars, M. T. Caldes, C. Guillot-Deudon, S. Jobic and L. Cario, Chem. Commun., 2019, 55, 6189–6192.
20. W. A. West and A. W. C. Menzies, J. Phys. Chem., 1929, 33, 1880–1892.
21. H. E. Swanson, N. T. Gilfrich, M. I. Cook, R. Stinchfield and P. C. Parks, Standard X-Ray Diffraction Powder Patterns, National Bureau of Standards Circular 539, United States of America, 1957, vol. 7.
22. I. Kawada, K. Kato and S. Yamaoka, Acta Crystallogr. Sect. A Cryst. Phys. Diffr. Theor. Gen. Crystallogr., 1975, 31, 2905–2906.
23. S. Yamaoka, J. T. Lemley, J. M. Jenks and H. Steinfink, Inorg. Chem., 1975, 14, 129–131.
24. H. D. Lutz and S. El Suradi, Z. Anorg. Allg. Chem., 1976, 425, 134–144.
25. H. Sawada and T. Yoshio, Z. Kristallogr. Cryst. Mater., 1990, 191, 161–172.
26. S. T. Weir, Y. K. Vohra and A. L. Ruoff, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 4221–4226.
27. P. Kayastha, G. Longo and L. D. Whalley, ACS Appl. Energy Mater., 2024, 7, 11326–11333.
28. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
29. A. J. Jackson, D. Tiana and A. Walsh, Chem. Sci., 2016, 7, 1082–1092.
30. M. Chase, NIST-JANAF Thermochemical Tables, American Institute of Physics, 4th edn, 1998.
31. T. Degen, M. Sadki, E. Bron, U. König and G. Nénert, Powder Diffr., 2014, 29, S13–S18.
32. M. Mayer, in AIP Conference Proceedings, AIP, Denton, Texas (USA), 1999, pp. 541–544.

---

Footnote

† Electronic supplementary information (ESI) available: RBS simulated spectra and S vapor pressure. See DOI: https://doi.org/10.1039/d5ta00798d

---