Open Access Article
Open Access ArticleA computational view on the thermochemical and electrochemical stability of ruthenium oxides†
Iratxe
Aguado-Ruiz‡
 ab,
Ricardo
Urrego-Ortiz‡
ab,
Ricardo
Urrego-Ortiz‡
 ab and
Federico
Calle-Vallejo
ab and
Federico
Calle-Vallejo
 *bc
*bc
aDepartment of Materials Science and Chemical Physics, Institute of Theoretical and Computational Chemistry (IQTCUB), University of Barcelona, C/Martí i Franquès 1, 08028 Barcelona, Spain
bNano-Bio Spectroscopy Group, European Theoretical Spectroscopy Facility (ETSF), Department of Advanced Materials and Polymers: Physics, Chemistry and Technology, University of the Basque Country UPV/EHU, Av. Tolosa 72, 20018 San Sebastián, Spain. E-mail: federico.calle@ehu.es
cIkerbasque, Basque Foundation for Science, Plaza de Euskadi 5, 48009 Bilbao, Spain
First published on 17th March 2025
Abstract
Ruthenium oxides (RuOx) display suitable activities for a number of electrocatalytic reactions, such as chlorine evolution and oxygen evolution. However, their corrosion resistance still ought to be enhanced and the instabilities are often attributed to the transformation of one Ru oxide into another. Density functional theory (DFT) calculations can help understand and improve the thermochemical and electrochemical stability of RuOx. However, in this work, we show that a wide variety of exchange-correlation functionals are visibly inaccurate for the thermochemistry of gas-phase and solid-state RuOx. The inaccuracies can be systematically mitigated, as they grow alongside the number of oxygen atoms in the compounds because of the repulsive interactions among Ru–O bonds. Furthermore, Pourbaix diagrams, which are electrochemical phase diagrams outlining the conditions of electrode stability, are shown to be significantly affected by these inaccuracies. Seamlessly, our simple correction scheme brings computational Pourbaix diagrams close to experimental results, giving confidence in the predictiveness of future stability studies.
1. Introduction
Ruthenium oxides (RuOx, x = 1–4) are a family of chemical compounds in which the metal atom displays a wide range of oxidation states, from +2 in RuO to +8 in RuO4. These oxides are relevant in diverse branches of chemistry, from nuclear energy to heterogeneous catalysis and electrochemistry.1–3 Among them, ruthenium dioxide (RuO2) is of particular importance due to its activity to electrocatalyze the chlorine and oxygen evolution reactions (CER and OER, respectively),4–8 the former being central in the chloralkali process, the latter in water electrolyzers, and both in competition during seawater electrolysis.9,10 In addition, RuO2 also helps catalyze the thermocatalytic Sumitomo process, in which HCl is oxidized to Cl2.3,11 In all these applications, efficient use of RuOx-based materials is crucial, as ruthenium is not particularly abundant in the Earth's crust,12 the chloralkali electrolysis is a notorious and energy-intensive industrial process, and water electrolyzers are key for producing green hydrogen.Consequently, efforts have been directed to investigate the factors governing the catalytic performance of RuO2, such as facet orientation,13 ligand effects,14 crystal structure,15 and doping.16,17 However, the chemical and structural features of RuO2 are interconnected in such a way that disclosing their effects on the catalytic activity is challenging from an experimental standpoint. Density functional theory (DFT) calculations coupled with thermodynamic models are valuable tools to address this matter, as they can be used to estimate the energies of reaction intermediates under different conditions, thus serving as a guide, support and supplement to experiments.17–20
In this context, it is paramount to properly assess the accuracy of DFT-calculated thermochemistry. In particular, the formation energies of oxides, gas-phase species, and OER intermediates have proved challenging for DFT,21–28 leading to inaccurate reaction energies, equilibrium potentials and adsorption energies that deviate from experimental observations.29,30 In addition, incorrect thermochemical predictions might lead to incorrect assessments of the stability of Ru-based electrodes, which are critical to ensure their suitability as catalysts, elucidate the state of the active sites under reaction conditions, and guarantee their durability.31–34 This calls for strategies that can swiftly pinpoint and rectify inaccurate results at the early stages of computational studies on these compounds.
In this work, we evaluate the DFT formation energies of several RuOx using exchange-correlation functionals of increasing complexity (GGAs, meta-GGAs, and hybrids) to evaluate if systematic errors exist and whether more sophisticated functionals necessarily lead to enhanced thermochemical predictions of Ru oxides. We unveil large errors that scale linearly with the number of oxygen atoms of the oxides and systematically prevent accurate thermochemical predictions. Moreover, we provide a simple but insightful model to rationalize this intriguing trend. Finally, by means of Pourbaix diagrams35 of the Ru–water system, we show the detrimental effects these errors have on electrochemical stability predictions and provide a handy procedure to align the DFT energies with experimental values.
2. Methodology
2.1 Computational methods
The total energies of the Ru-based species (Ru(g), Ru(s), RuO(g), RuO2(g), RuO2(s), RuO3(g) and RuO4(g)) in Fig. 1 were obtained with the Vienna Ab initio Simulation Package (VASP)36 using the Projector Augmented-Wave (PAW) method to describe ion–electron interactions.37 For that, we used three functionals at the level of the generalized gradient approximation (GGA): PBE,38 PW91,39 and RPBE;40 three meta-GGAs:41 SCAN,42 TPSS,43 and R2SCAN;44 and three hybrid functionals: PBE0,45 HSEsol,46 and HSE06.47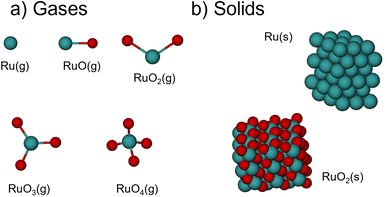 | ||
| Fig. 1 Schematics of (a) the gas-phase species and (b) the solids analyzed in this work. Green spheres represent ruthenium, and oxygen atoms are shown in red. | ||
All atoms in the compounds were allowed to relax in all directions until all the residual forces on them were below 0.01 eV Å−1. The reciprocal space was sampled using Monkhorst–Pack grids48 and only the Γ-point was considered for the molecules. Gaussian smearing was used at an electronic temperature of 0.001 eV to facilitate the convergence of the self-consistent cycles and all energies were extrapolated to 0 K. Spin unrestricted calculations were performed when necessary, namely for O2(g), Ru(g), and RuO(g). The molecules were simulated in cells of 15.00 Å × 15.10 Å × 15.20 Å, which ensured no interaction between the periodically repeated images.
Ru(s) was modelled in its hexagonal close-packed (hcp) structure while RuO2(s) was simulated in its rutile form. For the bulk calculations, all atoms were free to relax in all directions until all residual forces were below 0.05 eV Å−1. Test calculations using a tighter force criterion (0.01 eV Å−1) showed total energy differences for Ru(s) and RuO2(s) smaller than 0.0001 eV. The smearing was made using the Methfessel–Paxton method49 at an electronic temperature of 0.2 eV and all energies were subsequently extrapolated to 0 K. Based on the convergence test in Section S7,† we used a plane-wave energy cutoff of 450 eV for all calculations of molecules and solids.
2.2 Thermochemical calculations
The formation reaction of the compounds under study is defined in eqn (1), where all species are in their standard states and x = {0, 1, 2, 3, 4}. | (1) |
The free energy of formation for each compound 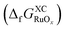 can be approximated using DFT-calculated data as follows:
can be approximated using DFT-calculated data as follows:
 | (2) |
2.3 Evaluating DFT errors
For a given compound RuOx, the deviation between the experimental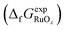 and DFT formation energies computed with a particular functional
and DFT formation energies computed with a particular functional  corresponds to the total error
corresponds to the total error  . Importantly,
. Importantly,  includes the errors in RuOx
includes the errors in RuOx and in the reactants of eqn (1) (
and in the reactants of eqn (1) ( and
and ), as shown in eqn (3).27,54–57
), as shown in eqn (3).27,54–57 | (3) |
In particular, the triplet state of O2(g) is commonly miscalculated by DFT, yielding substantial  values.21,25,58,59 Furthermore, previous studies have unveiled DFT errors above 0.5 eV in oxygen-containing gaseous species,60–62 such that large values of
values.21,25,58,59 Furthermore, previous studies have unveiled DFT errors above 0.5 eV in oxygen-containing gaseous species,60–62 such that large values of  are also expected. As GGAs usually describe metals better than molecules,27 it is customary to assume
are also expected. As GGAs usually describe metals better than molecules,27 it is customary to assume  as a first approximation, which might be reconsidered for hybrid functionals. Thus, reorganizing eqn (3) we have:
as a first approximation, which might be reconsidered for hybrid functionals. Thus, reorganizing eqn (3) we have:  , which indicates that the specific DFT error of each RuOx can be evaluated once the O2(g) errors are known. In practice,
, which indicates that the specific DFT error of each RuOx can be evaluated once the O2(g) errors are known. In practice,  is usually calculated semiempirically using the experimental water formation energy
is usually calculated semiempirically using the experimental water formation energy  .21,25,26,54,55 The DFT total errors and the individual molecular errors calculated for all functionals in this work are shown in Tables S2 and S3.†
.21,25,26,54,55 The DFT total errors and the individual molecular errors calculated for all functionals in this work are shown in Tables S2 and S3.†
3. Results and discussion
3.1 Energy–structure relationship
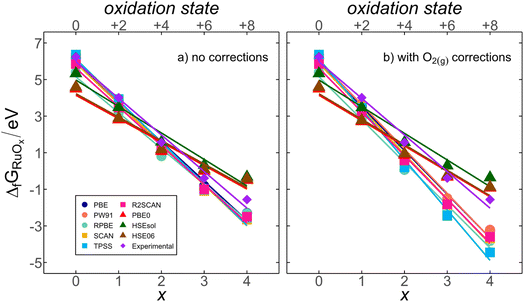
Ru displays increasing oxidation states as the number of oxygen atoms in the compound (x) grows from +2 in RuO(g) to +8 in RuO4(g). The experimental and DFT-calculated formation energies, with and without O2(g) corrections, show a strong correlation with x (or the oxidation state of Ru), as shown in Fig. 2. This suggests the existence of a systematic connection between chemical composition and energy for RuOx. In the following, we provide an energy-decomposition model63–65 to rationalize the linear relationships in Fig. 2. The model is based on three considerations:(1) The free energy of eqn (1) is  , and the free energies of the species include their internal energy, ZPE and entropic corrections, in line with eqn (2).
, and the free energies of the species include their internal energy, ZPE and entropic corrections, in line with eqn (2).
(2) The total energy of the oxide (ERuOx(g)) can be decomposed into the sum of the energy of Ru–O bonds plus an interaction energy Eint(x) between different Ru–O moieties: ERuOx(g) = xERu–O + Eint(x). As shown in Table S5,† the energy of the Ru–O bonds in RuOx can be approximated to the energy of RuO(g). Therefore ERuOx(g) ≈ xERuO(g) + Eint(x).
(3) Eint(x) is observed in Section S3† to scale linearly with x for all functionals, such that E(x)int ≈ αx + β, where α and β are functional-specific constants.
These three considerations lead to eqn (4):
 | (4) |
When the terms in eqn (4) are calculated using DFT and a specific functional, eqn (5) is obtained, where  and
and  .
.
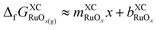 | (5) |
Eqn (5) explains the linear trends in Fig. 2a, in which free energies and oxygen content are shown to vary proportionally. Importantly, 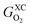 is the uncorrected free energy of O2(g). When O2(g) is corrected,
is the uncorrected free energy of O2(g). When O2(g) is corrected,  is replaced by
is replaced by  (“OC” stands for oxygen corrected), as shown in Fig. 2b. Table S1† shows the experimental and DFT-calculated formation energies obtained using eqn (2), without and with the O2(g) correction (
(“OC” stands for oxygen corrected), as shown in Fig. 2b. Table S1† shows the experimental and DFT-calculated formation energies obtained using eqn (2), without and with the O2(g) correction ( and
and  , respectively), for all scrutinized functionals. Table S9† contains the parameters of the fits in Fig. 2b and those obtained with the O2(g)-corrected version of eqn (5). Section S3† contains further details of the model.
, respectively), for all scrutinized functionals. Table S9† contains the parameters of the fits in Fig. 2b and those obtained with the O2(g)-corrected version of eqn (5). Section S3† contains further details of the model.
3.2 Trends in the gas-phase errors of RuOx
The total errors in the DFT-calculated energies of RuOx were calculated using eqn (3) for all the examined functionals. Upon correcting O2(g), the individual errors
were calculated using eqn (3) for all the examined functionals. Upon correcting O2(g), the individual errors 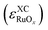 were also computed. Both
were also computed. Both 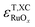 and
and  scale with the number of oxygen atoms in the oxide, as shown in Fig. 3a and b for the GGAs and meta-GGAs, and in Fig. 3c and d for hybrid functionals, respectively.
scale with the number of oxygen atoms in the oxide, as shown in Fig. 3a and b for the GGAs and meta-GGAs, and in Fig. 3c and d for hybrid functionals, respectively.
Fig. 3 unveils a striking difference between the analyzed functionals: the trends for GGAs and meta-GGAs have negative slopes while those of hybrid functionals display positive slopes. Eqn (5) and the definitions of  and
and  can be used to explain such opposing trends. Specifically, the magnitude and sign of the slopes depend on those in Fig. 2 in the way shown in eqn (6):
can be used to explain such opposing trends. Specifically, the magnitude and sign of the slopes depend on those in Fig. 2 in the way shown in eqn (6):
 | (6) |
Because  and
and  are negative in Fig. 2,
are negative in Fig. 2, 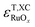 scales positively with x when
scales positively with x when 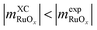 (see Table S9).† Once molecular oxygen has been corrected, we have:
(see Table S9).† Once molecular oxygen has been corrected, we have:
 | (7) |
Again, 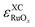 scales with a positive slope with x if
scales with a positive slope with x if 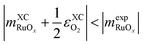 .
.
3.3 Mitigating gas-phase errors
Fig. 3 shows that the uncorrected formation energies entail large deviations from experimental values for all functionals. The trends in Fig. 3a have similar slopes of ∼−0.20 eV per O atom except for RPBE, which is nearly flat (0.04 eV per O atom). Meanwhile, hybrids exhibit an average slope of ∼0.66 ± 0.10 eV per O atom in Fig. 3c.In Fig. 3b and d, correcting  makes all GGAs and meta-GGAs display similar slopes of −0.46 ± 0.15 eV per O atom. For the hybrids, the average slope is now 0.59 ± 0.04 eV per O atom. As the oxygen error does not affect Ru(g), the intercepts remain unchanged in Fig. 3b and d compared to those in Fig. 3a and c. Capitalizing on the linear trends in Fig. 3b and d provided by the inexpensive structural descriptor x, a corrected DFT free energy
makes all GGAs and meta-GGAs display similar slopes of −0.46 ± 0.15 eV per O atom. For the hybrids, the average slope is now 0.59 ± 0.04 eV per O atom. As the oxygen error does not affect Ru(g), the intercepts remain unchanged in Fig. 3b and d compared to those in Fig. 3a and c. Capitalizing on the linear trends in Fig. 3b and d provided by the inexpensive structural descriptor x, a corrected DFT free energy  can be obtained:66
can be obtained:66
 | (8) |
 vs. x. In Table 1, we report such slopes and intercepts for all scrutinized functionals. We note that
vs. x. In Table 1, we report such slopes and intercepts for all scrutinized functionals. We note that  is a residual error stemming from the slight deviations of the calculated datapoints and the linear fits in Fig. 2. Such residual errors are shown for all functionals in Fig. 4, where we observe unsystematic, flat trends around 0 eV with mean and maximum absolute errors (MAE and MAX) close to chemical accuracy (∼0.04 eV). For instance, the uncorrected SCAN energy of formation for RuO4(g) entails an initial error of −2.12 eV, and after correcting with eqn (8), the residual error is only −0.14 eV. In addition, the average of the MAEs is 0.06 eV and the average of the MAXs is 0.11 eV. In sum, Fig. 4 attests to the removal of the systematic errors in RuOx observed in Fig. 3 by means of simple linear corrections based on the number of oxygen atoms in the oxide.
is a residual error stemming from the slight deviations of the calculated datapoints and the linear fits in Fig. 2. Such residual errors are shown for all functionals in Fig. 4, where we observe unsystematic, flat trends around 0 eV with mean and maximum absolute errors (MAE and MAX) close to chemical accuracy (∼0.04 eV). For instance, the uncorrected SCAN energy of formation for RuO4(g) entails an initial error of −2.12 eV, and after correcting with eqn (8), the residual error is only −0.14 eV. In addition, the average of the MAEs is 0.06 eV and the average of the MAXs is 0.11 eV. In sum, Fig. 4 attests to the removal of the systematic errors in RuOx observed in Fig. 3 by means of simple linear corrections based on the number of oxygen atoms in the oxide.
 and x for all functionals under study. All values are in eV
and x for all functionals under study. All values are in eV
| Functional | PBE | PW91 | RPBE | SCAN | TPSS | R2SCAN | PBE0 | HSEsol | HSE06 |
|---|---|---|---|---|---|---|---|---|---|
| δ XC | −0.39 | −0.43 | −0.34 | −0.47 | −0.75 | −0.39 | 0.61 | 0.54 | 0.61 |
| θ XC | −0.07 | 0.08 | −0.83 | −0.08 | 0.15 | −0.35 | −1.83 | −1.00 | −1.75 |
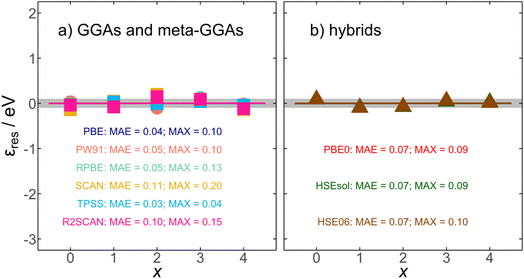 | ||
| Fig. 4 Residual errors (εres) obtained after correcting the DFT formation energies using eqn (8). Results are shown for (a) GGAs and meta-GGAs (circles and squares, respectively) and (b) hybrid functionals (triangles). The gray region spans ±0.1 eV around zero. The final MAE/MAX values (in eV) are reported for all scrutinized functionals. | ||
Fig. 5 summarizes the MAEs and MAXs when no corrections are applied, when O2(g) is corrected, and when O2(g) and the oxides are corrected using eqn (8). A noteworthy feature of Fig. 5 is that both MAE and MAX values increase after correcting O2(g) for all GGAs and meta-GGAs, reaching MAE/MAX of 1.5/2.9 eV, while hybrids show a slight improvement. Finally, mitigating the errors using eqn (8) leads to the orange data in Fig. 5a and b, which are remarkably close to the red dashed line marking chemical accuracy. In fact, the largest final MAE and MAX (0.11 and 0.20 eV, respectively) are in stark contrast with the largest initial MAE and MAX (1.5 and 2.9 eV, respectively), illustrating that the corrections based on x swiftly and inexpensively lower the substantial DFT errors to the scale of chemical accuracy for all functionals.
 | ||
| Fig. 5 (a) Mean absolute error (MAE) and (b) maximum absolute error (MAX) for different functionals when no gas-phase corrections are applied (blue), when only the O2(g) energy is corrected (green), and when O2(g) and RuOx are corrected using eqn (8) and Table 1 (orange). The red dashed lines mark the chemical accuracy (1 kcal mol−1 ≈ 0.04 eV). | ||
3.4 Solid-phase errors
In the previous sections, large gas-phase errors in the DFT-calculated energies of RuOx were unveiled, suggesting substantial deviations in reactions involving them. Although the analysis has focused so far on molecules, eqn (3) is also valid for solids. Bearing in mind that ,52 the functional-dependent error
,52 the functional-dependent error  was estimated using eqn (3), as shown in Table S4.† Furthermore, Fig. S1† shows a comparison against its gaseous counterpart
was estimated using eqn (3), as shown in Table S4.† Furthermore, Fig. S1† shows a comparison against its gaseous counterpart  . Encouragingly, the solid phase is better described than the gas phase; we did not observe any correlation between gas-phase and solid-state errors, and only for the meta-GGAs the magnitude of the solid-state error exceeds 0.3 eV. Indeed, the mean absolute values of
. Encouragingly, the solid phase is better described than the gas phase; we did not observe any correlation between gas-phase and solid-state errors, and only for the meta-GGAs the magnitude of the solid-state error exceeds 0.3 eV. Indeed, the mean absolute values of  and
and  calculated from Tables S3 and S4† are significantly different in all cases: 1.08 vs. 0.16 eV for GGAs, 1.06 vs. 0.82 eV for meta-GGAs, and 0.43 vs. 0.24 eV for hybrid functionals.
calculated from Tables S3 and S4† are significantly different in all cases: 1.08 vs. 0.16 eV for GGAs, 1.06 vs. 0.82 eV for meta-GGAs, and 0.43 vs. 0.24 eV for hybrid functionals.
3.5 Impact on electrochemistry
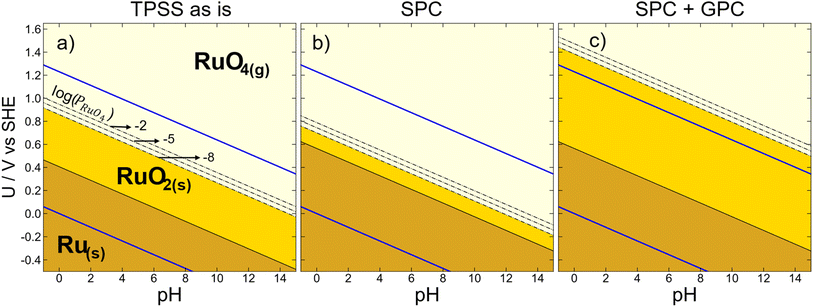
Stability and durability are necessary features of the materials used in electrochemical and electrocatalytic applications.67–70 Pourbaix diagrams are useful to assess the thermodynamic stability of materials in aqueous media as a function of potential and pH, allowing to anticipate regions of protection, passivation and corrosion.35 Importantly, as bulk and surface Pourbaix diagrams can be built entirely from DFT calculations,71–74 it is crucial to appraise the DFT errors and uncertainty if an accurate picture of stable phases under reaction conditions is sought after.75Below we illustrate the repercussions of DFT errors on the bulk Pourbaix diagram of the Ru–water system, considering the oxidations from Ru(s) to RuO2(s) and RuO4(g). This outlines a stability region for RuO2(s), which deserves special attention due to the negative impact of its dissolution to RuO4(aq) on the durability and catalytic performance for the OER.31,76–78 Importantly, the degradation pathway involves compounds in the gas and solid phases, such that different sorts of DFT errors should be simultaneously addressed. Because Fig. 3a and b hinted toward particularly large meta-GGA errors in the energies of RuO4(g) and RuO2(g), TPSS is used as a case study.
In Fig. 6, the TPSS-based Pourbaix diagram for the Ru–water system is shown at three correction stages: in Fig. 6a no corrections are taken into account, in Fig. 6b only the solid-phase correction of RuO2(s) is considered, and Fig. 6c includes both the solid-phase and gas-phase corrections of RuO2(s) and RuO4(g). We recall that the errors of RuO2(s) and RuO4(g) result upon correcting the energy of O2(g) in their formation reactions (eqn (1)). The three scenarios depict contrasting regions, so whether and how many DFT errors are included can lead to different conclusions. For instance, the “TPSS as is” region of Ru(s) is smaller than when solid-phase and/or gas-phase corrections are added, so uncorrected Ru(s) oxidation is not accurately predicted.
The solid-phase correction shortens the RuO2(s) region in Fig. 6b, so that its vertical span is 0.10 V, in contrast to the 0.46 V in Fig. 6a. When the gas-phase energy of RuO4(g) is also corrected, the RuO4(g) region is shifted upwards such that the RuO2(s) phase has now a vertical width of 0.82 V, as shown in Fig. 6c. To incorporate pressure effects in the gas phase, the dashed lines in Fig. 6 mark three different partial pressures of RuO4(g) (log(PRuO4(g)) = −2, −5, and −8). Besides, the blue lines delimit the water stability region in between O2(g) and H2(g) evolution. Table S10† contains the equilibrium potentials at the three correction stages in Fig. 6 for all functionals under study.
We close this section by stressing that additional phases can and ought to be included to enrich Fig. 6, whether they are gases, solids or aqueous species. In doing so, it is always advisable to properly assess the DFT errors since not only free molecules but also solids might be problematic.
4. Conclusions
DFT is widely employed to understand and improve the electrocatalytic performance of Ru-based electrodes, which display high activities for the CER and OER. Therefore, a proper description of the thermochemistry of Ru oxides is crucial to yield accurate predictions.In this study, we analyzed the DFT-calculated free energies of formation for several Ru oxides using various GGA, meta-GGA and hybrid functionals. The gas-phase errors are substantial and increase linearly with the number of oxygen atoms in the compounds. The slopes of GGAs and meta-GGAs are negative and around −0.46 eV per O atom, while those of hybrids are positive and close to 0.59 eV per O atom. We elaborated an energy-decomposition model that explains (i) the linear relationship between the number of oxygen atoms and the formation energies of Ru oxides and (ii) the positive and negative slopes of the error trends.
We capitalized on the systematicity of the errors to provide a swift and inexpensive correction scheme that lowers the absolute errors to values close to chemical accuracy. In addition, RuO2(s) errors were computed and found to be smaller than their gas-phase counterparts, displaying absolute values of ∼0.2 eV, except for the meta-GGAs for which the errors are larger than 0.6 eV.
Finally, the effects of solid-state and gas-phase DFT errors of RuOx on electrochemical stability were appraised by means of bulk Pourbaix diagrams including Ru(s), RuO2(s), and RuO4(g) phases. The resulting Pourbaix diagrams showed that uncorrected or partially corrected TPSS energies produce reshaped regions visibly deviating from the fully corrected picture. In fact, the stability region of RuO2(s) is underestimated if solids and molecules are not corrected.
All in all, relying on DFT without being aware of its inaccuracies might lead to faulty models of chemical, electrochemical and catalytic reactions involving Ru oxides. This work provides a rational, inexpensive and semiempirical scheme to detect and quantify such errors and align predictions with experiments. Finally, this work can be used in future studies as a starting point to unveil similar trends for other families of oxidized electrocatalysts and enhance their DFT modelling.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work received financial support from grants PID2021-127957NB-I00 and TED2021-132550B-C21, which are funded by the Spanish MCIN/AEI/10.13039/501100011033 and the European Social Fund Plus (ESF+). The project that gave rise to these results also received the support of a Ph.D. fellowship from “la Caixa” Foundation (ID 100010434, fellowship code LCF/BQ/DI22/11940040). FCV also acknowledges financial support through grant IT1453-22 “Grupos Consolidados UPV/EHU del Gobierno Vasco”. IAR thanks the Spanish MCIN for an FPI grant (PRE2022-103431). The use of supercomputing facilities at SURFsara was sponsored by NWO Physical Sciences, with financial support from NWO. We thank the Red Española de Supercomputación for providing computational resources through grants QHS-2025-1-0024, QHS-2024-3-0037 and QHS-2024-3-0025.References
- F. Miradji, S. Souvi, L. Cantrel, F. Louis and V. Vallet, Thermodynamic Properties of Gaseous Ruthenium Species, J. Phys. Chem. A, 2015, 119(20), 4961–4971, DOI:10.1021/acs.jpca.5b01645.
- C. Mun, L. Cantrel and C. Madic, Review of Literature on Ruthenium Behavior in Nuclear Power Plant Severe Accidents, Nucl. Technol., 2006, 156(3), 332–346, DOI:10.13182/NT156-332.
- K. Iwanaga, K. Seki, T. Hibi, K. Issoh, T. Suzuta, M. Nakada, Y. Mori and T. Abe, The Development of Improved Hydrogen Chloride Oxidation Process, R&D Report, Sumitomo Kagaku, 2004 Search PubMed.
- S. Trasatti, Electrocatalysis: Understanding the Success of DSA®, Electrochim. Acta, 2000, 45(15–16), 2377–2385, DOI:10.1016/S0013-4686(00)00338-8.
- S. Trasatti and G. Buzzanca, Ruthenium Dioxide: A New Interesting Electrode Material. Solid State Structure and Electrochemical Behaviour, J. Electroanal. Chem. Interfacial Electrochem., 1971, 29(2), A1–A5, DOI:10.1016/S0022-0728(71)80111-0.
- Y. Matsumoto and E. Sato, Electrocatalytic Properties of Transition Metal Oxides for Oxygen Evolution Reaction, Mater. Chem. Phys., 1986, 14(5), 397–426, DOI:10.1016/0254-0584(86)90045-3.
- S. Trasatti, Electrocatalysis in the Anodic Evolution of Oxygen and Chlorine, Electrochim. Acta, 1984, 29(11), 1503–1512, DOI:10.1016/0013-4686(84)85004-5.
- R. K. B. Karlsson and A. Cornell, Selectivity between Oxygen and Chlorine Evolution in the Chlor-Alkali and Chlorate Processes, Chem. Rev., 2016, 116(5), 2982–3028, DOI:10.1021/acs.chemrev.5b00389.
- W. T. Hong, M. Risch, K. A. Stoerzinger, A. Grimaud, J. Suntivich and Y. Shao-Horn, Toward the Rational Design of Non-Precious Transition Metal Oxides for Oxygen Electrocatalysis, Energy Environ. Sci., 2015, 8(5), 1404–1427, 10.1039/C4EE03869J.
- Y. Liu, Y. Wang and S. Zhao, Journey of Electrochemical Chlorine Production: From Brine to Seawater, Curr. Opin. Electrochem., 2023, 37, 101202, DOI:10.1016/j.coelec.2022.101202.
- D. Crihan, M. Knapp, S. Zweidinger, E. Lundgren, C. J. Weststrate, J. N. Andersen, A. P. Seitsonen and H. Over, Stable Deacon Process for HCl Oxidation over RuO2, Angew. Chem., Int. Ed., 2008, 47(11), 2131–2134, DOI:10.1002/anie.200705124.
- P. C. K. Vesborg and T. F. Jaramillo, Addressing the Terawatt Challenge: Scalability in the Supply of Chemical Elements for Renewable Energy, RSC Adv., 2012, 2(21), 7933, 10.1039/c2ra20839c.
- K. A. Stoerzinger, O. Diaz-Morales, M. Kolb, R. R. Rao, R. Frydendal, L. Qiao, X. R. Wang, N. B. Halck, J. Rossmeisl, H. A. Hansen, T. Vegge, I. E. L. Stephens, M. T. M. Koper and Y. Shao-Horn, Orientation-Dependent Oxygen Evolution on RuO2 without Lattice Exchange, ACS Energy Lett., 2017, 2(4), 876–881, DOI:10.1021/acsenergylett.7b00135.
- Y. Qin, T. Yu, S. Deng, X.-Y. Zhou, D. Lin, Q. Zhang, Z. Jin, D. Zhang, Y.-B. He, H.-J. Qiu, L. He, F. Kang, K. Li and T.-Y. Zhang, RuO2 Electronic Structure and Lattice Strain Dual Engineering for Enhanced Acidic Oxygen Evolution Reaction Performance, Nat. Commun., 2022, 13(1), 3784, DOI:10.1038/s41467-022-31468-0.
- Z. Xu and J. R. Kitchin, Tuning Oxide Activity through Modification of the Crystal and Electronic Structure: From Strain to Potential Polymorphs, Phys. Chem. Chem. Phys., 2015, 17(43), 28943–28949, 10.1039/C5CP04840K.
- H. Sun and W. Jung, Recent Advances in Doped Ruthenium Oxides as High-Efficiency Electrocatalysts for the Oxygen Evolution Reaction, J. Mater. Chem. A, 2021, 9(28), 15506–15521, 10.1039/D1TA03452A.
- N. B. Halck, V. Petrykin, P. Krtil and J. Rossmeisl, Beyond the Volcano Limitations in Electrocatalysis – Oxygen Evolution Reaction, Phys. Chem. Chem. Phys., 2014, 16(27), 13682–13688, 10.1039/C4CP00571F.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining Theory and Experiment in Electrocatalysis: Insights into Materials Design, Science, 2017, 355(6321), eaad4998, DOI:10.1126/science.aad4998.
- X. Liao, R. Lu, L. Xia, Q. Liu, H. Wang, K. Zhao, Z. Wang and Y. Zhao, Density Functional Theory for Electrocatalysis, Energy Environ. Mater., 2022, 5(1), 157–185, DOI:10.1002/eem2.12204.
- R. R. Rao, M. J. Kolb, N. B. Halck, A. F. Pedersen, A. Mehta, H. You, K. A. Stoerzinger, Z. Feng, H. A. Hansen, H. Zhou, L. Giordano, J. Rossmeisl, T. Vegge, I. Chorkendorff, I. E. L. Stephens and Y. Shao-Horn, Towards Identifying the Active Sites on RuO2 (110) in Catalyzing Oxygen Evolution, Energy Environ. Sci., 2017, 10(12), 2626–2637, 10.1039/C7EE02307C.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892, DOI:10.1021/jp047349j.
- J. I. Martínez, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Formation Energies of Rutile Metal Dioxides Using Density Functional Theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(4), 045120, DOI:10.1103/PhysRevB.79.045120.
- L. Wang, T. Maxisch and G. Ceder, Oxidation Energies of Transition Metal Oxides within the GGA + U Framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(19), 195107, DOI:10.1103/PhysRevB.73.195107.
- R. Christensen, H. A. Hansen, C. F. Dickens, J. K. Nørskov and T. Vegge, Functional Independent Scaling Relation for ORR/OER Catalysts, J. Phys. Chem. C, 2016, 120(43), 24910–24916, DOI:10.1021/acs.jpcc.6b09141.
- E. Sargeant, F. Illas, P. Rodríguez and F. Calle-Vallejo, Importance of the Gas-Phase Error Correction for O2 When Using DFT to Model the Oxygen Reduction and Evolution Reactions, J. Electroanal. Chem., 2021, 896, 115178, DOI:10.1016/j.jelechem.2021.115178.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, M. Mogensen and J. Rossmeisl, Trends in Stability of Perovskite Oxides, Angew. Chem., Int. Ed., 2010, 49(42), 7699–7701, DOI:10.1002/anie.201002301.
- R. Urrego-Ortiz, S. Builes, F. Illas and F. Calle-Vallejo, Gas-Phase Errors in Computational Electrocatalysis: A Review, EES Catal., 2024, 2(1), 157–179, 10.1039/D3EY00126A.
- I. C. Man, H. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3(7), 1159–1165, DOI:10.1002/cctc.201000397.
- L. G. V. Briquet, M. Sarwar, J. Mugo, G. Jones and F. Calle-Vallejo, A New Type of Scaling Relations to Assess the Accuracy of Computational Predictions of Catalytic Activities Applied to the Oxygen Evolution Reaction, ChemCatChem, 2017, 9(7), 1261–1268, DOI:10.1002/cctc.201601662.
- Z. Xu, J. Rossmeisl and J. R. Kitchin, A Linear Response DFT+U Study of Trends in the Oxygen Evolution Activity of Transition Metal Rutile Dioxides, J. Phys. Chem. C, 2015, 119(9), 4827–4833, DOI:10.1021/jp511426q.
- C. F. Dickens and J. K. Nørskov, A Theoretical Investigation into the Role of Surface Defects for Oxygen Evolution on RuO2, J. Phys. Chem. C, 2017, 121(34), 18516–18524, DOI:10.1021/acs.jpcc.7b03481.
- F. Studt, F. Abild-Pedersen, H. A. Hansen, I. C. Man, J. Rossmeisl and T. Bligaard, Volcano Relation for the Deacon Process over Transition-Metal Oxides, ChemCatChem, 2010, 2(1), 98–102, DOI:10.1002/cctc.200900194.
- K. Klyukin, A. Zagalskaya and V. Alexandrov, Role of Dissolution Intermediates in Promoting Oxygen Evolution Reaction at RuO2 (110) Surface, J. Phys. Chem. C, 2019, 123(36), 22151–22157, DOI:10.1021/acs.jpcc.9b03418.
- A. Zagalskaya and V. Alexandrov, Role of Defects in the Interplay between Adsorbate Evolving and Lattice Oxygen Mechanisms of the Oxygen Evolution Reaction in RuO2 and IrO2, ACS Catal., 2020, 10(6), 3650–3657, DOI:10.1021/acscatal.9b05544.
- M. Pourbaix, Atlas of Electrochemical Equilibria in Aqueous Solutions, National Association of Corrosion Engineers, Houston, Texas, 2nd edn, 1974 Search PubMed.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78(7), 1396, DOI:10.1103/PhysRevLett.78.1396.
- J. P. Perdew and Y. Wang, Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(23), 13244–13249, DOI:10.1103/PhysRevB.45.13244.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(11), 7413–7421, DOI:10.1103/PhysRevB.59.7413.
- J. Sun, M. Marsman, G. I. Csonka, A. Ruzsinszky, P. Hao, Y.-S. Kim, G. Kresse and J. P. Perdew, Self-Consistent Meta-Generalized Gradient Approximation within the Projector-Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(3), 035117, DOI:10.1103/PhysRevB.84.035117.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115(3), 036402, DOI:10.1103/PhysRevLett.115.036402.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91(14), 146401, DOI:10.1103/PhysRevLett.91.146401.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and Numerically Efficient r2SCAN Meta-Generalized Gradient Approximation, J. Phys. Chem. Lett., 2020, 11(19), 8208–8215, DOI:10.1021/acs.jpclett.0c02405.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for Mixing Exact Exchange with Density Functional Approximations, J. Chem. Phys., 1996, 105(22), 9982–9985, DOI:10.1063/1.472933.
- L. Schimka, J. Harl and G. Kresse, Improved Hybrid Functional for Solids: The HSEsol Functional, J. Chem. Phys., 2011, 134(2), 024116, DOI:10.1063/1.3524336.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, Screened Hybrid Density Functionals Applied to Solids, J. Chem. Phys., 2006, 124(15), 154709, DOI:10.1063/1.2187006.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B, 1976, 13(12), 5188–5192, DOI:10.1103/PhysRevB.13.5188.
- M. Methfessel and A. T. Paxton, High-Precision Sampling for Brillouin-Zone Integration in Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(6), 3616–3621, DOI:10.1103/PhysRevB.40.3616.
- W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Handbook of Chemistry and Physics, CRC Press/Taylor and Francis, Boca Raton, FL, 97th edn, 2016, DOI:10.1201/9781315380476.
- I. Nuta, C. Chatillon, F.-Z. Roki and E. Fischer, Gaseous Phase above Ru–O System: A Thermodynamic Data Assessment, Calphad, 2021, 75, 102329, DOI:10.1016/j.calphad.2021.102329.
- C. Chatillon, I. Nuta, F.-Z. Roki and E. Fischer, Chemical Thermodynamics of RuO2(s), J. Nucl. Mater., 2018, 509, 742–751, DOI:10.1016/j.jnucmat.2018.05.060.
- NIST Standard Reference Database Number 69, 2023, DOI:10.18434/T4D303.
- R. Urrego-Ortiz, S. Builes and F. Calle-Vallejo, Fast Correction of Errors in the DFT-Calculated Energies of Gaseous Nitrogen-Containing Species, ChemCatChem, 2021, 13(10), 2508–2516, DOI:10.1002/cctc.202100125.
- M. O. Almeida, M. J. Kolb, M. R. V. Lanza, F. Illas and F. Calle-Vallejo, Gas-Phase Errors Affect DFT-Based Electrocatalysis Models of Oxygen Reduction to Hydrogen Peroxide, ChemElectroChem, 2022, 9(12), e202200210, DOI:10.1002/celc.202200210.
- L. P. Granda-Marulanda, A. Rendón-Calle, S. Builes, F. Illas, M. T. M. Koper and F. Calle-Vallejo, A Semiempirical Method to Detect and Correct DFT-Based Gas-Phase Errors and Its Application in Electrocatalysis, ACS Catal., 2020, 10(12), 6900–6907, DOI:10.1021/acscatal.0c01075.
- R. Urrego-Ortiz, M. Almeida and F. Calle-Vallejo, Error Awareness in the Volcano Plots of Oxygen Electroreduction to Hydrogen Peroxide, ChemSusChem, 2024, e202400873, DOI:10.1002/cssc.202400873.
- S. Kurth, J. P. Perdew and P. Blaha, Molecular and Solid-State Tests of Density Functional Approximations: LSD, GGAs, and Meta-GGAs, Int. J. Quantum Chem., 1999, 75(4–5), 889–909, DOI:10.1002/(SICI)1097-461X(1999)75:4/5<889::AID-QUA54>3.0.CO;2-8.
- R. Urrego-Ortiz, S. Builes, F. Illas, S. T. Bromley, M. C. Figueiredo and F. Calle-Vallejo, Minimum Conditions for Accurate Modeling of Urea Production via Co-Electrolysis, Commun. Chem., 2023, 6(1), 1–10, DOI:10.1038/s42004-023-00990-7.
- R. Urrego-Ortiz, S. Builes and F. Calle-Vallejo, Impact of Intrinsic Density Functional Theory Errors on the Predictive Power of Nitrogen Cycle Electrocatalysis Models, ACS Catal., 2022, 12(8), 4784–4791, DOI:10.1021/acscatal.1c05333.
- A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, How Copper Catalyzes the Electroreduction of Carbon Dioxide into Hydrocarbon Fuels, Energy Environ. Sci., 2010, 3(9), 1311–1315, 10.1039/C0EE00071J.
- R. Christensen, H. A. Hansen and T. Vegge, Identifying Systematic DFT Errors in Catalytic Reactions, Catal. Sci. Technol., 2015, 5(11), 4946–4949, 10.1039/C5CY01332A.
- H. Umeyama and K. Morokuma, The Origin of Hydrogen Bonding. An Energy Decomposition Study, J. Am. Chem. Soc., 1977, 99(5), 1316–1332, DOI:10.1021/ja00447a007.
- C. Dupont, Y. Jugnet and D. Loffreda, Theoretical Evidence of PtSn Alloy Efficiency for CO Oxidation, J. Am. Chem. Soc., 2006, 128(28), 9129–9136, DOI:10.1021/ja061303h.
- F. Calle-Vallejo, P. Sautet and D. Loffreda, Understanding Adsorption-Induced Effects on Platinum Nanoparticles: An Energy-Decomposition Analysis, J. Phys. Chem. Lett., 2014, 5(18), 3120–3124, DOI:10.1021/jz501263e.
- R. Urrego-Ortiz, S. Builes and F. Calle-Vallejo, Automated versus Chemically Intuitive Deconvolution of Density Functional Theory (DFT)-Based Gas-Phase Errors in Nitrogen Compounds, Ind. Eng. Chem. Res., 2022, 61(36), 13375–13382, DOI:10.1021/acs.iecr.2c02111.
- J. Masa, C. Andronescu and W. Schuhmann, Electrocatalysis as the Nexus for Sustainable Renewable Energy: The Gordian Knot of Activity, Stability, and Selectivity, Angew. Chem., Int. Ed., 2020, 59(36), 15298–15312, DOI:10.1002/anie.202007672.
- S. Geiger, O. Kasian, M. Ledendecker, E. Pizzutilo, A. M. Mingers, W. T. Fu, O. Diaz-Morales, Z. Li, T. Oellers, L. Fruchter, A. Ludwig, K. J. J. Mayrhofer, M. T. M. Koper and S. Cherevko, The Stability Number as a Metric for Electrocatalyst Stability Benchmarking, Nat. Catal., 2018, 1(7), 508–515, DOI:10.1038/s41929-018-0085-6.
- N. Esfandiari, M. Aliofkhazraei, A. N. Colli, F. C. Walsh, S. Cherevko, L. A. Kibler, M. M. Elnagar, P. D. Lund, D. Zhang, S. Omanovic and J. Lee, Metal-Based Cathodes for Hydrogen Production by Alkaline Water Electrolysis: Review of Materials, Degradation Mechanism, and Durability Tests, Prog. Mater. Sci., 2024, 144, 101254, DOI:10.1016/j.pmatsci.2024.101254.
- T. Fuchs, V. Briega-Martos, J. Drnec, N. Stubb, I. Martens, F. Calle-Vallejo, D. A. Harrington, S. Cherevko and O. M. Magnussen, Anodic and Cathodic Platinum Dissolution Processes Involve Different Oxide Species, Angew. Chem., 2023, 135(34), e202304293, DOI:10.1002/ange.202304293.
- H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Surface Pourbaix Diagrams and Oxygen Reduction Activity of Pt, Ag and Ni(111) Surfaces Studied by DFT, Phys. Chem. Chem. Phys., 2008, 10(25), 3722, 10.1039/b803956a.
- Z. Wang, X. Guo, J. Montoya and J. K. Nørskov, Predicting Aqueous Stability of Solid with Computed Pourbaix Diagram Using SCAN Functional, npj Comput. Mater., 2020, 6(1), 160, DOI:10.1038/s41524-020-00430-3.
- K. S. Exner, J. Anton, T. Jacob and H. Over, Chlorine Evolution Reaction on RuO2(110): Ab Initio Atomistic Thermodynamics Study - Pourbaix Diagrams, Electrochim. Acta, 2014, 120, 460–466, DOI:10.1016/j.electacta.2013.11.027.
- T. Fuchs, J. Drnec, F. Calle-Vallejo, N. Stubb, D. J. S. Sandbeck, M. Ruge, S. Cherevko, D. A. Harrington and O. M. Magnussen, Structure Dependency of the Atomic-Scale Mechanisms of Platinum Electro-Oxidation and Dissolution, Nat. Catal., 2020, 3(9), 754–761, DOI:10.1038/s41929-020-0497-y.
- O. Vinogradova, D. Krishnamurthy, V. Pande and V. Viswanathan, Quantifying Confidence in DFT-Predicted Surface Pourbaix Diagrams of Transition-Metal Electrode–Electrolyte Interfaces, Langmuir, 2018, 34(41), 12259–12269, DOI:10.1021/acs.langmuir.8b02219.
- S. Cherevko, S. Geiger, O. Kasian, N. Kulyk, J.-P. Grote, A. Savan, B. R. Shrestha, S. Merzlikin, B. Breitbach, A. Ludwig and K. J. J. Mayrhofer, Oxygen and Hydrogen Evolution Reactions on Ru, RuO2, Ir, and IrO2 Thin Film Electrodes in Acidic and Alkaline Electrolytes: A Comparative Study on Activity and Stability, Catal. Today, 2016, 262, 170–180, DOI:10.1016/j.cattod.2015.08.014.
- C. Roy, R. R. Rao, K. A. Stoerzinger, J. Hwang, J. Rossmeisl, I. Chorkendorff, Y. Shao-Horn and I. E. L. Stephens, Trends in Activity and Dissolution on RuO2 under Oxygen Evolution Conditions: Particles versus Well-Defined Extended Surfaces, ACS Energy Lett., 2018, 3(9), 2045–2051, DOI:10.1021/acsenergylett.8b01178.
- H. Tamura and C. Iwakura, Metal Oxide Anodes for Oxygen Evolution, Int. J. Hydrogen Energy, 1982, 7(11), 857–865, DOI:10.1016/0360-3199(82)90003-9.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta09213a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |