DOI:
10.1039/D4TA08940E
(Communication)
J. Mater. Chem. A, 2025,
13, 11293-11299
Tuning ferrite nanoparticles for optimal inductive heating in thermal swing adsorption processes†
Received
17th December 2024
, Accepted 24th March 2025
First published on 24th March 2025
Abstract
By enabling faster regeneration of adsorbents and minimizing heat losses, inductive heating is key to improving the efficiency, capacity and carbon neutrality of temperature swing adsorption systems. For successful implementation of inductive heating, access to performant and chemically robust susceptor materials is essential. Combining performance with chemical stability is however challenging and current magnetic susceptors typically only achieve one of these requirements. This report presents a strategy for the complete optimization of ferrite nanoparticles, yielding susceptors with superior inductive heating performance and excellent chemical robustness. Superparamagnetic nickel–zinc ferrite nanoparticles with optimized heating performance within the boundary conditions imposed by inductive heating swing adsorption applications are synthesised and their heating performance was experimentally evaluated and rationalised. Chemical composition as well as the calcination temperature at which ferrite precursors are converted into the susceptor materials are demonstrated to be critical for maximizing the heat response. Tuning chemical composition and calcination temperature enabled enhancement of the specific absorption rate of a Ni(1−x)ZnxFe2O4 ferrite system by one order of magnitude. Ni0.6Zn0.4Fe2O4 nanoparticles (Ø 78 nm) synthesized at 900 °C generate an outstanding specific absorption rate of 113.7 W g−1 excited by a 135.7 Oe magnetic field alternating at 248 kHz. The optimization route is discussed and rationalized based on the identified induction heating mechanism.
Broader context
Heating is the most employed method for separation and purification of chemicals, accounting for 40% of the industrial energy consumption. Over 90% of this heat is generated from combustion of fossil fuels. Heating therefore stands out as one of the most CO2-intensive industrial unit operations. Induction heating can be an efficient solution to electrify industrial heating processes, offering a clean alternative to traditional heating methods. Within the range of separation processes employed in industry, temperature swing adsorption (TSA) is particularly CO2-intensive. Replacing classic TSA by inductive heating swing adsorption (IHSA) requires magnetic susceptors that are both energetically efficient and chemically stable in the harsh redox conditions that TSA systems are exposed to. Combining these two characteristics has proven to be very challenging. The most efficient susceptors currently available in literature are not chemically suitable for IHSA. This work shows how to generate magnetic susceptors that are chemically stable and exhibit one of the highest heating efficiencies among all materials reported. The presented Ni0.6Zn0.4Fe2O4 superparamagnetic ferrite nanoparticles generate 113.7 W of heat per gram of susceptor under realistic industrial conditions. This offers significant potential to electrify IHSA processes.
|
Introduction
Separation processes are of critical importance to industry and consume around 15% of the global energy use.1 Nearly the entirety of this energy is generated through the combustion of fossil fuels.2 Separation processes are consequently highly CO2-intensive. Replacing fossil energy with renewable electricity and combining that strategy with electrification presents a major opportunity towards achieving carbon neutrality.3 The urgency of this approach is reinforced by various pieces of binding legislation, such as the Paris Agreement (2015), the European Green Deal (2019), and the UK's Climate Change Act (2008).4–6 Temperature swing adsorption (TSA) is widely used in industry as a gas separation, purification and drying process. In TSA systems, heating is intensively applied to regenerate the adsorption bed, leading to the release of the gases and solvents adsorbed to it. In TSA applications, inductive heating has emerged as an alternative to classical approaches such as the regeneration of adsorption columns using hot gas streams or by incorporating steam-powered heating elements. Thus, IHSA is essentially a subclass of TSA processes in which the heat is supplied via induction. Besides CO2 abatement, inductive heating also provides significant benefits for process optimization, as adsorbents can be regenerated faster, with less power consumption and without diluting the adsorbed product.7,8 Additionally, inductive heating swing adsorption (IHSA) also boasts superior process safety as the heat is generated homogeneously inside the pellets (ESI-7†).9
Inductive heating is achieved by applying an alternating magnetic field to a ferro- or ferrimagnetic susceptor material. To enable its use in an IHSA setup (as depicted in Fig. 1A), susceptor (nano-)particles could be incorporated into an adsorbent material or pellets of that material.10 In an industrial context, not only the efficiency of heat generation achieved by the magnetic susceptors should be maximised, but also their chemical stability in the harsh redox environment typically encountered in TSA processes must be ensured. However, achieving a balance between performance and chemical stability is challenging, and most magnetic susceptors can only fulfil one of these requirements at a time. As an example, magnetite nanoparticles (Fe3O4) can produce an astonishing amount of 1 kW of heat per gram of susceptor in a 302 Oe magnetic field alternating at 300 kHz.11 However, these are inherently unfit for IHSA systems due to their oxidation-prone nature. Oxidation of magnetite produces hematite, which has a much lower inductive heating efficiency.12
 |
| | Fig. 1 (A) Schematic of IHSA setup operating a CO2/N2 separation process, (B) structure of a spinel ferrite unit cell, and (C) magnetisation curves displaying major and minor hysteresis loops. | |
Ferrites with redox-insensitive divalent cations exhibit very high chemical stability in the harsh conditions often encountered in industrial desorption/adsorption processes and are especially attractive for IHSA applications (ESI-6†).13,14 Ferrites are materials with the chemical formula MIIFe2O4, with MII being a divalent metal cation. They exhibit a spinel crystal structure with one tetrahedral (A-site) and two octahedral (B-site) metal sites, as illustrated in Fig. 1B. The interaction between the magnetic moments of the metals in these distinct sites imparts them ferrimagnetic properties, which can be used to locally generate heat in an IHSA process via induction heating.15 Previous work has shown that ferrites can only efficiently generate heat if their coercivity is tuned to the magnitude of the field generated by the induction coil. Substituting Co(II) with Ni(II) in CoFe2O4 ferrite allowed to decrease the coercivity of the material to a range in which very high specific absorption rates could be reached. Using a magnetic field of 257 Oe alternating at 248 Hz, CoFe2O4 ferrites (HC = 491 Oe) only delivered 8.2 W g−1, while NiFe2O4 ferrite nanoparticles (HC = 29.2 Oe) could deliver 43.8 W g−1.16,17 These values correspond to an intrinsic loss power (ILP) of, respectively, 0.08 mW g−1 kHz−1 kA−2 m−3 and 0.4 mW g−1 kHz−1 kA−2 m−3.
This report devises and experimentally demonstrates a theory-based strategy to generate redox-stable ferrite susceptors with superior inductive heating efficiency. Meticulous optimisation of the magnetic and morphological properties of ferrites is shown to enable a 6-fold increase in the heat generation efficiency achieved by ferrites, outperforming state-of-the-art induction heating systems based on other non-oxidizable susceptors. By tuning the chemical composition and synthesis parameters of the ferrites, the saturation magnetization, the coercivity and the magnetic domain size of a Ni(1−x)ZnxFe2O4 ferrite system were optimized to maximize heat generation. Partial substitution of Ni(II) with Zn(II) enables the increase of the saturation magnetization of the particles by reducing the antiparallel magnetic contribution of the sublattice formed by the tetrahedral sites in the ferrite structure. Combining this effect with optimal calcination to increase the magnetic domain size and slow down the magnetic relaxation in the systems, Ni0.6Zn0.4Fe2O4 nanoparticles (Ø 78 nm) with an outstanding specific absorption rate of 113.7 W g−1 were produced. This value corresponds to an intrinsic loss power of 3.9 mW g−1 kHz−1 kA−2 m−3, surpassing that of Mg-based ferrites.18–20
Results and discussion
When an alternating magnetic field (H) is applied to ferro- or ferrimagnetic particles, their magnetization (M) executes a hysteresis loop, as shown in the schematic magnetization curve displayed in Fig. 1C.21 Incorporating the particles in adsorbent pellets, this hysteresis can be exploited to provide heat to IHSA processes. The amount of heat generated in one field cycle (W) is directly correlated with the area within the hysteresis loop:22whereas the power (P) delivered depends also on the field cycling frequency (f):
Defined by eqn (1) and (2), the effectiveness of inductive heat generation strongly depends on the magnetic and morphological properties of the susceptor material, such as the coercivity (HC), saturation magnetization (MS), magnetic anisotropy (K), particle size and the size of magnetic domains in the susceptor particles. For a set field alternating at a specific frequency, the impact of these parameters on heat generation largely depends on the inductive heating mechanism which is exploited. In suspensions of nanosized susceptor particles, rotational Brownian motion is an important mechanism. In solid-state applications, hysteresis heating and Néel relaxation are the most relevant mechanisms, each manifesting in a different magnetic regime.23,24 Néel relaxation dominates in the superparamagnetic regime, whereas hysteresis heating becomes increasingly significant for susceptors with higher coercivity.
For Néel and Brownian relaxations of non-interacting single-domain magnetic nanoparticles, eqn (1) and (2) can be further reworked to explicitly show the dependence of P on the Néel (τN) and Brownian (τB) relaxation times:25
| |  | (3) |
With the effective relaxation time
τ defined as 1/
τ = 1/
τN + 1/
τB.
μ0,
ρ,
H0,
V,
kB,
T and
τ denote, respectively, the vacuum magnetic permeability, the mass density of the susceptor, the magnitude of the applied magnetic field, the volume of the magnetic particles, the Boltzmann constant and the temperature. The dependence of
τN and
τB on the magnetic and morphological parameters of the particles can be written as:
| |  | (4) |
| | 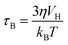 | (5) |
in which
η,
VH, and
τ0 are, respectively, the viscosity of the liquid the particles are immersed in, their hydrodynamic volume and the magnetic response time of a single-domain particle, known as the attempt time.
For hysteresis heating, the power delivered by susceptor particles of normalized differential susceptibility α = MS−1χH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) HC is given by:16,17
HC is given by:16,17
| |  | (6) |
Strategy for maximizing the inductive heating performance of magnetic susceptors
Eqn (3)–(6) set the overall landscape from which a strategy for complete optimisation of the heating performance of magnetic susceptors can be devised. This strategy is illustrated in Fig. 2. From eqn (3) and (6), it is clear that, regardless of the heating mechanism, the power generated per gram of susceptor, known as the specific absorption rate (SAR), can be increased by maximizing the saturation magnetization (MS) of the susceptors in a first optimization step. After maximizing MS, further rational optimization depends on the identification of the heating mechanism. While, regardless of the mechanism, the generation of induction heat crucially depends on the hysteretic behaviour of the magnetization, the origin of this behaviour depends on the type of mechanism being exploited. In Néel and Brownian relaxation, the hysteretic behaviour comes from the lagging response of M relative to changes in H. Therefore, heat is efficiently generated only when the relaxation times τN and τB are of the same order of magnitude as the timescale f−1 of the changes in the applied alternating magnetic field. For a fixed IHSA setup working with a defined frequency, optimizing SAR translates to optimizing the magnetic domain size for Néel relaxation (eqn (4)) and the particle size for Brownian relaxation (eqn (5)), accounting also for possible particle agglomeration. In hysteresis heating, the hysteretic behaviour responsible for the heating is the intrinsic DC hysteretic behaviour of ferri- or ferromagnetic susceptors. While the magnetic field alternates, the magnetization describes a (minor) hysteresis loop (see Fig. 1C) whose area is given by eqn (6). For a set IHSA system, optimization of SAR is achieved by finding the optimal fit between HC, α and the magnitude H0 of the alternating magnetic field.16,17
 |
| | Fig. 2 Optimization of the heating efficiency of ferrite materials can be achieved through (step 1) the maximization of their saturation magnetization (MS), (step 2) the determination of the involved heating mechanism and (step 3) a mechanism-dependent optimization of their morphological and magnetic properties. | |
Experimental optimization of Zn-substituted Ni ferrite for inductive heating
Increasing the saturation magnetization of ferrite nanoparticles implies modification of their chemical composition. Crystallite size can be influenced by calcination, while particle size of nanoparticles for Brownian heating can be influenced by modification of the synthesis conditions or by addition of stabilizing molecules.26,27
Optimizing the chemical composition of ferrites
Ferrites can host different divalent cations in their spinel structure. By meticulously adding redox-insensitive metal cations to their composition, the saturation magnetization of ferrites can be maximized while still keeping their chemical stability in redox environments. To demonstrate this strategy, a series of zinc-substituted ferrites (Ni1−xZnxFe2O4, x = 0–0.7, see Table 1) with similar size was synthesised and their heating efficiency was compared. To synthesise the nanoparticles, stoichiometric amounts of precursor salts of Ni2+, Zn2+ and Fe3+ were added dropwise to a pH-controlled alkaline solution to obtain a hydroxide precursor that was calcined at 600 °C for 6 hours under air.28,29 More details on the synthesis can be found in the ESI.† The magnetization curves and the magnetic parameters of the samples are shown in Fig. S3† and 3A, respectively. Going from NiFe2O4 to Ni0.6Zn0.4Fe2O4, the magnetization saturation increases from 32.1 to 72.7 emu g−1. As Zn(II) exhibits a higher preference to occupy the tetrahedral sites (A-sites) as compared to Fe, its introduction induces a higher Fe(III) occupancy in the octahedral sites (B-sites) as compared to Zn(II)-free ferrites.30 This induces a higher magnetization in the B magnetic sublattice. At the same time, due to its fully occupied 3d10 orbitals, Zn(II) lacks a magnetic moment, reducing the magnetization of the A magnetic sublattice. The result is a higher saturation magnetization for Zn(II)-containing ferrites until x = 0.4, as a consequence of the increased vector sum of the moments of the A- and B-sublattices. The changes in the magnetization of the sublattices also induce a decrease in the antiferromagnetic interaction between A and B sites and an increase in the interaction between B sites. This causes the spins in the B sites to cant as illustrated in the inset of Fig. 3A, an effect known as Yafet Kittel rearrangement.31,32 As a result, the saturation magnetization of ferrites decreases when the Zn fraction is increased beyond x = 0.4, reaching 42.9 emu g−1 in Ni0.3Zn0.7Fe2O4.33–35
Table 1 The saturation magnetization (MS), coercivity (HC), and particle size as a function of sample composition
| Sample composition |
M
S (emu g−1) |
H
C (Oe) |
Particle size (nm) |
| NiFe2O4 |
32.1 |
4.5 |
16.7 |
| Ni0.9Zn0.1Fe2O4 |
49.8 |
21 |
17.1 |
| Ni0.8Zn0.2Fe2O4 |
61.5 |
22 |
17.6 |
| Ni0.7Zn0.3Fe2O4 |
67.1 |
35 |
17.6 |
| Ni0.6Zn0.4Fe2O4 |
72.7 |
7 |
22.1 |
| Ni0.5Zn0.5Fe2O4 |
70.1 |
17 |
17.6 |
| Ni0.4Zn0.6Fe2O4 |
61.1 |
0.9 |
16.6 |
| Ni0.3Zn0.7Fe2O4 |
42.9 |
0 |
16.7 |
 |
| | Fig. 3 Evolution of the magnetic properties and hysteresis heat generated by Ni1−xZnxFe2O4 ferrites with varying Zn(II) substitution grades (x). (A) Saturation magnetization. The inset illustrates the Yafet–Kittel rearrangement leading to an increase in the canting angle αYK and a reduction in MS and in the SAR when x > 0.4. (B) SAR generated by the ferrites and their coercivity. | |
To evaluate the effectiveness of induction heating generation in the synthesized materials, the specific absorption rate (SAR) generated by the ferrite nanoparticles was measured in a magnetic field of 135.7 Oe alternating at 248 kHz. An aqueous suspension of ferrite nanoparticles was used in the measurements. The maximum SAR value was obtained when the saturation magnetization of the particles peaked, and 60.6 W g−1 is delivered by Ni0.6Zn0.4Fe2O4 ferrites. This represents a 4-fold increase in comparison with the 17 W g−1 generated by the Zn-free NiFe2O4 nanoparticles. Given the superparamagnetic behaviour of the particles as shown by their very low coercivity values, Brownian or Néel relaxation can be assigned as the heating mechanisms governing induction heat generation in these particles. With a 2-fold increase in MS, the 4-fold increase in SAR is explained by the quadratic dependence of SAR on the saturation magnetization, as described by eqn (3).
To evaluate the contribution of Brownian relaxation in the heat generation of the investigated systems, the SAR generated by the ferrites was measured in poly(ethylene glycol). As described by eqn (3) and (5), Brownian relaxation should be severely diminished upon a drastic increase in the viscosity (η) of the suspension medium. As seen from the SAR values in Table S1,† a maximum decrease of 20% in SAR has been observed for the particles in PEG (ηPEG = 105 ηH2O) as compared to water. This indicates that Néel relaxation is the dominant heat generation mechanism in all analysed systems.
While the overall increase in SAR can be explained by the smooth increase in the saturation magnetization of the ferrites when Zn(II) is introduced in their structure, the oscillations in the SAR curve, following the oscillations in the coercivity (see Fig. 3B), further indicate Néel relaxation as the major mechanism driving heat generation in these systems. In this mechanism, the magnetic relaxation time (eqn (4)) is directly dependent on the energy barrier (KV) to be overcome during reorientations of the magnetic domains in the particles. This energy barrier also influences the coercivity of the susceptor and an increase in coercivity indicates an increase in the magnetic anisotropy of the particles. This, in turn, causes an increase in the Néel relaxation time, which affects the SAR. The anti-correlation between the oscillations in SAR and HC (Fig. 3B) shows that a more efficient generation of heat in these systems is achieved by slowing down the magnetic reorientations of the magnetic domains in the particles. Further optimization could then be achieved by increasing the domain size, as hinted by eqn (4).
Tuning the domain size
After determining the chemical composition that optimizes the generation of heat by hysteresis losses, the size of the magnetic domains in the susceptor particles was optimized by changing the calcination temperature used to obtain the ferrite phase from the precursor hydroxides. The calcination temperature was varied between 400 and 1100 °C in the synthesis of Ni0.6Zn0.4Fe2O4 ferrites while keeping all other variables identical. Calcination induces particle growth and an increase in crystallinity (Table 2), as evidenced by the TEM micrographs in Fig. 4 and the PXRD patterns in Fig. S2.† Aside from particle growth, also the crystallite size inside the particles increases.
Table 2 Magnetic and morphological parameters of the Ni0.6Zn0.4Fe2O4 nanoparticles. The particle size was determined with TEM. The crystallite size was determined with synchrotron-based PXRD
| Calcination temperature (°C) |
M
S (emu g−1) |
H
C (Oe) |
Particle size (nm) |
Crystallite size (nm) |
| 400 |
58.2 |
0 |
11.7 |
13.9 |
| 500 |
64.6 |
2.4 |
15.8 |
16.4 |
| 600 |
72.7 |
7.2 |
16.4 |
17.3 |
| 700 |
78.4 |
59.4 |
29.2 |
27.3 |
| 800 |
84.8 |
85.7 |
48.2 |
47.6 |
| 900A |
87.8 |
49.7 |
— |
78.3 |
| 1100A |
3.0 |
0 |
— |
110.6 |
 |
| | Fig. 4 TEM micrographs representative of the morphology of the Ni0.6Zn0.4Fe2O4 particles obtained after calcination at (A) 500 °C, (B) 600 °C, (C) 700 °C, (D) 800 °C, (E) 900 °C and (F) 1100 °C. | |
The increase in particle and crystallite size also has implications for the magnetic properties of the particles. With a decrease in the surface/volume ratio of the susceptor particles, the saturation magnetization increases, an effect linked to the decreased fraction of surface spins with low long-range magnetic correlation with the neighbouring magnetic moments. This trend is most pronounced for small to medium-sized nanoparticles (<50 nm), after which the increase in MS levels off to the value of the bulk material.26,27,36,37 At a calcination temperature of 900 °C, the highest MS of 87.7 emu g−1 is achieved. While this value represents a 25% increase compared to the saturation magnetization of Ni0.6Zn0.4Fe2O4 obtained at 600 °C, it cannot account for the further 2-fold increase in SAR obtained by increasing the calcination temperature from 600 to 900 °C (Fig. 5). This result is rather an effect of the growth of the magnetic domains in the susceptor particles, which increases the energy barrier for magnetic reorientations of the magnetic domains, slowing them down as described by eqn (4). Upon a further increase in the calcination temperature over 900 °C, a decrease in SAR is observed, which is interpreted as originating from an over-increase in the size of the magnetic domains that freezes the magnetization of the susceptor. In fact, increasing the calcination temperature to 1100 °C results in a crystallite size of 110 nm, a 2-fold increase compared to the crystallite size of ferrites produced at 900 °C. This leads to a drastic increase in the magnetic domain volume, which then exponentially increases the Néel relaxation time governing the ability of the susceptor to reorient upon the application of the magnetic field.
 |
| | Fig. 5 (A) Magnetic properties and (B) SAR generated by the Ni0.6Zn0.4Fe2O4 ferrites nanoparticles obtained by calcination of the hydroxide precursor at different temperatures. | |
Performance assessment
Induction heating applications employing superparamagnetic nanoparticles mostly rely on Néel and/or Brownian relaxation of their magnetic moments. In these mechanisms, SAR quadratically scales with the magnetic field strength H02, as shown in eqn (3). Near the optimal operational conditions of the nanoparticles, SAR also scales linearly with the frequency of the applied alternating field. To enable comparison between SAR measurements carried out under different operational conditions, the intrinsic loss power (ILP = SAR H0−2f−1) is considered. To assess the heating performance of the here reported, optimized Ni0.6Zn0.4Fe2O4 ferrite nanoparticles against other magnetic materials, a compilation of susceptors reported elsewhere is provided in Table S3.†Fig. 6 shows the reported ILP as a function of the magnitude and frequency of the applied magnetic field. The highest ILP is obtained for magnetite (5.85 mW g−1 kHz−1 kA−2 m−3). However, under the redox conditions usually found in TSA applications, magnetite reduces to hematite, which has a low ILP of 0.53 mW g−1 kHz−1 kA−2 m−3. This compromises the use of magnetite in IHSA systems. The here reported nikel–zinc ferrites contain no oxidizable cations, ensuring long-term chemical stability under redox conditions. Among the non-oxidizable susceptors reported in the literature, the presented Ni0.6Zn0.4Fe2O4 material features the highest ILP. When calcined at 900 °C, these nanoparticles (Ø 78 nm) generate 114 W of heat per gram of susceptor in mild frequency and field conditions. This represents an ILP of 3.92 mW g−1 kHz−1 kA−2 m−3. Using non-oxidizable materials, comparably high ILP values have only been reported for MnFe2O4 (3.82 mW g−1 kHz−1 kA−2 m−3), CoFe2O4@MnFe2O4 core/shell particles (3.59 mW g−1 kHz−1 kA−2 m−3), and Mn0.5Zn0.5Fe2O4 (3.84 mW g−1 kHz−1 kA−2 m−3) operating, respectively, at 1.95 MHz, 500 and 178 kHz.18,20,38
 |
| | Fig. 6 Performance comparison (intrinsic loss power [mW g−1 kHz−1 kA−2 m−3]) between magnetic susceptors reported in the literature, including oxidizable (red) and non-oxidizable (green) materials. The here reported Ni0.6Zn0.4Fe2O4 ferrite nanoparticles (Ø 78 nm) calcined at 900 °C is depicted as a star (★). ILP values as a function of field strength and frequency. Please refer to Table S3† for the list of materials included in the comparison. | |
Conclusions
This study illustrates the potential for improving the inductive heating performance of ferrite susceptor particles and outlines a general strategy for achieving maximal performance within a set of boundary conditions. On the example of Zn(II) substituted Ni-ferrite, the report demonstrates how tuning the ferrite composition, assessing the heating mechanism and in function of the latter, optimising their morphological and magnetic properties leads to maximal performance at the frequency and magnitude of the induction field determined by an application. The full optimization allowed to increase the specific absorption rate of Ni(1−x)ZnxFe2O4 by almost one order of magnitude, shifting the performance from 20 W g−1 for pure NiFe2O4 to 114 W g−1 for a fully optimized Ni0.6Zn0.4Fe2O4.
Data availability
The data included in the figures are available free of charge in the KU Leuven institutional repository at: https://doi.org/10.7910/DVN/CIGRCD.
Author contributions
M. D. B. performed the synthesis of the materials, carried out the characterization of their heating efficiency, performed the TEM measurements and contributed to data analysis and writing of the manuscript. A. F. M. and E. B. carried out data analysis, interpretation and writing of the manuscript. J. H. carried out synthesis of materials with the guidance of M. D. B. R. J., S. B. and M. J. V. B. provided and carried out the SQUID measurements and supported the analysis of the magnetic properties of the materials. D. C. and V. D. provided and carried out the data acquisition and analysis of synchrotron-based XRD. J. D., J. A. M. and E. B. conceived, supervised and funded the project. All authors contributed to this work with discussions and with the writing of the final text.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
J. A. M. acknowledges the Flemish Government for long-term structural funding (Methusalem). S. B., R. J. and M. J. V. B. acknowledge funding by the FWO under the Excellence of Science program (grant No. G0J4922N), the Belgian interuniversity iBOF-project from KU Leuven (grant No. IBOF/23/065), and from the KU Leuven C1 program (grant No. C14/18/074). M. D. B., J. F. M. D., J. A. M., and E. B., acknowledge VLAIO for the financial support (HBC.2019.0109 & HBC.2021.0255). A. F. M. acknowledges support from the European Union's Horizon Europe programme through a Marie Skłodowska-Curie postdoctoral fellowship (No. 101063656, H2E). NMRCoRe acknowledges the Flemish government for financial support as an International Research Infrastructure (I001321N: Nuclear Magnetic Resonance Spectroscopy Platform for Molecular Water Research). This research was supported by the FWO infrastructure projects (AKUL13/19 and I000920N).
Notes and references
- D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435–437 CrossRef PubMed.
-
C. Philibert, Renewable Energy for Industry, International Energy Agency (IEA), Paris, 2017 Search PubMed.
- I. Azevedo, C. Bataille, J. Bistline, L. Clarke and S. Davis, Energy Clim. Change, 2021, 2, 100049 CrossRef CAS.
-
United Nations, The paris agreement, 2016.
-
European Commission, The european green deal, 2019.
-
United Kingdom of Great Britain and Northern Ireland, Climate Change Act 2008, 2008.
- M. Gholami, B. Verougstraete, R. Vanoudenhoven, G. V. Baron, T. Van Assche and J. F. M. Denayer, Chem. Eng. J., 2022, 431, 133380 CrossRef CAS.
- M. Schoukens, M. Gholami, G. V. Baron, T. Van Assche and J. F. M. Denayer, Chem. Eng. J., 2023, 459, 141587 CrossRef CAS.
- R. Grewal and M. Kumar, Mater. Today: Proc., 2022, 56, 2696–2703 Search PubMed.
- M. M. Sadiq, H. Li, A. J. Hill, P. Falcaro, M. R. Hill and K. Suzuki, Chem. Mater., 2016, 28, 6219–6226 Search PubMed.
- H. Gavilán, G. M. R. Rizzo, N. Silvestri, B. T. Mai and T. Pellegrino, Nat. Protoc., 2023, 18(3), 783–809 CrossRef PubMed.
- K. Newport, K. Baamran, A. A. Rownaghi and F. Rezaei, Ind. Eng. Chem. Res., 2022, 61, 18843–18853 Search PubMed.
- P. R. Kumar and S. Mitra, RSC Adv., 2013, 3, 25058–25064 RSC.
- S. Balgude, K. Patil, S. Moharil, M. Puranik, S. Kadam, P. Lokhande, S. Patange and P. More, ChemistrySelect, 2022, 7, e202200221 CrossRef CAS.
- S. B. Narang and K. Pubby, J. Magn. Magn. Mater., 2021, 519, 167163 CrossRef CAS.
- M. De Belder, A. F. Morais, N. De Vos, L. Van Meervelt, J. F. M. Denayer, J. A. Martens and E. Breynaert, Mater. Horiz., 2024, 11, 4144–4149 RSC.
- M. De Belder, A. F. Morais, N. De Vos, S. Basov, R. Joris, M. J. Van Bael, L. Van Meervelt, J. F. M. Denayer, J. A. Martens and E. Breynaert, Mater. Horiz., 2024, 11, 4828 RSC.
- A. Doaga, A. M. Cojocariu, W. Amin, F. Heib, P. Bender, R. Hempelmann and O. F. Caltun, Mater. Chem. Phys., 2013, 143, 305–310 Search PubMed.
- P. T. Phong, P. H. Nam, D. H. Manh and I. J. Lee, J. Magn. Magn. Mater., 2017, 433, 76–83 Search PubMed.
- J. H. Lee, J. T. Jang, J. S. Choi, S. H. Moon, S. H. Noh, J. W. Kim, J. G. Kim, I. S. Kim, K. I. Park and J. Cheon, Nat. Nanotechnol., 2011, 6(7), 418–422 CrossRef CAS PubMed.
- V. M. Khot, A. B. Salunkhe, N. D. Thorat, R. S. Ningthoujam and S. H. Pawar, Dalton Trans., 2012, 42, 1249–1258 Search PubMed.
- V. M. Khot, A. B. Salunkhe, N. D. Thorat, M. R. Phadatare and S. H. Pawar, J. Magn. Magn. Mater., 2013, 332, 48–51 CAS.
- A. E. Deatsch and E. E. Evans, J. Magn. Magn. Mater., 2014, 354, 163–172 CAS.
- S. Ota and Y. Takemura, J. Phys. Chem. C, 2019, 123, 28859–28866 CrossRef CAS.
- A. A. de Almeida, F. Fabris, G. S. da Silva, K. R. Pirota, M. Knobel and D. Muraca, ACS Appl. Mater. Interfaces, 2025, 17, 13083–13093 Search PubMed.
- L. Kumar and M. Kar, IEEE Trans. Magn., 2011, 47, 3645–3648 CAS.
- S. J. Olusegun, E. T. F. Freitas, L. R. S. Lara, H. O. Stumpf and N. D. S. Mohallem, Ceram. Int., 2019, 45, 8734–8743 CrossRef CAS.
- A. F. Morais, D. Nanclares, I. G. N. Silva, A. Duarte, F. A. Garcia, E. Breynaert and D. Mustafa, Nanoscale, 2021, 13, 11781–11792 RSC.
- A. F. Morais, I. G. N. Silva, B. J. Ferreira, A. C. Teixeira, S. P. Sree, H. Terraschke, F. A. Garcia, E. Breynaert and D. Mustafa, Chem. Commun., 2023, 59, 13571–13574 RSC.
- C. Venkataraju, G. Sathishkumar and K. Sivakumar, J. Magn. Magn. Mater., 2011, 323, 1817–1822 CAS.
- Y. Yafet and C. Kittel, Phys. Rev., 1952, 87, 290 CAS.
- N. S. S. Murthy, M. G. Natera, S. I. Youssef, R. J. Begum and C. M. Srivastava, Phys. Rev., 1969, 181, 969 CAS.
- S. F. Mansour, M. A. Abdo and F. L. Kzar, J. Magn. Magn. Mater., 2018, 465, 176–185 CAS.
- R. Topkaya, A. Baykal and A. Demir, J. Nanopart. Res., 2013, 15, 1–18 Search PubMed.
- R. Sharma, P. Thakur, M. Kumar, P. B. Barman, P. Sharma and V. Sharma, Ceram. Int., 2017, 43, 13661–13669 CAS.
- T. Kim and M. Shima, J. Appl. Phys., 2007, 101, 9–516 Search PubMed.
- T. Fan, D. Pan and H. Zhang, Ind. Eng. Chem. Res., 2011, 50, 9009–9018 CrossRef CAS.
- E. Mazarío, J. Sánchez-Marcos, N. Menéndez, M. Cañete, A. Mayoral, S. Rivera-Fernández, J. M. De La Fuente and P. Herrasti, J. Phys. Chem. C, 2015, 119, 6828–6834 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Alysson F.
Morais‡
ab,
Alysson F.
Morais‡
 ae,
Julie
Heyens
a,
Rikkie
Joris
c,
Sergey
Basov
ae,
Julie
Heyens
a,
Rikkie
Joris
c,
Sergey
Basov
 c,
Margriet J.
Van Bael
c,
Dmitry
Chernyshov
c,
Margriet J.
Van Bael
c,
Dmitry
Chernyshov
 d,
Vadim
Diadkin
d,
Joeri F. M.
Denayer
d,
Vadim
Diadkin
d,
Joeri F. M.
Denayer
 b,
Johan A.
Martens
b,
Johan A.
Martens
 ae and
Eric
Breynaert
ae and
Eric
Breynaert
 *ae
*ae



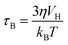
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) HC is given by:16,17
HC is given by:16,17





