Specific Cu₂O surfaces for electrocatalytic oxygen reduction reaction

Abstract

Examination of the facet effects of metal oxide crystals on the oxygen reduction reaction (ORR) has been inadequately investigated due to the limited availability of polyhedra that expose only specific surfaces. Here, cuprous oxide cubes, octahedra, and rhombic dodecahedra, exposing the respective {100}, {111}, and {110} surfaces, were incorporated into a matrix of carbon nanotubes (CNTs) to enhance electrical conductivity. The composites were evaluated for their electrocatalytic ORR activity. The rhombic dodecahedra/CNTs composite exhibited the highest ORR activity, followed by the octahedra/CNTs and then the cubes/CNTs. Commercial Cu₂O powder/CNTs showed notably lower ORR activity, demonstrating the importance of catalyst surface control for ORR performance. Koutecký–Levich plots showed that these Cu₂O polyhedra were highly selective towards the four-electron pathway in the ORR, whereas the commercial Cu₂O powder/CNTs catalyst proceeded via the two-electron pathway. Durability tests revealed a reversed trend, with the cubes/CNTs being the most stable electrocatalyst. Density functional theory (DFT) calculations indicated the weakest O₂ adsorption on the Cu₂O {110} surface. The free energy diagrams and 2D volcano plot further established the {110} surface as the most active towards ORR, while strong OH intermediate binding on the {100} and {111} surfaces led to lower theoretical limiting potentials and higher overpotentials. DFT results provided mechanistic insights to explain the experimental facet effects.

---

Introduction

Semiconductor crystals broadly exhibit facet-dependent electrical conductivity, photocatalytic activity, and optical behaviors.^1–10 For example, the {111} faces of a cuprous oxide crystal are highly electrically conductive, while its {100} faces are far less conductive.^1,2 The {110} faces of Cu₂O are actually insulating. The emergence of these facet effects is attributed to the presence of a surface layer with face-specific lattice variations, in addition to possible lattice constant changes in the crystal bulk, as revealed by synchrotron X-ray diffraction (XRD) patterns showing both bulk and surface layer lattice components, as well as lattice point images derived from high-resolution transmission electron microscopy (HR-TEM) images of Cu₂O, Ag₂O, MnS, and PbZrTiO₃ crystals.^11–14 The surface lattice variations are expected to affect charge transport across different surfaces, leading to significant changes in the conductivity and photocatalytic activity of the crystals. This lattice feature is also expected to influence electrochemical reactions, such as the oxygen reduction reaction, since oxygen molecules receive electrons through the catalyst particle. The oxygen reduction reaction plays a key role in fuel cells.

Considering the high cost of platinum-based electrocatalysts with superior ORR performance, transition metal oxide electrocatalysts have been explored as cost-effective and highly active alternatives.^15,16 To improve the electrical conductivity of transition metal oxide electrocatalysts, decoration or dispersion with metal nanoparticles, carbon-based materials, and conducting polymers is effective in enhancing interparticle conductivity and catalytic activity.^17–19 With regard to ORR activity, the exposed crystal faces should be a significant factor, especially considering the existence of face-related lattice variations in semiconductor crystals. Previously, Co₃O₄ spheres, octahedra, and truncated octahedra on reduced graphene oxide sheets were evaluated for ORR activity, with the octahedra showing the highest activity.²⁰ Carbon-dispersed Cu₂O nanocubes, truncated cubes, and nanoporous particles were also compared for ORR performance.²¹ However, it was not demonstrated that the polymers added to synthesize the Cu₂O crystals were completely removed. These Cu₂O particle morphologies, prepared by electrochemical deposition, were also examined for their ORR activities. However, the obtained polarization curves did not exhibit limiting currents.²² Au particle-decorated Cu₂O spheres, cubes, and multipods dispersed onto a carbon nanotube matrix were also employed for the oxygen reduction reaction.²³ However, a comprehensive understanding of the facet effects on the ORR activity of Cu₂O crystals is still lacking.

In this work, Cu₂O cubes, octahedra, and rhombic dodecahedra, exposing the {100}, {111}, and {110} faces, respectively, were mixed with a carbon nanotube matrix to form active electrocatalysts for the oxygen reduction reaction. Their ORR linear sweep voltammetry (LSV) polarization curves, after normalization for active surface area, were compared. The number of transferred electrons was determined for each sample. Chronoamperometric curves were obtained. Moreover, DFT calculations of oxygen adsorption energy on the three Cu₂O surfaces and the free energy changes associated with intermediate formation were performed to support the experimental results. An ORR activity map was also constructed.

Results and discussion

The reaction details and conditions for the syntheses of the Cu₂O cubes, octahedra and rhombic dodecahedra are available in the ESI.† Fig. S1 (ESI)† shows the product solution colors, and Table S1 (ESI)† lists the reagent amounts used. Because semiconductor band gaps are tuned by light absorption from both the crystal bulk and the surface layer, these samples showed discernably different colors.^13,24 The crystal bulk refers to the particle size. Scanning electron microscopy (SEM) images of the synthesized Cu₂O crystals and their size-distribution histograms are provided in Fig. S2 (ESI).† The particles demonstrated good size and shape uniformity. The average sizes of the cubes, octahedra and rhombic dodecahedra were approximately 234, 217 and 290 nm, respectively. Fig. S3 (ESI)† presents the XRD patterns of these Cu₂O crystals. The cubes displayed diffraction peaks that were shifted to higher 2θ angles relative to those of the rhombic dodecahedra, which was consistent with the synchrotron XRD results.¹¹ However, the octahedra did not give similar peak shifts. Here, the slight lattice constant changes naturally appeared with the different particle shapes to give rise to facet-dependent behaviors.

Initially, the electrochemical performance of these Cu₂O crystals was evaluated by determining the redox peak reversibility through the cyclic voltammetry curves of potassium ferricyanide (K₃[Fe(CN)₆]). Fig. S4 (ESI)† presents the CV curves. The redox peaks of [Fe(CN)₆]^3−/4− measured using these Cu₂O crystals did not show good reversibility, with less clear peak positions and low current densities. The octahedra delivered the largest current density, followed by the cubes and rhombic dodecahedra. This order was the same as the order of their electrical conductivity behaviors, so it is clear that their intrinsic electrical conductivity properties greatly affected the electrochemical performance.

To address the low electrochemical activity issue, electroconductive carbon black and carbon nanotubes were introduced to improve the overall stability and activity of the catalysts. Fig. 1 gives the SEM images of the Cu₂O cubes, octahedra, and rhombic dodecahedra, showing they were well dispersed in the CNT matrix. The Cu₂O particles still retained their shapes. The XRD patterns of the composites showed a diffraction peak from the CNTs (Fig. S5, ESI†). Interestingly, the diffraction peaks for the octahedra were shifted to slightly higher 2θ angles than those for the rhombic dodecahedra, so shape-related lattice constant changes could still be observed. Fig. S6 (ESI)† displays the measured cyclic voltammetry (CV) curves. The Cu₂O crystals mixed with carbon black and CNTs could all greatly improve the current density and reversibility of the [Fe(CN)₆]^3−/4− redox peaks, and mixing the crystals with CNTs produced higher current densities. Thus, the Cu₂O/CNT composite was used for the subsequent electroanalytical measurements.

Fig. 1 SEM images of Cu₂O (a) cubes, (b) octahedra, and (c) rhombic dodecahedra mixed with carbon nanotubes.

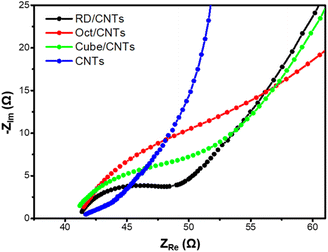
Electrochemical impedance spectroscopy (EIS) measurements were then performed to examine the impedance behavior of these catalysts. The Nyquist plots were fitted using a Randles circuit model to obtain the impedance values. Previously, the charge-transfer resistance (R_ct) values of the Cu₂O cubes, cuboctahedra, and rhombic dodecahedra without mixing with CNTs were in the range of 18.9 to 28.9 kΩ.³ As seen in Fig. 2, after mixing with the CNTs, all the Cu₂O catalysts exhibited very small impedance values. The trend for charge transfer was CNTs > octahedra/CNTs > cubes/CNTs > rhombic dodecahedra/CNTs. The R_ct values for the Cu₂O/CNTs were all approximately <10 Ω. Since the R_ct values were too small, the fitting results could only be estimated. By mixing with CNTs, the overall electrical conductivity and charge-transfer ability of the catalysts were greatly enhanced, rendering them more suitable for electrochemical experiments.

Fig. 2 Nyquist impedance plot of Cu₂O crystals in a CNT matrix.

Before conducting electrocatalytic ORR measurements with LSV and chronoamperometric analysis (CA) to evaluate the performance and stability of the Cu₂O/CNTs catalysts, the variation in the electrochemically active surface area of each sample needed to be considered. When comparing the catalytic performance of the catalysts, the measured current densities of the LSV curves had to account for differences in electrochemically active surface area (ECSA) to provide a more accurate evaluation of the facet effects on ORR activity. The double-layer capacitance (C_dl) was used to estimate the corresponding ECSA differences. The double-layer capacitance was determined from the CV curves using the following equation:

Δj(j_a − j_c)/2 = C_dl × v (1)

In a plot of charging current density, Δj(j_a − j_c)/2 was plotted against the scan rate (v), where j_a and j_c represented the anodic and cathodic current densities, respectively, at ΔE = 0.1 V (potential window was −0.05 V to 0.05 V vs. Ag/AgCl), and v represented the scan rate in mV s⁻¹. The slope of this plot provided the double-layer capacitance (C_dl). The non-Faradic current density based on the ECSA was then estimated using the following equation:

ECSA = C_dl/C_s (2)

where C_s represented the specific capacitance of the electrode.

The corresponding CV curves and a plot of charging current density Δj(j_a − j_c) vs. scan rate (v) are shown in Fig. S7 (ESI).† The C_dl values of the rhombic dodecahedra/CNTs, cubes/CNTs, octahedra/CNTs, commercial Cu₂O powder/CNTs, and CNTs were 7.28, 6.46, 6.32, 5.70, and 5.30 mF cm⁻², respectively (see Table S2, ESI†). To eliminate the ECSA effect, the ORR LSV curves were normalized using the following equation:

Normalized current density = current density/C_dl ratio (3)

In an alkaline environment, the oxygen reduction reaction proceeds via a four-electron pathway or a two-electron pathway. The standard reduction potential of O₂ to OH⁻, is 0.401 V versus the standard hydrogen electrode (SHE) for the direct four-electron pathway (eqn (4)).

O₂ + 2H₂O + 4e⁻ ⇌ 4OH⁻; E° = 0.401 V vs. SHE (4)

For the alternative two-electron pathway, O₂ is first reduced to peroxide ion and can be further reduced (eqn (5) and (6)).

O₂ + H₂O + 2e⁻ ⇌ HO₂⁻ + OH⁻; E° = −0.076 V vs. SHE (5)

H₂O + HO₂⁻ + 2e⁻ ⇌ 3OH⁻; E° = 0.878 V vs. SHE (6)

In an alkaline medium at 25 °C and at an O₂ pressure of 1 atm, is related to the reversible hydrogen electrode (RHE) through the following equation:

E_RHE = E_SHE + 0.059 × pH (7)

Fig. 3 shows the ORR steady-state linear sweep voltammetry polarization curves for different electrocatalysts in an O₂-saturated KOH electrolyte, with an oxygen flow at a scan rate of 5 mV s⁻¹ and an electrode rotating rate of 1600 rpm. The expected ORR limiting currents were observed for all the samples, showing the positive effect of stability and performance with the addition of CNTs. Compared with the CNTs and the commercial Cu₂O powder, which have large particle sizes and random morphologies, the Cu₂O polyhedra/CNTs exhibited notably better ORR catalytic activities, with the rhombic dodecahedra showing the largest limiting current density of −4.25 mA cm⁻², followed by the octahedra at −3.93 mA cm⁻² and the cubes at −3.67 mA cm⁻². This highlights the importance of catalyst surface control on catalytic activity.

Fig. 3 Normalized LSV polarization curves for the ORR using different catalysts.

Next, a series of linear sweep voltammetry polarization curves for the cubes, octahedra, and rhombic dodecahedra mixed with CNTs were obtained at a scan rate of 5 mV s⁻¹ and different rotating rates (i.e., 400, 600, 900, 1200, 1600, 2000, 2500, and 3600 rpm), as shown in Fig. 4. The data were recorded after scanning multiple times until the curves became stabilized, ensuring consistent and stable performance of the catalysts. These data were normalized with the ECSA for a better facet-related electrocatalytic activity comparison. It was found that the catalytic current increased progressively as the rotating rate increased. The rhombic dodecahedra/CNTs catalyst remained the most electrocatalytically active in terms of ORR performance, with current densities of −5.09 mA cm⁻² at 1600 rpm and −10.4 mA cm⁻² at 3600 rpm. The octahedra/CNTs also achieved a respectable limiting current density of −4.44 mA cm⁻² at 1600 rpm, while it was −3.81 mA cm⁻² at 1600 rpm for the cubes/CNTs (see Fig. S8, ESI†). This notable facet dependence in ORR activity may be due to the different interactions between the crystal facets and oxygen.

Fig. 4 LSV polarization curves for the ORR at different rotation speeds, the corresponding Koutecký–Levich plots (j⁻¹vs. ω^−1/2) at different potentials, and plots of the transferred electron numbers versus potentials for (a–c) Cu₂O cubes, (d–f) octahedra and (g–i) rhombic dodecahedra mixed with CNTs.

To further understand the ORR catalytic mechanism and kinetics, the LSV polarization curves at different rotating rates were used to obtain the Koutecký–Levich plots for the different potentials. The Koutecký–Levich plot is used in the study of electrode reaction kinetics and the evaluation of catalyst activity. As can be seen in Fig. 4, the corresponding Koutecký–Levich plots exhibited good linearity in the range of mass-transport control from 0.35 V to 0.5 V, demonstrating a first-order reaction characteristic with oxygen.

Next, the average number of electrons transferred (n) during the ORR was extracted from the Koutecký–Levich plot, which helps in determining whether the oxygen reduction reaction follows a four-electron or a two-electron reaction pathway through the Koutecký–Levich equation (eqn (8)).

1/J = 1/J_L + 1/J_K = 1/Bω^1/2 + 1/J_K (8)

where J, J_L, and J_K are the values of the experimentally measured current, diffusion-limiting current, and kinetic current density, respectively; ω is the angular rotating rate, and B is defined as:

B = 0.62nFAD_O^2/3v^−1/6C_O (9)

where n is the number of electrons transferred during the electrochemical reaction, F is the Faraday constant (96 485 C mol⁻¹), A is the electrode surface area of the rotating disk electrode (0.196 cm²), D_O is the diffusion coefficient of O₂ in 0.1 M KOH (1.9 × 10⁻⁵ cm² s⁻¹), v is the kinematic viscosity of the electrolyte (v = 0.01 cm² s⁻¹), and C_O is the bulk concentration of O₂ (1.2 × 10⁻⁶ mol cm⁻³). The value of n can be calculated from the slope of the J⁻¹vs. ω^−1/2 plot. As can also be seen in Fig. 4, the numbers of electrons transferred (n) for all the Cu₂O/CNTs catalysts were similar in the range of mass-transport control from 0.35 V to 0.55 V. The average values of n for the ORR with cubes, octahedra, and rhombic dodecahedra mixed with CNTs were about 3.6, 3.9, and 3.9, respectively. By contrast, for the commercial Cu₂O powder/CNTs and CNTs, the numbers of electrons transferred, as determined through the Koutecký–Levich plots, were about 2.5 and 2.1, respectively (Fig. S9, ESI†). Thus, these Cu₂O polyhedra all involved a four-electron reaction pathway and showed outstanding reaction selectivity in the ORR. Judging from the limiting current density, the onset potential (0.81 V vs. RHE), number of charges transferred, and E_1/2 at 0.66 V, Cu₂O rhombic dodecahedra mixed with CNTs was considered to be a superior ORR electrocatalyst among the reported ORR catalysts incorporating Cu₂O crystals.^21,22

The stability of the catalysts was evaluated by chronoamperometric (i–t) measurements for 6 h under a constant potential of 0.65 V vs. RHE at a rotating rate of 1600 rpm in O₂-saturated 0.1 M KOH solution. Fig. 5 shows that the cubes/CNTs sample retained 89.9% of its original current density after 6 h, showing it had the best stability. Meanwhile, the octahedra/CNTs catalyst retained 82.7% of its original current density, and the rhombic dodecahedra/CNTs catalyst displayed the fastest decay rate, retaining just 75.4% of its original current density. The gradual decrease in current density implied that the effect of any deposited Pt clusters on the working electrode was not a concern for this work. The CA measurements clearly showed that mixing with CNTs could improve the catalyst stability for the ORR. Mechanistically, the inferior stability of the rhombic dodecahedra/CNTs could be attributed to the {110} crystal surface of Cu₂O being more reactive with oxygen and self-oxidizing to CuO during the ORR. As the crystal surface changed, the current density in the CA curve gradually decreased. This further indicated that the rhombic dodecahedra/CNTs composite exhibited superior electrocatalytic performance and ORR catalytic activity compared to the other samples. Fig. S10 (ESI)† shows the SEM images of the Cu₂O crystals after the chronoamperometric measurements. Their morphologies had become less recognizable. However, the cubes maintained a better morphology than the octahedra and rhombic dodecahedra, so the cubes had better stability but lower reactivity. The X-ray fluorescence spectroscopic measurements showed no presence of Pt on the Cu₂O cubes/CNTs electrode after the chronoamperometric experiment (Fig. S11†). Fig. S12 (ESI)† provides SEM images of the three Cu₂O/CNTs samples after storing them for two months in sealed vials containing isopropanol. The cubes and octahedra still maintained their original morphologies, while the rhombic dodecahedra had been etched due to a possible reaction with trace oxygen in the isopropanol.

Fig. 5 Chronoamperometric curves for the Cu₂O/CNTs catalysts measured at 0.65 V vs. RHE in an O₂-saturated 0.1 M KOH solution.

Tafel plots offer the electrochemical kinetics relationship between the current (or reaction rate) and overpotential through the Tafel equation (eqn (10)).

η = a − b log i (10)

Under the cathodic reduction reaction, η is the overpotential (V), i is the current density (A m⁻²), a is a constant related to the magnitude of the forward and reverse current at equilibrium, and b is the Tafel slope (mV dec⁻¹). Fig. S13 (ESI)† gives the Tafel plots of the Cu₂O cubes, octahedra, and rhombic dodecahedra mixed with CNTs. The Tafel slopes for the cubes/CNTs, octahedra/CNTs, and rhombic dodecahedra/CNTs were 79.1, 75.6, and 73.1 mV dec⁻¹, respectively. These values were lower than the reported Tafel slopes for the Pt/C electrodes (80.4 and 98 mV dec⁻¹),^25,26 so the Cu₂O/CNTs catalysts could be more efficient in producing current with less overpotential in the electrocatalytic ORR than commercial Pt/C.

The adsorption strength of oxygen is strongly correlated with the oxygen reduction reaction performance. The oxygen adsorption energies (E_ads) on the three different Cu₂O surfaces were determined using density functional theory calculations. The computational details are provided in the ESI.† We initially investigated the O₂ adsorption behavior on the three Cu₂O surfaces, and the most stable geometric configurations are displayed in Fig. 6. The Cu–O distances between the O₂ and the surface were 3.14, 2.21, and 1.86 Å for the {100}, {110}, and {111} surfaces, respectively. O₂ molecules preferentially bound to the Cu atoms on the {110} and {111} surfaces. On the {100} surface, O₂ slightly bound to the saturated Cu atoms at a two-fold bridge site. The E_ads values of an O₂ molecule on the three Cu₂O facets followed the order: {110} (−0.09 eV) < {100} (−0.85 eV) < {111} (−1.66 eV). The weakest adsorption strength of oxygen on the {110} surface indicated that a smaller energy barrier was required to form the intermediate product OOH*, leading to the best ORR reactivity. Conversely, the strongest adsorption on the {111} surface could be attributed to the bonding nature of the unsaturated Cu atoms. Herein, the moderate adsorption energy of the {100} surface was mostly contributed by the bond distortion of the surface atoms, as shown in Fig. 6.

Fig. 6 The most stable O₂ adsorption configurations on Cu₂O (a) {100}, (b) {110}, and (c) {111} surfaces. The upper and lower panels show the top and side views, respectively.

The oxygen reduction reaction can involve four elementary steps (see ESI†). The free energy diagrams of the ORR intermediate products (OOH*, O*, OH*) at zero electrode potential (U = 0 V) and equilibrium electrode potential (U = 1.23 V) were evaluated. All the intermediate steps were exothermic at U = 0 V, implying that the ORR pathway was thermodynamically favorable (see Fig. 7a). Here * refers to the active site on the catalyst surface. The free energy of OOH* for the {110} surface (4.63 eV) was higher than that for the {100} (3.57 eV) and {111} (3.47 eV) surfaces, indicating a much weaker OOH* binding ability on the {110} surface. The same scenario could be observed for the O* and OH* intermediates. Significantly, the theoretical limiting potential (U_L), or the potential-limiting step, acquired from the minimum change in free energy for each reaction step, indicated that the ORR activity followed the trend {110} (0.29 V) > {100} (0.11 V) > {111} (0.03 V) surfaces. The limiting potential for the {110} surface was the * + O₂ + (H⁺ + e⁻) → OOH* step, while the limiting potential for the {100} and {111} surfaces was the OH* + (H⁺ + e⁻) → * + H₂O step. The highest U_L and the corresponding best ORR activity of the {110} surface among the three facets aligned well with the experimental observations. The {100} and {111} surfaces showed only a small difference in their ORR performance. In addition to the four-electron process, we also considered the free energy of the two-electron process (red line in Fig. 7a). The free energies of O* (ΔG_O*) among these three facets were much lower than that of H₂O₂, meaning that the oxygen reduction reaction preferred to proceed via the four-electron pathway, consistent with the experimental results.

Fig. 7 Free energy diagram for oxygen reduction on Cu₂O {100}, {110}, and {111} surfaces with (a) U = 0 V and (b) U = 1.23 V. The theoretical overpotential (η_ORR) and the corresponding potential-determining step are presented in panel (b).

Fig. 7b presents the free energy diagram at U = 1.23 V. The potential-determining steps (PDSs) and the corresponding overpotentials (η_ORR) of the ORR were obtained, where the PDS represented the key step with the maximum free energy rise during the ORR process. The PDS of the {110} surface was the transformation of O₂ to OOH* (* + O₂ + (H⁺ + e⁻) → OOH*), which differed from the other two facets (OH* + (H⁺ + e⁻) → * + H₂O). The order of the η_ORR values was: {110} (0.94 V) < {100} (1.12 V) < {111} (1.20 V). A lower η_ORR indicated improved ORR activity. Therefore, the results of the overpotential were consistent with the theoretical limiting potential.

Next, the ORR activity map, as developed by Nørskov et al., is shown in Fig. 8, which presents two important descriptors, namely ΔG_OOH* and ΔG_OH*.^27,28 The best ORR activity was located at ΔG_OH* = 1.23 eV and ΔG_OOH* = 3.69 eV, corresponding to the highest limiting potential (U_L = 1.23 V, see the red hill). Furthermore, the competitive free energies of the ORR steps distinguished the three PDSs into different regimes, which are bounded by the white dashed lines in Fig. 8. The free energies of the intermediates on the Cu₂O {100}, {110}, and {111} surfaces were respectively labeled on the 2D volcano plot. Evidently, the {110} surface possessed the best activity among the three Cu₂O facets, showing weak OOH* binding on the surface. On the other hand, the {100} and {111} surfaces, with small ΔG_OH* values, demonstrated strong OH* binding ability. This scenario could cause catalyst poisoning due to the hard desorption of OH*, resulting in non-ideal ORR activity. The positions of these three facets on the activity map confirmed the key PDSs in the entire ORR pathway, agreeing with the results from the free energy diagram at U = 1.23 V. Besides, these three facets exhibited a linear relationship between ΔG_OOH* and ΔG_OH*. ΔG_OOH* can be expressed as ΔG_OOH* = 0.975ΔG_OH* + 3.45. This behavior follows the linear scaling relation observed in other transition metal oxides and metal surfaces.^29,30 It could be noted that the slope of the scaling line was very close to 1, which implied that OOH* bound to the surface via a single bond.³¹ The scaling relationship and the descriptor-associated analysis can help explain the catalytic behavior and provide theoretical insight into the performance of the chemical reaction.

Fig. 8 2D volcano plot for the oxygen reduction reaction. The theoretical limiting potential represents the ORR activity.

Conclusions

Cu₂O cubes, octahedra, and rhombic dodecahedra blended with a matrix of carbon nanotubes were used as catalyst materials for the electrochemical oxygen reduction reaction. After normalization of the electrochemical active surface area, the rhombic dodecahedra delivered the highest current density, followed by the octahedra and cubes. Koutecký–Levich plots clearly showed that these Cu₂O/CNTs were highly selective toward the four-electron pathway in the ORR. The catalyst stability test showed that the cubes were the most stable, followed by the octahedra and then the rhombic dodecahedra. Oxygen interactions with surface Cu atoms likely contributed to the facet-related ORR performance. DFT calculations provided the adsorption strengths of the reactant on the three Cu₂O facets, showing that the weakest O₂ adsorption occurred on the {110} surface. The calculated free energy diagrams and 2D volcano plots also indicated that the {110} surface exhibited the best ORR activity. The {100} and {111} surfaces had a low theoretical limiting potential and high overpotential, attributed to the strong OH* binding on the surface, leading to less facile desorption of the intermediate species. The ORR free energy diagram also indicated the energetic preference of the four-electron pathway over the two-electron pathway.

Experimental section

Chemicals

Copper(II) chloride anhydrous (CuCl₂, 98%, Alfa Aesar), hydroxylamine hydrochloride (NH₂OH·HCl, 99%, Sigma-Aldrich), sodium hydroxide (NaOH, 98%, Honeywell), and sodium dodecyl sulfate (SDS, 99%, J. T. Baker) were used to synthesize Cu₂O crystals. Nafion™ perfluorinated resin solution (NR50, 5 wt% in a mixture of lower aliphatic alcohols and water, Sigma-Aldrich), isopropanol (≥99.8%, Duksan), Ketjenblack EC-300J (99%, TIMCAL) and multiwalled carbon nanotubes (99%, TIMCAL) were used for the electrode preparation. Potassium hydroxide (KOH, ≥85%, Honeywell), potassium chloride (KCl, 99%, J. T. Baker), and potassium hexacyanoferrate(III) (K₃[Fe(CN)₆], 99%, Sigma-Aldrich) were used for the electrolyte solution and electrochemical measurements. Copper(I) oxide powder (Cu₂O, 97%, Sigma-Aldrich) was added for comparison of the ORR activity. Ultrapure deionized water (18.2 M, Milli-Q) was used for all the solution preparations.

Preparation of the Cu₂O/CNT electrode

To enhance the effectiveness and accuracy of the electrocatalytic measurements, carbon nanotubes were added to prepare the electrode catalyst. CNTs have a high specific surface area, good stability, and high conductivity. Nafion is co-polymerized from tetrafluoroethylene and perfluorinated vinyl ether. Adding Nafion creates an ion-selective film on the electrode surface with good conductivity. The added CNTs and Nafion facilitate more reliable electrochemical measurements. First, 10 mg of Cu₂O nanocrystal powder, 10 mg of CNTs, and 1 mL of isopropanol were mixed in a 10 mL sample vial. Next, 20 μL of 5 wt% Nafion solution was dropped into the catalyst ink solution. After sonicating for 15 min and stirring for about 12 h, a homogeneous solution was obtained. Next, 10 μL of the catalyst ink solution was slowly applied onto the rotating disk electrode surface. The circular electrode surface area was 0.196 cm². The loading content was about 1.02 mg cm⁻². To make the ink rigidly attach to the RDE surface, the catalyst was slowly dried at room temperature for about 12 h.

Instrumentation

XRD patterns were collected using a Shimadzu XRD-6000 diffractometer with Cu Kα radiation. Cu₂O powder was loaded over glass for the XRD measurements. SEM images were taken using a JEOL JSM-7000F electron microscope. Electrochemical measurements were carried out using a Zahner Zennium E4 workstation and Thales Zahner XT software. The electrocatalytic oxygen reduction reaction was carried out using an RRDE-3A rotating ring disk electrode apparatus. A Thermo Scientific ARL QUANT’X EDXRF analyzer was used for the energy-dispersive X-ray fluorescence spectral measurements.

Electroanalytical experiment setup

For the electrochemical measurements, a Ag/AgCl (3 M NaCl solution) electrode was used as the reference electrode (RE), glassy carbon (GC, 0.0707 cm² area) as the working electrode (WE), and Pt wire as the counter electrode (CE). The working electrode was polished with 0.05 μm alumina powder and rinsed with distilled water and ethanol before use. As the supporting electrolyte, 0.1 M KCl was used. For the electrocatalytic ORR experiments, a Hg/HgO (1 M NaOH solution) electrode was used as the reference electrode, and a rotating disk electrode served as the working electrode. Also, 0.1 M KOH was used as the supporting electrolyte in the electrochemical cell.

The Hg/HgO electrode potentials could be converted to the reversible hydrogen electrode (RHE) scale according to the Nernst equation:

E (V vs. RHE) = E (V vs. Hg/HgO) + 0.098 + 0.059 × pH (11)

where the potential of Hg/HgO (1 M NaOH solution) was 0.098 V, and the pH value of 0.1 M KOH solution was 12.45, as measured by a SUNTEX SP-2300 pH meter. For conversion of the Ag/AgCl electrode potentials to the RHE potentials, the following equation was used.

E (V vs. RHE) = E (V vs. Ag/AgCl) + 0.197 + 0.059 × pH (12)

where the potential of Ag/AgCl (3 M NaCl solution) was 0.197 V, and the pH value of the 0.1 M NaCl solution was 7.0, as measured using the same meter.

Electrochemical property measurements

All the cyclic voltammogram and linear sweep voltammetry data were recorded after 10 CV cycles, when the curves became stable and corrected. For the CV curves, 5 mM K₃[Fe(CN)₆] in 0.1 M KCl electrolyte saturated with nitrogen gas was used. The scan rate was 10 mV s⁻¹, over the scanning potential window from −0.1 to 0.5 V (vs. Ag/AgCl). Different Cu₂O catalysts were loaded with 5 μL of catalyst ink solution on a glassy carbon working electrode surface (0.0707 cm² area).

Electrocatalytic ORR measurements

Polarization curves were obtained using linear sweep voltammetry with a scan rate of 5 mV s⁻¹ over the potential window from 0.9 to 0.3 V (vs. RHE) in 0.1 M KOH electrolyte saturated with oxygen. The catalyst loading amount was 10 μL. The rotation speeds for the rotating ring disk electrode were 400, 600, 900, 1200, 1600, 2000, 2500, and 3600 rpm, respectively.

Electrochemical impedance spectroscopy measurements

The onset potential in the EIS measurements was applied at 0.015 V (vs. Hg/HgO) in 0.1 M KOH electrolyte. The amplitude was 5 mV and the AC frequency was from 50 kHz to 0.1 Hz. The fitting model for the Nyquist plot was a Randles circuit.

Electrochemically active surface area analysis

The CV curves in the ECSA analysis were measured at scan rates of 20, 40, 60, 80, 100, 120, and 140 mV s⁻¹, respectively. The potential window was from −0.05 to 0.05 V (vs. Hg/HgO). The average current density (Δj = (j_a − j_c)/2) was determined at an average applied potential of 0 V (vs. Hg/HgO). The double-layer capacitance (C_dl) was then extracted from the corresponding CVs by plotting Δj against the scan rate (v).

Chronoamperometric measurements

This measurement probes the catalyst stability. The onset potential in the CA measurement was 0.65 V (vs. RHE). This potential would enable the oxygen reduction reaction. The disk rotation rate was 1600 rpm, and the CA measurement was recorded for 6 h in O₂-saturated 0.1 M KOH electrolyte.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support was provided by the National Science and Technology Council, Taiwan (NSTC 112-2113-M-007-016-MY3, 112-2221-E-A49-030, and 112-2112-M-018-005). J.-P. Chou and Y.-C. Lo thank the National Center for High-performance Computing (NCHC) for providing computational and storage resources. Y.-C. Lo also thanks the Center for Advanced Semiconductor Technology Research from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education in Taiwan.

References

1. C.-S. Tan, S.-C. Hsu, W.-H. Ke, L.-J. Chen and M. H. Huang, Nano Lett., 2015, 15, 2155–2160.
2. A.-T. Lee, C.-S. Tan and M. H. Huang, ACS Cent. Sci., 2021, 7, 1929–1937.
3. H.-H. Ma and M. H. Huang, J. Mater. Chem. C, 2023, 11, 5857–5866.
4. G. Kumar, C.-R. Chen, B.-H. Chen, J.-W. Chen and M. H. Huang, J. Mater. Chem. C, 2022, 10, 12125–12131.
5. G. Kumar, Z.-L. Chen, S. Jena and M. H. Huang, J. Mater. Chem. C, 2023, 11, 3885–3888.
6. G. Kumar, J.-W. Chen, H.-H. Ma, X.-F. Huang and M. H. Huang, J. Mater. Chem. C, 2022, 10, 10424–10428.
7. P.-L. Hsieh, G. Kumar, Y.-Y. Wang, Y.-J. Lu, L.-J. Chen and M. H. Huang, J. Mater. Chem. A, 2021, 9, 15354–15358.
8. P.-J. Chou, W.-Y. Yu, J.-C. Kao, Y.-C. Lo, J.-P. Chou and M. H. Huang, J. Mater. Chem. A, 2023, 11, 19514–19523.
9. Z.-L. Chen and M. H. Huang, J. Mater. Chem. A, 2023, 11, 22198–22205.
10. G. Kumar, H.-W. Sun and M. H. Huang, ACS Appl. Nano Mater., 2024, 7, 2155–2163.
11. B.-H. Chen, G. Kumar, Y.-J. Wei, H.-H. Ma, J.-C. Kao, P.-J. Chou, Y.-C. Chuang, I.-C. Chen, J.-P. Chou, Y.-C. Lo and M. H. Huang, Small, 2023, 19, 2303491.
12. C.-K. Chen, B.-H. Chen and M. H. Huang, Chem. Mater., 2023, 35, 7859–7866.
13. P.-S. Chang, B.-H. Chen, Y.-C. Lin, W.-T. Dai, G. Kumar, Y.-G. Lin and M. H. Huang, Small, 2024, 20, 2401558.
14. Y.-J. Chuang, A. Pal, B.-H. Chen, S. Jena, S. Suresh, Z.-H. Lin and M. H. Huang, Chem. Sci., 2025, 16, 3285–3295.
15. Y. Wang, J. Li and Z. Wei, J. Mater. Chem. A, 2018, 6, 8194–8209.
16. J. Du, C. Chen, F. Cheng and J. Chen, Inorg. Chem., 2015, 54, 5467–5474.
17. Z.-Q. Liu, H. Cheng, N. Li, T. Y. Ma and Y.-Z. Su, Adv. Mater., 2016, 28, 3777–3784.
18. W. Wang, H. Wang, Y. Yu, Z. Wu, M. Asif and H. Liu, Catal. Sci. Technol., 2018, 8, 480–485.
19. X.-Y. Yan, X.-L. Tong, Y.-F. Zhang, X.-D. Han, Y.-Y. Wang, G.-Q. Jin, Y. Qin and X.-Y. Guo, Chem. Commun., 2012, 48, 1892–1894.
20. J. Xiao, Q. Kuang, S. Yang, F. Xiao, S. Wang and L. Guo, Sci. Rep., 2013, 3, 2300.
21. Q. Li, P. Xu, B. Zhang, H. Tsai, S. Zheng, G. Wu and H.-L. Wang, J. Phys. Chem. C, 2013, 117, 13872–13878.
22. X. Zhang, Y. Zhang, H. Huang, J. Cai, K. Ding and S. Lin, New J. Chem., 2018, 42, 458–464.
23. A. Zhang, J. Wu, L. Xue, C. Li, S. Zeng, D. Caracciolo, S. Wang and C.-J. Zhong, ACS Appl. Mater. Interfaces, 2021, 13, 46577–46587.
24. J.-Y. Huang, M. Madasu and M. H. Huang, J. Phys. Chem. C, 2018, 122, 13027–13033.
25. H. Gong, S. Lu, P. Strasser and R. Yang, Electrochim. Acta, 2018, 283, 1411–1417.
26. J. Zhu, Q. Zhang, C. Wang, Y. Feng, Y. Zhang, G. Qi, L. Kang, J. Luo and X. Liu, Nanoscale, 2025, 17, 2709–2717.
27. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
28. J. A. Zamora Zeledón, M. B. Stevens, G. T. K. Gunasooriya, A. Gallo, A. T. Landers, M. E. Kreider, C. Hahn, J. K. Nørskov and T. F. Jaramillo, Nat. Commun., 2021, 12, 620.
29. H. Li, S. Kelly, D. Guevarra, Z. Wang, Y. Wang, J. A. Haber, M. Anand, G. T. K. K. Gunasooriya, C. S. Abraham, S. Vijay, J. M. Gregoire and J. K. Nørskov, Nat. Catal., 2021, 4, 463–468.
30. V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, ACS Catal., 2012, 2, 1654–1660.
31. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08855g

---