 Open Access Article
Open Access ArticleCharacterization of densification behavior and mechanical properties of solid electrolyte powders for all solid-state batteries†
Seung-Yong
Lee‡
 a,
Ji-Hoon
Han‡
a,
Ji-Hoon
Han‡
 bc,
Hyun-Woo
Gong
d,
Jae-pyoung
Ahn
d,
Kyung-Woo
Yi
b and
Young Whan
Cho
bc,
Hyun-Woo
Gong
d,
Jae-pyoung
Ahn
d,
Kyung-Woo
Yi
b and
Young Whan
Cho
 *c
*c
aMaterials Characterization Center, Korea Institute of Materials Science (KIMS), Changwon 51508, Republic of Korea
bDepartment of Materials Science and Engineering, Seoul National University, Seoul 08826, Republic of Korea
cCenter for Hydrogen Energy Materials, Korea Institute of Science and Technology (KIST), Seoul 02792, Republic of Korea. E-mail: oze@kist.re.kr
dAdvanced Analysis Center, Korea Institute of Science and Technology (KIST), Seoul 02792, Republic of Korea
First published on 17th February 2025
Abstract
A simple powder compression method was used to compare the mechanical properties of various argyrodite-type solid electrolytes. The Heckel plot's K values revealed differences in plastic deformation behavior, aligning qualitatively with nano-indentation test results.
All solid-state lithium batteries (ASSBs) have received great attention as next-generation batteries due to higher energy density and safety, in comparison with commercial lithium-ion batteries (LIBs).1,2 Unlike LIBs consisting of liquid-electrolytes, ASSBs use solid-electrolytes (SEs), which play the role of separators together with the intermediate medium for ion-transport between the anode and cathode. Generally, four types of SEs have been reported such as sulfides, oxides, halides, and polymers. Each has its own advantages and disadvantages.3
Among these, sulfide-based solid electrolytes have garnered the most attention due to their ease of formability and high ionic conductivity, making them close to commercialization. Various sulfide solid electrolytes, such as lithium argyrodite, have been studied so far; however, most of the research studies have focused on the energy performance aspect, such as ionic conductivity and electrochemical stability, with less attention to their mechanical properties related to physical compatibility with electrodes.4,5 Given that sulfide-based SEs can function both as a separator and an ion transport medium simply through the application of pressure at room temperature, the mechanical properties of the powder hold significant importance.6,7 SEs should comply with the applied force, especially compressive stress, during the manufacturing process, in which ASSB cells are manufactured with sufficient pressure to minimize residual voids and to maximize the solid–solid contact interface between the SE and the anode/cathode materials for lithium-ion transportation.8–10 The stress compliance of SEs is also significant under in-service conditions; the lattice contraction and expansion of electrode materials due to lithium-ion transportation during charge/discharge cycles can induce residual stress/strain on the solid–solid interfaces.11–15 Given that SEs have less ability for stress compensation, the residual stress/strain could result in microvoid/crack formation at the interfaces, leading to the degradation of ASSB performance.16–18 Recent research has reported that good stiffness of SEs enables compensation for the volume contraction/expansion of electrode materials effectively, minimizing internal charge transfer resistance induced by cracks and voids.1,5,8,11–15,19–23 These findings emphasize that the microstructure and mechanical properties of solid electrolytes are critical to achieving higher stability and performance in ASSLMBs by mitigating dendrite-induced short-circuit failures.
Accordingly, mechanical properties of SEs must be considered for the development and application of ASSBs. In previous studies,24–26 lattice elastic coefficients of SEs at the atomic-scale have been calculated through atomistic simulations. In actual manufacturing and in-service processes, however, macroscopic compressibility of SEs due to particle–particle and particle–void interactions will be more critical. In this study, comparative research was conducted on various sulfide SEs to evaluate stress compatibility by means of compression testing as well as by nano-indentation.
To understand the fundamentals of compression behavior of SE powders, the results of the representative commercial SE powder, Li6PS5Cl, are presented in Fig. 1. Fig. 1a indicates the total displacement (Δd) curve corresponding to the compressive stress (σ) and the inset shows the mold compression system with digital image correlation (DIC) analysis where the upper and lower plungers are speckle-patterned with SiO2 particles on carbon tape (see the ESI† section for further details regarding DIC). Compressive force is applied on the upper plunger, which moves down toward a zirconia mold, and then the displacement is quantitatively measured in real-time by tracking the distance variation between the upper and lower plungers by DIC analysis. The total displacement rapidly increases and then appears saturated with increasing compressive stress. Variation of the displacement is closely related to the reduction of the mold space volume filled with SE powders and voids. However, one should be cautious that the displacement is also affected by the elastic contribution of the plunger rod.
The total displacement, Δd, under compressive load can be expressed as eqn (1);
| Δd = Δdelastic + ΔhSE-powder = σL/E + ΔhSE-powder | (1) |
SE powder undergoes various stages during powder-to-pellet formation under compression, such as powder rearrangement and plastic and/or elastic deformation.31 To understand the compaction behavior of powders, the Heckel equation is widely used in various fields, especially in pharmaceutical powder compaction processes.32–37 Assuming that the particle-to-pellet formation under compression is derived from a first-order chemical reaction, where the voids are the reactants and the densification of the solid is the product, the Heckel equation is expressed as eqn (2);
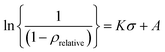 | (2) |
Fig. 2 shows the negative logarithmic (1 − ρrelative) vs. compressive stress curves of various SE powders. The Heckel plots of as-received commercial Li6PS5Cl together with that of the same powder after ball-milling are shown in Fig. 2a. The value of K in stage II of as-received commercial Li6PS5Cl powder is 32.3 (×10−4) and after ball milling, it slightly increases to 34.0 (±0.15). It is, however, noted that the ball-milled powder densifies relatively easily compared with the as-received powder. When compared to as-received commercial Li6PS5Cl powder (brown squares), the transition from stage II to III occurs at lower stress with the ball-milled commercial powder (purple circles). The compressive stress at 97% theoretical density of ball milled powder is 570 MPa while that of as-received powder is 650 MPa. It seems that as the particle size decreases, the voids are quickly filled with particles even under lower stress and thus densification of the pellet is accelerated, resulting in a reduced plastic deformation region (stage II) and an earlier transition to stage III. The milled powder approaches the theoretical density at significantly lower stress relative to as-received commercial powder while the K is approximately the same between these two powders. Given that the K is predominantly governed by intrinsic mechanical properties, such as the elastic modulus and/or plasticity, it is not uncommon to observe a comparable slope in SE powders with identical chemical compositions and crystal structures. When there is a significant difference in the morphology and/or size of the SE powders, however, it is natural to have different compacting behavior even if they have the same chemical composition and crystal structure.
When Cl− in Li6PS5Cl is replaced with Br−, the transition from stage II to III is delayed as shown in Fig. 2b. It is believed that the difference in the Heckel plot between Li6PS5Cl and Li6PS5Br is mainly derived from the change in the intrinsic mechanical properties of electrolyte itself, such as the elastic modulus and/or plasticity.32,33,36,37 As shown in Table 1, the compressive stress at 97% of the theoretical density of the Li6PS5Cl compact is lower than that of Li6PS5Br, which agrees well with the above result that the transition between stage II and III appears at relatively lower stress with Li6PS5Cl compared to Li6PS5Br.
| Li6PS5Br | Li6PS5Cl | Li5.15PS4.15(BH4)1.85 | Li5.55PS4.55(BH4)1.45 | |
|---|---|---|---|---|
| Slope, K (×10−4 MPa−1) | 25.0 (±0.16) | 29.1 (±0.14) | 37.0 (±0.11) | 41.3 (±0.11) |
| Compressive stress @ 97% theoretical density (MPa) | 725 | 675 | 570 | 510 |
The Heckel plots of BH4− substituted SE powders are also presented in Fig. 2b. Compared to Li6PS5Cl powder, the transition from stage II to III of these SE powders tends to accelerate. In the initial densification stage, the voids are large enough for the particles to simply rearrange and gradually fill them up. As the voids become smaller than the average particle size, however, particles have to change their shape or even break into smaller ones through plastic deformation or fragmentation to fill up the remaining empty spaces. The plastic deformation behavior is controlled by the yield strength and elastic modulus. In eqn (1) representing the Heckel plot, the K value represents the linear section in stage II and indicates the stress compatibility of the powders. The reciprocal of the K value physically represents a quantity proportional to the yield strength of the powder.32,33K values derived from the Heckel plot in Fig. 2b are presented in Table 1. Li6PS5Br has a lower K value compared to Li6PS5Cl. K values of BH4− substituted powders are much higher than those of Li6PS5Cl and Li6PS5Br. In addition, the compressive stresses at 97% theoretical density are much lower than those of Li6PS5Cl and Li6PS5Br. The K value will mainly depend on the chemical composition, which is closely related to the change in the yield strength. This indicates that it is much easier for BH4− substituted SE powders to plastically deform to produce a compact of near theoretical density at room temperature compared with common halide substituted argyrodites such as Li6PS5Cl and Li6PS5Br.
The elastic modulus (E) and hardness (H) are critical mechanical properties that govern the deformation behavior of materials. The elastic modulus reflects the stiffness of a material and its ability to resist elastic deformation under stress, while hardness indicates resistance to localized plastic deformation.38–41
To further characterize the mechanical properties of SE powders, the indentation hardness and elastic modulus of the pellets were measured using nano-indentation, and the results are shown in Table 2. For the measurements, the pellets were compressed close to the theoretical density, as determined from the Heckel plots. The surface morphology of the ion milled SE powder compacts for the nano-indentation test is shown in Fig. 3. There are some pores but the porosity measured by an image analysis method is not higher than 7%. The nano-indentation curves of Li6PS5Br are also given in Fig. 3e and f. While the elastic modulus of Li6PS5Cl is slightly higher than that of Li6PS5Br, the hardness of Li6PS5Br is higher than that of Li6PS5Cl. This suggests that the yield stress of Li6PS5Cl is lower than that of Li6PS5Br. This result agrees with those from the Heckel plot as the K of Li6PS5Cl is higher than that of Li6PS5Br. Both the elastic modulus and indentation hardness of the BH4− substituted SE powders are much lower compared to those of Li6PS5Cl and Li6PS5Br.
| Li6PS5Br | Li6PS5Cl | Li5.15PS4.15(BH4)1.85 | Li5.55PS4.55(BH4)1.45 | |
|---|---|---|---|---|
| Hardness (GPa) | 1.68 (±0.11) | 1.41 (±0.24) | 0.69 (±0.07) | 0.66 (±0.05) |
| Elastic modulus (GPa) | 30.5 | 27.6 | 15.6 | 19.1 |
| Porosity (%) | 2.5 | 2.5 | 7.3 | 4.7 |
| H/E (plasticity index) ×10−2 | 5.5 | 5.1 | 4.4 | 3.5 |
 | ||
| Fig. 3 (a–d) Porosity of cross-sections of different types of solid electrolyte pellets measured by SEM. The scale bar is 3 μm. The black spot, which resembles a pore-like feature, is an artifact caused by the ‘edge effect,’ as explained in detail in Fig. S3.† (e and f) Indentation curve of a synthesized sample. Measurements were taken at least five times at different locations for each sample. | ||
The lower elastic modulus and hardness of BH4−-substituted SEs result in earlier onset of plastic deformation under lower applied stress. This behavior facilitates efficient densification of the material by allowing voids to be filled with less energy, as shown in the Heckel plots and nano-indentation tests. This indicates that the BH4− substituted SE powders proceed with easier plastic deformation due to lower hardness and yield stress compared to Li6PS5Cl and Li6PS5Br. As a result, a lower stress is required to fill up the voids, leading to the transition to stage III at relatively lower compressive stress for BH4-substituted SE powders compared to Li6PS5Cl and Li6PS5Br.
The H/E ratio (plasticity index) can be derived from the hardness and elastic modulus obtained via nanoindentation.38–40,42–44 A higher value of H/E means that the material is more capable of absorbing greater energy in the elastic region, resulting in reduced plastic deformation. Li6PS5Cl typically exhibits a value of approximately 5.0 × 10−2, which aligns well with our result of 5.1 × 10−2.38–40,42–44 As shown in Table 2, a comparison of the H/E values of various electrolytes reveals that Li6PS5Br has the highest value of 5.5 × 10−2, whereas Li5.55PS4.55(BH4)1.45 displays the lowest value of 3.5 × 10−2. It is clear that the H/E is proportional to the inverse of the slope K from the Heckel plot. The H/E ratio, which reflects the balance between elasticity and plasticity, highlights that BH4−-substituted SEs have a higher tendency for plastic deformation, making them mechanically softer and more adaptable for densification during pellet formation. Therefore, it is concluded that the powder compression test is an effective method to evaluate the relative plasticity of solid electrolyte powders for all-solid-state batteries.
Conclusions
In this study, the mechanical behavior of argyrodite-type solid electrolyte powders with different chemical compositions was investigated and compared using both the powder compression and nano-indentation tests. These findings highlight the necessity of considering the mechanical properties, such as the elastic modulus and hardness, when selecting SEs. While lower values may facilitate manufacturability by reducing the required compression stress, it is nevertheless crucial to ensure that the material exhibits adequate stiffness and hardness in order to maintain structural integrity and prevent mechanical failures during battery operation. The presence of voids within solid electrolyte membrane layers during the manufacturing process, as well as under in-service conditions, is a critical issue which may significantly affect the performance and reliability of the cell. Therefore, in the manufacturing process of ASSBs, it is crucial to densify the electrolyte membrane close to the theoretical density. It would be advantageous to select powders with uniform and finer sizes, a higher elastic modulus, and a lower yield stress. On the other hand, the yield stress and the elastic modulus should be high enough to prevent short circuits induced by mechanical damage throughout the entire life in service. A simple powder compression test described in the present study is a quite useful method to compare basic mechanical properties of different solid electrolyte powders and is believed to be helpful in selecting appropriate conditions in the manufacturing process of solid electrolyte membranes for ASSBs.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Seung-Yong Lee and Ji-Hoon Han contributed equally to the preparation of this manuscript. Seung-Yong Lee contributed to the data curation, conceptualisation, formal analysis, investigation, validation, visualisation, and writing of the original draft. Ji-Hoon Han contributed to the data curation, conceptualisation, formal analysis, investigation, validation, visualisation, and writing the original draft. Hyun-Woo Gong contributed to the data curation. Jae-Pyung Ahn contributed to the data curation. Kyung-Woo Yi contributed to the supervision. Young Whan Cho contributed to the data curation, conceptualisation, formal analysis, investigation, validation, and writing of the original draft.Conflicts of interest
There are no conflicts to declare.Notes and references
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed.
- C. W. Sun, J. Liu, Y. D. Gong, D. P. Wilkinson and J. J. Zhang, Nano Energy, 2017, 33, 363–386 CrossRef CAS.
- S. Chen, D. Xie, G. Liu, J. P. Mwizerwa, Q. Zhang, Y. Zhao, X. Xu and X. Yao, Energy Storage Mater., 2018, 14, 58–74 CrossRef.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- A. Sakuda, A. Hayashi and M. Tatsumisago, Sci. Rep., 2013, 3, 2261 CrossRef PubMed.
- J.-M. Doux, Y. Yang, D. H. S. Tan, H. Nguyen, E. A. Wu, X. Wang, A. Banerjee and Y. S. Meng, J. Mater. Chem. A, 2020, 8, 5049–5055 RSC.
- W. D. Jung, J. S. Kim, Y. J. Kim, H. Jeong, D. Han, K. W. Nam, D. Ahn, D. H. Kwon, H. G. Jung, J. H. Lee and H. Kim, Adv. Funct. Mater., 2023, 33, 2211185 CrossRef CAS.
- L. L. Baranowski, C. M. Heveran, V. L. Ferguson and C. R. Stoldt, ACS Appl. Mater. Interfaces, 2016, 8, 29573–29579 Search PubMed.
- Z. Fu and E. Wachsman, J. Am. Ceram. Soc., 2023, 107, 1481–1489 CrossRef.
- G. Liu, W. Weng, Z. Zhang, L. Wu, J. Yang and X. Yao, Nano Lett., 2020, 20, 6660–6665 CrossRef CAS PubMed.
- D. K. Singh, A. Henss, B. Mogwitz, A. Gautam, J. Horn, T. Krauskopf, S. Burkhardt, J. Sann, F. H. Richter and J. Janek, Cell Rep. Phys. Sci., 2022, 3, 101043 Search PubMed.
- W. Zhang, D. A. Weber, H. Weigand, T. Arlt, I. Manke, D. Schroder, R. Koerver, T. Leichtweiss, P. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2017, 9, 17835–17845 CrossRef CAS PubMed.
- Y. Wang and W. H. Zhong, ChemElectroChem, 2014, 2, 22–36 CrossRef.
- Y. Huang, L. Zhao, L. Li, M. Xie, F. Wu and R. Chen, Adv. Mater., 2019, 31, e1808393 Search PubMed.
- M. Cronau, M. Szabo, C. König, T. B. Wassermann and B. Roling, ACS Energy Lett., 2021, 6, 3072–3077 Search PubMed.
- S. Kalnaus, N. J. Dudney, A. S. Westover, E. Herbert and S. Hackney, Science, 2023, 381 Search PubMed.
- Y. Liu, H. Su, Y. Zhong, M. Zheng, Y. Hu, F. Zhao, J. T. Kim, Y. Gao, J. Luo, X. Lin, J. Tu and X. Sun, Adv. Energy Mater., 2024, 14, 2400783 Search PubMed.
- X. Feng, P.-H. Chien, Y. Wang, S. Patel, P. Wang, H. Liu, M. Immediato-Scuotto and Y.-Y. Hu, Energy Storage Mater., 2020, 30, 67–73 Search PubMed.
- L. Zhou, A. Assoud, Q. Zhang, X. Wu and L. F. Nazar, J. Am. Chem. Soc., 2019, 141, 19002–19013 CrossRef CAS PubMed.
- W. D. Jung, J. S. Kim, S. Choi, S. Kim, M. Jeon, H. G. Jung, K. Y. Chung, J. H. Lee, B. K. Kim, J. H. Lee and H. Kim, Nano Lett., 2020, 20, 2303–2309 CrossRef CAS PubMed.
- K.-H. Ni, Z.-L. Chen and C.-C. Li, Acta Mater., 2024, 275, 120057 CrossRef CAS.
- J. Wu, W. Chen, B. Hao, Z. J. Jiang, G. Jin and Z. Jiang, Small, 2024, e2407983 Search PubMed.
- M. D'Amore, L. E. Daga, R. Rocca, M. F. Sgroi, N. L. Marana, S. M. Casassa, L. Maschio and A. M. Ferrari, Phys. Chem. Chem. Phys., 2022, 24, 22978–22986 RSC.
- Z. Deng, Z. Wang, I.-H. Chu, J. Luo and S. P. Ong, J. Electrochem. Soc., 2015, 163, A67–A74 CrossRef.
- Z. Q. Wang, M. S. Wu, G. Liu, X. L. Lei, B. Xu and C. Y. Ouyang, Int. J. Electrochem. Sci., 2014, 9, 562–568 CrossRef.
- I. M. B. Donald Peckner, Handbook of Stainless Steels, McGraw-Hill Book Company, New York, 1977 Search PubMed.
- T. L. G. H. E. Boyer, Metals Handbook, American Society for Metals, Metals Park, Ohio, 1985 Search PubMed.
- A. I. H. C. J. R. Davis, Metals Handbook. Volume 1, Properties and Selection : Irons, Steels, and High-Performance Alloys, ASM International, Materials Park, OH, 10 edn, 1990 Search PubMed.
- P. D. Harvey, Engineering Properties of Steel, American Society for Metals, Metals Park, Ohio, 1982 Search PubMed.
- C. Schneider, C. P. Schmidt, A. Neumann, M. Clausnitzer, M. Sadowski, S. Harm, C. Meier, T. Danner, K. Albe, A. Latz, W. A. Wall and B. V. Lotsch, Adv. Energy Mater., 2023, 13 CAS.
- A. Hassanpour and M. Ghadiri, Powder Technol., 2004, 141, 251–261 CrossRef CAS.
- C. Sun and D. J. Grant, Pharm. Dev. Technol., 2001, 6, 193–200 CrossRef CAS PubMed.
- M. U. Ghori and B. R. Conway, Br. J. Pharm., 2016, 1, 19–29 Search PubMed.
- R. W. Heckel, Trans. Metall. Soc. AIME, 1961, 221, 1001–1008 Search PubMed.
- P. Paronen, Drug Dev. Ind. Pharm., 1986, 12, 1903–1912 CrossRef CAS.
- J. M. Sonnergaard, Int. J. Pharm., 1999, 193, 63–71 CrossRef CAS PubMed.
- Y. T. Cheng and C. M. Cheng, Appl. Phys. Lett., 1998, 73, 614–616 CrossRef CAS.
- R. Yang, T. H. Zhang and Y. H. Feng, J. Mater. Res., 2010, 25, 2072–2077 CrossRef CAS.
- R. Yang, T. H. Zhang, P. Jiang and Y. L. Bai, Appl. Phys. Lett., 2008, 92 CAS.
- J. Musil, F. Kunc, H. Zeman and H. Poláková, Surf. Coat. Technol., 2002, 154, 304–313 CrossRef CAS.
- O. Tutusaus, J. Hempel, S. Thapa, K. Kim, K. E. Kweon, B. C. Wood, L. Hentz, R. C. Hill, R. Mohtadi and Y.-T. Cheng, PRiME, 2024 Search PubMed.
- B. D. Beake, Surf. Coat. Technol., 2022, 442, 128272 CrossRef CAS.
- F. M. El-Hossary, A. M. Abd El-Rahman, M. Raaif and D. A. Ghareeb, Appl. Phys. A:Mater. Sci. Process., 2016, 122, 242 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08604j |
| ‡ These authors contributed equally to the preparation of this manuscript. |
| This journal is © The Royal Society of Chemistry 2025 |


