Reduction of RuO₂ nanoparticles supported on silica by organic molecules: a strategy for nanoparticle redispersion

Abstract

High metal surface area is a critical parameter in metal-based supported heterogeneous catalysts. However, supported metal nanoparticle coalescence or sintering is inevitable and a cause for catalyst deactivation. While reversing the sintering process is challenging, it is an essential topic as this would further extend catalyst use and reduce the consumption of critical raw materials often used in catalysts, e.g., noble metals. The cyclic oxidation–reduction of supported metal nanoparticles is commonly reported as a method for redispersing supported metal nanoparticles. While multiple molecules can be used to reduce supported metal oxide nanoparticles, H₂ is the primary reducing agent used when performing redispersion via oxidation/reduction. Yet, replacing the H₂ with other organic molecules could significantly impact the redispersion phenomena as it is well-known that metal nanoparticles' configuration is affected by molecular adsorption. Herein, we explored organic molecules as reducing agents to reduce silica-supported ruthenium oxide nanoparticles (RuO₂/SiO₂). Six compounds were evaluated: methanol, ethanol, isopropanol, acetone, heptane, and cyclohexane, and the results were compared to the conventional reduction with H₂. The products and the energy released showed two pathways: (i) conversion of RuO₂ to metallic Ru due to oxidative dehydrogenation and oxidation of the reducing agents, and (ii) dehydrogenation of the organic molecules when enough metallic Ru is available. The energy released during reduction was substantially lower with organic molecules (27–85 kJ mol_RuO2⁻¹), as opposed to H₂ (156 kJ mol_RuO2⁻¹). In addition, smaller Ru nanoparticles resulted from the reduction of organic molecules (4.5–7.0 nm) instead of H₂ (11.9 nm). This observation was attributed to a redispersion phenomenon, which was not observed when using H₂, supported by the existence of clusters of small nanoparticles, which were, in turn, impacted by the kinetics of the reduction reaction. The Ru/SiO₂ catalyst was employed in the furfural hydrogenation reaction as a model reaction, where all catalysts reduced with organic compounds displayed a two-fold increase in activity compared to those reduced with H₂.

---

Introduction

The chemical and petrochemical industries heavily rely on metal-based heterogeneous catalysts, typically supported on high-surface-area inorganic materials, such as gamma-alumina, silica, and zeolites.¹ These catalysts are employed in reactions such as Fischer–Tropsch synthesis, methanol synthesis, hydrogenation, dehydrogenation, and catalytic reforming.² While high metal surface area is a critical parameter in metal-based heterogeneous catalysts as it defines the active surface for reaction,³ multiple phenomena can contribute to minimizing this parameter. For instance, supported metal nanoparticle coalescence or sintering is known to occur during reaction conditions, leading to a substantial decrease in the catalyst's active surface and its subsequential deactivation.^3–10 Reversing the sintering process is particularly challenging as thermodynamics favors the phenomenon with a driving force that increases exponentially with the decreasing particle size.¹¹

As the impact of catalyst deactivation by sintering is quite significant in industrial processes that use metal-supported catalysts, considerable effort has been dedicated to reversing this process as a catalyst recycling or regeneration strategy.¹¹ Indeed, the first references to the reactivation of metal catalysts date from the early 1940's.^12,13 Multiple methods exist in the literature for converting large nanoparticles into smaller ones. For instance, halogens like Cl and I in gas form, e.g., HCl, Cl₂, and ICH₃, among others, have been used to redisperse metal nanoparticles.¹⁴ Despite the success of this method, it can lead to the deposition of residual amounts of halogen in the catalyst, which alters its catalytic properties and can lead to deactivation.¹⁵ An alternative method for the redispersion of supported metal particles consists of submitting the catalyst to repeated cycles of oxidation/reduction. Unlike redispersion by halogen interaction, which occurs via increased mobility of halo-metal particles, redispersion by oxidation/reduction follows a “strain model” based on modifying the strain caused by the different densities of oxide and metal.¹¹ Thus, redispersion occurs when oxide and metal coexist in the particles. For this reason, short cycling times are typically used, particularly during the reduction stage when sintering is favored. While redispersion by oxidation/reduction has been extensively studied in the literature, the main focus has been on the impact of process conditions, such as temperature, treatment time, and metal nature.¹¹ A few studies also focused on using alternative reducing and oxidizing agents, particularly CO, as replacements for the standard H₂, which is known to favor sintering.^16,17 Using other molecules to promote the reduction of the oxide particles, in alternative to H₂, could help improve the efficiency of the oxidation/reduction strategy for metal redispersion.¹⁸

Even though the reduction of the metal oxide nanoparticles is generally done at high temperatures in the gas phase, typically via reaction with H₂,¹⁹ conditions which tend to favor sintering, a few other methods have been reported in the literature. For instance, supported metal oxides have been reduced at a laboratory scale via wet chemical reduction methods. Some typical alternative reducing agents are metal borohydrides (NaBH₄ and KBH₄),^20–25 hydrazine (N₂H₄),^26–29 and formaldehyde.^20,26,30,31 For instance, it has been shown that different reducing agents can modify the morphology and dispersion of platinum nanoparticles, which impacts catalytic activity.^32–34 Moreover, metal sintering has been observed to be more intense in H₂ when compared with NaBH₄ ^20,22 or hydrazine.²⁷ Metal–support interactions were also shown to affect the degree of sintering in the reduction using formaldehyde, with particle migration and coalescence being the prominent mechanism.²⁶ These reducing agents also allow mild reduction conditions,³⁵ which can potentially benefit the catalytic properties by promoting well-defined metal nanocrystal facets.³⁶ Nevertheless, some compounds present in these reducing agents, such as boron, sodium, and potassium, are partially impregnated in the catalyst and cause pore blockage and surface area reduction, ultimately affecting the catalytic performance.^20,24 Additionally, these compounds would face challenges for large-scale application since metal hydrides and hydrazine are toxic, explosive, and corrosive. Therefore, their application in the recycling of metal supported heterogeneous catalysts seems unlikely.

In the literature, the study of supported metal nanoparticle reductions is primarily focused on the metal particles with complete disregard for the fact that this process is a chemical reaction, where the supported metal oxide nanoparticles oxidize a molecule while being reduced simultaneously (redox reaction). Indeed, metal oxides are traditional oxidation catalysts employed, among other uses, in reactions such as methanol to formaldehyde, ethylene to ethylene oxide, propylene to acrylic acid, and catalytic oxidation of volatile organic compounds (VOCs).^37,38 Although the final product varies according to the organic molecule, it follows a redox reaction, where lattice oxygen is removed with the consequent formation of an anion vacancy, which is then regenerated by an oxidant, like O₂ (Mars–van Krevelen mechanism).³⁹ In the absence of an oxidant, it is expected the oxide is converted into metal, much like what already occurs with H₂. For example, Maia et al. demonstrated that Ni²⁺ is reduced to Ni⁰ through the oxidation of isobutane.⁴⁰ While examples of the supported metal oxide particle reduction through the oxidation of organic molecules are scarce, doing so could bring significant benefits for the recycling of metal catalysts via oxidation/reduction redispersion since the interaction between gas molecules and metal nanoparticles significantly impacts the particles shape enabling in some cases to stabilize metastable configurations,⁴¹ potentially helping to improve the metal dispersion.

In this view, we report the reduction of silica-supported ruthenium oxide nanoparticles (RuO₂/SiO₂) into their metallic form (Ru/SiO₂) through the oxidation of six organic molecules, viz., methanol, ethanol, isopropanol, acetone, heptane, cyclohexane, and H₂. A catalyst sample with a large RuO₂ nanoparticle size (16.2 nm) was used to evaluate the redispersion phenomena. The reduction process was studied from multiple perspectives, such as the products obtained from the oxidation of the multiple reducing agents by RuO₂, the energy released during the reaction, and the impact of the reduction process on the resulting Ru nanoparticles. Thus, providing the basis for a comprehensive view of the reduction process of supported RuO₂. Finally, the obtained metallic catalysts were used to promote the hydrogenation of furfural as a model reaction to understand the impact of the reduction process on the catalytic performance of the material.

Experimental

Materials

Methanol, anhydrous ethanol, isopropanol, acetone, heptane, and cyclohexane were acquired from Sigma Aldrich and used as received. Calcium oxalate monohydrate (98% – CaC₂O₄·H₂O – Sigma Aldrich) was used as a standard for calibration of mass and Pt/γ-Al₂O₃ (prepared by incipient wetness impregnation from H₂PtCl₆·xH₂O – Sigma Aldrich) for calibration of enthalpy.

Catalyst preparation

The catalyst was synthesized by the incipient wetness impregnation method (IWI), where the precursor RuCl₃·xH₂O (Sigma Aldrich) was added to the support SiO₂ (Alfa Aesar) to achieve 3% metal loading. After drying the remaining powder in air overnight at 105 °C, the solid was calcined at 500 °C (2 °C min⁻¹) for 5 h in static air (S = 197.0 m² g⁻¹, V_p = 1.0 cm³ g⁻¹, Ru (% weight) = 2.92).

Temperature-programmed reduction (TPR)

The catalyst samples (500 mg, particle size 0.425–0.600 mm) were placed inside a tubular quartz reactor, and the catalyst bed was located in the middle of the tubular furnace to ensure a homogeneous temperature profile. The samples were pre-treated at 400 °C for 30 min under argon (50 mL min⁻¹) prior to the experiment to remove adsorbed moisture. After, the samples were cooled down to 100 °C and heated to 375 °C at 4, 6, and 8 °C per minute under a continuous flow of reducing agent (5% in argon). The reducing agent gas mixture was prepared by bubbling argon (50 mL min⁻¹) through a saturator containing methanol, ethanol, isopropanol, acetone, heptane, or cyclohexane. The temperature of the saturator was controlled by a thermostatic bath and was modified to ensure the gas outlet composition was 5 vol% (saturator temperature: methanol (4 °C), ethanol (17 °C), isopropanol (23 °C), acetone (−11 °C), heptane (21 °C), or cyclohexane (5 °C). A mixture of 5% H₂ in N₂ was used to compare with the traditional reduction method. An SRS RGA300 quadrupole mass spectrometer (MS) monitored the gases formed online during the catalyst reduction, i.e., recording between 100 °C and 375 °C. The decomposition of CaC₂O₄·H₂O (50 mg) was used to calibrate used to calibrate the masses of H₂O (m/z = 18), CO (m/z = 28), and CO₂ (m/z = 44) (Fig. S1†) for the mass balance of oxygen.^42,43 The calibration was performed 3 times to ensure reproducibility. CO₂ (m/z = 44) has a fragment with m/z = 28, which was used to follow CO. The contribution of CO₂ fragmentation to m/z = 28 was experimentally measured to be 9% of m/z = 44 and was accounted for in the quantification of CO (m/z = 28).

Enthalpy of reaction

The temperature of the catalytic bed was measured online during the experiments by a K-type thermocouple located inside the reactor in direct contact with the bed. After each TPR experiment, a reference temperature (T_control) was determined by cooling the reactor to 100 °C under pure argon and then heating it again following the same ramp used for the TPR experiment. The difference in temperature between the experiments (ΔT = T_TPR − T_control) was plotted, and the area under the curve is related to the enthalpy of the reaction through correlation with a calibration standard.

The enthalpy of reduction of Pt/γ-Al₂O₃ with H₂ (ΔH_red = −103 kJ mol_H2⁻¹) was used as the standard for calibration.⁴⁴ The catalyst was prepared by incipient wetness impregnation (IWI) using γ-Al₂O₃ from Alfa Aesar. Three experiments with 500 mg of catalyst were conducted, and the temperature was measured in the catalytic bed. Three different metal concentrations were prepared (2%, 3%, and 5% weight) to obtain different amounts of heat released, and a standard curve was used as calibration (Fig. S2†). The concentration of Pt in the catalysts was verified by ICP measurements.

Activation energy

The activation energy of the reaction between silica-supported RuO₂ and the different reducing agents was determined by the Flynn–Wall–Ozawa method.^45,46 This model-free method allows for the calculation of the activation energy based on measuring the temperatures corresponding to fixed values of conversion at different heating rates, according to the equation below:⁴⁷
where, E_a = activation energy (J mol⁻¹), R = ideal gas constant (8.314 J mol⁻¹ K⁻¹), β = heating rate (K min⁻¹).

By plotting ln(β) against 1/T, the slopes give −E_a/R. Heating ramps of 4, 6 and 8 °C min⁻¹ were applied, and the plots were generated. The activation energy was estimated using the H₂O signal (m/z = 18) as a reference, which is produced with all reducing agents applied. Three different percentages of the H₂O peak area were used, i.e., 30%, 50%, and 70% for the calculations.

Nanoparticles characterization

Prior to XRD, HRTEM, and XPS analysis, 250 mg of catalyst samples were reduced in a 100 mL autoclave reactor (Parr model 4566C, Parr Instrument Company) with each one of the organic reducing agents (1.5 g) under 6 bar argon at their respective reduction temperatures (T_peak), for 1 h and without stirring. Following, the solvent was evaporated under argon flow at 350 °C for 30 minutes. The samples had minimal but some exposure to air prior to the analysis.

Powder XRD was performed on a Bruker D8 Advance MKII XRD diffractometer with Cu Kα radiation (λ = 1.54184 Å) operating at 30 kV and 25 mA. Data was collected with a range of 2θ from 10 to 80° and a step size of 0.01°.

The surface-averaged particle size distribution of samples treated with different reducing agents was determined by counting at least 200 particles from images obtained by high-resolution transmission electron microscopy (HRTEM) Hitachi HF5000 Cs-STEM/TEM and applying the formula (D = Σn_id_i³/Σn_id_i²), where D is the particle size (nm), n_i is the number of particles with diameter d_i.⁴⁸ The percentage of clusters of particles was determined based on the number of clusters identified while measuring the 200 particles. The cluster size was determined based on the number-averaged size (D = Σn_id_i/Σn_i). The line scanning measurements and elemental mapping of Ru, O and Si were obtained using the same equipment.

The surface chemistry of the catalysts was monitored by a Thermo Scientific™ Nexsa G2 X-ray photoelectron spectrometer (XPS) equipped with a monochromatic Al Kα (1486.6 eV). High-resolution core-level spectra of Si 2p, O 1s, C 1s Ru 3d, and Ru 3p were recorded using monochromated Al Kα X-rays (1486.6 eV) with a 30 eV pass energy. Charge neutralization was required for all samples. XPS analysis area was 400 μm spot mode, an ellipse of ca. 600 μm by 400 μm. Thermo Scientific™ Avantage Software was used to analyze and fit the data. The peaks were referenced to Si 2p fixed at 103.7 eV.

Furfural hydrogenation

The hydrogenation reactions were conducted in a 100 mL autoclave reactor (Parr model 4566C, Parr Instrument Company) under continuous stirring. The Ru/SiO₂ catalyst (250 mg) was reduced prior to the reaction with each one of the organic reducing agents (1.5 g) under 6 bar argon at their respective reduction temperatures (T_peak), for 1 h and without stirring. Following, the catalyst was dried via evaporative drying at 350 °C under a continuous argon flow. For H₂ reduction, 6 bar H₂ was used, and the same procedure was followed to allow for a comparison between the results. A control experiment was conducted where the catalyst was not reduced prior to the reaction. For the hydrogenation reaction, furfural (250 mg) and water (50 g) were injected into the reactor with the aid of a syringe to avoid exposing the catalyst to air. Before starting the test, the reactor was flushed with H₂ and pressurized at 6 bar. The reactor was heated to 80 °C with a 5 °C min⁻¹ ramp using an electric furnace, where the time was considered from the moment the temperature was reached. After 1 hour reaction time, the vessel was quenched to ambient temperature, and the gases were released.

The liquid samples were analyzed using a Shimadzu GC-2010 gas chromatograph coupled with a flame ionization detector (FID) with an HP-ULTRA-1 column (length: 25 m; internal diameter: 0.20 mm and film thickness: 0.33 μm). After catalyst removal via filtration, 3 μL was injected. The furfuryl alcohol mass yield was determined as follows: mass yield furfuryl alcohol = (final concentration of furfuryl alcohol/initial concentration of furfural) × 100.

Results and discussion

Oxidation of organic compounds during RuO₂/SiO₂ reduction

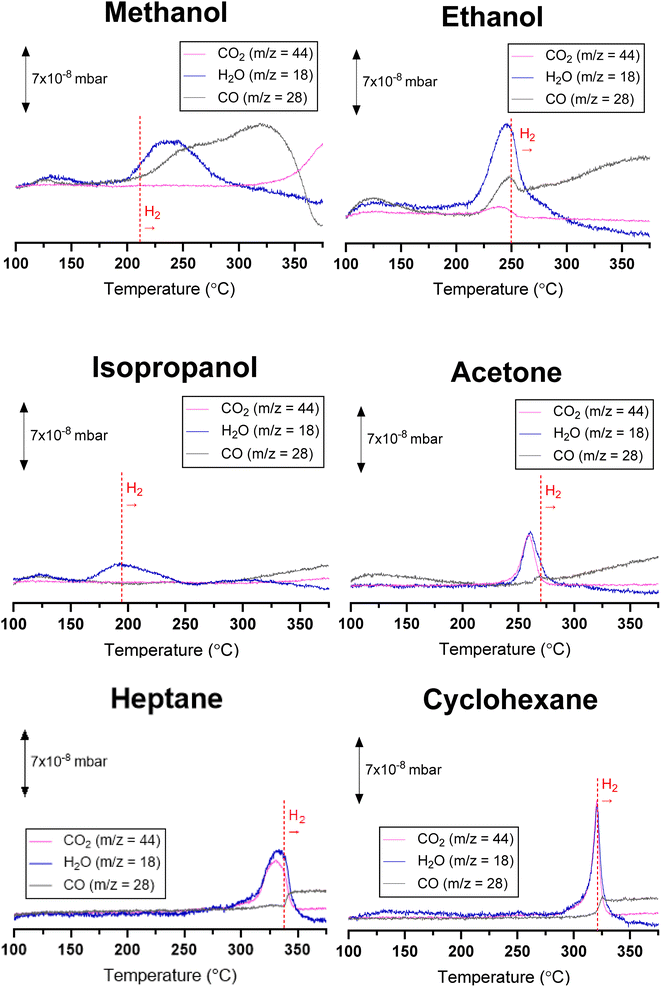
The reduction of RuO₂ particles deposited over SiO₂ (RuO₂/SiO₂) by methanol, ethanol, isopropanol, acetone, heptane, and cyclohexane was studied under increasing temperature, at 4, 6, and 8 °C min⁻¹. The profiles of H₂O (m/z = 18), CO (m/z = 28), and CO₂ (m/z = 44) obtained at 4 °C min⁻¹ are presented in Fig. 1. As a reference, RuO₂/SiO₂ was also reduced with 5% H₂ in N₂ (Fig. S3†), leading to a sole peak at 159 °C, as already reported in the literature.^49,50 The reduction of RuO₂/SiO₂ by the action of H₂ was accompanied by H₂O production, with no other products being detected.

Fig. 1 MS analysis of H₂O (m/z = 18), CO (m/z = 28), CO₂ (m/z = 44) obtained by temperature-programmed reduction (TPR) with different organic compounds at 5% molar concentration in argon using a heating ramp of 4 °C min⁻¹. The dashed lines show the temperature after which H₂ formation was observed.

Mass and energy balance

At least 74.4% of the mass of oxygen from the metal oxide could be accounted for in all the organic molecules evaluated (Fig. 2), indicating H₂O, CO, and CO₂ represent most of the products generated during reduction of RuO₂/SiO₂. Note that the oxygen from the oxygenated reducing agents (alcohols and acetone) has been discounted from the mass balance to account only for the oxygen removed from the metal oxide. While partial oxidation of the reducing agent molecule into products that are not detected could account for the missing oxygen, other phenomena, such as the well-known propensity of silica to be hydroxylated by H₂O,⁵¹ can reduce the amount of H₂O detected at the reactor outlet and contribute to higher experimental error, especially when RuO₂ reduction occurs at a lower temperature. Despite that, the large quantity of oxygen from RuO₂ accounted for in the products strongly indicates that oxide reduction is complete.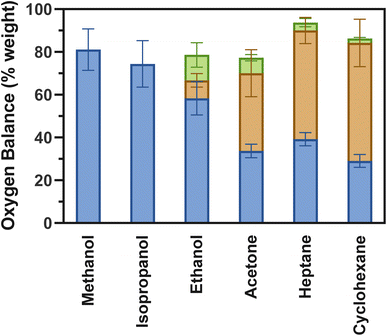

Fig. 2 Mass balance of oxygen from the reaction of RuO₂/SiO₂ with different organic compounds. Only the oxygen from RuO₂ is considered in these calculations and is based on the detected products: H₂O (blue), CO (green), CO₂ (orange). Calculated based on area of peaks in Fig. 1 and calibration curve (Fig. S1†).

The replacement of H₂ by the other reducing agents significantly altered the RuO₂/SiO₂ reduction profile (Fig. 1). Not only the temperature at which RuO₂/SiO₂ underwent reduction was shifted to higher temperatures, i.e., from 159 °C with H₂ to 193–332 °C depending on the molecule used (Table 1), but also, except for isopropanol, CO and CO₂ were detected in addition to H₂O (Fig. 1). Among the alternative reducing agents evaluated in this study, isopropanol presented the lowest temperature for reduction (193 °C), while the highest occurs with heptane (332 °C). Hence, the following order of reduction temperatures was obtained: isopropanol < methanol < ethanol < acetone < cyclohexane < heptane. In all cases, the continuous formation of H₂ (m/z = 2), characteristic of the dehydrogenation of organic compounds on metallic Ru, was observed after the peaks of H₂O, CO and/or CO₂ (Fig. S4†).

Table 1 Temperature of reduction (T_peak) and apparent activation energy (E_app) from the reduction of RuO₂/SiO₂ catalysts with 5% organic solvent in argon and 5% H₂ in nitrogen

Reducing agent	T peak (°C)	E app (kJ molRuO2^−1)
a This temperature was determined as the maximum of the peak from Fig. 3. b Apparent activation energy (Eapp) determined through the Flynn–Wall–Ozawa method.^45,46
H2	159	44.6 ± 2.3
Methanol	233	45.4 ± 0.7
Ethanol	244	74.7 ± 8.5
Isopropanol	193	34.3 ± 0.6
Acetone	261	68.7 ± 5.0
Heptane	332	56.8 ± 6.6
Cyclohexane	322	84.9 ± 6.5

---

The limited formation of H₂O, CO, and CO₂ in the presence of RuO₂/SiO₂ and reducing agents is a consequence of the limited supply of oxygen from RuO₂ particles. However, the variation in the temperatures and H₂O, CO₂, and CO formation profiles suggests not all reducing agents are oxidized by RuO₂ particles in the same way.

The apparent activation energy (E_app) for reduction of RuO₂ nanoparticles reduction, presented in Table 1, was estimated using the Flynn–Wall–Ozawa method (Fig. S5†).^45,46 The E_app for RuO₂/SiO₂ reduction using H₂ was estimated at 44.6 ± 2.3 kJ mol⁻¹, which is comparable with the value of 46.3 kJ mol⁻¹ reported in the literature, validating the method.⁵² As expected, the activation energy varies with the reducing agent, ranging from 34 to 85 kJ mol_RuO2⁻¹ in the following ascending order: isopropanol < H₂ ∼ methanol < heptane < acetone < ethanol < cyclohexane (Table 1). By definition, E_app provides information on the temperature dependence on a reaction. Consequently, higher activation energy indicates that, once reduction starts, it will be completed more quickly under dynamic temperature conditions. For instance, reduction with cyclohexane occurs more quickly than with heptane, despite both happening at similar temperatures. Thus, the wide range of E_app indicates different rates for the reduction of the nanoparticles, as discussed in later sections.

Redox reactions, such as the reduction of RuO₂/SiO₂, are exothermic. When H₂ is employed as the reducing agent, only one reaction is possible because of its chemical nature (2H₂ + RuO₂ → Ru + 2H₂O). However, multiple reactions occur when organic molecules are employed, resulting in a net ΔH_reaction that differs from that of any individual reaction. Thus, information about the heat released during this process assists in elucidating the reaction pathway.

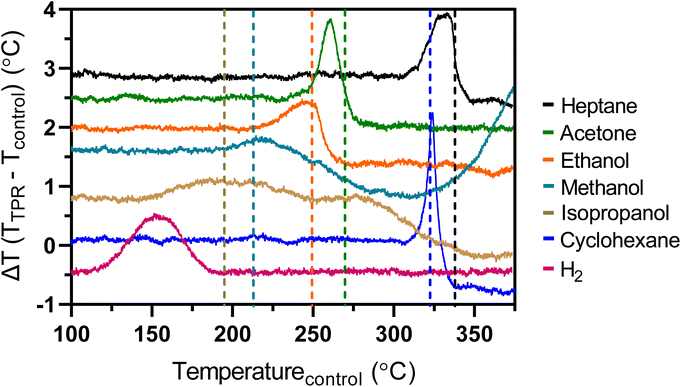
The temperature on the catalyst bed was measured for each TPR experiment (T_TPR), including H₂, and compared to the temperature of a control experiment without reduction (T_control), where only the effect of catalyst bed heating is considered (ΔT = T_TPR − T_control). In all cases, a temperature rise was observed when the reduction of RuO₂/SiO₂ to Ru/SiO₂ took place (Fig. 3). Once RuO₂/SiO₂ was reduced, the ΔT was inferior to that occurring just before reduction for all reducing agents, except for H₂. This negative baseline, i.e., ΔT_{before reduction} > ΔT_{after reduction}, indicates the occurrence of an endothermic reaction after reduction. Indeed, the formation of H₂ was observed for all reducing agents after reduction (Fig. 1 and S4†), indicating the occurrence of dehydrogenation, an endothermic reaction (Table 2). In addition, methanol oxidative dehydrogenation and ethanol dehydro-decarbonylation, for methanol and ethanol, respectively, are endothermic reactions and could explain the negative baseline for these compounds (Fig. 3 and Table 2). In the case of methanol, ΔT increased steadily for temperatures above ∼320 °C suggesting that an exothermic reaction takes place, such as reverse Boudouard reaction or water–gas shift (WGS).

Fig. 3 Temperature profiles of reduction using seven different reducing agents, including H₂, at 4 °C min⁻¹. The dashed lines represent the temperature after which H₂ formation was observed. Area under the curves represents the enthalpy of reaction.

Table 2 Enthalpy of reduction (ΔH_reaction) and reactions involved in the reduction of Ru/SiO₂ catalysts with H₂ and organic compounds

	ΔHreaction (kJ molRuO2^−1)	Reaction	Stoichiometry	ΔHreaction^a (kJ molRuO2^−1a or kJ molH2^−1b)
a The ΔHreaction were calculated based on eqn (S1) and (S2) and thermodynamic parameters from Table S1.
H2	−156 ± 19	Oxidation	2H2(g) + RuO2(s) → Ru(s) + 2H2O(g)	−164.8^a
Methanol	−42 ± 4	Oxidative dehydrogenation	CH3OH(g) + RuO2(s) → Ru(s) + 2H2O(g) + CO(g)	−80.8^a
		Oxidative dehydrogenation-2	2CH3OH(g) + RuO2(s) → Ru(s) + 2H2O(g) + 2CH2O(g)	−17.5^a
		Reverse methanol synthesis		42.2^b
Ethanol	−27 ± 8	Oxidation	C2H5OH(g) + 3RuO2(s) → 3Ru(s) + 3H2O(g) + 2CO2(g)	−112.0^a
		Oxidative dehydrogenation	2C2H5OH(g) + RuO2(s) → Ru(s) + 2H2O(g) + 2C2H4O(g)	−23.1^a
		Dehydro-decarbonylation		55.6^a
		Dehydrogenation		75.5^b
Isopropanol	−85 ± 12	Oxidative dehydrogenation	2C3H7OH(g) + RuO2(s) → Ru(s) + 2H2O(g) + 2C3H6O(g)	−120.0^a
		Dehydrogenation		26.6^b
Acetone	−43 ± 5	Oxidation	C3H6O(g) + 4RuO2(s) → 4Ru(s) + 3H2O(g) + 3CO2(g)	−100.0^a
		Oxidative dehydrogenation	2C3H6O(g) + RuO2(s) → Ru(s) + 2H2O(g) + 2C3H4O(g)	159.4^a
		Dehydrogenation		170.3^b
Heptane	−79 ± 10	Oxidation	C7H16(g) + 11RuO2(s) → 11Ru(s) + 8H2O(g) + 7CO2(g)	−94.9^a
		Oxidative dehydrogenation	2C7H16(g) + RuO2(s) → Ru(s) + 2H2O(g) + 2C7H14(g)	99.3^a
		Dehydrogenation		137.9^b
Cyclohexane	−41 ± 4	Oxidation	C6H12(g) + 9RuO2(s) → 9Ru(s) + 6H2O(g) + 6CO2(g)	−94.4^a
		Oxidative dehydrogenation	2C6H12(g) + RuO2(s) → Ru(s) + 2H2O(g) + 2C6H10(g)	77.1^a
		Dehydrogenation		126.7^b

---

The experimental enthalpies of reaction (ΔH_reaction) for the reduction of RuO₂/SiO₂ by each reducing agent, including H₂, are displayed in Table 2. As multiple reactions occur during the reduction of RuO₂/SiO₂, the overall experimental heat of reaction (ΔH_reaction), presented in Table 2, reflects the combination of these reactions. The enthalpy of each individual reaction considered to occur during the RuO₂/SiO₂ reduction process is also presented in Table 2.

The measured enthalpy of RuO_2/SiO₂ reduction by H₂ was −156 ± 19 kJ mol_RuO2⁻¹, in reasonable agreement with the theoretical value of −164.8 kJ mol⁻¹ in Table 2, validating the method. While the ΔH_reaction was highly dependent on the reducing agent, all organic molecules released significantly less heat during reduction than H₂. Hence, the following order can be established according to the heat released during the reduction of RuO₂/SiO₂: H₂ ≫ isopropanol ≈ heptane > methanol ≈ cyclohexane ≈ acetone > ethanol.

Reaction pathways for each reducing agent

Hydrocarbons. For heptane and cyclohexane, full oxidation is the primary pathway for reducing RuO₂/SiO₂ since slightly more water is produced than the expected for oxidative dehydrogenation. The typical mechanism for the oxidation of saturated hydrocarbons on metal surfaces starts with hydrogen extraction from a C–H bond, which is the limiting step of the reaction.⁵³ Hence, the higher energy required for the cleavage of C–H bonds in hydrocarbons is most likely related to the higher temperature necessary for the reducing agents to promote the reduction of RuO₂/SiO₂, i.e., T > 300 °C. After activation, the reaction proceeds quickly in noble metals under oxygen-rich conditions.⁵³ However, during RuO₂/SiO₂ reduction, oxygen supply is limited, which could explain the formation of CO. Still, CO formation is minimal and only occurs at later reduction stages, i.e., at a higher temperature, when oxygen availability in the system is reduced (Fig. 1). An increase of m/z = 28 observed after RuO₂ reduction could be due to cracking of heptane and cyclohexane to small molecules, like ethylene (m/z = 28).⁵⁴

The ΔH_reaction for the two hydrocarbons was inferior to the theoretical value of RuO₂ reduction via hydrocarbon oxidation (Table 2). While both compounds display similar heat of reaction for oxidation by RuO₂, oxidative dehydrogenation of cyclohexane (77.1 kJ mol_RuO2⁻¹) is less endothermic than that of heptane (99.3 kJ mol_RuO2⁻¹). However, the experimental ΔH_reaction for each compound indicates the reduction of RuO₂/SiO₂ by heptane is more exothermic (Table 2). Thus, hydrocarbon dehydrogenation, an endothermic phenomenon, contributes to the heat of reduction, as observed by the sharp fall in ΔT is observed at the same time H₂ starts being produced via dehydrogenation (Fig. 3). Thus, the overall energy released during the reduction of RuO₂/SiO₂ is counter-balanced by the endothermic nature of the dehydrogenation, which for cyclohexane starts at earlier stages of reaction than for heptane (Fig. 1), making the ΔH_reaction lower. Note that the endothermic contribution of the dehydrogenation to the ΔH_reaction will depend on the moment RuO₂/SiO₂ reduction started, the ΔH_reaction (Table 2), and the rate of reaction, which was not measured. Still, the difference between the ΔT baseline before and after reduction in Fig. 3 and the evolution of H₂ (Fig. S4†) can be used to compare the H₂ production rate between reducing agents.

Alcohols. The reduction of RuO₂/SiO₂ by alcohols occurs preferentially by the abstraction of hydrogen and consequent release of H₂O. For the alcohols evaluated, one can see the following trend of reducing temperature: isopropanol (193 °C) < methanol (233 °C) < ethanol (244 °C), indicating isopropanol is more easily activated than methanol and ethanol. Indeed, the C–C bond cleavage in isopropanol is not favored during oxidation. Consequently, only oxidative dehydrogenation occurs with this reducing agent, as confirmed by the observed formation of acetone (Fig. S6†).⁵⁵

For ethanol, the simultaneous formation of CO and CO₂ indicates C–C cleavage occurred during RuO₂/SiO₂ reduction. The higher temperature necessary for the activation of ethanol versus isopropanol (Table 1) could be explained by the higher reactivity of secondary alcohols, compared to primary alcohols. It is noteworthy that CO is not typically reported as a reaction product for ethanol oxidation, due to fast CO oxidation to CO₂ over RuO₂.⁵⁶ Yet, the limited supply of oxygen for oxidation in the system might hinder CO conversion to CO₂. Ethanol can also undergo dehydrogenative decarbonylation over metallic ruthenium, yielding CO, H₂, and CH₄,^57,58 as confirmed by the significant formation of CH₄ during and after reduction (Fig. S7†). Like cyclohexane and heptane, the ΔT drop observed when using ethanol coincided with the start of H₂ production (Fig. 3), suggesting dehydrogenation might also contribute to the lower ΔH_reaction.

In the specific case of methanol, CO and H₂O are predominant during RuO₂/SiO₂ reduction (Fig. 1), with formaldehyde (m/z = 29) being observed as well (Fig. S8†), suggesting the pathway goes through methanol oxidative dehydrogenation. Based on this, the CO generated by methanol decomposition (Fig. 1) was not considered in the oxygen mass balance (Fig. 2). In addition, an increase of m/z = 44 attributed to side reactions over Ru metal particles, was observed after RuO₂ reduction. Indeed, the water–gas shift reaction (CO + H₂O ⇌ CO₂ + H₂) between the water contained in the methanol or the reverse Boudouard reaction (2CO ⇌ CO₂ + C) could explain the formation of CO₂ after the reduction is complete. Like the other alcohols, the ΔT observed with methanol also declined after H₂ started to be produced, even though RuO₂/SiO₂ reduction was still underway (Fig. 1 and 3).

Acetone. The conversion behavior for acetone over RuO₂/SiO₂ was similar to that of cyclohexane and heptane since it was mainly converted to oxidation products. However, this molecule started to react with RuO₂/SiO₂ at 234 °C, indicating its activation was an intermediate between the alcohols and hydrocarbons, as expected according to the literature.⁵⁹ No products resulting from acetone aldol condensation (mesityl oxide) and acetone decarbonylation (methane) were observed, thus leaving dehydrogenation of acetone as the only plausible reaction to justify the observed formation of H₂. Still, acetone dehydrogenation has not been reported in the literature, as it requires the rearrangement of the molecule to prevent the carbon atom in the carbonyl group from forming more than four covalent bonds (octet rule). It is worth mentioning that isomerization of acetone into propanal, allyl alcohol, and propylene oxide has been reported in the literature, with acetone being the most stable of all isomers.⁶⁰ Yet, independently of the reaction mechanism involved in the monomolecular dehydrogenation of acetone, acrolein (2-propenal) is the most likely product for this reaction. While the molecular ion of acrolein (m/z = 56) was not measured, this molecule undergoes fragmentation into m/z = 28 (Fig. S9†), which increases at a rate similar to H₂ (Fig. S10†), thus suggesting acrolein is indeed formed.

Summary. The combined analysis of the oxygen mass balance and the ΔH_reaction during RuO₂/SiO₂ reduction revealed two simultaneous processes occur (Scheme 1). The first corresponds to the exothermic reduction of the RuO₂ nanoparticles promoted by oxidative dehydrogenation or oxidation of the reducing agent. Once enough metallic Ru is present to catalyze the dehydrogenation of the reducing agent, an endothermic process starts, which continues after the RuO₂ nanoparticles are completely reduced. In fact, at the later stages of the RuO₂ nanoparticles reduction occurs by direct oxidative dehydrogenation of the reducing agent, whose oxidation does not proceed due to the lack of oxygen in the nanoparticle, and/or by the oxidation of H₂ produced from the reducing agent dehydrogenation on a nearby metal site. Hence, the mechanism involved in reducing the RuO₂ nanoparticles is a function of the reduction level of the particles. The combination of both processes explains the significant reduction of the ΔH_reaction when comparing reducing agents to H₂, where the endothermic process does not occur. Nonetheless, it should be mentioned that even in the absence of the endothermic process, RuO₂/SiO₂ reduction via the oxidation of organic reducing agents should be less exothermic than H₂, as shown by the theoretical ΔH_reaction in Table 2.

Scheme 1 Simplified pathway of reactions involved during reduction of supported metal oxides using organic molecules.

Characterization of nanoparticles

The XRD pattern of RuO₂/SiO₂ and its comparison with the resulting catalysts after treatment with H₂ and organic molecules are presented in Fig. 4. The diffraction peaks of the initial sample are centered at 2θ = 27.8°, 34.8°, 39.9°, and 53.9°, which correspond to lattice plans of RuO₂ (110), (101), (200), and (211), respectively.⁶¹ Additionally, the peaks at 38.5°, 42.0°, 43.9°, 58.3°, 69.3° correspond to lattice plans of Ru⁰ (100), (002), (101), (102), and (110),⁶² respectively, and were observed in all the samples after treatment with organic compounds and H₂. Thus, suggesting RuO₂ was converted to metallic Ru. Furthermore, the absence of RuO₂ characteristic peaks after reduction independently of the reducing agent used, including H₂, indicates that all RuO₂ was reduced, as suggested previously.

Fig. 4 XRD patterns of RuO₂/SiO₂, compared with the results after the treatment with different organic reducing agents and H₂.

The variation of the Ru sharpness peaks in the XRD diffractograms (Fig. 4) indicates differences in the particle size of Ru nanoparticles between samples. Indeed, by applying the Scherrer equation (Table 3), it is possible to estimate the Ru nanoparticle size to 10.0 nm when using H₂ and 2.5–5.8 nm when using the organic molecules as reducing agents, indicating that reducing supported RuO₂ nanoparticles through the oxidation of organic molecules yields smaller Ru particles than with H₂.

Table 3 Particle size of RuO₂ deposited on SiO₂ and resulting Ru nanoparticles after reduction with each reducing agent

Reducing agent	Particle size^a (Scherrer equation) (nm)	Particle size (HR-TEM) (nm)	Particles in cluster^b (HR-TEM) (%)	Cluster size^b (HR-TEM) (nm)	Surface Ru concentration^c (% atom)	Surface C concentration^c (% atom)	Ru/C
a Calculated based on data from Table S2. b Clusters are agglomerates of nanoparticles. NA: not applicable. c Quantification based on Ru 3d and C 1s XPS signals. Complete surface composition in Table S4. XPS wide spectra, and Ru 3d/C 1s peak deconvolution spectra in Fig. S11 and S12, respectively.
None (RuO2/SiO2)	13.8	16.2 ± 6.0	N.A.	N.A.	0.19	1.4	0.13
H2	10.0	11.9 ± 3.4	0	N.A.	0.36	2.1	0.17
Methanol	4.5	4.7 ± 1.7	52	17.8 ± 8.3	0.32	1.0	0.32
Ethanol	2.5	5.3 ± 2.3	38	21.2 ± 10.9	0.46	1.6	0.28
Isopropanol	4.5	6.6 ± 2.9	64	22.1 ± 9.8	0.23	2.9	0.08
Acetone	4.4	4.9 ± 1.9	43	17.0 ± 9.4	0.43	1.3	0.43
Heptane	4.7	6.7 ± 2.9	26	19.3 ± 10.9	0.32	1.1	0.29
Cyclohexane	5.6	6.6 ± 1.9	4	35.8 ± 7.1	0.45	1.2	0.45

---

The samples were also analyzed by high-resolution transmission electron microscopy (HR-TEM) to determine their particle size distribution. Firstly, carbon deposit was not observed, which was further confirmed by the XPS analysis since the quantity of carbon is comparable to that from reduction with H₂ (Table 3). Additionally, the mapping of the samples was performed to verify if the RuO₂ nanoparticles reduction to Ru was complete, as suggested by XRD. The elemental mapping and line scanning (Ru, Si, and O) of the starting metal oxide catalyst and the reduced sample are presented in Fig. 5. When comparing the line scanning of the parent sample (RuO₂/SiO₂) with those of the reduced samples, it is possible to observe that the oxygen profile of the reduced samples does not follow that of Ru, unlike in the parent sample (Fig. 5A). Instead, oxygen is only observed in the presence of Si, clearly indicating no oxygen is present in the metal particles and that the reduction was complete independently of the reducing agent. Similarly, the lattice fringe distance of the parent RuO₂ nanoparticles was 3 Å (Fig. 5A), agreeing with the (110) plane of RuO₂,⁶³ while for the reduced samples (only represented in Fig. 5B) the distance was 2 Å, as in the (101) plane of hcp (hexagonally close packed) ruthenium.⁶⁴ The XPS results (Table 3) also confirm the predominance of Ru metallic nanoparticles. Note that the material was exposed to air for analysis; hence, surface oxidation is expected.

Fig. 5 HRTEM image of Ru particles, elemental mapping and EDS line scan (Ru, Si, O), and particle size histogram of Ru/SiO₂ catalysts reduced with (A) starting catalyst and catalyst reduced with (B) ethanol, (C) methanol, (D) isopropanol, (E) acetone, (F) heptane, (G) cyclohexane and (H) H₂. Arrows indicate the direction of the line scanning measurement.

The particle size distribution of the parent RuO₂/SiO₂ sample and reduced samples can be found in Fig. 5 and Table 3. In all cases, the average particle size of the starting metal oxide catalyst is larger (16.2 nm) than after reduction (4.7–11.9 nm), with the HRTEM results in agreement with those estimated through the Scherrer equation (Table 3). A decrease in the particle size is expected since Ru has a higher bulk density (12.2 g cm⁻³ at 20 °C) than RuO₂ (6.97 g cm⁻³ at 20 °C). Still, the estimated diameter of Ru particles obtained from 16.2 nm RuO₂ particles is 12.3 nm, as presented in Table S3.† While the H₂ reduced sample yields Ru nanoparticles with an average size comparable with the estimated size, i.e., 11.9 ± 3.4 nm vs. 12.3 nm respectively, using organic compounds as reducing agents yields significantly smaller particles. Consequently, the use of organic compounds led to a redispersion of the Ru nanoparticles over the SiO₂ support, while H₂ only transformed RuO₂ into Ru with minimal interference to the expected particle size. It is worth mentioning that when oxidation/reduction methods are employed to promote redispersion, particle size reduction occurs primarily during the oxidation stage.¹¹

Even though all the samples reduced via organic agents displayed redispersion of the Ru particles, clusters of small Ru nanoparticles, as shown in Fig. 5B, were observed. This same phenomenon was observed for all organic agents to different extents, but it was more pronounced with isopropanol, where 64% of the metal particles were such clusters (Table 3). On the other hand, only 4% of the Ru nanoparticles were agglomerated in clusters when using cyclohexane. The occurrence of nanoparticles as clusters increases in the following order: cyclohexane (4%) ≪ heptane (26%) < ethanol (38%) < acetone (43%) < methanol (52%) < isopropanol (64%). While the occurrence of these clusters varied significantly with the reducing agent, the average size of these clusters was quite similar, i.e., 17.0–22.1 nm, except for cyclohexane (35.8 nm), which can be justified by the low occurrence of clusters when using this reducing agent. It should be mentioned that no Ru nanoparticles cluster was found when using H₂ to reduce RuO₂/SiO₂.

Impact of reduction pathway on the characteristics of the nanoparticles

The differences in the particle size observed between H₂ and the reducing agents, the capacity of these compounds to promote the redispersion of Ru nanoparticles during reduction, and the occurrence of clusters of Ru nanoparticles suggest that organic reducing agents significantly modify the reduction process of supported RuO₂ nanoparticles. The mechanism of oxide nanoparticles undergoing reduction and possibly redispersion is complex and not fully understood. In simple terms, metal nuclei are formed at the nanoparticle's surface during metal oxide reduction, expanding during the reduction process.⁶⁵ The evolution of the reduction process depends on multiple aspects, especially the nature of the support and metal temperature,¹¹ the size of the metal nanoparticles, and, as shown by this work, the reducing agent or reducing atmosphere.

Reduction and oxidation of supported nanoparticles are often used to promote the redispersion of nanoparticles, i.e., decrease the nanoparticle size.^11,65,66 In the specific case of reduction, multiple mechanisms have been proposed in the literature, including atomic migration of metallic/metal oxide atoms, strong metal–support interaction (SMSI),⁶⁷ and differences between the interaction (wetting) of oxide and metal with the support.^65,66,68,69 In the specific case of RuO₂/SiO₂ system, no SMSI is expected under the experimental conditions due to the low temperature and low capacity of SiO₂ to strongly interact with RuO₂ or Ru. Similarly, atomic migration implies gas phase diffusion,⁶⁶ and both RuO₂ and Ru have very high boiling points, i.e., 1200 °C and 4150 °C, respectively, even considering typical depression due to the nanometric size of the particles. Finally, while the different affinities of the support with metal oxide (strong) and metal (weak), and the increase in the density of the nanoparticles (ρ_metal > ρ_{metal oxide}) can create stress in the particle and lead to cracks, this mechanism cannot explain the differences between the different reducing agents by itself.

The temperature at which nanoparticles are exposed is a critical parameter for redispersion and sintering phenomena.^11,70 While RuO₂ reduction was found to happen at different temperatures depending on the reducing agent used (Table 1), the samples used for the nanoparticles size measurement were all submitted to the same maximum temperature of 375 °C, which is lower than the typical temperatures reported to cause sintering, i.e., T > 400 °C.¹¹ Furthermore, reduction with H₂ led to the largest metal particles, while it displayed the lowest reduction temperature, i.e., T_reduction = 159 °C. Another important parameter that can contribute to significant changes in the local temperature of the supported nanoparticles is the energy released during the reduction process. It is well-established that excessive heat can cause sintering in metal-based catalysts due to the formation of thermodynamically favorable coarse-grained structures.⁷¹ The impact of the energy released during RuO₂ reduction in the Ru nanoparticle distribution, shown in Fig. 6, indicates that lower ΔH_reaction favors the formation of smaller particles. However, the highest ΔT observed in the reactor bed was ∼2.5 °C (Fig. 3), thus making it unlikely for the local temperature in the nanoparticle to be high enough to promote aggregation. Indeed, Ano et al. showed that a continuous supply of microwave radiation with a potency of ∼20–60 W was necessary to increase the local temperature of supported platinum nanoparticles by a couple of hundred degrees,⁷² with equally high values being reported to achieve similar local heating of nanoparticles in solutions.⁷³ On the other hand, reducing RuO₂ nanoparticles over silica only releases a few joules of energy, i.e., 5–23 J, during the several minutes the transformation takes place (Fig. 1 and 3). Thus, the energy released during the reduction process is more than two orders of magnitude smaller than the necessary for the local temperature of nanoparticles, i.e., T > 400 °C, to promote aggregation.

Fig. 6 Enthalpy of reaction (ΔH_reaction) versus average particle size for Ru/SiO₂ catalysts reduced with different reducing agents.

An important difference between the reduction process of RuO₂ promoted by the organic agents compared to H₂ is that two thermic processes happen at different stages, ultimately leading to the low ΔH_reaction observed. First, the oxidation or oxidative dehydrogenation of the reducing agent by the RuO₂ nanoparticles takes place (exothermic), followed by the dehydrogenation of the same reducing agent when enough Ru surface is available (endothermic). Thus, it could be hypothesized that redispersion was observed when using the organic compounds as reducing agents due to this two-stage process, rather than directly because of the released energy.

According to the nanoparticle reduction mechanism proposed by T. Wang and L. D. Schmidt,⁶⁵ cracks caused by elastic stress resulting from the higher density of the newly formed metal can be formed in oxide nanoparticles during the reduction process if the number of nucleation points is small, i.e., the reduction does not proceed homogeneously through the whole nanoparticle. If we take into consideration the difference in the cross-sectional area (σ, where ,⁷⁴ where M_w is the molecular weight, ρ is the density of the liquid, and N_A is the Avogadro number of the adsorbed organic molecules (σ = 0.18 nm² (methanol)–0.42 nm² (heptane)) and H₂ (σ = 0.14 nm²)), it would be expected that the number of nucleation points would be smaller when using the organic molecules to promote the reduction of the RuO₂ nanoparticles. Furthermore, each H₂ molecule only eliminates one atom of oxygen from the RuO₂ matrix while, except for isopropanol, all the remaining organic agents were proven to remove multiple oxygen atoms per molecule (Table 2). In addition, the intermediates formed during the oxidation of the organic molecules are more reactive than the parent molecule, thus increasing the driving force for RuO₂ reduction once the reaction starts. Therefore, the lower incidence of nucleation points linked to a faster driving force for reduction could explain the increased occurrence of “cracks” in the reduction of RuO₂ nanoparticles. This, in turn, would be linked to the higher occurrence of smaller nanoparticles and agglomerates when using organic reducing agents without justifying why these do not persist when using H₂.

The coalescence or sintering of nanoparticles is directly linked to the chemical potential of the metallic surface.^71,75 In general, the chemical potential of nanoparticles surface is impacted by the nature of the metal, the support, and the nanoparticle size, i.e., smaller nanoparticles have higher chemical potentials. Besides being related to the capacity of nanoparticles to sinter, the chemical potential also impacts the strength of the bond of each reaction intermediates to the metal surface.⁷⁵ As described earlier, during the reduction of RuO₂ nanoparticles by the organic reducing agents, the formation of H₂ from dehydrogenation was observed. Dehydrogenation at the later stages of reduction directly indicates the adsorption of the organic molecules on the newly formed metal surface. Note that metal nanoparticles are not rigid, and the interaction of adsorbed molecules with the surface of metallic nanoparticles was shown in multiple studies to significantly affect nanoparticle shape.^76–80

In addition, when the surface of the metal is completely clean, coalescence may happen.⁸¹ Hence, dehydrogenation intermediates covering the metal surface during the reaction process could explain the observed nanoparticle clusters and redispersion phenomenon. However, when using H₂, no reaction occurs after RuO₂ reduction is achieved, and any “cracks” formed on the nanoparticles readily disappear due to the high chemical potential of small nanoparticles. It is worth mentioning that the restructuration of metal catalysts via the detachment of smaller nanoparticles, clusters, or single atoms during catalytic reactions is not a new concept. For instance, Ananikov proposed that, in some cases, the actual catalytic center was constituted by smaller metal clusters or atoms detached from the nanoparticle surface into the solution (liquid phase reaction) to promote the reaction (cocktail concept).^80,82,83 Similarly, the atomic leaching of metal nanoparticles was observed through microscopy, as was metal nanoparticle reconstruction in the presence of different gas atmospheres.^80,84,85 According to the mechanisms mentioned earlier, forming isolated atoms (single atoms) is possible even though these were not observed.

While all organic compounds led to the formation agglomerated nanoparticle clusters, not all particles were contained in such agglomerates (Table 3). Indeed, the concentration of metal nanoparticles in clusters varied significantly with the type of organic reducing agent. For instance, only 4% of Ru particles were contained in clusters using cyclohexane, while 64% were observed for isopropanol. Fig. 7 shows the impact of the apparent activation energy (E_app) for reducing RuO₂ nanoparticles as a function of the occurrence of Ru nanoparticles in clusters. For the organic reducing agents, it can be observed that higher E_app leads to fewer clusters. Under increasing temperature conditions, a higher E_app is related to a faster reduction rate, as can be observed by comparing the reduction profiles of cyclohexane (high E_app) and isopropanol (low E_app) in Fig. 1. Therefore, a faster reduction rate of RuO₂ should favor the “cracking” of the nanoparticles during reduction, which ultimately can lead to the complete breaking of larger particles into new, smaller, and isolated metal nanoparticles. It should be noted that the H₂ does not behave similarly to the organic reducing agents since it does not have adsorbates after the oxide is fully reduced.

Fig. 7 Apparent activation energy (E_app) of the reduction of the RuO₂ nanoparticles supported on SiO₂versus the occurrence of nanoparticles in clusters. Dotted line represents trend of the data, excluding H₂.

Furfural hydrogenation – a model reaction

The hydrogenation of furfural to furfuryl alcohol was conducted to evaluate the catalytic performance of the metal nanoparticles obtained from the reduction of RuO₂/SiO₂ with each of the reducing agents. The need for metallic sites and the capacity to undergo hydrogenation by H₂ under temperatures below the temperature at which H₂ promotes RuO₂ reduction justify the use of this model reaction. Therefore, the hydrogenation of furfural into furfuryl alcohol was performed at 80 °C and under 6 bar H₂. The reaction was conducted using water as a solvent to eliminate the possibility of hydrogen transfer from the solvent to the substrate. A control experiment without prior reduction of the catalyst showed negligible (<3%) mass yield of furfuryl alcohol even after 1 hour reaction time.

The catalytic performance of the reduced catalyst for the furfural hydrogenation reaction clearly demonstrates that organic molecules can be used as reducing agents instead of H₂. When the catalyst was reduced with H₂ before the reaction, the activity was 1.5–3-fold lower than when the organic reducing agents were employed (Table 4). These results also eliminate the doubt over any possible decline in activity following catalyst fouling promoted by organic reducing agents, thus agreeing with the XPS and TEM data. A trend between activity and particle size after reaction is apparent, albeit not perfectly uniform across all data points. This could be attributed to the formation of particle clusters in all cases and for all images analyzed (not shown), which causes the adsorption of molecules to be non-linear.¹¹

Table 4 Activity at 1 hour reaction time (20–40% conversion) and particle size after hydrogenation of furfural, reaction conditions: 80 °C, 50 g water, 250 mg furfural, 250 mg catalyst

Reducing agent	Activity (molfurfural molRu^−1 h^−1)	Particle size after reaction (nm)	Furfuryl alcohol selectivity (%)
a Tetrahydrofurfuryl alcohol observed as side product.
H2	5.3	9.1 ± 2.5	67.8^a
Methanol	8.7	6.5 ± 2.1	100
Ethanol	15.4	2.9 ± 0.7	100
Isopropanol	16.4	6.0 ± 1.6	97.3^a
Acetone	13.3	4.6 ± 1.1	100
Heptane	16.9	5.1 ± 1.6	100
Cyclohexane	15.2	6.2 ± 1.7	100

---

Outlook

Most metals, such as ruthenium, used in catalysts are now labeled critical raw materials.⁸⁶ Thus, finding solutions for reusing such materials is of prime importance. Redispersion can be a simple method for restoring the catalytic properties of spent metal-based catalysts without using harsh chemicals and temperatures often employed in other methods.⁸⁷ This manuscript shows that using organic molecules to reduce metal oxides can significantly improve the redispersion phenomenon. Yet, the exact mechanism responsible for the enhanced redispersion still needs to be established. Nonetheless, the metal oxide nanoparticle reduction pathway is quite complex and highly dependent on the molecule undergoing oxidation.

Furthermore, metal oxides have different reactivities and interact differently with organic compounds, indicating that an optimal solution might be system-dependent. Therefore, further work is necessary to evaluate the limitations of this method. For instance, for RuO₂/SiO₂, all organic molecules required higher temperatures than H₂ to promote RuO₂ reduction. This fact could prevent using organic reducing agents to reduce transition metals, like Ni and Co, which undergo reduction by H₂ at much higher temperatures. Nevertheless, organic reducing agents represent a promising alternative to H₂ for reducing oxide nanoparticles, displaying a significant potential for recycling spent metal catalysts.

Conclusion

Organic compounds, namely, methanol, ethanol, isopropanol, acetone, heptane, and cyclohexane, were employed as alternative reducing agents to H₂ for reducing RuO₂ nanoparticles deposited on amorphous silica (RuO₂/SiO₂). The products resulting from the RuO₂/SiO₂ reduction process, and the energy released during this process revealed two reaction phenomena. First, the conversion of RuO₂ nanoparticles to metallic Ru took place, together with oxidative dehydrogenation and oxidation of the reducing agents. Second, when enough metallic Ru was present, the dehydrogenation of the organic molecules or reverse methanol synthesis took place. The combination of the two processes explained the significant reduction in the energy released during the reduction process when using the organic reducing agents as a replacement for H₂, i.e., 27–85 kJ mol_RuO2⁻¹vs. 156 kJ mol_RuO2⁻¹, respectively.

The characterization of the treated catalysts showed that all the molecules evaluated were capable of fully reducing the RuO₂ to metallic Ru. Additionally, the Ru nanoparticles were significantly smaller when employing the organic reducing agents when compared to H₂, i.e., 4.7–6.7 nm vs. 11.9 nm, respectively. Nonetheless, Ru nanoparticle clusters were observed when using organic reducing agents. The comparison of the Ru nanoparticle size with the parent RuO₂ indicated a redispersion phenomenon occurred when the organic reducing agents were employed. The redispersion of the Ru nanoparticles was attributed to the combination of the two reaction processes, i.e., oxidation of organic agent and its dehydrogenation during RuO₂ reduction, occurring during the oxide reduction. In addition, the kinetics of the RuO₂ reduction reaction were found to impact the occurrence of Ru nanoparticle clusters when employing organic molecules as reducing agents. A faster RuO₂ reduction was shown to favor isolated metal particles.

Furfural hydrogenation to furfuryl alcohol was used as a model reaction to evaluate the catalytic performance of the Ru nanoparticles. When organic reducing agents were employed instead of H₂, the Ru/SiO₂ catalyst displayed at least a two-fold increase in activity, depending on the molecule used. The capacity to actively promote the catalytic conversion of furfural clearly further confirms that the surface of the nanoparticles was not deactivated by fouling.

Data availability

Data for this article, including TEM images and particle size calculations, EDS line scanning raw data, XPS raw data, XRD raw data, BET raw data, furfural hydrogenation reaction GC data and calculations, and MS raw and process data are available at Zenodo repository at https://doi.org/10.5281/zenodo.14263889.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the Centre for Microscopy and Microanalysis at The University of Queensland and the Central Analytical Research Facility operated by Research Infrastructure (QUT). The first author acknowledges the financial support from an Australian Government Research Training Program (RTP) administered by The University of Queensland Graduate School. N. Batalha and M. Konarova would like to thank CNRS for supporting this research through the International Emerging Action project “HYSPILL”.

References

1. J. Hagen, in Industrial Catalysis: A Practical Approach, Wiley-VCH GmbH, Weinheim, Germany, 2015, pp. 261–298,  DOI:10.1002/9783527684625.ch8.
2. S. D. Jackson, A. K. A. AlAsseel, A. M. Allgeier, J. S. J. Hargreaves, G. J. Kelly, K. Kirkwood, C. M. Lok, S. Schauermann, S. R. Schmidt and S. K. Sengupta, in Hydrogenation: Catalysts and Processes, ed. C. M. Lok, De Gruyter, Berlin and Boston, 2018.
3. H. Wang and J. Lu, Chin. J. Chem., 2020, 38, 1422–1444.
4. M. D. Argyle and C. H. Bartholomew, Catalysts, 2015, 5, 145–269.
5. C. H. Bartholomew, Appl. Catal., A, 2001, 212, 17–60.
6. R. Pattabiraman, Appl. Catal., A, 1997, 153, 9–20.
7. Y. Y. Zhan, K. Song, Z. M. Shi, C. S. Wan, J. H. Pan, D. L. Li, C. Au and L. L. Jiang, Int. J. Hydrogen Energy, 2020, 45, 2794–2807.
8. O. S. Alexeev, S. Y. Chin, M. H. Engelhard, L. Ortiz-Soto and M. D. Amiridis, J. Phys. Chem. B, 2005, 109, 23430–23443.
9. J. Feng, H. Y. Fu, J. B. Wang, R. X. Li, H. Chen and X. J. Li, Catal. Commun., 2008, 9, 1458–1464.
10. P. Maki-Arvela and D. Y. Murzin, Appl. Catal., A, 2013, 451, 251–281.
11. K. Morgan, A. Goguet and C. Hardacre, ACS Catal., 2015, 5, 3430–3445.
12. L. A Mekler, Regeneration of solid contact material, US Pat., US2391327A, 1942.
13. J. N. Weiland, Regeneration of contact materials, US Pat., US2330462A, 1940.
14. F. Le Normand, A. Borgna, T. F. Garetto, C. R. Apesteguia and B. Moraweck, J. Phys. Chem., 1996, 100, 9068–9076.
15. J. Sá, A. Goguet, S. F. R. Taylor, R. Tiruvalam, C. J. Kiely, M. Nachtegaal, G. J. Hutchings and C. Hardacre, Angew. Chem., Int. Ed., 2011, 50, 8912–8916.
16. A. Kubacka, A. Martínez-Arias, M. Fernández-García, M. Di Michiel and M. A. Newton, J. Catal., 2010, 270, 275–284.
17. A. Kubacka, A. Iglesias-Juez, M. Di Michiel, M. A. Newton and M. Fernández-García, Phys. Chem. Chem. Phys., 2013, 15, 8640–8647.
18. J. Barbier, D. Bahloul and P. Marecot, J. Catal., 1992, 137, 377–384.
19. N. Pernicone and F. Traina, in Preparation of Catalysts II, Proceedings of the Second International Symposium, ed. B. Delmon, P. Grange, P. Jacobs and G. Poncelet, Elsevier, 1979, vol. 3, pp. 321–351.
20. J. Hajek, P. Maki-Arvela, E. Toukoniitty, N. Kumar, T. Salmi, D. Y. Murzin, L. Cerveny, I. Paseka and E. Laine, J. Sol-Gel Sci. Technol., 2004, 30, 187–195.
21. Y. Fang, L. S. Guo, Y. Cui, P. P. Zhang, Y. Yoneyama, G. H. Yang and N. Tsubaki, Chemistryselect, 2019, 4, 10447–10451.
22. T. Furusawa, M. Shirasu, K. Sugiyama, T. Sato, N. Itoh and N. Suzuki, Ind. Eng. Chem. Res., 2016, 55, 12742–12749.
23. S. Muhammad, W. L. Tan, N. H. H. Abu Bakar, M. Abu Bakar and M. M. Bettahar, React. Kinet., Mech. Catal., 2016, 118, 537–556.
24. R. B. Mane, S. T. Patil, H. Gurav, S. S. Rayalu and C. V. Rode, Chemistryselect, 2017, 2, 1734–1745.
25. N. H. H. Abu Bakar, M. M. Bettahar, M. Abu Bakar, S. Monteverdi and J. Ismail, Catal. Lett., 2009, 130, 440–447.
26. M. T. Schaal, J. Rebelli, H. M. McKerrow, C. T. Williams and J. R. Monnier, Appl. Catal., A, 2010, 382, 49–57.
27. A. G. Boudjahem, S. Monteverdi, M. Mercy and M. M. Bettahar, J. Catal., 2004, 221, 325–334.
28. R. Wojcieszak, S. Monteverdi and M. M. Bettahar, Colloids Surf., A, 2008, 317, 116–122.
29. M. M. Bettahar, R. Wojcieszak and S. Monteverdi, J. Colloid Interface Sci., 2009, 332, 416–424.
30. E. Groppo, G. Agostini, A. Piovano, N. B. Muddada, G. Leofanti, R. Pellegrini, G. Portale, A. Longo and C. Lamberti, J. Catal., 2012, 287, 44–54.
31. P.-H. Liao and H.-M. Yang, Catal. Lett., 2007, 121, 274–282.
32. H. Lee, S. E. Habas, S. Kweskin, D. Butcher, G. A. Somorjai and P. Yang, Angew Chem. Int. Ed. Engl., 2006, 45, 7824–7828.
33. S. M. Davis, F. Zaera and G. A. Somorjai, J. Catal., 1984, 85, 206–223.
34. Z. Jiang, Z. Zhang, W. Shangguan, M. A. Isaacs, L. J. Durndell, C. M. A. Parlett and A. F. Lee, Catal. Sci. Technol., 2016, 6, 81–88.
35. J. Qiu, H. Zhang, C. Liang, J. Li and Z. Zhao, Chemistry, 2006, 12, 2147–2151.
36. Z. N. Xu, J. Sun, C. S. Lin, X. M. Jiang, Q. S. Chen, S. Y. Peng, M. S. Wang and G. C. Guo, ACS Catal., 2013, 3, 118–122.
37. J. H. Teles, W. Partenheimer, R. Jira, F. Cavani, G. Strukul, R. Hage, J. W. de Boer, L. Gooßen, P. Mamone and O. A. Kholdeeva, in Applied Homogeneous Catalysis with Organometallic Compounds, ed. B. Cornils, W. A. Herrmann, M. Beller and R. Paciello, WILEY-VCH GmbH, 2017, pp. 465–568.
38. M. S. Kamal, S. A. Razzak and M. M. Hossain, Atmos. Environ., 2016, 140, 117–134.
39. H. H. Kung, in Transition Metal Oxides - Surface Chemistry and Catalysis, Elsevier, 1989, vol. 45, pp. 91–109.
40. A. J. Maia, E. B. Pereira, A. C. Sola, N. Homs, P. R. de la Piscina, B. Louis and M. M. Pereira, Mol. Catal., 2018, 458, 145–151.
41. X. Duan, Y. Han, B. Zhu and Y. Gao, Materials Today Catalysis, 2023, 3, 100032.
42. J. Rak, P. Skurski, M. Gutowski and J. Blazejowski, J. Therm. Anal., 1995, 43, 239–246.
43. D. Hourlier, J. Therm. Anal. Calorim., 2019, 136, 2221–2229.
44. C.-B. Wang, H.-K. Lin, S.-N. Hsu, T.-H. Huang and H.-C. Chiu, J. Mol. Catal. A: Chem., 2002, 188, 201–208.
45. J. H. Flynn, J. Therm. Anal., 1983, 27, 95–102.
46. J. H. Flynn and L. A. Wall, J. Res. Natl. Bur. Stand., Sect. A, 1966, 70, 487–523.
47. M. Venkatesh, P. Ravi and S. P. Tewari, J. Phys. Chem. A, 2013, 117, 10162–10169.
48. G. Bergeret and P. Gallezot, Particle Size and Dispersion Measurements, in Handbook of Heterogeneous Catalysis, 2008, ch. 3.1.2, pp. 738–765,  DOI:10.1002/9783527610044.hetcat0038.
49. P. G. J. Koopman, A. P. G. Kieboom and H. Vanbekkum, React. Kinet. Catal. Lett., 1978, 8, 389–393.
50. P. G. J. Koopman, A. P. G. Kieboom and H. Vanbekkum, J. Catal., 1981, 69, 172–179.
51. L. T. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38.
52. D. Ugur, A. J. Storm, R. Verberk, J. C. Brouwer and W. G. Sloof, J. Phys. Chem. C, 2012, 116, 26822–26828.
53. L. Ma, Y. Geng, X. Y. Chen, N. Q. Yan, J. H. Li and J. W. Schwank, Chem. Eng. J., 2020, 402, 125911.
54. G. Fau, N. Gascoin and J. Steelant, J. Anal. Appl. Pyrolysis, 2014, 108, 1–11.
55. I. Mangoufis-Giasin, O. Pique, P. Khanipour, K. J. J. Mayrhofer, F. Calle-Vallejo and I. Katsounaros, J. Catal., 2021, 400, 166–172.
56. H. Liu and E. Iglesia, J. Phys. Chem. B, 2005, 109, 2155–2163.
57. J. M. Sturm, C. J. Lee and F. Bijkerk, Surf. Sci., 2013, 612, 42–47.
58. M. Almohalla, E. Gallegos-Suarez, A. Arcoya, I. Rodríguez-Ramos and A. Guerrero-Ruiz, Catal. Sci. Technol., 2016, 6, 521–529.
59. J. Hermia and S. Vigneron, Catal. Today, 1993, 17, 349–358.
60. M. Elango, G. S. Maciel, F. Palazzetti, A. Lombardi and V. Aquilanti, J. Phys. Chem. A, 2010, 114, 9864–9874.
61. R. Z. Jiang, D. T. Tran, J. T. Li and D. Chu, Energy Environ. Mater., 2019, 2, 201–208.
62. T. Mitsui, K. Tsutsui, T. Matsui, R. Kikuchi and K. Eguchi, Appl. Catal., B, 2008, 81, 56–63.
63. H. Z. Liu, G. L. Xia, R. R. Zhang, P. Jiang, J. T. Chen and Q. W. Chen, RSC Adv., 2017, 7, 3686–3694.
64. S. Agarwal and J. N. Ganguli, RSC Adv., 2014, 4, 11893–11898.
65. T. Wang and L. D. Schmidt, J. Catal., 1981, 70, 187–197.
66. J. E. Stulga, P. Wynblatt and J. K. Tien, J. Catal., 1980, 62, 59–69.
67. R. T. K. Baker, E. B. Prestridge and R. L. Garten, J. Catal., 1979, 59, 293–302.
68. R. M. J. Fiedorow and S. E. Wanke, J. Catal., 1976, 43, 34–42.
69. R. M. J. Fiedorow, B. S. Chahar and S. E. Wanke, J. Catal., 1978, 51, 193–202.
70. T. W. Hansen, A. T. DeLaRiva, S. R. Challa and A. K. Datye, Acc. Chem. Res., 2013, 46, 1720–1730.
71. Y. Dai, P. Lu, Z. Cao, C. T. Campbell and Y. Xia, Chem. Soc. Rev., 2018, 47, 4314–4331.
72. T. Ano, S. Tsubaki, A. Liu, M. Matsuhisa, S. Fujii, K. Motokura, W.-J. Chun and Y. Wada, Commun. Chem., 2020, 3, 86.
73. S. Merabia, S. Shenogin, L. Joly, P. Keblinski and J.-L. Barrat, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15113–15118.
74. S. Brunauer and P. H. Emmett, J. Am. Chem. Soc., 1935, 57, 1754–1755.
75. Z. Mao and C. T. Campbell, ACS Catal., 2021, 11, 8284–8291.
76. P. Nolte, A. Stierle, N. Y. Jin-Phillipp, N. Kasper, T. U. Schulli and H. Dosch, Science, 2008, 321, 1654–1658.
77. G. Li, K. Fang, Y. Chen, Y. Ou, S. Mao, W. Yuan, Y. Wang, H. Yang, Z. Zhang and Y. Wang, J. Catal., 2020, 388, 84–90.
78. L. Piccolo, Catal. Today, 2021, 373, 80–97.
79. R. Cheula, M. Maestri and G. Mpourmpakis, ACS Catal., 2020, 10, 6149–6158.
80. A. S. Galushko and V. P. Ananikov, ACS Catal., 2024, 14, 161–175.
81. J. Liu, M. Wang, P. Liu, R. Sun, Y. Yang and G. Zou, Comput. Mater. Sci., 2021, 190, 110265.
82. D. B. Eremin and V. P. Ananikov, Coord. Chem. Rev., 2017, 346, 2–19.
83. V. P. Ananikov and I. P. Beletskaya, Organometallics, 2012, 31, 1595–1604.
84. P. L. Hansen, J. B. Wagner, S. Helveg, J. R. Rostrup-Nielsen, B. S. Clausen and H. Topsøe, Science, 2002, 295, 2053–2055.
85. V. Beermann, M. E. Holtz, E. Padgett, J. F. de Araujo, D. A. Muller and P. Strasser, Energy Environ. Sci., 2019, 12, 2476–2485.
86. European Commission: Directorate-General for Internal Market, Entrepreneurship and SMEs, M. Grohol and C. Veeh, Study on the critical raw materials for the EU 2023 – final report, Report ET-07-23-116-EN-N, Publications Office of the European Union, 2023.
87. S. K. Padamata, A. S. Yasinskiy, P. V. Polyakov, E. A. Pavlov and D. Y. Varyukhin, Metall. Mater. Trans. B, 2020, 51, 2413–2435.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08563a

---