Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An electrochemical oscillator for harvesting near room temperature waste heat†
Basanta
Ghimire‡
 ab,
Mihir
Parekh‡
ab,
Mihir
Parekh‡
 *ab,
Herbert
Behlow
ab,
Morteza
Sabet
*ab,
Herbert
Behlow
ab,
Morteza
Sabet
 bc,
Sriparna
Bhattacharya
bc,
Sriparna
Bhattacharya
 ab,
Nawraj
Sapkota
ab,
Pankaj Singh
Chauhan
d,
Abha
Misra
d and
Apparao M.
Rao
ab,
Nawraj
Sapkota
ab,
Pankaj Singh
Chauhan
d,
Abha
Misra
d and
Apparao M.
Rao
 *ab
*ab
aDepartment of Physics and Astronomy, Clemson University, 118 Kinard Laboratory, Clemson, South Carolina, USA. E-mail: mihirp@clemson.edu; arao@clemson.edu; basantg@clemson.edu; hbehlow@clemson.edu; nsapkot@clemson.edu
bClemson Nanomaterials Institute, Clemson University, 81 Technology Drive, Anderson, South Carolina, USA. E-mail: bbhatta@g.clemson.edu
cDepartment of Automotive Engineering, Clemson University, 4 Research Dr, Greenville, South Carolina, USA. E-mail: ssabet@clemson.edu
dDepartment of Instrumentation and Applied Physics, Indian Institute of Science, Bengaluru, Karnataka, India. E-mail: pschauhan.89@gov.in; abha@iisc.ac.in
First published on 15th January 2025
Abstract
We present Soret effect-driven electrochemical devices that generate >1 V with a mere 10 K temperature difference with the cold end at room temperature, i.e., a thermopower α > 100 mV K−1 – almost four to five times the record to date [Adv. Energy Mater., 2019, 9, 1901085]. We show that α depends not only on the electrolyte composition but also on the electrode porosity and microstructure, which has remained an understudied area of research. Interestingly, our devices show novel voltage oscillations (unlike electrochemical oscillations observed previously, which were a result of either (a) stochastic single-molecule electrochemistry or (b) redox reactions) arising from an interplay between ionic diffusion and ionic migration within the electric double-layer, highlighting the potential for novel applications. Notably, the real-world use of TRECO is demonstrated by (a) facile continuous operation, (b) harvesting body heat (∼825 mV obtained for a temperature difference of 6 K), and (c) powering a pocket calculator using a single large format TRECO cell to harvest waste heat from warm continuously operating lab equipment.
Broader contextWhile shifting towards renewable energy sources is one way of tackling global warming, harvesting waste heat (nearly two-thirds of primary energy is wasted as heat) is another way of reducing greenhouse gas emissions. Harvesting high-grade waste heat using thermoelectric generators based on the Seebeck effect has been explored for a while, but harvesting the ubiquitous near-room temperature waste heat (e.g., waste heat from hot mobile phones, laptops, body heat, etc.) has remained a challenge. In this work, we (a) develop Soret effect-driven thermally rechargeable electrochemical oscillators (TRECOs) to harvest near room temperature ultra-low grade waste heat, (b) demonstrate a record high (beating the previous best by a factor >4) thermopower (i.e., the voltage generated per unit temperature difference) of ∼0.1 V K−1, (c) elucidate the fundamental physics underlying the previously unobserved voltage oscillations during discharge (implying that TRECO could be used for novel applications such as generating voltage pulses, or to generate oscillating waveforms, etc.) and (d) demonstrate TRECO's potential for real-time applications by powering a pocket calculator and developing a TRECO based wearable arm-band. All of the above is attributed to electrode microstructure and porosity – previously unexplored areas of study for Soret effect-driven devices. |
1 Introduction
Increasing greenhouse gas emissions and the already apparent global warming have led to a tectonic shift in the ways of generating electricity. While the prudent shift from fossil fuel-based power plants to renewable energy is expected to decrease greenhouse gas emissions, harvesting waste heat1 adds another dimension to our efforts toward combating climate change. For every 3 J of primary energy, nearly 2 J is lost as waste heat.2 Conventional methods of electricity generation, such as thermal/nuclear power plants, often generate high-grade waste heat, which could be harvested using electronic thermoelectric materials, although not with desired efficiencies. However, alternative methods such as solar photovoltaics and wind energy generate ultra-low grade waste heat, which could be harvested using ionic thermoelectric cells based on their redox reactions3 or the Soret effect.4–8 Thermogalvanic cells based on redox reactions utilize temperature-dependent entropy difference (and thus, voltage difference) to drive electrochemical reactions at the electrodes in opposite directions. For example, if an aqueous solution containing ferricyanide/ferrocyanide redox couple3 is used as the electrolyte, the redox reaction proceeds in opposite directions on hot and cold electrodes (due to temperature-dependent entropy difference and reaction Gibbs free energy), which drives the electrochemical reactions.3 On the other hand, the Soret effect utilizes thermophoretic mobility differences between oppositely charged ions to generate a charge separation within the cell, thus leading to voltage generation. Li et al.9 utilized the Soret effect in ionic thermoelectric cells and reported a thermopower of 24 mV K−1 at room temperature – one of the highest thermopowers reported to date. Here, we present Soret-based ionic cells that exhibit a thermopower of 50–110 mV K−1 (depending upon the electrode type), which is more than two-to-four times the previously highest reported thermopower. While we also used cellulose-based separators like Li et al.,9 we measured such high thermopowers primarily due to our choice of electrode material and its microstructure, which has been a previously neglected area of study. Few previous publications on electrode microstructure have either focused on thermogalvanic cells,10,11 or replaced the electrode itself12 (rather than electrode microstructure of the same electrode material) for Soret effect-based cells. Our cells open up possibilities for harvesting, transmitting, and instantaneously utilizing ultra-low-grade waste heat, thus helping us address one of the five grand thermal challenges of the 21st century.13 Ultra-low-grade waste heat harvesting and long-distance transmission for instantaneous utilization could not yet be realized because neither ionic nor electronic thermoelectric cells exhibited sufficiently high thermopower. However, using cells with a thermopower of 50–110 mV K−1, the possibility of harvesting abundant solar energy (the earth receives more solar energy in one hour than humanity utilizes in one year,14 which is mostly lost as waste heat) is within our reach.In addition to the high thermopower discussed above, our ionic thermoelectric cells exhibited novel and previously unreported oscillations in the output voltage during their galvanostatic discharge. In particular, our thermally charged cells exhibited voltage oscillations in the presence or absence of a temperature gradient across them during discharge, implying an electrochemical origin for the oscillations. Hence, we refer to our ionic thermoelectric cell as a thermally rechargeable electrochemical oscillator or TRECO. In other words, TRECO is an electrochemical oscillator that can be charged by maintaining a low-temperature difference across its two electrodes. While electrochemical oscillations have been observed previously, they were found to arise from either (i) an interplay of multiple processes governing redox reactions,15–19e.g., lithium titanate anodes in lithium-ion batteries, or (ii) stochastic single-molecule electrochemical processes,20–26e.g., electrochemistry on zeptoliter volumes of hexamineruthenium(III) chloride on a Pt ultra-microelectrode. However, electrodes and electrolytes in TRECO do not undergo redox reactions (the cyclic voltammetry data shown in Fig. S1† do not exhibit any peaks corresponding to redox reactions), pointing towards a novel origin of electrochemical oscillations in TRECO.
Our study shows that TRECO generates voltage due to charge separation, leading to oppositely charged double-layers at the two electrode–electrolyte interfaces. While the nature of the oscillations depends on discharge current and electrode porosity, the oscillations are also present in TRECOs with nonporous electrodes, although to a lesser extent. Thus, the possibility of oscillations arising purely from stochastic single-molecule electrochemistry within pores just large enough to trap single solvation shell structures can also be ruled out. The nonporous electrodes ensure that single-molecule electrochemical processes do not occur, as the entire electrode surface is essentially exposed to the electrolyte. We find that (i) the interplay between Fick's diffusion (diffusion due to concentration gradient) and ion migration due to the electrostatic forces within the electric double-layer (EDL) at the electrode–electrolyte interfaces and (ii) electrode microstructure and porosity together are responsible for the voltage oscillations. As a result, choosing electrodes with appropriate microstructures helped us observe (a) extraordinarily high thermopower at room temperatures (temperature difference between cold and hot ends being ∼10 K) and (b) voltage oscillations (which were observed both with and without the temperature gradient). A detailed description and discussion elucidating the link between electrode microstructure and these two novel effects form the backbone of this work. Notably, we also demonstrate TRECO's ability to power a calculator in real-time with (i) a TRECO module made up of four coin cells connected electrically in series, (ii) a single large format TRECO cell, which harvests waste heat from a continuously operating laboratory vacuum pump, (iii) a wearable arm-band based on a single TRECO coin cell.
This study advances the field of low-grade-waste heat recovery and thermal energy harvesting in multiple ways: (a) we uncovered the effect of electrode microstructure and porosity on the thermopower, which was previously an understudied areas of research, (b) our focus on electrode microstructure and porosity helped us improve over the previous thermopower record by a factor of 4, (c) we observed novel voltage oscillations (and elucidated the physics behind the oscillations) during discharge, which were not reported previously.
2 Results and discussion
2.1. Application of a thermal gradient across TRECO
To control the temperature at the two ends of the TRECO in a coin cell format, an in-house setup consisting of two copper blocks, one of which had an embedded resistive heater (Fig. 1a) was designed. The resistive heater was connected to a PID controller that maintained the copper block at a constant temperature of 310 K. The other copper block was held at room temperature (300 K). The TRECO coin cell was placed between the two copper blocks, thus establishing a ∼10 K temperature difference across the TRECO, which enables thermodiffusion (as shown in Fig. 1b) to drive ions from the bulk electrolyte toward the electrode–electrolyte interfaces. This creates charge separation and activates Fick's diffusion (Fig. 1b) within the bulk electrolyte. The materials used to fabricate our symmetric TRECO coin cells are described in the Methods section (ESI†) and Fig. S2† (separator), and Fig. 1c, S3 and S4† (electrodes). Three types of porous electrodes (CD1, CD2, and Bucky Paper (BP)) were used in this study, and Fig. 1c, S3 and S4† show their respective pore size distribution derived from gas physisorption measurements. The insets show the corresponding scanning electron micrographs.2.2. Open circuit behavior: thermal charging of the TRECO
Application of a ∼10 K temperature difference across the TRECO coin cell resulted in a time-varying open circuit voltage (OCV), shown in Fig. 2. The OCV across TRECO was recorded every 30 s with a Keithley 2400 multimeter that was controlled using LabVIEW. Fig. 2a–c, respectively, show OCV as a function of time for TRECO coin cells using the CD1, CD2, and BP electrodes, which suggest that the OCV and its temporal behavior depend not only on the electrolyte but also on the electrode materials and their porosity. In comparison to previously reported time-dependent OCV (Fig. 2d),9 the TRECO cells delivered a much higher voltage and exhibited a longer stability duration. To quantify ‘voltage stability’, the following criteria were used: voltage should be within ±10% of a chosen value close to its peak. For e.g. (i) in Fig. 2a, voltage is within 10% of the maximum value of 1022 mV within 1.85 to 10.7 minutes and is within ±10% of 800 mV (i.e., within 720 to 880 mV), from 11.1 to 100 minutes (ii) in Fig. 2b, voltage is within 10% of the maximum value of around 793 mV between 424 and 624 minutes (i.e., approximately 200 minutes), and is within ±10% of 750 mV (i.e., between 675 and 825 mV) from 424 to 919 minutes, and (iii) for Fig. 2c, it is within 10% of 500 mV (i.e., between 450 mV and 500 mV) for 100 minutes, the highest voltage is around 540 mV in Fig. 2c, and the voltage is within 10% of the average voltage of 513 mV for the entire duration of 100 minutes. In Fig. 2b, the maximum negative voltage was achieved after a much longer initial wait, as opposed to the short initial wait in the case of CD1 and BP. This suggests that even though the electrolyte and the separator are the same in all these cases, the electrode microstructure and porosity govern the temporal behavior of the OCV. The long stability durations reported above are sufficient enough to power applications.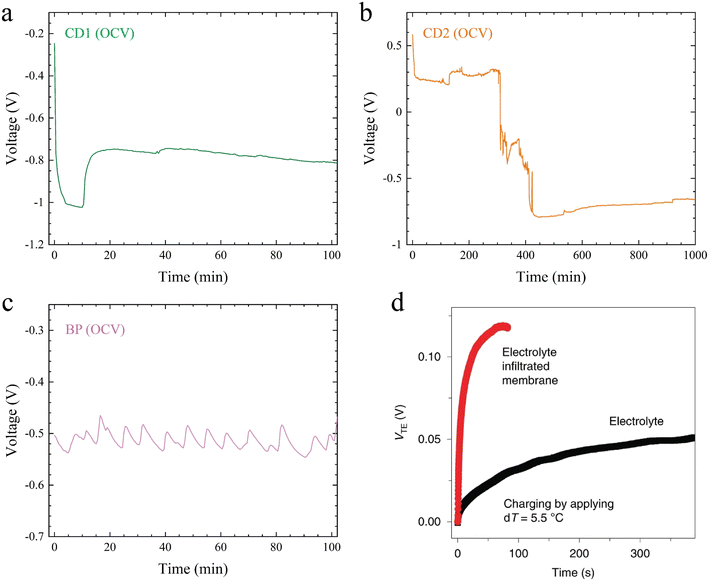 | ||
| Fig. 2 Open circuit voltage as a function of time for TRECO coin cells (temperature difference was set to 10 K before inserting the cell in the setup shown in Fig. 1a) with cellulose obtained from delignified wood as the separator, an aqueous electrolyte containing sodium chlorite and polyethylene oxide, and (a) CD1, (b) CD2, and (c) BP electrodes. (d) Open circuit behavior as a function of time for a cell with Pt electrodes with a 5.5 K temperature difference (adapted from ref. 9). | ||
The dependence of OCV on electrode material and porosity is not unexpected. The Soret effect generates a potential difference via charge separation, which depends not only on the ion (Na+, ClO2−) diffusivity and thermophoretic mobility but also on the EDL structure at the electrode–electrolyte interfaces. The EDL structure depends largely on the electrode microstructure; hence, the electrode material and its porosity play an important role in governing the generated OCV in any ionic thermoelectric cell, such as those used previously (e.g., ref. 27) or the TRECO. The maximum (by magnitude) observed OCV for the three different electrode types and their corresponding thermopowers are listed in Table 1. It should be noted that most previous studies utilizing the Soret effect to harvest low-grade waste heat have not reported the temporal behavior of OCV at a fixed temperature difference.1,29–31 Moreover, the previous literatures focused primarily on electrolyte optimization for increasing the OCV and thermopower. However, as pointed out above, OCV depends not only on time but also on the electrode material and porosity.
The reproducibility of thermopower and its dependence on the applied temperature difference are shown in Tables S1† and 2, respectively. The large OCV and thermopower are (i) generally attributed to large differences in ionic diffusivities and thermophoretic mobilities and (ii) interestingly enough, to electrode porosity also. The sodium (Na+) and chlorite ions (ClO2−) are the cations and anions present in our aqueous electrolyte. Polar hydroxyl groups within the cellulose separator and ether groups within polyethylene oxide (PEO) favor Na+ movement over ClO2− ions.9 Moreover, the ionic size difference is expected to affect ionic diffusivity. Thermophoretic mobility difference and electrode porosity are the other factors contributing to charge separation. Moreover, within the EDL present in the electrode pores, the existing large electric field (arising from charge separation) drives ion migration in a direction opposite to Fick's diffusion (Fig. 1b). The electric field leads to an electrostatic attraction between the electrodes and the ions within the double-layer, thus holding the ions close to the electrodes. Nonetheless, Fick's diffusion tends to drive the ions away from the electrodes. As shown in Fig. 1b, this interplay between Fick's diffusion and Soret effect in the electrolyte and Fick's diffusion and ion migration in the EDL dynamically changes an ion's position, leading to the fluctuating OCV. The mechanisms leading to voltage fluctuations in TRECOs under open circuit conditions are similar to those responsible for the self-discharge of electric double-layer capacitors. In electric double-layer capacitors, voltage drops during the rest period due to charge redistribution32 within the pores of the porous electrodes and within the electrolyte. The charges redistribute because, during the charging process, the slow ionic movement does not allow ions to diffuse into the deepest pores present within the electrode, leading to ion concentration gradients within the electrode (porous part of the electrode) and within the electrolyte. Fick's law drives ions from regions of high concentration to low concentration, resulting in charge redistribution. While the voltage drops smoothly in electric double-layer capacitors owing to charge redistribution, the TRECO's voltage exhibits a stochastic behavior due to the multiple phenomena, namely, the Soret effect (which pushes ions towards the electrodes and its pores) and Fick's diffusion (which pushes the ions in the opposite direction). This complex interplay of ion flux motion and the pore size distribution in the electrode and the separator leads to non-linearities in TRECO's voltages as a function of temperature gradient (Table 2). A movie (SM1†) highlighting the similarities and differences between the electrical charging of an electric double-layer capacitor and the thermal charging of TRECO can be found in the ESI† section.
| Temperature difference (ΔT) | Open circuit voltage (V) |
|---|---|
| 0 K | ∼0 V |
| 7.5 K | −0.490 V |
| 10 K | −0.84 V |
It is well known that in an electric double-layer capacitor (EDLC), the capacitance is highly dependent upon the pore size distribution within the electrode material. Pores with sizes of the order of the solvated ions essentially ensure a minimum distance between the solid electrode material and the ion within the EDL, thus increasing the capacitance.33 However, pore sizes smaller than ionic sizes can inhibit the ions from entering the pores, thus lowering the utilized electrode surface area and, hence, the capacitance. Therefore, akin to EDLCs, our TRECO cells based on CD1 and CD2 electrodes (cf.Fig. 1c and S3†) display an increased thermopower than BP electrodes with relatively larger pores (Fig. S4†).
2.3. Electrochemical oscillations during discharge (with the temperature gradient present across the electrodes)
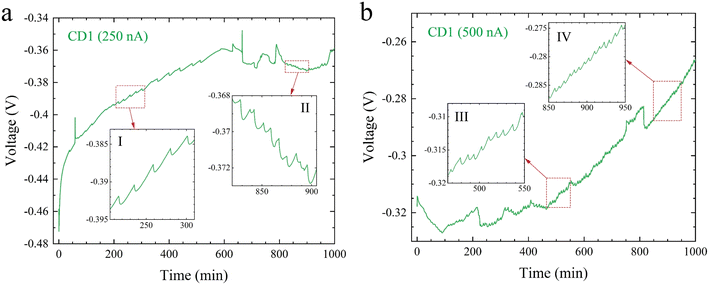
Temporal voltage behavior of our TRECO coin cells was studied for constant discharge currents with CD1, CD2, and BP electrodes. The temporal voltage characteristics (voltage was recorded every 30 s with a Keithley 2400 multimeter, which was controlled using LabVIEW) are shown in Fig. 3, S5 and S6† for CD1, CD2, and BP electrodes, respectively. A closer look at these figures suggests that irrespective of the electrode material and discharge current, the voltage does not exhibit a monotonic rise but instead shows voltage oscillations (shown as insets in Fig. 3, S5 and S6†). Notably, the oscillations observed during discharge and the open circuit voltage fluctuations do not arise solely due to temperature fluctuations associated with the PID controller because if voltage oscillations during discharge/fluctuations during OCV arose purely from temperature fluctuations, the time period of fluctuation/oscillation would have been the same across Fig. 3, 2a–c, 3a, b, S5 and S6.† Fig. S7† and the related discussion explain PID controller's effect on voltage oscillations. While the time period of voltage oscillations is several minutes for most cases, a fast Fourier transform (FFT) analysis of the voltage oscillations shown in insets I–VI in Fig. 3a, b and S8a† was performed and is shown in Fig. S9 and Table S2† (movie SM2, Fig. S10, and Table S3† delineate the effect of the PID controller on voltage oscillations). Notably, the oscillation amplitude correlates with the electrode material. It must also be noted that both the time period and amplitude of oscillations are much larger than the recording interval (30 s) and the least count of the voltmeter (0.1 μV), respectively. These oscillations could arise from phenomena occurring within the (i) bulk of the electrolyte or (ii) the EDL. The EDL width in these cells may be greater than the Debye length34 because of charge separation induced by the Soret effect. However, the EDL width will still be much smaller than the inter-electrode distance.2.4. Theoretical models to investigate the origin of voltage oscillations
To investigate the origin of the oscillations, first, we modeled the bulk electrolyte (i.e., the electrolyte domain between the double-layers near the electrodes, which is an open system as it excludes the electrodes and the double-layer). Within the bulk electrolyte,4 | (1) |
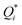 represents the heat of diffusion (thermophoretic mobility). The subscript i varies with the studied ionic species, viz., i ∈ {Na+, ClO2−}. The first term on the right-hand side of eqn (1) represents Fick's diffusion, and the second term represents the flux contributions arising from the Soret effect (i.e., thermodiffusion). Given that the prepared TRECO cells were CR2032-type coin cells and that all the studies were performed near room temperature (∼300 K), Fick's diffusion has a timescale of about 1000 s, and thermodiffusion occurs over 25
represents the heat of diffusion (thermophoretic mobility). The subscript i varies with the studied ionic species, viz., i ∈ {Na+, ClO2−}. The first term on the right-hand side of eqn (1) represents Fick's diffusion, and the second term represents the flux contributions arising from the Soret effect (i.e., thermodiffusion). Given that the prepared TRECO cells were CR2032-type coin cells and that all the studies were performed near room temperature (∼300 K), Fick's diffusion has a timescale of about 1000 s, and thermodiffusion occurs over 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s, the derivation of which is shown in the ESI† section. Since the voltage oscillations have a time period of the order of a few minutes, this analysis suggests that thermodiffusion is too slow to contribute to the observed voltage oscillations despite maintaining a temperature difference of ∼10 K even during discharge, which is quite surprising. Since having at least two competing effects is necessary for oscillations, the starkly distinct orders of magnitude suggest that the competition between Fick's diffusion and the Soret effect within the bulk electrolyte does not cause oscillations during discharge.
000 s, the derivation of which is shown in the ESI† section. Since the voltage oscillations have a time period of the order of a few minutes, this analysis suggests that thermodiffusion is too slow to contribute to the observed voltage oscillations despite maintaining a temperature difference of ∼10 K even during discharge, which is quite surprising. Since having at least two competing effects is necessary for oscillations, the starkly distinct orders of magnitude suggest that the competition between Fick's diffusion and the Soret effect within the bulk electrolyte does not cause oscillations during discharge.
To investigate the origin of oscillations further, we leverage the equivalent circuit model of the TRECO shown in Fig. 4.
In Fig. 4, Rdiff refers to the ionic diffusion resistance within the electrolyte, RSoret is the resistance to thermodiffusion within the electrolyte, Rdl1, Rdl2, Cdl1, and Cdl2 represent double-layer resistances and capacitances at the two electrode–electrolyte interfaces, respectively. While Rext is the resistance of the external connections, and I is the discharge current applied during the galvanostatic discharge of the TRECO, I1, I2, I3, I4, I5, V1, V2, V3, and V4 are assumed to vary temporally. Although the double-layer resistances, double-layer capacitances, and bulk electrolyte resistances (ionic diffusion and thermodiffusion resistance) typically vary with voltage, we assume they are constant or weakly varying. This is because the amplitude of a single voltage oscillation, for most cases, is on the order of 1 mV, which is much smaller than the TRECO voltage of ∼1 V. V1 − V4 gives the measured TRECO voltage, and for voltage to oscillate, d(V1 − V4)/dt (i.e., the slope of voltage versus time curve) should exhibit a change of sign, i.e., vary from negative to positive or vice versa. Solving the equivalent circuit model suggests that
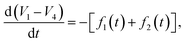 | (2) |
| f1(t)Cdl1Rdl1 + f2(t)Cdl2Rdl2 + ∫[f1(t) + f2(t)]dt = I(Rdl1 + Rdl2), | (3) |
The temporal nature of I1, I4 (and I2, I5) drives the oscillations. A typical RC parallel circuit shows an exponential voltage profile (with respect to time), both during charging and discharging. Since RC circuits have represented the double-layers, the voltage oscillations imply charging–discharging of the double-layers (charging and discharging seem to happen in unequal amounts as the device as a whole is being discharged and the oscillations are riding on a typical discharge profile). Charging of the double-layer implies ions moving towards the electrode–electrolyte interface (ionic migration dominates over Fick's diffusion (cf.Fig. 1b)), and ions move away from the electrode–electrolyte interface during discharge of the double-layer (Fick's diffusion dominates over ionic migration within the double-layer (cf.Fig. 1b)). This leads to a change of sign for I1, I4, which further leads to voltage oscillations as can be seen from eqn (2) and (3). This shows that the origin of voltage oscillations is electrochemical in nature. Thus, the order of magnitude analysis and the equivalent circuit model predict that the voltage oscillations (a) do not require the temperature gradient during discharge, (b) should exist irrespective of the chosen electrode, electrolyte, and separator material's porosity, and microstructure, and (c) may be observed even during electrical charging of a typical supercapacitor. This is because the electric double-layer is present at all electrode–electrolyte interfaces. We performed additional experiments described in the next section to confirm this prediction.
2.5. Experimental observations of voltage oscillations irrespective of the temperature gradient, electrode, electrolyte, separator materials' porosity, and microstructure
The analysis of our equivalent circuit model based on Fig. 4 suggests that the origin of the voltage oscillations is electrochemical in nature, which is validated via two experiments: (a) a TRECO cell with CD1 electrodes was charged via a temperature difference of ∼10 K across its electrodes and discharged at 500 nA in the absence of the thermal gradient, and (b) a TRECO cell with BP electrodes was charged at 100 nA without the application of any thermal gradient. While experiment (a) used delignified wood soaked in an aqueous solution of NaClO2 and PEO as the separator, in the experiment (b), a Celgard polypropylene separator and a 1 M solution of tetraethyl-ammonium tetrafluoroborate (TEABF4) in acetonitrile (AN) were used as the electrolyte. As shown in Fig. 5a and b, the temporal voltage profile obtained for both experiments exhibited voltage oscillations, confirming that voltage oscillation is not an artifact of the (i) Soret effect and/or (ii) choice of electrode/electrolyte material. Furthermore, the presence of voltage oscillations, even in the absence of thermal gradients, further confirms the fact that voltage oscillations do not arise due to temperature fluctuations associated with the PID controller. Moreover, it also shows that voltage oscillations are present during both charge and discharge processes, thus confirming the role played by the EDL (which exists during both charge and discharge) at the electrode–electrolyte interfaces. The initial absence of oscillations in Fig. 5b is attributed to insufficient ion concentration within the EDL. As the ionic concentration within the EDL gradually builds up with charge separation, electrostatic forces and diffusion tend to act against each other, thus leading to oscillations.Fig. 5a exhibits the presence of voltage oscillations in the positive voltage regime close to its maximum voltage. However, oscillations are absent during the initial monotonic voltage rise, which is unlike the oscillations observed in the negative voltage regimes in Fig. 3a and b but is similar to the phenomenon shown in Fig. S8a.† A comparison of Fig. 3a, b and S8a† indicate that a high current of 1000 nA (the magnitude is different and depends upon the material's microstructure, as can be seen from Fig. S8a–d†) discharges the cell too quickly, not allowing sufficient time for ions to migrate back into the EDL. The ions diffuse out of the EDL (step I in Fig. 6) via the electrolyte (step II in Fig. 6) to the opposite electrode (step III in Fig. 6), thus switching polarity. With reversed polarity, the discharging current acts like a charging current for the cell, thus increasing the electrostatic attraction for ions within the EDL, which overcomes the concentration gradient effects and prevents the ions from diffusing out of the EDL once again. While Fig. 3a and b show the presence of oscillations even before the cell switches polarity due to discharge; their absence before a polarity switch in Fig. 5a at a low discharge current of 500 nA shows that the EDL dynamics is different in the presence or absence of temperature gradient (this is expected as the Soret effect helps in creating charge separation and hence we have more ions in the EDL with temperature gradient than in the case of no temperature gradient). Therefore, we hypothesize that a lower discharge current might exhibit oscillations before switching polarities in the absence of thermal gradients during discharge. This hypothesis is confirmed in Fig. 5c.
The above models and experiments confirm the role of the EDL in voltage oscillations. EDL characteristics depend upon the electrode material, microstructure, and porosity. Furthermore, the different oscillation patterns exhibited by TRECO cells with CD1, CD2, and BP electrodes confirm the role of choice of electrode material, microstructure, and porosity. Since the oscillations are seen with multiple electrode/electrolyte materials and varying microstructures and porosities, it seems that voltage oscillations might occur in any porous electrode, irrespective of the microstructure. However, the question still remains as to whether porous electrodes are necessary for observing voltage oscillations. This question becomes even more relevant if we extend the proposed models16–18 to EDL. The authors of ref. 16–18, through their models, showed that voltage oscillations occur because lithium ions shift from one particle to another during the lithiation processes within the two-phase regime.16–18 A simple extrapolation of this concept to TRECO suggests that voltage oscillations may be due to ions shifting from one pore to another within the electrode. However, as shown in Fig. 5d, a simple experiment with nonporous stainless-steel electrodes, cellulose obtained from delignified wood and soaked in an aqueous solution of sodium chlorite and PEO suggests that electrochemical oscillations can be observed even in cells with nonporous electrodes. We suggest that the ions find it hard to escape the EDL due to an interplay between Fick's diffusion and ionic migration due to electrostatic forces.
While this confirms the role of EDL, the role of porosity cannot be ruled out because, in porous electrodes, the double-layer structure itself depends on the porosity (if we have pore sizes of the order of Debye length, which is the case for CD1, CD2, and BP electrodes). Additionally, pores with sizes of the order of ionic sizes might also act like a physical trap for ions, thus making it harder for ions to leave the pore during the discharge and contributing to oscillations. In summary, the oscillations in porous electrodes result from porosity and the dynamic EDL structure, but the dynamic EDL structure is the sole cause for oscillations in nonporous electrodes. A detailed theoretical formulation35,36 explaining the complex dependence of voltage fluctuations under open circuit conditions (thermal charging) and voltage oscillations under galvanostatic discharge conditions on ionic diffusivities/mobilities is presented in the ESI† section under the title ‘Effect of ionic mobility on charging/discharging timescales, voltage fluctuations during open circuit conditions, and oscillations during discharge’. Additionally, a detailed explanation regarding the role of electrode microstructure and porosity in governing the electric double-layer structure, and hence the thermopower and voltage oscillations, has been presented in the ESI.†
2.6. Continuous operation using TRECO
Continuous operation of a cell, as defined in ref. 12, requires a change of device polarity because a change in device polarity essentially implies that ions have completely shifted from one electrode to the other. In ref. 12, the change in device polarity was achieved by switching to a different type of electrode, which can sometimes be tedious, especially for coin cell or pouch cell formats, which are the commercially used formats.One way to think of change in polarity is that it may be achieved via very large amplitude voltage oscillations where the peak-to-peak voltage difference is greater than the initial voltage before the polarity flip. However, such oscillations would imply that
(1) ions within the electric double-layer managed to not only escape the electric double-layer,
(2) but also reach the electric double-layer at the other electrode–electrolyte interface,
(3) then escape the electric double-layer at the other electrode–electrolyte interface and
(4) eventually reach the original electric double-layer in which they were present before the initial polarity flip.
This would only be possible when the ionic migration due to electrostatic forces is negligible compared to the diffusion flux. However, such a case would have never given rise to voltage oscillations during discharge at all because the oscillations arise due to a competition between the ionic migration and Fick's diffusion within the electric double-layer. Thus, the key to achieving continuous operation is flipping the polarity twice (once from initial to opposite and then back to initial). The polarity flips may be achieved easily by splitting the task into two steps, each step accounting for one polarity flip, as elaborated in the next to next paragraph below.
As shown in Fig. 5a and S8a–c,† the change in device polarity for TRECO can be easily achieved by discharging the cell at high currents. As explained in Fig. 6, discharging the cell at a high current ensures that the electronic movement through the external circuit is extremely fast (compared to the ionic movement through the electrolyte). This rapidly changes the electric field magnitude within the electric double-layer at the electrode–electrolyte interface, thus reducing the electrostatic attraction between the electrodes and oppositely charged ions. This alters the balance between Fick's diffusion and ionic migration within the electric double-layer, and hence, instead of observing voltage oscillations within the same polarity, the voltage first flips sign, making ions switch their location (from one electric double-layer to another) and then we observe voltage oscillations with flipped polarity. This is because, with flipped polarity, the current initially acting as a discharge current now starts to act as a charging current, thus increasing the electrostatic attraction between the electrodes and oppositely charged ions and holding them tightly enough to prevent a further flip of polarity.
To ensure continuous operation, the device polarity must be returned to the original polarity (i.e., polarity before the high current discharge was started). That may further be achieved (cf.Fig. 7) by flipping the sign of the current. This allows us to control the final voltage, as different voltages may be easily achieved after the initial and second polarity flip, as is evident from Fig. S8b and c.† Notably, our scheme does not require any change within the device itself, unlike the scheme proposed in ref. 12. Furthermore, achieving back the same voltage before the initial change of electrodes was performed in ref. 12 would require them to either have both sets of electrode materials with same thermopower in magnitude and opposite in sign or adjusting the temperature difference. Adjusting the temperature difference is not always possible in real-world settings where the application governs the hot end temperature and the cold end temperature is often room temperature. Thus, our proposed continuous operation scheme in this paper is more facile regarding its real-world applicability.
2.7. Powering a pocket calculator using a TRECO module
While the voltage oscillates during discharge, the amplitude of voltage oscillations (∼1 mV) is negligible compared to TRECO's voltage (∼1 V). Moreover, constant current discharge at 500 nA (for CD1) suggests that within 1000 minutes of discharge, the TRECO voltage only drops by about ∼60–75 mV. This, thus, shows that the amount of energy stored within the TRECO coin cell is much larger than the device reported in ref. 9, which discharged without any oscillations in less than 3 minutes. Thus, TRECO is capable of powering devices for long durations despite the oscillating voltage because the amplitude of voltage oscillations is much smaller than TRECO's OCV. This was confirmed by developing a TRECO module to power a calculator, as described below.As shown in Fig. 8a and b, a TRECO module was assembled by connecting four TRECO coin cells (electrically in series and thermally in parallel), and its top and bottom faces were held at 313 K and room temperature (300 K), respectively. Thus, a temperature difference of 13 K was applied across the two terminals of the module. The module's output was sufficient to power a calculator (whose battery was removed) in real-time, as shown in movies SM3 and SM4† (uploaded). We also performed experiments by connecting resistors as loads across TRECO. The corresponding experimental procedure is described under the section ‘Discharging TRECO coin cells using a constant resistance load’ in the ESI,† and the average power and energy dissipated in the resistors are tabulated in Table S4.†
2.8. Powering a pocket calculator using a large format TRECO cell
As shown in Fig. 8c and d, we used a large format cell (with an areal footprint of approximately 6.25 times the footprint of a single CR2032 coin cell) placed on a hot vacuum pump in our lab (the vacuum pump continuously operates as it is connected to the glove box) to power the pocket calculator. Approximately 1 V was obtained as the open circuit voltage (OCV) for ΔT = 8–9 K, and the obtained short circuit current (Isc) was 200 μA. An additional movie capturing this demonstration (ESI, movie SM5†) has been added to the ESI.†2.9. Wearable TRECO armband
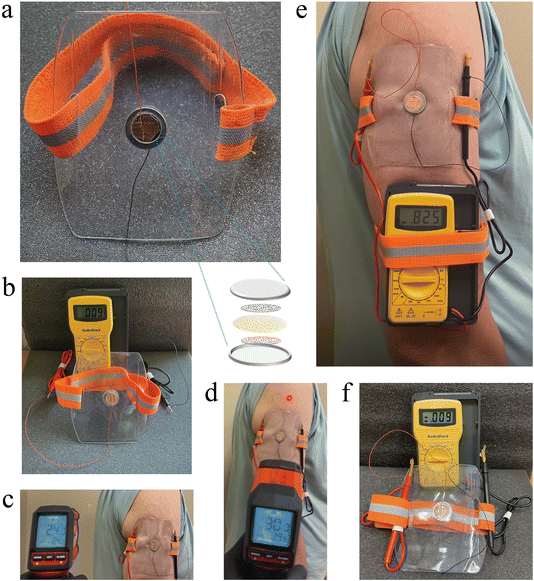
Wearable devices such as health-monitoring gadgets are integrating technology into daily life, enabling continuous health monitoring, enhanced communication, and improved productivity. Uninterrupted power from natural sources may be key to unlocking wearables' potential. The heat produced by our bodies, as a natural and sustainable energy source, is ideal for powering wearables in an uninterrupted fashion. To this end, we demonstrated that TRECO harvests ultra low-grade heat from the body for power generation, potentially replacing TEGs.Fig. 9 illustrates the details of a wearable arm-band powered by a single TRECO coin cell. Fig. 9a shows an arm badge pouch, typically used for holding ID cards during sports, repurposed to contain the TRECO coin cell. Two concentric circular holes were made in the pouch to expose the top and bottom surfaces of the coin cell to human skin (hot end) and air (cold end), respectively. Before attaching the arm-band to the human arm (i.e., ΔT = 0 K), the TRECO coin cell exhibited a negligible initial voltage, as seen in Fig. 9b. The room temperature and skin temperature were measured using an infrared thermometer (Fig. 9c and d), highlighting a temperature difference of approximately 6 K between the hot and cold ends of the TRECO coin cell. As shown in Fig. 9e, the TRECO coin cell generated about 825 mV from a small temperature difference of 6 K. Finally, Fig. 9f shows that the voltage returned to 9 mV after the TRECO coin cell was disconnected from the human arm. Informed consent was obtained from the human participant before the experiment, and a video capturing the experiment is included in the ESI section (ESI, movie SM6†).
2.10. Efficiency of TRECO
Efficiency for TRECO devices may be calculated via 2 methodologies: (a) power efficiency and (b) energy efficiency. A detailed explanation regarding both calculation methodologies has been provided in the ESI.†Fig. 10 shows that amongst Soret-based ionic thermoelectric generator systems, TRECO has one of the highest energy efficiencies. Additionally, TRECO exhibits the highest thermopower amongst all Soret-based ionic thermoelectric generators. | ||
| Fig. 10 Energy efficiency versus thermopower for TRECO and other state-of-the-art Soret effect-based ionic thermoelectric generators such as the ones based on PSSNa,37 PSSH,38 ionic liquids,30 PEO:NaOH27 electrolytes, ferricyanide/ferrocyanide redox couple3 based ionic thermoelectric and electronic thermoelectrics based on PEDOT:PSS39 and Bi2Te3 (ref. 37). Amongst Soret effect-based ionic thermoelectrics, TRECO has one of the highest efficiencies and the highest thermopower. | ||
3 Conclusions
This work demonstrated Soret effect-based ionic thermoelectric cells that can harvest ultra-low-grade waste heat near room temperature in real time. With a temperature difference of ∼10 K between the two electrodes, open circuit voltages greater than 1 V were recorded, thus resulting in a thermopower >100 mV K −1. We (i) proposed and demonstrated a continuous operation scheme for TRECO for its real-world utility, (ii) successfully harvested waste heat from a warm vacuum pump to power a pocket calculator using a single large format TRECO cell, (iii) developed a wearable TRECO arm-band which generated ∼825 mV when strapped on a human arm, and (iv) observed novel ‘electrochemical voltage oscillations’ while discharging the devices. These oscillations were observed, irrespective of electrode microstructure, electrode–electrolyte pair, and electrode porosity. Models and experiments both suggest that within the electric double-layer at the electrode–electrolyte interface, the electric field-driven ionic migration and concentration gradient-driven diffusion compete with each other, thus making it harder for the ions to escape the double-layer, leading to voltage oscillations. TRECO's novel mode of operation underscores its potential for novel applications.Data availability
The data that support the findings of this study are available from corresponding authors upon reasonable request.Author contributions
Conceptualization: MP and AMR; data curation: BG and MP; formal analysis: MP, SB, and MS; methodology: MP, HB, and AMR; investigation: BG, MP, MS, HB, SB, and NS; funding acquisition: AMR and AM; supervision: MP and AMR; visualization: MS; writing-original draft: MP, writing-review and editing: MP, AMR, SB, MS, HB, NS, BG, PSC, and AM.Conflicts of interest
The authors declare that a patent application corresponding to this work has been filed with USPTO and is pending evaluation.Acknowledgements
Prof. A. M. and Prof. A. M. R. acknowledge the funding from IUSSTF/JC-146/2019. All authors acknowledge the Instrument Shop (Mr Barrett Barker and his team-members) operated by the Department of Physics and Astronomy, Clemson University, for fabricating the in-house built TRECO test setup. We acknowledge Dr Jeffrey N. Anker, Department of Chemistry, Clemson University, for discussing the equivalent circuit model. Furthermore, we are indebted to Dr Laszlo Kish, Department of Electrical and Computer Engineering, Texas A & M University, for his advice on fast Fourier transform (FFT) and other invaluable feedback about the manuscript. All the authors acknowledge Mr Sam Parler, Mr Kevin Coleman, and Mr Jim Kaplan from Cornell Dubilier Electronics, South Carolina, for providing porous Al foils used as CD1 and CD2 electrodes in this study. We acknowledge Dr Kelliann Koehler for helping with the BET characterization of the electrode materials.References
- H. Cheng, X. He, Z. Fan and J. Ouyang, Flexible Quasi-Solid State Ionogels with Remarkable Seebeck Coefficient and High Thermoelectric Properties, Adv. Energy Mater., 2019, 9, 1901085 CrossRef.
- B. M. Mahlalela, C. Liu, K. Li and Y. Zhu, Electric Power Generation Potential Based on Waste Heat and Geothermal Resources in South Africa, in 44th Workshop on Geothermal Reservoir Engineering, 2019, vol. 214 Search PubMed.
- R. Hu, et al., Harvesting Waste Thermal Energy Using a Carbon-Nanotube-Based Thermo-Electrochemical Cell, Nano Lett., 2010, 10, 838–846 CrossRef CAS PubMed.
- D. Zhao, A. Würger and X. Crispin, Ionic thermoelectric materials and devices, J. Energy Chem., 2021, 61, 88–103 CrossRef CAS.
- J. Chipman, The Soret effect, J. Am. Chem. Soc., 1926, 48, 2577–2589 CrossRef CAS.
- M. A. Rahman and M. Z. Saghir, Thermodiffusion or Soret effect: historical review, Int. J. Heat Mass Transfer, 2014, 73, 693–705 CrossRef.
- W. Köhler and K. I. Morozov, The Soret Effect in Liquid Mixtures – A Review, J. Non-Equilib. Thermodyn., 2016, 41, 151–197 Search PubMed.
- E. D. Eastman, Theory of the Soret effect, J. Am. Chem. Soc., 1928, 50, 283–291 CrossRef CAS.
- T. Li, et al., Cellulose ionic conductors with high differential thermal voltage for low-grade heat harvesting, Nat. Mater., 2019, 18, 608–613 CrossRef CAS PubMed.
- I. Burmistrov, et al., High Seebeck coefficient thermo-electrochemical cell using nickel hollow microspheres electrodes, Renewable Energy, 2020, 157, 1–8 CrossRef CAS.
- X. Wang, et al., Direct thermal charging cell for converting low-grade heat to electricity, Nat. Commun., 2019, 10, 4151 CrossRef CAS PubMed.
- C. Chi, et al., Reversible bipolar thermopower of ionic thermoelectric polymer composite for cyclic energy generation, Nat. Commun., 2023, 14, 306 CrossRef CAS PubMed.
- A. Henry, R. Prasher and A. Majumdar, Five thermal energy grand challenges for decarbonization, Nat. Energy, 2020, 5, 635–637 CrossRef CAS.
- M. Grant Norton, A Modern History of Materials: From Stability to Sustainability, 2023 Search PubMed.
- M. Rudolph, M. Hromadova and R. de Levie, Demystifying an Electrochemical Oscillator, J. Phys. Chem. A, 1998, 102, 4405–4410 CrossRef CAS.
- Z. Xu, F. Hu, D. Li and Y. Chen, Electrochemical Oscillation during Galvanostatic Charging of LiCrTiO4 in Li-Ion Batteries, Materials, 2021, 14, 3624 CrossRef CAS PubMed.
- D. Li, et al., Electrochemical Oscillation in Li-Ion Batteries, Joule, 2018, 2, 1265–1277 CrossRef CAS.
- T. Lan, Q. Qiao, F. Hu, D. Li and Y. Chen, Electrochemical Oscillation during the Galvanostatic Charging of Li4Ti5O12 in Li-Ion Batteries, J. Phys. Chem. C, 2021, 125, 14549–14558 CrossRef CAS.
- Y. Mukouyama, M. Kikuchi and H. Okamoto, Bromide ions induced chaotic behavior in H2O2–H2SO4–Pt electrochemical system, J. Solid State Electrochem., 2005, 9, 290–295 CrossRef CAS.
- F.-R. F. Fan and A. J. Bard, Electrochemical Detection of Single Molecules, Science, 1995, 267, 871–874 CrossRef CAS PubMed.
- I. J. Cutress, E. J. F. Dickinson and R. G. Compton, Electrochemical random-walk theory, J. Electroanal. Chem., 2011, 655, 1–8 CrossRef CAS.
- J. Lu, Y. Fan, M. D. Howard, J. C. Vaughan and B. Zhang, Single-Molecule Electrochemistry on a Porous Silica-Coated Electrode, J. Am. Chem. Soc., 2017, 139, 2964–2971 CrossRef CAS PubMed.
- P. Sun and M. V. Mirkin, Electrochemistry of Individual Molecules in Zeptoliter Volumes, J. Am. Chem. Soc., 2008, 130, 8241–8250 CrossRef CAS PubMed.
- M. A. G. Zevenbergen, P. S. Singh, E. D. Goluch, B. L. Wolfrum and S. G. Lemay, Stochastic Sensing of Single Molecules in a Nanofluidic Electrochemical Device, Nano Lett., 2011, 11, 2881–2886 CrossRef CAS PubMed.
- S. G. Lemay, S. Kang, K. Mathwig and P. S. Singh, Single-Molecule Electrochemistry: Present Status and Outlook, Acc. Chem. Res., 2013, 46, 369–377 CrossRef CAS PubMed.
- F.-R. F. Fan, J. Kwak and A. J. Bard, Single Molecule Electrochemistry, J. Am. Chem. Soc., 1996, 118, 9669–9675 CrossRef CAS.
- D. Zhao, et al., Ionic thermoelectric supercapacitors, Energy Environ. Sci., 2016, 9, 1450–1457 RSC.
- S. L. Kim, J.-H. Hsu and C. Yu, Thermoelectric effects in solid-state polyelectrolytes, Org. Electron., 2018, 54, 231–236 CrossRef CAS.
- H. Wang, U. Ail, R. Gabrielsson, M. Berggren and X. Crispin, Ionic Seebeck Effect in Conducting Polymers, Adv. Energy Mater., 2015, 5, 1500044 CrossRef.
- M. Bonetti, S. Nakamae, M. Roger and P. Guenoun, Huge Seebeck coefficients in nonaqueous electrolytes, J. Chem. Phys., 2011, 134(11), 114513 CrossRef CAS PubMed.
- D. Zhao, et al., Polymer gels with tunable ionic Seebeck coefficient for ultra-sensitive printed thermopiles, Nat. Commun., 2019, 10, 1093 CrossRef PubMed.
- H. A. Andreas, Self-Discharge in Electrochemical Capacitors: A Perspective Article, J. Electrochem. Soc., 2015, 162, A5047–A5053 CrossRef CAS.
- J. Chmiola, et al., Anomalous Increase in Carbon Capacitance at Pore Sizes Less Than 1 Nanometer (1979), Science, 2006, 313, 1760–1763 CrossRef CAS PubMed.
- J. Wu, Understanding the Electric Double-Layer Structure, Capacitance, and Charging Dynamics, Chem. Rev., 2022, 122, 10821–10859 CrossRef CAS PubMed.
- P. S. Chauhan, et al., Influence of electrolyte on the photo-charging capability of a ZnO–FTO supercapacitor, J. Mater. Chem. A, 2024, 12, 22725–22736 RSC.
- J. P. de Souza, A. Levy and M. Z. Bazant, Electroneutrality breakdown in nanopore arrays, Phys. Rev. E, 2021, 104, 044803 CrossRef CAS PubMed.
- H. Wang, et al., Ionic Thermoelectric Figure of Merit for Charging of Supercapacitors, Adv. Electron. Mater., 2017, 3, 1700013 CrossRef.
- S. L. Kim, H. T. Lin and C. Yu, Thermally Chargeable Solid-State Supercapacitor, Adv. Energy Mater., 2016, 6, 1600546 CrossRef.
- O. Bubnova, et al., Optimization of the thermoelectric figure of merit in the conducting polymer poly(3,4-ethylenedioxythiophene), Nat. Mater., 2011, 10, 429–433 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08559k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |