Phase behavior, crystal structure, and superprotonic conductivity of Cs[(H₂PO₄)_1−2y(HPO₄)_y]: phosphate deficient analogs to cubic CsH₂PO₄ in the (1 − x)CsH₂PO₄–xCs₂HPO₄ system

Abstract

A systematic study of the (1 − x)CsH₂PO₄–xCs₂HPO₄ system has been carried out to explore the possibility of modifying the phase behavior of CsH₂PO₄ in the high temperature, superprotonic regime. Materials with x from 0 to 0.20 were characterized by in situ X-ray powder diffraction, simultaneous thermal analysis, and electrical impedance spectroscopy under a range of steam partial pressures. From these data, the phase diagram between CsH₂PO₄ (x = 0) and Cs₃(H_1.5PO₄)₂ (x = 0.5) was determined. The system displays eutectoid behavior, with an invariant point defined by a temperature of 192.0 ± 1.4 °C and a composition of x = 0.17 ± 0.01. At the eutectoid temperature, monoclinic CsH₂PO₄ combines with Cs₃(H_1.5PO₄)₂ to form α′′-CDP, a cubic variant of superprotonic CsH₂PO₄, in which Cs : P exceeds 1 : 1. This surprising result implies that cubic CsH₂PO₄, which crystallizes in the CsCl structure-type, can support a large excess of Cs. Rietveld structure refinement, along with a lattice parameter that decreases with increasing Cs content, reveals that the chemistry is accommodated via the presence of phosphate vacancies rather than Cs interstitials. Charge balance is presumed to be maintained via a concomitant decrease in the average number of protons per phosphate group. Accordingly, the stoichiometry of α′′-CDP is described as CsH_2−3y(PO₄)_1−y, and the phosphate vacancy concentration can be at least as high as 17% (x = 0.20). The conductivity of the α′′-CDP materials is comparable to that of stoichiometric, superprotonic CDP, while providing access to a substantially wider temperature range of superprotonic transport. This study reveals the potential for creating advanced proton conductors using cation:anion off-stoichiometry as a new design principle.

---

1. Introduction

The candidate pool for technologically relevant solid acid materials with superprotonic phases remains small.¹ In such materials, superionic transport of protons is facilitated by polyanion group reorientation and rapid proton hops between such groups.² The prototypical compound in this class is CsH₂PO₄ (cesium dihydrogen phosphate, CDP), a material that adopts at ambient conditions a monoclinic, P2₁/m structure, that is effectively proton insulating and transitions at 228 °C to a cubic, Pm3̄m phase of the CsCl structure-type, in which the phosphate groups are rotationally disordered. Above the transition, the conductivity rises to technologically significant levels, reaching a value of 2.5 × 10⁻² S cm⁻¹ at 250 °C.³ High conductivity in the intermediate temperature region between 100 and 300 °C is considered highly desirable^4,5 (the temperatures are high enough to support high rates for catalytic reaction rates and yet low enough to limit thermally induced degradation), and CsH₂PO₄ has the highest proton conductivity in this regime of any known material except for In-doped SnP₂O₇.^5,6 As such, CsH₂PO₄ (either alone or as a composite with a second component) has been demonstrated in a range of electrochemical energy technologies, including hydrogen fuel cells,^7–9 direct alcohol fuel cells,¹⁰ electrolyzers,¹¹ electrochemical cells for both CO₂ (ref. 12 and 13) and N₂ reduction,¹⁴ and ammonia to hydrogen convertors.¹⁵ While these developments show promise towards commercial realization, CDP suffers from various drawbacks, in particular, the limited window of thermal stability of the superprotonic phase and the need to supply high levels of steam to prevent decomposition.^16,17 These drawbacks have motivated efforts to discover alternative superprotonic materials.¹

Constraints in identifying new candidates arise from the limited number of physically realizable compounds with desired crystal-chemical features (i.e., structures formed of polyanion groups linked by hydrogen bonds), as well as the chemical instability of materials with suitable hydrogen bonding configurations when exposed to device operating conditions. Such instabilities include dehydration, as noted is encountered in CDP,^16,17 reduction by hydrogen, as encountered in sulfate and selenate solid acids,^18,19 and oxidation, as encountered in CsHPO₃H.²⁰ Of these, dehydration of CDP can be considered the most likely to be overcome via chemical modification. In contrast, sulfate/selenate reduction and phosphite oxidation are inherent to the nature of the polyanion group. Of possible bulk chemical modifications to CDP, Rb and K substitutions have been explored but have not generated promising materials.²¹ While RbH₂PO₄ (rubidium dihydrogen phosphate, RDP) is entirely miscible in CDP, its introduction increases the temperature of the superprotonic transition, increases susceptibility to dehydration, and decreases the conductivity in the superprotonic phase. The solubility limit of KH₂PO₄ into CDP is not fully established, but across the measured incorporation range, the conductivity of the cubic phase again decreases with increasing K substitution. Thus, these relatively straightforward approaches to modifying CDP have not proven successful. An alternative to modifying the bulk chemistry is to pursue composites, and such approaches have shown signs of promise,²² but they cannot be expected to influence the inherent thermodynamics of CDP dehydration.¹⁶

We recently discovered a new strategy for modifying the crystal chemical behavior of cubic CsH₂PO₄ in which the Cs ions are replaced, not by Rb or K ions, but instead, and rather remarkably, by protons.²³ The structure, in this case, hosts Cs vacancies which are charge balanced by an increase in the average number of protons per phosphate group. The chemical formula can accordingly be described as Cs_1−x[(H₃PO₄)_x(H₂PO₄)_1−x], reflecting the structural defects that result from the chemical modification. This Cs-deficient phase, denoted α-CDP, can be considered a solid solution between CsH₂PO₄ and H₃PO₄ and can accommodate as much as 22% of the Cs⁺ being replaced by H⁺. The phase behavior in the CsH₂PO₄–H₃PO₄ system has relevance for technological applications due to the occurrence of a eutectoid transition between monoclinic CDP and the compound Cs₇(H₄PO₄)(H₂PO₄)₈ (ref. 24) (hepta-cesium tretra-hydroxyphosphonium octa-dihydrogenphosphate, CPP) at a temperature of 155 °C. The solvus temperature delineating the boundary between the two-phase region encompassing monoclinic CsH₂PO₄ and α-CDP and the single-phase α-CDP region falls monotonically with x, from 228 °C for stoichiometric CDP, to 155 °C at x = 0.18, the composition which defines the eutectic point. Critically important to exploiting this phase behavior, the conductivity in much of the two-phase region comprising monoclinic CDP(m) and α-CDP approaches that of stoichiometric, superprotonic CDP. Thus, essentially superprotonic behavior is observed upon traversing the eutectoid at 155 °C, rather than being limited to temperatures above the solvus.²³ While the extension of the high conductivity phase to lower temperatures is desirable, these phosphate excess compositions were found to be more susceptible to dehydration than stoichiometric CDP and thus they provide limited technological value.

In parallel with the discovery of proton-substituted CsH₂PO₄, we have found that cubic RbH₂PO₄ can be modified, in an inverse sense, via alkali ion substitution of the protons.²⁵ In this case, solid solution behavior is effectively observed between RbH₂PO₄ and Rb₃PO₄, and the cubic structure accommodates the excess alkali ions via an even more surprising feature, the presence of phosphate ion vacancies. Charge balance is maintained by a reduction in the average number of protons per phosphate group relative to RbH₂PO₄, and the chemical formula is most appropriately described as phosphate-deficient Rb[(H₂PO₄)_1−2y(HPO₄)_y]. At least 20% of the phosphate sites can be vacant in the cubic phase. The eutectoid point in this system occurs at 242 °C and y = 0.16. In the stoichiometric material, the superprotonic phase is only reliably observed under high total pressure.²⁶ When it is heated under total 1 atm pressure, regardless of the steam partial pressure, dehydration precedes the superprotonic transition, which has been estimated to occur (as a metastable transformation) at ∼280 °C.^27,28 Chemical modification by introducing excess Rb enables access to the cubic superprotonic phase without recourse to high pressure conditions. However, the stability window is extremely narrow, extending only approximately 3 °C beyond the eutectoid temperature under a steam partial pressure of 0.88 atm.²⁵

These observations raise the possibility of the existence of phosphate-deficient cubic CDP, a material that would be analogous to phosphate-deficient cubic RDP,²⁵ found in the RDP-Rb₃PO₄ system. Such a material would be essentially the inverse of our previously reported cesium-deficient phase²³ and ideally, it would both extend the superprotonic conductivity regime to low temperatures and enhance the thermal stability relative to stoichiometric CDP. Two compounds are known along the pseudo-binary composition line between CDP and Cs₃PO₄, Cs₃(H_1.5PO₄)₂ (ref. 29) and Cs₂HPO_4.³⁰ High temperature mixtures of either of these compounds, or their crystalline hydrates, with stoichiometric CsH₂PO₄ would be expected to yield phosphate deficient α-CDP, should it be a thermodynamically accessible phase. Ponomareva and Bagryantseva³¹ have recently studied mixtures of stoichiometric CDP and Cs₂HPO₄·2H₂O, with up to 0.5 mole fraction of the latter phase. These authors reported that, at ambient temperature, the mixtures yielded composites of stoichiometric CDP and anhydrous, stoichiometric Cs₃(H_1.5PO₄)₂. Moreover, the conductivities of the mixtures, as measured on heating, were greater than that of stoichiometric CDP at temperatures below its superprotonic transition of 228 °C. The thermal stability was also reported to be improved in the composites relative to neat CDP. The authors attributed the enhanced proton transport to the presence of highly conductive interfacial regions between CDP and Cs₃(H_1.5PO₄)₂ and emphatically not to solid solution behavior.³¹ This interpretation stands counter to our discovery of a solid solution region in the analogous Rb system²⁵ and motivates a definitive analysis of the phase behavior between CDP and Cs₃PO₄.

In the present study, we use thermal analysis, in situ X-ray diffraction, and impedance spectroscopy to establish the characteristics of the (1 − x)CsH₂PO₄–xCs₂HPO₄ system between x = 0 and 0.5, a chemical composition space that is bound at x = 0 by CDP and at x = 0.5 by Cs₃(H_1.5PO₄)₂. While for ease, the stoichiometry of a single-phase material in this composition space can be written as Cs_1+xH_2−xPO₄, this formula does not represent the crystallography of the material discovered. Instead, in analogy to the behavior found in the (1 − x)RbH₂PO₄–xRb₂HPO₄ system,²⁵ the stoichiometry in the cubic phase is written as Cs[(H₂PO₄)_1−2y(HPO₄)_y] to reflect the crystallographic features, specifically, the presence of phosphate vacancies. It is to be noted that, formally, the previously reported Cs-deficient Cs_1−x[(H₃PO₄)_x(H₂PO₄)_1−x] compositions and the present materials lie in the same phase space. To differentiate these regions of chemical space with respect to stoichiometric CsH₂PO₄, we introduce the notation α′ to indicate cation deficiency (previous work²³) and α′′ to indicate phosphate deficiency (this study).

2. Methods

2.1 Sample preparation

Samples of overall composition Cs_1+xH_2−xPO₄, up to x = 0.3, were prepared by combining the requisite quantities of CsH₂PO₄ and Cs₃(H_1.5PO₄)₂. Because both precursors, particularly Cs₃(H_1.5PO₄)₂, are hygroscopic, both were grown as moderately sized crystals from aqueous solution, using methods described elsewhere,^32,33 thereby minimizing the contribution of surface adsorbed H₂O to the precursor mass. The starting compounds Cs₂CO₃ (Thermo Scientific, 99.9% metals basis) and H₃PO₄ (Sigma-Aldrich, 85 wt%, 99.99% metals basis) were used for precursor preparation without further purification. To promote the reaction between the two precursor phases in the subsequent analyses, the precursor powders were ground, pressed into compacts, and annealed at 240 °C under 0.4 atm pH₂O for several hours, and the process repeated. Following these steps, the true phase fractions of precursor components in the samples were established by X-ray powder diffraction (XRD) and model refinement as described below. Samples used for transport studies were handled in a glove box in order to minimize the contribution of surface adsorbed water to the conductivity.

2.2 X-ray diffraction

X-ray diffraction patterns of the samples prepared for thermal analysis and conductivity measurements were collected under ambient conditions using a Rigaku Ultima IV diffractometer (Cu source), a measurement range of 15° to 60°, a scan speed of 5° min⁻¹, and a scan step size of 0.02°. All patterns showed a mixture of monoclinic CsH₂PO₄ (ref. 34) and Cs₃(H_1.5PO₄)₂·2H₂O.³⁵ Data were analyzed by Rietveld refinement to determine the relative amounts of these phases and establish the precise chemistry of each sample, with an estimated uncertainty in x of 0.01.

Elevated temperature, in situ X-ray diffraction under controlled pH₂O was performed on a Rigaku Smartlab 9 kW Gen3 with a Cu source (15° to 60° 2θ range, 10° min⁻¹ scan speed, variable step size between 0.08–0.20°) and an Anton Paar XRK900 furnace attachment. Compositions examined were x = 0.06, 0.15 and 0.20. Prior to the introduction of humidity, measurements were performed at a few selected temperatures between ambient and 150 °C. The heating rate between measurement conditions was 10 °C min⁻¹, and the samples were equilibrated for 30 min after reaching the targeted temperature prior to data collection. At 150 °C, water vapor was introduced to the system using 30 sccm of N₂ carrier gas, and diffraction data were collected following a 30 min equilibration period. In all cases, it was found that the introduction of humidity did not impact the crystalline structures. The sample was then heated to a calibrated temperature of 192 °C (set 190 °C), and diffraction patterns were measured at 2–5 °C intervals (2 °C min⁻¹ between steps) to a given maximum temperature that was composition dependent. At each measurement temperature, following a 30 min equilibration period, the data collection was repeated every ten minutes until evolution was complete; only final diffraction patterns are reported.

Refinement of structural parameters from the X-ray data was performed using the GSAS-II program and the relevant crystallographic information files.^34,35 The histogram scale factor, sample displacement, lattice parameters, and crystallite sizes were each refined in addition to the phase fractions. The instrument parameters were fixed using an independent measurement of a LaB₆ standard.

2.3 Thermal analysis

Simultaneous thermogravimetric and differential scanning calorimetry (TGA/DSC) measurements were performed using a Netzsch STA (simultaneous thermal analyzer) 449F3. Powder samples, roughly 40 mg in mass, were compacted in the Pt sample pan to ensure particle–particle contact. The water partial pressure, pH₂O, in these experiments was controlled using the integrated water vapor furnace of the STA and was set to values ranging from 0.1 to 0.7 atm (balance Ar). Five compositions between x = 0.03 and 0.20 were characterized under 0.4 atm, nine between x = 0.03 and 0.30 were measured under 0.7 atm, and the x = 0.16 composition was studied under six gas conditions, from dry to pH₂O = 0.7 atm. The total gas flow rate was between 130 and 350 sccm, depending on the requirements for achieving the target pH₂O. Initial heating was performed under dry Ar up to 130 °C. After 1 h of equilibration at this temperature, water vapor was introduced, and the sample allowed to equilibrate for another hour. Following this equilibration the heating rate was set to 1 °C min⁻¹ and data collected to a maximum temperature of 350 °C. All thermal events of interest occurred at temperatures well above 130 °C, and artifacts in the profiles due to the introduction of steam are ignored in the analysis by reporting only data acquired at higher temperatures. The dry measurement of the x = 0.16 composition (identified to be the eutectoid composition) was performed under neat Ar supplied at a rate of 20 sccm, with the heating rate again set to 1 °C min⁻¹ and a maximum temperature of 350 °C. DSC results obtained at low to moderate pH₂O (0.1 to 0.4 atm) were used as calibration standards to ensure self-consistency across STA and diffraction measurements. Relative to the nominally recorded temperatures, this calibration procedure resulted in modifications of no more than 2 °C to the XRD data and no more than 4 °C to the high pH₂O STA data.

2.4 Electrical impedance spectroscopy

Electrical impedance measurements were made on five compositions, from x = 0 to 0.18. While the conductivity of the end-member CsH₂PO₄ (x = 0) has been reported a number of times in the prior literature,^{3,21,32,36–38} we include new measurements of this compound for completeness and method validation. For each composition, enough material was synthesized to fabricate and characterize three 0.8 g pellets. In an Ar environment glovebox, samples were pulverized and mixed in a mortar and pestle and then loaded into a 14.85 mm diameter die. The loaded die was transferred to a uniaxial press outside of the glovebox, and the sample then subjected to a pressure of 98 kPa for 5 minutes. Final densities of the resulting compacts were greater than 95% of theoretical in all cases, with thicknesses of approximately 1.4 mm. The compacts were polished with 2000 grit sandpaper and Ag electrodes (100 nm) were sputtered onto each face using a Denton Desk Sputter IV. Samples were positioned into in-house constructed holders for placement into a furnace, and care was taken to apply a similar gripping force on each sample. Sample dimensions, which can be impacted by the force of the holder, were measured before and after impedance characterization, and diameters were found to differ only by tens of micrometers in all cases.

Impedance spectra were collected on heating. Upon reaching 150 °C, 0.4 atm pH₂O, carried by N₂, was introduced into the sample furnace and the system allowed to equilibrate; continuously recorded impedance data indicated that equilibrium had been reached after approximately one hour. Spectra were then collected in 15 °C temperature steps up to 190 °C, with three measurements recorded at each temperature over a thirty-minute period. Upon reaching 190 °C, the temperature steps were decreased to 3 °C, the number of measurements recorded at each temperature increased to four, and the measurement period increased to forty-minutes. The maximum measurement temperature was 257 °C. Upon cooling, the gas was changed to dry N₂ at 150 °C to prevent condensation. Slight differences in conductivity between humid and dry conditions were observed at 150 °C; to enable focus on the impact of the phase changes (which occur in any case at temperatures above which surface hydration effects impact conductivity), only the conductivity data collected above 150 °C are reported.

The resulting data were analyzed in terms of equivalent circuit models using the software package ZView. At lower temperatures the data were described using a single, parallel (RQ) circuit, where R is a resistor and Q is a constant phase element. At higher temperatures, the data were described using a series RW circuit, where W is a Warburg impedance element. From the fitted resistances, corresponding conductivities were computed using the post-measurement dimensions of the samples. The conductivities for each composition were averaged to derive averaged transport values and estimated uncertainties.

3. Results

3.1 Phase behavior

The phase diagram determined for the (1 − x)CsH₂PO₄–xCs₂HPO₄ system between end-members CsH₂PO₄ (x = 0) and Cs₃(H_1.5PO₄)₂ (x = 0.5) is presented in Fig. 1. Representative XRD and STA data that support the proposed phase behavior are presented in Fig. 2–4. The key feature of the phase diagram is the occurrence of a eutectoid reaction between stoichiometric, monoclinic CsH₂PO₄ and stoichiometric Cs₃(H_1.5PO₄)₂ at 192.0(14) °C and x = 0.17(1). Following crystallographic notation, the number in parentheses corresponds to the uncertainty in the final digit(s). Reflected in the diagram is the transition of stoichiometric CDP to its cubic phase at 228 °C. In the case of Cs₃(H_1.5PO₄)₂, high temperature studies of this material have shown that no superprotonic transition occurs prior to decomposition,³³ despite its crystallographic similarity to compounds such as Rb₃H(SeO₄)₂ (ref. 39) which display a trigonal superprotonic phase.

Fig. 1 Phase diagram between CsH₂PO₄ and Cs₃(H_1.5PO₄)₂ as determined from STA and in situ XRD experiments. For ease of description, the composition space is defined according to (1 − x)CsH₂PO₄–xCs₂HPO₄.

Fig. 2 In situ XRD patterns of the materials with composition (a and b) x = 0.06, (c and d) x = 0.15; and (e and f) x = 0.20 in the system (1 − x)CsH₂PO₄–xCs₂HPO₄ at (a, c and e) 150 °C, below the eutectoid transition, and (b, d and f) 197 °C, above the transition. The composition x = 0.15 is close to the eutectoid composition, and at 197 °C, almost all of the material has transformed to cubic α-CPD. Data are collected under flowing pH₂O = 0.4 atm, balance N₂.

Fig. 3 Cubic lattice parameters of α′′-CDP materials: (a) temperature dependence, with filled data points corresponding to single phase regions and half-filled data points to single phase regions; and (b) composition dependence at 192 °C, where values are extrapolated from (a). The data for stoichiometric CDP (x = 0) are from Ikeda et al.²¹ Uncertainties in the values as derived from Rietveld refinement are smaller than the size of the datapoints.

Fig. 4 STA profiles of representative materials in the (1 − x)CsH₂PO₄–xCs₂HPO₄ system collected under pH₂O = 0.4 atm: (a) x = 0.05 (in the hypoeutectoid region); (b) x = 0.16 (close the eutectoid composition); and (c) x = 0.20 (in the hypereutectoid region). Each material displays a DSC anomaly at ∼192 °C in the absence of mass loss.

The diffraction patterns, Fig. 2, show the phase behavior for the three compositions studied by in situ XRD (x = 0.06, 0.15 and 0.20) at temperatures that are below (150 °C) and above (197 °C) the eutectoid transition. At 150 °C, all three samples are fully described as mixtures of stoichiometric monoclinic CsH₂PO₄ and stoichiometric Cs₃(H_1.5PO₄)₂. The mutual insolubility of these phases is demonstrated by the insensitivity of the cell volumes to composition (see ESI Fig. S1†). Above the transition, the x = 0.15 composition displays a pattern dominated by a cubic phase, the peaks of which are readily indexed as simple cubic with a lattice parameter of a ≈ 4.9 Å. The peak intensities are similar to those of cubic superprotonic CsH₂PO₄,^21,34,40 though the stoichiometry of the material characterized here clearly differs. The occurrence of a small amount of monoclinic CsH₂PO₄ in the pattern indicates that the eutectoid composition is slightly rich in Cs₂HPO₄ relative to x = 0.15 and is the basis for the estimated value of x = 0.17(1) for the invariant point. The patterns of the x = 0.06 and x = 0.20 materials at 197 °C reveal the presence of two phases, consistent with the proposed phase diagram of Fig. 1. In particular, at x = 0.06, stoichiometric monoclinic CsH₂PO₄ appears alongside the cubic, CsH₂PO₄-like phase, and at x = 0.20, the two phases are stoichiometric Cs₃(H_1.5PO₄)₂ and the cubic compound. At sufficiently high temperatures, only cubic patterns are obtained from these compositions (see examples presented in ESI Fig. S2†). Data points indicated on the phase diagram, Fig. 1, reflect the phases observed in the complete set of in situ diffraction studies.

The cubic, CsH₂PO₄-like compound that occurs at 192 °C has a stoichiometry globally described as Cs_1.16H_1.84PO₄ and is deficient in phosphate relative to stoichiometric CsH₂PO₄. It forms at a temperature substantially lower than the superprotonic transition temperature of 228 °C of stoichiometric CsH₂PO₄, highlighting the potential for engineering the phase behavior via chemical modifications. An indication of the crystallographic nature of the phosphate-deficient compositions is given by comparison of their lattice parameters to those of stoichiometric, cubic CsH₂PO₄, Fig. 3, where it is evident that the phosphate deficiency is accompanied by a substantial decrease in cell parameter.

Particularly striking in Fig. 3(a) are the distinct temperature trends in the apparent thermal expansion coefficients of the different compositions. Within the two-phase region, these coefficients differ from each other not only in magnitude, but also in sign, whereas within the single-phase region, the thermal expansion behavior is similar across all four compositions. In the specific case of the x = 0.16 composition (for which the widest temperature range in the single-phase region could be accessed) the thermal expansion coefficient is 3.57(12) × 10⁻⁵ K⁻¹, as referenced to the cell parameter at 242 °C, almost identical to the reported value of 3.92(11) × 10⁻⁵ K⁻¹ of CDP.²¹ Extrapolation of the lattice parameters in the single-phase regions to a common temperature of 192 °C reveals that the cell parameter of Cs_1+xH_2−xPO₄ contracts approximately linearly with composition, x, Fig. 3(b), with a slope of −0.41(3) Å/x (in fractional units). This decrease argues against a structure in which Cs ions are located in interstitial sites and suggests instead the presence of phosphate vacancies, similar to what has been observed in Rb-rich α′′-RDP.²⁵

The lattice contraction with increasing cesium excess also explains the anomalous lattice parameter trends in the two-phase regions, Fig. 3(a). In the case of the hypoeutectoid material (x = 0.06) the heightened apparent thermal expansion reflects the diminishing extent of cesium excess as the composition moves along the solvus line towards stoichiometric CDP. Conversely, the hypereutectoid material (x = 0.20) displays an apparent negative thermal expansion because cesium excess in the cubic phase increases with temperature, as given by the hypereutectoid solvus. The material near the eutectoid composition displays nearly linear expansion, consistent with the minimal temperature range over which it exists within a two-phase region. The lattice parameter of the cubic phase at this composition is slightly above the extrapolation from the single-phase region, representing a very minor inconsistency with identification of x = 0.15 as being slightly rich in Cs relative to the eutectoid composition. The asymmetry between the x = 0.06 and the x = 0.20 compositions in terms of deviation from simple thermal expansion can also be explained in terms of the phase behavior, Fig. 1. The solvus line is shallow in the hypoeutectoid region, indicating a strong change in composition of α′′-CDP with temperature, whereas in the hypereutectoid region it is steep, indicating limited change in composition. Estimation of the positions of the solvus lines from the lattice parameters reproduces the qualitative features of the phase diagram (Fig. S3†).

The thermal analysis, Fig. 4, revealed a clear transition at 191–193 °C that is independent of composition and occurs in the absence of any mass loss. As averaged across all measurements (see ESI Fig. S4 and S5†), the transition occurs at 192.0(14) °C. The DSC profile of the x = 0.05 composition in particular, displays a classic eutectoid feature⁴¹ in which a sharp peak is followed by a long tail, which then concludes with another sharp, though less intense, peak. The latter corresponds to the solvus temperature beyond which the material is entirely within the high temperature phase. In principle, quantitative determination of the phase diagram is possible using such features of the DSC profiles, however, this requires appropriate homogenization of the reactant phases. Due to the availability of in situ diffraction data, the positions of the solvus lines in Fig. 1 are instead obtained on the basis of phase detection in the diffraction patterns.

Significant from an application perspective, the results in Fig. 4 (collected under pH₂O = 0.4 atm) indicate a relatively wide stability range for α′′-CDP, extending well past the eutectoid temperature. As expected, the decomposition temperature depends on pH₂O, as evident in the profiles for the x = 0.16 composition measured at several values of pH₂O, Fig. 5. Under dry Ar, the dehydration almost entirely obscures the polymorphic transition, underscoring the importance of ensuring the presence of finite pH₂O when conducting measurements on solid acid materials. The results also demonstrate the variability in the features of the DSC signal due to differences in sample homogenization. Nevertheless, the onset of the eutectoid transition occurs at an invariant temperature of 191–193 °C, confirming indisputably that the transformation is not a result of dehydration. Decomposition under 0.4 atm pH₂O occurs at 271(2) °C and is elevated to 282(2) °C under 0.7 atm pH₂O, Fig. 6. Furthermore, within the uncertainty of the measurement, the dehydration tendency is independent of composition, x.

Fig. 5 STA profiles of the material with composition x = 0.16, close to the eutectoid composition, in the (1 − x)CsH₂PO₄–xCs₂HPO₄ system measured under six different gas conditions ranging from (a) dry Ar; to (f) 0.7 atm, as indicated. In the absence of humidification, the polymorphic transition is convoluted with decomposition. With increasing pH₂O, the decomposition is increasingly suppressed.

Fig. 6 Decomposition temperature of materials in the (1 − x)CsH₂PO₄–xCs₂HPO₄ system: (a) as a function of pH₂O with x = 0.1; and (b) as a function of composition, x, at pH₂O values indicated.

3.2 Structure of α′′-CDP

The global stoichiometry of α′′-CDP (for example, Cs_1.16H_1.84PO₄ at the eutectoid point) can, in principle, be accommodated in the CsCl structure of superprotonic CsH₂PO₄ in a variety of ways. These include the placement of the Cs in interstitial sites, the presence of anti-site defects in which Cs replaces a phosphate group, or the occurrence phosphate vacancies that are charge balanced by phosphate groups with a diminished number of protons than in stoichiometric CDP. As argued in the case of α′′-RDP,²⁵ cation interstitials and antisite defects are extremely unlikely due to the strain and electrostatic energy penalties such features would introduce. Furthermore, as noted above, with increasing x, the cell parameter of Cs_1+xH_2−xPO₄, decreases, eliminating the possibility of Cs interstitials as the mechanism for accommodating excess Cs in the structure, as these would be expected to expand the lattice. Accordingly, the structure is proposed to form in a manner similar to that of α′′-RDP, which hosts phosphate vacancies,²⁵ and the stoichiometry can be denoted Cs[(H₂PO₄)_1−2y(HPO₄)_y] with y = 1 − 1/(1 + x) or (equivalently) CsH_2−3y(PO₄)_1−y. Here, the average number of protons per phosphate group is (2 − 3y)/(1 − y) and decreases as the Cs excess increases, maintaining overall charge balance.

Rietveld analysis of data collected for the x = 0.15 composition at 222 °C, in which only the cubic phase was detected, yielded the structure shown in Fig. 7 and parameters provided in Table 1. In the refinement steps, the P and O occupancies were fixed to the values implied by the structural interpretation (i.e., 0.84 and 0.1417, respectively). Isotropic displacement parameters for all atoms were refined, with the displacement parameter for O fixed at 1.07 times that of P, as has been reported for stoichiometric, cubic CDP. The oxygen was placed on the 24l site of stoichiometric CDP and the free coordinates allowed to vary under the restraint of a P–O bond distance of 1.54 Å. The final refinement statistics were R_wp = 8.34%, R_bragg = R_F = 4.02%, GOF = 6.34, indicating the model to be satisfactory. The difficulty in obtaining full powder randomization at high temperatures at which grain growth occurs and the limited number of peaks in the pattern conspire to produce slightly unrealistic crystallographic parameters, including a relatively short P–O distance of 1.38(1) Å.

Fig. 7 Rietveld refinement result from measurement of the x = 0.16 composition at 222 °C. Insets show the refined structure, corresponding to a stoichiometry of CsH_1.59(PO₄)_0.86 with 14% of the phosphate sites unoccupied. Left inset is the average structure, with all oxygen sites shown; right inset displays a single representative phosphate orientation.

Table 1 Fractional atomic coordinates and displacement parameters of α′′-Cs_1+xH_2−xPO₄ at x = 0.15 and T = 222 °C. Structure adopts space group Pm3̄m with a = 4.89517(9) Å. The P–O bond distance is 1.38(1) Å. Numbers in parentheses reflect the uncertainty in the final digit(s) of the quoted values

Atom	x	y	z	Site	Occupancy^a	Uiso (Å^2)
a Fixed to match global chemistry.b Tied to the Uiso of P by a multiplicative factor of 1.073.
Cs	0	0	0	1a	1	0.098(1)
P	½	½	½	1b	0.8696	0.010(3)
O	½	0.244(1)	0.380(2)	24l	0.1449	0.011(3)^b

---

3.3 Conductivity

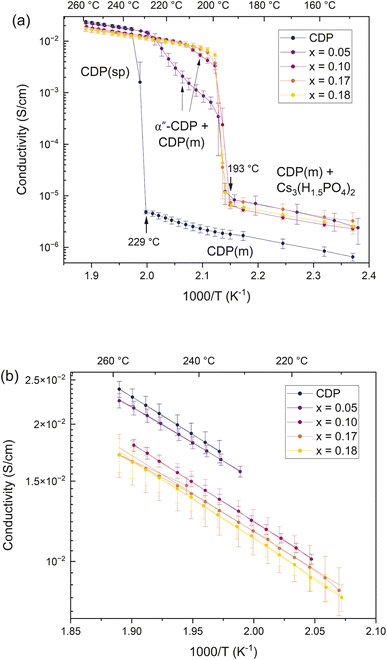
The temperature dependent conductivities of the materials of composition x = 0, 0.05, 0.10, 0.17, and 0.18 are shown in Fig. 8 (as averaged over the three samples measured at each composition). In neat (stoichiometric) CsH₂PO₄, the superprotonic transition at 229 °C is clearly captured. In each of the phosphate deficient compositions, a noticeable jump in conductivity occurs at 193 °C, corresponding to the eutectoid transition. In the x = 0.05 material, the impact of the two-phase mixture is evident as a superlinear (concave upwards) increase in conductivity with temperature in the Arrhenius representation, which then reverts to linearity in the single-phase region above about 225 °C. The behavior of the x = 0.10 material is similar, but the increase in conductivity on reaching the eutectoid temperature is larger, and the temperature range over which the conductivity is superlinear is narrower, concluding at about 215 °C. These features are entirely consistent with the proposed phase diagram, Fig. 1; specifically, with its global composition closer to that of the eutectoid invariant composition, the x = 0.10 material forms a greater proportion of α′′-CDP at the transition and has a lower solvus temperature than the x = 0.05 material. The final two compositions, x = 0.17 and x = 0.18, are close to the eutectoid, and no region of two-phase behavior can be discerned.

Fig. 8 Conductivities of representative materials in the (1 − x)CsH₂PO₄–xCs₂HPO₄ system collected under pH₂O = 0.4 atm: (a) Arrhenius presentation showing behavior over the temperature range 150–260 °C; and (b) behavior in the superprotonic phase space.

Within the single-phase region, the conductivities of the phosphate-deficient α′′-CDP materials are comparable to that of stoichiometric CDP. However, as highlighted in Fig. 8(b), there is a slight decrease in conductivity with increasing phosphate deficiency. The activation energy for transport across the four α′′-CDP materials falls in the range of 0.37 to 0.39 eV and the pre-exponential term – ln(A) in the expression σ = A/T exp(−E_a/kT) – falls in the range of 10.4 to 10.9/ln(S cm⁻¹ K⁻¹) (ESI Fig. S6†). Overall, these values are similar to the properties of stoichiometric superprotonic CDP, E_a = 0.36(4) eV and ln(A) = 10.4(1)/ln(S cm⁻¹ K⁻¹), as measured here and as reported in the prior literature.^3,21 Given the margin of uncertainty of the experiments, it is not possible to establish whether the slight decline in conductivity in α′′-CDP with composition is due to a change in activation energy or change in pre-exponential factor or both (see ESI Fig. S5† for a comparison of the three CDP samples characterized). The presence of phosphate vacancies in Cs[(H₂PO₄)_1−2y(HPO₄)_y] might plausibly be expected to decrease the conductivity due to the disruption of the proton transport pathway and the overall decrease in proton concentration on a per unit cell basis. On the other hand, the decrease in cell parameter suggests a decrease in jump distance. Such factors evidently largely cancel out, producing a relatively weak composition dependence. At 200 °C, the conductivities of the near-eutectoid compositions are ∼6.5 × 10⁻³ S cm⁻¹, technologically attractive values.

4. Discussion

The observation here that superprotonic cubic CDP can occur in a chemistry in which Cs ions effectively replace protons implies that the surprising behavior previously observed in the RDP-Rb₃PO₄ system²⁵ is not unique to Rb. The result mirrors our previous demonstration in a separate study of the cubic phase of CDP that the inverse can occur, that protons can effectively replace Cs ions.²³ In both types of chemistries, the phosphate : alkali ion ratio differs from 1 : 1, and the ‘off-stoichiometry’ is accommodated by the generation of vacancies, either on the phosphate sites (as observed here and in the analogous Rb system²⁵) or on the alkali ion site (as observed in the CDP-H₃PO₄ system²³). In all cases, the phase behavior is eutectoid in nature, and there is a large increase in conductivity at the eutectoid temperature, which lies well below the superprotonic transition of the stoichiometric material.

At a more granular level, the behavior of the (1 − x)CsH₂PO₄–xCs₂HPO₄ system uncovered here bears similarities and distinctions to the phase behavior of the analogous (1 − x)RbH₂PO₄–xRb₂HPO₄ system²⁵ and to the mirror system (1 − x)CsH₂PO₄–xH₃PO₄.²³ Considering first the direct Rb analog, the first compound along the pseudo binary line from RbH₂PO₄ to Rb₂HPO₄ is Rb₅H₇(PO₄)₄ (x = 0.25), whereas in the Cs case, the compound Cs₅H₇(PO₄)₄ does not form and, ignoring hydrates, the closest compound to CDP is Cs₃(H_1.5PO₄)₂ (x = 0.5). Nevertheless, the eutectoid compositions are rather similar, occurring at x = 0.17 for Cs and at x = 0.19 for Rb. In both systems, the eutectoid temperature is ∼93% that of the transition temperature of the stoichiometric material, hinting at an underlying thermodynamic universality. Moreover, in neither the Cs or Rb systems has the limit of phosphate deficiency been established. In α′′-CDP we show here that at least 17% of the phosphate sites can be unoccupied (x = 0.20). In α′′-RDP at least 20% (x = 0.25)²⁵ can be supported, as observed by the transformation of Rb₅H₇(PO₄)₄ to the cubic phase. In the Cs system, Cs₃(H_1.5PO₄)₂ is presumably too deficient in P to directly transform to α′′-CDP. Significantly, however, in a previous study of Cs₃(H_1.5PO₄)₂ we found that exposure to high temperature induced exsolution of a small quantity of a cubic, CDP-like phase at 190 °C with a lattice parameter of 4.91 Å that decreased with temperature.³³ We noted in that work that the lattice parameter of the exsolved phase was too small and its dependence on temperature too anomalous to correspond to conventional cubic CsH₂PO₄ (which has a cell parameter of 4.96 Å at 230 °C and displays conventional thermal expansion), but we could not offer an explanation for the observation. It can now be concluded that the material obtained was α′′-CDP and that its anomalous thermal expansion is due to increasing nonstoichiometry, as occurs for the hypereutectoid composition shown in Fig. 3(a). Elucidation of the complete phase behavior, inclusive of the high temperature transformations of Cs₃(H_1.5PO₄)₂, awaits a future study.

Turning to a comparison to the phosphate-rich (1 − x)CsH₂PO₄–xH₃PO₄ system, the discussion is facilitated via reference to the comprehensive phase diagram, Fig. 9, that includes both cesium deficient²³ and phosphate deficient (this work) regions relative to stoichiometric CDP. The eutectoid temperature in the cesium deficient side of the diagram is 155 °C, just 85% of the transition temperature of stoichiometric CDP. However, whereas dehydration behavior in the phosphate deficient compositions (α′′-CDP, this work) is largely independent of Cs : P ratio, in the cesium deficient materials (α′-CDP, previous study), the dehydration temperature rapidly decreases with increasing nonstoichiometry, effectively overshadowing the technological benefits of access to superprotonic behavior at reduced temperatures. An intriguing feature of the cesium deficient system is the occurrence of the unusual compound Cs₇(H₄PO₄)(H₂PO₄)₈ (CPP), a 4 × 4 × 4 superstructure of cubic CDP in which one in eight of the Cs⁺ cations is replaced by the polyphosphate group H₄PO₄⁺.²⁴ CPP forms upon reaction of CsH₅(PO₄)₂ and CsH₂PO₄ at 90 °C and is stable only up to 180 °C, beyond which it transforms to α′-CDP. As in the phosphate deficient systems, the limit of site non-stoichiometry in α′-CDP has not been established, though it is known to be at least x = 0.22 (22% of the Cs sites are unoccupied), corresponding to the stoichiometry of CPP.

Fig. 9 Comprehensive phase diagram between CsH₅(PO₄)₂ and Cs₃(H_1.5PO₄)₂ spanning Cs deficient²³ and phosphate deficient (this work) regions relative to stoichiometric CsH₂PO₄. CPP is the compound Cs₇(H₄PO₄)(H₂PO₄)₈.²⁴ The temperature at which Cs₃(H_1.5PO₄)₂ forms from Cs₃(H_1.5PO₄)₂·2H₂O, which depends on steam partial pressure, is not well-characterized and has not been indicated. The positions of the solvus lines have uncertainty on the order of ±0.1 in composition (x, y) or equivalently ±10 °C in temperature. The invariant transition temperatures, on the other hand, are known to within ±1.5 °C. At high temperature, the CsCl structure-type of cubic CsH₂PO₄ can support at least 22% vacancies on the Cs site (α′-CDP) and at least 20% vacancies on the phosphate site (α′′-CDP). Charge balance is achieved via modulation of the average number of protons per phosphate group.

In all three systems discussed here, cell parameter emerges as a key indicator of material stoichiometry. In the phosphate-deficient α′′-CDP compositions, cell parameter decreases linearly with phosphate deficiency. In the analogous Rb system, reduction was also observed, but due to the limited access to the single phase α′′-RDP region, the precise dependence of cell volume on phosphate deficiency could not be determined.²⁵ For α′′-CDP, the trend is clearly captured at several temperatures. In the mirror chemical space of phosphate excess, the lattice parameter in α′-CDP increases with increasing off-stoichiometry.²³ The effect appears to reflect a weakening of the overall ionic bonding, reminiscent of the chemical expansion that occurs when variable valence oxides undergo reduction.^42,43 Somewhat surprisingly, the chemical expansion/contraction values of α′-CDP and α′′-CDP are each on the order of 0.4 Å/x in magnitude, indicating that Cs vacancies and phosphate vacancies have essentially mirrored impacts on the structure.

In terms of technological implementation, α′′-CDP offers a clear advantage over α′-CDP of our prior study due to its higher thermal stability, comparable to that of stoichiometric CDP. The conductivities of the near-eutectoid compositions in both systems correspond to those that would be approximately obtained by Arrhenius extrapolation of the conductivity of stoichiometric cubic CDP to lower temperatures. Whether the α′′-CDP compositions offer advantages over stoichiometric CDP via operability at reduced temperatures remains to be seen. While reduced temperatures can have negative impacts on catalytic reaction rates, catalyst impurity tolerance, and proton conductivity, they typically decrease degradation rates and increase system lifetime. Additionally, with the thermodynamic driving force for decomposition unchanged, humidification requirements to prevent material decomposition are relaxed at lower temperatures, which can decrease the energy penalty of heating steam, both because less steam is required and because it must be heated to a lower temperature.

5. Summary and conclusions

A systematic study of the (1 − x)CsH₂PO₄–xCs₂HPO₄ system in the range x = 0 to 0.20 has been carried out. The system displays eutectoid behavior, with an invariant point defined by a temperature of 192.0 ± 1.4 °C and a composition of x = 0.17 ± 0.01. In its cubic phase, CsH₂PO₄ can support a large cesium excess via the presence of phosphate vacancies that are charge balanced by a decrease in the proton concentration. In essence, Cs ions replace protons in the material stoichiometry, and the chemical formula is most appropriately described as Cs[(H₂PO₄)_1−2y(HPO₄)_y], with y = 1 − 1/(1 + x). Evidence of phosphate vacancies rather than cesium interstitials is found in the behavior of the cubic lattice parameter, which decreases with increasing off-stoichiometry. The thermal stability against dehydration is insensitive to phosphate deficiency, whereas the conductivity of the α′′-CDP approaches that of stoichiometric, superprotonic CDP. Thus, the materials, particularly those with near-eutectoid compositions, provide meaningful access to a wider temperature range for application than stoichiometric CDP.

This work demonstrates that the surprising phase behavior recently recognized in the (1 − x)RbH₂PO₄–xRb₂HPO₄ system, in which phosphate vacancies in a cubic superprotonic phase were first recognized,²⁵ is not unique to Rb. In combination with our separate previous study of the (1 − x)CsH₂PO₄–xH₃PO₄ system,²³ the present work further shows that superprotonic CDP can exist over a wide stoichiometry range, including both cesium rich and cesium deficient compositions. Thus, off-stoichiometric compositions can be considered a new framework for designing advanced superprotonic materials. Recognition of off-stoichiometric behavior in α-CDP and α-RDP systems moreover rationalizes previous results in the literature described as heterogeneous doping, in which excess phosphoric acid has been used to influence the properties of a base solid acid, e.g., CsH₂PO₄.⁴⁴ It also reconciles the otherwise surprising occurrence of superprotonic phase transitions in compounds such as Rb₅H₇(PO₄)₄,^25,45 for which high symmetry cannot be readily envisioned with fully occupied cation and anion sites. Even more broadly, the combined observations in the CDP and RDP systems indicate that the chemical phase space available for the development of new superprotonic materials can be widened by shifting focus from line (stoichiometric) compounds that form at ambient conditions towards solid solution phases that occur at high temperatures.

Data availability

The data supporting the conclusions of this article have been included either in the main text or as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support has been provided by the National Science Foundation (OAC-2118201, DMR-1807234, and DGE-1842165). This work made use of the J. B. Cohen X-Ray Diffraction facility at Northwestern University, supported by the NSF MRSEC program (NSF DMR-2308691).

References

1. P. Zguns, K. Klyukin, L. S. Wang, G. Xiong, J. Li, S. M. Haile and B. Yildiz, Energy Environ. Sci., 2024, 17, 5730–5742.
2. A. I. Baranov, Crystallogr. Rep., 2003, 48, 1012–1037.
3. S. M. Haile, C. R. I. Chisholm, K. Sasaki, D. A. Boysen and T. Uda, Faraday Discuss., 2007, 134, 17–39.
4. Q. Li, R. He, J. O. Jensen and N. J. Bjerrum, Chem. Mater., 2003, 15, 4896–4915.
5. T. Hibino, J. Ceram. Soc. Jpn., 2011, 119, 677–686.
6. Y. Matsuda, J. Nakajima, Y. Inoue, A. Ishikawa, N. Ueta, D. Mori, S. Taminato, N. Imanishi, T. Fukushima and S. Higashimoto, Inorg. Chem., 2024, 63, 8018–8025.
7. D. A. Boysen, T. Uda, C. R. I. Chisholm and S. M. Haile, Science, 2004, 303, 68–70.
8. T. Uda and S. M. Haile, Electrochem. Solid-State Lett., 2005, 8, A245–A246.
9. L. S. Wang and S. M. Haile, Adv. Mater. Interfaces, 2024, 11.
10. T. Uda, D. A. Boysen, C. R. I. Chisholm and S. M. Haile, Electrochem. Solid-State Lett., 2006, 9, A261–A264.
11. N. Fujiwara, H. Nagase, S. Tada and R. Kikuchi, ChemSusChem, 2021, 14, 417–427.
12. E. Christensen, I. M. Petrushina, A. V. Nikiforov, R. W. Berg and N. J. Bjerrum, J. Electrochem. Soc., 2020, 167, 5.
13. E. Christensen, R. W. Berg, R. Krüger and N. J. Bjerrum, J. Electrochem. Soc., 2023, 170, 5.
14. S. Nagaishi, R. Hayashi, A. Hirata, R. Sagara and J. Kubota, Sustain. Energy Fuels, 2024, 8, 14.
15. D. K. Lim, A. B. Plymill, H. Paik, X. Qian, S. Zecevic, C. R. I. Chisholm and S. M. Haile, Joule, 2020, 4, 2338–2347.
16. A. Ikeda and S. M. Haile, Solid State Ionics, 2012, 213, 63–71.
17. Y.-K. Taninouchi, T. Uda, Y. Awakura, A. Ikeda and S. M. Haile, J. Mater. Chem., 2007, 17, 3182–3189.
18. R. B. Merle, C. R. I. Chisholm, D. A. Boysen and S. M. Haile, Energy Fuels, 2003, 17, 210–215.
19. T. Uda, D. A. Boysen and S. M. Haile, Solid State Ionics, 2005, 176, 127–133.
20. C. R. I. Chisholm, R. B. Merle, D. A. Boysen and S. M. Haile, Chem. Mater., 2002, 14, 3889–3893.
21. A. Ikeda, D. A. Kitchaev and S. M. Haile, J. Mater. Chem. A, 2014, 2, 204–214.
22. M. Gupta, K. K. Zhang and K. V. Huang, Energy Adv., 2025, 4, 424–434.
23. L. S. Wang, S. V. Patel, E. Truong, Y.-Y. Hu and S. M. Haile, Chem. Mater., 2022, 34, 1809–1820.
24. L. S. Wang, S. V. Patel, S. S. Sanghvi, Y. Y. Hu and S. M. Haile, J. Am. Chem. Soc., 2020, 142, 19992–20001.
25. G. Xiong, L. S. Wang and S. M. Haile, Mater. Horiz., 2023, 10, 5555–5563.
26. D. A. Boysen, S. M. Haile, H. J. Liu and R. A. Secco, Chem. Mater., 2004, 16, 693–697.
27. A. A. Gaydamaka, V. G. Ponomareva and I. N. Bagryantseva, Solid State Ionics, 2019, 329, 124–130.
28. Z. K. Li and T. B. Tang, Mater. Res. Bull., 2010, 45, 1909–1915.
29. V. Ponomareva, I. Bagryantseva, B. Zakharov, N. Bulina, G. Lavrova and E. Boldyreva, Acta Crystallogr., Sect. C, 2017, 73, 773–779.
30. G. Lavrova, N. Bulina, V. Minkov and A. Matvienko, Russ. J. Inorg. Chem., 2016, 61, 284–290.
31. V. G. Ponomareva and I. N. Bagryantseva, Solid State Ionics, 2019, 329, 90–94.
32. D. A. Boysen, S. M. Haile, H. Liu and R. A. Secco, Chem. Mater., 2003, 15, 727–736.
33. S. Sanghvi and S. M. Haile, Solid State Ionics, 2020, 349, 115291.
34. C. E. Botez, J. D. Hermosillo, J. Zhang, J. Qian, Y. Zhao, J. Majzlan, R. R. Chianelli and C. Pantea, J. Chem. Phys., 2007, 127, 194701.
35. M. Weil and B. Stöger, Monatsh. Chem., 2020, 151, 1317–1328.
36. A. I. Baranov, V. P. Khiznichenko, V. A. Sandler and L. A. Shuvalov, Ferroelectrics, 1988, 81, 1147–1150.
37. J. Otomo, N. Minagawa, C.-j. Wen, K. Eguchi and H. Takahashi, Solid State Ionics, 2003, 156, 357–369.
38. D. Aili, Y. Gao, J. Han and Q. Li, Solid State Ionics, 2017, 306, 13–19.
39. A. Pawlowski, C. Pawlaczyk and B. Hilczer, Solid State Ionics, 1990, 44, 17–19.
40. W. Bronowska and A. Pietraszko, Solid State Commun., 1990, 76, 293–298.
41. L. Rycerz, J. Therm. Anal. Calorim., 2013, 113, 231–238.
42. D. S. Tsvetkov, V. V. Sereda, D. A. Malyshkin, I. L. Ivanov and A. Y. Zuev, J. Mater. Chem. A, 2022, 10, 6351–6375.
43. D. Marrocchelli, N. H. Perry and S. R. Bishop, Phys. Chem. Chem. Phys., 2015, 17, 10028–10039.
44. V. G. Ponomareva and G. V. Lavrova, Solid State Ionics, 2017, 304, 90–95.
45. A. A. Gaydamaka, V. G. Ponomareva and I. N. Bagryantseva, Ionics, 2019, 25, 551–557.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08426h

---