Highly efficient thermoelectric converters based on metalloporphyrin nanotubes

Abstract

Novel devices based on porphyrin nanotubes may lead to a wide range of uses in electronic functionality and thermoelectric conversion. π-Conjugated metallo-porphyrin nanotubes have been designed with a configuration of oppositely charged porphyrin molecules, which leads to oscillatory bandgaps as a function of the diameter of the nanotube. We focus in this work on bottom-up porphyrin nanotubes, rather different from conventional carbon nanotubes, making them favorable candidates as precursors for nanotube devices. We exploited the asymmetric band gap feature to design configurations of stacked six-metalloporphyrin rings connected by butadiyne to form a periodic nanotube structure with different metallic atoms (Zn, Fe, and Fe–Cl). The electronic transport properties given by the transmission coefficients show that porphyrin nanotubes with Zn produce step-like features located asymmetrically relative to the Fermi energy (E_F), which lead to huge enhancements of the thermoelectric performance. The highest values obtained for the thermopower and the electronic figure of merit can also be obtained for many different positions of E_F, which makes Zn-porphyrin nanotubes an optimal candidate for designing novel thermoelectric devices.

---

1. Introduction

The organization of metallo-porphyrin molecules in one-dimensional nanostructures, like for instance nanotubes, is of great interest for several properties that can incorporate discrete π-conjugated electronic systems,^1–7 tunable bandgaps⁸ and quantum confinement effect in self-assembled binary porphyrin structures.⁹ Such structures can have different forms, like for example stacked and cyclic nanorings of six butadiyne (C4)-linked porphyrin units (labeled c-P6).¹⁰ Notice that the use of other linkers (C0 and C2), both along the circumference of the nanotube or along the nanotube axis, is also possible; however, in the first case (circumference), the use of smaller linkers would cause additional tension that would make it necessary to use more porphyrin units along that direction; in the second case (axis), the use of other conjugate linkers would modify the electronic structure (although probably not too much, since the electrons would still find it easy to delocalize along the conjugate states), but a more detailed investigation is beyond the scope of this article. More recently, a π-conjugated porphyrin nanotube was synthesized, and it was observed that additionally stacking two (c-P6) nanorings forms a tube (labeled t-P12), which clearly transforms the optical properties due to an increase in the conjugation, followed by metalation with zinc.¹¹ The increase in conjugation affects the optical properties because when the porphyrin nanoring structures are coupled strongly, leading to conjugate states all over the circumference, light of different frequencies can be absorbed by delocalized excited states over the entire circumference, similar to a regular π-system, instead of more localized states located on each porphyrin unit. Recent DFT calculations have also shown details of the electronic properties of porphyrin nanotubes and, in particular, abnormal and highly oscillatory bandgaps of these structures upon increasing their size were observed.¹¹ Moving one step beyond, the use of porphyrin tubes in nanodevices currently faces great challenges, not only in their design and fabrication, but also in controlling their structural and functional properties. Notice as well that the use of porphyrins in structures like nanotubes makes them easier to handle and connect to terminals, compared to other structures such as single molecules and combinations of them. Also, the use of nanotube structures increases their tunability by introducing factors such as the chirality and the diameter of the nanotube and by making it easier to use other methods such as chemical doping,¹² which adds more freedom to the design of specific thermoelectric materials based on porphyrins. Regarding thermoelectric properties, the consideration of p-type materials, like carbon nanotube-based thermoelectric devices, has remarkably increased in recent years.^13–18 The specific use of porphyrins in novel structures changes their electronic properties and can lead, as we will see, to sharp features in the electronic structure around the Fermi level; such features are different from those observed in other porphyrin systems (such as e.g. resonances in single molecule systems), leading to rather different thermoelectric performances (higher performance, in many cases). This is then the first study of the thermoelectric performance of such structures.

The route to convert waste heat into electric power is through thermoelectric materials specifically designed for that.^19–22 Waste heat can be harnessed in different ways and through different devices, including thermal sensors,^23–25 aerospace applications^26,27 and energy conversion devices.^28–31 In particular, through the Seebeck effect, it is possible to generate electricity from sources of waste heat, which is represented by the thermopower coefficient S = −ΔV/ΔT, where ΔV is the voltage difference generated across a device from a temperature difference ΔT. The efficiency of a thermoelectric converter is defined in terms of the dimensionless figure of merit ZT = S²GT/k, where G is the electrical conductance (which represents the conduction of an electric current across a device) and k is the thermal conductance (which represents the conduction of heat across a device). The aim is to design devices with ZT as high as possible, but finding strategies for minimizing the denominator (k) and maximizing the numerator (S and G) of ZT is currently a big challenge. New alternatives have then to be explored, such as the use of organic materials, whose thermoelectricity has been extensively studied in the last few years. For instance, the room-temperature thermopower S of semiconducting single-walled carbon nanotubes (SWCNTs) (160–170 μV K⁻¹),³² the thermopower (∼70 μV K⁻¹) and the figure of merit (∼0.11 at 305 K) of p-type metallic SWCNT films³³ and the thermopower of metalloporphyrin/SWCNT complex composite films (47 μV K⁻¹) were measured.³³

In this paper, we examine the potential of metalloporphyrin nanotubes for thermoelectric performance. The proposed structures, shown in Fig. 1, are made of a one-dimensional supercell of hollow metalloporphyrin nanotubes with three types of transition metal centers (Zn, Fe, and Fe–Cl); in this last case, a Cl atom is bonded to the Fe atom in the center of each molecule; notice that we use Cl because this is a halogen atom that leads to precise oxidation/reduction changes between Fe(II) and Fe(III), i.e. to the absorption of one electron, see ref. 34. In such structures, the hollow metalloporphyrin nanotube, which has a length L = 6.7 nm and a diameter D = 2.7 nm, is made of butadiyne-linked porphyrin nanorings. Different views of the calculated geometries are also shown in Fig. S1 of the ESI.† The coupled states of these nanorings make the electrons highly delocalized between them.³⁵ Such a particular electronic structure leads to a wide range of optoelectronic properties⁹ and can also be exploited to make electronic and thermoelectric devices. In particular, to exploit the potential of these periodic structures as thermoelectric converters, it is necessary to find asymmetric step-function and narrow delta-function like features in the electronic structure that can lead to high thermoelectric performance,^36–39 as we shall see. In order to understand and clarify the role of such features in the thermoelectric performance, we present a discussion in the ESI.†

Fig. 1 The relaxed supercell of a 30-hollow metalloporphyrin nanotube made of 1260 atoms. Three possible structures corresponding to three metallic atoms (Zn, Fe, and Fe–Cl), which vary for each structure.

2. Computational method

We used density functional theory (DFT) as implemented in the SIESTA code.⁴⁰ We employed the generalized gradient approximation (GGA-PBE) as the exchange and correlation functional,⁴¹ double-zeta polarized basis sets to span the valence states and norm-conserving pseudoatomic orbitals to get rid of the core electrons. Notice that a better description of the d states of Fe would still be possible by using DFT + U, since the strong on-site Coulomb repulsion would substantially affect the electronic interactions in the localized d-orbitals. All results were also calculated with such correction, with a U of 4.5 eV. A similar effect would also be induced by more sophisticated functionals, like HSE06, which would open the band gap, but we found that in these cases the results were quantitatively and qualitatively very similar, so we decided not to include it. Notice as well that the use of functionals with dispersion corrections would not be necessary in this case, since no van der Waals interactions are considered in single nanotubes. We defined a real-space grid with a plane-wave cut-off of 200 Ry and relaxed all geometries until all atomic forces were smaller than 0.02 eV Å⁻¹. We also used the GOLLUM quantum transport code⁴² to calculate the transmission T(E) and the corresponding thermoelectric coefficients from the electronic structure provided by SIESTA.

3. Results and discussion

3.1. DFT calculations

Five nanoring units with six metallo-porphyrins were stacked to form the nanotube. We also considered different metallic atoms (Zn, Fe, and Fe–Cl) as central atoms in the metallo-porphyrins. For all these cases, the structures are completely relaxed, leading to the nanotubes shown in Fig. 1 (different views of the calculated geometries are shown in Fig. S1 of the ESI†). The relaxations are carried out without problem and the nanotubes always relax to the same structure, which shows that they are stable (also confirmed by experiments).⁶ Notice that in some cases (PFe and PFe–Cl), there is some deviation from planarity. This deviation is real, as already found for other molecules⁴³ and not an artifact of the simulations.

Fig. S2–S4 of the ESI† show the frontier molecular orbitals (FMOs) of the PZn, PFe, and PFe–Cl nanorings, respectively. Red corresponds to the positive and blue to the negative regions of the wave function. The plots show that the HOMO of the PZn ring is distributed through the pathways of the π-system, while for the LUMO is delocalized across their pyrrole subunits.

The butadiyne linkers (C4) between the 6-porphyrin nanoring have frontier orbitals in antiphase, which is similar to that of the 12-porphyrin nanotube.^6,44 However, the FMOs are distributed through the pyrrole subunits of porphyrins with scarcity around the metal center Fe(II) and significant reduction across the C4-linkers of the PFe(II) nanoring.

For the PFe(III) complexed with Cl⁻, the HOMO is often distributed cross the π-system and the C4-linkers, whereas the LUMO is partially distributed and the FMOs resemble that of the C4-linkers in the PFe(II) nanoring. Notice that the donation of electrons from the HOMO PFe populates the counter ion Cl, while for the LUMO of PFe–Cl, there are two bare chloride atoms.

For each unit cell of the metallo-porphyrin nanoring structure in Fig. 2 (right-hand panels), the electronic band structure (left-hand panels) and the density of states (DOS) (central panels) were calculated. The calculations show that the PZn nanoring structure has an electronic structure with an energy gap of ∼1 eV at the Fermi energy. The bandgap appears for this particular size (6 porphyrin units around the tube).¹¹ For the metal center with Fe, however, panel (b) shows that the energy gap moves below the Fermi energy E_F, which makes this nanotube metallic. Finally, for the PFe(III)-complex, which has the presence of Cl⁻ counter anions that capture electrons, the energy gap shifts above the E_F, which makes it metallic as well, as shown in panel (c). Notice as well that the gap is always direct, since the top of the valence band coincides with the bottom of the conduction band.

Fig. 2 (a)–(c) right: the DFT calculated optimized geometry of the unit cell for 6-metallo-porphyrin nanoring structures with different metallic atoms (Zn, Fe, and Fe–Cl), (a)–(c) middle: the density of states (DOS) and (a)–(c) left: the band structure for all structures, respectively. The dashed lines indicate the Fermi level.

For each metalloporphyrin nanotube (PZn, PFe and PFe–Cl) in Fig. 2, the transmission T(E) was calculated, as can be seen in Fig. 3. Since these structures are periodic, T(E) in all these cases is equal to the number of open channels and is given by a series of step functions. Fig. 3(a) shows that for the porphyrin nanotube with Zn atoms an asymmetric step-function in the transmission T(E) appears around Fermi energy, while for the nanotube with Fe atoms a series of steps related to bands of the metal atom and the molecule appear. Finally, for the PFe nanotube in the presence of a Cl⁻ counter anion, a broad and asymmetric structure forms around the Fermi level. Notice that, in particular, steps near the Fermi level likely lead to high thermoelectric performance. It is then convenient to study how the thermoelectric coefficients change with the position of Fermi energy E_F relative to the original one E^DFT_F. This can be achieved experimentally, by using electrostatic or electrochemical environments or by doping, i.e. by varying for instance the transition metal in the center of the porphyrin.

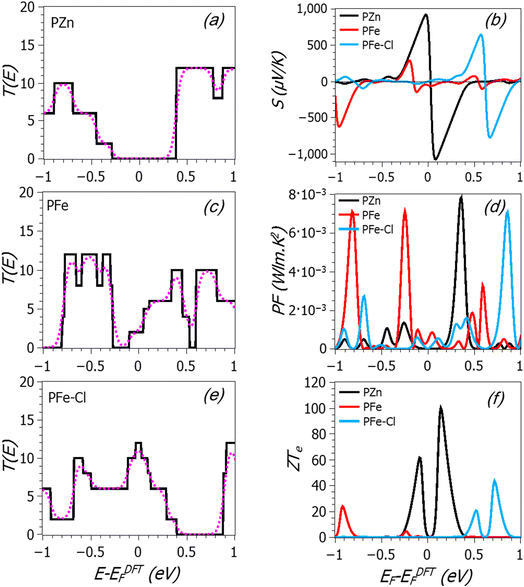Fig. 3 For the metallo-porphyrin nanotube structures of Fig. 1, the black solid line in each panel shows the calculated transmission coefficient T(E) versus energy for (a) PZn, (c) PFe and (e) PFe–Cl. The pink dotted curves show the room-temperature electrical conductance. (b), (d) and (f) The thermopower S, power factor PF = σS² and electronic figure of merit ZT_e over a range of Fermi energies.

Once the transmission coefficient T(E) is obtained, then the room-temperature electrical conductances (pink dotted curves in the left-hand panels of Fig. 3) and the thermoelectric coefficients (panel (b) in Fig. 3) can be calculated using eqn (S3) to (S6) in the ESI.† The variation of the conductance, both electrical and thermal, is easy to understand by looking at the transmission, since this quantity roughly follows it. The thermopower follows the derivative, so it reaches high values when there are sharp variations in the transmission. In particular, if the Fermi level is on the right (left) of a sharp feature, the thermopower is positive (negative). Notice as well that the transmission for all these systems has in general peaks close to the Fermi level, as opposed to typical carbon nanotubes, which have a gap or a flat transmission around it (leading to poorer thermoelectric performance). Fig. 3 also shows the power factor (PF = σ²S) in panel (d), and the electronic figure of merit ZT_e in panel (f) over a range of Fermi energies. The calculations show that for the PZn nanotube, the asymmetric-located feature in T(E) around the Fermi level leads to the highest positive and negative thermopower magnitudes: S = +760 μV K⁻¹ at E_F − E^DFT_F = 0 eV and S = 1065 μV K⁻¹ at E_F − E^DFT_F = 0.07 eV. The explanation for such high values is that the Fermi energy after p-doping (metal into porphyrin) at the PZn lies close to the HOMO, so that the metal causes the Fermi energy to lie closer to the HOMO, in a region of a steep slope for the transmission function. This behaviour is shown in Fig. 3(a), where the Zn atom causes the energy levels of the porphyrin nanotube to increase in energy and therefore the HOMO resonance moves closer to the Fermi energy, leading to an increase in the slope and hence to a more negative Seebeck coefficient. Meanwhile, in the case of PFe, the step-function remarkably decreases (around −0.2 eV) accompanied by a broad delta-function (∼0.6 eV) moving away from DFT-Fermi energy, leading to a decrease in the slope and this produces low thermopower at E_F = E^DFT_F. For porphyrin nanotubes with Fe–Cl, the step-function shifts away from Fermi energy to higher energies and a broad delta function emerges over a range of Fermi energies resulting in a decrease in the slope and this also produces a low thermopower. For porphyrin nanotubes with Fe and Fe–Cl, S shows values of −52 and +1.7 μV K⁻¹ at E_F = E^DFT_F, respectively. As before, both the magnitude and the sign of thermopower depend on the location of Fermi energy and rather high values can appear for certain E_F. For instance, for the nanotube with Fe atoms, the thermopower is −285 μV K⁻¹ at E_F − E^DFT_F = −0.2 eV, while for the nanotube with Fe–Cl, it can reach +628 μV K⁻¹ at E_F − E^DFT_F = 0.58 eV and −770 μV K⁻¹ at E_F − E^DFT_F = 0.67 eV. These values are much higher than those typically found in molecular electronic systems or similar systems such as nanowires of molecules,^45,46 or other systems made of periodic arrays of nanoscale elements.⁴⁷ Such high values of thermopower would allow the fabrication of much more efficient heat-to-electricity converters, coolers and other systems with applications in several industries, ranging from domestic systems to the automobile or aerospace industries.

Regarding the figure of merit, the porphyrin nanotube in the presence of Zn has the highest value of ZT_e (around 100), which reflects its thermopower and conductance. Such high values make the PZn nanotube a favourable material for thermoelectric devices. Notice as well that for bulk systems, the figure of merit ZT = S²σT/k involves two crucial quantities, which are the power factor (PF = S²σ) and the total thermal conductivity (k), where k includes both electron and phonon contributions (this differs from ZT_e = S²σT/k_e, where k_e has only contributions from electrons). The quantity PF = S²σ, known as the power factor, can also be calculated to have an idea of its contribution to ZT. The conductivity is σ = GL/A, where L is the length of the molecular device and A is the cross-sectional area. In this work, we use L = 6.7 nm and A = 7.4 nm². These values come from the length and cross-section used in the simulations. Above that length, the nanotube is assumed to be connected seamlessly to metallic electrodes. The results show that the highest power factor is obtained at E_F − E^DFT_F = 0.35 eV (PF = 8 × 10⁻³ W m⁻¹ K⁻²) in the case of the PZn nanotube. For PFe, the power factor is 7 × 10⁻³ W m⁻¹ K⁻² at E_F − E^DFT_F = −0.25 eV. A similar value is found at E_F − E^DFT_F = 0.86 eV for the PFe nanotube in the presence of a Cl⁻ counter anion. These values are higher than the measured value of the single-walled carbon nanotube/ZnTPP, which was found to be 247 × 10⁻⁶ W m⁻¹ K⁻².³³

Finally, the temperature dependence of the thermoelectric coefficients was also calculated. The electrical conductance G, thermopower S and power factor PF = σS² are shown over a range of temperatures T and evaluated at the DFT-Fermi energy, as shown in Fig. 4(a)–(c). As can be seen, the electrical conductance strongly decreases as the temperature increases, which is a consequence of the temperature window covering larger portions with small conductance as it increases (i.e. as the derivative of the Fermi distribution becomes wider). The thermopower has a similar trend for PZn, although the decrease is smaller and sustained, while it is roughly constant or decreases (it becomes more negative) a little for the other two cases; the decrease or increase of this quantity depends on the introduction of more sharp features into the temperature window. Finally, the power factor decreases for all cases except for the PFe system, where it increases due mainly to the increase of the absolute value of the thermopower in this case. Also, the electronic contributions to the thermal conductance (k_e) and figure of merit ZT_e as a function of temperature T are shown in Fig. 5(a) and (b). The electronic thermal conductance of PFe–Cl and PFe nanotubes increases with temperature due to the covering of the temperature window of more features as it increases, while the highest temperature-dependent figure of merit, which is a combination of all previous quantities, occurs for the PZn nanotube, with the highest values given at high temperatures (>300 K).

Fig. 4 Electrical conductance G (a), thermopower S (b) and power factor PF = σS² (c) as a function of temperature T, evaluated at E_F − E^DFT_F = 0 eV.

Fig. 5 Electronic contribution to the thermal conductance (k_e) (a) and the figure of merit ZT_e (b) over a range of temperatures T.

3.2. DFT + U calculations

To describe accurately the electronic properties in porphyrin nanoring, DFT-density of states (DOS) calculations for the PFe and PFe–Cl rings were carried out using GGA-PBE, GGA + U and the hybrid functional GGA-HSE06. The results of the HSE06 calculation are similar to those of GGA for PFe around the DFT-Fermi energy, while largest differences are observed with GGA + U (as shown in Fig. S5 and S6 in the ESI†). Comparing GGA and HSE06, we found that HSE06 changed the size of the energy gaps of the PFe and PFe–Cl rings. For the PFe ring, the PBE band gap is located below the DFT-Fermi energy, as shown in Fig. 2(b), and has a value of 0.8 eV, whereas the HSE06 energy gap reduces it to approximately 0.2 eV, as shown in Fig. S5(c).† In case of the PFe–Cl ring, the PBE band gap lies roughly 0.75 eV above the Fermi energy (Fig. 2(c)), while with HSE06 it disappears and a new energy gap below the Fermi energy appears with a value of ∼0.1 eV, as shown in Fig. S6(c).†

Using DFT + U combined with Green's function formalism, the transmission T(E) was calculated for periodic PFe and PFe–Cl nanotube structures. The calculation shows that the step-functions like T(E)s shifted about 0.2 eV close to DFT-Fermi energy for the PFe nanotube, as shown in Fig. 6(a), while for the PFe–Cl, Fig. 6(b) shows a higher broad asymmetric delta-function (about 1.6 eV) than those in PFe (about 0.6 eV) around the Fermi energy.

Fig. 6 The black solid line shows the DFT + U calculation of the transmission coefficient T(E) versus energy for the metallo-porphyrin nanotube structures (a) PFe and (b) PFe–Cl. The pink dotted curve shows the room-temperature electrical conductance.

This particular feature (steps near E_F) is favorable for enhancing the thermoelectric properties and again using transmission T(E) based GGA + U functional, the thermoelectric coefficients were calculated, as shown in Fig. 7(a)–(d). The higher room-temperature thermopower S and power factor PF were observed for the PFe nanotube at E_F − E^DFT_F = −3.4 eV (near the step-function), with values of +262 μV K⁻¹ and 6.3 × 10⁻³ W m⁻¹ K⁻², respectively. These higher values are accompanied by lower electronic thermal conductance k_e = 3.5 × 10⁻¹⁰ W K⁻¹, resulting in a higher electronic figure of merit ZT_e = 6.2. Meanwhile for the PFe in the presence of the counter ion Cl⁻, a higher thermoelectric coefficient appears within the range of Fermi energies E_F − E^DFT_F from 0.8 to 0.94 eV, which lies near the step-function of transmission. This leads to a change in the sign and the magnitude of thermopower S = −487 μV K⁻¹, increases the value of the power factor 7.5 × 10⁻³ W m⁻¹ K⁻² and enhances the electronic figure of merit to ZT_e = 18. This ability to enhance the thermoelectric coefficients of metalloporphyrin nanotubes depends on the consideration of the full efficiency figure of merit ZT by taking into account the total thermal conductance (κ = κ_e + κ_ph), where κ_ph is the phonon thermal conductance and ZT = σS²T/k. Therefore, to determine the full efficiency ZT, the κ_ph value needs to be considered. A comparison between GGA and GGA + U calculations is found in Fig. (S13–S20) of the ESI.†

Fig. 7 The room-temperature thermoelectric coefficients calculation using DFT + U for the PFe and PFe–Cl nanotubes: (a) thermopower S, (b) power-factor PF = σS², (c) electronic thermal conductance k_e and (d) electronic figure of merit ZT_eversus Fermi energy.

4. Conclusions

We have demonstrated the possibility to design metalloporphyrin nanotube thermoelectric devices with particular electronic properties such as specific band gap values and band structures by varying the central metallic atom of the porphyrin unit and the type of self-assembly formation (nanotubes, in this case). These variations can highly affect the transmission and therefore tune the thermoelectric properties. Our aim was to examine three cases of metalloporphyrin nanotubes (PZn, PFe, and PFe–Cl), with induced asymmetric step-functions around the Fermi level in the transmission coefficients. Finding such features can significantly improve the thermoelectric performance.

GGA calculations show that asymmetrically located features in the transmission lead to rather high positive or negative values of the thermopower for many values of E_F − E^DFT_F. The PZn nanotube exhibited the best thermoelectric performance with a rather high room-temperature thermopower of S = +760 μV K⁻¹ at the DFT-Fermi energy. The thermopower can also switch sign to negative, with the highest negative magnitude of S = −1065 μV K⁻¹ at E_F − E^DFT_F = 0.07 eV. Notice that the sign of the thermopower depends on the type of feature that is at the Fermi level; if such a feature has a “positive slope” (i.e. the feature is below the Fermi level), the thermopower is negative, while it is positive in the opposite case. Since the Fermi level scan can cover both types of features, the thermopower switch sign in various cases. The resulting PFe and PFe–Cl thermopowers range from +628 μV K⁻¹ at E_F − E^DFT_F = 0.58 eV to −770 μV K⁻¹ at E_F − E^DFT_F = 0.67 eV. On the other hand, the highest power factor, 8 × 10⁻³ W m⁻¹ K⁻², was found for the PZn nanotube at E_F − E^DFT_F = 0.35 eV, which is much higher than the measured value of single-walled carbon nanotube/ZnTPP composites (247 × 10⁻⁶ W m⁻¹ K⁻²), improving therefore the thermoelectric properties of such systems and the degree of miniaturization over mixtures of different nanoscale elements.³³ Finally, the porphyrin nanotube with Zn has the highest value of ZT_e, much higher than other nanoscale systems. All these rather high thermoelectric coefficients make these nanotubes favourable materials for thermoelectric conversion, with promising performance for thermoelectric applications.

For GGA + U calculations, particular features near the Fermi level enhance the thermoelectric properties, giving rise to higher room-temperature thermopower S and power factor PF for PFe nanotubes at E_F − E^DFT_F = −3.4 eV (near the step-function), with values +262 μV K⁻¹ and 6.3 × 10⁻³ W m⁻¹ K⁻², respectively. Something similar is found for the thermal conductance, k_e = 3.5 × 10⁻¹⁰ W K⁻¹, and the electronic figure of merit ZT_e = 6.2. Meanwhile for PFe–Cl, higher thermoelectric coefficients occur within the range of Fermi energies E_F − E^DFT_F from 0.8 to 0.94 e, near the step-function of transmission. This leads to a change in the sign and magnitude of thermopower S = −487 μV K⁻¹ and increases the value of the power factor 7.5 × 10⁻³ W m⁻¹ K⁻², while also increasing the figure of merit to ZT_e = 18. This shows that the inclusion of U is necessary in this case, as it leads to different results (higher thermoelectric performances).

Data availability statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author contributions

Qusiy H. Al-Galiby, Laith A. Algharagholy, Hatef Sadeghi and V. M. García-Suárez were involved in interpreting the results, writing and commenting the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

Qusiy H. Al-Galiby and Laith A. Algharagholy acknowledge the Iraqi Ministry of Higher Education and Scientific Research, University of Al-Qadisiyah and University of Sumer for the support. Hatef Sadeghi acknowledges the UKRI for Future Leaders Fellowship numbers MR/S015329/2 and MR/X015181/1. V. M. García-Suárez thanks the European Union and the Spanish Ministry of Science, Innovation and Universities for funding through the project MCINN-24-PCI2024-153437.

References

1. Z. Wang, C. J. Medforth and J. A. Shelnutt, Self-metallization of photocatalytic porphyrin nanotubes, J. Am. Chem. Soc., 2004, 126(51), 16720–16721.
2. Z. Wang, C. J. Medforth and J. A. Shelnutt, Porphyrin nanotubes by ionic self-assembly, J. Am. Chem. Soc., 2004, 126(49), 15954–15955.
3. S. Vlaming, et al., Exciton spectra and the microscopic structure of self-assembled porphyrin nanotubes, J. Phys. Chem. B, 2009, 113(8), 2273–2283.
4. Q. Zhao, et al., Out-of-plane coordinated porphyrin nanotubes with enhanced singlet oxygen generation efficiency, Sci. Rep., 2016, 6(1), 31339.
5. G. Zhu, et al., Curvature-dependent selectivity of CO2 electrocatalytic reduction on cobalt porphyrin nanotubes, ACS Catal., 2016, 6(9), 6294–6301.
6. R. Haver and H. L. Anderson, Synthesis and properties of porphyrin nanotubes, Helv. Chim. Acta, 2019, 102(1), e1800211.
7. S. Idrees, et al., Porphyrin nanotubes based on a hydrogen-bonded organic framework, Nanoscale, 2022, 14(39), 14630–14635.
8. V. Posligua, et al., Band structures of periodic porphyrin nanostructures, J. Phys. Chem. C, 2018, 122(41), 23790–23798.
9. R. Franco, et al., Molecular organization in self-assembled binary porphyrin nanotubes revealed by resonance Raman spectroscopy, Phys. Chem. Chem. Phys., 2010, 12(16), 4072–4077.
10. M. Hoffmann, et al., Enhanced p conjugation around a porphyrin [6] nanoring, Angew. Chem., Int. Ed. Engl., 2008, 47(27), 4993.
11. S. I. Allec, N. V. Ilawe and B. M. Wong, Unusual bandgap oscillations in template-directed π-conjugated porphyrin nanotubes, J. Phys. Chem. Lett., 2016, 7(13), 2362–2367.
12. M. Nishinaka, et al., n-Type Carbon Nanotubes Doped by Cross-Linked Organic Superbase for Stable Thermoelectric Materials, Energy Mater. Adv., 2024, 5, 0123.
13. J. L. Blackburn, et al., Carbon-nanotube-based thermoelectric materials and devices, Adv. Mater., 2018, 30(11), 1704386.
14. C. Meng, C. Liu and S. Fan, A promising approach to enhanced thermoelectric properties using carbon nanotube networks, Adv. Mater., 2010, 22(4), 535–539.
15. A. D. Avery, et al., Tailored semiconducting carbon nanotube networks with enhanced thermoelectric properties, Nat. Energy, 2016, 1(4), 1–9.
16. Q. Jin, et al., Flexible layer-structured Bi₂Te₃ thermoelectric on a carbon nanotube scaffold, Nat. Mater., 2019, 18(1), 62–68.
17. F. Ren, et al., Thermoelectric and mechanical properties of multi-walled carbon nanotube doped Bi_0.4Sb_1.6Te₃ thermoelectric material, Appl. Phys. Lett., 2013, 103(22), 221907.
18. W. Zhou, et al., High-performance and compact-designed flexible thermoelectric modules enabled by a reticulate carbon nanotube architecture, Nat. Commun., 2017, 8(1), 14886.
19. L. E. Bell, Cooling, heating, generating power, and recovering waste heat with thermoelectric systems, science, 2008, 321(5895), 1457–1461.
20. E. Garofalo, et al., Waste heat to power: technologies, current applications, and future potential, Energy Technol., 2020, 8(11), 2000413.
21. H. Jouhara, et al., Waste heat recovery technologies and applications, Therm. Sci. Eng. Prog., 2018, 6, 268–289.
22. A. Chiolerio, et al., Waste heat to power conversion by means of thermomagnetic hydrodynamic energy harvester, Appl. Energy, 2020, 277, 115591.
23. A. Van Herwaarden and P. Sarro, Thermal sensors based on the Seebeck effect, Sensor. Actuator., 1986, 10(3–4), 321–346.
24. A. Kirihara, et al., Flexible heat-flow sensing sheets based on the longitudinal spin Seebeck effect using one-dimensional spin-current conducting films, Sci. Rep., 2016, 6(1), 23114.
25. Y. Zhao, et al., Ultrasensitive Photothermal Spectroscopy: Harnessing the Seebeck Effect for Attogram-Level Detection, Nano Lett., 2023, 23(17), 7883–7889.
26. S. Boccardi, F. Ciampa and M. Meo, Design and development of a heatsink for thermo-electric power harvesting in aerospace applications, Smart Mater. Struct., 2019, 28(10), 105057.
27. A. Sarris, B. Bhatti and F. Ciampa, Thermoelectric energy harvesting using vapour chamber coolers for aerospace applications, J. Intell. Mater. Syst. Struct., 2022, 33(12), 1602–1612.
28. A. S. Arico, et al., Nanostructured materials for advanced energy conversion and storage devices, Nat. Mate., 2005, 4(5), 366–377.
29. J. M. Cullen and J. M. Allwood, Theoretical efficiency limits for energy conversion devices, Energy, 2010, 35(5), 2059–2069.
30. L. Huang, et al., Fiber-based energy conversion devices for human-body energy harvesting, Adv. Mater., 2020, 32(5), 1902034.
31. W. Li, J. Liu and D. Zhao, Mesoporous materials for energy conversion and storage devices, Nat. Rev. Mater., 2016, 1(6), 1–17.
32. Y. Nakai, et al., Giant Seebeck coefficient in semiconducting single-wall carbon nanotube film, Appl. Phys. Express, 2014, 7(2), 025103.
33. Y. Zhou, et al., High performance p-type organic thermoelectric materials based on metalloporphyrin/single-walled carbon nanotube composite films, J. Power Sources, 2019, 423, 152–158.
34. Q. H. Al-Galiby, et al., Tuning the thermoelectric properties of metallo-porphyrins, Nanoscale, 2016, 8(4), 2428–2433.
35. M. Rickhaus, et al., Single-acetylene linked porphyrin nanorings, J. Am. Chem. Soc., 2017, 139(46), 16502–16505.
36. L. A. Algharagholy, et al., Tuning thermoelectric properties of graphene/boron nitride heterostructures, Nanotechnology, 2015, 26(47), 475401.
37. C. J. Lambert, H. Sadeghi and Q. H. Al-Galiby, Quantum-interference-enhanced thermoelectricity in single molecules and molecular films, C. R. Phys., 2016, 17(10), 1084–1095.
38. H. Sadeghi, S. Sangtarash and C. J. Lambert, Enhanced thermoelectric efficiency of porous silicene nanoribbons, Sci. Rep., 2015, 5(1), 9514.
39. H. Sadeghi, S. Sangtarash and C. J. Lambert, Enhancing the thermoelectric figure of merit in engineered graphene nanoribbons, Beilstein J. Nanotechnol., 2015, 6(1), 1176–1182.
40. J. M. Soler, et al., The SIESTA method for ab initio order-N materials simulation, J. Phys.: Condens. Matter, 2002, 14(11), 2745.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
42. J. Ferrer, et al., GOLLUM: a next-generation simulation tool for electron, thermal and spin transport, New J. Phys., 2014, 16(9), 093029.
43. Q. Al-Galiby, et al., Exploiting the extended π-system of perylene bisimide for label-free single-molecule sensing, J. Mater. Chem. C, 2015, 3(9), 2101–2106.
44. P. Neuhaus, et al., A molecular nanotube with three-dimensional π-conjugation, Angew. Chem., 2015, 127(25), 7452–7456.
45. M. Paulsson and S. Datta, Thermoelectric effect in molecular electronics, Phys. Rev. B:Condens. Matter Mater. Phys., 2003, 67(24), 241403.
46. L. Rincón-García, et al., Thermopower measurements in molecular junctions, Chem. Soc. Rev., 2016, 45(15), 4285–4306.
47. J. Deb, et al., Thermoelectric properties of pristine graphyne and the BN-doped graphyne family, ACS Omega, 2021, 6(31), 20149–20157.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08282f

---