Tuning of the ionic conductivity of Ba₇Nb₄MoO₂₀ by pressure: a neutron diffraction and atomistic modelling study

Abstract

Ba₇Nb₄MoO₂₀ is a hexagonal perovskite derivative that exhibits both high oxide-ion and proton conductivity. The high oxide-ion conductivity results from the presence of disordered flexible MO_x (x = 3, 4, 5) units within the palmierite-like layer. The high proton conductivity arises from the dynamic and rotational flexibility of the MO_x units that results in disorder of the proton defects, high proton mobility and low energy diffusion pathways. Herein, using a combination of neutron diffraction experiments and atomistic modelling simulations, we demonstrate that both the crystal structure and ion transport of Ba₇Nb₄MoO₂₀ can be tuned by applying pressure. Applying pressure results in a reduction in the fraction of MO₄ tetrahedra within the P–L layer with a concomitant increase in the fraction of MO₆ octahedra. Density functional theory and molecular dynamics simulations using a newly developed machine-learned forcefield reveal a significant decrease in oxide-ion transport with increasing pressure whilst proton transport is comparatively unaffected.

---

Introduction

Oxide-ion and proton conductors are important materials for applications in energy generation and storage technologies such as ceramic fuel cells (CFCs) and solid oxide electrolysers (SOECs). Fuel cells are of particular interest due to their ability to produce clean energy from renewable resources whilst exhibiting high efficiencies compared to traditional combustion technologies.^1–5 However, the high operating temperatures (>700 °C) required for sufficient ionic conduction through commercially available electrolytes pose technical challenges for CFCs such as poor durability of components and higher costs.^1–5 Therefore, research has focussed on the development of materials which exhibit high conductivities at lower temperatures (300–600 °C).

One such material is Ba₇Nb₄MoO₂₀ which exhibits a significant bulk dual-ion conductivity of 4.0 × 10⁻³ S cm⁻¹ at 510 °C, as well as excellent stability over a range of oxygen partial pressures.⁶ Ba₇Nb₄MoO₂₀ crystalises in the P3̄m1 space group and can be described as a cation-deficient 7H hexagonal perovskite derivative formed by the intergrowth of 12R perovskite layers and palmierite-like (P–L) layers.^6,7 The O1 and O2 sites are only partially occupied due to the short O1–O2 distances, which results in mixed coordination of M1 sites along the P–L layers. This arrangement indicates that there is a random distribution of M1O₄ tetrahedral units and M1O₆ octahedral units across the average crystal structure. The adjacency of the O1 and O2 sites may however suggest that the oxide ions along the P–L layer are positionally disordered resulting in variable local geometries of the M1O_x polyhedra (x = 4, 5, 6).

The M1 and M2 sites shown in Fig. 1, are also only partially occupied with the cations distributed across both sites leading to four possible stacking configurations which are randomly positioned along the structural layers.^6,8,9 This configuration disrupts the stacking of the palmierite-like and 12R perovskite units due to the disorder of the cationic vacancies.^6,9 The oxide ion and cation disorder within the crystal structure is responsible for the significant ionic conductivity of Ba₇Nb₄MoO_20. The partially occupied oxygen sites as well as the intrinsic vacancies along the P–L layer provides a pathway for oxide-ion migration, whilst the proximity of these sites as well as the flexibility of the M1O_x polyhedral units facilitates proton migration.⁶

Fig. 1 Average crystal structure of Ba₇Nb₄MoO₂₀ which is composed of alternating 12R perovskite and palmierite-like (P–L) layers. Colours: green, Ba; blue, M1; pink, M2; purple, M3 and M4; yellow, O1; orange, O2; and red, O3, O4, and O5. The O1 and O2 sites are partially occupied resulting in variable coordination of the M1 cations along the P–L layers.

Under dry conditions the O1 site is predominately occupied, and the oxygen vacancies are mainly distributed on the O2 site. Water absorption occurs via the hydration of these intrinsic oxygen vacancies on the P–L layer which results in the formation of protonic defects. The Rietveld fit to the P3̄m1 model from variable temperature neutron diffraction data shows a thermal rearrangement of the fractional occupancies of the O1 and O2 sites.⁶ Above 300 °C the O1 site occupancy increases resulting in an increase in lower coordination environments.⁶ This structural rearrangement is likely due the uptake of water in which the presence of a proton between an oxygen site and M1 site forces a redistribution of cations from the M1 site to the vacant M2 site. Upon heating, water is lost from the P–L layer which causes the cations to move back to the M1 site and a consequent increase in the O1 occupancy.⁹ These findings are similar to that of the related Ba₃NbMoO_8.5 phase which has an average structure that is a disordered hybrid of the 9R hexagonal perovskite (A₃B₃O₉) and palmierite (A₃B₂O₈) structures.^8,10–15 The palmierite structure is derived from the 9R polytype by replacing the AO₃ cubic layer with an oxygen deficient layer AO₂. This disrupts the trimers of face-sharing BO₆ octahedra which are connected through corner sharing in the 9R polytype resulting in the formation of layers of BO₄ tetrahedra separated by octahedral vacancies. The vacancies within the Ba₃NbMoO_8.5 structure are split across the M1 and M2 sites as well as the O1 and O2 sites which leads to variable coordination environment of the M1 site (M1O_x). Upon increasing temperature, the ratio of M1O_x tetrahedra:octahedra increases and a decrease in activation energy is observed as well as improved ionic conductivity.¹²

The effect of pressure on the crystal structure of Ba₃NbMoO_8.5 has also been reported. The results show a structural reorganisation in favour of the O2 site which increases the average number of octahedra within the structure and therefore the occurrence of 9R-type regions. Above 5.2 GPa it is thought that the palmierite contribution will be completely suppressed as the O3 position is empty.¹⁴ The bulk modulus of Ba₃NbMoO_8.5 was found to be significantly lower than typical layered oxide materials and closer to halide materials suggesting that the structure exhibits high flexibility and compressibility.

Here, we report the effect of applied pressure on the crystal structure and ion transport properties of Ba₇Nb₄MoO₂₀ and how these structural changes may affect its conductivity. The results show that upon increasing pressure the O2 site occupancy increases whereas the O1 site occupancy decreases. Under ambient conditions the average number of (Mo, Nb)O₄ tetrahedra and (Mo, Nb)O₆ octahedra are 80.3% and 19.7% respectively. At ∼4.9 GPa the number of tetrahedra decreases to 63.8% as the number of octahedra increases to 36.2%. It has previously been reported that introducing excess oxygen (which increases the O2 site occupation) by aliovalent doping of Nb⁵⁺ by W⁶⁺, Mo⁶⁺ and Cr⁶⁺ enhances the oxide-ion conductivity of Ba₇Nb₄MoO₂₀ considerably.^16–18 However, density functional theory (DFT) and molecular dynamics (MD) simulations reveal that oxide-ion transport is substantially reduced with increasing pressure whilst proton transport is only weakly affected. Our results demonstrate how pressure can be used to tune the structure and conductivity of Ba₇Nb₄MoO₂₀.

Experimental

Samples of Ba₇Nb₄MoO₂₀ were synthesised via the solid-state reaction method. Stoichiometric amounts of BaCO₃ (99.999%, Aldrich), Nb₂O₅ (99.99%, Aldrich), and MoO₃ (99.5 + %, Aldrich) were ground, pressed into a pellet, heated at 1050 °C for 48 h, and then cooled to room temperature at 5 °C min⁻¹. The heating step was repeated until a phase pure product was obtained. The purity of the sample was confirmed using a PANalytical Empyrean diffractometer equipped with a Cu Kα tube and a Johansson monochromator. Data were recorded in the range 10°< 2θ < 120° with a step size of 0.013°.

High pressure time-of-fight (TOF) neutron powder diffraction data were collected at room temperature on the PEARL diffractometer at the ISIS Neutron and Muon Facility (Rutherford Appleton Laboratory, Harwell, Oxford, UK). Initially 137 mg of Ba₇Nb₄MoO₂₀ sample was sealed in a 6 mm vanadium can for data collection under ambient conditions. The powder sample was then sealed in a null scattering titanium–zirconium alloy gasket using highly neutron transparent zirconia-toughened alumina (ZTA) anvils along with a lead pressure marker and 4 : 1 perdeuterated methanol : ethanol as a pressure medium. A Paris Edinburgh (PE) press was used to apply selected loads between 6 and 60 tonnes to the sample. The time-of-fight (TOF) range was 1500–19900 μs using the 90° detector banks with a collection time of 4 hours for each loading. The GSAS/EXPGUI software was used to perform Rietveld analysis on the obtained data.^19,20 The pressure was determined by using a pressure–volume–temperature parameterisation of the lead equation of state in the form of the Birch–Murnaghan equation (Pb PVT BMEOS4).²¹ The unit cell parameter of the lead phase extracted from preliminary neutron refinements was implemented into this model to determine the pressure. TOF neutron powder diffraction data were then collected on the Ba₇Nb₄MoO₂₀ sample without the lead pressure marker present at a range of pressures −0.93(5) GPa, 1.65(5) GPa, 3.29(6) GPa, 3.56(6) GPa, 4.06(8) GPa, and 4.89(8) GPa. The time-of-fight (TOF) range was 1500–19900 μs using the 90° detector banks with a collection time of 9–12 hours for each pressure. The relationship between normalised volume and pressure was fitted with a Birch–Murnaghan function using the EosFit7-GUI software, from which the bulk modulus (B₀) of Ba₇Nb₄MoO₂₀ could be extracted.

Minimum bounding ellipsoid analysis was performed using the PIEFACE software to evaluate the relaxation of the average metal polyhedral units upon increasing pressure.²² The polyhedral distortion was quantified by the standard deviation, σ(R), of three primary ellipsoid radii, R1, R2 and R3.

Computational methods

The Vienna ab initio simulation package (VASP) was used to carry out the DFT simulations.²³ A 2 × 2 × 1 k-point mesh was used with a plane wave energy cutoff of 600 eV for static optimisations. 2 × 2 × 1 supercells of Ba₇Nb₄MoO₂₀ were used to calculate the volume. Ab initio molecular dynamics (AIMD) simulations using the NVT ensemble were carried out on the relaxed supercell with a plane wave energy cutoff of 450 eV and a Γ-centered 1 × 1 × 1 k-mesh. To model wet conditions, AIMD simulations were carried out on a Ba₇Nb₄MoO₂₀–0.5H₂O supercell containing 268 ions. A timestep of 1 fs and the Nose–Hoover thermostat were used. Simulations were performed at three strains (−0.05, 0 and 0.05) and four temperatures (300–1200 K at 300 K intervals). Snapshots were extracted from a production run of 10 ps at 0.1 ps intervals, i.e., 100 structures for each temperature and strain, resulting in a total of 1200 training structures.

The training and evaluation of moment tensor potentials were performed using the MLIP-3 package, and molecular dynamics (MD) simulations were performed using the LAMMPS package.^24–27 At the first stage, a moment tensor potential of the 16th level was pretrained using the data collected from AIMD. The potential includes 2068 fitting parameters. The root mean square error in energy per atom, forces and stresses between DFT and the fitted MTP are 3.6 meV, 0.39 eV Å⁻¹ and 0.91 kBar, respectively. The lattice parameters (a and c) of Ba₇Nb₄MoO₂₀ are similar between DFT (5.96 and 16.82 Å, respectively) and the MTP (5.97 and 16.80 Å, respectively). To study the diffusion coefficients of Ba₇Nb₄MoO₂₀ under dry and wet conditions and pressures, MD NVT simulations were performed using the fitted MTP on 4 × 4 × 2 supercells at a 1 ns time scale. Ten MD simulations were run at each temperature.

The nudged elastic band (NEB) method was applied to calculate the oxygen vacancy migration pathways and energy barriers.^28,29 The energy of the electronic ground state was converged to within 10⁻⁶ eV and the cutoff energy and convergence tolerance were set to 600 eV and 10⁻⁵ eV Å⁻¹, respectively. Five intermediate images were generated through linear interpolation between the initial and final structures, with a spring constant of −5 eV Å⁻¹.

Results and discussion

Influence of pressure on global and local structure

The X-ray diffraction pattern on the sample prepared for the neutron diffraction study showed that Ba₇Nb₄MoO₂₀ could be indexed with the P3̄m1 space group, with unit cell parameters of a = 5.86076(5) Å and c = 16.5230(2) Å. The sample was stored at room temperature in air with no decomposition observed. Fig. 2 shows the neutron diffraction data and Rietveld fit for Ba₇Nb₄MoO₂₀ at 0 and ∼4.9 GPa. The average structure of Ba₇Nb₄MoO₂₀ as reported in ref. 6 was employed as the initial model for the Rietveld refinements (Table S1†). The Ba atoms are situated at three different Wycoff sites; Ba1 at 1a, Ba2 and Ba4 at 2d and Ba3 at 2c. Due to their similar neutron scattering lengths, the Nb/Mo cations are assumed to be distributed over the metal sites M1, M2, M3 at Wyckoff site 2d, and M4 at Wyckoff site 1b, as it is not possible to resolve their individual scattering contributions.

Fig. 2 Rietveld refinement fits to the P3̄m1 model of Ba₇Nb₄MoO₂₀ from neutron diffraction data at 0 GPa (top) and 4.9 GPa (bottom). Black crosses show the observed data, the red line is the Rietveld fit and the green line is the background function, the blue line shows the difference between the calculated and observed data. Vertical pink lines show the reflection positions for Ba₇Nb₄MoO₂₀. Vertical cyan and black lines show the refection positions of Al₂O₃ and ZrO₂ phases respectively. The 0 Gpa dataset was collected from a V-can, and the 4.9 GPa dataset from the Paris-Edinburgh press.

The occupancies of the Ba and M3 and M4 sites refined to within ± 1% of the full occupancy and were therefore fixed at 1. The fractional occupancies of the M1 and M2 sites were refined. Due to the proximity of the O1 and O2 sites simultaneous occupation of these positions is not possible and therefore partial occupancies were also refined. The oxygen atoms are situated at two different Wyckoff sites; O1, O3, O4, O5 at 6i, and O2 at 3e. The O3, O4 and O5 positions refined to within ± 1% of the full occupancy and were therefore fixed at 1.

The atomic displacement parameters were modelled isotopically for all atoms at every pressure. A constraint was applied on the U_iso values for all the Ba atoms (1–4) to be the same. Similarly, the U_iso values for all the Nb/Mo atoms were also constrained to be the same. A constraint was also placed on the O1/O2 fractional occupancies so that as they varied, the overall oxygen stoichiometry would remain equal to 20. An excellent Rietveld refinement fit using this model was observed at all pressures and no additional peaks or evidence of a phase transition was observed. The statistical parameters at ∼0 GPa and 4.9 GPa were found to be χ² = 5.336, R_p = 1.96%, wR_p = 2.28% and χ² = 0.790, R_p = 3.1%, wR_p = 2.82% respectively. Tables of refined atomic positions, cell parameters and agreement factors are displayed in Table S1.† Additional phases of Al₂O₃ and ZrO₂ were present in the sample environment and have been represented by extra reflection markers in Fig. 2.

The unit cell parameters a = b ≠ c all decrease linearly upon increasing pressure with no anomalies observed (Table S1†). The axial compressibility, k, of the cell parameters were determined from the linear fit of the normalised plots a/a₀ (Fig. S1†) and c/c₀ (Fig. S2†). Values of k = 3.14 × 10⁻³ GPa⁻¹ and k = 3.51 × 10⁻³ GPa⁻¹ were obtained for a and c respectively, revealing that the compression is slightly anisotropic (the axial compressibility ratio is 1.12), and the structure is more elastic along the c axis. This is expected as it is typical for perovskites to be elastically anisotropic under pressure. However, there are a few materials that exhibit isotropic compression such as the related Ba₃NbMoO_8.5 phase.¹⁴

A second order Birch–Murnaghan isothermal equation of state has been fitted to the normalised plot of V/V₀ shown in Fig. 3, with the pressure derivative K fixed at 4. The bulk modulus, B₀ was determined to be 92.8(2) GPa using the EOSfit7 software for a refined V₀ value of 491.6(4) ų. This is somewhat lower than most oxide perovskites which typically exhibit a bulk modulus of >150 GPa.³⁰ DFT calculations were also performed to predict the bulk modulus using a third-order Birch–Murnaghan equation of state. The obtained value of 82 GPa at 0 K, is in good agreement with the experimental value. Our newly developed moment tensor potential model also predicts a bulk modulus of 82 GPa at 0 K, which is consistent with the value obtained from DFT calculations demonstrating the reliability of our model.

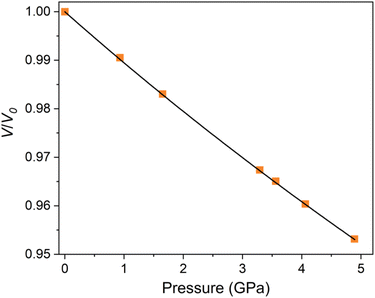Fig. 3 Variation of normalised unit cell volume with pressure for Ba₇Nb₄MoO_20. The data is fit with a second order Birch–Murnaghan equation of state.

The related hexagonal perovskite derivative Ba₃NbMoO_8.5 exhibits an even lower bulk modulus value of 50(2) GPa which is comparable to that of halide perovskites which typically exhibit a bulk modulus of 30–50 GPa.^14,31 The lower concentration of vacancies in the Ba₇Nb₄MoO₂₀ crystal structure compared to the related Ba₃NbMoO_8.5 phase is likely the reason why the Ba₇Nb₄MoO₂₀ exhibits a higher bulk modulus and is therefore harder to compress than Ba₃NbMoO_8.5.

The significant ionic conductivity of Ba₇Nb₄MoO₂₀ is associated with the anion and cation disorder within the structure. This disorder results in flexible MO_x polyhedra which accommodate the intrinsic oxygen vacancies and protonic defects. These anionic and cationic vacancies are distributed over the M1/M2 and O1/O2 sites and the fractional occupancies of these sites were refined. The Ba1–4, M3/M4 and O3–5 site occupancies were all fixed at 1. At ambient pressure the refined fractional occupancies of the M1/M2 and O1/O2 sites were found to be in good agreement as previously reported for this material.⁶ As determined both experimentally and computationally, when pressure is applied, the occupancy of the O1 position decreases whilst the occupancy of the O2 site increases, as shown in Fig. 4. It has previously been reported that by increasing the Mo : Nb cation ratio and therefore increasing the site occupancy of the O2 interstitial oxygen within Ba₇Nb₄MoO₂₀ enhances the oxide-ion conductivity of Ba₇Nb₄MoO_20. Ba₇Nb_3.9Mo_1.1O_20.05 is reported to exhibit significant oxide-ion conductivity of 5.8 × 10⁻⁴ S cm⁻¹ at lower temperatures ∼310 °C.¹⁶ At intermediate temperatures ∼600 °C, Ba₇Nb_3.9Mo_1.1O_20.05 exhibits a bulk conductivity of 5.1 × 10⁻³ S cm⁻¹, higher than that of the undoped phase which exhibits a bulk conductivity of ∼1.9 × 10⁻³ S cm⁻¹ under dry conditions.^6,16

Fig. 4 Influence of pressure on O1 (orange) and O2 (blue) fractional occupancies from the Rietveld fit to the P3̄m1 model from neutron diffraction data collected on the PEARL diffractometer (left) and MD simulations at 300 K (right).

Under ambient conditions the average number of (Mo,Nb)O₄ tetrahedra and (Mo,Nb)O₆ octahedra within the palmierite-like layer of Ba₇Nb₄MoO₂₀ is 80.3% and 19.7%, respectively. At ∼4.9 GPa the number of tetrahedra decreases to 63.8% as the number octahedra increases to 36.2%. The change in the occupancy of the O1 and O2 sites with pressure has the reverse effect compared to the influence of temperature. As reported previously, upon heating, the fractional occupancy of the O1 site increases whilst the occupancy of the O2 site simultaneously decreases. At temperatures > 500 °C the O1 site is fully occupied and the O2 site is empty.⁶ The variation of the fractional occupancies of the M1 and M2 positions with pressure are shown in Fig. S3 and S4.† Overall, there is a slight decrease in the M1 occupancy accompanied by a slight increase in the M2 occupancy.

Upon increasing pressure, the Ba1–O2 bond length decreases linearly which is expected as it lies along the a axis which also decreases linearly with compression. The Ba1–O3, Ba2–O4, Ba3–O5, Ba4–O4, Ba4–O5, M1–O1, M1–O2 and M4–O5 bonds all show a general decrease upon compression (Table S2†). The remaining bond lengths show no clear observable trends.

Polyhedral distortion can play a role in influencing the ionic conductivity of materials. It has previously been reported for the Ba₃MM’O_8.5 related phase that the polyhedral distortion is a result of the second-order Jahn–Teller distortion which is higher in magnitude for cations with a smaller ionic radius and larger formal charge.^32–34 This is why Mo⁶⁺ is a more effective distorter than Nb⁵⁺ and W⁶⁺ and why the activation energy for the bulk conductivity is lower for Ba₃MoNbO_8.5 compared to Ba₃WNbO_8.5 and Ba₃W_1.2Nb_0.8O_8.6 phases, as a more distorted environment can improve oxide-ion diffusion. Upon increasing pressure, the octahedral environment of the related Ba₃NbMoO_8.5 phase undergoes a decrease in distortion and the angles O1–M1–O2 and O2–M1–O2 which define its octahedral environment tend towards 90° (the ideal octahedra geometry).³⁵ Conversely, the tetrahedra become more distorted with increasing pressure for this phase.

The PIEFACE software package was used to determine the minimum bounding ellipsoid at every pressure. By fitting the smallest bounding ellipsoid around the polyhedra, the polyhedral distortion σ(R), ellipsoidal shape parameter (S) and metal cation displacement (d) can be determined. The results are displayed in Tables S4–S6, Fig. S5 and S6.† The polyhedral distortion σ(R) for the M1O₆ octahedra decreases from 0.0819 at 0 GPa to 0.0783 at 4.9 GPa (Fig. S5†). Therefore, the M1O₆ octahedra appear to become slightly less distorted with pressure which is expected as the average number of octahedra increases. The polyhedral distortion, σ(R), for the M2O₆ octahedra also decreases from 0.1371 at 0 GPa to 0.0916 at 4.9 GPa (Fig. S6†). This is supported by the decrease in the O3–M2–O4 angle towards 90° upon increasing pressure (Table S3†).

Upon increasing pressure, the displacement of the M1 cation shows no discernible trend meaning that the decrease in M1–O1/O2 bond is purely a result of compression rather than the M1 cation moving closer to the O1/O2 positions. This is also confirmed by the refined atomic parameter z, where no clear trend is observed with increasing pressure. The shape parameter, S, describes whether the minimum bounding is a perfect sphere S = 0, axially compressed S < 0 or axially stretched S > 0. In general, octahedra can be described by an oblate ellipsoid (S < 0) and tetrahedra by a prolate bound ellipsoid (S > 0). Upon increasing pressure, the ellipsoid shape parameter, S, for the M1O₆ octahedra increases from −0.0842 at 0 GPa to −0.08094 at 4.9 GPa (Fig. S5†). Both the polyhedral distortion, σ(R), and the shape parameter, S, for the M1O₄ tetrahedra show no discernible trends.

Influence of pressure on short- and long-range ion transport

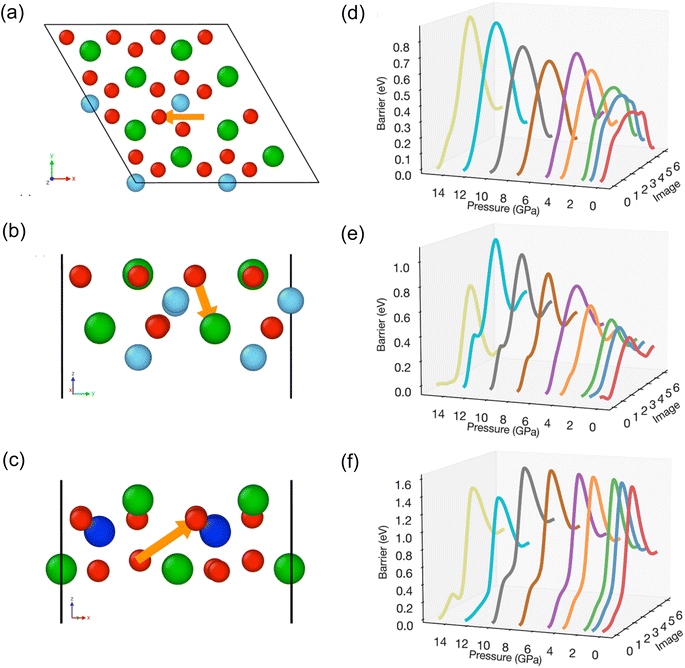
We can't currently determine the ionic conductivity of Ba₇Nb₄MoO₂₀ under the applied pressures used in the neutron diffraction experiment. To determine how the changes in crystal structure would affect both the oxide-ion and proton conductivity, we have performed atomistic modelling simulations. NEB were employed to understand and quantify the impact of pressure (ranging from 0 to 15 GPa) on short-range oxide-ion transport in Ba₇Nb₄MoO₂₀. Three representative oxygen hopping pathways were considered, as shown in Fig. 5(a–c), and their corresponding energy barriers are presented in Fig. 5(d–f). With increasing pressure, the energy barriers for all migrations generally rise, indicating a reduced tendency for oxide-ion diffusion.

Fig. 5 (a–c) NEB pathways for three oxygen migrations considered. Colours: green, Ba; blue, Mo; aqua, Nb and red, O. The orange arrows indicate the oxygen pathways between oxygen sites: (a) O5–O5 (2.95 Å), (b) O5–O4 (2.59 Å) and (c) O3–O1 (3.55 Å). (d–f) Corresponding energy barriers for the three oxygen migrations calculated as a function of pressure.

For the O5–O5 pathway, the barrier increases from 0.32 eV at 0 GPa to 0.88 eV at 15 GPa. Likewise, for the O5–O4 transition, the barrier increases from 0.34 eV to 0.70 eV at 15 GPa. At higher pressures (i.e., 10 GPa and above), the barrier becomes sharper and more pronounced. In contrast, the O3–O1 transition shows a high barrier of 1.46 eV at 0 GPa, and the effect of pressure on this pathway is less pronounced. As previously reported for the Ba₃MoNbO_8.5 phase, increasing pressure results in higher relative bond valence energy barriers, a trend consistent with our NEB calculations.¹⁴

The differences in energy between the initial and final states of the NEB pathways also generally exhibit an increasing trend with increasing pressure. For example, for the O5–O5 transition, the difference in energy between the initial and final states increases from 0.01 eV at 0 GPa to 0.20 eV 4.9 GPa. Considering both this energy difference and the energy barrier for the forward transition, the magnitude of the reverse barrier for this transition shows minimal change in this range (∼0.4 eV). When the pressure exceeds 5 GPa, since the energy of the final structure is very close to that of the initial structure, both the forward and reverse transitions become equally likely to occur. This behaviour highlights how increasing pressure significantly affects both the migration barriers and the stability of the final vacancy configuration. It is noteworthy that kinks appear on the energy barrier curves, which are indicative of local minima along the migration pathway. For the O5–O5 transition, kinks are present at 0 GPa but disappear by 3.6 GPa, while for the O5–O4 and O3–O1 transitions, the kinks become more pronounced when the pressure exceeds 5 GPa.

In addition to the individual hopping events considered above, long-range oxide-ion and proton diffusion were assessed using large-scale MD simulations. Arrhenius plots of the calculated oxide-ion and proton diffusion and their corresponding activation energies as a function of pressure are presented in Fig. 6. For oxide-ion diffusion, as presented in Fig. 6(a), there is a clear decrease in diffusion with increasing pressure, with the highest diffusion coefficient of 4.98 × 10⁻⁸ cm² s⁻¹ occurring at 0 GPa and the lowest of 6.86 × 10⁻⁹ cm² s⁻¹ at 10 GPa (for 500 °C). This is in good agreement with the NEB results presented above. Interestingly, despite the reduced oxide-ion mobility with pressure, the activation energy for oxide-ion transport significantly decreases from 0.33 eV at 0 GPa to 0.23 eV at 0.9 GPa and then further decreases with increasing pressure up to 10 GPa (Fig. 6(b)).

Fig. 6 Arrhenius plots of (a) oxide-ion and (b) proton diffusion and their (c) corresponding activation energies as a function of pressure, respectively.

To explore these findings further, we calculated the average O–O separation at 800 K from our MD simulations, as shown in Fig. S7.† At 0 GPa, the distribution exhibits a prominent peak at around 2.90 Å and two smaller peaks at 2.68 Å and 3.08 Å. With increasing pressure, the small peak at 3.08 Å gradually diminishes until it is no longer observable at >7.5 GPa. The second small peak at 3.08 Å becomes increasingly more well defined up to ∼4.9 GPa before disappearing at >10 GPa. The main peak at 2.90 Å shifts towards a shorter separation distance (to the left) as the pressure continues to increase, indicating a compression of the O–O separation under higher pressures. This compression trend becomes more prominent at pressures above 10 GPa, where the primary peak becomes broader and shifts to lower values, reflecting a more compact and uniform oxygen sublattice in the system. These results indicate a clear change in the mechanism of oxide-ion transport in the system because of pressure, with the distinct shorter and longer O–O distances at 0 GPa becoming more uniform. The overall smaller average O–O distances at higher pressures could be expected to induce lower activation energies, as observed, but also higher diffusion coefficients, which are not observed. Furthermore, the increasing pressure also results in smaller bottlenecks for oxide-ion transport, which contribute to the orders of magnitude decreases in diffusion found from the MD simulations in Fig. 6(a).

For proton diffusion (Fig. 6(b)), in contrast, there is no clear trend, and the influence of pressure is reduced compared to its impact on oxide-ion diffusion. While the diffusion coefficients and activation energies for proton transport show some fluctuations, the overall changes are relatively small, indicating that the proton migration mechanism is only mildly affected by the structural changes induced by pressure. Overall, our calculations show that the combination of temperature and pressure exerts a synergistic effect on ion transport in Ba₇Nb₄MoO₂₀.

Conclusions

We have reported the effect of applied pressure on the crystal structure and ion transport of Ba₇Nb₄MoO₂₀. The results show a continuous linear decrease of the unit cell parameters upon increasing pressure. The compressibility of Ba₇Nb₄MoO₂₀ is higher than that of typical layered oxide material as it exhibits a much lower bulk modulus of 92.8(2) demonstrating the flexibility and tuneability of this material. Upon increasing the pressure from 0 GPa to 4.9 GPa, the interstitial O2 site fractional occupancy increases from 0.179 to 0.309 whereas the O1 site occupancy decreases from 0.243 to 0.179 so that the number of octahedra within the palmierite-like layer increases from 19.7% to 36.2%. This is the reverse effect to what has previously been observed for increasing temperature as the structure undergoes a thermal reorganisation of the fractional occupancies of the O1 and O2 sites in favour of the O1 site.

To determine the influence of the structural changes in the P–L layer with applied pressure on the ionic conductivity, density functional theory and molecular dynamics simulations using a newly developed machine-learned forcefield have been performed. NEB results show an increase in the energy barriers for oxide-ion migration which is most likely a result of the reduced number of tetrahedra in the P–L layer and hence a decrease in the number of low energy pathways for oxide-ion migration, as previously reported for Ba₃NbMoO_8.5.¹⁴ The results would suggest a critical number of tetrahedral and interstitial (octahedral) oxide-ion sites are required for high oxide-ion conductivity in Ba₇Nb₄MoO₂₀. MD simulations give further insight and show that oxide-ion diffusion is further reduced with applied pressure because of the smaller bottlenecks for oxide-ion transport. Surprisingly the proton transport is relatively unaffected by changes to the crystal structure upon applying pressure. Combined, the experimental and computational results give further insight into oxide-ion and proton conductivity in Ba₇Nb₄MoO₂₀.

Data availability

Data for this article, including the description of data and experimental team are available at https://doi.org/10.5286/ISIS.E.RB2310096.

Author contributions

ACM and JAD conceptualised the study. VW and DT synthesised the sample and conducted the neutron diffraction experiment with guidance from CJR. VW analysed the neutron diffraction data with guidance from ACM and CJR. YZ carried out the simulations and analysed the results with guidance from JAD. All authors contributed to the writing of the original draft and subsequent editing of the paper.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission. This research was supported by the Leverhulme Trust (grant number RPG-2022-175) and EPSRC (Grant no. EP/X011941/1 (A. C. M.) and EP/X010422/1 (J. A. D.). We also acknowledge STFC-GB for provision of beamtime at the ISIS under the experiment number RB2310096, doi: https://doi.org/10.5286/ISIS.E.RB2310096.

References

1. L. Malavasi, C. A. J. Fisher and M. S. Islam, Chem. Soc. Rev., 2010, 39, 4370–4387.
2. B. C. Steele and A. Heinzel, Nature, 2001, 414, 345–352.
3. A. J. Jacobson, Chem. Mater., 2009, 22, 660–674.
4. K. V. Kordesch and G. R. Simader, Chem. Rev., 1995, 95, 191–207.
5. L. Fan, Z. Tu and S. H. Chan, Energy Rep., 2021, 7, 8421–8446.
6. S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle, J. T. S. Irvine, P. A. Connor, C. Savaniu, C. Ritter and A. C. Mclaughlin, Nat. Mater., 2020, 19, 752–757.
7. E. García-González, M. Parras and J. M. González-Calbet, Chem. Mater., 1999, 11, 433–437.
8. S. Fop, K. S. McCombie, R. I. Smith and A. C. Mclaughlin, Chem. Mater., 2020, 32, 4724–4733.
9. S. Fop, J. A. Dawson, A. D. Fortes, C. Ritter and A. C. McLaughlin, Chem. Mater., 2021, 33, 4651–4660.
10. S. Fop, J. M. Skakle, A. C. McLaughlin, P. A. Connor, J. T. S. Irvine, R. I. Smith and E. J. Wildman, J. Am. Chem. Soc., 2016, 138, 16764–16769.
11. K. S. McCombie, E. J. Wildman, S. Fop, R. I. Smith, J. M. Skakle and A. C. Mclaughlin, J. Mater. Chem. A, 2018, 6, 5290–5295.
12. M. S. Chambers, K. S. McCombie, J. E. Auckett, A. C. Mclaughlin, J. T. S. Irvine, P. A. Chater, J. S. O. Evans and I. R. Evans, J. Mater. Chem. A, 2019, 7, 25503–25510.
13. A. Gilane, S. Fop, F. Sher, R. I. Smith and A. C. Mclaughlin, J. Mater. Chem. A, 2020, 8, 16506–16514.
14. B. Sherwood, C. J. Ridley, C. L. Bull, S. Fop, J. M. S. Skakle, A. C. McLaughlin and E. Wildman, J. Mater. Chem. A, 2021, 9, 6567–6574.
15. D. N. Tawse, A. Gilane, S. Fop, A. Martinez-Felipe, F. Sher, R. I. Smith and A. C. Mclaughlin, Inorg. Chem., 2021, 60, 13550–13556.
16. M. Yashima, T. Tsujiguchi, Y. Sakuda, Y. Yasui, Y. Zhou, K. Fujii, S. Torii, T. Kamiyama and S. J. Skinner, Nat. Commun., 2021, 12, 556.
17. Y. Suzuki, T. Murakami, K. Fujii, J. R. Hester, Y. Yasui and M. Yashima, Inorg. Chem., 2022, 61, 7537–7545.
18. Y. Sakuda, J. R. Hester and M. Yashima, J. Ceram. Soc. Japan., 2022, 130, 442–447.
19. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
20. A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratory Report,LAUR, 86–748, 1994.
21. A. D. Fortes, RAL Technical Report, RAL-TR-2019-002, 2019.
22. J. Cumby and J. P. Attfield, Nat. Commun., 2017, 8, 14235.
23. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
24. A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173.
25. I. S. Novikov, K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, Mach. Learn.: Sci. Technol., 2020, 2, 025002.
26. E. Podryabinkin, K. Garifullin, A. Shapeev and I. Novikov, J. Chem. Phys., 2023, 159, 084112.
27. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
28. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
29. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
30. A. S. Verma and A. Kumar, J. Alloys Compd., 2012, 541, 210–214.
31. M. Li, T. Liu, Y. Wang, W. Yang and X. Lü, Matter Radiat. Extremes, 2020, 5, 018201.
32. S. Fop, K. S. McCombie, E. J. Wildman, J. M. Skakle and A. C. Mclaughlin, Chem. Commun., 2019, 55, 2127–2137.
33. M. Kunz and I. D. Brown, J. Solid State Chem., 1995, 115, 395–406.
34. M. T. Dunstan, A. F. Pavan, V. V. Kharton, M. Avdeev, J. A. Kimpton, V. A. Kolotygin, E. V. Tsipis and C. D. Ling, Solid State Ionics, 2013, 235, 1–7.
35. N. P. Juraj and S. I. Kirin, Coord. Chem. Rev., 2021, 445, 214051.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08133a

---