A two-step strategy improves the wide-temperature-range thermoelectric performance of Mg_3+xBi_1.29Sb_0.7Te_0.01

Abstract

Mg₃Bi₂-based thermoelectric materials have attracted significant attention due to the absence of volatile and expensive chalcogen elements like Te, along with their potential for high thermoelectric performance near room temperature. However, stabilizing the Mg content and optimizing the preparation process remain key challenges in further improving their thermoelectric properties. In this study, we employ a two-step method to progressively enhance the near-room-temperature performance of Mg₃Bi₂-based thermoelectric materials. First, by fine-tuning the excess Mg, we achieve a p-to-n type transition, optimizing carrier concentration and mobility, which leads to a substantial improvement in the power factor. Next, by modifying the high-temperature sintering process to create a well-structured microstructure, we increase grain size without compromising the system composition, further enhancing room-temperature electron mobility for faster electron transport. As a result, the room-temperature power factor of Mg_3.4Bi_1.29Sb_0.7Te_0.01 sintered at 1073 K significantly increases from 6.5 to 16 μW cm⁻¹ K⁻², while the figure of merit value at 323 K increases from 0.2 to nearly 0.5, with the peak figure of merit at 500 K approaching 0.9, reaching one of the highest values reported for similar materials.

---

Introduction

Thermoelectric materials, which enable the direct conversion of heat into electrical energy, have garnered significant research interest due to their unique energy conversion mechanisms and wide-ranging applications.¹ The efficiency of thermoelectric devices is dictated by the performance of these materials,² typically measured by the dimensionless figure of merit ZT = S²σT/(κ_l + κ_e) = S²σT/κ, where S, σ, κ_l, κ_e, κ, and T represent the Seebeck coefficient, electrical conductivity, lattice thermal conductivity, electronic thermal conductivity, thermal conductivity, and absolute temperature, respectively.³ Enhancing thermoelectric performance, therefore, requires a high S²σ and low κ.⁴ Over the past few decades, various thermoelectric materials have been explored, including near-room-temperature materials (e.g., Bi₂Te₃ and Ag₂Q, where Q = S, Se, Te),^5–7 mid-temperature materials (e.g., PbSe, SnTe, and GeTe),^8–10 and high-temperature materials (e.g., SiGe alloys and half-Heusler alloys),^11,12 all of which exhibit relatively high ZT values within their respective temperature ranges. While Bi₂Te₃, PbTe and SnSe have shown promising performance in near-room- and mid-temperature ranges, their commercialization is hindered by the volatility and toxicity of chalcogen elements (Te, Pb, and Se), along with high production costs.¹³ Consequently, non-toxic, low-cost Mg₃(Sb,Bi)₂-based thermoelectric materials have emerged as a promising alternative.¹⁴

Mg₃Sb₂-based thermoelectric materials belong to the Zintl phase structure and are distinguished by their low bandgap and low κ.¹⁵ The inherently low κ_l is attributed to the instability of Mg atoms within the layers and the highly disordered quasi-layered crystal structure.¹⁶ However, the volatility and high vapor pressure of Mg result in a significant number of Mg vacancies (V_Mg), which impede electron transport and substantially degrade the thermoelectric performance.¹⁷ In 2016, Tamaki et al.¹⁸ successfully achieved n-type conductive Mg₃Sb₂ by introducing excess Mg, while Imasato et al.¹⁹ later conducted a more detailed investigation into its thermoelectric properties at varying Mg contents. Studies have shown that excess Mg and electron doping can achieve stable n-type conductivity.²⁰ The multi-valley characteristic of n-type conductivity notably improves its electrical transport properties compared to p-type, with the highest ZT of Mg₃Sb₂-based thermoelectric materials being achieved in compositions such as Mg₃Sb_1.5Bi_0.49Te_0.01 + 10% Nb²¹ and Mg_3.2In_0.005Sb_1.5Bi_0.49Te_0.01.²² However, these high ZT values of Mg₃Sb₂-based thermoelectric materials occur at elevated temperatures (above 700 K), while their thermoelectric performance in the low-to-mid temperature range remains poor, limiting their effectiveness for near-room-temperature applications.

Researchers have found that introducing Bi into Sb sites can modify the Bi/Sb alloy ratio, reduce the bandgap, and shift the temperature range of high ZT values closer to room temperature.^23,24 Bi doping also induces lattice strain, enhancing phonon scattering and lowering the κ. As a result, significant research focusing on n-type thermoelectric materials based on Bi-doped Mg₃Sb₂ has emerged. To further enhance its thermoelectric performance, researchers are exploring both interface engineering and doping modifications. On one front, researchers optimize grain size and the chemical composition and structure near grain boundaries using techniques such as Mg vapor annealing,²⁵ Nb wetting phases,²⁶ introducing carbon nanotubes at grain boundaries,²⁷ and employing nano-sintering aids like Mg₂Cu to lower grain boundary barriers.²⁸ On the other front, researchers enhance electrical properties through doping, such as substituting Sb/Bi sites with S,²⁹ Se,³⁰ or Te,¹⁸ or doping the Mg sites with group III and lanthanide elements like Y,³¹ Sc,³² La,³³ and Nd.³⁴ While these doping strategies generally increase the carrier concentration (n), they often impact the carrier mobility (μ). Thus, the challenge remains in optimizing thermoelectric performance without compromising the μ. Additionally, further research into process improvements to enhance the performance of Mg₃Bi₂ across a wide temperature range continues to be a key focus. While previous research on the sintering process has primarily focused on high Sb compositions,^35,36 the low melting point and high volatility of Bi are likely to hinder the Mg₃Bi₂ alloying process and exacerbate Mg volatility. Therefore, a more detailed investigation of Mg content and the sintering process under high Bi composition is crucial.

In general, achieving stable n-type conductivity requires an excess of Mg, with the required amount depending on the synthesis method. Once the n-type conduction threshold is reached, fine-tuning of Mg content becomes crucial for optimizing the thermoelectric performance. This study highlights a significant enhancement in the wide-temperature-range thermoelectric performance of Mg₃Bi₂-based materials using a straightforward two-step method. By precisely controlling the Mg content to optimize σ and adjusting the high-temperature sintering process to engineer the microstructure, grain boundary resistance was reduced, and the room-temperature μ was improved, enabling faster electron transport. The results show that the power factor of Mg_3.4Bi_1.29Sb_0.7Te_0.01 sintered at 1073 K increased significantly, with the room-temperature S²σ rising from 6.5 to 16 μW cm⁻¹ K⁻², nearly a threefold improvement. Due to the remarkable improvement in electrical properties, the ZT value at 323 K increased from 0.2 to nearly 0.5, while the peak ZT at 500 K approached 0.9, reaching one of the highest values reported for similar materials (Table S1, ESI†).^30,37–44

Results and discussion

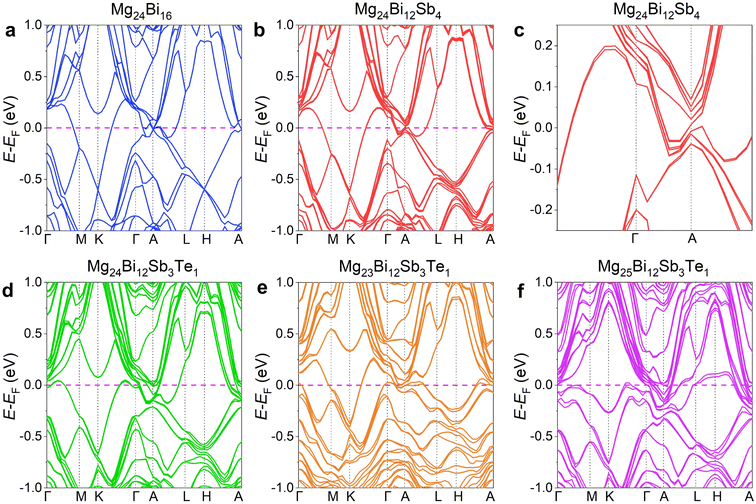
In the experimental process, the issue of increased V_Mg due to Mg volatilization is typically addressed by introducing excess Mg. The extent of Mg volatilization depends not only on the sintering temperature, heating rate, and holding time but may also be influenced by the Bi/Sb elemental ratio, with higher Bi content increasing the likelihood of Mg volatilization during sintering. To achieve high-performance n-type conductivity near room temperature, it is essential to precisely control the amount of excess Mg and the sintering temperature to optimize the thermoelectric performance and microstructure. This study first investigated the effect of excess Mg levels on the thermoelectric performance and microstructure of the material. To assess the impact of excess Mg on thermoelectric properties, Mg_3.2Bi_1.3Sb_0.7 was selected as the base composition, given its high preliminary S²σ (Fig. S1, ESI†). A small amount of Te (1%) was then doped to regulate n.^45–47 The rationality of this composition was first verified using first-principles density functional theory (DFT). Fig. 1 presents the computational results of Mg₃Bi₂-based thermoelectric compounds, including the calculated band structures of Mg₂₄Bi₁₆, Mg₂₄Bi₁₂Sb₄, Mg₂₄Bi₁₂Sb₃Te, Mg₂₃Bi₁₂Sb₃Te, and Mg₂₅Bi₁₂Sb₃Te. In Fig. 1a, the electronic structure of Mg₂₄Bi₁₆ shows an overlap between the conduction band and valence band without a clear direct bandgap, indicating that Mg₂₄Bi₁₆ has an electronic structure similar to that of metals. After partially substituting Bi with Sb, the electronic structure of Mg₂₄Bi₁₂Sb₄, as shown in Fig. 1b, exhibits band splitting due to the different electronic orbitals of Bi and Sb. A magnified view in Fig. 1c shows that the conduction band and valence band no longer overlap, and a small direct bandgap emerges, with the bottom of the conduction band and the top of the valence band located at the same position. As the Sb content increases, the direct bandgap progressively widens and eventually transitions into an indirect bandgap, where the bottom of the conduction band and the top of the valence band are positioned at different locations in momentum space, as shown in the electronic structures of Mg₂₄Bi₄Sb₁₂ and Mg₂₄Sb₁₆ (Fig. S2a and b, ESI†). In Fig. 1d, the electronic structure of Mg₂₄Bi₁₂Sb₃Te shows that Te shifts the Fermi level towards the conduction band, enhancing n-type conductivity in the system. We also examined the effects of V_Mg and additional Mg atoms (e.g., interstitial Mg, Mg_i). Fig. 1e and f illustrate the electronic structures of Mg₂₃Bi₁₂Sb₃Te and Mg₂₅Bi₁₂Sb₃Te, showing that V_Mg shifts the Fermi level towards the valence band, indicating a tendency for the system to exhibit p-type conductivity. Conversely, additional Mg atoms (e.g., Mg_i) shift the Fermi level towards the conduction band, similar to the effect of Te, promoting n-type conductivity. Thus, ensuring enough Mg to minimize the formation of V_Mg is one of the primary objectives of this study. However, in actual samples, due to the high volatility of Mg, the nominal composition Mg₃Bi_1.29Sb_0.7Te_0.01 may exhibit p-type conductivity due to the presence of V_Mg. Therefore, the first step in our study focuses on optimizing electrical transport performance by adjusting the amount of excess Mg to achieve stable n-type conductivity.

Fig. 1 Computational results of Mg₃Bi₂-based thermoelectric compounds. Calculated band structures of (a) Mg₂₄Bi₁₆, (b) Mg₂₄Bi₁₂Sb₄, (c) magnified Mg₂₄Bi₁₂Sb₄, (d) Mg₂₄Bi₁₂Sb₃Te, (e) Mg₂₃Bi₁₂Sb₃Te, and (f) Mg₂₅Bi₁₂Sb₃Te.

To explore the optimized excess amount of Mg, we prepared a series of samples with nominal compositions of Mg_3+xBi_1.29Sb_0.7Te_0.01 (x = 0.2, 0.3, 0.4, and 0.5). The phase information of these bulk samples was analyzed using room-temperature X-ray diffraction (XRD) after hot-pressing at 973 K, as shown in Fig. 2a. The XRD patterns, recorded over a 2θ range from 20 to 60°, were compared with standard peaks corresponding to pure Mg₃Bi₂. All diffraction peaks can be indexed to the α-Mg₃Bi₂ phase with a P3̄m1 space group and an anti-α-La₂O₃ structure.⁴² Within the detection limits, a few minor secondary phase peaks are present, likely attributed to unreacted elemental substances or the MgO secondary phase, which is commonly found in Mg₃(Bi, Sb)₂ materials.²⁹ However, MgO, as an insulating material, scatters both carriers and phonons, resulting in its effects on and contributions to the thermoelectric properties effectively canceling each other out. Fig. 2b presents the magnified XRD patterns with a 2θ range from 20 to 26°. The diffraction peaks shift to the left as Mg content increases up to x = 0.4, after which the peaks begin to shift to the right. The leftward shift for x < 0.4 is caused by lattice expansion due to the reduction of V_Mg. However, when x > 0.4, the diffraction peak shifts to the right. This shift can be attributed to changes in the crystal structure, likely caused by modifications in the atomic arrangement within the crystal lattice due to the presence of excess magnesium. Fig. 2c shows a SEM image of the freshly fractured surface of the Mg_3.4Bi_1.29Sb_0.7Te_0.01 sample, revealing a dense structure with no visible defects or pores, indicating successful sintering and good material compactness. The sample also exhibits a characteristic layered structure, which originates from its typical rhombohedral crystal structure (space group: P3̄m1), comprising alternating layers of [Mg²(Sb/Bi)²]²⁻ and Mg²⁺ ions.³⁰ For further reference, Fig. S3 (ESI†) shows SEM images of fractured surfaces taken from other positions of Mg_3.4Bi_1.29Sb_0.7Te_0.01, confirming the presence of uniform layered and dense structures throughout the material.

Fig. 2 Characterization and thermoelectric performance of Mg_3+xBi_1.29Sb_0.7Te_0.01. (a) X-ray diffraction (XRD) patterns with a 2θ range from 20 to 60°. (b) Magnified XRD patterns with a 2θ range from 20 to 26°. (c) Scanning electron microscopy (SEM) image of the fractured surface of Mg_3.4Bi_1.29Sb_0.7Te_0.01. Temperature-dependent (d) electrical conductivity (σ) and (e) Seebeck coefficient (S). (f) x-Dependent carrier concentration (n) and mobility (μ) at room temperature. Temperature-dependent (g) power factor (S²σ). (h) Total thermal conductivity (κ), and (i) ZT.

To further investigate the impact of excess Mg on the thermoelectric performance of the material, Fig. 2d and e present the temperature-dependent σ and S of Mg_3+xBi_1.29Sb_0.7Te_0.01 (x = 0.2, 0.3, 0.4, and 0.5) samples. As shown in Fig. 2e, as x increases from 0.2 to 0.3, the S value shifts from positive to negative, indicating a transition from p-type to n-type conduction at x > 0.3. Additionally, with increasing Mg content, (the σ decreases and then increases due to a conduction type shift caused by the reduction of V_Mg) the σ increases and reaches a maximum at x = 0.4, where the highest σ is achieved across the entire tested temperature range. However, when the Mg content becomes too high (e.g., x = 0.5), σ drops (the reasons for which will be analyzed subsequently). To explain the changes in electrical properties, the room-temperature n and μ as a function of x are further plotted in Fig. 2f. In n-type conduction, the n increases almost monotonically with increasing x, as the low formation energy of V_Mg leads to numerous V_Mg and increasing the Mg content significantly suppresses the V_Mg, reducing vacancy-electron trapping and thus enhancing n. As seen in Fig. 2f, the μ first increases and then decreases with increasing x. This behavior can also be attributed to the influence of V_Mg and Mg_i. In Mg₃(Sb,Bi)₂-based thermoelectric materials, V_Mg is the primary defect in the matrix, causing strong ionized impurity scattering, which affects the μ. The initial rise in μ is mainly due to the reduction of V_Mg migration and accumulation. However, at x = 0.5, the significant increase in n (primarily attributed to excess elemental impurities, predominantly resulting from the introduction of excess Mg, which leads to the formation of interstitial Mg)^48,49 intensifies scattering between carriers and around impurity-phase interfaces, hindering the free movement of carriers, which explains the drop in σ. As shown in Fig. 2d, when x = 0.4, σ initially increases and then decreases with rising temperature, indicating a transition in the carrier scattering mechanism. Specifically, the ionization scattering-dominated region (σ ∝ T^1.5) occurs below 450 K, while the acoustic phonon scattering-dominated region (σ ∝ T^−1.4) emerges above 450 K. The temperature dependence of Mg_3.4Bi_1.29Sb_0.7Te_0.01 closely aligns with theoretical predictions (σ ∝ T^1.5 for ionization scattering and σ ∝ T^−1.5 for acoustic phonon scattering) across different temperature ranges. Overall, the simultaneous increase in both n and μ improves the σ significantly, leading to a peak S²σ of about 18.3 μW cm⁻¹ K⁻² at 531 K for x = 0.4, as shown in Fig. 2g. It is evident that a moderate excess of Mg enhances S²σ, while an excessive amount of Mg results in a decrease in μ due to increased impurity levels, lowering S²σ.

Fig. 2h shows the thermal transport properties of Mg_3+xBi_1.29Sb_0.7Te_0.01 (x = 0.2, 0.3, 0.4, and 0.5) samples. Due to the onset of the bipolar thermal diffusion effect, the κ decreases at lower temperatures and then increases at higher temperatures.⁴¹ Notably, in n-type conducting samples, an increase in magnesium content results in an increase in κ, reaching its peak value at x = 0.4. To explain these changes, Fig. S4a and b (ESI†) present the temperature-dependent κ_e and κ_l, respectively. With increasing Mg content, κ_e increases for x = 0.3 to 0.5 and then decreases, closely following the behavior of σ, thus explaining the variations in κ. The observed increase in κ_l may be attributed to the formation of Mg-rich inclusions in certain regions due to excess Mg, which typically have higher κ_l.¹⁹Fig. 2i compares the temperature-dependent ZT values. Due to the significant enhancement of S²σ, the ZT value of Mg_3.4Bi_1.29Sb_0.7Te_0.01 is substantially higher than that of other samples across the entire temperature range. The ZT value reaches a peak of 0.97 at 580 K and 0.21 at room temperature.

Building upon the optimized composition of Mg_3.4Bi_1.29Sb_0.7Te_0.01, further improvements in its thermoelectric performance near room temperature were achieved by fine-tuning the sintering temperature. To examine the phase composition, XRD characterization was performed on bulk samples of Mg_3.4Bi_1.29Sb_0.7Te_0.01 sintered at different temperatures (973, 1023, and 1073 K). Fig. 3a shows the XRD patterns within the 2θ range of 20–60°. Consistent with previous findings, nearly all diffraction peaks correspond to α-Mg₃Bi₂ peaks with the P3̄m1 space group. In Fig. 3b, a magnified view of the XRD patterns reveals that the (101) peak shifts towards higher diffraction angles, indicating a potential shrinkage of the unit cell. To further assess the lattice parameters, Rietveld refinement of the XRD results was conducted, as shown in Fig. 3c. As the sintering temperature increases, the values of a and c decrease from 4.664 and 7.404 Å at 973 K to 4.638 and 7.371 Å at 1073 K. Assuming that the sample composition remains constant, the reduction in lattice constants (unit cell shrinkage) can be attributed to the formation of V_Mg during sintering, as higher sintering temperatures are more likely to induce Mg volatilization, or meet the energy threshold for V_Mg formation.

Fig. 3 Characterization of Mg_3.4Bi_1.29Sb_0.7Te_0.01 fabricated at different hot-press temperatures (973, 1023, and 1073 K). (a) XRD patterns with a 2θ range from 20 to 60°. (b) Magnified XRD patterns with a 2θ range from 20 to 26°. (c) Determined lattice parameters. SEM images of the sample surfaces etched with HNO₃ after hot-pressing at (d) 973 K, (e) 1023 K, and (f) 1073 K. (g–i) Corresponding grain size distributions.

Fig. 3d–i display SEM images of HNO₃-etched sintered samples and corresponding grain size statistics. The increase in sintering temperature results in a significant growth in grain size. The average grain sizes of the samples sintered at 973, 1023, and 1073 K were measured to be 3.19, 7.49, and 8.49 μm, respectively. Additionally, electron backscattered diffraction (EBSD) analysis (Fig. S5, ESI†) confirmed the grain size, showing a trend consistent with the SEM results. Typically, larger grain sizes correspond to a reduction in grain boundary density, which reduces carrier scattering at grain boundaries and subsequently improves μ, enhancing electrical performance. Furthermore, the grain size of the samples sintered at 1073 K showed a minimal increase compared to those sintered at 1023 K. This may be because the grain size of Mg₃(Bi, Sb)₂ is already within the large grain range. Therefore, the increase in sintering temperature is insufficient to significantly promote further grain growth, resulting in a noticeably reduced growth rate. It is important to note that sintering temperatures above 1073 K can cause considerable compositional changes, potentially damaging the samples; therefore, 1073 K was set as the maximum sintering temperature in this study.

We further investigated the micro- and nano-morphological characteristics of the Mg_3.4Bi_1.29Sb_0.7Te_0.01 sample sintered at 1073 K. Fig. 4a presents the X-ray energy spectrometer (EDS) mapping of the main phase elements in the polished bulk sample, revealing a uniform distribution of elements on the micron scale, without significant segregation. Fig. 4b shows an SEM image of the fresh fracture surface of the sample, where a dense layered structure remains visible despite the elevated sintering temperature. Fig. 4c shows a transmission electron microscopy (TEM) image of a focused ion beam (FIB)-cut sample, with a macroscopic image of the FIB sample provided in Fig. S6 (ESI†). Dense nanograins are clearly observed in Fig. 4c, and the corresponding fast Fourier transform (FFT) pattern, shown in Fig. 4d, exhibits the overlapping ring diffraction pattern typical of nanocrystalline polycrystalline materials. Fig. 4e and f present TEM images taken from different sites, demonstrating that nanocrystals within large grains are prevalent throughout the sample. At the nanoscale, lattice defects, such as lattice distortions, are visible, deviating from normal lattice patterns at this sintering temperature. As shown in Fig. 4g, lattice defects at the intersection of the (110) and (102) crystal planes may be attributed to the formation of microscopic dislocations and vacancy accumulations, possibly caused by the loss of specific atoms on these planes (e.g., Mg). Additionally, significant lattice twists and distortions are evident, which induce greater lattice strain, effectively scattering phonons and reducing the κ_l, as seen in Fig. 4h. Fig. 4i shows a grain boundary between nanocrystals, which, although smooth, displays a high degree of misalignment, indicating a relatively disordered orientation between the nanocrystals. These abundant grain boundaries effectively scatter low-frequency phonons, further reducing the κ_l.

Fig. 4 Micro/nanostructural characterization of Mg_3.4Bi_1.29Sb_0.7Te_0.01 fabricated at a hot-press temperature of 1073 K. (a) SEM image of the polished surface and the corresponding X-ray energy spectrometer (EDS) maps of individual elements. (b) SEM image of the fractured surface. (c) Transmission electron microscopy (TEM) image of the sample prepared using the focused ion beam (FIB) technique. (d) Corresponding fast Fourier transform (FFT) pattern. (e and f) TEM images taken from other sites within one sample. (g and h) High-resolution TEM (HRTEM) images showing the lattice distortions. (i) HRTEM image showing the grain boundary.

Fig. 5a and b show the temperature-dependent σ and S of Mg_3.4Bi_1.29Sb_0.7Te_0.01 samples sintered at different temperatures of 973, 1023, and 1073 K. As shown in Fig. 5a, σ continuously decreases with increasing temperature (σ ∝ T^−1.53 below 573 K), exhibiting characteristics of a degenerate semiconductor, where phonon scattering serves as the dominant carrier scattering mechanism. With increasing sintering temperature, the σ near room temperature significantly improves, indicating that higher sintering temperatures enhance near-room-temperature electrical transport. This suggests that reducing grain boundary intensity can effectively prevent carrier scattering in the low-temperature region.⁵⁰ For instance, the σ of the sample sintered at 1073 K increases from 341 to 712 S cm⁻¹ at room temperature, representing an increase of approximately 200%. Noticeable differences in σ between the samples sintered at 973, 1023, and 1073 K are evident near room temperature, whereas the σ values at high temperatures are comparable. This result suggests that in the mid-to-high temperature range, grain boundary scattering diminishes, and phonon scattering becomes one of the primary factors affecting μ. The stability of grain boundaries at high temperatures may also influence scattering effects; for example, grain boundaries might migrate, rearrange, or form new defect structures at high temperatures, potentially altering their scattering capacity. As shown in Fig. 5b, due to the bipolar effect at high temperatures, the S initially increases and then decreases with rising temperature. A slight increase in S is visible with increasing sintering temperature. Therefore, the S²σ is greatly enhanced in the near-room-temperature region (Fig. 5c). At room temperature, the S²σ of the sample sintered at 973 K is only 6.61 μW cm⁻¹ K⁻², while the S²σ of the sample sintered at 1073 K increases to 16.84 μW cm⁻¹ K⁻², representing an increase of approximately 254%.

Fig. 5 Thermoelectric performance of Mg_3.4Bi_1.29Sb_0.7Te_0.01, fabricated at different hot-press temperatures of 973, 1023, and 1073 K. Temperature-dependent (a) electrical conductivity (σ) and (b) Seebeck coefficient (S), and (c) S²σ. Room-temperature (d) carrier concentration (n) and mobility (μ) and (e) effective mass (m*). Temperature-dependent (f) κ, (g) electrical thermal conductivity (κ_e), (h) lattice thermal conductivity (κ_l), and (i) ZT.

To understand the variations in electrical properties, Fig. 5d presents the room-temperature n and μ. As the sintering temperature increases, the room-temperature μ values of the samples sintered at 1023 K and 1073 K are significantly higher than that of the sample sintered at 973 K. For example, at room temperature, μ increases from 10 cm² V⁻¹ s⁻¹ at 973 K to 145 cm² V⁻¹ s⁻¹ at 1023 K and 204 cm² V⁻¹ s⁻¹ at 1073 K. This improvement is primarily attributed to the reduction in grain boundary scattering for the carriers, despite a decrease in n due to the increase in V_Mg caused by the higher sintering temperatures. As shown in Fig. 5e, the increase in sintering temperature also results in a reduction in the effective mass (m*) of the carriers, as calculated using the single parabolic band (SPB) model.⁵¹ This is largely due to the decrease in n, further suggesting that no significant energy filtering effect is present. Consequently, with the improvement in μ, σ increases significantly, leading to a marked enhancement in S²σ.

Fig. 5f–h show the temperature-dependent κ, κ_e, and κ_l for the Mg_3.4Bi_1.29Sb_0.7Te_0.01 samples sintered at 973, 1023, and 1073 K, respectively. The κ_e was estimated using the Wiedemann–Franz law (κ_e = LσT), where L represents the Lorenz number estimated using the single parabolic band (SPB) model.⁵² As shown in Fig. 5g, the temperature-dependent κ_e increases, primarily due to the corresponding increase in σ. Fig. 5h illustrates that as the sintering temperature increases, the κ_l also shows a noticeable increase. This can be attributed to the increase in grain size, where the reduction in grain boundary intensity weakens phonon scattering. Additionally, a crossover is observed in the κ_l region beyond 632 K. This phenomenon can be attributed to the higher carrier concentration in the sample sintered at 973 K, which results in a more pronounced bipolar thermal effect, thereby increasing its κ_l. Overall, the increase in sintering temperature slightly increases the κ, as depicted in Fig. 5f. However, despite this increase in κ, the S²σ significantly improves, leading to a notable enhancement in the near-room-temperature ZT values for the samples sintered at 1023 K and 1073 K. Fig. 5i shows the temperature-dependent ZT values, with the ZT reaching 0.5 at room temperature, an improvement of 238%. The peak ZT remains high at 531 K, approaching a value of 0.9. Meanwhile, the samples have demonstrated excellent thermal cycling stability, showing no significant changes in performance after 20 cycles of testing. Regarding chemical stability, the samples exhibit relative stability in air but show sensitivity to water, as detailed in Fig. S7–S10 in the ESI.†

Conclusion

This study utilized a two-step method to progressively enhance the thermoelectric performance of Mg₃Bi₂-based materials over a broad temperature range near room temperature. First, by adjusting the excess Mg content, we achieved a transition from p-type to n-type conduction while optimizing n and μ, leading to a significant increase in ZT, with a peak ZT value of ∼1 at 573 K. In the second step, we fine-tuned the sintering temperature during the high-temperature sintering process, engineering a microstructure that increased grain size without altering the system's composition. This further improved electron mobility near room temperature. Consequently, the ZT value at 323 K rose from 0.2 to nearly 0.5, with a peak ZT close to 0.9 at 500 K. This work provides valuable insights for optimizing the preparation of Mg₃Bi₂-based materials and serves as a useful reference for future improvement strategies.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Foundation of Shaanxi University of Science & Technology (Grant No. 2017GBJ-03). The authors are thankful for the financial support from the Australian Research Council, and QUT Capacity Building Professor Program, and acknowledge the National Computational Infrastructure, supported by the Australian government, for providing computational resources and service. This work was enabled by the use of the Central Analytical Research Facility hosted by the Institute for Future Environments at QUT. The authors acknowledge the support from the Xi'an International Science and Technology Cooperation Base of Semiconductor Thermoelectric Materials and Devices.

References

1. J. He and T. M. Tritt, Science, 2017, 357, eaak9997.
2. Y. Xiao and L.-D. Zhao, Science, 2020, 367, 1196–1197.
3. Q. Yang, S. Yang, P. Qiu, L. Peng, T.-R. Wei, Z. Zhang, X. Shi and L. Chen, Science, 2022, 377, 854–858.
4. B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, J. Pennycook Stephen and J. He, Science, 2021, 371, 830–834.
5. W. Chen, X.-L. Shi, M. Li, T. Liu, Y. Mao, Q. Liu, M. Dargusch, J. Zou, G. Q. M. Lu and Z.-G. Chen, Science, 2024, 386, 1265–1271.
6. T.-R. Wei, P. Qiu, K. Zhao, X. Shi and L. Chen, Adv. Mater., 2023, 35, 2110236.
7. Q.-X. Hu, W.-D. Liu, L. Zhang, H. Gao, D.-Z. Wang, T. Wu, X.-L. Shi, M. Li, Q.-F. Liu, Y.-L. Yang and Z.-G. Chen, Adv. Energy Mater., 2024, 14, 2401890.
8. M. Rakshit, D. Jana and D. Banerjee, J. Mater. Chem. A, 2022, 10, 6872–6926.
9. J. Sun, Y. Zhang, Y. Fan, X. Tang and G. Tan, Chem. Eng. J., 2022, 431, 133699.
10. X. Zhang, Z. Bu, S. Lin, Z. Chen, W. Li and Y. Pei, Joule, 2020, 4, 986–1003.
11. H. Lai, Y. Peng, M. Wang, R. Shi, J. Chen, C. Liu, Y. Wang, L. Miao and H. Wei, J. Adv. Ceram., 2023, 12, 228–241.
12. G. Rogl and P. F. Rogl, Crystals, 2023, 13, 1152.
13. X.-L. Shi, J. Zou and Z.-G. Chen, Chem. Rev., 2020, 120, 7399–7515.
14. Z. Zhou, G. Han, X. Lu, G. Wang and X. Zhou, J. Magnesium Alloys, 2022, 10, 1719–1736.
15. X. Chen, H. Wu, J. Cui, Y. Xiao, Y. Zhang, J. He, Y. Chen, J. Cao, W. Cai, S. J. Pennycook, Z. Liu, L.-D. Zhao and J. Sui, Nano Energy, 2018, 52, 246–255.
16. L. Wu, Z. Zhou, G. Han, B. Zhang, J. Yu, H. Wang, Y. Chen, X. Lu, G. Wang and X. Zhou, Chem. Eng. J., 2023, 475, 145988.
17. K. Imasato, M. Wood, S. Anand, J. J. Kuo and G. J. Snyder, Adv. Energy Sustainability Res., 2022, 3, 2100208.
18. H. Tamaki, H. K. Sato and T. Kanno, Adv. Mater., 2016, 28, 10182–10187.
19. K. Imasato, S. Ohno, S. D. Kang and G. J. Snyder, APL Mater., 2018, 6, 016106.
20. P. Ying, L. Wilkens, H. Reith, N. P. Rodriguez, X. Hong, Q. Lu, C. Hess, K. Nielsch and R. He, Energy Environ. Sci., 2022, 15, 2557–2566.
21. J.-W. Li, Z. Han, J. Yu, H.-L. Zhuang, H. Hu, B. Su, H. Li, Y. Jiang, L. Chen, W. Liu, Q. Zheng and J.-F. Li, Nat. Commun., 2023, 14, 7428.
22. L. Wang, W. Zhang, S. Y. Back, N. Kawamoto, D. H. Nguyen and T. Mori, Nat. Commun., 2024, 15, 6800.
23. X. Shi, X. Zhang, A. Ganose, J. Park, C. Sun, Z. Chen, S. Lin, W. Li, A. Jain and Y. Pei, Mater. Today Phys., 2021, 18, 100362.
24. K. Imasato, S. D. Kang, S. Ohno and G. J. Snyder, Mater. Horiz., 2018, 5, 59–64.
25. M. Wood, J. J. Kuo, K. Imasato and G. J. Snyder, Adv. Mater., 2019, 31, 1902337.
26. T. Luo, J. J. Kuo, K. J. Griffith, K. Imasato, O. Cojocaru-Mirédin, M. Wuttig, B. Gault, Y. Yu and G. J. Snyder, Adv. Funct. Mater., 2021, 31, 2100258.
27. Z. Liang, C. Xu, H. Shang, M. Ning, T. Tong, S. Song, W. Ren, X. Shi, X. Liu, F. Ding, J. Bao, D. Wang and Z. Ren, Adv. Energy Mater., 2023, 13, 2301107.
28. J. Lei, K. Zhao, J. Liao, S. Yang, Z. Zhang, T.-R. Wei, P. Qiu, M. Zhu, L. Chen and X. Shi, Nat. Commun., 2024, 15, 6588.
29. J. Zhang, L. Song, K. A. Borup, M. R. V. Jørgensen and B. B. Iversen, Adv. Energy Mater., 2018, 8, 1702776.
30. X. Mo, J. Liao, G. Yuan, S. Zhu, X. Lei, L. Huang, Q. Zhang, C. Wang and Z. Ren, J. Magnesium Alloys, 2022, 10, 1024–1032.
31. X. Shi, T. Zhao, X. Zhang, C. Sun, Z. Chen, S. Lin, W. Li, H. Gu and Y. Pei, Adv. Mater., 2019, 31, 1903387.
32. J. Zhang, L. Song and B. B. Iversen, Angew. Chem., Int. Ed., 2020, 59, 4278–4282.
33. K. Imasato, M. Wood, J. J. Kuo and G. J. Snyder, J. Mater. Chem. A, 2018, 6, 19941–19946.
34. J. Zhang, L. Song and B. B. Iversen, Adv. Sci., 2020, 7, 2002867.
35. T. Kanno, H. Tamaki, H. K. Sato, S. D. Kang, S. Ohno, K. Imasato, J. J. Kuo, G. J. Snyder and Y. Miyazaki, Appl. Phys. Lett., 2018, 112, 033903.
36. S. Chen, J. Wei, Z. Kang, X. Miao, D. An, W. Fan and C. Dun, Chem. Eng. J., 2024, 490, 151404.
37. K. Imasato, S. D. Kang and G. J. Snyder, Energy Environ. Sci., 2019, 12, 965–971.
38. J. Mao, H. Zhu, Z. Ding, Z. Liu, G. A. Gamage, G. Chen and Z. Ren, Science, 2019, 365, 495–498.
39. Z. Liang, C. Xu, H. Shang, Q. Zhu, F. Ding, J. Mao and Z. Ren, Mater. Today Phys., 2021, 19, 100413.
40. Z. Liu, W. Gao, H. Oshima, K. Nagase, C.-H. Lee and T. Mori, Nat. Commun., 2022, 13, 1120.
41. N. Qu, Y. Zhu, J. Zhu, K. Yu, F. Guo, Z. Liu, Q. Zhang, W. Cai and J. Sui, J. Magnesium Alloys, 2024, 12, 4538–4546.
42. H. Cho, S. Y. Back, N. Sato, Z. Liu, W. Gao, L. Wang, H. D. Nguyen, N. Kawamoto and T. Mori, Adv. Funct. Mater., 2024, 34, 2407017.
43. X. Li, C. Sun, K. Yang, D. Liang, X. Ye, W. Song, W. Xu, W. Zhao and Q. Zhang, Small, 2024, 20, 2311478.
44. K. Yang, X. Li, C. Sun, W. Song, W. Zhao and Q. Zhang, Adv. Funct. Mater., 2024, 34, 2315886.
45. L. Yin, C. Chen, F. Zhang, X. Li, F. Bai, Z. Zhang, X. Wang, J. Mao, F. Cao, X. Chen, J. Sui, X. Liu and Q. Zhang, Acta Mater., 2020, 198, 25–34.
46. M. Ozen, M. Yahyaoglu, C. Candolfi, I. Veremchuk, F. Kaiser, U. Burkhardt, G. J. Snyder, Y. Grin and U. Aydemir, J. Mater. Chem. A, 2021, 9, 1733–1742.
47. C. Xu, M. Jian, Z. Liang, B.-H. Lei, S. Song, F. Zhang, D. J. Singh, Z. Feng and Z. Ren, Nano Energy, 2023, 106, 108036.
48. J.-S. Liang, X.-L. Shi, Y. Peng, W.-D. Liu, H.-Q. Yang, C.-Y. Liu, J.-L. Chen, Q. Zhou, L. Miao and Z.-G. Chen, Adv. Energy Mater., 2022, 12, 2201086.
49. S. Ohno, K. Imasato, S. Anand, H. Tamaki, S. D. Kang, P. Gorai, H. K. Sato, E. S. Toberer, T. Kanno and G. J. Snyder, Joule, 2018, 2, 141–154.
50. J. J. Kuo, S. D. Kang, K. Imasato, H. Tamaki, S. Ohno, T. Kanno and G. J. Snyder, Energy Environ. Sci., 2018, 11, 429–434.
51. J. Zhu, X. Zhang, M. Guo, J. Li, J. Hu, S. Cai, W. Cai, Y. Zhang and J. Sui, Npj Comput. Mater., 2021, 7, 116.
52. H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08026b

‡ These two authors contribute equally.

---