Structural evolution of Prussian blue analogues A_xMFe(CN)₆ upon intercalation of Na and K

Abstract

Prussian blue analogues (PBAs) are promising cathode candidates for sodium-ion and potassium-ion batteries; however, the complicate phase transitions occurring during charge/discharge affect intercalation dynamics and long-term stability. We discuss the structural evolution using hybrid-exchange DFT calculations to provide a theoretical foundation for the structural distortions in PBAs. The fully optimized geometries of PBAs A_xMFe(CN)₆ with different alkali metals (A = Na, K), transition metals (M = Mn, Fe) and intercalation levels (x) are compared and analysed through ligand field theory. The results evidence a 2-D like distortion of the hexacyanoferrate framework at low intercalation levels, and a 3-D like distortion at high concentrations, with stable superstructural arrangements of the intercalated ions. The correlations between framework distortion and the position of alkali metal ions are elucidated and rationalised by considering the combined effect of ionic sizes and the transition metal redox sequence.

---

1 Introduction

Prussian blue analogue (PBA) materials, built on the hexacyanoferrate [Fe^(II)(CN)₆]⁴⁻ metal complex, contain redox-active transition metal ions embedded in a flexible framework with tuneable structure, composition and properties. They have attracted attention for multiple application areas, such as beyond-lithium-ion batteries,^1,2 (electro-)catalysis³ and gas storage.^4,5 The most general composition of PBAs can be expressed as A_xM[′(CN)₆]_1−y·y□·zH₂O where M and M′ are transition metal (TM) ions that build a three-dimensional network of octahedral sites, corner-sharing through the cyano ligands; this framework may enclose intercalated species A that can be alkali or multivalent ions as well as molecular species, while the symbol □ represents [M′(CN)₆] vacancies. H₂O can be present either directly bonded to the M ions adjacent to the [M′(CN)₆] vacancies or in the interstices containing the A species, respectively termed coordinated or zeolitic water. In this work we consider the effect of intercalation and transition metal type on the structure of PBA materials without vacancies and water, whose composition can therefore be expressed as A_xM[M′(CN)₆].

PBAs are metal–organic framework analogues of double-perovskites A₂BB′X₆, where the mononuclear anions X are replaced by cyano ligands. The two transition metal ions are coordinated end-on with the C or N side of the CN⁻ ligands, generating different ligand fields and yielding a low-spin (LS) electronic configuration for the C-coordinated M′ site and a high-spin (HS) electronic state for the N-coordinated M, respectively.⁶ As for (double) perovskites, the regiotype PBA structure is cubic, with an FCC crystallographic unit cell containing 4 M and 4 M′ sites. The M[M′(CN)₆] framework provides loose migration channels along the 〈100〉 direction (∼3.2 Å in diameter, depending on the metal ions employed) and interstitial sites (∼4.6 Å in diameter) for (de-)intercalation of both cations and molecular species. The robust perovskite-like structure of PBAs ensures long lifetime stability as batteries cathodes. However, the easy replacement of transition metals in PBAs leads to not only tuneable redox behaviour but also complex structural distortions.¹ The effect of ionic sizes on structural distortions in ABX₃ perovskites is well captured by the Goldschmidt tolerance factor 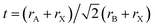;⁷ given the much larger size of the A sites in PBAs compared to perovskites, all PBA compounds with monoatomic intercalants have t < 1 and undergo distortions corresponding to octahedral tilting, that can be described using the Glazer notation.⁸ In addition to forming larger voids for intercalation, the diatomic CN molecular bridge between metal sites provides a “double hinge” link between octahedra that can bend at both the C and N sites and potentially extend the structural distortion possibilities available for traditional perovskites.

The structural evolution behaviour of PBAs was studied under various conditions. The negative thermal expansion (NTE) of MPt(CN)₆ (M = Mn, Fe, Co, Ni, Cu, Zn, Cd) reveals the relationship between PBA framework flexibility and transition metal M radius along with temperature change.⁹ Boström reported the F4̄3m → P4̄n2 → Pn phase transition for AMnCo(CN)₆ (A = Rb or Cs) at different pressures. The larger Cs induces a higher phase transition pressure than the smaller Rb. The effect of vacancies and water on the Fm3̄m to R3̄ phase transition pressure was also discussed.¹⁰ The phase transitions from high symmetry cubic (Fm3̄m and F4̄3m) to P4̄n2 and R3̄ are induced by octahedral tilting corresponding to Glazer notations a⁰a⁰c⁺ and a⁻a⁻a⁻, respectively.

When employed as a battery cathode material, the concentration (x) of alkali metal ions in A_xM[M′(CN)₆] cycles between 0 and 2, corresponding to the fully deintercalated (charged) and intercalated (discharged) state, respectively. In fully deintercalated PBAs [MM′(CN)₆], the M–N–C–M′ units are straight, i.e. there is no tilting of MN₆ or M′C₆ octahedra, corresponding to Glazer notation a⁰a⁰a⁰. Upon intercalation, octahedra in A_xMM′(CN)₆ (0 < x < 2) tilt and thus result in a phase transition from cubic or tetragonal to monoclinic and rhombohedral.¹¹ Because of the variable concentration of intercalants, x, during battery cycling applications, the effect of intercalation on the PBA structure deserves attention. Beyond relative ionic sizes, factors that determine the structural transition during intercalation include Coulomb interactions between the intercalated ions and the cyano ligands as well as ligand field theory and covalent bond strength between the two TMs and the cyano ligands.¹² At low concentration x, the intercalant interaction with the M–N–C–M′ framework is not strong enough to induce a phase transition for the entire structure, which results in a straight M–N–C–M′ framework (no octahedral tilting, a⁰a⁰a⁰) or only local octahedral tilting.¹³ However, structural distortions of PBAs at low concentrations (0 < x ≤ 1) have not been explained sufficiently. There is no mechanism to predict and explain stable positions of interstitial cations in PBAs at low concentrations.

In this work, we study Fe-containing PBAs A_xMFe(CN)₆ with different HS transition metals (M = Mn or Fe), interstitial cation types (A = Na or K) and concentrations (x). We only consider defect-free PBA frameworks, without hexacyanoferrate vacancies or coordinated water, to focus on the intrinsic distortions of the PBA framework upon intercalation. The similarities and differences of the above PBAs in the fully (de-)intercalated state are discussed first. We then examine the dependence of structural distortion and alkali metal position at low concentrations (0 < x ≤ 1). Our finding reveals how the PBAs framework distortions are affected by the alkali metal and transition metal types at low concentrations.

2 Computational details

DFT calculations were performed using the CRYSTAL17 package.¹⁴ The crystallographic unit cell, comprising four A_xMFe(CN)₆ (A = Na or K and M = Fe or Mn) formula units, i.e., a cell containing 8 A sites was used for all calculations, with periodic boundary conditions. All structures have been fully geometry optimized using the P₁ space group to avoid any symmetry constraint. A selected number of geometry optimizations have been followed by calculations of Γ-point phonons in the harmonic approximation, to ensure the dynamic stability of the structures identified. Indeed, none of the phonon calculations produced imaginary modes; a representative example of phonon calculation output is reported in Table S1.† At the end of the geometry optimisation, the structures were analysed using the FINDSYM program of the ISOTROPY Software Suite,¹⁵ to identify their space group.

Electronic exchange and correlation were described using the PBE0 hybrid-exchange functional, which includes 1/4 Hartree–Fock (HF) exchange to attenuate the self-interaction error (SIE) in the open-shell TM ions.¹⁶ Commensurate grids for reciprocal space integration were generated by the Pack–Monkhorst method with shrinking factor IS = 4. Density of States (DOS) plots were calculated using a denser k-point grid (shrinking factor IS = 8). The default values were used for the truncation of bielectronic integrals (corresponding to TOLINTEG = 7 7 7 7 14), SCF convergence and geometry optimizations. All-electron basis sets of triple zeta plus polarization quality were used for all atoms, retrieved from the CRYSTAL online database using the following tags: (C_m-6-311G(d)_Heyd_2005),¹⁷, (N_m-6-311G(d)_Heyd_2005),¹⁷ (Na_8-511 G_dovesi_1991),¹⁸ (K_86-511 G_dovesi_1991),¹⁸ (Mn_86-411d41 G_towler_1992),¹⁹ and (Fe_86-411d41 G_towler_1992a).²⁰ When multiple open-shell ions are present, only the ferromagnetic spin arrangement was considered.

To investigate the structure stability and mechanistic details of intercalation/deintercalation processes, all inequivalent configurations of the Na and K intercalants at each concentration x were calculated, corresponding to different arrangements of the alkali metal ions in the 8 available sites, to determine the presence of stable superlattice structures of intermediate composition. The relative energy ΔE_AxMFe(CN)6 of each configuration is compared with a weighted average of fully deintercalated and intercalated PBAs, using the equation below:

where E(A_xMFe(CN)₆), E(A₀MFe(CN)₆) and E(A₂MFe(CN)₆) are the calculated energies of composition A_xMFe(CN)₆, fully deintercalated and fully intercalated PBAs, respectively. Examining the convex-hull behaviour of ΔE_AxMFe(CN)6 as a function of x indicates whether intermediate compositions of particular stability are expected to occur during the (de-)intercalation process.

3 Results

Before discussing the results of our calculations, we introduce the nomenclature that we employ in this section of the paper. To classify the different intercalation sites of the PBA lattice we refer to the regiotype Fm3̄m structure. The fundamental units of the A_xMFe(CN)₆ PBA structure, suitable for describing intercalation, are the M₄Fe₄(CN)₁₂ “sub-cubes” formed by alternate HS-M and LS-Fe sites at the corners, with CN⁻ ligands along the sides. One such sub-cube is shaded in Fig. 1. Each sub-cube encompasses one intercalation site A.

Fig. 1 Schematic of the cubic A_xMFe(CN)₆ structure, with labelling of the intercalation sites employed in this work. Sub-cube and window secondary building units are highlighted.

Adjacent sub-cubes along the 〈100〉, 〈010〉 and 〈001〉 directions are separated by “windows” formed by four Fe–C–N–M sides, as shown in Fig. 1. Migration of the intercalant A between adjacent sub-cubes occurs through one of these windows. Within each sub-cube, the actual location of the intercalant A can vary and occurs either at the centre or displaced along high symmetry directions; these are denoted using the Wyckoff notation of the different sites in the Fm3̄m cell. The centre of the sub-cube is surrounded by 12 equidistant CN ligands and is denoted as the 8c site. If the A ions displace from 8c sites along the 〈111〉 direction towards either the C-coordinated LS-Fe or the N-coordinated HS-TM they occupy 32f and 32f′ sites, respectively. The centre of the windows is indicated as 24d, while the sites between the centre of the sub-cube (8c) and the centre of the windows (24d) are labelled as 48g.

Two main types of structural distortions may occur in PBAs: one driven by the electronic configuration of the TM ions that may undergo Jahn–Teller (J–T) like distortions as discussed in the framework of ligand field theory, and another associated with tilting of the octahedra associated with steric and Coulomb interactions of the intercalated A ions – mostly with the cyano ligands of the PBA framework. Their relative importance, and hence the equilibrium structure of the PBA material overall, depends on the type of TM ions (M and Fe here) and the type and concentration of intercalated species (A, x).

We start our discussion of DFT results with two model systems: the intercalant-free material with x = 0, which is subject to only J–T like distortions, and the A₂MnFe(CN)₆ compound where neither the HS-Mn^II nor the LS-Fe^II ions are J–T distorted; hence distortions are only due to the presence of the A ions.

3.1 Fully deintercalated MFe(CN)₆

In the optimised structure, the fully deintercalated PBAs FeFe(CN)₆ and MnFe(CN)₆ have straight Fe–C–N–Mn linkages. This geometry maximises orbital overlap in the hexacyanoferrate ion [Fe^II(CN)₆]⁴⁻ and enhances the Coulomb interaction between the N end of the hexacyanoferrate ions and the second TM site. No tilting of FeC₆ or MN₆ octahedra occurs, corresponding to Glazer notation a⁰a⁰a⁰. No alkali metal ions are present to interact with the cyano ligands and disturb this high-symmetry arrangement. The equilibrium geometry of FeFe(CN)₆ is Fm3̄m, corresponding to a cubic crystal system (Fig. 2a). However, MnFe(CN)₆ exhibits a tetragonal I4/mmm space group as shown in Fig. 2b. The d⁴ high-spin electronic configuration of trivalent Mn causes an elongation of the axial bonds in MnN₆ octahedra due to a pronounced J–T distortion, which results in different Mn–N bond lengths (2.21 Å and 1.96 Å, respectively) and lattice parameters (c = 10.60 Å and a = b = 10.06 Å) along the z-axis compared to the xy-plane. Although low-spin trivalent Fe exhibits a small J–T effect arising from the t_2g states, it is not strong enough to induce appreciable distortions and FeFe(CN)₆ retains its cubic symmetry. The lattice parameters and bond lengths of FeFe(CN)₆ and MnFe(CN)₆ are compared in Table 1. The square window of FeFe(CN)₆ is bigger than the windows in the xy plane and smaller than those in the xz and yz planes of MnFe(CN)₆. The size of the window surrounded by four octahedra is critical in determining ion mobility during charge/discharge and the stable position of alkali metal ions at low concentrations.

Fig. 2 Optimized geometry of (a) FeFe(CN)₆ and (b) MnFe(CN)₆ and d orbital electron configurations of LS-Fe, HS-Fe and HS-Mn.

Table 1 Equilibrium lattice parameters, volume per formula unit and bond lengths in intercalant-free MFe(CN)₆

	FeFe(CN)6	MnFe(CN)6
Space group	Fm3̄m	I4/mmm
a = b (Å)	10.28	10.06
c (Å)		10.60
α = β = γ (°)	90	90
Volume (Å^3 per f.u.)	271.74	268.46
Fe–C (in xy plane) (Å)	1.92	1.91
Fe–C (in z plane) (Å)		1.93
M–N (in xy plane) (Å)	2.06	1.96
M–N (in z plane) (Å)		2.21

---

3.2 Fully intercalated A₂MFe(CN)₆

We first consider the Mn compounds A₂MnFe(CN)₆, where neither N-coordinated divalent Mn (d⁵, HS) nor C-coordinated divalent Fe (d⁶, LS) is expected to incur J–T distortion. Indeed, all our geometry optimisations result in octahedra with six identical Fe–C or Mn–N bond distances. A summary of the calculated equilibrium structural parameters for the fully intercalated compounds is reported in Table 2.

Table 2 Lattice parameters, volume per formula unit, M–N–C angle and Fe–C and M–N bond lengths of fully intercalated PBAs A₂MFe(CN)₆ (A = Na or K and M = Mn or Fe) with the space group P2₁/c (including two formula units)

	K2FeFe(CN)6	Na2FeFe(CN)6	K2MnFe(CN)6	Na2MnFe(CN)6
a (Å)	6.91	6.58	6.95	6.62
b (Å)	7.29	6.93	7.34	6.96
c (Å)	12.13	11.70	12.20	11.79
β (°)	124.05	123.96	124.24	124.00
Volume (Å^3 per f.u.)	253.42	221.44	257.14	225.35
∠M–N–C (°)	149	134	146	133
Fe–C (Å)	1.89	1.88	1.89	1.88
M–N (Å)	2.17	2.18	2.23	2.23

---

When all the sub-cubes are occupied by K, corresponding to the composition K₂MnFe(CN)₆, a combination of octahedral tilting and alkali metal displacements results in a phase transition from cubic to monoclinic, with the space group P2₁/c. The tilting of the octahedra can be described by Glazer notation a⁻a⁻c⁺, which means that the octahedra rotate along all three x, y, and z axes, with two out-of-phase and one in-phase tilting, as shown in Fig. 3b and c. The Fe–C–N–Mn framework bends almost exclusively at the N atom position; the Fe–C–N angles show small changes (within 3° variation from 180°), while all the Mn–N–C angles decrease from 180° to ∼146°. The K ions displace from the centre of the sub-cubes (position 8c) along the 〈111〉 direction towards Mn, into positions 32f′. When Na is intercalated, no significant differences in Fe–C and M–N bond lengths are observed compared to the K-intercalated PBA as both TM sites have the same d orbital electron configuration. However, tilting becomes more obvious with Mn–N–C angles of ∼133°, which results in smaller lattice parameters and volume compared to the K-intercalated PBAs. This is consistent with the tilting angle prediction based on the Goldschmidt tolerance.

Fig. 3 (a) Optimised geometry of K₂MnFe(CN)₆, space group P2₁/c. (b) Views of out-phase tilting and (c) in-phase tilting of octahedra in K₂MnFe(CN)₆ along different axes.

In K₂FeFe(CN)₆, the Fe–C–N–Fe framework distortion is similar to that discussed for K₂MnFe(CN)₆, with Mn–N–C angles of 149° and only minor deviations in the Fe–C–N angle. A small J–T distortion in N-coordinated divalent Fe (d⁶, HS) causes a very small difference in Fe–N bond lengths (2.17 Å in the xy plane and 2.18 Å along the z axis, respectively). Similar to the Mn PBA, upon replacing K with Na there are no significant differences in Fe–C and Fe–N bond lengths but tilting becomes more pronounced, resulting in Fe–N–C angles of ∼134°.

In brief, the Fe–C and M–N bond lengths are affected by the transition metal valence and d orbital electron configurations, while the size of the interstitial ions leads to significant volumetric changes due to different degrees of octahedral tilting, occurring almost exclusively at the N angles.

Since both the tilting of octahedra and the displacement of the intercalated ions have components in all three x, y, z directions, we identify the distortion in fully intercalated PBAs as three-dimensional (3-D).

3.3 Partially intercalated A_xMFe(CN)₆ (50%, 25% and 12.5% occupation)

Despite the FeFe(CN)₆ and MnFe(CN)₆ host compounds exhibiting similar geometry in their fully (de-)intercalated states, the sequence of redox processes accompanying intercalation occurs differently in the two materials. Two redox couples are available: Fe²⁺/Fe³⁺ at the C-coordinated LS-Fe site that is common to both compounds, and M²⁺/M³⁺ at the N-coordinated HS site that is different in the Fe and Mn compounds examined. The order in which the two metal sites are oxidised upon removal of Na and K intercalants can be determined by examining the local density of states (LDOS) at the two transition metal sites in the fully intercalated state. The examples of K₂MFe(CN)₆ are shown in Fig. 4. The first metal ion to be oxidised is the one whose occupied d levels are closest to the Fermi level. In K₂FeFe(CN)₆ these correspond to the minority spin t_2g states of the HS-Fe^II (N-coordinated) ion, while in K₂MnFe(CN)₆, electrons at the top of the valence band reside in the fully occupied t_2g states of LS-Fe^II (C-coordinated). These electrons are the first to be extracted during depotassiation; hence oxidation occurs first at HS-Fe in K₂FeFe(CN)₆ and at LS-Fe in K₂MnFe(CN)₆. In the half-intercalated state, corresponding to x = 1, the 3+ TM site is therefore N-coordinated in A₁FeFe(CN)₆ and C-coordinated in A₁MnFe(CN)₆. This will likely affect the stable intercalation sites and lattice distortions, as the cationic intercalants Na⁺ and K⁺ have different Coulomb interactions with the 2+ and 3+ TM sites, which are located on opposite sides in the two frameworks.

Fig. 4 Total and atom-projected density of states (DOS) for (a) K₂FeFe(CN)₆ and (b) K₂MnFe(CN)₆.

Let us consider the stable structure of the two PBA frameworks at the 50% intercalation level, corresponding to the composition A₁MFe(CN)₆. With only 4 of the 8 available sub-cubes in the crystallographic PBA cell being occupied, several different configurations are possible. These have all been considered for each combination of A (Na and K) and M (Mn and Fe) ions, and in the following we examine those with lowest calculated energy.

In all the stable structures, the position of the intercalated A⁺ ions is displaced from the 8c centre of the sub-cubes towards the 24d sites (centre of the windows), i.e. in positions 48g, as shown in Fig. 5a, d, g and j. How close the A⁺ ions are to the plane of the window depends on the actual size of the intercalant and of the two TM ions (which in turn determines the size of the window). The smaller Na is located much closer to the window plane, with distances of ∼0 Å and 0.49 Å in the Na₁MnFe(CN)₆ and Na₁FeFe(CN)₆ frameworks, compared to the larger K, whose respective distances are of 1.6 Å and 2.0 Å. The difference between the Mn- and Fe-containing PBAs is due to the longer Fe–Mn distances (∼5.28 Å) compared to Fe–Fe (∼5.08 Å). Therefore, at a 50% intercalation level, the intercalants displace towards the windows and the distance of the alkali metal ions from the window plane is determined by the relative sizes of the alkali metal ions and window.

Fig. 5 Side views and top views of partially intercalated A_xMFe(CN)₆ (A = Na or K, M = Mn or Fe) with x = 1 (a, d, g and j); x = 0.5 (b, e, h and k); x = 0.25 (c, f, i and l).

Once in proximity of the window, the alkali metal ions induce Fe–CN–M framework distortions, due to the strong Coulomb interaction between the positive metal ions and the N atoms that represent the negative pole of the cyano ligands. This interaction rotates the four octahedra that define the window in such a way that the four nearest N atoms displace towards the alkali metal ions in the 24d/48g sites. The distortion occurs exclusively within the plane of the window that hosts the intercalated ion, without significantly affecting the cyano ligands along the perpendicular axis. Since both alkali metal displacement and octahedral tilting occur along the same direction, we refer to this perturbation of the PB framework as a two-dimensional (2-D) distortion.

A closer inspection of the in-plane octahedral tilting, shown in Fig. S1,† indicates that the tilting around one A⁺ intercalant, causes the adjacent windows to become unstable for intercalation. Each cyano ligand represents the edge between two adjacent windows in the 〈001〉 plane; displacement of the N-end of the ligand in one direction to maximise the interaction with the A⁺ ion in position 24d/48g automatically prevents displacement in the opposite direction. Half intercalation (x = 1) is therefore the highest concentration at which alkali metals occupy 24d/48g sites and form a 2D distorted structure, in a chessboard-like arrangement. In addition to occupying only alternate 24d/48g sites, in the lowest energy structure, the intercalated alkali metal ions are distributed on alternate sides of the window-plane, in such a way as to reduce the mutual Coulomb repulsion.

Reducing the intercalant content further to 25% occupation, corresponding to the composition A_0.5MFe(CN)₆, stable superstructural arrangements in the distribution of the occupied sub-cubes become even more apparent. While in A₁MFe(CN)₆ all sites of each TM sublattice have the same oxidation state, in A_0.5MFe(CN)₆ only half the metal sites of one sublattice (LS-Fe for M = Fe; HS-Mn for M = Mn) are oxidised to the 3+ state, the other half retaining in the 2+ oxidation state. These structures retain the 2D intercalation and distortion pattern discussed above for the materials with 50% occupation, but they contain alternate layers with LS-Fe or HS-Mn ions in 2+ and 3+ oxidation states, respectively, as shown in Fig. 5b. HS-Mn^III is strongly J–T distorted, and windows containing Mn^III at one of the vertices can be built on the long or short Mn–N bonds. Intercalation of both Na and K occurs in the larger windows that contain the long Mn–N bonds, oriented in the 〈100〉 or 〈010〉 directions (the 〈010〉 direction is illustrated in Fig. 5 and referred to in the following discussion). The alkali metal ions move closer to the square window plane of the reduced layer due to the balance of Coulomb interactions. Therefore, we observe a close association between the positions of the intercalated ions and the reduced TM sites.

The Fe–C and Fe–N bond distances show limited variation between 2+ and 3+ oxidation states, which induces little structural strain at 25% concentration of the intercalants when alternating planes with 2+ and 3+ Fe are present. For Mn-HS instead, the Mn–N bond distances from the metal in 2+ and 3+ oxidation states are significantly different. In Na_0.5MnFe(CN)₆, Mn^II has nearly identical Mn–N bond distances of ∼2.2 Å in all three directions; J–T distorted Mn^III, instead, has long Mn–N bonds of 2.2 Å along the z direction and short bonds of ∼2.0 Å in the xy-plane. The alternation of planes with 2+ and 3+ Mn ions in the stable configuration of the intercalated Na and K ions, therefore, creates a structural strain in the 〈100〉 direction connected by alternate long and short Mn–N bonds. This strain is accommodated through a rotation of the Mn₆ octahedra around the z axis as shown in Fig. 5h and k. This new tilting distortion in materials with mixed-valence Mn ions is not due to the size mismatch between the intercalant radius and size of the interstices available, but rather due to the size mismatch between the different octahedral sites in the same TM sublattice. Such a distortion mode is expected to occur in A_xMnFe(CN)₆ in the entire range of 0 < x < 1, where mixed-valence Mn ions are present. At x = 0.25, the tilting of MnN₆ octahedra produces a wave-like distortion of the (larger) Mn-reduced layer and forms deeper pockets around the windows where the intercalated Na and K ions are located. The intrinsic structural strain discussed above is expected to destabilise A_xMnFe(CN)₆ PBA phases with mixed-valent Mn, i.e., in the composition range of 0 < x < 1.

In the phase with a 25% intercalation level, each window occupied by one of the intercalated ions has a centre of inversion: the two ions of each sublattice located at opposite corners have the same oxidation state. This symmetrical arrangement leads to intercalated ions being located at or directly above the centre of the window. When the intercalant concentration is below 25%, however, this symmetry constraint stops existing, which leads to a new change in the equilibrium structure. We exemplify this situation using PBAs with a 12.5% intercalation level, of composition A_0.25MFe(CN)₆, obtained when only one intercalated ion (hence only one reduced TM ion) is present in each crystallographic PBA unit cell. Let us consider what happens if the intercalated A ion is located at or above the centre of one of the square windows. Because only one of the 4 corner TM sites of the window is reduced at this intercalation level, the window is no longer centrosymmetric; two TM ions of the same sublattice at opposite corners will have different oxidation states. Due to electrostatic reasons, the positively charged A⁺ ion displaces off-centre and towards the reduced TM site. This displacement affects the strength of the A–N interactions in opposite ways, depending on whether the reduced TM site is Fe-LS (i.e., in A_0.25FeFe(CN)₆ – Fig. 6a) or Mn-HS (i.e., in A_0.25MnFe(CN)₆ – Fig. 6b). In the case illustrated in Fig. 6a, the attraction of the A⁺ intercalant to the negative poles of the cyano ligands and to the reduced TM site acts in opposite directions, resulting in small off-centre displacements of the intercalant; instead, in the case of Fig. 6b, the two electrostatic forces on A⁺ act in the same direction, yielding more pronounced off-centering. The off-centre movement is larger for K⁺ than for Na⁺ since K⁺ resides further above the window plane and is less constrained by a 2D distortion. The net result is a displacement of K from the 8c centre of its sub-cube that has components both in the direction of the square window and perpendicular to it, resulting in an equilibrium position close to the 32f′ site along the 〈111〉 diagonal of the sub-cube in K_0.25MnFe(CN)₆; K in K_0.25FeFe(CN)₆ and Na in both Mn and Fe PBAs, instead, has a prevalent 2D-like equilibrium position, although displaced off-centre from the high symmetry 8c/48g/24d line. At concentrations of x ≤ 0.25, each intercalated ion is separated from the next intercalant by at least one empty interstice in each direction; tilting of octahedra to accommodate size mismatches at the TM sites are observed, but they are localised around the reduced TM site and do not cause collective phase transitions in the overall PBA lattice.

Fig. 6 Effect of Na–N interaction on displacement to C-coordinated (a) and N-coordinated (b) transition metal corners.

In summary, calculations considering different types and concentrations of intercalated ions in PBAs reveal a complex sequence of local and long-ranged structural distortions and the occurrence of stable superlattices that are much richer than those available for the isoreticular perovskites. This behaviour will clearly affect both energetics and dynamics of intercalation processes, as well as the stability of PBA cathodes under operational conditions, and will need to be considered in the design of optimal PBA-based materials for energy storage.

3.4 Energy considerations

Having investigated how the PBA structure reacts to the concentration of intercalated Na⁺ and K⁺ ions, we now discuss the effect that the induced phase transitions have on the intercalation energy and mechanistic details. To this goal, we calculate the relative energies ΔE_AxMFe(CN)6 of intermediate phases and plot the “convex hull” diagrams of energies as a function of intercalant content x.

The results for each combination of Na, K, Fe and Mn are shown in Fig. 7. The calculated energy of different configurations of the intercalants at the same concentration x are illustrated by separate points in the diagrams. These diagrams illustrate whether superstructures of intermediate compositions are stable and expected to occur during (dis-)charge processes.

Fig. 7 Relative intercalation energy ΔE_AxMFe(CN)6 for the PBAs A_xMFe(CN)₆ examined (A = Na or K, M = Mn or Fe) as a function of intercalation level x. The background color indicates the ion that is redox active at each value of x: red for HS-Mn, light blue for LS-Fe, and dark blue for HS-Fe.

We note in Fig. 7 that, irrespective of the type of intercalant or high-spin TM site, the structure with 50% intercalation is always the most stable, by up to 0.2 eV per formula unit (i.e. ∼0.8 eV per crystallographic unit cell). As discussed earlier, this is the highest concentration that allows for the 2-D intercalation geometry and 2-D distortion pattern of the PBA lattice. This is therefore the most stable local arrangement. Deviations from this structure incur lattice frustration and are unstable.

Relative to the stable superstructure with x = 1, intercalation of K (Fig. 7b and d) yields unstable PBA compounds in both the low (0 < x < 1) and high level of intercalation (1 < x < 2); these materials may be expected to decompose into a K-rich or a K-poor phase during (dis-)charge. If the intercalation is controlled by thermodynamic factors, this two phase behaviour is expected to yield flat intercalation voltage plateaus over the 0 < x < 1 and 1 < x < 2 composition ranges, during which a K-rich phase grows at the expense of a K-poor phase during intercalation. This voltage profile corresponds to experimental observations, e.g., ref. 21 and 22. Such two-phase behaviour may be detrimental to the dynamics of ion transport, and thermodynamic control may not be achieved upon fast charge/discharge. Intercalation of Na, instead, shows nearly a linear variation of energy as a function of Na content for the Fe-based PBA Na_xFeFe(CN)₆, as shown in Fig. 7c. Upon thermodynamic control of Na intercalation in FeFe(CN)₆, we would expect single phase behaviour and a disordered distribution of Na in the host lattice; this process may show a sloping voltage with increasing Na intercalation, but suffers less from kinetic limitations. The smooth slope voltage profile corresponding to the single-phase reaction is observed for Na_xFeFe(CN)₆ and at high intercalation levels in Na_xMnFe(CN)₆.^23,24 However, Na_xMnFe(CN)₆ shown in Fig. 7a,, shows two phase behaviour in the low intercalation region (0 < x < 1), where our results indicate structural frustration due to size mismatch between reduced and oxidised HS-Mn ions in the same TM sublattice.

4 Conclusions

We have presented the structural evolution of A_xFeFe(CN)₆ and A_xMnFe(CN)₆ during Na and K (de-)intercalation obtained from DFT calculations. The phase behaviour is more complex than that observed in isoreticular perovskites. We have identified 2-D and 3-D structural distortion modes, whose boundary occurs at 50% occupation, i.e. x = 1 in the composition A_xMFe(CN)₆. Alkali metal ions occupy 48g sites in half-intercalated PBAs, corresponding to displacements in the 〈100〉 direction from the centre of the sub-cubes to the centre of the windows of the PBA lattice. At low concentrations (x < 1), the structure contains alternating layers of reduced and oxidised Fe-LS (in A_xFeFe(CN)₆) or Mn-HS (in A_xMnFe(CN)₆); the size mismatch in the Mn–N distances induces a wave-like distortion of the reduced layer in A_xMnFe(CN)₆. At a given intercalation level x, the equilibrium position of the alkali metal ions depends not only on their ionic sizes but also on the redox sequence of the transition metals. The displacement of alkali metal ions towards the N- or C-coordinated reduced TM site either enhances or contrasts the attraction towards the N end of the cyano ligands. This enhanced detail on the structural evolution of PBA materials during (de-)intercalation is critical to understand and rationalise thermodynamic stability and mechanistic aspects of their electrochemical application in energy storage. Further studies are needed to understand the structural evolution of PBA compounds in the presence of lattice defects such as vacancies and water, to provide insights into material design.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

No conflict of interest exits in the submission of this manuscript, and the manuscript has been approved by all authors for publication. I would like to declare on behalf of my co-authors that the work described is original research that has not been published previously, and is not under consideration for publication elsewhere, in whole or in part. All the authors listed have approved the manuscript that is enclosed.

Acknowledgements

The authors acknowledge the use of the UCL Kathleen High Performance Computing Facility (Kathleen@UCL), and its associated support services, in the completion of this work.

References

1. K. Hurlbutt, S. Wheeler, I. Capone and M. Pasta, Joule, 2018, 2, 1950–1960.
2. G. Oh, J. Kim, S. Kansara, H. Kang, H.-G. Jung, Y.-K. Sun and J.-Y. Hwang, J. Energy Chem., 2024, 93, 627–662.
3. B. Nayebi, K. P. Niavol, B. Nayebi, S. Y. Kim, K. T. Nam, H. W. Jang, R. S. Varma and M. Shokouhimehr, Mol. Catal., 2021, 514, 111835.
4. S. S. Kaye and J. R. Long, J. Am. Chem. Soc., 2005, 127, 6506–6507.
5. S. S. Kaye, H. J. Choi and J. R. Long, J. Am. Chem. Soc., 2008, 130, 16921–16925.
6. F. S. Hegner, J. R. Galan-Mascaros and N. Lopez, Inorg. Chem., 2016, 55, 12851–12862.
7. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
8. A. M. Glazer, Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
9. K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 7009–7014.
10. H. L. B. Boström, I. E. Collings, D. Daisenberger, C. J. Ridley, N. P. Funnell and A. B. Cairns, J. Am. Chem. Soc., 2021, 143, 3544–3554.
11. A. Zhou, W. Cheng, W. Wang, Q. Zhao, J. Xie, W. Zhang, H. Gao, L. Xue and J. Li, Adv. Energy Mater., 2021, 11, 2000943.
12. P. Xiao, J. Song, L. Wang, J. B. Goodenough and G. Henkelman, Chem. Mater., 2015, 27, 3763–3768.
13. Y. Wang, B. Hou, X. Cao, S. Wu and Z. Zhu, J. Electrochem. Soc., 2022, 169, 010525.
14. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima and S. Salustro, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360.
15. H. T. Stokes and D. M. Hatch, J. Appl. Crystallogr., 2005, 38, 237–238.
16. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
17. J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101.
18. R. Dovesi, C. Roetti, C. Freyria-Fava, M. Prencipe and V. Saunders, Chem. Phys., 1991, 156, 11–19.
19. M. Towler, N. Allan, N. M. Harrison, V. Saunders, W. Mackrodt and E. Apra, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 5041.
20. M. Catti, G. Valerio and R. Dovesi, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 51, 7441.
21. X. Ma, Y. Guo, C. Yu, X. Chen, L. Gui, N. Cheng, J. Sun, P. Chen, J. Chen and Z. Zi, J. Alloys Compd., 2022, 904, 164049.
22. L. Deng, J. Qu, X. Niu, J. Liu, J. Zhang, Y. Hong, M. Feng, J. Wang, M. Hu and L. Zeng, Nat. Commun., 2021, 12, 2167.
23. X. Wu, Y. Luo, M. Sun, J. Qian, Y. Cao, X. Ai and H. Yang, Nano Energy, 2015, 13, 117–123.
24. Y. Shang, X. Li, J. Song, S. Huang, Z. Yang, Z. J. Xu and H. Y. Yang, Chem, 2020, 6, 1804–1818.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta07755e

---