Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigation of charge transfer models on the evolution of phases in lithium iron phosphate batteries using phase-field simulations†
Souzan
Hammadi
 a,
Peter
Broqvist
a,
Peter
Broqvist
 *a,
Daniel
Brandell
*a,
Daniel
Brandell
 a and
Nana
Ofori-Opoku
a and
Nana
Ofori-Opoku
 *b
*b
aDepartment of Chemistry –Ångström Laboratory, Uppsala University, 75121 Uppsala, Sweden. E-mail: peter.broqvist@kemi.uu.se
bDepartment of Materials Science and Engineering, Brockhouse Institute for Materials Research, McMaster University, Hamilton, L8S 1L4, Canada. E-mail: noforiopoku@mcmaster.ca
First published on 17th December 2024
Abstract
Charge transfer is essential for all electrochemical processes, such as in batteries where it is facilitated through the incorporation of ion–electron pairs into solid crystals. The low solubility of lithium (Li) in some of these host lattices cause phase changes, which for example happens in FePO4. This results in the growth of interfacial patterns at the mesoscale between a Li-poor and Li-rich phase, FePO4 and LiFePO4 respectively. Conventionally, the effect of charge transfer on the evolution of these phases is usually modelled using the Butler–Volmer equation. However, the exponentially increasing current–overpotential relation in this formalism becomes problematic for battery systems operating under high currents. In this study, we implement a phase-field model to investigate two electrochemical reaction models: the Butler–Volmer and the Marcus–Hush–Chidsey formulation. We assess their effect on the spatial and temporal evolution of the FePO4 and LiFePO4 phases. Both reaction models demonstrate similar microstructural patterns in equilibrium. Nevertheless, a significant increase in current density is caused by using the Butler–Volmer expression, leading to an accelerated reaction rate at high overpotentials and an exaggerated delithiation. Furthermore, we show that including anisotropic elastic strain fields in the phase-field model accelerates the delithiation process, reaching the bulk mass transport limitation faster. These elastic effects, when included in the overpotential, can cause the current density to exceed its limits, a problem inherently mitigated by the Marcus–Hush–Chidsey model.
Introduction
Li-ion batteries are built on the functionality of intercalation compounds. The incorporation of ions into solid crystal lattices can result in the formation of new interfaces within the electrode materials upon phase transition. This occurs, for example, in LiFePO4; as lithium (Li) ions intercalate into the material, a transition occurs between the Li-poor FePO4 (FP) and the Li-rich LiFePO4 (LFP) phase with coherency strain between the two due to differences in lattice parameters.1–4 This active battery material exhibits a voltage profile characteristic of phase-changing materials – a steady line that obscures details about the microstructural evolution.To uncover more information on this phase-change and its spatial and temporal progression, capturing the FP-LFP interface is necessary, which requires modelling techniques at the mesoscale level. One such technique is the phase-field model, where a diffuse interface is introduced and minimized according to a multivariate energy functional.5–7 Phase-field models have their origins in Cahn–Hilliard theory, Landau–Ginzburg theory of phase transitions, and van der Waals theory of dense fluids. The evolution of concentration and chemical potential – and other possible fields of interest – are described by differential equations, which can be solved by using numerical methods, such as finite element methods (FEM). When employing phase-field models to describe electrochemical systems, the description of the charge transfer reaction is of critical importance.
Phase-field models have previously been applied to model the phase transition in LFP with the charge transfer defined by Butler–Volmer (BV) kinetics.8–12 The BV model, which is conventionally employed in electrochemistry, relates the electrode surface potential to ionic transfer, described by an exponentially increasing current density.13 While this equation has a simplistic mathematical form and is often valid at low currents, it should be acknowledged that it was developed for metal electrodes, and not for intercalation compounds or for high current applications.
Mesoscale models using BV kinetics have shown that the phase change in LFP strongly depends on the rate of Li insertion,8–12 which has also been observed experimentally.14 High charge transfer rates increase the solubility of Li in LFP beyond its thermodynamic equilibrium, which suppresses the phase transition and thereby the FP-LFP interface formation.8,11 Increasing the Li solubility enhances the performance of the corresponding Li-ion battery, as these interfaces otherwise introduce macroscopic coherency strain and thereby potential mechanical damage. However, since the BV relation describes an exponentially increasing current, it might strongly exceed the charge transfer limit. This, in turn, exaggerates the solubility of Li in FP, and thereby renders an erratic description of the intercalation process and the evolution of the mechanical stress and strain fields in the material. This is particularly important for today's state-of-the art batteries that operate under fast charging conditions.
One way to avoid mechanical damage in a battery is by choosing electrode materials that have high Li solubility, showcasing a solid solution during Li incorporation. However, recent studies have shown that such single phase materials can experience so-called “kinetic” phase transitions in the bulk. This was shown for single particle Nb14W3O44 (NWO) electrodes under operating conditions.15 Similar behaviour have been observed in Li(Ni,Mn,Co)O2 (NMC) and Li(Ni,Co,Al)O2 (NCA) systems.16–18 This suggests that strain effects extend beyond systems undergoing phase transitions in equilibrium and in some cases become more pronounced under fast charging conditions.
It is under these conditions that the BV expression breaks down. The BV model is empirically based on transition state theory and follows Tafel behaviour only at low overpotentials. The main parameters of the BV relation, i.e. the exchange current density and the transfer coefficient, are generally obtained experimentally through iterative fitting of current–voltage data and do not correspond to intrinsic material properties. The exchange current density in particular is a key property, being the pre-exponential factor that can determine the magnitude of the current. The complexity of accurately capturing this parameter is highlighted by the widely varying values reported in the literature, which differ by several orders of magnitude.19–22 This is particularly challenging in phase changing electrode materials, where classical electro-analytical models fail to accurately capture the non-linear relation of reaction and diffusion.23
Other more fundamental charge transfer models may be necessary for systems undergoing fast kinetic processes. This was reported already back in 1991 by Chidsey who used the Marcus–Hush formulation to describe electron charge transfer at metal-electrolyte interfaces.24 The resulting formulation has the advantage of being independently parameterized from first-principle models while also reproducing the experimentally observed curved potential dependence, i.e., a plateauing current with higher overpotential.25 This curved potential dependence has been experimentally validated for LFP battery electrodes.22,26 Similarly, it has been shown for Li metal anodes,27 Zn electrodeposition28 and recently also for LixCoO2 (LCO) and LixNi1/3Co1/3Mn1/3O2 (NMC111).25,29
In previous research utilizing the MHC formalism on intercalation compounds, the focus has been on understanding the role of different electrochemical reaction models on interface morphology.30 However, these have largely excluded the effects of bulk transport-limited interfacial pattern formation and elastic strain effects. In this work, we include both these effects in a spatially and time resolved phase-field model while rigorously evaluating the use of BV and MHC kinetics for the delithiation of LFP. Although studies using BV formulation have divulged valuable insights into the phase changing behaviour in LFP, their findings are all qualitative. Our objective is to investigate the impact of these different electrochemical reaction models on phase evolution by doing a side-by-side comparison. We demonstrate that both models predict similar microstructural patterns and highlight a shift in kinetics where the systems under BV conditions evolve more rapidly. The MHC formulation naturally limits the current density, providing a more reliable approach for describing fast-charging conditions.
Methodology
In this work, the phase-field model developed by Tang and coworkers10,31 has been implemented in the open source finite element software FEnICS.32,33 Parameters are presented in Table 1. A one-particle system of LFP is defined, where the (0 1 0) plane is artificially in contact with an electrolyte assumed to have an infinite Li reservoir. This assumes no mass transport limitation in the electrolyte. For simplicity, only the delithiation process is considered, as it has been shown in previous work that reduction processes undergo additional constraints on the current density.34 The change in Li concentration, c, in the particle is defined by the Cahn–Hilliard equation, which varies with the gradient of chemical potential, μ, | (1) |
| Variable | Description | Value | Source |
|---|---|---|---|
| V m | Molar volume | 4.38 × 10−5 m3 mol−1 | 10 |
| Ω | Regular solution coefficient | 12 × 103 J mol−1 | 10 |
| T | Temperature | 298 K | — |
| R | Gas constant | 8.3145 J mol−1 K−1 | — |
| κ | Gradient energy term | 1.68 × 10−10 J m−1 | 10 and 35 |
| D | Diffusion coefficient | 1 × 10−15 m2 s−1 | 10 |
| σ | Interfacial energy | 0.072 J m−2 | 10 and 35 |
| μ eq | Equilibrium chemical potential | −2.11 × 10−5 J m−3 | — |
| Δϕ | Applied potential | 100–500 mV | — |
| L | Interface width/length unit | 1 nm | — |
| ε 011, ε022, ε033 | Eigenstrains (LFP as reference) | 5.0%, 3.6%, −1.9% | 10 and 36 |
| E | Young's modulus | 125.7 × 109 Pa | 10 |
| ν | Poisson's ratio | 0.252 | 10 and 37 |
| α | Transfer coefficient (BV) | 0.5 | — |
| k BV0 | Rate constant (BV) | 2.035 × 10−4 s−1 | 22 |
| k MHC0 | Rate constant (MHC) | 2.062 × 10−4 s−1 | 22 |
| λ | Reorganizational energy (MHC) | 8.3RT J mol−1 | 22 |
| τ | Correction parameter (MHC) | 3.358 | — |
The mobility of the Li ions is denoted as M = DVm/RT, were D is the Li diffusion coefficient, Vm is the molar volume, R the gas constant and T the system temperature. The chemical potential, μ, in turn is the variational derivative of an energy functional consisting of a local thermodynamic free energy density term, elastic energy density, and a gradient energy that penalizes the interface,38
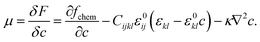 | (2) |
The chemical free energy, fchem, is defined as a regular solution model,
| fchem = RT/Vm[c ln(c) + (1 − c)ln(1 − c)] + Ω/Vmc(1 − c), | (3) |
 | (4) |
 is defined by the Young's modulus E, and ν, Poisson's ratio.
is defined by the Young's modulus E, and ν, Poisson's ratio.
The regular solution model, eqn (3), is presented in Fig. 1a. The height and shape of the activation barrier defined by the model is characterized by the Ω parameter, which directly affects the phase changing behaviour. The addition of elastic strain energy to the regular solution model, decreases the barrier height. Overall, this is seen more clearly in the differential free energy, ∂f/∂c, in Fig. 1b and its effect on the phase diagram in Fig. 1c.
 | ||
| Fig. 1 The effect of elasticity on the free energy, (a) the regular solution model (eqn (3)) and the addition of isotropic elastic energy (eqn (4)) (b) differential free energy and (c) phase diagram also including the spinodal of the regular solution model. The elastic energy by Cogswell et al.9 is included for reference. | ||
Note that an anisotropic elastic free energy, which we have in this system, would give a directionality of the free energy in which the barrier might be smaller or vary in different directions. The lowest value for  of 0.19 GPa was derived by Cogswell et al.9 and is included as a reference to highlight this anisotropic effect (see Fig. 1). The strain (σ) fields are solved for using the equation of linear elasticity,
of 0.19 GPa was derived by Cogswell et al.9 and is included as a reference to highlight this anisotropic effect (see Fig. 1). The strain (σ) fields are solved for using the equation of linear elasticity,
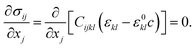 | (5) |
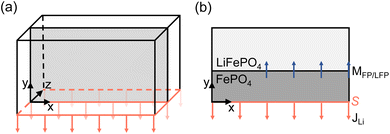
In this study, we investigate charge transfer phenomena occurring at the particle boundary. The weak form of eqn (1) naturally contains a boundary integral term of the gradient in chemical potential. A change in concentration in the system is thus induced by a change in potential. To model the charge transfer as a flux through the surface S, a Neumann boundary condition is defined as,
 | (6) |
 | (7) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) = μ + FΔϕ) and the equilibrium electrode potential is the chemical potential of the system at equilibrium (Eeq = μeq).40 This gives,
= μ + FΔϕ) and the equilibrium electrode potential is the chemical potential of the system at equilibrium (Eeq = μeq).40 This gives,| η = Eeq − E = μeq − μ − FΔϕ, | (8) |
The BV formulation allows for an exponentially increasing current with overpotential in its unconstrained form. In contrast, the MHC model predicts a plateauing current density. There are extension of the BV expression, e.g. the so-called BV + film,41 which mimics the curved Tafel plot but does not follow the experimentally derived current23 and voltage data.42 For the MHC formulation, we employ the recent simplification proposed by Zeng, which streamlines a more complex integral solution.26 Note that the parameters, including the reorganizational energy λ and the overpotential η, have been non-dimensionalized in this formulation.
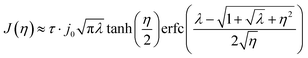 | (9) |
The analytical kinetic models are presented in Fig. 2, where the MHC model has been adjusted to match the BV at low potentials by an additional constant τ similarly to what is done by Bai et al.22 There are also simpler, polynomial-like, approximations that can be made for the MHC expression.43 Although this requires fitting a polynomial expression for each system, it is likely to make solving the entire model less computationally demanding. We will see however, that simulations employing eqn (9) are not that much more demanding than using the BV expression in eqn (7).
 | ||
| Fig. 2 Current density as a function of an applied potential, as described by the Butler–Volmer (BV) and Marcus–Hush–Chidsey (MHC) models, using the parameters given in Table 1. The latter model has been adjusted to fit the former at low potentials. | ||
The kinetic models are parameterized by the exchange current density, j0, and for the MHC formulation, by the reorganizational energy, λ. These are material specific parameters that have been experimentally determined for the LFP system by Bai et al.22
The presented charge transfer rates [s−1] in Table 1 have been converted into a current density [A m−2] according to the following relation,
 | (10) |
Additionally, we define the cell voltage as,
 | (11) |
The total current is obtained as the integral of the concentration at the activate surface of the particle, S,
 | (12) |
In this study, we choose to include the charge transfer rate at only the electrode boundary to highlight the effect of bulk transport-limited interfacial pattern formation. Bulk transport is particularly relevant in microsized particles, commonly found in today's commercial Li-ion batteries.
However, it is also worth noting that different methods exist for modelling charge transfer by varying the flux condition, stemming from studies on the phase evolution of LFP electrodes. Imaging studies on large LFP particles reveal the presence of a diffusion limited interface.44 Another investigation shows that the motion of the phase boundary is constrained by both surface insertion and bulk diffusion, occurring in various directions.45 To account for this type of Li surface insertion, one can add the charge transfer rate directly to the Cahn–Hilliard equation as a source term.9,11 Within this so-called depth-averaging approximation, the dynamics of surface-reaction-limited (SRL) processes result in a charge transfer rate that is concentrated at phase boundaries, extending to the surface through channels of rapid bulk diffusion.46 As a result, the bulk Li concentration quickly adjusts to match the surface concentration. This depth-averaging approximation circumvents restrictions imposed by bulk mass transport limitation, allowing for delithiation without phase transition though a solid solution pathway. The model setup resembles a 3D domain, see Fig. 3, where the whole bottom surface is perpendicular to the charge transfer rate direction, but the charge transfer rate also reaches the moving FF-LFP interface. This type of approximation is particularly important when modelling nanosized particles, that are known for exhibiting this solid solution at high rates,14 and is not used in this study.
All equations are non-dimensionalized and scaled using an energy barrier defined as H = σ/L [J m−3], the length-scale L = 1 nm and time-scale t = l2/D. For higher performance, dynamic adaptive meshing and a basic scheme for adaptive time-stepping are employed. Simulations are carried out using both the BV and MHC formulations at different applied potentials and rate constants k/k0, both with and without coherency strain. The computational domain size is 128 × 64 nm if not stated otherwise and periodic boundary conditions are applied in the [1 0 0] direction.
Results and discussion
As Li depletes from the surface of LFP, a complex interplay of coexisting driving forces shapes the outcome of the phase-field model. These driving forces are described by the chemical potential in eqn (2), which has three main contributions. First, the chemical free energy, where the activation barrier's shape and height dictate the ease of phase transition. Second, the anisotropic elastic contribution alters and reduces this barrier while also introducing macroscopic strain fields-the more interfaces, the greater the strain. Third, the gradient energy that penalizes the formation of interfaces in the bulk.The system's evolution out of equilibrium is governed by the dynamics over this free energy landscape. In the absence of coherency strain, a planar interface forms, as shown in the inset of Fig. 4a, where the blue and red regions are the FP and LFP phase respectively.
Fig. 4a shows the decrease in Li over time, where the BV simulations proceed more rapidly at higher applied potentials. The voltage profile in Fig. 4b demonstrates the familiar planar form distinct for LFP, except a discontinuity at approximately 88% Li which is attributed to the formation of the new interface.47 The phase change occurs at approximately 88.3–88.4% Li for the MHC calculations and 88.3–90.2% Li for the BV calculations. Higher overpotentials shift the transition slightly to higher concentrations, more so for the BV relation. The current in Fig. 4 varies by several orders of magnitude between the BV and MHC simulations.
The exchange current densities used in these simulations, derived from the rate constants provided by Bai et al.22 (k/k0 = 1), are three orders of magnitude lower then the ones employed by Yang and Tang for the BV formulation10 whose model we are employing in this study. The planar interface growth observed is consistent with their findings.10 However, in our simulations (see Fig. 4a), delithiation proceeds over several hours in real time compared to the seconds reported by Yang and Tang, due to the significantly lower charge transfer rate magnitude. As expected, the MHC simulation reaches a limit at 400 mV (see Fig. 4a) and the delithiation process does not proceed faster despite increasing the applied potential to 500 mV. We have reached the limit corresponding to the MHC plateau shown in Fig. 2. In contrast, the BV simulation proceeds at a much faster rate at higher overpotentials.
Simulations using the same rate constants of k/k0 = 1 but now also including coherency strain are presented in Fig. 5a. Similarly, we present the change in Li concentration over time, the voltage and current profile. Despite the more complex form of the MHC boundary equation, the wall time of the computed solutions are only ∼5% slower than their BV counterparts. In these simulations, the coherency strain contributes an additional term to the overpotential, as seen in eqn (2) and (8), which will inherently increase its value. This is why lower applied potentials, (ΔΦ = 1–200 mV) are used in these simulations. Contrary to earlier observations in Fig. 4a, the change in Li concentration over time in Fig. 5a, d and e follows an exponential decay, and the delithiation process proceeds more rapidly. The voltage profile in Fig. 5b now has a sloped line, which has been linked to the influence of elastic free energy.9,48 The discontinuity indicating the phase transition is now shifted to a lower Li concentration of around 80%. This is to be expected, as higher Li solubility in both phases is predicted by the equilibrium phase diagram when elastic free energy is included, see Fig. 1c.
The simulations with coherency strain in Fig. 5 showcase different microstructural patterns compared to the more simple planar interface seen in Fig. 4 when no coherency is included. The corresponding snapshots of the BV simulation can be found in the ESI.† Snapshots of the microstructural evolution, see inset in Fig. 5a, show the new FP phase region initiating at two isolated points, growing upwards and then expanding laterally in the [1 0 0] direction. The misfit strain is higher in this direction, see Table 1 which makes this lateral growth non-preferable. All simulations at this rate constant, both the MHC and BV, show similar microstructural patterns but evolve at different rates. The BV simulation at 200 mV has initially three initiation points, with the third region eventually growing into the two adjacent ones.
To observe how the microstructure evolves with higher charge transfer rate, simulations have been conducted at higher rate constants. Results from rate constants on the order of 100–101 (k/k0 = 104–105) are presented in Fig. 5d–f and g–i. With increased charge transfer rate, delithiation proceeds more rapidly. Phase initiation now occurs at multiple sites, giving rise to wedge-shaped perturbations (see insets in Fig. 5d and g, respectively).
Larger perturbations grow at the cost of smaller ones, which is a common coalescence phenomenon. The higher the rate constant k, the more initiation sites are formed until they are no longer isolated but instead connected into a wave-like shape, see insert in Fig. 5g. The BV simulations give rise to more such initiation sites, as the current density is higher. This leads to a different microstructure and strain field, as seen in Fig. 6.
Snapshots of the strain field for the other simulations are included in the ESI.† At low and high charge transfer rates, similar strain fields are observed. However, at intermediate rates, there is a noticeable difference between the two models. The voltage profile indicates an earlier shift in phase transition points at higher concentrations, and the current profiles differ significantly. The BV expression results in much higher currents which is anticipated.
Interestingly, the voltage transition is smoother at higher charge transfer rate magnitude (k/k0 = 104 in Fig. 5e and k/k0 = 105Fig. 5h), and no discontinuity appears at the phase transition. Instead these points have been marked out specifically at the applied potentials ΔΦ = 1 mV and 200 mV by observation of the microstructural phase-field data.
The discontinuities seen in the voltage profile characterizing the point of phase transition, are more distinct at lower charge transfer rate magnitudes. In contrast, the resulting smoother voltage profiles observed at higher charge transfer rate suggests a change in the phase transition mechanism. Note that the voltage is directly proportional (linearly) to the total chemical potential in the system through eqn (11). The voltage profile is therefore linked to the free energy formulation, which maps out the energy landscape described by the phase-diagram in Fig. 1. This phase-diagram is characterized by the solubility lines (the coexistence curve) and the spinodal (defined by δ2f/δc2 = 0). Between the coexistence curve and the spinodal, phase transitions occur by overcoming an activation barrier (first-order) and are characterized by nucleation and subsequent growth. Within the spinodal this barrier ceases to exist (second-order).
These two types of transitions can also be examined from a thermodynamic perspective, by considering the discontinuities in the derivatives of free energy. At the phase transition point, a discontinuous first derivative indicates a first-order transition, while a continuous first derivative but a discontinuous second derivative indicates a second-order transition.49 Using this definition, we can directly distinguish between these transitions through the simulated voltage profile, revealing which parts of the energy landscape are accessed as current magnitudes change.
This demonstrates that we do not have spinodal decomposition at low charge transfer rates but rather an activated first order phase transition. The shift to a second order transition decreases the Li solubility and shifts the phase boundaries outward, as if expanding the spinodal region seen in Fig. 1c. Once this shift happens and the activation barrier disappears at k/k0 = 104, Fig. 5g, evenly growing perturbations emerge.
Eventually, a point is reached where delithiation proceeds at a similar rate despite an increasing overpotential. This is reached at k/k0 = 105, see Fig. 5g, and is due to bulk mass transport limitation. The FP/LFP phase boundary cannot move faster than the diffusion limit and when the charge transfer rate magnitude is sufficiently high, both the BV and MHC reach this state. At this stage, both systems delithiate at the same rate and showcase the same microstructural pattern. The differences can be found in the second derivative of the chemical potential during the formation and initial growth of the new phase. The early-stage mechanisms of these reaction rate models at this bulk limit seem however to have little effect on the resulting interfacial evolution.
Because of the pronounced anisotropy in the strain field, 3D simulations were performed to enable the field to develop in the third dimension. In a system exhibiting wave-like growth behaviour, the introduction of the third dimension allows the system to become more dispersed, as shown in Fig. 7. Compared to its 2D counterpart in Fig. 5g, this charge transfer rate magnitude generates a spinodal-like pattern at the charge transfer rate surface which the 2D simulation does not indicate. However, when an even higher charge transfer rate magnitude is applied, the 3D simulation follows the trend and displays the wave-like patterns also seen in 2D (Fig. 5g). BV simulations of the same settings are presented in the ESI.†
To quantify the effect of the anisotropic elastic strain and the uneven growing interface on the time evolution, we conducted a simulation without coherency strain at high charge transfer rate using both the BV and MHC formulation. As shown in Fig. 8, the fastest delithiation of this system after reaching the mass transport limit with a planar phase front, is approximately 17 times slower than for the system with coherency strain.
The accelerated delithiation caused by anisotropic coherency strain is a result of the reduced energy barrier for phase transition and an increased Li solubility, as illustrated in the phase diagram in Fig. 1c. Moreover, the presence of curved interfaces increases the interfacial area/length, further accelerating the process. The system tends to favour configurations without interfaces, due to the penalty associated with the gradient energy term in eqn (2).
All our presented results have demonstrated phase transitions no matter the applied charge transfer rate magnitude. Previous studies, both experimental and theoretical, demonstrate a system where at a critical current, the delithiation can proceed through a pathway of no phase transition.9,14,50 Simulations can reproduce this phenomenon by using SRL dynamics in which the charge transfer rate enters the Cahn–Hilliard equation as a source term9,11,46 instead of a charge transfer rate boundary condition as is done in this study. In our setup, in Fig. 7, phase transitions at the surface boundary experiencing charge transfer can be completely bypassed at a high enough charge transfer rate. However, the rest of the bulk is still limited by the mobility of the FP/LFP phase front, determined by the Li diffusivity.
In our study, we push the system to the point of bulk mass transport limitation within the electrode, using this as our benchmark. It is however questionable if reaching this limit is feasible in reality due to mass transport constraints in the electrolyte. Our one-particle system requires significantly higher rate constants than those predicted by Bai et al.22 Specifically, the required rate constants are five orders of magnitude greater than the experimentally derived values. The BV and MHC models are originally reaction models used to describe planar electrodes. Further complications arise from the architecture of a battery electrode, which is a porous agglomeration of particles adhered together with a conductive carbon coating. The mass transport in the porous layer formed by the particles may dominate the voltage output51 making the derived parameters highly uncertain.
It is important to note that the choice of kinetic model becomes even more important when strain effects are present. Linear elasticity adjusts the chemical potential of the system and thus the current magnitude, see eqn (2) and (8). The BV expression increases exponentially with no limit, realizing a much larger current magnitude in comparison to the MHC formulation. This directly affects the long range phase evolution in LFP (see Fig. 6) and thus its electrochemical performance as a battery electrode.
Incorporation of Li ions into solid lattices inherently induces strain, however this does not always lead to long-range mesoscopic effects. Other battery chemistries exhibit similar behaviour as LFP, for example Li2MnO3 (LMO).52 This material has a higher operating voltage than LFP which enables higher energy density. However, phase changes cause an increased strain in the solid crystal which eventually leads to mechanical damage hindering its practical use. Another example of an electrode that undergoes phase transition is Li4Ti5O12 (LTO),53 a system that is recognized for experiencing minimal strain compared to LFP and has been effectively modelled without accounting for linear elasticity.54
However, fast charging conditions can introduce higher concentration gradients which accumulates strain. This has been seen in the NWO system, mentioned in the introduction of this work. The phase-field model employed to investigate this system experiencing a so-called “kinetic” phase transition did not include strain energy due to the lack of material parameters available in literature.15 A BV expression was employed to model charge transfer and front velocity of the phase movement was approximately two times faster than the experimental one. Opting for a lower diffusion coefficient gave better agreement. However, the discrepancy may very well have been due to the current magnitude imposed by the BV expression.
The limited application of alternative theories like the MHC theory might stem from the unavailability of key parameters, such as the rate constant and reorganizational energy. However, new computational and experimental frameworks are being developed to tackle this issue.25,29
The mechanical properties are not the only anisotropic factors in the LFP system. First principles modelling studies has produced a broader form of the chemical free energy as compared to the regular solution model in Fig. 1.55 Other studies suggest that the thermodynamic description, fitted to experimental voltage data, exhibits an asymmetrical free energy form with a third local minimum.48,56 The impact of kinetics depends on the form of the energy landscape, making various free energy formulations worth exploring.
Finally, we summarize our observations and comment on the differences seen with the two electrochemical reaction models. Three distinct growth patterns are observed in the phase-field model with coherency strain in Fig. 5, (i) isolated pillars growing laterally (Fig. 5a), (ii) uniformly growing wedge-shaped regions (Fig. 5d) and (iii) a connected wave-like interfacial front (Fig. 5g). Higher charge transfer rate results in more initiation points for phase transition. Both electrochemical reaction models show these growth patters, however shifted in time and charge transfer rate magnitude where the BV simulation discharges faster and shows more initiation points at lower currents. This leads to different microstructures depending on which kinetic model that is used, see Fig. 6. At high charge transfer rate magnitudes, the transition is bypassed at the surface perpendicular to the charge transfer rate. Both the BV and MHC formulation converge to the same results due to the bulk mass transport limitation inherent in the dynamics of the model.
Conclusions
We have performed a side-by-side comparison of BV and MHC kinetics using a phase-field model considering bulk mass transport limited interfacial pattern formation and anisotropic elastic strain effects. The main outcome of this studied system is that both the BV and the MHC electrochemical reaction models exhibit similar microstructural behaviour. The BV model evolves more rapidly as it has an exponentially increasing overpotential–current relation. Eventually, at high charge transfer rates, both the BV and MHC formulations converge to the same bulk mass transport limit.The addition of anisotropic coherency strain has also been particularly highlighted as it directly affects the energy landscape and thereby the impact of the applied kinetics. This effect is clearly demonstrated in the equilibrium phase diagram, showing a decrease in the energy barrier and an increased Li solubility. However, high charge transfer rates shifts the system out of equilibrium and the phase change occurs at much higher Li content during delithiation. Rapid kinetics facilitates the change from a first order to a second order phase transition where nucleation is no longer necessary, leading to evenly growing perturbations.
The exponentially increasing current density results in a current profile that is highly exaggerated in comparison to the MHC model. In turn, MHC kinetics has a natural limit on the current density that can be defined from first principles, making it more reliable especially at higher overpotentials. Exploring various rate constants within the range presented in this study would provide valuable insights into the impact of microstructural evolution in LiFePO4.
Data availability
The code and data analysis scripts are available and can be found at GitHub [https://github.com/souzanha/LiFePO4-phase-field].Author contributions
Souzan Hammadi: conceptualization, methodology, software, data curation, visualization, writing – original draft, Nana Ofori-Opoku: supervision, conceptualization, methodology, software, writing – original draft, Daniel Brandell: funding acquisition, supervision, writing – original draft, Peter Broqvist: funding acquisition, supervision, conceptualization, writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project was funded by the Swedish Electromobility Center, the National Strategic e-Science Program eSSENCE and STandUP for Energy. Computations were performed on resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) at the National Supercomputer Centre (NSC). N. O. acknowledges funding support from the Natural Science and Engineering Council of Canada (NSERC).References
- A. Yamada, H. Koizumi, N. Sonoyama and R. Kanno, Electrochem. Solid-State Lett., 2005, 8, A409 CrossRef.
- A. Yamada, H. Koizumi, S. I. Nishimura, N. Sonoyama, R. Kanno, M. Yonemura, T. Nakamura and Y. O. Kobayashi, Nat. Mater., 2006, 5(5), 357–360 CrossRef PubMed.
- J. L. Dodd, R. Yazami and B. Fultz, Electrochem. Solid-State Lett., 2006, 9, A151 CrossRef.
- C. Delacourt, P. Poizot, J.-M. Tarascon and C. Masquelier, Nat. Mater., 2005, 4, 254–260 CrossRef.
- N. Moelans, B. Blanpain and P. Wollants, CALPHAD:Comput. Coupling Phase Diagrams Thermochem., 2008, 32, 268–294 CrossRef.
- M. Plapp, Handbook of Crystal Growth, 2nd edn, 2015, vol. 1, pp. 631–668 Search PubMed.
- N. Provatas and K. Elder, Phase-Field Methods in Materials Science and Engineering, Wiley-VCH, 2010 Search PubMed.
- P. Bai, D. A. Cogswell and M. Z. Bazant, Nano Lett., 2011, 11, 22 Search PubMed.
- D. A. Cogswell and M. Z. Bazant, ACS Nano, 2012, 6, 2215–2225 CrossRef.
- K. Yang and M. Tang, J. Mater. Chem. A, 2020, 8, 3060–3070 RSC.
- S. Daubner, M. Weichel, D. Schneider and B. Nestler, Electrochim. Acta, 2022, 421, 140516 CrossRef.
- W. B. Andrews and K. Thornton, MRS Bull., 2024, 49, 644–654 CrossRef.
- E. J. Dickinson and A. J. Wain, J. Electroanal. Chem., 2020, 872, 114145 CrossRef.
- H. Liu, F. C. Strobridge, O. J. Borkiewicz, K. M. Wiaderek, K. W. Chapman, P. J. Chupas and C. P. Grey, Science, 2014, 344(6191), 1252817 CrossRef.
- A. J. Merryweather, Q. Jacquet, S. P. Emge, C. Schnedermann, A. Rao and C. P. Grey, Nat. Mater., 2022, 21, 1306–1313 CrossRef PubMed.
- J. Park, H. Zhao, S. D. Kang, K. Lim, C.-C. Chen, Y.-S. Yu, R. D. Braatz, D. A. Shapiro, J. Hong, M. F. Toney, M. Z. Bazant and W. C. Chueh, Nat. Mater., 2021, 20, 991–999 CrossRef PubMed.
- H. Hyun, K. Jeong, H. Hong, S. Seo, B. Koo, D. Lee, S. Choi, S. Jo, K. Jung, H. Cho, H. N. Han, T. J. Shin and J. Lim, Adv. Mater., 2021, 33(51), 2105337 CrossRef.
- A. Grenier, P. J. Reeves, H. Liu, I. D. Seymour, K. Märker, K. M. Wiaderek, P. J. Chupas, C. P. Grey and K. W. Chapman, J. Am. Chem. Soc., 2020, 142, 7001–7011 CrossRef PubMed.
- C. Heubner, M. Schneider and A. Michaelis, J. Power Sources, 2015, 288, 115–120 CrossRef.
- H. Munakata, B. Takemura, T. Saito and K. Kanamura, J. Power Sources, 2012, 217, 444–448 CrossRef.
- J. Hu, W. Li, Y. Duan, S. Cui, X. Song, Y. Liu, J. Zheng, Y. Lin, F. Pan, J. Hu, W. Li, Y. Duan, S. Cui, X. Song, Y. Liu, J. Zheng, Y. Lin and F. Pan, Adv. Energy Mater., 2017, 7, 1601894 CrossRef.
- P. Bai and M. Z. Bazant, Nat. Commun., 2014, 5(1), 1–7 Search PubMed.
- D. Fraggedakis, M. McEldrew, R. B. Smith, Y. Krishnan, Y. Zhang, P. Bai, W. C. Chueh, Y. Shao-Horn and M. Z. Bazant, Electrochim. Acta, 2021, 367, 137432 CrossRef.
- C. E. Chidsey, Science, 1991, 4996, 919–922 CrossRef.
- J. Halldin Stenlid, P. Žguns, D. Vivona, A. Aggarwal, K. Gordiz, Y. Zhang, S. Pathak, M. Z. Bazant, Y. Shao-Horn, A. Baskin and J. W. Lawson, ACS Energy Lett., 2024, 9, 3608–3617 CrossRef.
- Y. Zeng, R. B. Smith, P. Bai and M. Z. Bazant, J. Electroanal. Chem., 2014, 735, 77–83 CrossRef.
- D. T. Boyle, X. Kong, A. Pei, P. E. Rudnicki, F. Shi, W. Huang, Z. Bao, J. Qin and Y. Cui, ACS Energy Lett., 2020, 5, 701–709 CrossRef.
- D. A. Cogswell, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2015, 92, 011301 CrossRef PubMed.
- Y. Zhang, D. Fraggedakis, T. Gao, S. Pathak, D. Zhuang, C. Grosu, Y. Samantaray, A. R. Neto, S. R. Duggirala, B. Huang, Y. G. Zhu, L. Giordano, R. Tatara, H. Agarwal, R. M. Stephens, M. Z. Bazant and Y. Shao-Horn, Lithium-ion intercalation by coupled ion-electron transfer, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-d00cp-v2.
- D. Fraggedakis and M. Z. Bazant, J. Chem. Phys., 2020, 152, 184703 CrossRef.
- M. Tang, J. F. Belak and M. R. Dorr, J. Phys. Chem. C, 2011, 115, 4922–4926 CrossRef.
- Automated Solution of Differential Equations by the Finite Element Method, ed. A. Logg, K.-A. Mardal and G. Wells, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, vol. 84 Search PubMed.
- M. S. Alnaes, J. Blechta, J. Hake, A. Johansson, B. Kehlet, A. Logg, C. Richardson, J. Ring, M. E. Rognes and G. N. Wells, Archive of Numerical Software, 2015, 3(100), 9–23 Search PubMed.
- J. E. Guyer, W. J. Boettinger, J. A. Warren and G. B. McFadden, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021604 CrossRef PubMed.
- A. Abdellahi, O. Akyildiz, R. Malik, K. Thornton and G. Ceder, J. Mater. Chem. A, 2014, 2, 15437–15447 RSC.
- N. Meethong, H. Y. S. Huang, S. A. Speakman, W. C. Carter and Y. M. Chiang, Adv. Funct. Mater., 2007, 17, 1115–1123 CrossRef.
- R. Hill, Proceedings of the Physical Society. Section A, 1952, 65, 349 CrossRef.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28(2), 258–267 CrossRef.
- J. W. Cahn, Acta Metall., 1961, 9, 795–801 CrossRef.
- S. W. Boettcher, S. Z. Oener, M. C. Lonergan, Y. Surendranath, S. Ardo, C. Brozek and P. A. Kempler, ACS Energy Lett., 2021, 6, 261–266 CrossRef.
- M. Doyle, J. Newman, A. S. Gozdz, C. N. Schmutz and J. Tarascon, J. Electrochem. Soc., 1996, 143, 1890–1903 CrossRef.
- R. B. Smith and M. Z. Bazant, J. Electrochem. Soc., 2017, 164, E3291–E3310 CrossRef.
- J. Zhang, A. F. Chadwick and P. W. Voorhees, J. Electrochem. Soc., 2023, 170, 120503 CrossRef.
- J. Wang, Y. C. K. Chen-Wiegart, C. Eng, Q. Shen and J. Wang, Nat. Commun., 2016, 7(1), 1–7 Search PubMed.
- L. Hong, L. Li, Y. K. Chen-Wiegart, J. Wang, K. Xiang, L. Gan, W. Li, F. Meng, F. Wang, J. Wang, Y. M. Chiang, S. Jin and M. Tang, Nat. Commun., 2017, 8(1), 1–13 CrossRef.
- G. K. Singh, G. Ceder and M. Z. Bazant, Electrochim. Acta, 2008, 53, 7599–7613 CrossRef.
- M. Wagemaker, F. M. Mulder, A. Van Der Ven, M. Wagemaker, F. M. Mulder and A. Van Der Ven, Adv. Mater., 2009, 21, 2703–2709 CrossRef PubMed.
- A. Van der Ven, K. Garikipati, S. Kim and M. Wagemaker, J. Electrochem. Soc., 2009, 156, A949 CrossRef.
- D. A. Porter, K. E. Easterling and K. E. Easterling, Phase Transformations in Metals and Alloys (Revised Reprint), CRC Press, 2009 Search PubMed.
- R. C. Kurchin, D. Gandhi and V. Viswanathan, J. Phys. Chem. Lett., 2023, 14, 7802–7807 CrossRef PubMed.
- E. Kätelhön, L. Chen and R. G. Compton, Appl. Mater. Today, 2019, 15, 139–144 CrossRef.
- P. J. Phillips, J. Bareño, Y. Li, D. P. Abraham and R. F. Klie, Adv. Energy Mater., 2015, 5(23), 1501252 CrossRef.
- H. Zhang, Y. Yang, H. Xu, L. Wang, X. Lu and X. He, InfoMat, 2022, 4(4), e12228 CrossRef.
- A. Vasileiadis, N. J. J. de Klerk, R. B. Smith, S. Ganapathy, P. P. R. M. L. Harks, M. Z. Bazant and M. Wagemaker, Adv. Funct. Mater., 2018, 28(16), 1705992 CrossRef.
- R. Malik, F. Zhou and G. Ceder, Nat. Mater., 2011, 10, 587–590 CrossRef PubMed.
- A. T. Phan, A. E. Gheribi and P. Chartrand, Can. J. Chem. Eng., 2019, 97, 2224–2233 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06444e |
| This journal is © The Royal Society of Chemistry 2025 |