Structural and thermodynamic analysis of triple conducting ceramic materials BaCo_0.4Fe_0.4Zr_0.2−XY_XO_3−δ

Abstract

Triple ionic–electronic conductors, capable of concurrent conduction of protons, oxygen ions, and electrons, are promising cathodes in ceramic fuel cells. Though thoroughly studied, extensive evaluation and explanation of their transport phenomena are crucial for guiding future research. In this work, the structure, composition, and formation enthalpies of BaCo_0.4Fe_0.4Zr_0.2−XY_XO_3−δ (BCFZY_X, X = 0, 0.05, 0.1, 0.15, 0.2) are correlated with its trends in defect mobility. Three compositions of BCFZY_X, X = 0, 0.1, 0.2, are measured under X-ray diffraction and neutron powder diffraction to reveal a common cubic perovskite structure with increasing oxygen vacancy concentration upon increasing yttrium concentration. Formation enthalpies obtained by high-temperature calorimetry reveal a general destabilization of this perovskite structure with yttrium substitution, with deviations at the endmember compositions. Further analysis suggests that high yttrium substitution causes yttrium–vacancy pairs to be more energetically favorable than randomized oxygen vacancies. This phenomenon, along with changes in oxygen vacancy concentration, helps explain observed trends in oxygen-ion and proton mobility in the compositional suite as well as criteria for the selection of high performing, durable protonic ceramic fuel cell materials.

---

1. Introduction

The design of efficient materials for energy conversion and storage applications is a critical challenge facing modern materials science.^1–3 Perovskite ceramic materials, including mixed ionic–electronic conductors, have shown great potential for use in gas separation membranes, fuel cells, and catalysis.^4–8 Among these, triple ionic–electronic conductors (TIECs), known to concurrently transport protons, oxide ions, and electrons under humid oxidizing conditions, are especially interesting due to their high ionic transport at low-to-intermediate temperatures.

Among relevant TIECs, BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ (BCFZY_0.1) and its closely related derivatives are among the most widely studied in the field.⁹ It is known that BCFZY_0.1 can incorporate a wide range of metal ion dopants^10,11 and substitutions,^12–16 as well as withstand broad changes in metal-ion and oxygen non-stoichiometry.^17,18 Our recent work has focused on changing the dopant levels of Zr and Y in the BaCo_0.4Fe_0.4Zr_0.2−XY_XO_3−δ (BCFZY_X) compositional series to understand the dopant effects on ionic and electronic mobility and surface kinetics of these materials.^19,20 Shin, et al. have performed a similar study focusing on varying the levels of multivalent dopants Co and Fe to understand similar phenomena.²¹ Focusing on incremental changes in dopant levels helps reveal the properties which produce high-performance cathode materials in oxide-based fuel cells.

The properties of TIEC materials, including defect mobility and surface exchange reactions, can be significantly affected by oxygen vacancies^22–28 and structural changes.^29–32 Understanding these effects is crucial for the design and optimization of new materials with improved properties. Neutron powder diffraction (NPD) is a powerful tool to understand the structure of these materials. NPD has an additional benefit of probing low atomic weight elements, like lithium and oxygen, unlike traditional X-ray diffraction (XRD). Because of this resolution, the absolute oxygen vacancy concentration can be measured, which is important for TIEC materials with multivalent cations such as Co and Fe, as the vacancy concentration cannot be calculated without knowing the valence state.^33,34 Combined with relative probing of vacancy concentration using methods like thermogravimetric analysis (TGA), the nominal composition of these materials can be elucidated throughout its working temperature ranges.

A method used to correlate the structure, defect chemistry, and mobility properties of solid oxide materials is the measurement of enthalpy of formation from the oxides by high temperature oxide melt solution calorimetry.³⁵ Previous efforts have correlated interesting property changes with respect to composition in perovskites,³⁶ fluorites,³⁷ and other-structured oxide ceramics.^38,39 A general trend is emerging which suggests defect mobility and thermodynamic stability are negatively correlated up to a certain level of substitution, after which structural changes inhibit the further improvement of mobility throughout these complex systems. Indeed, this work supports this trend.

In this study, we present the trends in structure, oxygen vacancy concentration, and enthalpy of formation from the oxides with respect to yttrium concentration. NPD revealed the increase in oxygen vacancy concentration with increases in aliovalent doping. Enthalpy of formation from the oxides was measured using high temperature oxide melt solution calorimetry. These thermodynamic data give new insights to the defect chemistry of BCFZY_X; changes in trends in the enthalpy of formation from the oxides in this BCFZY_X perovskite series suggest causes for the optimum concentration for surface and bulk-level defect mobility, which, among the compositions studied, occurs at 10% B-site doping Y³⁺ for Zr⁴⁺.

2. Methods

2.1 Material synthesis

BaCo_0.4Fe_0.4Zr_0.2−XY_XO_3−δ (BCFZY_X) materials with 0 ≤ X ≤ 0.2 were synthesized using a wet chemistry sol–gel method.⁴⁰ Stoichiometric amounts of precursor nitrates were dissolved in distilled water. Citric acid and EDTA were then added to the solution in a ratio of citric acid : EDTA : metal of 1.5 : 1.5 : 1 as chelating agents. While stirring, ammonium hydroxide was added to the solution until the solution achieved a pH of 9. The solution was heated at 80 °C until a gel formed and was subsequently placed in an oven at 150 °C for 36 h. The resultant complex was fired at 1000 °C for 10 h to remove organic residues and calcine the perovskite phase.

To ensure full calcination of the perovskite phase, membranes of each composition were synthesized by pressing the powder at 160 MPa for two minutes into 15 mm diameter pellets. Pellets were covered with their own calcined powder to reduce the potential for Ba loss during sintering. All samples were sintered at 1275 °C for 8 h in air to form dense membranes. These membranes were subsequently crushed for future measurements.

2.2 Structural characterization

The phase assemblages of all the samples were measured using powder XRD (Hitachi SmartLab Powder Diffractometer) equipped with Cu Kα radiation. NPD was also used to characterize BaCo_0.4Fe_0.4Zr_0.2O_3−δ (BCFZ), BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ (BCFZY_0.1), and BaCo_0.4Fe_0.4Y_0.2O_3−δ (BCFY) at ambient and high temperature using the PEARL diffractometer available at Delft University of Technology.⁴¹ The constant-wavelength diffractometer employs a Ge monochromator and wavelength of λ = 1.667 Å was used. Samples were measured at RT and at 800 K. Samples consisted of sintered pellets that were crushed and ground, loaded in a cylindrical vanadium sample can (50 mm length, 6 mm inner diameter) and sealed under air. The NPD patterns were recorded over a 2θ range from 11° to 158°. Each diffraction pattern was collected for about 3 hours. Rietveld refinements of XRD and NPD data were performed using the software JANA 2006.⁴²

2.3 Thermogravimetry

Thermogravimetric analysis (TGA) was performed using a PerkinElmer TGA8000. Samples were measured to determine the oxygen loss characteristics of each sample at high temperatures. Approximately 20 mg of powdered, sintered pellets were utilized for the measurement. Samples were loaded and the temperature was increased to 200 °C at a heating rate of 50 °C min⁻¹ and held for 30 minutes to remove adsorbed water from the surface of the material. Next, the temperature was increased to 950 °C at a heating rate of 10 °C min⁻¹. This measurement was performed in both air and nitrogen as the purge gas to quantify the weight loss in oxidizing and reducing conditions.

2.4 Quantification of chemical composition

The metals content of each sample was measured using ICP-MS (Thermo X Series II). Approximately 10 mg of each BCFZY_X powder was dissolved in 10 mL of 2% HNO₃ to give solutions containing 10–500 ng mL⁻¹ of each element. Calibration standards were prepared in 2% HNO₃ by diluting single-element plasma standards. The ICP-MS analysis yielded a limit of detection (LOD) of 0.066, 0.027, 0.376, 0.064, and 0.012 ng mL⁻¹ for ¹³⁷Ba, ⁵⁹Co, ⁵⁶Fe, ⁹⁰Zr, and ⁸⁹Y, respectively. Measured concentrations of each ion in the BCFZY_X solutions were always one to three orders of magnitude larger than the LODs. Each dissolution and each analysis was repeated in triplicate, except for BCFZ which was repeated in duplicate, which yielded standard deviations of the calculated molar ratios of less than 1%. Oxygen content in the samples is estimated from thermogravimetric analysis and Rietveld analysis of the BCFZY_X powders measured via NPD.

2.5 High-temperature oxide melt solution calorimetry

Formation enthalpy is a fundamental thermodynamic property which may be used as a gauge of phase stability. Calorimetry is the only direct means to access the formation enthalpy from the oxides and the standard heats of formation from the elements, which it does through the application of appropriate thermochemical cycles. In this method, the total heat effect of drop solution (ΔH_ds) includes the heat of solution (ΔH_sln) and heat content (ΔH_T) of the sample. The drop solution enthalpy for each sample was measured using an AlexSys 1000 (Setaram^®) superbill twin Tian-Calvet high temperature solution calorimeter at 700 °C. Hand-pressed sample pellets (nominally 4–6 mg) were dropped from room temperature into molten sodium molybdate (3Na₂O–4MoO₃) (20 g) solvent. Oxygen was flushed through the glassware assembly at 40 mL min⁻¹ and bubbled through the solvent at 4–5 mL min⁻¹. Flushing ensures constant vapor pressure above the solvent, while bubbling aids dissolution. Experiments were replicated for each sample to achieve statistical relevance (typically not less than 8 measurements) which produced the mean enthalpy of drop solution (ΔH_ds). The reported mean measurement uncertainties were computed as two standard deviations. Calibration was done against the known heat content of trace metal grade alpha-alumina (Sigma Aldrich, 99.999%). The calorimetry and calibration methods have been described previously.^43–46

2.6 Computational methods

To calculate the enthalpy of formation from oxides of BCFZY_X materials, spin-polarized DFT calculations were conducted using the Vienna Ab Initio Simulation Package (VASP).⁴⁷ The calculations employed the generalized gradient approximation (GGA) for the exchange–correlation functional, incorporating a Hubbard U correction within the PBE framework.^48–50 The U values in PBE + U method were consistent as those from the Materials Project:⁵¹U = 5.3 eV for Fe and 3.32 eV for Co. Core electrons were described using projector augmented wave (PAW) pseudopotentials.⁵² The calculations were performed with an energy cutoff of 500 eV. A 4 × 4 × 1 Monkhorst–Pack⁵³k-point mesh in the Brillouin zone was used for a 2 × 2 × 10 supercell of the primitive perovskite unit, containing a total of 200 atoms with 4 different cation configurations in order to cancel out the cation arrangement effects. This somewhat unusual supercell was used so that we could exactly match the desired oxygen stoichiometries. For the binary oxides, Monkhorst–Pack k-point mesh of 8 × 8 × 8, 8 × 8 × 8, 5 × 5 × 5, 5 × 5 × 5 and 3 × 3 × 3 were used for BaO (space group Fm3̄m), CoO (space group F4̄3m), Fe₂O₃ (space group R3̄c), ZrO₂ (space group P2₁/c) and Y₂O₃ (space group Ia3̄) respectively.

The 200-atom supercell was also used to calculate the binding energy of an oxygen vacancy and a Y atom by calculating the difference between two cells, one with Y–vacancy close (nearest neighbors), Y–vacancy intermediate and one with Y–vacancy far (separated as widely as possible in the cell, here 4.63 Å). The coordinates for the three calculations have been included in the ESI† as POSCAR_Y_Vac_Close, POSCAR_Y_Vac_Intermediate and POSCAR_Y_Vac_Far and the location of the vacancy (removed oxygen) being studied are included with the label “Vac” (this line must be removed to run these files in VASP). The binding energy of a 40-atom unit cell and a 320-atom supercell, with the same Y–vacancy close and Y–vacancy far distances as in DFT calculations, was additionally calculated using molecular dynamics (MD) simulations with Interatomic Potentials (M3Gnet).⁵⁴ The cohesive energy of metal oxide compositions under air conditions (Co₃O₄ with space group R3̄m, Fe₂O₃ with space group R3̄c, and Y₂O₃ with space group Ia3̄) was calculated using data extracted from the Materials Project.⁵¹

3. Results

3.1 Structural analysis

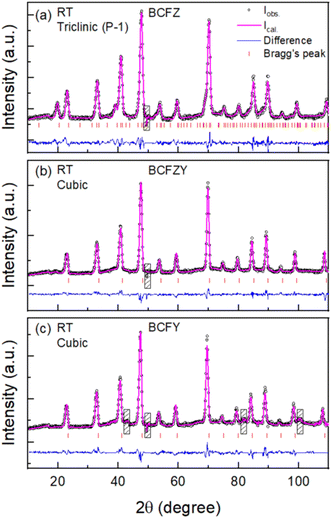
Fig. 1 shows the Rietveld refinement of the room temperature XRD patterns, where all the peaks in each pattern are indexed using the cubic Pm3̄m space group, which is consistent with previous reports.^12,40,55,56 The refined lattice parameters are shown in the respective figures, demonstrating that the Y³⁺ substitution for Zr⁴⁺ caused a lattice expansion of ∼0.003 nm (about 2.4% expansion by volume) as the yttrium content is increased to X = 0.2. This increase is expected due to the larger ionic radius of Y³⁺ compared to Zr⁴⁺, and the magnitude of expansion is reasonably consistent with our and others' previous syntheses of BCFZY_X.^{12,19,20,40,57} The goodness of fit parameters for BCFZ, BCFZY and BCFY are 1.2, 1.1 and 1.1, respectively, which shows the high quality of fit for all the samples.

Fig. 1 Rietveld refined powder X-ray diffraction patterns of (a) BaCo_0.4Fe_0.4Zr_0.2O_3−δ (BCFZ), (b) BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ (BCFZY), and (c) BaCo_0.4Fe_0.4Y_0.2O_3−δ (BCFY).

Powder neutron diffraction measurements were performed on all three compositions at 27 °C and 500 °C. Fig. 2a–c shows the NPD patterns for BCFZ, BCFZY and BCFY. As confirmed from the room temperature XRD, the crystal system for all compositions is cubic with only slight variation in lattice parameters. Therefore, one can expect to see similar peak patterns at all compositions in the absence of additional structural or magnetic ordering.

Fig. 2 Neutron powder diffraction patterns for (a) BaCo_0.4Fe_0.4Zr_0.2O_3−δ (BCFZ), (b) BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ (BCFZY) and (c) BaCo_0.4Fe_0.4Y_0.2O_3−δ (BCFY) recorded at 27 and 500 °C.

However, while comparing the NPD for different samples as a function of temperature, several interesting features emerge. First, for BCFZ, as shown in Fig. 2a, two extra peaks at lower 2θ values of ∼20° and ∼40° can be seen, unlike the other two samples at room temperature. Since these additional peaks appear only at lower 2θ angle, and because the XRD data do not demonstrate peaks at the same d-spacings, they are associated with long range magnetic ordering of Co/Fe spins. Further, magnetic ordering is confirmed when these peaks disappear at high temperatures. Simple observation suggests that the high temperature data belongs to the paramagnetic phase of BCFZ where Co/Fe spins are randomly orientated. The dashed line at 2θ values at ∼20° and ∼40° in Fig. 2a highlights the absence of magnetic peaks in the high temperature data. The presence of magnetic field was confirmed in BCFZ using Mössbauer spectroscopy. As shown in ESI Fig. S1,† BCFZ was the only observed composition with magnetic hyperfine splitting, while the other BCFZY_X compositions exhibited only quadrupole splitting. On close observation of the NPD patterns, it is clear that the same magnetic ordering peaks are present, though just above background, in BCFZY_0.1 but are absent in BCFY. This phenomenon is not observed in the Mössbauer spectroscopy, although it is possible that iron does not play a role in the material's magnetism as yttrium is doped into the structure, and that Co is the primary magnetic ion. The presence of magnetic peaks in the Zr containing samples, unlike in BCFY, indicates that the onset of magnetic ordering is linked to Zr doping in the studied compounds and the ordering becomes stronger with increasing Zr content.

Another prominent feature of the NPD data is the presence of 3 additional peaks with increased intensity at elevated temperature (500 °C) for the BCFY sample. The FWHM of the peaks is quite broad and the peaks cannot be indexed using any high temperature phase reported for this family of structures. Therefore, we attribute these to interference due to the beam clipping some component of the furnace, creating additional diffraction peaks.

The high temperature NPD of each composition was subjected to Rietveld fitting using cubic symmetry to extract the structural parameters in the paramagnetic region. For refining the NPD data of BCFY, we have excluded several broad peaks that appeared at this temperature at higher 2θ angle. Fig. 3 shows the fitted NPD patterns measured at 500 °C. In the crystal structure, the Ba ions reside at the 1a (0, 0, 0) position while the Co/Fe/Zr/Y ions are located at the 1b (0.5, 0.5, 0.5). The oxygen ion is situated at the 3c (0.5, 0.5, 0) position. In addition to refining the peak shapes, background, lattice parameters and other global parameters, the data enabled refinement of the oxygen site occupancy as well as the displacement parameters for the transition metal ions and oxygen. Table 1 presents the occupancies and displacement parameter values for each ion for the data measured at 500 °C. Since Co, Fe, Zr and Y are all randomly distributed on the 1b site, the refinement included a restraint keeping the displacement parameters for Co, Fe and Zr/Y the same. The refined compositions are BaCo_0.4Fe_0.4Zr_0.2O_2.32, BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_2.28 and BaCo_0.4Fe_0.4Y_0.2O_2.27.

Fig. 3 Rietveld refinements of high temperature (500 °C) NPD patterns for (a) BaCo_0.4Fe_0.4Zr_0.2O_3−δ (BCFZ), (b) BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ (BCFZY) and (c) BaCo_0.4Fe_0.4Y_0.2O_3−δ (BCFY) using cubic symmetry. The hatched regions show the excluded regions from the refinement.

Table 1 Refined values of oxygen occupancy, and thermal parameters at 500 °C for different compounds using cubic symmetry Pm3̄m using NPD data

Composition	BaCo0.4Fe0.4Zr0.2O3−δRwp = 5.04 and Rp = 3.96		BaCo0.4Fe0.4Zr0.1Y0.1O3−δRwp = 5.17 and Rp = 3.94		BaCo0.4Fe0.4Y0.2O3−δRwp = 5.72 and Rp = 4.46
Atom	Occupancy	Uiso	Occupancy	Uiso	Occupancy	Uiso
Ba	1	0.0355(13)	1	0.0313(12)	1	0.0386(13)
Co/Fe/Zr/Y	0.4/0.4/0.2/0	0.0467(13)	0.4/0.4/0.1/0.1	0.0452(12)	0.4/0.4/0/0.2	0.0539(13)
O	0.773(7)	0.0437(11)	0.760(7)	0.0479(11)	0.756(7)	0.0580(13)

---

The NPD data collected at room temperature has also been fitted to extract the temperature variation of the lattice parameters, shown in Fig. 4. The NPD pattern of BCFZ was fitted in the triclinic setting (P-1) to include the satellite reflections coming from magnetic ordering using the incommensurate propagation vector k = (0.295, 0.5, 0). With the available data quality, the complete refinement of the magnetic structure was not possible, and future studies would benefit from neutron diffraction studies of single crystals to enable determination of the spin structure for the given incommensurate propagation vector. Table 2 shows the values of the displacement parameters at room temperature.

Fig. 4 Room temperature NPD patterns for (a) BaCo_0.4Fe_0.4Zr_0.2O_3−δ (BCFZ) (b) BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ (BCFZY) and (c) BaCo_0.4Fe_0.4Y_0.2O_3−δ (BCFY). The NPD pattern of BCFZ is fitted using triclinic setting (P-1) to include magnetic reflections whereas the data of BCFZY and BCFY was fitted using cubic symmetry. The hatched regions show the excluded regions from the refinement.

Table 2 Thermal parameters and occupancies for different cations at room temperature using the Rietveld fit NPD data with cubic symmetry

Composition	BaCo0.4Fe0.4Zr0.2O3−δRwp = 5.05 and Rp = 4.06		BaCo0.4Fe0.4Zr0.1Y0.1O3−δRwp = 5.40 and Rp = 4.20		BaCo0.4Fe0.4Y0.2O3−δRwp = 5.72 and Rp = 4.46
Atom	Occupancy	Uiso	Occupancy	Uiso	Occupancy	Uiso
Ba	1	0.0279(14)	1	1.5459(11)	1	0.0210(12)
Co/Fe/Zr/Y	0.4/0.4/0.2/0	0.0412(14)	0.4/0.4/0.1/0.1	2.5556(12)	0.4/0.4	0.0342(13)
O	0.792(9)	0.0361(12)	0.782(7)	2.713(2)	0.766(8)	0.0379(13)

---

The oxygen occupancies were also refined. While comparing the values of oxygen occupancies, one can see a clear increase in oxygen vacancy content with increasing temperature. Table 3 compares the room temperature values of δ with high temperature values. A small increase in δ values at elevated temperature is consistent with the TGA results as discussed later.

Table 3 Oxygen vacancy (δ) as a function of temperature

Sample	δ (27 °C)	δ (500 °C)
BaCo0.4Fe0.4Zr0.2O3−δ	0.624(9)	0.681(7)
BaCo0.4Fe0.4Zr0.1Y0.1O3−δ	0.654(7)	0.720(7)
BaCo0.4Fe0.4Y0.2O3−δ	0.702(8)	0.732(7)

---

Temperature dependence of the lattice parameters and oxygen vacancies as a function of temperature along with the thermal expansion coefficient values for each sample is shown in Fig. 5a–c. The lattice expands on heating as evident from significant increase in lattice parameters values. As mentioned above, the oxygen vacancies increase slightly in each sample at 500 °C as compared to room temperature data. The thermal expansion coefficient shows a maximum for the equally co-doped sample BCFZY_0.1.

Fig. 5 Temperature dependence of (a) lattice parameters, (b) oxygen vacancies and (c) thermal expansion coefficient as a function of X for BaCo_0.4Fe_0.4Zr_0.2−XY_XO_3−δ.

Using the oxygen vacancy concentration refined from room temperature NPD as an initial starting value, the vacancy concentration at the operating temperature (500 °C) is estimated using thermogravimetric analysis. The values from TGA are then compared to the refined vacancy concentration from NPD at 500 °C. Fig. 6a displays mass as a function of temperature for BCFZ, BCFZY, and BCFY. A small mass loss occurred during the drying process, followed by mass increase from 300 to 450 °C (approx.), and then continuous mass loss above 450 °C. Mass gain over the intermediate temperature range suggests oxidation of the multivalent metal cations due to oxygen uptake, as observed in other ferrite and cobaltite materials.^58–60 On comparison with TGA in inert conditions (pure N₂) as shown in ESI Fig. S2,† mass gain is not observed, supporting this hypothesis of oxidation. Subsequent mass loss indicates thermal reduction as a result of metal cations releasing their bound oxygen from the structure. In terms of mass loss, little difference is evident in the TGA profiles for these samples, however oxygen vacancy formation appears greater in the presence of Y-substitution, particularly in BCFZY_0.1. The mass loss is used to estimate oxygen vacancy concentration (δ_TGA) using eqn (1).^12,61

Here, M_FW is the molar mass of the BCFZY_X composition, M_O is the molar mass of oxygen, m_T is the mass at temperature T, m_i is the initial mass after drying, and δ_i,NPD is the initial oxygen vacancy concentration calculated from NPD at room temperature. Using these initial vacancy concentration calculations, the plot of oxygen vacancy concentration against sample temperature is plotted in Fig. 6b. These values are compared between NPD (δ_NPD) and TGA (δ_TGA) in Table 4. Notably, the TGA vacancy estimation showed relatively similar differences in δ between the room temperature and elevated temperature measurements across the three materials, all about 0.02 atoms per formula unit at 500 °C. In BCFY, the difference between TGA and NPD vacancy concentration values is within 0.01 atoms per formula unit, indicating good agreement between the two measurement methods. However, the difference in NPD and TGA vacancy concentration is noticeably greater for BCFZY_0.1 and BCFZ, as shown in the percent difference in the final column of Table 4. The fast temperature ramp on the TGA may not allow for full equilibration of the oxygen concentration, potentially leading to this difference. A future study would use a slower ramp rate to again compare the TGA and NPD methods.

Fig. 6 Thermogravimetric analysis of three BCFZY_X materials, showing (a) weight loss as a function of temperature, and (b) oxygen vacancy concentration calculated from weight loss, with initial vacancy concentration calculated from neutron powder diffraction.

Table 4 Calculated oxygen vacancy concentrations from TGA and NPD

	δ i,NPD 27 °C	δ NPD 500 °C	δ TGA 500 °C	ΔNPD (δNPD,500 − δNPD,27)	ΔTGA (δTGA,500 − δNPD,27)	(ΔNPD − ΔTGA)/ΔNPD
BCFZ	0.624(9)	0.681(7)	0.647(5)	0.056(8)	0.022(8)	60%
BCFZY0.1	0.654(7)	0.720(7)	0.669(3)	0.066(0)	0.014(6)	78%
BCFY	0.702(8)	0.732(7)	0.727(2)	0.029(9)	0.024(4)	18%

---

3.2 Calorimetry

Five BCFZY_X compositions were measured with high temperature oxide melt solution calorimetry in molten sodium molybdate at 700 °C under continuous oxygen flow. The samples fully dissolved in the sodium molybdate melt within 35 to 40 minutes as evidenced by the heat flow peaks returning to baseline without baseline shifts, tailing, or other anomalies. Table 5 presents two thermochemical cycles, which compute the formation enthalpy from the oxides (ΔH_f,ox) as well as the standard formation enthalpy from the elements (ΔH_el) for each sample. The former uses the measured mean drop solution enthalpies of the samples and the binary oxides (BaO, CoO, Co₃O₄, FeO, Fe₂O₃, ZrO₂, and Y₂O₃) and the latter from the elements. Table 6 summarizes the mean drop solution enthalpies (ΔH_ds) of the five BCFZY_X compositions.

Table 5 Thermochemical cycles used to compute the enthalpy of formation from the oxides and elements at 25 °C for the BaCo_0.4Fe_0.4Zr_0.2−XY_XO_3−δ (X = 0, 0.05, 0.10, 0.15, 0.20) samples^a

Reactions	ΔH (kJ mol^−1)
a Notations: s = solid and sln = solution. Measurement mean uncertainty was calculated as a two-standard deviation. The content of Co and Fe in BaCo0.4Fe0.4Zr0.2−XYXO3−δ are merely representative of the BCFZYX target.
(1) BaCo0.4Fe0.4Zr(0.2−X)YXO(3−δ)(s,25°C) → BaO(sln,700°C) + aCoO(sln,700°C) + (⅓)bCo3O4(sln,700°C) + nFeO(sln,700°C) + (½)mFe2O3(sln,700°C) + (0.2 − X)ZrO2(sln,700°C) + (½)XY2O3(sln,700°C) + 0.25O2(g,700°C)	ΔH1 = ΔHds (BCFZYX)
(2) BaO(s,25°C) → BaO(sln,700°C)	ΔH2 = ΔHds (BaO) = −185.30 ± 3.12 (ref. 62)
(3) CoO(s,25°C) → CoO(sln,700°C)	ΔH3 = ΔHds (CoO) = 15.66 ± 0.59 (ref. 63)
(4) Co3O4(s,25°C) → Co3O4(sln,700°C)	ΔH4 = ΔHds (Co3O4) = 271.05 ± 3.72 (ref. 64)
(5) FeO(s,25°C) → FeO(sln,700°C)	ΔH5 = ΔHds (FeO) = −85.21 ± 0.92 (ref. 65)
(6) Fe2O3(s,25°C) → Fe2O3(sln,700°C)	ΔH6 = ΔHds (Fe2O3) = 95.63 ± 0.50 (ref. 65)
(7) ZrO2(s,25°C) → ZrO2(sln,700°C)	ΔH7 = ΔHds (ZrO2) = 19.5 ± 0.9 (ref. 66)
(8) Y2O3(s,25°C) → Y2O3(sln,700°C)	ΔH8 = ΔHds (Y2O3) = −120.07 ± 2.5 (ref. 67)
Calculated ΔH f,ox (25 °C) of BCFZY X from binary oxides:
BaO(s) + aCoO(s) + (⅓)bCo3O4(s) + nFeO(s) + (½)mFe2O3(s) + (0.2 − X)ZrO2(s) + (½)XY2O3(s) + 0.25O2(g) → BaCo0.4Fe0.4Zr(0.2−X)YXO(3−δ)(s)
ΔH9 = ΔHf,ox = ΔH2 + aΔH3 + (⅓)bΔH4 + nΔH5 + (½)mΔH6 + (0.2 − X)ΔH7 + (½)XΔH8 − ΔH1
Calculated ΔH f,el (25 °C) from the elements and the ΔH f,ox of BCFZY X
Ba(s) + aCo(II)(s) + (⅓)bCo(II,III) + nFe(II)(s) + (½)mFe(III)(s) + (0.2 − X)Zr(s) + XY(s) + 1.5O2(g) → BaCo0.4Fe0.4Zr(0.2−X)YXO(3−δ)(s)
ΔHf,el = ΔH9 + ΔHf,el(BaO) + aΔHf,el(CoO) + (⅓)bΔHf,el(Co3O4) + nΔHf,el(FeO) + (½)mΔHf,el(Fe2O3) + (0.2 − X)ΔHf,el(ZrO2) + (½)XΔHf,el(Y2O3)

---

Table 6 The enthalpy of drop solution, the formation enthalpy from the oxides, and the standard formation enthalpy from the elements of the measured solid solution samples that correspond to the general formula BaCo_0.4Fe_0.4Zr_0.2−XY_XO_3−δ with X = 0, 0.05, 0.10, 0.15, 0.20

Target stoichiometry	ΔHds (kJ mol^−1)^a	ΔHf,ox^b (kJ mol^−1)	ΔHf,el^c (kJ mol^−1)
a The measurement mean of multiple experiments, as shown in parentheses, yields the enthalpy of drop solution (ΔHds). The reported uncertainty is the two-standard deviation of the measurement average. For the enthalpies of formation from oxides and elements, uncertainties are the propagated errors computed as the square root of the sum of the squares. b ΔHf,ox = enthalpy of formation from the binary oxides. c ΔHf,el = enthalpy of formation from the elements. Ancillary data used in the thermochemical cycles to compute the standard heats of formation are from Robie and Hemingway.^68 Thermochemical values for a comparative BZY sample are from the research group of Alexandra Navrotsky.^62
BaCo0.4Fe0.4Zr0.2O3−δ	−50.57 ± 2.08 (7)	−95.60 ± 5.57	−1072.90 ± 10.95
BaCo0.4Fe0.4Zr0.15Y0.05O3−δ	−60.27 ± 1.08 (6)	−99.63 ± 5.28	−1069.68 ± 10.81
BaCo0.4Fe0.4Zr0.1Y0.1O3−δ	−70.19 ± 1.66 (6)	−96.94 ± 5.43	−1033.27 ± 10.88
BaCo0.4Fe0.4Zr0.05Y0.15O3−δ	−82.43 ± 1.47 (8)	−92.92 ± 5.37	−1011.43 ± 10.85
BaCo0.4Fe0.4Y0.2O3−δ	−90.05 ± 1.64 (8)	−96.96 ± 5.42	−1002.25 ± 10.88
BaZr0.80Y0.20O2.90 (Navrotsky 2014)	−85.53 ± 3.95 (8)	−92.89 ± 5.7	−1634.94 ± 10.63

---

Using the oxygen nonstoichiometry, the average valence state for Co and Fe can be elucidated in each measured sample. Extra steps are taken to decouple each valence for Co and Fe. Mössbauer spectroscopy (Table S1†) was used to calculate the ratio of binary oxides in Fe. The ratio of binary oxides in Co was estimated using a charge balance based on the valence states of all other metal cations with the oxygen concentration elucidated from neutron powder diffraction. In intermediate compositions BCFZY_0.05 and BCFZY_0.15, the oxygen vacancy concentration is estimated using a linear interpolation. To characterize and correlate thermodynamic and transport phenomena for these complex oxides, accurate elemental composition is paramount. Using the above methods, the reported compositions are the best estimates possible for the actual composition of each sample. Compositions used for these thermodynamic analyses are given in Table S2.† For the following analyses, only binary oxides of Co and Fe with valence (II) and (III) are considered, as the binary oxides with valence (IV) are not stable and have not been characterized by thermochemical methods.

As presented in Table 6 and Fig. 7a, the enthalpy of formation from oxides and elements are both strongly exothermic and are thus favorable with respect to their binary oxides. The standard formation enthalpy from the elements decreases in stability tracking inversely with the Y content increase and directly with the decrease in Zr. The stability of these compositions is less favorable with simple mixing of the elements. They are all significantly less thermodynamically stable in their standard formation from the elements that the BZY (ΔH_f,el = −1634.94 ± 10.63 kJ mol⁻¹) that is not substituted with the transition metals, Co and Fe. The increasingly negative drop solution enthalpies indicate dissolution tendency and track directly with the increasing Y content. Although not a hard and fast rule, typically increased favorability of sample dissolution corresponds to decreased stability of the phase, and in this case would produce an increasingly endothermic trend in the enthalpy of formation from the oxides for perovskite samples with increasing Y-substitution. The expected trend holds for the three intermediate phases, BCFZY_0.05, BCFZY_0.1, and BCFZY_0.15. However, the endpoint compositions BCFZ (ΔH_ds = −50.57 ± 2.08 kJ mol⁻¹ and ΔH_f,ox = −95.60 ± 5.57 kJ mol⁻¹) and BCFY (ΔH_ds = −90.05 ± 1.64 kJ mol⁻¹ and ΔH_f,ox = −96.96 ± 5.42 kJ mol⁻¹) break the expected trend for the mixing of binary oxides to form these two samples and, in spite of the large 40 kJ mol⁻¹ difference in drop solution enthalpy, the ΔH_f,ox remains relatively constant.

Fig. 7 (a) Enthalpies of drop solution (left axis, left-facing arrow) as measured in sodium molybdate at 700 °C and formation enthalpies from the oxides at 25 °C (right axis, right-facing solid arrow) and (b) comparison of empirical enthalpies of formation from the oxides with DFT calculations, as a function of X yttrium content in BCFZY solid solutions. Reported uncertainty values were calculated as two standard deviations from the mean for both experimental and DFT plotted data.

Comparison between the empirical and the DFT-calculated enthalpy of formation from the oxides is shown in Fig. 7b. All DFT-calculated values are within 15% of the experimentally determined values, indicating good agreement between the model and experimental data. The DFT data show many similarities to the experiments in the first four compositions. Specifically, DFT also predicts a slight decrease in ΔH_f,ox from BCFZ (ΔH_f,ox,DFT = −112.14 ± 4.46 kJ mol⁻¹) to BCFZY_0.05 (ΔH_f,ox,DFT = −113.69 ± 1.46 kJ mol⁻¹), followed by a general increase to BCFZY_0.15 (ΔH_f,ox,DFT = −105.53 ± 1.02 kJ mol⁻¹). This significant increase in ΔH_f,ox from BCFZY_0.05 to BCFZY_0.15 closely matches between the empirical data and predicted DFT calculations. However, DFT calculations appear to underestimate the ΔH_f,ox in the final BCFY composition. Overall, the BCFZY_X compositions are relatively close to previously reported values for yttrium-doped barium zirconate in both drop solution enthalpy and enthalpy of formation from the oxides.⁵²

4. Discussion

Neutron diffraction revealed that this compositional suite of materials has high oxygen vacancy concentration, especially compared to other ionic conductors such as BaZr_1−XY_XO_3−δ and Ce_1−XGd_XO_2−δ.^62,69,70 Previous neutron diffraction studies on a similar mixed ionic–electronic material Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ showed similar levels of initial oxygen non-stoichiometry of δ ≈ 0.6.³⁴ From a structural symmetry standpoint, Ba²⁺ is a large cation, meaning that larger B-site cations are necessary for structural stability/symmetry of the cubic perovskite system. As redox state in Fe/Co is reduced, the ionic radius is increased given the same spin state.⁵⁷ It is therefore structurally favorable for the lattice to contain reduced redox states of Fe/Co, which are closer to the ionic radius of Zr⁴⁺, as suggested in this work. In recent studies in this system, specifically on BCFZY_0.1, iodometry has suggested a wide range of oxygen vacancy concentrations from δ = 0.23 to δ = 0.5,^12,17,18 lower than the value reported here, leaving wide uncertainty of the actual vacancy concentration of this composition. Other work on BaCoO_3−δ and BaCo_0.5Fe_0.5O_3−δ have shown that high vacancy concentrations (δ = 0.78 and δ = 0.84, respectively) are necessary for cubic perovskite symmetry, supporting this work;^71–73 at lower vacancy concentrations with more oxidized metal cation redox states, the structural symmetry is reduced to hexagonal. Contrary to this work, these compounds were synthesized in reducing conditions, though the compositions were shown to be stable in air until 220 °C through TGA measurements.⁷¹ It is possible that the larger and univalent Zr⁴⁺ and Y³⁺ cations in the BCFZY_X system help stabilize the lattice across a wide range of temperatures. These works also present an interesting question on the upper-bound of vacancy concentration for compositions synthesized in air.

Although it is known that small changes in dopant concentration have notable effects on transport properties in BCFZY_X, the underlying reasons for the trends in transport phenomena have not been clearly defined in literature. Neutron diffraction revealed that the three compositions are structurally quite similar; all compositions exhibit cubic perovskite symmetry with only small changes in lattice parameter across the compositional range. The substitution of yttrium for zirconium increases the lattice parameter, which increases ionic hopping distance and therefore can decrease ionic conductivity. This phenomenon is observed in oxide ion conductivity (σ_O²⁻) given in Table 7. The same trend is not observed in proton conductivity (σ_H⁺); it is more likely that localized atomic changes caused by Y for Zr doping are the main cause for the optimal proton conductivity observed in BCFZY_0.1, as discussed later. Additionally, neutron diffraction showed increasing oxygen vacancy concentration with increasing yttrium doping. Increased vacancy content likely increases the available sites for surface exchange, increasing oxygen surface exchange (k_O,chem)and hydroxyl surface exchange (k_OH,chem)as noted in Table 7. The increased vacancy concentration also decreases the available B–O bonds in the system, thus decreasing the electronic conductivity (σ_e⁻).

Table 7 Values of selected conductivity and electrochemical kinetic parameters at 600 °C, previously measured. Electronic conductivity (σ_e⁻) from total conductivity measured via four-point probe with ionic components subtracted.²⁰ Proton conductivity (σ_H⁺) is estimated from hydrogen permeation measurements.¹⁹ Oxide ion conductivity (σ_O²⁻) is estimated from oxygen permeation measurements.²⁰ Chemical oxygen surface exchange coefficient (k_O,chem) and hydroxyl surface exchange coefficient (k_OH,chem) are measured using electrochemical conductivity relaxation^19,20

Composition	σ e^− (S cm^−1)	σ H^+ (S cm^−1)	σ O^2− (S cm^−1)	k O,chem (cm s^−1)	k OH,chem (cm s^−1)
BCFZ	2.63	8.48 × 10^−4	7.56 × 10^−2	7.3 × 10^−4	8.62 × 10^−5
BCFZY0.1	1.71	3.23 × 10^−3	3.56 × 10^−2	2.8 × 10^−3	2.26 × 10^−4
BCFY	1.23	2.7 × 10^−3	1.41 × 10^−2	4.6 × 10^−3	3.91 × 10^−4

---

Thermodynamic destabilization of the perovskite phase was expected with aliovalent substitution of Y³⁺ for Zr⁴⁺ in this series. This trend was expected in part due to the endothermic effects of increasing number of oxygen vacancies as well as local lattice strain caused by the larger size of Y³⁺ compared to Zr⁴⁺ and Co/Fe multivalent ions. In Fig. 7, the experimental enthalpy of formation from the oxides exhibits this trend in the three intermediate compositions. However, the endpoint compositions BCFZ and BCFY show interesting deviations from the expected trend. Some of the deviations can be explained by the larger changes in barium concentration at the endmembers. However, when only accounting for the barium concentration change, the roughly linear trend still cannot be resolved compared to the three intermediate concentrations. BCFZ shows greater endothermicity than expected. Observations from literature suggest difficulties for this composition to achieve cubic symmetry, including lower symmetry structures and secondary phases.^19,74,75 This difficulty may provide some explanation for why BCFZ is more endothermic than expected.

In BCFY, the greater exothermicity from expected may be the result of vacancy-dopant association, where the yttrium atom becomes associated with the vacancy it forms, and therefore yttrium–vacancy pairs become more energetically stable than randomized vacancies. This phenomenon has also been hypothesized by high temperature oxide melt solution calorimetry in other fluorite and perovskite structures.^76–79 Vacancy association is typically correlated with decreases in conductivity of mobile ions due to the trapping of vacancies, reducing the number of available mobile defects for kinetic transport.^80,81 Vacancy association can especially be supported by the previously measured proton conductivity of the BCFZY_X series, where BCFZY_0.1 (X = 0.1) exhibited the highest proton conductivity followed by a decrease with increased yttrium doping as shown in Table 7 and Fig. S3.¹⁹† Yttrium–vacancy association is also noted in BZY, where proton conductivity reaches a relative maximum at X = 0.2 and decreases once vacancy association (suggested from high temperature solution calorimetry) is present at X = 0.3 and greater.^62,70 Like in BZY,⁸² the vacancy-dopant association in BCFY outweighs the increased propensity for proton uptake from yttrium incorporation¹⁹ and leads to its decreased proton conductivity. A similar explanation may also apply to the increased exothermicity of BCFZY_0.05 against BCFZ, where some local vacancy-dopant association is occurring with the introduction of Y³⁺. However, in this case, the propensity for proton uptake from Y³⁺ incorporation outweighs the local association effect, so proton conductivity increases.

Vacancy association was investigated using computational approaches. Density functional theory (DFT) calculations of an O vacancy next to and farther from Y in a 200-atom unit cell of BaCo_0.4Fe_0.4Y_0.2O₃ show a binding energy of −2.22 eV, a very strong repulsion. This result contradicts expectations from electrostatics, where Y and oxygen vacancies in the perovskite lattice should attract due to the negative charge of Y and the positive charge of the oxygen vacancies. The result is also inconsistent with the size effects expected from the larger Y atoms. The ionic radii for B-site cations in the perovskite system are Y³⁺ (0.90 Å), Co⁴⁺ (0.53 Å) and Fe⁴⁺ (0.58 Å). The comparably larger ionic radii of Y³⁺ compared to Co⁴⁺ and Fe⁴⁺ would be expected to attract oxygen vacancies to reduce the strain in the system, effectively helping the larger Y³⁺ fit by creating space nearby. However, the binding energy is consistent with the stronger metal–oxygen bond of Y compared to Co or Fe. Specifically, we can estimate the bond strengths by dividing the cohesive energy of each phase by the number of metal–oxygen bonds, which gives: Y₂O₃ cohesive energy/bond = −19.53 eV/12 bonds = −1.68 eV/bond; Co₃O₄ cohesive energy/bond = −9.03 eV/18 bonds = −0.50 eV/bond, and Fe₂O₃ cohesive energy/bond = −8.54 eV/12 bonds = −0.71 eV/bond, as calculated using DFT (see Methods). We therefore believe that it is the strong yttrium–oxygen bond compared to the other metals that attracts the oxygen, or equivalently, repels the vacancy in this estimation.

To ensure a robust calculation of the binding energy of yttrium–vacancy pair, an additional binding energy calculation was performed for a configuration where the distance of Y and the oxygen vacancy was intermediate between the near and far case. This calculation yielded a binding energy of −1.91 eV, consistent with the repulsion decreasing as the vacancy moves farther away from nearby yttrium. Additionally, the M3Gnet universal machine learning potential was used to evaluate the binding energy of the yttrium–vacancy pair. Oxygen vacancies adjacent to and farther from yttrium in a 40-atom and 320-atom unit cell of BaCo_0.4Fe_0.4Y_0.2O₃ showed the same binding energy of −0.89 eV. This result is potentially quite approximate as the potential was not fit to vacancy binding data but is qualitatively consistent with the DFT in that it shows strong repulsion between the yttrium and the oxygen vacancy and no strong dependence on the size of the cell used in the study. These DFT and M3Gnet calculations are not consistent with the attractive yttrium–vacancy binding that has been posited in the explanations above. It is possible that some other effect underlies the above thermodynamic and kinetic observations, or that the complex magnetic, electron localization, redox, and correlated electron effects that may be occurring in the BaCo_0.4Fe_0.4Y_0.2O₃ are poorly enough captured by the PBE DFT and M3Gnet that they get the wrong sign for the yttrium–vacancy binding. Overall, although opposite in potential, a strong association is suggested with yttrium in both the computational work (Y–O bond) and the experimental work (Y–Vac bond), each of which could decrease mobile species in the lattice. More work is needed in this area to develop a robust and consistent understanding.

In terms of oxygen transport, BCFZY_X shows a clear tradeoff between bulk oxygen conductivity and surface exchange^19,20 as shown in Table 7 and Fig. S4.† The increase in oxygen surface exchange can be explained by the increased vacancy concentration with increasing yttrium concentration, allowing for more sites for oxygen incorporation. For bulk transport, we can see the reduced oxygen diffusion kinetics with increasing yttrium concentration by considering the oxygen ionic diffusion coefficient, D_O²⁻. Using the previously determined oxygen ionic conductivity,²⁰σ_O²⁻, and the Nernst–Einstein equation,^83,84D_O²⁻ can be calculated:

where K_B is the Boltzmann constant, T is the specified temperature, N_O²⁻ is the number of carrier ions per unit volume, Z_O²⁻ is the valence of the oxygen ion, and e is the elementary electron charge. The number of carrier ions per unit volume can be calculated using the equationwhere ρ is the material density, A is Avogadro's number, δ is the vacancy concentration, and M is the material's molecular weight. Given that these materials are cubic perovskite, which is a primitive cubic cell, the equation can be further reduced towhere a is the material lattice parameter. Increasing yttrium results in an overall decrease in diffusivity, as shown in Fig. 8. Here, the carrier ion concentration is estimated using TGA nonstoichiometry values, while the lattice parameter is estimated using the thermal expansion coefficient from Fig. 5c. Although the oxygen ion conductivity was previously measured using a chemical gradient, it is reasonable to estimate the diffusion coefficient using this value, as shown previously.⁸⁵ Indeed, at 600 °C, the estimated diffusion values for BCFZY_0.1 (1.07 × 10⁻⁷ cm² s⁻¹) reasonably agree with tracer diffusion measurements of BCFZY_0.1 from a previous study (5.4 × 10⁻⁸ cm² s⁻¹).²¹ Additionally, the estimated value is on par with other known oxide-ion conductors.^86,87 These comparisons further suggest the rationality for this estimation of oxygen ion diffusivity in these materials.

Fig. 8 Estimated oxygen ionic self-diffusivity as a function of temperature from 550–700 °C, using structural data and previously determined oxygen ion conductivity measurements.

Based on both the observed thermodynamic and structural phenomena, the observed trends in oxygen mobility are supported by the increased hopping distance due to the increases in lattice parameter from BCFZ to BCFY and the hypothesis of dopant vacancy association, leading to increased vacancy immobilization around the Y ion.^62,80,81,88 This estimation is also supported by the assertion that increased vacancy content decreases the ionic mobility.⁸⁹ The trend observed with the ionic diffusion coefficient aligns reasonably well with the previously measured chemical diffusion coefficient, D_O,chem, except at low temperatures, as shown in Fig. S4.† The low temperature measurements of the chemical diffusion for BCFZ may be hindered by the low surface exchange coefficient at low temperatures. If BCFZ was surface limited in this measurement, this could potentially skew the bulk diffusivity to be lower than expected.²⁰

5. Conclusions

This work analyzed trends in the enthalpy of formation from the oxides as a function of oxygen vacancy and structure effects through the application of high temperature solution calorimetry, XRD, TGA, and neutron powder diffraction. The results were then correlated with previously measured proton and oxygen kinetics in the BCFZY_X perovskite ceramic compositional suite. All compositions exhibit a cubic perovskite structure which shows increasing oxygen vacancy concentration with increasing yttrium substitution. It is hypothesized through the thermochemical data that the increase in yttrium for zirconium substitution induces dopant-vacancy association, correlating with a decrease in defect mobility in the fully yttrium-doped BCFY.

Data availability

The data supporting this article have been included as part of the ESI† with additional data available upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project was funded by the Department of Energy, National Energy Technology Laboratory an agency of the United States Government, through an appointment administered by the Oak Ridge Institute for Science and Education. Neither the United States Government nor any agency thereof, nor any of its employees, nor the support contractor, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. The authors would like to acknowledge Boris Merkies at TU Delft for his work on the Mössbauer spectroscopy measurements. JHD was supported in part by an International Research Experiences for Students program through National Science Foundation Award #1952528. KSB was supported in part by an appointment to the NETL Research Participation Program, sponsored by the U.S. Department of Energy and administered by the Oak Ridge Institute for Science and Education.

References

1. E. Fabbri, D. Pergolesi and E. Traversa, Chem. Soc. Rev., 2010, 39, 4355–4369.
2. J. Irvine, J. L. M. Rupp, G. Liu, X. Xu, S. Haile, X. Qian, A. Snyder, R. Freer, D. Ekren, S. Skinner, O. Celikbilek, S. Chen, S. Tao, T. H. Shin, R. O'Hayre, J. Huang, C. Duan, M. Papac, S. Li, V. Celorrio, A. Russell, B. Hayden, H. Nolan, X. Huang, G. Wang, I. Metcalfe, D. Neagu and S. G. Martín, J. Phys., 2021, 3, 031502.
3. J. W. Choi and D. Aurbach, Nat. Rev. Mater., 2016, 1, 16013.
4. J. Kim, S. Sengodan, S. Kim, O. Kwon, Y. Bu and G. Kim, Renew. Sustain. Energy Rev., 2019, 109, 606–618.
5. R. Merkle, M. F. Hoedl, G. Raimondi, R. Zohourian and J. Maier, Annu. Rev. Mater. Res., 2021, 51, 461–493.
6. U. Balachandran, B. Ma, P. S. Maiya, R. L. Mieville, J. T. Dusek, J. J. Picciolo, J. Guan, S. E. Dorris and M. Liu, Solid State Ionics, 1998, 108, 363–370.
7. J. Sunarso, S. S. Hashim, N. Zhu and W. Zhou, Prog. Energy Combust. Sci., 2017, 61, 57–77.
8. N. Kochetova, I. Animitsa, D. Medvedev, A. Demin and P. Tsiakaras, RSC Adv., 2016, 6, 73222–73268.
9. L. R. Tarutina, M. A. Gordeeva, D. E. Matkin, M. T. Akopian, G. N. Starostin, A. V. Kasyanova, A. P. Tarutin, N. A. Danilov, I. A. Starostina, D. A. Medvedev and Z. Shao, Chem. Eng. J., 2024, 490, 151615.
10. M. Liang, F. He, C. Zhou, Y. Chen, R. Ran, G. Yang, W. Zhou and Z. Shao, Chem. Eng. J., 2021, 420, 127717.
11. M. Liang, Y. Song, D. Liu, L. Xu, M. Xu, G. Yang, W. Wang, W. Zhou, R. Ran and Z. Shao, Appl. Catal., B, 2022, 318, 121868.
12. M. S. Alam, I. Kagomiya and K. Kakimoto, Ceram. Int., 2023, 49, 11368–11377.
13. H. Lv, Z. Jin, R. Peng, W. Liu and Z. Gong, Ceram. Int., 2019, 45, 23948–23953.
14. Y. Xu, F. Hu, Y. Guo, J. Zhang, Y. Huang, W. Zhou, J. Sun, B. He and L. Zhao, Sep. Purif. Technol., 2022, 297, 121482.
15. J. Ma, F. Zhu, Y. Pan, H. Zhang, K. Xu, Y. Wang and Y. Chen, Sep. Purif. Technol., 2022, 288, 120657.
16. Z. Xu, J. Yu and W. Wang, Membranes, 2022, 12, 831.
17. R. Ren, Z. Wang, C. Xu, W. Sun, J. Qiao, D. W. Rooney and K. Sun, J. Mater. Chem. A, 2019, 7, 18365–18372.
18. X. Kuai, G. Yang, Y. Chen, H. Sun, J. Dai, Y. Song, R. Ran, W. Wang, W. Zhou and Z. Shao, Adv. Energy Mater., 2019, 9, 1902384.
19. J. H. Duffy, H. W. Abernathy and K. S. Brinkman, J. Mater. Chem. A, 2023, 11, 8929–8938.
20. J. H. Duffy, Y. Meng, H. W. Abernathy and K. S. Brinkman, Membranes, 2021, 11, 766.
21. Y. Shin, Y. Kim, M. Sanders, S. P. Harvey, M. Walker and R. O'Hayre, J. Mater. Chem. A, 2022, 10, 24839–24853.
22. D. Poetzsch, R. Merkle and J. Maier, Adv. Funct. Mater., 2015, 25, 1542–1557.
23. H. Takahashi, I. Oikawa and H. Takamura, J. Phys. Chem. C, 2018, 122, 6501–6507.
24. X. Wang, W. Li, C. Zhou, M. Xu, Z. Hu, C.-W. Pao, W. Zhou and Z. Shao, ACS Appl. Mater. Interfaces, 2023, 15, 1339–1347.
25. R. Ren, Z. Wang, X. Meng, X. Wang, C. Xu, J. Qiao, W. Sun and K. Sun, ACS Appl. Energy Mater., 2020, 3, 4914–4922.
26. L. Zhang, B. Pang, S. Hu, Z. Cao, P. Zhang, X. Zhu and W. Yang, Int. J. Hydrogen Energy, 2023, 48, 10180–10190.
27. F. Feng, W. Yang, Q. Zheng, J. Milewski, L. Zhao, C. Wang and Y. Guo, Energy Fuels, 2021, 35, 8953–8960.
28. M. A. Gomez, Z. Lin, S. Lin, Y. Tian, A. van Bokkelen and M. Valerio, J. Phys. Chem. C, 2020, 124, 27954–27964.
29. M. Coduri, M. Karlsson and L. Malavasi, J. Mater. Chem. A, 2022, 10, 5082–5110.
30. M. Mogensen, D. Lybye, N. Bonanos, P. Hendriksen and F. Poulsen, Solid State Ionics, 2004, 174, 279–286.
31. J. Ding, J. Balachandran, X. Sang, W. Guo, J. S. Anchell, G. M. Veith, C. A. Bridges, Y. Cheng, C. M. Rouleau, J. D. Poplawsky, N. Bassiri-Gharb, R. R. Unocic and P. Ganesh, Chem. Mater., 2018, 30, 4919–4925.
32. J. F. Basbus, M. D. Arce, F. R. Napolitano, H. E. Troiani, J. A. Alonso, M. E. Saleta, M. A. González, G. J. Cuello, M. T. Fernández-Díaz, M. P. Sainz, N. Bonanos, C. E. Jimenez, L. Giebeler, S. J. A. Figueroa, A. Caneiro, A. C. Serquis and L. V. Mogni, ACS Appl. Energy Mater., 2020, 3, 2881–2892.
33. S. McIntosh, J. F. Vente, W. G. Haije, D. H. A. Blank and H. J. M. Bouwmeester, Solid State Ionics, 2006, 177, 833–842.
34. S. McIntosh, J. F. Vente, W. G. Haije, D. H. A. Blank and H. J. M. Bouwmeester, Chem. Mater., 2006, 18, 2187–2193.
35. A. Navrotsky, AIP Conf. Proc., 2000, 535, 288–296.
36. J. Cheng, A. Navrotsky, X. D. Zhou and H. U. Anderson, J. Mater. Res., 2005, 20, 191–200.
37. H. J. Avila-Paredes, T. Shvareva, W. Chen, A. Navrotsky and S. Kim, Phys. Chem. Chem. Phys., 2009, 11, 8580–8585.
38. M. Zhao, Y. Xu, L. Shuller-Nickles, J. Amoroso, A. I. Frenkel, Y. Li, W. Gong, K. Lilova, A. Navrotsky and K. S. Brinkman, J. Am. Ceram. Soc., 2019, 102, 4314–4324.
39. H. Xu, L. Wu, J. Zhu and A. Navrotsky, J. Nucl. Mater., 2015, 459, 70–76.
40. C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Science, 2015, 349, 1321–1326.
41. L. Van Eijck, L. D. Cussen, G. J. Sykora, E. M. Schooneveld, N. J. Rhodes, A. A. Van Well and C. Pappas, J. Appl. Crystallogr., 2016, 49, 1398–1401.
42. V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr. - Cryst. Mater., 2014, 229, 345–352.
43. A. Navrotsky, MRS Bull., 1997, 22, 35–41.
44. A. Navrotsky, Engineering, 2019, 5, 366–371.
45. A. Navrotsky, Phys. Chem. Miner., 1997, 24, 222–241.
46. A. Navrotsky, J. Am. Ceram. Soc., 2014, 97, 3349–3359.
47. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
48. J. Hubbard, Proc. R. Soc. London, Ser. A, 1963, 276, 238–257.
49. V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808.
50. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
51. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
52. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
53. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
54. C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728.
55. M. Shang, J. Tong and R. O'Hayre, RSC Adv., 2013, 3, 15769.
56. L. Zhang, J. Shan and Q. Wang, J. Alloys Compd., 2019, 771, 221–227.
57. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767.
58. F. Dong, Y. Chen, D. Chen and Z. Shao, ACS Appl. Mater. Interfaces, 2014, 6, 11180–11189.
59. V. Cascos, J. A. Alonso and M. T. Fernández-Díaz, Materials, 2016, 9, 1–12.
60. A. Aguadero, J. A. Alonso, D. Pérez-Coll, C. De La Calle, M. T. Fernández-Díaz and J. B. Goodenough, Chem. Mater., 2010, 22, 789–798.
61. J. I. Lee, K. Y. Park, H. Park, H. Bae, M. Saqib, K. Park, J. S. Shin, M. Jo, J. Kim, S. J. Song, E. D. Wachsman and J. Y. Park, J. Power Sources, 2021, 510, 230409.
62. M. D. Gonçalves, P. S. Maram, R. Muccillo and A. Navrotsky, J. Mater. Chem. A, 2014, 2, 17840–17847.
63. L. Wang, A. Navrotsky, R. Stevens, B. F. Woodfield and J. Boerio-Goates, J. Chem. Thermodyn., 2003, 35, 1151–1159.
64. N. H. Perry, T. O. Mason, C. Ma, A. Navrotsky, Y. Shi, J. S. Bettinger, M. F. Toney, T. R. Paudel, S. Lany and A. Zunger, J. Solid State Chem., 2012, 190, 143–149.
65. K. I. Lilova, F. Xu, K. M. Rosso, C. I. Pearce, S. Kamali and A. Navrotsky, Am. Mineral., 2012, 97, 164–175.
66. A. V. Radha, O. Bomati-Miguel, S. V. Ushakov, A. Navrotsky and P. Tartaj, J. Am. Ceram. Soc., 2009, 92, 133–140.
67. P. Zhang, A. Navrotsky, B. Guo, I. Kennedy, A. N. Clark, C. Lesher and Q. Liu, J. Phys. Chem. C, 2008, 112, 932–938.
68. R. A. Robie and B. S. Hemingway, Thermodynamic Properties of Minerals and Related Substances at 298.15 K and 1 Bar (10⁵ pascals) Pressure and at Higher Temperatures, 1995.
69. T. S. Zhang, J. Ma, H. Cheng and S. H. Chan, Mater. Res. Bull., 2006, 41, 563–568.
70. D. Han and T. Uda, J. Mater. Chem. A, 2018, 6, 18571–18582.
71. O. Mentré, M. Iorgulescu, M. Huvé, H. Kabbour, N. Renaut, S. Daviero-Minaud, S. Colis and P. Roussel, Dalton Trans., 2015, 44, 10728–10737.
72. A. Diatta, C. V. Colin, R. Viennois, M. Beaudhuin, J. Haines, P. Hermet, A. van der Lee, L. Konczewicz, P. Armand and J. Rouquette, J. Am. Chem. Soc., 2024, 146, 15027–15035.
73. S. W. Strauss, I. Fankuchen and R. Ward, J. Am. Chem. Soc., 1951, 73, 5084–5086.
74. K. Efimov, O. Czuprat and A. Feldhoff, J. Solid State Chem., 2011, 184, 1085–1089.
75. O. Czuprat, M. Arnold, S. Schirrmeister, T. Schiestel and J. Caro, J. Membr. Sci., 2010, 364, 132–137.
76. J. Cheng and A. Navrotsky, J. Solid State Chem., 2004, 177, 126–133.
77. W. Chen and A. Navrotsky, J. Mater. Res., 2006, 21, 3242–3251.
78. M. Aizenshtein, T. Y. Shvareva and A. Navrotsky, J. Am. Ceram. Soc., 2010, 93, 4142–4147.
79. S. Buyukkilic, T. Shvareva and A. Navrotsky, Solid State Ionics, 2012, 227, 17–22.
80. M. S. Khan, M. S. Islam and D. R. Bates, J. Phys. Chem. B, 1998, 102, 3099–3104.
81. K. Huang, R. S. Tichy and J. B. Goodenough, J. Am. Ceram. Soc., 1998, 81, 2565–2575.
82. E. Fabbri, D. Pergolesi, S. Licoccia and E. Traversa, Solid State Ionics, 2010, 181, 1043–1051.
83. S. Kotsantonis and J. A. Kilner, Solid State Ionics, 2011, 192, 168–171.
84. P. J. Gellings and H. J. M. Bouwmeester, The CRC Handbook of Solid State Electrochemistry, CRC Press, 1997.
85. S. Y. Jeon, M. B. Choi, H. N. Im, J. H. Hwang and S. J. Song, J. Phys. Chem. Solids, 2012, 73, 656–660.
86. L. Wang, R. Merkle and J. Maier, J. Electrochem. Soc., 2010, 157, B1802.
87. L. Wang, R. Merkle, J. Maier, T. Acartürk and U. Starke, Appl. Phys. Lett., 2009, 94, 1–4.
88. S. Imashuku, T. Uda, Y. Nose, G. Taniguchi, Y. Ito and Y. Awakura, J. Electrochem. Soc., 2009, 156, B1.
89. Z. Li, X. Mao, D. Feng, M. Li, X. Xu, Y. Luo, L. Zhuang, R. Lin, T. Zhu, F. Liang, Z. Huang, D. Liu, Z. Yan, A. Du, Z. Shao and Z. Zhu, Nat. Commun., 2024, 15, 9318.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06417h

‡ These authors contributed equally to this work.

---