 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Amorphous-like thermal conductivity and high thermoelectric figure of merit in “π” SnS and SnSe†
Min
Zhang
 a,
Ioanna
Pallikara
ab,
Joseph M.
Flitcroft
a,
Ioanna
Pallikara
ab,
Joseph M.
Flitcroft
 a and
Jonathan M.
Skelton
a and
Jonathan M.
Skelton
 *a
*a
aDepartment of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK. E-mail: jonathan.skelton@manchester.ac.uk
bSchool of Chemical and Process Engineering, University of Leeds, Woodhouse Lane, Leeds LS2 9JT, UK
First published on 3rd January 2025
Abstract
We present a detailed first-principles characterisation of the thermoelectric performance of the cubic “π” phases of SnS and SnSe. The complex structures push the “particle-like” contribution to the lattice thermal conductivity, κlatt, below the amorphous limit, resulting in an ultra-low κlatt from room temperature upwards. The cubic symmetry supports larger Seebeck coefficients than the orthorhombic phases, but higher carrier effective masses and stronger electron scattering require high doping levels to optimise the conductivity and power factors. For π SnSe, we predict a low-temperature n-type figure of merit, ZT, comparable to Bi2Te3, and a high-temperature ZT competitive with the flagship orthorhombic SnSe. These results demonstrate the exceptional promise of these systems as high-performance thermoelectrics, and highlight structural complexity as a route to optimising low-temperature ZT by minimising the κlatt.
1 Introduction
With over half of global energy wasted as heat,1,2 practical heat recovery is critical from both an environmental and economic standpoint. Thermoelectric (TE) power directly converts heat to electricity through the Seebeck effect in a TE material, with potential applications to energy harvesting and for improving energy efficiency at multiple scales.2 The performance of a TE material is expressed by the dimensionless figure of merit ZT:2,3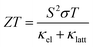 | (1) |
A variety of materials have been studied as prospective TEs including chalcogenides, skutterudites, half-Heuslers, zintl compounds, clathrates, oxides, and oxychalcogenides (ref. 9 and references therein). The current industry-standard materials for low- and high-temperature applications are based on Bi2Te3 (ZT ≃ 1 from 350–450 K,2ZT up to 1.9 reported for nanostructured (Bi1−xSbx)Te3 alloys10,11) and PbTe (ZT up to 2.2 at 915 K with endotaxial nanostructuring12). However, the low abundance of Te precludes widespread adoption, and thus alternative materials composed of more abundant elements are critical.2
The discovery of high ZT in orthorhombic SnSe (up to 2.6 in single crystals13 and 3.1 in polycrystalline samples14) has led to considerable interest in the group IV–VI sulphides and selenides. The favourable electrical properties of these materials are well established from the use of SnS as a photovoltaic (PV) absorber material,15 and SnS and SnSe both show unusually low κlatt associated with the high-temperature Pnma → Cmcm phase transition.16–19 However, the “headline” ZT in orthorhombic SnSe is only achieved at high temperature, whereas many potential applications require the recovery of low-grade waste heat,2 and so orthorhombic SnSe cannot replace Bi2Te3.
While the thermoelectric performance of orthorhombic SnS and SnSe is well characterised, the IV–VI chalcogenides display a rich structural chemistry, with several potential phases that could show superior low-temperature performance (Fig. 1).21–23 Among these, the recently-discovered metastable cubic “π” phase of SnS and SnSe24–26 have shown considerable potential for PV applications.27–29 A recent study of the IV–VI chalcogenides also revealed new structural–property relationships that suggest the π structure should lend itself to low κlatt.23 The potential thermoelectric performance of the π phases has been explored in several computational studies,30–32 but significant approximations in the calculations mean the results are at best indicative.
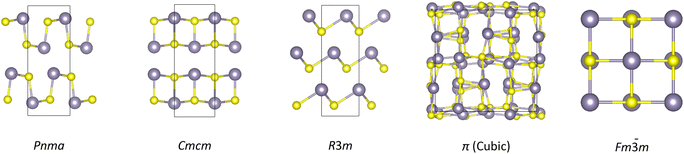 | ||
Fig. 1 Structures adopted by the group IV–VI monochalcogenides: orthorhombic Pnma and Cmcm, rhombohedral R3m, and cubic π (P213) and rocksalt (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) phases. These images were prepared using VESTA.20 m) phases. These images were prepared using VESTA.20 | ||
We have developed a fully ab inito workflow for predicting ZT, by combining state-of-the-art approaches to computing the S, σ, κel and κlatt,33–35 which we and others have validated against multiple classes of TE materials including chalcogenides,36,37 oxides38–40 and oxychalcogenides.41,42 In this study, we apply this workflow to obtain high-quality reference predictions of the thermoelectric performance of π SnS and SnSe. π SnS and SnSe have lower κlatt and higher (absolute) S than the corresponding orthorhombic phases, but at the cost of higher carrier effective masses, stronger electron scattering, and lower σ, which requires heavier doping to offset. The majority of the κlatt occurs through intraband tunnelling characteristic of amorphous materials,43,44 leading to very low thermal conductivity at and above room temperature. With n-type doping at the level achieved in experiments on p-type SnS and SnSe,45,46 π SnSe has a low-temperature ZT comparable to Bi2Te3 and a high-T ZT competitive with orthorhombic SnSe, resulting in a large average ZT for low- to mid-temperature applications. More generally, these findings highlight targeting structural complexity as a viable strategy for suppressing the low-T κlatt in TE materials to optimise the ZT toward more widespread heat-recovery applications.
2 Computational methods
Calculations were performed using plane-wave density-functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP) code.47 Initial structures of π SnS and SnSe were taken from previous work22 and optimised to tight tolerances of 10−8 eV on the total energy and 10−2 eV Å−1 on the forces. PBEsol+D3 (ref. 48 and 49) was used to describe electron exchange and correlation, as this has been shown to provide an accurate description of the structure and dynamics of these materials.21 Projector-augmented wave (PAW) pseudopotentials50,51 were used to describe the ion cores, with the valence configurations: Sn – 5s25p2, S – 3s23p4, and Se – 4s24p4. A plane-wave basis with a kinetic-energy cutoff of 600 eV was employed with a 4 × 4 × 4 Γ-centred Monkhorst–Pack k-point mesh52 to model the valence electrons.Phonon and κlatt calculations were performed using the Phonopy and Phono3py codes.35,53 The second-order (harmonic) force constants were obtained using a displacement step of 10−2 Å and 2 × 2 × 2 supercell expansions with 512 atoms. The third-order (anharmonic) force constants were computed using a step of 3 × 10−2 Å and the 64-atom unit cells. Phonon dispersion curves were obtained by interpolating the frequencies along q-point paths between the high-symmetry points in the P213 Brillouin zone. Atom-projected density of states (PDoS) curves were obtained from frequencies evaluated on uniform Γ-centered q-point grids with 24 × 24 × 24 subdivisions. The “particle-like” contribution to the κlatt was determined by solving the phonon Boltzmann transport equation (BTE) within the single-mode relaxation-time approximation (SM-RTA), using modal properties computed on 10 × 10 × 10 Γ-centered q-point grids. Testing on smaller 8 × 8 × 8 meshes confirmed the SM-RTA and full linarised BTE solution54 are quantitatively similar (Fig. S1, ESI†). The “wave-like” intraband tunnelling contribution to the κlatt was additionally obtained by solving the Wigner transport equation.43,44
The S, σ and κel were determined by solving the electron BTE within the momentum relaxation-time approximation (MRTA) as implemented in the AMSET code.34 Accurate electronic bandgaps, Eg, and uniform band structures were obtained using non-self-consistent HSE06.55,56 Energy- and momentum-dependent electron relaxation times were estimated from the rates of acoustic deformation potential (ADP), ionized impurity (IMP), piezoelectric (PIE), and polar optical phonon (POP) scattering.34 The deformation potentials were determined from single-point calculations on deformed structures generated with AMSET. The elastic constant matrices C, high-frequency/static dielectric constants ε∞/εS, Born effective-charge tensors Z* and piezoelectric tensors e(0) were obtained using the finite differences and density-functional perturbation theory (DFPT) approaches in VASP.57,58 All properties were computed with PBEsol+D3 apart from the ε∞, which were computed using non-self-consistent HSE06. The POP frequencies ωpo were calculated by combining the phonon frequencies at q = Γ from Phonopy with the Z* from DFPT.58k-point convergence tests and validation of non-self-consistent HSE06 are provided in Table S1.†
Finally, defect calculations were performed to investigate potential dopants for the π phases, requiring additional calculations on a set of reference elemental metals and metal chalcogenides/halides and a series of Pnma and π SnS and SnSe models with atomic substitutions. A list of reference systems, and the chosen k-point meshes, are provided in Table S2.†
Additional details of the calculations and analysis performed in this work, including key equations, are provided in Section 1 of the ESI.†
3 Results and discussion
3.1 Structure, dynamics and lattice thermal conductivity
The structural chemistry of the Group IV–VI oxides and chalcogenides is strongly influenced by the stereochemical activity of the valence ns2 lone pair on the tetrel T2+ cations. This gives rise to five structure types across the TCh series (T = Ge/Sn/Pb, Ch = S/Se/Te), viz. a high-symmetry cubic rocksalt phase (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m spacegroup), two low-symmetry orthorhombic phases (Pnma, Cmcm), and intermediate-symmetry rhombohedral and cubic π phases (R3m/P213) (Fig. 1).
m spacegroup), two low-symmetry orthorhombic phases (Pnma, Cmcm), and intermediate-symmetry rhombohedral and cubic π phases (R3m/P213) (Fig. 1).
The heavier PbCh form the rocksalt structure, in which the Pb2+ cations adopt a centrosymmetric octahedral environment with six equal Pb–Ch bond lengths and the 6s2 lone pairs are inactive. For GeS/GeSe and SnS/SnSe, the “strain” induced by placing the Ge2+/Sn2+ in a centrosymmetric environment leads to an energetic preference for the orthorhombic Pnma structure, where the “pseudo-2D” layered structure and three-coordinate geometry allow the 4s2/5s2 lone pairs to project into an interlayer void space. The R3m phase adopted by GeTe, and by SnTe at low temperature, lies between these extremes, with a cation off-centering along the rocksalt {111} direction giving three short and three long T–Te bonds and a partial relaxation of the strain in the higher-symmetry phase.
The π structure is a distorted 2 × 2 × 2 expansion of the eight-atom rocksalt conventional cell, and differs significantly from the rhombohedral phase in that it retains a cubic P213 spacegroup but with a larger primitive cell with na = 64 atoms. The Pnma structure has one unique Sn site with one short and two long bonds to chalcogen atoms (Table S3†). In contrast, the π structure has four Sn sites, with 2 × 4 atoms in rhombohedral-like sites with three equivalent Sn–Ch distances and the other 2 × 12 in sites with three different Sn–Ch bond lengths.
We predict optimised lattice constants of a = 11.38 and 11.77 Å for π SnS and SnSe, respectively, which are within 2% of the measured a = 11.6 and 11.97 Å.24,26 Previous studies have shown that both π phases are dynamically stable (i.e. there are no imaginary modes in the phonon dispersion curves) and energetically metastable with respect to the orthorhombic phases of SnS and the orthorhombic and rocksalt phases of SnSe.21,22,31,59 Our calculated phonon spectra confirm the dynamical stability, with real frequencies across the Brillouin zone (Fig. 2 and S2†).
 | ||
| Fig. 2 Phonon dispersion and density of states (DoS) of π SnS. The blue and orange shaded regions show the projections of the DoS onto the Sn and S atoms, respectively. | ||
Using the SM-RTA we predict room-temperature κlatt from “particle-like” transport, κp, of 0.26 and 0.18 W m−1 K−1 for π SnS and SnSe. These are well below the averaged values of 0.96–5.01 W m−1 K−1 for IV–VI chalcogenides in the other structure types in Fig. 1 obtained from similar calculations.23 We previously showed that low κlatt in the IV–VI chalcogenides arises from a balance of low phonon group velocities and a large “phase space” of energy- and momentum-conserving phonon scattering pathways, favoured by structure types with large primitive cells, and strong three-phonon interactions, favoured in structures where the T2+ are constrained to locally-symmetric environments.23 Separating the κp into harmonic (group velocity) and weighted-average lifetime components, κ/τCRTA and τCRTA, confirms the large unit cell of the π structure reduces the group velocities by ∼75–80% compared to the Pnma phases (Fig. 3(a)). The τCRTA of π SnS and SnSe are also around 30 and 50% smaller above 300 K (Fig. 3(b)). We stress that we only use the CRTA model to determine a weighted-average lifetime to compare materials, and we do not use this approximation to calculate the κlatt. Comparison of the “phase space” functions ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2(ω) indicate that the π phases show comparable numbers of scattering pathways to the Pnma phases, but with higher spectral weight at low frequency (Fig. 3(c)). This does not follow the trend with unit-cell size in our previous study,23 indicating that the larger numbers of energy-conserving scattering channels potentially enabled by the denser phonon dispersions may be offset by momentum conservation restrictions from the higher cubic symmetry. The calculated
2(ω) indicate that the π phases show comparable numbers of scattering pathways to the Pnma phases, but with higher spectral weight at low frequency (Fig. 3(c)). This does not follow the trend with unit-cell size in our previous study,23 indicating that the larger numbers of energy-conserving scattering channels potentially enabled by the denser phonon dispersions may be offset by momentum conservation restrictions from the higher cubic symmetry. The calculated ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) place the anharmonicity in the π phases between the Pnma and R3m phases (Fig. 3(d)), which can be ascribed to 25% of the Sn atoms being in more constrained rhombohedral-like environments (cf. Table S3†).
place the anharmonicity in the π phases between the Pnma and R3m phases (Fig. 3(d)), which can be ascribed to 25% of the Sn atoms being in more constrained rhombohedral-like environments (cf. Table S3†).
 | ||
Fig. 3 Analysis of the “particle-like” thermal conductivity, κp, of π SnS and SnSe using the models employed in our previous studies.23,60,61 (a)/(b) Separation of the scalar average κp into a harmonic term κ/τCRTA (a) and weighted-average lifetime τCRTA (b). The κ/τCRTA and τCRTA are indicative of differences in the phonon group velocities and lifetimes, respectively. (c) Scaled average number of energy- and momentum-conserving three-phonon scattering channels (“phase space”, ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2) as a function of frequency. (d) Weighted-average three-phonon interaction strengths 2) as a function of frequency. (d) Weighted-average three-phonon interaction strengths ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) compared to other IV–VI chalcogenides, including Pnma SnS and Ge/Sn selenides and tellurides in the crystal phases shown in Fig. 1. Where applicable, ranges are indicated by error bars. The data for Pnma SnS and SnSe in (a)–(c) are taken from our previous work.61 The compared to other IV–VI chalcogenides, including Pnma SnS and Ge/Sn selenides and tellurides in the crystal phases shown in Fig. 1. Where applicable, ranges are indicated by error bars. The data for Pnma SnS and SnSe in (a)–(c) are taken from our previous work.61 The ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) in (d) are taken from our previous study,23 but include the in (d) are taken from our previous study,23 but include the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) for Pnma SnS from ref. 61. for Pnma SnS from ref. 61. | ||
The dense phonon dispersions result in very small intraband spacing (cf.Fig. 2), which, combined with the short lifetimes, suggests “wave-like” heat transport through intraband tunnelling, characteristic of amorphous materials, is likely to be significant.43,44 The condition suggested in ref. 44 is:
 | (2) |
 | ||
| Fig. 4 Lattice thermal conductivity κlatt of π SnS and SnSe. (a) Contribution of “particle-like” and “wave-like” transport κp/κw to the total κlatt of π SnSe. (b) Comparison of the scalar average κlatt of π SnS and SnSe to the orthorhombic Pnma phases. For the two Pnma phases, we show both the orientationally-averaged κlatt (solid lines) and the κlatt along the layering direction (crystallographic b axis; dashed lines). Data for the Pnma phases were taken from our previous work61 and the κlatt were recalculated to include the κw contribution. | ||
To the best of our knowledge the κlatt of π SnS and SnSe have not been measured. We previously predicted a room-temperature lattice thermal conductivity of 0.13 W m−1 K−1 for π SnS.62 However, this calculation did not account for intraband tunneling and is equivalent to the κp obtained in the present study. Using the data from ref. 62, we obtain a κw of 0.32 W m−1 K−1 and a total κlatt of 0.45 W m−1 K−1 (Fig. S6†), which is 26% lower than predicted in the present work. One possible explanation for this discrepancy is the use of a dispersion correction in the present calculations, which has a small but noticeable effect on the phonon dispersion (Fig. S7†).61 This can be ascribed to the ∼3.3% smaller equilibrium volume predicted with the dispersion correction, since the phonon frequencies, and, by extension, κlatt, can be highly sensitive to the volume.63
Related to this point, the anharmonicity in the π phases could indicate large thermal expansion, which could have a significant impact on the κlatt. Using the quasi-harmonic phonon calculations in our previous work,22 we estimate volume expansions of 4.1 and 4.3%, relative to the athermal equilibrium volume, V0, for π SnS and SnSe, respectively, at T = 900 K (Fig. S8†). Given the large cost of computing the third-order force constants, it is not feasible to perform “full” κlatt calculations at these expanded cell volumes. Instead, we adopt the approximate model used in our previous work,61,64 and combine harmonic phonon calculations at 3.5/6.6 and 3.4/6.5% expanded volumes of π SnS and SnSe, respectively, from the calculations in ref. 22 with the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) obtained at V
obtained at V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) V0 in the present work (see Section 1.4 of the ESI†). This method accounts for the effect of thermal expansion on the phonon group velocities and three-phonon scattering phase space, under the assumption that the average three-phonon interaction strengths are similar to those at the equilibrium volume. Expansion of the unit cell leads to a reduction in the phonon frequencies and, consequently, the κlatt (Fig. S9–S12†). With a ∼3.5% expanded volume, we predict a reduction in κlatt of around 13% at T = 900 K (24% at a larger ∼6.5% expanded volume), due mostly to a reduction in the κw (Fig. S11/S12†). We therefore conclude that thermal expansion may have a moderate impact on the κlatt of the π phases, and that our predicted κlatt at high T is likely to be overestimated. For π SnS, we predict that a 3.5% volume expansion will reduce the κlatt by 18% at 300 K, which suggests that differences in the predicted V0 largely do account for the discrepancy between the present work and our previous calculation.62
V0 in the present work (see Section 1.4 of the ESI†). This method accounts for the effect of thermal expansion on the phonon group velocities and three-phonon scattering phase space, under the assumption that the average three-phonon interaction strengths are similar to those at the equilibrium volume. Expansion of the unit cell leads to a reduction in the phonon frequencies and, consequently, the κlatt (Fig. S9–S12†). With a ∼3.5% expanded volume, we predict a reduction in κlatt of around 13% at T = 900 K (24% at a larger ∼6.5% expanded volume), due mostly to a reduction in the κw (Fig. S11/S12†). We therefore conclude that thermal expansion may have a moderate impact on the κlatt of the π phases, and that our predicted κlatt at high T is likely to be overestimated. For π SnS, we predict that a 3.5% volume expansion will reduce the κlatt by 18% at 300 K, which suggests that differences in the predicted V0 largely do account for the discrepancy between the present work and our previous calculation.62
Other computational studies31,32 predicted room-temperature κlatt of 5.15 and 2.54/0.86 W m−1 K−1 for π SnS and SnSe using the Slack model,65 but the larger predictions suggest this model is likely not appropriate for these systems. On the other hand, ref. 31 predicted thermal conductivities of 0.49 and 0.32 W m−1 K−1 for π SnS and SnSe using the Cahill model for the minimum thermal conductivity,66 which are remarkably similar to the present calculations.
3.2 Electrical transport
The calculated electronic band structures and DoS of π SnS and SnSe (Fig. S13†) are comparable to previous studies67,68 and yield direct bandgaps of Eg = 1.61 and 1.28 eV that are an excellent match to experimental measurements25,26 and previous calculations.31,67 The σ, S and κel of the π phases were calculated as a function of temperature and an extrinsic carrier concentration n (“doping level”) by solving the electron BTE33 with energy- and monentum-dependent electron scattering rates from four scattering processes common to semiconductors.34 With this approach, we estimate per-state electron lifetimes, which is an improvement on previous computational studies that have determined the σ and κel with respect to an unknown, fixed or state-independent relaxation times.30–32The doping level is a key parameter for optimising the electrical properties of semiconductor thermoelectrics.3Pnma SnS and SnSe can be both p-type (hole) and n-type (electron) doped14,15,45,69–72 at n up to 5 × 1019 cm−3.45,46,71Fig. 5 shows the predicted σ, absolute |S|, PF S2σ and κel of the π and Pnma36,37 phases of SnS and SnSe, for p- and n-type doping with n = 1016–1020 cm−3 and T = 700 K. This temperature was chosen to be well below the high-temperature Pnma → Cmcm phase transitions in orthorhombic SnS and SnSe (T = 878/807 K73).
 | ||
| Fig. 5 Predicted electrical properties of π SnS and SnSe as a function of extrinsic carrier concentration n (“doping level”) at T = 700 K: (a) electrical conductivity σ, (b) absolute Seebeck coefficient |S|, (c) power factor S2σ (PF), and (d) electronic thermal conductivity κel. Data for p- and n-type doping are shown by solid and dashed lines respectively. Predicted orientationally-averaged properties for Pnma SnS and SnSe taken from our previous studies36,37 are shown for comparison. | ||
The π phases are predicted to have 10–20× lower σ with p-type doping, and ∼10× lower σ with n-type doping, than their Pnma counterparts (Fig. 5(a)). This is partially offset by a 1.5–2× larger |S| (Fig. 5(b)), but the net result is that the Pnma phases have up to 8× larger PFs at a reference n = 4 × 1019 cm−3. As for the Pnma phases,37 we predict larger σ but comparable |S| with n-type doping, yielding reasonable PFs of 1.1 and 1.4 mW m−1 K−2 for π SnS and SnSe, respectively, that can be enhanced to 1.7 and 2.3 mW m−1 K−2 at a larger n = 1020 cm−3 (Fig. 5(c)). On the other hand, at higher n the κel are proportional to the σ through the Wiedemann–Franz law,
| κel = LσT | (3) |
The electrical conductivity is given by:
 | (4) |
 , obtained from a weighted average over the bands that contribute to the transport. The Seebeck coefficient is related to the Seebeck effective mass
, obtained from a weighted average over the bands that contribute to the transport. The Seebeck coefficient is related to the Seebeck effective mass  and n according to:3
and n according to:3 | (5) |
 and
and  for the Pnma and π phases of SnS and SnSe were determined according to the procedure in ref. 74 at a nominal n = 4 × 1019 cm−1 and T = 700 K, and are presented in Table S4.† We calculate
for the Pnma and π phases of SnS and SnSe were determined according to the procedure in ref. 74 at a nominal n = 4 × 1019 cm−1 and T = 700 K, and are presented in Table S4.† We calculate  between 1.1–2.5 me for the π phases, which are ∼5−10× larger than the corresponding 0.15–0.27 me for the Pnma phases. On the other hand, the
between 1.1–2.5 me for the π phases, which are ∼5−10× larger than the corresponding 0.15–0.27 me for the Pnma phases. On the other hand, the 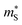 of the π phases are 3–4× larger than those of the Pnma phases. These differences partially account for the lower conductivity and higher Seebeck coefficients of the π phases. Furthermore, the
of the π phases are 3–4× larger than those of the Pnma phases. These differences partially account for the lower conductivity and higher Seebeck coefficients of the π phases. Furthermore, the  for electrons are around 30 and 45–50% lower than holes in the Pnma and π phases, respectively, whereas the
for electrons are around 30 and 45–50% lower than holes in the Pnma and π phases, respectively, whereas the 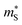 differ by <10%, which explains the larger predicted n-type conductivity and power factors.
differ by <10%, which explains the larger predicted n-type conductivity and power factors.
The  and
and 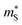 can be used to calculate the Fermi surface complexity factor
can be used to calculate the Fermi surface complexity factor  , where
, where 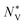 is the effective valley degeneracy, i.e. the number of band extrema involved in the transport, and K* is the effective anisotropy factor that describes the shape of the carrier pockets in the Fermi surface.74 The
is the effective valley degeneracy, i.e. the number of band extrema involved in the transport, and K* is the effective anisotropy factor that describes the shape of the carrier pockets in the Fermi surface.74 The  shows a strong correlation to the maximum power factor, and values above ∼10 are characteristic of materials such as the lead chalcogenides where features of the electronic structure are known to contribute significantly to the thermoelectric performance.74–76 We calculate
shows a strong correlation to the maximum power factor, and values above ∼10 are characteristic of materials such as the lead chalcogenides where features of the electronic structure are known to contribute significantly to the thermoelectric performance.74–76 We calculate  for p-type Pnma SnS/SnSe and 8.2/11 for the n-type materials, while the larger
for p-type Pnma SnS/SnSe and 8.2/11 for the n-type materials, while the larger 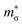 of the π phases result in 60–80% smaller values of 1.1/1.7 and 3.2/3.7. This implies that the electronic structures of the Pnma phases show features that are beneficial for the thermoelectric properties, and that these features are largely absent in the π phases. While we do not calculate the NV or K explicitly, the values of
of the π phases result in 60–80% smaller values of 1.1/1.7 and 3.2/3.7. This implies that the electronic structures of the Pnma phases show features that are beneficial for the thermoelectric properties, and that these features are largely absent in the π phases. While we do not calculate the NV or K explicitly, the values of 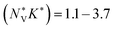 predicted for the π phases suggest either a low effective valley degeneracy and/or an effective anisotropy K < 1.
predicted for the π phases suggest either a low effective valley degeneracy and/or an effective anisotropy K < 1.
Furthermore, comparing the carrier mobilities as a function of n indicates the μ are also an order of magnitude lower in the π phases (Fig. S14/S15†). The μ of both the Pnma and π phases is limited by polar-optic phonon (POP) scattering36,37 (Fig. S14–S17†), for which the scattering rates are proportional to the POP frequency ωpo and inversely proportional to the high-frequency and static dielectric constants ε∞/εS.34,77 The π phases have larger ωpo and smaller ε, which both favour stronger scattering. The lower σ of the π phases can therefore be explained both by larger carrier masses, as discussed above, and stronger (POP) carrier scattering.
The temperature dependence of the electrical properties is typically secondary to doping level. At the larger n required to obtain reasonable PFs, the S2σ of the π phases decrease with temperature due to a metallic-like decrease in σ typical of heavily-doped (“degenerate”) semiconductors (Fig. S18/S19†). As in the Pnma phases, this is partially offset by an increase in the |S|,36,37 but for n-type π-SnSe there is a ∼30% reduction in the PF, from ∼2 to 1.4 mW m−1 K−2, between 300–700 K at our reference n = 4 × 1019 cm−3.
There have been a limited number of experimental studies on the π phases for photovoltaic applications. Measurements on thin films of n-type π SnS yielded a conductivity of 0.1 S cm−1 at 673 K and n = 3.7 × 1017 cm−3,78 which is comparable to our predicted 0.7 S cm−1. Similarly, measurements on Sn(S0.45Se0.55) films obtained a p-type conductivity of 2 × 10−2 S cm−1 at 723 K and n = 1016 cm−3,79 which falls between our predicted σ = 0.9 × 10−2 and 6 × 10−2 S cm−1 for π SnS and SnSe. Nair et al. reported that the room-temperature σ of Pnma SnS and SnSe are 2–3 orders of magnitude larger than the corresponding π phases,28 which is qualitatively consistent with our findings. The Seebeck coefficients of 485 and 314 μV K−1 measured for p-type SnS–SnSe and SnS–SnSe–SnS stacks, with n = 9 × 1015 and 1015 cm−3 respectively,80 are less than half the maximum we predict. Our calculations on both π structures suggest the S change sign with temperature at low n, which could account for this discrepancy (Fig. S18/S19†).
We predict Seebeck coefficients of |S| ≃ 300–600 μV K−1 at carrier concentrations between 1019–1020 cm−3, which are similar to the calculations in ref. 31. However, the electron lifetimes in ref. 31 were calculated from the deformation potential, and do not account for the dominant POP scattering, so the predicted conductivity is significantly larger than in the present study. Our predictions of higher σ and PFs with n-type doping are also qualitatively consistent with the “reduced” values from the calculations in ref. 30.
3.3 Thermoelectric figure of merit
Combining the S, σ, κel and κlatt allows us to predict the figure of merit ZT as a function of doping level and temperature (eqn (1)) For n-type π SnSe, an industrially-viable ZT > 1 can be obtained at T as low as 300 K, and ZT ≃ 3, comparable to state-of-the-art experiments on orthorhombic SnSe,14 can be obtained at high temperature (Fig. 6(b)). With n = 4 × 1019 cm−3 we predict maximum ZT, ZTmax, of 1.6 and 2.4 for n-type π SnS and SnSe, respectively, close to the orthorhombic Pnma → Cmcm transition temperatures of 878 and 800 K73 (Table S4†). These are larger than the ZTmax of the p-type Pnma phases predicted by similar calculations, and very similar to the n-type ZTmax (Table S4†).36,37 Larger n = 1020 cm−3 improve the limiting electrical conductivity and PFs of the π phases, yielding significantly improved ZTmax of 2.2 and 3. Both the Pnma and π phases are predicted to show superior performance with n-type doping,37 but the differences are much larger in the π phases, with p-type ZT > 1 only attainable at high T and large n (Fig. S20 and Table S5†).Previous theoretical studies have predicted p-type ZT of 0.83 and 1.2 for π SnS and SnSe, respectively, at 800 K31 and ZT between 0.74 and 1 between 300–900 K for π SnSe.30,32 At the same T = 800 K and n = 1020 cm−3 employed in ref. 31, we predict larger p-type ZT = 1.21 and comparable ZT = 1.25 for π SnS and SnSe. This study also predicted higher S2σ with p-type doping, in contrast to our results, which is likely due to the neglect of POP scattering when calculating the σ as noted above. The calculated ZT in ref. 30 are obtained by neglecting the κlatt entirely, while ref. 32 estimates the κlatt with the Slack model and uses a constant electron relaxation time to calculate the σ and κel, all of which are likely to be poor approximations. However, since neither study specifies the carrier concentration(s) at which the ZT were calculated, it is impossible to compare to our calculations.
While many flagship thermoelectrics perform best at high temperature, the majority of applications require good low-T performance.2 We predict π SnSe to have ZT = 1.1 and 1.3 at 300 K, with n = 4 × 1019 and 1020 cm−3, respectively, which are ∼2–3× larger than p-type Pnma SnSe (Fig. 7(a)). The “device efficiency” η of a thermoelectric generator is given by:2
 | (6) |
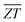 is the average ZT for the p- and n-type couple over the temperature range Tc → Th. The continuous increase in the ZT with temperature results in a
is the average ZT for the p- and n-type couple over the temperature range Tc → Th. The continuous increase in the ZT with temperature results in a  that increases continuously up to ∼1.9 and 2.3 at Th = 800 K with the two doping levels (Fig. 7(b)). In contrast, the slower rise in ZT with temperature in Pnma SnSe means
that increases continuously up to ∼1.9 and 2.3 at Th = 800 K with the two doping levels (Fig. 7(b)). In contrast, the slower rise in ZT with temperature in Pnma SnSe means  is only achieved when Th ≥ 650 K. Our results therefore show that n-type π SnSe, given a suitable doping level, could display viable thermoelectric performance for a wide range of low-to-mid temperature applications.
is only achieved when Th ≥ 650 K. Our results therefore show that n-type π SnSe, given a suitable doping level, could display viable thermoelectric performance for a wide range of low-to-mid temperature applications.
 | ||
Fig. 7 Thermoelectric efficiency of n-type π SnS and SnSe. (a) Figure of merit ZT as a function of temperature. (b) Average figure of merit  as a function of the hot-side temperature Th with a cold-side temperature Tc = 300 K. Solid and dashed lines show the predicted as a function of the hot-side temperature Th with a cold-side temperature Tc = 300 K. Solid and dashed lines show the predicted  obtained at doping levels of n = 4 × 1019 and 1020 cm−3 respectively. The predicted orientationally-averaged obtained at doping levels of n = 4 × 1019 and 1020 cm−3 respectively. The predicted orientationally-averaged  of p-type Pnma SnS and SnSe with n = 4 × 1019 cm−3 are shown for comparison. These data were taken from our previous studies,36,37 but the lattice thermal conductivities κlatt were recalculated to include the intraband tunnelling contribution κw. of p-type Pnma SnS and SnSe with n = 4 × 1019 cm−3 are shown for comparison. These data were taken from our previous studies,36,37 but the lattice thermal conductivities κlatt were recalculated to include the intraband tunnelling contribution κw. | ||
A similar contrast is seen between π and Pnma SnS, i.e. the π phase performs better at low T and therefore shows a higher  over a wide temperature range. However, the generally lower ZT means the threshold of
over a wide temperature range. However, the generally lower ZT means the threshold of  is not reached until Th = 675 K (500 K with n = 1020 cm−3). However, for larger Th = 880 K we predict reasonable
is not reached until Th = 675 K (500 K with n = 1020 cm−3). However, for larger Th = 880 K we predict reasonable  of 1.2 and 1.5 at the two doping levels. For applications where sulphide-based TEs are preferred, exploring doping strategies to maximise the n of π SnS may therefore be facile.
of 1.2 and 1.5 at the two doping levels. For applications where sulphide-based TEs are preferred, exploring doping strategies to maximise the n of π SnS may therefore be facile.
In order to realise our predictions experimentally, the key challenges of synthesising and stabilising the π phases, and optimising the electrical properties, will need to be addressed. π SnS and SnSe have been prepared in nanoparticulate and thin-film form with a variety of techniques including chemical bath deposition (CBD),81 solution synthesis,25,82 spray pyrolysis,83,84 and aerosol-assisted chemical vapour deposition (AACVD).85 A number of experiments have examined thermal stability, with the consensus that π SnS transforms to the Pnma phase on heating to around 600 K or higher.82,84,85 If the stability “window” cannot be widened, π SnS and SnSe could only be used for low-temperature applications.
The structural preferences of the IV–VI chalcogenides can be understood in terms of the stereochemical activity of the tetrel lone pair, which is driven by the interaction between the tetrel and chalcogen atoms.86 Generally, the lighter chalcogenides prefer lower-symmetry phases (e.g. SnS/SnSe and GeS/GeSe adopt the orthorhombic Pnma phase), while heavier chalcogenides prefer higher-symmetry phases (e.g. SnTe, GeTe and the Pb chalcogenides adopt the rhombohedral and rocksalt phases). Previous studies have found that π SnS is closer to the convex hull than π SnSe (ΔG = 2.3 and 3 kJ per mol per F.U. at 300 K).21,22,68 The existence of a direct conversion pathway to the orthorhombic phase has not, to our knowledge, been established, but we have previously considered conversion to the structurally-similar rocksalt phases and obtained energy barriers of 8.5 and 2.2 kJ per mol F.U. for π SnS and SnSe.22 Based on this, admittedly incomplete, information, we suggest that the π phases might be stabilised by elements that favour the Pnma/R3m-like local geometry over the six-coordinate geometry in the rocksalt phases. This suggests that a SnS/SnSe solid solution could be used to stabilise π SnSe, or that alloying with GeS or GeSe could be used to stabilise the π phases of both Sn chalcogenides.
Literature on the relevant properties of the π phases is currently sparse, and the largest n-type carrier concentrations of 4 × 1017 reported to date78 are orders of magnitude lower than we predict are required to achieve high thermoelectric performance. p-type orthorhombic SnS and SnSe have been prepared with n up to 4 × 1019 cm−3,45,46 and experiments on n-doped SnSe have reported comparable n up to 5 × 1019 cm−3.71 Established dopants for the Pnma phases include Na and Ag (p-type),45,46,64 and the halogens Cl and Br (n-type).15,87–89 Several studies have also investigated Sb and Bi as potential n-type dopants, with reported n up to ∼4 × 1019 cm−3.90,91
To determine whether these six dopants might be used to optimise the carrier concentrations of the π phases, we performed a series of calculations to compare the doping energies Ed for substitution into Pnma and π SnS/SnSe (Section 1.6 and Table S6, ESI†). For p-type doping, we predict a negative Ed for Na at the concentrations of ∼3 at% in our models, due to the relative instability of elemental Na, whereas we predict Ed of 1.3–1.5 eV for Ag. The negative Ed for Na is likely due to our not having considered all possible competing phases, but the contrast between the predicted Ed of Na and Ag is nonetheless qualitatively consistent with experiments, where large p-type n have been obtained with Na doping45,46 but a recent study of Ag-doped SnS found that high doping levels of up to 2.78 at% led to segregation of an Ag2SnS3 secondary phase.64 For Cl and Br we predict Ed of 1.5–1.7 and 1.4–1.7 eV, respectively, which compare to values of 0.8–1.1 and 0.6–0.9 eV for Sb and Bi. This suggests that n-type doping by metal substitution at the Sn site may be more facile than halide substitution at the chalcogen site. The calculations predict that all six dopants should fully ionise and not form localised defect levels (Table S6 and Fig. S21–S24†). We note, however, that experiments have shown that Sb can act as an amphoteric dopant,92 with substitution at both the cation and anion sites (Sb3+/Sb3−), and the present calculations do not account for possible substitution at the chalcogen site. It is also unclear whether Bi may show similar amphoteric behaviour.
We predict similar Ed for Na and Ag in SnS and SnSe, but notably higher Ed for the majority of the electron donors in SnS, which suggests that SnSe can be more easily n-type doped. Excluding Na, for which we predict negative Ed for all four materials, we predict 5 and 16% larger Ed for Ag in π SnS and SnSe, respectively, compared to the Pnma phases, and 3–20% larger Ed for the four n-type dopants. This suggests the π phases may be slightly more difficult to dope than their Pnma counterparts, but otherwise have similar defect chemistry, as might be expected given the similar local structures. To further assess the stability of the metal dopants, we calculated the precipitation energies Ep for exsolution of the metal chalcogenide in the presence of a chalcogen reservoir (Table S6†). With the exception of the Ep for Na2S/Na2Se from Pnma SnS and SnSe, which are 70 and 30 meV, respectively, the Ep are negative, indicating that large concentrations of the dopants may not be accommodated unless kinetically trapped. Finally, as a basic “sanity check” on our values, we also compared the formation energies Ef for the metal chalcogenides, including Pnma SnS and SnSe, to both the Materials Project calculations93,94 and to experimental data where available95–101 (Table S7†). We find generally good agreement, which provides some level of confidence in our predicted Ed/Ep.
Based on our analysis, we tentatively suggest that it should be possible to dope π SnS and SnSe to achieve at least n ≈ 5 × 1019 cm−3 using Na as a p-type dopant and Sb or Bi as n-type dopants. However, a comprehensive analysis of the defect chemistry should include intrinsic defects, in particular Sn vacancies, and different charge states. A further consideration is also the impact of doping on the (meta)stability of the π phases, since the generally higher Ed could provide an additional driving force for conversion to the Pnma phase. However, since the π phases are likely to be kinetically formed and trapped, the effect of the dopants on the kinetics of formation and/or the energy barrier to conversion to other phases may be more important considerations. We defer a more comprehensive exploration of these issues to a future study.
4 Conclusions
This work has provided detailed ab inito reference predictions of the transport properties and thermoelectric figure of merit of π SnS and SnSe.As predicted by a previous analysis of the lattice thermal conductivity of the IV–VI chalcogenides, the complex structure lowers the particle-like transport below the amorphous limit, and the shallow temperature dependence of the intraband tunnelling transport leads to κlatt much lower than other chalcogenides at room temperature, and κlatt competitive with that along the layering direction in the orthorhombic phases at high T. The cubic structures support larger absolute Seebeck coefficients than the Pnma phases, but larger carrier effective masses and stronger polar-optic phonon scattering lead to low conductivity, and n-type doping with carrier concentrations on the order of 4 × 1019 cm−3, and ideally larger, are required to obtain reasonable power factors. If this is achievable, we predict that π SnSe could show ZT > 1, competitive with Bi2Te3,9 at room temperature, and ZT as high as 3 at 800 K, matching state-of-the-art experiments on Pnma SnSe.14 With a typical 300 K cold-side temperature, this strong low-temperature performance results in a much higher average ZT than we predict for p-type Pnma SnSe, making π SnSe suitable for a wide range of low- to mid-temperature applications. The predicted performance of π SnS is also considerably better than p-type Pnma SnS, such that a  could be achieved for mid-temperature applications if the n can be optimised.
could be achieved for mid-temperature applications if the n can be optimised.
Despite being discovered almost a decade ago, the potential TE performance of the π monochalcogenides has not yet been uncovered, due to a combination of experiments focusing on photovoltaic applications and computational predictions using unsuitable approximations.30–32 Among the latter, there are likely few circumstances where neglecting the κlatt in the ZT equation would be reasonable.30 The Slack model significantly overestimates the κlatt of the π phases compared to solving the Wigner transport equation, although the Cahill model works remarkably well.31 Finally, unless a reasonable estimate of an electron relaxation time can be obtained (e.g. from experiments102,103), our results suggest electronic transport calculations within the constant relaxation-time approximation cannot be relied upon for quantitative predictions.32 On the other hand, the good match between our predicted σ and experimental measurements suggests phenomenological models for the electron scattering may be adequate provided they capture the dominant scattering mechanism(s) (POP scattering for Pnma and π SnS/SnSe).
While there are potential challenges around stabilising and heavily doping the π phases, in our view the exceptional predicted TE performance, and in particular the ultra-low κlatt, warrants further investigation. On the last point, this study evidences the successful strategy of targeting structural complexity as a route to achieving low room-temperature κlatt and high low-temperature ZT. If our understanding of the IV–VI chalcogenides generalises to the related group IV oxides and V–VI sesquioxides/sesquichalcogenides, further investigation of the low-symmetry orthorhombic phases of the Sb2Ch3 and Bi2Ch3, or ternary IV–V oxides in the pyrochlore and derived structure types,38 could be rewarding.
Data availability
Raw data from this study will be made available to download free of charge after publication from an online repository at https://doi.org/10.17632/6j4vvf5py4. Our analysis code is available on GitHub at https://github.com/skelton-group/ZT-Calc-Workflow.Author contributions
Conceptualisation – JMS; methodology – all authors; data curation – all authors; formal analysis and investigation – all authors; writing (original draft) – all authors; writing (review and editing) – all authors; funding acquisition – JMS. All authors have read and agreed to the published version of the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MZ is supported by a CSC studentship (202006700004). JMS and JMF are supported by a UK Research and Innovation Future Leaders Fellowship (MR/T043121/1, MR/Y033973/1), and JMS previously held a University of Manchester Presidential Fellowship. This work used the ARCHER2 UK National Supercomputing Service via the UK Mateirals Chemistry Consortium (Engineering and Physical Sciences Research Council EP/R029431 and EP/X035859).Notes and references
- A. Firth, B. Zhang and A. Yang, Appl. Energy, 2019, 235, 1314–1334 CrossRef.
- R. Freer and A. V. Powell, J. Mater. Chem. C, 2020, 8, 441–463 RSC.
- G. Tan, L.-D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149 CrossRef CAS PubMed.
- Y. Takagiwa, Y. Pei, G. Pomrehn and G. Snyder, Appl. Phys. Lett., 2012, 101, 092102 CrossRef.
- Q. Zhang, H. Wang, W. Liu, H. Wang, B. Yu, Q. Zhang, Z. Tian, G. Ni, S. Lee and K. Esfarjani, et al. , Energy Environ. Sci., 2012, 5, 5246–5251 RSC.
- Y. Pei, Z. M. Gibbs, A. Gloskovskii, B. Balke, W. G. Zeier and G. J. Snyder, Adv. Energy Mater., 2014, 4, 1400486 CrossRef.
- J. M. Skelton, JPhys Energy, 2020, 2, 025006 CrossRef CAS.
- J. Qu, A. Balvanz, S. Baranets, S. Bobev and P. Gorai, Mater. Horiz., 2022, 9, 720–730 RSC.
- R. Freer, D. Ekren, T. Ghosh, K. Biswas, P. Qiu, S. Wan, L. Chen, S. Han, C. Fu, T. Zhu, A. K. M. A. Shawon, A. Zevalkink, K. Imasato, G. J. Snyder, M. Ozen, K. Saglik, U. Aydemir, R. Cardoso-Gil, E. Svanidze, R. Funahashi, A. V. Powell, S. Mukherjee, S. Tippireddy, P. Vaqueiro, F. Gascoin, T. Kyratsi, P. Sauerschnig and T. Mori, JPhys Energy, 2022, 4, 022002 CrossRef CAS.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, Science, 2008, 320, 634–638 CrossRef CAS PubMed.
- S. I. Kim, K. H. Lee, H. A. Mun, H. S. Kim, S. W. Hwang, J. W. Roh, D. J. Yang, W. H. Shin, X. S. Li, Y. H. Lee, G. J. Snyder and S. W. Kim, Science, 2015, 348, 109–114 CrossRef CAS PubMed.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, nature, 2014, 508, 373–377 CrossRef CAS.
- C. Zhou, Y. K. Lee, Y. Yu, S. Byun, Z.-Z. Luo, H. Lee, B. Ge, Y.-L. Lee, X. Chen and J. Y. Lee, et al. , Nat. Mater., 2021, 20, 1378–1384 CrossRef CAS PubMed.
- I. Suzuki, S. Kawanishi, T. Omata and H. Yanagi, JPhys Energy, 2022, 4, 042002 CrossRef CAS.
- C. W. Li, J. Hong, A. F. May, D. Bansal, S. Chi, T. Hong, G. Ehlers and O. Delaire, Nat. Phys., 2015, 11, 1063–1069 Search PubMed.
- J. M. Skelton, L. A. Burton, S. C. Parker, A. Walsh, C.-E. Kim, A. Soon, J. Buckeridge, A. A. Sokol, C. R. A. Catlow, A. Togo and I. Tanaka, Phys. Rev. Lett., 2016, 117, 075502 CrossRef PubMed.
- U. Aseginolaza, R. Bianco, L. Monacelli, L. Paulatto, M. Calandra, F. Mauri, A. Bergara and I. Errea, Phys. Rev. Lett., 2019, 122, 075901 CrossRef CAS PubMed.
- U. Aseginolaza, R. Bianco, L. Monacelli, L. Paulatto, M. Calandra, F. Mauri, A. Bergara and I. Errea, Phys. Rev. B, 2019, 100, 214307 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. M. Skelton, L. A. Burton, F. Oba and A. Walsh, J. Phys. Chem. C, 2017, 121, 6446–6454 CrossRef CAS.
- I. Pallikara and J. M. Skelton, Phys. Chem. Chem. Phys., 2021, 23, 19219–19236 RSC.
- S. K. Guillemot, A. Suwardi, N. Kaltsoyannis and J. M. Skelton, J. Mater. Chem. A, 2024, 12, 2932–2948 RSC.
- R. Abutbul, A. Garcia-Angelmo, Z. Burshtein, M. Nair, P. Nair and Y. Golan, CrystEngComm, 2016, 18, 5188–5194 RSC.
- R. E. Abutbul, E. Segev, L. Zeiri, V. Ezersky, G. Makov and Y. Golan, RSC Adv., 2016, 6, 5848–5855 RSC.
- R. E. Abutbul, E. Segev, S. Samuha, L. Zeiri, V. Ezersky, G. Makov and Y. Golan, CrystEngComm, 2016, 18, 1918–1923 RSC.
- U. Chalapathi, B. Poornaprakash and S.-H. Park, Sol. Energy, 2016, 139, 238–248 CrossRef CAS.
- P. Nair, A. Garcia-Angelmo and M. Nair, Phys. Status Solidi A, 2016, 213, 170–177 CrossRef CAS.
- E. Barrios-Salgado, L. A. Rodríguez-Guadarrama, M. L. Ramón García, L. G. Martínez, M. Nair and P. Nair, Phys. Status Solidi A, 2017, 214, 1700036 CrossRef.
- F. K. Butt, B. U. Haq, S. ur Rehman, R. Ahmed, C. Cao and S. AlFaifi, J. Alloys Compd., 2017, 715, 438–444 CrossRef CAS.
- S. U. Rehman, F. K. Butt, Z. Tariq, X. Zhang, J. Zheng, G. Naydenov, B. Ul Haq and C. Li, Int. J. Energy Res., 2021, 45, 6369–6382 CrossRef CAS.
- M. A. Sattar, N. Al Bouzieh, M. Benkraouda and N. Amrane, Beilstein J. Nanotechnol., 2021, 12, 1101–1114 CrossRef CAS PubMed.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222 CrossRef CAS.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- J. M. Flitcroft, I. Pallikara and J. M. Skelton, Solids, 2022, 3, 155–176 CrossRef CAS.
- M. Zhang, J. M. Flitcroft, S. K. Guillemot and J. M. Skelton, J. Mater. Chem. C, 2023, 11, 14833–14847 RSC.
- W. Rahim, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2020, 8, 16405–16420 RSC.
- W. Rahim, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2021, 9, 20417–20435 RSC.
- A. Z. Khan, J. M. Flitcroft and J. M. Skelton, Adv. Mater., 2024, 5, 652–664 RSC.
- K. Brlec, K. B. Spooner, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2022, 10, 16813–16824 RSC.
- J. M. Flitcroft, A. Althubiani and J. M. Skelton, JPhys Energy, 2024, 6, 025011 CrossRef CAS.
- M. Simoncelli, N. Marzari and F. Mauri, Nat. Phys., 2019, 15, 809–813 Search PubMed.
- M. Simoncelli, N. Marzari and F. Mauri, Phys. Rev. X, 2022, 12, 041011 Search PubMed.
- L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu and V. P. Dravid, et al. , Science, 2016, 351, 141–144 CrossRef CAS PubMed.
- W. He, D. Wang, J.-F. Dong, Y. Qiu, L. Fu, Y. Feng, Y. Hao, G. Wang, J. Wang and C. Liu, et al. , J. Mater. Chem. A, 2018, 6, 10048–10056 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- L. Chaput, Phys. Rev. Lett., 2013, 110, 265506 CrossRef PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- J. M. Skelton, D. S. Gunn, S. Metz and S. C. Parker, J. Chem. Theory Comput., 2020, 16, 3543–3557 CrossRef CAS PubMed.
- S. Baroni and R. Resta, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7017–7021 CrossRef CAS.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- U. Argaman, R. E. Abutbul, Y. Golan and G. Makov, Phys. Rev. B, 2019, 100, 054104 CrossRef CAS.
- J. Tang and J. M. Skelton, J. Phys.: Condens. Matter, 2021, 33, 164002 CrossRef CAS.
- J. M. Skelton, J. Mater. Chem. C, 2021, 9, 11772–11787 RSC.
- J. M. Skelton, L. A. Burton, A. J. Jackson, F. Oba, S. C. Parker and A. Walsh, Phys. Chem. Chem. Phys., 2017, 19, 12452–12465 RSC.
- J. M. Skelton, D. Tiana, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, J. Chem. Phys., 2015, 143, 064710 CrossRef PubMed.
- Y. Liu, J. M. Skelton, X. Xia, Y. Zhu, D. J. Lewis and R. Freer, J. Mater. Chem. C, 2024, 12, 508–520 RSC.
- G. A. Slack, Solid State Phys., 1979, 34, 1–71 CAS.
- D. G. Cahill and R. O. Pohl, Annu. Rev. Phys. Chem., 1988, 39, 93–121 CrossRef CAS.
- J. M. Skelton, L. A. Burton, F. Oba and A. Walsh, APL Mater., 2017, 5, 036101 CrossRef.
- E. Segev, U. Argaman, R. E. Abutbul, Y. Golan and G. Makov, CrystEngComm, 2017, 19, 1751–1761 RSC.
- X. Shi, Z.-G. Chen, W. Liu, L. Yang, M. Hong, R. Moshwan, L. Huang and J. Zou, Energy Storage Mater., 2018, 10, 130–138 CrossRef.
- X. Shi, A. Wu, T. Feng, K. Zheng, W. Liu, Q. Sun, M. Hong, S. T. Pantelides, Z.-G. Chen and J. Zou, Adv. Energy Mater., 2019, 9, 1803242 CrossRef.
- S. Chandra, U. Bhat, P. Dutta, A. Bhardwaj, R. Datta and K. Biswas, Adv. Mater., 2022, 34, 2203725 CrossRef CAS PubMed.
- X. Yang, W.-H. Gu, W.-J. Li, Y.-X. Zhang, J. Feng and Z.-H. Ge, J. Phys. Chem. Solids, 2023, 172, 111077 CrossRef CAS.
- T. Chattopadhyay, J. Pannetier and H. G. Von Schnering, J. Phys. Chem. Solids, 1986, 47, 879–885 CrossRef CAS.
- Z. M. Gibbs, F. Ricci, G. Li, H. Zhu, K. Persson, G. Ceder, G. Hautier, A. Jain and G. J. Snyder, npj Comput. Mater., 2017, 3, 8 CrossRef.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem., Int. Ed., 2016, 55, 6826–6841 CrossRef CAS.
- M. K. Brod and G. J. Snyder, J. Mater. Chem. A, 2021, 9, 12119–12139 RSC.
- H. Fröhlich, Adv. Phys., 1954, 3, 325–361 CrossRef.
- K. Jeganath, N. J. Choudhari, G. S. Pai, A. Rao and Y. Raviprakash, Mater. Sci. Semicond. Process., 2020, 113, 105050 CrossRef CAS.
- F. D. B. Sánchez, M. T. S. Nair and P. K. Nair, Semicond. Sci. Technol., 2023, 39, 015003 CrossRef.
- E. Barrios-Salgado, L. A. Rodríguez-Guadarrama, A. R. Garcia-Angelmo, J. C. Álvarez, M. Nair and P. Nair, Thin Solid Films, 2016, 615, 415–422 CrossRef CAS.
- A. Garcia-Angelmo, R. Romano-Trujillo, J. Campos-Álvarez, O. Gomez-Daza, M. Nair and P. Nair, Phys. Status Solidi A, 2015, 212, 2332–2340 CrossRef CAS.
- J. Breternitz, R. Gunder, H. Hempel, S. Binet, I. Ahmet and S. Schorr, Inorg. Chem., 2017, 56, 11455–11457 CrossRef CAS PubMed.
- S. Polivtseva, I. O. Acik, A. Katerski, A. Mere, V. Mikli and M. Krunks, Phys. Status Solidi C, 2016, 13, 18–23 CrossRef CAS.
- S. Polivtseva, A. Katerski, E. Kärber, I. O. Acik, A. Mere, V. Mikli and M. Krunks, Thin Solid Films, 2017, 633, 179–184 CrossRef CAS.
- M. Guc, J. Andrade-Arvizu, I. Y. Ahmet, F. Oliva, M. Placidi, X. Alcobé, E. Saucedo, A. Pérez-Rodríguez, A. L. Johnson and V. Izquierdo-Roca, Acta Mater., 2020, 183, 1–10 CrossRef CAS.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- Y. Iguchi, K. Inoue, T. Sugiyama and H. Yanagi, Inorg. Chem., 2018, 57, 6769–6772 CrossRef CAS PubMed.
- X. Hu, W. He, D. Wang, B. Yuan, Z. Huang and L.-D. Zhao, Scr. Mater., 2019, 170, 99–105 CrossRef CAS.
- L. Su, T. Hong, D. Wang, S. Wang, B. Qin, M. Zhang, X. Gao, C. Chang and L.-D. Zhao, Mater. Today Phys., 2021, 20, 100452 CrossRef CAS.
- X.-L. Shi, K. Zheng, W.-D. Liu, Y. Wang, Y.-Z. Yang, Z.-G. Chen and J. Zou, Adv. Energy Mater., 2018, 8, 1800775 CrossRef.
- A. T. Duong, V. Q. Nguyen, G. Duvjir, V. T. Duong, S. Kwon, J. Y. Song, J. K. Lee, J. E. Lee, S. Park, T. Min, J. Lee, J. Kim and S. Cho, Nat. Commun., 2016, 7, 13713 CrossRef CAS PubMed.
- C. Yamamoto, X. He, T. Katase, K. Ide, Y. Goto, Y. Mizuguchi, A. Samizo, M. Minohara, S. Ueda, H. Hiramatsu, H. Hosono and T. Kamiya, Adv. Funct. Mater., 2021, 31, 2008092 CrossRef CAS.
- A. Jain, G. Hautier, S. P. Ong, C. J. Moore, C. C. Fischer, K. A. Persson and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045115 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- A. Glibo, M. Reda, Y. Surace, D. M. Cupid and H. Flandorfer, J. Alloys Compd., 2023, 969, 172320 CrossRef CAS.
- R. Colin and J. Drowart, Trans. Faraday Soc., 1964, 60, 673–683 RSC.
- G. Lindberg, A. Larsson, M. Råberg, D. Boström, R. Backman and A. Nordin, J. Chem. Therm., 2007, 39, 44–48 CrossRef CAS.
- T. L. Brundzia and O. J. Klep, Econ. Geol., 1988, 83, 174–181 CrossRef.
- P. Scardala, V. Piacente and D. Ferro, J. Less-Common Met., 1990, 162, 11–21 CrossRef CAS.
- G. K. Johnson, G. Papatheodorou and C. E. Johnson, J. Chem. Therm., 1981, 13, 745–754 CrossRef CAS.
- V. R. Sidorko, L. V. Goncharuk and R. V. Antonenko, Powder Metall. Met Ceram., 2008, 47, 234–241 CrossRef CAS.
- Y. Liu, J. M. Skelton, X. Xia, Y. Zhu, D. J. Lewis and R. Freer, J. Mater. Chem. C, 2024, 12, 508–520 RSC.
- Y. Zhu, J. M. Skelton, D. J. Lewis and R. Freer, JPhys Energy, 2024, 6, 025027 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Includes further details of the calculations and analysis performed in this work, and additional data in figures and tables to support the results and discussion. See DOI: https://doi.org/10.1039/d4ta05815a |
| This journal is © The Royal Society of Chemistry 2025 |

