Efficient soft-chemical synthesis of large van-der-Waals crystals of the room-temperature ferromagnet 1T-CrTe₂

Abstract

We herein report on a fast and convenient soft-chemical synthesis approach towards large 1T-CrTe₂ van-der-Waals crystals. This compound is formed X-ray diffraction pure, with a complete conversion within just over 2 h from flux-grown LiCrTe₂ crystals using diluted acids. Due to the availability of high-quality single crystals, we have confirmed the crystal structure for the first time by single-crystal X-ray diffraction experiments. For the acid deintercalated 1T-CrTe₂ crystals, we find long-range ferromagnetic order with a Curie temperature of T_C = 318 K. We further revealed the magnetic structure of 1T-CrTe₂ using low-temperature neutron powder diffraction experiments and determined the magnetic Hamiltonian using density functional theory. X-ray diffraction experiments of post-annealed crystals suggest a thermal stability of 1T-CrTe₂ up to at least 100 °C. Our findings expand the synthesis methods for 1T-CrTe₂ crystals, which hold promise for integrated room-temperature spintronics applications.

---

1 Introduction

Spintronics is an emerging research field to provide the future high-capacity data storage and fast data processing required in information technology.¹ Their development is accompanied by the discovery and enhanced synthesis of van-der-Waals (vdW) materials, thereby allowing the fabrication of spintronic devices in the 2D limit.^2–5 Advanced synthesis methods and especially soft-chemical methods have emerged as indispensable tools to synthesize many of the most promising 2D and van-der-Waals materials for applications.^6–11

One of the most promising candidates for 2D spintronic devices is the vdW material 1T-CrTe₂. Bulk 1T-CrTe₂ has been reported to have a ferromagnetic transition temperature of slightly above room temperature with Curie temperatures ranging between T_C = 300 K and 320 K.^12–15 Moreover, 1T-CrTe₂ exhibits large magnetic moments, pronounced perpendicular anisotropy, and a spin-split band structure in its magnetic properties.^15,16 Its high Curie temperature has been reported to be nearly retained down to the monolayer level, supported by strong magnetic anisotropy and weak interlayer interactions.^15,17 Additionally, 1T-CrTe₂ films were reported to function as efficient spin injectors when combined with other 2D materials like topological insulators and semimetals, facilitating the exploration of new spintronics properties.^2,18–20 These characteristics position 1T-CrTe₂ with an exceptional prospect for applications in room-temperature spintronics. The quality of the materials used in these devices is the cornerstone of their further development, which novel synthesis strategies can improve.

Apart from 1T-CrTe₂ other Cr_xTe_y phases have been reported including CrTe,²¹ Cr₄Te₅,²² Cr₃Te₄,^23,24 Cr₂Te₃,^25–27 Cr_1+1/3Te₂,^28,29 Cr₅Te₈,^30–34 Cr₃Te₅,³⁵ and CrTe₃.³⁶ In contrast to 1T-CrTe₂, these phases are not vdW materials and thermodynamic products, which can be obtained by reactions of Cr and Te in their respective ratio via solid-state synthesis. The products of these reactions can be exemplary summarized in phase diagrams such as that by Ipser et al.³⁷

In addition to this, the synthesis of the meta-stable phase 1T-CrTe₂ has also been reported using two categories of synthesis methods: (i) bottom-up and (ii) top-down approaches. On the one hand, (i) bottom-up syntheses of few-layered or monolayer 1T-CrTe₂ have been reported by either using chemical vapor deposition (CVD) directly from the elements onto a substrate¹⁷ or molecular beam epitaxy (MBE) from either the elements,³⁸ or from CrCl₂ and elemental Te.¹⁸ Reported (ii) top-down approaches for both crystals and powders, on the other hand, start with the synthesis of the ternary KCrTe₂ from the elements, which in a second step is then deintercalated using I₂ dissolved in acetonitrile.^12–15

Employing other soft-chemical deintercalation methods – as demonstrated exemplarily in the synthesis of the superconductor 2M-WS₂ – can potentially improve crystallinity and enhance exchange interactions. In the specific case of 2M-WS₂, Song et al. advanced the deintercalation techniques used for K_0.5WS₂ with acids.³⁹ Earlier, 2M-WS₂ was synthesized using K₂Cr₂O₇ and H₂SO₄,^40,41 or using H₂ for the reduction and subsequent residual deintercalation with I₂.⁴² Hence, expanding the top-down soft-chemical synthesis of vdW materials can play a crucial role in the future fabrication of high-quality quantum materials.

The growth of single crystals via soft-chemical methods is influenced by the size and quality of the initial crystal, particularly during processes like deintercalation. A recent advance has been the successful growth of large, high-quality LiCrTe₂ crystals using a metal flux composed of Li/Te, which serves as a solvent for Cr.⁴³ Building on this foundation, we report the synthesis and detailed characterization of large 1T-CrTe₂ crystals synthesized by soft-chemical methods. We employed three different deintercalation techniques: diluted acids, Milli-Q water, and I₂ in acetonitrile, with each being assessed for its impact on the final product. The acid-assisted approach emerged as particularly effective due to its short reaction time of just over two hours, producing large, high-quality 1T-CrTe₂ crystals. This method enabled us to confirm the crystal structure from single-crystal X-ray diffraction data. The resulting acid deintercalated crystals exhibit a ferromagnetic ordering temperature of T_C = 318 K. In contrast, deintercalation with I₂/acetonitrile, requires several days for large crystals to complete, which is significantly longer than the swift acid method. Diffraction experiments of post-annealed samples further elucidate the thermal transitions of 1T-CrTe₂. Neutron diffraction experiments allowed us to solve the magnetic structure of 1T-CrTe₂. Finally, we used density functional theory to establish a magnetic Hamiltonian for 1T-CrTe₂ that clearly confirms our magnetic measurements.

2 Experimental

2.1 Synthesis

Single crystals of LiCrTe₂ were synthesized as previously reported from Li (granulates, Sigma-Aldrich, 99%), Cr (powder, Alfa Aesar, 99.95%) and Te (pieces, Alfa Aesar, 99.999%) using a metal flux method.⁴³ For the deintercalation in aqueous solutions either 1 M H₂SO₄, 2 M HCl, 2 M HNO₃ or Milli-Q water with a ratio of 10 mg LiCrTe₂ per 1 ml of the respective solution were used. The reagents were allowed to react for 30 min after which the solution was replaced three times with 5 ml of Milli-Q water in intervals of 30 min. Finally, the crystals were rinsed twice in acetonitrile (Sigma-Aldrich, ≥99.9%), which was then removed under reduced pressure. The crystals were transferred into an argon-filled glovebox. For the deintercalation using I₂, a 0.04 M solution of I₂ (granulates, Honeywell Fluka, ≥99.8%) in dry acetonitrile (Thermo scientific, 99.9%) was used to yield a ratio of LiCrTe₂ to I₂ of 1 : 1. The crystals were subsequently washed with dry acetonitrile to remove LiI and excess I₂ and then dried under reduced pressure. All acids used were diluted with Milli-Q water from 37% HCl (Fisher Scientific, laboratory reagent grade), 65% HNO₃ (carlo erba, for analysis) and 96% H₂SO₄ (carlo erba, for analysis).

2.2 Powder X-ray diffraction (PXRD)

PXRD data were collected using a Rigaku SmartLabXE diffractometer with Cu-K_α radiation (λ = 1.54187 Å) on a D/teX Ultra 250 detector in Bragg Brentano geometry in the 2θ range of 5° to 80°. Capillary measurements were performed on the same instrument in Debye–Scherrer geometry with Cu-K_α radiation. Crystals were ground into fine powders, mixed with Apiezon N Grease, and filled into quartz capillaries with an outer diameter of 0.8 mm. Powder refinements were conducted using the Rietveld method in the Fullprof Suite package software.⁴⁴

2.3 Single crystal X-ray diffraction (SXRD)

Single crystal X-ray diffraction (SXRD) experiments were performed under N₂ cooling at 120 K on a Rigaku XtaLab Synergy-S diffractometer using Mo K_α radiation (λ = 0.71072 Å). The experiment was performed on a small fragment which was carefully cut from a larger crystal using a scalpel. Pre-experiment screenings, data collection, data reduction, and absorption correction were performed using the program suite CrysAlisPro.⁴⁵ The crystal structure was solved with the dual space method in SHELXT.⁴⁶ The least square refinement of F² was performed using SHELXL⁴⁷ within the Olex2 crystallography software.⁴⁸

2.4 Scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDS)

Electron images were obtained from a JEOL JSM-IT800 Scanning electron microscope with an acceleration voltage of 20 kV. Energy dispersive X-ray spectroscopy (EDS) data was collected with an X-Max^N 80 detector from Oxford Instruments. Stoichiometry calculations are based on ten points on three crystals each.

2.5 Magnetization experiments

Magnetization vs. temperature and magnetization vs. magnetic field measurements were carried out in a Physical Property Measurement System in a cryogen-free system (PPMS DynaCool) from Quantum Design equipped with the vibrating sample magnetometer (VSM) option. The measurements were performed in a temperature range of T = 1.8–380 K in the sweep mode at rates of 5 K min⁻¹ and 50 Oe s⁻¹ in the range of −9 T to 9 T. Arrott plots were created using magnetization versus field data with a sweeping rate of 40 Oe s⁻¹ between 2 T and 0 T.

2.6 Neutron powder diffraction

Neutron powder diffraction experiments were performed on the High-Resolution Powder Diffractometer at the Swiss Spallation Neutron Source from the Paul Scherrer Institute in Villigen, Switzerland.⁴⁹ Crushed 1T-CrTe₂ deintercalated from LiCrTe₂ using 1 M H₂SO₄ was sealed in a vanadium sample container with a diameter of 6 mm using indium wire in a helium glovebox. Diffraction data were collected at T = 1.6 K with wavelengths of 1.886 Å and 1.494 Å as well as at T = 323 K with a wavelength of 1.886 Å. The patterns obtained were refined using the Rietveld method using the Fullprof Suite package. The magnetic symmetry was analyzed using ISODISTORT in the ISOTROPY software.^50,51

2.7 Calculations

The Hamiltonian of 1T-CrTe₂ was determined by density functional theory-based energy mapping.^52,53 We use the all electron full potential local orbital (FPLO) code⁵⁴ for all density functional theory calculations, in combination with the generalized gradient approximation (GGA) exchange and correlation functional.⁵⁵

2.8 Post-annealing experiments

40 mg of 1T-CrTe₂ synthesized by deintercalation with 1 M H₂SO₄ was placed in an Al₂O₃ crucible and were sealed in quartz ampules under 300 mbar of Ar. The quartz ampules were placed for 20 h in preheated ovens at temperatures of 250 °C, 325 °C, 400 °C, and 500 °C and consequently quenched in air.

3 Results and discussion

3.1 Acid-assisted deintercalation of LiCrTe₂

In Fig. 1a, the schematic of the reaction of LiCrTe₂ with acids is shown. LiCrTe₂ reacts with the acid, i.e. H⁺ ions to result in a redox reaction, in which H⁺ are reduced to H₂, while the chromium is oxidized from Cr(III) to Cr(IV). The reaction can be followed visually within minutes, as illustrated in Fig. 1b for the case of 1 M H₂SO₄.

Fig. 1 Acid-assisted synthesis of 1T-CrTe₂: (a) Scheme of the deintercalation reaction of LiCrTe₂ with an acid and the respective cell parameters of LiCrTe₂ (ref. 56) based on synchrotron data and 1T-CrTe₂ based on our SXRD data. (b) Images of the deintercalation process of LiCrTe₂ crystals in diluted 1 M H₂SO₄ with the respective time stamps.

Visually, the reaction of LiCrTe₂ with diluted H₂SO₄, HCl, HNO₃, and Milli-Q water was found to progress in a similar fashion for all of these solutions. Upon contact, the formation of H₂ gas was observed, ending after approximately 5 min. When washing the crystals with Milli-Q water after 30 min no further formation of gas was observed except in the case of HNO₃, which then ended again within 5 min. The second generation of gas when using HNO₃ could indicate an incomplete deintercalation. During the deintercalation process, all diluted acid solutions first turned slightly purple but, after being transferred to a separate vial, then became clear within approximately 24 h.

All synthesized crystals using diluted acids are attracted by a neodymium permanent magnet once it is brought into proximity at room-temperature. This is in agreement with the previously reported room-temperature ferromagnetism for 1T-CrTe₂. The diameter of the crystals obtained was equal to or close to the initial LiCrTe₂ crystals. The size of the LiCrTe₂ used for deintercalation reached diameters up to 8 mm, which was the diameter of the crucible used for the synthesis. However, we visually observe more phase boundaries due to the lattice strains induced by the structural distortions of the LiCrTe₂ crystals in the periodic changes of the deintercalated crystal (compare, e.g., ref. 57).

Perpendicular to the c axis, the crystals can split during the deintercalation. All the obtained crystals are gray with a metallic luster. The crystals show a pronounced layered appearance due to the underlying layered 2D crystal structure.

PXRD measurements of deintercalated LiCrTe₂ using diluted H₂SO₄, HCl, HNO₃, and, for comparison, Milli-Q water and I₂ in acetonitrile (after 14 days, see discussion below) – are depicted in Fig. 2. These samples deintercalated using H₂SO₄, HCl, HNO₃, and also I₂/acetonitrile show comparatively sharp peaks in the PXRD patterns. The reflections in the H₂O-deintercalated sample are wider, implying less crystallinity, and the intensities of the (00l) reflections are slightly off, and we observe Te as a clear impurity phase, indicating the partial decomposition of LiCrTe₂ upon reaction with H₂O. These findings match the comparative deintercalation attempts in the KWS₂/2M-WS₂ system, in which different soft-chemical methods also yielded products with similar purity and physical properties.³⁹ Further analyses have been conducted on the sample deintercalated with H₂SO₄. The properties observed in these measurements are likely very similar to those crystals deintercalated with diluted HCl and HNO₃ because of the nearly identical diffraction patterns.

Fig. 2 Comparative PXRD patterns of 1T-CrTe₂ synthesized via various deintercalation reactions: (a) PXRD patterns of 1T-CrTe₂ synthesized by deintercalation of LiCrTe₂ in diluted H₂SO₄, HCl, HNO₃, Milli-Q water and I₂ in acetonitrile. The latter pattern was obtained with a capillary measurement instead of reflection mode, which resulted in additional reflections marked with a star, due to Apiezon N Grease used for dilution. A PXRD measurement of the Apiezon N Grease alone in a capillary is depicted in the ESI.† (b) Rietveld refinement of 1T-CrTe₂ synthesized using a 1 M solution of H₂SO₄.

The Rietveld refinement, depicted in Fig. 2b was conducted on the PXRD-pattern of the H₂SO₄-deintercalated sample based on the respective SXRD crystal structure. The pattern shows no signs of impurities and was refined with χ² = 5.7318. Our Rietveld-refined cell parameters, namely a = 3.7875(2) Å, c = 6.10323(6) Å, are in excellent agreement with the refined SXRD unit cell parameters discussed below. The peak positions match the patterns and also match the PXRD patterns of all deintercalation methods, hence they all yielded 1T-CrTe₂ crystals. An exemplary image of an H₂SO₄ deintercalated crystal is depicted in Fig. 2b. Images of deintercalated crystals with the other methods are depicted in the ESI.†

Overall, we show that acid-assisted deintercalation methods of LiCrTe₂ yield phase-pure 1T-CrTe₂ crystals.

3.2 Deintercalation using iodine in acetonitrile

Single crystals of 1T-CrTe₂ were also synthesized by the adaptation of the I₂ in acetonitrile pathway for the deintercalation of LiCrTe₂ (compare, e.g. ref. 13). The synthesis of high quality 1T-CrTe₂ crystals by this approach was found to be feasible, however significantly slower and accompanied by the presence of Te. These Te impurities are always observed after the deintercalation with I₂/acetonitrile, while we do not observe it for the acid deintercalation reaction. The PXRD pattern of flux-grown LiCrTe₂ indicates the presence of small amounts of LiTe₃, which might react with I₂ to Te. The synthesis of millimeter-sized single crystals took 14 days. Shorter reaction times led to products that were not fully deintercalated. In Fig. 3a, we show the PXRD patterns of crystals with an approximate size of 5 × 3 × 0.5 mm, which were deintercalated with a 0.04 M solution of I₂ in acetonitrile for 1, 4, 8 and 14 days. LiCrTe₂ and 1T-CrTe₂ are best identified in the patterns by the peaks at about 13.2° 2θ and 29.3° 2θ for LiCrTe₂ or 14.5° 2θ and 30.9° 2θ for 1T-CrTe₂. After 1 day, peaks corresponding to 1T-CrTe₂ have much smaller intensities than those of LiCrTe₂. This is also the case after 4 days. After 8 days, the intensity ratio changes, suggesting more 1T-CrTe₂ than LiCrTe₂ is present in the crystal. Only after a duration of 14 days, does the PXRD pattern show no presence of LiCrTe₂ suggesting the deintercalation process to be complete. Rietveld refinements of all patterns were conducted to estimate the ratio of LiCrTe₂ and 1T-CrTe₂ present in the crystal. The molar percentages are depicted in a graph against deintercalation time in Fig. 3b. The PXRD experiments quantify the percentage of LiCrTe₂ from 100% to 55% after 1 day, to 40% after 4 days, to 13% after 8 days, and to 0% after 14 days.

Fig. 3 I₂/acetonitrile deintercalation of LiCrTe₂: (a) PXRD patterns of LiCrTe₂ and products obtained by deintercalating LiCrTe₂ with a solution of I₂ in acetonitrile for 1, 4, 8, and 14 days. Stars indicate reflections due to Apiezon N Grease used for capillary preparation and triangles reflections due to impurities of LiTe₃. A PXRD measurement of the Apiezon N Grease alone in a capillary is depicted in the ESI.† Next to the patterns are photographs of the crystals taken on millimeter-sized graph paper. (b) Plot of the molar ratios of LiCrTe₂ to 1T-CrTe₂ as a function of time. The mass ratios of LiCrTe₂, 1T-CrTe₂, and Te were derived from Rietveld refinements of the PXRD patterns shown in (a) and converted to molar ratios, with Te excluded for simplicity. The sum of molar percentages of LiCrTe₂ and 1T-CrTe₂ was scaled up to 100%. Dashed lines represent a pseudo-exponential fit, with additional fitting information provided in ESI Fig. 3.†

Upon examining the photographs of the crystals following different deintercalation durations, one can optically observe a dark-gray center surrounded by a light-gray outer ring (see photographs in Fig. 3a). As the deintercalation time increases, the light-gray region expands, correlating with the formation of 1T-CrTe₂ as confirmed by the powder X-ray diffraction (PXRD) results. Song et al. had found for the deintercalation of polycrystalline KCrSe₂ powder using I₂ in acetonitrile a linear progression with time, and suggested a 0^th order kinetics reaction in agreement with the K⁺ diffusing towards the edges during the deintercalation.⁵⁸ The course of the molar percentages of 1T-CrTe₂ and LiCrTe₂ observed here for millimeter sized crystals matches instead an exponential change, which hints towards 1st order kinetics, yet the effect of the crystal defects as well as varying crystal sizes cannot be quantified and could have led to this different assumption in kinetics.

Overall, it can be certainly stated that the overall time necessary for the deintercalation of large LiCrTe₂ crystals using I₂/acetonitrile is significantly higher than for the acid-assisted deintercalation.

3.3 Diffraction and crystal structure

For the first time we were able to confirm the crystal structure of 1T-CrTe₂, which was proposed based on X-ray powder diffraction data by Freitas et al., using SXRD experiments. SXRD could be performed on crystals synthesized within just over 2 h using diluted H₂SO₄. The best structural model is found to be in the trigonal space group P3̄m1. The unit cell parameters at 120 K were found to be almost identical with a = b = 3.7823(3) Å, c = 6.0203(5) Å for the diluted acid deintercalation. The full crystallographic data is listed in Table 2. The crystal structure is depicted in Fig. 1a and shows the characteristic layers of the vdW material. Since the Te atoms are arranged octahedrally around the Cr and the Cr–Cr distances within the layers are identical, the 1T polytype can be attributed to this structure. As expected, the Cr–Cr interlayer distance of 6.0205(5) Å in 1T-CrTe₂ clearly decreased compared to about 6.585 Å in LiCrTe₂. The unit cell consists of two fully occupied crystallographic sites: The 1b Wyckoff position, x = 0, y = 0, z = 1/2, is occupied by Cr whereas Te can be found in the 2d Wyckoff position at x = 2/3, y = 1/3, z = 0.2420(3) as listed in Table 1.

Table 1 Refined coordinates and assigned Wyckoff position of Cr and Te in 1T-CrTe₂ based on a SXRD measurement at 120 K

Atom	Wyckoff	Occ.	x	y	z
Cr	1b	1	0	0	1/2
Te	2d	1	2/3	1/3	0.2420(3)

---

Table 2 Crystallographic data for single crystals of 1T-CrTe₂ synthesized by deintercalation of LiCrTe₂ with diluted H₂SO₄

SXRD refinement	1T-CrTe2
Formula	CrTe2
CCDC collection code	2376663
Structure type	CdI2
Mol. wt. (g mol^−1)	307.20
Crys. syst.	Trigonal
Space group	P3̄m1(164)
a (Å)	3.7823(3)
c (Å)	6.0203(5)
V (Å^3)	74.587(13)
Z	1
Calculated density (g cm^−1)	6.839
Temperature (K)	120
Diffractometer	Synergy, Dualflex, HyPix-Arc 150
Radiation	Mo-Kα
Crystal color	Gray
Crystal description	Plate
Crystal size (mm^3)	0.24 × 0.19 × 0.03
Linear absorption coefficient (mm^−1)	22.658
Scan mode	ω scan
Recording range θ (°)	3.264–40.432
h range	−5–5
k range	−6–6
l range	−10–10
Nb. of measured reflections	5693
Data reduction
Completeness (%)	100
Nb. of independent reflections	208
R int	0.0954
Absorption corrections	Spherical
Independent reflections	202
With I ≥ 2.0σ
Refinement
R 1 (obs/all) (%)	0.0688/0.0694
wR 2 (obs/all) (%)	0.1855/0.1858
GooF	1.335
No. of refined parameters	6
Difference Fourier residues (e^− Å^−3)	−4.232 to +11.618

---

The crystal structure of 1T-CrTe₂ from crystals deintercalated using diluted H₂SO₄ was solved with reasonable data reduction and refinement parameters with R_int = 0.0954, R₁ = 0.0678, and wR_R2 = 0.1757. The model has a significant residual electron density of +11.08 e⁻ Å⁻³. However, this is located at such close distance to the heavy Te atoms that no additional atom can be reasonably placed in the vdW gap. Both the absence of electron densities between the vdW layers as well as the significant shorter c-axis correspond to the successful deintercalation of Li. Elevated reduction and refinement parameters are most likely the result of the significant mosaicity. Reconstructions of the hk0, h0k and 0kl planes of SXRD datasets on crystals deintercalated with diluted acid and I₂ in acetonitrile are depicted in the ESI,† showing similar mosaicity.

Summarized PXRD analysis shows the successful synthesis of 1T-CrTe₂ using diluted acids and iodine in acetonitrile. The previously suggested crystal structure based on powder refinements has been confirmed using SXRD.

3.4 Microscopic analysis

The stoichiometric ratio of Cr to Te was studied using EDS measurements and was found to be nearly ideal with a ratio of Cr = 1.000 ± 0.010 to Te = 1.942 ± 0.018. In Fig. 4a, we show an exemplary EDS map with an even distribution of Cr and Te. After exfoliation with Scotch tape, the stoichiometric ratio did not change. This stoichiometry differs significantly from other reported Cr_xTe_y species; EDS therefore substantiates the successful synthesis of CrTe₂. Further, EDS data together with the absence of substantial shrinkage of the crystal sizes upon deintercalation, indicate no significant dissolution of Cr or Te in 1 M H₂SO₄ during the short deintercalation period of 30 min.

Fig. 4 Microscopic analysis of 1T-CrTe₂ synthesized by deintercalation of LiCrTe₂ in H₂SO₄: EDS map of 1T-CrTe₂ after exfoliation with Scotch tape (a). SEM images of 1T-CrTe₂. Yellow frames indicate the frame of the respective image with increased magnification. (b) Shows images with magnifications of ×50, ×1000 and ×3000 taken perpendicular to the crystal's surface. (c) Shows a side view on a crystal at an angle of about 45° with magnifications of ×50, ×1000 and ×3000.

The microstructure of a representative acid deintercalated crystal is depicted in Fig. 4b and c. The top-view (b) shows the surface on different scales of the 1T-CrTe₂ crystal. Large areas, i.e., single crystalline domains, can be observed. These areas are interrupted by cracks. These are expected, and likely even unavoidable, by soft-chemical methods in vdW materials (compare, e.g., ref. 57 and 59). The angle-view (c) highlights the layered nature of the resulting crystal, but also emphasizes the presence of disorder, i.e., turbostratic disorder, as the layers have irregular spacings at the edges. This lamellar crystal habitus matches the layered 2D crystal structure of the vdW material. One possible explanation for the irregular spacings at the edges is that the evolved gas leaves the interlayer space towards the edges of the crystal into the solution, applying a perpendicular force on the 1T-CrTe₂ layers. This irregular spacing is likely connected to the mosaicity observed in the SXRD measurement.

Overall, the microscopic analysis confirmed the expected stoichiometric ratio of about 1 : 2 of Cr to Te of 1T-CrTe₂ and showed the layered nature of the vdW-material.

3.5 Magnetic properties of 1T-CrTe₂

In Fig. 5, we show the magnetic properties of 1T-CrTe₂ as-prepared using acid-assisted deintercalation from a 1 M solution of H₂SO₄. The temperature-dependent magnetization in an external magnetic field of μ₀H = 2 T is shown in Fig. 5a, which reveals the pronounced transition of 1T-CrTe₂ to a ferromagnetic state above room temperature. The transition temperatures were determined from the derivatives dM/dT at T_C = 325 K for H‖c and dM/dT at T_C = 321 K for H⊥c. To quantify the transition temperature of 1T-CrTe₂ crystals more accurately, an Arrott plot^7,60,61 is utilized, as depicted in Fig. 5b. The Arrott plot – resulting from mean field theory for magnetism – corresponds to a M²vs. H/M measurement at fixed temperatures. It is the measurement procedure to (i) provide evidence for the existence of a ferromagnetic long-range ordered state, as well as (ii) for a precise determination of the Curie temperature T_C of a ferromagnet. The M²vs. H/M linear behavior that can be extended to the origin of the coordination system for T_C = 318 K corresponds to the Curie temperature. Here, this value for the acid deintercalated 1T-CrTe₂ is in agreement with the first derivative of the magnetization and with earlier reports of Curie temperatures between T_C = 300 K and 320 K.^12–15,62

Fig. 5 Magnetic properties of H₂SO₄-deintercalated 1T-CrTe₂: (a) temperature-dependent magnetization of 1T-CrTe₂ synthesized by deintercalation of LiCrTe₂ in diluted H₂SO₄ along the easy axis (H⊥c) and hard axis (H‖c) measured from 1.8 K and 380 K at 2 T, and their derivatives. The ferromagnetic transition temperature was precisely determined at 318 K using an Arrott plot, (b), which was constructed from the field-dependent magnetic moment up to 2 T between 315 K and 321 K. Field-dependent magnetic moment between −2 T and 2 T along the hard axis, (c), and easy plane, (d).

The field-dependent magnetization measurements are presented in Fig. 5c and d for T = 1.8 K, 300 K, 325 K, and 380 K with the external magnetic field parallel and perpendicular to the c axis respectively. For the measurements with the field along the c axis, at T = 1.8 K we observe a clear ferromagnetic behavior displaying a hysteresis loop. Above the Curie temperature, the field-dependent magnetization is linear, as expected in the paramagnetic state. In this orientation of the crystal there is no saturation of the magnetization observed up to μ₀H = 9 T as this corresponds to the hard axis (see ESI†).

With the magnetic field perpendicular to the c axis, corresponding to the easy plane, no prominent hysteresis can be observed, and the magnetization almost saturates above T_C = 318 K. We estimate a saturation moment of around 2.1 μ_B by extrapolation that is found above μ₀H = 9 T. This is in agreement with the theoretical moment of Cr⁴⁺ of ≈2.82 μ_B based on the spin only formula with n being the number of unpaired electrons. Saturation magnetization, as well as direction of the hard axis, are in agreement with earlier reports on samples of 1T-CrTe₂ from KCrTe₂ using I₂/acetonitrile.^12–15,62

The magnetic properties of 1T-CrTe₂ prepared via acid-assisted deintercalation from 1 M H₂SO₄ demonstrate a transition to a ferromagnetic state above room temperature with a Curie temperature of T_C = 318 K, confirmed through temperature-dependent magnetization, Arrott plots, and field-dependent magnetization measurements.

3.6 Neutron powder diffraction

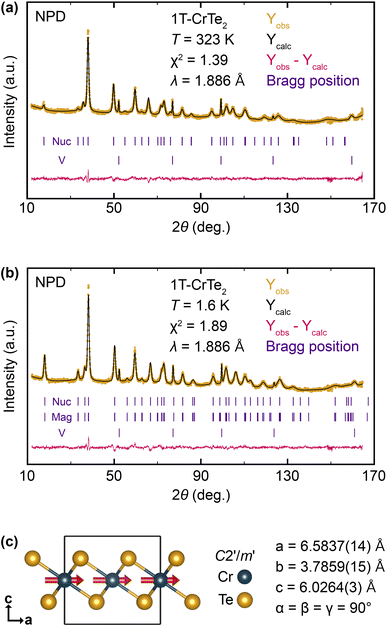
In Fig. 6, we show the results of neutron powder diffraction experiments that we have performed on finely ground 1T-CrTe₂ crystals, which were synthesized using diluted 1 M H₂SO₄. Experiments have been conducted both at T = 1.6 K and 323 K, above T_C = 318 K. Above the ferromagnetic transition temperature, we successfully refined the diffraction pattern using only the nuclear component, as shown in Fig. 6a. At T = 1.6 K, the obtained pattern is well described by introducing a magnetic phase with contributions to the neutron powder pattern at the same 2θ values as the nuclear part. Based on the nuclear model, four different magnetic space groups (MSG) can be envisioned using ISODISTORT from the ISOTROPY software,^50,51 which are listed in the ESI.† The highest symmetric space group P3̄m′1 was rejected since it would not allow for intensity of the (00n) reflections, whereas we observed strong magnetic contributions to the (001) reflection. Considering the remaining space groups, we found the long-range magnetic structure is best described in C2′/m′ with the cell parameters a = 6.5829(15) Å, b = 3.7869(17) Å, c = 6.0262(3) Å and α = β = γ = 90°. Relative to the nuclear structure, a basis transformation with [(2, 1, 0), (0, 1, 0), (0, 0, 1)] was applied.

Fig. 6 Rietveld refinement of neutron diffraction patterns of H₂SO₄-deintercalated 1T-CrTe₂. (a) Refined pattern obtained at T = 323 K based on two phases: a nuclear part (Nuc) on the basis of SXRD data and the sample container made of vanadium (COD code: 1506411). (b) Refined pattern obtained at T = 1.6 K based on three phases: a nuclear part (Nuc) on the basis of SXRD data, a magnetic contribution (Mag) with the space group C2′/m′ and the sample contained made of vanadium. (c) Graphical representation of the magnetic structure with parallel orientation of the magnetic moments of Cr represented by red arrows.

Fig. 6c depicts a graphical representation of the resulting magnetic structure. It comprises two occupied atom sites with Te located at (2/3, 0, 0.747) and Cr at (0, 0, 0.5). The single magnetic Cr site has a magnetic moment of μ_Cr = 1.329(14)μ_B, which is comparatively low for Cr(+IV) because of the absence of an applied field. Refinement of the magnetic moment vector has led to two solutions which can be considered equally valid based on the obtained value of χ². A first solution has a magnetic moment vector with contributions both in x-direction (m_x = 1.311(14)μ_B) and z-direction (m_z = 0.56(5)μ_B), was refined with χ² = 1.89 and described in more detail in the ESI.† A second solution has only a contribution of the magnetic moment in the x-direction (m_x = 1.329(14)μ_B) and was refined with χ² = 1.92 (Table 3). The second solution with the magnetic moments aligned in the ab-plane is the appropriate model, as it agrees better with the observed strong anisotropy between in-plane and out-of-plane magnetization (Fig. 5c and d), but also agrees with our fully relativistic energy calculations of the ferromagnetic spins as function of the quantization axis, where the spins clearly prefer to be in the ab plane over the c axis (see discussion below and ESI†).

Table 3 Comparison of refined parameters of neutron powder diffraction data on H₂SO₄-deintercalated 1T-CrTe₂ collected at 1.6 K and 323 K

	1.6 K	323 K
a (Å)	3.79550(12)	3.7860(3)
c (Å)	6.0262(3)	6.1213(6)
V (Å^3)	75.181(5)	75.985(10)
μ Cr (μB)	1.329(14)	—
R p	1.40	1.69
R wp	1.80	2.10
R exp	1.30	1.78
χ ^2	1.92	1.39

---

The neutron powder diffraction experiments on 1T-CrTe₂ crystals synthesized using diluted 1 M H₂SO₄ reveal that the long-range magnetic structure at 1.6 K is best described by the C2′/m′ space group, with Cr atoms having a magnetic moment of μ_Cr ≈ 1.33 μ_B.

3.7 Calculated magnetic couplings

We would now like to obtain additional information about 1T-CrTe₂ using DFT electronic structure calculations. The basic idea of the energy mapping technique we use is that all the information about the way the Cr ions interact magnetically is contained in energies of broken symmetry solutions for different spin arrangements. In addition, if we include spin orbit coupling, DFT energies also contain information about the magnetic anisotropy of the material. One crucial aspect of 1T-CrTe₂ is that it is a metal. This makes magnetic interactions potentially long-range so that our energy mapping approach has to be extended far beyond the nearest neighbor in the Cr triangular lattice. Given the availability of a precise crystalline model of 1T-CrTe₂, we further investigate the magnetic properties of this compound by determining the Heisenberg Hamiltonian where S_i are spin operators and J_ij are Heisenberg Hamiltonian parameters. The Heisenberg Hamiltonian parameters J_ij represent the strength and nature of the exchange interactions between the spins of the Cr ions. These parameters are influenced by the electronic structure and the spatial arrangement of the atoms.

We use the well-established approach of density functional theory (DFT) energy mapping, which has previously yielded excellent results for the related compound LiCrTe₂ (ref. 43) as well as for other chromium magnets.^63,64 The method implies that we calculate 40 spin configurations with distinct energies for a 3 × 2 × 2 supercell and fit their GGA + U energies with the Heisenberg Hamiltonian. This allows us to resolve the seven exchange couplings shown in Fig. 7 for seven values of the onsite Coulomb interaction U.

Fig. 7 (a) Exchange interactions of 1T-CrTe₂ determined by DFT energy mapping using a DFT + U exchange correlation functional, as function of the on-site interaction strength U. (b) Seven relevant exchange paths for CrTe₂.

Our findings indicate that within the triangular lattice formed by Cr ions in the ab plane, the three exchange interactions, denoted as J₁, J₃, and J₅, are ferromagnetic (negative), suggesting that these interactions favor parallel alignment of neighboring spins. Additionally, the interlayer couplings J₂, J₄, J₆, and J₇ are predominantly ferromagnetic. This dominance of ferromagnetic interactions both within the plane and between layers corroborates the experimentally observed ferromagnetic order in 1T-CrTe₂. Hence, our calculations confirm that the magnetic measurements of 1T-CrTe₂ reveal predominantly ferromagnetic in-plane and interlayer exchange interactions.

Interestingly, we find in-plane second (J₃) and third neighbor (J₅) couplings to be substantial in 1T-CrTe₂. Thus, the high ordering temperature found in the 1T-CrTe₂ monolayer is probably due both to strong single ion anisotropy as well as important longer range exchange interactions.⁶⁵ Meanwhile, the interlayer exchange in 1T-CrTe₂ is not found to be small in our calculations; this is reasonable because the interlayer Cr–Cr distance of 6.0203 Å is small compared to alkali chromium ditellurides, and there are reasonable Cr–Te–Te–Cr exchange paths. Thus, from our calculations we do not find interlayer exchange to be weak, and we can still give valid reasons why the monolayer displays long-range magnetic order. The details on the DFT energy mapping are presented in the ESI.†

Our calculations confirm that 1T-CrTe₂ exhibits predominantly ferromagnetic in-plane and interlayer exchange interactions, with significant second and third neighbor couplings contributing to the high ordering temperature, and the interlayer exchange being substantial due to the relatively small Cr–Cr distance and viable Cr–Te–Te–Cr exchange paths.

3.8 Thermal decomposition

To investigate the thermal stability and decomposition of acid-assisted deintercalated 1T-CrTe₂ we post-annealed ground powders of acid deintercalated 1T-CrTe₂ crystals under Ar atmosphere. PXRD patterns of the psot-annealed samples are depicted in Fig. 8. The temperatures investigated were inspired by DSC and DTA experiments, which are enclosed in the ESI.†

Fig. 8 PXRD patterns showing the thermal stability of 1T-CrTe₂ after tempering at 100 °C for two weeks, and at 250 °C, 325 °C, 400 °C, and 500 °C for 20 hours. Stars indicate an unidentified phase, potentially resembling CrTe₃, and Bragg positions of identified phases are shown below the patterns.

Acid deintercalated 1T-CrTe₂ was found thermally stable at least up to 100 °C for two weeks, after which no significant change of the PXRD pattern compared to the untempered sample was observed. Tempering at 250 °C resulted in the appearance of reflections that correspond to elemental Te in addition to 1T-CrTe₂. The observation can be rationalized with the loss of Te from 1T-CrTe₂ due to its thermal degradation. In the PXRD patterns of the samples annealed at 325 °C and 400 °C we observe the formation of phases closely related to a Cr-rich composition, corresponding to the thermodynamic stable phases Cr₂Te₃ and Cr₅Te₈. The PXRD pattern can be well explained with these structures present. These two phases differ primarily by the amount of Cr that occupies the vdW gap of 1T-CrTe₂, and can be interpreted as a Te-deficient version of the 1T phase, which is well in agreement with the observed Te loss upon thermal treatment. Based on PXRD alone, the clear identification of these two phases from one another is challenging due to their structural similarity. The corresponding reflections in the PXRD pattern that were annealed at 325 °C and 400 °C shift slightly relative to each other and there is a difference in their relative intensities, most prominently at 29.7° 2θ and 30.4° 2θ. Given the continuous loss of Te it is likely that at the phase transition 1 the 1T-CrTe₂ phase decomposes into the Te-poorer Cr₂Te₃ phase, which at higher temperatures decomposes into the even slightly Te-poorer Cr₅Te₈.

Due to the large number of (meta)-stable Cr_xTe_y with stoichiometries close to 1T-CrTe₂ the thermal decomposition of bulk 1T-CrTe₂ and its products is likely a highly complicated process which should be closer investigated in the future. Nevertheless, our observations quantify the thermal decomposition of bulk 1T-CrTe₂ between 100 °C and 250 °C. Henceforth, the annealing of these acid deintercalated 1T-CrTe₂ crystals for device fabrication of any sort might be critical in order not to decompose the phase of interest.

The post-annealing experiments reveal that 1T-CrTe₂ remains stable up to 100 °C, begins to decompose with the formation of elemental Te at 250 °C, and forms Cr-rich phases Cr₂Te₃ and Cr₅Te₈ at higher temperatures due to thermal degradation and Te loss.

4 Conclusions

In this work, we have expanded the top-down synthesis strategies to yield large, X-ray-pure single crystals of the room-temperature ferromagnetic vdW material 1T-CrTe₂. This includes the soft-chemical deintercalation of flux-grown LiCrTe₂, which allowed the synthesis of large crystals with diameters up to 8 mm, using diluted acids as well as a solution of I₂ in acetonitrile. We found the deintercalation of LiCrTe₂ using I₂ to be a slow process, i.e. for millimeter-sized crystals the synthesis took up to 14 days, making the acid-assisted deintercalation an efficient and significantly faster alternative, which only took just over 2 h for millimeter-sized. The quality of these acid deintercalated crystals has been found to be high so that we could – for the first time – resolve the crystal structure of 1T-CrTe₂ from SXRD data.

We find for the acid deintercalated 1T-CrTe₂ well-defined magnetic properties with a ferromagnetic transition temperature of T_C = 318 K. We have resolved its long-range magnetic ferromagnetic order, using neutron diffraction, which is best described in the magnetic space group C2′/m′, with the moments aligned in the ab-plane. Applying DFT-based energy mapping to 1T-CrTe₂, we determined a Heisenberg Hamiltonian with strong ferromagnetic in-plane couplings, including substantial longer range exchange. We find significant interlayer couplings that are also predominantly ferromagnetic. Besides, we obtain a single ion anisotropy that makes 1T-CrTe₂ strongly easy plane. Our calculations can explain the high Curie temperature of the bulk material and give clues why even the monolayer has a high Curie temperature. Finally, our post-annealing experiments of 1T-CrTe₂ suggest a thermal transition of 1T-CrTe₂ into a Cr-richer phase between 100 °C and 250 °C marking an important annealing temperature for possible future device fabrications.

In conclusion, the soft-chemical deintercalation of LiCrTe₂ using diluted acids yields high-quality crystals of 1T-CrTe₂ within a short deintercalation time of 2 h. Future exfoliation of these crystals can be expected to yield few-layered or monolayered samples, which hold promise for the fabrication of room-temperature spintronic devices.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

FvR designed the experiments. KR synthesized the crystals. KR, CW, CB, and VP conducted the experiments. HOJ performed the electronic structure calculations. All authors contributed to the analysis of the data. FvR and KR wrote the manuscript with contributions from all the authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Enrico Giannini and Radovan Cerny for the helpful discussions, Kerry-Lee Paglia for help with the DSC measurement. Part of this work was performed at the Swiss Spallation Neutron Source (SINQ), Paul Scherrer Institut (PSI), Villigen, Switzerland. This work was supported by the Swiss National Science Foundation under Grant No. PCEFP2_194183. The background image in the graphical abstract is by Berend de Kort viahttps://www.pexels.com.

Notes and references

1. J. F. Sierra, J. Fabian, R. K. Kawakami, S. Roche and S. O. Valenzuela, Nat. Nanotechnol., 2021, 16, 856–868.
2. Y. Ou, W. Yanez, R. Xiao, M. Stanley, S. Ghosh, B. Zheng, W. Jiang, Y.-S. Huang, T. Pillsbury, A. Richardella, C. Liu, T. Low, V. H. Crespi, K. A. Mkhoyan and N. Samarth, Nat. Commun., 2022, 13, 2972.
3. L. Alegria, H. Ji, N. Yao, J. Clarke, R. J. Cava and J. R. Petta, Appl. Phys. Lett., 2014, 105, 053512.
4. Z. Wang, D. Sapkota, T. Taniguchi, K. Watanabe, D. Mandrus and A. F. Morpurgo, Nano Lett., 2018, 18, 4303.
5. F. Wu, I. Gutiérrez-Lezama, S. A. López-Paz, M. Gibertini, K. Watanabe, T. Taniguchi, F. O. von Rohr, N. Ubrig and A. F. Morpurgo, Adv. Mater., 2022, 34, 2109759.
6. B. V. Lotsch, Annu. Rev. Mater. Res., 2015, 45, 85–109.
7. S. A. López-Paz, Z. Guguchia, V. Y. Pomjakushin, C. Witteveen, A. Cervellino, H. Luetkens, N. Casati, A. F. Morpurgo and F. O. von Rohr, Nat. Commun., 2022, 13, 4745.
8. T. McQueen, T. Berry, J. Chamorro, A. Ghasemi, W. A. Phelan, E. Pogue, L. Pressley, M. Sinha, V. J. Stewart, T. Tranet al., Fundamentals of Quantum Materials: A Practical Guide to Synthesis and Exploration, 2021.
9. F. O. Von Rohr, H. Ji, F. A. Cevallos, T. Gao, N. P. Ong and R. J. Cava, J. Am. Chem. Soc., 2017, 139, 2771–2777.
10. X. Song, G. Cheng, D. Weber, F. Pielnhofer, S. Lei, S. Klemenz, Y.-W. Yeh, K. A. Filsinger, C. B. Arnold and N. Yao, et al. , J. Am. Chem. Soc., 2019, 141, 15634–15640.
11. H. Sun, D. N. Woodruff, S. J. Cassidy, G. M. Allcroft, S. J. Sedlmaier, A. L. Thompson, P. A. Bingham, S. D. Forder, S. Cartenet and N. Mary, et al. , Inorg. Chem., 2015, 54, 1958–1964.
12. X. Sun, W. Li, X. Wang, Q. Sui, T. Zhang, Z. Wang, L. Liu, D. Li, S. Feng, S. Zhong, H. Wang, V. Bouchiat, M. Nunez Regueiro, N. Rougemaille, J. Coraux, A. Purbawati, A. Hadj-Azzem, Z. Wang, B. Dong, X. Wu, T. Yang, G. Yu, B. Wang, Z. Han, X. Han and Z. Zhang, Nano Res., 2020, 13, 3358.
13. D. C. Freitas, R. Weht, A. Sulpice, G. Remenyi, P. Strobel, F. Gay, J. Marcus and M. Núñez-Regueiro, J. Phys.: Condens. Matter, 2015, 27, 176002.
14. A. Purbawati, J. Coraux, J. Vogel, A. Hadj-Azzem, N. Wu, N. Bendiab, D. Jegouso, J. Renard, L. Marty, V. Bouchiat, A. Sulpice, L. Aballe, M. Foerster, F. Genuzio, A. Locatelli, T. O. Menteş, Z. V. Han, X. Sun, M. Núñez-Regueiro and N. Rougemaille, ACS Appl. Mater. Interfaces, 2020, 12, 30702.
15. A. Purbawati, S. Sarkar, S. Pairis, M. Kostka, A. Hadj-Azzem, D. Dufeu, P. Singh, D. Bourgault, M. Nuñez-Regueiro, J. Vogel, J. Renard, L. Marty, F. Fabre, A. Finco, V. Jacques, L. Ren, V. Tiwari, C. Robert, X. Marie, N. Bendiab, N. Rougemaille and J. Coraux, ACS Appl. Electron. Mater., 2023, 5, 764.
16. A. Otero Fumega, J. Phillips and V. Pardo, J. Phys. Chem. C, 2020, 124, 21047.
17. X. Zhang, Q. Lu, W. Liu, W. Niu, J. Sun, J. Cook, M. Vaninger, P. F. Miceli, D. J. Singh, S.-W. Lian, T.-R. Chang, X. He, J. Du, L. He, R. Zhang, G. Bian and Y. Xu, Nat. Commun., 2021, 12, 2492.
18. L. Meng, Z. Zhou, M. Xu, S. Yang, K. Si, L. Liu, X. Wang, H. Jiang, B. Li, P. Qin, P. Zhang, J. Wang, Z. Liu, P. Tang, Y. Ye, W. Zhou, L. Bao, H.-J. Gao and Y. Gong, Nat. Commun., 2021, 12, 809.
19. X. Zhang, S. C. Ambhire, Q. Lu, W. Niu, J. Cook, J. S. Jiang, D. Hong, L. Alahmed, L. He and R. Zhang, et al. , ACS Nano, 2021, 15, 15710.
20. S. Fragkos, P. Pappas, E. Symeonidou, Y. Panayiotatos and A. Dimoulas, Appl. Phys. Lett., 2022, 120, 182402.
21. M. Wang, L. Kang, J. Su, L. Zhang, H. Dai, H. Cheng, X. Han, T. Zhai, Z. Liu and J. Han, Nanoscale, 2020, 12, 16427.
22. L.-Z. Zhang, A.-L. Zhang, X.-D. He, X.-W. Ben, Q.-L. Xiao, W.-L. Lu, F. Chen, Z. Feng, S. Cao, J. Zhang and J.-Y. Ge, Phys. Rev. B, 2020, 101, 214413.
23. R. Chua, J. Zhou, X. Yu, W. Yu, J. Gou, R. Zhu, L. Zhang, M. Liu, M. B. H. Breese, W. Chen, K. P. Loh, Y. P. Feng, M. Yang, Y. L. Huang and A. T. S. Wee, Adv. Mater., 2021, 33, 2103360.
24. M. Yamaguchi and T. Hashimoto, J. Phys. Soc. Jpn., 1972, 32, 635.
25. M. Bian, A. N. Kamenskii, M. Han, W. Li, S. Wei, X. Tian, D. B. Eason, F. Sun, K. He, H. Hui, F. Yao, R. Sabirianov, J. P. Bird, C. Yang, J. Miao, J. Lin, S. A. Crooker, Y. Hou and H. Zeng, Mater. Res. Lett., 2021, 9, 205.
26. J. Zhong, M. Wang, T. Liu, Y. Zhao, X. Xu, S. Zhou, J. Han, L. Gan and T. Zhai, Nano Res., 2022, 15, 1254.
27. T. Hashimoto, K. Hoya, M. Yamaguchi and I. Ichitsubo, J. Phys. Soc. Jpn., 1971, 31, 679.
28. K. Lasek, P. M. Coelho, P. Gargiani, M. Valvidares, K. Mohseni, H. L. Meyerheim, I. Kostanovskiy, K. Zberecki and M. Batzill, Appl. Phys. Rev., 2022, 9, 011409.
29. R. Saha, H. L. Meyerheim, B. Göbel, B. K. Hazra, H. Deniz, K. Mohseni, V. Antonov, A. Ernst, D. Knyazev, A. Bedoya-Pinto, I. Mertig and S. S. P. Parkin, Nat. Commun., 2022, 13, 3965.
30. W. Bensch, O. Helmer and C. Näther, Mater. Res. Bull., 1997, 32, 305.
31. Y. Wang, J. Yan, J. Li, S. Wang, M. Song, J. Song, Z. Li, K. Chen, Y. Qin, L. Ling, H. Du, L. Cao, X. Luo, Y. Xiong and Y. Sun, Phys. Rev. B, 2019, 100, 024434.
32. C. Chen, X. Chen, C. Wu, X. Wang, Y. Ping, X. Wei, X. Zhou, J. Lu, L. Zhu, J. Zhou, T. Zhai, J. Han and H. Xu, Adv. Mater., 2022, 34, 2107512.
33. B. Tang, X. Wang, M. Han, X. Xu, Z. Zhang, C. Zhu, X. Cao, Y. Yang, Q. Fu, J. Yang, X. Li, W. Gao, J. Zhou, J. Lin and Z. Liu, Nat. Electron., 2022, 5, 224.
34. Z.-L. Huang, W. Kockelmann, M. Telling and W. Bensch, Solid State Sci., 2008, 10, 1099.
35. M. Huang, L. Gao, Y. Zhang, X. Lei, G. Hu, J. Xiang, H. Zeng, X. Fu, Z. Zhang, G. Chai, Y. Peng, Y. Lu, H. Du, G. Chen, J. Zang and B. Xiang, Nano Lett., 2021, 21, 4280.
36. K. O. Klepp and H. Ipser, Angew Chem. Int. Ed. Engl., 1982, 21, 2004.
37. H. Ipser, K. L. Komarek and K. O. Klepp, J. Less-Common Met., 1983, 92, 265.
38. J.-J. Xian, C. Wang, J.-H. Nie, R. Li, M. Han, J. Lin, W.-H. Zhang, Z.-Y. Liu, Z.-M. Zhang, M.-P. Miao, Y. Yi, S. Wu, X. Chen, J. Han, Z. Xia, W. Ji and Y.-S. Fu, Nat. Commun., 2022, 13, 257.
39. X. Song, B. Hoff, R. Singha, J. W. Stiles, G. Skorupskii, J. F. Khoury, G. Cheng, F. Kamm, A. J. Uzan, S. Dulovic, S. Wu, F. Pielnhofer, N. Yao and L. M. Schoop, Chem. Mater., 2023, 35, 5487.
40. F. Wypych, K. Sollmann and R. Schöllhorn, Mater. Res. Bull., 1992, 27, 545.
41. Z. Guguchia, D. J. Gawryluk, M. Brzezinska, S. S. Tsirkin, R. Khasanov, E. Pomjakushina, F. O. von Rohr, J. A. Verezhak, M. Z. Hasan and T. Neupert, et al. , npj Quantum Mater., 2019, 4, 50.
42. Z. Lai, Q. He, T. H. Tran, D. V. M. Repaka, D.-D. Zhou, Y. Sun, S. Xi, Y. Li, A. Chaturvedi, C. Tan, B. Chen, G.-H. Nam, B. Li, C. Ling, W. Zhai, Z. Shi, D. Hu, V. Sharma, Z. Hu, Y. Chen, Z. Zhang, Y. Yu, X. Renshaw Wang, R. V. Ramanujan, Y. Ma, K. Hippalgaonkar and H. Zhang, Nat. Mater., 2021, 20, 1113.
43. C. Witteveen, E. Nocerino, S. A. López-Paz, H. O. Jeschke, V. Y. Pomjakushin, M. Månsson and F. O. von Rohr, J. Phys.: Mater., 2023, 6, 035001.
44. J. Rodriguez-Carvajal, Phys. B, 1993, 192, 55–69.
45. O. D. Rigaku, Crysalis Pro, Rigaku Oxford Diffraction Ltd, Yarnton, Oxfordshire, England, 2015.
46. G. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
47. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3.
48. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339.
49. P. Fischer, G. Frey, M. Koch, M. Könnecke, V. Pomjakushin, J. Schefer, R. Thut, N. Schlumpf, R. Bürge, U. Greuter, S. Bondt and E. Berruyer, Phys. B, 2000, 276–278, 146.
50. H. T. Stokes, D. M. Hatch and B. J. Campbell, ISODISTORT, ISOTROPY Software Suite, https://iso.byu.edu.
51. H. T. Stokes, D. M. Hatch and B. J. Campbell, J. Appl. Crystallogr., 2006, 39, 607.
52. H. O. Jeschke, F. Salvat-Pujol, E. Gati, N. H. Hoang, B. Wolf, M. Lang, J. A. Schlueter and R. Valentí, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 094417.
53. H. O. Jeschke, H. Nakano and T. Sakai, Phys. Rev. B, 2019, 99, 140410.
54. K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743.
55. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
56. E. Nocerino, C. Witteveen, S. Kobayashi, O. K. Forslund, N. Matsubara, A. Zubayer, F. Mazza, S. Kawaguchi, A. Hoshikawa, I. Umegaki, J. Sugiyama, K. Yoshimura, Y. Sassa, F. O. von Rohr and M. Månsson, Sci. Rep., 2022, 12, 21657.
57. J. Peng, J. Wu, X. Li, Y. Zhou, Z. Yu, Y. Guo, J. Wu, Y. Lin, Z. Li and X. Wu, et al. , J. Am. Chem. Soc., 2017, 139, 9019.
58. X. Song, S. N. Schneider, G. Cheng, J. F. Khoury, M. Jovanovic, N. Yao and L. M. Schoop, Chem. Mater., 2021, 33, 8070.
59. H. Chung, Y. Li, M. Zhang, A. Grenier, C. Mejia, D. Cheng, B. Sayahpour, C. Song, M. H. Shen and R. Huang, et al. , Chem. Mater., 2022, 34, 7302.
60. A. Arrott, Phys. Rev., 1957, 108, 1394.
61. R. Lefèvre and F. O. von Rohr, Chem. Mater., 2022, 34, 2352.
62. F. Fabre, A. Finco, A. Purbawati, A. Hadj-Azzem, N. Rougemaille, J. Coraux, I. Philip and V. Jacques, Phys. Rev. Mater., 2021, 5, 034008.
63. P. Ghosh, Y. Iqbal, T. Müller, R. T. Ponnaganti, R. Thomale, R. Narayanan, J. Reuther, M. J. P. Gingras and H. O. Jeschke, npj Quantum Mater., 2019, 4, 63.
64. H.-X. Xu, M. Shimizu, D. Guterding, J. Otsuki and H. O. Jeschke, Phys. Rev. B, 2023, 108, 125142.
65. S. Jenkins, L. Rózsa, U. Atxitia, R. F. L. Evans, K. S. Novoselov and E. J. G. Santos, Nat. Commun., 2022, 13, 6917.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2376663. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ta05649c

---