Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Afterglow quenching in plasma-based dry reforming of methane: a detailed analysis of the post-plasma chemistry via kinetic modelling†
Joachim
Slaets
 ,
Eduardo
Morais
,
Eduardo
Morais
 and
Annemie
Bogaerts
and
Annemie
Bogaerts
 *
*
Research Group PLASMANT, Department of Chemistry, University of Antwerp, Universiteitsplein 1, BE-2610 Wilrijk-Antwerp, Belgium. E-mail: annemie.bogaerts@uantwerpen.be
First published on 28th January 2025
Abstract
We have developed a kinetic model to investigate the post-plasma (afterglow) chemistry of dry reforming of methane (DRM) in warm plasmas with varying CO2/CH4 ratios. We used two methods to study the effects of plasma temperature and afterglow quenching on the CO2 and CH4 conversion and product selectivity. First, quenching via conductive cooling is shown to be unimportant for mixtures with 30/70 and 50/50 CO2/CH4 ratios, while it affects mixtures containing excess CO2 (70/30) by influencing radical recombination towards CO2, H2 and H2O, as well as the water gas shift reaction, decreasing the CO2 conversion throughout the afterglow. This is accompanied by shifts in product distribution, from CO and H2O to CO2 and H2, and the magnitude of this effect depends on a combination of plasma temperature and quenching rate. Second and more importantly, quenching via post-plasma mixing of the hot plasma effluent with fresh cold gas yields a significant improvement in conversion according to our model, with 258% and 301% extra conversion for CO2 and CH4, respectively. This is accompanied by small changes in product selectivity, which are the result of interrupted reaction pathways at lower gas temperatures in the afterglow. Effectively, the post-plasma mixing can function as a heat recovery system, significantly lowering the energy cost through the additional conversion ensued. With this approach, our model predicts that energy consumption can be lowered by nearly 80% in comparison to DRM under the same plasma conditions without mixing.
Sustainability spotlightThis paper describes plasma-based dry reforming of methane (DRM), converting CO2 and CH4 into CO and H2, which can be used to produce more complex chemicals. This supports a circular economy, by using CO2 and biogas as a feedstock, while reducing emissions and dependence on fossil fuels. Plasma reactors are ideal in this scenario as they can operate on renewable electricity and easily couple to intermittent energy supplies. In this work, we evaluate different post-plasma quenching methods via chemical kinetics modelling to develop a better understanding of chemical pathways in plasma-based DRM, crucial to advance this technology and bring it closer to industry. Our work contributes to UN sustainable development goals: industry, innovation, and infrastructure (SDG-9) and climate action (SDG-13). |
1. Introduction
CO2 and CH4 are both major greenhouse gases that play an important role in climate change. Therefore, reducing emissions of these gases is an important challenge. Beyond lower emissions, utilising these gases in new chemical processes can provide a sustainable source of raw materials, creating a circular economy.1 As such, targeting the dry reforming of methane (DRM) (R1) can help to convert CO2 and CH4 into more useful molecules, in this case, a mixture of CO and H2 (syngas). In turn, syngas can be used as a building block for more complex, value-added chemicals, for example in the Fischer–Tropsch process to synthesise a variety of hydrocarbons.2–4| CO2 + CH4 → 2CO + 2H2, ΔH0 = 247 kJ mol−1 | (R1) |
The use of plasma reactors for DRM offers many benefits. It is a fully electrified process, allowing the reactors to operate using renewable energy. Also, it can be quickly switched on/off, and scaled according to energy availability and demand, making it suitable for peak shaving.5–7 As a young and promising technology for gas conversion, plasma has been extensively researched in the last decade.
Considerable research effort goes into the optimisation of specific plasma parameters. Various distinct plasma types and reactor configurations have been studied under varying operating conditions – such as flow rate, applied power, reactor geometry, gas mixtures, etc.6 Warm plasma reactors, including gliding arc (GA), microwave (MW), atmospheric pressure glow discharges (APGDs) or nanosecond pulsed discharges (NPDs) can generate high gas temperatures, reaching several 1000 K.5,6 While the gas conversion is typically driven by thermal chemistry, they are more energy efficient than cold plasmas, like dielectric barrier discharges.5,6,8 In these warm plasmas, the downstream gas temperature (i.e., the afterglow or post-plasma region, outside of the plasma zone) may still be sufficiently high to enable reaction pathways that can influence reactor performance in different manners. For instance, this effect could trigger reverse reactions, reducing the overall conversion and altering the product distribution.9 On the other hand, it can also be used to enhance the conversion and product yield.9 Thus, recent studies have increasingly focussed on the post-plasma region of these reactors, to build a better understanding of the effects at play and improve the overall performance.
In CO2 plasmas, it has been demonstrated that CO2 conversion locally within the plasma can approach 100%.10,11 However, reverse reactions in the post-plasma region (namely recombination of CO with O radicals) have been found to reduce this significantly, with measured conversions as low as 25%.10,11 Rapid quenching of the high gas temperature has been shown to be a successful strategy to curtail these reverse reactions.12–15 Three different modes can be identified for post-plasma quenching.9 First, in absolute quenching, the plasma-generated product molecules are preserved, while the radical species recombine to reform the reactants, i.e., leading to a net reduction in the conversion. Second, in ideal quenching, the conversion achieved in the plasma zone is retained by inducing the radicals to react towards products. The third quenching mode is called super-ideal quenching, where not only the high conversions are maintained, but they can be further boosted. Super-ideal quenching can be achieved when the gas is cooled faster than the time required for vibrational–translational (VT) relaxations to occur, creating a VT non-equilibrium.9 The vibrational energy trapped in the gas molecules can stimulate endothermic reactions, allowing for conversion gains during the quenching. This super-ideal quenching mode will not be considered in this work, as it can only be attained under very specific conditions and in systems with a strong VT non-equilibrium character.11 This is not the case for the atmospheric plasmas studied in this work, as it has been shown that VT non-equilibrium is limited to pressures below or equal to 25 mbar.16
There is a diverse range of quenching methods and several studies have investigated the use of a constricting nozzle, for example.13–15 This device can cool down the gas by rapid expansion, creating eddies in the fluid flow which improve gas mixing and heat transfer.14,15,17 For CO2, the conversion gain from this strategy can vary significantly (between 2 and 30%), depending strongly on the operating conditions and nozzle design. The largest additional conversion was seen by Hecimovic et al.15 who measured an increase in CO2 conversion from 5 to 35%, following nozzle implementation. Subsequently, this setup was modelled by Van Alphen et al.18 confirming these findings, indicating that a cooling rate of ∼107 K s−1 was achieved, significantly enhancing CO2 conversion. A similar nozzle approach was modelled by Yang et al.,17 reaching the same conclusions.
Further research attempted quenching using liquid-cooled devices to reduce the temperature of the gas stream from the plasma region. A two-stage cooling system used by Wang et al.19 improved the CO2 conversion from 6.6 to 19.5%. Another design, which uses a liquid-cooled rod in the reactor outlet to achieve the post-plasma cooling, was used by Kim et al.12 who reported that the CO2 conversion increased from 30.1 to 36.1% upon implementation of this strategy. The same approach was also tested for DRM, leading to interesting findings: both the CO2 and CH4 conversion were observed to drop compared to the uncooled plasma reactor.20 The reported maximum decrease in total conversion occurred at a CO2/CH4 ratio of 3/1, from 23.4 to 22.6%. On the other hand, upon employing the quenching rod, selectivity towards H2 was boosted, while that towards H2O dropped. The selectivity effect was attributed to the inhibition of the reverse water gas shift (RWGS) in the colder post-plasma region, preventing CO2 and H2 from reacting to CO and H2O. While the drop in conversion has a negative effect on the energy cost, the selectivity gain towards H2 (observed for mixtures with higher CH4 fractions) can outpace the negative effect on conversion, resulting in a lower energy cost for syngas production.
Another approach to consider is the introduction of new gas in the afterglow region, such as through a secondary inlet. Hyun Cho et al.21 injected cold CH4 in the afterglow of a CO2 plasma to achieve conversion, effectively separating the DRM reaction into a two step process. They claim the main advantage of this method is the increase in energy consumption selectivity. The energy injected through the plasma decomposes only CO2 rather than CH4, yielding higher CO2 conversion and higher syngas energy conversion efficiency compared to the direct DRM reaction in the plasma. While their work specifically focusses on this two step DRM process, this secondary inlet can be an interesting strategy to apply, even without changing the overall gas mixture. The remaining heat in the plasma effluent can be recovered and used to convert the newly introduced gas, potentially improving the performance of the system, while it also provides cooling to the afterglow.
While a comparison with current industrial processes involving DRM and quenching would provide valuable context for the broader application of this research, this theoretical study specifically focuses on understanding the fundamental mechanisms of post-plasma effects in warm plasmas, opening avenues for future experiments and benchmarking.
In this work, we aim to explore the effects of these post-plasma quenching methods on the chemical kinetics for DRM, and elucidate the mechanisms involved in the observed conversion and selectivity trends. Our model incorporates two distinct approaches to post-plasma quenching: (i) heat removal from the system (emulating the introduction of a cooled rod, hence conductive cooling), and (ii) the mixing of cold gas in the post-plasma region (emulating the introduction of a nozzle, or simply adding cold gas in the afterglow). In the interest of model versatility and relevance, we do not limit our work to specific reactor designs or operating conditions; instead we focus specifically on warm plasma conditions, which are indeed known to yield the best performance for DRM.6 To this end, we study a wide range of conditions, with plasma temperatures between 2000–4000 K and three different CO2/CH4 ratios, i.e., stoichiometric (50/50), excess CH4 (30/70) and excess CO2 (70/30). We compare different degrees of gas cooling, achieved with both methods, and evaluate the effects of the ensuing temperature decrease on conversion, selectivity and energy cost. Our primary objective is to obtain a better understanding of the post-plasma kinetics upon gas cooling. These insights can help experimentalists towards potential improvements and new reactor designs for further advancement of plasma-based DRM technologies.
2. Model description
2.1. Simulation details
In this work, we use a zero-dimensional chemical kinetics model which allows us to conduct an in-depth (yet general) study of multiple conditions and approaches, while also running simulations independent of a specific reactor configuration. The calculations were performed using the ZDPlasKin22 code, which is described in Section 2.3.The simulation domain consists of a plasma region and a subsequent post-plasma (or afterglow) region, with the latter being the main focus of this work. A schematic overview of the simulations is given in Fig. 1a, illustrating the plasma zone with a constant temperature, followed by the afterglow in which the gas temperature decreases, as the hot gas is quenched. We simulate (i) fast conductive cooling and (ii) mixing with cold unconverted gas (see Fig. 1b) as distinct quenching methods.
 | ||
| Fig. 1 (a) Schematic overview of the simulation domain, showing the plasma and post-plasma/afterglow zones, plasma temperature (Tpl) and residence time (tres, which is typically around 10 ms).23,24 (b) Schematic overview of the enhanced mixing approach, indicating the plasma and post-plasma/afterglow zones. The cold unconverted gas is only added after the plasma, either from a peripheral region around the plasma zone or from a secondary inlet. The important points in the simulations are compared in the Results and discussion section. (A) Corresponds to the end of the plasma zone (at the plasma temperature, immediately before the temperature drop), and (B) to the end of the afterglow after all quenching has taken place. | ||
In the plasma, gas temperatures between 2000–4000 K are assumed, which is the typical temperature range for many warm plasmas.6 The residence time in the plasma zone was set to 10 ms, which is a reasonable assumption following the works of Van Alphen et al.23 and Dahl et al.24 These conditions are also consistent with our previous work25 (focused on DRM plasma kinetics), which demonstrated that within the studied temperature range, the kinetics is dominated by thermal chemistry, meaning that electron impact processes can be neglected. Therefore, the DRM thermal kinetics suffices to describe the plasma region, simplifying the simulations. In terms of applicability, this approach broadens the potential of our results, since the gained insights can be expanded beyond plasma-specific conditions. To demonstrate the effects in the post-plasma region, we present the important parameters (species concentrations, conversion and selectivity) at points A and/or B (indicated in Fig. 1), as a function of the plasma temperature.
As mentioned above, two quenching approaches are tested within the post-plasma region, which divides our work into two main parts: (i) in the first approach, we model an afterglow system which is cooled through conductive heat loss (from point A to point B), aiming to study the effects of temperature decrease on the reaction kinetics. This conductive cooling is enhanced with a factor, c, (1, 10 and 100) with more details given in Section 2.3. (ii) In the second approach, the cooling stems from mixing room-temperature gas with the hot afterglow, introducing ‘fresh’ and ‘cold’ gas molecules which will reduce the overall gas temperature. In this study, the cold gas mixture introduced post-plasma is identical to the unconverted gas mixture. The freshly added CO2 and CH4 molecules will be dissociated by the relatively high temperatures in the afterglow, resulting in altered kinetic pathways and extra overall conversion.
Since this mixing approach does not consider conductive heat loss to the reactor walls, i.e., the post-plasma region is assumed to be perfectly thermally insulated, the addition of cold gas is the only factor that influences the gas temperature and in turn the kinetics. Hence, without other means to decrease the gas temperature, optimal conditions are created to attain the highest possible conversion of the added gas. This is due to the redistribution of the available energy over more gas molecules, since this quenching method does not remove heat from the system. Thus, to guarantee a realistic cooling and a temperature drop sufficient to stop all reactions, a large amount of cold gas must be added. In our case, we found that adding a cold gas stream nine times larger than the initial flow (i.e., diluting the fraction that travelled through the plasma to 10%) meets this criterion. We change the mixing time between 1, 10 and 100 ms to modulate the cooling strength, which is further explained in Section 2.3. This results in temperature gradients in the afterglow similar to the conductive cooling approach.
By studying these two quenching approaches in our model, i.e., the enhanced thermal conductivity (or fast conductive cooling) and enhanced post-plasma mixing, we aim to provide insights into the reaction kinetics in post-plasma DRM processes. We note that these approaches are not directly comparable to experimental conditions, thus the trends and general findings resulting from the model are more relevant than the absolute values.
2.2. DRM chemistry
The species and reaction scheme used in this work is the same as in our previous work.25 However, as mentioned above, based on our previous study, our present simulations only consider thermal kinetics; hence electrons and ions and their respective reactions are not included. This amounts to a total of 40 species and 728 reactions. These species are listed in Table 1, and a list of the reactions with the corresponding rate coefficients and respective references is provided in the ESI (Table S3, at the end of the document).† The main dissociation pathways under the tested plasma conditions vary depending on the gas composition.25 For CO2, dissociation primarily occurs through reactions with H radicals, while in mixtures with an excess of CO2, reactions with O and OH radicals also contribute significantly. In the case of CH4, dissociation predominantly proceeds through reactions with H or neutral species (M). Additionally, in mixtures with excess CO2, OH radicals play a role, and in mixtures with excess CH4, C2H radicals also contribute to the dissociation process.| C |
| O, O2, O3 |
| H, H2 |
| CO, CO2 |
| CH, CH2, CH3, CH4, C2H, C2H2, C2H3, C2H4, C2H5, C2H6 |
| OH, H2O, HO2, H2O2 |
| CH2CH2OH, CH2CO, CH2OH, CH3CH2O, CH3CH2OH, CH3CHO, CH3CHOH, CH3CO, CH3COOH, HCCO, CH3O, CH3OH, CH3OO, CH3OOH, COOH, HCHO, HCO, HCOOH |
2.3. Equations in the model
The calculations are performed using the ZDPlasKin22 code, which uses the DVODE solver26 to solve the mass conservation equation for each species included in the model (eqn (1)). The first term on the right-hand side calculates the change in number density with respect to time (∂n/∂t) for species (s) due to a chemical reaction (i). aRs,i and aLs,i are the coefficients of species s on the right and left side of reaction i, respectively, and Ri is the corresponding reaction rate, which is explained in ESI (Section S1 and eqn (S1)).† More details on the reaction rates, alongside a complete list of all reactions in the kinetics scheme and corresponding references, are given in ESI (Table S3 and Section S2).† | (1) |
The standard mass conservation expression (based on the first term on the right-hand side) is expanded with two other terms to include an additional source term and a correction for gas expansion (see ESI, Section S1 and eqn (S2)†). The former is used to introduce new species in the system upon mixing with unconverted gas (as explained in Section 2.1) based on a rate (Rmix) and the fraction added of each species in the model (xmix,s). These species are limited to CO2 and CH4, and their fractions are defined by the CO2/CH4 gas mixing ratio, i.e., 30/70, 50/50 and 70/30. The mixing rate (Rmix) is defined as a source term that represents species transport from the surrounding cold unconverted gas flow into the modelled plasma effluent volume (as shown in Fig. 1b). This is given in eqn (2), where nmix is the total number density of gas that is added during the mixing process, τmix is the characteristic mixing time, tAG is the time in the afterglow and α is the gas expansion factor. The dilution of 10% (i.e., flow of unconverted mixing gas being nine times higher than the plasma effluent) is used in all conditions, which results in nmix = 2.25 × 1020 cm−3, equal to nine times the initial number density at 293.15 K and 1 atm. Because the mixing is given by an exponential function, it only tends to zero asymptotically (never actually becoming zero). For reference, 99% of the mixing has occurred at 4.61, 46.1 and 461 ms in the afterglow for the characteristic times of 1, 10 and 100 ms.
 | (2) |
 .27,28 However, due to the 0D nature of our model, these D and L parameters do not have a physical meaning. In the interest of simplifying the analysis, we directly specify the τmix values, rather than having them defined by a combination of D and L values. Therefore, the τmix values used in this study are not intended to be correlated to diffusion, instead they are selected to emulate cooling rates consistent with those observed in the other quenching methods since the focus of our study is on the effect of the cooling rate on the kinetics.
.27,28 However, due to the 0D nature of our model, these D and L parameters do not have a physical meaning. In the interest of simplifying the analysis, we directly specify the τmix values, rather than having them defined by a combination of D and L values. Therefore, the τmix values used in this study are not intended to be correlated to diffusion, instead they are selected to emulate cooling rates consistent with those observed in the other quenching methods since the focus of our study is on the effect of the cooling rate on the kinetics.
All simulations are conducted at a constant pressure of 1 atmosphere, and this is directly linked to the absolute number densities for each species in the model. There are two factors that influence the total number density in the system: temperature and chemical reactions. As chemical reactions take place, and the gas temperature changes, the gas needs to expand or contract accordingly if the number density changes, to maintain a constant pressure. This is achieved with the Rexpansion term in eqn (1), which is further explained in the ESI (Section S1).†
The gas expansion is monitored throughout the simulation using eqn (3), which represents the ratio of the mass density (ρ) at the start of the simulation and the end. The mass density is the summation of the products of the number density (nj) and mass (mj) of each species (j) in the model.
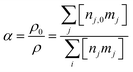 | (3) |
While the temperature is kept constant in the plasma portion of the simulation, in the post-plasma portion the heat balance equation is solved to calculate the temperature self-consistently. ZDPlasKin normally considers a system at constant volume by using the ratio of specific heats to describe the isochoric heat capacity. However, in this model we consider a system at constant pressure, and therefore the isobaric heat capacity is included instead, thus accounting for volumetric expansion. This heat balance equation is given in eqn (4), in which Rgas is the universal gas constant, cp,mix is the heat capacity of the mixture (see ESI, Section S1 and eqn (S3)†), dT/dt represents the change in temperature with respect to time, Qreaction is the heat gained or lost as a result of reactions, while Qconductive and Qmixing represent the conductive heat losses and the heat losses resulting from post-plasma mixing, respectively. When quenching through conductive cooling is investigated, the Qconductive term is used, while the Qmixing term is set to zero. Conversely, in the case of quenching through mixing, the Qmixing term is used and the Qconductive term is zero.
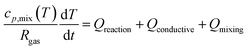 | (4) |
The heat exchange due to reactions (Qreaction) is calculated using eqn (5), with Ng the total number density of the heavy species in the simulation, Ri the reaction rate of reaction i and εi the reaction enthalpy of reaction i (see ESI, Section S1 and eqn (S4)†).
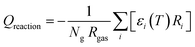 | (5) |
The conductive heat loss is calculated using eqn (6), in which T is the gas temperature, T0 is the reference wall temperature (293.15 K), kB the Boltzmann constant, r the radius of the plasma (chosen as 1 cm), λmix the thermal conductivity of the gas mixture (see ESI, Section S1 and eqn (S5)†) and c an additional factor to artificially increase the external cooling (varied between 1, 10 and 100). This additional c-factor is similar to the one used by Vermeiren et al.11 The equation assumes a parabolic temperature profile with T being the radially average temperature and T0 the temperature at the wall.29 This provides a basic approximation of the temperature in the afterglow. The exact and precise value, however, is not the main focus of our study, as the most important effect here is the cooling rate on the kinetics. For the simulations that investigate post-plasma mixing, this conductive cooling term is set to zero. This is done to emulate a perfectly insulated system, which will isolate the effects of mixing by eliminating competition with conductive cooling. This ensures that the gas temperature remains at high values for a longer time, thus creating the optimal conditions for conversion of the freshly mixed gas.
 | (6) |
Finally, when applying post-plasma mixing, additional species are added to the afterglow without the removal of other species, which effectively increases the size of the system. Besides, since these new species do not have the same temperature, an amount of energy is required to equalise the temperature of these species to the rest of the system, which affects the heat balance. This is accounted for in the mixing heat term (Qmixing) defined by eqn (7), in which Rmix is the mixing rate, xmix,s is the fraction of species s in the mixed gas (both explained above already), Hfs is the temperature-dependent enthalpy of species s (obtained from McBride et al.30 and Burcat et al.31), T is the gas temperature and T0 is the temperature of the mixing gas (293.15 K). In the first set of conditions, where enhanced conductive cooling is used to quench the afterglow, no mixing is used and therefore this Qmixing term is zero.
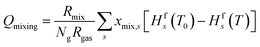 | (7) |
The metrics of conversion, yield and selectivity of various species are presented for different simulated conditions, following the recommendations of Wanten, et al.32 The conversion of the initial gases CO2 and CH4 is calculated using eqn (8), where nins and nouts are the number density of species s (CO2 or CH4) entering and leaving the simulations, and α is the gas expansion factor. For the simulations where mixing was considered, the initial number density includes both the original and the additional gas densities.
 | (8) |
In the Results and discussion section, we plot the selectivity of the product species as a function of the plasma temperature, to show its effects on the product distribution. The selectivity is calculated using eqn (9), where A is the base-atom (C, H or O in this case) and μAs and μAi are the numbers of the base-atom in product s and reactants i, respectively.32 The base-atom is required to differentiate between the number of each atom type in the gas mixture, which eventually become the products. For example, the selectivity of CO can be calculated relative to the amount of C (from CO2 and CH4) or O (from CO2) present in the simulations. Therefore, multiple selectivity values can be calculated for one product. By definition, the sum of all selectivity values must be 100%, which is the case for each base-atom.32 To simplify the understandability and presentation of the results, we display only one value for each product, prioritising the base-atoms in the following order: first carbon (C), then hydrogen (H), and finally oxygen (O). In some cases, product selectivities for different base-atoms are shown in the same figure, thus it is important to keep in mind that the sum of the selectivity can be above 100%. Once again, the results will focus on the individual products and general trends, but not the total sum. This strategy is commonly used in the case of simulations with mixing, to present changes in product distribution regardless of the achieved conversion.32
 | (9) |
Besides conversion and selectivity, another important evaluated metric is the energy cost of the process. To this end, we calculated energy cost of conversion, as the ratio between the energy input and the obtained conversion. In practice, the lower the energy cost, the more energy efficient the process is. In our case, because we set a constant plasma temperature, no energy input is defined. Therefore, we utilise a minimum energy input (MEI), which is defined as the enthalpy difference between the initial state (CO2 and CH4 at 293.15 K) and the state in the plasma (at the fixed temperature). This represents the minimum possible energy required to obtain this state. It is calculated using eqn (10), in which Hfs is the formation enthalpy of species s, ns is the species density, α is the gas expansion factor and NA is Avogadro's constant. The formation enthalpy is determined from the thermodynamic data from McBride et al.30 and Burcat et al.31 We use this MEI concept to define the minimum energy cost of conversion (MEC) (eqn (11)), which represents the minimum energy cost achievable for these conditions. χtot is the weighted average of the CO2 and CH4 conversion relative to their initial concentrations. Even though this cannot be compared to experimental data (as the calculations do not consider energy loss processes), this parameter allows us to compare between our different operating conditions and evaluate their potential.
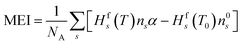 | (10) |
 | (11) |
For the simulations with post-plasma mixing, we also calculate the additional conversion (χadditional), which represents the relative increase in conversion between the end of the plasma and the end of the post-plasma region. This is determined using eqn (12), in which χend and χplasma are the conversion at the end of the simulation and at the end of the plasma region, respectively, and D is the dilution degree from mixing (10%, as explained above). Note that when the conversion does not change in the afterglow, χadditional will be 0%; and in the case of recombination, χadditional will be negative. Finally, this equation does not distinguish between further conversion of gas treated by the plasma or conversion of mixed gas in the hot afterglow.
 | (12) |
3. Results & discussion
3.1. Post-plasma cooling
We first analyse the results from simulations where conductive cooling is applied post-plasma. The extent of cooling (and thus quenching) is modulated by the factor c, as described in the previous section. For the three investigated CO2/CH4 ratios (30/70, 50/50, 70/30) and the three different c-factors (1, 10, 100), the resulting gas cooling can be observed in the temperature profiles shown in Fig. S1–S3 in ESI (Section S3).† In turn, this gives rise to cooling rates in the order of 105–108 K s−1 (see panels b, d and f in the abovementioned figures) at the start of the afterglow. This magnitude of cooling rate has been proven to be beneficial for the conversion of CO2,17,18 which bodes well for this theoretical study of DRM.The differences observed in the temperature profiles across the three CO2/CH4 ratios are ascribed to the lesser and greater proportion of CO2 or CH4 in the mixture, which affects the thermal conductivity and heat capacity (leading to changes in the temperature profiles). When slower cooling is considered (c-factor = 1), exothermic radical recombination occurs at high temperature, rendering undisturbed temperature profiles and resulting in a smooth decrease. In the case of faster conductive cooling (i.e., larger c-factors), these exothermic reactions are forced to occur at lower temperatures, deaccelerating the temperature drop at certain points in the afterglow. We do not focus on these absolute temperature profiles in the afterglow for comparing the kinetics, conversion or selectivity results, instead we focus on the overall trends, which provide a more qualitative comparison. Higher-dimensional fluid models would offer a more realistic and detailed simulation of these plasma systems, enabling more quantitative and space-resolved insights into the post-plasma effects. However, these models also introduce significant complexity and tend to be more specific to particular setups or reactor geometries. This lies beyond the scope of this work, as our focus is on gaining in-depth knowledge on the overall kinetics, hence we consider our simpler and more universal modelling approach better suited for this work. Note that for plasma temperatures near 2000 K, a steady state has not yet been fully reached within the simulated plasma residence time. Therefore, unreacted CO2 and CH4 and intermediate species from incomplete conversion can still be present.
 | ||
| Fig. 2 Selectivity of the main species (above 5%) as a function of the plasma temperature, for the 50/50 CO2/CH4 ratio and c-factor of 1 (no enhanced cooling), at the end of the plasma zone (point A in Fig. 1; dotted lines) and end of the afterglow (point B in Fig. 1; solid lines). The CO curves (both at the end of the plasma and afterglow) and H2 curves at the end of the afterglow largely overlap. Also, the H2O and C2H2 selectivity curves overlap both at the end of the plasma and afterglow. Near full conversion of CO2 and CH4 is observed under all conditions, at the end of the plasma, and maintained till the end of the afterglow. | ||
When the cooling degree is increased by a ten- or hundred-fold (c = 10, 100), we observe the same behaviour (see Fig. S4†), with only negligible alterations in minor product species (H2O, C2H2 and CH4). In summary, our model suggests that for a 50/50 CO2/CH4 mixture, quenching is not required to maintain the conversion reached in the afterglow, while the main products are consistently CO and H2.
 | ||
| Fig. 3 Selectivity of the main species (above 5%) as a function of the plasma temperature, for the 30/70 CO2/CH4 ratio and c-factor of 1 (no enhanced cooling), at the end of the plasma zone (point A in Fig. 1; dotted lines) and end of the afterglow (point B in Fig. 1; solid lines). Full conversion of CO2 and CH4 is observed under all conditions (except for 2000 K, as explained in the text). | ||
When the cooling rate for this mixture is increased, the main products predicted by the model continue to be H2, CO and C2H2, without any new products being formed (see Fig. S5†). However, the C2H4 selectivity is reduced to 1.3% for both c-factors 10 and 100 (compared to 2.5% at c = 1). In conclusion, for 30/70 CO2/CH4 mixtures, these results also reveal that quenching of the afterglow is not beneficial for conversion and has a negligible effect on the species distribution.
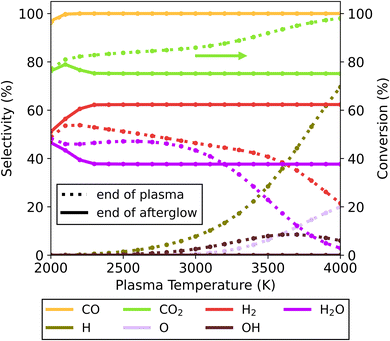 | ||
| Fig. 4 Selectivity of the main species (above 5%) as a function of the plasma temperature, for the 30/70 CO2/CH4 ratio and c-factor of 1 (no enhance cooling), at the end of the plasma zone (point A in Fig. 1; dotted lines) and end of the afterglow (point B in Fig. 1; solid lines). Full conversion of CH4 is observed under all conditions, but not for CO2, and therefore the CO2 conversion is also plotted (right y-axis). | ||
In the lower range of plasma temperatures (<3000 K), radical concentrations are rather low (only small fractions of H and OH are present). Despite radical recombination being limited, there is a notable shift in product distribution – with the formation of H2 and CO2 being favoured over that of CO and H2O, through the occurrence of the water gas shift (WGS) reaction (R2). For instance, at 2500 K the conversion of CO2 decreases from 84 to 75% due to WGS, while simultaneously the H2 selectivity increases from 51 to 62% and the H2O selectivity decreases from 47 to 38%.
| CO + H2O → CO2 + H2 | (R2) |
For higher plasma temperatures, higher CO2 conversions can be achieved in the plasma, up to 98% at 4000 K. This is accompanied by considerable formation of H, OH and O radicals, instead of H2O and H2. At this temperature, the low H2O concentrations limit the occurrence of WGS. However, between 2300 and 4000 K, we observe approximately the same product distribution at the end of the afterglow, regardless of the initial plasma temperature, which is further explained in the next paragraph. Also noteworthy is that all extra CO2 conversion originating from the higher plasma temperatures is lost again in the afterglow upon gas cooling. This negates the supposed benefits of high plasma temperatures for CO2 conversion, as in this case this effect alone is counteracted in the afterglow region. This is aligned with results for pure CO2 conversion without quenching of Vermeiren et al.11 where significant recombination is demonstrated to reduce the conversion to similar levels, regardless of the gas temperature obtained in the plasma.
These recombination reactions and pathways are further explored by analysing the evolution of key species over time in the afterglow for the 4000 K plasma temperature case (Fig. 5 below). Owing to the presence of O, OH and H radicals produced in the plasma for the 70/30 CO2/CH4 ratio, multiple recombination processes can occur. The two most straightforward processes are the O + CO reaction to CO2 and H + H to H2. Aside from these, a reaction of minor importance occurs between O and H to form OH, with the OH selectivity peaking at 8.5% around 1.8 ms. Subsequently, these OH radicals are important to further produce H2O, which has a maximum selectivity of 46% at 9.9 ms. At this point the system has reached a state similar to the equilibrium composition at around 2500 K (also obtained at the end of the plasma for plasma temperatures of 2000–3000 K, cf.Fig. 4). Since the kinetics up to this point significantly outpaces the cooling rate, differences in cooling have minimal impact. The temperature is still sufficient to allow further reactions, and the WGS reaction reduces the H2O selectivity again before it plateaus at 38%. This is the result of the kinetics eventually slowing down, effectively halting all reactions and reaching the final steady state. Because this part of the temperature profile is similar, regardless of the starting plasma temperature (Fig. S12 in ESI†) the overall chemical changes are also similar, resulting in overall similar product distributions across the entire temperature range. The CO selectivity is constant at 100%, and as this is the only main C-containing species, the C-based selectivity remains constant. However, the absolute amount of CO does decrease (not shown in the figure) as the CO2 conversion drops due to WGS.
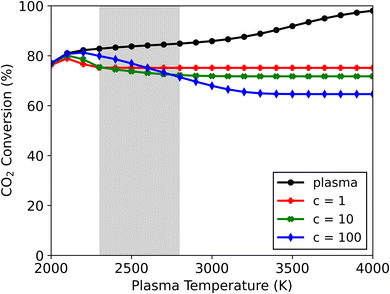
Upon increasing the cooling factor to 10 and 100, radical recombination towards CO2 continues to be observed in the afterglow in all cases for this mixture (see Fig. S6†). The lower end of the plasma temperature range (T < 2100 K) remains largely unaffected by the magnitude of cooling. This is also where the highest CO2 conversions are attained upon cooling implementation (see Fig. 6) – with 79, 80 and 81% conversion for c-factors of 1, 10 and 100, and at 2100, 2100 and 2200 K, respectively. These conversions lie slightly below those found in the plasma, signalling only a small amount of CO + O recombination. This can be attributed to the small amount of radicals present, combined with the relatively low plasma temperatures, which upon quenching in the afterglow will drastically limit recombination reactions. Therefore, at these temperatures the effect of the WGS reaction is small, which in turn preserves the higher CO2 conversions obtained in the plasma (alongside the CO and H2O products).
At plasma temperatures exceeding 2800 K, the opposite effect is observed. A shift in the afterglow reaction mechanisms promotes the formation of CO2 and H2 over that of H2O. As shown in Fig. 6, the CO2 conversion drops with increasing cooling, only reaching 72 and 65% (for c-factors of 10 and 100, respectively) at a plasma temperature of 4000 K, compared to 75% for c = 1. Consequently, this allows for more H2 to be produced – with a selectivity of 66 and 74% for c-factors of 10 and 100, respectively, compared to 62% for c = 1 (see Fig. S6†). This enhanced H2 formation, combined with lower CO2 conversions, improves the syngas ratio, from 0.45 to 0.59. The product selectivities and chemical pathways are consistent with those observed at a c-factor of 1 (Fig. 5). However, the faster decrease in temperature in the afterglow (at c = 10 and c = 100) forces radical recombination to occur predominantly at lower temperatures (see Fig. S7†), which favours the recombination of O with CO to CO2, over the reaction with H to OH, which subsequently forms H2O. In this case, the rapid temperature drop slows the recombination reactions of the H radicals which results in an overlap between the radical recombination and WGS reaction steps. A part of the H radicals remains as free radicals even at lower temperatures (>1000 K, where for the slower cooling all reactions have ceased around 1500 K). The presence of these radicals keeps the system reactive at these lower temperatures which changes the pathways and the final steady state the system reaches. The more H remains as radicals rather than reacting to H2O in the first stage, the higher the amount of H2 (and CO2) in the final product distribution. Because of this, the system evolves towards a different steady state compared to the slower cooling in Fig. 5. For plasma temperatures between 2300 and 2800 K, there is effectively a transition zone (see Fig. 6), where these opposing effects (faster cooling limiting the WGS reaction and the shift in radical combination pathways) compete. In this zone, the overall CO2 conversion is dependent on the combined influences of cooling and plasma temperature.
In conclusion, the mixture with excess CO2 (70/30) clearly exhibits distinct behaviour compared to the other mixtures (50/50 and 30/70), as the CO2 conversion is shown to decrease drastically in the afterglow upon cooling. The drop in conversion is worsened by increasing the cooling rate to quench the hot gas in the afterglow. The lower CO2 conversions coincide with changes in product distribution, with CO and H2O being favoured at the lower end of the plasma temperature range, while CO2 and H2 are dominant at the higher end.
The latter effect is similar to the observations noted by Kwon et al.20 from their quenching rod experiment. They also reported higher selectivity towards H2 (instead of H2O) alongside a lower CO2 conversion. Even though they attributed this result to the suppression of RWGS (i.e., further limiting conversion of CO2 with H2 in the afterglow), our model suggests a different mechanism could be responsible for the observed shift. Their experiments presumably have plasma temperatures above 2800 K, where the CO2 conversion decreases as a result of quenching the post-plasma region (as seen in Fig. 6). Under these conditions, our calculations show significant radical recombination towards CO2 regardless of quenching, however by accelerating the temperature drop (i.e., stronger cooling) different species are favoured, as illustrated in Fig. 5 and S7.† While we trust these modelled results, we are aware that other experimental factors (which cannot be captured by our 0D model) may influence the reaction kinetics.
Targeting this effect to synthesise higher H2 concentrations (over H2O) at higher plasma temperatures is certainly beneficial, as H2O is an unwanted side product. A H2-richer product mixture improves the overall value of the effluent. The ensuing lower CO2 conversion is an unfortunate side effect, but not a major issue as the remaining CO2 requires post-processing in a separation step in either case (as complete conversion cannot be achieved). However, a detailed process optimisation study and an in-depth economic analysis are necessary to determine the more cost-effective targets.
Another important consideration is the role of the afterglow in further converting CO2 and CH4 when a steady state is not achieved in the plasma (due to a shorter residence time, for example). This is a plausible scenario for the lower end of the temperature range, in which case quenching of the hot gas can suppress further dissociations in the afterglow, also lowering the conversion.
The energy input (see Fig. S8†) ranges between 7.5 and 37 kJ L−1 depending on gas mixture (CO2/CH4 ratio) and plasma temperatures, i.e., higher temperature values correspond to higher energy inputs, since more energy is required to reach higher temperatures, leading to greater dissociation into radicals. From this minimum energy input (eqn (10)), we calculated the minimum energy cost for CO2 and CH4 conversion (eqn (11)), based on the total conversion reached at the end of the afterglow for the different cooling strengths (c-factors) (see Fig. S9†). This energy cost is approximately equal to the energy input, which is logical as the conversion of both CO2 and CH4 in the plasma zone is approximately 100% in all cases. The exception is the 70/30 CO2/CH4 ratio (where the CO2 conversion is lower than 100%, as shown in Fig. 6) which has a total conversion between 75 and 87% depending on plasma temperature and cooling strength. In this specific case, the minimum energy cost increases with the cooling strength, however, the overall difference is less than 3.4 kJ L−1.
Our results clearly suggest it is best to maintain a plasma temperature as low as possible (while still being sufficiently high to fully convert the reactants) to obtain the lowest minimum energy costs. Also, an interesting analysis is the comparison of our results to the target energy cost of 4.27 eV per molecule (17.1 kJ L−1), which was proposed by Snoeckx and Bogaerts6 for competitiveness with existing technologies. This would suggest that plasma temperatures above 3000 K should be avoided, as such systems could not meet this energy target, while temperatures below 3000 K could meet this target.
However, it must be noted that these insights should be nuanced when comparing this idealised system to experimental conditions. Firstly, our calculations only consider the minimum energy input, and not the total energy input of the process or reactor setup, which in reality is higher since energy loss channels are present (such as heat loss from the plasma) and the efficiency of the power supply is not 100%. Under experimental conditions, these factors will contribute to a higher energy cost. Secondly, this approach only accounts for the gas that is interacting with the plasma, i.e., it assumes that 100% of the gas flow is treated by the plasma. However, experimentally, the power deposition in the reactor is localised and non-uniform, which results in only a fraction of the gas flow to be treated by the plasma. This also results in a temperature gradient across the plasma, of which parts can operate at more ideal conditions with respect to energy cost. On the other hand, this could also create regions with less ideal conditions, by either operating at a too high temperature (above 3000 K, as discussed above) or too low to achieve considerable conversion at the periphery of the plasma, and both effects would increase the energy cost again. Ultimately, the above experimental intricacies will probably lead to a higher energy input requirement, which according to our results will not be reflected in an enhanced overall conversion; on the contrary, it will probably result in an increased energy cost.
3.2. Post-plasma mixing
While for the above study of quenching via fast cooling, we assumed all gas passes through the plasma discharge, this is unlikely since experimental setups are not completely and homogeneously filled with plasma.34–36 Instead, what is most likely is the existence of a peripheral colder zone surrounding the plasma, where reactant conversion is significantly lower. When these two zones remain separated, the results of the previous section apply specifically to the plasma and its effluent only, albeit the overall conversion will be significantly lower than those predicted by the model. On the other hand, this colder surrounding gas flow can mix with the plasma effluent in the hot afterglow, which will lead to additional thermal conversion, improving the overall output of the reactor. This effect is targeted in some reactors by introducing a nozzle to force these two distinct layers of gas to mix.14,15,17In this section, we apply our model to explore this effect theoretically, by adding unconverted cold gas in the hot afterglow of a DRM plasma. To this end, we consider a perfectly insulated system, which makes gas mixing the only factor influencing the temperature. This represents the ideal and best-case scenario to target maximum additional conversion of the added gas. The plasma effluent is diluted to 10%, which corresponds to adding nine times the amount of initial gas during the afterglow region. As this dilution lowers the temperature to below 1000 K (at the end of the mixing stage), thermal reactions are effectively halted. We investigate three different mixing rates, modulated through the mixing time (τmix) set to 1, 10 or 100 ms. Further explanation regarding the implementation of the mixing is given in the model description (Section 2.3). The plasma zone assumed before the mixing has been described in the previous section, with temperatures ranging from 2000 to 4000 K and three distinct CO2/CH4 ratios.
An overview of the temperatures and cooling rates throughout the afterglow for different gas mixtures, plasma temperatures and characteristic mixing times, is shown in Fig. S10–S12 in the ESI,† demonstrating that the highest cooling rates vary between 105 and 108 K s−1, depending on the specific conditions. This is a similar range to that observed in the previous section.
For the plasma temperature of 2000 K, the overall change in the afterglow is negligible. As the plasma temperature is increased, the extra conversion for both CO2 and CH4 also rises, with a maximum additional conversion, relative to the conversion in the plasma, of 230% for CO2 (at 4000 K and a 30/70 CO2/CH4 ratio) and 275% for CH4 (at 4000 K and a 70/30 ratio). This increasing trend is logical, as the initial higher afterglow temperatures allow the newly added CO2 and CH4 to experience a longer residence time at elevated temperatures, in turn converting a larger fraction of the mixed gas. In all three gas mixtures, the principal radical in the afterglow is H, which also plays a crucial role in the initial dissociation processes within the plasma. Expectedly, the additional conversion is driven upon reaction of these H radicals with CO2 and CH4via reactions (R3) and (R4), respectively. This can also be correlated to the plasma temperature: as the temperature is raised, higher concentrations of H radicals are available in the afterglow, thereby increasing the conversion.
| CO2 + H → CO + OH | (R3) |
| CH4 + H → CH3 + H2 | (R4) |
The most notable effect is seen for the 70/30 CO2/CH4 ratio, which also undergoes the greatest extent of recombination to CO2, decreasing the overall conversion when quenching with fast cooling was considered (see Fig. 6 in Section 3.1.3). This detrimental effect is circumvented with the post-plasma mixing, by shifting the reaction pathways towards dissociation instead of recombination. The increase in CO2 density acts to reduce the net recombination reaction of CO and O, and instead CO2 conversion is further enhanced by reaction with H radicals (reaction (R3)).
Regarding the other mixing rates (i.e., τmix = 1 and 100 ms), the same trends discussed above are observed, however the additional conversion is closely linked to the mixing rate. At the largest mixing rate (τmix = 1 ms), the system achieves the lowest additional conversion, with maximum values of 202 and 252% for CO2 and CH4, respectively, while at the lowest mixing rate (τmix = 100 ms), the conversion rises to 258 and 301% for CO2 and CH4, respectively. These results are again logical and are in line with the explanation given above for the effect of plasma temperature. With stronger mixing, the temperature experiences a faster decrease, thus the reactants have a shorter residence time at sufficiently high temperature to be converted.
These results demonstrate that post-plasma mixing can indeed be beneficial, especially upon coupling of high plasma temperatures with slow mixing. This mixing effect should be nuanced with respect to common experimental conditions, where perfect insulation described in our model is unattainable. As a consequence, heat loss to the reactor walls will increase the overall cooling in the afterglow, thereby diminishing the overall benefit. Nevertheless, the above results provide qualitative insights into how post-plasma mixing can improve the conversion.
For the stoichiometric CO2/CH4 ratio of 50/50, syngas is still the main component of the product stream (see Fig. 8). The lowest selectivity is observed at 2000 K and the slowest mixing (τmix = 100 ms), with 74 and 81% for H2 and CO, respectively. This can be ascribed to incomplete reactant conversion, forming H2O and C2H2 with 16 and 17% selectivity, respectively. These results are similar to those discussed in the previous section, without post-plasma mixing. The selectivity of the latter species is reduced with increasing plasma temperature, as ‘more complete’ conversion can occur in the plasma. This increases the selectivity towards syngas, reaching a maximum at 2300 K – with H2 and CO exhibiting 87 and 93% selectivity, respectively. This corresponds to a C2H2 and H2O selectivity of 6.4 and 7.2%, which again increases for higher plasma temperatures, and this can be explained as follows. Since H2O and C2H2 are intermediate species in the DRM process (occurring at temperatures between 1500 K and 2500 K),25 these species can be formed in the post-plasma region of higher plasma temperatures when mixing is implemented. As the plasma temperature drops in the afterglow (due to mixing), it reaches the above-mentioned optimum range for C2H2 and H2O formation, forming these intermediates. However, as the mixing continues, the temperature decreases further, inhibiting the pathways that convert H2O and C2H2 to H2 and CO. Hence the former species remain as final products.
The effect of the mixing rate on the product distribution is directly related to the plasma temperature (Fig. 8). For plasma temperatures below 2700 K, increasing the mixing rate favours the formation of syngas. The acceleration of the temperature drop simply results in less influence of the already small additional conversion to H2O and C2H2. Above 3000 K, the opposite effect is seen, with the product selectivity shifting towards H2O and C2H2 (in detriment of syngas). This can be ascribed to the exponential mixing rate, rendering a stronger temperature decrease in the early part of the afterglow (closer to the plasma zone) than that experienced in the later part. As such, the relative contribution of H2O and C2H2 at the tail end of the temperature profile becomes larger, increasing their selectivity.
The formation of these products can be further explained by the species selectivity profiles throughout the afterglow in Fig. 9 for the plasma temperature of 4000 K and τmix = 100 ms. In the early afterglow, the remaining H radicals (formed in the plasma zone) are consumed in the direct conversion of the added CO2 and CH4 to CO and H2. As outlined above in reactions (R3) and (R4) (see Section 3.2.1), these H radicals react with both CO2 and CH4 – being the main driving force for the additional conversion. This also causes a shift in the selectivity from H to H2. The secondary product species (C2H2 and H2O) only emerge later in the afterglow, coinciding with a drop in H2 and CO selectivity. The selectivity towards H2O remains below 1% until 15.9 ms in the afterglow, and at this point the original flow is diluted to 43% and the temperature has dropped from 4000 K to 2675 K. As the temperature decreases further, the H2O selectivity increases up to a maximum of 8.7%, while simultaneously C2H2 is also formed (with 7.4% selectivity). This is when steady state is reached, and the temperature has dropped to approximately 1550 K. Continuing dilution from this point onwards only decreases the gas temperature further, as all reactions are halted; and thus the H2O and C2H2 species will be seen in the final products. For the lower plasma temperatures or faster mixing, the same processes occur, but to a smaller extent due to the reduced residence time in the afterglow, which allows for a lesser extent of chemical reactions.
The work of Sun et al.37 discusses mixing between the plasma effluent and a surrounding gas stream, using a reactor network model for a microwave plasma setup for DRM with a 1/1 ratio of CO2/CH4 and compared to their experimental findings. The difference in model description and higher plasma temperature (5000–5900 K) make a direct comparison difficult. However, they reported similar product distributions, mainly syngas production with smaller fractions of H2O and C2H2.
The gas mixtures with different ratios exhibit the same overall effect, with the intermediate species (H2O, C2H2 and C2H4) emerging as final products because the abrupt temperature drop in the afterglow slows down the kinetics, resulting in incomplete conversion pathways.
For the 30/70 CO2/CH4 ratio (see Fig. 10), the products shift more towards C2H2 (at the expense of CO), because of the higher CH4 fraction compared to the 50/50 ratio. H2 is the main product with selectivity between 78 and 85%, while the selectivity of CO is slightly lower (between 54 and 59%), and C2H2 becomes a significant product – with selectivity between 32 and 44%. The remaining products are H2O and C2H4, with selectivity ranging from 0.19 to 4.2% and from 0.70 to 10%, respectively.
Akin to the 50/50 CO2/CH4 ratio, the highest selectivity towards H2 and CO is observed at 2100 K and faster mixing. However, at the 30/70 CO2/CH4 ratio, C2H4 formation does not follow this trend, since it exhibits the highest selectivity at the lowest mixing rate and highest plasma temperature. A transition from C2H2 to C2H4 can be noticed in the afterglow when the temperature drops from 1775 to 1230 K for a plasma temperature of 4000 K and τmix = 100 ms (see Fig. 11). This occurs through reactions with H2(R5) or with H and CH4 with C2H3 as an intermediate ((R6) and (R7)).
| C2H2 + H2(+M) → C2H4(+M) | (R5) |
| C2H2 + H(+M) → C2H3(+M) | (R6) |
| C2H2 + CH4 → C2H3 + CH3 | (R7) |
This transition to C2H4 proceeds at lower temperatures than the other afterglow processes (e.g., the additional CO2 and CH4 conversion and the formation of C2H2 and H2O), and therefore much later in the post-plasma region. This can be ascribed to a combination of longer residence times (due to slower mixing) with high C2H2 concentrations (achieved at high CH4 ratios), driving the reactions towards C2H4. When optimising the process, C2H2 and especially C2H4 are worth considering, as they are also valuable products.
Finally, we consider the 70/30 CO2/CH4 ratio (see Fig. S13†) whose selectivity trends are the least affected by the plasma temperature and mixing speed. The main product is CO, reaching a selectivity between 95 and 100%, while H2 and H2O range from 49 to 53% and from 45 to 48%, respectively. In this mixture, C2H2 is formed as a minor product with selectivity between 0.063 and 4.9%. For the lower plasma temperatures (below 2500 K), increasing the mixing speed (accelerating the temperature drop) favours the formation of syngas. However, the product selectivity shifts towards H2O and C2H2 above 2500 K. Again, this can be ascribed to the exponential mixing rate, which causes a stronger temperature decrease in the early afterglow and limits H2 and CO formation. In the later afterglow, the relative formation of H2O and C2H2 is increased as the tail end of the temperature profile becomes larger, resulting in higher H2O and C2H2 selectivity.
To summarise, the selectivity results for the three CO2/CH4 ratios suggest that post-plasma mixing does not yield drastic changes to the product distribution in DRM plasmas. Across the studied range of plasma temperatures and mixing rates, the selectivity of the products varies by less than 10%. The main products across all mixtures are still syngas (H2 and CO), with also high fractions of H2O or C2H2 being observed for mixtures with excess CO2 or CH4, respectively. Additionally, incomplete conversion of the freshly added gas in the afterglow leads to the formation of small quantities of C2Hy and/or H2O depending on the gas mixture (C2H2 and H2O for the 50/50 ratio, C2H2 for excess CO2, and H2O and C2H4 for excess CH4).
Overall, we would recommend elevated plasma temperatures (4000 K or even higher) combined with slow mixing, to maximize the (additional) CO2 and CH4 conversion and reach a high syngas yield. Indeed, at elevated plasma temperatures, our results suggest the additional conversion of the mixed gas is directly coupled to a partial selectivity shift from syngas towards secondary products (H2O, C2H2 and C2H4), with the slowest mixing (τmix = 100 ms) showing the higher syngas selectivity. Despite this, the overall syngas yield is still significantly improved by the additional conversion, which can be industrially more interesting than a slightly higher syngas selectivity. On the other hand, the absolute maximum selectivity towards syngas is obtained for a plasma temperature of ∼2200 K coupled to a fast mixing rate (τmix = 1 ms) of fresh gas in the afterglow. However, the model suggests the effects of both quenching methods are negligible at these conditions.
Considering the non-uniformity of the plasma, there will likely be deviations from an ideal condition. For instance, inevitable temperature gradients will also alter the overall selectivity, as the conversion process occurs across a range of different temperatures. In addition, it is important to recognize the possible formation of solid carbon (and ensuing operational challenges) for gas mixtures with excess CH4,20,38–41 which can result from C2H2 and C2H4 formation, as these are important precursor species.23,42,43 This phenomenon has not been accounted for in our study. Nonetheless, the aforementioned results offer qualitative insights into the influence of post-plasma mixing on product selectivities.
In this case, only 10% of the total gas flow is treated directly with plasma (instead of the complete gas flow), hence the minimum energy input is ten times lower compared to the previous conditions in Section 3.1.4 (Fig. S8†). The minimum energy input ranges between 0.75 and 3.7 kJ L−1, increasing with targeted plasma temperature and depending on the CO2/CH4 ratio.
The calculated minimum energy cost of conversion for the three different gas mixtures is shown in Fig. 12, with the optimal results achieved for the slowest mixing (τmix = 100 ms). The energy cost slightly decreases with rising plasma temperature for all gas mixtures. The 30/70 CO2/CH4 ratio has the highest overall minimum energy cost. It decreases from 10.9 to 10.4 kJ L−1 when the plasma temperature is raised from 2000 to 4000 K. The stoichiometric (50/50) and 70/30 ratios have slightly lower values which follow the same trend, decreasing from 9.6 to 9.1 kJ L−1 and from 8.8 to 8.4 kJ L−1, respectively. Increasing the mixing rate tempers the additional conversion, increasing the minimum energy cost (see Fig. 12). At 2000 K, the difference in energy cost between τmix = 100 ms and 1 ms is less than 0.5 kJ L−1, for all mixtures, because the impact of mixing is very minor. For higher plasma temperatures the effects of mixing are more significant. Indeed, as the faster mixing limits the additional conversion, the minimum energy cost rises, which increases the energy cost disparity between τmix = 100 ms and 1 ms to 1.4–1.5 kJ L−1 at 2900 K, depending on the gas mixture.
These results contrast those discussed in Section 3.1.4 (in the absence of mixing), where the energy cost always increased with plasma temperature. The higher temperatures reached in those results are unfavourable due to overheating of the gas, not having the option to be reused effectively. However, by applying mixing, additional conversion can be achieved, creating a use for this excess heat. For a plasma temperature of 4000 K, the mixing allows a reduction in energy cost of between 19 and 29 kJ L−1 (depending on the CO2/CH4 ratio) compared to the results discussed in Section 3.1.4, which corresponds to a relative drop in energy cost of 68 to 78%. Note that when a high fraction of gas is treated in the reactor, one can argue that it is equally useful to increase the flow rate through the plasma to decrease the specific energy input, thereby operating at a lower temperature, which can still achieve the same conversion, instead of using post-plasma mixing. However, for reactors in which the treated gas fraction is limited, increasing the mixing with the surrounding unconverted gas does have a benefit on the overall performance (for the same energy input).
The nuances previously discussed should also be applied here. As our results are derived from an idealised setup, the actual energy cost in the experiments will be higher because of various thermal losses and non-uniformity of the plasma. Also, our modelling approach considers a discrete temperature difference between the high temperature plasma zone and the cold surrounding gas, which are eventually mixed in the post-plasma region. In plasma reactors, a temperature gradient will exist on the interface between the two zones. On the one hand, this will increase the overall energy input assuming the same plasma fraction and temperature. However, on the other hand, partial conversion can also occur in this gradient zone as temperatures will approach that of the plasma. Although uncaptured by the model, this effect will also influence the overall effect of mixing in the post-plasma region. This aspect of mixing is subject to further research, possibly using higher dimensional modelling that allows for more detailed studies of heat transport phenomena. Moreover, since a certain degree of post-plasma mixing will already be present in experimental setups, this effect is intrinsically always in place. As a result, further enhancing this mixing will be less beneficial than predicted by our model (since the model assumes no prior mixing). This is supported by Sun et al.,37 who determined in their reactor network model for a DRM microwave setup that the heat loss to the wall is on a longer timescale than the mixing and subsequent reactions. Consequently, mixing plays an integral role in the reforming process within their system. These observations reinforce the importance of accounting for this effect.
Nevertheless, mixing the hot plasma effluent with cold new gas has the potential to greatly improve the system's energy efficiency. This strategy represents an effective implementation of a heat recovery system, reusing the energy applied in the plasma by harnessing the generated heat post-plasma, which would otherwise just be dissipated and lost. Furthermore, this strategy could also be combined with a complete heat recovery system, reusing the energy for preheating the plasma, so that the applied plasma power can effectively (all) be used for the chemical conversion. This can both be thought as an optimisation method, particularly well-suited for setups with localised, high temperature plasmas. Therefore, post-plasma mixing is an important consideration in the design and optimisation of reactors for DRM processes and further development of plasma technology in general.
4. Conclusion
In this work, we studied the post-plasma DRM kinetics for warm plasmas, in a wide range of plasma temperatures, and for different CO2/CH4 ratios and cooling/mixing methods. Firstly, we evaluated enhanced conductive cooling to decrease the afterglow temperature, thereby gaining insights into the effect of heat quenching on the DRM chemistry.A negligible effect of quenching was found for CO2/CH4 mixtures with ratios of 50/50 and 30/70, which maintained the near 100% conversion through the afterglow regardless of the quenching rate. However, for mixtures with excess CO2 (70/30), 100% conversion could only be achieved in the plasma region at temperatures of 4000 K. Our model indicates that the conversion diminishes throughout the afterglow, due to the occurrence of radical recombination reactions towards CO2, H2 and H2O, and a subsequent water gas shift reaction. For plasma temperatures below 2300 K, only the water gas shift reaction is relevant and its effect is reduced with faster quenching rates, resulting in more CO and H2O formation. On the other hand, for higher plasma temperatures (above 2800 K) the effect of water gas shift is minor compared to the radical recombination reactions. Increasing the quenching rate in the afterglow forces these radical recombination pathways to occur at lower temperatures, favouring the formation of CO2 (and H2) over H2O. While this effect is detrimental in terms of CO2 conversion, the syngas ratio (H2/CO) is enhanced and the concentration of unwanted H2O is simultaneously lowered, thus producing a more valuable effluent. This may be beneficial in terms of energy use towards production of these desired species. In general, we can conclude that heat quenching in the afterglow of DRM plasmas only has a significant impact for mixtures with excess CO2. Regarding the minimum energy cost of conversion, our calculations suggest that it is best to keep the plasma temperature as low as possible, around 2000 K, considering the assumption of a homogeneous plasma at a constant temperature. This is explained by the minor difference in total overall conversion, which shows only a slight variation with plasma temperature, whereas the minimum energy required to achieve these higher temperatures increases significantly.
Furthermore, we showed that implementing post-plasma mixing of cold fresh CO2 and CH4 can significantly boost the overall output of syngas (and other side products). This method essentially allows to recover energy from the plasma and use it to convert more reactant gas, improving the overall performance. The additional conversion rises with plasma temperature and slower mixing, reaching a maximum additional conversion, relative to the conversion in the plasma, of 258 and 301% for CO2 and CH4, respectively, within the tested parameter ranges in this study. The model also shows that stronger mixing limits the additional conversion, which is logical since the faster the mixing, the shorter the residence times at sufficiently elevated temperature (which is the main conversion driver). The post-plasma mixing also leads to minor changes in product selectivity. Upon the temperature drop, brought forth by the mixing, the conversion pathways are interrupted. Consequently, this leads to low selectivity towards intermediate species (H2O and C2H4 for the 30/70 ratio, H2O and C2H2 for the 50/50 ratio and C2H2 for the 70/30 ratio).
Our model reveals that significant reductions in energy cost are theoretically possible (up to 78%) by implementing this ‘heat recovery system’ through post-plasma mixing. However, under experimental conditions, heat transfer from the gas to the reactor wall can reduce the overall benefit by limiting the additional conversion compared to our idealised conditions. Nonetheless, our study demonstrates that post-plasma mixing can create opportunities to optimise DRM in warm plasmas.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant Agreement No. 810182 – SCOPE ERC Synergy project), the VLAIO-Catalisti-ICON project BluePlasma (Project No. HBC.2022.0445) and through long-term structural funding (Methusalem). The computational resources and services used in this work were provided by the HPC core facility CalcUA of the Universiteit Antwerpen, and VSC (Flemish Supercomputer Center), funded by the Research Foundation – Flanders (FWO) and the Flemish Government. We also thank Matthias Albrechts, Björn Loenders, Stein Maerivoet, Elizabeth Mercer, and Ivan Tsonev for their expertise and feedback.References
- R. M. Cuéllar-Franca and A. Azapagic, Carbon capture, storage and utilisation technologies: A critical analysis and comparison of their life cycle environmental impacts, J. CO2 Util., 2015, 9, 82–102 CrossRef.
- G. Centi, E. A. Quadrelli and S. Perathoner, Catalysis for CO2 conversion: a key technology for rapid introduction of renewable energy in the value chain of chemical industries, Energy Environ. Sci., 2013, 6, 1711–1731 RSC.
- D. Pakhare and J. Spivey, A review of dry (CO2) reforming of methane over noble metal catalysts, Chem. Soc. Rev., 2014, 43, 7813–7837 RSC.
- D. Leckel, Diesel Production from Fischer−Tropsch: The Past, the Present, and New Concepts, Energy Fuels, 2009, 23, 2342–2358 CrossRef CAS.
- A. Bogaerts and E. C. Neyts, Plasma Technology: An Emerging Technology for Energy Storage, ACS Energy Lett., 2018, 3, 1013–1027 CrossRef CAS.
- R. Snoeckx and A. Bogaerts, Plasma technology – a novel solution for CO2 conversion?, Chem. Soc. Rev., 2017, 46, 5805–5863 RSC.
- Y. Vadikkeettil, Y. Subramaniam, R. Murugan, P. V. Ananthapadmanabhan, J. Mostaghimi, L. Pershin, C. Batiot-Dupeyrat and Y. Kobayashi, Plasma assisted decomposition and reforming of greenhouse gases: A review of current status and emerging trends, Renewable Sustainable Energy Rev., 2022, 161, 112343 CrossRef CAS.
- A. Bogaerts and G. Centi, Plasma Technology for CO2 Conversion: A Personal Perspective on Prospects and Gaps, Front. Energy Res., 2020, 8, 1–23 CrossRef.
- A. Fridman, Plasma Chemistry, Cambridge University Press, 2008 Search PubMed.
- A. J. Wolf, F. J. J. Peeters, P. W. C. Groen, W. A. Bongers and M. C. M. van de Sanden, CO2 Conversion in Nonuniform Discharges: Disentangling Dissociation and Recombination Mechanisms, J. Phys. Chem. C, 2020, 124, 16806–16819 CrossRef CAS.
- V. Vermeiren and A. Bogaerts, Plasma-Based CO 2 Conversion: To Quench or Not to Quench?, J. Phys. Chem. C, 2020, 124, 18401–18415 CrossRef CAS.
- H. Kim, S. Song, C. P. Tom and F. Xie, Carbon dioxide conversion in an atmospheric pressure microwave plasma reactor: Improving efficiencies by enhancing afterglow quenching, J. CO2 Util., 2020, 37, 240–247 CrossRef CAS.
- E. R. Mercer, S. Van Alphen, C. F. A. M. van Deursen, T. W. H. Righart, W. A. Bongers, R. Snyders, A. Bogaerts, M. C. M. van de Sanden and F. J. J. Peeters, Post-plasma quenching to improve conversion and energy efficiency in a CO2 microwave plasma, Fuel, 2023, 334, 126734 CrossRef CAS.
- J. Li, X. Zhang, J. Shen, T. Ran, P. Chen and Y. Yin, Dissociation of CO2 by thermal plasma with contracting nozzle quenching, J. CO2 Util., 2017, 21, 72–76 CrossRef CAS.
- A. Hecimovic, F. A. D'Isa, E. Carbone and U. Fantz, Enhancement of CO2 conversion in microwave plasmas using a nozzle in the effluent, J. CO2 Util., 2022, 57, 101870 CrossRef CAS.
- A. W. van de Steeg, T. Butterworth, D. C. M. van den Bekerom, A. F. Silva, M. C. M. van de Sanden and G. J. van Rooij, Plasma activation of N 2 , CH 4 and CO 2 : an assessment of the vibrational non-equilibrium time window, Plasma Sources Sci. Technol., 2020, 29, 115001 CrossRef CAS.
- T. Yang, J. Shen, T. Ran, J. Li, P. Chen and Y. Yin, Understanding CO 2 decomposition by thermal plasma with supersonic expansion quench, Plasma Sci. Technol., 2018, 20, 065502 CrossRef.
- S. Van Alphen, A. Hecimovic, C. K. Kiefer, U. Fantz, R. Snyders and A. Bogaerts, Modelling post-plasma quenching nozzles for improving the performance of CO2 microwave plasmas, Chem. Eng. J., 2023, 462, 142217 CrossRef CAS.
- K. Wang, S. Ceulemans, H. Zhang, I. Tsonev, Y. Zhang, Y. Long, M. Fang, X. Li, J. Yan and A. Bogaerts, Inhibiting recombination to improve the performance of plasma-based CO2 conversion, Chem. Eng. J., 2024, 481, 148684 CrossRef CAS.
- H. Kwon, T. Kim and S. Song, Dry reforming of methane in a rotating gliding arc plasma: Improving efficiency and syngas cost by quenching product gas, J. CO2 Util., 2023, 70, 102448 CrossRef CAS.
- C. Hyun Cho, J. H. Kim, J. K. Yang, I. S. Park, Y.-S. Choi and I. J. Kang, Dry reforming process using microwave plasma generator with high carbon dioxide conversion efficiency for syngas production, Fuel, 2024, 361, 130707 CrossRef CAS.
- S. Pancheshnyi, B. Eismann, G. J. M. Hagelaar and L. C. Pitchford, Computer Code ZDPlasKin, University of Toulouse, LAPLACE, CNRS-UPSINP, Toulouse, France, 2008, http://www.zdplaskin.laplace.univ-tlse.fr Search PubMed.
- S. Van Alphen, F. Jardali, J. Creel, G. Trenchev, R. Snyders and A. Bogaerts, Sustainable gas conversion by gliding arc plasmas: a new modelling approach for reactor design improvement, Sustainable Energy Fuels, 2021, 5, 1786–1800 RSC.
- J. K. Dahl, A. W. Weimer, A. Lewandowski, C. Bingham, F. Bruetsch and A. Steinfeld, Dry Reforming of Methane Using a Solar-Thermal Aerosol Flow Reactor, Ind. Eng. Chem. Res., 2004, 43, 5489–5495 CrossRef CAS.
- J. Slaets, B. Loenders and A. Bogaerts, Plasma-based dry reforming of CH4: Plasma effects vs. thermal conversion, Fuel, 2024, 360, 130650 CrossRef CAS.
- P. N. Brown, G. D. Byrne and A. C. Hindmarsh, VODE: A Variable-Coefficient ODE Solver, SIAM J. Sci. Stat. Comput., 1989, 10, 1038–1051 CrossRef.
- M. A. Lieberman and A. J. Lichtenberg, Principles of Plasma Discharges and Materials Processing, Wiley, 2005 Search PubMed.
- M. Albrechts, I. Tsonev and A. Bogaerts, Can post-plasma CH 4 injection improve plasma-based dry reforming of methane? A modeling study, Green Chem., 2024, 26, 9712–9728 RSC.
- V. Guerra, E. Tatarova, F. M. Dias and C. M. Ferreira, On the self-consistent modeling of a traveling wave sustained nitrogen discharge, J. Appl. Phys., 2002, 91, 2648–2661 CrossRef CAS.
- B. J. McBride, M. J. Zehe and S. Gordon, NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species, National Aeronautics and Space Administration, 2002 Search PubMed.
- A. Burcat and B. Ruscic, Third millennium ideal gas and condensed phase thermochemical database for combustion (with update from active thermochemical tables), Argonne, IL, 2005 Search PubMed.
- B. Wanten, R. Vertongen, R. De Meyer and A. Bogaerts, Plasma-based CO2 conversion: How to correctly analyze the performance?, J. Energy Chem., 2023, 86, 180–196 CrossRef CAS.
- P. L. Spath and D. C. Dayton, Preliminary Screening – Technical and Economic Assessment of Synthesis Gas to Fuels and Chemicals with Emphasis on the Potential for Biomass-Derived Syngas, Golden, CO (United States), 2003 Search PubMed.
- M. Ramakers, G. Trenchev, S. Heijkers, W. Wang and A. Bogaerts, Gliding Arc Plasmatron: Providing an Alternative Method for Carbon Dioxide Conversion, ChemSusChem, 2017, 10, 2642–2652 CrossRef CAS PubMed.
- R. Vertongen and A. Bogaerts, How important is reactor design for CO2 conversion in warm plasmas?, J. CO2 Util., 2023, 72, 102510 CrossRef CAS.
- I. Tsonev, H. Ahmadi Eshtehardi, M.-P. Delplancke and A. Bogaerts, Importance of geometric effects in scaling up energy-efficient plasma-based nitrogen fixation, Sustainable Energy Fuels, 2024, 8, 2191–2209 RSC.
- H. Sun, J. Lee and M. S. Bak, Experiments and modeling of atmospheric pressure microwave plasma reforming of a methane-carbon dioxide mixture, J. CO2 Util., 2021, 46, 101464 CrossRef CAS.
- S. Kelly, E. Mercer, R. De Meyer, R.-G. Ciocarlan, S. Bals and A. Bogaerts, Microwave plasma-based dry reforming of methane: Reaction performance and carbon formation, J. CO2 Util., 2023, 75, 102564 CrossRef CAS.
- R. B. Raja, R. Sarathi and R. Vinu, Selective Production of Hydrogen and Solid Carbon via Methane Pyrolysis Using a Swirl-Induced Point–Plane Non-thermal Plasma Reactor, Energy Fuels, 2022, 36, 826–836 CrossRef CAS.
- N. Lu, D. Sun, Y. Xia, K. Shang, B. Wang, N. Jiang, J. Li and Y. Wu, Dry reforming of CH4–CO2 in AC rotating gliding arc discharge: Effect of electrode structure and gas parameters, Int. J. Hydrogen Energy, 2018, 43, 13098–13109 CrossRef CAS.
- R. B. Raja, A. C. Halageri, R. Sankar, R. Sarathi and R. Vinu, Dry Reforming of Methane Using a Swirl-Induced Plasma Discharge Reactor, Energies, 2023, 16, 1823 CrossRef CAS.
- K. De Bleecker, A. Bogaerts and W. Goedheer, Aromatic ring generation as a dust precursor in acetylene discharges, Appl. Phys. Lett., 2006, 88, 151501 CrossRef.
- K. De Bleecker, A. Bogaerts and W. Goedheer, Detailed modeling of hydrocarbon nanoparticle nucleation in acetylene discharges, Phys. Rev. E, 2006, 73, 026405 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4su00676c |
| This journal is © The Royal Society of Chemistry 2025 |