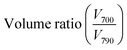Frustrated crystallization kinetics in marginally mismatched binary self-assembly driven by depletion interactions†
Sk
Tahmid Shahriar
 a,
Chris
Feltman
b,
Sean
Machler
c and
Nabila
Tanjeem
a,
Chris
Feltman
b,
Sean
Machler
c and
Nabila
Tanjeem
 *c
*c
aDepartment of Mechanical Engineering, California State University, Fullerton, Fullerton, California 92831, USA
bDepartment of Mathematics, California State University, Fullerton, Fullerton, California 92831, USA
cDepartment of Physics, California State University, Fullerton, Fullerton, California 92831, USA. E-mail: ntanjeem@fullerton.edu
First published on 16th May 2025
Abstract
We investigate two-dimensional crystal assemblies formed by a binary mixture of colloidal particles with a size ratio of 0.88 and driven by short-ranged depletion interactions. Our experiments show that the orientational order of the assembly decreases with an increasing fraction of impurity particles, reaching up to 18% reduction in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture compared to a monodisperse suspension. We observe slower growth rate and arrested dynamics in the binary mixture, whereas the monodisperse sample follows a two-step nucleation and growth mechanism. We performed molecular dynamics simulations to calculate the minimum energy states for different size ratios and number ratios of the binary mixture. The simulation results predict a compromised translational order but sustained orientational order in a binary mixture with a size ratio as high as 0.88. From the combined experimental and numerical results, we conclude that the disordered assemblies found in a binary mixture originate from the frustration in assembly kinetics rather than topological frustration when there is a marginal mismatch between the two particle sizes.
1 binary mixture compared to a monodisperse suspension. We observe slower growth rate and arrested dynamics in the binary mixture, whereas the monodisperse sample follows a two-step nucleation and growth mechanism. We performed molecular dynamics simulations to calculate the minimum energy states for different size ratios and number ratios of the binary mixture. The simulation results predict a compromised translational order but sustained orientational order in a binary mixture with a size ratio as high as 0.88. From the combined experimental and numerical results, we conclude that the disordered assemblies found in a binary mixture originate from the frustration in assembly kinetics rather than topological frustration when there is a marginal mismatch between the two particle sizes.
1. Introduction
Studies on colloidal self-assembly are instrumental in developing fundamental insights into material phases and designing applications by leveraging the mechanical and optical properties of the assembled phases.1–5 The simplest components of colloidal self-assembly are monodisperse particles whose size, shape, interparticle interactions, and concentration determine the properties of the assembled phases. To realize greater complexity in the phase behavior and assembly kinetics, suspensions made of two different particle sizes, i.e., binary mixtures, have been employed in numerous experimental and computational studies.6–13 Binary assemblies are the simplest model of polydisperse colloids that are the closest approximation to colloidal suspensions found in nature and relevant for many industrial applications. Insights gained from binary assembly experiments can be applied to understand the formation of metal alloys at the atomic scale14,15 and to design materials with the desired crystalline structure.16–20 Therefore, interest in understanding binary colloidal self-assembly for a wide range of experimental parameters, including particle size ratios, materials, compositions, spatial confinement, and interparticle interaction potentials, is rising rapidly.An important determinant of colloidal self-assembly is the nature of the interparticle interaction potential. While hard sphere assembly has been a common choice for studying phase behavior, assembly mechanisms that involve engineering the attractive potential between particles by tuning electrostatic, DNA-hybridization, and depletion interactions have become increasingly popular.21–23 Specifically, self-assembly driven by depletion forces allows for tuning the strength and the range of the attractive interaction potential simply by varying the assembly components, hence it has been employed for programming the structures of colloidal clusters.24–28 Another important aspect of depletion interaction is that its strength depends on the geometry of the particles and the nearby surfaces; this property allows the formation of two-dimensional colloidal crystals on a surface whose curvature is smaller than the particle curvature.29,30 Therefore, depletion-induced self-assembly has been an attractive choice for investigating 2D colloidal crystallization mechanisms on flat and curved surfaces.31,32 Such systems have a diverse set of applications involving photonic crystals,27,33 semiconducting particle assembly,34 chiral nanomaterials,31,35 photonic balls,36,37 and colloidal epitaxy.10,38 Despite significant interest, it is yet unknown how depletion-driven 2D colloidal crystallization is affected by particle polydispersity, the simplest case of which is a binary system comprised of two different particle sizes.
Here, we investigate two-dimensional binary colloidal self-assembly driven by a short-ranged depletion interaction potential, where the ratio of the small particle diameter to the large particle diameter is  , and the range of the attractive interaction potential is only 4% of the particle diameter. Prior work on binary colloidal self-assembly in the presence of depletion interactions investigated the phase behavior in bulk,39–41 observed eutectic crystallization,42,43 and the formation of colloidal gels.44,45 Toyotama et al. found phase-separated eutectic crystals for a size ratio of particles (0.83) that was closer to our system but driven by a long-ranged interaction potential (80% of particle diameter). Pandey et al. investigated self-assembly with short-ranged depletion interaction (4% of particle diameter) in a binary mixture of particles with a size ratio of 0.49 and observed the formation of 3D colloidal gels and arrested particle dynamics. To our knowledge, no experiments have explained the formation of 2D binary crystals driven by short-ranged depletion interactions, especially in the presence of a small asymmetry in the particle sizes. Therefore, we performed a combination of experimental and computational investigation to elucidate how the size ratio and the relative concentrations of the two particle species determine the structural order and the assembly kinetics.
, and the range of the attractive interaction potential is only 4% of the particle diameter. Prior work on binary colloidal self-assembly in the presence of depletion interactions investigated the phase behavior in bulk,39–41 observed eutectic crystallization,42,43 and the formation of colloidal gels.44,45 Toyotama et al. found phase-separated eutectic crystals for a size ratio of particles (0.83) that was closer to our system but driven by a long-ranged interaction potential (80% of particle diameter). Pandey et al. investigated self-assembly with short-ranged depletion interaction (4% of particle diameter) in a binary mixture of particles with a size ratio of 0.49 and observed the formation of 3D colloidal gels and arrested particle dynamics. To our knowledge, no experiments have explained the formation of 2D binary crystals driven by short-ranged depletion interactions, especially in the presence of a small asymmetry in the particle sizes. Therefore, we performed a combination of experimental and computational investigation to elucidate how the size ratio and the relative concentrations of the two particle species determine the structural order and the assembly kinetics.
We found that the orientational hexatic order parameter of the self-assembled binary monolayer reduces by 18% in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture compared to a monodisperse suspension. Additionally, the binary mixture exhibits much slower growth kinetics that is accompanied by cooperative particle motion. To explain the experimental findings, we developed a molecular dynamics simulation model to identify the minimum energy states of a 2D binary assembly driven by a short-range attractive interaction potential. The model shows that for a mixture with a greater particle size difference, i.e.,
1 binary mixture compared to a monodisperse suspension. Additionally, the binary mixture exhibits much slower growth kinetics that is accompanied by cooperative particle motion. To explain the experimental findings, we developed a molecular dynamics simulation model to identify the minimum energy states of a 2D binary assembly driven by a short-range attractive interaction potential. The model shows that for a mixture with a greater particle size difference, i.e.,  , the hexatic order parameter decreases with an increasing fraction of impurity particles and reaches the minimum value for the 1
, the hexatic order parameter decreases with an increasing fraction of impurity particles and reaches the minimum value for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture. However, for a binary mixture where the particle sizes are much closer, i.e.,
1 mixture. However, for a binary mixture where the particle sizes are much closer, i.e., 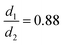 , the orientational hexatic order parameter in the 1
, the orientational hexatic order parameter in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture ratio sample remains the same as the sample with minimal impurity. However, in this case, a reduction in the translational order, as characterized by the average bond length, is observed. The disagreement between the computational and experimental results can be attributed to the assembly kinetics that distinguish the 1
1 mixture ratio sample remains the same as the sample with minimal impurity. However, in this case, a reduction in the translational order, as characterized by the average bond length, is observed. The disagreement between the computational and experimental results can be attributed to the assembly kinetics that distinguish the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture from a monodisperse sample. Although both samples grow in amorphous states during the first part of the assembly process, the monodisperse sample starts forming stable crystallites following two-step nucleation,30 whereas the binary sample continues to grow in the amorphous state until the assembly attains high surface coverage and the particles become dynamically arrested. Our results provide a new insight into binary assemblies in cases where the mismatch in the particle sizes is marginal—the frustration in assembly kinetics, rather than the topological frustration, is the key factor that determines the structural order of the assembly.
1 mixture from a monodisperse sample. Although both samples grow in amorphous states during the first part of the assembly process, the monodisperse sample starts forming stable crystallites following two-step nucleation,30 whereas the binary sample continues to grow in the amorphous state until the assembly attains high surface coverage and the particles become dynamically arrested. Our results provide a new insight into binary assemblies in cases where the mismatch in the particle sizes is marginal—the frustration in assembly kinetics, rather than the topological frustration, is the key factor that determines the structural order of the assembly.
2. Methods
2.1 Preparation of colloidal particle mixtures
Fluorescent polymer microspheres with two different diameters, d1 = 700 nm (Fluoro-Max G700, green beads purchased from Fisher Scientific Inc.) and d2 = 790 nm (Fluoro-Max R800, red beads purchased from Fisher Scientific Inc.) were used to prepare the binary mixture samples. Each of the particle suspensions was washed two times before usage. During each wash cycle, a total of 1 mL particle suspension (1% solids) was centrifuged (using Eppendorf 5430) for 5 minutes at 6500 rpm, the supernatant was removed, and the particles were re-suspended in 1 mL of Milli-Q water. The particles were redispersed in the suspension through vortex-mixing for 15–20 s. Once the microsphere suspensions were prepared, they were mixed with an aqueous 36.5 mM of sodium dodecyl sulfate (SDS, purchased from Sigma Aldrich) solution for the depletion-induced self-assembly experiments. A stock solution of 100 mM SDS was first prepared by dissolving 288.38 mg of SDS in 10 mL of Milli-Q water. Then the SDS solution was diluted to 73 mM by mixing 36.9 μL Milli-Q water with 100 μL of the stock SDS solution. Binary mixtures with different volume ratios were prepared as described below:Monodisperse sample: the green beads (Fluoro-Max G700) with a diameter of d1 = 700 nm were used to study the self-assembly of a monodisperse suspension. Five μL of the 1% particle suspension was mixed with an equal volume of 73 mM of SDS. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture: 10 μL of 73 mM SDS solution was mixed with 5 μL of 700 nm green beads and 5 μL of 790 nm red beads. 9
1 binary mixture: 10 μL of 73 mM SDS solution was mixed with 5 μL of 700 nm green beads and 5 μL of 790 nm red beads. 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture: 9 μL of 700 nm green beads and 1 μL of 790 nm red beads were mixed with 10 μL of 73 mM SDS solution. 19
1 binary mixture: 9 μL of 700 nm green beads and 1 μL of 790 nm red beads were mixed with 10 μL of 73 mM SDS solution. 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture: 19 μL of 700 nm green beads and 1 μL of 790 nm red beads were mixed with 20 μL of 73 mM SDS solution. 39
1 binary mixture: 19 μL of 700 nm green beads and 1 μL of 790 nm red beads were mixed with 20 μL of 73 mM SDS solution. 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture: 39 μL of 700 nm green beads and 1 μL of 790 nm red beads were mixed with 40 μL of 73 mM SDS solution.
1 binary mixture: 39 μL of 700 nm green beads and 1 μL of 790 nm red beads were mixed with 40 μL of 73 mM SDS solution.
The number ratios of the two particles in a binary mixture can be calculated based on the volume ratios of the two mixtures  , particle sizes (Dp), the density of the particles (ρb) and the fluid (ρf) using the following equation:
, particle sizes (Dp), the density of the particles (ρb) and the fluid (ρf) using the following equation:
 | (1) |
2.2 Sample chamber preparation and imaging
After the colloidal particles were mixed with SDS, the solution was transferred to a sample chamber for observation under a microscope. A 2-D sample cell was prepared by making a sandwich of a 24 × 50 mm cover glass (purchased from VWR, no. 1) and a 22 × 22 mm cover glass (purchased from VWR, no. 1). First, both cover glasses were pretreated in a UVO Cleaner (Jelight Model 30) for 5 minutes. A thin plastic film spacer and a 22 × 22 mm micro cover glass were placed on top of the 24 × 50 mm cover glass, and the corners of the chamber were sealed by applying the optical adhesive NOA 61 (Norland). The sample cell was then re-treated in the UVO Cleaner again for a minute. The particle suspension (about 10 μL) was injected into the thin gap between the two cover glasses. Finally, the sample cell was completely sealed by applying a 5-minute epoxy (Devcon).The sample cells were imaged using an optical microscope immediately after sealing them. The imaging was performed using an inverted Olympus ix83 microscope equipped with a 100× (N.A. = 1.45) objective lens. Images were captured using the open-source software Fiji and its plug-in Micro-Manager 2.0. The green particles were captured using a 470 nm/525 nm (excitation/emission) filter set, and the red particles were captured using a 560 nm/630 nm filter set.
The expected number ratios of the two particles in the mixture  calculated using eqn (1), and the observed number ratios measured from the self-assembled monolayers are summarized in Table 1.
calculated using eqn (1), and the observed number ratios measured from the self-assembled monolayers are summarized in Table 1.
2.3 Image processing and analysis
 , where θjk is the angle between the vector rjk that connects particle k to particle j, and the x-axis. An existing Python library (PairCorrelation) was used to calculate the radial distribution function g(r) from colloidal crystal images.
, where θjk is the angle between the vector rjk that connects particle k to particle j, and the x-axis. An existing Python library (PairCorrelation) was used to calculate the radial distribution function g(r) from colloidal crystal images.
| χ4(t) = N [〈Q(t)2〉t − 〈Q(t)〉t2] |
A particle was defined as mobile if its displacement at a time interval Δt is greater than a threshold displacement 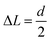 , where d is the average particle diameter. The temporal fluctuations of Q(t) was calculated from 100 images captured at every 30 s of time intervals.
, where d is the average particle diameter. The temporal fluctuations of Q(t) was calculated from 100 images captured at every 30 s of time intervals.
2.4 Molecular dynamics simulation
 | (2) |
Interaction between type 2 (large) particles:
 | (3) |
Interaction between type 1 (small) and type 2 (large) particles:
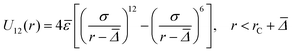 | (4) |
The finite diameters of the smaller and the larger particles were represented by Δ1 + σ and Δ2 + σ, respectively. Five different size ratios m = 0.80, 0.82, 0.84, 0.86, 0.88 were applied to simulate different degrees of asymmetry in particle sizes. The values of Δ2 and ![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) were calculated for each m and for a fixed value of Δ1 (all parameters listed in Table 2). The value of σ was calculated from the experimental estimate of the range of depletion interaction – 4% of the diameter of the smaller particles, i.e.,
were calculated for each m and for a fixed value of Δ1 (all parameters listed in Table 2). The value of σ was calculated from the experimental estimate of the range of depletion interaction – 4% of the diameter of the smaller particles, i.e., 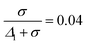 . Since the ratio of the interaction strengths,
. Since the ratio of the interaction strengths,  is true for depletion forces, ε2 and
is true for depletion forces, ε2 and ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) were calculated from the values of ε1 and m. The cutoff distance rc was chosen to be approximately 1.5 [(Δ1 + σ) + (Δ2 + σ)] to reduce the computation time.
were calculated from the values of ε1 and m. The cutoff distance rc was chosen to be approximately 1.5 [(Δ1 + σ) + (Δ2 + σ)] to reduce the computation time.
 cases. The following equations were solved to calculate N1 and N2.
cases. The following equations were solved to calculate N1 and N2. | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 is the total area covered by all particles in the simulation box, and
000 is the total area covered by all particles in the simulation box, and | (6) |
N
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 (small N2 (small![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) large) large) |
N 1 | N 2 | |
|---|---|---|---|
| m = 0.80 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 713 |
273 |
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 420 |
2381 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
9808 | 9827 | |
| m = 0.82 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 727 |
272 |
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572 572 |
2353 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 102 102 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 077 077 |
|
| m = 0.84 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 727 |
272 |
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 757 757 |
2449 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836 836 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
|
| m = 0.86 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 732 732 |
273 |
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 769 769 |
2435 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 607 607 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 639 |
|
| m = 0.88 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 727 |
283 |
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947 947 |
2459 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976 976 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984 984 |
|
 to
to  over a period of 5 × 105 iterations, with the time step of each iteration, τ = 0.001 s. We confirmed that closely packed crystalline structures were found at the end of the simulation period for every set of parameters (Table 3). We found that the energy reaches the minimum for all simulations that were performed for longer than 105 iterations (for both τ = 0.01 and τ = 0.001). The minimum energy value was also consistent with the one found using conjugate gradient energy minimization on LAMMPS (Fig. S1, ESI†).
over a period of 5 × 105 iterations, with the time step of each iteration, τ = 0.001 s. We confirmed that closely packed crystalline structures were found at the end of the simulation period for every set of parameters (Table 3). We found that the energy reaches the minimum for all simulations that were performed for longer than 105 iterations (for both τ = 0.01 and τ = 0.001). The minimum energy value was also consistent with the one found using conjugate gradient energy minimization on LAMMPS (Fig. S1, ESI†).
3. Results and discussions
First, we investigated the depletion-induced phase behavior of a monodisperse colloidal particle suspension (diameter d1 = 700 nm, 0.5% w/w) mixed with different concentrations of the depletant, sodium dodecyl sulfate (SDS). The SDS surfactants form micelles at above the critical micelle concentration (8.2 mM) and induce attractive depletion interactions between the polystyrene spheres and the flat glass surface, as well as between the polystyrene spheres themselves.31,48 The Asakura–Osawa depletion interaction potential between two objects can be expressed as:49UAO(r) = −ρkBTVov(r), where ρ is the number density of the depletant micelles and Vov is the overlap of the excluded volumes. Because the overlap volume between a flat surface and a sphere is greater compared to the overlap volume between two spheres, the particles first weakly adsorb to the flat glass wall at the bottom of the sample chamber and then form closely packed structures.30–32,48,50–52We find no evidence of self-assembly at SDS concentrations below 30 mM (Fig. S2, ESI†). The particles remain in a fluid phase with SDS concentration of 30 mM and in a fluid-crystal co-existent phase at 32 mM (Fig. 1a). We observe the formation of polycrystalline monolayers that cover the entire glass surface with higher SDS concentration of 34 mM (estimated particle–particle bond energy Eb ≈ −Umin ≈ 5.6kBT, ESI,† Section S2) and 36.5 mM (Eb ≈ 6.1kBT). The particle–particle interaction is even stronger at 38 mM and 42 mM of SDS, resulting in gel formation. From the phase behavior, we conclude that equilibrium assembly can take place through multiple particle binding and unbinding events only when the SDS concentration is in the range of 34–36.5 mM. We estimated the range of the attractive interaction to be about 4.84% of particle diameter by analysing a snapshot of the assembled colloidal crystals (Fig. S3, ESI†). The average center-to-center distance between nearest neighbors was found to be about 734 nm, only 34 nm larger than the particle diameter (700 nm).
Next, we studied 2D binary assemblies by mixing 34 mM of SDS with polystyrene microspheres of two different diameters, d1 = 700 nm and d2 = 790 nm, (Fig. 1b and c). The polydispersity index of the polystyrene particles was less than 3%, as reported by the supplier. Both particles, small and large, remain stable in the suspension at the applied concentration (0.5% w/w, volume fraction ϕ = 0.005) on their own as well as when mixed with each other (Fig. S4 and S5, ESI†). The structure and dynamics of the self-assembled monolayers were observed in real-time using an optical microscope (Olympus ix83) equipped with fluorescence imaging capabilities and a 100× oil immersion objective lens (NA = 1.45). Particles with diameter d1 = 700 nm and d2 = 790 nm were identified from their fluorophore labels – green and red colors, respectively. The self-assembled monolayers formed after leaving the mixture solution in a sealed sample chamber for several hours (Fig. 1d). Since the height of our sample cell (about 360 μm) was much larger than the particle diameter, we do not expect to observe any effect of the hydrodynamic interactions resulting from the spatial confinement. The observed number ratio of the two particles  in the self-assembled monolayer was found to be very close to the expected number ratio calculated from the volume ratio of the two suspensions (Table 1). The small difference could be due to the marginally stronger interaction potential between the larger particles and their lower diffusivity and higher sedimentation rate.
in the self-assembled monolayer was found to be very close to the expected number ratio calculated from the volume ratio of the two suspensions (Table 1). The small difference could be due to the marginally stronger interaction potential between the larger particles and their lower diffusivity and higher sedimentation rate.
We investigated how the mixing ratio of the two types of particles impact the crystalline order of the formed layers. The difference in crystalline order is evident from the corresponding Voronoi diagrams and the radial distribution function g(r), as shown in Fig. 2. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture (700 nm
1 mixture (700 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 nm) sample exhibit more 5- and 7-fold defects (Fig. 2a) and reduced heights in higher-order peaks compared to the 39
790 nm) sample exhibit more 5- and 7-fold defects (Fig. 2a) and reduced heights in higher-order peaks compared to the 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (700 nm
1 (700 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 nm) mixture sample (Fig. 2b). The hexatic order parameter can be used to quantify the degree of six-fold rotational symmetry around every particle,
790 nm) mixture sample (Fig. 2b). The hexatic order parameter can be used to quantify the degree of six-fold rotational symmetry around every particle,  . The average
. The average  was calculated from micrographs of particles at five different positions in a sample, each consisting of about 7500 particles, after 22 h of observation. While the polycrystalline structures in the 39
was calculated from micrographs of particles at five different positions in a sample, each consisting of about 7500 particles, after 22 h of observation. While the polycrystalline structures in the 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture had a higher average hexatic order of
1 mixture had a higher average hexatic order of  , the 1
, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture showed a much lower value of
1 mixture showed a much lower value of  (distributions of |ψ6| shown in in Fig. S6, ESI†). The lack of crystalline order was consistently observed in samples with different particle concentrations –
(distributions of |ψ6| shown in in Fig. S6, ESI†). The lack of crystalline order was consistently observed in samples with different particle concentrations –  in a 0.13% (w/w) particle suspension and
in a 0.13% (w/w) particle suspension and  in a 0.25% (w/w) suspension (Fig. S7, ESI†). This result clearly indicates that the self-assembled structures transition from crystalline to amorphous for a higher fraction of impurities and thereby offers a mechanism for precise tuning of the crystalline order in 2D colloidal assemblies.
in a 0.25% (w/w) suspension (Fig. S7, ESI†). This result clearly indicates that the self-assembled structures transition from crystalline to amorphous for a higher fraction of impurities and thereby offers a mechanism for precise tuning of the crystalline order in 2D colloidal assemblies.
Although it may not be surprising that the addition of impurities frustrates crystalline order in binary assemblies, there are two possible mechanisms behind this frustration. The first one is a topological frustration induced by the size mismatch that would reduce the crystallinity of the equilibrium states. And the second one is a kinetic frustration induced by the specific crystal growth mechanism that restricts the assembly from reaching its equilibrium state.
To investigate the possibility of topological frustration, we developed a molecular dynamics simulation model that allows us to identify the equilibrium assembly structures for a wider range of parameters. The simulation was performed using the open-source molecular dynamics simulation package LAMMPS.53 The different sizes of the particles were implemented by using shifted Lennard-Jones (LJ) potentials (eqn (2)–(4)), where Δ1 + σ represents the diameter of the smaller particles (green) and and Δ2 + σ represents the diameter of the larger particles (red).54 The range of the attractive interaction potential was fixed at 4% of the smaller particle diameter to mimic the experimental range of attractive potential (about 34 nm).48,55 The shapes of the applied LJ potential between different particle pairs are shown in Fig. 3a.
We identified the minimum energy states of the 2D assembly for different size ratios,  by performing simulated annealing. We observe a reduction in the average hexatic order,
by performing simulated annealing. We observe a reduction in the average hexatic order,  , with increasing fractions of impurities, specifically for cases where the difference in the particle sizes was larger (smaller m). For example,
, with increasing fractions of impurities, specifically for cases where the difference in the particle sizes was larger (smaller m). For example, 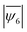 decreases from 0.89 to 0.69 as the mixture ratio varies from 90
decreases from 0.89 to 0.69 as the mixture ratio varies from 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 when the simulation is performed at m = 0.80 (Fig. 3b). However, the average hexatic order
1 when the simulation is performed at m = 0.80 (Fig. 3b). However, the average hexatic order  does not decrease when two particle types have closely matched diameters, i.e., m = 0.88 – a size ratio that represents the experimental sample. The assembled structures found at the minimum energy states are shown in Fig. 3c – polycrystalline structures and clearly separated grain boundaries form when the fraction of impurities is small (90
does not decrease when two particle types have closely matched diameters, i.e., m = 0.88 – a size ratio that represents the experimental sample. The assembled structures found at the minimum energy states are shown in Fig. 3c – polycrystalline structures and clearly separated grain boundaries form when the fraction of impurities is small (90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for both m = 0.80 and m = 0.88. In contrast, randomly distributed defects and voids are observed in the 50% mixture ratio (1
1) for both m = 0.80 and m = 0.88. In contrast, randomly distributed defects and voids are observed in the 50% mixture ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) sample (Voronoi diagrams in Fig. S8, ESI†). The constant
1) sample (Voronoi diagrams in Fig. S8, ESI†). The constant  value in the 1
value in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the 90
1 and the 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture for m = 0.88 indicates that the energy cost of the grain boundaries in the 90
1 mixture for m = 0.88 indicates that the energy cost of the grain boundaries in the 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture matches the energy cost of the voids in the 1
1 mixture matches the energy cost of the voids in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture. As the mismatch in particle diameters becomes larger, e.g., for m = 0.80, the number of defects increases, causing a significant reduction (22%) in the average hexatic order. The computational results indicate that the formation of amorphous solids in the presence of a large size mismatch can be explained primarily from the energetics of the system. This finding is consistent with prior experiments that observed glass formation in binary samples with a size ratio of 0.77 and 0.81.47,56
1 mixture. As the mismatch in particle diameters becomes larger, e.g., for m = 0.80, the number of defects increases, causing a significant reduction (22%) in the average hexatic order. The computational results indicate that the formation of amorphous solids in the presence of a large size mismatch can be explained primarily from the energetics of the system. This finding is consistent with prior experiments that observed glass formation in binary samples with a size ratio of 0.77 and 0.81.47,56
Additionally, we quantified the translational order of the assembled structures by quantifying the distributions of the center-to-center distance between neighboring particles, DB. As shown in Fig. 3d and e, the average  and the standard deviation of the distribution, δDB gradually increases with the increasing fraction of impurities (both for = 0.80 and m = 0.88). This increase is more prominent in the presence of large size mismatch as demonstrated in Fig. 3f. The finding indicates that the translational order is more sensitive to marginal mismatches in particle diameters than the orientational hexatic order. Although the asymmetric bond lengths between particle pairs reduce the average translational order, the deviation is not high enough to compromise the mean orientational order in the 1
and the standard deviation of the distribution, δDB gradually increases with the increasing fraction of impurities (both for = 0.80 and m = 0.88). This increase is more prominent in the presence of large size mismatch as demonstrated in Fig. 3f. The finding indicates that the translational order is more sensitive to marginal mismatches in particle diameters than the orientational hexatic order. Although the asymmetric bond lengths between particle pairs reduce the average translational order, the deviation is not high enough to compromise the mean orientational order in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture for m = 0.88. Therefore, the simulation results confirm that a marginal size mismatch (such as m = 0.88) cannot introduce enough topological frustration to reduce the hexatic order of a binary mixture sample as high as 18%.
1 binary mixture for m = 0.88. Therefore, the simulation results confirm that a marginal size mismatch (such as m = 0.88) cannot introduce enough topological frustration to reduce the hexatic order of a binary mixture sample as high as 18%.
To strengthen our conclusion, we examined the hexatic order for the m = 0.88 sample numerically for an even shorter range of attractive interaction – 0.22% of the particle diameter. We found that the hexatic order shows only a 2% reduction when the number ratio varies from 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. S9, ESI†), much smaller compared to the 18% reduction observed in the experiment. We also examined the thermodynamic equilibrium states by exciting the ground state crystal structures with an increased temperature of kBT. We found that the hexatic orders of all mixture ratios (90
1 (Fig. S9, ESI†), much smaller compared to the 18% reduction observed in the experiment. We also examined the thermodynamic equilibrium states by exciting the ground state crystal structures with an increased temperature of kBT. We found that the hexatic orders of all mixture ratios (90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 9
1, 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1
1, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) decrease equally from 0.89 to 0.82 at room temperature, yet any notable reduction was absent in the 1
1) decrease equally from 0.89 to 0.82 at room temperature, yet any notable reduction was absent in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sample compared to the 90
1 sample compared to the 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sample (Fig. S9, ESI†). Therefore, we conclude that the near equilibrium structures computed in the simulations do not explain why we observe a large reduction of
1 sample (Fig. S9, ESI†). Therefore, we conclude that the near equilibrium structures computed in the simulations do not explain why we observe a large reduction of  (18%) in the m = 0.88 sample when the mixture ratio changes from 90
(18%) in the m = 0.88 sample when the mixture ratio changes from 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
Therefore, we shift our focus to the investigation of the crystal growth mechanism to explore the possibility of kinetic frustration. In Fig. 4a, the mean hexatic order plot is shown for samples with a few different volume ratios – 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 19
1, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 9
1, 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1
1, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, observed at different times and assembled with different SDS concentrations (i.e., different bond energy). We find the general trend of gradually decreasing
1, observed at different times and assembled with different SDS concentrations (i.e., different bond energy). We find the general trend of gradually decreasing  with increasing fraction of “impurity” (790 nm, red) particles. We also notice that the addition of impurities slows down the crystallization process. The sample with a higher SDS concentration (36.5 mM, Eb ≈ 6.1kBT) reaches its maximum crystalline state within about 90 min for all mixture ratios. In contrast, the sample with lower SDS concentration (34 mM, Eb ≈ 5.6kBT) crystallizes slowly, especially when impurities are added (compare the dark blue and cyan curves on Fig. 4a). In this case, a monodisperse sample crystallizes with
with increasing fraction of “impurity” (790 nm, red) particles. We also notice that the addition of impurities slows down the crystallization process. The sample with a higher SDS concentration (36.5 mM, Eb ≈ 6.1kBT) reaches its maximum crystalline state within about 90 min for all mixture ratios. In contrast, the sample with lower SDS concentration (34 mM, Eb ≈ 5.6kBT) crystallizes slowly, especially when impurities are added (compare the dark blue and cyan curves on Fig. 4a). In this case, a monodisperse sample crystallizes with  within only 3 h; however, the 19
within only 3 h; however, the 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture ratio takes about 22 h to obtain a similarly higher magnitude of
1 mixture ratio takes about 22 h to obtain a similarly higher magnitude of  . It is expected that the average hexatic order for a sample with higher bond energy will be slightly smaller, because of the more frequent nucleation from different sites (the black curve is situated lower than the dark blue curve). Notably, we observe that the hexatic order of the 1
. It is expected that the average hexatic order for a sample with higher bond energy will be slightly smaller, because of the more frequent nucleation from different sites (the black curve is situated lower than the dark blue curve). Notably, we observe that the hexatic order of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture is low for both SDS concentrations, regardless of the long observation time of up to 22 h. Upon close examination of the assembled structures in the 19
1 mixture is low for both SDS concentrations, regardless of the long observation time of up to 22 h. Upon close examination of the assembled structures in the 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sample (Eb ≈ 5.6kBT after 22 h), we notice that the ordered regions of the assembly consist mostly of the 700 nm particles (green) while the 790 nm particles (red) locate themselves in between the boundaries of different crystalline grains. All these observations indicate that the crystallization pathway is different in a suspension with large number of impurities compared to a monodisperse suspension.
1 sample (Eb ≈ 5.6kBT after 22 h), we notice that the ordered regions of the assembly consist mostly of the 700 nm particles (green) while the 790 nm particles (red) locate themselves in between the boundaries of different crystalline grains. All these observations indicate that the crystallization pathway is different in a suspension with large number of impurities compared to a monodisperse suspension.
Colloidal crystallization driven by short-ranged depletion interaction is known to follow a two-step nucleation pathway, distinct from the mechanism explained in the classical nucleation theory.30 Savage et al. found that especially at a high area fraction, the assembly first forms amorphous clusters and grows in that state until a sudden increase in the hexatic order occurs resulting a crystalline state. The mechanism behind this two-step nucleation was explained by the reduction of the line tension in the intermediate amorphous phase that compensates for the lower bulk energy caused by the short interaction range. This is indeed what we observe in the crystallization pathway of the monodisperse sample (Fig. 4b and c) – the assembly first grows in the amorphous state, and then stable crystallites start developing at about 40 min, which eventually grow and form boundaries between multiple crystalline grains (at t = 60 min, Fig. 4c). However, in the binary sample, growth in this amorphous state continues for the entire timespan of the assembly, as depicted by the slow growth curve in Fig. 4b and the snapshots in Fig. 4c. The absence of two-step nucleation is binary mixtures is likely due to the size mismatch that causes a further reduction of the bulk energy in a binary simple compared to a monodisperse sample – as evident from the calculation of higher nucleation barrier in binary systems.57 From the hexatic order plots during the early stage of crystal growth (0–60 min, Fig. 4b), we observe the signature of a two-step growth mechanism only in the monodisperse suspension. Both the monodisperse and the binary mixture show a linear growth for the first 20 min, followed by a non-linear growth in the monodisperse sample and a continued linear growth in the binary sample (full field of view images and longer time growth characterization shown in Fig. S10 and S11, ESI†). We also examined different intermediate mixture ratios, such as 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5
1, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 3
1, and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. S12, ESI†) – although we observe the formation of stable grains via two-step nucleation in the 9
1 (Fig. S12, ESI†) – although we observe the formation of stable grains via two-step nucleation in the 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture sample, it becomes a rarer event when the fraction of the impurities increases in the 5
1 mixture sample, it becomes a rarer event when the fraction of the impurities increases in the 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures. From all the observations, it is reasonable to conclude that the second step of nucleation is much more likely to occur in a region where a critical number of particles with the same size can gather. Since it takes long time for this gathering to occur in the presence of the impurities, the 19
1 mixtures. From all the observations, it is reasonable to conclude that the second step of nucleation is much more likely to occur in a region where a critical number of particles with the same size can gather. Since it takes long time for this gathering to occur in the presence of the impurities, the 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 9
1 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures exhibit slower rates of growth in reaching their maximum
1 mixtures exhibit slower rates of growth in reaching their maximum  value (Fig. 4a), and the 1
value (Fig. 4a), and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture remain frustrated for the entire timespan of observation (with a maximum
1 mixture remain frustrated for the entire timespan of observation (with a maximum  of only 0.63 after 22 h, Fig. 4a).
of only 0.63 after 22 h, Fig. 4a).
We verified that the major impact caused by the impurities is the two-step nucleation, and not the difference in deposition rate or the formation of second layers. The rate at which the particles attach to the surface, i.e., the deposition rate remains equal for both samples during the early stage of growth (Fig. S13, ESI†). The growth only slows down after 40 min for the binary sample due to the lack of available space for deposition. Therefore, we can conclude that the deposition rate is not the cause of kinetic frustration in the binary samples. Furthermore, the growth of second layers is only observed on top of a highly crystalline first layer, which acts a solid surface and induce a depletion interaction between the first layer and the second layer (Fig. S14a, ESI†). We do not observe any second layer formation in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary sample because of the highly amorphous first layer, indicating that the second layer cannot induce the kinetic frustration either.
1 binary sample because of the highly amorphous first layer, indicating that the second layer cannot induce the kinetic frustration either.
Finally, we quantify the particle dynamics in the amorphous layer of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
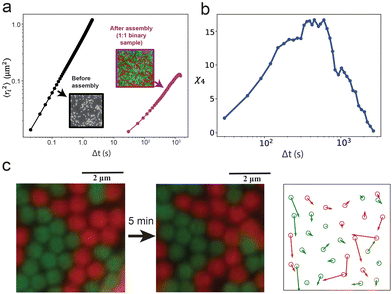
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture to identify any signature of arrested dynamics. The microscopic dynamics of the amorphous state was captured after the assembly continued for 80 min (Movie S1, ESI†). While freely diffusing particles before assembly take 1 s to move 1 μm2 (mean-squared displacement), the particles in the assembled layer of the binary sample take about 970 s to move only 0.1 μm2 (Fig. 5a). Additionally, we observe multiple partial vacancies in the assembly and cooperative particle movement adjacent to the locations of the partial vacancies. An example of the cooperative motion is presented and quantified in Fig. 5c. Because of the remarkably short interaction range, particles fail to interact with each other across a partial vacancy and continue to rearrange their positions locally due to their Brownian motions. These local movements result in continuous hopping of the vacancy locations (Fig. 5c and Movie S1, ESI†). Because of the high surface coverage, the fluctuating particles can support the relocation of their nearest neighbors, causing the cooperative movement observed in certain spots. Particle motion of this nature contributes to the overall arrested dynamics, which is a common feature observed near glass transition.58,59 The four-point susceptibility, χ4, calculated from a 50 μm × 30 μm region of the sample (Fig. S15, ESI†) shows a peak near 600 s (Fig. 5b), demonstrating the signature of spatiotemporal heterogeneity in colloidal glasses.47 Furthermore, when a stronger interaction potential is applied by increasing the concentration of the depletant micelles, the binary sample forms colloidal gels (Fig. S16, ESI†), transitioning from one nonequilibrium phase to another.
1 binary mixture to identify any signature of arrested dynamics. The microscopic dynamics of the amorphous state was captured after the assembly continued for 80 min (Movie S1, ESI†). While freely diffusing particles before assembly take 1 s to move 1 μm2 (mean-squared displacement), the particles in the assembled layer of the binary sample take about 970 s to move only 0.1 μm2 (Fig. 5a). Additionally, we observe multiple partial vacancies in the assembly and cooperative particle movement adjacent to the locations of the partial vacancies. An example of the cooperative motion is presented and quantified in Fig. 5c. Because of the remarkably short interaction range, particles fail to interact with each other across a partial vacancy and continue to rearrange their positions locally due to their Brownian motions. These local movements result in continuous hopping of the vacancy locations (Fig. 5c and Movie S1, ESI†). Because of the high surface coverage, the fluctuating particles can support the relocation of their nearest neighbors, causing the cooperative movement observed in certain spots. Particle motion of this nature contributes to the overall arrested dynamics, which is a common feature observed near glass transition.58,59 The four-point susceptibility, χ4, calculated from a 50 μm × 30 μm region of the sample (Fig. S15, ESI†) shows a peak near 600 s (Fig. 5b), demonstrating the signature of spatiotemporal heterogeneity in colloidal glasses.47 Furthermore, when a stronger interaction potential is applied by increasing the concentration of the depletant micelles, the binary sample forms colloidal gels (Fig. S16, ESI†), transitioning from one nonequilibrium phase to another.
4. Conclusions
We investigated the self-assembly of 2D binary colloidal crystals driven by short-ranged depletion interaction and in the presence of a marginal mismatch in the particle diameters. Our computational findings indicate that the minimum energy states maintain a high orientational order in a binary sample when the size ratio of the small to the large particle is 0.88. However, our experiments show a significant reduction (of about 18%) of the orientational order parameter in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture compared to the monodisperse suspension. The order reduces gradually as the fraction of the impurity particles increases in the binary mixture. By carefully examining the crystallization kinetics, we find that the two-step nucleation mechanism that drives crystallization in the presence of short-ranged depletion interaction is responsible for the observed phenomenon. After growing in the amorphous state during the first step, the monodisperse sample enters the second nucleation step to rapidly form stable crystallites while the binary sample continues to grow in the amorphous state until the particle dynamics becomes arrested. These results have important implications for our general understanding of the mechanisms behind amorphous solid formation that originate from thermodynamic, kinetic, or topological conditions. Our findings on 2D binary assembly demonstrate that the frustration in growth kinetics can dominate over the topological frustration when a small mismatch in particle size is introduced. Leveraging this kinetic pathway of colloidal glass formation can stimulate progress in the fundamental studies on glass transitions59–62 as well as applications focused on photonic glasses.63–65 In addition, the binary mixtures with intermediate volume ratios (19
1 binary mixture compared to the monodisperse suspension. The order reduces gradually as the fraction of the impurity particles increases in the binary mixture. By carefully examining the crystallization kinetics, we find that the two-step nucleation mechanism that drives crystallization in the presence of short-ranged depletion interaction is responsible for the observed phenomenon. After growing in the amorphous state during the first step, the monodisperse sample enters the second nucleation step to rapidly form stable crystallites while the binary sample continues to grow in the amorphous state until the particle dynamics becomes arrested. These results have important implications for our general understanding of the mechanisms behind amorphous solid formation that originate from thermodynamic, kinetic, or topological conditions. Our findings on 2D binary assembly demonstrate that the frustration in growth kinetics can dominate over the topological frustration when a small mismatch in particle size is introduced. Leveraging this kinetic pathway of colloidal glass formation can stimulate progress in the fundamental studies on glass transitions59–62 as well as applications focused on photonic glasses.63–65 In addition, the binary mixtures with intermediate volume ratios (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 9
1 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) allow the nucleation of small crystallites whose growth is then inhibited by the presence of the impurities. Applications of this self-limiting formation of crystal grains could enable the design of polycrystalline and epitaxial colloidal materials10,66–69 with precisely tuned optical and mechanical properties.
1) allow the nucleation of small crystallites whose growth is then inhibited by the presence of the impurities. Applications of this self-limiting formation of crystal grains could enable the design of polycrystalline and epitaxial colloidal materials10,66–69 with precisely tuned optical and mechanical properties.
Author contributions
S. T. S. performed the experiments, analyzed the experimental data, and prepared the manuscript. C. F. performed the Molecular Dynamics simulations. S. M. developed the computational methods used for image processing and data analysis. N. T. supervised the project and prepared the manuscript.Data availability
The data that support the findings of this study are available from the corresponding author, Nabila Tanjeem, upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the support from the National Science Foundation (NSF), award no. CBET – 2301692.References
- P. N. Pusey and W. van Megen, Phase Behaviour of Concentrated Suspensions of Nearly Hard Colloidal Spheres, Nature, 1986, 320(6060), 340–342, DOI:10.1038/320340a0.
- B. Li, D. Zhou and Y. Han, Assembly and Phase Transitions of Colloidal Crystals, Nat. Rev. Mater., 2016, 1(2), 15011, DOI:10.1038/natrevmats.2015.11.
- P. J. Lu and D. A. Weitz, Colloidal Particles: Crystals, Glasses, and Gels, Annu. Rev. Condens. Matter Phys., 2013, 4(1), 217–233, DOI:10.1146/annurev-conmatphys-030212-184213.
- V. N. Manoharan, Colloidal Matter: Packing, Geometry, and Entropy, Science, 2015, 349(6251), 1253751, DOI:10.1126/science.1253751.
- V. J. Anderson and H. N. W. Lekkerkerker, Insights into Phase Transition Kinetics from Colloid Science, Nature, 2002, 416(6883), 811–815, DOI:10.1038/416811a.
- P. Bartlett, R. H. Ottewill and P. N. Pusey, Superlattice Formation in Binary Mixtures of Hard-Sphere Colloids, Phys. Rev. Lett., 1992, 68(25), 3801–3804, DOI:10.1103/PhysRevLett.68.3801.
- P. Bartlett, R. H. Ottewill and P. N. Pusey, Freezing of Binary Mixtures of Colloidal Hard Spheres, J. Chem. Phys., 1990, 93(2), 1299–1312, DOI:10.1063/1.459142.
- M. Sato, Two-Dimensional Binary Colloidal Crystals Formed by Particles with Two Different Sizes, Sci. Rep., 2022, 12(1), 12370, DOI:10.1038/s41598-022-16806-y.
- J. Yu, Q. Yan and D. Shen, Co-Self-Assembly of Binary Colloidal Crystals at the Air−Water Interface, ACS Appl. Mater. Interfaces, 2010, 2(7), 1922–1926, DOI:10.1021/am100250c.
- J. Nozawa, S. Uda, A. Toyotama, J. Yamanaka, H. Niinomi and J. Okada, Growth and One-Dimensional Heteroepitaxy of Binary Colloidal Crystals, Cryst. Growth Des., 2020, 20(5), 3247–3256, DOI:10.1021/acs.cgd.0c00078.
- S. Lopez-Godoy, P. Díaz-Leyva and A. Kozina, Self-Assembly in Binary Mixtures of Spherical Colloids, Adv. Colloid Interface Sci., 2022, 308, 102748, DOI:10.1016/j.cis.2022.102748.
- L. D. Yao, H. Y. Chen, Y. Shi, Y. Liang and T. H. Zhang, Synchronized Fractionation and Phase Separation in Binary Colloids, Soft Matter, 2020, 16, 9042–9046, 10.1039/D0SM00751J.
- Y. Li, J. R. Royer, J. Sun and C. Ness, Impact of Granular Inclusions on the Phase Behavior of Colloidal Gels, Soft Matter, 2023, 19(7), 1342–1347, 10.1039/D2SM01648F.
- D. M. Herlach, Colloids as Model Systems for Metals and Alloys: A Case Study of Crystallization, Eur. Phys. J.: Spec. Top., 2014, 223(3), 591–608, DOI:10.1140/epjst/e2014-02111-5.
- Y. Hu, D. Lan, G. Dai, H. Jiang, L. Duan and B. Wei, Study on Crystallization Kinetics of Binary Alloys through Model Colloidal Mixtures, J. Alloys Compd., 2010, 504, S243–S246, DOI:10.1016/j.jallcom.2010.02.151.
- F. S. Diba, A. Boden, H. Thissen, M. Bhave, P. Kingshott and P.-Y. Wang, Binary Colloidal Crystals (BCCs): Interactions, Fabrication, and Applications, Adv. Colloid Interface Sci., 2018, 261, 102–127, DOI:10.1016/j.cis.2018.08.005.
- M. Á. Fernández-Rodríguez, R. Elnathan, R. Ditcovski, F. Grillo, G. M. Conley, F. Timpu, A. Rauh, K. Geisel, T. Ellenbogen, R. Grange, F. Scheffold, M. Karg, W. Richtering, N. H. Voelcker and L. Isa, Tunable 2D Binary Colloidal Alloys for Soft Nanotemplating, Nanoscale, 2018, 10(47), 22189–22195, 10.1039/C8NR07059H.
- Z. Zhang, G. Yi, P. Li, X. Zhang, Z. Wan, X. Wang, C. Zhang and Y. Zhang, Recent Advances in Binary Colloidal Crystals for Photonics and Porous Material Fabrication, J. Phys. Chem. B, 2021, 125(22), 6012–6022, DOI:10.1021/acs.jpcb.1c03349.
- E. V. Shevchenko, D. V. Talapin, N. A. Kotov, S. O’Brien and C. B. Murray, Structural Diversity in Binary Nanoparticle Superlattices, Nature, 2006, 439(7072), 55–59, DOI:10.1038/nature04414.
- P. Wang, Q. Qiao, Y. Zhu and M. Ouyang, Colloidal Binary Supracrystals with Tunable Structural Lattices, J. Am. Chem. Soc., 2018, 140(29), 9095–9098, DOI:10.1021/jacs.8b05643.
- M. E. Leunissen, C. G. Christova, A.-P. Hynninen, C. P. Royall, A. I. Campbell, A. Imhof, M. Dijkstra, R. van Roij and A. van Blaaderen, Ionic Colloidal Crystals of Oppositely Charged Particles, Nature, 2005, 437(7056), 235–240, DOI:10.1038/nature03946.
- W. B. Rogers, W. M. Shih and V. N. Manoharan, Using DNA to Program the Self-Assembly of Colloidal Nanoparticles and Microparticles, Nat. Rev. Mater., 2016, 1(3), 16008, DOI:10.1038/natrevmats.2016.8.
- M. Liu, X. Zheng, V. Grebe, D. J. Pine and M. Weck, Tunable Assembly of Hybrid Colloids Induced by Regioselective Depletion, Nat. Mater., 2020, 19, 1354–1361, DOI:10.1038/s41563-020-0744-2.
- S. Sacanna, W. T. M. Irvine, P. M. Chaikin and D. J. Pine, Lock and Key Colloids, Nature, 2010, 464(7288), 575–578, DOI:10.1038/nature08906.
- Y. Wang, Y. Wang, X. Zheng, G.-R. Yi, S. Sacanna, D. J. Pine and M. Weck, Three-Dimensional Lock and Key Colloids, J. Am. Chem. Soc., 2014, 136(19), 6866–6869, DOI:10.1021/ja502699p.
- D. Hinrichs, R. Himstedt and D. Dorfs, The Size-Selective Interaction of Key and Lock Nanocrystals Driven by Depletion Attraction at the Nanoscale, Nanoscale, 2018, 10(21), 9899–9907, 10.1039/C8NR01893F.
- S. Park, H. Hwang and S.-H. Kim, Direct Determination of the Phase Diagram of a Depletion-Mediated Colloidal System, J. Am. Chem. Soc., 2022, 144(40), 18397–18405, DOI:10.1021/jacs.2c06715.
- A. Parola and L. Reatto, Depletion Interaction between Spheres of Unequal Size and Demixing in Binary Mixtures of Colloids, Mol. Phys., 2015, 113(17–18), 2571–2582, DOI:10.1080/00268976.2015.1046529.
- G. Onuh, D. Harries and O. Manor, Depletion-Induced Self-Assembly of Colloidal Particles on a Solid Substrate, Langmuir, 2024, 40(16), 8554–8561, DOI:10.1021/acs.langmuir.4c00186.
- J. R. Savage and A. D. Dinsmore, Experimental Evidence for Two-Step Nucleation in Colloidal Crystallization, Phys. Rev. Lett., 2009, 102(19), 198302, DOI:10.1103/PhysRevLett.102.198302.
- N. Tanjeem, W. H. Wilkin, D. A. Beller, C. H. Rycroft and V. N. Manoharan, Geometrical Frustration and Defect Formation in Growth of Colloidal Nanoparticle Crystals on a Cylinder: Implications for Assembly of Chiral Nanomaterials, ACS Appl. Nano Mater., 2021, 4(10), 10682–10691, DOI:10.1021/acsanm.1c02126.
- G. Meng, J. Paulose, D. R. Nelson and V. N. Manoharan, Elastic Instability of a Crystal Growing on a Curved Surface, Science, 2014, 343(6171), 634–637, DOI:10.1126/science.1244827.
- L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Cubic Crystals from Cubic Colloids, Soft Matter, 2011, 7(9), 4139–4142, 10.1039/C0SM01246G.
- D. Baranov, A. Fiore, M. van Huis, C. Giannini, A. Falqui, U. Lafont, H. Zandbergen, M. Zanella, R. Cingolani and L. Manna, Assembly of Colloidal Semiconductor Nanorods in Solution by Depletion Attraction, Nano Lett., 2010, 10(2), 743–749, DOI:10.1021/nl903946n.
- G. Wu, H. Cho, D. A. Wood, A. D. Dinsmore and S. Yang, Confined Assemblies of Colloidal Particles with Soft Repulsive Interactions, J. Am. Chem. Soc., 2017, 139(14), 5095–5101, DOI:10.1021/jacs.6b12975.
- R. Ohnuki, M. Sakai, Y. Takeoka and S. Yoshioka, Optical Characterization of the Photonic Ball as a Structurally Colored Pigment, Langmuir, 2020, 36(20), 5579–5587, DOI:10.1021/acs.langmuir.0c00736.
- Y. Zhao, L. Shang, Y. Cheng and Z. Gu, Spherical Colloidal Photonic Crystals, Acc. Chem. Res., 2014, 47(12), 3632–3642, DOI:10.1021/ar500317s.
- R. Ganapathy, M. R. Buckley, S. J. Gerbode and I. Cohen, Direct Measurements of Island Growth and Step-Edge Barriers in Colloidal Epitaxy, Science, 2010, 327(5964), 445–448, DOI:10.1126/science.1179947.
- J. Zhou, J. S. van Duijneveldt and B. Vincent, Two-Stage Phase Separation in Ternary Colloid– Polymer Mixtures, Phys. Chem. Chem. Phys., 2011, 13(1), 110–113, 10.1039/C0CP01523G.
- A. Kozina, D. Sagawe, P. Díaz-Leyva, E. Bartsch and T. Palberg, Polymer-Enforced Crystallization of a Eutectic Binary Hard Sphere Mixture, Soft Matter, 2011, 8(3), 627–630, 10.1039/C1SM06699D.
- J. A. Bonham, M. A. Faers and J. S. van Duijneveldt, Binary and Ternary Mixtures of Microgel Particles, Hard Spheres and Non-Adsorbing Polymer in Non-Aqueous Solvents, Colloids Surf., A, 2018, 536, 180–190, DOI:10.1016/j.colsurfa.2017.07.022.
- A. Kozina, P. Díaz-Leyva, T. Palberg and E. Bartsch, Crystallization Kinetics of Colloidal Binary Mixtures with Depletion Attraction, Soft Matter, 2014, 10(47), 9523–9533, 10.1039/C4SM02193B.
- A. Toyotama, T. Okuzono and J. Yamanaka, Spontaneous Formation of Eutectic Crystal Structures in Binary and Ternary Charged Colloids Due to Depletion Attraction, Sci. Rep., 2016, 6(1), 23292, DOI:10.1038/srep23292.
- R. Pandey and J. C. Conrad, Dynamics of Confined Depletion Mixtures of Polymers and Bidispersed Colloids, Soft Matter, 2013, 9(44), 10617–10626, 10.1039/C3SM51879E.
- I. Zhang, R. Pinchaipat, N. B. Wilding, M. A. Faers, P. Bartlett, R. Evans and C. P. Royall, Composition Inversion in Mixtures of Binary Colloids and Polymer, J. Chem. Phys., 2018, 148(18), 184902, DOI:10.1063/1.5023393.
- J. C. Crocker and D. G. Grier, Methods of Digital Video Microscopy for Colloidal Studies, J. Colloid Interface Sci., 1996, 179(1), 298–310, DOI:10.1006/jcis.1996.0217.
- T. Narumi, S. V. Franklin, K. W. Desmond, M. Tokuyama and E. R. Weeks, Spatial and Temporal Dynamical Heterogeneities Approaching the Binary Colloidal Glass Transition, Soft Matter, 2011, 7(4), 1472–1482, 10.1039/C0SM00756K.
- R. W. Perry, M. C. Holmes-Cerfon, M. P. Brenner and V. N. Manoharan, Two-Dimensional Clusters of Colloidal Spheres: Ground States, Excited States, and Structural Rearrangements, Phys. Rev. Lett., 2015, 114(22), 228301, DOI:10.1103/PhysRevLett.114.228301.
- S. Asakura and F. Oosawa, On Interaction between Two Bodies Immersed in a Solution of Macromolecules, J. Chem. Phys., 1954, 22(7), 1255–1256, DOI:10.1063/1.1740347.
- J. H. Sun, G. H. Zhang, A. Plummer, C. Martin, N. Tanjeem, D. R. Nelson and V. N. Manoharan, Colloidal Crystallization on Cones, Phys. Rev. Lett., 2025, 134(1), 018201, DOI:10.1103/PhysRevLett.134.018201.
- A. D. Dinsmore and A. G. Yodh, Entropic Confinement of Colloidal Spheres in Corners on Silicon Substrates, Langmuir, 1999, 15(2), 314–316, DOI:10.1021/la981243w.
- J. R. Savage, D. W. Blair, A. J. Levine, R. A. Guyer and A. D. Dinsmore, Imaging the Sublimation Dynamics of Colloidal Crystallites, Science, 2006, 314(5800), 795–798, DOI:10.1126/science.1128649.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS – a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales, Comput. Phys. Commun., 2022, 271, 108171, DOI:10.1016/j.cpc.2021.108171.
- N. Tanjeem, D. M. Hall, M. B. Minnis, R. C. Hayward and G. M. Grason, Focusing Frustration for Self-Limiting Assembly of Flexible, Curved Particles, Phys. Rev. Res., 2022, 4(3), 033035, DOI:10.1103/PhysRevResearch.4.033035.
- T. D. Iracki, D. J. Beltran-Villegas, S. L. Eichmann and M. A. Bevan, Charged Micelle Depletion Attraction and Interfacial Colloidal Phase Behavior, Langmuir, 2010, 26(24), 18710–18717, DOI:10.1021/la103701k.
- T. Eckert and E. Bartsch, Glass Transition Dynamics of Hard Sphere like Microgel Colloids with Short-Ranged Attractions, J. Phys.: Condens. Matter, 2004, 16(42), S4937, DOI:10.1088/0953-8984/16/42/011.
- S. R. Ganagalla and S. N. Punnathanam, Free Energy Barriers for Homogeneous Crystal Nucleation in a Eutectic System of Binary Hard Spheres, J. Chem. Phys., 2013, 138(17), 174503, DOI:10.1063/1.4802777.
- J. Yun, B. Chun, H. W. Jung and J. C. Hyun, Emergence of Cooperative Particle Dynamics in Quasi-Two-Dimensional Glass-Forming Colloidal Suspensions, Phys. Fluids, 2024, 36(1), 013311, DOI:10.1063/5.0181383.
- S. Vivek, C. P. Kelleher, P. M. Chaikin and E. R. Weeks, Long-Wavelength Fluctuations and the Glass Transition in Two Dimensions and Three Dimensions, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(8), 1850–1855, DOI:10.1073/pnas.1607226113.
- G. L. Hunter and E. R. Weeks, The Physics of the Colloidal Glass Transition, Rep. Prog. Phys., 2012, 75(6), 066501, DOI:10.1088/0034-4885/75/6/066501.
- E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Three-Dimensional Direct Imaging of Structural Relaxation Near the Colloidal Glass Transition, Science, 2000, 287(5453), 627–631, DOI:10.1126/science.287.5453.627.
- J. M. Lynch, G. C. Cianci and E. R. Weeks, Dynamics and Structure of an Aging Binary Colloidal Glass, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78(3), 031410, DOI:10.1103/PhysRevE.78.031410.
- A. F. Demirörs, E. Poloni, M. Chiesa, F. L. Bargardi, M. R. Binelli, W. Woigk, L. D. C. de Castro, N. Kleger, F. B. Coulter, A. Sicher, H. Galinski, F. Scheffold and A. R. Studart, Three-Dimensional Printing of Photonic Colloidal Glasses into Objects with Isotropic Structural Color, Nat. Commun., 2022, 13(1), 4397, DOI:10.1038/s41467-022-32060-2.
- S. G. Romanov, S. Orlov, D. Ploss, C. K. Weiss, N. Vogel and U. Peschel, Engineered Disorder and Light Propagation in a Planar Photonic Glass, Sci. Rep., 2016, 6(1), 27264, DOI:10.1038/srep27264.
- G. Shang, M. Eich and A. Petrov, Photonic Glass Based Structural Color, APL Photonics, 2020, 5(6), 060901, DOI:10.1063/5.0006203.
- F. A. Lavergne, S. Diana, D. G. A. L. Aarts and R. P. A. Dullens, Equilibrium Grain Boundary Segregation and Clustering of Impurities in Colloidal Polycrystalline Monolayers, Langmuir, 2016, 32(48), 12716–12724, DOI:10.1021/acs.langmuir.6b02683.
- J. D. Hutchinson and R. P. A. Dullens, Grain Rotation in Impurity-Doped Two-Dimensional Colloidal Polycrystals, Phys. Rev. Mater., 2024, 8(7), 075603, DOI:10.1103/PhysRevMaterials.8.075603.
- J. Nozawa, S. Uda, H. Niinomi, J. Okada and K. Fujiwara, Heteroepitaxial Growth of Colloidal Crystals: Dependence of the Growth Mode on the Interparticle Interactions and Lattice Spacing, J. Phys. Chem. Lett., 2022, 13(30), 6995–7000, DOI:10.1021/acs.jpclett.2c01707.
- S. Yang, Y. G. Kim, S. Park and S.-H. Kim, Structural Color Mixing in Microcapsules through Exclusive Crystallization of Binary and Ternary Colloids, Adv. Mater., 2023, 35(38), 2302750, DOI:10.1002/adma.202302750.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00433k |
| This journal is © The Royal Society of Chemistry 2025 |