 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bubbling and mixing of vibrated and non-vibrated gas-fluidized active granular matter
Oscar J.
Punch
 *a,
Michael W.
Jordan
*a,
Michael W.
Jordan
 ab,
Angelina S.
Moncrieffe
ab,
Angelina S.
Moncrieffe
 a,
Qiang
Guo
a,
Qiang
Guo
 c and
Christopher M.
Boyce
c and
Christopher M.
Boyce
 *a
*a
aDepartment of Chemical Engineering, Columbia University, New York 10027, USA. E-mail: ojp2117@columbia.edu; cmb2302@columbia.edu
bColumbia Climate School, Columbia University, New York 10027, USA
cState Key Laboratory of Mesoscience and Engineering, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China
First published on 16th April 2025
Abstract
Numerical simulations are used to study the effect of varying magnitudes of active matter force on non-vibrated and vertically vibrated gas-fluidized granular materials. We observe that if the ratio of active matter force to gravity is less than 1, but above 0, gas bubbles produced by fluidization generally increase in size which promotes mixing. However, if the ratio of active matter force to gravity exceeds 1, then the active matter force suppresses bubbling and the mixing is poorer. Furthermore, we find that if the active matter force significantly exceeds 1, the mixing can be enhanced despite no bubbling, owing to diffusion. By vertically vibrating the granular bed, and subsequently producing structured bubbling, we find that bubbles persist for larger active matter force, which we attribute to the larger bubble size observed for structured bubbling as compared to chaotic bubbling. Finally, we present a non-dimensional regime map describing the transition of sub-diffusive, diffusive, and advective transport regimes depending on the balance of active matter force to drag force to gravitational force for fluidized active granular materials.
1 Introduction
Active matter comprises any system which is out of thermal equilibrium and does not consist of a time-reversal symmetry.1 For many systems, this manifests in the form of self-propulsion using stored energy. These active materials are ubiquitous owing to the many living creatures on Earth, and span a wide range of length scales from microscopic bacteria2 to larger-scale animals, as commonly observed in schooling fish.3 Specifically, active granular materials are a more recent field of study comprised of self-driven non-biological granular materials, for which Brownian motion is negligible (>1 μm diameter), that are typically less than 10 mm in diameter. Recently, active matter has found a host of interest due to the emergence of soft robotics4,5 and colloidal robots6 which can either be randomly driven or coherently driven. Coherently-driven task-orientated active materials are of significant interest to the biomedical engineering field for accomplishing complex tasks such as site-specific drug delivery7 or clogged artery cleaning.8 Other engineering applications of active materials include biomimetics of fish and lizards to improve locomotion maneuverability9 and navigation of challenging terrains.10,11 Fascinating phenomena has also been reported for randomly driven granular robots such as clustering at the corners in bounded systems,12 and elastically banded-together pairs active granular materials have even been shown to be able to solve complex situations such as mazes.13Random walk active matter can also exist for biological samples in granular length scales and systems, such as black soldier fly larvae14 which have been suggested as a promising method for efficient composting and livestock feed.15 The farming and harvesting of these fly larvae, as minilivestock, produces additional challenges with processing and so many sub-optimal methods such as tray farming and physical carrying are often used to grow and transport these materials, and it is still unclear how to best feed them.16 As such, understanding the physical transport of active granular matter is key to improve process efficiency for minilivestock farms. Yet, surprisingly, active granular matter is seldom studied from an engineering point of view.
Fluidization is a common technique to improve the process handling of granular materials, where the weight of the particles is supported (or exceeded) by the drag force imparted by a gas flow acting against gravity.17 Recently, the coupling of vertical vibration and gas-fluidization in traditional fluidized beds has been shown to further improve heat transfer18 and mixing19 compared to non-vibrated gas-fluidized beds. Vertically vibrated gas-fluidized beds have also been shown to replicate a host of traditional fluid dynamics phenomena such as Rayleigh–Taylor instabilities,20 Rayleigh–Bérnard convection,21 Faraday waves,22 drafting–kissing–tumbling,23 as well as structure other chaotic phenomena such as spout oscillation.24,25 Specifically, vertical vibration (or pulsed-gas flow) at certain frequencies and amplitudes can be used to form transient solid regions of the bed which channels the gas flow, producing bubbles positioned at specific nodes and antinodes in a triangular lattice arrangement.26–30 This is commonly referred to as structured bubbling and has critical implications in improving gas-fluidization by increasing control over bubble size, position, uniformity, and rate.26 Despite these promising findings, the field of structured bubbling is still nascent and so it is unclear what limitations there are with the method. Furthermore, to the best of the authors knowledge, no studies have yet considered how the presence of an active matter force may affect the bubbling for structured or unstructured bubbling.
The computational fluid dynamics-discrete element method (CFD-DEM) is a numerical simulation technique commonly used to simulate fluidized granular materials.31 CFD-DEM models the fluid using an Eulerian grid and the particles as discrete Lagrangian points. The volume-averaged Navier–Stokes equations are solved over each cell and particle contacts are resolved using Hertzian contact theory; the fluid and particles are then coupled using an interphase momentum exchange.32 A key advantage of CFD-DEM is the opportunity it provides to explore a vast parametric space, which may be challenging to do experimentally, as well as resolve parameters which are tricky to quantify experimentally, such as particle drag force. It is well-known that the choice of drag model33 and contact parameters34 is key for accurate simulation of fluidized systems. However, a recent study also showed that the choice of vibration modeling is critically important for accurately simulating vertically vibrated gas-fluidized beds; with vibrating the walls and a virtual plate acting as a distributor providing the highest accuracy.35
In this work we use numerical CFD-DEM simulations to investigate the bubbling and mixing of actively driven particles in both a vertically vibrated and non-vibrated gas-fluidized bed. The active force is randomly determined from a Gaussian distribution about mean zero after particle–particle contact, where the magnitude of the active force is controlled by the standard deviation of the Gaussian distribution. As such, the particles are essentially active underdamped Ornstein-Uhlenbeck particles.36 We reveal that three key regimes exist for bubbling through active granular materials: (i) active matter force less than gravity for which bubble diameter is increased and mixing is promoted, (ii) active matter force in parity with gravity for which bubbles still exist but are significantly smaller and mixing is worsened, and finally (iii) active matter force which is larger than gravity for which bubbles are completely suppressed yet mixing is increased over (ii), but slightly less than (i). Additionally, we find that the balance of drag force, active force, and gravitational force is key for describing the transport regime the system is in (advective, diffusive, or sub-diffusive).
2 Methods
Numerical simulations are conducted using the open-source multiphase Eulerian–Lagrangian framework MFiX37 using the method commonly referred to as the computational fluid dynamics-discrete element method (CFD-DEM). The governing equations for MFiX with an in-house active matter force implementation are now presented.2.1 Governing equations
First, let us consider a binary collision between two fluidized particles which do not initially contain an active force as shown in Fig. 1. As the particles approach, particle motion is governed by gravitational force (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) G) and drag force (
G) and drag force (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D), assuming the particles do not already have an active matter force from contacting another particle recently. During particle collision, the particles experience a contact force (
D), assuming the particles do not already have an active matter force from contacting another particle recently. During particle collision, the particles experience a contact force (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) C), which is governed by Hertzian contact theory, and an active matter force (
C), which is governed by Hertzian contact theory, and an active matter force (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A) is applied onto the particles. The active matter force is anisotropic in x, y, and z. As the particles separate, they remain ‘active’ until they contact another particle, at which point a new active matter force is applied to the particle, or the active matter force is set to zero if τ ≡ Δt = 0.0005 s passes. This implementation of the active matter force is commonly referred to as a finite correlation time (τ) and helps ensure the system remains numerically stable. As such, the force on a single particle i at any time is given by
A) is applied onto the particles. The active matter force is anisotropic in x, y, and z. As the particles separate, they remain ‘active’ until they contact another particle, at which point a new active matter force is applied to the particle, or the active matter force is set to zero if τ ≡ Δt = 0.0005 s passes. This implementation of the active matter force is commonly referred to as a finite correlation time (τ) and helps ensure the system remains numerically stable. As such, the force on a single particle i at any time is given by | (1) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) C = 0 if particle i is not currently contacting another particle and
C = 0 if particle i is not currently contacting another particle and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A = 0 if particle i has not contacted another particle within Δt ≥ τ. Eqn (1) is similar to those in literature for the modeling of vibrated active-granular materials,38 with the inclusion of a drag force term, and neglecting a friction term on the left-hand side of our equation as the friction due to the fluid phase (air) is negligible. We now briefly discuss the implementation of each of these forces.
A = 0 if particle i has not contacted another particle within Δt ≥ τ. Eqn (1) is similar to those in literature for the modeling of vibrated active-granular materials,38 with the inclusion of a drag force term, and neglecting a friction term on the left-hand side of our equation as the friction due to the fluid phase (air) is negligible. We now briefly discuss the implementation of each of these forces.
To resolve the contact force (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) C) between particles we use a Hertzian contact model with a soft-sphere implementation.39 For particle–particle contact between particles i and j, the Hertzian contact model has the form
C) between particles we use a Hertzian contact model with a soft-sphere implementation.39 For particle–particle contact between particles i and j, the Hertzian contact model has the form
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) C,ij = (knδnij − γn C,ij = (knδnij − γn![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) nij) + (ktδtij − γt nij) + (ktδtij − γt![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) tij), tij), | (2) |
The fluid and the particles are two-way coupled using the volume-averaged Navier–Stokes equations with an interphase momentum exchange term (![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) ) as per,
) as per,
 | (3) |
 | (4) |
![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) = β( = β(![[U with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0055_20d1.gif) g − g − ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p). p). | (5) |
Here, t is time, εg is the gas void fraction, ρg is the gas density, ![[U with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0055_20d1.gif) g is the gas velocity, P is the gas pressure, and
g is the gas velocity, P is the gas pressure, and  is the gas stress tensor. β is an empirically derived fluid drag law for which we implement the Gidaspow drag function.41 As such, β is given by
is the gas stress tensor. β is an empirically derived fluid drag law for which we implement the Gidaspow drag function.41 As such, β is given by
 | (6) |
 | (7) |
 | (8) |
 | (9) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) d is the drag force over each particle in a cell as per
d is the drag force over each particle in a cell as per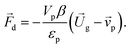 | (10) |
We model the particle active matter force (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A) using a Gaussian distribution, for which the probability density function is given as per
A) using a Gaussian distribution, for which the probability density function is given as per
 | (11) |
2.2 Numerical setup
The simulation domain is shown in Fig. 2 and the simulation parameters are given in Table 1. The fluid (air) is introduced into the domain using a mass-inlet boundary condition on the bottom xz-plane and exits due to an atmospheric pressure outlet condition on the top xz-plane. All other walls use a no-slip boundary condition, which is important for accurate simulation of structured bubbling in fluidized beds.40 The simulations consist of approximately 1.5 million spherical 400–600 μm diameter particles. The particle diameter range is given by a Gaussian distribution centered on dp = 500 μm, matching prior experimental work,26 and each fluid grid has characteristic lengths of ≈3dp. Prior to fluidization, the particles form a bed height of 0.06 m and are loosely packed. The bed height is significantly lower than real gas-fluidized beds for two key reasons: (i) computational limitations and (ii) matching that of a previous study for non-active particles.26 Each simulation is run for a total of 12 s of simulation time (≈150 hours of wall-clock time on 80 cores). The first 4 seconds of the simulations are discarded to allow for the system to reach pseudo steady-state.| Parameters | Symbol | Value |
|---|---|---|
| Domain | ||
| Geometry | W, H, Z | 0.2 × 0.16 × 0.01 m |
| Number of CFD cells | N W , NH, NZ | 100 × 80 × 5 |
| Vibration frequency | f | 5 Hz |
| Vibration amplitude | A | 4.5 mm |
| CFD time step | t CFD | 1 × 10−4 s |
| DEM time step | t DEM | 1 × 10−6 s |
| Gas | ||
| Gas density | ρ g | 1.2 kg m−3 |
| Gas viscosity | μ g | 1.8 × 10−5 Pa s |
| Inlet gas vel. | U/Umf | 0–1.4 |
| Outlet gas pressure | P | 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 Pa 325 Pa |
| Drag law model | — | Gidaspow |
| Solid | ||
| Number of particles | N p | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599 599![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 353 353 |
| Particle diameter | d p | 400–600 μm |
| Particle density | ρ p | 2500 kg m−3 |
| Particle contact model | — | Hertzian |
| Friction coefficient | μ p | 0.35 |
| Young's modulus | Y | 1 × 106 Pa |
| Poisson's ratio | ν | 0.35 |
| Coeff. of restitution | e p−p | 0.90 |
| Active matter std. dev. | σ | 0–1 × 10−4 n |
Two primary methods have been proposed to model vertical vibration in numerical simulations for vibrated gas-fluidized beds: (i) oscillating the y-component of gravity20,26 and (ii) using a virtual distributor of particles which physically moves up and down whilst also physically moving the walls of the domain.35 In reality, the particles experience a vibration force due to friction with the walls acting orthogonal to the axis of vibration and a vibration force which acts normal due to contact with the base of the fluidized bed (often the distributor). To mimic realistic vibration propagation through the bed, we employ the most-accurate vibration method from the current literature35 where we physically displace an stl file which spans the base of the fluidized bed as per,
ystl = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(2πft). sin(2πft). | (12) |
vy = 2πfA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos(2πft). cos(2πft). | (13) |
2.3 Non-dimensional parameters & data processing
Several non-dimensional parameters are used later which we now discuss. Firstly, we commonly report the ratio of non-dimensional vibration strength relative to gravity as per | (14) |
 | (15) |
 | (16) |
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≤ 3.1) is large compared to many real biological samples (e.g.
A ≤ 3.1) is large compared to many real biological samples (e.g. ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≈ 0.4 for black soldier fly larvae14).
A ≈ 0.4 for black soldier fly larvae14).
To quantify the structuring of the bubbling we use Pearson's correlation coefficient,44 which has been shown to be an indicative measure of structured bubbling repetition.26 The correlation coefficient is given as per,
 | (17) |
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) is the mean void fraction throughout the entire domain consisting of particles of interest (i.e. not including the vibrating distributor or the freeboard region above the particle bed), and ε and ε′ are for time t and t + 4π, respectively, as previous work has shown that structured bubbling repeats every 2 vibration cycles.26 It should be noted that χ = 1 for perfectly repeated structured bubbling, and χ = 0 for no repetition whatsoever. For clarity, in this work we only consider a single vibration frequency of f = 5 Hz, and so the difference between t and t + 4π is always Δt = 0.4 s.
is the mean void fraction throughout the entire domain consisting of particles of interest (i.e. not including the vibrating distributor or the freeboard region above the particle bed), and ε and ε′ are for time t and t + 4π, respectively, as previous work has shown that structured bubbling repeats every 2 vibration cycles.26 It should be noted that χ = 1 for perfectly repeated structured bubbling, and χ = 0 for no repetition whatsoever. For clarity, in this work we only consider a single vibration frequency of f = 5 Hz, and so the difference between t and t + 4π is always Δt = 0.4 s.
We also quantify the effective bubble diameter by
 | (18) |
 | (19) |
To quantify particle mixing we use the Lacey mixing index45 which is given by
 | (20) |
 | (21) |
| S0 = ϕm(1 − ϕm), | (22) |
 | (23) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2〉, which is defined as the Euclidean distance for the same particle centroid, relative to its initial starting position, and is given as
2〉, which is defined as the Euclidean distance for the same particle centroid, relative to its initial starting position, and is given as | (24) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) has coordinates in x, y, and z.
has coordinates in x, y, and z.
3 Results
3.1 Bubbling dynamics
We first consider the bubbling dynamics in the system for a non-dimensional active matter force ranging from![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 0 to
A = 0 to ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 3.1. Fig. 3 shows a time-series of the void fraction for a slice through the central z-plane of the particle bed over two vibration cycles (φ = 4π) or the equivalent time for the non-vibrated case (i.e. Δt = 0.4 s) with varying magnitude non-dimensional active matter force. The time period of Δt = 0.4 s ≡ Δφ = 4π is chosen to highlight the repetitive structured nature of the bubbles for the vibrated cases. It should be noted that we omit the virtual distributor from these (and subsequent) images. When there is no active matter force present and the system is not vibrated, the bubbles rise with no clear repetition in position or homogeneity in size which is well-understood to be a key characteristic of the mathematically chaotic bubbling dynamics typically observed in bubbling gas-fluidized beds.46,47 Comparatively, when the system is vertically vibrated at these conditions a periodic lattice (with period 4π) of bubbles are formed at specific points with an additional row of bubbles forming at the antinodes between bubble centroids at φ = 2π. These structured bubble patterns have been shown to exist for a range of frequencies and amplitudes, where the degree of structuring is highly dependent on f and A. Here we specifically pick operating conditions which produce coincide with a high degree of structuring.
A = 3.1. Fig. 3 shows a time-series of the void fraction for a slice through the central z-plane of the particle bed over two vibration cycles (φ = 4π) or the equivalent time for the non-vibrated case (i.e. Δt = 0.4 s) with varying magnitude non-dimensional active matter force. The time period of Δt = 0.4 s ≡ Δφ = 4π is chosen to highlight the repetitive structured nature of the bubbles for the vibrated cases. It should be noted that we omit the virtual distributor from these (and subsequent) images. When there is no active matter force present and the system is not vibrated, the bubbles rise with no clear repetition in position or homogeneity in size which is well-understood to be a key characteristic of the mathematically chaotic bubbling dynamics typically observed in bubbling gas-fluidized beds.46,47 Comparatively, when the system is vertically vibrated at these conditions a periodic lattice (with period 4π) of bubbles are formed at specific points with an additional row of bubbles forming at the antinodes between bubble centroids at φ = 2π. These structured bubble patterns have been shown to exist for a range of frequencies and amplitudes, where the degree of structuring is highly dependent on f and A. Here we specifically pick operating conditions which produce coincide with a high degree of structuring.
As the active matter force increases, the bubble shape begins to deform. Instead of symmetrical ellipsoidal bubbles, the bubbles take the shape of wider horizontal bands with lower overall void fraction. For non-vibrated fluidized beds, the bubbles are formed by gas channeling into small voids, which in turn increases the size of these void regions, and the drag force on particles maintains the semi-circular bubble roof. Here, we reason that the formation of these horizontal bands is due to the particles in the roof of the bubble pushing away from each other due to the active force, elongating the bubble horizontally. This all suggests that the addition of an active matter force inhibits structured bubbling when ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≫ 1, and has negligible effect on bubble structuring when
A ≫ 1, and has negligible effect on bubble structuring when ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≤ 0.3, indicating an intermediate
A ≤ 0.3, indicating an intermediate ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A type regime between these bounds for which the bubbles are structured but bubble size is dependent on active matter force adding an additional mechanism to control structured bubbling.
A type regime between these bounds for which the bubbles are structured but bubble size is dependent on active matter force adding an additional mechanism to control structured bubbling.
To more quantitatively compare the structured and non-structured cases, we now investigate the effect of varying the active matter force on key bubble characteristics. Fig. 4 shows the effect of varying active matter on effective bubble diameter, Deff, correlation coefficient, χ, and bubble aspect ratio, AR. As the active matter force increases, the effective bubble diameter generally tends towards getting smaller for both the non-vibrated and vibrated cases, as the bubbles become wider (i.e. increasing Ar), where eventually at high ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A no bubbles exist, and long horizontal voids propagate through the system. We attribute this general decrease in effective bubble diameter to the active force preventing particles from aggregating in certain areas, to form bubbles in others. As such, this is akin to the particles being perfectly evenly spread out and homogeneously fluidized. Surprisingly, there is a slight increase in effective bubble diameter for small
A no bubbles exist, and long horizontal voids propagate through the system. We attribute this general decrease in effective bubble diameter to the active force preventing particles from aggregating in certain areas, to form bubbles in others. As such, this is akin to the particles being perfectly evenly spread out and homogeneously fluidized. Surprisingly, there is a slight increase in effective bubble diameter for small ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A in both non-vibrated and vibrated cases, which we hypothesize is due to the active matter force not being large enough to suppress bubbling, but large enough that particles will actively move outwards of bubbles increasing the average bubble diameter. The correlation coefficient at
A in both non-vibrated and vibrated cases, which we hypothesize is due to the active matter force not being large enough to suppress bubbling, but large enough that particles will actively move outwards of bubbles increasing the average bubble diameter. The correlation coefficient at ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 0.3 is similar to the non-active (
A = 0.3 is similar to the non-active (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 0) cases for both the vibrated and non-vibrated systems. When the active matter force is near parity with gravity (i.e.
A = 0) cases for both the vibrated and non-vibrated systems. When the active matter force is near parity with gravity (i.e. ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 0.6, 0.9), bubbles can still exist in the system but the structuring is significantly reduced and so a lower correlation coefficient is observed for the vibrated case. Finally, when the active matter force exceeds gravity, (
A = 0.6, 0.9), bubbles can still exist in the system but the structuring is significantly reduced and so a lower correlation coefficient is observed for the vibrated case. Finally, when the active matter force exceeds gravity, (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A > 1), bubbles are seldom formed, due to a reduction in locally solid regions, which in-turn makes the system highly structured.
A > 1), bubbles are seldom formed, due to a reduction in locally solid regions, which in-turn makes the system highly structured.
We postulate that the bubbling dynamics in active granular systems is highly dependent on the ratio of active matter force to gravity and three primary regimes are identified: low ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A (
A (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A < 0.5) where bubbling is negligibly affected by the active matter force and repetitive structuring can still exist, intermediate
A < 0.5) where bubbling is negligibly affected by the active matter force and repetitive structuring can still exist, intermediate ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A (0.5 <
A (0.5 < ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A < 1) where bubbles still form but the active force significantly affects the size and structuring of the bubbles, and finally high
A < 1) where bubbles still form but the active force significantly affects the size and structuring of the bubbles, and finally high ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A (
A (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A > 1) where the bubbles are completely suppressed due a higher average void fraction in the bed and no locally solid regions, but bed structuring is highly repetitive.
A > 1) where the bubbles are completely suppressed due a higher average void fraction in the bed and no locally solid regions, but bed structuring is highly repetitive.
We now attempt to explain why structured bubbling is not observed for the highly active cases (e.g. ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≥ 1.2). Fig. 5 shows the non-dimensionalized particle contact force,
A ≥ 1.2). Fig. 5 shows the non-dimensionalized particle contact force, ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) C on particles over a period of two vibration cycles, φ = 4π. During structured bubbling, a densely packed solid-like region is formed beneath bubbles due to particle convection patterns packing particles close together. This close packing causes high particle contact forces, which can be described in a continuum manner as a high particle pressure. Gas flow avoids these higher packing regions, as they provide more resistance to flow (Darcy's Law) and thus the gas flows into the spaces between them creating a new row of bubbles and forming the distinct triangular lattice pattern associated with structured bubbling. When an active matter force is present, the particles are still compacted due to the vibration; however, due to the active matter force, the active particles generate large velocities, contacting more non-active particles, and thus repel each other and prevent the dense packing of particles needed to form these solid-like regions (Fig. 5b and c). Without discrepancies in packing fraction below bubbles, there is nothing to drive a new bubble away from forming directly below the previous row of bubbles and thus structured bubbling no longer forms. When the active matter force is sufficiently high (
C on particles over a period of two vibration cycles, φ = 4π. During structured bubbling, a densely packed solid-like region is formed beneath bubbles due to particle convection patterns packing particles close together. This close packing causes high particle contact forces, which can be described in a continuum manner as a high particle pressure. Gas flow avoids these higher packing regions, as they provide more resistance to flow (Darcy's Law) and thus the gas flows into the spaces between them creating a new row of bubbles and forming the distinct triangular lattice pattern associated with structured bubbling. When an active matter force is present, the particles are still compacted due to the vibration; however, due to the active matter force, the active particles generate large velocities, contacting more non-active particles, and thus repel each other and prevent the dense packing of particles needed to form these solid-like regions (Fig. 5b and c). Without discrepancies in packing fraction below bubbles, there is nothing to drive a new bubble away from forming directly below the previous row of bubbles and thus structured bubbling no longer forms. When the active matter force is sufficiently high (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 3.1), the particle packing fraction is entirely horizontally homogeneous and the gas flow is homogeneously distributed. A now flat void forms every vibration cycle as the downward motion of the distributor plate creates a void pocket which is then sustained by upward gas flow.
A = 3.1), the particle packing fraction is entirely horizontally homogeneous and the gas flow is homogeneously distributed. A now flat void forms every vibration cycle as the downward motion of the distributor plate creates a void pocket which is then sustained by upward gas flow.
3.2 Mean squared displacement
To understand the effect of this bubble suppression for highly active granular fluidized systems, we now analyze the mean squared displacement. For non-fluidized active systems, the mean squared displacement (MSD) is proportional to the square of time when the particle motion is ballistic (i.e. 〈![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2〉 ∼ t2) but is proportional with time when particle motion is diffusive (i.e. 〈
2〉 ∼ t2) but is proportional with time when particle motion is diffusive (i.e. 〈![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2〉 ∼ t). However, for an advection dominated system MSD is proportional to ∼t2. Fig. 6 shows the MSD for varying active matter force for both the non-vibrating and vibrating gas-fluidized systems. The MSD for all non-vibrating cases is proportional to ∼t for short time, suggesting that discrete particle contacts are causing particles to generate an active matter force propelling particles and the system is diffusion dominated. For t > 1 s, the MSD is proportional to ∼t2 as gas percolates through the system conveying the particles. Interestingly, the same trend is not observed for the vibrating cases for which the MSD of all cases is proportional to ∼t. For both the non-vibrated and vibrated systems, the higher
2〉 ∼ t). However, for an advection dominated system MSD is proportional to ∼t2. Fig. 6 shows the MSD for varying active matter force for both the non-vibrating and vibrating gas-fluidized systems. The MSD for all non-vibrating cases is proportional to ∼t for short time, suggesting that discrete particle contacts are causing particles to generate an active matter force propelling particles and the system is diffusion dominated. For t > 1 s, the MSD is proportional to ∼t2 as gas percolates through the system conveying the particles. Interestingly, the same trend is not observed for the vibrating cases for which the MSD of all cases is proportional to ∼t. For both the non-vibrated and vibrated systems, the higher ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A cases have a hump in the MSD over time every 0.2 s, which corresponds to the time taken for a void to move through the bed. Additionally, there appears to be a general trend of the MSD decreasing with increasing
A cases have a hump in the MSD over time every 0.2 s, which corresponds to the time taken for a void to move through the bed. Additionally, there appears to be a general trend of the MSD decreasing with increasing ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A. This observation of an increasing active matter force decreasing the MSD may seem counterintuitive, as the opposite is observed for purely active non-fluidized systems for which advection is negligible, but can be explained by the realization that the bubbling is significantly suppressed for the highly active cases compared to the non-active case, due to the higher localized void fraction. Additionally, we believe that the increase in MSD for the small active matter force systems, relative to the non-active systems, is due to an increase in bubble diameter. Of significant note is that even small changes in
A. This observation of an increasing active matter force decreasing the MSD may seem counterintuitive, as the opposite is observed for purely active non-fluidized systems for which advection is negligible, but can be explained by the realization that the bubbling is significantly suppressed for the highly active cases compared to the non-active case, due to the higher localized void fraction. Additionally, we believe that the increase in MSD for the small active matter force systems, relative to the non-active systems, is due to an increase in bubble diameter. Of significant note is that even small changes in ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A have a significant effect on particle motion, even when it is smaller than gravity (and thus drag force).
A have a significant effect on particle motion, even when it is smaller than gravity (and thus drag force).
We propose that whether the particles are in an advection or diffusion dominated regime is dependent on the magnitude of the three forces governing them, |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) G|, |
G|, |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D|, and |
D|, and |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A|, relative to each other. That is, of course to say, that if
A|, relative to each other. That is, of course to say, that if ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D is the only force acting on the particles, transport must be advective. Likewise if only
D is the only force acting on the particles, transport must be advective. Likewise if only ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) G is acting on the particles, they will of course be stationary (i.e. no transport). Using the data presented in Fig. 6, and additional simulations, we now present in Fig. 7 a ternary diagram of the transition between the sub-diffusive (〈Δr〉 = tα, where α < 1), diffusion (〈Δr2〉 ∼ t), and advection (〈Δr2〉 ∼t2) transport regimes depending on the mean forces acting over all the particles. It should be noted that |
G is acting on the particles, they will of course be stationary (i.e. no transport). Using the data presented in Fig. 6, and additional simulations, we now present in Fig. 7 a ternary diagram of the transition between the sub-diffusive (〈Δr〉 = tα, where α < 1), diffusion (〈Δr2〉 ∼ t), and advection (〈Δr2〉 ∼t2) transport regimes depending on the mean forces acting over all the particles. It should be noted that |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) G|, |
G|, |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D|, and |
D|, and |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A| are normalized by the total mean force acting on the particles in a simulation,
A| are normalized by the total mean force acting on the particles in a simulation, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) T (i.e.
T (i.e. ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) T =
T = ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) G +
G + ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D +
D + ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A) such that they can be plotted on a ternary diagram. When |
A) such that they can be plotted on a ternary diagram. When |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D| < 0.5 and |
D| < 0.5 and |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) G| > 0.5, the particles are sub-diffusive for all |
G| > 0.5, the particles are sub-diffusive for all |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A| as the active matter force is not sufficiently large to overcome gravitational force, and so particle motion is largely limited to the two components of planar motion (i.e. x and z). Conversely, when |
A| as the active matter force is not sufficiently large to overcome gravitational force, and so particle motion is largely limited to the two components of planar motion (i.e. x and z). Conversely, when |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) G| < 0.5, the particle motion is either driven by advection (if |
G| < 0.5, the particle motion is either driven by advection (if |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D| < 0.5) or diffusion (if |
D| < 0.5) or diffusion (if |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D| < 0.5), depending on two things: the ratio of |
D| < 0.5), depending on two things: the ratio of |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D|/|
D|/|![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A|, and the minimum fluidization velocity, Umf. If the system is above Umf, the ratio of |
A|, and the minimum fluidization velocity, Umf. If the system is above Umf, the ratio of |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A|/
A|/![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D must be significantly larger for the system to exist in a diffusive regime (|
D must be significantly larger for the system to exist in a diffusive regime (|![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A|/|
A|/|![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D| ≈ 9). Comparatively, below Umf, the system exhibits diffusive behavior with ratios of |
D| ≈ 9). Comparatively, below Umf, the system exhibits diffusive behavior with ratios of |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A|/
A|/![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D as little as |
D as little as |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A|/
A|/![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D ≈ 0.2. While we realise that it can be challenging to know
D ≈ 0.2. While we realise that it can be challenging to know ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D a priori, we reason that that this ternary diagram is still quite useful as
D a priori, we reason that that this ternary diagram is still quite useful as ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) G is trivial to solve and |
G is trivial to solve and |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) A| is often known, and thus for an approximated range of
A| is often known, and thus for an approximated range of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) D, the particle transport scaling can be known a priori.
D, the particle transport scaling can be known a priori.
3.3 Mixing dynamics
It's well understood that for traditional fluidized beds, a decrease in bubble diameter corresponds to decreased mixing rates.48 Additionally, while the results presented previously on MSD over time (Fig. 6) suggest how varying the active matter force will affect how much the particles mix, it is still not clear how this mixing will proceed. As such, we now investigate the mixing dynamics by coloring the particles based on their initial starting position. Firstly, we consider the vertical mixing in the system by equal partitioning the particles in the y-axis. Fig. 8 shows a time series of the vertical mixing in the bed for both the non-vibrated and vibrated systems. Over time, all the cases show some degree of mixing, but the degree of mixing varies significantly. Generally, as the active matter force increases, there appears to be less vertical mixing. However, it is challenging to say conclusively from qualitative comparison alone, as both![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 0 and low
A = 0 and low ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≤ 0.6 cases appear sufficiently mixed. Additionally, it appears that the lowest vibration cases are becoming mixed more quickly, whilst the highest vibration cases are becoming mixed more slowly, compared to their non-vibrated counterpart.
A ≤ 0.6 cases appear sufficiently mixed. Additionally, it appears that the lowest vibration cases are becoming mixed more quickly, whilst the highest vibration cases are becoming mixed more slowly, compared to their non-vibrated counterpart.
 | ||
| Fig. 8 Time series of the vertical mixing over 8 s for varying active matter cases for (a) a non-vibrated gas-fluidized bed and (b) a vertically vibrated gas-fluidized bed. | ||
It also appears that the method of mixing is vastly different as the active matter force increases. For low active matter force cases, the particles mix vertically due to bubble wake transport drawing particles upwards and consequently pulling particles to the sides of bubbles downwards. As such, fingering-type mixing patterns are formed as can be seen for the ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 0 cases in Fig. 8(a)
A = 0 cases in Fig. 8(a)![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 0 at t = 1 s and t = 2 s or (b)
A = 0 at t = 1 s and t = 2 s or (b) ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 0 at t = 1 s. However, for more active cases (i.e.
A = 0 at t = 1 s. However, for more active cases (i.e. ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 1.2) the particle mixing forms symmetric roll patterns, regardless of if the bed is vibrated or not. These symmetric roll patterns are well-documented in vibrated granular materials49 and have been attributed to granular convection, but the authors are unaware of any work on convective rolls for non-vibrated active granular matter. While these active granular convective rolls are interesting, we make no attempt to explain their origin and instead suggest that they require further mechanistic study to be better understood. For the
A = 1.2) the particle mixing forms symmetric roll patterns, regardless of if the bed is vibrated or not. These symmetric roll patterns are well-documented in vibrated granular materials49 and have been attributed to granular convection, but the authors are unaware of any work on convective rolls for non-vibrated active granular matter. While these active granular convective rolls are interesting, we make no attempt to explain their origin and instead suggest that they require further mechanistic study to be better understood. For the ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 3.1 cases, the convective rolls are not as clear. Instead, the particles are transported by the voids pushing particles above them upwards until the void passes through the particles, at which point the particles then fall vertically through the void. During this void rising, particles contact and generate active forces, which has the effect of causing the particles to slowly diffuse into each other.
A = 3.1 cases, the convective rolls are not as clear. Instead, the particles are transported by the voids pushing particles above them upwards until the void passes through the particles, at which point the particles then fall vertically through the void. During this void rising, particles contact and generate active forces, which has the effect of causing the particles to slowly diffuse into each other.
In complement to investigating the vertical mixing, we also consider the horizontal mixing. Fig. 9 shows a time series of the horizontal mixing over time for varying active matter cases for both the non-vibrated and vibrated gas-fluidized bed. There is less mixing in the horizontal direction, compared to the vertical direction, owing to the minimal gas velocity (and thus advection) in the x-direction. The presence of a small amount of active force (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A = 0.6) appears to significantly improve mixing for both the non-vibrated and vibrated cases, which we attribute to a slightly decrease in structuring and increase in bubble diameter. For an advection dominated system, the horizontal mixing of particles requires the particles to be conveyed orthogonally to the primary direction of the gas flow, which is best achieved for larger, more structured, bubbles. However, for systems with a higher active matter force (
A = 0.6) appears to significantly improve mixing for both the non-vibrated and vibrated cases, which we attribute to a slightly decrease in structuring and increase in bubble diameter. For an advection dominated system, the horizontal mixing of particles requires the particles to be conveyed orthogonally to the primary direction of the gas flow, which is best achieved for larger, more structured, bubbles. However, for systems with a higher active matter force (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≥ 1.2) we observe that the vertical vibration worsens the mixing as the gas flow propagates through the bed as horizontally homogeneous voids, rather than bubbles, and thus there is no forcing of the particles horizontally.
A ≥ 1.2) we observe that the vertical vibration worsens the mixing as the gas flow propagates through the bed as horizontally homogeneous voids, rather than bubbles, and thus there is no forcing of the particles horizontally.
 | ||
| Fig. 9 Time series of the horizontal mixing over 8 s for varying active matter cases for (a) non-vibrated gas-fluidized bed and (b) a vertically vibrated gas-fluidized bed. | ||
We now use the Lacey mixing index, Mr, to quantify the mixing within the cases. Fig. 10 shows the Lacey mixing index in the horizontal (Mx) and vertical (My) direction over time for the varying active matter force cases with and without vertical vibration. When a small active matter force is present (Fig. 10a–c and i–k), ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≤ 0.6, the vertically vibrated systems mix significantly quicker than the non-vibrated systems in both the vertical and horizontal directions. When the active matter force is near parity with gravity (0.9 ≤
A ≤ 0.6, the vertically vibrated systems mix significantly quicker than the non-vibrated systems in both the vertical and horizontal directions. When the active matter force is near parity with gravity (0.9 ≤ ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≤ 1.2), the vibrated and non-vibrated cases have a similar mixing index over time indicating that the cases mix at similar rates. However, when the active matter force is large relative to gravity (
A ≤ 1.2), the vibrated and non-vibrated cases have a similar mixing index over time indicating that the cases mix at similar rates. However, when the active matter force is large relative to gravity (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≥ 1.8), the gradient of the mixing index over time in both the vertical and horizontal directions is decreased for the vibrated cases, compared to the non-vibrated cases. Furthermore, the system is becoming more mixed (both vertically and horizontally) at t = 8 s as the active matter force increases further.
A ≥ 1.8), the gradient of the mixing index over time in both the vertical and horizontal directions is decreased for the vibrated cases, compared to the non-vibrated cases. Furthermore, the system is becoming more mixed (both vertically and horizontally) at t = 8 s as the active matter force increases further.
These few examples of mixing for non-vibrated and vibrated active systems make several things clear: circular bubbles mix particles well because they lift particles up continuously in their wake and push particles to their sides horizontally. Larger bubbles lead to more mixing and thus vibration, which produces larger bubbles, leads to more mixing than unstructured bubbling with no vibration and no active matter force. For an active matter force of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≤ 0.6, the active matter force increases bubble size, subsequently increasing mixing. If
A ≤ 0.6, the active matter force increases bubble size, subsequently increasing mixing. If ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A > 0.6, particles can no longer pack together closely above and below bubbles, as needed for circular bubbles to form, and long horizontal voids are formed instead. These horizontal voids simply lift particles up before shortly dropping them down in nearly the same place, and thus the mixing decreases significantly. When the system is vibrated, the uniform particle motion across the entire horizontal cross-section of the bed causes flat voids spanning the entire width of the bed to form, and thus mixing becomes even worse at high
A > 0.6, particles can no longer pack together closely above and below bubbles, as needed for circular bubbles to form, and long horizontal voids are formed instead. These horizontal voids simply lift particles up before shortly dropping them down in nearly the same place, and thus the mixing decreases significantly. When the system is vibrated, the uniform particle motion across the entire horizontal cross-section of the bed causes flat voids spanning the entire width of the bed to form, and thus mixing becomes even worse at high ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A for the vibrated case compared to the non-vibrated case. It should be noted that even though the timescale for mixing is small here (Δt = 8 s), this change in time is long for self-mixing among like particles and is also long compared to many other timescales in the system such as bubble rise time or finite correlation time. As such, we do not expect that simulations run for significantly longer times would yield vastly different results, but note that this is likely untrue for binary active granular materials.
A for the vibrated case compared to the non-vibrated case. It should be noted that even though the timescale for mixing is small here (Δt = 8 s), this change in time is long for self-mixing among like particles and is also long compared to many other timescales in the system such as bubble rise time or finite correlation time. As such, we do not expect that simulations run for significantly longer times would yield vastly different results, but note that this is likely untrue for binary active granular materials.
4 Conclusions
In this work we have investigated the bubbling and mixing of vibrated and non-vibrated gas-fluidized active granular materials through numerical CFD-DEM simulations. Simulations reveal that the if the active matter force is small relative to gravity (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≤ 0.6), the bubble diameter generally increases compared to non-active systems and vertical vibration aids both horizontal and vertical mixing. Comparatively, when the active matter force is much larger than gravity (
A ≤ 0.6), the bubble diameter generally increases compared to non-active systems and vertical vibration aids both horizontal and vertical mixing. Comparatively, when the active matter force is much larger than gravity (![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) A ≥ 1.8), active forces reduce locally solid regions in the bed, which suppresses bubbling and vertical vibration hinders vertical and horizontal mixing in the bed. These findings suggest that vertical vibration of active matter, as a means to enhance mixing efficiency, should only be implemented if the active matter force is small compared to gravity. One key limitation of this work is how it translates when the particles are small such that interparticle (van der Waals) forces are significant, e.g. Geldart group C particles. We believe this warrants further mechanistic study, but may be challenging using a CFD-DEM approach.
A ≥ 1.8), active forces reduce locally solid regions in the bed, which suppresses bubbling and vertical vibration hinders vertical and horizontal mixing in the bed. These findings suggest that vertical vibration of active matter, as a means to enhance mixing efficiency, should only be implemented if the active matter force is small compared to gravity. One key limitation of this work is how it translates when the particles are small such that interparticle (van der Waals) forces are significant, e.g. Geldart group C particles. We believe this warrants further mechanistic study, but may be challenging using a CFD-DEM approach.
This study naturally leads to other new questions which we believe are worthy of follow studies such as:
• What is the effect of other forces which may inhibit structured bubbling? e.g. liquid bridge cohesion or triboelectric charging. What is the effect of particle shape and deformability?
• Does this work hold for structured bubbling formed using pulsed gas rather than vertical vibration?
• Is the behavior of gas-fluidized active granular materials also dependent on confining geometry, as many traditional active materials are?
• How do gas-fluidized active granular materials behave with significant size distribution differences?
• What is the effect of horizontal vibration on gas-fluidized active granular materials.
Finally, we make no effort in this work to attempt to describe the varying states of transport which can exist for gas-fluidized active material using a continuum approach, as is commonly done for many works on active materials, but this is of course necessary for simulating many real-world processes for which the particles may number in the tens of millions and as such cannot be modeled using a discrete approach due to computational limitations.
Author contributions
O. J. P., M. W. J., and A. S. M. conducted and analyzed the simulations. O. J. P. and Q. G. designed the numerical model. All authors contributed to the writing of the manuscript.Data availability
Raw data and numerical model implementation in MFiX for this study can be found at the repository https://github.com/ojp2117/ActiveMatterCFDDEM/tree/main.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
This work was funded by the Office of Naval Research (ONR) Grant No. N00014-23-1-2041 and National Science Foundation Grants No. 2144763 and 2150296, and Sloan Foundation Grant G-2021-17054.References
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- G. M. Viswanathan, M. G. Da Luz, E. P. Raposo and H. E. Stanley, The physics of foraging: an introduction to random searches and biological encounters, Cambridge University Press, 2011 Search PubMed.
- D. Weihs, Nature, 1973, 241, 290–291 CrossRef.
- B. Saintyves, M. Spenko and H. M. Jaeger, Sci. Rob., 2024, 9, eadh4130 CrossRef PubMed.
- D. I. Goldman and D. Zeb Rocklin, Sci. Rob., 2024, 9, eadn6035 CrossRef PubMed.
- A. T. Liu, M. Hempel, J. F. Yang, A. M. Brooks, A. Pervan, V. B. Koman, G. Zhang, D. Kozawa, S. Yang and D. I. Goldman, et al. , Nat. Mater., 2023, 22, 1453–1462 CrossRef CAS PubMed.
- G. Bonacucina, M. Cespi, M. Misici-Falzi and G. F. Palmieri, J. Pharm. Sci., 2009, 98, 1–42 CrossRef CAS PubMed.
- Z. Ye and B. Wang, Recent Progress in Medical Miniature Robots, Elsevier, 2025, pp. 265–286 Search PubMed.
- S. C. Van Den Berg, R. B. Scharff, Z. Rusák and J. Wu, HardwareX, 2022, 12, e00320 CrossRef PubMed.
- C. Li, T. Zhang and D. I. Goldman, Science, 2013, 339, 1408–1412 CrossRef CAS PubMed.
- C. Li, A. O. Pullin, D. W. Haldane, H. K. Lam, R. S. Fearing and R. J. Full, Bioinspiration Biomimetics, 2015, 10, 046003 CrossRef PubMed.
- S. Lévay, A. Katona, H. Löwen, R. C. Hidalgo and I. Zuriguel, arXiv, 2024, preprint, arXiv:2412.14419 DOI:10.48550/arXiv.2412.14419.
- Y. Xi, T. Marzin, R. B. Huang, T. J. Jones and P.-T. Brun, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2410654121 CrossRef CAS PubMed.
- H. Ko, G. J. Cassidy, O. Shishkov, E. Aydin, D. L. Hu and D. I. Goldman, Front. Phys., 2021, 9, 734447 CrossRef.
- A. Van Huis and L. Gasco, Science, 2023, 379, 138–139 CrossRef CAS PubMed.
- I. G. Lopes, V. Wiklicky, E. Ermolaev and C. Lalander, Waste Manage., 2023, 172, 25–32 CrossRef PubMed.
- J. F. Davidson and D. L. Keairns, Fluidization: Proceedings of the Second Engineering Foundation Conference, Trinity College, Cambridge, England 2-6 April 1978, CUP Archive, 1978, vol. 2.
- Q. Guo, S. Chiu, W. Da and C. M. Boyce, AIChE J., 2023, 69, e17970 CrossRef CAS.
- J. Omidi, O. J. Punch, Q. Guo and C. M. Boyce, Powder Technol., 2024, 438, 119648 CrossRef CAS.
- C. P. McLaren, T. M. Kovar, A. Penn, C. R. Müller and C. M. Boyce, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9263–9268 CrossRef CAS PubMed.
- Q. Guo, Y. Zhang, T. M. Kovar, K. Xi and C. M. Boyce, Soft Matter, 2022, 18, 3323–3327 RSC.
- Q. Guo, W. Da, R. Wu, Y. Zhang, J. Wei and C. M. Boyce, Phys. Rev. E, 2023, 107, 034603 CrossRef CAS PubMed.
- O. J. Punch, Q. Guo, M. Gueye, J. Omidi, M. W. Jordan, J. M. Sanghishetty and C. M. Boyce, Phys. Rev. E, 2025, 111, L013403 CrossRef CAS PubMed.
- O. J. Punch, B. N. Cabrera, C. Spitler and C. M. Boyce, Chem. Eng. J., 2024, 495, 153459 CrossRef CAS.
- O. J. Punch, C. Spitler, B. N. Cabrera, M. W. Jordan, A. Khan and C. M. Boyce, Ind. Eng. Chem. Res., 2025, 64, 2433–2445 CrossRef CAS.
- Q. Guo, Y. Zhang, A. Padash, K. Xi, T. M. Kovar and C. M. Boyce, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2108647118 CrossRef CAS PubMed.
- J. M. Sanghishetty, N. M. Russ, C. Spitler, Q. Guo, D. Nagaraj, R. S. Farinato and C. M. Boyce, Soft Matter, 2024, 20, 5221–5236 RSC.
- V. Francia, K. Wu and M.-O. Coppens, Chem. Eng. Process., 2021, 159, 108143 CrossRef CAS.
- V. Francia, K. Wu and M.-O. Coppens, Chem. Eng. Sci., 2022, 248, 117189 CrossRef CAS.
- M.-O. Coppens and J. R. van Ommen, Chem. Eng. J., 2003, 96, 117–124 CrossRef CAS.
- C. Kloss, C. Goniva, A. Hager, S. Amberger and S. Pirker, Prog. Comput. Fluid Dyn., Int. J., 2012, 12, 140–152 CrossRef.
- M. A. El-Emam, L. Zhou, W. Shi, C. Han, L. Bai and R. Agarwal, Arch. Comput. Methods Eng., 2021, 1–42 Search PubMed.
- C. Loha, H. Chattopadhyay and P. K. Chatterjee, Chem. Eng. Sci., 2012, 75, 400–407 CrossRef CAS.
- R. Moreno-Atanasio, B. Xu and M. Ghadiri, Chem. Eng. Sci., 2007, 62, 184–194 CrossRef CAS.
- Q. Guo, J. Tian, R. Huang and C. M. Boyce, Chem. Eng. Sci., 2024, 298, 120445 CrossRef CAS.
- L. L. Bonilla, Phys. Rev. E, 2019, 100, 022601 CrossRef CAS PubMed.
- M. Syamlal, W. Rogers and T. J. O’Brien, MFIX Documentation Theory Guide, 1993 Search PubMed.
- A. R. Sprenger, C. Scholz, A. Ldov, R. Wittkowski and H. Löwen, Commun. Phys., 2023, 6, 301 CrossRef.
- S. R. Schwartz, D. C. Richardson and P. Michel, Granular Matter, 2012, 14, 363–380 CrossRef.
- L. A. Vandewalle, V. Francia, K. M. Van Geem, G. B. Marin and M.-O. Coppens, Chem. Eng. J., 2022, 430, 133063 CrossRef CAS.
- J. Ding and D. Gidaspow, AIChE J., 1990, 36, 523–538 CrossRef CAS.
- S. Ergun, Chem. Eng. Prog., 1952, 48, 89 CAS.
- C. Y. Wen, Fluid Particle Technology, Chem. Eng. Progress. Symposium Series, 1966, pp. 100–111 Search PubMed.
- K. Pearson, Philos. Trans. R. Soc., A, 1896, 253–318 Search PubMed.
- P. Lacey, Chem. Eng. Res. Des., 1997, 75, S49–S55 CrossRef.
- C. M. Van den Bleek and J. C. Schouten, Chem. Eng. J., 1993, 53, 75–87 CAS.
- C. S. Daw, W. F. Lawkins, D. J. Downing and N. E. Clapp Jr, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 1179 CrossRef PubMed.
- S. Cooper and C. J. Coronella, Powder Technol., 2005, 151, 27–36 CrossRef CAS.
- E. Ehrichs, H. Jaeger, G. S. Karczmar, J. B. Knight, V. Y. Kuperman and S. R. Nagel, Science, 1995, 267, 1632–1634 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |








