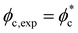Open Access Article
Open Access ArticleField-driven reversible networks from colloidal rods†
José
Fojo
 ab,
Rodolfo
Subert
c,
Laura
Rodríguez-Arco
bd,
Modesto T.
López-López
ab,
Rodolfo
Subert
c,
Laura
Rodríguez-Arco
bd,
Modesto T.
López-López
 bd,
Marjolein
Dijkstra
*c,
Carla
Fernández-Rico
*e and
Laura
Alvarez
bd,
Marjolein
Dijkstra
*c,
Carla
Fernández-Rico
*e and
Laura
Alvarez
 *a
*a
aCNRS, Univ. Bordeaux, CRPP, UMR5031, 33600 Pessac, France. E-mail: laura.alvarez-frances@u-bordeaux.fr
bUniversidad de Granada, Departamento de Física Aplicada, Campus de Fuentenueva, E-18071 Granada, Spain
cSoft Condensed Matter & Biophysics, Debye Institute for Nanomaterials Science, Utrecht University, The Netherlands. E-mail: m.dijkstra@uu.nl
dInstituto de Investigación Biosanitaria Ibs.GRANADA, E-18014 Granada, Spain
eDepartment of Materials, ETH Zürich, 8093 Zurich, Switzerland. E-mail: carla.fernandezrico@mat.ethz.ch
First published on 30th April 2025
Abstract
Highly interconnected percolated networks are interesting structures for materials with enhanced transport and mechanical properties. While percolated networks of anisotropic particles have been explored at the nanoscale, achieving highly interconnected structures at the microscale remains challenging. In this work, we explore the controlled assembly of rod-like polymer colloids under external fields leading to reversible quasi-2D networks. By varying voltage and frequency, we modulate the pore size and thickness of the network. We find that field-driven attractive interactions enable percolation at lower area fractions than predicted for non-interacting rods. Monte Carlo simulations incorporating dipolar interactions and electrostatic boundary conditions confirm the field-induced transition from isotropic to aligned rod configurations, supporting the emergence of percolated networks. This work presents a simple and robust approach for assembling reconfigurable colloidal networks with controlled connectivity, offering new strategies for designing adaptive soft materials.
1 Introduction
Colloidal self-assembly provides a powerful route for the bottom-up construction of intricate microstructures, mimicking nature's ability to create complex structures from simple building blocks.1,2 The ability to precisely tune the interactions, shape, and size of colloidal particles enables the rational design of materials with tailored structures, including superlattices,3,4 colloidal crystals5 and percolated networks.6,7 Percolated networks are particularly interesting, as their interconnected structures provide continuous pathways for efficient (electrical or thermal) transport and mechanical contacts for improved mechanical properties.8–10Percolated or interconnected structures have been extensively studied in nano- and microscopic systems. Colloidal gels formed in dense suspensions of spherical particles exhibit kinetic percolation where short-range attractive interactions mediate particle aggregation, resulting in fractal-like structures and arrested phase separation.11–16 The strength of particle interaction in colloidal gels can significantly reduce the critical percolation threshold17 – concentration at which an interconnected path appears – as supported by theoretical predictions.18,19
While percolation in isotropic spherical colloids mainly depends on the strength of the interactions, percolation in anisotropic systems also accounts for geometrical factors.20–22 For instance, in systems of carbon nanotubes (CNTs) interacting via excluded volume interactions, percolation depends on the concentration and aspect ratio of the nanotubes.23–25 Moreover, similar to their spherical counterparts, the percolation threshold in these systems decreases in the presence of depletion-induced weak interactions,26–29 but also when the rod polydispersity increases, as supported by theoretical studies.20,23–25
External fields provide an alternative approach to induce percolation in colloidal systems.30 Electric and magnetic fields enable reversible modulation of interparticle interactions and facilitate the directed assembly of complex structures. While interconnected networks have been observed in systems of colloidal spheres actuated by electric fields,31,32 the network formation of anisotropic particles—such as dielectric rods, dumbbells,33–37 ellipsoids, or Janus rods38–42—under electric field actuation remains largely unexplored. Since electric fields enable in situ control over particle interactions, they provide a unique route to modulate network connectivity and reversibility, which is essential for designing materials with tunable mechanical and transport properties.
In this work, we explore the directed self-assembly of colloidal rods using AC electric fields to achieve percolated networks. We demonstrate that by tuning the frequency and amplitude of the applied field, we can control the balance between electrohydrodynamic forces and dipolar interactions, resulting in tunable quasi-two-dimensional networks, as supported by Monte Carlo simulations. Our system reveals reversible transitions between disordered planar phases and continuum networks, providing new insights into designing porous materials with controllable network properties, for smart materials’ design.43,44
2 Materials and methods
2.1 Polymeric SU8-rods suspension synthesis
We use a previously described method to synthesize the fluorescent colloidal SU-8 polymer rods.45 In a typical synthesis, a 250 ml beaker with an inner diameter of 5 cm was filled with 110 ml of glycerol. A mixer (Heidolph RZR 2021) equipped with a high-shear impeller with a diameter of 3.5 cm was then introduced into glycerol. We started the high shear-mixing process by applying 1500 rpm—corresponding to a shear stress of 518 Pa to the glycerol phase, and immediately after, approximately 0.1 g of SU-8 50 viscous photoresist (Michrochem) was dropped from a spatula into the gap between the inner wall of the beaker and the impeller, resulting in a turbid dispersion. To synthesise fluorescent SU-8 rods, the dye was previously mixed with the SU-8 50 epoxy-based photoresist resin at a mass ratio of 10 mg dye (Rhodamine) g−1 SU-8 50. The high-shear mixing of glycerol and the SU-8 50 was continued for 10 min. The resulting non-Brownian SU-8 rod-like particles in glycerol were directly exposed to sonication for 1–3 h to break them into smaller colloidal rods. These colloidal SU-8 rods were subsequently photo-crosslinked by exposing them to UV light with a wavelength of 365 nm for 30 min to yield chemically stable rods that can be dispersed in both aqueous and non-aqueous solvents. To remove the glycerol, the colloidal SU-8 rods were washed by repeated centrifugation and redispersion cycles at 3000 × g for 40 min using water containing 0.2 wt% SDS (Sodium dodecyl sulfate). Any large or irregularly shaped rods were easily removed by sedimentation in water under gravity for an hour. Finally, the resulting colloidal SU-8 rods with length (L) of 6–10 μm and diameter (d) of 0.5–1 μm were kept in water containing 0.2 wt% SDS to prevent aggregation during long-time storage. Previous to the experiments with AC fields, the SU-8 rods suspension was centrifuged and redispersed in MilliQ water three times, with no added salt and conductivity (σm = 5.5 × 10−5 S m−1). In this work, the colloidal suspension is dispersed in MilliQ water with no added salt, where the surface charge of the SU8-rods is around ζ = −30 mV.2.2 Sample cell preparation
To build the experimental cell, we first clean coverslips (0.7 mm thickness and 24 × 36 mm, Menzel Gläser, Germany) by sonicating them for 5 min in ethanol, then 5 min in pure MiliQ water, and drying them with compressed air. Then, we sputter-coated the slides on one side with 3 nm of chromium-Cr and 10 nm of Gold-Au (SAFEMATIC, Switzerland). We functionalize the metal surface with a solution of 10 mg ml−1 Polystyrene-sulfonate (PSS) for 10 min to avoid attractive electrostatic interactions between the substrate and the particles followed by the removal of PSS excess, rinsing with MilliQ water. A droplet (7.4 μl) of the SU8-rods suspension with a concentration of 0.1% w/v in pure MilliQ water is deposited on the bottom conductive coverslip within a 9 mm-circular opening of a 0.12 mm-thick sealing spacer (Grace Bio-Labs SecureSeal, USA), and then closed with a top electrode with the conductive side facing the sample. The top and bottom electrodes are connected to a signal generator (Keysight 33500B Waveform Generator Trueform). Thanks to the thin metal layers coating the coverslips, the electrodes remain transparent, and we perform real-time image acquisition while the AC electric field is applied perpendicularly to the conductive coverslips. We perform the experiments with an average particle area fraction of ≈40%. For this, we tilt the experimental cell overnight with an angle of 10 and wait until the particles accumulate due to gravity. Once the desired area fraction is achieved, we place the sample flat for the following experiments.2.3 AC electric field experiments and analysis
We characterized the SU8-rods assembly behaviour under different voltage conditions by applying a sinusoidal AC field ranging between 1–10 Vpp voltage-per-peak (8333–83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 V m−1) and 1–10 kHz perpendicular to the electrodes. We observe the SU8-rods labelled with Rhodamine with 10×, 20× and 40× objectives and an LED light source (cool LED pE excitation system λ = 550 nm) and an inverted optical microscope (Olympus IX71). Images and videos were taken with a Hamamatsu Orca 4.2 camera, with 100 ms exposure times. For further quantification of the sedimentation of the SU8-rods and their behaviour under AC fields, we use a confocal microscope (Zeiss LSM 980 Airyscan with camera Zeiss Axiocam 705 mono). A z-step of 0.62 μm was used, but due to the mismatch of the refractive index, a correction factor k = nwater/nair was necessary for 3D reconstruction of the confocal stacks. The structural quantification was performed using pre-optimized particle tracking algorithms (Python) and Image J.
333 V m−1) and 1–10 kHz perpendicular to the electrodes. We observe the SU8-rods labelled with Rhodamine with 10×, 20× and 40× objectives and an LED light source (cool LED pE excitation system λ = 550 nm) and an inverted optical microscope (Olympus IX71). Images and videos were taken with a Hamamatsu Orca 4.2 camera, with 100 ms exposure times. For further quantification of the sedimentation of the SU8-rods and their behaviour under AC fields, we use a confocal microscope (Zeiss LSM 980 Airyscan with camera Zeiss Axiocam 705 mono). A z-step of 0.62 μm was used, but due to the mismatch of the refractive index, a correction factor k = nwater/nair was necessary for 3D reconstruction of the confocal stacks. The structural quantification was performed using pre-optimized particle tracking algorithms (Python) and Image J.
2.4 Theoretical framework
When an external electric field is applied to a suspension of polymeric colloidal rods in water, charge redistribution around the particle surfaces induces polarization, resulting in a dipole moment that aligns with the field direction and remains perpendicular to the electrode surfaces. In the quasi-static regime, the characteristic charge relaxation time is given by the Maxwell–Wagner time , where εm, σm are the permittivity and conductivity of the medium and εp, σp are those of the particles. For polymer-based colloidal rods in Milli-Q water, this relaxation time corresponds to a critical frequency fc = 1/2πτMW ≈ 105 Hz. At frequencies f ≪ fc, the system behaves as a suspension of dipolar rods with field-induced dipole moments aligned with the field, as polarization equilibrates almost instantaneously. While this assumption holds for low applied potentials, the dependence of the permittivities and conductivities on the external field strength may introduce nonlinear effects. In particular, electrohydrodynamic (EHD) effects may dominate when the fluid motion driven by electric field interactions exceeds the random thermal motion of colloidal particles as was discussed by Ristenpart et al.,46 and later studied for a variety of colloidal systems by Wung et al.37,47,48 This defines a threshold for the onset of field-induced hydrodynamic interactions. The characteristic velocity associated with EHD flows, arising from electro-osmotic effects, is given by
, where εm, σm are the permittivity and conductivity of the medium and εp, σp are those of the particles. For polymer-based colloidal rods in Milli-Q water, this relaxation time corresponds to a critical frequency fc = 1/2πτMW ≈ 105 Hz. At frequencies f ≪ fc, the system behaves as a suspension of dipolar rods with field-induced dipole moments aligned with the field, as polarization equilibrates almost instantaneously. While this assumption holds for low applied potentials, the dependence of the permittivities and conductivities on the external field strength may introduce nonlinear effects. In particular, electrohydrodynamic (EHD) effects may dominate when the fluid motion driven by electric field interactions exceeds the random thermal motion of colloidal particles as was discussed by Ristenpart et al.,46 and later studied for a variety of colloidal systems by Wung et al.37,47,48 This defines a threshold for the onset of field-induced hydrodynamic interactions. The characteristic velocity associated with EHD flows, arising from electro-osmotic effects, is given by  , where E0 is the applied field strength, η the dynamic viscosity of water, and f the frequency of the applied field. This expression illustrates how EHD flows arise from the interaction between the oscillating field and the induced charge distributions near the colloidal surface, where the inverse dependence on f arises because, at higher frequencies, charge redistribution lags behind the field oscillations, reducing the impact of EHD flows. A competing effect is thermal diffusion, which sets the characteristic velocity for Brownian motion
, where E0 is the applied field strength, η the dynamic viscosity of water, and f the frequency of the applied field. This expression illustrates how EHD flows arise from the interaction between the oscillating field and the induced charge distributions near the colloidal surface, where the inverse dependence on f arises because, at higher frequencies, charge redistribution lags behind the field oscillations, reducing the impact of EHD flows. A competing effect is thermal diffusion, which sets the characteristic velocity for Brownian motion  . For EHD effects to dominate, the electro-osmotic velocity must exceed the characteristic velocity associated with diffusion. This condition leads to a threshold electric field
. For EHD effects to dominate, the electro-osmotic velocity must exceed the characteristic velocity associated with diffusion. This condition leads to a threshold electric field  . This condition indicates that stronger fields are required to drive EHD effects as the frequency increases. Thus, the threshold voltage scales as
. This condition indicates that stronger fields are required to drive EHD effects as the frequency increases. Thus, the threshold voltage scales as 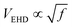 . In our experimental observations with colloids with thickness σ = 1 μm, suspended in water with permittivity εm ≃ 78ε0 and viscosity η ∼ 10−3 Pa s, and electrodes separated by a distance L ∼ 100 μm, confirm that for frequencies in the range 1 kHz < f < 10 kHz, the threshold voltage falls within 8 V < VEHD < 25 V. These results reveal two distinct regimes. In the first regime, EDH effects dominate, characterized by repulsive interactions, as we will show in Section 3.5. In the quasi-static regime, polarization occurs on a lower scale. This analysis can be further refined to clarify the transition between these regimes. In the quasi-static regime, each rod acquires a permanent dipole moment that remains aligned with the electric field, ensuring minimal energy when the rods are oriented parallel to the field. However, the presence of an electrode significantly alters the interaction landscape by introducing mirror dipoles, an essential theoretical construct required to satisfy the boundary conditions of the system. These mirror dipoles induce two key effects: first, an attractive interaction between each rod and its mirror image, drawing the rods toward the electrode, and second, an effective attraction between neighboring rods in a planar configuration due to cross-interactions with their respective mirror charges. Thus, in the absence of gravity, planar configurations are energetically unfavorable due to dipolar interactions, which favor standing rods. However, when gravitational effects are included, sedimentation competes with thermal diffusion, and we can quantify this balance through the Péclet number
. In our experimental observations with colloids with thickness σ = 1 μm, suspended in water with permittivity εm ≃ 78ε0 and viscosity η ∼ 10−3 Pa s, and electrodes separated by a distance L ∼ 100 μm, confirm that for frequencies in the range 1 kHz < f < 10 kHz, the threshold voltage falls within 8 V < VEHD < 25 V. These results reveal two distinct regimes. In the first regime, EDH effects dominate, characterized by repulsive interactions, as we will show in Section 3.5. In the quasi-static regime, polarization occurs on a lower scale. This analysis can be further refined to clarify the transition between these regimes. In the quasi-static regime, each rod acquires a permanent dipole moment that remains aligned with the electric field, ensuring minimal energy when the rods are oriented parallel to the field. However, the presence of an electrode significantly alters the interaction landscape by introducing mirror dipoles, an essential theoretical construct required to satisfy the boundary conditions of the system. These mirror dipoles induce two key effects: first, an attractive interaction between each rod and its mirror image, drawing the rods toward the electrode, and second, an effective attraction between neighboring rods in a planar configuration due to cross-interactions with their respective mirror charges. Thus, in the absence of gravity, planar configurations are energetically unfavorable due to dipolar interactions, which favor standing rods. However, when gravitational effects are included, sedimentation competes with thermal diffusion, and we can quantify this balance through the Péclet number 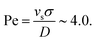 The sedimentation velocity is estimated using Stokes’ law, is
The sedimentation velocity is estimated using Stokes’ law, is  while the diffusion coefficient, obtained from the Stokes–Einstein relation
while the diffusion coefficient, obtained from the Stokes–Einstein relation  , where the mass density difference45 is Δρ = 280 kg m−3. Since Pe > 1, sedimentation is the dominant process, forcing rods into a predominantly planar orientation. In this configuration, the stronger induced dipolar attractions, combined with the polydispersity of the system and the pointed tips of the rods, may play a crucial role in stabilizing the observed percolated network structures. In Section 3.2, we will test this hypothesis by performing Monte Carlo simulations in the zero-frequency limit, systematically comparing the equilibrium structures obtained from initially standing and planar rod configurations to assess the role of sedimentation-driven alignment to the electrode.
, where the mass density difference45 is Δρ = 280 kg m−3. Since Pe > 1, sedimentation is the dominant process, forcing rods into a predominantly planar orientation. In this configuration, the stronger induced dipolar attractions, combined with the polydispersity of the system and the pointed tips of the rods, may play a crucial role in stabilizing the observed percolated network structures. In Section 3.2, we will test this hypothesis by performing Monte Carlo simulations in the zero-frequency limit, systematically comparing the equilibrium structures obtained from initially standing and planar rod configurations to assess the role of sedimentation-driven alignment to the electrode.
3 Results and discussion
3.1 AC field-driven colloidal rods continuum networks
In Fig. 1(a), we show a schematic representation of the experimental system studied in this work. First, we place a diluted suspension of fluorescent SU-8 rods with average length L = 6.2 ± 3 μm, average diameter D = 1.5 ± 0.5 μm, and average aspect ratio L/D = 8 ± 2 of polydispersity of ≈20% (see Fig. 1(b)), into a custom-made electric cell of 120 μm thickness (see Materials and methods). The aspect ratio used in these experiments is distinctively bigger than previous experiments of anisotropic inorganic colloidal particles under electric fields,34,37,40 where typical aspect ratios L/D < 5. Due to the small gravitational length of the particles (Lg = kBT/mg ≈ 44 nm), rods sediment close to the bottom electrode and form a quasi-two-dimensional system (see Supplementary Movie S1, ESI†), where particles can explore all orientations within the plane (see Fig. 1(c)). To increase the particle volume fraction to ≈0.4 (see Fig. 1(c)), we equilibrate the sample at a 10 tilt overnight (see Materials and methods).In the absence of electric fields, the particles show isotropic ordering as expected for low packing of colloidal rods (Fig. 1(c)).45 Remarkably, after applying an AC electric field perpendicular to the bottom electrode at 1 kHz and voltage-per-peak of <4 Vpp, we observe the formation of a porous interconnected and continuous network, extending through the whole field of view of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μm2 (Fig. 1(d) and Supplementary Movie S2, ESI†). The rods are attracted to the bottom electrode due to the interaction with their dipole image, as we will discuss later in detail, with the long axis parallel to it. These networks are formed by strands of locally planar assemblies of aligned rods, with high local ordering yet without exhibiting significant global order on larger scales (Fig. 1(e)). In this configuration, some of the rods lie on top of the 2D layer, depending on their initial state without the field. The presence of the rods close to the bottom electrode distorts the electric field asymmetrically, leading to field gradients along the axes of the rods, especially near the tips. This distortion enhances field intensity due to geometric effects.49,50 The asymmetric field distortion results in the development of induced dipoles on the rods,51 which generates stronger electric fields at the rod tips, driving attractive tip–body and tip–tip interactions. We have additionally performed control experiments using SU8-spheres from the initial synthetic protocol at the same area fraction (Fig. S2, ESI†), where only isolated particle clusters form as previously studied for spheres under AC fields.37,52 Although the process of interconnected network formation could be interpreted as kinetic phase separation driven by out-of-equilibrium dynamics, in Section 3.4 we will argue that the steady-state nature of the network supports a distinct mechanism reliant on field-induced connectivity rather than dynamic clustering or segregation.
000 μm2 (Fig. 1(d) and Supplementary Movie S2, ESI†). The rods are attracted to the bottom electrode due to the interaction with their dipole image, as we will discuss later in detail, with the long axis parallel to it. These networks are formed by strands of locally planar assemblies of aligned rods, with high local ordering yet without exhibiting significant global order on larger scales (Fig. 1(e)). In this configuration, some of the rods lie on top of the 2D layer, depending on their initial state without the field. The presence of the rods close to the bottom electrode distorts the electric field asymmetrically, leading to field gradients along the axes of the rods, especially near the tips. This distortion enhances field intensity due to geometric effects.49,50 The asymmetric field distortion results in the development of induced dipoles on the rods,51 which generates stronger electric fields at the rod tips, driving attractive tip–body and tip–tip interactions. We have additionally performed control experiments using SU8-spheres from the initial synthetic protocol at the same area fraction (Fig. S2, ESI†), where only isolated particle clusters form as previously studied for spheres under AC fields.37,52 Although the process of interconnected network formation could be interpreted as kinetic phase separation driven by out-of-equilibrium dynamics, in Section 3.4 we will argue that the steady-state nature of the network supports a distinct mechanism reliant on field-induced connectivity rather than dynamic clustering or segregation.
3.2 Monte Carlo simulations on network formation of dipolar rods
To gain deeper insight into the self-assembly and network formation of colloidal rods under an applied electric field, we perform Monte Carlo simulations of a model system consisting of 150 polarized rods at a surface coverage of 40%. Each rod has an aspect ratio of L/D = 8 and is modeled as a rigid chain of hard spheres, where each sphere carries its own dipole moment with pair interaction | (1) |
 is the dimensionless interaction strength, where p is the dipole moment induced by the external electric field.
is the dimensionless interaction strength, where p is the dipole moment induced by the external electric field.
The dipoles are consistently oriented perpendicular to the two parallel conducting electrodes as they are induced by the field. To satisfy the electrostatic boundary condition that requires the electric field to be perpendicular to the electrode surfaces, we account for an infinite series of periodic image dipoles within the electrodes.53 This approach, effectively mimicking an extended periodic boundary in the direction normal to the electrodes, allows for treating the long-range dipolar interactions with the standard Ewald summation framework.54 As shown in Fig. 2(a), although mirror images will attract the rods towards one of the two electrodes and two neighboring planar dipoles near an electrode experience a weak attractive interaction due to the interaction with their neighbouring particles mirror images that overcome dipolar repulsion, the ground state is the standing configuration. In Fig. 2(b) and (c), we compare low-field and high-field configurations in the absence of gravity, presenting both side and top views. At low field strengths, the rods behave as an isotropic fluid, experiencing only weak attraction to their mirror images, which keeps them near one of the electrodes. As the field strength increases, the fraction of standing rods gradually increases, indicating a transition toward a more aligned standing state (see Supplementary Section S1, Fig. S7, S8 and Movies S5, S6, ESI† for more details). To bias the rods towards a planar configuration, we introduce a gravitational energy Ug = Pe·h with h the height from the bottom electrode, which allows to tune the sedimentation-diffusion competition effectively matching the experimental Péclet number, Pe = 1.2. As shown in Fig. 2(d), the rod orientation distribution exhibits a clear separation, with the vast majority of rods adopting either a fully planar or fully standing configuration. This realization demonstrates that gravity strongly biases the system toward planar alignment, inducing weak dipolar attractions between planar rods at large applied voltages, highlighting the interplay between electrostatic and gravitational effects in determining the systems structural organization.
3.3 Experimental network characterization with varying AC field conditions
We focus now on exploiting the behaviour of the emergent two-dimensional network regime at varying frequencies and voltages (Fig. 3(a) and (b)). We start quantifying the changes in the network structure by measuring the dependence of the porosity (ϕp) and network thickness (LN) as a function of frequency (1–8 kHz) and voltage amplitudes (2–8 Vpp). Here, porosity (ϕp) represents the fraction of void – pore – area relative to the total area of the image, ranging between 0 and 1. It is defined as the ratio , where AV is the void area and AT is the total area of the image, including the solid and void components. We identified the pore regions and their associated pore area (Ad) using image analysis (Fig. 3(c) and (d)). The thickness of the network (LN) is defined by measuring the lateral distance of the connecting paths over the network. Overall, we observe increased porosity with frequency, which saturates above 4 kHz and becomes sharper at higher voltages. (Fig. 3(e) and Supplementary Movie S3, ESI†). Simultaneously, the thickness LN decreases with increasing frequency (Fig. 3(f)), causing an important change in the network structure as the network skeleton is reduced in diameter. In addition, we observe a complex evolution of the pore area Ap, characterized by the emergence of smaller pores as the network begins to break, alongside the formation of larger pores that expand in size and shape as the network fragments. Consequently, the distribution of Ap becomes broader at higher frequencies (see Fig. S3, ESI†). Most importantly, this measurement is very sensitive to the size of the region of interest, as the pores may extend over larger areas.
, where AV is the void area and AT is the total area of the image, including the solid and void components. We identified the pore regions and their associated pore area (Ad) using image analysis (Fig. 3(c) and (d)). The thickness of the network (LN) is defined by measuring the lateral distance of the connecting paths over the network. Overall, we observe increased porosity with frequency, which saturates above 4 kHz and becomes sharper at higher voltages. (Fig. 3(e) and Supplementary Movie S3, ESI†). Simultaneously, the thickness LN decreases with increasing frequency (Fig. 3(f)), causing an important change in the network structure as the network skeleton is reduced in diameter. In addition, we observe a complex evolution of the pore area Ap, characterized by the emergence of smaller pores as the network begins to break, alongside the formation of larger pores that expand in size and shape as the network fragments. Consequently, the distribution of Ap becomes broader at higher frequencies (see Fig. S3, ESI†). Most importantly, this measurement is very sensitive to the size of the region of interest, as the pores may extend over larger areas.
During our experiments, we observe rods aligning with the applied electric field – standing – as we increase the frequency. We quantify the population of standing rods (rods) thanks to their distinct circular shape and higher fluorescence intensity when they stand up (Fig. 3(g)). This behaviour is consistent with previous observations for microscopic rods,33,34,36 arising when the charges around the particle build a dipole resulting in the alignment of the particles along the direction of the applied E. Thus, a standing rod aligns its long axis parallel to the electric field with an angle between the rod and the bottom slide of θ = 0, while a planar dimer aligns its long axis perpendicularly to the field θ = π/2. In this case, LN is affected by the standing rods, as only planar rod-like particles contribute to the network. As we will see in the next section, this is a key event that affects the network structure. Overall, together with frequency changing the applied field strength provides an additional handle to modify the structural properties of the SU8-rod monolayer.
3.4 Rod rearrangement and network connectivity
As previously mentioned, the network structure is significantly influenced by the effect of the electric field E on the particle orientation. In Fig. 4(a)–(c), we illustrate the impact of the electric field on the same region of the network. As frequency (and voltage) increase, the rods tend to align with E, leading to the breaking of the network and a decrease in its thickness.The effect of the rods standing up on the overall network connectivity is quantified by measuring the parameter G, as shown in Fig. 4(d). Here, G represents the largest connected component within the network, defined as the subset of nodes where every node is accessible from any other node through a sequence of connected edges. The presence of a large, dominant component indicates a highly interconnected structure, suggesting that a significant fraction of the system's nodes form a continuous, traversable path. At frequencies between f = 1–6 kHz and for voltages above 6 Vpp, the connectivity of the system is highest (G > 0.75), and we observe a continuous network where the rods connect to form a path across the system, resulting in a percolated planar network. When G < 0.75, we start observing a bigger population of isolated clusters of planar rods, and a decrease of percolated clusters spanning over the field of view as the network starts disconnecting. The degree of connectivity is inversely related to the applied frequency, as the network transitions into thinner, more spaced structures while the rods align with the field and orient perpendicular to the plane, as sketched in Fig. 4(c). The percolated network forms above a certain planar-rod area fraction threshold for a fixed field condition. Thus, the connectivity will decrease with increasing standing rods (rods) and it will increase with increasing LN (see Fig. S3, ESI†).
This behaviour aligns with theoretical predictions on percolation networks in two-dimensional suspensions of rods.55 For a system of sticks with a given aspect ratio L/D – accounting for the polydispersity of the system – there is a theoretical critical concentration  at which the system transitions from isolated clusters of rods to a configuration where there is, at least, one percolating cluster. Increasing the concentration of rods increases the likelihood of intersections, facilitating percolation. Based on this, we estimate the critical percolation area fraction
at which the system transitions from isolated clusters of rods to a configuration where there is, at least, one percolating cluster. Increasing the concentration of rods increases the likelihood of intersections, facilitating percolation. Based on this, we estimate the critical percolation area fraction  of non-interacting rods to be ≈35%, taking into account the polydispersity (≈20%) and aspect ratio (L/D ≈ 10) of our system (see Fig. S4 and ESI† for more details). We compare the approximated theoretical value with the experimental area fraction of planar rods contributing to the network as (
of non-interacting rods to be ≈35%, taking into account the polydispersity (≈20%) and aspect ratio (L/D ≈ 10) of our system (see Fig. S4 and ESI† for more details). We compare the approximated theoretical value with the experimental area fraction of planar rods contributing to the network as ( ) using the ratio
) using the ratio  (Fig. 3(g)). We represent the conditions of frequency and voltage at which we start observing at least one percolated path of rods under the influence of the AC electric field, and we count the planar rods to estimate
(Fig. 3(g)). We represent the conditions of frequency and voltage at which we start observing at least one percolated path of rods under the influence of the AC electric field, and we count the planar rods to estimate  . When
. When  , the experimental percolation threshold in area fraction is equal to the theoretical prediction for non-interacting rods. Here, percolation starts to take place in our system at much lower area fractions (
, the experimental percolation threshold in area fraction is equal to the theoretical prediction for non-interacting rods. Here, percolation starts to take place in our system at much lower area fractions ( ) with respect to non-interacting rods and above a certain threshold of frequency and voltage. This decrease in percolation threshold rises due to the intrinsic polydispersity of the system and the AC field-driven attractive interactions of the rods, driving the rods assembly.
) with respect to non-interacting rods and above a certain threshold of frequency and voltage. This decrease in percolation threshold rises due to the intrinsic polydispersity of the system and the AC field-driven attractive interactions of the rods, driving the rods assembly.
As estimated by van der Shoot and coworkers, ϕc decreases when the polydispersity increases for a fixed average rod length. Specifically, in our system, the percolation threshold is governed by the weight-average rod length 〈L〉w, which is greater than the mean length ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) due to the longer rods contributing more heavily to connectivity. For a Gaussian distribution, the weight-average length is
due to the longer rods contributing more heavily to connectivity. For a Gaussian distribution, the weight-average length is  , which shows that even small variances lead to a decrease in the ϕc. Here, with a mean rod length of L = 6.2 μm, and standard deviation of 3 μm, we estimate at least a 20% reduction in the ϕc due to polydispersity. Moreover, the presence of the AC-driven attractive interactions further reduces the ϕc and influences the network structure (see ESI† for more details), since rods come into contact and aggregate more efficiently, as it happens for sticky rods.23,24,56,57 It is important to note that this process is reversible, both when the field is switched off and when transitioning between different field conditions. By adjusting the electric field, colloidal interactions can be directly manipulated to achieve similar effects by altering the interparticle potential.
, which shows that even small variances lead to a decrease in the ϕc. Here, with a mean rod length of L = 6.2 μm, and standard deviation of 3 μm, we estimate at least a 20% reduction in the ϕc due to polydispersity. Moreover, the presence of the AC-driven attractive interactions further reduces the ϕc and influences the network structure (see ESI† for more details), since rods come into contact and aggregate more efficiently, as it happens for sticky rods.23,24,56,57 It is important to note that this process is reversible, both when the field is switched off and when transitioning between different field conditions. By adjusting the electric field, colloidal interactions can be directly manipulated to achieve similar effects by altering the interparticle potential.
3.5 Phase behavior of SU8-rods under AC electric fields
In this section, we summarize and rationalize the behaviour of the SU8-rods under the actuation of an AC electric field perpendicular to the plane at various field conditions. For this, we build a complete phase behaviour diagram at an initial fixed SU8-rod area fraction of isotropic rods (≈40%), and we vary the amplitude of the voltage-per-peak (Vpp) and frequency (f), while observing the sample under fluorescence microscopy (Fig. 5(a)). We observe four main states: 2D-network (star), isolated clusters (triangle), expanded aligned planar phase (square), and standing rods (circles) as depicted in Fig. 5(b) and (c).The isotropic state is reminiscent of monolayers of colloidal rods in the absence of an electric field or when the voltage is negligible in this system, in this case, V < 2 Vpp, (<16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 667 V m−1). At frequencies mostly above 1 kHz and voltages above 2 Vpp, an unprecedented 2D-percolated network arises due to the complex interaction between the anisotropic particles. This is in stark contrast with previous works, where the main features observed in the MHz regime are standing rods aligned with the electric field,33,34 or planar aggregates in coexistence with standing particles in the kHz regime for dielectric dumbbells.37 The observed percolation behaviour in this work is characteristic of polydisperse systems with attractive interactions, which, in this case, are finely tuned by the applied electric field. The network disconnects with increasing frequency into clusters, up to the full disconnection due to all the rods standing up.
667 V m−1). At frequencies mostly above 1 kHz and voltages above 2 Vpp, an unprecedented 2D-percolated network arises due to the complex interaction between the anisotropic particles. This is in stark contrast with previous works, where the main features observed in the MHz regime are standing rods aligned with the electric field,33,34 or planar aggregates in coexistence with standing particles in the kHz regime for dielectric dumbbells.37 The observed percolation behaviour in this work is characteristic of polydisperse systems with attractive interactions, which, in this case, are finely tuned by the applied electric field. The network disconnects with increasing frequency into clusters, up to the full disconnection due to all the rods standing up.
Finally, we observe a counter-intuitive network expansion at 1 kHz above a certain voltage (>4 Vpp). Increasing the amplitude of the voltage, one would expect an increase in the magnitude of the established interactions at 1 kHz in the already existing porous structure, thus magnifying the close packing of the rods within the skeleton of the network. This behaviour could be understood by the dominating EHD-induced repulsive forces at this frequency when increasing the voltage amplitude, as the flows around the rods are extensile/repulsive (see Fig. S5 and Movie S4, ESI†). This is consistent with the regimes mentioned in Section 2.4. The magnitude of the flow uEHD increases with the applied electric field at 1 kHz, as uEHD ∝ E2, generating a strong repulsive force that disrupts the previously formed network into a 2D planar highly packed conformation when increasing voltage. We observe the opposite behavior at higher frequencies within the voltages of our experimental setup, also evidenced by the PIV analysis (Fig. S5 and Movie S4, ESI†). We observe an effective attraction of the tracers towards the surface of the rod, evidencing a decrease of the repulsive EHD flows as uEHD ∝ 1/f,46 with of dipole–dipole interactions between the rod and the tracer particles dominating.
Thus, in this scenario, the interplay between dipole–dipole interactions and frequency-dependent electrohydrodynamic flows might explain why repulsion dominates at low frequencies, while dipole-attractive interactions overcome weak EHD forces at higher frequencies, leading to network formation as supported numerically. This balance results in a percolating structure with enough connectivity to span the system, as also seen for spheres.32
4 Conclusions
Our study highlights the versatility of AC electric fields in tuning interparticle interactions to control the reversible formation of 2D-percolated networks of colloidal rods. We demonstrate that percolation occurs at lower effective area fractions than predicted for non-interacting rods of similar dimensions, emphasizing the critical role of field-induced attractive interactions. These interactions, driven by induced dipole–dipole effects, act as a tunable mechanism for “stickiness,” reminiscent of the weak attractive forces that lower percolation thresholds in carbon nanotube (CNT) systems. The percolation network can be precisely controlled by adjusting the frequency and amplitude of the applied AC electric field. Frequency modulates the orientation of the rods, with higher frequencies aligning rods perpendicular to the plane, thereby reducing their contribution to the planar network. Conversely, increasing the voltage amplitude enhances the strength of the field-induced dipole interactions, effectively increasing the “stickiness” between rods and promoting network connectivity. To confirm that these attractive interactions arise from dipolar forces, we performed Monte Carlo simulations of dipolar rods confined between two parallel electrodes. The simulations show that the mirror–image interactions induced by the conducting boundaries lead to effective rod–rod attractions, facilitating network formation. These results support the experimental observations, demonstrating that the percolated networks reach a steady state after the electric field is applied, confirming that the observed behavior represents a stable, equilibrium-driven configuration rather than a phase separation. Our results also reveal a reversible transition from a connected network to a disordered planar expansion phase, providing a mechanism to dynamically modulate pore size. By leveraging the principles of continuum percolation, our approach provides a robust framework to design percolated structures with tunable connectivity and porosity. This work opens pathways for creating advanced porous materials with reconfigurable architectures.Author contributions
Author contributions are defined based on the CRediT (Contributor Roles Taxonomy) and listed alphabetically. Conceptualization: L. A.; formal analysis: L. A., J. F., C. F. R. R. S.; funding acquisition: L. A., J. F., L. R. A., M. T. L. L.; investigation: L. A., M. D., J. F., C. F. R., R. S.; methodology: L. A., J. F., project administration: L. A. software: L. A., J. F., R. S., M. D.; supervision: L. A., L. R. A.; validation: L. A., M. D., J. F., C. F. R., R. S., M. D.; visualization: L. A., J. F., R. S., writing – original draft: L. A., J. F., R. S.,; writing – review, and editing: L. A., J. F., C. F. R., L. R. A., M. T. L. L., R. S.Data availability
Data and codes are available upon request to the authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. A. thanks Philippe Poulin for insightful and exciting discussions. L. A. thanks IdEX University of Bordeaux for funding. J. F. and L. R. A. acknowledge financial support by grant PID2019-105930GA-I00 funded by, Spanish Ministry of Science and Innovation (2019). This article is dedicated to Prof. Stephan Egelhaaf in recognition of his significant contributions to the Soft Matter community and his role as a dedicated and supportive mentor.Notes and references
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- V. N. Manoharan, Science, 2015, 349, 1253751 CrossRef PubMed.
- F. Grillo, M. A. Fernandez-Rodriguez, M.-N. Antonopoulou, D. Gerber and L. Isa, Nature, 2020, 582, 219–224 CrossRef CAS PubMed.
- M. Liu, X. Zheng, V. Grebe, M. He, D. J. Pine and M. Weck, Angew. Chem., Int. Ed., 2021, 60, 5744–5748 CrossRef CAS PubMed.
- M. He, J. P. Gales, E. Ducrot, Z. Gong, G.-R. Yi, S. Sacanna and D. J. Pine, Nature, 2020, 585, 524–529 CrossRef CAS PubMed.
- F. Evers, R. D. L. Hanes, C. Zunke, R. F. Capellmann, J. Bewerunge, C. Dalle-Ferrier, M. C. Jenkins, I. Ladadwa, A. Heuer, R. Castañeda-Priego and S. U. Egelhaaf, Eur. Phys. J.: Spec. Top., 2013, 222, 2995–3009 Search PubMed.
- L. L. Treffenstädt, N. A. M. Araújo and D. de las Heras, Soft Matter, 2018, 14, 3572–3580 RSC.
- X. Zhang, W. Tan, T. Carey, B. Wen, D. He, A. Arbab, A. Groombridge, F. Smail, J. de La Verpilliere, C. Yao, Y. Wang, X. Wei, H. Liu, S. Xie, F. Torrisi, M. D. Volder, W. Zhou and A. Boies, Nano Res., 2023, 16, 12821–12829 CrossRef CAS.
- A. G. Rösch, F. Giunta, M. M. Mallick, L. Franke, A. Gall, J. Aghassi-Hagmann, J. Schmalian and U. Lemmer, Adv. Theory Simul., 2021, 4, 2000284 CrossRef.
- J. L. Silverberg, A. R. Barrett, M. Das, P. B. Petersen, L. Bonassar and I. Cohen, Biophys. J., 2014, 107, 1721–1730 CrossRef CAS PubMed.
- S. Reynaert, P. Moldenaers and J. Vermant, Langmuir, 2006, 22, 4936–4945 CrossRef CAS PubMed.
- P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503 CrossRef CAS PubMed.
- E. Zaccarelli, P. J. Lu, F. Ciulla, D. A. Weitz and F. Sciortino, J. Phys.: Condens. Matter, 2008, 20, 494242 CrossRef.
- R. F. Capellmann, N. E. Valadez-Pérez, B. Simon, S. U. Egelhaaf, M. Laurati and R. Castañeda-Priego, Soft Matter, 2016, 12, 9303–9313 RSC.
- A. Villada-Balbuena, G. Jung, A. B. Zuccolotto-Bernez, T. Franosch and S. U. Egelhaaf, Soft Matter, 2022, 18, 4699–4714 RSC.
- H. Tsurusawa, S. Arai and H. Tanaka, Sci. Adv., 2024, 6, eabb8107 CrossRef PubMed.
- S. Griffiths, F. Turci and C. P. Royall, J. Chem. Phys., 2017, 146, 014905 CrossRef PubMed.
- Y. C. Chiew and E. D. Glandt, J. Phys. A: Math. Gen., 1983, 16, 2599–2608 CrossRef.
- M. A. Miller and D. Frenkel, Phys. Rev. Lett., 2003, 90, 135702 CrossRef PubMed.
- I. Balberg, C. H. Anderson, S. Alexander and N. Wagner, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 3933–3943 CrossRef.
- A. L. R. Bug, S. A. Safran and I. Webman, Phys. Rev. Lett., 1985, 54, 1412–1415 CrossRef PubMed.
- U. Alon, I. Balberg and A. Drory, Phys. Rev. Lett., 1991, 66, 2879–2882 CrossRef PubMed.
- A. V. Kyrylyuk and P. van der Schoot, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 8221–8226 CrossRef CAS PubMed.
- S. Mertens and C. Moore, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 061109 CrossRef PubMed.
- J. Lin, H. Chen, L. Liu and R. Zhang, Phys. A, 2020, 544, 123564 CrossRef.
- P. D. Gennes, J. Phys., Lett., 1976, 37, 1–2 CrossRef.
- B. Vigolo, C. Coulon, M. Maugey, C. Zakri and P. Poulin, Science, 2005, 309, 920–923 CrossRef CAS PubMed.
- C. Zakri and P. Poulin, J. Mater. Chem., 2006, 16, 4095–4098 RSC.
- M. Meloni, M. J. Large, J. M. G. Domínguez, S. Victor-Román, G. Fratta, E. Istif, O. Tomes, J. P. Salvage, C. P. Ewels, M. Pelaez-Fernandez, R. Arenal, A. Benito, W. K. Maser, A. A. K. King, P. M. Ajayan, S. P. Ogilvie and A. B. Dalton, Nat. Commun., 2022, 13, 6872 CrossRef CAS PubMed.
- A. van Blaaderen, M. Dijkstra, R. van Roij, A. Imhof, M. Kamp, B. W. Kwaadgras, T. Vissers and B. Liu, Eur. Phys. J.: Spec. Top., 2013, 222, 2895–2909 Search PubMed.
- H. Carstensen, A. Krämer, V. Kapaklis and M. Wolff, Soft Matter, 2022, 18, 6222–6228 RSC.
- A. K. Agarwal and A. Yethiraj, Phys. Rev. Lett., 2009, 102, 198301 CrossRef PubMed.
- B. Liu, T. H. Besseling, M. Hermes, A. F. Demirörs, A. Imhof and A. V. Blaaderen, Nat. Commun., 2014, 5, 3092 CrossRef PubMed.
- B. W. Kwaadgras, T. H. Besseling, T. J. Coopmans, A. Kuijk, A. Imhof, A. V. Blaaderen, M. Dijkstra and R. V. Roij, Phys. Chem. Chem. Phys., 2014, 16, 22575 RSC.
- A. Kuijk, T. Troppenz, L. Filion, A. Imhof, R. van Roij, M. Dijkstra and A. van Blaaderen, Soft Matter, 2014, 10, 6249–6255 RSC.
- A. F. Demirörs, F. Eichenseher, M. J. Loessner and A. R. Studart, Nat. Commun., 2018, 8, 1872 CrossRef PubMed.
- F. Ma, S. Wang, L. Smith and N. Wu, Adv. Funct. Mater., 2012, 22, 4334–4343 CrossRef CAS.
- J. P. Singh, P. P. Lele, F. Nettesheim, N. J. Wagner and E. M. Furst, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 50401 CrossRef PubMed.
- R. S. Hendley, L. Zhang and M. A. Bevan, Soft Matter, 2022, 18, 9273 RSC.
- K. Chaudhary, J. J. J. Arez, Q. Chen, S. Granick and J. A. Lewis, Soft Matter, 2014, 10, 1320 RSC.
- A. Azari, J. Crassous, A. M. Mihut, E. Bialik, P. Schurtenberger, J. Stenhammar and P. Linse, Langmuir, 2017, 33, 27 CrossRef PubMed.
- S. K. Panda, S. Debata, N. A. Kherani and D. P. Singh, Soft Matter, 2024, 20, 3971–3979 RSC.
- R. Kato, T. Mikami and T. Kato, Adv. Mater., 2024, 36, 2404396 CrossRef CAS PubMed.
- Y. Huang, C. Wu, J. Chen and J. Tang, Angew. Chem., Int. Ed., 2024, 63, e202313885 CrossRef CAS PubMed.
- C. Fernández-Rico, T. Yanagishima, A. Curran, D. G. A. L. Aarts and R. P. A. Dullens, Adv. Mater., 2019, 31, 1807514 CrossRef PubMed.
- W. D. Ristenpart, I. A. Aksay and D. A. Saville, J. Fluid Mech., 2007, 575, 83–109 CrossRef CAS.
- M. Mak, M. H. Zaman, R. D. Kamm and T. Kim, Nat. Commun., 2016, 7, 10323 CrossRef CAS PubMed.
- F. Ma, S. Wang, H. Zhao, D. T. Wu and N. Wu, Soft Matter, 2014, 10, 8349–8357 RSC.
- M. Mittal, P. P. Lele, E. W. Kaler and E. M. Furst, J. Chem. Phys., 2008, 129, 3345 CrossRef PubMed.
- E. V. Yakovlev, K. A. Komarov, K. I. Zaytsev, N. P. Kryuchkov, K. I. Koshelev, A. K. Zotov, D. A. Shelestov, V. L. Tolstoguzov, V. N. Kurlov, A. V. Ivlev and S. O. Yurchenko, Sci. Rep., 2017, 7, 13727 CrossRef PubMed.
- A. F. Demirö, J. Rô and J. Crassous, Soft Matter, 2017, 13, 3182 RSC.
- F. Nadal, F. Argoul, P. Hanusse, B. Pouligny and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 061409 CrossRef PubMed.
- S. H. L. Klapp, Mol. Simul., 2006, 32, 609–621 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, Inc., USA, 2nd edn, 2001 Search PubMed.
- I. Balberg and N. Binenbaum, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 3799–3812 CrossRef.
- R. H. J. Otten and P. van der Schoot, J. Chem. Phys., 2011, 134, 094902 CrossRef PubMed.
- M. A. Bissett, Y. Deng, I. A. Kinloch and W. W. Sampson, Adv. Theory Simul., 2023, 6, 2300131 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00218d |
| This journal is © The Royal Society of Chemistry 2025 |