Spontaneous rolling of a soft sphere on a vertical soft substrate

Abstract

On perfectly vertical surfaces, rolling is conventionally deemed impossible without external torque. While various species like geckos and spiders exhibit vertical locomotion, they cannot achieve rolling; instead, they fall. In this study, we demonstrate the spontaneous rolling of a soft polyacrylamide sphere on a soft polydimethylsiloxane (PDMS) substrate held vertically at a 90° incline, given specific elasticity values for the materials. Our experiments uncover a slow rolling motion induced by a dynamically changing contact diameter and a unique contact asymmetry. The advancing edge behaves like a closing crack, while the receding edge acts as an opening crack. Utilizing adhesion hysteresis theories and crack propagation models, we explain how this contact asymmetry generates the necessary torque and friction to maintain rolling, preventing either pinning or falling. The findings challenge the traditional understanding of vertical surface interactions and open new avenues for exploring soft-on-soft contact systems. This novel phenomenon has potential implications for designing advanced materials and understanding biological locomotion on vertical surfaces.

---

1. Introduction

From automobile wheels to the game of billiards, rolling is ubiquitous. Typically, we observe rolling on horizontal or inclined surfaces. Revisiting introductory physics textbooks:¹ when a rigid glass sphere, for instance, of mass m is gently dispensed on an inclined plane of a similar rigid material, the sphere will roll down freely due to gravity for any inclination angle 0° < θ_S < 90°. But what happens when θ_S = 90°, i.e., a perfectly vertical surface? The intuitive answer is that the sphere will undergo free fall without any contact with the surface unless it has an initial roll (see Movie S1, ESI†). This is because, on a perfectly smooth vertical surface, the normal force at the contact interface (or point), i.e., mg cos 90° is zero, resulting in no static friction force to generate the torque needed for rolling. Typically, rigid-on-rigid contacts have little to no adhesion.² For scenarios, where adhesion is significant,³ the rigid sphere will either stick to the surface or slide down.

On the other extreme, a millimetric liquid water droplet will wet a perfectly vertical surface, forming a downward elongated profile and exhibiting finite contact angle hysteresis, which is the difference in contact angles between the advancing and receding edges (see Movie S2, ESI†). The droplet may either remain pinned in its original position or slide down freely while maintaining contact with the surface (see Movie S2, ESI†). Under special circumstances, for instance, on an inclined micro-nano textured superhydrophobic substrate, droplets may display irregular rolling and tumbling motion.⁴ The question is whether this overarching notion of inability of objects to roll on surfaces when θ_S = 90° still holds true when both objects and underlying surfaces are made of elastic material (non-rigid) whose elasticity can be tuned at will? At least, when the underlying substrate is soft, a rigid cylinder can sustain spontaneous rolling for an inclination angle of 90°, as first demonstrated by Barquins.⁵ Further works by Barquins and coworkers have elaborated on the different facets of the observed rolling motion under various normal loads and inclination angles.^6,7 In this work, while exploring soft-on-soft contact/wetting systems across a broad range of both top and bottom contacting pair elasticity, we report a scenario where a soft sphere exhibits spontaneous rolling motion on a soft substrate held vertically at a 90° incline without any externally imparted torque. In the following sections, we first present our experimental findings and then unravel the governing principles of this unique phenomenon by invoking a theory based on crack propagation and adhesion hysteresis.

2. Materials and methods

2.1. Materials

The elastic polyacrylamide (PAAm) spheres are realized using an in-house recipe involving a delicate mix of acrylamide (monomer), N,N′-methylene-bis-acrylamide (BIS) (crosslinker), and 2,4,6-tri-methyl benzoyldiphenylphosphine oxide (TPO) (initiator)⁸ (Fig. S1, ESI†). By tuning the monomer in weight percentages of 4 to 30, we impart varying degree of elasticity, i.e., Young's modulus E₁, which upon rheology mesaurements were found to be varying between 0.0017 kPa to 169.7 kPa (Fig. S2, ESI†). As our working substrates, we use freshly cleaned microscope glass slides and glass substrates coated with two different commercially available PDMS: Sylgard 184 and Sylgard 527 with monomer:crosslinker ratios of 10 : 1 and 1 : 1, respectively. Consequently, we prepare 1 mm thick soft coatings with Young's modulus, E₂ = 2242 kPa and E₂ = 3 kPa, confirmed using rheology measurements (Fig. S3, ESI†). By varying the elasticity of both the elastic spheres and the substrates, we thus vary the effective elasticity of the contact interface, E* = [(1 − ν₁²)/E₁+ (1 − ν₂²)/E₂]⁻¹, where ν₁ ≈ 0.5 and ν₂ ≈ 0.5 are the Poisson's ratio of the top and bottom pair, respectively.⁸ Additional details of PAAm fabrication can be found in our previous works^8,9 as well as in the ESI.†

2.2. Methods

We conduct our experiments by gently depositing 1 mm radius polyacrylamide spheres/drops (mass, m = 4 mg) on the working substrates kept vertically at 90° inclination with precise control using the software-controlled rotating stage of a commercial goniometer (DSA30, Kruss). As control experiments, we also deposited similarly sized water droplets. Static pinned or sliding configurations of PAAm sphere/drops and water droplets on the working substrates were observed using conventional shadowgraphy using DSA Kruss' in-built CCD camera coupled with a macro lens, achieving a spatial resolution of 22–25 μm per pixel.

The rolling experiments were performed using shadowgraphy with three different settings. First, moderate magnification experiments were performed with a high-speed camera (FASTCAM AX-200, Photron) operating at acquisition rates of 50–60 frames per second and coupled with a 4× microscope objective lens and an adapter tube providing a spatial resolution of 7–8 μm per pixel (see Movies S3–S6, ESI†). These experiments provide the optimal spatio-temporal resolution and are thus used for extracting key features (advancing/receding edges, velocity, and contact angles) of the rolling dynamics. Second, higher magnification rolling experiments were performed using a similar configuration albeit with a 10× long-working distance objective lens (Optem), providing a spatial resolution of 2 μm per pixel (see Movie S7, ESI†). These recordings provide a close up of the advancing and receding edges and thus a lower field of view. However, these recordings are not used for extracting key features of the rolling dynamics. Lastly, lower magnification (1×) recordings were performed using DSA Kruss' in-built CCD camera at 10 frames per second acquisition rate and a spatial resolution of 22–25 μm/pixel (see Movies S8 and S9, ESI†). These recordings have a larger field of view and exhibits the point of dispensing and extended rolling. Again, these are not used for extracting key features of the rolling dynamics. To enhance observation of the rolling motion, we conducted additional experiments by dispersing 100 μm sized microplastics on the PDMS substrates along the rolling path. These microplastics adhered to the rolling PAAm sphere, acting as markers to help visualize the rolling motion (see Movie S6, ESI†). Note that the microplastics do not create or sustain the rolling motion in any form and the initial PDMS location where the PAAm sphere was placed contained no microplastics (see Movie S6, ESI†). Overall, we repeated the rolling experiments 15–20 times to ensure consistency.

Image processing was conducted using an edge detection algorithm in Python.^9,10 Briefly, shadowgraphy rendered the PAAm sphere dark against a bright background. Consequently, we scanned each frame along the line separating the rolling PAAm sphere from the substrate. The first pixel below a threshold intensity value identified the advancing edge position when scanning from the bright background. Similarly, scanning from the opposite direction located the receding edge position. The threshold intensity typically ranged between 70 a.u. and 100 a.u., depending on the image acquisition rate and illumination conditions. Dynamic contact angles at the advancing and receding edges were determined using either a tangent fit or a first-order polynomial fit. To identify the contact asymmetry, a circle was fitted over the PAAm profile to locate its center, and the center's x-coordinate was projected onto the contact interface. Alternatively, the x-coordinate of the outermost advancing point at the central axis can be extracted using edge detection (similar to that performed for advancing/receding edges) and upon subtracting the PAAm sphere's radius, we can identify the center. For rolling experiments without microplastics as markers, a random protrusion or shape irregularity at the periphery of the rolling PAAm sphere is tracked over successive frames to determine angular velocity.

3. Results

3.1. Pinning and sliding outcomes

Before delving into the conditions which causes self rolling, here we briefly describe the non-rolling outcomes for liquids like water and PAAm spheres with different elasticity on vertical substrates. For weakly elastic PAAm spheres, i.e., E₁ = 0.0017 kPa, we observe that they behave as polymeric liquids and completely wet the substrates like a water droplet.⁹ Consequently, for the substrates held vertically, they mostly remain pinned (Fig. 1a). This behavior is similar to water droplets which mostly remain pinned on the soft, PDMS substrates (Fig. 1b) whereas they slide down on glass substrates (see Movie S2, ESI†). The outcome depends on the substrate's wettability and the presence of local surface heterogeneities¹¹ or contact line induced local deformation (for the soft PDMS coatings)^12–14 which favors pinning rather than sliding. Since the focus of the present work is more on the rolling motion, we do not elaborate further on the pinning or sliding outcomes. With increasing PAAm elasticity, we observe morphologies intermediate between wetting and contact with gradually decreasing PAAm-substrate contact diameter d and increasing contact angle (Fig. 2 and Fig. S4, ESI†). However, they still remain either pinned or exhibit sliding behavior. For E₁ = 15.8 kPa, the elastic spheres exhibit the Hertz/Johnson–Kendall–Roberts (JKR) like contact configuration;^2,3 though still pinned to the substrates held vertically (Fig. 2). One would assume that with increasing elasticity, since the contact diameter tends to zero and the contact angles tend to 180°, the spheres would eventually fall off. However, for the stiffest PAAm sphere used in the study, i.e., E₁ = 169.7 kPa, we observe an interesting outcome: the spheres exhibit steady rolling (see Movies S3–S9, ESI†) on the relatively stiffer PDMS substrate (E₂ = 2242 kPa) held vertically while remaining pinned on the glass and the relatively softer PDMS substrate (E₂ = 3 kPa) (Fig. 2).

Fig. 1 (a) Static pinned configuration of a 1 mm radius PAAm drop with 4 wt% monomers (elasticity, E₁ = 0.0017 kPa) on vertical substrates: glass (first column), PDMS substrates (elasticity, E₂ = 2242 kPa) (second column), and PDMS substrates (elasticity, E₂ = 3 kPa) (third column). (b) Snapshot while sliding of a 1 mm radius water droplet on a vertical glass substrate (first column). Static pinned configuration of a 1 mm radius water drop on vertical substrates: PDMS substrates (elasticity, E₂ = 2242 kPa) (second column), and PDMS substrates (elasticity, E₂ = 3 kPa) (third column). The dashed lines demarcate the PAAm/water with the substrate. Scale bars represent 1 mm.

Fig. 2 Static pinned configurations of 1 mm radius PAAm spheres of different elasticity, E₁ on vertical glass substrates and PDMS substrates of different elasticity, E₂. The dashed lines demarcate the PAAm with the substrate. d represents the contact diameter. Scale bars represent 1 mm.

3.2. Spontaneous rolling

Fig. 3 shows the snapshots of the rolling event (see also Movie S3, ESI†). Note that we conducted rolling experiments using shadowgraphy under different magnifications. However, to facilitate subsequent image processing and analysis, we chose only those experiments performed at 50–60 frames per second acquisition rates and using a 4× magnification microscope objective lens providing a spatial resolution of 7–8 μm per pixel (see Methods). For ease of analysis, without any loss of generality, we choose a window of the rolling event where the rolling sphere is completely visible and has traversed a vertical distance of approximately 1 mm in 2 seconds. Consequently, we extract crucial dynamical features like evolution of the advancing edge x_A, receding edge x_R, center-of-mass x_COM, and contact diameter d (Fig. 4(a)). We also extract the contact angles at the advancing edge θ_A and the receding edge θ_R. As the sphere rolls down, we observe an almost linear growth of the advancing and receding edges as well as the center-of-mass (Fig. 4(b)) indicating a steady velocity and a negligible acceleration. Upon subsequent analysis, we observe that the average center-of-mass velocity v_COM,avg and the average angular velocity ω_avg are 0.51 mm s⁻¹ and 0.94 rad s⁻¹, respectively. Here, note that . Thus, the observed motion is rolling with slipping rather than pure rolling. This feature becomes more evident from our rolling experiments with microplastics aiding in measuring ω with higher accuracy (Movie S6 and Fig. S5, ESI†). In contrast to rigid body rolling where the contact diameter is fixed during rolling, here interestingly, we observe that the contact diameter is not fixed during the rolling sequence and continuously changes, oscillating about a mean value of 285 ± 21 μm (Fig. 4(c)). Further, we observe that the dynamic contact angles at both the edges are greater than 160° with the contact angle at the advancing edge consistently larger than at the receding edge with an average hysteresis δθ = θ_A − θ_R = 2.9° ± 1.6° (Fig. 4(d)). We note that the continuous variation of the contact diameter indicates a continuous creation and destruction of the interface creating the torque and friction necessary to sustain this rolling motion.

Fig. 3 Experimental snapshots highlighting the rolling of a 1 mm radius PAAm sphere (elasticity, E₁ = 169.7 kPa) on a vertical PDMS substrate (elasticity, E₂ = 2242 kPa). The frames are separated by 2 seconds. The scale bars represent 1 mm.

Fig. 4 (a) Experimental snapshot during rolling of a 1 mm radius PAAm sphere (E₁ = 169.7 kPa) on a vertical PDMS substrate (E₂ = 2242 kPa). The location of the advancing contact edge, receding contact edge, and the center-of-mass are highlighted as x_A, x_R, and x_COM, respectively. θ_A and θ_R are the contact angles at the advancing and receding edge, respectively. d is the contact diameter. The arrow denotes the direction of motion. The scale bar represents 0.5 mm. (b) Evolution of the advancing edge x_A, receding edge x_R, and the center-of-mass x_COM. Note that the location of the receding edge at the first frame is considered the origin, i.e., x = 0. Error bars are avoided for clarity. Measurement error is 7–8 μm. (c) Evolution of the contact diameter d. (d) Evolution of the contact angles at the advancing edge θ_A and the receding edge θ_R.

3.3. Adhesion hysteresis

Upon closer inspection, we noticed that the contact interface is not completely axisymmetric unlike its static counterpart on a horizontal substrate (Fig. 5(a)–(c)). By fitting a circle over the sphere profile in successive frames, we reveal the asymmetry in the contact diameter (see also Methods). This aids us in identifying the two unequal semi-circles with radii a₁ and a₂, where the subscripts 1 and 2 represents the contact radius in the receding and advancing edge, respectively and a₁ + a₂ = d (Fig. 5(a) and (b)). Consequently, we observe that a₁ and a₂ oscillate about mean values of 159 ± 16 μm and 126 ± 13 μm, respectively with a₁ consistently larger than a₂ (Fig. 5(d)). Using this observation of contact asymmetry, we invoke established crack theory and previous works by Dominik and Tielens,¹⁵ Kendall,¹⁶ and Krijit and co-workers¹⁷ to interpret the rolling motion.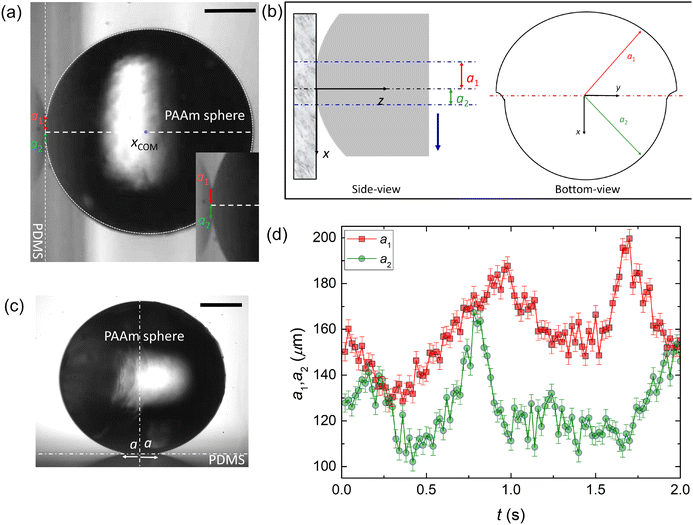

Fig. 5 (a) Experimental snapshot during rolling of a 1 mm radius PAAm sphere (elasticity, E₁ = 169.7 kPa) on a vertical PDMS substrate (elasticity, E₂ = 2422 kPa). The asymmetric contact interface is highlighted using the fitted circle (white dotted line) along the center-of-mass x_COM enabling extraction of the two unequal contact radii a₁ and a₂. Inset shows a close up of the contact interface. Scale bar represents 0.5 mm. (b) Side-view and bottom-view schematic of the contact asymmetry. The blue arrow represents the direction of roll. (c) Static configuration of a similar 1 mm radius PAAm sphere (elasticity, E₁ = 169.7 kPa) on a horizontal PDMS substrate (elasticity, E₂ = 2422 kPa). The symmetric contact interface is highlighted using equal contact radius a. Scale bar represents 0.5 mm. (d) Evolution of a₁ and a₂ for the rolling of the PAAm elastic sphere (E₁ = 169.7 kPa) on a vertical PDMS substrate (E₂ = 2242 kPa), i.e., corresponding to the analysis in Fig. 4.

As the sphere rolls down, crack propagates through the contact interface, acting like an adhesive joint. Consequently, the crack at the advancing (leading) edge continuously closes whereas the crack at the receding (trailing) edge continuously opens resulting in the observed contact asymmetry. A rough estimate of this crack opening and closing velocity can be obtained from evaluating dx_R/dt (receding edge) and dx_A/dt (advancing edge) whose magnitudes averaged over the rolling duration are 0.50 mm s⁻¹ and 0.52 mm s⁻¹, respectively (Fig. S6, ESI†). Interestingly, these velocities are approximately the same as the average velocity of the center-of-mass, i.e., v_COM,avg = 0.51 mm s⁻¹. Higher magnification visualization of the rolling event confirms this crack opening/closing phenomenon (see Movie S7, ESI†).

The strain energy release rate associated with the crack propagation process can be expressed as, , where G₁ and G₂ are the energy release rates at the receding (crack opening) and advancing (crack closing) edges, respectively, and G₁−G₂ represents the adhesion hysteresis.¹⁶ Here, δ is the common indentation depth shared by both contact radii, a₁ and a₂. A natural consequence of the adhesion hysteresis is a finite torque and as a result, a finite friction force. In other words, rolling can only occur if G₁−G₂ > 0, i.e., the energy required for opening the crack is higher than that required to close it. Using the contact asymmetry and the differential strain energy release rates, Dominik et al. exhibited how the pressure distribution varies along the contact interface generating a torque about the y-axis (Fig. 5(b)), most pronounced at the periphery of the receding part of the contact interface.¹⁵ This torque which essentially counters mgR can be expressed as, τ = C₀R(a₁G₁ − a₂G₂) (see detailed derivation in ESI† and also ref. 17). Note that in the expression of torque, the prefactor C₀ can vary between 0.5 to 2 depending on the geometry of the contacting pairs. For sphere-sphere contacts, C₀ = π/2. In the present study, we consider the mean of these limits, i.e., C₀ = 1.25. Consequently, we can express the friction force f as f = C₀(a₁G₁ − a₂G₂). Thus, the force balance reads ma_COM = mg − f where a_COM is the linear acceleration of the center-of-mass.

Before proceeding with further analysis, here we make certain considerations relevant to the problem. First, typically the indentation depth δ is significant for static, horizontal contacts.^2,3 However, for the present vertical contact configuration and subsequent rolling, it is negligible due to the continuous rolling motion providing negligible time for the indentation to form. Thus, we assume a_1,2² ≫ Rδ. Further, so far, we have considered the static Young's modulus for describing the elastic properties of the contacting pairs (see ESI†). However, during rolling, the PAAm sphere induces contact on the underlying PDMS substrate at a finite angular velocity ω_avg = 0.94 rad s⁻¹ ≈ 0.15 Hz. Thus, we calculate the effective elasticity E* as E*|_ω=0.15Hz = [(1 − ν₁²)/E₁|_ω=0.15Hz + (1 − ν₂²)/E₂|_ω=0.15Hz]⁻¹. As a result, for the specific combination of PAAm elastic sphere and PDMS substrate which exhibits the rolling motion, we have E₁|_ω=0.15Hz = 405 kPa and E₂|_ω=0.15Hz = 2316 kPa providing E*|_ω=0.15Hz = 457 kPa (see also Fig. S7, ESI†).

In Fig. 6, we reveal the variation of the experimentally calculated friction force f over the duration of rolling event. Since f is a function of a₁ and a₂, it also oscillates about a mean value f_avg = 38.7 μN during the course of rolling. Note that since v_COM ∼ 10⁻⁴ m s⁻¹ and a_COM ∼ 10⁻⁴ m s⁻², ma_COM ≪ mg Thus, from the force balance expression, it is expected that f ≈ mg which is reflected in our experiments where f_avg = 38.7 μN ≈ mg = 39.2 μN. Thus, for rolling on a 90° incline, the average friction force is just enough to balance the weight of the rolling sphere. Conversely, the torque expression reads mgR − fR = Iα and is perfectly balanced since Iα ≪ mgR, fR. Here I = (2/5)mR² + (1/2)mR² is the moment of inertia, α is the angular acceleration, and Iα ∼ 10⁻⁶ μN m⁻¹ whereas mgR, fR ∼ 10⁻²μN m⁻¹.

Fig. 6 Evolution of computed friction force f for the rolling of a PAAm sphere (E₁ = 169.7 kPa) on a vertical PDMS substrate (E₂ = 2242 kPa). f_avg and mg are the average friction force and weight of the PAAm sphere, respectively. Inset shows the free body diagram of the process.

3.4. Energy analysis

Here, we perform a conservation of energy analysis to interpret this rolling motion. To do so, we consider two instances at the beginning and end of the chosen window of the rolling event shown in Fig. 3 and analyzed subsequently in Fig. 4–6. The energy balance dictates where I is the moment of inertia and Δh ≈ 1 mm is the vertical distance traversed by the rolling sphere in the chosen window. Here, the subscripts i and f represent the initial and final states, respectively. Upon performing an order of magnitude analysis, we observe that , f_avgΔh ∼ [scr O, script letter O](10⁻² μN m⁻¹) and . Thus, the energy balance simplifies to mgΔh = f_avgΔh which aligns with our previous force balance analysis, i.e., mg ≈ f_avg (Fig. 6). In essence, the observed rolling motion satisfies conservation of energy, where the potential energy is entirely dissipated by the work done by the kinetic friction. At the same time, our energy analysis theoretically indicates that the rolling motion will continue as long as there is a finite Δh inducing finite, non-zero potential energy. This is confirmed in our experiments, where we observed rolling events terminating at Δh = 4 mm (see Movie S8, ESI†) as well as events where the sphere rolled down with Δh > 15 mm, exceeding the substrate's length eventually (see Movie S9, ESI†). Therefore, for rolling to terminate, additional dissipation mechanisms due to physical and chemical heterogeneities at the contact interface are essential.

4. Discussions

In the preceding sections, we analyzed the conditions that sustain the rolling motion. Here, we briefly discuss the probable reasons for the onset of rolling. Initially, after the PAAm sphere is deposited, G₁ < G_op where G_op is the critical strain energy required to open the crack at the trailing edge.^15,16 Rolling begins only when G₁ overcomes G_op, causing the crack to open at the trailing edge and leading to the adhesion hysteresis necessary to initiate rolling. Factors contributing to this include mechanical events like high strain rates at the trailing edge or chemical events such as molecular rearrangement at the contact interface.¹⁸ Conversely, a similar condition can also prematurely terminate the rolling; if G₁ instantaneously drops below G_op, the crack at the trailing edge fails to open, stopping the roll. To provide a quantitative estimate of the approximate magnitude of G_op, we probe the work of adhesion w between the contacting pairs. Using the static contact radii (a) values of the PAAm spheres (E₁ = 169.7 kPa) on the PDMS substrates (E₂ = 2242 kPa), measured on horizontal substrates as well on vertical ones after rolling terminates, we extract w using the JKR theory i.e., w = 2a³E*/9πR = 46.5 ± 3.5 mJ m⁻². Consequently, we observe that during rolling both G₁ and G₂ are higher than w (Fig. 7, ESI†). Further, estimating w provides us with a critical value of the work of adhesion between any two contacting pairs of finite elasticity below which rolling should ideally be possible. In comparison, Barquins and coworkers observed a critical work of adhesion value of 52 mJ m⁻² for their combination of rigid cylinder and natural rubber substrate.^6,7 Note that for other elasticity combinations used in the present study where no rolling was observed, using the JKR theory and static contact radii values, we similarly calculate the work of adhesion and observed w ≥ 61 mJ m⁻².

Fig. 7 Evolution of strain energy release rates, G₁ (crack opening, receding edge) and G₂ (crack closing, advancing edge) for the rolling of the PAAm elastic sphere (E₁ = 169.7 kPa) on a vertical PDMS substrate (E₂ = 2242 kPa), i.e., corresponding to the analysis in Fig. 5 and using the relation, 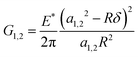. The work of adhesion w between the contacting pairs is shown for clarity. Note that here t = 0 does not represent the onset of rolling.

Here, we elaborate on the role of slip in the observed rolling. To do so, we first aim to quantify the relevant slip velocity. Consequently, we first draw an analogy with conventional rigid-body rolling with slipping on rigid, horizontal surfaces. For such cases, a finite velocity is observed at the contact point, i.e., the slip velocity, commonly expressed as v_slip = v_COM − ωR (Fig. 8a). Consequently the velocity at the apex of the rolling sphere typically is v_COM + ωR. However, for the present soft rolling, instead of a singular contact point, a contact region exists whose average velocity should ideally reflect the slip velocity. Previously, we have highlighted the evolution of the advancing edge, receding edge and the center-of-mass. Here, we also extract the evolution of the apex point of the rolling sphere and calculate its instantaneous translation velocity, i.e., v_T = dx_T/dt (Fig. 8b). For the sake of simplicity, we consider the average instantaneous velocity of the advancing edge and the receding edge, i.e., (v_A + v_R)/2 to be representative of the slip velocity. Upon comparison of the different relevant velocities (Fig. 8c), we observe that the average contact region velocity i.e., (v_A + v_R)/2 mirrors the evolution of the center-of-mass velocity, v_COM, and does not converge to the theoretical value of v_COM,avg − ω_avgR (Fig. 8c). Here, note that as previously mentioned, for the experiments shown in Fig. 3, v_COM,avg = 0.51 mm s⁻¹ and ω_avgR = 0.15 mm s⁻¹, yielding v_COM,avg − ω_avgR = 0.36 mm s⁻¹. At the same time, we observe that velocity at the apex point monotonically decreases and converges to the value of v_T = 0.64 mm s⁻¹ = v_COM,avg + ω_avgR. Thus, we observe that in contrast to conventional rigid-body rolling with slipping, v_COM,avg − ω_avgR does not hold in soft rolling due to a finite contact region even though v_COM,avg + ω_avgR still holds due to a singular apex point. Further, it is likely that slippage here occurs intermittently. This fact can be observed from Fig. 8c, where a subtle increase in both v_COM and (v_A + v_R)/2 occurs at t ≈ 0.25 s indicating the possible onset of slip. Upon comparing with the contact asymmetry (Fig. 5d, t ≈ 0.25 s) and strain energy release rates (Fig. 7, t ≈ 0.25 s), we observe that roughly before the onset of slip, a₂ approaches a₁ and exceeds it momentarily. Thus, the corresponding G₂ approaches and exceeds G₁ momentarily. Upon subsequent analysis, we observe that here , where Δa_c is the critical displacement required to sustain steady rolling.¹⁷ Thus, Δa momentarily dropping below the critical value may have induced momentary pinning (at a time scale below the current resolution), followed by the slip phase. Furthermore, since both Δa and ΔG diminishes, friction is also observed to drop significantly at the onset of slip (Fig. 6, t ≈ 0.25 s). A similar analysis can potentially explain other instances of intermittent slippage.

Fig. 8 (a) Schematic of rigid-body rolling with slipping on horizontal surfaces. (b) Schematic of present soft vertical rolling. Here, x_A, x_R, x_COM, and x_T are the locations of the advancing edge, receding edge, center-of-mass, and apex point, respectively. v_A = dx_A/dt, v_R = dx_R/dt, v_COM = dx_COM/dt, and v_T = dx_T/dt are the respective instantaneous velocities. ω is the angular velocity. Evolution of (v_A + v_R)/2, v_COM, and v_T for rolling of the PAAm elastic sphere (E₁ = 169.7 kPa) on a vertical PDMS substrate (E₂ = 2242 kPa), i.e., corresponding to the analysis in Fig. 4.

Lastly, we highlight that multiple experiments revealed that the average center-of-mass (or even the contact edges) velocities varied in a rather small range, i.e., between 0.46 mm s⁻¹ and 2.52 mm s⁻¹, with occasional velocity enhancement due to intermittent slippage. Thus, highlighting the dependence of strain energy release rates and friction (or dissipation) on the relevant velocity scales is beyond the scope of the present work. To perform such an analysis, a broad variation in velocity is crucial which can only be achieved by factors like imparting external forces, varying the inclination angle, or varying the mass (or radius) of the soft sphere.

5. Conclusion

In conclusion, using experiments and theory, we highlight the conditions under which rolling of a soft sphere can occur on a soft substrate held at a 90° incline without any externally imparted torque. Using shadowgraphy, we first performed experiments where PAAm spheres of different elasticity E₁ were dispensed on vertical PDMS substrates of different elasticity E₂. The spontaneous rolling motion was observed only for a unique combination of material elasticity, i.e., E₁ = 169.7 kPa (PAAm) and E₂ = 2242 kPa (PDMS). Whereas making either of them softer resulted in either pinning or sliding outcomes, making them sufficiently rigid promoted a free-fall. Additionally, this unique elasticity combination renders a work of adhesion value of 46.5 mJ m⁻² favoring rolling. Further, we observed the rolling motion to be rolling with slipping rather than pure rolling with an average center of mass velocity varying between 0.46 mm s⁻¹ and 2.52 mm s⁻¹, and the average angular velocity varying between 0.9 rad s⁻¹ and 2.4 rad s⁻¹, across multiple experimental runs. Subsequent analysis revealed that the PAAm-PDMS contact diameter continuously changes during rolling and exhibits an asymmetry at the same time. High magnification experiments and theoretical arguments showed that this contact asymmetry is due to adhesion hysteresis at the interface, which continuously opens at one end and closes at the other, similar to a crack. The resulting pressure asymmetry generates the torque and friction force necessary to sustain continuous rolling motion. We provided detailed theoretical formulations of the pressure asymmetry induced friction force and combined it with our experimental findings to establish the relevant force balance. The force balance demonstrated that the average friction force delicately balances the weight of the rolling sphere, sustaining contact during rolling and preventing free fall. Finally, our conservation of energy analysis perfectly complemented the force balance, reinforcing our conclusions.

It is noteworthy to mention that apart from some precedence of rigid cylinders rolling on a perfectly vertical soft surface,^5–7 existing theoretical studies^19,20 have demonstrated the feasibility of liquid droplets rolling down an inclined plane, supported by experimental evidence.^4,20 Given the deformability of liquid droplets and their ability to maintain contact over a finite area, it might be possible for them to roll on a vertical, defect-free, superhydrophobic surface. However, to the best of our knowledge, no experimental evidence has been reported for this phenomenon. Until such evidence is presented, soft-on-soft contact systems may be the most effective method to enable a spherical object to self-roll on a 90° incline. In our previous work, we highlighted how exploiting soft-on-soft contact systems, specifically material elasticity, bridged adhesion and wetting.⁸ Similarly, the present work indicates that modulating elasticity can bridge sliding and free-fall outcomes, guiding us in formulating a unifying framework to better understand motion on a vertical surface.

Finally, we emphasize that the findings of the present work extends beyond mere scientific curiosity. They offer a promising avenue towards the design of soft micro rovers for navigating unpredictable terrain during space exploration. Additionally, understanding this type of rolling motion is relevant for N-body simulations of dust aggregate compression in protoplanetary discs.²¹ Such aggregates consist of spherical monomers whose rolling-driven mutual interactions are crucial for understanding compression.^21,22

Author contributions

S. K. M. conceived the study. S. M. and A-R. K. performed the experiments. S. M. and A.-R. K. analyzed the data. All authors discussed the results. S. M. wrote the manuscript with inputs from all the authors. B. Z. and S. K. M. supervised the research.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors thank Prof. Michael K. C. Tam (Department of Chemical Engineering, University of Waterloo) for providing the dynamic shear rheometer. B. Z. acknowledges the support of NSERC RGPIN-2019-04650. S. K. M acknowledges the support of the Discovery Grant (NSERC, RGPIN-2024-03729). Finally, the authors acknowledge the use of Microsoft's Copilot (version GPT-4) for paraphrasing and proof reading parts of the manuscript.

References

1. D. Halliday, R. Resnick and J. Walker, Fundamentals of physics, John Wiley & Sons, 2013.
2. H. Hertz, J. Reine Angew. Math., 1882, 92, 22.
3. K. L. Johnson, K. Kendall and A. D. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313.
4. R. Mukherjee, A. S. Berrier, K. R. Murphy, J. R. Vieitez and J. B. Boreyko, Joule, 2019, 3, 1360–1376.
5. M. Barquins, J. Adhes., 1988, 26, 1–12.
6. F. Robbe-Valloire and M. Barquins, Int. J. Adhes. Adhes., 1998, 18, 29–34.
7. J.-C. Charmet and M. Barquins, Int. J. Adhes. Adhes., 1996, 16, 249–254.
8. A.-R. Kim, S. Mitra, S. Shyam, B. Zhao and S. K. Mitra, Soft Matter, 2024, 20, 5516–5526.
9. S. Mitra, A.-R. Kim, B. Zhao and S. K. Mitra, Langmuir, 2024, 40, 18968–18976.
10. M. van Gorcum, B. Andreotti, J. H. Snoeijer and S. Karpitschka, Phys. Rev. Lett., 2018, 121, 208003.
11. J. Joanny and P.-G. De Gennes, J. Chem. Phys., 1984, 81, 552–562.
12. E. R. Jerison, Y. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2011, 106, 186103.
13. S. Mitra, S. Misra, T. Tran and S. K. Mitra, Langmuir, 2022, 38, 7750–7758.
14. Q. Vo, S. Mitra, M. Lin and T. Tran, J. Colloid Interface Sci., 2024, 664, 478–486.
15. C. Dominik and A. Tielens, Philos. Mag. A, 1995, 72, 783–803.
16. K. Kendall, Wear, 1975, 33, 351–358.
17. S. Krijt, C. Dominik and A. Tielens, J. Phys. D: Appl. Phys., 2014, 47, 175302.
18. Y. Chen, C. Helm and J. Israelachvili, J. Phys. Chem., 1991, 95, 10736–10747.
19. L. Mahadevan and Y. Pomeau, Phys. Fluids, 1999, 11, 2449–2453.
20. D. Richard and D. Quéré, Europhys. Lett., 1999, 48, 286.
21. A. Kataoka, H. Tanaka, S. Okuzumi and K. Wada, Astron. Astrophys., 2013, 554, A4.
22. C. Dominik and A. Tielens, Astrophys. J., 1997, 480, 647.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01490a

---