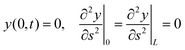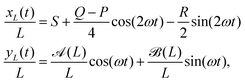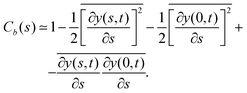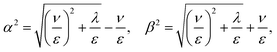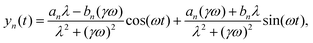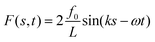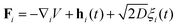Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Active-like dynamics of worm-like chains driven by an external traveling-wave force
Fabio
Cecconi
 *ab,
Andrea
Puglisi
*ab,
Andrea
Puglisi
 c,
Massimiliano
Viale
c,
Massimiliano
Viale
 cd and
Dario
Lucente
cd and
Dario
Lucente
 d
d
aCNR-Institute for Complex Systems, Via dei Taurini 19, 00185 Rome, Italy. E-mail: fabio.cecconi@cnr.it
bINFN, Sezione di Roma, Piazzale Aldo Moro 2, 00185 Rome, Italy
cCNR-Institute for Complex Systems, P.le Aldo Moro 2, 00185 Rome, Italy
dDepartment of Mathematics and Physics, University of Campania “Luigi Vanvitelli”, Viale Lincoln 5, 81100 Caserta, Italy
First published on 26th May 2025
Abstract
We present a simplified theory for semiflexible flagella under the action of a traveling-wave perturbation that emulates the organized active forces generated by molecular motors, capable of inducing beating patterns to the filament. By modeling the flagellum as a worm-like chain (WLC), we explore the interplay (competition) between the externally applied perturbation and the intrinsic bending rigidity of the filament. Our analysis aims to understand how this interplay can lead to a selection of conformations with the spatiotemporal behavior resembling the beating dynamics of axonemes such as those in sperm tails, in Chlamydomonas cilia, or eukaryotic flagella in general. Through a systematic analysis of the WLC's response to traveling-wave perturbations, we try to identify the key parameters that mostly influence the mechanical waveform profiles.
1 Introduction
Flagella are relatively slender structures found in various living organisms playing a crucial role in motility and locomotion. While bacterial flagella are usually passive filaments actuated by motors located at their base,1 eukaryotic flagella such as the cilia in organisms like Chlamydomonas or the tails of sperm cells are active filaments powered by numerous molecular motors distributed along their length.2Flagella serve, in general, as the primary swimming apparatus that, by wiggling and rotating, enables microorganisms to move through fluid environments. Besides propulsion,3 they perform, along with cilia and bio-filaments, a variety of other biological processes,4 that include, for instance, movement of fluids and particles, pathogens removal, e.g. mucus clearance in lung tissue,5,6 embryogenesis (cell signaling, tissue development and patterning),7–9 mechanotransduction10 and sensory reactions to environmental stimuli.11
The complex dynamics of flagella have attracted researchers for decades, inspiring investigations into the fundamental mechanical principles that govern their biological function. In recent years, interest has also grown for the theoretical and experimental study of dynamical fluctuations in the flagellum beating pattern, which is periodic only on average.12–15 This research is driven by the natural need for knowledge but also by the goal of emulating their working efficiency in engineered micro-scale devices and macroscopic biomimetic systems.10 Several theoretical approaches have been developed or applied to address the wide range of flagella shapes and their complex dynamics,16 as well as to explain and interpret a plethora of experimental evidence and observations.17,18 Theory includes mechanical description based on the elasticity of flexible rod-like and slender bodies,19–23 computational methods24–26 and simple theoretical frameworks borrowed by active polymer physics,27–30 each suited to account for the specific phenomenology of various types of flagella. In particular, the bending rigidity of long linear biomolecules, flagella, and biofilaments in general, is a crucial characteristic that significantly assists their biological functions, and such molecular stiffness is naturally assumed essential for the precise functional control of the beating dynamics. From this perspective, theoretical and computational models that accurately incorporate this bending rigidity are essential for capturing, mechanical, physical, and structural aspects of such functional dynamics.
Therefore, models of semiflexible polymers, which account for the stiffness of biopolymers like actin filaments, proteins, and DNA,31–33 are also useful for describing flagella. This stiffness arises from the valence angles in their backbone structure.34 However, these models are more difficult to handle theoretically, as they require additional constraints like preserving a fixed chain length.
A very popular approach resorts to employing the so-called “worm-like chain” (WLC) models representing a minimal yet meaningful physical approach to implementing bending rigidity, as they describe flexible elongated structures characterized by a certain persistence length.35,36 This property has strongly motivated the modeling of flagella as active persistent polymers,28,29,37 idealized as chains of units (molecular motors) that, through their organized or synchronized activity, determine the shape and the right collective dynamics to confer motility to the flagellum.30,38
From a hydrodynamical point of view, the locomotion is possible because the viscous friction of the fluid along slender bodies is anisotropic;39 indeed, the hydrodynamic forces acting on slender bodies are predominantly anisotropic due to the different resistance encountered along and perpendicular to their length. This effect is embodied in the slender-body theory,40 which simplifies the approach by focusing only on the body's centerline, especially when viscous forces dominate (low Reynolds number). The investigation of the complex interplay between hydrodynamics and elasticity in biofilament fluctuations has led to the elastohydrodynamic formulations of flagellar motion that inspired a series of interdisciplinary studies. Besides the seminal works by K. E. Machin41 on the propagation of elastic waves along flagella, other interesting contributions include ref. 42 on the bending modulus measurement of microtubules and ref. 43 exploring the behavior of actin filaments under external oscillatory driving and viscous drag.
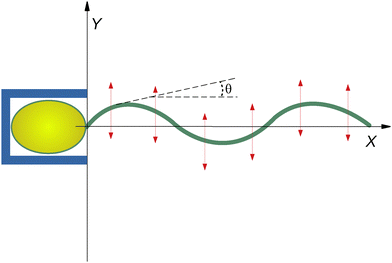
The implications of anisotropic hydrodynamic friction are essential to understanding biological propulsion and designing micro-scale devices. Although this issue is highly significant, it will not be addressed here because we are mainly interested in the dynamics of beating. Therefore, we only consider the situation in which the first monomer of the filament is anchored to a fixed point. Note that a similar condition has been realized experimentally,13 in which sperm cells were confined within microscopic cages (Fig. 1). Since this setup forbids natation, tail conformations can be assumed to be weakly affected by the anisotropies of the hydrodynamic drag.
Therefore, we study through simulations and theory a simplified, yet not trivial, version of an anchored flagellum depicted in Fig. 1 constrained to move in the 2D planar geometry and subject to the effects of a traveling-wave force representing an idealized version of the coherent activity of molecular motors during beating dynamics. In particular, we will analyze how spatially periodic conformational shapes of flagella can emerge from the interplay between its rigidity and the spatiotemporal periodicity of the driving.44,45 To maintain the analysis as simple as possible, we consider a monochromatic traveling-wave force, as in ref. 46, characterized by a wavelength λ (i.e. wavevector k = 2π/λ) and an oscillation frequency ω. The study is performed at different ω and k to show how these parameters affect the flagellum wave-form selection.
Our simple choice of the force hn is due to the requirement that the continuum model, we will use to explain certain regimes of flagellum dynamics, be fully solvable. One might question whether such functional form and direction are compatible with the notion of active force, since: (i) the force is decoupled from the chain conformations; (ii) it always oscillates in a constant direction (y-axis). In its widest definition, an active force is an additional degree of freedom coupled to the system leading to out of equilibrium dynamics. In the literature, it is common practice to represent active forces as coloured noises independent of the conformation,30,46,47 but any representation that breaks detailed-balance is legitimate.
Additionally, it can be noted that in the approximation we will work with, weakly bending (small deformation from the straight conformation), the force directed along the y-axis is the relevant part of the force that is oriented as the normal to the flagellum. In this sense, it is reasonable to interpret hn as the local average force exerted by molecular motors on a small segment of the filament. To further emphasize the concept, let us notice that molecular motors acting on a filament constitute additional degrees of freedom beyond those representing the filament. Moreover, each dynein exerts a shear force on a microtubule doublet, which is internal to the filament, such a shear force converts instantaneously into a bending (i.e. almost transversal) excitation inducing local curvature due to internal constraints.
The paper is structured as follows. In Section 2, we introduce the computational two-dimensional model of the flagellum, along with its continuum theoretical version, which provides a useful framework for interpreting the simulation results. Section 3 discusses the dynamics of the flagellum, analyzing the computational results in terms of parameters (ω,k) that define the monochromatic active force. Finally, conclusions are drawn in Section 4.
2 Flagellum models
2.1 Computational model
In our approach, the flagellum is portrayed as a 2-dimensional chain of N + 1 beads of mass m connected by stiff elastic springs of finite extension b. As the first bead is anchored to the origin, r0 = 0, the system cannot translate but can explore the full range of bending fluctuations. The bending energy introduces a penalty whenever three consecutive beads lose their alignment. The potential energy of the system is defined by the function48–50 | (1) |
We consider the overdamped regime of the system when coupled to a weak thermal bath, so the equation of motion of each bead is
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(knb − ωt)) is a deterministic space-modulated and time-periodic perturbation (active-like force)52 that, in our simplified scheme, confers to the flagellum a transversal beating dynamics. In the following, we set f0 = B/20 in all simulations and theoretical analysis to consider the active force as a relatively small perturbation with respect to bending and stretching interactions. The active force hn(t) competes with the bending rigidity in generating transversal undulatory fluctuations of the chain with a spatial modulation depending on the wave number k. We choose k = (2π/L)m where L = Nb is the length of the flagellum in terms of monomers and m is a positive integer defining the number of expected oscillations applied to the flagellum. This choice guarantees that the active force is spatially periodic over the polymer length L and implies a zero net force as easily verified,
sin(knb − ωt)) is a deterministic space-modulated and time-periodic perturbation (active-like force)52 that, in our simplified scheme, confers to the flagellum a transversal beating dynamics. In the following, we set f0 = B/20 in all simulations and theoretical analysis to consider the active force as a relatively small perturbation with respect to bending and stretching interactions. The active force hn(t) competes with the bending rigidity in generating transversal undulatory fluctuations of the chain with a spatial modulation depending on the wave number k. We choose k = (2π/L)m where L = Nb is the length of the flagellum in terms of monomers and m is a positive integer defining the number of expected oscillations applied to the flagellum. This choice guarantees that the active force is spatially periodic over the polymer length L and implies a zero net force as easily verified,  In addition, we assume local isotropic dissipation with friction coefficient γ and neglect long-range hydrodynamic interactions.
In addition, we assume local isotropic dissipation with friction coefficient γ and neglect long-range hydrodynamic interactions.
As already mentioned in the introduction, a rigorous dynamical formulation would require anisotropic drag.32,53 However, as we clearly show in Appendix D, the weakly bending regime we consider in simulation and theoretical analysis, where the motion is predominantly transverse, implies that only the normal drag enters the leading-order dynamics.
Here, the role of γ in the dynamics is to provide a time scale, i.e. the rate of energy dissipation due to the friction with the solvent, and then it can be set γ = 1 in the simulations without loss of generality. Nevertheless, in the following theoretical analysis, we leave it indicated to keep track of the correct physical units of the observables; we also anticipate that the theory will neglect the Gaussian noise.
This is because, in our simulations, the noise is completely overwhelmed by the forcing hn, i.e. f02 ≫ γT. However, although small, its presence is necessary for running Brownian dynamics simulations.54
Along the same lines as the work by Machin,41 we are interested in understanding how the interplay between bending rigidity and active forcing selects the resulting polymer conformations and in describing their relevant spatiotemporal patterns.55,56 In the papers,32,53 the same issue is studied under the effects of localized forces, applied to one of the endpoints of the flagellum, and under anisotropic hydrodynamic drag. Let us notice that, while hydrodynamics plays an important role in generating self-propulsion, it does not contributes significantly in the beating dynamics, which is instead mostly influenced by mechanical aspects (see Appendix D), especially when driven by an extended force like the one we consider.
For this reason, we first perform Brownian simulations54 of the chain in an isotropic medium through the Langevin eqn (2). Then, to better clarify the role of the perturbation parameters (k,ω), we support the computational results with a theoretical analysis based on the continuous model discussed below. The left panels of Fig. 2 and 3 give the first qualitative idea about the beating phenomenology of the system by showing several conformations assumed by the flagellum sampled in simulations over one period, 2π/ω, of the forcing. When k = m(2π/L), the flagellum can sustain undulations of wavelength λ = L/m as one can see from the number of bumps along the conformations. The tail, instead, cannot follow the spatial periodicity due to the great moment of the external force on the free-end region making the tail perform considerable excursions.
 | ||
| Fig. 2 Snapshots of the flagellum stationary dynamics (left panels) compared with the corresponding conformations obtained from the approximated theory eqn (4) (right panels), for a chain of length L = Nb (N = 40, b = 1) and bending modulus B = 10. The different colors indicate six sampling times that are equally spaced within a force-cycle 2π/ω. The comparison is done for active perturbations of wavevector 5(2π/L) and small, moderate, and high frequencies ω = 0.01, 0.10, 1.0. | ||
 | ||
| Fig. 3 Same conditions of Fig. 2, but higher bending stiffness, B = 20. | ||
Moreover, simulations indicate that at low frequencies, ω ≲ 10−2, the flagellum oscillates over time but shows little undulation. In contrast, at high frequencies, ω ≳ 1, it becomes more spatially modulated and undergoes a “stiffening” transition, assuming a more rod-like conformation. This occurs because its mechanical structure can no longer sustain and follow high-frequency modes. The transition is evident from the “cigar-like” shape seen in the final left panels of Fig. 2 and 3.
2.2 Continuum model
The continuum formulation of model (2) can be derived from the explicit expression of the internal forces obtained by direct differentiation of the potential (1) | (3) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p2, being
p2, being ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p the persistence length of the stiff polymer. As customary, we parameterize the curve with the arc length bn → s measured from the origin coinciding with the hinged point (see Fig. 1).
p the persistence length of the stiff polymer. As customary, we parameterize the curve with the arc length bn → s measured from the origin coinciding with the hinged point (see Fig. 1).
The equation of motion governing the evolution of the system's coordinate r(s,t) = x(s,t)ex + y(s,t)ey is straightforwardly derived from the monomers's eqn (3) after performing the continuum limits rn − rn−1 → b ∂r(s)/∂s. In this way, the first term of eqn (3) formally represents the discrete first derivative of the function G(x), whereas the last term is the discrete 4-th derivative of r(s) and neglecting the contribution of the Gaussian noise, this leads to
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ks − ωt)). For consistency with the simulation setup, we have to assume: h(0,t) ≡ 0 because the external force on the hinged monomer is null. The boundary conditions for eqn (4) corresponding to a tethered-hinged polymer in the origin (s = 0), and free at the other end (s = L), can be derived from eqn (3) by adding the “virtual” monomers r−1, rN+1, rN+2, which must satisfy specific relations such that the equations of motion for the “actual” monomers r1, rN−1, rN can be treated as bulk eqn (3). This trick ensures the same description of the dynamics across the entire polymer chain, including the boundaries. Such conditions are, obviously, r0 = 0 and
sin(ks − ωt)). For consistency with the simulation setup, we have to assume: h(0,t) ≡ 0 because the external force on the hinged monomer is null. The boundary conditions for eqn (4) corresponding to a tethered-hinged polymer in the origin (s = 0), and free at the other end (s = L), can be derived from eqn (3) by adding the “virtual” monomers r−1, rN+1, rN+2, which must satisfy specific relations such that the equations of motion for the “actual” monomers r1, rN−1, rN can be treated as bulk eqn (3). This trick ensures the same description of the dynamics across the entire polymer chain, including the boundaries. Such conditions are, obviously, r0 = 0 and| r1 − 2r0 + r−1 = 0 |
| rN+1 − 2rN + rN−1 = 0 |
which, to the continuum, leads to r(0,t) = 0 and
 | (5) |
2.3 Weakly bending approximation
The weakly bending approximation (WBA)59,64 is a convenient approach to recovering extensibility; it assumes the flagellum undergoes only small deviations from a straight or rod-like conformation, likewise, the active force is considered small enough to remain consistent with the weakly bending regime. In our case, we see that WBA provides a satisfactory scheme for interpreting computational results. As customary in WBA, a convenient parameterization of the flagellum centerline is r(s,t) = (s + u(s,t),y(s,t)), where u is a small longitudinal deviation from x = s, with a small derivative as well, ∂su(s) ≪ 1.Such a parameterization is required to satisfy the inextensibility constraint
| |∂sr|2 = [1 + ∂su(s,t)]2 + [∂sy(s,t)]2 = 1, | (6) |
 | (7) |
 | (8) |
 | (9) |
 | (10) |
with νeff small and positive parameter that has to be determined. As already mentioned, νeff could be considered as a Lagrangian multiplier (within the approximation g constant) which implements inextensibility constraint of the flagellum. However, since we are already working within the WBA framework, which approximates this constraint, we need only to determine a reasonable value of ν from the simulation data (see next section). As a consequence, ν naturally turns out to be a function of the ω and k, νeff = νeff(k,ω) of the active force, like it always happens when a stiff polymer undergoes the action of an external driving (shear flow, pulling, or active random force).37,65,66
In the rest of the paper, for simplicity, we use ν instead of νeff.
Besides the need to reproduce numerical simulations, another guess for the presence of the stretching term stems from the observation that by plugging the condition (7) into eqn (6) implies that |∂sr|2 ≃ 1 + (∂sy)4/4, thus |∂sr| is allowed to take on values slightly larger than 1. This is consistent with our expectation regarding the role of the term g(|∂sr|) in eqn (4).
Definitely, our analytical estimate of the flagellum conformations in the WBA is given by eqn (10) together with eqn (8). The solution to eqn (10) can be obtained by an expansion37,58
 | (11) |
 | (12) |
 | (13) |
The amplitudes of each mode are independent and evolve according to the following equation
 | (14) |
| an = f0〈cos(ks),ψn(s)〉, bn = f0〈sin(ks),ψn(s)〉, | (15) |
Their explicit expression is
 | (16) |
 | (17) |
 | (18) |
After putting all the terms together and using the ψn(s), we obtain the full solution of the y-profile of the flagellum that can be rearranged into the very simple expression
y(s,t) = ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) k,ω(s)cos(ωt) + k,ω(s)cos(ωt) + ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) k,ω(s)sin(ωt) k,ω(s)sin(ωt) | (19) |
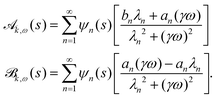 | (20) |
The amplitudes ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) k,ω(s) and
k,ω(s) and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) k,ω(s) play the role of a response of the system to a given forcing with spatiotemporal periodicity k,ω: high or low values of those amplitudes indicate if the traveling-wave perturbation is consistent with or is attenuated by the bending rigidity of the flagellum. Such amplitudes seem to be suppressed by increasing ω, therefore in large ω regimes, the dynamics of the flagellum is expected to become noise-dominated and it loses the periodic behavior. In other terms, the flagellum response to high-frequency active forces resembles a low-pass filter for which high-frequency perturbations are strongly attenuated, or in a more structural sense, this corresponds to a “straightening” crossover.
k,ω(s) play the role of a response of the system to a given forcing with spatiotemporal periodicity k,ω: high or low values of those amplitudes indicate if the traveling-wave perturbation is consistent with or is attenuated by the bending rigidity of the flagellum. Such amplitudes seem to be suppressed by increasing ω, therefore in large ω regimes, the dynamics of the flagellum is expected to become noise-dominated and it loses the periodic behavior. In other terms, the flagellum response to high-frequency active forces resembles a low-pass filter for which high-frequency perturbations are strongly attenuated, or in a more structural sense, this corresponds to a “straightening” crossover.
It is also interesting to remark that the flagellum acts as a sort of “spectral device” which decomposes a “monochromatic” perturbation of parameters (k,ω) into a superposition of responses characterized by a set of numbers {αn,λn}∞n=1 where αn (and βn that is strictly connected to it) plays the role of a generalized wave vector and λn is the corresponding “vibration” frequency.
For visualizing the impact of the wave number, k, on the flagellum properties we plot, in Fig. 4, the coefficients (16) and (17) of the active-force expansion in eigenmodes as a function of αn.
 | ||
Fig. 4 Coefficients, eqn (16) and (17) plotted versus αn, of the perturbation f0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ks − ωt) expanded into the orthonormal eigenfunctions ψn(s). The thick black vertical line marks the wave-number k of the spatiotemporal forcing, k = 5(2π/L) and k = 10(2π/L). The blue line indicates the amplitude sin(ks − ωt) expanded into the orthonormal eigenfunctions ψn(s). The thick black vertical line marks the wave-number k of the spatiotemporal forcing, k = 5(2π/L) and k = 10(2π/L). The blue line indicates the amplitude 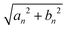 of the n-th eigenmode. The picture resembles a “spatial-resonance” scenario because the maximal variation of coefficients occurs around k, even if the other contributions can not be considered negligible. of the n-th eigenmode. The picture resembles a “spatial-resonance” scenario because the maximal variation of coefficients occurs around k, even if the other contributions can not be considered negligible. | ||
The coefficient an (black dots) displays oscillations that intensify as αn approaches k (marked by the thick vertical line), whereas bn (red dots) exhibits a growth towards k without oscillations, undergoing a sign change when crossing k. The behavior of 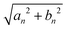 , which is a sort of composite envelope of an and bn, distinctly reveals a pronounced peak at k.
, which is a sort of composite envelope of an and bn, distinctly reveals a pronounced peak at k.
These plots closely resemble a “spatial resonance” scenario, because the maximal variation of an and bn occurs around a neighborhood of k, even though the remaining contributions are not negligible. This suggests that the flagellum modes with αn ≃ k are the most sensible to the perturbation.
In the following section, we discuss the simulation results on the flagellum beating behavior by using the above continuum string theory as a reference and interpretative basis.
3 Results
We run simulations of a flagellum according to eqn (2) for N + 1 = 41 monomers (beads), the first of which is anchored to the origin, forming a hinged restrain, by numerically integrating eqn (2) for each monomer forming the flagellum. We select K = 100, as a reasonable choice for granting inextensibility, and consider different bending modulus B and active cycles, 2π/ω. The time step is chosen to be of the order of h ≃ 10−4 to avoid instabilities of the Brownian dynamics code (Euler scheme) within the whole explored range of parameters. The flagellum is initialized by aligning all the monomers to the x-axis in their relaxed configuration: xn = nb, (n = 0,…,N). Main observables needed to characterize the flagellum dynamics were sampled and eventually averaged over a time 10(2π/ω), i.e. for ten forcing cycles, after discarding a transient of about 106 time steps to allow the system's relaxation onto a robust stationary regime.The left panels of Fig. 2 and 3 show snapshots of flagellum conformations from simulations for three values of ω, with B = 10 and B = 20 respectively, while the right panels report the corresponding theoretical flagellum conformations obtained by solving eqn (10) and using eqn (8) to reconstruct the x-coordinate in the WBA. The reasonable agreement between simulation and theory has been possible by adjusting the coefficient ν of the stretching term. For calibrating ν, we compared the motion of the flagellum tail (last monomer) with its theoretical prediction from eqn (10). The beating oscillations of the tail observed in the simulations and displayed in Fig. 5 (black dots), can be described by the following simple evolutionary laws
x(t) = x0 + ax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ωt) + bx cos(2ωt) + bx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2ωt) sin(2ωt) | (21) |
y(t) = ay![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) + by cos(ωt) + by![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt). sin(ωt). | (22) |
 | ||
| Fig. 5 Trajectory of the tail position xL(t),yL(t) of a flagellum of N + 1 = 41 beads (length L = Nb), bending rigidity B = 20 and under a active perturbation with k = 5, ω = 0.10. Black dots are the simulated data and the red curves represent the fit with eqn (21) and (22). | ||
As we will see in the following, the frequency doubling of the x coordinate is a natural consequence of the quasi-inextensibility of the flagellum. This phenomenon has also been observed in simulations of wall-anchored semiflexible polymers under oscillatory shear flow.56
The amplitude of the y(t) signal is 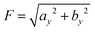 whose numerical value can be obtained by a fitting procedure to the simulation time series, see Fig. 5. The effective value of ν is such that F2 ≃
whose numerical value can be obtained by a fitting procedure to the simulation time series, see Fig. 5. The effective value of ν is such that F2 ≃ ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 2(L) +
2(L) + ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 2(L), where
2(L), where
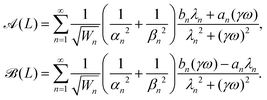 | (23) |
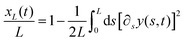 | (24) |
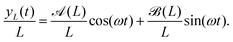 | (25) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (L)2 +
(L)2 + ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) (L)2 from the semiflexible flagellum theory
(L)2 from the semiflexible flagellum theory
| ω | 0.01 | 0.10 | 1.0 |
| B = 10 | ν = 0.1696 | ν = 0.1950 | ν = 0.5632 |
| B = 20 | ν = 0.3375 | ν = 0.3710 | ν = 0.7150 |
 | ||
| Fig. 6 Trajectory described during the beating process by the position of the tail (last-monomer) of a flagellum with N = 40 monomers of length b = 1, for two bending constants and two frequencies as indicated in the panels. The motion recalls a bi-lobed Lissajous figure, the points are the simulation results, whereas the curves are the predicted trajectory described by eqn (26a) and (26b). The red-thick Lissajuous figures correspond to the optimal ν reported in Table 1. For comparison, we also plot the dashed blue lines corresponding to the flagellum with ν = 0 to underscore the important role of the stretching contribution. | ||
The dashed lines in Fig. 6 represent the theoretical Lissajous plots that by tuning ν converge and overlap with the simulation data.
The scattering (spread) observed in the simulation data is presumably due to the interplay of chaos and thermal noise which we do not investigate here. The reader can refer to ref. 67 for a discussion of possible chaotic behaviors in anchored polymers driven by a localized oscillating force. It is, however, clear that on passing from ω = 0.01 to ω = 0.10, the positions of the tail turn out to be more scattered, even if the thermal noise in the simulation is the same. This is an intriguing role of the active forcing at high frequencies, which introduces a sort of “stochastization effect” that dominates over the small thermal noise, as shown in eqn (19).
It is interesting to discuss how the bi-lobed Lissajous-like behavior of the tail emerges in terms of the continuum theory from eqn (24) and (25). Fig. 6 shows that such Lissajous figures are characterized by a frequency ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, corresponding to a frequency doubling of the x-motion: ωx = 2ωy. Indeed, the frequencies of a Lissajous' figure are known to satisfy the relationship
1, corresponding to a frequency doubling of the x-motion: ωx = 2ωy. Indeed, the frequencies of a Lissajous' figure are known to satisfy the relationship
| Nx·ωx = Ny·ωy, |
This ratio is expected as a straightforward consequence of the quasi-inextensibility of the chain, in fact by substituting eqn (25) into eqn (24), and expressing formally the integrals as L〈⋯〉, we get
P = 〈[![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ′(s)]2〉, Q = 〈[ ′(s)]2〉, Q = 〈[![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ′(s)]2〉, R = 〈 ′(s)]2〉, R = 〈![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ′(s) ′(s)![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ′(s)〉, ′(s)〉, |
| cos2(ωt) = [1 + cos(2ωt)]/2 |
| sin2(ωt) = [1 − cos(2ωt)]/2 |
xL(t)/L = S + Sx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ωt + Δx) cos(2ωt + Δx) | (26a) |
yL(t)/L = Sy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt + Δy), cos(ωt + Δy), | (26b) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Δx) = (Q − P)/4, Sx
cos(Δx) = (Q − P)/4, Sx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Δx) = R/2 and Sy
sin(Δx) = R/2 and Sy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Δy) =
cos(Δy) = ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (L)/L, Sy
(L)/L, Sy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Δy) =
sin(Δy) = ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) (L)/L. In conclusion, the tail's behavior can be mathematically explained by considering that the solution (8) and (19) evaluated at s = L results in a combination of sin(ωt) and cos(ωt) which can be rearranged in the form (26a) and (26b). Moreover, the shape figure depends not only on the frequency (2
(L)/L. In conclusion, the tail's behavior can be mathematically explained by considering that the solution (8) and (19) evaluated at s = L results in a combination of sin(ωt) and cos(ωt) which can be rearranged in the form (26a) and (26b). Moreover, the shape figure depends not only on the frequency (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and amplitude ratio (Sx
1) and amplitude ratio (Sx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sy) but also on the phase shift, Δ = Δy − Δx.
Sy) but also on the phase shift, Δ = Δy − Δx.
It's worth noting that each internal monomer of the flagellum also undergoes a similar type of Lissajous motion, albeit the greatest amplification is observed in the free tail.
Another quantity often used to characterize the dynamical response of the flagellum and its conformational properties is the end-to-end distance, which for the hinged system to the origin simply reads
| Ree2(t) = x2(L,t) + y2(L,t). |
 | ||
| Fig. 7 Simulated time course (black) of the squared end-to-end distance Ree2 of a flagellum with N + 1 = 41 beads each of diameter b = 1, corresponding to a length L = Nb. The chain has a bending rigidity strength B = 10 and perturbation k = 5, ω = 0.01 and ω = 0.10. The simulations show a periodic behavior with a main frequency ω that is double the forcing frequency. The red curve represents the expected Ree2 obtained by the solution (8) and (19). | ||
3.1 Spatial modulation
So far, we have analyzed the influence of the force cycle, defined by ω, on the flagellum beating dynamics, now, we would like to focus on the role of k in shaping the spatial conformation of the flagellum. To check if the spatial modulation induced by the perturbation is sustained by the filament dynamics, we computed the bond–bond correlation starting from the hinged point, x0 = 0, y0 = 0, | (27) |
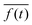 indicates the time average, which in our case, coincides with the average over a period, 2π/ω, of the active force. Fig. 8 presents the simulated data for Cb(n) (black points) averaged over a long equilibrium run at low temperature T = 0.001, corresponding to a flagellum of bending stiffness B = 10, (upper panel) and B = 20 (lower panel) both perturbed with frequency ω = 0.10. Cb(n) exhibits five peaks, consistent with the oscillations imposed by the active-force wave number, k = 5(2π/L), indicating that the chain's stiffness can support the external modulation.
indicates the time average, which in our case, coincides with the average over a period, 2π/ω, of the active force. Fig. 8 presents the simulated data for Cb(n) (black points) averaged over a long equilibrium run at low temperature T = 0.001, corresponding to a flagellum of bending stiffness B = 10, (upper panel) and B = 20 (lower panel) both perturbed with frequency ω = 0.10. Cb(n) exhibits five peaks, consistent with the oscillations imposed by the active-force wave number, k = 5(2π/L), indicating that the chain's stiffness can support the external modulation.
 | ||
| Fig. 8 Bond–bond correlation C(n) for filaments of N = 40 monomers, with bending stiffness B = 10 and B = 20, both having the same ω = 0.10. Black dots represent simulation data, while red dots represent theoretical predictions. Both the simulation and theoretical plots reveal spatial modulation with five peaks, consistent with the active-force wave number k = 5(2π/L), where L = Nb. The average is taken over a long equilibrium simulation run at temperature T = 0.001. The red plots, drawn from eqn (29), show a pattern of peaks similar to the simulation data. | ||
Simulations also show that the bond orientation becomes more correlated as the bending stiffness increases, this is expected since the persistence length is higher for B = 20. The faster decay of the correlation for B = 10 is also indicative of weaker persistence, and a “visual estimate” of the persistence length of the flagellum can be obtained from the onset of a large deviation of the tail region from the horizontal dashed line.
A theoretical prediction of bond–bond correlation behavior can be obtained from the continuum model by using the following formula
 | (28) |
In the WBA, the bond vector can be written as
By using eqn (19) and the average properties of trigonometric functions over a period, after simple algebraic manipulations, C(s) can be recast to the form
 | (29) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and
and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) are the expressions in eqn (23). Notice that correctly Cb(s = 0) = b2 = 1, as expected from the “quasi-inexensibility” of the flagellum bonds.
are the expressions in eqn (23). Notice that correctly Cb(s = 0) = b2 = 1, as expected from the “quasi-inexensibility” of the flagellum bonds.
For a comparison, Fig. 8 also displays the corresponding quantity Cb(s) derived from the continuum model, eqn (29) (red points). Although a precise quantitative agreement between Cb(n) and Cb(s) is lacking especially in the tail region where the application of WBA is questionable, it is noteworthy that they exhibit five similar oscillations driven by the active forcing modulation, k = 5(2π/L).
This suggests that the qualitative structure of the beating dynamics remains consistent when passing from the discrete to the continuum models.
4 Conclusions
The main purpose of this study was to investigate the selection of flagella conformations arising from the bending resistance of a slender semi-flexible structure to an extended force (mimicking the activity of molecular motors) and driving its evolution across different spatiotemporal patterns characterized by ω,k.In particular, we developed an effective mechanical theory, that upon “tuning” the longitudinal stretching term, can explain (at least qualitatively) some important features of the beating dynamics observed in the simulation, such as the bond–bond spatial correlation and temporal oscillation of the flagellum tail which, in a certain frequency range of the active force, describes Lissajous' figures of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 frequency ratio. The theory clearly explains that such a 2
1 frequency ratio. The theory clearly explains that such a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 frequency ratio arises from a frequency doubling of the x-oscillation, which in turn, is a natural consequence of the chain inextensibility.
1 frequency ratio arises from a frequency doubling of the x-oscillation, which in turn, is a natural consequence of the chain inextensibility.
Furthermore, our theoretical analysis sheds light on the ranges of ω and k of the active force required to confer a prescribed spatial modulation to the flagellum and produce a significant effect on its beating dynamics. Indeed, as explained in Section 2.2, for high-frequencies forcing (ω ≫ 1) the amplitude of periodic modulations of transversal profile y(s,t) is largely suppressed, and thermal fluctuations dominate the flagellum dynamics.
Additionally, the wavelength, 2π/k, of the active forcing must be consistent with the persistence length, lp, of the flagellum, as high levels of spatial modulation cannot be energetically sustained by a system with a given bending stiffness, see Appendix C for a less qualitative argument. Such a result could play a key role in designing bio-inspired self-propelled engines.
We also provided evidence (see Appendix D) that, as long as WBA holds, anisotropies in hydrodynamical interaction, which are crucial for self-propulsion, play a little role in the selection of conformations of flagella.
Although the modeling of active-like dynamics is not fully realistic from a biological point of view, we expect that the theory could be generalized to describe different scenarios, including cases where the active force has true “internal” origin by modeling the action of molecular motors distributed along the flagella. Thus, this work constitutes a first step towards more realistic description of active bio-filaments giving insight into the mechanism that arises from the interplay between mechanical and active forces, which is responsible for their conformation dynamics.
Data availability
The source files for Fig. 2–8 of the manuscript are available at https://github.com/cecconif/flagellum-wlc-data. Each file can be opened using the graphical software Grace, which can be found and downloaded from the site https://plasma-gate.weizmann.ac.il/Grace/. Such files also contain, at the end, the raw data used to generate the figures.Conflicts of interest
There are no conflicts to declare.Appendices
A Derivation of the eigenmodes
In this appendix, we derive the eigenmodes which are solutions of the equation | (30) |
Since eqn (30) is linear, its solution requires solving the associated characteristic polynomial
| εμ4 − 2νμ2 − λn = 0, |
then, it is straightforward to obtain the following algebraic identities
| β2 − α2 = 2ν/ε | (31) |
| λ = εα4 + 2να2 = εβ4 − 2νβ2. | (32) |
Then the general solution of eqn (30) can be written as
ψ(s) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(αs) + B sin(αs) + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(βs) + C sinh(βs) + C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(αs) + D cos(αs) + D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosh(βs); cosh(βs); | (33) |
α2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(αL)A − β sin(αL)A − β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(βL)B = 0 sinh(βL)B = 0 |
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(αL)A − α cos(αL)A − α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosh(βL)B = 0, cosh(βL)B = 0, |
To exclude the nontrivial solution A = B = D = 0, the determinant of the coefficient matrix should be zero, therefore we have the condition α3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(αL)cosh(βL) = β3
sin(αL)cosh(βL) = β3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(αL)sinh(βL) that can be recast to
cos(αL)sinh(βL) that can be recast to
α3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(αL) = β3 tan(αL) = β3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tanh(βL) tanh(βL) | (34) |
After simple algebraic manipulations, we obtain from eqn (33) the final expression of the eigenfunctions (Fig. 9),
 | (35) |
W
n
being a normalization constant such that
 | (36) |
B Solution of the mode amplitude equation
We derive the evolution of the n-th mode amplitude, yn(t), that obeys the equation | (37) |
after a change of variable t − z → z
and expanding cos[ω(t − z)] and sin[ω(t − z)], we obtain
| yn(t) = (anZ1 − bnZ2)cos(ωt) + (anZ2 + bnZ2)sin(ωt) |
Thus re-arranging, we can write
which is the searched solution, eqn (18) of the main text.
The same expression could have been obtained, by substituting the test function (similar to the known term) yn(t) = C1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) + C2
cos(ωt) + C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) into eqn (37) and choosing the coefficients C1, C2 to make both members equal.
sin(ωt) into eqn (37) and choosing the coefficients C1, C2 to make both members equal.
C A simple criterium
In this appendix, we discuss a simple energetic argument that justifies the physical limits of the flagellum response.The argument compares the energy of a perturbation mode and the energy of the flagellum solution (11), using the continuum energy formula59
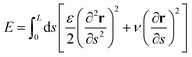 | (38) |
where, the pre-factor 2f0/L is the necessary scale to make the amplitude of F(s,t) and the flagellum longitudinal oscillation y(s,t) of the same order. When substituted into eqn (38), F(s,t) requires an energetic cost
This cost has to be compared with the energy of the flagellum solution, which can be computed using its expansion in eigenmodes, which due to their orthogonality, yields (11)
note that, with respect to the expressions (16) and (17), the forcing amplitude, f0, has been factored out, thus we obtain
 | (39) |
In other words, if E(k) is too large due to a high value of k, we introduce too much energy into the system, which must be balanced by choosing a small ω, and vice versa, if k is too small, it requires a very large ω.
This situation is also critical because, at high frequencies, the system dynamics are significantly attenuated, leading to a decoupling between the flagellum's dynamics and the fast oscillating perturbation: in this regime, the flagellum perceives this rapid oscillation as additional “noise”.
D Anisotropic hydrodynamic drag
In this appendix, we justify neglecting anisotropic effects of the drag coefficient used in our model of flagellar dynamics. The overdamped anisotropic dynamics of the i-th bead of the flagellum is governed by the stochastic differential equation,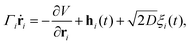 | (40) |
| Γiṙi = γ‖(ṙi·ti)ti + γ⊥(ṙi·ni)ni. | (41) |
and normal vector ni·ti = 0 referred to bead i, with the boundary condition on the last bead tN+1 = tN.
By inverting Γi, or equivalently projecting eqn (40) along ti and ni we obtain the Brownian dynamics in the anisotropic drag
 | (42) |
is the total effective force.
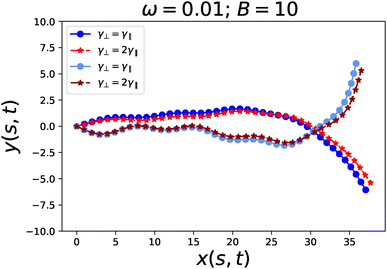
Eqn (42) was integrated using the same Euler scheme to obtain the flagellum conformations presented in Fig. 10. The comparison shows that the conformations are weakly affected by drag anisotropy. This observation is further supported by looking at the trajectories of the terminal monomer, which form Lissajous figures that remain essentially unchanged, apart from a slight adjustment in their aspect ratio (see Fig. 11).
A similar conclusion could have been derived from the theoretical side by using the WBA. Indeed, let us consider the continuum model, eqn (4),
 | (43) |
| Γ = γ‖ttT + γ⊥nnT | (44) |
According to eqn (7), when the weakly bending approximation holds, t and n can be parametrized as
 | (45) |
Inserting these expressions into eqn (44) leads to
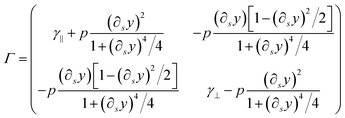 | (46) |
 | (47) |
 | (48) |
 | (49) |
 | (50) |
The above theoretical considerations are also confirmed by numerical simulation, as shown in Fig. 10 and 11.
In conclusion, both simulation results and theoretical analysis indicate that drag anisotropy plays a minor role when the system is anchored and unable to swim. In this constrained scenario, the absence of net translation suppresses the influence of anisotropic drag on the flagellum's dynamics and conformations.
Acknowledgements
The authors are grateful to A. Cavagna for stimulating discussions and his precious remarks and suggestions, we also thank L. Caprini for a critical reading of the manuscript. F. C., A. P., M. V. acknowlege funding from the Italian Ministero dell'Università e della Ricerca under the programme PRIN 2022 (“re-ranking of the final lists”), number 2022KWTEB7, cup B53C24006470006.Notes and references
- N. Wadhwa and H. C. Berg, Bacterial motility: machinery and mechanisms, Nat. Rev. Microbiol., 2022, 20(3), 161–173 CrossRef CAS PubMed.
- W. Gilpin, M. S. Bull and M. Prakash, The multiscale physics of cilia and flagella, Nat. Rev. Phys., 2020, 2(2), 74–88 CrossRef.
- J. B. Keller and S. I. Rubinow, Swimming of flagellated microorganisms, Biophys. J., 1976, 16(2), 151–170 CrossRef CAS PubMed.
- S. Khan and J. M. Scholey, Assembly, functions and evolution of archaella, flagella and cilia, Curr. Biol., 2018, 28(6), R278–R292 CrossRef CAS PubMed.
- L. E. Kuek and R. J. Lee, First contact: the role of respiratory cilia in host-pathogen interactions in the airways, Am. J. Physiol.: Lung Cell. Mol. Physiol., 2020, 319(4), L603–L619 CrossRef CAS PubMed.
- X. M. Bustamante-Marin and L. E. Ostrowski, Cilia and mucociliary clearance, Cold Spring Harbor Perspect. Biol., 2017, 9(4), a028241 CrossRef PubMed.
- J. I. Arellano, S. M. Guadiana, J. J. Breunig, P. Rakic and M. R. Sarkisian, Development and distribution of neuronal cilia in mouse neocortex, J. Comp. Neurol., 2012, 520(4), 848–873 CrossRef CAS PubMed.
- C. Boehlke, F. Kotsis, V. Patel, S. Braeg, H. Voelker, S. Bredt, T. Beyer, H. Janusch, C. Hamann and M. Gödel, et al., Primary cilia regulate mTORC1 activity and cell size through lkb1, Nat. Cell Biol., 2010, 12(11), 1115–1122 CrossRef CAS PubMed.
- G. Wheway, L. Nazlamova and J. T. Hancock, Signaling through the primary cilium, Front. Cell Dev. Biol., 2018, 6, 8 CrossRef PubMed.
- D. E. Jaalouk and J. Lammerding, Mechanotransduction gone awry, Nat. Rev. Mol. Cell Biol., 2009, 10(1), 63–73 CrossRef CAS PubMed.
- P. P. Lele, B. G. Hosu and H. C. Berg, Dynamics of mechanosensing in the bacterial flagellar motor, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(29), 11839–11844 CrossRef CAS PubMed.
- R. Ma, G. S. Klindt, I. H. Riedel-Kruse, F. Jülicher and B. M. Friedrich, Active phase and amplitude fluctuations of flagellar beating, Phys. Rev. Lett., 2014, 113(4), 048101 CrossRef PubMed.
- C. Maggi, F. Saglimbeni, V. C. Sosa, R. Di Leonardo, B. Nath and A. Puglisi, Thermodynamic limits of sperm swimming precision, PRX Life, 2023, 1(1), 013003 CrossRef.
- R. Ferretta, R. Di Leonardo and A. Puglisi, Thermal fluctuations for a three-beads swimmer, Phys. Rev. Res., 2024, 6(3), 033117 CrossRef CAS.
- A. Sharma, B. M. Friedrich and V. F. Geyer, Active fluctuations of axoneme oscillations scale with number of dynein motors, Proc. Natl. Acad. Sci. U.S.A., 2024, 121(46), e2406244121 CrossRef CAS PubMed.
- F. Wang, A. M. Burrage, S. Postel, R. E. Clark, A. Orlova, E. J. Sundberg, D. B. Kearns and E. H. Egelman, A structural model of flagellar filament switching across multiple bacterial species, Nat. Commun., 2017, 8(1), 960 CrossRef PubMed.
- B. L. Carroll, T. Nishikino, W. Guo, S. Zhu, S. Kojima, M. Homma and J. Liu, The flagellar motor of vibrio alginolyticus undergoes major structural remodeling during rotational switching, eLife, 2020, 9, e61446 CrossRef CAS PubMed.
- D. F. Blair, Flagellar movement driven by proton translocation, FEBS Lett., 2003, 545(1), 86–95 CrossRef CAS PubMed.
- C. R. Calldine, Change of waveform in bacterial flagella: the role of mechanics at the molecular level, J. Mol. Biol., 1978, 118(4), 457–479 CrossRef.
- M. Hines and J. J. Blum, Three-dimensional mechanics of eukaryotic flagella, Biophys. J., 1983, 41(1), 67–79 CrossRef CAS PubMed.
- C. Moreau, L. Giraldi and H. Gadêlha, The asymptotic coarse-graining formulation of slender-rods, bio-filaments and flagella, J. R.Soc., Interface, 2018, 15(144), 20180235 CrossRef PubMed.
- P. K. Purohit, M. E. Arsenault, Y. Goldman and H. H. Bau, The mechanics of short rod-like molecules in tension, Int. J. Non-Linear Mech., 2008, 43(10), 1056–1063 CrossRef.
- A. Taloni, D. Vilone and G. Ruta, General theory for plane extensible elastica with arbitrary undeformed shape, Int. J. Eng. Sci., 2023, 193, 103941 CrossRef.
- A. Kitao and H. Hata, Molecular dynamics simulation of bacterial flagella, Biophys. Rev., 2018, 10(2), 617–629 CrossRef CAS PubMed.
- A. Arkhipov, P. L. Freddolino, K. Imada, K. Namba and K. Schulten, Coarse-grained molecular dynamics simulations of a rotating bacterial flagellum, Biophys. J., 2006, 91(12), 4589–4597 CrossRef CAS PubMed.
- R. H. Dillon, L. J. Fauci, C. Omoto and X. Yang, Fluid dynamic models of flagellar and ciliary beating, Ann. N. Y. Acad. Sci., 2007, 1101(1), 494–505 CrossRef PubMed.
- G. Zhu, L. Gao, Y. Sun, W. Wei and L.-T. Yan, Non-equilibrium structural and dynamic behaviors of active polymers in complex and crowded environments, Rep. Prog. Phys., 2024, 87(5), 054601 CrossRef CAS PubMed.
- A. Ghosh and N. S. Gov, Dynamics of active semiflexible polymers, Biophys. J., 2014, 107(5), 1065–1073 CrossRef CAS PubMed.
- R. Samatham, K. J. Kim, D. Dogruer, H. R. Choi, M. Konyo, J. D. Madden, Y. Nakabo, J.-D. Nam, J. Su, S. Tadokoro, et al., Active polymers: an overview, Electroactive polymers for robotic applications: Artificial muscles and sensors, 2007, pp. 1–36 Search PubMed.
- R. G. Winkler and G. Gompper, The physics of active polymers and filaments, J. Chem. Phys., 2020, 153(4), 040901 CrossRef CAS PubMed.
- J. Käs, H. Strey, J. X. Tang, D. Finger, R. Ezzell, E. Sackmann and P. Janmey, F-actin, a model polymer for semiflexible chains in dilute, semidilute, and liquid crystalline solutions, Biophys. J., 2016, 70(2), 609–625 CrossRef PubMed.
- C. H. Wiggins, D. Riveline, A. Ott and R. E. Goldstein, Trapping and wiggling: elastohydrodynamics of driven microfilaments, Biophys. J., 1998, 74(2), 1043–1060 CrossRef CAS PubMed.
- C. K. Ober, Shape persistence of synthetic polymers, Science, 2000, 288(5465), 448–449 CrossRef CAS PubMed.
- D. Hofmann, L. Fritz, J. Ulbrich and D. Paul, Molecular modelling of amorphous membrane polymers, Polymer, 1997, 38(25), 6145–6155 CrossRef CAS.
- O. Kratky and G. Porod, Röntgenuntersuchung gelöster fadenmoleküle, Recl. Trav. Chim. Pays-Bas, 1949, 68(12), 1106–1122 CrossRef CAS.
- A. Marantan and L. Mahadevan, Mechanics and statistics of the worm-like chain, Am. J. Phys., 2018, 86(2), 86–94 CrossRef CAS.
- T. Eisenstecken, G. Gompper and R. G. Winkler, Conformational properties of active semiflexible polymers, Polymers, 2016, 8(8), 304 CrossRef PubMed.
- S. F. Schoeller and E. E. Keaveny, From flagellar undulations to collective motion: predicting the dynamics of sperm suspensions, J. R.Soc., Interface, 2018, 15(140), 20170834 CrossRef PubMed.
- E. Lauga, The fluid dynamics of cell motility, Cambridge University Press, 2020, vol. 62 Search PubMed.
- R. G. Cox, The motion of long slender bodies in a viscous fluid part 1. general theory, J. Fluid Mech., 1970, 44(4), 791–810 CrossRef.
- K. E. Machin, Wave propagation along flagella, J. Exp. Biol., 1958, 35(4), 796–806 CrossRef.
- H. Felgner, R. Frank and M. Schliwa, Flexural rigidity of microtubules measured with the use of optical tweezers, J. Cell Sci., 1996, 109(2), 509–516 CrossRef CAS PubMed.
- D. Riveline, C. H. Wiggins, R. E. Goldstein and A. Ott, Elastohydrodynamic study of actin filaments using fluorescence microscopy, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56(2), R1330 CrossRef CAS.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Microscopic artificial swimmers, Nature, 2005, 437(7060), 862–865 CrossRef CAS PubMed.
- P. V. Bayly, B. L. Lewis, P. S. Kemp, R. B. Pless and S. K. Dutcher, Efficient spatiotemporal analysis of the flagellar waveform of Chlamydomonas reinhardtii, Cytoskeleton, 2010, 67(1), 56–69 CrossRef CAS PubMed.
- Z. El Khiyati, R. Chesneaux, L. Giraldi and J. Bec, Steering undulatory micro-swimmers in a fluid flow through reinforcement learning, Eur. Phys. J. E:Soft Matter Biol. Phys., 2023, 46(6), 43 CrossRef CAS PubMed.
- T. Eisenstecken, G. Gompper and R. G. Winkler, Internal dynamics of semiflexible polymers with active noise, J. Chem. Phys., 2017, 146(15), 154903 CrossRef PubMed.
- C. M. Marques and G. H. Fredrickson, Rigid Gaussian chains i: The scattering function, J. Phys. II, 1997, 7(12), 1805–1816 CrossRef CAS.
- G. T. Barkema, D. Panja and J. M. J. Van Leeuwen, Semiflexible polymer dynamics with a bead-spring model, J. Stat. Mech.:Theory Exp., 2014, 2014(11), P11008 CrossRef.
- S. Zeng, M. Chinappi, F. Cecconi, T. Odijk and Z. Zhang, Dna compaction and dynamic observation in a nanopore gated sub-attoliter silicon nanocavity, Nanoscale, 2022, 14(33), 12038–12047 RSC.
- J. Kierfeld, O. Niamploy, V. Sa-Yakanit and R. Lipowsky, Stretching of semiflexible polymers with elastic bonds, Eur. Phys. J. E:Soft Matter Biol. Phys., 2004, 14, 17–34 CrossRef CAS PubMed.
- G. Saggiorato, L. Alvarez, J. F. Jikeli, U. B. Kaupp, G. Gompper and J. Elgeti, Human sperm steer with second harmonics of the flagellar beat, Nat. Commun., 2017, 8(1), 1415 CrossRef PubMed.
- G. De Canio, E. Lauga and R. E. Goldstein, Spontaneous oscillations of elastic filaments induced by molecular motors, J. R.Soc., Interface, 2017, 14(136), 20170491 CrossRef PubMed.
- G. A. Huber and J. A. McCammon, Brownian dynamics simulations of biological molecules, Trends Chem., 2019, 1(8), 727–738 CrossRef CAS PubMed.
- L. Natali, L. Caprini and F. Cecconi, How a local active force modifies the structural properties of polymers, Soft Matter, 2020, 16(10), 2594–2604 RSC.
- A. Lamura, R. G. Winkler and G. Gompper, Wall-anchored semiflexible polymer under large amplitude oscillatory shear flow, J. Chem. Phys., 2021, 154(22), 224901 CrossRef CAS PubMed.
- R. G. Winkler, P. Reineker and L. Harnau, Models and equilibrium properties of stiff molecular chains, J. Chem. Phys., 1994, 101(9), 8119–8129 CrossRef CAS.
- R. A. Harris and J. E. Hearst, On polymer dynamics, J. Chem. Phys., 1966, 44(7), 2595–2602 CrossRef CAS.
- B. Obermayer and E. Frey, Tension dynamics and viscoelasticity of extensible wormlike chains, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 80(4), 040801(R) CrossRef PubMed.
- R. E. Goldstein and S. A. Langer, Nonlinear dynamics of stiff polymers, Phys. Rev. Lett., 1995, 75(6), 1094 CrossRef CAS PubMed.
- D. Panja, G. T. Barkema and J. M. J. van Leeuwen, Efficient simulation of semiflexible polymers, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2015, 92(3), 032603 CrossRef PubMed.
- K. Soda, Dynamics of stiff chains. i. equation of motion, J. Phys. Soc. Jpn., 1973, 35(3), 866–870 CrossRef.
- S. R. Aragon and R. Pecora, Dynamics of wormlike chains, Macromolecules, 1985, 18(10), 1868–1875 CrossRef CAS.
- S. L. Poelert and A. A. Zadpoor, Analytical and numerical methods for capturing the thermal fluctuations of semiflexible polymers, Macromol. Theory Simul., 2012, 21(6), 357–371 CrossRef CAS.
- R. G. Winkler, Conformational and rheological properties of semiflexible polymers in shear flow, J. Chem. Phys., 2010, 133(16), 164905 CrossRef PubMed.
- X. Liao, P. K. Purohit and A. Gopinath, Extensions of the worm-like-chain model to tethered active filaments under tension, J. Chem. Phys., 2020, 153(19), 194901 CrossRef CAS PubMed.
- A. K. Chattopadhyay and D. Marenduzzo, Dynamics of an anchored polymer molecule under an oscillating force, Phys. Rev. Lett., 2007, 98(8), 088101 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |