 Open Access Article
Open Access ArticleContinuum mechanics of differential growth in disordered granular matter
Noemie S.
Livne†
 a,
Tuhin
Samanta†
a,
Tuhin
Samanta†
 b,
Amit
Schiller†
a,
Itamar
Procaccia
bc and
Michael
Moshe
b,
Amit
Schiller†
a,
Itamar
Procaccia
bc and
Michael
Moshe
 *a
*a
aRacah Institute of Physics, The Hebrew University of Jerusalem, Jerusalem, 9190, Israel. E-mail: michael.moshe@mail.huji.ac.il
bDept. of Chemical Physics, The Weizmann Institute of Science, Rehovot, 76100, Israel
cSino-Europe Complexity Science Center, School of Mathematics, North University of China, Shanxi, Taiyuan, 030051, China
First published on 6th June 2025
Abstract
Disordered granular matter exhibits mechanical responses that occupy the boundary between fluids and solids, lacking a complete description within a continuum theoretical framework. Recent studies have shown that, in the quasi-static limit, the mechanical response of disordered solids to external perturbations is anomalous and can be accurately predicted by the theory of “odd dipole screening.” In this work, we investigate responsive granular matter, where grains change size in response to stimuli such as humidity, temperature, or other factors. We develop a geometric theory of odd dipole-screening, incorporating the growth field into the equilibrium equation. Our theory predicts an anomalous displacement field in response to non-uniform growth fields, confirmed by molecular dynamics simulations of granular matter. Although the screening parameters in our theory are phenomenological and not derived from microscopic physics, we identify a surprising relationship between the odd parameter and Poisson's ratio. This theory has implications for various experimental protocols, including non-uniform heating or wetting, which lead to spatially varying expansion fields.
1 Introduction
A densely packed assembly of elastic grains that forms a jammed granular material is able to withstand external shear stress similarly to solid materials. Unlike conventional solids, stress in the jammed state is transmitted through force chains – networks of particles in contact that selectively bear the external load.1 Close to the jamming point only a fraction of the particles participate in these chains. Consequently, when grains undergo volume expansion due to thermal, humidity,2 or other environmental changes, the mechanical impact varies depending on its position within the force chain network.3 Therefore, the mechanical state of a growing and responsive granular material is expected to deviate significantly from that of elastic-like growing solids.4–6 The main objective of this work is to study the effect of growth on granular matter using a continuum theoretical framework. A central objective in the theory of granular matter is the development of a complete continuum framework that accurately describes the complex phenomenology exhibited by granular materials. Attempts along this line include the description of active and passive granular matter in, or at the verge of, mechanical equilibrium.7–12A key challenge in developing continuum theories for disordered granular materials is that their response to mechanical perturbations involves plastic events, characterized by localized particle rearrangements that relax internal stresses. Unlike crystalline solids, where plastic deformations can be described using dislocation theory, the lack of long-range order in disordered solids necessitates alternative approaches to model plasticity. Several theoretical frameworks have been proposed, including Eshelby inclusions,13,14 shear transformation zones (STZs),15,16 and elasto-plastic models,17–19 all of which aim to capture the collective rearrangement of particles under stress. However, these models do not provide a closed-form continuum theory that generalizes classical elasticity to describe deformation and displacement fields in amorphous solids. In contrast, recent studies have demonstrated that, despite the microscopic complexity of granular materials, their averaged equilibrium response can be effectively described using a continuum mechanical screening framework, where mechanical relaxations are modeled as interacting elastic charges.20–22
More specifically, in this theory, plastic rearrangements adjust the material's reference state and induce elastic charges that mediate strain relaxation. These charges obey conservation laws. Just as in electrostatics, where local rearrangements of charge generate electrostatic dipoles or higher-order multipoles, in mechanics, the lowest-order multipole allowed by conservation laws is the quadrupole.23 The effect of mechanical screening by plastic rearrangements is therefore described as a distribution of quadrupolar elastic charges.
When the nucleation energy of quadrupoles is high, such as when the system is under large pressure, the theory aligns with the elastic-like behavior of disordered solids. Conversely, when the nucleation energy is low, quadrupoles can organize non-uniformly, and screening is instead dominated by the nucleation of mechanical dipole-charges, an extension of dislocations to disordered solids.23–25 In this regime, mechanical screening leads to an anomalous response to external loads, where displacement fields deviate qualitatively from classical elasticity. For instance, while the elastic response to the inflation of a small, confined region is that of an Eshelby inclusion, experiments have shown that inflating a single particle in a jammed granular solid induces spatially oscillating displacement fields that were accurately predicted by mechanical screening theory.26 These predictions, along with other anomalies, have also been confirmed in numerical simulations of disordered granular and glassy materials.20,27 This continuum framework based on mechanical screening thus provides a novel pathway for extending continuum mechanics to describe the mechanical implications of growth in disordered granular materials.
Another key characteristic of disordered granular matter is the existence of non-vanishing work cycles, even in the presence of reversible plastic events.28,29 Due to the glassy structure of the energy landscape, it has been shown that after a closed loop in deformation space, the system does not return to its original microscopic state. As a result, energy is not conserved within the standard continuum framework, it may either be released or stored, leading to an apparent violation of energy conservation from a macroscopic perspective. This issue is naturally resolved if one explicitly accounts for the microscopic degrees of freedom associated with plastic events, but doing so contradicts the goal of developing an effective continuum description of disordered granular matter. A more recent theoretical advancement has revealed that mechanical screening in the presence of a glassy energy landscape, where energy conservation is effectively violated, can be formulated in terms of odd screening.30 The case of odd-quadrupole screening is equivalent to odd-elasticity, and introduces no new phenomenology. Contrary to that is the extension of mechanical screening theory to odd-dipole screening, a framework that leads to new phenomenology with anomalous displacement fields that deviate from previous odd or conservative predictions. These theoretical predictions have been experimentally confirmed in sheared granular materials.30 Therefore, to study the effect of growth in disordered granular matter, we focus below on incorporating growth fields into the framework of odd-dipole screening.
To analyze the mechanical response of disordered granular matter to nonuniform growth fields, we employ both analytical and numerical methods. On the analytical side, we extend the theory of odd dipole-screening to incorporate arbitrary growth fields, and focus on the specific setup wherein growth is induced by diffusive mechanisms, such as temperature or humidity variations, and derive explicit predictions for the resulting displacement fields. As a case study, we consider thermal expansion driven by a uniform heat source with a fixed-temperature boundary condition. We demonstrate that the resulting geometric state of the system corresponds to a flattened spherical configuration. This process is illustrated in Fig. 1, which presents the displacement fields across three regimes: elastic, screened, and odd-screened (see figure caption for details). On the numerical side, we perform molecular dynamics simulations of jammed granular matter experiencing a growth field by expanding the size of each grain according to the prescribed growth profile.
A fundamental aspect of the odd dipole-screening theory is the emergence of two screening moduli that accompany the classical elastic moduli. While we do not derive these moduli from microscopic interactions, our analysis uncovers a significant and nontrivial relationship between the measured screening and elastic moduli observed in simulations.
The remainder of this paper is structured as follows: in Section 2, we review the dipole-screening theory and extend it to account for differential growth, subsequently generalizing it to the odd-screening regime. Section 3 introduces the specific growth field considered in this study and presents the corresponding analytical solution. Section 4 describes our numerical simulations, where we systematically vary both growth fields under fixed physical conditions and physical conditions under a fixed growth field. Finally, in Section 5, we compare our theoretical predictions with the molecular dynamics simulations of differentially growing disordered granular matter and find excellent agreement between theory and simulations.
2 Theoretical framework
The following sections introduce the theory of dipole screening, its extension to incorporate growth, and finally, the generalization to odd-screening. Our starting point is an energy functional that accounts for both elastic strains and the nucleation of plastic rearrangements. To address the inherent coupling between elastic and plastic deformations encoded in the displacement field when measured relative to an initial state, we adopt a geometric approach wherein the reference state evolves in response to mechanical perturbations. This framework not only resolves complications arising from mixing elastic and plastic deformation modes in the displacement field, but also provides a direct pathway for incorporating growth. Finally, we extend the dipole screening constitutive relation to include symmetry-breaking terms, thereby generalizing the theory to account for odd screening.2.1 Geometric screening
This section reviews the main aspects of the theory of geometric screening introduced in ref. 22, which established a theoretical linkage between screening theory and geometric elasticity.31Assuming that the configuration prior to the application of the expansion profile is flat and stress free, its rest configuration is described by a Euclidean reference metric η. The energetic cost of a deformation is due to the elastic strain, which measures deviations from the reference metric.31 We assume that the reference metric can change in response to growth or mechanical perturbations, and as in ref. 22, we define a temporary reference metric ḡ = η + q where q is an anelastic strain that describes the particle rearrangements. The elastic strain is then:
 | (1) |
 , where
, where ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) is the elastic tensor encoding material Young modulus Y and Poisson's ratio ν
is the elastic tensor encoding material Young modulus Y and Poisson's ratio ν | (2) |
We further take into account the nucleation cost of the quadrupolar perturbation field. It was shown in ref. 22 that a hierarchy of screening modes is expected, from no screening in pure elasticity, through quadrupole, dipole, and monopole screening effectively forming a liquid-like state. Our focus in this work is on dipole screening which was shown to describe the phenomenology of disordered granular matter very well. Specifically, when the nucleation cost of a single quadrupolar charge is negligible, e.g. at small pressures, the multipole expansion of elastic charges allows the nucleation of dipoles with finite cost by non-uniformly distributing a field of quadrupolar charges32
Pdip = Div![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q. Q. | (3) |
Here, the quadrupole charge field is determined by the anelastic strain through Qαβ = εαμεβνqμν. The nucleation energy will have the form  , where ΛP is a tensor that encodes material properties, and in homogeneous and isotropic media is proportional to η
, where ΛP is a tensor that encodes material properties, and in homogeneous and isotropic media is proportional to η
 | (4) |
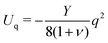 , otherwise, the nucleation cost of the quadrupolar field would not be negligible compared to Up (this is due to the appearance of q in (1)). Finally, we have the total energy density
, otherwise, the nucleation cost of the quadrupolar field would not be negligible compared to Up (this is due to the appearance of q in (1)). Finally, we have the total energy density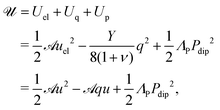 | (5) |
 | (6) |
 | (7) |
 | (8) |
| Pdip = κ(d − d0) | (9) |
 , and d0 is a constant of integration. Substituting into the equilibrium eqn (8) it reduces to a closed form equation for the displacement field,
, and d0 is a constant of integration. Substituting into the equilibrium eqn (8) it reduces to a closed form equation for the displacement field, | (10) |
2.2 Differential growth in screened solids
In geometric terms, applying an isotropic expansion profile ϕ(x) to every area element ΔS0 such that ΔS = ϕ(x)ΔS0 corresponds to assigning a new initial reference metric ḡ0 = ϕ(x)η, where η is the Euclidean metric that described the flat two-dimensional sample before it was deformed. The sample then responds through particle rearrangements and elastic deformation, reaching a new equilibrium configuration described by g. Because both the initial and final configurations are flat, as before, the original metric η and the actual metric g are related by a well-defined displacement field d, through (6).While the elastic energy remains in the form of (5), the full strain is modified. The elastic strain now satisfies
 | (11) |
 | (12) |
2.3 Odd dipole screening
Unlike elastic solids, which relax to a well-defined global energy minimum, granular materials are characterized by rough energy landscapes with many meta-stable states.28,33,34 As a result, performing a closed loop of deformations that returns the system to its macroscopic state can still lead to a net change in energy due to microscopic rearrangements. While this process is not dissipative in the traditional sense, it does not conserve energy either.In a previous work,30 the simplest possible non-conservative yet non-dissipative extension of the theory was introduced by coupling the mechanical response to the microscopic response field, specifically by adding an odd term to the coupling in (9). While still consistent with homogeneity and isotropy, it was shown that odd dipole screening is accompanied by spontaneous breakdown of chiral symmetry, and accounts for the amount of work that is extracted or loaded into the material upon completing a closed trajectory in configuration space. This hypothesis was experimentally verified in ref. 30, demonstrating its relevance to real systems. In our work, we test this generalization through simulations, focusing on an unrelated prediction of the theory.
Adding an odd term to the coupling in (9) introduces an antisymmetric component to the relationship. Instead of simply scaling by a constant, the coupling between Pdip and d now involves multiplication by a scaled rotation matrix:
 | (13) |
Consequently, the generalized equation for the displacement becomes
 | (14) |
It is interesting to note that similar anti-symmetric terms exist in the electrostatic analog of non-hermitian dielectrics. In that case the dielectric tensor consists of an anti-symmetric term that quantifies energy loss or gain.35,36 However, we emphasize that the odd dipole-screening mechanism developed in ref. 30 differs fundamentally from the recently studied odd-mechanics in driven granular matter.9 While the former describes an asymmetric constitutive relation between the displacement and dipoles, which effectively violates translational symmetry, the latter preserves this translational symmetry and relates stresses with strains a-symmetrically, ultimately leading to odd-elasticity.
3 Problem setup and analytical solution
To specify the growth function ϕ, we consider a specific model of thermal expansion in a system exposed to uniform heat source and fixed temperature on the boundary, with the temperature satisfying a diffusion equation.24 We show that in that situation the Gaussian curvature corresponding to the reference metric ḡ0 = ϕ(x)η is a constant, and we analyze the equilibrium equation with the corresponding growth field (14).3.1 Expansion due to a diffusive field
The following results apply to any system where a diffusive field induces isotropic expansion. Consider an isotropic and homogeneous elastic material with a thermal expansion parameter α. Then, a spatially varying temperature field T(x) induces a non-uniform thermal expansion. We assume that the material was initially at a uniform temperature T0 and stress-free in the plane. For a temperature change δT = T − T0, a segment of length![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) expands according to
expands according to ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ′ =
′ = ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (1 + αδT), where α is the thermal expansion coefficient. In the case of a non-uniform temperature field T(x), this relation generalizes for an infinitesimal length element d
(1 + αδT), where α is the thermal expansion coefficient. In the case of a non-uniform temperature field T(x), this relation generalizes for an infinitesimal length element d![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) as d
as d![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ′ = d
′ = d![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (1 + αdT). Due to the isotropy of the material, the deformation results in a conformally flat metric of the form ḡ0 = e2α(T−T0)η. The Gaussian curvature associated with this metric is given by
(1 + αdT). Due to the isotropy of the material, the deformation results in a conformally flat metric of the form ḡ0 = e2α(T−T0)η. The Gaussian curvature associated with this metric is given by![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) G = −αΔg0T = −αe−2α(T−T0)ΔT, G = −αΔg0T = −αe−2α(T−T0)ΔT, | (15) |
The temperature field T is not arbitrary but determined as a solution to the heat equation, subject to appropriate boundary conditions. The precise form of this equation depends on the microscopic model of heat transport. If the heat flux is defined in the laboratory (spatial) frame, the Laplacian operator is taken with respect to the spatial metric of the deformed configuration. Conversely, if the flux is defined in the material (reference) frame, the Laplacian is computed with respect to the reference metric. In the limit of small temperature variations, both formulations yield nearly identical results. For simplicity, and although alternative models could be considered, we adopt the latter approach here and formulate the heat equation in the reference frame. For a detailed discussion, see ref. 37.
In the reference manifold, the thermo-elastic problem requires solving a time-dependent heat equation while accounting for the intrinsic metric ḡ0
 | (16) |
![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) the material's thermal diffusivity. This relation highlights the intrinsic coupling of geometry and temperature, which can be highly nontrivial. However, in steady state with a time-independent heat source, the equation simplifies to
the material's thermal diffusivity. This relation highlights the intrinsic coupling of geometry and temperature, which can be highly nontrivial. However, in steady state with a time-independent heat source, the equation simplifies to![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) Δḡ0T + Q = 0. Δḡ0T + Q = 0. | (17) |
Using (15), this gives
 | (18) |
Thus, when expansion is driven by a diffusive field with a constant, spatially uniform source term, and the resulting expansion remains small and linear in the inducing field, the induced metric will have constant positive Gaussian curvature. Specifically, from eqn (18), the radius of curvature R of the resulting geometry is given by  . Note that if the heat equation were instead formulated in the lab frame, then for small temperature variations the Laplace–Beltrami operator reduces, to leading order, to the standard Laplacian. This approximation justifies the validity of the result even in that setting. For a circular elastic sample, this implies that its intrinsic geometry corresponds to that of a spherical cap with curvature set by the diffusion and expansion parameters. For a granular disordered matter, this reference state will not survive, and it will experience further plastic deformations that will modify it.
. Note that if the heat equation were instead formulated in the lab frame, then for small temperature variations the Laplace–Beltrami operator reduces, to leading order, to the standard Laplacian. This approximation justifies the validity of the result even in that setting. For a circular elastic sample, this implies that its intrinsic geometry corresponds to that of a spherical cap with curvature set by the diffusion and expansion parameters. For a granular disordered matter, this reference state will not survive, and it will experience further plastic deformations that will modify it.
3.2 Determining the expansion field
To use (12), we need an expansion profile ϕ(x) that induces an intrinsic Gaussian curvature of 1/R2 when applied to a disc of radius rout. Given the problem's rotational symmetry and the requirement that the expansion field is positive, we can denote ϕ(x) = e2φ(r). Substituting into (15), we now seek φ(r) such that | (19) |
The general solution to this equation is
 | (20) |
 | (21) |
To ensure the deformation doesn’t alter the total area – and thus maintains a constant pressure – we choose c2 accordingly. This leaves us with the final expansion field
 | (22) |
3.3 Solving for the displacement field
Having determined the expansion field (22), we now turn to solving (14) for the displacement field. In the limit where the imposed radius of curvature R is large compared to system size rout, the analytical solution takes the form| dr(r) = αrJ1(r/l1) + βrJ1(r/l2) + γrr, |
| dθ(r) = αθJ1(r/l1) + βθJ1(r/l2) + γθr, | (23) |
Sketches of representative solutions for even (θκ = 0) and odd (θκ ≠ 0) screening modes are depicted in Fig. 1(d) in dashed and solid lines respectively. In the next section, we outline the simulation protocol used to test these results.
4 Molecular dynamics simulations of 2D jammed disordered granular matter
For the simulation protocol, we employed four sizes of frictionless disks, of radii 0.4, 0.5, 0.6, and 0.7, placed randomly in a circular disk of initial radius rout = 75, all in dimensionless units. There are N = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 discs in all. An initial area fraction below the jamming threshold was chosen, and then the outer radius was isotropically reduced to achieve a finite chosen pressure. Open source code large-scale atomic/molecular massively parallel simulator (LAMMPS) are used to perform the simulations. In these, the normal contact force is a Hertzian force with force-constant Kn = 2000 and the viscoelastic damping constant for normal contact γn = 100. The mass of each disk is 1. The tangential contact force is zero since the system has no friction. Using Newton's second law of motion with damping, the system is relaxed to mechanical equilibrium after each step, i.e., the total force on each disk is minimized to be smaller than 10−6. Once a mechanically stable configuration is reached at a desired pressure, each disc is inflated according to eqn (22), and subsequently mechanical equilibration follows, and the resulting displacement field measured. The displacement field depends on both r and θ, and we decompose it into the radial component dr(r,θ) and the angular component dθ(r,θ). Finally, comparison with the theoretical functions as shown in Fig. 2 is obtained by angle averaging,
000 discs in all. An initial area fraction below the jamming threshold was chosen, and then the outer radius was isotropically reduced to achieve a finite chosen pressure. Open source code large-scale atomic/molecular massively parallel simulator (LAMMPS) are used to perform the simulations. In these, the normal contact force is a Hertzian force with force-constant Kn = 2000 and the viscoelastic damping constant for normal contact γn = 100. The mass of each disk is 1. The tangential contact force is zero since the system has no friction. Using Newton's second law of motion with damping, the system is relaxed to mechanical equilibrium after each step, i.e., the total force on each disk is minimized to be smaller than 10−6. Once a mechanically stable configuration is reached at a desired pressure, each disc is inflated according to eqn (22), and subsequently mechanical equilibration follows, and the resulting displacement field measured. The displacement field depends on both r and θ, and we decompose it into the radial component dr(r,θ) and the angular component dθ(r,θ). Finally, comparison with the theoretical functions as shown in Fig. 2 is obtained by angle averaging, 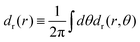 , and similarly for the tangential component.
, and similarly for the tangential component.
5 Results
To test our theoretical predictions we performed numerical simulations of disordered granular matter consisting of frictionless disks. In our simulations we started from an unjammed state and reduced the outer radius of the domain to achieve a target pressure. In each simulation we imposed a growth field and allowed the system to relax until it reached a new equilibrium state. The displacement field is measured between the equilibrium state prior to growth to that after it. To compare the measured displacement field with our predictions we perform an angle-averaging of the radial and tangential displacement components of each particle. We estimate the error at each radius as the root-mean-square deviation within annular bins used for averaging the displacement fields.Dipole screening in general, and odd-screening in particular, is expected to take place when quadrupole nucleation costs are very low. We therefore expect elastic-like behavior to take place, for example, at high pressures and odd-dipole screening at low pressures. In Fig. 2 we show two typical examples of displacement fields at low and high pressures. The comparison between theory and simulations require a simultaneous fit for dr and dθ with respect to three fitting parameters: κ, θκ and ν. We see that theory and simulations are in excellent agreement with our expectation and with the theoretical predictions.
In the high pressure case, the response is quasi-elastic as shown in Fig. 2(a). In this case, the fitting parameters are κ = 0 and ν = −0.1. In the low pressure case, the response is anomalous, and it breaks chiral symmetry with a non-vanishing tangential displacement, as shown in Fig. 2(b). The fitting parameters are κ = 0.026, θκ ≈ π/6 and ν = 0.35. We see that the effect of odd coupling is moderate, with an angle of π/6 between the inducing displacement and induced dipole.
We continue with a systematic study of the anomalous response to non-uniform growth, and its dependence on the controlled parameters: the radius of curvature R and the pressure P. We start by varying the pressure in systems with a fixed growth field that corresponds to a radius of curvature R = 450. Three representative examples are shown in the left panels of Fig. 3(a and b), showing that pressure controls the level of screening. For example, we see that the tangential displacement component decreases in amplitude as the pressure increases. We continue by varying the radius of curvature R in systems with fixed pressure P = 0.005. Three representative examples are shown in the right panels of Fig. 3(c and d), showing that curvature also controls the level of screening. For example, we see that the displacement amplitude decreases as the radius of curvature increases, as expected. In both curvature-controlled or pressure-controlled systems, the agreement between theoretical predictions and observations is very good. Interestingly, it seems that the odd coupling is also affected by the pressure and radius of curvature. To better quantify this impression we plot the fitted moduli as function of the controlled parameter. For example, in the case of pressure controlled simulations, we plot κ, θκ and ν as function of the imposed radius of curvature R, as shown in Fig. 4.
In this figure we see explicit dependence of the screening moduli and Poisson's ratio on the imposed radius of curvature. In principle, the screening parameters and the Poisson's ratio are emergent properties that depend on microscopic properties, e.g. particle size ratios. The dependence of these emergent properties can be a complicated function of the microscopic parameters. While currently we do not have a derivation of such functions, we observe that the ratio between the odd phase and the Poisson's ratio is nearly constant, θκ/ν = 1.1. Investigation of these relations, and understanding which microscopic parameters determine them, requires further numeric simulations and experiments with varying microscopic properties, such as particle size ratios and more. Such an investigation is left for future research.
Next we study the dependence of screening moduli on the imposed pressure for fixed R. For presentation purposes we plot the screening moduli as function of Φ = ln(P−1), see Fig. 5. We find that at large pressures (low Φ) the effect of dipole screening disappear, with quasi-elastic behavior and κ = 0. In this regime θκ is meaningless. At lower pressures screening mechanism is dominated by odd-dipoles, and finite values for κ and θκ are observed. This implies the possibility of a transition or a crossover from a quasi-elastic regime to an odd-dipole screening regime.38,39
6 Discussion
In summary, in this work we have shown that the recently developed theory of odd-dipole-screening30 accurately predicts the functional form of the displacement field in responsive granular matter. A main feature of the theory is that it describes materials that do not conserve energy. The success of the theory implies that the numerical model of the disordered granular assembly do not conserve energy, as expected from a material with glassy energy landscape.As a linear theory, the theory is expected to hold for small deformations. Therefore, we limited the numerical simulations to small growth fields, that is, the radius of curvature induced by the growth is much larger than rout. We expect that when these become more comparable, nonlinear terms will need to be included into eqn (14), but this beyond the scope of the present work.
The growth protocol studied in this work is a continuum generalization of the particle-inflation protocol studied in previous works on anomalous mechanics in disordered solids.26 There, the quasi-elastic response to a single-particle inflation had the property that it depended only on geometric properties. Therefore, elastic moduli could not be extracted in the quasi-elastic regime. Here we show that the quasi-elastic response to the growth protocol ϕ(x) depends on Poisson's ratio. The numerical simulations revealed that the Poisson's ratio is negative in the quasi-elastic regime, and positive in the odd-screening regime. This suggests that the Poisson's ratio may serve as an indicator for the onset of dipole screening.
Two characteristic properties of odd-dipole screening have emerged in response to the specific growth profile imposed on the system in this work. First, spatial oscillations in the displacement field were observed, consistent with experimental findings for a single inclusion.26 Second, chiral symmetry was broken, in agreement with experimental observations supporting the odd-dipole screening theory.30 While the precise details of the displacement field depend on the specific growth profile, these key features are expected to persist more generally, governed primarily by physical conditions such as pressure and disorder.
A key gap between our theoretical framework and the observed phenomenology is the lack of a clear, physically intuitive explanation for the anomalous behavior—such as the inward displacement. Developing such an intuitive picture would likely involve establishing connections between the displacement field, force chains, induced charges, and other structural descriptors of granular matter. Bridging the microscopic mechanisms with the emergent macroscopic displacement fields remains an open challenge and a topic of ongoing research that we are actively pursuing.
Last but not least, we note that the growth protocol in this work was fully prescribed. In reality, growth and mechanics are strongly coupled.40–42 Our theory lays the foundations for a future theory that couples the dynamics of the growth field and the mechanical state of the growing system.
Appendix A. analytical solution for the displacement field of “flattened granular sphere”
In the limit rout ≪ R, the leading order contribution of the non-homogeneous term due to ϕ(x) is proportional to , and the equation is
, and the equation is | (24) |
The explicit solution that satisfies this equation with the stated boundary conditions is
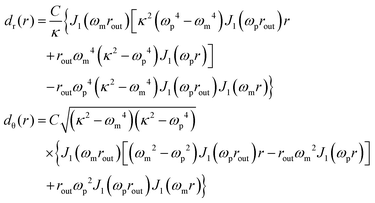 | (25) |
 | (26) |
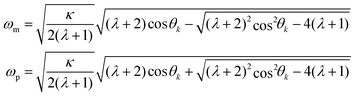 | (27) |
Author contributions
NL and MM developed the theoretical framework by combining non-euclidean elasticity with the theory of odd-dipole screening. AS developed the theory in its first stages. TS performed numerical simulations. NL and TS analyzed the data. MM and IP supervised the theoretical and numerical work correspondingly. NL, TS, IP and MM wrote the manuscript.Data availability
The data supporting this article is included in the manuscript in Fig. 2–5.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MM NL and AS have been supported by Israel Science Foundation Grant No. 1441/19. TS and IP have been supported by the joint grant between the Israel Science Foundation and the National Science Foundation of China, and by the Minerva Foundation, Munich, Germany. This research was supported in part by grant NSF PHY-2309135 to the Kavli Institute for Theoretical Physics (KITP).Notes and references
- H. M. Jaeger, S. R. Nagel and R. P. Behringer, Rev. Mod. Phys., 1996, 68, 1259–1273 CrossRef.
- C. Ovalle and P.-Y. Hicher, Geosci. Front., 2020, 487–494 CrossRef.
- C.-H. Liu and S. R. Nagel, J. Phys.: Condens. Matter, 1994, 6, A433 CrossRef CAS.
- A. Goriely and M. Ben Amar, Phys. Rev. Lett., 2005, 94, 198103 CrossRef PubMed.
- A. Goriely, M. Robertson-Tessi, M. Tabor and R. Vandiver, Mathematical modelling of biosystems, 2008, pp. 1–44 Search PubMed.
- M. S. El Youssoufi, J.-Y. Delenne and F. Radjai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051307 CrossRef CAS PubMed.
- R. Blumenfeld, Phys. Rev. Lett., 2004, 93, 108301 CrossRef PubMed.
- J. N. Nampoothiri, M. D’Eon, K. Ramola, B. Chakraborty and S. Bhattacharjee, Phys. Rev. E, 2022, 106, 065004 CrossRef CAS PubMed.
- R. Huang, R. Mandal, C. Scheibner and V. Vitelli, arXiv, 2023, preprint, arXiv:2311.18720 DOI:10.48550/arXiv.2311.18720.
- A. Bera, M. Baggioli, T. C. Petersen, T. W. Sirk, A. C. Y. Liu and A. Zaccone, PNAS Nexus, 2024, 3, gae315 CrossRef PubMed.
- V. Vaibhav, A. Bera, A. C. Y. Liu, M. Baggioli, P. Keim and A. Zaccone, Nat. Commun., 2025, 16, 55 CrossRef CAS PubMed.
- R. Blumenfeld, Phys. Rev. E, 2024, 109, 014901 CrossRef CAS PubMed.
- J. D. Eshelby, Proc. R. Soc. London, Ser. A, 1957, 241, 376–396 Search PubMed.
- J. Ashwin, O. Gendelman, I. Procaccia and C. Shor, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022310 CrossRef PubMed.
- M. L. Falk and J. S. Langer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 7192–7205 CrossRef CAS.
- J. S. Langer and M. L. Manning, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 056107 CrossRef CAS PubMed.
- A. Nicolas, E. E. Ferrero, K. Martens and J.-L. Barrat, Rev. Mod. Phys., 2018, 90, 045006 CrossRef CAS.
- S. Rossi, G. Biroli, M. Ozawa, G. Tarjus and F. Zamponi, Phys. Rev. Lett., 2022, 129, 228002 CrossRef CAS PubMed.
- M. Ozawa, L. Berthier, G. Biroli, A. Rosso and G. Tarjus, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6656–6661 CrossRef CAS PubMed.
- K. Schreiber Re’em, MSc thesis, The Hebrew University of Jerusalem, 2021.
- A. Lematre, C. Mondal, M. Moshe, I. Procaccia, S. Roy and K. Screiber-Re’em, Phys. Rev. E, 2021, 104, 024904 CrossRef PubMed.
- N. S. Livne, A. Schiller and M. Moshe, Phys. Rev. E, 2023, 107, 055004 CrossRef CAS PubMed.
- R. Kupferman, M. Moshe and J. P. Solomon, Arch. Ration. Mech. Anal., 2015, 216, 1009–1047 CrossRef.
- M. Moshe, E. Sharon and R. Kupferman, arXiv, 2014, preprint, arXiv:1409.6594 DOI:10.48550/arXiv.1409.6594.
- M. Moshe, I. Levin, H. Aharoni, R. Kupferman and E. Sharon, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10873–10878 CrossRef CAS PubMed.
- C. Mondal, M. Moshe, I. Procaccia, S. Roy, J. Shang and J. Zhang, Chaos, Solitons Fractals, 2022, 164, 112609 CrossRef.
- C. Mondal, M. Moshe, I. Procaccia and S. Roy, Phys. Rev. E, 2023, 108, L042901 CrossRef CAS PubMed.
- C. Reichhardt, I. Regev, K. Dahmen, S. Okuma and C. J. O. Reichhardt, Phys. Rev. Res., 2023, 5, 021001 CrossRef CAS.
- A. Szulc and I. Regev, Phys. Rev. Res., 2024, 6, 033129 CrossRef CAS.
- Y. Cohen, A. Schiller, D. Wang, J. Dijksman and M. Moshe, arXiv, 2023, preprint, arXiv:2310.09942 DOI:10.48550/arXiv.2310.09942.
- E. Efrati, E. Sharon and R. Kupferman, Soft Matter, 2013, 9, 8187–8197 RSC.
- M. Moshe, E. Sharon and R. Kupferman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 062403 CrossRef PubMed.
- M. Mungan, S. Sastry, K. Dahmen and I. Regev, Phys. Rev. Lett., 2019, 123, 178002 CrossRef CAS PubMed.
- I. Regev, I. Attia, K. Dahmen, S. Sastry and M. Mungan, Phys. Rev. E, 2021, 103, 062614 CrossRef CAS PubMed.
- L. D. Landau, J. S. Bell, M. Kearsley, L. Pitaevskii, E. Lifshitz and J. Sykes, Electrodynamics of continuous media, elsevier, 2013, vol. 8 Search PubMed.
- L. Friedland and I. Bernstein, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 1680 CrossRef.
- M. E. Gurtin, E. Fried and L. Anand, The mechanics and thermodynamics of continua, Cambridge University Press, 2010 Search PubMed.
- Y. Jin, I. Procaccia and T. Samanta, Phys. Rev. E, 2024, 109, 014902 CrossRef CAS PubMed.
- A. Zaccone, Theory of disordered solids, Springer, Cham, 2023, vol. 1015, pp. 179–211 Search PubMed.
- P. Gniewek, C. F. Schreck and O. Hallatschek, Phys. Rev. Lett., 2019, 122, 208102 CrossRef CAS PubMed.
- B. I. Shraiman, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3318–3323 CrossRef CAS PubMed.
- S. Al Mosleh, A. Gopinathan and C. Santangelo, Soft Matter, 2018, 14, 8361–8371 RSC.
Footnote |
| † NL TS and AS contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |





