Stiffening of a fibrous matrix after recovery of contracted inclusions

Abstract

Disordered fibrous matrices in living tissues are subjected to forces exerted by cells that contract to pull on matrix fibers. To maintain homeostasis or facilitate disease progression, contracted cells often push on matrix fibers as they recover their original sizes. Recent advances have shown that matrix geometry encodes loading history into mechanical memory independently of plasticity mechanisms such as inter-fiber cohesion or fiber yielding. Conceptualizing cells as inclusions undergoing sequential contraction and recovery, prior work documented matrix remodeling surrounding a solitary recovered inclusion. However, because the remodeling induced by the contraction of multiple inclusions differs from that caused by a single contracted inclusion, we investigate how matrix remodeling occurs when multiple contracted inclusions recover simultaneously, a scenario that more accurately reflects real tissues containing many closely spaced cells. Using mechanics-based computational models of fibrous matrices embedded with clusters of inclusions, we studied the mechanical remodeling of the matrix during the simultaneous recovery of inclusions after contraction. The results revealed permanent mechanical remodeling of the matrix within the cluster, with stiffening observed in areas of the matrix enclosed by closely spaced inclusions. This stiffening was driven by microstructural changes in matrix geometry and was corroborated in experiments, where collagen matrices permanently remodeled by the contraction and recovery of closely spaced embedded cells also exhibited stiffening. By enriching the understanding of memory formation in fibrous matrices, this study opens new possibilities for estimating cell forces on matrix substrates and refining metamaterial design strategies.

---

Introduction

Fibrous matrices, constituted of randomly organized fibers, are widely prevalent in natural environments, manifesting in diverse forms, including the cellular cytoskeleton,^1–3 tissue extracellular matrices,⁴ blood clots,⁵ neurofilaments,⁶ and biomaterials such as silk proteins,⁷ mycelium,⁸ and bamboo,⁹ among others. These matrices, regardless of the specific constitutive model of the individual fibers, exhibit nonlinear elasticity under deformation.^10,11 This nonlinear elasticity arises from a complex interplay between stretched and buckled fibers, leading to either strain stiffening^12–23 or strain softening^24,25 of the matrix. Most mechanics models,^26–30 which treat matrix fibers as elastic beams while excluding traditional plasticity mechanisms such as inter-fiber cohesion or the possibility of fiber yielding, assume that matrix responses remain elastic, with fibers returning to their original orientation and stress-free state once deformation is removed. However, recent research,^31,32 including our own,³³ challenges this elasticity assumption by showing that the intricate geometry of these matrices encodes signatures of past loading histories to establish a mechanical memory independent of traditional plasticity, similar to that observed in granular and amorphous materials.³⁴

Biopolymer fibrous matrices in tissues contain closely spaced cells that act as mechanical actuators, applying tension by pulling on matrix fibers.^26,35–37 To study this mechanical interaction, previous theoretical and experimental studies have modeled cells as contracting inclusions.^{24,26,38–43} The contraction of a solitary inclusion can either soften or stiffen the matrix.^38,40 When multiple contracting inclusions are present, the matrix typically softens,²⁴ unless the constrained external boundaries of the matrix drive a stiffening response.^44,45 In some contexts, the mechanical interactions between cells and the matrix are further complicated by contracted cells expanding to recover their original pre-contraction size, thereby pushing on the matrix. This phenomenon is commonly observed in cancer cells during the onset of invasion.^46,47 Likewise, in functional tissues such as muscle and adipose, sequences of cellular contraction followed by recovery are essential to maintain homeostasis.^48,49 Conceptualizing cells as inclusions, our recent work³³ demonstrated that the recovery of a solitary contracted inclusion activates a geometry-driven microstructural deformation mechanism within the matrix, distinct from traditional plasticity, which contributes to the permanent mechanical remodeling of the matrix. However, these insights remain incomplete, as real tissues typically consist of many closely spaced cells rather than solitary ones. Predictions of matrix remodeling surrounding a single recovered inclusion (or cell) cannot be directly extended to multiple recovered inclusions (or cells) due to the nonlinearity and complexity of memory formation in matrices, particularly given the prior understanding that multiple contracted inclusions remodel the matrix very differently than a single contracted inclusion.²⁴ Consequently, the mechanical response of the matrix when multiple contracted inclusions recover simultaneously remains uncertain, necessitating further investigation.

In this study, we employed mechanics-based computational models of inclusion-matrix systems to examine how the simultaneous recovery of multiple contracted inclusions influences the mechanical remodeling of the matrix. Clusters of contractile inclusions mimicking cells were embedded in fibrous matrix models designed as an intricate network of fibers to replicate the structure of fibrous collagen, with fibers modeled as linear elastic beams in finite element software (similarly to ref. 23,50,51) enabling the analysis of mechanical properties in the matrix regions enclosed by the inclusions within the cluster. By assessing the deformation and stress states of the constituent fibers during inclusion recovery, our investigations revealed permanent mechanical remodeling of the matrix inside the cluster, wherein the centers of inclusions moved closer together. This remodeling occurred independently of traditional plasticity mechanisms and was attributed to geometric confinement generated by a microstructural gradient formed in the matrix during inclusion contraction surrounding the cluster, facilitating the remodeling of the matrix within the cluster during inclusion recovery. Notably, as a cluster of closely spaced inclusions contracted and recovered, the remodeled matrix within the cluster consistently exhibited a stiffening response. We corroborated this model-predicted stiffening in experiments, where floating collagen I matrices permanently remodeled by the contraction and recovery of closely spaced embedded cells exhibited a stiffening response.

Results and discussion

Establishing minimal inclusion-matrix models

To gain an understanding of the mechanical response of a fibrous matrix during the simultaneous recovery of multiple embedded contracted inclusions, we employed minimal inclusion-matrix models (Fig. 1). The matrix was modeled as a quasi-two-dimensional discrete fiber network resembling fibrous matrices of collagen with randomly organized fibers, building on an established algorithm.^{24,41,52–54} Within the matrix, approximately three fibers were permanently welded at each node, each node being capable of transmitting both forces and moments. Embedded within the matrix were several circular contractile inclusions, each with a diameter twice the average fiber length (L_f) of the matrix, mimicking the typical length scale of contractile cells in soft tissue extracellular matrices.³⁹ These minimal inclusion-matrix models were chosen due to their documented efficiency in capturing the evolving microstructures and nonlinear mechanical responses characteristic of three-dimensional fibrous matrices.^24,41,54 In finite element simulations, matrix fibers were linear elastic Timoshenko beams, highly susceptible to bending, stretching, and buckling, while contractile inclusions were continuum linear elastic bodies. To preclude any plasticity mechanisms, no cohesive interactions were allowed between fibers, and it was ensured that stretched fibers did not yield. The simulations involved two quasistatic load steps: first, the inclusions contracted; second, they recovered to their original sizes, with inclusions maintaining kinematic compatibility and force equilibrium with the matrix in both steps. The external boundaries of the matrix remained free throughout both steps. In the deformed matrix, we characterized the kinematic states of the fibers, focusing especially on fiber buckling because of its importance in dictating the mechanical response of matrices, as we will explore further in subsequent subsections. The extent of buckling in fibers—referred to as defects in this study—was quantified by measuring their excess length, defined as the difference between each fiber's contour and its node-to-node distance.^{18,19,23,24,55} More intricate details about the finite element model and the characterization of matrix fibers and matrix states are provided in the Methods.

Fig. 1 Matrix with a cluster of inclusions. (a) A representative matrix containing a cluster of inclusions, each with a diameter of 2L_f, spaced ≈3.5L_f apart. (b) Simplified matrix model used in this study, showing a cluster with four inclusions, each spaced ≈3.5L_f from their nearest neighbors. The inclusions first contracted simultaneously and then recovered, while the external edges of the matrix remained free. L_f denotes the average matrix fiber length.

Extending this framework to more complex scenarios, as prior studies have shown, when embedded inclusions form a closely spaced cluster in the matrix (e.g., Fig. 1(a)), they modulate the mechanics of the matrix they enclose.^24,56 Building on our prior work,³³ which demonstrated that a matrix containing an isolated inclusion undergoing sequential contraction and recovery induces buckling-mediated mechanical instabilities in matrix fibers, here we found that matrices with multiple inclusions introduce even more instabilities, posing numerical challenges and increasing computational cost (see Methods, with details in Supplemental Notes, ESI†). To address these challenges while maintaining numerical efficiency and ensuring that the model captures the essential mechanics of the confined matrix, we employed a cluster of four closely spaced inclusions (Fig. 1(b) and 2(a)), each with a diameter of D = 2L_f, positioned ≈3.5L_f apart. This spacing closely resembled the inter-inclusion spacings considered in dense clusters investigated in previous studies.^24,56,57 These inclusions underwent sequential contraction and recovery, with the external boundaries of the matrix remaining free. The matrix region confined by these four inclusions (Fig. 2(b)) served as a representative system for understanding the mechanics of the matrix within a larger inclusion cluster, establishing it as our region of interest for mechanical analysis.

Fig. 2 Foundational insights as cluster of inclusions contracts. (a), (b) Enlarged view of a representative matrix (from Fig. 1(b)) surrounding the inclusion cluster before contraction, with panel b highlighting the region of interest between inclusions (indicated by a purple diamond in panel a). δ_ref denotes the initial inter-inclusion spacing. (c), (d) Representative matrix after inclusions contracted 60%, with panel d showing the region of interest. Inter-inclusion spacing reduces to δ₁. (e) Relative decrease in spacing between nearest inclusions (δ₁/δ_ref < 1) as inclusions contract. (f) Total length of defects (ξ_c) produced in the region of interest at various inclusion contraction levels (ε_r). Values of ξ_c were normalized by L_f. Color bar indicates inclusion contraction levels (ε_r) for the data points in panels e and f. An alternative representation of δ₁/δ_ref and ξ_c/L_f with ε_r on the abscissa is shown in ESI,† Fig. S3a and b. Data points in panels e and f represent means from seven independent matrices. ESI,† Fig. S4a and b shows the spread of the data. Background colors in panels a–d are employed solely to enhance the graphic contrast of matrix fibers.

Matrix mechanics under tension from multiple contracted inclusions

To facilitate subsequent analysis aimed at understanding the mechanical response of a fibrous matrix during the simultaneous recovery of multiple contracted inclusions, we initially sought to reproduce the established behavior of matrices during inclusion contraction, as outlined in prior studies.^24,38,42 Simultaneous contraction of inclusions, applying radial strains (ε_r) ranging from 4% to 60%, induced tension in the matrix. Matrix fibers oriented radially toward each inclusion (Fig. 2(c) and (d)), resulting in visible alignment between adjacent inclusions along lines connecting their centers. These fiber reorientations occurred simultaneously with axial compression and pronounced fiber buckling circumferential to the inclusions, especially in regions between the inclusions (Fig. 2(d)). As the inclusions contracted, they moved closer together (δ₁ < δ_ref; Fig. 2(a), (c) and (e)), consistent with a previous study,²⁴ and the spacing between inclusions decreasing as ε_r increased (Fig. 2(e)) as expected. The translation of the inclusion centers, reflecting the fidelity of our model in which contracted inclusions maintained force equilibrium and kinematic compatibility with the matrix, promoted fiber buckling between inclusions. Fiber buckling represents mechanical instabilities, which we consider as defects in this study. These defects, quantitatively defined by the excess length of fibers, were aggregated from all fibers within the region confined by contracted inclusions to calculate the total length of defects (ξ_c). At elevated levels of ε_r, these defects intensified (Fig. 2(f)) and contributed to the densification and mechanical softening of the confined matrix (ESI,† Fig. S1), corroborating prior studies.^24,25,58,59

Recovery of inclusions drives matrix remodeling

As the contracted inclusions expanded to recover their original size (Fig. 3(a)–(d) and ESI,† Fig. S2), two key observations emerged. First, the inter-inclusion distance after recovery remained similar to that at the onset of recovery (δ₂ ≈ δ₁; Fig. 3(e)), indicating a permanent reduction in the inter-inclusion spacing compared to the reference spacing (δ₂/δ_ref < 1; Fig. 3(f)). Second, the recovery process produced new buckling-mediated defects (ξ_r; Fig. 3(g)), relative to the contracted state, within the region of interest between the inclusions (Fig. 3(d)). Both the decrease in δ₂/δ_ref and the increase in ξ_r intensified as the levels of inclusion contraction (ε_r) increased, despite the absence of explicit plasticity mechanisms in the model such as inter-fiber cohesion or fiber yielding. Recovery-induced defects (ξ_r) superimposed those generated during inclusion contraction (ξ_c; Fig. 2(f)) to form cumulated permanent defects (ξ; Fig. 3(h)).

Fig. 3 Recovery of the contracted inclusions. (a), (b) Representative matrix with inclusions contracted by 60%, showing reduced inter-inclusion spacing (δ₁). Panel b highlights the region of interest between inclusions. (c), (d) Matrix after inclusions have recovered, with inter-inclusion spacing (δ₂) remaining similar to δ₁. Panel d depicts the region of interest. (e) Ratios of inter-inclusion spacing after recovery (δ₂) to before recovery (δ₁). (f) Ratios of inter-inclusion spacing after recovery (δ₂) to the spacing in the reference matrix (δ_ref). (g), (h) Total length of defects produced during the recovery process (ξ_r, panel g) and total length of permanent defects (ξ, panel h) within the region of interest (from panel d). Both ξ_r and ξ are normalized by L_f. Permanent defects (ξ) represent the sum of defects produced during inclusion contraction (ξ_c; Fig. 2(f)) and inclusion recovery (ξ_r). The color bar adjacent to the plots in panels e–h represents the inclusion contraction levels (ε_r) for the data points, while an alternative presentation of the data points plotted against ε_r on the abscissa is provided in ESI,† Fig. S3c–f. (i, j) Increase in the buckling-mediated defects in fibers during recovery of inclusions (Δξ_f > 0), highlighted in red, with intensity (color bar) reflecting the extent of the increase in defects; darker red fibers are more buckled than lighter red ones. Panel i depicts the area surrounding the recovered inclusions, while panel j focuses on the region between recovered inclusions; values of Δξ_f are normalized by L_f. For panels c, d, i, and j, the recovered inclusion diameter of 2L_f serves as the scale bar. Background colors in panels a–d are used solely to enhance visual contrast. Each data point in panels e–h represents averages from seven independent matrices; ESI,† Fig. S4c–f shows the spread of the data.

The production of defects during inclusion recovery, evidenced by an increase in the excess lengths of individual fibers (Δξ_f > 0; Fig. 3(i) and (j)), resulted in permanent deformation indicative of the permanent mechanical remodeling of the matrix. This phenomenon conceptually aligns with findings from our recent study,³³ which demonstrated that the recovery of a solitary contracted inclusion similarly remodeled the surrounding matrix.

To investigate the mechanisms contributing to the persistence of defects in the matrix, we examined the matrix microstructure during inclusion contraction and recovery. Prior to contraction, the matrix fibers were randomly oriented (Fig. 2(a)). Upon contraction, the matrix surrounding and between the inclusions assumed distinct alignments (Fig. 3(a)). Closer inspection revealed two categories of fiber alignment near the cluster: the first occurred between adjacent contracted inclusions, where fibers aligned along the axis connecting their centers, and the second involved fibers surrounding the inclusion cluster, which adopted radial alignment relative to the geometric center of the cluster.

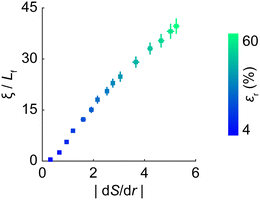
We sought to understand the spatial changes in the matrix microstructure surrounding the contracted cluster. To achieve this, we quantified the microstructural state by measuring the radial alignment of fibers surrounding the cluster relative to its center using an order parameter S (see Methods and ESI,† Fig. S5) and evaluated the spatial gradient of S with respect to the radial distance r from the cluster center (|dS/dr|; Fig. 4(b)), referred to here as the microstructural gradient. Across all levels of inclusion contraction assessed in this study, we typically observed a pronounced gradient in the region immediately surrounding the contracted cluster extending from r ≈ 2.5L_f to r ≈ 5.5L_f (highlighted in yellow in Fig. 4(a)), with higher inclusion contraction leading to a higher gradient (Fig. 4(b)); see Supplemental Note 1 (ESI†) for the rationale behind selecting this specific region surrounding the cluster.

Fig. 4 Recovering inclusions amidst gradient in microstructure. (a) A representative matrix with fibers surrounding the cluster showing pronounced radial alignment with respect to the cluster center (highlighted in yellow). In this case, the inclusions contracted by 60%. (b) Normalized microstructural alignment gradient, |dS/dr|, calculated in the region immediately surrounding the cluster, spanning r ≈ 2.5L_f to r ≈ 5.5L_f from the cluster center (region highlighted yellow in panel a), for different levels of inclusion contraction (see color bar). The magnitudes of the gradient emulate a sharp reduction in radial fiber alignment moving radially outward from the cluster. (c) Matrix in the immediate vicinity of the 60% contracted inclusions, showing both the region between the inclusions and surrounding the cluster (zoomed-in view of the highlighted region in panel a). Fibers are color-coded to indicate axial compression (blue) or tension (orange), with the majority under tension. (d)–(h) Matrix between and surrounding the cluster as inclusions gradually recover to their original size. Grey arrows highlight the radial confinement imposed by the microstructural gradient. Surrounding the cluster, the number of fibers in compression (blue) increases progressively as inclusions recover from panels d to h. (i) Evolution of the confining pressure (force per unit peripheral length; grey arrows in panels d–h) as the inclusions progress toward recovery. Each data point in panel b represents averages from seven independent matrices, with the standard error of these averages provided in ESI,† Fig. S5.

During the recovery of inclusions, the high microstructural gradient surrounding the cluster (Fig. 4(a)–(c)) exerted a confining pressure (grey arrows, Fig. 4(d)–(h)), which gradually increased as the recovery of inclusions progressed (Fig. 4(i)). This confinement restricted the outward radial movement of fibers, creating a compressed region surrounding the cluster where compressive axial strain built up in the fibers, ultimately leading to their buckling. This process was evidenced by the progressive increase in the proportion of compression fibers (colored blue) as the inclusions expanded toward their recovered state (Fig. 4(d)–(g)). At full recovery (Fig. 4(h)), some tension fibers re-emerged both surrounding and within the cluster, a phenomenon attributed to post-buckling distortions in already buckled fibers, with severely distorted fibers transitioning to tension, as detailed in the next subsection. Further confirming the buckling collapse and subsequent postbuckling distortions of fibers, slight disruptions in the radial alignment of fibers immediately surrounding the recovered cluster were observed (ESI,† Fig. S6).

The microstructural gradient surrounding the cluster induced geometric confinement that, by restricting the movement of radially aligned fibers during the recovery process, prevented the inclusion centers from reverting to their original positions prior to contraction. The immobilization of inclusion centers during recovery helped preserve the buckling-mediated defects generated during contraction (ξ_c) within the region of interest between the inclusions. Additionally, the recovering boundary of the inclusions intensified the geometric confinement, akin to biaxial compression, further exacerbating fiber buckling within the region between the inclusions (Fig. 4(d)–(h)). This exacerbated buckling led to increased fiber excess lengths (defects), with new defects (ξ_r) superimposing existing ones (ξ_c) to form permanent defects (ξ). Permanent defects (ξ) within the cluster increased with the increase in the microstructural gradient surrounding the cluster at the onset of recovery (Fig. 5). As this geometric gradient was determined by the level of inclusion contraction prior to recovery (Fig. 4(b)), greater inclusion contraction resulted in more pronounced permanent defects within the cluster after recovery (Fig. 5). This phenomenon underscores a history-dependent response of fibrous matrices in multi-inclusion systems.

Fig. 5 History-dependent behavior in the matrix, reflected as the microstructural gradient (|dS/dr|) surrounding the contracted cluster (Fig. 4(b)), which is driven by the level of inclusion contraction, modulates the extent of permanent defects (ξ) produced within the recovered cluster (i.e., between the recovered inclusions). ξ is normalized by L_f. Each data point represents the mean from seven independent matrices, with error bars showing the standard errors of these means. The color bar indicates inclusion contraction levels (ε_r) prior to recovery.

These history-dependent permanent defects in the matrix, arising without the activation of explicit plasticity mechanisms, resonate with a recent continuum model^31,32 suggesting that fibrous materials may inherently retain loading history through geometry alone. The mechanism we uncovered, wherein the persistence of fiber buckling is facilitated by the geometric gradient pursuant to the loading history of the matrix, offers a nuanced perspective on mechanical memory formation in disordered fibrous materials.

A summary of the analysis framework, outlining the formation and persistence of defects during inclusion recovery, is provided in Table 1 (Appendix A) for clarity.

Defects tune matrix properties within the recovered cluster

Next, we explored how permanent defects (ξ) influence the properties of the matrix between the recovered inclusions. Within the region of interest encompassed by the recovered inclusions in the cluster (e.g., Fig. 3(d)), we considered permanent buckling-mediated defects (ξ) as an internal variable that carries the mechanical memory of fiber kinematics, building on our prior study.³³ The greater the inclusion contraction (ε_r) prior to recovery, the greater the permanent defects (ξ), leading to increased matrix density (ρ; Fig. 6(a)) and a greater impartation of geometric randomness in the matrix topography, measured as heterogeneity (χ; Fig. 6(b)). We define ρ as the fiber density and χ as the total spectral energy of the permanent displacement field, both measured in the matrix region between recovered inclusions as detailed in the Methods. Under biaxial compression due to the confinement of recovered inclusions, the matrix confined between the inclusions (e.g., Fig. 3(d)) exhibited typical compression behavior. The extent of permanent defects, determined by inclusion contraction levels, dictated whether the matrix exhibited a softening or stiffening mechanical response, indicated respectively by a negative or positive value of incremental bulk stiffness (k; Fig. 6(c)). Adopting an incremental measure of stiffness, as detailed in the Methods, focused our analysis on how variations in ξ modulate the bulk internal resistance of the matrix within the defined region of interest. Softening (k < 0) typically occurred when ε_r ≤ 10%, driven by fiber buckling dominating matrix mechanics. In contrast, stiffening (k > 0) arose from pronounced boundary effects of advancing inclusion boundaries, marked by a buildup of tension within severely post-buckled fibers (a parallel measurement of incremental shear modulus also exhibited this stiffening; see ESI,† Fig. S7). Representative configurations of permanently deformed matrix states, depicted in Fig. 6(d)–(f) (also ESI,† Fig. S8), demonstrate the buildup of the proportion of tension fibers (L_eff/L_t) as the levels of ε_r prior to recovery increase; this increase in tension fibers was associated with elevated matrix stiffness (Fig. 6(g)). In capturing the role of permanent defects on matrix properties, increasing permanent defects (ξ) were accompanied by enhancements in both heterogeneity (χ; Fig. 6(b)) and stiffness (k; Fig. 6(c)), suggesting that escalating matrix heterogeneity contributes to the observed stiffness enhancements (Fig. 6(h)). This trend is further supported by the density of states of the remodeled matrix (Supplemental Note 2, ESI†), which characterizes how the mechanical states of the matrix are distributed across soft and stiff states. Lower heterogeneity levels were associated with an abundance of soft states dominated by buckling defects, manifested as a peak in the density of states (ESI,† Fig. S10). As heterogeneity increased, this peak diminished, marking a mechanical transition toward stiff states, where postbuckled fibers under confinement governed the response. Further underscoring the importance of defect-mediated heterogeneity in driving stiffening, the observed stiffness values far exceeded the theoretical bound expected from mere densification⁶⁰ (ESI,† Fig. S11).

Fig. 6 Defects modulate matrix properties between recovered inclusions. (a), (b) Higher inclusion contraction (ε_r) leads to greater permanent defects (ξ), densification (ρ; panel a), and increased geometric heterogeneity (χ; panel b). Density is normalized by the density of the reference matrix, ρ_ref, and heterogeneity is normalized by the heterogeneity at the lowest ε_r, χ₀. To avoid singularity, χ was normalized by χ₀ at the minimum ε_r, as by definition χ = 0 when ε_r = 0 (see accompanying text and Methods). (c) Permanent defects dictate the incremental bulk stiffness (k) of the matrix. The matrix stiffened at ε_r > 10%. Stiffness is normalized against the maximal mean stiffness (k_max) of the independent matrices studied. ξ is normalized by L_f in panels a–c. (d)–(f) Representative matrix between the recovered inclusions, showing fibers under axial tension (orange) and compression (blue). As inclusions underwent greater contraction prior to recovery, more tension fibers developed in the matrix, as seen from panels d to f. (g) During stiffening (k > 0), the proportion of fibers under tension (L_eff/L_t) increased. (h) Elevated heterogeneity (panel b) is associated with increasing stiffness (panel c). Each data point in panels a–c, g, and h corresponds to means from seven independent matrices (standard errors of data in ESI,† Fig. S9). Error bars in panels c, g, and h represent standard errors. The color bar indicates inclusion contraction levels prior to recovery for data points in panels a–c, g, and h.

Therefore, as demonstrated in a matrix with a cluster of four closely spaced inclusions (Fig. 1–6), the contraction and subsequent recovery of each inclusion led to a marked reduction in inter-inclusion spacing, inducing multiaxial compression within the matrix between inclusions. As the inclusions contracted, the inclusion centers moved closer together, and a geometric gradient emerged in the surrounding matrix, generating confining pressure that prevented the inclusions from moving apart during recovery (Fig. 4(h)). This compressive confinement exacerbated fiber buckling within the encompassed matrix between inclusions and helped trigger severe postbuckling distortion in fibers. As the inclusions continued to recover against increasing confining pressure (Fig. 4(i)), additional strain energy was transferred into the encompassed matrix due to the work done by the recovering inclusions against the confining pressure. The encompassed matrix attempted to redistribute this strain energy within fibers. The minimally deformed buckled fibers of the encompassed matrix could no longer gain additional strain energy from axial compression. Furthermore, the low bending rigidity of fibers (see Methods) posed a limiting constraint on the storage of bending strain energy. To accommodate the excess strain energy arising from the compressive confinement, a subset of postbuckled fiber segments, highly distorted by geometric confinement, began to take on axial tension (Fig. 6(e) and (f)). This mechanical transition is a natural consequence of energy balance in light of the fibers’ inability to sustain further compression or bending, making axial tension in confined segments of distorted fibers the only viable energy storage option (Supplemental Note 3, ESI†). The emergence of axial tension in fiber segments drove the stiffening mechanical response of the encompassed matrix between the recovered inclusions (Fig. 6(g)). Although this stiffening draws parallels to a prior study,⁵⁶ in which stiffening was driven by fiber tension induced by steric repulsion between inert inclusions when the inclusions were externally forced closer together, our mechanism is fundamentally different. Rather than externally forcing the inclusion centers closer, we imposed radial contraction followed by the recovery of inclusions, wherein a geometry-driven confining pressure kept the inclusions from moving apart during recovery. The encompassed matrix stiffened due to tension in fibers that arose from the geometric confinement of postbuckled fibers—thus revealing a novel stiffening mechanism for fibrous matrices elucidated in this study.

To investigate whether the initial inter-inclusion spacing (δ_ref) influences matrix stiffening between recovered inclusions, we conducted a parametric study inspired by prior research on the role of spacing in matrix remodeling.^61,62 The initial spacing between inclusions was varied from 3.5L_f to 5L_f and 7L_f, designated as cases 1, 2, and 3, respectively (Fig. 7(a), (c) and (e)). Compared to the denser cluster (case 1), the contraction of inclusions in sparser clusters (cases 2 and 3) induced a weaker microstructural gradient surrounding the cluster (Fig. 7(g)) and reduced the forces between inclusions, as predicted by a prior study.²⁴ Consequently, inclusion centers in sparser clusters moved closer together less efficiently (ESI,† Fig. S12a). Furthermore, the relative increase in the matrix area enclosed by inclusions in sparser clusters introduced a size effect, a factor known to influence matrix mechanics.^63–68 Collectively, these factors delayed the onset and reduced the extent of stiffening in the matrix enclosed by sparser clusters compared to the denser cluster; nevertheless, all cases eventually exhibited stiffening at high levels of permanent defects modulated by the proportion of tension fibers (ESI,† Fig. S12b–g), indicating that although the size effect influenced the degree of stiffening it did not prevent the stiffening response.

Fig. 7 Effect of initial inter-inclusion spacing. (a)–(f) Matrices with inclusions at varying initial spacings: 3.5L_f in panels a, b (case 1); 5L_f in panels c, d (case 2); and 7L_f in panels e, f (case 3). Panels a, c, and e show matrices before inclusion contraction, while panels b, d, and f display matrices after inclusion recovery. In these representative examples, inclusions contracted by 60% prior to recovery. (g) Compared to case 1, greater initial spacings (δ_ref) in cases 2 and 3 resulted in weaker microstructural gradients (|dS/dr|) in the regions spanning ≈3L_f immediately surrounding the cluster (see insets). The selection of this specific region surrounding the cluster across cases follows the rationale in Supplemental Note 1 (ESI†). (h) As permanent defects (ξ) accumulate, case 1 demonstrates strain stiffening (k > 0), whereas cases 2 and 3 exhibit softening (k < 0). Inset: Stiffening associates with the proportion of tension fibers (L_eff/L_t), with a high likelihood of buckled fibers transitioning to tension in case 1 due to severe distortion. k_max corresponds to maximal stiffness in case 1. Each data point in panels g and h (including inset) represents averages from seven independent matrices. The color bar indicates inclusion contraction levels prior to recovery for data points in panels g and h. ξ is normalized by L_f in panel h.

Given that the stiffening trend in the matrix between recovered inclusions was unaffected by matrix size, we rigorously tested the influence of inclusion boundaries alone, independent of size effects, on this stiffening mechanism. To this end, we studied a constant region of interest size, equivalent to that of the densest cluster (case 1; Fig. 7(a) and (b)), across the sparser clusters (cases 2 and 3; Fig. 7(c)–(f)), thereby eliminating size effects and isolating the influence of proximity to inclusion boundaries on the matrix. Results showed that the stiffening observed between closely spaced inclusions at ε_r > 10% (case 1) was absent when inclusions were sparsely spaced in cases 2 and 3 (Fig. 7(h)). In these sparser clusters, a weaker microstructural gradient resulted in less permanent defects, leading to a softening of the matrix as the length of defects increased. This softening was primarily due to fiber buckling, without the severe post-buckling distortions that characterized the matrix in the densest cluster (case 1; Fig. 7(h), inset). Thus, the proximity to inclusion boundaries was crucial for achieving a compression-stiffening response, otherwise buckling-mediated softening would prevail. Even fully constraining the remote external boundaries of the matrix did not preclude this stiffening response (ESI,† Fig. S13), further highlighting the dominant role of local boundary proximity in driving compression-stiffening.

Recovery of cell forces stiffens biopolymer matrix

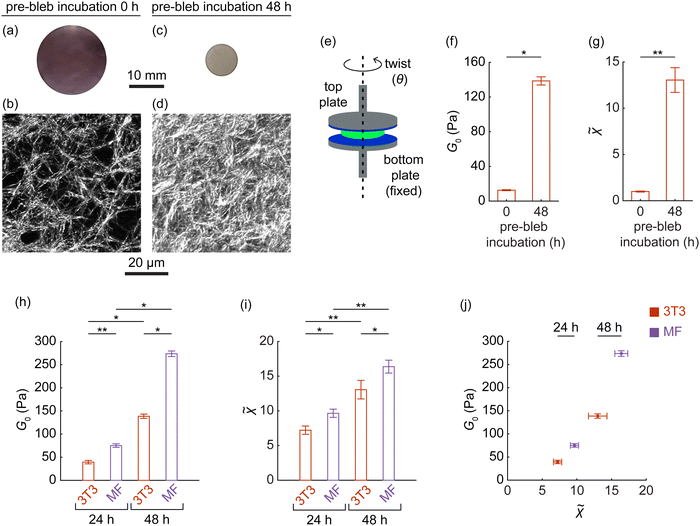
Our models demonstrated that when a dense cluster of four inclusions underwent contraction and recovery, the matrix between them typically stiffened. This history-dependent stiffening originated from compressive confinement exerted by the surrounding matrix on the recovered cluster (Fig. 4). When considered alongside findings from our recent study,³³ which demonstrated that even a solitary inclusion after recovery experiences similar compressive confinement, this suggests that the phenomenon is consistent across different cluster sizes. Consequently, our results suggest that larger clusters containing more than four inclusions would similarly experience compressive confinement during the recovery of contracted inclusions, leading to the stiffening of the encompassed matrix within these larger clusters. Building on these predictions, we designed an experiment to verify whether such history-dependent stiffening could be observed in real materials. Using sparse random fibrous matrices of collagen I (2 mg mL⁻¹) embedded with cells mimicking contracting inclusions, we sought to replicate the responses observed in the models. To facilitate this, we optimized the cell seeding density to 0.5 million cells per mL, ensuring it was high enough for measurable stiffening yet low enough to prevent inter-cell contact and to avoid reaching the maximal density threshold of the matrix, as established by a prior parametric study.⁶²

Experimentation commenced with NIH 3T3 fibroblasts embedded in disk-shaped matrices with free external boundaries, measuring 20 mm in diameter and 1.3 mm in thickness. We prepared two categories of cell-embedded matrices in which cell behavior was modulated using the cell force inhibitor, blebbistatin, which permeated the matrices to reach the cells.

In the first category of cell-embedded matrices, blebbistatin was added immediately after cell seeding, rendering the cells inert and preventing them from contracting and exerting tension on the matrix. Consequently, the cell-embedded matrices retained their original diameter of 20 mm and thickness of 1.3 mm as cast (Fig. 8(a) and (b)).

Fig. 8 Cell-mediated history response in biopolymer matrix. (a) Cell-embedded matrix of collagen (2 mg mL⁻¹) with free external boundaries embedded with 3T3 fibroblasts at a seeding density of 0.5 million per mL; cells were prevented from contracting by immediate application of blebbistatin after seeding. (b) Representative confocal microscope image of matrix fibers from panel a. (c) Matrix from panel a showing permanent radial contraction of 53% after 48 h of cellular contraction, followed by release of cell forces by blebbistatin. (d) Representative confocal microscope image of matrix fibers from panel c, indicating densification. (e) Schematic of a shear rheometer showing the matrix with relaxed cells (green) mounted between parallel plates (grey), separated by glutaraldehyde-treated coverslips (blue) to prevent slippage. The top plate axially twists the cell-embedded matrix to apply a shear strain of γ = 0.35% at the outer edge, measuring the shear modulus G₀ of the cell-embedded matrix. The diameters of the disk-shaped matrices, measured from their digital images using ImageJ software, were smaller than the 25 mm diameter of the rheometer plates, as shown. (f), (g) After 48 h of contraction by 3T3 cells, followed by the release of cell forces, the permanently deformed matrix exhibited an increase in modulus G₀ (panel f) and an increase in geometric heterogeneity [small chi, Greek, tilde] (panel g). For a 48-h incubation, cell-embedded matrices were appropriately incubated (see Methods) before being mounted between the rheometer plates. (h), (i) Modulus (G₀, panel h) and heterogeneity ([small chi, Greek, tilde], panel i) of matrices embedded with fibroblasts (3T3) and myofibroblasts (MF) applying tension for 24 and 48 h, followed by cell force release by blebbistatin. (j) For permanently deformed matrices, stiffness (panel h) increased at higher heterogeneity levels (panel i). In panels f and h, each data point represents at least four independent samples, and in panels g and i, at least six independent samples. Error bars indicate the standard error of the mean. * and ** indicate significance with p ≤ 0.05 and p ≤ 0.01, respectively.

In the second category of cell-embedded matrices, after allowing the cells to contract and apply tension for 48 h, cell tension triggered global volumetric contraction of the cell-embedded matrices. The expulsion of water from the cell-embedded matrices as they were contracting was rapid, facilitated by the use of sparse matrices with large pore sizes containing water, unlike the hyaluronic acid prevalent in real extracellular matrices.^42,69,70 As a result, the contraction of the cell-embedded matrices remained quasi-static, akin to our models. The contracted cells were subsequently treated with blebbistatin, enabling them to expand and release the tension⁷¹ on the matrix, akin to the recovering inclusions in our models. The final result was a profound and permanent radial contraction of the cell-embedded matrices by ≈53% (Fig. 8(c)) and a reduction in thickness by ≈35%, leading to a marked ≈6× densification of the matrix between cells (Fig. 8(d) and ESI,† Fig. S14, S15).

To assess the incremental shear modulus of cell-embedded matrices from both categories, we mounted each cell-embedded matrix on the parallel plates of a shear rheometer (Fig. 8(e)) and applied a low shear strain of 0.35% through a small axial twist (see Methods). This setup ensured that stiffness measurements remained unaffected by potential size effects,⁶⁸ as the sizes of all cell-embedded matrices exceeded 40 fiber lengths. The shear modulus (G₀) was 13 Pa in the absence of cell tension in the first category of cell-embedded matrices (e.g., Fig. 8(a)) and increased by ≈11-fold to 139 Pa after the release of cell tension in the second category (e.g., Fig. 8(c)), demonstrating significant stiffening (Fig. 8(f)). This stiffening was not solely attributable to the densification of the matrix between cells, as G₀ exhibited a stronger-than-linear dependence on matrix density (ESI,† Fig. S15), exceeding the theoretical bound predicted from the linear scaling of modulus with density.⁶⁰ Instead, the stiffening of a cell-embedded contracted matrix arose as the matrix between inclusion-mimicking cells stiffened (Fig. 6(c) and ESI,† Fig. S7), modulated by severely post-buckled fibers between cells taking on tension as predicted by our model (Fig. 6(g)).

With our model linking this stiffening (Fig. 8(f)) to fiber defects from severe post-buckling distortion (Fig. 6(g)), we sought to quantify in experiments the role of these distorted fibers in orchestrating the stiffening. Challenged by the difficulty of segmenting individual fibers in a highly heterogeneous matrix⁷² to accurately measure fiber defects, we instead quantified microstructural heterogeneity by analyzing fluctuations in pixel-level image intensities, where higher fluctuations indicate greater heterogeneity, drawing inspiration from previous studies.^73,74 Given the pronounced heterogeneity at sub-fiber scales,⁷⁵ we measured microstructural heterogeneity ([small chi, Greek, tilde]) at approximately 0.2 fiber lengths (6.6 μm), both in the absence of cell tension in the first category of matrices (e.g., Fig. 8(b)) and after the release of cell tension in the second category of matrices following 48 h of cell-induced tension (e.g., Fig. 8(d)). Results revealed an ≈13-fold increase in heterogeneity ([small chi, Greek, tilde]; Fig. 8(g)) of permanently deformed matrices (i.e., those in the second category), corroborating the elevated heterogeneity trends predicted by our models (Fig. 6(b)). This increase in the parameter [small chi, Greek, tilde] is particularly sensitive to the heterogeneity arising from the dense accumulation of defects in distorted fibers, as confirmed by our additional study showing no increase in [small chi, Greek, tilde] from mere densification through the deposition of undeformed fibers (ESI,† Fig. S16). Therefore, in light of the established understanding that cell–matrix interactions are primarily mechanical with minimal collagen synthesis⁷⁶ or degradation⁷⁷ during the 48-h incubation period, our findings show that cellular tension resulted in enduring changes in stiffness (Fig. 8(f)) and heterogeneity (Fig. 8(g)) that persisted even after cellular tension had been released, thereby imparting mechanical memory within the matrix.

Recognizing the cell-induced history responses of the matrix in our experimental setup, we assessed the potential of this system to empirically link these responses to the extent of cell tension. We conducted repeated experiments with two cell types of differing contractility—3T3 fibroblasts and highly contractile intestinal myofibroblasts⁷⁸ (Applied Biological Materials Inc., T0565). In assessing the permanent mechanical remodeling of the matrix after 24 and 48 h of cell-induced tension and its subsequent release, we found that myofibroblasts consistently induced greater stiffening than the 3T3 cells at both time points (Fig. 8(h)). Furthermore, increasing cell-generated forces by extending the duration of cell contraction from 24 to 48 h significantly enhanced matrix stiffness for both cell types, highlighting that stiffening serves as a marker of mechanical memory within the matrix, linked to the magnitude of cellular forces exerted during its loading history, regardless of cell type. Similarly to stiffness, microstructural heterogeneity within the permanently deformed matrix also increased with elevated cellular forces (Fig. 8(i)). This suggests that enhancements in matrix stiffness were accompanied by increases in heterogeneity (Fig. 8(j)), aligning with our model prediction (Fig. 6(h)). Thus, the stiffening response of the matrix, driven by closely spaced cells (mimicking inclusions) undergoing contraction and recovery, intensified with increasing levels of cell contraction prior to recovery, reflected in the accumulation of permanent defects that manifested as increased geometric heterogeneity within the matrix.

While these findings substantiate the core predictions of our model, we recognize that its simplifications and assumptions necessitate a careful assessment of the model's limitations. First, real fibrous matrices exhibit plasticity mechanisms absent from our model, including interfiber crosslinking under mechanical forces, fiber yielding upon excessive stretching,^79–81 and fiber bundle opening under strain.⁸² These processes likely contribute to mechanical memory in experiments, suggesting that observed responses arise from both plasticity-driven effects and the geometry-driven memory predicted by our model. Second, our model, designed as a minimal system with four closely spaced inclusions, captures the fundamental physics of the problem but does not yield an exact quantitative match with experiments on multi-cell matrices. Future extensions incorporating more inclusions and addressing numerical challenges (see Supplemental Notes 4 and 5, ESI†) will enable a broader exploration of mechanical memory in fibrous matrices. Third, our simulations were quasi-two-dimensional, whereas experiments involve fully three-dimensional matrices. The rigor of our model ensures that the mechanisms of fiber buckling and postbuckling distortions remain qualitatively similar, and the predicted heterogeneity-driven stiffening was corroborated by experiments. However, the degree of stiffening was somewhat lower in experiments, likely due to the more localized influence of distorted fibers. Fourth, in contrast to the quasistatic conditions in our model and experiments, real biopolymer matrices often consist of a composite of collagen fibers and hyaluronic acid. This composition can suppress fiber buckling⁴² and initiate a time-dependent mechanical response, presenting challenges in directly comparing our quasi-static predictions. Fifth, unlike our model's fixed stiffness contrast between inclusions and matrix fibers, cell stiffness in real tissues varies with contraction and recovery,⁸³ complicating the cell–matrix interactions. Despite these limitations, our findings highlight the independent role of matrix geometry, beyond conventional plasticity, in encoding mechanical memory within disordered fibrous matrices.

Conclusions

Our numerical studies revealed that when a cluster of closely spaced inclusions underwent contraction and recovery, the matrix between them stiffened. This remodeling arose from a spontaneously formed alignment gradient in the matrix microstructure during inclusion contraction, which induced compressive confinement on the inclusion cluster during recovery, leading to multiaxial compression in the matrix within the cluster. This state of compression was exacerbated when the initial inter-inclusion spacing was small, bringing the matrix to a mechanical state wherein it stiffens. While this stiffening behavior may resemble prior studies where inert inclusions in fibrous matrices were forced closer together under uniaxial compression,^56,57 our approach fundamentally differed. Here, the inclusion centers permanently moved closer together without external forcing, driven solely by the contraction and recovery of the inclusions.

Extending a recent study that suggested the contraction of multiple closely spaced inclusions typically softens the matrix,²⁴ our study demonstrated that the matrix stiffens as those contracted inclusions recover. Combining our numerical findings with experimental corroboration that stiffening occurs in disordered biopolymer matrices with closely spaced cells upon the release of cell tension, we demonstrate the potential of the matrix to record cell loading history. These results underscore the pivotal role of matrix geometry in driving mechanical memory formation, alongside traditional plasticity mechanisms such as inter-fiber cohesion and fiber yielding. Looking ahead, this geometry-driven mechanical memory provides promising directions for estimating cell forces on synthetic fibrous substrates lacking traditional plasticity mechanisms (for example, ref. 84) and refining design strategies for fibrous metamaterials.^85,86

Methods

Inclusion-matrix models and finite element simulations

We used quasi-two-dimensional discrete fiber models to emulate fibrous matrices of collagen with randomly organized fibers, employing an algorithm developed and validated in previous studies.^{24,41,52–54} Several circular contractile inclusions were embedded in the matrix (Fig. 1(a) and (b)) to mimic contracting cells, following established modeling strategies.³⁰ The matrix-generating algorithm utilized a simulated annealing-based optimization approach to move nodes and swap fibers between different nodes in two dimensions, iterating until it achieved a prescribed average fiber length (L_f) and a nodal connectivity of 3.4. This nodal connectivity is a subisostatic value, below Maxwell's isostatic threshold of twice the system dimensionality,⁸⁷ and is consistent with observations from collagen imaging studies.^52,88 During deformation, matrix fibers were allowed to cross without connecting, maintaining the structural fidelity of three-dimensional collagen. The external dimensions of the matrix models were set to 23L_f. The algorithm to generate the matrix is freely available in a public repository at the link provided in the Data and Code Availability statement. These quasi-two-dimensional models efficiently captured evolving microstructures and nonlinear mechanical responses characteristic of three-dimensional fibrous matrices,^24,41,54 consistent with the demonstrated applicability of two-dimensional models for replicating the mechanics of three-dimensional fibrous matrices.^{18,23,30,89,90}

In finite element simulations, fibers were modeled as linear elastic Timoshenko beams. To replicate the mechanical properties typical of fibers in collagen matrices,^18,19,91,92 the shear stiffness of fibers was set to half the axial stiffness, with a bending-to-axial stiffness ratio of 1 × 10⁻⁴, making the fibers highly susceptible to bending. A mesh convergence study (ESI,† Fig. S17) demonstrated that discretizing each fiber into two three-node quadratic beam elements was sufficient to capture essential fiber mechanics while preventing numerical locking. Our prior work^23,24,93 also indicated the effectiveness of this discretization approach, further supporting its adoption here. Welded nodes connected the fibers, transmitting both forces and moments. While nodes remained permanently welded, ensuring no changes in the nodal connectivity of fibers, they were permitted to translate spatially in response to mechanical strain; this configuration enabled fibers to realign through both rigid body movements and elastic deformations, such as axial stretching, compression, bending, and buckling. Circular inclusions with diameter 2L_f, mimicking the typical size of cells in fibrous extracellular matrices in soft tissues,³⁹ were embedded using established techniques.^24,94 Briefly, in order to maintain the structural fidelity of the three-dimensional matrix, fibers intersecting the inclusion periphery were trimmed, while those passing through were preserved. The inclusions were discretized into three-node continuum triangular elements, with two-node linear beam cross-links rigidly connecting them to the matrix. Inclusions transfer forces and moments to the surrounding matrix. To ensure that the strain in each inclusion matched the strain on the matrix, we assigned the inclusions and cross-links stiffness values tenfold greater than the axial stiffness of the matrix fibers. An ill-conditioning test confirmed that this setup did not skew stiffness measurements in the permanently deformed matrix (ESI,† Fig. S18). This design preserved the circular geometry of the inclusions during their uniform radial contraction and recovery.

Finite element simulations were performed in Abaqus (Dassault Systèmes), employing two load steps. In the first step the inclusions contracted while in the second, they recovered to their original sizes. Throughout both steps, the external matrix boundaries remained free. The inclusions were modeled as continuum linear elastic bodies, ensuring force equilibrium and kinematic compatibility with the matrix during contraction and recovery, consistent with ref. 24. This was achieved using Abaqus's thermal loading feature to impose a prescribed radial strain on the inclusions. This approach contrasted with some prior studies,^27–30,80 in which inclusion contraction was simulated by moving boundary nodes to ensure kinematic compatibility but without guaranteeing force equilibrium with the matrix. Our method accurately captured inclusion-matrix mechanical interactions under free external boundaries. Here, engineering strain represent the radial strain (ε_r) of the inclusions, following practices from prior studies.^23,50 The simulations were conducted on an implicit dynamic quasi-static solver with the nonlinear geometry option enabled to account for large local deformations and mechanical instabilities within the matrix, as described in prior studies.^{23,24,41,75,93} Further justification for employing the implicit dynamic solver is provided in Supplemental Note 4 (ESI†). While employing a slightly underdamped system allowed physically relevant fiber buckling events to occur without excessive smoothing, our choice of damping parameters and adaptive time stepping maintained quasi-static conditions by keeping the kinetic-to-strain-energy ratio below ≈5% for numerical stability, yet above ≈0.5% to avoid artificial viscoelastic effects (Supplemental Note 5 and Fig. S19, ESI†). Every simulation presented in this study was conducted using seven independent inclusion-matrix models, each created with a distinct random seed for assembling the fibers within the matrix.

Characterizing matrix mechanics in numerical models

Fiber mechanical states. The extent of fiber buckling, where buckled fibers are referred to as defects in this study, was measured as the excess length between a fiber's contour and its node-to-node distance. The sum total of the excess lengths across all fibers in a defined region of interest represented the total length of defects, ξ_c, produced during inclusion contraction. Similarly, during inclusion recovery, additional defects imparted on individual fibers were quantified as the increase in excess lengths, Δξ_f, and their sum across all fibers in the region of interest represented the total length of defects produced by the inclusion recovery process alone, ξ_r. Finally, the total length of permanent defects in the region of interest, ξ, was calculated as the sum of the defects produced during inclusion contraction, ξ_c, and those produced during inclusion recovery, ξ_r. To report the proportion of tension fibers in the matrix region of interest, the total length of tension fibers, L_eff, within the region of interest was measured using established strategies^21,23 and normalized by the total length of all fibers, L_t, in the same region.

Microstructural gradient. To quantify changes in the matrix microstructure following the contraction of inclusions, we calculated the spatial variation in fiber alignment (S) with respect to the radial distance r from the geometric center of the inclusion cluster. This spatial variation, referred to as the microstructural gradient, is denoted as dS/dr. The parameter S is defined as the average extent to which fibers align radially with the cluster center, relative to their reference orientation, within the region surrounding the cluster (ESI,† eqn (S3)). Absolute value of dS/dr was normalized by multiplying with the average fiber length, L_f.

Several alternative methods exist for quantifying fiber orientation in two-dimensional fibrous matrices, including mean intercept length, line fraction deviation, Fourier transform method, and structure tensor analyses, among others.⁹⁵ While these approaches primarily capture global orientation distributions or anisotropy, our parameter S quantifies the relative radial alignment of fibers with respect to the cluster center, providing a localized measure of orientation change due to mechanical forces. Conceptually, S shares similarities with the structure tensor in that both describe average fiber alignment. However, whereas the structural tensor represents a second-order orientation distribution, S is a first-order measure that directly quantifies relative radial alignment and enables the computation of its spatial gradient (|dS/dr|), allowing us to track localized microstructural evolution.

Matrix density and heterogeneity. To assess matrix density, ρ, we employed a kernel density estimation of material points distributed along the fibers, where dense aggregations of material points indicate high matrix density, building on methodologies described in ref. 96. To evaluate the impact of permanent defects on geometric randomness in the permanently deformed matrix, we measured a heterogeneity parameter χ, analogous to metrics used in prior studies to characterize heterogeneous displacement fields in fibrous matrices.^{54,75,97–100} To quantify χ, we performed the Fourier transform of the absolute permanent displacement field within the region of interest, calculating the energy of displacement fluctuations across wave numbers. The sum of these energies represented the total spectral energy of the displacement field (ESI,† eqn (S4)), reflecting the geometric heterogeneity induced by the contraction and recovery processes of the inclusions.

Matrix stiffness. The incremental bulk stiffness (k) of the matrix region of interest was determined after each load step (i.e., following the radial contraction and subsequent recovery of inclusions at a given contraction level) by calculating the second-order derivative of the total strain energy of all constituent fibers with respect to their total defects (ξ), capturing changes in internal resistance to incremental increases in fiber defects (ESI,† eqn (S5)). This method is inspired by ref. 101, with broader conceptual parallels to incremental stiffness measures used in architected materials design.¹⁰²

In fibrous matrices, the mechanical response is dictated by the local kinematic states of individual fibers, necessitating descriptors that extend beyond classical strain measures. Previous studies have introduced new internal variables to capture fiber-level kinematics such as fiber rotation³¹ and fiber buckling,³³ which influence matrix behavior at length scales spanning multiple fibers. Building on this framework, we define ξ, the total excess length of all fibers due to their persistent buckling defects, as an internal variable that characterizes the evolving mechanical state of the matrix region of interest.

Since the fibers of the encompassed matrix within the cluster retain a random spatial organization throughout deformation (Fig. 2(d) and 3(d)), defect accumulation occurs without directional bias at the bulk scale of this encompassed matrix. As a result, ξ serves as an isotropic microstructural descriptor of bulk-like deformation in fibrous matrices. Consequently, the second-order derivative of the strain energy with respect to ξ provides a measure of the incremental bulk stiffness of the encompassed matrix within the cluster, offering a bulk-like stiffness descriptor that generalizes bulk modulus concepts for disordered fibrous matrices in a physically meaningful way.

Experiments on collagen matrices

Collagen matrix with embedded cells. NIH 3T3 fibroblasts and intestinal myofibroblasts (Applied Biological Materials Inc., T0565) were cultured in high-glucose Dulbecco's Modified Eagle's Medium supplemented with 10% fetal bovine serum and 1 × Penicillin–Streptomycin at 37 °C in a 5% CO₂ atmosphere until they reached 90% confluency. For experiments in the collagen matrices, cells were detached from the dish using 0.05% Trypsin-EDTA, centrifuged at 150g for 5 min, and resuspended in fresh culture media prior to cell count measurements using a hemocytometer. Each cell type was cultured and processed separately in their respective experiments, with NIH 3T3 fibroblasts or intestinal myofibroblasts seeded at a density of 0.5 million per mL into neutralized rat tail collagen I (Corning, Inc.) matrices with a final collagen concentration of 2 mg mL⁻¹ and an average fiber length of 32 μm, based on prior protocols.^39,103 These cell–collagen mixtures were cast into disks 20 mm in diameter and 1.3 mm in thickness on pluronic acid-coated glass-bottom dishes in order to prevent fiber adhesion to the glass. Following polymerization at 22 °C for 30 min, the matrix formed a sparse, randomly organized fibrous structure (Fig. 8(b)). Cell culture media was added to help detach the matrices from the glass surfaces. The cell-embedded matrices were then incubated for either 24 or 48 h, as detailed in the Results, to allow cells to adhere to the matrix and apply local tension to fibers, thereby inducing global matrix contraction. Following the specified incubation periods, matrices were treated with blebbistatin (concentration 100 μM) in order to release the cell-induced tension in the fibers.¹⁰⁴ A control set of matrices was prepared in which the development of cell tension was immediately inhibited after seeding the cells in the matrix by applying blebbistatin.

Rheometry of the cell-embedded matrix. A commercial rheometer (DHR-3, TA Instruments) characterized the stiffness of the cell-embedded matrices, both with and without being remodeled by cells, at 22 °C. The disk-shaped matrices were firmly gripped between two glass coverslips that had been functionalized with 0.5% glutaraldehyde and 0.5% (3-aminopropyl)triethoxysilane in order to prevent slip. Coverslips were affixed to the 25 mm flat plates of the rheometer with double-sided adhesive tapes. The spacing between plates was zeroed for calibration, then adjusted to mount the sample (matrix). The permanently deformed matrices varied in diameter from 9–12 mm and thickness from 350–650 μm, contrasting with their original dimensions of 20 mm diameter and 1.3 mm thickness prior to cell contraction. Following a prior study,¹⁶ the matrices were probed using a step input low shear strain of 0.35% by axially twisting them, as schematically depicted in Fig. 8(e). This method introduced a controlled incremental, low magnitude strain to the matrices that had already exhibited residual deformation, ensuring that the incremental response not only remained linear within the viscoelastic limits but also stayed above the noise floor of the rheometer¹⁰⁵ (ESI,† Fig. S20b and c). The rheometer measured the relaxation modulus as a function of time beginning when the constant probing strain was applied, and these data were fitted to the standard linear solid model to determine G₀, the modulus immediately after applying the probing strain. This modulus, G₀, reflects the linear tangent modulus—or the incremental modulus—at the residual strain of the remodeled matrix. This measure conceptually aligns with the incremental measures of stiffness employed in our computational models. Further details on the computation of G₀ are in ESI,† Fig. S20a and b.

Imaging matrix fibers. Matrix fibers were visualized using a Zeiss LSM 710 confocal microscope equipped with a Ti-Sapphire Laser (Spectra Physics Mai Tai). Second harmonic generation confocal imaging was performed by exciting the matrices with a two-photon laser tuned to 780 nm, using a 40 × water immersion objective with a numerical aperture of 1.2 (Zeiss). To assess the heterogeneity of the matrix geometry, image stacks were acquired with a step size of 1 μm and scanned at 1024 × 1024 pixels with a pixel size of 0.208 × 0.208 μm², and recorded on Zen software. Matrix heterogeneity was analyzed by subdividing each image into 32 × 32 pixel subsets (6.6 × 6.6 μm²) and computing the Fourier transform of pixel intensities for each subset to quantify the fluctuation energy of intensity across wave numbers. The aggregate of these energy values provided the total spectral energy of the intensity field for each subset, which was then averaged across all subsets within an image to quantify the geometric heterogeneity of the matrix ([small chi, Greek, tilde]; ESI,† eqn (S6)), reflecting its permanently remodeled state following the contraction and recovery of cells. For each matrix sample, [small chi, Greek, tilde] was averaged across five representative images from distinct regions of interest. In the Results, [small chi, Greek, tilde] was normalized by the average matrix heterogeneity measured under conditions of inhibited cell contraction.

Statistical analysis

Statistical analysis was performed using MATLAB R2023b, with the Wilcoxon rank-sum test applied for comparisons between two groups. This test was selected because it is suitable for assessing differences between independent groups when normality cannot be assumed. Statistical significance was defined as p ≤ 0.05, with * and ** denoting p ≤ 0.05 and p ≤ 0.01, respectively.

Nomenclature

The following terms are used consistently throughout the paper.

Fibrous matrix (matrix)	Structure constituted by an intricate network of fibers.
Fibers (matrix fibers)	Fibers that constitute the fibrous matrix.
Mechanical remodeling	Mechanical strain-driven structural deformation of the fibrous matrix, independent of biochemical activity. Permanent deformation arising purely from geometric effects is referred to as permanent mechanical remodeling.

Variables in numerical simulations

L f	Average fiber length in the fibrous matrix.
ε r	Inclusion radial contraction.
δ ref	Reference inter-inclusion spacing in the cluster.
δ 1	Inter-inclusion spacing in the contracted cluster.
δ 2	Inter-inclusion spacing in the recovered cluster.
ξ c	Total length of fiber defects (excess lengths) produced by inclusion contraction within the cluster.
Δξf	Defect (excess length) in individual fibers produced during inclusion recovery.
ξ r	Total length of defects inside the cluster produced during inclusion recovery.
ξ	Total length of permanent defects within the recovered cluster.
L eff	Total length of fibers under axial tension within the recovered cluster.
L t	Total length of all fibers within the recovered cluster.
S	Relative radial alignment of fiber with the geometric center of the cluster.
r	Radial distance from the cluster center.
ρ	Physical fiber density of the matrix within the cluster.
χ	Geometric randomness imparted in the matrix due to inclusion contraction and recovery.
k	Incremental bulk stiffness of the matrix within the cluster.

Data availability

The supporting data for this study are included in the main text and ESI.† The code for generating the fibrous matrix is publicly available at https://github.com/jknotbohm/fiber_network_model. Scripts for finite element input file generation and experimental image processing, along with representative examples, are available at https://github.com/mainak-git-cloud/inclusion_matrix_models.

Conflicts of interest

The authors have no conflicts of interest to declare.

Appendix A

Table 1 Matrix mechanics during inclusion recovery

Step	Description	Key observations
Recovery of cluster inclusions	Inclusions recover their original size.	Permanent reduction in inter-inclusion spacing.
Geometric confinement surrounding cluster	A high microstructural gradient generates confining pressure surrounding the cluster, leading to fiber buckling during inclusion recovery.	Inclusions recover against increasing confining pressure, inducing post-buckling distortions in matrix fibers within the recovered cluster.
Defect generation within cluster	Recovery induces new buckling-mediated defects that superimpose pre-existing defects from inclusion contraction.	Accumulation of permanent defects.
History-dependent response	The magnitude of permanent defects reflects the loading history of the matrix.	Higher inclusion contraction and a steeper microstructural gradient result in more pronounced permanent defects.

---

Acknowledgements

MS and CL acknowledge the support from Charles Bell, Catherine Bracken and Barbara Bell. AWJ is a Chan Zuckerberg Biohub Chicago Investigator.

References

1. P. A. Janmey, The cytoskeleton and cell signaling: component localization and mechanical coupling, Physiol. Rev., 1998, 78(3), 763–781.
2. A. Bausch and K. Kroy, A bottom-up approach to cell mechanics, Nat. Phys., 2006, 2(4), 231–238.
3. B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Taylor & Francis Group, New York, 2007.
4. L. D. Muiznieks and F. W. Keeley, Molecular assembly and mechanical properties of the extracellular matrix: A fibrous protein perspective, Biochim. Biophys. Acta, Mol. Basis Dis., 2013, 1832(7), 866–875.
5. N. Laurens, P. d Koolwijk and M. De Maat, Fibrin structure and wound healing, J. Thromb. Haemostasis, 2006, 4(5), 932–939.
6. Y.-C. Lin, N. Y. Yao, C. P. Broedersz, H. Herrmann, F. C. MacKintosh and D. A. Weitz, Origins of elasticity in intermediate filament networks, Phys. Rev. Lett., 2010, 104(5), 058101.
7. Z. Shao and F. Vollrath, Surprising strength of silkworm silk, Nature, 2002, 418(6899), 741.
8. M. R. Islam, G. Tudryn, R. Bucinell, L. Schadler and R. Picu, Morphology and mechanics of fungal mycelium, Sci. Rep., 2017, 7(1), 13070.
9. P. G. Dixon and L. J. Gibson, The structure and mechanics of moso bamboo material, J. R. Soc., Interface, 2014, 11(99), 20140321.
10. P. Onck, T. Koeman, T. Van Dillen and E. van der Giessen, Alternative explanation of stiffening in cross-linked semiflexible networks, Phys. Rev. Lett., 2005, 95(17), 178102.
11. C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nonlinear elasticity in biological gels, Nature, 2005, 435(7039), 191–194.
12. B. A. Roeder, K. Kokini, J. E. Sturgis, J. P. Robinson and S. L. Voytik-Harbin, Tensile mechanical properties of three-dimensional type i collagen extracellular matrices with varied microstructure, J. Biomech. Eng., 2002, 124(2), 214–222.
13. P. A. Janmey, M. E. McCormick, S. Rammensee, J. L. Leight, P. C. Georges and F. C. MacKintosh, Negative normal stress in semiflexible biopolymer gels, Nat. Mater., 2007, 6(1), 48–51.
14. A. E. Brown, R. I. Litvinov, D. E. Discher, P. K. Purohit and J. W. Weisel, Multiscale mechanics of fibrin polymer: gel stretching with protein unfolding and loss of water, Science, 2009, 325(5941), 741–744.
15. D. Vader, A. Kabla, D. Weitz and L. Mahadevan, Strain-induced alignment in collagen gels, PLoS One, 2009, 4(6), e5902.
16. S. Münster, L. M. Jawerth, B. A. Leslie, J. I. Weitz, B. Fabry and D. A. Weitz, Strain history dependence of the nonlinear stress response of fibrin and collagen networks, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(30), 12197–12202.
17. O. V. Kim, R. I. Litvinov, J. W. Weisel and M. S. Alber, Structural basis for the nonlinear mechanics of fibrin networks under compression, Biomaterials, 2014, 35(25), 6739–6749.
18. A. J. Licup, S. Münster, A. Sharma, M. Sheinman, L. M. Jawerth, B. Fabry, D. A. Weitz and F. C. MacKintosh, Stress controls the mechanics of collagen networks, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(31), 9573–9578.
19. M. Vahabi, A. Sharma, A. J. Licup, A. S. Van Oosten, P. A. Galie, P. A. Janmey and F. C. MacKintosh, Elasticity of fibrous networks under uniaxial prestress, Soft Matter, 2016, 12(22), 5050–5060.
20. R. Picu, S. Deogekar and M. Islam, Poisson's contraction and fiber kinematics in tissue: insight from collagen network simulations, J. Biomech. Eng., 2018, 140(2), 021002.
21. A. Mann, R. S. Sopher, S. Goren, O. Shelah, O. Tchaicheeyan and A. Lesman, Force chains in cell-cell mechanical communication, J. R. Soc., Interface, 2019, 16(159), 20190348.
22. H. Reda, K. Berkache, J. Ganghoffer and H. Lakiss, Dynamical properties of random fibrous networks based on generalized continuum mechanics, Waves Random Complex Media, 2020, 30(1), 27–53.
23. M. Sarkar and J. Notbohm, Evolution of force chains explains the onset of strain stiffening in fiber networks, J. Appl. Mech., 2022, 89(11), 111008.
24. M. Sarkar, B. M. Burkel, S. M. Ponik and J. Notbohm, Unexpected softening of a fibrous matrix by contracting inclusions, Acta Biomater., 2024, 177, 253–264.
25. A. Zakharov, M. Awan, A. Gopinath, S.-J. J. Lee, A. K. Ramasubramanian and K. Dasbiswas, Clots reveal anomalous elastic behavior of fiber networks, Sci. Adv., 2024, 10(2), eadh1265.
26. G. Grekas, M. Proestaki, P. Rosakis, J. Notbohm, C. Makridakis and G. Ravichandran, Cells exploit a phase transition to mechanically remodel the fibrous extracellular matrix, J. R. Soc., Interface, 2021, 18(175), 20200823.
27. R. S. Sopher, H. Tokash, S. Natan, M. Sharabi, O. Shelah, O. Tchaicheeyan and A. Lesman, Nonlinear elasticity of the ecm fibers facilitates efficient intercellular communication, Biophys. J., 2018, 115(7), 1357–1370.
28. E. Ban, H. Wang, J. M. Franklin, J. T. Liphardt, P. A. Janmey and V. B. Shenoy, Strong triaxial coupling and anomalous Poisson effect in collagen networks, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(14), 6790–6799.
29. D. Humphries, J. Grogan and E. Gaffney, Mechanical cell-cell communication in fibrous networks: the importance of network geometry, Bull. Math. Biol., 2017, 79, 498–524.
30. J. Notbohm, A. Lesman, P. Rosakis, D. A. Tirrell and G. Ravichandran, Microbuckling of fibrin provides a mechanism for cell mechanosensing, J. R. Soc., Interface, 2015, 12(108), 20150320.
31. A. Favata, A. Rodella and S. Vidoli, An internal variable model for plastic remodeling in fibrous materials, Eur. J. Mech. A/Solids, 2022, 96, 104718.
32. A. Favata, A. Rodella and S. Vidoli, Emerging anisotropy and tethering with memory effects in fibrous materials, Mech. Mater., 2024, 190, 104928.
33. M. Sarkar and C. Laukaitis, A. Wagoner Johnson, Geometry-driven mechanical memory in a random fibrous matrix, J. Appl. Mech., 2025, 92(4), 041010.
34. J. D. Paulsen and N. C. Keim, Mechanical memories in solids, from disorder to design, Annu. Rev. Condens. Matter Phys., 2024, P 16, 035544.
35. E. Bell, B. Ivarsson and C. Merrill, Production of a tissue-like structure by contraction of collagen lattices by human fibroblasts of different proliferative potential in vitro, Proc. Natl. Acad. Sci. U. S. A., 1979, 76(3), 1274–1278.
36. L. K. Wrobel, T. R. Fray, J. E. Molloy, J. J. Adams, M. P. Armitage and J. C. Sparrow, Contractility of single human dermal myofibroblasts and fibroblasts, Cell Motil. Cytoskeleton, 2002, 52(2), 82–90.
37. P. Lu, K. Takai, V. M. Weaver and Z. Werb, Extracellular matrix degradation and remodeling in development and disease, Cold Spring Harbor Perspect. Biol., 2011, 3(12), a005058.
38. B. Burkel and J. Notbohm, Mechanical response of collagen networks to nonuniform microscale loads, Soft Matter, 2017, 13(34), 5749–5758.
39. B. Burkel, M. Proestaki, S. Tyznik and J. Notbohm, Heterogeneity and nonaffinity of cell-induced matrix displacements, Phys. Rev. E, 2018, 98(5), 052410.
40. M. Proestaki, A. Ogren, B. Burkel and J. Notbohm, Modulus of fibrous collagen at the length scale of a cell, Exp. Mech., 2019, 59(9), 1323–1334.
41. M. Proestaki, B. Burkel, E. E. Galles, S. M. Ponik and J. Notbohm, Effect of matrix heterogeneity on cell mechanosensing, Soft Matter, 2021, 17, 10263–10273.
42. M. Proestaki, M. Sarkar, B. M. Burkel, S. M. Ponik and J. Notbohm, Effect of hyaluronic acid on microscale deformations of collagen gels, J. Mech. Behav. Biomed. Mater., 2022, 135, 105465.
43. S. Natan, Y. Koren, O. Shelah, S. Goren and A. Lesman, Long-range mechanical coupling of cells in 3d fibrin gels, Mol. Biol. Cell, 2020, 31(14), 1474–1485.
44. G. Chaudhary, A. Ghosh, N. A. Bharadwaj, J. G. Kang, P. V. Braun, K. S. Schweizer and R. H. Ewoldt, Thermoresponsive stiffening with microgel particles in a semiflexible fibrin network, Macromol, 2019, 52(8), 3029–3041.
45. S. Adam, A. Mohanan, S. Bakshi, A. Ghadai and S. Majumdar, Network architecture dependent mechanical response in temperature responsive collagen-pnipam composites, Colloids Surf., B, 2023, 227, 113380.
46. K. M. Wisdom, K. Adebowale, J. Chang, J. Y. Lee, S. Nam, R. Desai, N. S. Rossen, M. Rafat, R. B. West and L. Hodgson, et al., Matrix mechanical plasticity regulates cancer cell migration through confining microenvironments, Nat. Commun., 2018, 9(1), 4144.
47. A. Saraswathibhatla, D. Indana and O. Chaudhuri, Cell-extracellular matrix mechanotransduction in 3d, Nat. Rev. Mol. Cell Biol., 2023, 24(7), 495–516.
48. R. C. Webb, Smooth muscle contraction and relaxation, Adv. Physiol. Educ., 2003, 27(4), 201–206.
49. A. Sakers, M. K. De Siqueira, P. Seale and C. J. Villanueva, Adipose-tissue plasticity in health and disease, Cell, 2022, 185(3), 419–446.
50. M. Islam and R. Picu, Effect of network architecture on the mechanical behavior of random fiber networks, J. Appl. Mech., 2018, 85(8), 081011.
51. H. Hatami-Marbini and M. Rohanifar, Nonlinear mechanical properties of prestressed branched fibrous networks, Biophys. J., 2021, 120(3), 527–538.
52. S. B. Lindström, D. A. Vader, A. Kulachenko and D. A. Weitz, Biopolymer network geometries: Characterization, regeneration, and elastic properties, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82(5), 051905.
53. S. B. Lindström, A. Kulachenko, L. M. Jawerth and D. A. Vader, Finite-strain, finite-size mechanics of rigidly cross-linked biopolymer networks, Soft Matter, 2013, 9(30), 7302–7313.
54. P. Grimmer and J. Notbohm, Displacement propagation in fibrous networks due to local contraction, J. Biomech. Eng., 2018, 140(4), 041011.
55. A. Sharma, A. Licup, R. Rens, M. Vahabi, K. Jansen, G. Koenderink and F. MacKintosh, Strain-driven criticality underlies nonlinear mechanics of fibrous networks, Phys. Rev. E, 2016, 94(4), 042407.
56. J. L. Shivers, J. Feng, A. S. van Oosten, H. Levine, P. A. Janmey and F. C. MacKintosh, Compression stiffening of fibrous networks with stiff inclusions, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(35), 21037–21044.
57. A. S. van Oosten, X. Chen, L. Chin, K. Cruz, A. E. Patteson, K. Pogoda, V. B. Shenoy and P. A. Janmey, Emergence of tissue-like mechanics from fibrous networks confined by close-packed cells, Nature, 2019, 573(7772), 96–101.
58. J. Hafner, D. Grijalva, A. Ludwig-Husemann, S. Bertels, L. Bensinger, A. Raic, J. Gebauer, C. Oelschlaeger, M. Bastmeyer, K. Bieback, C. Lee-Thedieck and N. Willenbacher, Monitoring matrix remodeling in the cellular microenvironment using microrheology for complex cellular systems, Acta Biomater., 2020, 111, 254–266.
59. P. K. Viji Babu, C. Rianna, U. Mirastschijski and M. Radmacher, Nano-mechanical mapping of interdependent cell and ECM mechanics by AFM force spectroscopy, Sci. Rep., 2019, 9, 12317.
60. M. A. Meyers and K. K. Chawla, Mechanical behavior of materials, Cambridge university press, 2008.
61. P. Fernandez and A. R. Bausch, The compaction of gels by cells: a case of collective mechanical activity, Integr. Biol., 2009, 1(3), 252–259.
62. U. Doha, O. Aydin, M. S. H. Joy, B. Emon, W. Drennan and M. T. A. Saif, Disorder to order transition in cell-ECM systems mediated by cell-cell collective interactions, Acta Biomater., 2022, 154, 290–301.
63. A. Shahsavari and R. Picu, Size effect on mechanical behavior of random fiber networks, Int. J. Solids Struct., 2013, 50(20–21), 3332–3338.
64. K. Berkache, S. Deogekar, I. Goda, R. Picu and J.-F. Ganghoffer, Construction of second gradient continuum models for random fibrous networks and analysis of size effects, Compos. Struct., 2017, 181, 347–357.
65. K. Berkache, S. Deogekar, I. Goda, R. C. Picu and J.-F. Ganghoffer, Identification of equivalent couple-stress continuum models for planar random fibrous media, Continuum Mech. Thermodyn., 2019, 31, 1035–1050.
66. K. Berkache, S. Deogekar, I. Goda, R. C. Picu and J.-F. Ganghoffer, Homogenized elastic response of random fiber networks based on strain gradient continuum models, Math. Mech. Solids, 2019, 24(12), 3880–3896.
67. S. Tyznik and J. Notbohm, Length scale dependent elasticity in random three-dimensional fiber networks, Mech. Mater., 2019, 138, 103155.
68. J. Merson and R. Picu, Size effects in random fiber networks controlled by the use of generalized boundary conditions, Int. J. Solids Struct., 2020, 206, 314–321.
69. K. J. Wolf and S. Kumar, Hyaluronic acid: incorporating the bio into the material, ACS Biomater. Sci. Eng., 2019, 5(8), 3753–3765.
70. F. Burla, J. Tauber, S. Dussi, J. van Der Gucht and G. H. Koenderink, Stress management in composite biopolymer networks, Nat. Phys., 2019, 15(6), 549–553.
71. J.-C. Lien and Y.-l Wang, Cyclic stretching-induced epithelial cell reorientation is driven by microtubule-modulated transverse extension during the relaxation phase, Sci. Rep., 2021, 11(1), 14803.
72. J. S. Bredfeldt, Y. Liu, C. A. Pehlke, M. W. Conklin, J. M. Szulczewski, D. R. Inman, P. J. Keely, R. D. Nowak, T. R. Mackie and K. W. Eliceiri, Computational segmentation of collagen fibers from second-harmonic generation images of breast cancer, J. Biomed. Opt., 2014, 19(1), 016007.
73. D. Gibson and P. Gaydecki, Definition and application of a Fourier domain texture measure: applications to histological image segmentation, Comput. Bio.l Med., 1995, 25(6), 551–557.
74. A. van der Schaaf and J. H. van Hateren, Modelling the power spectra of natural images: statistics and information, Vision Res., 1996, 36(17), 2759–2770.
75. M. Sarkar and J. Notbohm, Quantification of errors in applying dic to fiber networks imaged by confocal microscopy, Exp. Mech., 2022, 62(7), 1175–1189.
76. K. E. Kubow, R. Vukmirovic, L. Zhe, E. Klotzsch, M. L. Smith, D. Gourdon, S. Luna and V. Vogel, Mechanical forces regulate the interactions of fibronectin and collagen i in extracellular matrix, Nat. Commun., 2015, 6(1), 8026.
77. Y. Zhu, C. M. Sköld, X. Liu, H. Wang, T. Kohyama, F.-Q. Wen, R. F. Ertl and S. I. Rennard, Fibroblasts and monocyte macrophages contract and degrade three-dimensional collagen gels in extended co-culture, Respir. Res., 2001, 2, 295.
78. H. Kawasaki, T. Ohama, M. Hori and K. Sato, Establishment of mouse intestinal myofibroblast cell lines, World J. Gastroenterol., 2013, 19(17), 2629.
79. J. Kim, J. Feng, C. A. Jones, X. Mao, L. M. Sander, H. Levine and B. Sun, Stress-induced plasticity of dynamic collagen networks, Nat. Commun., 2017, 8(1), 842.
80. E. Ban, J. M. Franklin, S. Nam, L. R. Smith, H. Wang, R. G. Wells, O. Chaudhuri, J. T. Liphardt and V. B. Shenoy, Mechanisms of plastic deformation in collagen networks induced by cellular forces, Biophys. J., 2018, 114(2), 450–461.
81. M. Zhang, Y. Chen, F.-P. Chiang, P. I. Gouma and L. Wang, Modeling the large deformation and microstructure evolution of nonwoven polymer fiber networks, J. Appl. Mech., 2019, 86(1), 011010.
82. F. Burla, S. Dussi, C. Martinez-Torres, J. Tauber, J. van der Gucht and G. H. Koenderink, Connectivity and plasticity determine collagen network fracture, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(15), 8326–8334.
83. B. Deng, Z. Zhao, W. Kong, C. Han, X. Shen and C. Zhou, Biological role of matrix stiffness in tumor growth and treatment, J. Transl. Med., 2022, 20(1), 540.
84. M. D. Davidson, E. Ban, A. C. Schoonen, M.-H. Lee, M. D'Este, V. B. Shenoy and J. A. Burdick, Mechanochemical adhesion and plasticity in multifiber hydrogel networks, Adv. Mater., 2020, 32(8), 1905719.
85. J. Huang, J. Zhang, D. Xu, S. Zhang, H. Tong and N. Xu, From jammed solids to mechanical metamaterials: A brief review, Curr. Opin. Solid State Mater. Sci., 2023, 27(1), 101053.
86. D. Rayneau-Kirkhope, S. Bonfanti and S. Zapperi, Density scaling in the mechanics of a disordered mechanical meta-material, Appl. Phys. Lett., 2019, 114(11), 111902.
87. J. C. Maxwell, L. on the calculation of the equilibrium and stiffness of frames, London, Edinburgh Dublin Philos. Mag. J. Sci., 1864, 27(182), 294–299.
88. S. Arzash, J. L. Shivers, A. J. Licup, A. Sharma and F. C. MacKintosh, Stress-stabilized subisostatic fiber networks in a ropelike limit, Phys. Rev. E, 2019, 99(4), 042412.
89. S. Goren, Y. Koren, X. Xu and A. Lesman, Elastic anisotropy governs the range of cell-induced displacements, Biophys. J., 2020, 118(5), 1152–1164.
90. H. Hatami-Marbini and M. Rohanifar, Mechanical response of composite fiber networks subjected to local contractile deformation, Int. J. Solids Struct., 2021, 228, 111045.
91. J. Feng, H. Levine, X. Mao and L. M. Sander, Alignment and nonlinear elasticity in biopolymer gels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91(4), 042710.
92. A. S. Van Oosten, M. Vahabi, A. J. Licup, A. Sharma, P. A. Galie, F. C. MacKintosh and P. A. Janmey, Uncoupling shear and uniaxial elastic moduli of semiflexible biopolymer networks: compression-softening and stretch-stiffening, Sci. Rep., 2016, 6, 19270.
93. M. Sarkar and J. Notbohm, Bioinspired fiber networks with tunable mechanical properties by additive manufacturing, J. Appl. Mech., 2023, 90(8), 081010.
94. M. Islam and R. Picu, Random fiber networks with inclusions: The mechanism of reinforcement, Phys. Rev. E, 2019, 99(6), 063001.
95. E. A. Sander and V. H. Barocas, Comparison of 2d fiber network orientation measurement methods, J. Biomed. Mater. Res., Part A, 2009, 88(2), 322–331.
96. B. E. Vestal, N. E. Carlson and D. Ghosh, Filtering spatial point patterns using kernel densities, Spat. Stat., 2021, 41, 100487.
97. D. A. Head, A. J. Levine and F. MacKintosh, Deformation of cross-linked semiflexible polymer networks, Phys. Rev. Lett., 2003, 91(10), 108102.
98. D. Head, A. Levine and F. MacKintosh, Mechanical response of semiflexible networks to localized perturbations, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72(6), 061914.
99. P. L. Chandran and V. H. Barocas, Affine versus non-affine fibril kinematics in collagen networks: theoretical studies of network behavior, J. Biomech. Eng., 2006, 128(2), 259–270.
100. H. Hatami-Marbini and R. Picu, Scaling of nonaffine deformation in random semiflexible fiber networks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77(6), 062103.
101. N. Parvez, J. Merson and R. Picu, Stiffening mechanisms in stochastic athermal fiber networks, Phys. Rev. E, 2023, 108(4), 044502.
102. C. Liu, J. Lertthanasarn and M.-S. Pham, The origin of the boundary strengthening in polycrystal-inspired architected materials, Nat. Commun., 2021, 12(1), 4600.
103. B. Burkel, B. A. Morris, S. M. Ponik, K. M. Riching, K. W. Eliceiri and P. J. Keely, Preparation of 3D collagen gels and microchannels for the study of 3D interactions in vivo, J. Visualized Exp., 2016, 111, 53989.
104. M. Kovács, J. Tóth, C. Hetényi, A. Málnási-Csizmadia and J. R. Sellers, Mechanism of blebbistatin inhibition of myosin ii, J. Biol. Chem., 2004, 279(34), 35557–35563.
105. R. H. Ewoldt, M. T. Johnston and L. M. Caretta, Experimental Challenges of Shear Rheology: How to Avoid Bad Data, Springer, New York, 2015, ch. 6, pp. 207–241.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00087d

---