Open Access Article
Open Access ArticleDesigning soft and tough multiple-network elastomers: impact of reversible radical deactivation on filler network architecture and fracture toughness†
Aaliyah Z.
Dookhith
 ,
Zidan
Zhang
,
Zidan
Zhang
 ,
Venkat
Ganesan
,
Venkat
Ganesan
 and
Gabriel E.
Sanoja
and
Gabriel E.
Sanoja
 *
*
McKetta Department of Chemical Engineering, The University of Texas at Austin, Austin, TX 78712, USA. E-mail: gesanoja@che.utexas.edu
First published on 28th April 2025
Abstract
Polymer networks are crucial for engineering and biomedical applications; however, their excessive brittleness in the absence of viscoelastic dissipation limits their use in applications requiring high temperatures and water concentrations. Multiple-networks, consisting of a stiff and pre-stretched “filler” network phase embedded within a soft and extensible “matrix” network, offer a promising route to overcome this limitation; yet, the relationship between “filler” network architecture and fracture toughness remains unknown. Here, we synthesized three poly(ethyl acrylate) “filler” networks via free radical polymerization (FRP), RAFT, and ATRP, and assessed the interplay between “filler” network architecture, irreversible chain breakage, and fracture toughness by labelling their crosslinks with fluorogenic mechanophores. These networks had similar elastic chain densities but distinct chain length distributions and mesoscopic structures. They were used to prepare multiple-networks, whose structure and mechanical properties were evaluated using mechanical tests, confocal microscopy, reactive Monte Carlo, and coarse-grained molecular dynamics simulations. Our results reveal that “filler” networks synthesized by RAFT and ATRP yield more brittle multiple-networks than those made by FRP, primarily due to the reduced average extensibility of their “filler” network chains. Their narrower chain length distributions in the load-bearing phase promote strain hardening but compromise energy dissipation through molecular friction and chain breakage, as well as fracture toughness. Overall, these findings underscore the need for advanced gelation methods that provide control over elastic chain distributions within networks, as, without such improvements, the use of RAFT and ATRP may result in long curing times, opacity, and a greater tendency to fracture.
Introduction
Polymer networks are irreplaceable in engineering and biomedical applications, such as elastomers in rubber tires, dampers, and seals;1 hydrogels in contact lenses and superabsorbent diapers;2 and pressure-sensitive-adhesives (PSAs) in labels, band-aids, and double-sided tape.3 These materials feature elastic moduli E ranging from 1 kPa to 1 MPa and can sustain large deformations near pre-existing defects or cracks.4–6 However, at high temperatures or solvent concentrations, they readily break, precluding their use in applications such as water purification membranes,7 hydrogels for artificial prosthetics and drug delivery,8 solid polymer electrolytes for energy conversion and storage devices,9 and electro-adhesives for advanced manufacturing.10 In these conditions, the polymer segmental dynamics facilitate ion or small-molecule transport, but the networks exhibit limited viscoelastic dissipation, which leads to localized stresses, crack nucleation, and fracture. Designing polymer networks that are both soft and tough under these conditions is critical for developing advanced materials in emerging energy, healthcare, and manufacturing applications.A common practice to design soft and tough polymer networks is to embed stiff carbon black or silica particles within a rubber-like polymer matrix.11 This approach leads to an uneven load distribution between the stiff and soft phases,12 which helps mitigate the nucleation and growth of cracks. However, probing this load distribution under increasing strain is challenging because of load transfer from the stiff particles to the soft matrix, molecular-scale damage, and large-strain cavitation.13–15 Gaining insight into this load distribution, along with its evolution and impact on energy dissipation and fracture, is essential for establishing structure–property relationships and designing next-generation polymer networks.
We aim to understand and control the load distribution, energy dissipation, and fracture toughness of soft and tough polymer networks, leveraging three recent advances in polymer science. First, the introduction of double-network hydrogels and multiple-network elastomers by Gong et al. and Ducrot et al.,16,17 which consist of a stiff and brittle “filler” network phase embedded within a soft and extensible “matrix” network. These materials result from sequential polymerization and swelling steps, which isotropically pre-stretch the “filler” network chains to a stretch ratio λ0; and have mechanical properties governed by an uneven load distribution between the stiff and soft phases, just like conventional filled networks.18–22
Specifically, at small strains, the “filler” network carries the load within its chains; while at large strains, these chains elongate and break, transferring the load to the “matrix” network. Therefore, the mechanical properties of these materials closely depend on the pre-stretch of the “filler” network chains, λ0, as well as the architecture (i.e., topology) and interconnectivity between the “filler” and “matrix” networks. For instance, when the “filler” network chains elongate to their contour lengths, the multiple-networks undergo strain-hardening; and when they break, the multiple-networks dissipate significant energy and exhibit enhanced toughness.17,21–23 Thus, we consider multiple-networks as ideal systems for designing soft and tough polymer networks by focusing on the impact of polymerization methods on gelation.
The second important development is the use of reversible deactivation radical polymerizations (RDRPs) such as reversible addition–fragmentation transfer (RAFT), atom transfer radical polymerization (ATRP), and nitroxide-mediated polymerization (NMP) to structurally tailor and engineer polymer networks.24,25 These techniques provide control over the molecular weight, dispersity, and microstructure of linear polymers (i.e., comonomer sequence) and can influence the topology of polymer networks. Fukuda,26,27 Billingham and Armes,28,29 Matyjaszewski,30–33 Allonas and Croutxé-Barghorn,34,35 and their coworkers have demonstrated that RDRPs prevent the formation of “dead” gels or clusters at the early stages of monomer-crosslinker copolymerization, shifting the percolation threshold to higher vinyl group conversions and narrowing the chain length distribution within the networks. These RDRPs were conducted at either high crosslinker, ≈85 mol%,34,35 or high solvent concentrations, ≈50 wt%,36,37 resulting in polymer networks with mechanical properties ranging from stiff and brittle to soft and tacky.
More recently, one of our investigations showed that conducting RAFT and ATRP copolymerizations at lower crosslinker concentrations and under bulk conditions (i.e., without solvent) also induces sol–gel demixing at high vinyl group conversions (i.e., microsyneresis), resulting in polymer networks with crosslinker-rich and crosslinker-poor mesophases that form at the late stages of gelation, an opaque appearance, and elastomer-like mechanical properties (i.e., Young's modulus, E ∼ 1 MPa, and fracture toughness, Gc ∼ 100 J m−2).38 Therefore, we consider RDRPs to be promising techniques for controlling the architecture of both single- and multiple-networks, and understanding their impact on load distribution, energy dissipation, and mechanical properties.
The third important development is the use of mechanochemistry as a tool to map and quantify damage in polymers.39–44 This approach involves incorporating force-responsive probes, known as mechanophores, at load-bearing points within polymer networks, such as the crosslinks. These probes selectively activate at forces similar to those required to break a covalent bond, inducing changes in the photophysical properties of the bulk in response to force. For example, force-induced chemical reactions can turn these probes into fluorophores, with fluorescence detectable under a confocal microscope.45–48 This fluorescence provides a direct damage measure and is particularly useful for studying fracture.23,47,49–52 Hence, we consider this fluorogenic mechanochemistry technique a powerful tool for unraveling the impact of “filler” network architecture, as controlled by RDRPs, on load distribution, damage, energy dissipation, and fracture toughness of multiple-networks.
Before proceeding, we deem it important to highlight two key bodies of work on the structure–property relationships of these multiple-networks. The first is by Kawauchi et al., which examined the effect of “filler” network heterogeneities on the fracture toughness of double-network hydrogels.53 This study revealed that “filler” networks with no or large-scale heterogeneities, ξ > 300 nm, synthesized by monomer-crosslinker copolymerization in either good or poor solvents, offered more brittle double-networks than those with moderately sized heterogeneities, ξ = 10–300 nm, where ξ represents the correlation length of the spatial heterogeneities within the “filler” network.
The second study, by Slootman et al., investigated the impact of “filler” network pre-stretch, λ0, on the fracture toughness of multiple-network elastomers.23 Their results demonstrated that pre-stretched “filler” network chains improve the high-temperature (i.e., low-rate) fracture toughness of multiple-networks by facilitating damage delocalization ahead of cracks and improving the load transfer efficiency between the “filler” and “matrix” networks. Namely, this work illustrated that when the “filler” network pre-stretch exceeds λ0 > 1.6, the “matrix” network can more effectively carry the load transferred upon “filler” network breakage, delaying the transition from random (i.e., mean-field) to localized (i.e., correlated) “filler” network scission, crack nucleation, and fracture.
In addition, Slootman et al. demonstrated that rate and temperature strongly influence this damage delocalization mechanism, highlighting the critical role played by viscoelasticity in energy dissipation, bulk deformation, and fracture.23 Their findings showed that multiple-networks dissipate energy through both viscoelasticity and damage, with the number of broken “filler” network chains per unit area of propagated crack, Σx, scaling with the effective stretch of the “filler” network chains at the fracture point, λcλ0, Σx ∼ exp(α·λcλ0), where α = 1.75. This effective stretch, λcλ0, depends on both the loading rate and temperature, indicating that viscoelasticity and damage are inherently coupled in dissipating energy ahead of cracks.
With these considerations in mind, we hypothesized that RDRPs such as RAFT and ATRP could offer control over the “filler” network architecture, as well as the resulting load transfer mechanism, energy dissipation, and fracture toughness of multiple-networks. To validate this hypothesis, we synthesized a series of polymer networks via free radical copolymerization (FRP), RAFT, and ATRP, using ethyl acrylate (EA) as the monomer and 1,4-butanediol diacrylate (BDA) as the crosslinker. These networks were similar to those reported in our previous work, where we showed that RAFT and ATRP lead to a different interplay between elasticity (i.e., Young's modulus) and strain-hardening than FRPs.38 Here, we used these networks as “filler” phases in multiple-network systems, focusing specifically on how their architecture impacts energy dissipation and fracture toughness.
Through mechanical testing, mechanochemistry, reactive Monte-Carlo (RMC) and coarse-grained molecular dynamics (CGMD) simulations, we show that, at the same crosslink density, νx, (i.e., modulus, E, or pre-stretch ratio λ0), “filler” networks synthesized via RAFT and ATRP result in more brittle multiple-networks than those synthesized by FRP. The reversible deactivation of radical chain ends during gelation leads to the formation of crosslinker-rich and crosslinker-poor mesophases, along with narrower chain length distributions within the crosslinker-rich, load-bearing phase (i.e., lower average chain extensibility, λh). This reduced chain extensibility limits the load transfer efficiency between the “filler” and “matrix” networks, and decreases the energy dissipated per broken “filler” network bond ahead of cracks, thereby reducing overall toughness. These results inform the molecular design of soft and tough polymer networks, underscoring the need for advanced polymerization methods that offer control over elastic chain distribution, mesoscopic architecture, and load transfer efficiency of multiple-networks.
Experimental
Materials
Unless otherwise specified, all chemicals were used as received. Ethyl acrylate (EA) and 1,4-butanediol diacrylate (BDA) were sourced from TCI America; 2-hydroxy-2-methylpropiophenone (HMP), cyanomethyl dodecyl trithiocarbonate (CTA), ethyl α-bromoisobutyrate (EBiB) copper(I) bromide (CuBr), tris[2-(dimethylamino)ethyl]amine (Me6TREN), anhydrous THF, triethylamine, acryloyl chloride, hydroquinone, magnesium sulfate and anhydrous ethyl acetate from Millipore Sigma; basic aluminum oxide, toluene, dichloromethane (DCM), sodium chloride, sodium bicarbonate and anhydrous DMSO from VWR; and the π-extended anthracene-maleimide adduct, diol precursor of the fluorogenic mechanophore (DACL), from Concept Life Sciences.EA (100 mL) and BDA (25 mL) were purified by elution over basic aluminum oxide. Purified EA, BDA and as-received HMP, CTA, EBiB, and Me6TREN were placed in dry septum-sealed bottles, sparged with N2 for 45 min, and transferred into a N2-filled glovebox.
Synthesis of fluorogenic mechanophore
The fluorogenic mechanophore (DACL) was synthesized following the procedure reported by Göstl et al.45 Briefly, the diol precursor (50 mg, 0.11 mmol) was dissolved in anhydrous THF (2 mL) and activated with excess triethylamine (160 μL, 1.1 mmol). Separately, acryloyl chloride (90 μL, 1.1 mmol) was dissolved in anhydrous THF (3 mL) in a round-bottom flask pre-cooled in an ice bath. The diol solution was then added dropwise to the acryloyl chloride solution, and the reaction mixture was allowed to proceed overnight at room temperature.The following day, DI water (25 mL) was added to the reaction mixture, and the product was extracted with DCM (25 mL). The organic layer was washed with saturated sodium bicarbonate (3 × 25 mL) and saturated sodium chloride (3 × 25 mL), dried with magnesium sulfate, filtered, and used to dissolve hydroquinone (1 mg, 0.01 mmol). Finally, DCM was evaporated under vacuum, yielding the mechanophore crosslinker, DACL, as a pale-yellow solid. This mechanophore was dried overnight in a vacuum oven at room temperature, resulting in a reaction yield of 85% (see 1H NMR in Fig. S1, ESI†).
Synthesis of filler networks
Polymer networks were synthesized in a N2-filled glovebox, following a procedure introduced by Ducrot et al.17,54,55 and detailed in our previous work.38 The concentration of propagating clusters was fixed at approximately 0.1 mol% through the concentration of initiator (FRP and ATRP) or chain transfer agent (RAFT).For FRP, monomer EA, crosslinker BDA (0.5 mol%), and initiator HMP (0.1 mol%) were mixed in a 20 mL scintillation vial and transferred to a mold composed of two PET-covered glass plates sealed with a silicone rubber spacer approximately 0.1 cm thick. Instead, for RAFT and ATRP, the mixture consisted of monomer EA, crosslinker BDA (1.0 mol%), initiator HMP (0.02 mol%), CTA agent (0.1 mol%), and toluene (10%v/v); and monomer EA, crosslinker BDA (1.0 mol%), initiator EBiB (0.07 mol%), catalyst CuBr (0.007 mol%), ligand Me6TREN (0.028 mol%), and DMSO (10% v/v). Importantly, ATRP polymerizations were conducted directly on glass, as their kinetics were too slow to prevent diffusion of the EA monomer within the PET layer and excessive adhesion of the networks (see a detailed summary of the polymerization conditions in Table S1, ESI†).
For networks labelled with fluorogenic mechanophores, a small fraction of crosslinker BDA, 0.02 mol%, was substituted with the mechanophore crosslinker (see a detailed summary of the polymerization conditions in Table S3, ESI†), just like in previous work.47 This substitution resulted in networks with the same mechanical properties as those synthesized without mechanophore, consistent with the findings of Slootman et al.47 (see representative stress–stretch curves in Fig. S10 and S11, ESI†).
The copolymerizations were initiated with UV light (365 nm, 0.30 mW cm−2) and carried out until approximately 100% conversion: 2 h, 24 h, and 48 h for networks synthesized by FRP, RAFT, and ATRP, respectively. These times were determined from the kinetics of EA polymerization reported in Dookhith et al.38
The resulting polymer networks were removed from the glovebox and dried under vacuum oven overnight at 30 °C. These networks had dimensions of approximately 8 × 4 × 0.1 cm3 and gel fractions above 99%.
Synthesis of multiple networks
Multiple-networks were synthesized in a N2-filled glovebox according to a procedure introduced by Ducrot et al.17,54,55 and detailed in our previous work.38 Briefly, the filler networks were swollen to equilibrium with a solution of monomer EA (99.98 mol%), crosslinker BDA (0.01 mol%) and initiator HMP (0.01 mol%) for 2 h, and transferred to a mold composed of two PET-covered glass plates sealed with a silicone spacer (≈0.1 cm thick). The polymerizations were initiated by irradiation with UV light (365 nm, 0.30 mW cm−2) and conducted for 2 h.The resulting multiple-networks were transferred outside of the glovebox and dried overnight under vacuum at 30 °C. These networks had dimensions dictated by the filler network pre-stretch, λ0, and gel fractions above 99%.
Following Millereau et al., this procedure was adjusted to fine tune the pre-stretch the “filler” network, leveraging the composition of the EA solution with ethyl acetate solvent to control the swelling, Q, and pre-stretch ratios, λ0 = Q−1/3.21
Visualization of phase separation in filler networks
Polymer networks were punch-cut into cylindrical specimens of 8 mm diameter, cleaned with ethanol and optical paper, and placed on a glass slide. Then, a Zeiss Axio Scope A1 microscope was used to examine their structure, acquiring brightfield images with a 20× LD Plan – Neofluar objective.Rheology
Polymer networks were punch-cut into cylindrical specimens of 8 mm diameter, and their rheological properties were evaluated in a discovery HR-2 rheometer equipped with stainless steel flat plates of the same diameter. Frequency sweeps from 0.1 to 100 rad s−1 at temperatures from 30 to 75 °C were performed within the linear viscoelastic regime at a strain of 0.10%. Master curves for the storage, G′, and loss, G′′, moduli were constructed by time-temperature-superposition (TTS), using a reference temperature of 30 °C and horizontal aT, and vertical, bT, shift factors.Uniaxial tension
Polymer networks were punch-cut into dog-bone shaped specimens of 20 mm gauge-length, 4 mm width, and approximately 1.3 mm thickness. These specimens were marked with two dots of white paint and then deformed with an Instron 34TM5 equipped with a 100 N load cell and a video extensometer. The initial stretch rate was varied between 3 × 10−4 and 3 × 10−2 s−1, and the temperature between 23 and 75 °C.The resulting force–displacement curves were used to compute the stress, σ, and stretch, λ, according to:
 | (1) |
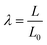 | (2) |
The stress–stretch curves were used to estimate the Young's modulus, E, according to:
 | (3) |
And the stress–stretch curves of the multiple-networks were fitted to Gent's hyperelastic model to estimate the strain hardening, λm, according to:
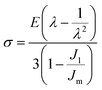 | (4) |
Uniaxial tensile tests were conducted by triplicate at each stretch rate and temperature to determine the average and 95% confidence interval of the modulus, E, and strain hardening, λm.
Single-edge notch crack propagation tests
Polymer networks were punch-cut into dog-bone shaped specimens of 20 mm gauge length, 4 mm width, and approximately 1.3 mm thickness. These specimens were cut with a fresh razor blade to introduce a crack of ≈1 mm length, marked with two dots of white paint, and deformed with an Instron 34TM5 equipped with a 100 N load cell and a video extensometer. The initial stretch rate was varied between 3 × 10−4 and 3 × 10−2 s−1 and the temperature between 23 and 75 °C.The resulting force–displacement curves were used to compute the engineering stress, σ, and stretch, λ, according to eqn (1) and (2).
The fracture toughness or critical energy release rate, Gc, was calculated using the Greensmith model:56
 | (5) |
 .
.
Single-edge notch fracture tests were conducted by triplicate at each stretch rate and temperature to determine the average and 95% confidence interval of the fracture toughness, Gc.
Damage quantification through mechanochemistry
Fractured specimens were cleaned with ethanol and optical paper, and then taped to a Petri dish using double-sided tape. Fluorescent images were acquired on a Nikon AXR (Galvano and Resonant Scanner) confocal system equipped with a CFI60 Plan Apochromat Lambda D 20× N.A. 0.80, W.D. 0.80 mm, F.O.V. 25 mm, DIC, spring-loaded objective lens. π-Extended anthracene fluorophores were excited with a 405-nm laser, and their fluorescent emission recorded in the 424–524 nm range. The optical magnification was set to 20×, resulting in 2048 × 2048 raw images (0.43 μm pixel−1). 3D scans were collected from the specimen surface (i.e., plane of maximum intensity) through a 300 μm depth using a step size of 20 μm.The fluorescence intensity was used to estimate the number of broken monolayers of “filler” network chains following a previously established procedure.47,49 Briefly, a calibration curve was used to determine the number density of activated mechanophores, ϕ(x,y,z), which was assumed to represent the number density of broken “filler” network bonds. This assumption was thoroughly discussed by Slootman et al.,47 who evaluated the force-induced fluorescence of pol(methyl acrylate) networks labeled with different mechanophore fractions and subjected to uniaxial deformation or single-edge notch crack propagation at various rates and temperatures. Their results indicated that, within the range of mechanophore concentrations, strain rates, and temperatures considered in this work, the force-induced fluorescence serves as a representative measure of chain breakage and damage (see Appendices 6 and 7 in Slootman et al., 1H NMR spectrum for calibration molecule in Fig. S2 and representative calibration curve in Fig. S12, ESI†). The calculation was done according to:
 | (6) |
This density of broken “filler” network bonds was averaged across the imaged plane, xz, to calculate the distribution of broken “filler” network chains within the multiple-networks,  , where Lx = 880 μm is the dimension of the imaged volume along the crack propagation direction, x.
, where Lx = 880 μm is the dimension of the imaged volume along the crack propagation direction, x.
This damage profile, ϕ(y,z), was integrated along the penetration depth, Ly = 300 μm, to estimate the number of broken “filler” network bonds per unit area of propagated crack, Σx(z):
 | (7) |
Averaging Σx(z) along the imaged thickness, Lz = 300 μm, offers a measure of the number of broken “filler” network bonds per unit area of propagated crack,  .
.
This Σx was normalized by the areal density of “filler” network chains, Σ0, to determine the number of Lake–Thomas monolayers that break upon fracture,  (see image processing details in Fig. S13, ESI†). Here, Σ0 was calculated according to:
(see image processing details in Fig. S13, ESI†). Here, Σ0 was calculated according to:
 | (8) |
Reactive Monte-Carlo and coarse-grained molecular dynamics simulations
Reactive Monte-Carlo (RMC) and coarse-grained molecular dynamics (CGMD) simulations were conducted following procedures from our recent work and are described in detail in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38,57
38,57
The polymerization scheme used in the RMC for FRP, RAFT, and ATRP utilized an initiator concentration of 0.2%. This scheme differentiated RAFT and ATRP by varying the termination rate constant (see details in ESI†). The crosslinker concentrations were set to 0.5% (FRP) and 1.0% (RAFT and ATRP). The simulation box contained 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 monomers, and the reaction probabilities for initiation, propagation, and termination reactions were based on previously reported values.38,57
250 monomers, and the reaction probabilities for initiation, propagation, and termination reactions were based on previously reported values.38,57
The RMC simulations were conducted until 98% vinyl group conversion. The resulting polymer networks were then mapped onto a coarse-grained bead-spring representation, purging unreacted monomers and initiators. The polymer network number density was then maintained at 0.85σ−3.
In the coarse-grained simulations, pairwise interactions between beads were modelled by the repulsive, truncated-shifted Lennard-Jones (LJ) potential:
 | (9) |
The connectivity between beads was modelled using the finite extensible nonlinear elastic (FENE) potential:
 | (10) |
The rigidity of the strands was described using a bending potential:
| Ubendi,i+1 = kBTKbend(1 − (ni·ni+1)) | (11) |
The equilibration of the coarse-grained polymer network was conducted under the canonical ensemble (NVT). Specifically, Langevin dynamics were integrated using the velocity Verlet algorithm58 with a timestep of Δt = 0.005τ and a duration of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ, where τ is the timescale in the coarse-grained simulation described as
000τ, where τ is the timescale in the coarse-grained simulation described as  , where m = 1.0 is the mass of the coarse-grained bead. After equilibration, a topological analysis was conducted to determine the elastically active chains, explicitly accounting for the Scanlan-Case criterion.59
, where m = 1.0 is the mass of the coarse-grained bead. After equilibration, a topological analysis was conducted to determine the elastically active chains, explicitly accounting for the Scanlan-Case criterion.59
After equilibration, the bending potential was removed, and the FENE potential was replaced with a breakable quartic bond potential, which allows for chain scission during uniaxial deformation:
| Uquartic = Kquartic(r − Rc)2(r − Rc − B1)(r − Rc − B2) + U0 | (12) |
After switching the FENE bond potential to the breakable quartic potential, the polymer network was re-equilibrated for 2500τ under the NPT ensemble. The temperature and pressure were set to T = 1.5 and P = 1.0, using a Nosé–Hoover barostat.61 Such a choice ensures that the number density of all three systems is maintained around 0.85σ−3 (see Fig. S31, ESI†). Subsequently, uniaxial deformation was performed under the NPT ensemble until the stretch ratio reached at least λ = 21, with an elongation rate of 5 × 10−5τ−1. Simulation results were averaged over five ensembles with completely different initial configurations for statistical purposes. All coarse-grained molecular dynamics simulations were conducted using LAMMPS (Update 1, 2nd Aug 2023).62
Results and discussion
“Filler” networks synthesized by RDRPs have different molecular and mesoscopic structures than analogues synthesized by FRP
We synthesized three polymer networks by UV-initiated radical copolymerization of ethyl acrylate (EA) monomer and 1,4-butanediol diacrylate crosslinker (BDA), using FRP, RAFT, or ATRP. Detailed synthetic conditions are located in the Materials and methods section and ESI,† but their primary difference lies in the crosslinker concentration: 0.5 mol% for FRP and 1.0 mol% for RAFT and ATRP. These differences reflect variations in the initiation, propagation, and termination rates inherent to each polymerization method but ultimately yield networks with similar small-strain mechanical properties (see detailed discussion in Zhang et al.57).These networks were rubbery at room temperature, with a glass transition temperature, Tg ≈ −18 °C. Moreover, based on rubber elasticity and Flory–Rehner theories,63 they were indistinguishable, featuring the same elastic modulus, E ≈ 0.89 ± 0.02 MPa, and swelling ratio Q ≈ 4.0, in an athermal solvent like ethyl acrylate. Thus, they had the same volumetric and areal densities of elastically active chains: νx ≈ 7.1 × 1025 m−3 and Σ0 ≈ 2.3 × 1017 m−2.
However, both the structure and optical properties of these networks differed. RAFT- and ATRP-synthesized networks were opaque due to sol–gel demixing during gelation, consisting of crosslinker-rich and crosslinker-poor phases. In addition, the early-stage kinetics of RAFT and ATRP resulted in networks with narrower chain length distributions and higher load-bearing capacities in the crosslinker-rich phase, which formed under higher local crosslinker concentrations and percolated throughout the network (see properties in Table 1, images in Fig. 1A, stress–strain curves in Fig. 1B, and elastic chain distributions estimated from reactive Monte-Carlo simulations in Fig. 1C).
| Mechanism | E [MPa] | Q | ν x [1025 m−3] | Σ 0 [1017 m−2] | λ h |
|---|---|---|---|---|---|
| FRP | 0.9 | 4.0 | 7.1 | 2.3 | 4.9 |
| RAFT | 0.9 | 4.0 | 7.1 | 2.3 | 3.9 |
| ATRP | 0.9 | 4.0 | 7.1 | 2.3 | 3.7 |
 | ||
| Fig. 1 Properties of “filler” networks: optical, mechanical and molecular (A) filler networks synthesized by RAFT and ATRP appear opaque, suggesting phase-separation into crosslinker-rich and crosslinker-poor phases. (B) These networks, as well as that synthesized by FRP, exhibit similar mechanical properties in the low-deformation regime. Specifically, they have comparable elastic modulus E ≈ 0.9 MPa, indicating equivalent densities of elastically active chains. (C) However, at the molecular scale, these three networks likely differ in their chain length distributions, with RAFT- and ATRP- synthesized networks having narrower chain length distributions than that synthesized via FRP, based on reactive Monte Carlo simulations (see distributions in a log–log scale in Fig. S29, ESI†). Reprinted (adapted) from Dookhith et al.34 Copyright 2024 American Chemical Society. | ||
These structural differences were reported in Dookhith et al.,38 and, here, we hypothesize that they should impact the fracture properties of multiple-networks.
“Filler” networks synthesized by RAFT and ATRP offer more brittle multiple-networks than analogues synthesized by FRP
Inspired by the seminal work of Gong et al. on double-network hydrogels and Ducrot et al. on multiple-network elastomers,16,17 we interpenetrated these “filler” networks within a soft and loosely crosslinked “matrix” network, synthesized by FRP of EA and BDA (0.01 mol%) using HMP (0.01 mol%) as a photoinitiator (see scheme in Fig. 2A). These multiple-networks were also rubbery at room temperature, with a glass transition temperature, Tg ≈ −18 °C. They had the same pre-stretch ratio, λ0 = Q−1/3 = 1.6 (see swelling ratio in Fig. S3, ESI†), and Young's modulus, E = 1.30 ± 0.03 MPa, but exhibited distinct strain hardening. Specifically, the multiple-networks containing “filler” networks synthesized by RAFT and ATRP strain hardened at λm,RAFT ≈ λm,ATRP ≈ 2.4 ± 0.2, whereas that containing a “filler” network synthesized by FRP did so at λm,FRP = 3.1 ± 0.1 (see rheological master curves in Fig. 2B, stress–stretch curves in Fig. 2C, and summary of multiple-network properties in Table 2).| “Filler” network | E [MPa] | λ 0 | λ m | G c [J m−2] |
|---|---|---|---|---|
| FRP | 1.3 | 1.6 | 3.1 | 1200 |
| RAFT | 1.3 | 1.6 | 2.3 | 740 |
| ATRP | 1.3 | 1.6 | 2.4 | 760 |
In Dookhith et al.,38 we noted that these differences in large-strain mechanical properties likely arise from variations in the average extensibility of the “filler” network chains, λh, in line with the analyses reported by Millereau et al. and Kong et al. (see Table 1),21,64 and molecular and mesoscopic structures. Here, we examine their impact on fracture toughness, as measured by the critical energy release rate, Gc.
Remarkably, at a temperature of 23 °C and an initial loading rate of 3 × 10−3 s−1, the multiple-networks based on “filler” networks synthesized by RAFT and ATRP were more brittle than that based on a “filler” network synthesized by FRP, with Gc,RAFT = 740 ± 40 J m−2, Gc,ATRP = 760 ± 50 J m−2 and Gc,FRP = 1200 ± 40 J m−2. At other rates and temperatures, similar differences in fracture behavior were observed despite variations in Gc due to viscoelastic dissipation (see Fig. 3, representative stress–stretch curves in Fig. S4 and S7, S8, critical stretch ahead of the crack in Fig. S9, and statistics in Table S2, ESI†). Thus, multiple-networks composed of “filler” networks synthesized by RAFT and ATRP appeared to be less effective at dissipating energy than that with a “filler” network synthesized by FRP, presumably due to less efficient load transfer from the “filler” to the “matrix” network.
To us, these observations were interesting given the similar viscoelastic behavior of the multiple-networks in both linear amplitude oscillatory shear rheology and step-cyclic loading. The storage and loss moduli, G′ and G′′, were indistinguishable over a wide range of reduced frequencies, aTω, and the stress–stretch curves showed negligible hysteresis under step-cyclic loads (see rheological master curves in Fig. 2B, stress–stretch curves in Fig. S5 and shift factors in Fig. S6, ESI†). Thus, we consider this family of materials to be both identically and nearly perfectly elastic in bulk, with all differences in dissipation mechanisms (i.e., viscoelasticity and damage) confined to the large-strain region ahead of a crack – similar linear rheology but different nonlinear response.
“Filler” networks synthesized by RAFT and ATRP lead to a different interplay between viscoelasticity and damage ahead of cracks
Having examined the impact of “filler” network architecture on the fracture toughness, Gc, we now focus on its effect on the load transfer efficiency and energy dissipation mechanisms ahead of cracks. This efficiency was evaluated by labelling the “filler” networks with fluorogenic mechanophores and imaging the regions next to the fracture surfaces with a confocal microscope. Details on the mechanophore synthesis and quantification are provided in the Materials and methods section, as well as in Göstl et al.,45 Slootman et al.,23,47 and Sanoja et al.;49 but, briefly, we estimated the (i) number of activated mechanophores per unit area of propagated crack, Σx, from a calibration curve and the Young's modulus, E, of the “filler” network; and (ii) the number of broken “filler” network monolayers per unit area of propagated crack,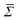 , from the prediction of the Lake and Thomas model, Σ0.65 This number of activated mechanophores was considered representative of the number of broken “filler” network bonds, in line with Slootman et al. (see a detailed discussion of this assumption in Appendices 6 and 7 of Slootman et al., as well as in the recent theoretical work of Dubach et al.).47,66
, from the prediction of the Lake and Thomas model, Σ0.65 This number of activated mechanophores was considered representative of the number of broken “filler” network bonds, in line with Slootman et al. (see a detailed discussion of this assumption in Appendices 6 and 7 of Slootman et al., as well as in the recent theoretical work of Dubach et al.).47,66
Consistent with the measured Gc, the multiple-networks composed of “filler” networks synthesized by RAFT, ATRP, and FRP experienced different extents of damage during fracture,  . For example, at a loading rate of 3 × 10−3 s−1 and temperature of 23 °C, the multiple-networks with “filler” networks synthesized by RAFT and ATRP evolved larger, more delocalized damage zones than that with a “filler” network synthesized by FRP, with
. For example, at a loading rate of 3 × 10−3 s−1 and temperature of 23 °C, the multiple-networks with “filler” networks synthesized by RAFT and ATRP evolved larger, more delocalized damage zones than that with a “filler” network synthesized by FRP, with  ,
,  , and
, and  . Additionally, at lower loading rates and higher temperatures, all multiple-networks exhibited less, more localized damage likely due to reduced, large-strain viscoelastic dissipation ahead of cracks (see Fig. 4, representative confocal images and damage profiles in Fig. S14–S17 (ESI†), and estimates of damage delocalization length scale in Fig. S18 and S19, ESI†). Therefore, the multiple-networks composed of “filler” networks synthesized by RAFT and ATRP incurred more damage than that composed of a “filler” network synthesized by FRP, despite being more brittle.
. Additionally, at lower loading rates and higher temperatures, all multiple-networks exhibited less, more localized damage likely due to reduced, large-strain viscoelastic dissipation ahead of cracks (see Fig. 4, representative confocal images and damage profiles in Fig. S14–S17 (ESI†), and estimates of damage delocalization length scale in Fig. S18 and S19, ESI†). Therefore, the multiple-networks composed of “filler” networks synthesized by RAFT and ATRP incurred more damage than that composed of a “filler” network synthesized by FRP, despite being more brittle.
To us, this observation was particularly interesting because the fracture toughness, Gc, often increases with the damage-zone size,  , in fracture mechanics. Specifically, the fracture toughness is typically described by the equation Gc = G0 (1 + f(aTv)), where G0 is the intrinsic fracture toughness and a function of damage, and f(aTv) is a viscoelastic toughness enhancement that depends on the reduced crack propagation velocity, aTv.67–71 Within this framework, the intrinsic fracture energy, G0, is defined as the energy required to break a monolayer of elastically active chains across the crack plane. According to Lake and Thomas,65 this energy is given by G0 = NxUbΣ0, where Nx is the average elastic chain length, Ub is the energy of a C–C bond, and Σ0 is the areal density of elastically active chains along the fracture plane (see crack velocities in Table S3 (ESI†) and related analyses of fracture toughness and damage in Fig. S20 and S21, ESI†).
, in fracture mechanics. Specifically, the fracture toughness is typically described by the equation Gc = G0 (1 + f(aTv)), where G0 is the intrinsic fracture toughness and a function of damage, and f(aTv) is a viscoelastic toughness enhancement that depends on the reduced crack propagation velocity, aTv.67–71 Within this framework, the intrinsic fracture energy, G0, is defined as the energy required to break a monolayer of elastically active chains across the crack plane. According to Lake and Thomas,65 this energy is given by G0 = NxUbΣ0, where Nx is the average elastic chain length, Ub is the energy of a C–C bond, and Σ0 is the areal density of elastically active chains along the fracture plane (see crack velocities in Table S3 (ESI†) and related analyses of fracture toughness and damage in Fig. S20 and S21, ESI†).
However, our results challenge this description, revealing a larger damage zone, in terms of broken “filler” network chains, for the more brittle multiple-networks, as well as a dependence of the damage zone on both rate and temperature. They indicate that the total energy dissipated per broken “filler” network bond, Gc/Σx, depends on the method used to synthesize the “filler” network, irrespective of the loading rate and temperature. For instance, at a temperature of 23 °C and a rate of 3 × 10−3 s−1, Gc/Σx,RAFT = 1.2 ± 0.3 × 10−17 J per chain, Gc/Σx,ATRP = 0.9 ± 0.5 × 10−17 J per chain, and Gc/Σx,FRP = 2.4 ± 0.6 × 10−17 J per chain. In comparison, at 75 °C and the same loading rate of 3 × 10−3 s−1, Gc/Σx,RAFT = 0.9 ± 0.6 × 10−17 J per chain, Gc/Σx,ATRP = 0.8 ± 0.5 × 10−17 J per chain, and Gc/Σx,FRP = 2.6 ± 1.0 × 10−17 J per chain (see energy dissipated per filler chain under different fracture conditions in Fig. S27, ESI†).
From “filler” network synthesis to multiple-network fracture: a molecular picture
Based on these results, we pose a molecular picture of fracture, which closely aligns with that of Slootman et al.23 and is inspired by the damage models of Brown and Tanaka.18,19 In this picture, fracture results from (i) random and (ii) correlated scission of “filler” network bonds, followed by (iii) breakage of the “matrix” network; that is, from load transfer from the “filler” to the “matrix” network and the associated energy dissipation. In their seminal work, Slootman et al. demonstrated that the “filler” network pre-stretch, λ0, is critical in this load transfer efficiency, controlling the formation of a stable damage zone, energy dissipation, and fracture.23 Here, we focus on the influence of “filler” network architecture, as dictated by the gelation method, on the fracture toughness.Let us first examine the impact of “filler” network architecture on the size of the damage zone, Σx, which, in damage models, is typically governed by the effective stretch within the “filler” network, λλ0, relative to the maximum extensibility of the “filler” network chains, λh.72–74 This ratio measures the probability of breaking a chain within the “filler” network and was evaluated at the fracture point, λcλ0/λh, which depends on both rate and temperature because of viscoelastic dissipation (see variation in λc with rate and temperature in Fig. S9 (ESI†) and changes in toughness and damage with λc in Fig. S21, ESI†).
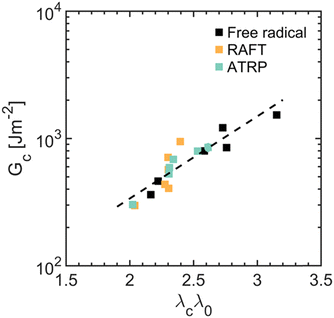
In line with damage models, our results indicate that the probability of breaking a “filler” network bond controls the size of the damage zone, Σx, revealing a master curve between Σx and λcλ0/λh, which scales as Σx ∼ exp(β·λcλ0/λh), with β = 6.9 ± 1.5 (see Fig. 5). This scaling exponent is similar to that reported by Slootman et al. for another family of multiple-networks composed of a “filler” network synthesized by FRP and having a modulus of E = 1 MPa, β = 6.3 ± 1.2 (see Fig. S26, ESI†).23
This result highlights two key points. First, the coupling between viscoelasticity and damage, as measured by β, is independent of the “filler” network architecture. All multiple-networks consist of poly(ethyl acrylate) chains, presumably featuring the same friction coefficient and intermolecular interactions when elongated from their undeformed configuration to their contour length. Second, “filler” networks synthesized by RAFT and ATRP experience more damage than those synthesized by FRP when fractured at the same effective stretch, λcλ0; likely due to the reduced average extensibility of the “filler” network chains, λh, resulting from the controlled gelation methods and their impact on the architecture.
With this picture in mind, we can now discuss the impact of “filler” network structure on the fracture toughness of multiple-networks, Gc. Unlike the size of the damage zone, Σx, which depends on the fracture stretch of the “filler” network relative to its average contour length, this fracture toughness, Gc, depends only on the fracture stretch of the “filler” network, λcλ0, and collapses onto a master curve described by Gc ∼ exp(γ·λcλ0), with γ = 1.5 ± 0.4 (see Fig. 6). This curve suggests that viscoelasticity ultimately governs energy dissipation, dictating the fracture behavior of multiple-networks. Namely, multiple-networks with distinct “filler” network architectures exhibit similar fracture toughness as long as their filler network chains experience a similar fracture stretch, λcλ0. Reducing the average extensibility of the “filler” network chains through an RDRP method, such as RAFT and ATRP, thus compromises both (i) the energy dissipated as the “filler” network chains extend from their relaxed configuration to their fracture length (i.e., from λ0 to λ0λc, which dictates viscoelasticity), as well as (ii) the energy released as the “filler” network chains progressively break as they approach their contour length (i.e., from λ0/λh to λ0λc/λh, which governs damage).
The impact of RAFT and ATRP on “filler” network architecture and multiple-network fracture is then two-fold. First, RAFT and ATRP lower the average extensibility of the “filler” network chains, resulting in higher chain breakage probabilities at the crack front and in multiple-networks with larger damage zones. Second, RAFT and ATRP lead to “filler” networks with limited large-strain viscoelastic dissipation ahead of the crack, ultimately promoting multiple-network fracture. Thus, RAFT- and ATRP-synthesized “filler” networks localize stress and transition from random to correlated chain breakage at lower deformations than that synthesized by FRP, compromising energy dissipation and fracture toughness.
Coarse-grained molecular dynamics simulations
Having painted this molecular picture of fracture, we now address whether variations in the “filler” network structure at the molecular or mesoscopic length scales have a greater impact on the toughness. Ideally, to isolate the impact of these variations, we would synthesize networks with uniform mesoscopic structures (i.e., without crosslinker-rich and crosslinker-poor mesophases) using FRP, ATRP, and RAFT. However, synthesizing such networks proved challenging; all networks synthesized by RAFT and ATRP turned opaque due to sol–gel demixing at the late stages of gelation.Nevertheless, our observations suggest that variations in chain length distributions within the load-bearing phase of the “filler” network play a more significant role than the mere presence of crosslinker-rich and crosslinker-poor mesophases. After all, RAFT- and ATRP-synthesized networks differ significantly in light transmittance (T ≈ 67% for “filler” network synthesized by RAFT and T ≈ 19% for the “filler” network synthesized by ATRP) but exhibit a similar relationship between viscoelasticity, damage, and fracture toughness (see images in Fig. 1A, master curves in Fig. 5 and 6, and visualization of phase separation in filler and multiple networks in Fig. S28, ESI†). Furthermore, the crosslinker-rich phase within the “filler” network, which forms during the early, reaction-controlled stages of gelation, should carry most of the load; both because it percolates and constitutes the majority phase, and because it consists, on average, of shorter chains than the crosslinker-poor phase.
To support this picture, we generated three networks by reactive Monte-Carlo simulations and deformed them in uniaxial tension through coarse-grained molecular dynamics simulations. As in experiments, these networks had similar elastic chain densities but different chain length distributions due to reversible radical deactivation during gelation (see Fig. 1C). Simulation details are provided in the Materials and methods section, as well as in Dookhith et al. and Zhang et al.,38,57 but briefly, the reactive Monte-Carlo simulations generated networks through a three-dimensional bond fluctuation model (3DBFM), while the coarse-grained molecular dynamics offered stress–strain curves and damage evolution estimates under uniaxial deformation, leveraging a quartic bond potential to quantify chain breakage. Importantly, these simulations focused exclusively on the crosslinker-rich phase of the “filler” networks, neglecting both the matrix network and any coexisting phases within the architecture. As discussed earlier, the crosslinker-rich phase forms during the early, reaction-controlled stages of gelation and should carry most of the load within the “filler” network.
Interestingly, our simulation results show tensile curves consistent with networks having similar elastic chain densities but distinct chain length distributions. These networks exhibited indistinguishable Young's moduli but different strain hardening and failure (i.e., maximum stress) points (see Fig. 7A and Fig. S32, ESI†). Additionally, networks synthesized by RAFT and ATRP start to damage at lower strains than those synthesized by FRP (see Fig. 7B), suffering more chain breakage events, particularly among shorter chains, when subjected to a similar stretch. Lastly, the simulations unveil a mismatch between the number of chain breakage events and the associated energy dissipation, with networks synthesized by RAFT and ATRP dissipating less energy per chain elongation and breakage event than that synthesized by FRP, rendering them more brittle. This mismatch likely underpins the differences in fracture toughness between the multiple-networks. RAFT- and ATRP-synthesized “filler” networks may experience more chain breakage events ahead of cracks but do not necessarily dissipate more energy. Since their broken chains are, on average, shorter, they are unable to store and dissipate as much energy as that synthesized by FRP, in line with the Lake and Thomas model (see the cumulative average length of the broken chains in Fig. 7C).65
The picture that emerges from these coarse-grained MD simulations is thus qualitatively similar to that posed through mechanochemistry experiments. RAFT and ATRP offer networks with narrower chain length distributions within the crosslinker-rich, load-bearing phase, which, on average, have a limited ability to dissipate and store energy. These networks suffer chain breakage events at lower strains than those synthesized by FRP, experiencing an accelerated transition from random to correlated chain scission, rapidly localizing stress (i.e., inefficiently transferring it from the “filler” to the “matrix” network), and readily undergoing crack nucleation and fracture (see estimates of this transition in Fig. S33 and S34, ESI†). Therefore, at the same elastic chain density, νx, RAFT and ATRP seemingly afford more brittle networks than conventional FRP (see Scheme 1).
Concluding remarks
We investigated the impact of “filler” network architecture on the fracture toughness of multiple-networks, leveraging recent advances in RDRPs and mechanochemistry to synthesize three families of polymer networks (i) labelled with fluorogenic mechanophores and (ii) having similar elastic chain densities, νx, but different chain length distributions and mesoscopic structures.Using mechanical testing, confocal microscopy, reactive Monte-Carlo, and coarse-grained molecular dynamics simulations, we showed that these networks offered multiple-networks with distinct load transfer efficiency, energy dissipation, and fracture toughness. Specifically, “filler” networks synthesized by RAFT and ATRP resulted in more brittle multiple-networks than that made by FRP due to the reduced average extensibility of their elastic chains, which lowers both the energy stored per chain in its fully elongated state and the energy dissipated through viscoelastic chain friction as the chains stretch from their relaxed, Gaussian configuration to their contour length.
This result has important implications for both polymer science and fracture mechanics, bridging the gelation kinetics with the network architecture and fracture toughness. First, it reveals an inherent trade-off between strain hardening and fracture toughness, which arises from the gelation method and its impact on the elastic chains density and chain length distribution. Networks with narrower chain lengths, particularly within the load-bearing phase, may strain harden at lower strains but are more susceptible to damage and fracture. Second, it highlights differences in the damage zone in terms of the number of chain breakage events and the energy dissipated upon such breakage. Ahead of a crack, numerous short chains may break, but these events do not necessarily dissipate much energy and afford toughness. Finally, it highlights challenges raised by RAFT, ATRP, and other living polymerization methods (e.g., ring-opening polymerizations75–77) in manufacturing soft and tough elastomers (i.e., with elastic modulus and fracture toughness on the order of 1 MPa and 1000 J m−2).78,79 Relative to FRP, these techniques offer slower gelation rates and opaque and embrittled networks, particularly at high temperatures.
Overall, this result underscores the need to develop new techniques that offer high gelation rates and controlled molecular architectures, both to advance understanding of the interplay between gelation, structure, and mechanical properties and to guide the molecular design of advanced networks for emerging applications.
Further, it highlights two aspects that require future work. First, the generality of our results, since we focused on three “filler” networks synthesized via FRP, ATRP, and RAFT under very restricted crosslinker and initiator concentrations. Second, their validity under other conditions of minimal viscoelastic dissipation, such as the high-water concentrations typical of hydrogels. Addressing these points could deepen our understanding of the fundamental synthesis–structure–property relationships governing the mechanical properties of polymer networks.
Author contributions
Conceptualization (A. Z. D. and G. E. S.), data curation (A. Z. D. and Z. Z.), data analysis (A. Z. D., Z. Z., V. G., and G. E. S.), funding acquisitions (V. G., and G. E. S.), investigation (A. Z. D., and Z. Z.), methodology (A. Z. D., Z. Z., V. G., and G. E. S.), resources (V. G., and G. E. S.), supervision (V. G., and G. E. S.), validation (A. Z. D., Z. Z., and G. E. S.), visualization (A. Z. D. and G. E. S.), writing – original draft (A. Z. D.), writing – review and editing (A. Z. D., Z. Z., V. G. and G. E. S.).Data availability
Data for this article, including experimental data, reactive Monte Carlo simulations, and coarse-grained molecular dynamics simulations are available at the Texas Data Repository at https://doi.org/10.18738/T8/OVB8P1.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge Costantino Creton and K. Ravi-Chandar for helpful discussions. G. E. S. thanks the Welch Foundation for financial support (F-2210), and V. G. the Welch Foundation (F-1599), the donors of the American Chemical Society Petroleum Research Fund (66812-ND7) and the National Science Foundation (DMR-2225167).Notes and references
- A. N. Gent, in Engineering with Rubber, ed. A. N. B. T.-E. Gent and R. Gent, Carl Hanser Verlag GmbH & Co. KG, München, 3rd edn, 2012, pp. I–XVIII Search PubMed.
- Hydrogels in Medicine and Pharmacy, ed. N. A. Peppas, CRC Press, 2019 Search PubMed.
- C. Creton, MRS Bull., 2003, 28, 434–439 CrossRef CAS.
- C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 046601 CrossRef.
- C. Creton, Macromolecules, 2017, 50, 8297–8316 CrossRef CAS.
- R. Long, C.-Y. Hui, J. P. Gong and E. Bouchbinder, Annu. Rev. Condens. Matter Phys., 2021, 12, 71–94 CrossRef.
- G. M. Geise, D. R. Paul and B. D. Freeman, Prog. Polym. Sci., 2014, 39, 1–42 CrossRef CAS.
- X. Zhao, X. Chen, H. Yuk, S. Lin, X. Liu and G. Parada, Chem. Rev., 2021, 121, 4309–4372 CrossRef CAS PubMed.
- D. T. Hallinan and N. P. Balsara, Annu. Rev. Mater. Res., 2013, 43, 503–525 CrossRef CAS.
- H. J. Kim, L. Paquin, C. W. Barney, S. So, B. Chen, Z. Suo, A. J. Crosby and R. C. Hayward, Adv. Mater., 2020, 32, 1–7 Search PubMed.
- S. K. Kumar, B. C. Benicewicz, R. A. Vaia and K. I. Winey, Macromolecules, 2017, 50, 714–731 CrossRef CAS.
- Y. Chen, A. Kovalenko, A. Brûlet, B. Bresson, A. Lantheaume, L. Olanier and C. Creton, Macromolecules, 2023, 56, 5336–5345 CrossRef CAS.
- H. Zhang, A. K. Scholz, J. de Crevoisier, F. Vion-Loisel, G. Besnard, A. Hexemer, H. R. Brown, E. J. Kramer and C. Creton, Macromolecules, 2012, 45, 1529–1543 CrossRef CAS.
- H. Zhang, A. K. Scholz, F. Vion-Loisel, Y. Merckel, M. Brieu, H. Brown, S. Roux, E. J. Kramer and C. Creton, Macromolecules, 2013, 46, 900–913 CrossRef CAS.
- J. A. Gohl, T. J. Wiley, H.-C. Chang, C.-C. Chang and C. S. Davis, Front. Soft Matter, 2023, 3, 1–10 Search PubMed.
- J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Adv. Mater., 2003, 15, 1155–1158 CrossRef CAS.
- E. Ducrot, Y. Chen, M. Bulters, R. P. Sijbesma and C. Creton, Science, 2014, 344, 186–189 CrossRef CAS.
- H. R. Brown, Macromolecules, 2007, 40, 3815–3818 CrossRef CAS.
- Y. Tanaka, Europhys. Lett., 2007, 78, 56005 CrossRef.
- J. P. Gong, Soft Matter, 2010, 6, 2583 RSC.
- P. Millereau, E. Ducrot, J. M. Clough, M. E. Wiseman, H. R. Brown, R. P. Sijbesma and C. Creton, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9110–9115 CrossRef CAS.
- Y. Chen, G. Sanoja and C. Creton, Chem. Sci., 2021, 12, 11098–11108 RSC.
- J. Slootman, C. J. Yeh, P. Millereau, J. Comtet and C. Creton, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, 1–11 CrossRef.
- H. Gao and K. Matyjaszewski, Prog. Polym. Sci., 2009, 34, 317–350 CrossRef CAS.
- J. Cuthbert, A. C. Balazs, T. Kowalewski and K. Matyjaszewski, Trends Chem., 2020, 2, 341–353 CrossRef CAS.
- N. Ide and T. Fukuda, Macromolecules, 1997, 30, 4268–4271 CrossRef CAS.
- N. Ide and T. Fukuda, Macromolecules, 1999, 32, 95–99 CrossRef CAS.
- I. Bannister, N. C. Billingham, S. P. Armes, S. P. Rannard and P. Findlay, Macromolecules, 2006, 39, 7483–7492 CrossRef CAS.
- C.-D. Vo, J. Rosselgong, S. P. Armes and N. C. Billingham, Macromolecules, 2007, 40, 7119–7125 CrossRef CAS.
- H. Gao, K. Min and K. Matyjaszewski, Macromolecules, 2007, 40, 7763–7770 CrossRef CAS.
- H. Gao, W. Li and K. Matyjaszewski, Macromolecules, 2008, 41, 2335–2340 CrossRef CAS.
- H. Gao, A. Miasnikova and K. Matyjaszewski, Macromolecules, 2008, 41, 7843–7849 CrossRef CAS.
- H. Gao, P. Polanowski and K. Matyjaszewski, Macromolecules, 2009, 42, 5925–5932 CrossRef CAS.
- E. Goldbach, X. Allonas, L. Halbardier, C. Ley and C. Croutxé-Barghorn, Eur. Polym. J., 2023, 197, 112335 CrossRef CAS.
- E. Goldbach, X. Allonas, C. Croutxé-Barghorn, C. Ley, L. Halbardier and G. L’Hostis, Eur. Polym. J., 2023, 188, 111947 CrossRef CAS.
- A. Beziau, A. Fortney, L. Fu, C. Nishiura, H. Wang, J. Cuthbert, E. Gottlieb, A. C. Balazs, T. Kowalewski and K. Matyjaszewski, Polymer, 2017, 126, 224–230 CrossRef CAS.
- J. Cuthbert, S. V. Wanasinghe, K. Matyjaszewski and D. Konkolewicz, Macromolecules, 2021, 54, 8331–8340 CrossRef CAS.
- A. Z. Dookhith, Z. Zhang, V. Ganesan and G. E. Sanoja, Macromolecules, 2024, 57, 8698–8711 CAS.
- A. L. Black, J. M. Lenhardt and S. L. Craig, J. Mater. Chem., 2011, 21, 1655–1663 RSC.
- J. Li, C. Nagamani and J. S. Moore, Acc. Chem. Res., 2015, 48, 2181–2190 CrossRef CAS PubMed.
- R. Göstl, J. M. Clough and R. P. Sijbesma, in Mechanochemistry in Materials, ed. Y. C. Simon and S. L. Craig, The Royal Society of Chemistry, 2018, pp. 53–75 Search PubMed.
- N. Deneke, M. L. Rencheck and C. S. Davis, Soft Matter, 2020, 16, 6230–6252 RSC.
- Y. Chen, G. Mellot, D. van Luijk, C. Creton and R. P. Sijbesma, Chem. Soc. Rev., 2021, 50, 4100–4140 RSC.
- G. E. Sanoja and C. Creton, Annu. Rev. Chem. Biomol. Eng., 2025 DOI:10.1146/annurev-chembioeng-092220-113154.
- R. Göstl and R. P. Sijbesma, Chem. Sci., 2016, 7, 370–375 RSC.
- M. Stratigaki, C. Baumann, L. C. A. van Breemen, J. P. A. Heuts, R. P. Sijbesma and R. Göstl, Polym. Chem., 2020, 11, 358–366 RSC.
- J. Slootman, V. Waltz, C. J. Yeh, C. Baumann, R. Göstl, J. Comtet and C. Creton, Phys. Rev. X, 2020, 10, 041045 CAS.
- S. He, M. Stratigaki, S. P. Centeno, A. Dreuw and R. Göstl, Chem. – Eur. J., 2021, 27, 15889–15897 CrossRef CAS PubMed.
- G. E. Sanoja, X. P. Morelle, J. Comtet, C. J. Yeh, M. Ciccotti and C. Creton, Sci. Adv., 2021, 7, 1–23 Search PubMed.
- X. P. Morelle, G. E. Sanoja, S. Castagnet and C. Creton, Soft Matter, 2021, 17, 4266–4274 RSC.
- J. Ju, G. E. Sanoja, M. Y. Nagazi, L. Cipelletti, Z. Liu, C. Y. Hui, M. Ciccotti, T. Narita and C. Creton, Phys. Rev. X, 2023, 13, 021030 CAS.
- J. Ju, G. E. Sanoja, L. Cipelletti, M. Ciccotti, B. Zhu, T. Narita, C. Yuen Hui and C. Creton, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, 2017 Search PubMed.
- Y. Kawauchi, Y. Tanaka, H. Furukawa, T. Kurokawa, T. Nakajima, Y. Osada and J. P. Gong, J. Phys.:Conf. Ser., 2009, 184, 012016 CrossRef.
- E. Ducrot, H. Montes and C. Creton, Macromolecules, 2015, 48, 7945–7952 CrossRef CAS.
- E. Ducrot and C. Creton, Adv. Funct. Mater., 2016, 26, 2482–2492 CrossRef CAS.
- H. W. Greensmith, J. Appl. Polym. Sci., 1963, 7, 993–1002 CrossRef CAS.
- Z. Zhang, J. Krajniak, A. Z. Dookhith, Y. Tian, H. S. Sachar, N. Marioni, T. J. Duncan, J. Liu, G. E. Sanoja and V. Ganesan, Macromolecules, 2025, 58, 3168–3187 CrossRef CAS.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS.
- J. Scanlan, J. Polym. Sci., 1960, 43, 501–508 CrossRef CAS.
- T. Ge, F. Pierce, D. Perahia, G. S. Grest and M. O. Robbins, Phys. Rev. Lett., 2013, 110, 098301 CrossRef PubMed.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, New York, 1953 Search PubMed.
- V. A. Kong, T. A. Staunton and J. E. Laaser, Macromolecules, 2024, 57, 4670–4679 CAS.
- G. J. Lake and A. G. Thomas, Proc. R. Soc. A, 1967, 300, 108–119 CAS.
- F. F. C. Dubach, W. G. Ellenbroek and C. Storm, J. Polym. Sci., 2021, 59, 1188–1199 CrossRef CAS.
- A. N. Gent, Langmuir, 1996, 12, 4492–4496 CrossRef CAS.
- B. N. J. Persson and E. A. Brener, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2005, 71, 036123 CAS.
- C.-Y. Hui, B. Zhu and R. Long, J. Mech. Phys. Solids, 2022, 159, 104748 Search PubMed.
- B. N. J. Persson, G. Carbone, C. Creton, G. Heinrich and T. Tada, Extreme Mech. Lett., 2024, 68, 102143 CrossRef.
- S.-Q. Wang, Z. Fan, A. Siavoshani, M. Wang and J. Wang, Extreme Mech. Lett., 2025, 74, 102277 CrossRef.
- M. Bacca, C. Creton and R. M. McMeeking, J. Appl. Mech., 2017, 84, 1–7 CrossRef.
- F. J. Vernerey, R. Brighenti, R. Long and T. Shen, Macromolecules, 2018, 51, 6609–6622 CrossRef CAS PubMed.
- S. R. Lavoie, P. Millereau, C. Creton, R. Long and T. Tang, J. Mech. Phys. Solids, 2019, 125, 523–549 CrossRef CAS.
- A. Z. Dookhith, N. A. Lynd, C. Creton and G. E. Sanoja, Macromolecules, 2022, 55, 5601–5609 CrossRef CAS.
- A. Z. Dookhith, N. A. Lynd and G. E. Sanoja, Macromolecules, 2023, 56, 40–48 CrossRef CAS.
- M. Yasir, B. Hu, T.-C. Lin and K. Matyjaszewski, Langmuir, 2025, 41, 378–382 CrossRef CAS PubMed.
- A. Bagheri, C. M. Fellows and C. Boyer, Adv. Sci., 2021, 8, 2003701 CrossRef CAS PubMed.
- V. A. Bobrin, J. Zhang, N. Corrigan and C. Boyer, Adv. Mater. Technol., 2023, 8, 2201054 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00045a |
| This journal is © The Royal Society of Chemistry 2025 |