Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic field-induced transitions and phase diagram of aggregate structures in a suspension of polydisperse cubic haematite particles†
Kazuya
Okada
 *a and
Akira
Satoh
b
*a and
Akira
Satoh
b
aDepartment of Mechanical Engineering, Saitama Institute of Technology, Fukaya, Japan. E-mail: kokada@sit.ac.jp; Fax: +81-48-585-6902; Tel: +81-48-585-6902
bDepartment of Mechanical Engineering, Akita Prefectural University, Yurihonjo, Japan
First published on 2nd April 2025
Abstract
We investigated a polydisperse cubic haematite particle suspension in an external magnetic field and examined the dependence of magnetic field-induced transitions on the standard deviation of the particle size distribution using quasi-two dimensional Monte Carlo simulations. In the case of smaller polydispersity, stable clusters tend to form owing to stable face-to-face contact. In this case, however, larger magnetic particle–particle interaction strengths are necessary. Since the applied magnetic field enables the magnetic moment of each particle to incline in the field direction, it enhances the formation of chain-like clusters. In the case of larger polydispersity, compared to the smaller polydispersity cases, particle aggregates are formed even in the region of smaller magnetic particle–particle interactions. In this case, small particles combine with a growing cluster composed of large particles to form larger clusters. However, these small particles tend to disturb the internal structure of the particle aggregates, leading to chain-like clusters with narrower widths than those in the case of smaller polydispersity. These characteristics of the particle aggregates confirm that the broadness of polydispersity in a magnetic cubic particle suspension is applicable for controlling the internal structure and regime transition in the internal structure of particle aggregates. This may be an important feature in the development of surface modification techniques using magnetic cubic particle suspensions.
Introduction
Desired magnetic particle suspensions are generated by dispersing fine particles with appropriate magnetic properties and geometrical shapes in non-magnetic fluids. These suspensions have attracted significant attention in various engineering fields owing to their unique physical properties, such as particle aggregation, magnetically induced heat generation, characteristic orientational features, and magnetorheological behaviours, which are induced by the complex relationship between the magnetic properties of the particles and an applied magnetic field. The applications of magnetic particle suspensions are diverse in various fields, including magnetically controlled fluid devices in fluid engineering,1,2 magnetic hyperthermia treatments, drug delivery systems in biomedical engineering,3–6 visibility improvement methods in environmental resource engineering,7,8 and surface modification techniques in colloid and surface engineering.9–11To optimise the design and performance of devices utilising magnetic particle suspensions, clarifying their physical properties under various conditions is crucial. The orientational characteristics of magnetic particles and the internal structure of particle aggregates are known to significantly vary depending on the influence of an external magnetic field. This demonstrates that understanding the behaviour of magnetic particles in the presence of an applied magnetic field is essential to obtain a successful application of magnetic suspensions. In the present study, we conducted simulations to develop a surface modification technology, which may be a key factor in generating new multi-functionalised particles using magnetic and non-magnetic materials. The primary issue in the development of surface modification technology is controlling the orientational characteristics of magnetic particles and the regime change in particle aggregates on the material surface (i.e. magnetic field-induced transitions). Many researchers have investigated the aggregation phenomena and magnetic field-induced transitions on a two-dimensional (2D) plane by focusing on magnetic spherical particles.9–13 These studies clarified that spherical particles tend to form ring-like or curved chain-like clusters with point-to-point contact in a dilute system. These clusters were unstable and could be easily collapsed by the influence of flow fields or magnetic fields. In recent years, since magnetic particles can be synthesised with various geometric shapes, research subjects have expanded to magnetic non-spherical particles, such as rod-like,14,15 disc-like,16,17 cube-like,18–25 and peanut-like23,25 particles. Among these, cube-like particles allow for three distinct magnetisation models such as, plane direction, edge direction, and diagonal direction. These magnetisation characteristics are expected to significantly influence the internal structure of aggregates. Additionally, magnetic cube-like particles naturally aggregate in a face-to-face configuration. This face-to-face contact promotes the formation of closely-packed isotropic clusters, which tend to remain stable under flow fields or magnetic fields. This suggests that, compared to magnetic spherical and rod-like particle suspensions, cubic particle suspensions may exhibit distinct physical characteristics. Furthermore, the unique cubic shape enhances stability on material surfaces, potentially facilitating self-assembly on the surfaces. These distinctive shape and magnetization characteristics of cubic particles have motivated extensive research on cubic particle suspensions.24,26–28 Along this research trend, several researchers have investigated the internal structure of aggregates in cubic particle suspensions. Donaldson and Kantorovich studied optimal particle arrangements within clusters in a quasi-2D system without an external magnetic field using molecular dynamics simulations.24 Using the same simulation method, Brics et al. explored energetically favourable structures in an external magnetic field.26 Linse studied cubic haematite particles with three different magnetisation characteristics to investigate magnetic field-induced transitions.27 Their research clarified that cubic particles magnetized in the plane direction favour ring-like or curved chain-like structures, similar to conventional spherical particles. Under an external magnetic field, these structures transformed into single chain-like structures aligned with the field direction. In contrast, cubic particles magnetized along diagonal direction formed closely-packed clusters that expand into a square-lattice structure with face-to-face contact. As the magnetic field strength increased, these clusters transformed into chain-like clusters with offset face-to-face contact. Notably, these chain-like clusters could connect with neighbouring clusters, growing into thicker chain-like clusters. Thus, the internal structure of aggregates changes significantly due to their distinctive particle shape and magnetization characteristics of the cubic particles magnetized in the diagonal direction. This feature is not observed in suspensions composed of particles that form aggregates with point-to-point contact. While these studies considered monodisperse systems for simplicity in simulations, a complex system of polydispersity has not been investigated sufficiently. Any real suspension exhibits some degree of polydispersity, and therefore, it is essential to understand its effects when applying the findings of previous studies to real suspensions.
In our previous study,29 through 2D MC simulations, we elucidated the internal structure of particle aggregates and magnetic field-induced transitions on a material surface in a monodisperse suspension composed of cubic haematite particles. We clarified that cubic particles form stable closely-packed clusters with face-to-face contact, leading to rapid transitions within a certain narrow magnetic field range. This rapid magnetic field-induced transition is unique to a cubic particle system. Therefore, at the next step, clarification regarding the influence of the polydispersity of such a suspension on the aforementioned physical characteristics may be imperative.
As the magnitude of the magnetic moment of the particles is proportional to the particle volume, the polydispersity of the magnetic particles is expected to significantly affect the aggregate structures in magnetic–particle systems. Based on this consideration, in our subsequent study,30 we considered a suspension composed of polydisperse cubic haematite particles but focused on the situation where a magnetic field was absent. This is because, even in the case of a monodisperse system, magnetic cubic particles are expected to form complex clusters. Therefore, expanding on our previous investigation, in this study, we clarified the aggregation phenomena at a deeper level in the presence of an applied magnetic field.
Finally, we briefly describe several simulation studies31–38 on suspensions composed of polydisperse magnetic particles under an applied magnetic field. Kruse et al. studied polydisperse ferrofluids and investigated their microstructure in an external magnetic field.31 Kristóf and Szalai found that in weak and moderate magnetic fields, the magnetisation of a polydisperse system is higher than that of a monodisperse system.32 Ivanov et al. conducted molecular dynamics and MC simulations to examine the magnetisation curve of a polydisperse ferrofluid at various concentrations.34 Using the cluster-moving MC method, Aoshima and Satoh investigated the aggregation phenomena in a suspension composed of polydisperse ferromagnetic particles both in the absence and presence of an applied magnetic field.35,36 Li et al. examined a polydisperse system with a Gaussian distribution, focusing on the aggregation patterns of magnetic particles under an external magnetic field.37 They clarified the roles of large and small particles in polydisperse system. The probability of aggregation increased with particle size, as larger particles are more likely to aggregate. In contrast, smaller particles primarily attached to clusters formed by larger particles and did not play a major role in cluster formation. However, these studies primarily focus on a magnetic spherical particle suspension with polydispersity, and research on a suspension of magnetic non-spherical particles is scarce. Rosenberg et al. challenged the investigation on the effects of polydispersity in a suspension composed of disc-like particles using molecular dynamics simulations.38 They demonstrated that, compared to monodisperse systems, polydisperse systems exhibit more pronounced nematic-like ordering even under weaker magnetic fields. This finding may emphasize the importance of exploring how polydispersity affects phase transition phenomena in a cubic particle system.
The cubic haematite particles have significantly weak magnetisation compared to that of magnetite particles. Consequently, haematite particles with nano order generally do not significantly aggregate to form clusters. However, when the particle size reaches the submicron scale, particles tend to sediment and form self-assembly on the bottom surface.19–22 Therefore, we investigate a polydisperse suspension composed of cubic haematite particles with submicron order in the presence of an external magnetic field. We conducted quasi-2D MC simulations to investigate the influence of particle size polydispersity on the internal structure of the particle aggregates. In particular, we focused on these characteristics in the presence of a magnetic field to investigate the magnetic field-induced transitions by evaluating the order parameters and phase diagrams.
Model of cubic haematite particles and the coordinate system
Although the magnetic dipole moment within a haematite cube is not fully oriented diagonally,39 we employed a simplified model of cubic haematite particles,21 as shown in Fig. 1(a). A cubic particle i with a side length di has a magnetic dipole moment mi = mini = (|mi|ni) pointing diagonally at the particle centre. The magnetic moment was fixed to the particle and oriented from the blue part of the cube towards the red part. To assess the cluster formation, the criterion side length was defined as (1 + 2rclstr)di for each cubic particle. If these enlarged cubic particles overlapped, they were regarded as clusters. From the viewpoint of developing a surface modification technology, we investigated the internal structure of aggregates in a 2D system. However, a purely 2D model could not capture the 3D rotation of the particles caused by diffusion and magnetic interactions. Therefore, we employed a quasi-2D system,27 as shown in Fig. 1(b), where the centre of each cubic particle was constrained to a 2D plane, although the particles had full three-dimensional rotational ability. In the images of the aggregate structures, cubic layers are not shown for a more straightforward understanding of the internal structure of the aggregates. In the Results and discussion section, we present images viewed from the positive z-axis (normal to the plane). A uniform magnetic field, H = Hh = (|H|h), was applied along the positive direction of the y-axis. We assume that the particle sizes follow a normal distribution with a mean side length d0 and standard deviation σ. This particle size distribution was treated discretely in the usual manner in the simulations. Further information on the particle size distribution is provided in Appendix A1. With respect to the synthesis of a haematite cubic dispersion, excellent monodispersity can be obtained, where particle size distribution has a mean side length of 0.9 μm and a standard deviation of 0.09 μm.21 | ||
| Fig. 1 Particle model and coordinate system: (a) cubic particle i with magnetic moment mi located at the centre of the particle; (b) quasi-2D system of polydisperse cubic haematite particles. | ||
To obtain a stable suspension composed of magnetic particles, the magnetic particles in the base liquid are coated with repulsive layers such as steric or electric double layers, which prevented excessive particle aggregation. However, for cubic haematite particles with significantly weak magnetisation, a stable suspension can be obtained without surfactants.21 Thus, the cubic particles are not coated with a steric layer. This approach is justified by the fact that the MC method is not a dynamic simulation method and therefore does not require repulsive layers to prevent excessive particle overlap.
MC simulations
Formulation of interaction energies for a polydisperse system
For the present MC simulations, formulation of magnetic particle–particle and particle–field interaction energies was necessary. However, since we focused on a polydisperse system, the conventional interaction energy equations for monodisperse systems were not directly applicable.40,41 Therefore, the energy equations were modified as ref. 35 and 36 | (1) |
| U(H)i = −kTξini·H/H, | (2) |
 | (3) |
 | (4) |
Cluster-moving MC method
The MC simulations were conducted in a canonical ensemble, where the number of particles N, system volume V, and temperature T remained constant. We simulated the random translation and rotation of cubic particles according to the Metropolis algorithm.42 The decision to accept or reject a new microscopic state depends on the total potential energy U of the system, which is expressed as | (5) |
This problem arises because the characteristic times for single particle motion and cluster motion differ significantly. If a cluster behaves like a single particle, the characteristic time of cluster motion is much longer than that of single particle motion. That is, the conventional MC method only captures physical phenomena described within the timescales of the characteristic time of single particle motion. Therefore, obtaining physically reasonable aggregate structures using the conventional MC method is not straightforward. For the system to promptly attain an equilibrium state from an initial configuration, we introduced a procedure for the translational movement of clusters into the ordinary Metropolis algorithm—known as the cluster-moving MC method,43 wherein the trial movement of the clusters follows the principles of the Metropolis algorithm. In the simulations, cluster formation was assessed by simultaneously evaluating whether an overlap occurred between the enlarged cubic particles described in the previous section (‘Formulation of interaction energies for a polydisperse system’).
Quantitative evaluation for magnetic field-induced transitions and orientational characteristics of particles
We employed the order parameters S(e)4 and Sny to discuss the magnetic field-induced transitions and orientational characteristics of cubic haematite particles. | (6) |
 | (7) |
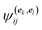 is the angle between the direction vectors ek and el of the cubic particles i and j. We focused on three orthogonal unit vectors (e1, e2, e3) that represent the plane direction vectors of an arbitrary cubic particle, as shown in Fig. 2(a). The relationship between the unit vector of the magnetic moment and the three orthogonal plane direction vectors for any given particle is expressed as
is the angle between the direction vectors ek and el of the cubic particles i and j. We focused on three orthogonal unit vectors (e1, e2, e3) that represent the plane direction vectors of an arbitrary cubic particle, as shown in Fig. 2(a). The relationship between the unit vector of the magnetic moment and the three orthogonal plane direction vectors for any given particle is expressed as | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψij) is expressed as P4(cos
ψij) is expressed as P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψij) = (35
ψij) = (35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos4
cos4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψij − 30
ψij − 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψij + 3)/8. The stability of the face-to-face contact and the alignment of the magnetic moment with the direction of the magnetic field were evaluated using S(e)4 and Sny, respectively. The order parameter S(e)4 yields S(e)4 = 0 for a disordered particle arrangement shown in Fig. 2(b), and S(e)4 = 1 if all faces of the cubic particles are oriented parallel to each other shown in Fig. 2(c) and (d). The order parameter Sny affords Sny = 1 if the directions of the magnetic moments of all cubic particles align exactly with the magnetic field direction, as shown in Fig. 2(d). By evaluating these two order parameters simultaneously, it is possible to distinguish between Fig. 2(c) and (d). Specifically, when the S(e)4 value is large but the Sny value is small, closely packed face-to-face clusters are predicted; however, when both the S(e)4 and Sny values are large, chain-like clusters with an offset face-to-face arrangement are expected.
ψij + 3)/8. The stability of the face-to-face contact and the alignment of the magnetic moment with the direction of the magnetic field were evaluated using S(e)4 and Sny, respectively. The order parameter S(e)4 yields S(e)4 = 0 for a disordered particle arrangement shown in Fig. 2(b), and S(e)4 = 1 if all faces of the cubic particles are oriented parallel to each other shown in Fig. 2(c) and (d). The order parameter Sny affords Sny = 1 if the directions of the magnetic moments of all cubic particles align exactly with the magnetic field direction, as shown in Fig. 2(d). By evaluating these two order parameters simultaneously, it is possible to distinguish between Fig. 2(c) and (d). Specifically, when the S(e)4 value is large but the Sny value is small, closely packed face-to-face clusters are predicted; however, when both the S(e)4 and Sny values are large, chain-like clusters with an offset face-to-face arrangement are expected.
Specification of parameters for performing simulations
Unless otherwise specified, we used the following parameter values to perform the cluster-moving MC simulations. For a comparison with the results obtained in the absence of a magnetic field,30 we adopted similar parameters for the system. The volumetric fraction of the particles was ϕV = 0.1, and the number of particles was N = 1225. The cutoff distance for calculating the magnetic interaction energies between the particles was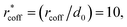 and the distance for the cubic layer was
and the distance for the cubic layer was  . The non-dimensional parameters λ0, ξ0, and the standard deviation σ* = (σ/d0) were set within the ranges of 0–15, 1–15, and 0.05–0.35, respectively. The values of λ0 and ξ0 were selected based on experimental data for cubic haematite particles, ensuring that the simulations accurately reflected realistic conditions. Detailed comparisons of these parameters with experimental data are provided in Appendix A2. MC simulations were carried out up to 2
. The non-dimensional parameters λ0, ξ0, and the standard deviation σ* = (σ/d0) were set within the ranges of 0–15, 1–15, and 0.05–0.35, respectively. The values of λ0 and ξ0 were selected based on experimental data for cubic haematite particles, ensuring that the simulations accurately reflected realistic conditions. Detailed comparisons of these parameters with experimental data are provided in Appendix A2. MC simulations were carried out up to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC steps, and the averaging procedure was performed using the final 40% of the simulation data. The maximum random translational distance and rotational angle were set as Δr = 0.1di and Δθ = (5°/180°)π, respectively. The cluster-moving algorithm was applied every 20 MC steps, up to the initial 1
000 MC steps, and the averaging procedure was performed using the final 40% of the simulation data. The maximum random translational distance and rotational angle were set as Δr = 0.1di and Δθ = (5°/180°)π, respectively. The cluster-moving algorithm was applied every 20 MC steps, up to the initial 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC steps. The maximum random translational distance of a cluster was set as Δrclstr = 0.1d0. As the initial configuration, a microscopic state with randomly arranged and oriented particles was employed (Fig. S1 and Video S1, ESI†). As the boundary condition, a periodic boundary condition in the x-axis and y-axis directions was employed.
000 MC steps. The maximum random translational distance of a cluster was set as Δrclstr = 0.1d0. As the initial configuration, a microscopic state with randomly arranged and oriented particles was employed (Fig. S1 and Video S1, ESI†). As the boundary condition, a periodic boundary condition in the x-axis and y-axis directions was employed.
Our previous study,29 which focused on a monodisperse system, clarified that isotropic closely packed clusters formed under zero magnetic field transform into thick chain-like clusters along the magnetic-field direction as the magnetic-field strength increases. This magnetic field-induced transition occurs because of the alignment of the magnetic moments of the constituent particles within the clusters along the magnetic-field direction. As described above, we focused on magnetic field-induced transitions in a polydisperse system, and thus, we investigated the magnetic field region, where the transition phenomena occurred, and the effect of polydispersity on the orientational characteristics of the magnetic moments of the particles.
Results and discussion
Magnetic field-induced transition phenomenon in a polydisperse system with a small standard deviation
In the case of a relatively weak magnetic interaction strength λ0 = 10 (Fig. 3), chain-like clusters grow along the field direction as the magnetic field strength increases. Although not shown as a figure, we have confirmed that unstable aggregate structures with weak face-to-face contact are formed in the absence of external magnetic field (ξ0 = 0).30 In a weak applied magnetic field (ξ0 = 1), as shown in Fig. 3(a), magnetic cubic particles aggregate to form network aggregate structures. Since the strength of the magnetic field is comparable to the thermal energy kT, the magnetic moments are not strongly restricted by the field direction, resulting in network formation. As the magnetic field strength increases to ξ0 = 5 (Fig. 3(b)) thick chain-like clusters are formed along the direction of the magnetic field. This is because in addition to the magnetic interactions between the constituent particles within the clusters, the magnetic field restricts the magnetic moments in the field direction. Thus, these interactions overwhelmed the thermal motion, which promoted the growth of chain-like clusters along the field direction. However, the magnetic particle–particle interaction strength is not sufficiently strong (λ0 = 10) and leads to a loosely arranged face-to-face contact configuration within the chain-like clusters.
In the case of a strong magnetic interaction strength λ0 = 15 (Fig. 4) with a weak applied magnetic field (ξ0 = 1), as shown in Fig. 4(a), closely packed clusters are stably formed as the magnetic particle–particle interaction strength is overwhelmingly dominant. As the magnetic field strength increases to ξ0 = 5, the closely packed clusters with almost perfect face-to-face contact in Fig. 4(a) are transformed into thick chain-like clusters with offset face-to-face contact. This transformation can be explained as follows: since the magnetic particle–particle interaction strength is stronger than the magnetic particle–field interaction strength (Fig. 4(a)), the magnetic moments are not fully aligned with the field direction, leading to the formation of closely packed clusters that do not incline in a specific direction. The magnetic field with increased strength (ξ0 = 5) induces the closely packed clusters to incline in the field direction, resulting in the formation of thick chain-like clusters (Fig. 4(b)). Moreover, a comparison with Fig. 3(b) for λ0 = 10 reveals that a stronger magnetic particle–particle interaction results in a denser internal structure of the chain-like clusters.
These results confirmed that the external magnetic field promoted the growth of thick chain-like clusters along the field direction. Notably, the formation of chain-like clusters was promoted by an external magnetic field even under relatively weak magnetic interactions between the particles. For λ0 < 10, where significant aggregates are not formed, unstable chain-like clusters tend to form, as shown in Fig. 13 in the Appendix A3. Similar results were observed in our previous study on monodisperse systems.29 Therefore, we believe that this level of polydispersity (σ* = 0.05) does not significantly influence the internal structure of the aggregates. The magnetic field-induced transition and orientational characteristics of the magnetic moments described above were quantitatively evaluated using the order parameters described in the next section.
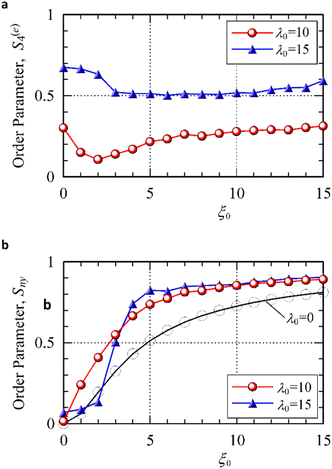
In the case of λ0 = 10, the S(e)4 curve in Fig. 5(a) initially decreases to a minimum of approximately S(e)4 ≃ 0.11 at ξ0 = 2 and then gradually increases to S(e)4 ≃ 0.31 at ξ0 = 15. This indicates that unstable aggregates with weak face-to-face contact initially collapse and then reform into chain-like clusters with offset face-to-face contact. Moreover, since the magnetic moments of the particles were more strongly aligned with the field direction with increasing magnetic field strength, the Sny curve in Fig. 5(b) gradually increased. The magnetic interactions between the constituent particles within the chain-like clusters contributed to the alignment of the magnetic moments in the direction of the magnetic field. Therefore, the Sny values for λ0 = 10 were larger than those for λ0 = 0, where only single particles remained in the system.
In the case of λ0 = 15, the S(e)4 curve in Fig. 5(a) initially decreased to S(e)4 ≃ 0.50 at ξ0 = 3, remained around this value up to ξ0 = 10, and then gradually increased to S(e)4 ≃ 0.59 at ξ0 = 15. This suggested that the closely packed clusters with almost perfect face-to-face contact transformed into thick chain-like clusters with offset face-to-face contact. Notably, this transformation occurred within a narrow magnetic-field range without complete collapse. Thus, the S(e)4 curve did not decrease significantly. This magnetic field-induced transition occurring within a narrow range of ξ0 can also be evaluated from the Sny curve in Fig. 5(b). The Sny curve for λ0 = 15 sharply increased in the range of 2 ≲ ξ0 ≲ 4, indicating that the transition phenomenon occurred within this magnetic-field range.
In this study, we quantitatively evaluated the magnetic field-induced transition in an aggregate structure composed of polydisperse cubic haematite particles with a small standard deviation. These results clarified that the transition phenomenon occurred within a narrow range of magnetic field strengths.
Influence of polydispersity on aggregate structures in an external magnetic field
First, we discuss the case where the magnetic particle–particle interaction strength is relatively weak λ0 = 10. In the system with σ* = 0.15 (Fig. 6(a)), many particles contributed to the formation of chain-like clusters. In contrast, in the system with σ* = 0.35 (Fig. 6(b)), larger particles formed chain-like clusters, whereas smaller particles relatively remained as single particles. This is because the magnitude of the magnetic moment is proportional to the particle volume. As shown in eqn (3), stronger magnetic particle–particle interactions occurred between larger particles, resulting in an aggregate structure composed of larger particles. Similar characteristics were observed in the absence of an external magnetic field.30 Moreover, as shown in eqn (4), the magnitude of the magnetic moment influences the particle–field interaction, and consequently, the directions of the magnetic moments of smaller particles are not strongly aligned with the magnetic field direction; thus, they orient randomly, giving rise to the tendency to move solely.
Next, we discuss the case of a stronger interaction λ0 = 15. As shown in Fig. 7(a) and (b), as the standard deviation σ* increases, the chain-like clusters become thinner, and network aggregate structures are formed in the system. This characteristic arises because the direction of the magnetic moments of larger particles is governed by magnetic particle–particle interactions rather than by magnetic particle–field interactions. Hence, a stronger magnetic field is required to align the magnetic moments of larger particles with the field direction. Therefore, in a system with a large standard deviation (σ* = 0.35), as shown in Fig. 7(b), network aggregate structures are formed instead of thick chain-like clusters. Moreover, smaller particles do not contribute to the formation of particle aggregates and remain as single particles even in a strong magnetic interaction system. These results indicated that in systems with a large standard deviation of the particle size distribution, larger particles mainly contribute to the formation of aggregate structures under an external magnetic field, whereas smaller particles do not significantly contribute to the formation of clusters. Similar findings were observed in our previous study on a polydisperse system in the absence of a magnetic field.30 Even in the case of λ0 < 10, larger particles aggregate to form network-like clusters and thin chain-like structures, as shown in Fig. 13 in Appendix A3. Furthermore, the present results suggest that a stronger magnetic field is vital for magnetic field-induced transitions in polydisperse systems than in monodisperse systems. This is due to the significantly strong magnetic particle–particle interactions between larger particles. In the next section, we present a quantitative evaluation of the magnetic-field range for the transition phenomenon in terms of the order parameter Sny.
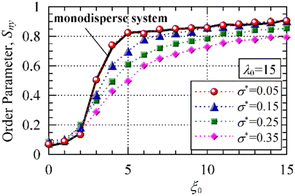
In the region of ξ0 ≲ 2, regardless of the standard deviation σ*, isotropic closely packed aggregates with face-to-face contact were formed, as shown in Fig. 4(a). The directions of the magnetic moments of the particles are governed by strong magnetic interactions between neighbouring particles, which lead to low values of Sny in all systems with different standard deviations. As the magnetic field increased, the closely packed aggregates collapsed and transformed into chain-like clusters along the magnetic field. Thus, the Sny curves tend to increase with increasing values of ξ0.
In the range of σ* ≲ 0.05, minor polydispersity does not influence magnetic field-induced transitions as the Sny curve for σ* = 0.05 is in good agreement with that for σ* = 0. Polydisperse systems with a larger standard deviation require a stronger magnetic field for magnetic field-induced transitions. Thus, in the region of 2 ≲ ξ0 ≲ 10, the Sny curves with larger standard deviations increased more gradually with increasing values of ξ0. In the range of ξ0 ≳ 10, although many magnetic moments aligned with the direction of the magnetic field, the magnetic moments of smaller particles were not strongly restricted to the field direction. This resulted in smaller values of Sny as the standard deviation increased.
These results demonstrate that a polydisperse system with a large standard deviation requires a strong magnetic field to induce magnetic field-induced transitions. This characteristic has not been observed in a conventional spherical particle system. There is a significant difference in the magnetic field-induced transition phenomenon between spherical and cubic particle systems. Spherical particles tend to form ring-like or curved chain-like clusters with point-to-point contact under no applied magnetic field.9,12 These clusters are unstable and can be easily collapsed by the influence of magnetic fields. Regardless of the polydispersity, these clusters transform into chain-like clusters along the magnetic field direction in a weak magnetic field.35,36 On the other hand, cubic particles form stable closely-packed clusters with a face-to-face contact, leading to rapid transitions within a certain narrow magnetic field range.
In the case of σ* = 0.05, the number of single particles was N1 ≃ 1.6, and the distribution pattern remained similar to that of the monodisperse system. This quantitatively indicates that, as shown in Fig. 4(b), the aggregate structures are composed of a large number of particles in the system. Thus, in the range of σ* ≲ 0.05, polydispersity does not significantly affect the internal structure in the system. In contrast, as the standard deviation increased to σ* = 0.15, 0.25, and 0.35, the number of single particle N1 increased significantly. In particular, in the case of σ* = 0.35, as shown in Fig. 7(b), numerous small particles were scattered without combining with grown aggregates, leading to N1 ≃ 180. In particular, approximately 15% of the particles remained as individual particles, without contributing to the formation of clusters.
These results indicate that the polydispersity significantly influences the number of particles that do not contribute to aggregate formation under an external magnetic field. In particular, the number of single particles increases with increasing polydispersity. This demonstrates that it is necessary to manage the polydispersity in order to obtain the desired aggregate structures. However, if the smallest particles in the system are large enough to exhibit strong magnetic particle–particle interactions, different aggregation behaviours would be expected. This scenario corresponds to the results for λ0 ≫ 15, where is beyond the scope of the present study. As provided in Appendix A1, the range of λ0 we considered here corresponds to cubic particles with the side length d0 = 0.5–0.9. In other words, our conclusion can be applied to only suspensions composed of cubic particles with submicron order.
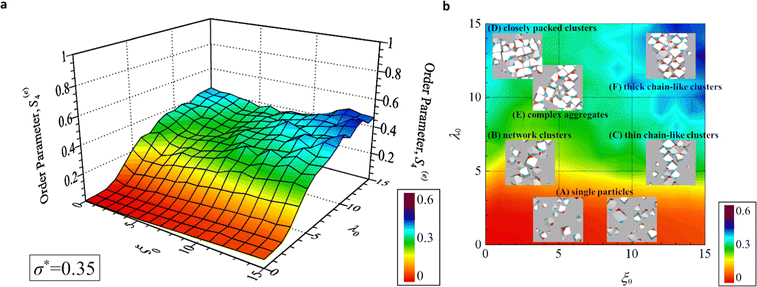
First, we focus on a polydisperse system with a small standard deviation (σ* = 0.05), as shown in Fig. 10. For the weak magnetic interaction strength λ0 ≲ 5 (Fig. S2 and Video S2, ESI†), the order parameter S(e)4 exhibited relatively small values independent of the field strength ξ0, implying that almost all the particles remained as (A) single particles without aggregating to form clusters. As the magnetic field strength increased, the magnetic moments of single particles tended to be restricted to the field direction, which led to a slight increase in the order parameter. For the intermediate magnetic interaction strength 5 ≲ λ0 ≲ 10 (Fig. S3 and Video S3, ESI†), the internal structures changed into two typical regimes dependent on the field strength. In particular, in the weak magnetic field region, (B) network clusters were formed because the magnetic interactions between the particles were not adequately strong to form stable aggregates. However, because of the unstable face-to-face contact between neighbouring particles, the order parameter was slightly higher than that of a single-particle system. In the strong magnetic-field region, the formation of (C) thin chain-like clusters is promoted along the field direction, resulting in an increase in the order parameter. For the strong magnetic interaction strength 10 ≲ λ0 ≲ 15 (Fig. S4 and Video S4, ESI†), the internal structure is classified into three typical regimes. In the weak magnetic-field region, (D) closely packed clusters were stably formed, resulting in large order parameter values. As the magnetic-field strength increased, the closely packed clusters first collapsed and finally transform into (F) thick chain-like clusters through (E) complex aggregate structures. Thus, the order parameter value first decreased and then increased with increasing values of ξ0.
Next, we focused on a polydisperse system with a large standard deviation (σ* = 0.35), as shown in Fig. 11. In the region where λ0 ≲ 2 (Fig. S5 and Video S5, ESI†), the S(e)4 values remained small, as in the case of σ* = 0.05, because all the particles in the system behaved as (A) single particles. In contrast, the distribution for λ0 ≳ 3 in Fig. 11 exhibited different characteristics compared to those in the case of σ* = 0.05 in Fig. 10.
In the region where 3 ≲ λ0 ≲ 12 (Fig. S6 and Video S6, ESI†), larger S(e)4 values were observed in all the field regions, which is in contrast to those observed for σ* = 0.05 shown in Fig. 10. This suggests that, in a system with more significant polydispersity, larger particles can aggregate to form (B) network clusters or (C) thin chain-like clusters. Conversely, in the region where λ0 ≳ 12 (Fig. S7 and Video S7, ESI†), the order parameter S(e)4 values were smaller in all the regions of field strength than those in the previous case of σ* = 0.05. This suggests that the smaller particles play a role in disturbing the order of the face-to-face contact configuration, leading to smaller order parameter values. In particular, the stability of face-to-face contact diminishes when smaller particles are trapped within (D) closely packed clusters or (F) thick chain-like clusters formed by larger particles.
Based on these results and the discussion in this section, we summarise the dependence of the internal structure of the particle aggregates on the broadness of polydispersity, field strength, and magnetic interactions between the particles. The main clusters formed in the system can be classified into six types of configurations: (A) single particles, (B) network clusters, (C) thin chain-like clusters, (D) closely packed clusters, (E) complex aggregates (magnetic field-induced transition regions), and (F) thick chain-like clusters. The main configuration that appeared in the system depended on the broadness of polydispersity. In the case of smaller polydispersity, stable clusters tend to form owing to strong face-to-face contact; however, in this case, larger magnetic particle–particle interaction strengths are necessary. In the case of larger polydispersity value, particle aggregates are formed even in regions of smaller magnetic particle–particle interactions. However, the stability of the internal structure diminishes because the smaller particles trapped in a cluster tend to disturb cluster formation.
Conclusion
We investigated a polydisperse cubic haematite particle suspension in an external magnetic field and examined the dependence of magnetic field-induced transitions on the standard deviation of the particle size distribution using quasi-2D MC simulations. The present study expands our previous work on systems29 into a polydispersity system, where many factors are expected to determine the internal structure of particle aggregates and the transition in aggregated regimes. As expected, an external magnetic field promoted the growth of thick chain-like clusters along the field direction, which is a common feature of polydispersity. However, a polydisperse system with a larger standard deviation requires a stronger magnetic field to induce magnetic field-induced transitions in the internal structure of the particle aggregates. The internal structure of the particle aggregates, observed in the images, can be classified into the following typical configurations: (A) single particles, (B) network clusters, (C) thin chain-like clusters, (D) closely packed clusters, (E) complex aggregates (magnetic field-induced transition region), and (F) thick chain-like clusters. The preferred configuration is dependent on the broadness of polydispersity, magnetic-field strength, and magnetic particle–particle interaction strength. In the case of smaller polydispersity, stable clusters tend to form owing to strong face-to-face contact; however, in this case, larger magnetic particle–particle interaction strengths are necessary. As the applied magnetic field enables the magnetic moment of each particle to incline in the field direction, it enhances the formation of chain-like clusters. In the case of larger polydispersity, compared to smaller polydispersity cases, particle aggregates are formed even in the region of smaller magnetic particle–particle interactions. In this case, small particles combine with a growing cluster composed of large particles to form larger clusters. However, these small particles tend to disturb the internal structure of the particle aggregates; as a result, widths of chain-like clusters are narrower than those in the case of smaller polydispersity. Based on these particle aggregate characteristics, we conclude that the broadness of polydispersity in a suspension composed of magnetic cubic particles with submicron order is potentially applicable as a tool for obtaining the desired internal structure and regime transition in the internal structure of particle aggregates. This may be an important feature in the development of a surface modification technique using a magnetic cubic particle suspension with polydisperse particle size.The phase diagram obtained in the present study provides the basic internal structure of aggregates in a cubic polydisperse system; however, this may not be applicable to a 3D system. In a 3D system, it is necessary to consider gravitational effects. Larger particles are subject to stronger gravity, which leads to more complex phenomena. For example, small particles trapped in clusters formed by larger particles may sediment together with the clusters. Additionally, because the MC approach cannot capture dynamic behaviours, other dynamics simulation methods such as Brownian dynamics or multi-particle collision dynamics would be required.
Author contributions
Kazuya Okada: writing the original draft, visualisation, data curation, conceptualisation, methodology, software, validation, formal analysis, and investigation. Akira Satoh: writing – review and editing, conceptualisation, methodology, software, validation, formal analysis, investigation.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Appendices
A1. Discrete normal distribution for assigning particle sizes
In simulations of polydisperse systems, assigning the particle size distribution discretely is a common process.34–37 A finite number of particle sizes were selected to represent the range of particle diameters in the system. In particular, the given normal distribution was discretely approximated by a series of rectangles, where each rectangle has a width of Δd = σ/10. This infinitesimal width describes the original distribution with sufficient accuracy. As an example, Fig. 12 shows the discrete particle size distribution for the case of σ* = (σ/d0) = 0.35. | ||
| Fig. 12 Particle size distribution for σ* = 0.35. The particle size distribution follows a normal distribution with a mean side length d0 and standard deviation σ*. | ||
A2. Comparison of non-dimensional parameters with experimental data
The non-dimensional parameters λ0 and ξ0 were set within the wide range of λ0 = 0–15 and ξ0 = 1–15, which were determined from the following experimental data of cubic haematite particles. We assumed the liquid temperature to be T = 293 K; the mass density of haematite as ρ = 5.25 × 103 kg m−3;44 the remanent magnetisation of haematite as σr = 0.2 A m2 kg−1;45 the magnitude of the magnetic field as H = 35 A m−1; the side length of the cube as d0 = 0.5–0.9 μm,21 with Boltzmann's constant k = 1.38 × 10−23 J K−1; and the permeability of free space μ0 = 1.26 × 10−6 Wb m−1 A−1. Using these typical values, the non-dimensional parameters are calculated as λ0 ≃ 3.4 to 20 and ξ0 ≃ 1.4 to 8.3.A3. Magnetic field-induced transitions for the case of weak magnetic particle–particle interaction strengths
Fig. 13 shows particle aggregates for the weak magnetic particle–particle interaction strength: A2(a) σ* = 0.05, λ0 = 5, ξ0 = 1, A2(b) σ* = 0.05, λ0 = 5, ξ0 = 5, A2(c) σ* = 0.35, λ0 = 3, ξ0 = 1 and A2(d) σ* = 0.35, λ0 = 3, ξ0 = 5.In a polydisperse system with a small standard deviation σ* = 0.05, due to weak magnetic interactions, chain-like clusters with unstable face-to-face contact tend to form, as shown in Fig. 13(a) and (b). The magnetic field promotes the formation of chain-like clusters along the field direction (Fig. S3 and Video S3, ESI†).
In a polydisperse system with a large standard deviation σ* = 0.35, even in the case of λ0 = 3, strong magnetic interactions act between larger particles. Larger particles aggregate to form network-like clusters and thin chain-like structures, as shown in Fig. 13(c) and (d). Notably, chain-like clusters tend to grow larger as the strength of the external magnetic field increases (Fig. S6 and Video S6, ESI†).
Acknowledgements
We would like to thank Editage (https://www.editage.jp) for English language editing.Notes and references
- W. A. Bullough, Electro-Rheological Fluids, Magneto-Rheological Suspensions and Associated Technology, World Scientific, Singapore, 1996 Search PubMed.
- N. M. Wereley, Magnetorheology: Advances and Applications, Royal Society of Chemistry, London, 2013 Search PubMed.
- A. M. Schmidt, Colloid Polym. Sci., 2007, 285, 953–966 Search PubMed.
- Y. I. Golovin, S. L. Gribanovsky, D. Y. Golovin, N. L. Klyachko, A. G. Majouga, A. M. Master, M. Sokolsky and A. V. Kabanov, J. Controlled Release, 2015, 219, 43–60 CAS.
- F. Mishima, S. Fujimoto, S. Takeda, Y. Izumi and S. Nishijima, J. Magn. Magn. Mater., 2007, 310, 2883–2885 CAS.
- S. Takeda, F. Mishima, S. Fujimoto, Y. Izumi and S. Nishijima, J. Magn. Magn. Mater., 2007, 311, 367–371 CAS.
- P. I. Girginova, A. L. Daniel-da-Silva, C. B. Lopes, P. Figueira, M. Otero, V. S. Amaral, E. Pereira and T. Trindade, J. Colloid Interface Sci., 2010, 345, 234–240 CAS.
- H. Vojoudi, A. Badiei, S. Bahar, G. M. Ziarani, F. Faridbod and M. R. Ganjali, J. Magn. Magn. Mater., 2017, 441, 193–203 CrossRef CAS.
- J. M. Tavares, J. J. Weis and M. M. T. da Gama, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 061201 CrossRef CAS.
- J. M. Dempster, R. Zhang and M. Olvera de la Cruz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 042305 CrossRef PubMed.
- K. Theis-Bröhl, P. Gutfreund, A. Vorobiev, M. Wolff, B. P. Toperverg, J. A. Dura and J. A. Borchers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 11, 4695–4704 Search PubMed.
- P. D. Duncan and P. J. Camp, J. Chem. Phys., 2004, 121, 11322–11331 CrossRef CAS PubMed.
- A. T. Pham, Y. Zhuang, P. Detwiler, J. E. S. Socolar, P. Charbonneau and B. B. Yellen, Phys. Rev. E, 2017, 95, 052607 CrossRef PubMed.
- J. L. C. Domingos, F. M. Peeters and W. P. Ferreira, Phys. Rev. E, 2017, 96, 012603 CrossRef.
- M. Aoshima and A. Satoh, J. Colloid Interface Sci., 2006, 293, 77–87 CrossRef CAS.
- D. Lisjak and S. Ovtar, J. Phys. Chem. B, 2013, 117, 1644–1650 CAS.
- M. Ozaki, N. Ookoshi and E. Matijević, J. Colloid Interface Sci., 1990, 137, 546–549 CAS.
- M. V. Kovalenko, M. I. Bodnarchuk, R. T. Lechner, G. Hesser, F. Schäffler and W. Heiss, J. Am. Chem. Soc., 2007, 129, 6352–6353 CrossRef CAS.
- L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Soft Matter, 2011, 7, 4139–4142 RSC.
- J. M. Meijer, F. Hagemans, L. Rossi, D. V. Byelov, S. I. R. Castillo, A. Snigirev, I. Snigireva, A. P. Philipse and A. V. Petukhov, Langmuir, 2012, 28, 7631–7638 CrossRef CAS PubMed.
- M. Aoshima, M. Ozaki and A. Satoh, J. Phys. Chem. C, 2012, 116, 17862–17871 CrossRef CAS.
- S. I. R. Castillo, C. E. Pompe, J. van Mourik, D. M. A. Verbart, D. M. E. Thies-Weesie, P. E. de Jongh and A. P. Philipse, J. Mater. Chem. A, 2014, 2, 10193–10201 RSC.
- J. W. J. de Folter, E. M. Hutter, S. I. R. Castillo, K. E. Klop, A. P. Philipse and W. K. Kegel, Langmuir, 2014, 30, 955–964 CrossRef CAS PubMed.
- J. G. Donaldson and S. S. Kantorovich, Nanoscale, 2015, 7, 3217–3228 RSC.
- J. M. Meijer and L. Rossi, Soft Matter, 2021, 17, 2354–2368 CAS.
- M. Brics, V. Šints, G. Kitenbergs and A. Cēbers, Phys. Rev. E, 2022, 105, 024605 CAS.
- P. Linse, Soft Matter, 2015, 11, 3900–3912 CAS.
- H. R. Vutukuri, F. Smallenburg, S. Badaire, A. Imhof, M. Dijkstra and A. Van Blaaderen, Soft Matter, 2014, 10, 9110–9119 CAS.
- K. Okada and A. Satoh, Mol. Phys., 2017, 115, 683–701 CAS.
- K. Okada and A. Satoh, Mol. Phys., 2024, e2323628 Search PubMed , in press, .
- T. Kruse, A. Spanoudaki and R. Pelster, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 054208 CrossRef.
- T. Kristóf and I. Szalai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 041109 CrossRef PubMed.
- T. Kristóf and I. Szalai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 041105 CrossRef PubMed.
- A. O. Ivanov, S. S. Kantorovich, E. N. Reznikov, C. Holm, A. F. Pshenichnikov, A. V. Lebedev, A. Chremos and P. J. Camp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 061405 CrossRef.
- M. Aoshima and A. Satoh, J. Colloid Interface Sci., 2004, 280, 83–90 CrossRef CAS PubMed.
- M. Aoshima and A. Satoh, J. Colloid Interface Sci., 2005, 288, 475–488 CrossRef CAS PubMed.
- X. L. Li, K. L. Yao and Z. L. Liu, Int. J. Mod. Phys. B, 2009, 23, 5307–5323 CrossRef CAS.
- M. Rosenberg, Ž. Gregorin, P. H. Boštjančič, N. Sebastián, D. Lisjak, S. S. Kantorovich, A. Mertelj and P. A. Sánchez, J. Mol. Liq., 2020, 312, 113293 CrossRef CAS.
- L. Rossi, J. G. Donaldson, J. M. Meijer, A. V. Petukhov, D. Kleckner, S. S. Kantorovich, W. T. M. Irvine, A. P. Philipse and S. Sacanna, Soft Matter, 2018, 14, 1080–1087 CAS.
- A. Satoh, Introduction to Molecular-Microsimulation of Colloidal Dispersions, Elsevier, Amsterdam, 2003 Search PubMed.
- A. Satoh, Introduction to Practice of Molecular Simulation: Molecular Dynamics, Monte Carlo, Brownian Dynamics, Lattice Boltzmann and Dissipative Particle Dynamics, Elsevier, Amsterdam, 2010 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987 Search PubMed.
- A. Satoh, J. Colloid Interface Sci., 1992, 150, 461–472 CrossRef CAS.
- J. M. Meijer, D. V. Byelov, L. Rossi, A. Snigirev, I. Snigireva, A. P. Philipse and A. V. Petukhov, Soft Matter, 2013, 9, 10729–10738 RSC.
- M. Ozaki, in Surface and Colloid Science, ed. E. Matijević and M. Borkovec, Springer, Boston, 2004, 17, 1–26 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01516a |
| This journal is © The Royal Society of Chemistry 2025 |