Enhancing spray retention using cloaked droplets to reduce pesticide pollution

Abstract

Enhancing agrochemical spray retention on plant surfaces would have tremendous benefits to global health and the environment. The bouncing of sprayed pesticide droplets from hydrophobic leaves is a major source of water and soil pollution, and the resultant overuse of pesticides is a human health hazard and a financial burden for farmers. Here we report on the development of sustainable agricultural sprays consisting of cloaked droplets that significantly enhance droplet retention on plant surfaces. By leveraging wetting dynamics, we create cloaked droplets that consist of an ultra-thin food and environmentally safe oil layer (<1% by volume) that encapsulates water droplets. We develop a fundamental understanding of the dynamics of cloaked droplet impact and retention on superhydrophobic surfaces. Using high-speed imaging, we capture how the oil cloak transforms into a wetting ridge that pins the droplets and suppresses their rebound. We span a wide range of impact conditions, oils, oil viscosities, and oil volume fractions to demonstrate the robustness of the approach. By considering a balance of kinetic energy, the work of adhesion, and viscous dissipation in this four-phase system, we develop a physical model that allows us to establish a regime map for rebound suppression. Finally, these findings are implemented into a prototype sprayer which leads to a ∼5-fold reduction in spray waste on crop leaves. We believe that our spray approach can greatly reduce agrochemical pollution as well as pesticide and surfactant usage.

---

Introduction

The use of agrochemicals like pesticides has enabled increased agricultural yield and contributed to development around the globe. Spraying is the most common method to deliver agrochemicals like pesticides to plants, but poor spray retention is one of the most important inefficiencies in pesticide application.¹ Sprayed droplets bounce or roll off of hydrophobic plant leaves, causing a large majority of what is sprayed to find its way to the environment.^2,3 Pesticides are found in 90% of agricultural run-off streams, which subsequently contaminate 50% of shallow wells and 33% of major deep aquifers in the United States.⁴ A recent study has shown that 31% of all global agricultural soil is at high risk of pesticide pollution.⁵ These excess pesticides not only affect soil chemistry but also cause the death of non-target organisms and damage soil microbiomes that are responsible for replenishing plant nutrients in the soil.⁶ Acute poisoning has been linked to tens of thousands of deaths per year and millions of illnesses.⁷ Once in the environment, pesticides have significant impact on public health, causing diseases like cancer, neurological conditions, and birth defects.⁷ The health impacts of pesticides are especially felt in the developing world, where a lack of personal protective equipment makes them even more dangerous.^7,8 In addition to having heavy global health and environmental costs, pesticides represent a major financial burden for farmers. Over $60 billion dollars of pesticides are used globally as they can contribute up to 30% of the production costs of certain crops.⁹ Fruit, vegetable, cereal, and nut crops all require a wide variety of pesticides to maintain crop health and yield. Pesticide expenditures for crops like tomatoes and strawberries can be as high as $800 and $1500 per acre, respectively, which is comparable to the profits achievable from selling those crops.¹⁰ Thus, there is an urgent need to reduce pesticide waste and overuse, and promoting spray retention offers a direct pathway to accomplish this.

The impact and bouncing of a liquid droplet on hydrophobic and superhydrophobic surfaces have been studied extensively.^11–20 In agricultural sprays, droplet sizes range from 50–600 μm, and droplet impact velocities range from 1–8 m s⁻¹, which corresponds to a Weber number range of 1–600.^21–23 During impact, such droplets undergo expansion driven by inertial forces and retraction that is driven by surface tension.^20,24,25 Whether the droplet sticks or bounces is determined by surface properties, such as surface energy and leaf micro-texture and droplet properties like surface tension, viscosity, density, and impact velocity. Several works have proposed methods to increase droplet retention on plant surfaces. These methods include using (i) adjuvants to modify the surface tension of droplets, (ii) compounds that change the viscosity or extensional rheology of droplets, (iii) additives that can disrupt the waxy coatings on leaf surfaces locally and promote adhesion, (iv) chemicals that generate microscopic pinning sites for droplets to stick or (v) physical charged interactions to promote droplet adhesion.

Surfactants are the most widely used adjuvants that aim to enhance spray coverage and retention.²⁶ While their effect on improving the spreading of droplets on plant surfaces under static conditions is well documented, their ability to reduce the dynamic surface tension of impacting droplets and suppress their rebound is more complex.^27,28 Recent work has shown that only specialized surfactants can diffuse to the droplet interface fast enough to reduce the dynamic surface tension of droplets during impact and arrest rebound.^29,30 In addition, surfactants suffer from a lack of universality as they must be chemically stable with a diverse range of pesticide chemistries. As they reduce surface tension, they also make the sprayed droplets smaller, which exacerbates pesticide drift and run-off.^31,32 Smaller droplets also tend to evaporate more quickly, which leads to product loss, especially for volatile pesticides.²⁶ Finally, some surfactants that are used in agriculture can be more environmentally and biologically toxic than the active ingredients in the pesticides. For example, the addition of ethoxylated amine surfactants to Roundup® makes these formulations cause more mitochondrial damage and necrosis in human cells and become more toxic towards non-target organisms than the active ingredient – glyphosate alone.^33–40

Viscosity modifying adjuvants that utilize viscous dissipation during impact to prevent the droplets from bouncing off offer limited improvement to spray retention efficiency on plant surfaces.⁴¹ High molecular weight polymer-based adjuvants that can modulate the extensional viscosity of droplets have also been shown to enhance droplet and spray retention (2–20% enhancements to spray retention on leaf and engineered surfaces).^42,43 However, in addition to the limited enhancement offered by this method, the need for the careful control of the pH of such formulations presents a significant barrier to robust implementation.^44,45 Electrostatic sprayers that physically charge spray droplets and introduce an attractive force towards grounded plant surfaces help reduce drift rather than droplet retention, but these units suffer from high costs that limit applicability.^46,47 Finally, prior work from our group has used polyelectrolytes to enhance droplet retention on plants.⁴⁸ In this approach, positively and negatively charged molecules are added to the sprayed liquid. The oppositely charged compounds undergo a precipitation reaction in situ, creating microscopic pinning sites on an otherwise hydrophobic surface. While the approach has led to significant improvements in droplet retention both in the lab and in field trials, the need to keep the charged additives separated until they reach the plant surface requires a significant retrofit to the sprayers.

Unlike the above approaches, which are either unsustainable, toxic, non-universal, or expensive, plant-based oils hold great promise as adjuvants that can promote droplet retention.²⁶ Oils have been used in agriculture for centuries as they possess insecticidal and fungistatic properties.^49,50 Vegetable oils are generally recognized as safe and are understood to pose no risks to the environment, and are widely used in food products and in agriculture.^51–53 Since they are readily degradable by microbes in the soil, these oils have a much lower environmental footprint than synthetic agrochemicals.⁵⁴ Their impact on crop health is well understood, and they are not phytotoxic when used appropriately.⁴⁹ Some oils are more robust against resistance development in pests, and some plant oils have minimal impact on non-target insects like honeybees.^55,56

As spray adjuvants, the lower surface energy of oils makes them stick more easily to hydrophobic leaves compared to water. Oils are predominantly formulated as oil-in-water emulsions, necessitating the use of surfactants – which have the drawbacks mentioned above – and the need for complex agitation methods at the point of use.²⁶ In comparison to oil-in-water emulsions, water-in-oil emulsions (>10% oil by volume) have been found to be more effective in enhancing retention. However, the need for surfactants and the potential for phytotoxicity of such large oil contents limit the applicability of such formulations.⁵⁷ Compound droplet impact work has consistently been shown to suppress droplet rebound without the need for surfactants or emulsification.^58–64 In this work, we explore the limits of small oil fractions (<1% by volume) wherein the oil forms a cloak around the water droplet, and investigate the applicability of this surfactant-free approach to suppressing droplet bouncing on real hydrophobic plant leaves.

In Fig. 1(c)–(e), we show time-lapse images of water droplets sprayed using an agricultural sprayer onto a cabbage leaf for 3 seconds. The nozzle in this case produces droplets with a volume median diameter between 341–403 μm at velocities between 5–10 m s⁻¹ (see Methods). Some droplets pin wherever there are defects on the leaf, but a majority of the sprayed water bounces off, highlighting the problem of poor droplet retention in conventional agrochemical spraying (Movie S1, ESI†). In contrast, Fig. 1(f)–(h) demonstrate the effectiveness of cloaking water drops with ∼1% of soybean oil, a ubiquitous plant-based oil, which (i) is used in food products, (ii) is approved by the EPA for agricultural use, (iii) has minimal impact on the environment and (iv) is inexpensive.^52,53,65 With a third of the spraying time, we achieve significantly more droplet retention and more uniform coverage on the leaf (Movie S2, ESI†). As shown in Fig. 1(i), the cloaked droplets result in a five-fold reduction in spray usage to reach a given coverage, indicating the promise of this simple, inexpensive, and environmentally sustainable approach to reducing pesticide waste.

Fig. 1 Oil cloaking leads to enhanced droplet retention on crops. Schematics of the experimental set-ups used to spray (a) DI water and (b) oil-cloaked water droplets onto leaves. See Fig. S1 (ESI†) for a full schematic and image of the prototype sprayer. Unlike conventional water sprays, which bounce off of hydrophobic leaf surfaces, droplets that are cloaked in minute quantities of a plant-derived oil (ex: soybean oil ≤ 1%) stick to leaves uniformly. (c)–(e) Time-lapse images of water sprayed using a commercial agricultural sprayer onto a cabbage leaf for 3 seconds. Some droplets pin and accumulate, but a majority of what is sprayed bounces off of the leaf (see Movie S1, ESI†). (f)–(h) Time-lapse images of water droplets cloaked with soybean oil (∼1% oil by volume) sprayed onto a cabbage leaf for 1 second. (i) Leaf coverage expressed as a percentage of total leaf area covered with water droplets demonstrates a ∼5× reduction in spray to reach similar coverage levels, indicating significant reductions in pesticide waste are possible. Measurement of leaf coverage is discussed in the Materials and methods section.

To fully understand this approach's potential to enhance droplet retention, we study it systematically with superhydrophobic surfaces. These surfaces that minimize droplet pinning represent the most extreme case that agricultural sprays can encounter. Studying enhancements in droplet retention in this extreme case would provide a conservative benchmark for our methodology. We examine droplet impact dynamics at a variety of agriculturally relevant spray velocities and Weber numbers and systematically study the effect of cloaking with different oils of varying surface tension and viscosity. We explore the effect of oil fraction and present a simple thermodynamic framework to explain the rebound suppression observed with oil cloaked droplets. Finally, we test a practical embodiment of this system and demonstrate significant improvements in spray retention on minimally pinning superhydrophobic surfaces and crop leaves.

Results

Single water droplets of different diameters were created by forcing liquids through needles of different gauges. The oil cloaks were applied using a secondary needle, as shown in Fig. 2. The flow rates of all fluids were controlled using syringe pumps (see Methods). The impact velocities were changed by controlling the release height of the dispensed droplets. Silicon nanograss surfaces were used as model superhydrophobic surfaces in this work.⁶⁶ The surfaces had an average texture size and spacing of around 200 nm, and they were functionalized with different hydrophobic modifiers (see Methods). The advancing and receding contact angles of DI water on this substrate were 163.9° and 159.3° respectively on the octadecyltrichlorosilane (OTS) coated surfaces and 166.6° and 164.8° on the trichloro(1H,1H,2H,2H-perfluorooctyl)silane (FS) coated surfaces respectively. The impact experiments were observed using a Photron Fastcam SA1.1 high-speed camera.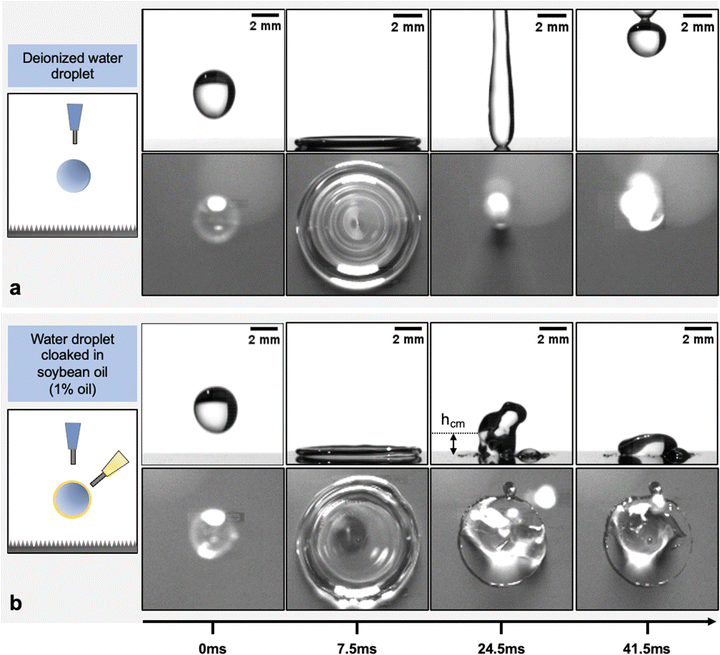

Fig. 2 Single droplet impact on a minimally-pinning superhydrophobic surface. Schematics of the experimental set-ups used to study droplet impact are shown in the left column. All droplets are released from 8 cm height, resulting in an impact speed of ∼1.25 m s⁻¹. Time-lapse images of impacts of (a) a DI water droplet and (b) a water droplet cloaked with soybean oil (1% oil by volume) from the side and top-down views. The DI water droplet undergoes a symmetric retraction phase and maintains a high contact angle with the surface until eventually bouncing off (see Movies S3 and S4, ESI†). The oil cloaked droplet undergoes a nearly identical expansion phase; however, the droplet pins during retraction and experiences a significant reduction in its receding contact angle. This pinning leads to the suppression of the rebound and leaves the droplet adhered to the surface, and constrains the maximum rebound height of the center of mass (h_cm) (see Movies S5 and S6, ESI†).

Fig. 2(a) shows time-lapse images of a water droplet (diameter ≈ 3 mm and impact speed ≈1.25 m s⁻¹) impacting on a minimally pinning surface from the side and top-down views. The droplet behaves as expected, going through a symmetric retraction phase and completely rebounding from the surface (Movies S3 and S4, ESI†). Fig. 2(b) shows droplet impacts under identical conditions with droplets that are cloaked in 1% soybean oil by volume. While the expansion phase is nearly identical in terms of the maximum diameter and the expansion time, the retraction phase in the cloaked case is markedly different (Movies S5 and S6, ESI†). During retraction, the cloaked droplet's contact line is pinned by a ridge of oil at the outermost interface between the droplet and the surface, as shown in Fig. 2(b). The ridge forms during the impact event as oil is carried to the contact line. Such wetting ridges are typically found on water droplets that are placed on oil films, oil-infused surfaces, and other soft substrates as it minimizes the total surface energy of the multi-phase system.⁶⁷ The presence of oil in the ridge is evidenced given that the dynamic retracting contact angle (Movies S5 and S6, ESI†) and the static contact angle of water droplets contacting the visible oil ridge (Fig. 2(b)) are markedly lower than the receding contact angle of pure water on the superhydrophobic surface (ESI,† Fig. S4). The pinning due to the ridge significantly reduces the retraction speed of the contact line and causes the droplet to stick to the surface. The retarded yet non-zero contact line retraction that we observe differs from the behavior observed by Han et al., wherein oil-cloaked droplets exhibit complete contact line pinning without any retraction on nano-porous superhydrophobic surfaces.⁶⁴ Fig. S2 (ESI†) demonstrates that the retraction behavior of oil-cloaked droplets on hydrophobic plant leaves matches more closely the behavior we observe on our superhydrophobic non-porous surface, motivating the continued use of this surface and further investigation of rebound suppression.

Our setup allows us to track the maximum height of the droplet's center of mass (h_cm), offering a quantitative measurement to track rebound suppression (see Methods). Illustratively, h_cm is labeled in Fig. 2(b). To confirm that the spreading phases of the impacts are undisturbed and to study the dynamics of rebound suppression more thoroughly, we conducted drop impact experiments with nine different oils of varying viscosities and surface tensions.

Fig. 3(a) shows the time evolution of the contact diameter of droplets (D(t)) normalized by their initial diameter D₀ for six representative oil cloaking conditions. These experiments were all conducted at 1% oil fraction by volume and at an impact velocity of ≈1.25 m s⁻¹ on a minimally pinning surface, functionalized with OTS. Only the control DI water droplet loses contact with the surface after rebound under these conditions as all the oil cloaks were successful in suppressing rebound. The observations in Fig. 2 are further confirmed here, as the expansion phase is approximately identical in terms of maximum droplet diameter and the expansion time for all the droplets. During the retraction phase, the contact lines of the cloaked droplets begin to pin to the surface and slow down the receding front. Fig. 3(b) shows the normalized maximum diameter for impact experiments with different oil cloaks, droplet sizes, and impact velocities. The Weber numbers of the droplets were varied from 45–639 and the Reynolds numbers from 1972–7875 to span agriculturally relevant conditions. For this regime, the normalized maximum diameter at full expansion scales as shown in eqn (1).

where We is the Weber number and Re is the Reynolds number, as was shown in previous studies for droplet impact on superhydrophobic surfaces.^13,68,69 Once again, we observe that the maximum diameters are nearly identical for cases with and without oil cloaks and follow the trend indicated by eqn (1). This demonstrates that the expansion phase of the droplet impacts is largely unaffected by the presence of an oil cloak at a variety of impact velocities and for different oils.

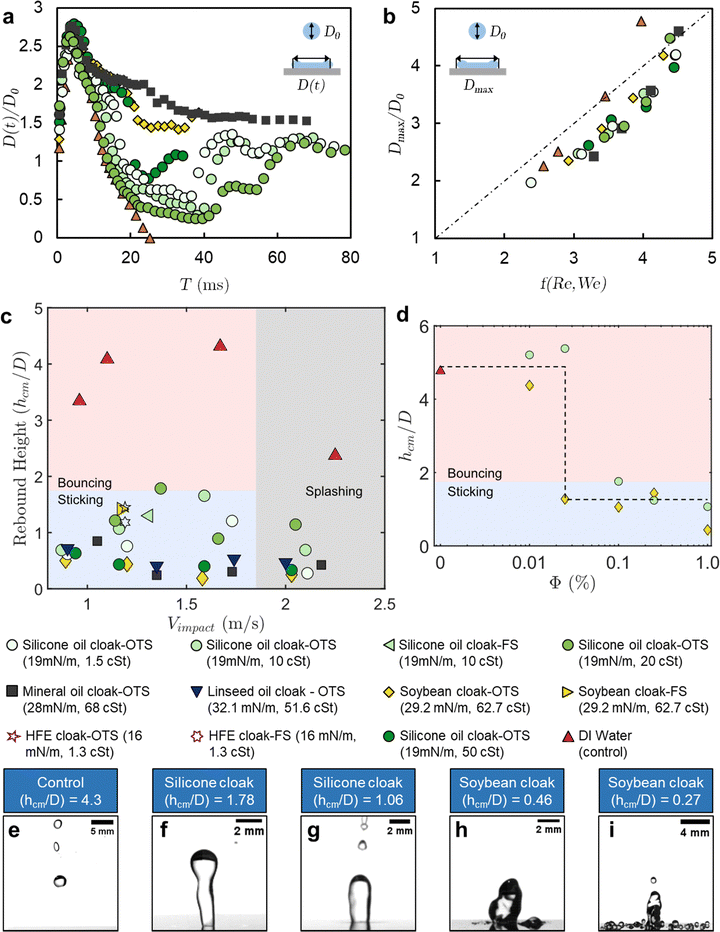Fig. 3 Droplet impact dynamics and retention behavior. (a) Normalized contact diameter as a function of time for six different oil cloaks for an impact velocity ≈1.25 m s⁻¹. Complete rebound is only observed for the pure water drop as contact is always maintained for all the oil-cloaked droplets (1% oil by volume). (b) Normalized maximum diameter as a function of the correlation function f(We,Re). The weber number spanned 45–639 in our experiments. (c) The rebound height of the center of mass of droplets (h_cm) is normalized by droplet diameter (D) for different impact velocities, oils, and oil viscosities. All oil cloaked droplets had an oil fraction of 1% by volume and diameters ≈3 mm. The bouncing transition is defined at h/D = 1.75, where the droplet lifts off the surface completely. All the oils helped suppress droplet rebound at a variety of impact velocities. (d) Rebound height of the center of mass of droplets (h_cm) normalized by droplet diameter (D) for different impact experiments is plotted as a function of oil volume fraction in cloaked droplets. 10 cSt silicone oil and soybean oil were chosen as representative oils, and both demonstrate the robustness of rebound suppression even for droplets with 0.1% of oil by volume (see Movies S9–S13, ESI†). (e)–(i) Snapshots of the highest points of the centers of mass of droplets during retraction or rebound for selected experiments. The labels for these snapshots indicate the oils used and the normalized rebound heights.

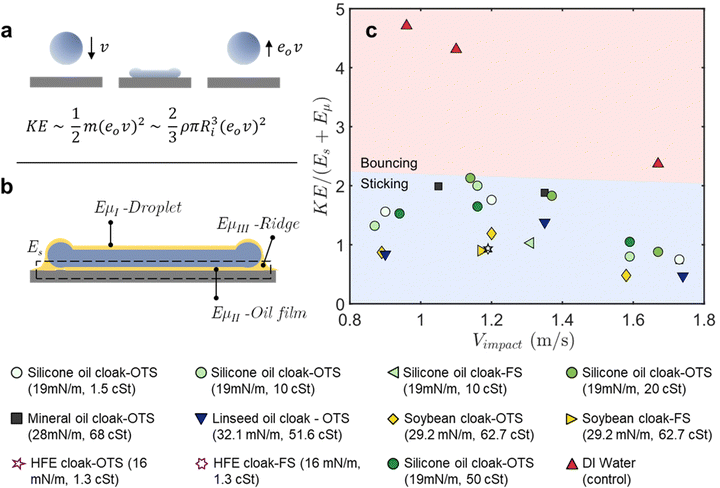
Focusing our attention now on the retraction phase and the rebound behavior of cloaked droplets, we revisit the maximum height (h_cm) of the droplet's center of mass. Using the highspeed videos of the droplet impacts, we measure the h_cm of the droplets and normalize it by the initial droplet diameter D₀ (see Methods for the estimation of the center of mass). Fig. 3(c) plots the normalized rebound height for various impact velocities, oil cloaking conditions, and surface functionalizations. In all of these experiments, the oil fraction was kept constant at 1% by volume for the cloaked droplets. This plot demonstrates the robustness of the approach in promoting droplet retention. Regardless of the type of the oil, the oil viscosity, or oil surface tension, all the cases with cloaking led to droplets sticking on superhydrophobic surfaces for velocities from 0.8–2.3 m s⁻¹, which correspond to the agriculturally relevant We ∼ 81–646. Oil viscosities were varied between 1.3 cSt and 68 cSt, as any oil that is too viscous would be difficult to work with in practice, and oils of too high viscosity can lead to less uniform coating and pose barriers to leaf processes.⁷⁰ The surface tensions of the oil were varied as much as possible, between 16 mN m⁻¹ to 32 mN m⁻¹.

We observe a general trend of increased rebound suppression for increasing viscosities, though this trend reverses when the viscosity becomes very high (∼500 cP), possibly due to the timescale of oil spreading increasing beyond the timescale of the droplet impact (see Movie S16, ESI†). At the higher end of the impact velocities we explored, we observe splashing of both the DI water droplets and the oil cloaked droplets. Interestingly while the satellite droplets in the control case scatter off the surface (Movie S7, ESI†), nearly all the satellite droplets in the oil-cloaked case adhere to the surface (Movie S8, ESI†). Typically, smaller droplet sizes that are more prone to drift are chosen to enhance coverage on plant surfaces.²⁶ These results indicate that our methodology could enable the use of large droplets that are resistant to drift while still benefiting from enhanced coverage afforded by satellite droplets. Fig. 3(d) demonstrates the effect of the oil fraction for two representative oils of low and high viscosity. Both oils are effective at preventing retention at 0.1% by volume, furthering the practical robustness of our approach. This volume of oil is comparable to the total amount of adjuvants currently used in agricultural spraying, including when oil-in-water emulsions are employed.²⁶

Movies S9–S13 and Fig. S3 (ESI†) indicate some of the complexities that arise at lower oil fractions. As the volume fraction reaches 0.1%, we notice that the ridge of oil that pins the droplet becomes discontinuous. This ridge is no longer evident when the oil fractions go below 0.1%. At these volume fractions, the average contact angle during the retraction phase also changes drastically from about 30° to about 140° (as seen in Video S4 and Fig. S3, ESI†). At 0.01% volume fraction, the retraction phase is comparable to that of a DI water droplet, indicating that there is a minimum amount of oil needed for the approach to be effective. Fig. 3(e)–(i) show some examples of the maximum normalized rebound height for different impact conditions to highlight the distinction between the bouncing, sticking, and splashing regimes.

Discussion

We have been able to demonstrate that oil-cloaking offers a simple yet robust approach to enhance droplet retention on superhydrophobic surfaces. We have shown improved retention over a range of agriculturally relevant impact conditions for a wide range of oils, oil viscosities, and oil volume fractions. However, it is also clear from the top-down videos of these impacts (Videos S6 and S9–S13, ESI†) that the mechanisms that govern retraction dynamics are fairly complex. There are several macroscopic and microscopic pinning events that lead to energy dissipation during the retraction phase. These videos indicate the formation of an oil ridge plays a key role in pinning the droplets to the surface. However, it is also evident that the thickness, continuity, and symmetry of the ridge are highly variable. While explaining the explicit dynamics of this system will require more examination of the fluidic and interfacial interactions at play, here we use a simple analysis of thermodynamic states to explain droplet retention – which is the fundamental experimental outcome we care most about.

We can consider an impacting droplet in two states: (i) at the maximum diameter during impact and (ii) after the droplet has rebounded. We first focus on the latter state for a pure water droplet without an oil cloak. When a water droplet rebounds from a superhydrophobic surface, its rebounding kinetic energy (KE) can be expressed as a function of its incoming velocity (v) and the coefficient of restitution (e₀), as shown in Fig. 4(a). This quantity KE therefore represents the approximate energy which must be dissipated to ensure rebound suppression. For water droplets on a superhydrophobic surface, the coefficient of restitution is a function of the Weber number, as seen in Fig. S5 (ESI†),^71,72 allowing easy calculation of KE.

Fig. 4 Sticking–bouncing transition for droplet impacts (a) as a pure water droplet rebounds from a superhydrophobic surface, it carries kinetic energy that can be expressed in terms of the coefficient of restitution (e₀), the incoming velocity (v), and the mass of the droplet (m). (b) To arrest the rebound of such a droplet and make it stick to a surface, this kinetic energy must be removed from the droplet by the work of adhesion (E_s) and viscous dissipation (E_μI + E_μII + E_μIII), shown here for a cloaked droplet at maximum extension. (c) The data points correspond to droplet impacts at different droplet velocities and oil cloaks. The shaded regions correspond to the different experimental outcomes. The vertical axis plots a ratio of the kinetic energy of rebound of a DI water droplet for each experimental condition and the sum of the work of adhesion and the viscous dissipation. This demonstrates that in the case of oil-cloaking, the work of adhesion and the viscous dissipation is comparable to the rebound kinetic energy, which leads to sticking.

To assess the ability of our cloaked oil droplet to dissipate this energy quantity KE, we return to the other state of interest as shown in Fig. 4(b), where an oil-cloaked droplet reaches its maximum diameter. We can consider two types of energy dissipation mechanisms, one due to contact line pinning and another due to viscous dissipation in the ridge.

The work of adhesion (E_s) – the term that captures the amount of work needed to overcome contact line pinning and remove a droplet from a surface – can be written in terms of the surface tension of the fluid in contact with the surface (σ), the receding contact angle of the droplet (θ_r) and the maximum radius of the droplet on the surface (R_max) as shown in eqn (2).^73–75

E_s ∼ σ₀(1 + cos(θ_r))πR_max² (2)

In the cloaked cases, we assume that the entire contact area with the surface is covered by oil during the impact event. This is a reasonable assumption given the fact that the oil is preferentially wetting on the surface compared to water. Moreover, the retracting contact angle of the droplet remains below 90 degrees throughout the entire retraction phase (Videos S5–S8, ESI†), far lower than that of pure water and indicating the presence of oil (see Fig. S4, ESI†). We also choose to model dissipation in experiments where the oil fraction was 1%; as at lower volume fractions, the situation is more complex due to the discontinuity of the oil ridge during the impact event. The second dissipation mechanism is only present in the oil cloaked cases and is due to the viscosity of the oil cloak itself. Using prior work on the viscous dissipation rate due to the oil cloak on droplets, we can express the viscous dissipation rate as a sum of three terms, dissipation in the oil cap (), dissipation in the oil film underneath the droplet () and dissipation in the oil ridge (), as shown in equation set 3.⁶⁷In the equations above, μ_w and μ₀ represent the viscosities of the water and oil, respectively. U_r represents the velocity of the retracting droplet, t is the thickness of the oil film underneath the droplet, R_max is the maximum contact radius of the droplet in its fully expanded state and t_ret is the retraction time for the droplet to go from its maximum diameter to its final contact diameter. Comparing the relative magnitude of these terms, we can see that the viscous dissipation rate in the oil ridge at the contact line of the receding droplet would be the dominant term (see ESI†). We note here that the dissipation in the water drop does not need to be considered in this energy balance as it is already accounted for in the coefficient of restitution. Using this framework, if the sum of the work of adhesion and the viscous dissipation is similar in magnitude to the kinetic energy of rebound which would have been available in the absence of an oil cloak, then the droplet will stick, and if the theoretical rebound kinetic energy is much greater than the sum of these terms, the droplet should bounce.^25,76

Fig. 4(c) plots the rebound kinetic energy normalized by the sum of the work of adhesion and the viscous dissipation for each experimental condition that our model is applicable to. We explicitly do not plot data points that fall in the splashing regime as our estimate of the coefficient of restitution does not apply to those data points. We also do not consider oil volume fractions <1%, given that the oil might not cover the entire interfacial area in those cases. For each droplet, we estimate the rebound kinetic energy that would be carried by a water droplet of similar size and incoming velocity using the coefficient of restitution. We estimate the work of adhesion and the viscous dissipation using the maximum contact diameter observed during each droplet impact. The contact angle used in this case is the quasi-static receding angle of the cloaked droplets on the superhydrophobic surface, as reported in ESI,† Fig. S4. We observe that the sum of the work of adhesion and viscous dissipation is of the same order as the rebound kinetic energy for all the cloaked droplets, indicating that the work of adhesion and viscous dissipation are significant enough to suppress droplet rebound. In contrast, for DI water droplets, their kinetic energies are several times larger than the sum of the dissipative terms, explaining why they bounce.

We have demonstrated that oil cloaking is an extremely simple, effective, and robust method to promote droplet retention on superhydrophobic surfaces. Having explored a wide regime of fluidic and interfacial parameters with single droplet impacts, we sought to implement our knowledge into a prototype that could be used to demonstrate practical enhancements to spray retention. We developed a prototype that involved two overlapping nozzles, one for the water and another for the oil (see Methods).

To test the ability of our sprayer to enhance retention in the most extreme case, we sprayed both water and soybean oil–cloaked water droplets onto a large minimally pinning surface, functionalized with OTS. A schematic and image of the prototype cloaked-droplet sprayer is shown in Fig. S1 (ESI†). In order to measure retention performance in terms of mass, we weighed the retained mass of droplets in both cases. Fig. 5(a) shows a photograph of the end result of spraying water drops onto the surface for 3 seconds. As expected, almost all the water drops sprayed onto the superhydrophobic surface bounce off (see Movie S14, ESI†). Fig. 5(b) shows a photograph of the end result of spraying water drops cloaked in ∼1% soybean oil by volume for 3 seconds. Almost immediately after spraying commences, the cloaked water drops begin sticking to the surface (see Movie S15, ESI†), and by the end of 3 seconds, we measure a nearly 100-fold enhancement in retained mass (Fig. 5(c)) for the case of soybean oil. Fig. 5(c) also shows retention data for experiments where oil cloaked droplets were only sprayed for 1 and 2 seconds. We find that this trend is consistent for other vegetable oils that are commonly used in agriculture, such as canola or cottonseed oil, further illustrating the robustness of our approach.^51,52 These experiments show the potential of this technology to greatly reduce the amount of pesticides sprayed, as with even a third of the spray time, the technique allows for 7 to 14-fold enhancements in mass retention based on the oil used. Crucially, these enhancements are achieved with food-safe oils that are inexpensive, widely used, and safe for the environment, farmworkers, and crops. These oils are also known to be widely compatible with pesticide chemistries, delay evaporation of agrochemical spray droplets, and promote foliar uptake of pesticides.^26,49

Fig. 5 Water and oil-cloaked water droplets sprayed on a superhydrophobic surface and different crop leaves. (a) The end result of spraying a 6-inch superhydrophobic wafer with DI water through a conventional agricultural spray nozzle for 3 seconds (see Movie S14, ESI†). (b) The same wafer after 3 s of spraying oil cloaked (1% by volume – soybean oil) droplets generated by the same spray nozzle (see Movie S15, ESI†). (c) Retained mass of droplets on the minimally pinning superhydrophobic surface for different spray times and different oil cloaks. (d)–(g) Snapshots to demonstrate the coverage attainable with 1 second of spraying with soybean oil-cloaked droplets on (d) cabbage, (e) kale, (f) lettuce, and (g) spinach leaves. (h) Mass of droplets retained on the leaf normalized by leaf area and spray time are compared on four crop leaves for pure water, and soybean oil cloaked droplets (∼1% by volume).

In Fig. 1, we demonstrated the ability of our prototype sprayer to reduce spray waste in terms of surface coverage on cabbage leaves. In order to demonstrate the ability of our sprayer to enhance the retained mass, we spray three more crop leaves (kale, spinach, and lettuce), and the end result of 1 s of spraying on all the leaves is shown in Fig. 5(d)–(g). The total retained mass of droplets is normalized by the area of the leaf and the spraying time for both DI water and soybean oil cloaked water droplets and is presented in Fig. 5(h). We observe >3-fold enhancements in normalized retained mass across leaves, demonstrating the wide practical applicability of our approach in enhancing droplet retention.

In conclusion, we have demonstrated a simple, environmentally sustainable, inexpensive, and effective approach to enhance the retention of sprays on hydrophobic and superhydrophobic surfaces. By cloaking droplets in minute quantities of oil (<1% by volume), we demonstrate robust rebound suppression on two types of superhydrophobic surfaces with nine different oils that span a wide range of viscosities and surface tensions across agriculturally relevant impact conditions. We were able to demonstrate the rebound suppression with as little as 0.1% oil by volume per droplet. By modeling the viscous and surface energy-based dissipation during the impacts of these cloaked droplets, we were able to provide a physical understanding of the rebound suppression across our experiments. Finally, we translated these findings into a prototype sprayer which was able to demonstrate up to a 102-fold enhancement in retention on superhydrophobic surfaces and up to a 5-fold reduction in waste when spraying on crop leaves. These enhancements were achieved using food and environmentally safe vegetable oils, and the methodology presented here demonstrates great promise in reducing the human health and environmental impact of pesticides.

Materials and methods

Single cloaked droplet generation

Two separate syringe pumps (Harvard Apparatus, PHD Ultra) were used to flow the water and oil which formed the cloaked droplets. The water syringe pump was connected to a 24-gage stainless steel needle (Vita Needle Company) positioned vertically at a specified height above the superhydrophobic substrate. The water flow rate was held constant at 0.4 mL min⁻¹ such that the water exited the 24-gage needle as discrete droplets. A 27-gage needle (Vita Needle Company) was connected to the oil syringe pump and placed beneath the water needle. Fig. 2(b) shows the relative needle placement, roughly to scale. The needles are positioned such that the water droplet emerging from the 24-gage needle contacts the tip of the oil needle for less than one second before the water droplet pinches off, allowing sufficient time for the oil to cloak the water droplet. The oil flowrate set on the oil syringe pump was varied in the range of 4 μL min⁻¹ and 0.04 μL min⁻¹ to achieve oil volume fractions between 1% and 0.01%, respectively. Impacts of the droplets on the superhydrophobic surface were recorded with a Photron Fastcam SA1.1.

Confirming low volume fractions of oil

All the volume fractions of oil were confirmed by running the syringe pumps until the syringes were emptied and recording the time taken.

Hydrophobizing needles

For oil volume fractions <1%, the stainless-steel needles were hydrophobized to prevent any wicking losses. The stainless-steel needles were hydrophobized by submerging them for 24 hours in a solution of 5 mM fluoroalkyl (C10) phosphonic acid (SP-06-003, obtained from Specific Polymers) solvated in methanol. A flat stainless-steel control surface subjected to the same conditions had a water–air contact angle of >90° confirming successful functionalization.

Contact angle and surface tension measurements

Contact angles and surface tensions were measured using a Ramé-Hart contact angle goniometer.

Impact velocity, center of mass, and coefficient of restitution estimation

Impact velocity and center of mass (COM) data was extracted from the high-speed videos via image analysis of each frame. Care was taken when lighting the background and surface such that the edges of the droplet were the darkest features of the video. This enabled the use of a simple thresholding method to create a mask of the droplet's outline. For each row of pixels in the droplet mask, the width of the mask was taken to be the local diameter of the droplet under the assumption that the droplet remained axisymmetric at all times. The partial mass of each row was calculated as the mass of a disk one pixel thick. The mass average of these partial masses weighted by their vertical position yielded the COM. The impact velocity was calculated by differentiating the frame-by-frame vertical COM with respect to time and taking the velocity just before impact. Because the rebound velocity of a droplet is highly variable throughout the rebound process, an alternative definition of the coefficient of restitution was established, where . By using the maximum COM height of the droplet after a rebound to calculate an equivalent velocity, a much more reliable value is obtained.

Cloaked droplet sprayer

In order to test the coverage of leaf surfaces by an agriculturally relevant spray, a reservoir of deionized water was pressurized at 2 atm (30 psi) and flowed through a TG-1 TeeJet Full Cone Spray Tip (Spray Smarter), with the resulting spray directed at the leaf. A distance of approximately 75 cm was maintained between the sprayer and leaf. An AA250AUH Automatic Spray Nozzle (Spraying Systems) was installed just upstream of the spray tip to control the spray time by switching on and off. The water droplets from the primary nozzle were cloaked in oils using a secondary airbrush sprayer. Care was taken to ensure that the overlap angle of the two nozzles ensured that none of the oil from the secondary sprayer contaminated the surfaces directly (see ESI,† Fig. S1). The flow rates of both fluids were controlled to ensure 1% cloaking oil by volume.

Evaluating leaf coverage (Fig. 1(i))

Manual annotation was performed to identify the area of the leaf which was covered by water droplets as shown in ESI,† Fig. S6, which was divided by the total area of the leaf to yield the coverage fraction. Note that in the case of the oil-cloaked spray, some area is wetted by spreading oil but does not have water droplets: this area is not counted as contributing to the leaf coverage.

Author contributions

Conceptualization: V. J., K. K. V. Investigation: V. J., S. R. Methodology: V. J., S. R., S. P. Visualization: V. J., S. R. Funding acquisition: K. K. V. Supervision: K. K. V. Writing: V. J. Writing – review and editing: V. J., S. P., S. R. K. K. V.

Data availability

The authors declare that the data supporting the findings of this study are available within the paper and its ESI.† Any additional information that supports the findings of this study are available from the corresponding author upon reasonable request. Dropbox link to supplementary videos: https://www.dropbox.com/scl/fo/aaqmlc9xfcpuu2odbwvcl/AO2TnyQF-Hp1bWkprHXMaDU?rlkey=7t8yxcwynykxpc6iuk0m292r5&dl=0.

Conflicts of interest

V. J., S. R., S. P., and K. K. V. are inventors on a patent application related to this work titled “Compositions, Articles, Devices, and Methods Related to Droplets Comprising A Cloaking Fluid” filed by MIT (PCT/US2022/048062). V. J. and K. K. V. are cofounders and have an equity interest in AgZen Inc. V. J. and K. K. V. acknowledge board positions with AgZen Inc. The authors declare that they have no other competing interests.

References

1. G. Matthews, Pesticide Application Methods, 2008.
2. D. Pimentel and L. Levitan, BioScience, 1986, 36, 86–91.
3. H. B. Pionke and D. E. Glotfelty, Water Res., 1989, 23, 1031–1037.
4. R. J. Gilliom, Pesticides in the Nation's Streams and Ground Water, 1992–2001 Geological Survey (US), 2007.
5. F. H. M. Tang, M. Lenzen, A. McBratney and F. Maggi, Nat. Geosci., 2021, 14, 206–210.
6. W. Aktar, D. Sengupta and A. Chowdhury, Interdiscip. Toxicol., 2009, 2, 1–12.
7. U. Ahlborg, M. Akerblom, G. Ekstrom, C. Hogstedt, T. Kjellstrom and O. Pettersson, Public Health Impact of Pesticides Used in Agriculture, World Health Organization, England, 1990.
8. L. Goldmann, Childhood pesticide poisoning: Information for advocacy and action, United Nations Environment Programme (UNEP), 2004.
9. N. L. Brooks, Electronic Report from the Economic Research Service Statistical Bulletin Number 974-2 Characteristics and Production Costs of U.S. Cotton Farms, U.S. Department of Agriculture, 2001.
10. J. Fernandez-Cornejo, R. Nehring, C. Osteen, S. Wechsler, A. Martin and A. Vialou, Pesticide Use in U.S. Agriculture: 21 Selected Crops, 1960–2008, U.S. Department of Agriculture, 2014.
11. D. Richard and D. Quéré, Europhys. Lett., 2000, 50, 769–775.
12. A. Lafuma and D. Quéré, Nat. Mater., 2003, 2, 457–460.
13. C. Clanet, C. Béguin, D. Richard and D. Quéré, J. Fluid Mech., 2004, 517, 199–208.
14. D. Bartolo, C. Josserand and D. Bonn, J. Fluid Mech., 2005, 545, 329–338.
15. D. Quéré, Rep. Prog. Phys., 2005, 68, 2495–2532.
16. C. Duez, C. Ybert, C. Clanet and L. Bocquet, Nat. Phys., 2007, 3, 180–183.
17. J. De Ruiter, J. M. Oh, D. Van Den Ende and F. Mugele, Phys. Rev. Lett., 2012, 108, 074505.
18. X. Deng, F. Schellenberger, P. Papadopoulos, D. Vollmer and H. J. Butt, Langmuir, 2013, 29, 7847–7856.
19. J. C. Bird, R. Dhiman, H. M. Kwon and K. K. Varanasi, Nature, 2013, 503, 385–388.
20. C. Peng, Z. Chen and M. K. Tiwari, Nat. Mater., 2018, 17, 355–360.
21. D. Nuyttens, M. De Schampheleire, P. Verboven, E. Brusselman and D. Dekeyser, Trans. ASABE, 2009, 52, 1471–1480.
22. G. J. Dorr, A. J. Hewitt, S. W. Adkins, J. Hanan, H. Zhang and B. Noller, Crop Prot., 2013, 53, 109–117.
23. S. Kooij, R. Sijs, M. M. Denn, E. Villermaux and D. Bonn, Phys. Rev. X, 2018, 8, 031019.
24. J. Fukai, Y. Shiiba, T. Yamamoto, O. Miyatake, D. Poulikakos, C. M. Megaridis and Z. Zhao, Phys. Fluids, 1995, 7, 236–247.
25. D. Bartolo, C. Josserand and D. Bonn, J. Fluid Mech., 2005, 545, 329–338.
26. F. Whitford and G. Lindner, Adjuvants and the Power of the Spray Droplet Droplet Improving the Performance of Pesticide Applications, Purdue Extension, 2014.
27. R. E. Gaskin, K. D. Steele and W. A. Forster, N. Z. Plant Prot., 2005, 58, 179–183.
28. X. Zhang and O. A. Basaran, J. Colloid Interface Sci., 1997, 187, 166–178.
29. M. Aytouna, D. Bartolo, G. Wegdam, D. Bonn and S. Rafai, Exp. Fluids, 2010, 48, 49–57.
30. H. Hoffman, R. Sijs, T. De Goede and D. Bonn, Phys. Rev. Fluids, 2021, 6, 033601.
31. M. C. Butler Ellis, C. R. Tuck and P. C. H. Miller, Colloids Surf., A, 2001, 180, 267–276.
32. R. Sijs and D. Bonn, Pest Manage. Sci., 2020, 76, 3487–3494.
33. K. A. Krogh, B. Halling-Sørensen, B. B. Mogensen and K. V. Vejrup, Chemosphere, 2003, 50, 871–901.
34. R. Mesnage, B. Bernay and G. E. Séralini, Toxicology, 2013, 313, 122–128.
35. M. J. L. Castro, C. Ojeda and A. F. Cirelli, Environ. Chem. Lett., 2014, 12, 85–95.
36. R. Mesnage, N. Defarge, J. Spiroux de Vendômois and G. E. Séralini, Food Chem. Toxicol., 2015, 84, 133–153.
37. J. P. Myers, M. N. Antoniou, B. Blumberg, L. Carroll, T. Colborn, L. G. Everett, M. Hansen, P. J. Landrigan, B. P. Lanphear, R. Mesnage, L. N. Vandenberg, F. S. Vom Saal, W. V. Welshons and C. M. Benbrook, Environ. Health: Global Access Sci. Source, 2016, 15, 1–13.
38. R. Mesnage and M. N. Antoniou, Front. Public Health, 2018, 5, 361.
39. R. Mesnage, C. Benbrook and M. N. Antoniou, Food Chem. Toxicol., 2019, 128, 137–145.
40. Bloomberg – Bayer's Roundup Costs Could Top $16 Billion as Provisions Mount, https://www.bloomberg.com/news/articles/2021-07-29/bayer-to-set-aside-4-5-billion-for-potential-roundup-claims, (accessed January 2025).
41. D. B. Smith, S. D. Askew, W. H. Morris, D. R. Shaw and M. Boyette, Trans. ASAE, 2000, 43, 255–259.
42. V. Bergeron, D. Bonn, J. Y. Martin and L. Vovelle, Nature, 2000, 405, 772–775.
43. A. Riseman and J. M. Frostad, Phys. Fluids, 2021, 33, 032107.
44. V. Bergeron, C. R. Phys., 2003, 4, 211–219.
45. A. Riseman and J. M. Frostad, Phys. Fluids, 2021, 33, 032107.
46. M. K. Patel, Eng. Agric. Environ. Food, 2016, 9, 92–100.
47. R. Salcedo, J. Llop, J. Campos, M. Costas, M. Gallart, P. Ortega and E. Gil, Crop Prot., 2020, 127, 104964.
48. M. Damak, M. N. Hyder and K. K. Varanasi, Nat. Commun., 2016, 7, 1–9.
49. C. E. Bogran, S. Ludwig and B. Metz, Using Oils As Pesticides, AgriLIFE Extension, 2006.
50. M. Stoytcheva, Pesticides in the Modern World – Pesticides Use and Management, InTech, Croatia, 2011.
51. Fact Sheet for Flower and Vegetable Oils, U.S. EPA, 1993.
52. Biopesticides Fact Sheet for Plant Oils – U.S. EPA Office of Pesticide Programs, https://www3.epa.gov/pesticides/chem_search/reg_actions/registration/fs_G-114_01-Jul-01.pdf, (Accessed January 2025).
53. Vegetable Oils in Food Technology: Composition, Properties and Uses, ed. F. D. Gunstone, John Wiley & Sons, 2nd edn, 2011.
54. A. Cornish, N. S. Battersby and R. J. Watkinson, Pestic. Sci., 1993, 37, 173–178.
55. R. Pavela, Advances in Plant Biopesticides, 2014, pp. 347–359.
56. I. M. da Silva, J. C. Zanuncio, B. P. Brügger, M. A. Soares, A. J. V. Zanuncio, C. F. Wilcken, W. de, S. Tavares, J. E. Serrão and C. S. Sediyama, Sci. Rep., 2020, 10, 1–8.
57. L. Zheng, C. Cao, L. Cao, Z. Chen, Q. Huang and B. Song, J. Agric. Food Chem., 2018, 66, 16.
58. N. Blanken, M. S. Saleem, C. Antonini and M. J. Thoraval, Sci. Adv., 2020, 6, eaay3499.
59. P. Gao and J. J. Feng, J. Fluid Mech., 2011, 682, 415–433.
60. N. Blanken, M. S. Saleem, M.-J. Thoraval and C. Antonini, Curr. Opin. Colloid Interface Sci., 2021, 51, 101389.
61. D. Liu and T. Tran, Appl. Phys. Lett., 2019, 115, 073702.
62. H. R. Liu, C. Y. Zhang, P. Gao, X. Y. Lu and H. Ding, J. Fluid Mech., 2018, 854, R6.
63. D. Liu and T. Tran, Appl. Phys. Lett., 2018, 112, 203702.
64. X. Han, W. Li, H. Zhao, J. Li, X. Tang and L. Wang, Nat. Commun., 2021, 12, 3154.
65. B. P. Baker, J. A. Grant and R. Malakar-Kuenen, Soybean Oil Profile, New York State Integrated Pest Management Program, 2018.
66. C. Dorrer and J. Rühe, Adv. Mater., 2008, 20, 159–163.
67. J. D. Smith, R. Dhiman, S. Anand, E. Reza-Garduno, R. E. Cohen, G. H. McKinley and K. K. Varanasi, Soft Matter, 2013, 9, 1772–1780.
68. J. B. Lee, N. Laan, K. G. de Bruin, G. Skantzaris, N. Shahidzadeh, D. Derome, J. Carmeliet and D. Bonn, J. Fluid Mech., 2016, 786, R41–R411.
69. M. Damak and K. Varanasi, Phys. Rev. Fluids, 2018, 3, 093602.
70. J. M. Baker, Environ. Pollut., 1970, 1, 27–44.
71. A.-L. Biance and G. Lagubeau, J. Fluid Mech., 2006, 554, 47–66.
72. Z. Wang and N. Koratkar, Understanding and Controlling Wetting Phenomena at the Micro/Nanoscale, Nanotechnologies for the Life Sciences, 2011.
73. P. Laplace, Traité de mécanique céleste, 1799.
74. B. Thomas Young and M. D. For Sec, Philos. Trans. R. Soc. London, 1805, 95, 65–87.
75. J. Gibbs, The collected works, 1928.
76. P. K. Sharma and H. N. Dixit, Phys. Fluids, 2020, 32, 112107.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01496k

---