 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of matrix stiffness on microstructure evolution and magnetization of magneto-active elastomers
Mehran
Roghani
 *ab,
Dirk
Romeis
*ab,
Dirk
Romeis
 a,
Dmitry
Borin
c and
Marina
Saphiannikova
a,
Dmitry
Borin
c and
Marina
Saphiannikova
 ab
ab
aLeibniz-Institut für Polymerforschung Dresden e.V., Hohe Strasse 6, Dresden, 01069, Germany. E-mail: Roghani@ipfdd.de
bFaculty of Mechanical Science and Engineering, Dresden University of Technology, Dresden, 01062, Germany
cInstitute of Mechatronic Engineering, Chair of Magnetofluiddynamics, Measuring and Automation Technology, Dresden University of Technology, Dresden, 01062, Germany
First published on 21st January 2025
Abstract
Field-induced microstructure evolution can play an important role in defining the coupled magneto-mechanical response of Magneto-Active Elastomers (MAEs). The behavior of these materials is classically modeled using mechanical, magnetic and coupled magneto-mechanical contributions to their free energy function. If the MAE sample is fully clamped so it cannot deform, the mechanical coupling is reduced to the internal microscopic deformations caused by the particles moving and deforming the elastic medium that surrounds them. In the present study, we build on a unified mean-field theoretical approach which takes the microscopic elastic energy into account. Combined with experiment, this approach reveals how microstructure evolution affects the magnetization behavior of isotropic MAEs. MAE disks with various matrix stiffness and volume fraction of particles were fabricated and the magnetization curves were measured by vibrating sample magnetometry. We demonstrate that the idea of columnar structures forming from randomly distributed particles upon the application of an external magnetic field provides an effective approach in modeling microstructure evolution in these materials. Our unified mean-field model, using few and physically meaningful parameters, shows good quantitative agreement with the experimental data on magnetization and magnetic differential susceptibility of MAE samples. More importantly, our model can estimate microstructure evolution in highly filled samples, for which measurements are very challenging. Since changes in magnetization and stiffness are both driven by microstructural evolution, a quantitative relationship can be established between the two effects, as they represent different macroscopic manifestations of the same microscopic process. Therefore, our model can be used in conjunction with magnetization measurements to predict the mechanical modulus of MAEs without the need for elastic testing.
1 Introduction
The promising applications of Magneto-Active Elastomers (MAEs) in high-tech fields such as medical devices,1,2 soft robotics,3,4 and active surfaces5,6 arise from their modifiable material properties. The key to the adaptability of MAEs lies in the magnetizable micro-particles embedded within a soft elastomeric matrix. In MAEs made with magnetically soft particles, such as carbonyl iron (ferromagnets with negligible remanent magnetization), the magnetic forces between the particles can be controlled by the strength of the applied magnetic field, leading to changes in their relative positions.7 This field-induced microstructure evolution has been linked to alterations in the elastic and magnetic properties of MAEs, as observed in various studies.8–10The phenomenon of microstructure evolution, which is most prominent in isotropic and elastically soft MAEs, has been visualized using metallographic microscopy11 and X-ray micro-computed tomography.12 These studies revealed that the randomly distributed particles come together upon the application of an external magnetic field. They form columnar structures with the principal axis aligned along the magnetic field lines. However, the formation of columnar structures has only been observed in MAEs with low particle content (<1%) due to the limitations of imaging in highly filled samples. To gain insight into microstructure evolution in highly filled samples, other methods must be used. For example, with ultra-small-angle neutron scattering, Belyaeva et al.13 showed that the distribution of particles gets more anisotropic with increasing magnetic load, which indicates the formation of elongated aggregates of particles.
The mechanical implication of microstructure evolution in MAEs is the transition of the elastic properties from isotropic to anisotropic.8 A consensus has emerged that matrix elasticity plays a key role in microstructure evolution.14 In a soft matrix, particles can move more freely, facilitating significant microstructure evolution, whereas in a stiff matrix, their positions remain practically fixed. This phenomenon has been extensively studied using various experimental testing procedures. In uniaxial extension or compression tests on soft samples, an increase in the Young's modulus is observed along the direction of the magnetic field, while the modulus perpendicular to the field remains effectively unchanged.8 In shear tests performed with rheometers, an increase in the shear modulus is observed, a phenomenon commonly referred to as the magnetorheological effect.15
From a modeling perspective, capturing the link between elastic behavior and microstructure evolution in soft MAEs has been particularly challenging, especially when using Finite Element Methods (FEM). This originates from the computational complexity arising in representative volume elements (RVEs), when rigid particles in a soft environment move around and come close to each-other.16 A modeling technique capable of investigating microstructure evolution is molecular dynamics (MD).17–21 For instance, Sanchez et al.22 used a coarse grained MD approach for simulating an MAE film and found stiff samples have a lower initial susceptibility compared to soft samples. In another work focusing on magnetic gels by Ryzhkov et al.,23 the MD simulations showed that different particle arrangements impact the magnetization behavior of samples with magnetic chains of various sizes. The samples with long chains of particles showed a lower magnetization compared to the samples with shorter chains. While MD provides valuable insights into the changes in magnetic and mechanical properties of MAEs, it comes with some drawbacks. The method is computationally expensive and restricted to microscopic and mesoscopic simulations, making it incapable of accounting for the effects of a sample's shape on the behavior. Consequently, making quantitative comparisons with experimental data using MD remains challenging.
Recently, we have introduced a unified mean-field model,24 based on analytical homogenization,25 which accounts for microstructure evolution and its impact on the behavior of MAEs. The model is computationally efficient and has the ability to take into account the macroscopic shape effects on the behavior of the sample in addition to microscopic effects. In previous works,24,26 we demonstrated that this model is not only capable of accurately predicting experimental observations of the magnetorheological effect and magnetically induced deformation of MAEs using just a few physically meaningful parameters, but also offers valuable insights into how microstructure evolution influences these phenomena.
For magnetic composites that do not undergo microstructure evolution due to a stiff matrix, the magnetization behavior is predominantly governed by the magnetization of the particles, their volume fraction, and their initial distribution.25 However, in composites where micro-particles can move under magnetic loading, the effective properties are less straightforward to determine. For magneto-rheological fluids (MRFs), the impact of microstructure evolution has been extensively studied, revealing that the effective susceptibility of the material becomes dependent on its viscosity.27 The effect of microstructure evolution on the magnetization behavior of isotropic MAEs was first examined experimentally by Stepanov et al.11 using two samples with elastic moduli of 60 and 400 kPa. Their results indicated higher susceptibility in the softer sample, leading the authors to conclude that particle motion is responsible for the active properties of MAEs, as evidenced by the correlation between magnetic and mechanical hysteresis. In another approach, Stepanov et al.28 immobilized the particles within an MAE by cooling it to 200 K and compared its magnetization to a sample at 290 K, where particle motion is less hindered. They also froze a sample under applied magnetic field and showed that while the sample frozen outside the magnetic field has a lower initial susceptibility, the magnetic behavior of the sample at 290 K is very close to the sample frozen under magnetic field. Later, Bodnaruk et al.29 confirmed the results of Stepanov et al.28 by performing similar experiments with different cooling temperatures. Additionally, they measured the magnetic anisotropy of MAE samples with microstructure evolution. Borin and Stepanov30 conducted systematic measurements of initial susceptibility in MAEs with different particle volume fractions and matrix types (liquid, elastic, and quasi-solid) allowing various degrees of particle mobility. The authors found that initial susceptibility depends on both matrix elasticity and particle volume fraction. Recently, Borin et al.31 investigated the effect of matrix elasticity on the magnetization and differential susceptibility of MAEs as well as magnetic hysteresis and how repeated magnetization cycling of the samples affects the magnetic behavior. The study demonstrated that the magnetic properties of soft MAEs are affected by reversible and irreversible particle mobility in the sample.
To date, theoretical models that consider the effect of microstructure evolution on the magnetic behavior of MAEs made with magnetically soft particles have primarily focused on explaining the magnetic hysteresis phenomenon. For example Zubarev et al.32 developed a lattice based dipole model for soft magnetic gels to capture the macroscopic magnetic hysteresis of these materials. Also, Vaganov and Raikher33 utilised first-order reversal curve analysis and a model based on two particles in an elastomeric matrix to study the magnetic hysteresis of soft MAEs. However, only few theoretical studies have examined how matrix stiffness affects the degree of microstructure evolution and magnetization in MAEs. Clark et al.34 experimentally measured the magnetization of MAE samples with magnetically soft particles and varying matrix stiffness, complementing these measurements with a simple two-dipole model that captures the trends of the observed phenomena.
In the following, we demonstrate that our unified mean-field model quantitatively describes the effects of microstructure evolution on the magnetization of MAE samples with varying matrix stiffness and particle volume fraction, in agreement with experimental data. To achieve this, we rely on analytical homogenization of the magnetic properties which takes into account the evolution of microstructure due to the formation of columnar structures under a magnetic field. The magnetization of nine samples, made with three distinct matrix stiffness levels and three particle volume fractions, was measured using a vibrating sample magnetometer (VSM). We compare the magnetization curves and differential susceptibilities obtained from the experiments with theoretical predictions. The extent of microstructure evolution, which our model quantifies as an increased particle volume fraction within columnar structures, and the resulting magnetorheological effect are investigated.
2 Unified mean-field theory
We model the magneto-mechanical behavior of MAEs using a self-consistent field approach that captures the evolving magnetic and elastic properties simultaneously.26 This method efficiently incorporates both macro-scale (sample shape and deformation) and micro-scale (particle arrangement and its evolution) contributions to these coupled properties.Here, we study disk shaped samples that are completely clamped, so they cannot deform (for details see the experiment section). The samples are placed in a uniform magnetic field H0 generated between the electromagnet poles of a VSM. The symmetry axis of the disks aligns with the direction of the magnetic field lines as shown in Fig. 1.
The general form of the free energy density of an MAE sample can be written as:26
ΨMAE(F, ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) ) = Ψmech(F, ) = Ψmech(F, ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) ) + Ψmag(F, ) + Ψmag(F, ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) ) + Ψmic( ) + Ψmic(![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) ), ), | (1) |
![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) :
:ΨMAE(![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) ) = Ψmag( ) = Ψmag(![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) ) + Ψmic( ) + Ψmic(![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) ). ). | (2) |
In the following we give a detailed definition of these two remaining terms.
2.1 Magnetic energy
Assuming our sample becomes homogeneously magnetized under the external magnetic field![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0, the magnetic energy density can be written only based on the scalar values of the local magnetic field H and the external magnetic field H0 (both are along the x axis as shown in Fig. 1). The magnetic energy density takes the form:
0, the magnetic energy density can be written only based on the scalar values of the local magnetic field H and the external magnetic field H0 (both are along the x axis as shown in Fig. 1). The magnetic energy density takes the form: | (3) |
Following the leading-order approximation where field inhomogeneities are neglected, the particle magnetization M, the external field H0 and the local field H are related via:36
| H = H0 − (1/3 − ϕfmacro − fmicro)M, | (4) |
 | (5) |
Chougale et al.38 used mean-field approximation to estimate the microstructure factor fmicro for columnar structures (right part of Fig. 1) that takes the analytical form:
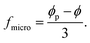 | (6) |
In our model, ϕp and ϕ indicate the local particle volume fraction and the total volume fraction of particles in a sample (see Fig. 1). They are linked to the volume fraction of the columnar structures ϕc through the following relation:
 | (7) |
In the absence of magnetic loading, the sample is isotropic ϕp = ϕ, resulting in fmicro = 0. The value of fmicro increases as the particles condense more and more into the columns. This results in the magnetic energy decreasing as fmicro increases, and thus we can conclude that columnar structures are more favorable in terms of the magnetic energy compared to an isotropic state in which the particles are randomly distributed.
The relation between M and H is a material property of the magnetizable particles. The carbonyl iron particles used in the experiment show a negligible magnetic hysteresis, as measured in a previous study.39 Therefore, we use the Fröhlich–Kennelly function to capture the saturating non-hysteretic behavior in this work:25
 | (8) |
2.2 Micro-mechanical energy
As explained previously, the formation of columns within the sample is magnetically favorable. In our previous works, we demonstrated that a mechanical energy penalty is necessary to regulate microstructure evolution, because without such penalty the particles form dense columns even in vanishingly small magnetic fields. This micro-mechanical energy function, for both initially isotropic and anisotropic magneto-active elastomers, is presented in our previous works24,26 as the Hookean form: | (9) |
 | (10) |
The micro-mechanical parameter km in eqn (9) and (10) provides the ability to tune the degree of microstructure evolution.
To calculate the elastic modulus of the columns, we use an effective medium theory recently presented by Lefevre and Lopez-Pamies40 for composites made with spherical inclusions:
 | (11) |
3 Experiment
MAE samples for the experiments were made of two-component silicone rubber Elastosil RT623 (Wacker Chemie AG, Germany). To adjust the stiffness of the matrix, it was diluted with M1000 silicone oil (GE Bayer Silicones, Germany) in different proportions before crosslinking. BASF CC carbonyl iron powder with magnetically soft spherical micro-particles (average diameter of ∼4 μm) was used as magnetic filler. The procedure for manufacturing the samples is reported in detail elsewhere.39 The samples fabricated for the experiments had matrix stiffnesses (shear modulus) of ∼10, 40, and 110 kPa and particle volume fractions of ∼0.05, 0.2, and 0.35. The specified values of the matrix shear modulus were obtained within a quasi-static torsion test of a reference non-filled specimens considering the linear response of the material.41The magnetic measurements were carried out at room temperature (T = 23 °C) using the Lake Shore VSM 7407s vibration magnetometer calibrated with a nickel sphere. In the measurements, a disc shaped sample with a diameter of ∼4.65 mm and height ∼1 mm was fixed on the LakeShore 730933 sample holder with a disc flat bottom perpendicular to an external magnetic field.
The magnetic moment of the samples was measured using a VSM in continuous data acquisition mode, with an averaging period of 1 second per point. The magnetization was calculated based on the sample volumes; however, the exact volumes slightly differ from the mold dimensions due to manufacturing variations. Ideally, samples with the same particle volume fraction should exhibit identical saturation magnetization at high magnetic fields. In practice, however, we observe small discrepancies in saturation magnetization, caused by these volume differences. To resolve this issue, we slightly adjust the calculated height of each sample to ensure that samples with the same particle volume fraction ϕ have identical saturation magnetization:
| Mϕ∞ = 0.98ϕM∞, | (12) |
4 Results and discussion
The values of applied magnetic field H0, matrix shear modulus Gm, volume fraction ϕ, and aspect ratio γ of the samples are fixed by the experimental conditions. The volume fraction of particles inside the columns ϕp can be obtained by minimizing the free energy given in eqn (2). Knowing ϕp, we can calculate the local magnetic field H and the magnetization of the particles M using eqn (4) and (8). The magnetization of the sample Me = ϕM is then compared to the experimentally acquired magnetization values. The saturation magnetization of the particles was experimentally determined to be approximately M∞ = 1500 kA m−1, and this value is used in our model. The parameters that are used to fit the experiment in our model are: the initial susceptibility of the particles χ, the micro-mechanical parameter km, and the effective medium theory parameters α and β. Their values are found using the least square curve fitting technique and are presented in Table 1. This set of fit parameters is used to evaluate the model for comparison with the experimental results for all the samples.| Parameter | Description | Value |
|---|---|---|
| χ | Initial susceptibility of the particles | 84.7 |
| k m | Micro-mechanical parameter | 1.8 |
| α | Effective medium theory parameter | 0.7 |
| β | Effective medium theory parameter | −2.0 |
The increase of local volume fraction ϕp with an increasing external magnetic field serves as an indicator of microstructure evolution in our model. The behavior of ϕp(H0) is depicted in Fig. 2 for the magnetization fit to the experiment. The horizontal dashed lines represent the sample's volume fraction ϕ, while the colors indicate the matrix stiffness according to experimental characterization. Blue lines correspond to samples with a matrix shear modulus of Gm = 10 kPa, red lines with Gm = 40 kPa, and green lines with Gm = 110 kPa. This color coding is retained through all the figures for consistency. The most visible trend in this figure is a reduction in the magnitude of microstructure evolution for samples with higher volume fraction of particles ϕ. An increase in matrix stiffness Gm also results in a smaller magnitude of microstructure evolution. Also, for higher values of Gm, the external magnetic field H0 at which ϕp reaches a plateau (indicating no further microstructure evolution) increases.
In Fig. 3, we show the measured magnetization for disk shaped MAE samples and the corresponding values predicted by our model. Each sub-plot corresponds to samples with the same volume fraction of particles. In the sub-plots, we see that the slope in the linear zone (near H0 = 0) of the magnetization curves is similar. Their behavior also coincides in the saturation zone (near H0 = M∞) by design as explained in the experiment section. However, we observe that the stiffness of the matrix influences the behavior in the transition zone (the magnetic fields at which the behavior changes from linear to saturating). The samples with a softer matrix have a higher magnetization in this zone compared to the samples with a stiffer matrix. We see that the sensitivity of the magnetization behavior to matrix stiffness is more pronounced for samples with lower fractions of particles. This experimentally observed phenomenon is captured by our model too. It can be explained by considering the microstructure evolution in Fig. 2. There, we observed that the samples with the lowest volume fraction have the most microstructure evolution. Also, among the samples with low ϕ, the softest sample experiences the highest increase of ϕp. From eqn (4) and (6), we can conclude that an increase in ϕp directly leads to an increase in the local magnetic field H which is responsible for particle magnetization. In the saturation zone, no effects of matrix stiffness on magnetization are observed due to two effects: (1) microstructure evolution has stopped, and (2) particle magnetization reaches saturation and no longer changes with increasing magnetic field.
Another interesting trend, when Fig. 3 is compared to Fig. 2, is that the magnetization of the samples saturates at a higher external magnetic field than the field at which microstructure evolution stops. This is related to the form of the micro-mechanical energy function presented in this study. In our previous work,26 we used the sample's shear modulus Giso in the micro-mechanical energy, which remains unchanged under a magnetic field. However, in this work, the shear modulus of the columnar structures Gc is used, as explained in the theory section, and it increases during magnetic loading since it is a function of ϕp. In our previous work,26 it was predicted that the magnetization saturates at the same external field at which microstructure evolution stops, because fmicro was the only parameter depending on ϕp in the micro-mechanical energy. However, in this study, both Gc and fmicro are functions of ϕp, introducing a greater penalty to microstructure evolution. This explains the different external field strengths at which microstructure evolution halts and magnetization saturates.
By taking the derivative of the sample magnetization Me with respect to H0, we obtain the differential susceptibility of the samples, as plotted in Fig. 4. In each sub-plot, the samples have the same volume fraction of particles but differ in matrix stiffness. This representation clearly shows that samples with the same volume fraction exhibit the same initial magnetization slope, but then the softer samples experience an uptake in their susceptibility. This uptake is most pronounced for the sample with the lowest volume fraction (ϕ = 0.05) and the softest matrix (Gm = 10 kPa). Higher particle volume fractions or increased matrix stiffness result in a reduced uptake of susceptibility, as both factors create a stiffer medium around the particles, restricting their movement (lower microstructure evolution as seen in Fig. 2). In the experimental results (symbols), the stiffer samples show a very low uptake in their susceptibility, whereas our model still predicts a noticeable uptake (solid lines). This discrepancy arises from the form of the micro-mechanical energy term, which is based on coarse approximations. Using a more complex function for ψmic than the one presented in eqn (10) would possibly allow for a closer agreement with the experiment. Such improved relationship could be developed through further micro-mechanical simulations but is beyond the scope of this work. Another observation from Fig. 4 is that the decreasing slope immediately after the uptake becomes steeper for softer samples and lower values of ϕ, as seen both in experimental results and model predictions. Additionally, the susceptibility curves for samples with the same volume fraction cross each other at the same point after the uptake. This crossing happens at lower magnetic fields for samples with lower particle volume fractions: ∼310 kA m−1 for ϕ = 0.05, ∼390 kA m−1 for ϕ = 0.2 and ∼460 kA m−1 for ϕ = 0.35. As the samples with lower volume fraction have a larger uptake in low magnetic fields, they reach saturation magnetization faster and thus their susceptibility decreases more steeply before saturation.
To evaluate our model's performance across extreme ranges of matrix stiffness, we consider two more cases in the appendix: an MRF sample and a sample of epoxy resin with infused particles. Magnetorheological fluids, where magnetic particles are highly mobile, undergo significant microstructure evolution. In contrast, for MAE samples with rigid matrices, like epoxy, particle movement is strongly restricted, preventing microstructure evolution. The measured magnetic behavior of these samples, along with the model predictions, is presented in Appendix A.
As discussed in the introduction, the magnetorheological effect in MAEs is another important aspect of these materials that our model can predict. Since fitting the magnetization data with our model provides a measure of microstructure evolution (as shown in Fig. 2), we can calculate the effective modulus of the columnar structures inside the sample. This allows us to assess the mechanical reinforcement resulting from the formation of dense columns and its impact on the sample's modulus EL along the magnetic field direction. Using the rules of mixture we estimate:26
| EL = (1 − ϕc)Em + ϕcEc, | (13) |
In Fig. 5, we observe that the sample with the stiffest matrix and highest particle volume fraction shows an increase of nearly 4 MPa (from 2 MPa to 6 MPa in Fig. 5, top) in its modulus parallel to the magnetic field, representing the largest absolute increase among the samples. The increase in modulus for the softer samples, however, shows a monotonous decline with respect to decreasing matrix modulus. When examining the relative increase of the modulus EL/Esio, we find that the sample with the softest matrix exhibits the highest magnetorheological effect, with a field-induced modulus increase that is 10 times greater than the initial modulus of the sample without an applied magnetic field. Here, the order of the curves with respect to their matrix stiffness changes from the top sub-plot and we see that the stiffest sample undergoes the smallest relative magnetorheological effect. Looking at the effect of particle volume fraction on the relative magnetorheological effect in the samples with the same matrix modulus (Fig. 5 bottom), we see that the samples with ϕ = 0.20 and ϕ = 0.35 have nearly identical initial slopes of EL/Eiso in low magnetic fields, but they deviate from each other around H0 ∼ 200 kA m−1. The sample with the lowest volume fraction does not experience a significant magnetorheological effect, despite having the largest increase in ϕp among all the samples (see Fig. 2). There are two reasons for this. First, while the local volume fraction ϕp increases significantly, the volume fraction of the columns ϕc decreases substantially according to the relation shown in eqn (7). Second, although the lowest filled sample exhibits the largest increase in ϕp, the value of ϕp is still far from the tight packing volume fraction ϕmax, at which the effective elastic modulus increases dramatically. This also explains why the softest sample with the highest particle volume fraction experiences the highest relative magnetorheological effect, since despite not having the largest increase in ϕp, its ϕp comes closest to ϕmax.
5 Summary and outlook
In summary, we have applied our unified mean-field model to predict the magnetization behavior of MAEs undergoing microstructure evolution using few and physically meaningful parameters. The magnetic energy contribution is taken into account with dipolar mean field approach. Since the samples are clamped during magnetic loading, the macro-scale mechanical energy contribution is disregarded. The energy spent on the microscale to move the particles inside their elastomeric surrounding is crucial in modeling these materials. A very effective way to model this microstructure evolution is by assuming columnar structures forming from randomly distributed particles upon the application of an external magnetic field. The micro-mechanical energy is introduced to regulate the extent of microstructure evolution based on key factors such as the magnetic field strength, volume fraction of particles, and the elastic modulus of the matrix. In previous works,24,26 we have shown that a simple Hookean-spring formulation for this micro-mechanical energy is sufficient in explaining magnetorheological effects and huge deformations in these materials. In this paper, we refine this formulation by making the micro-mechanical energy a function of the elastic modulus of the columns rather than the modulus of the isotropic samples. This adjustment allows us to explain the increase of susceptibility in low magnetic fields for very soft MAE samples as measured by VSM. A closer evaluation of how well our model predicts the experimental magnetic behavior is made by analyzing the derivative of magnetization with respect to the external magnetic field (differential susceptibility). The model accurately predicts the magnetization response for the softest sample. However, for stiffer samples, the model does not sufficiently suppress the magnetization uptake, as seen in the experiments. We attribute this discrepancy to the simplified form of the micro-mechanical energy, which likely has a more complex relationship with elasticity and particle volume fraction. Another potential source of discrepancy could be our assumption of homogeneous magnetic field inside the samples. Looking ahead, more detailed microscale simulations of microstructure evolution could provide more clarity on the form of the micro-mechanical energy term, leading to a more precise description of the macroscale magnetization behavior of MAEs. Additionally, this term could account for the observed magnetic hysteresis in MAEs caused by microstructure evolution. Finally we estimated the magnetorheological effect for all the samples. This can be useful in predicting the magnetically reinforced modulus of these materials in situations where mechanical testing is not possible.Author contributions
Mehran Roghani: conceptualization, methodology, formal analysis, investigation, writing – original draft, software, visualization, Dirk Romeis: conceptualization, methodology, writing – review & editing, Dmitry Borin: investigation, data curation, writing – original draft, Marina Saphiannikova: conceptualization, methodology, writing – review & editing, supervision, funding acquisition.Data availability
Processed and published data for this article will be archived with a persistent URL by software DOXIS4 (archive and document management system) hosted at the Leibniz Institute of Polymer Research Dresden.Conflicts of interest
There are no conflicts to declare.Appendix
Model performance for extreme matrix stiffness ranges
To evaluate the performance of our model across extreme ranges of matrix stiffness, we examine an MRF sample and an MAE sample with an epoxy matrix, both with a particle volume fraction of 0.05. The magnetization and differential susceptibility for these samples are compared. The model predictions for these cases are based on the same parameters as those applied to the elastomer-based samples discussed in the main text (see Table 1). Moreover, for the MRF sample, the matrix shear modulus Gm is set to a very low value (1 μPa) to reproduce an environment in which microstructure evolution is not hindered at all. For the epoxy-based sample, Gm is set to 1 GPa to reproduce an environment in which microstructure evolution is strongly suppressed.As it is seen in the top part of Fig. 6, the saturation magnetization in the measurements is matched to the predicted values by varying the sample heights. This is to make sure that the measured value of the sample's saturation magnetization matches ϕM∞ and agrees with the behavior of the elastomer samples with the same volume fraction in Fig. 3. In the bottom of Fig. 6, we observe that the sharp measured peak in susceptibility for the MRF sample is not fully captured by our model. This discrepancy may be due to the fully mobile particles in the fluid which can easily touch and form clusters. In such cases, the assumption of dipolar interactions between particles may no longer hold. Instead, higher-order interactions,45–48 which are significantly stronger, may dominate, leading to a much sharper susceptibility peak due to microstructure evolution. Despite this limitation, the predictions of our model agree well with the magnetic data measured after this peak.
For the epoxy sample, we notice that the initial susceptibility is slightly higher than that of elastomer-based samples with the same particle volume fraction. This can be explained by the fact that micro-particles in epoxy resin are mixed much worse than in silicone matrix, also due to rapid polymerization. Therefore, particle agglomerates are present in the material, resulting in higher initial susceptibility and a slight uptake in susceptibility. This increase occurs despite the absence of microstructure evolution, as the particles are fixed in the stiff matrix. Except this uptake, the model predictions agree well with the experimental measurements. This highlights the robustness of our model in predicting magnetization behavior across a spectrum of samples, from liquid to rigid.
Acknowledgements
Financial support via Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) research project 380321452/GRK2430 (‘Interactive Fiber Rubber Composites’) is gratefully acknowledged.References
- Y. Sun, W. Zhang, J. Gu, L. Xia, Y. Cao, X. Zhu, H. Wen, S. Ouyang, R. Liu and J. Li, Nat. Commun., 2024, 15, 1839, DOI:10.1038/s41467-024-46046-9
.
- X. Liu, L. Wang, Y. Xiang, F. Liao, N. Li, J. Li, J. Wang, Q. Wu, C. Zhou and Y. Yang, Sci. Robot, 2024, 9, eadh2479, DOI:10.1126/scirobotics.adh2479
.
- M. Reiche, L. Zentner, D. Borin, F. Becker and T. Becker, IEEE Robot. Autom. Lett, 2024, 1–6, DOI:10.1109/LRA.2024.3448213
.
- W. Han, W. Gao and X. Wang, ACS Appl. Mater. Interfaces, 2024, 16, 30396–30407, DOI:10.1021/acsami.4c04586
.
- R. Kriegl, M. Jezeršek, G. Kravanja, L. Hribar, S. M. Mukhi, G. Kokot, I. Drevenšek-Olenik and M. Shamonin, Smart Mater. Struct., 2024, 33, 067001, DOI:10.1088/1361-665X/ad41a9
.
- I. Straus, G. Kravanja, L. Hribar, R. Kriegl, M. Jezeršek, M. Shamonin, I. Drevensek-Olenik and G. Kokot, Materials, 2024, 17, 1550, DOI:10.3390/ma17071550
.
- T. Gundermann and S. Odenbach, Smart Mater. Struct., 2014, 23, 105013, DOI:10.1088/0964-1726/23/10/105013
.
- Z. Varga, G. Filipcsei and M. Zrnyi, Polymer, 2006, 47, 227–233, DOI:10.1016/j.polymer.2005.10.139
.
- Y. Han, W. Hong and L. E. Faidley, Int. J. Solids Struct., 2013, 50, 2281–2288, DOI:10.1016/j.ijsolstr.2013.03.030
.
- D. Y. Borin and S. Odenbach, J. Magn. Magn. Mater., 2017, 431, 115–119, DOI:10.1016/j.jmmm.2016.07.055
.
- G. Stepanov, D. Y. Borin, Y. L. Raikher, P. Melenev and N. Perov, J. Phys.: Condens. Matter, 2008, 20, 204121, DOI:10.1088/0953-8984/20/20/204121
.
-
D. Borin and S. Odenbach, Magnetic Soft Matter: Fundamentals and Applications, The Royal Society of Chemistry, 2023, ch. 8, pp. 213–228 Search PubMed
.
- I. A. Belyaeva, J. Klepp, H. Lemmel and M. Shamonin, Appl. Sci., 2021, 11, 4470, DOI:10.3390/app11104470
.
- M. Lokander and B. Stenberg, Polym. Test., 2003, 22, 677–680, DOI:10.1016/S0142-9418(02)00175-7
.
- G. Stepanov and P. Storozhenko, Bull. Russ. Acad. Sci.: Phys., 2024, 88, 570–576, DOI:10.1134/S1062873823706323
.
- T. A. Nadzharyan, M. Shamonin and E. Y. Kramarenko, Polymers, 2022, 14, 4096, DOI:10.3390/polym14194096
.
- M. Tarama, P. Cremer, D. Y. Borin, S. Odenbach, H. Löwen and A. M. Menzel, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042311, DOI:10.1103/PhysRevE.90.042311
.
- A. Ryzhkov, P. Melenev, C. Holm and Y. L. Raikher, J. Magn. Magn. Mater., 2015, 383, 277–280, DOI:10.1016/j.jmmm.2014.11.008
.
- O. V. Stolbov and Y. L. Raikher, Arch. Appl. Mech., 2019, 89, 63–76, DOI:10.1007/s00419-018-1452-0
.
- P. A. Sánchez, T. Gundermann, A. Dobroserdova, S. S. Kantorovich and S. Odenbach, Soft Matter, 2018, 14, 2170–2183, 10.1039/C7SM02366A
.
- G. Pessot, M. Schümann, T. Gundermann, S. Odenbach, H. Löwen and A. M. Menzel, J. Phys.: Condens. Matter, 2018, 30, 125101, DOI:10.1088/1361-648X/aaaeaa
.
- P. A. Sánchez, E. S. Minina, S. S. Kantorovich and E. Y. Kramarenko, Soft Matter, 2019, 15, 175–189, 10.1039/C8SM01850B
.
- A. V. Ryzhkov, P. V. Melenev, M. Balasoiu and Y. L. Raikher, J. Chem. Phys., 2016, 145, 074905, DOI:10.1063/1.4961299
.
- M. Roghani, D. Romeis and M. Saphiannikova, Soft Matter, 2023, 19, 6387–6398, 10.1039/D3SM00906H
.
- D. Romeis and M. Saphiannikova, J. Magn. Magn. Mater., 2023, 565, 170197, DOI:10.1016/j.jmmm.2022.170197
.
- M. Roghani, D. Romeis, G. Glavan, I. A. Belyaeva, M. Shamonin and M. Saphiannikova, arXiv, 2025, preprint, arXiv:2501.09353 DOI:10.48550/arXiv.2501.09353.
- K. Shu, C. Wang, W. Li, T. Bussell and J. Ding, Curr. Opin. Electrochem., 2020, 21, 297–302, DOI:10.1016/j.coelec.2020.03.004
.
- G. Stepanov, D. Y. Borin, S. Odenbach and A. Gorbunov, Solid State Phenom., 2009, 152, 190–193, DOI:10.4028/www.scientific.net/SSP.152-153.190
.
- A. V. Bodnaruk, A. Brunhuber, V. M. Kalita, M. M. Kulyk, P. Kurzweil, A. A. Snarskii, A. F. Lozenko, S. M. Ryabchenko and M. Shamonin, Polymer, 2019, 162, 63–72, DOI:10.1016/j.polymer.2018.12.027
.
- D. Borin and G. Stepanov, Phys. Sci. Rev., 2022, 7, 1119–1140, DOI:10.1515/psr-2019-0126
.
- D. Borin, M. Vaganov and S. Odenbach, J. Magn. Magn. Mater., 2024, 589, 171499, DOI:10.1016/j.jmmm.2023.171499
.
- A. Y. Zubarev, D. Chirikov, D. Y. Borin and G. Stepanov, Soft Matter, 2016, 12, 6473–6480, 10.1039/C6SM01257D
.
- M. V. Vaganov and Y. L. Raikher, J. Phys. D: Appl. Phys., 2020, 53, 405002, DOI:10.1088/1361-6463/ab9674
.
- A. T. Clark, D. Marchfield, Z. Cao, T. Dang, N. Tang, D. Gilbert, E. A. Corbin, K. S. Buchanan and X. M. Cheng, APL Mater., 2022, 10, 041106, DOI:10.1063/5.0086761
.
- D. Romeis and M. Saphiannikova, Polymers, 2021, 13, 1372, DOI:10.3390/polym13091372
.
- D. Romeis, S. A. Kostrov, E. Y. Kramarenko, G. V. Stepanov, M. Shamonin and M. Saphiannikova, Soft Matter, 2020, 16, 9047–9058, 10.1039/D0SM01337D
.
- M. Sato and Y. Ishii, J. Appl. Phys., 1989, 66, 983–985, DOI:10.1063/1.343481
.
- S. Chougale, D. Romeis and M. Saphiannikova, Materials, 2022, 15, 645, DOI:10.3390/ma15020645
.
- D. Borin, G. Stepanov and E. Dohmen, Arch. Appl. Mech., 2019, 89, 105–117, DOI:10.1007/s00419-018-1456-9
.
- V. Lefèvre and O. Lopez-Pamies, Extreme Mech. Lett., 2022, 55, 101818, DOI:10.1016/j.eml.2022.101818
.
- D. Borin, N. Kolsch, G. Stepanov and S. Odenbach, Rheol. Acta, 2018, 57, 217–227, DOI:10.1007/s00397-018-1071-2
.
- S. Chougale, D. Romeis and M. Saphiannikova, J. Magn. Magn. Mater., 2021, 523, 167597, DOI:10.1016/j.jmmm.2020.167597
.
- D. Ivaneyko, V. Toshchevikov, M. Saphiannikova and G. Heinrich, Condens. Matter Phys., 2012, 15, 33601, DOI:10.5488/CMP.15.33601
.
- D. Ivaneyko, V. Toshchevikov, M. Saphiannikova and G. Heinrich, Soft Matter, 2014, 10, 2213–2225, 10.1039/C3SM52440J
.
- A. Biller, O. Stolbov and Y. L. Raikher, J. Appl. Phys., 2014, 116, 114904, DOI:10.1063/1.4895980
.
- A. Biller, O. Stolbov and Y. L. Raikher, J. Phys.:Conf. Ser., 2018, 012001, DOI:10.1088/1742-6596/994/1/012001
.
- A. M. Biller, O. V. Stolbov and Y. L. Raikher, Phys. Rev. E, 2024, 110, 064501, DOI:10.1103/PhysRevE.110.064501
.
- D. Yaremchuk, D. Ivaneyko and J. Ilnytskyi, J. Magn. Magn. Mater., 2024, 589, 171554, DOI:10.1016/j.jmmm.2023.171554
.
| This journal is © The Royal Society of Chemistry 2025 |






