Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing cage dynamics in concentrated hard-sphere suspensions and glasses with high frequency rheometry†
Thanasis
Athanasiou
 ab,
Baicheng
Mei
ab,
Baicheng
Mei
 *c,
Kenneth S.
Schweizer
*cd and
George
Petekidis
*c,
Kenneth S.
Schweizer
*cd and
George
Petekidis
 *ab
*ab
aInstitute of Electronic Structure & Laser, FORTH, Heraklion, 70013, Greece. E-mail: georgp@iesl.forth.gr
bDepartment of Materials Science and Engineering, University of Crete, Heraklion, 70013, Greece
cDepartment of Material Science and Materials Research Laboratory, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA. E-mail: bcmei@illinois.edu; kschweiz@illinois.edu
dDepartment of Chemistry and Department of Chemical & Biomolecular Engineering, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA
First published on 18th February 2025
Abstract
The cage concept, a central microscopic mechanism for glassy dynamics, has been utilized in concentrated colloidal suspensions to describe a number of phenomena. Here, we probe the evolution of cage formation and shear elasticity with increasing volume fraction in hard sphere suspensions, with emphasis on the short-time dynamics. To this end, we utilize linear viscoelastic (LVE) measurements, by means of conventional rotational rheometers and a home-made HF piezo-rheometer, to probe the dynamic response over a broad range of volume fractions up to the very dense glassy regime in proximity to random close packing. We focus on the LVE spectra and times shorter than those corresponding to the dynamic shear modulus G′ plateau, where the system approaches transient localization and cage confinement. At these short times (higher frequencies), a dynamic cage has not yet fully developed and particles are not (strictly) transiently localized. This corresponds to an effective solid-to-liquid transition in the LVE spectrum (dynamic moduli) marked by a high frequency (HF) crossover. On the other hand, as the volume fraction increases caging becomes tighter, particles become more localized, and the onset of the localization time scale becomes shorter. This onset of transient localization to shorter times shifts the HF crossover to higher values. Therefore, the study of the dependence of the HF crossover properties (frequency and moduli) on volume fractions provides direct insights concerning the onset of particle in-cage motion and allows direct comparison with current theoretical models. We compare the experimental data with predictions of a microscopic statistical mechanical theory where qualitative and quantitative agreements are found. Findings include the discovery of microscopic mechanisms for the crossover between the two exponential dependences of the onset of the localization time scale and the elastic shear modulus at high volume fractions as a consequence of emergent many body structural correlations and their consequences on dynamic constraints. Moreover, an analytic derivation of the relationship between the high frequency localized short-time scale and the elastic shear modulus is provided which offers new physical insights and explains why these two variables are experimentally observed to exhibit nearly-identical behaviors.
1. Introduction
Brownian hard sphere colloidal suspensions are one of the simplest model soft matter systems with their structure and dynamics extensively studied.1–3 Nevertheless, although simple in terms of constituents and their interactions, these systems still pose challenges4,5 as they exhibit rich structural, thermodynamic and mechanical behaviors especially upon increasing the volume fraction towards their maximum value or a random close packing (RCP) state. In the concentrated regime, where particle surfaces approach to distances far less than their radii on average, many body interactions dominate, affecting microstructure, quiescent dynamics, and viscoelasticity. These many body correlations impose significant theoretical challenges. The nature of the glass transition is still a debated topic with advances being made by comparing the physics of colloidal suspensions with molecular glass formers.6–10 While in theory, hard core interactions are defined by an infinite repulsion at contact and zero at larger distances, in a real system such as sterically stabilized polymethylmethacrylate (PMMA) spheres,11 the repulsion pair potential cannot be infinitely steep12 and the softness induced by the steric layer may affect the viscoelastic response at higher frequencies.13In the colloidal regime, time scales are set by the elementary Brownian time τ0 (=R2/6D0), where R is the particle radius, D0 = kBT/6πηsR is the Stokes–Einstein–Sutherland self-diffusion coefficient at infinite dilution, kB is the Boltzmann constant, T is the absolute temperature, and ηs is the solvent viscosity. As the particle volume fraction increases from the dilute limit, particles start to interact via solvent-mediated hydrodynamic and excluded volume (entropic) interactions and hence the microscopic particle dynamics slow down. Eventually, at volume fractions around ϕ ≈ 0.4,14 the dynamics split into two distinct relaxation modes, one on a short length and hence a short time scale (often referred to as β-relaxation in the mode-coupling theory (MCT) framework) within the first neighbor distances and the other on a larger length and hence a longer time scale, the so-called α-relaxation, where particles diffuse beyond their first neighbor shell.15,16 At the onset of the thermodynamically metastable17 regime at ϕ ≈ 0.49, the two relaxation processes start to strongly separate in time.5 At the phenomenologically deduced glass transition volume fraction, typically cited to occur at ϕ ≈ 0.58 and determined based on the (arbitrary) practical longest time scale of a measurement or extrapolated fits of an “ideal” MCT critical power law, the inverse long-time diffusion constant and the related zero-shear viscosity exhibit a sharp increase. Taking the cage model as a reference15 the two relaxation modes have different origins: the β-relaxation is linked to in-cage rattling18,19 and the structural α-relaxation is linked to thermally activated hopping or cage escape. This mobility reduction is also reflected in the mean squared displacement (MSD), 〈Δr2(t)〉 = 〈|r(t) − r(0)|2〉, where r(t) denotes the particle position at time t and the bracket represents an ensemble average over all particle trajectories under consideration. At higher volume fractions (ϕ > 0.58) and intermediate time scales (between α and β-relaxation), single particle motion becomes even more strongly coupled to the structure and dynamics of neighboring particles, and its subdiffusive character on intermediate time and length scales becomes more prominent. This is the regime where the localization plateau emerges, thereby separating the dynamics into long-time and short-time regimes with their diffusion coefficients DL and DS20–23 corresponding to the α-relaxation and β-relaxation, respectively. Interestingly, the term β-relaxation was originally used in molecular glass formers to describe the relaxation modes that are extrinsic to the nature of glass transition.24 It is noted that the β-relaxation can refer to different microscopic dynamical processes in thermal molecular glasses and hard sphere colloidal glasses; however, in both cases they reflect the more short-time and local motions in each system, but at different values of absolute length- and time-scales. In the colloidal field – hence in this work – it refers to the particle in-cage motion.
A similar behavior is exhibited in linear viscoelastic (LVE) spectra where dynamic moduli at low- and high-frequencies (long- and short-times, respectively) are separated by the caging plateau which thereby defines the intermediate time dynamically relaxed elastic shear modulus G′, as has been shown in previous studies.25–27 When the probing frequency is decreased sufficiently (at frequencies often inaccessible to commercial rheometers), the suspension exhibits a liquid-like behavior marked by the low-frequency (LF) G′, G′′ crossover with a time scale, 1/ωc-LF. A similar phenomenology, but for a completely different reason, is exhibited at elevated frequencies. During such short-time observations the system behaves in a liquid like manner as the measured LVE corresponds to the particle in-cage diffusivity. This is reflected in the rheological response which exhibits a second solid-to-liquid transition and a relevant high frequency (HF) G′, G′′ crossover at a frequency, ωc-HF > 1/τ0 ≫ ωc-LF.
A significant amount of work in the literature has focused on the long-time α-relaxation process and the caging plateau which is the manifestation of the kinetic glass transition and the transiently localized state, respectively. The α-relaxation has been the epicenter of a debate concerning whether the literally frozen dynamics predicted by MCT28 is true or whether the cage has a finite lifetime due to the presence of ergodicity-restoring thermally activated hopping processes5 as predicted by other theories.29 The latter is generally acknowledged to be the case based on dynamic scattering experiments30,31 and direct trajectory observations.32,33 To the best of our knowledge, no systematic study has quantitatively linked the rheological signature of colloidal glasses at high frequencies with the theoretical description of short-time relaxation. Hence, its connection with an elastic shear modulus remains elusive.
In this work, we focus on microscopic times and in particular a measure of the time scale for the onset of transient localization, τloc, and its relationship with 1/ωc-HF obtained from macroscopic rheology. In the case of monodisperse spheres, the LF crossover can be modeled using a single element Maxwell fluid where the relevant time scale is defined by the moduli crossover frequency. This Maxwell relaxation is linked to the long-time diffusion coefficient.34 However, this is not the case for the HF crossover where its prediction is more challenging.35 The HF crossover clearly sets a time scale, τc-HF = 1/ωc-HF, and a corresponding modulus, Gc-HF = G′(ωc-HF) = G′′(ωc-HF), that marks the practical solid to liquid crossover transition and should reflect the characteristic dynamics within a cage length-scale. We explore the behavior of the HF crossover by performing intermediate and high frequency small amplitude oscillatory shear experiments in a HS colloidal suspension where the volume fraction is systematically increased.
There are many direct36 and indirect37,38 methods to obtain high frequency LVE data, with their own merits and limitations. High frequency oscillatory shear is not possible with most commercial rheometers which are limited to frequencies up to around 200 rad s−1. We utilize high frequency rheometry by means of an in-house developed piezo rheometer (PZR) capable of extending the accessible frequency range of up to 7000 rad s−1, thus probing faster dynamics.39 The volume fraction dependence of Gc-HF and ωc-HF extracted from the LVE spectra is compared with the predictions of the nonlinear Langevin equation (NLE) theory within the dynamic free energy framework40,41 and the physical mechanisms underlying our Gc-HF and ωc-HF measurements are elucidated. The relationship between LVE and dynamics is briefly described in Section 2 where the relevant time scales are defined. Section 3 presents the background on NLE theory followed by the description of materials and methods in Section 4. Theoretical predictions of NLE theory and experimental rheological data are compared and discussed in Section 5, before concluding in the last Section 6.
2. High frequency LVE and in-cage dynamics
The classic Stokes–Einstein–Sutherland (SE) equation relates the solvent viscosity to the single particle self-diffusion constant in the dilute limit.21 By generalizing this equation, Mason et al. related the MSD to the frequency-dependent complex modulus G* (ω) given by ref. 27 and 42: | (1) |
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 2(t)〉 is the Fourier transform of the MSD. Hence,
2(t)〉 is the Fourier transform of the MSD. Hence, | (2) |
 | (3) |
 | (4) |
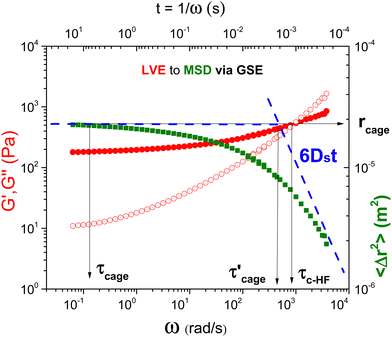 | ||
| Fig. 1 Typical LVE spectrum (left Y axis), G′ (solid circles) and G′′ (open circles) of a colloidal glass in the HF regime measured with a commercial rotational rheometer MCR702 and a homemade PZR up to an angular frequency of 4000 rad s−1. The corresponding MSD (right Y axis, solid squares) is obtained by rearranging eqn (2) and (3). Abscissa is either angular frequency (bottom) or the corresponding observation time t = 1/ω (top). An indication of the dynamic cage size, rcage, can be provided by the MSD plateau. The corresponding times for the high frequency cross-over and approach to the cage limits are also indicated by the vertical arrows. | ||
Fig. 1 presents the interrelation, viaeqn (1)–(4), of a measured LVE spectrum to the corresponding particle MSD for a hard sphere colloidal glass. The sample used as an example here is a suspension of PMMA particles of a hydrodynamic radius Rh of 151 nm in a viscous solvent (squalene) with a volume fraction ϕ of 0.63. At long times (low frequencies), particles are localized within a cage localization length, rcage, determined by the plateau of the MSD. This localization length is linked to the plateau modulus of G′ via the GSE relationship. At short times (high frequencies), the MSD slope approaches a linear dependence on time. The corresponding volume fraction dependent short-time diffusion coefficient, Ds(ϕ), at such high volume fractions, is expected to be about one order of magnitude slower than the dilute suspension (bare) SE diffusion coefficient, D0. A localization time is defined as the time required for a particle to sufficiently explore its environment, i.e. to “feel” its cage constraints and become transiently localized by its nearest neighbors. This process represents a transition of the MSD from diffusive to highly sub-diffusive, and the corresponding localization time can be crudely estimated as  where rcage is the displacement related to the dynamical cage size, as defined by the MSD long-time plateau. Still particles need, on average, significantly longer time to reach a distance equal to rcage; this time was qualitatively introduced above and is indicated as τcage in Fig. 1. From this simple graphical representation, it is clear that this microscopic localization time
where rcage is the displacement related to the dynamical cage size, as defined by the MSD long-time plateau. Still particles need, on average, significantly longer time to reach a distance equal to rcage; this time was qualitatively introduced above and is indicated as τcage in Fig. 1. From this simple graphical representation, it is clear that this microscopic localization time 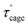 and the τc-HF deduced from macroscopic linear viscoelastic measurements at the high frequency G′, G′′, cross-over point, are comparable and potentially interrelated.
and the τc-HF deduced from macroscopic linear viscoelastic measurements at the high frequency G′, G′′, cross-over point, are comparable and potentially interrelated.
We should point out here that the microscopic dynamics deduced from the high frequency LVE measurement (shown in Fig. 1) could in principle be measured by optical microscopy or dynamic light scattering (DLS), when the latter probes, under certain contrast conditions, the self-intermediate scattering function and therefore particle self-diffusion. In this sense, hydrodynamic effects present in quiescent colloidal systems affect the dynamics probed both in LVE and DLS in the same way. On the other hand, under non-linear shear (not utilized here), hydrodynamic interactions would strongly affect the microstructure and microscopic dynamics.
3. Nonlinear Langevin equation theory
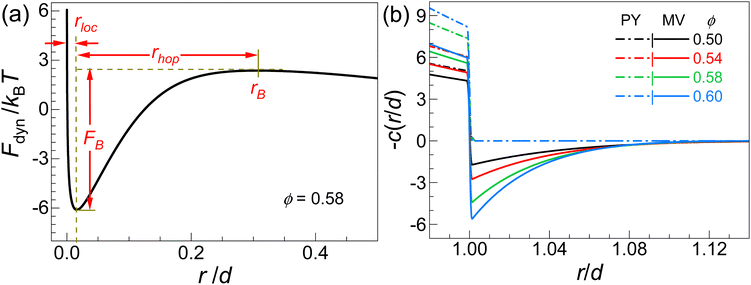
Within the dynamical, “ideal” MCT, a glass transition picture for hard sphere colloidal glass formers, the long-time diffusivity, DL(ϕ), approaches zero experimentally at ϕg ∼ 0.58 for monodisperse spheres. This is typically only inferred via an extrapolation from experimental and simulation data by fitting to a presumed functional form, e.g., the critical inverse power law of MCT. On the other hand, a finite slow α-relaxation has been detected at higher volume fractions of slightly polydisperse particles where it is argued the α time crosses over to an activated form.30,45 In contrast to this “ideal” MCT glass transition picture, the nonlinear Langevin equation (NLE) theory predicts a non-zero DL of up to ϕRCP. This is due to the thermally activated hopping of particles over an entropic barrier (computed microscopically) that always restores ergodicity via cage escape, in principle, at long enough times.46 This is qualitatively consistent with experimental observations43 for the out-of-cage diffusion which is predicted to freeze only at RCP, avoiding MCT singularities which have been estimated by various methods to lie in the interval of 0.64 ≫ ϕ > 0.515. The precise value of the latter number depends on the structural input to MCT and the statistical mechanical level of a MCT-like analysis47 employed, but is always below RCP. The short-time diffusivity, Ds(ϕ), remains finite and measurable even upon approaching ϕRCP ∼ 0.64 for monodisperse spheres due to local in-cage particle diffusion since some internal free volume is still available.Within the NLE theory, the entropic barrier emerges from the prediction of a spatially resolved effective dynamic free energy, Fdyn(r), where r is the scalar particle displacement from its initial position, and the negative gradient of the dynamic free energy defines an effective force on a particle due to all surrounding particles. It is calculated based solely on the equilibrium structural input via the radial distribution or pair correlation function, g(r), or its Fourier analogue, the static structure factor S(q),40,41 and is given as follows:
 | (5) |
 term in eqn (5)), and smooth decaying, negative contribution, finite at r = 0 (the second term in eqn (5)) due to interparticle interactions and correlations which favors particle localization. The minimum of the dynamic free energy defines a simple measure of the transient localization length rloc in the cage. The combination of the two contributions in eqn (5) leads to an entropic (for hard spheres) activation barrier in dimensionless units, βFB (see Fig. 2(a)), beyond a volume fraction of ∼0.43 that must be surmounted via thermally driven hopping to achieve out of-cage motion and ultimately structural relaxation and long distance Fickian diffusion. However, the barrier is only of order of kBT or less until the volume fraction approaches the onset of the thermodynamically metastable regime at ϕ ∼ 0.49, and hence activated dynamics emerge only sufficiently deep in the metastable regime where the barrier is significantly higher than kBT.
term in eqn (5)), and smooth decaying, negative contribution, finite at r = 0 (the second term in eqn (5)) due to interparticle interactions and correlations which favors particle localization. The minimum of the dynamic free energy defines a simple measure of the transient localization length rloc in the cage. The combination of the two contributions in eqn (5) leads to an entropic (for hard spheres) activation barrier in dimensionless units, βFB (see Fig. 2(a)), beyond a volume fraction of ∼0.43 that must be surmounted via thermally driven hopping to achieve out of-cage motion and ultimately structural relaxation and long distance Fickian diffusion. However, the barrier is only of order of kBT or less until the volume fraction approaches the onset of the thermodynamically metastable regime at ϕ ∼ 0.49, and hence activated dynamics emerge only sufficiently deep in the metastable regime where the barrier is significantly higher than kBT.
The required structural input (S(q) and c(q)) for hard sphere fluids in eqn (5) can be calculated from the Ornstein–Zernike (OZ) integral equation:48
 | (6) |
The OZ-MV theory for monodisperse hard sphere fluids predicts a structural and thermodynamic crossover at ϕs of ∼0.60 associated with new types of many body effects.52 The distinctive changes of all equilibrium properties are in good accord with simulations and experiments.52 As true of all approximate integral equation theories, the location of RCP is not captured correctly and is typically (well) beyond 0.644. For the OZ-MV theory, it is found at ϕRCP ∼ 0.77. Though far beyond the correct value of 0.644, it is much closer to the correct value than well studied integral equation theories such as OZ-PY, or popular empirical representations such as the Carnahan–Starling model, which both locate the incompressible RCP state at ϕ = 1. Moreover, it has been argued that the new physics emerges in the deeply metastable state (e.g. ϕ > 0.60) but well below the RCP volume fraction is not affected to leading order by the too large value predicted for ϕRCP.52
Given the dynamic free-energy from eqn (5), the mean time required for a tagged particle to displace “downhill” from its initial position to the minimum (localized state) in the overdamped limit (no inertia) can be computed by using Kramers mean first passage time theory53,54 as
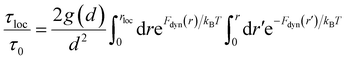 | (7) |
 | (8) |
4. Materials and experimental methods
Sterically stabilized nearly hard-sphere PMMA particles with a hydrodynamic radius Rh of 264 nm dispersed in squalene (Sigma Aldrich, Germany) were utilized as the primary sample. Steric stabilization is realized by chemically grafted poly-hydro-stearic acid chains (≈10 nm). Squalene was chosen as a solvent for its high boiling point and its refractive index proximity to PMMA in order to prevent evaporation and minimize any remaining van der Waals attractions, respectively. Its relatively high viscosity enhances torque signals but most importantly slows down the in-cage dynamics allowing the high frequency crossover to be accessible to conventional rotational rheometers such as MCR501, MCR702 (Anton-Paar, Austria) and ARES (TA Instruments, USA), and our in-lab developed high frequency piezorheometer (PZR). MCR702 was fitted with cone–plate geometry and utilized in a separated motor transducer mode to minimize the tool and sample inertia effects.39 The solvent shear viscosity was measured with a DMA 4100 M viscometer (Anton Paar, Austria) and found to be ηs = 13.32 mPa s at T = 23 °C. The particle hydrodynamic radius was confirmed by dynamic light scattering measurements in the dilute regime.The size polydispersity (standard deviation over the mean) of our samples is around 10% which suppresses crystallization. Different volume fractions were prepared from a single random close packing (RCP) batch, created by centrifugation. Starting from RCP, which was taken to be ϕRCP ≈ 0.67 (for a 10% polydisperse particles),59 the sample was successively diluted from about 0.64 to 0.45, with a total of 38 discrete samples progressively prepared, ensuring an accurate determination of the volume fraction among each other and relative to the initial RCP sample. More recent work60 suggest that the RCP volume fraction for 10% polydisperse hard spheres is in the range of 0.638–0.658 depending on the compression rate (or the centrifugation speed in our experimental protocol), i.e. clearly lower than that estimated by Schaertl et al.59 which we use in this study, for consistency with our previous work.25
Aging at these systems is weak and affects mainly G′′ at the lower frequency-end as short time in-cage dynamics are essentially age-independent;39,61,62 hence, the system is considered within the experimental time scales as time invariant. Particle swelling can induce significant uncertainties and therefore the stock sample was left at rest for two months after solvent exchange and then centrifuged to RCP. After solvent addition, the vial was placed on a rolling mixer for sufficiently long period depending on the concentration. Once the particle dispersion was completed, followed by a rest time of 12 hours, the sample was loaded on the rheometer. A reduction of the rest time was required for the less concentrated samples (ϕ < 0.58) to prevent sedimentation. All measurements were completed within 2 hours upon loading with no shear induced rejuvenation, i.e. no steady or oscillatory pre-shear.
To accurately determine the HF moduli crossover small amplitude oscillatory shear measurements were performed with 20 points per decade in the frequency regime of interest. Each dynamic frequency sweep measurement was performed at an optimum strain amplitude (ranging from 2% to 0.8%) in order to achieve significant torque signals and keep perturbation below the linear limit determined by dynamic strain sweeps. A weak evolution of the moduli was observed in very dense samples (ϕ > 0.6) within the first 30 minutes. At longer times, the LVE spectra and particularly the HF crossover were found to be time independent. Plate–plate 25 mm geometry was utilized in the very dense samples to overcome difficulties related to loading a stiff sample. Less concentrated samples were measured with cone-plate 50 mm geometry in the ARES rheometer.
5. Results and discussion
Dynamic frequency sweeps were utilized to capture the LVE spectrum of these hard sphere suspensions as the volume fraction is systematically decreased. The angular frequency and the modulus of the HF crossover were the parameters of specific interest. Hence, the conventional MCR702 or ARES data were complemented by measurements in the PZR when needed, i.e., at very concentrated samples where the HF crossover is detected at higher frequencies, beyond the range of conventional rheometers.The LVE spectra of three samples (out of the total 38 measured) are shown in Fig. 3. The most concentrated sample with ϕ = 0.64 exhibits the HF crossover at 586 rad s−1 while at lower frequencies the caging plateau emerges. As ϕ is decreased to 0.617, still in the nonequilibrium glassy regime, ωc-HF decreases and falls within the frequency range of the MCR702 instrument. This frequency decrease of the HF crossover reflects the cage enlargement and the less frequent exploration of cage boundaries exhibited by the particles as their concentration is reduced. The caging plateau is shifted to even lower frequencies with no indication of a LF crossover at the lower frequencies reached, (0.1 rad s−1). In contrast, at ϕ = 0.545, the LF crossover becomes faster and the HF crossover becomes slower; hence, both are now accessible with our conventional rotational rheometers. In this low volume fraction but still in the metastable regime, the cage becomes larger and weaker as the entropic barrier height decreases resulting in more frequent out-of-cage hopping events.
5.1. Short-time dynamics: theory and experiment
Kramers theory is used to predict the mean first passage time for a particle to displace “downhill” on the dynamic free energy from r = 0 to rloc (see Fig. 2(a) and eqn (7)) and thereby reach its transiently localized state40 and become “caged”, thereby defining the localization time, τloc. The theoretical predictions can be compared with the experimental time (or frequency) of the HF crossover obtained from LVE measurements. This comparison is shown in Fig. 4 where the behavior of ωc-HF for the entire ϕ range probed (panel (a)) and the NLE theory predictions for ωloc = 1/τloc from eqn (7) (panel(b)) are depicted. Interestingly, our experimental results reveal two exponential regimes with a much stronger exponential increase at ultra-high volume fractions. In particular, the experimental data for ϕ > 0.60 show an exponential increase as ωc-HF ∼ exp(61ϕ), while for lower volume fractions (still high in an absolute sense), the slope is a factor of 2 smaller, per ωc-HF ∼ exp(31ϕ). Data enclosed in the dashed rectangle, corresponding to the even lower volume fraction regime (0.53 < ϕ < 0.55), depart from exp(31ϕ) behavior and will be discussed later.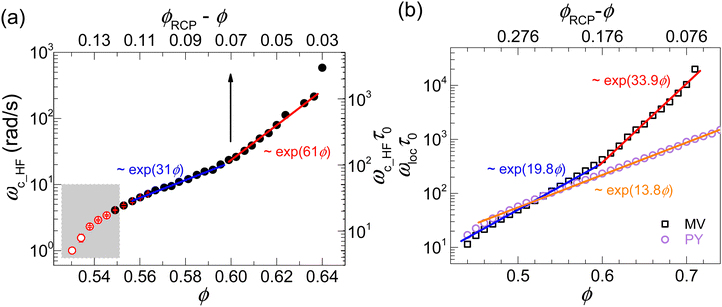 | ||
| Fig. 4 Volume fraction dependence of (a) the HF crossover frequency obtained from small amplitude oscillatory shear experiments scaled by the bare Brownian time (τ0 = R2/6D0) (right axis) and unscaled (left axis) and (b) the dimensionless localization frequency (τ0/τloc) related to the in-cage dynamics calculated from the NLE theory (eqn (7)) with MV closure approximation (open squares) and PY closure (open circles), where the y-axis (ω) is also normalized by 1/τ0. The lines in both (a) and (b) indicate the different slopes as denoted. The vertical arrow in (a) indicates the experimental distance from RCP for the critical volume fraction for the change of slopes. Data points in (a) shown in open red symbols (shaded area) are discussed below in Fig. 8. The top horizontal scale in panel (b) indicates the distance in the volume fraction from the OZ-MV theory predicted RCP volume fraction. | ||
The NLE theory predictions for monodisperse hard sphere fluids in Fig. 4(b) for the localization time τloc are expressed in units of the elementary bare time scale, which, as discussed above, for a colloidal suspension is τ0 = R2/D0 where D0 is the dilute suspension Stokes–Einstein diffusion constant. Results are plotted as the dimensionless ωloc = 1/τloc, and are in good semi-quantitative accord with the experimental data. In particular, the two exponential behaviors are predicted, and the ratio of the exponential slope parameters is comparable to that of the experimental data (a factor of ∼2), albeit smaller in an absolute magnitude sense. Moreover, the absolute value of ϕ at the crossover between the 2 exponential regimes is nearly the same for theory and experiments, occurring at a value of ϕ ∼ 0.6. Notably, this change of slope only appears when the structural input to NLE theory is from OZ-MV theory, as indicated by the black squares in Fig. 4(b). Moreover, the exponential growth laws have a theoretical basis in OZ-MV theory which predicts multiple structural metrics (including the density correlation length objectively deduced from h(r) = g(r) − 1) to grow exponentially in the metastable regime.63 On the other hand, the dynamical predictions that use OZ-PY theory structural input in Fig. 4(b) (purple circles) exhibit a single exponential regime, a direct reflection of the absence of the new emergent many-body attraction in the direct correlation function in OZ-PY theory.52 Thus, the crossover of the two exponential regimes observed in experiments is attributed to the importance of the new structural many-body effects on the dynamic caging process that leads to particle localization in the highly dense metastable or so-called deep glass state.
The theoretically predicted Gc-HF corresponds to the value of the elastic shear modulus in the localized state and is computed using eqn (8). This is effectively a MCT calculation albeit within the simpler single particle based “naïve” version.52 The theoretical dynamic shear modulus also exhibits two regimes with a change in slope at ϕs = 0.6, consistent with the experimental findings, as shown in Fig. 5. This qualitative behavior has been observed in earlier work25 and attributed to a rheological signature of the glass transition that was shifted to a higher volume fraction (compared to the nominal at ϕ ≈ 0.58) due to particle polydispersity. The present theory clearly predicts the same behavior for monodisperse spheres if the effective many body attractions in c(r) contained in the MV closure are included. Therefore, the two exponential regimes in Gc-HF(φ) and ωcr_HF(φ) observed experimentally are again a consequence of the importance of many-body effects in local packing structural correlations and elastic stress storage which is strongly coupled to slow density fluctuations. This implies that these many body interactions, although not negligible at ϕ smaller but close to 0.6 (see Fig. 2(b)), become very important at higher volume fractions and dominate at ϕ > 0.6 (see Fig. S1, ESI†).
 | ||
| Fig. 5 Volume fraction dependence of (a) the HF crossover modulus obtained from experiments with hard spheres, Rh = 264 nm, dispersed in squalene at T = 23 °C and (b) the normalized elastic shear modulus calculated theoretically from eqn (8) with MV closure approximation (open squares) and PY closure (open circles), where the y-axis is normalized over thermal energy per volume to allow comparison with theory. The lines indicate the different slopes as shown in Fig. 4. The vertical arrow in (a) indicates the experimental distance from RCP at the critical volume fraction where data exhibit a change of the power law slope. The top horizontal scale in panel (b) indicates the distance in the volume fraction from the OZ-MV theory predicted RCP volume fraction. | ||
If the experimental and theoretical results in Fig. 4 and 5 are compared quantitatively, then one should note that the shear modulus results of the latter have been extended to higher volume fractions (up to about 0.72). This high value (for all integral equation theories) is still well below the RCP volume fractions predicted by the OZ-MV theory as discussed above and in depth in ref. 52. We do not believe that this caveat affects the model predictions at lower volume fractions, as has also been discussed in ref. 49. Nevertheless, both the experimental and theoretical data plotted as a function of the distance to their corresponding RCP volume fractions are presented in Fig. 4 and 5, even though we do not expect that this distance is the controlling factor that determines the new physics for Brownian colloids. Indeed, we emphasize that the second exponential regime in G′ (as well as in the high cross over frequency) emerges from the theory well below the theoretical RCP. For the experiments, we note that although the absolute volume fraction values depend on the value of φrcp used, the relative distance to rcp, φrcp − φs, is not affected. Moreover, direct comparison of theory results for a monodisperse hard sphere model with the polydisperse colloid experimental system inevitably involves some (modest) quantitative uncertainty. It is to within these caveats that all quantitative comparisons of theory and experiments at a fixed common value of the absolute volume fraction should be viewed.
Overall, we believe that our findings above contribute to a deeper understanding of the nature and origin of the dynamical cage concept as it relates to the correlated pair structure. One can identify a characteristic crossover volume fraction of ϕ ∼ 0.6 in various dynamic properties (Fig. 4 and 5) as ϕs defined above based purely on a qualitative change of the structure and thermodynamics in the deeply metastable regime, which signals when a new type of many body effects become dominant. This deduction relates to simulation findings that indicate, irrespective of the existence or not of an MCT-like glass transition volume fraction, the emergence of a distinct type of dynamic and structural response in a high volume fraction regime approaching RCP but well below it ref. 52 and 64–66. On the experimental side, this volume fraction regime is identified with a type of nonequilibrium glassy state as defined in a practical sense where (i) crystallization (if particles are monodisperse) is practically suppressed, (ii) the α relaxation is long enough (though presumably not infinite) that is practically out of the experimental window (see extrapolation shown in Fig. S2, ESI†), and (iii) a solid like response is observed at all practical time scales. In colloidal suspensions, this volume fraction (usually denoted as ϕg) is typically estimated to be ∼0.58–0.6, with the exact value depending on the particle polydispersity, compression rate, and/or other experimental or simulation conditions.
Returning to the primary issue of the relatively short time and length scale dynamics, an important question is whether there is any intuitive theoretical understanding of why ωloc behaves so similarly to the dynamic shear modulus G in Fig. 5, a trend observed in our experiments. In order to provide an answer, we explore different technical simplifications of the NLE theory since we do not directly theoretically analyze the frequency-dependent moduli. First, we note that the theoretical result for ωlocτ0 in Fig. 4(b) was numerically calculated based on eqn (7) with a specific input from the dynamic free energy of eqn (5), an approach we call Method-I. As discussed above in the theoretical background section, Fdyn(r) contains two contributions, one favoring delocalization and one favoring localization, and both are included in Method-I. Regarding the short-time and -length scales associated with particle displacements that reach the localized caging state, activated barrier crossing processes are entirely irrelevant, suggesting that the first contribution might dominate to leading order. One can thus simplify the dynamic free energy to  . Substituting this in eqn (7), and employing the correctly computed value of rloc from the full theory, one can obtain a different estimate of ωlocτ0, an approach we call Method-II. A third approach follows from noting that the dynamic free energy near its minimum is, by definition, parabolic, per an Einstein amorphous solid. This suggests considering the harmonic approximation
. Substituting this in eqn (7), and employing the correctly computed value of rloc from the full theory, one can obtain a different estimate of ωlocτ0, an approach we call Method-II. A third approach follows from noting that the dynamic free energy near its minimum is, by definition, parabolic, per an Einstein amorphous solid. This suggests considering the harmonic approximation 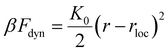 where the spring constant K0 is the curvature at the localization length scale rloc predicted by the full NLE theory, an approach we call Method-III.
where the spring constant K0 is the curvature at the localization length scale rloc predicted by the full NLE theory, an approach we call Method-III.
To test the robustness of our theoretical analyses, the results of these three different approximate methods are compared in Fig. 6. We found that Methods II and III deliver very similar results as that shown in Fig. 4(b): two exponential regimes with the crossover at nearly the same volume fraction. Moreover, all slopes in the same ϕ range are nearly identical for all three Methods. This agreement provides support for the idea that, although the theory does not explicitly analyze the frequency dependent shear modulus, the extraction of related information from the dynamic free energy reports information physically akin to the experimental ωloc, a conclusion in accord with our a priori physical expectations.
To test the level of quantitative agreement between the functional form of the predicted results based on the different methods, the results of Methods II and III are vertically shifted to align them with the predictions based on Method I. Encouragingly, the inset of Fig. 6 shows that a well-collapsed master curve is obtained. Thus, the short time or high frequency behavior associated with cage formation and the onset of particle location discussed in Fig. 4(a) from experiments and in Fig. 4(b) from the NLE theory, can be interpreted as corresponding to a physical picture of particle motion akin to a damped, Brownian, localized vibrational-like downhill motion. Finally, analytic insight can be obtained based on Method-II since the integral of eqn (7) can be exactly performed, thereby yielding 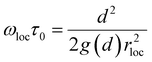 . This result provides explicit physical insight into what controls the inverse localization time: the dynamic localization length, and the contact value of g(r) which amplifies the pure solvent friction, ζSE, to that felt by a translating colloid in concentrated suspensions, ζs, due to independent binary collisions on short-length and -time scales
. This result provides explicit physical insight into what controls the inverse localization time: the dynamic localization length, and the contact value of g(r) which amplifies the pure solvent friction, ζSE, to that felt by a translating colloid in concentrated suspensions, ζs, due to independent binary collisions on short-length and -time scales 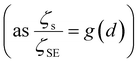 .40 In addition, it has been well established previously, both numerically and analytically,58 that the dynamic elastic shear modulus within the NMCT framework is predicted to obey a microrheology-like relationship to the inverse square localization length rloc−2, per
.40 In addition, it has been well established previously, both numerically and analytically,58 that the dynamic elastic shear modulus within the NMCT framework is predicted to obey a microrheology-like relationship to the inverse square localization length rloc−2, per 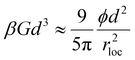 . Combining this with the above relationship
. Combining this with the above relationship  we obtain an interesting connection between the shear modulus and the short-time frequency as βGd3 ∝ ϕg(d)ωlocτ0.
we obtain an interesting connection between the shear modulus and the short-time frequency as βGd3 ∝ ϕg(d)ωlocτ0.
For further perspective, we note that in the framework of NLE theory, an analytic relationship between the localization length and the contact value g(d) was deduced58 as  . Combining this relationship with the above results of
. Combining this relationship with the above results of  and
and 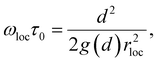 we predict that both the elastic shear modulus and the short time dimensionless frequency ωlocτ0 obey a power law relationship with the contact value g(d). This is a physically appealing result given that the rate of collisions in a hard sphere fluid scales with the contact value, and that stresses in hard sphere fluids are associated with impulsive “forces” and hence particles being in contact. This consistency physically explains why βGd3 and ωlocτ0 behave so similarly in Fig. 4 and 5, e.g., slope changes in the two exponential growth laws and crossover position.
we predict that both the elastic shear modulus and the short time dimensionless frequency ωlocτ0 obey a power law relationship with the contact value g(d). This is a physically appealing result given that the rate of collisions in a hard sphere fluid scales with the contact value, and that stresses in hard sphere fluids are associated with impulsive “forces” and hence particles being in contact. This consistency physically explains why βGd3 and ωlocτ0 behave so similarly in Fig. 4 and 5, e.g., slope changes in the two exponential growth laws and crossover position.
Furthermore, by combining the above analytic relationships, we obtain βGd3 ∝ ϕg(d)ωlocτ0 = ϕ0.33(ωlocτ0)1.33. Within the theory, this power law relationship between G and ωlocτ0 is easy to test based on numerical calculations, as shown in Fig. 7(b), where one sees that it works extremely well, although the power law exponent in numerical calculation is slightly larger, ∼1.53. To validate this power law prediction further, we plot the HF crossover modulus obtained from experiments (Gcr-HF) as a function of the crossover frequency (ωcr_HF) in Fig. 7(a). Remarkably, the data do obey a power law relationship with an exponent of 1.25, modestly lower than the numerically and analytically obtained values of ∼1.53 and ∼1.33, respectively.
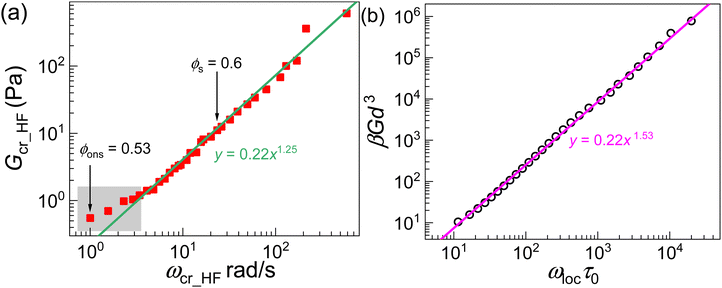 | ||
| Fig. 7 Modulus at the high frequency crossover as a function of the corresponding frequency in (a) experimental (red solid squares) and (b) theoretical (black open circles) data. The plot verifies the theoretically inspired power law relationship between the dimensionless shear modulus and ωlocτ0. Solid lines indicate the power law fits with slope values as indicated. Vertical arrows in (a) indicate the characteristic volume fractions, ϕons and ϕs, discussed in the text. The shaded area in (a) indicates the lower volume fraction regime data shown also in Fig. 4. | ||
Given the origin of the analytical theoretical relationships deduced above, we suggest that they may be relevant to other spherical particle systems with different interparticle interactions, for example in dense suspensions, sticky spheres and perhaps thermal liquids. However, it is often difficult to measure the contact value g(d) experimentally for nanoparticles or colloidal fluids, and essentially impossible for thermal liquids. Moreover, strong repulsive intermolecular interactions are generally not literally hard core. In the latter case, one could replace g(d) with the first maximum value of g(r). Future experiments can test the power law relationship of Fig. 7 in other complex systems such as viscous molecular liquids.
5.2. Long-time dynamics: experiments and theory
In contrast to the high frequency crossover, the LF crossover shifts to shorter times as the volume fraction is decreased and hence becomes visible in the frequency range of the ARES rheometer, as shown in Fig. 8 for a volume fraction of 0.539. This shift is due to cage escape as these events become faster and more frequent. Consequently, as ϕ is decreased, the two crossovers tend to approach each other along the frequency axis until they merge. This behavior is in analogy with molecular glass formers, where the slow glassy α-mode and the more fluid-like β-mode time scales converge at sufficiently high temperatures above the kinetic glass transition temperature.67The LF and HF crossover times and their merging point as derived from LVE measurements are shown in Fig. 9(a). For comparison, the short and long characteristic inverse times, 1/τloc and 1/τhop as calculated using Kramers mean first passage time theory within the NLE framework and which, as discussed above, arise from different parts of the spatially resolved dynamic free energy, are shown in Fig. 9(b). As mentioned earlier, the mean α process hopping time τhop is calculated from the same formula as the localization time (τloc in eqn (7))68,69 but the integration range is from rloc to rB corresponding to the displacement required for the particle to surmount the entropic barrier in Fig. 2(a) per activated hopping dynamics. Indeed, the microscopic times τloc and τhop increase and decrease, respectively, with dilution until they become equal at ϕ ≈ 0.43, the NMCT transition point. At this volume fraction (merging point derived from theory), the barrier approaches zero, and in its vicinity the barrier is less than kBT and hence the idea of activated dynamics loses its physical meaning.
Overall, the theoretical results are in good agreement with the experimental observations considering the practical uncertainties stemming from aging of low frequency dynamics, ϕ determination, and errors associated with the measurement itself. We interpret this volume fraction deduced from the theory as defining the onset or emergence of dynamic caging, ϕons. The corresponding experimentally deduced value where the two cross-over frequencies merge takes place at around 0.53 (with distance from RCP, ϕRCP − ϕ = 0.14) for the present polydisperse sample. We note that this is comparable with a freezing volume fraction of 0.494 (where ϕRCP − ϕ = 0.146) for monodisperse hard spheres.70,71 Therefore, freezing as deduced from the experimental linear viscoelasticity data and the onset of cage formation volume fraction, ϕons, as determined from the theoretical model, seems to coincide to the leading order with the merging of the two characteristic times scales of the in-cage localization and out-of-cage escape.
We note that the merging point in the experimental and theoretical data takes place at similar, but not the same, volume fractions. The reason is well known; the NMCT predicts the dynamic crossover to activated motion at a quantitatively too low volume fraction due to its single particle nature. This theoretical point has been analyzed in great depth long ago.40,46 Moreover, the theory studies monodisperse hard spheres, while the experiments employ polydisperse samples which generically delay the emergence of slow dynamics to higher volume fractions. From the NLE perspective, for ϕ lower than the crystallization volume fraction, the hard sphere suspension behaves in a more liquid-like manner since activated caging effects are not really important because the entropic barrier is only of order the thermal energy or less. In this regime, the non-self-consistently determined55 friction associated with independent binary collisions and weak-caging are dominant. By the same token, from the theoretical perspective, ϕons marks a dynamic crossover that signals the onset of a barrier larger than kBT, and a nontrivial separation of the minimum and maximum values of the dynamic free energy. Hence, this is the minimum volume fraction where short- and long-time dynamics begin to be separated by a caging plateau-like feature, although in practice clear observation of such a separation requires a barrier well beyond 1–2kBT, and hence a volume fraction beyond 0.5.
Below, but still near, ϕons, the experiments and theory agree that a continuous relaxation is observed, with short and long-time diffusion still distinguishable but not well separated by a clear caging plateau. Moreover, Ds and DL are comparable (although not identical) and affected by a binary collisions, hydrodynamic effects, plus the non-self-consistent weak-caging friction effects discussed above.55 Samples with volume fractions lower than ϕons, such as the sample with ϕ = 0.449 in Fig. 8, exhibit no moduli crossover, i.e. they behave in a liquid-like manner with G′′ > G′ at all time scales. Nevertheless, despite the absence of a moduli crossover, the LVE spectrum is not featureless; the moduli approach more at a certain frequency where tan(δ) attains a minimum value (see Appendix A.2). This frequency seems to set a time scale with a different volume fraction dependence than the moduli crossover frequency above ϕons. In this regime, there is a “loose caging” effect imposed by neighboring particles; constraints are very weak, with barrier below 1 kBT, and this is reflected in the dynamics with an absence of the typical caging plateau but still a clear separation of short and long diffusivity. At much lower volume fractions (not probed here), Ds and DL approach each other and eventually at the dilute limit become equal to its bare value, D0.
In addition to the near quantitative agreement of experiments with NLE theory predictions for the volume faction dependence of the high frequency cross-over, ωc-HF, and corresponding elastic modulus Gc-HF (Fig. 4 and 5), similar agreement between experiments and theory is observed for the approach of the frequencies ωc-H and ωc-LF, identified with model predictions for 1/τloc and 1/τhop, respectively. As seen in Fig. 9, these follow an exponential increase (ωc-HF or 1/τloc) or decrease (ωc-LF or 1/τhop) as a function of ϕ with larger exponents (as in the case of G′), higher for the LF (long-time hopping relaxation) than the HF (short-time cage localization time) and different in absolute values in experiments and theory. Interestingly, we found out that the LF-to-HF exponent ratio of roughly a factor of two (110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61) observed in experiments is in good accord with that predicted by theory (36.6
61) observed in experiments is in good accord with that predicted by theory (36.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19.8).
19.8).
6. Conclusions
The characteristic time scales derived from the experimental G′ and G′′ data dynamic crossovers at high and low frequencies of very dense hard sphere like colloidal suspensions have been determined for an extensive range of volume fractions. Overall, very good qualitative (and in some cases near quantitative) agreement of the distinctive trends is found with the predictions of the microscopic NLE theory, based on the spatially resolved dynamic free energy concept. The characteristic frequencies exhibit a double exponential increase with volume fraction with semi-quantitative agreement between experiments and theory. Two distinct volume fractions have been identified as ϕons and ϕs. The former, ϕons, signals the merging point of short- and long-time dynamics and marks the onset of activated caging at a volume fraction of about 0.53 in the present polydisperse particle experiments. As expected, this value lies above that predicted by the single particle dynamics NLE theory for monodisperse hard sphere fluids. The latter, ϕs, is derived in experiments from the change of a slope in the volume fraction increase of ωc-HF or Gc-HF. It can be identified as an experimental dynamic crossover volume fraction that is connected theoretically with the emergence within OZ-MV theory of a new type of structural many-body effect as manifested in effective attraction in the direct correlation function, c(r). Both the NLE theory and experiments agree that the dynamic crossover for ωc-HF and Gc-HF takes place at ϕ ∼ ϕs = 0.6. A caveat is that this quantitative agreement should be taken cautiously given that the theory analyzes monodisperse hard sphere fluids while the experimental studies polydisperse colloidal suspensions. Overall, the experiments and theory indicate the existence of a regime above ϕs with a distinct character than that of the modestly metastable fluid below, ϕs, which is crucial at very high volume fractions in determining the formation of a long-lived cages with implications for the microscopic dynamics and linear rheology. Experimentally, this is identifiable with the non-equilibrium glass in the sense that the viscoelastic response is solid like at all finite frequencies probed. On the theoretical side, it is linked to distinct dynamic, structural and thermodynamic behavior predicted to emerge in the equilibrated deeply metastable (or “deep glass”) regime associated with new many body packing effects. Thus, the question of whether ϕs can be identified with the experimentally deduced kinetic glass transition volume fraction, ϕg, where hard sphere suspensions are expected to transit to an effectively arrested state, and whether this is indeed identical with an observable property sense to the equilibrated deep glass regime analyzed by the theory, remains open.What is new in our modeling is the application of NLE theory with the accurate MV (rather than the PY) closure employed for the required structural input to make predictions consistent with our new experimental findings based on a wide volume fraction range, robust experimental data. One can also argue that this agreement provides additional new support for the dynamic free energy concept at the heart of NLE theory (which to date has focused on longer time and length scale processes than those studied here), and the important structural many body effects captured by the MV closure which are critical for quantifying dynamic caging constraints.
The presented new analytical theoretical results have also provided a microscopic physical basis for the mechanism of the experimentally observed nearly-identical behaviors of the high frequency (short time) localized dynamics time scale and the dynamic shear modulus. The physical picture is based on the small distance aspects of the spatially resolved dynamic free energy and is akin to dynamics describable as a damped, Brownian, localized vibrational-like “downhill” motion towards the transient localized state with the frictional resistance related to short time dissipative independent binary collisions.
Constraints by neighbors are evident in the rheological data at volume fractions below ϕons. The frequency where the two moduli approach more (τtanδ minima) sets a time scale, and hence provides important information that can be explored theoretically and experimentally in future work. In a similar manner, a systematic study of HF data of attractive glasses will provide insights into cage formation in the presence of competing attractive interparticle interactions and physical bond formation which reflects a rich interplay between entropic and enthalpic contributions in dynamic cage arrest. Further extension of the present work could aim to correlate ϕons and ϕs with other characteristic volume fractions in glass forming suspensions8 where it has been proposed that local domains of cooperatively moving particles become more rigid with increasing ϕ and eventually percolate leading to a glassy, solid-like response. Overall, we anticipate that the data presented here, which were obtained by simple rheological experiments and interpreted in terms of NLE theory, will aid in developing a deeper understanding of the dynamical caging mechanism and the glass transition phenomenon.
Finally, we note that previous results based on ECNLE theory63,72 showed that the mean α relaxation time of a deeply supercooled liquid (or metastable glass for hard spheres, ϕ > 0.58) can be directly related to the dynamic shear modulus in an exponential manner. This result emerges from not only τhop involving the local cage barrier, but also inclusion of the longer range collective elastic barrier which is of critical importance. Combining this exponential behavior with the relationship found here between 1/τloc and the dynamic shear modulus G′, an exponential connection between the mean α relaxation time and 1/τloc is predicted. Most importantly, both the α relaxation time and the fast process relaxation rate 1/τloc can, in principle, be measured experimentally over a wide range of degrees of metastability, which can provide an experimental test for the proposed exponential connection. This is of particular interest for supercooled thermal liquids where the measurement of G′ at relatively high and intermediate temperatures is difficult.
Author contributions
The authors contributed to this publication as follows: TA: writing – original draft, conceptualization, investigation (experiments), and data curation. BM: investigation (theory), writing – review & editing, and data curation. KS: conceptualization (theory), writing – review & editing, and supervision (theory). GP: conceptualization, writing – review & editing, and supervision.Data availability
We would like state that data for this article will be available at Zenodo data repository.Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A.1. High frequency scaling and volume fraction consistency
The weak power law dependence of G′ is sensitive to local interactions (Schroyen et al. 2019) and hence is strongly affected by the steric layer of colloids that induce deviations from ideal hard sphere interactions.73,74 The slope of G′ at frequencies above the HF crossover is typically 0.3 for hairy (sterically stabilized) particles.39,75 Furthermore, the volume fraction response of the total complex viscosity deduced at high frequencies can be used to determine the effective volume fraction of the suspension.The uncertainties and the various methods of ϕ determination are well discussed in the literature.76 Given that all samples were prepared from the same initial batch by sequential dilution, the uncertainties in the relative ϕ are minimized. The reduced high frequency viscosity is given by  where ηs = 13.3 mPa s for squalene at 23 °C, and
where ηs = 13.3 mPa s for squalene at 23 °C, and  is the limiting value of the real part of the complex viscosity obtained from oscillatory shear. Once this is known, the theoretical volume fraction can be calculated77,78 according to:
is the limiting value of the real part of the complex viscosity obtained from oscillatory shear. Once this is known, the theoretical volume fraction can be calculated77,78 according to:
 | (9) |
 as the plateau value has not been fully attained (Fig. 10) or to particle polydispersity that would affect the quantitative accuracy of eqn (9). However, the relative volume fractions are proven to be consistent. This indicates reasonably good agreement of experimental data and theoretical predictions with a potential shift of experimental volume fractions by 0.03 would not significantly change any of the main findings of this work.
as the plateau value has not been fully attained (Fig. 10) or to particle polydispersity that would affect the quantitative accuracy of eqn (9). However, the relative volume fractions are proven to be consistent. This indicates reasonably good agreement of experimental data and theoretical predictions with a potential shift of experimental volume fractions by 0.03 would not significantly change any of the main findings of this work.
| Determined from RCP | Prediction of eqn (9) | Deviation |
|---|---|---|
| 0.64 | 0.665 | 0.025 |
| 0.62 | 0.649 | 0.029 |
| 0.609 | 0.639 | 0.029 |
| 0.6 | 0.628 | 0.028 |
Appendix A.2 Low volume fraction (ϕ < ϕons) samples with no dynamic crossover
At volume fractions below ϕons (∼0.53 in experiments, see Fig. 8), the dynamic moduli do not exhibit a crossover, but they do approach each other at a certain frequency and this is clearly detected as a minimum of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = G′′/G′ as shown in Fig. 11(a). This frequency marks a time scale defined as τtanδ = 1/ωtanδ. At this time scale, the constraints felt by a tagged particle due to its neighboring particles are maximized, and this can be viewed as a “loose caging effect”. At shorter and longer times, particle mobility appears higher. Interestingly, ωtanδ exhibits the opposite trend from ωc-HF as shown in Fig. 11(b). This suggests that the characteristic time is related to the transition from in-cage (β-relaxation) to out-of-cage (α-relaxation) motion. Below ϕons, this is identified in experiments by τtanδ increasing with φ, whereas above ϕons, ωc-HF is related to the time scale of cage exploration decreases with φ as shown in Fig. 8. Such non-monotonic behavior, with a maximum at ϕons, is in reminiscent of the time scale τB determined from dynamic light scattering data (or from the self-intermediate scattering function) as the transition time scale between α and β-relaxations around the glass transition volume fraction by van Megen & Underwood.79
δ = G′′/G′ as shown in Fig. 11(a). This frequency marks a time scale defined as τtanδ = 1/ωtanδ. At this time scale, the constraints felt by a tagged particle due to its neighboring particles are maximized, and this can be viewed as a “loose caging effect”. At shorter and longer times, particle mobility appears higher. Interestingly, ωtanδ exhibits the opposite trend from ωc-HF as shown in Fig. 11(b). This suggests that the characteristic time is related to the transition from in-cage (β-relaxation) to out-of-cage (α-relaxation) motion. Below ϕons, this is identified in experiments by τtanδ increasing with φ, whereas above ϕons, ωc-HF is related to the time scale of cage exploration decreases with φ as shown in Fig. 8. Such non-monotonic behavior, with a maximum at ϕons, is in reminiscent of the time scale τB determined from dynamic light scattering data (or from the self-intermediate scattering function) as the transition time scale between α and β-relaxations around the glass transition volume fraction by van Megen & Underwood.79
Acknowledgements
We thank A. B. Schofield (University of Edinburgh, UK) for kindly providing the PMMA particles. We also thank Aris Papagianopoulos (EIE, Greece) for data conversion in Fig. 1. GP and TA acknowledge support from the Twinning project FORGREENSOFT (Number: 101078989 under HORIZON WIDERA-2021-ACCESS-03). KSS acknowledges support from the Army Research Office via a MURI grant with Contract No. W911NF-21-0146. A CC-BY public copyright license has been applied by the authors to the present document and will be applied to all subsequent versions up to the Author Accepted Manuscript (alternatively final peer-reviewed manuscript accepted for publication) arising from this submission, in accordance with the grant's open access conditions.References
- J. Mewis and N. J. Wagner, Colloidal suspension rheology, Cambridge University Press, Cambridge, 2012, vol. 10 Search PubMed.
- W. B. Russel, W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal dispersions, Cambridge University Press, 1991 Search PubMed.
- N. J. Wagner and J. Mewis, Theory and applications of colloidal suspension rheology, Cambridge University Press, 2021 Search PubMed.
- C. P. Royall, P. Charbonneau, M. Dijkstra, J. Russo, F. Smallenburg and T. Speck, et al., Colloidal hard spheres: triumphs, challenges, and mysteries, Rev. Mod. Phys., 2024, 96(4), 045003 CrossRef.
- L. Berthier and G. Biroli, Theoretical perspective on the glass transition and amorphous materials, Rev. Mod. Phys., 2011, 83(2), 587–645 CrossRef.
- L. Berthier and D. R. Reichman, Modern computational studies of the glass transition, Nat. Rev. Phys., 2023, 1–15 Search PubMed.
- G. Biroli and J. P. Garrahan, Perspective: the glass transition, J. Chem. Phys., 2013, 138(12), 12A301 CrossRef PubMed.
- B. Li, K. Lou, W. Kob and S. Granick, Anatomy of cage formation in a two-dimensional glass-forming liquid, Nature, 2020, 587(7833), 225–229 CrossRef PubMed.
- A. Vila-Costa, M. Gonzalez-Silveira, C. Rodríguez-Tinoco, M. Rodríguez-López and J. Rodriguez-Viejo, Emergence of equilibrated liquid regions within the glass, Nat. Phys., 2023, 19(1), 114–119 Search PubMed.
- O. Dauchot, F. Ladieu and C. P. Royall, The glass transition in molecules, colloids and grains: universality and specificity, C. R. Phys., 2024, 24(S1), 25–56 Search PubMed.
- L. Antl, J. W. Goodwin, R. D. Hill, R. H. Ottewill, S. M. Owens and S. Papworth, et al., The preparation of poly(methyl methacrylate) latices in non-aqueous media, Colloids Surf., 1986, 17(1), 67–78 CrossRef.
- G. Bryant, S. R. Williams, L. Qian, I. K. Snook, E. Perez and F. Pincet, How hard is a colloidal “hard-sphere” interaction?, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66(1), 060501 CrossRef PubMed.
- W. J. Frith, T. A. Strivens and J. Mewis, Dynamic mechanical properties of polymerically stabilized dispersions, J. Colloid Interface Sci., 1990, 139(1), 55–62 CrossRef.
- W. Van Megen, Comparison of dynamic light scattering measurements and mode-coupling theory for the tagged particle dynamics of a hard-sphere suspension, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76(6), 061401 CrossRef.
- P. N. Pusey, Liquids, freezing and the glass transition, North-Holland, Amsterdam, 1991 Search PubMed.
- P. N. Pusey, Colloidal glasses, J. Phys.: Condens. Matter, 2008, 20(49), 494202 CrossRef.
- M. D. Ediger and P. Harrowell, Perspective: supercooled liquids and glasses, J. Chem. Phys., 2012, 137(8), 080901 CrossRef PubMed.
- A. Donev, S. Torquato and F. H. Stillinger, Pair correlation function characteristics of nearly jammed disordered and ordered hard-sphere packings, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71(1), 011105 CrossRef.
- W. Gotze and L. Sjogren, Relaxation processes in supercooled liquids, Rep. Prog. Phys., 1992, 55(3), 241 CrossRef.
- J. F. Brady, The rheological behavior of concentrated colloidal dispersions, J. Chem. Phys., 1993, 99(1), 567–581 CrossRef.
- J. K. Dhont, An introduction to dynamics of colloids, Elsevier, 1996, vol. 2 Search PubMed.
- W. van Megan, S. M. Underwood, R. H. Ottewill, N. S. J. Williams and P. N. Pusey, Particle diffusion in concentrated dispersions, Faraday Discuss. Chem. Soc., 1987, 83, 47–57 RSC.
- G. Nägele, Viscoelasticity and diffusional properties of colloidal model dispersions, J. Phys.: Condens. Matter, 2002, 15(1), S407 CrossRef.
- G. P. Johari, Intrinsic mobility of molecular glasses, J. Chem. Phys., 1973, 58(4), 1766–1770 CrossRef.
- N. Koumakis, A. Pamvouxoglou, A. S. Poulos and G. Petekidis, Direct comparison of the rheology of model hard and soft particle glasses, Soft Matter, 2012, 8(15), 4271 RSC.
- T. G. Mason and D. A. Weitz, Linear viscoelasticity of colloidal hard sphere suspensions near the glass transition, Phys. Rev. Lett., 1995, 75(14), 2770 CrossRef PubMed.
- T. G. Mason and D. A. Weitz, Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids, Phys. Rev. Lett., 1995, 74(7), 1250 CrossRef CAS PubMed.
- J. Reinhardt, F. Weysser and M. Fuchs, Comment on “Probing the equilibrium dynamics of colloidal hard spheres above the mode-coupling glass transition”, Phys. Rev. Lett., 2010, 105(19), 199604 CrossRef CAS.
- K. S. Schweizer and E. J. Saltzman, Entropic barriers, activated hopping, and the glass transition in colloidal suspensions, J. Chem. Phys., 2003, 119(2), 1181–1196 CrossRef CAS.
- G. Brambilla, D. El Masri, M. Pierno, L. Berthier, L. Cipelletti and G. Petekidis, et al., Probing the equilibrium dynamics of colloidal hard spheres above the mode-coupling glass transition, Phys. Rev. Lett., 2009, 102(8), 085703 CrossRef CAS.
- W. Van Megen, T. C. Mortensen, S. R. Williams and J. Müller, Measurement of the self-intermediate scattering function of suspensions of hard spherical particles near the glass transition, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58(5), 6073 CrossRef CAS.
- E. R. Weeks and D. A. Weitz, Properties of cage rearrangements observed near the colloidal glass transition, Phys. Rev. Lett., 2002, 89(9), 095704 CrossRef PubMed.
- J. E. Hallett, F. Turci and C. P. Royall, Local structure in deeply supercooled liquids exhibits growing lengthscales and dynamical correlations, Nat. Commun., 2018, 9(1), 3272 CrossRef.
- A. J. Banchio, G. Nägele and J. Bergenholtz, Viscoelasticity and generalized Stokes–Einstein relations of colloidal dispersions, J. Chem. Phys., 1999, 111(18), 8721–8740 CrossRef CAS.
- M. Siebenbürger, M. Fuchs, H. Winter and M. Ballauff, Viscoelasticity and shear flow of concentrated, noncrystallizing colloidal suspensions: comparison with mode-coupling theory, J. Rheol., 2009, 53(3), 707–726 CrossRef.
- B. Schroyen, D. Vlassopoulos, P. Van Puyvelde and J. Vermant, Bulk rheometry at high frequencies: a review of experimental approaches, Rheol. Acta, 2020, 59, 1–22 CrossRef CAS.
- T. Hecksher, D. H. Torchinsky, C. Klieber, J. A. Johnson, J. C. Dyre and K. A. Nelson, Toward broadband mechanical spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(33), 8710–8715 CrossRef PubMed.
- Q. Li, K. A. Dennis, Y. F. Lee and E. M. Furst, Two-point microrheology and diffusing wave spectroscopy, J. Rheol., 2023, 67(6), 1107–1118 CrossRef.
- T. Athanasiou, G. K. Auernhammer, D. Vlassopoulos and G. Petekidis, A high-frequency piezoelectric rheometer with validation of the loss angle measuring loop: application to polymer melts and colloidal glasses, Rheol. Acta, 2019, 58(9), 619–637 CrossRef.
- E. J. Saltzman and K. S. Schweizer, Transport coefficients in glassy colloidal fluids, J. Chem. Phys., 2003, 119(2), 1197–1203 CrossRef.
- K. S. Schweizer, Derivation of a microscopic theory of barriers and activated hopping transport in glassy liquids and suspensions, J. Chem. Phys., 2005, 123(24), 244501 CrossRef.
- T. G. Mason, Estimating the viscoelastic moduli of complex fluids using the generalized Stokes–Einstein equation, Rheol. Acta, 2000, 39(4), 371–378 CrossRef.
- L. Cipelletti and L. Ramos, Slow dynamics in glassy soft matter, J. Phys.: Condens. Matter, 2005, 17(6), R253 CrossRef.
- T. M. Squires and T. G. Mason, Fluid mechanics of microrheology, Annu. Rev. Fluid Mech., 2010, 42, 413–438 CrossRef.
- D. El Masri, G. Brambilla, M. Pierno, G. Petekidis, A. B. Schofield and L. Berthier, et al., Dynamic light scattering measurements in the activated regime of dense colloidal hard spheres, J. Stat. Mech.: Theory Exp., 2009, 2009(07), P07015 Search PubMed.
- E. J. Saltzman and K. S. Schweizer, Activated hopping and dynamical fluctuation effects in hard sphere suspensions and fluids, J. Chem. Phys., 2006, 125(4), 44509 CrossRef PubMed.
- C. Luo and L. M. Janssen, Glassy dynamics of sticky hard spheres beyond the mode-coupling regime, Soft Matter, 2021, 17(33), 7645–7661 RSC.
- J. P. Hansen and I. R. McDonald, Theory of simple liquids: with applications to soft matter, Academic Press, 2013 Search PubMed.
- L. Verlet, Integral equations for classical fluids: I. The hard sphere case, Mol. Phys., 1980, 41(1), 183–190 CrossRef.
- L. Verlet, Integral equations for classical fluids: II. Hard spheres again, Mol. Phys., 1981, 42(6), 1291–1302 CrossRef.
- Y. Zhou, B. Mei and K. S. Schweizer, Integral equation theory of thermodynamics, pair structure, and growing static length scale in metastable hard sphere and Weeks-Chandler-Andersen fluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2020, 101(4), 042121 CrossRef PubMed.
- S. Chaki, B. Mei and K. S. Schweizer, Theoretical analysis of the structure, thermodynamics, and shear elasticity of deeply metastable hard sphere fluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2024, 110(3), 034606 CrossRef.
- P. Hänggi, P. Talkner and M. Borkovec, Reaction-rate theory: fifty years after Kramers, Rev. Mod. Phys., 1990, 62(2), 251 CrossRef.
- H. A. Kramers, Brownian motion in a field of force and the diffusion model of chemical reactions, Physica, 1940, 7(4), 284–304 CrossRef.
- R. Verberg, I. M. De Schepper and E. G. D. Cohen, Viscosity of colloidal suspensions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 55(3), 3143 CrossRef.
- B. Mei, Y. Zhou and K. S. Schweizer, Thermodynamics–structure–dynamics correlations and nonuniversal effects in the elastically collective activated hopping theory of glass-forming liquids, J. Phys. Chem. B, 2020, 124(28), 6121–6131 CrossRef.
- S. Mirigian and K. S. Schweizer, Elastically cooperative activated barrier hopping theory of relaxation in viscous fluids. I. General formulation and application to hard sphere fluids, J. Chem. Phys., 2014, 140(19), 194506 CrossRef PubMed.
- K. S. Schweizer and G. Yatsenko, Collisions, caging, thermodynamics, and jamming in the barrier hopping theory of glassy hard sphere fluids, J. Chem. Phys., 2007, 127(16), 164505 CrossRef.
- W. Schaertl and H. Sillescu, Brownian dynamics of polydisperse colloidal hard spheres: equilibrium structures and random close packings, J. Stat. Phys., 1994, 77, 1007–1025 CrossRef.
- M. Hermes and M. Dijkstra, Jamming of polydisperse hard spheres: the effect of kinetic arrest, Europhys. Lett., 2010, 89(3), 38005 CrossRef.
- P. Ballesta and G. Petekidis, Creep and aging of hard-sphere glasses under constant stress, Phys. Rev. E, 2016, 93, 042613 CrossRef.
- A. R. Jacob, E. Moghimi and G. Petekidis, Rheological signatures of aging in hard sphere colloidal glasses, Phys. Fluids, 2019, 31(8), 087103 CrossRef.
- B. Mei, Y. Zhou and K. S. Schweizer, Experimental test of a predicted dynamics–structure–thermodynamics connection in molecularly complex glass-forming liquids, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(18), e2025341118 CrossRef.
- S. Torquato, T. M. Truskett and P. G. Debenedetti, Is random close packing of spheres well defined?, Phys. Rev. Lett., 2000, 84(10), 2064 CrossRef PubMed.
- R. D. Kamien and A. J. Liu, Why is Random Close Packing Reproducible?, Phys. Rev. Lett., 2007, 99(15), 155501 CrossRef PubMed.
- G. Parisi and F. Zamponi, Mean-field theory of hard sphere glasses and jamming, Rev. Mod. Phys., 2010, 82(1), 789–845 CrossRef.
- R. G. Larson, The structure and rheology of complex fluids, Oxford university press, New York, 1999, vol. 150 Search PubMed.
- B. Mei, T. W. Lin, G. S. Sheridan, C. M. Evans, C. E. Sing and K. S. Schweizer, Structural relaxation and vitrification in dense cross-linked polymer networks: simulation, theory, and experiment, Macromolecules, 2022, 55(10), 4159–4173 CrossRef.
- Y. Zhou, B. Mei and K. S. Schweizer, Activated relaxation in supercooled monodisperse atomic and polymeric WCA fluids: simulation and ECNLE theory, J. Chem. Phys., 2022, 156(11), 114901 CrossRef PubMed.
- G. L. Hunter and E. R. Weeks, The physics of the colloidal glass transition, Rep. Prog. Phys., 2012, 75(6), 066501 CrossRef PubMed.
- P. N. Pusey, Colloidal Suspensions in Liquids, Freezing, and the Glass Transition, Les Houches, 1991 Search PubMed.
- B. Mei, Y. Zhou and K. S. Schweizer, Experimental tests of a theoretically predicted noncausal correlation between dynamics and thermodynamics in glass-forming polymer melts, Macromolecules, 2021, 54(21), 10086–10099 CrossRef.
- A. Ikeda, L. Berthier and P. Sollich, Disentangling glass and jamming physics in the rheology of soft materials, Soft Matter, 2013, 9(32), 7669 RSC.
- J. Mewis and P. Haene, Prediction of rheological properties in polymer colloids, Wiley Online Library, 1993. pp. 213–225 Search PubMed.
- T. Shikata and D. S. Pearson, Viscoelastic behavior of concentrated spherical suspensions, J. Rheol., 1994, 38(3), 601–616 CrossRef.
- W. C. Poon, E. R. Weeks and C. P. Royall, On measuring colloidal volume fractions, Soft Matter, 2012, 8(1), 21–30 RSC.
- Z. Cheng, J. Zhu, P. M. Chaikin, S. E. Phan and W. B. Russel, Nature of the divergence in low shear viscosity of colloidal hard-sphere dispersions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65(4), 041405 CrossRef PubMed.
- A. Sierou and J. F. Brady, Accelerated Stokesian Dynamics simulations, J. Fluid Mech., 2001, 448 Search PubMed.
- W. Van Megen and S. M. Underwood, Glass transition in colloidal hard spheres: measurement and mode-coupling-theory analysis of the coherent intermediate scattering function, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1994, 49(5), 4206 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01428f |
| This journal is © The Royal Society of Chemistry 2025 |