Open Access Article
Open Access ArticleNonlinear behavior of stochastic athermal fiber networks with elastic–plastic fibers†
Syed N.
Amjad
 ,
Nishan
Parvez
,
Nishan
Parvez
 and
Catalin R.
Picu
and
Catalin R.
Picu
 *
*
Department of Mechanical, Aerospace and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180, USA. E-mail: picuc@rpi.edu; Tel: +1 518 276 2195
First published on 19th March 2025
Abstract
Stochastic fiber networks form the structural component of network materials, which are broadly encountered in engineering and biology. Apparent elastic–plastic behavior, characterized by a yield point and softening at larger strains, is observed in some of these materials. A range of mechanisms, some of which being unrelated to fiber plasticity, may cause this behavior. In this work we investigate network plasticity caused by the plastic deformation of fibers and develop a comprehensive perspective on its relationship with network structural parameters. We determine the scaling of the yield stress and yield strain with network parameters emphasizing differences between the affine and non-affine deformation regimes. The non-linear response of the network is more complex when fiber plasticity takes place than in the purely elastic case. We describe four non-linear regimes and their dependence on network parameters. Further, we evaluate the dissipation and residual strains resulting upon loading–unloading cycles for a variety of networks and discuss design strategies for maximizing energy dissipation. Finally, we provide guidelines for the interpretation of experimental results and discuss ways to distinguish between various mechanisms that may cause a yield point and apparent elastic–plastic behavior.
1. Introduction
Many biological and man-made materials have a stochastic network of fibers as their main structural component. Examples include the extracellular matrix,1 connective tissue2 and blood vessel walls,3 whose mechanical behavior is defined by their underlying collagen and elastin networks, as well as nonwovens,4 paper and cellulose products5 and various types of nanopapers6–12 made from diverse types of fibers including polymeric, cellulose, chitin and carbon nanotubes. These diverse materials have mechanical behavior defined by the respective networks, a unifying view of which is presented in ref. 13.When tested in shear or uniaxial tension, network materials exhibit one of two types of response: biological materials show, in general, hyperelastic-type behavior, with increasing tangent stiffness with stretch,14–16 while many of the engineering materials listed in the previous paragraph show a concave stress–stretch curve, with an apparent yield point followed by softening.17–21
The non-linear behavior of networks with linear elastic fibers and non-dissociating crosslinks is generally understood.22–25 The response is linear elastic at small strains and is characterized by Young's modulus E0 (regime I). Exponential stiffening is observed in regime II; in this regime, the tangent stiffness, Et, is proportional to the (nominal) stress, S, Et = dS/dλ ∼ S (λ is the stretch in uniaxial loading, which is related to the uniaxial strain, ε, as λ = 1 + ε). A subsequent regime III of power law stiffening is reported at larger stretches when the nominal stress is used, but this regime is absent if the Cauchy stress is used instead.26 These conclusions apply to tensile and shear loading.
Occurrence of diffuse damage may reduce the tangent stiffness in any of the three regimes. Localization of diffuse damage leads to the emergence of a peak stress in the nominal stress–stretch curve, S(λ), and eventually to global failure.27,28 Strain localization is precluded in network materials without damage due to the strong stiffening.
The key parameters used to define the network structure include the network density (total length of fiber per unit volume, in 3D, or area, in 2D), ρ, the crosslink number density, ρb, the mean connectivity (average number of fiber segments connected at a crosslink), z, and fiber properties (e.g. for linear elastic fibers of circular cross-section, the fiber material modulus, Ef, and the diameter, d). This is a minimum set of structural parameters for networks without preferential fiber orientation, although the structure being stochastic, additional parameters may be defined. These parameters may be used to form non-dimensional groups which are then placed in relation to the descriptors of macroscopic behavior,29–31 such as E0 and Et. For the type of networks considered in this work, the most useful such parameter is w = log10(ρd2).32,33 It has been shown30,34 that deformation is approximately affine and E0/Ef ∼ ρd2 when w is large, while in the opposite situation, deformation is non-affine and E0/Ef ∼ ρxd4, with x = 2 for the type of networks considered here. Exponent x depends on the network structure and the dimensionality of the embedding space.29–33,35 The affine-non-affine transition takes place in the vicinity of a threshold w0; w0 = −0.6 for the networks considered here, as discussed further in Section 3.2. The fact that E0 ∼ Efd2 ∼ EfAf (where Af is the cross-sectional area of fibers) in the affine limit, for w > w0, implies that the primary deformation mode of fibers is axial. Likewise, E0 ∼ Efd4 ∼ EfIf (where If is the axial moment of inertia with respect to one of the centroidal axes of the fiber cross-section) in non-affine cases, for w < w0, implies that fibers deform predominantly in bending.
Engineering athermal network materials, such as nonwovens4,36–39 and nanopapers,6–12,40 exhibit softening at a point of the stress–stretch curve, S(λ), that resembles the yield point of metals, Sny, while the peak stress, Snu, is larger and occurs at larger stretches. This apparent yield point was attributed heuristically to the onset of fiber plasticity. However, other mechanisms may lead to the same macroscopic behavior. For example, it was shown that friction in nonwoven mats of thin elastic fibers leads to a yield point phenomenon and the corresponding yield stress increases with increasing friction.41 This mechanism also provides strain hardening beyond the yield point. Cohesive interactions between fibers promote fiber bundling and the organization of the network of fibers into a network of fiber bundles.42 The mechanical behavior of such structures is controlled mainly by cohesive forces at relatively small stretches, and by the network at larger stretches. However, it was shown that cohesive interactions may also lead to the emergence of an apparent yield point which increases with increasing the strength of cohesion.43 Stiffening may be observed beyond the yield point due to the continued fiber alignment during straining. Yet, another type of yield point phenomenon is observed in interpenetrating network (IPN).44,45 These are networks composed of two sub-networks, each being formed by a different type of fibers (or molecules, in the case of molecular IPN), with both sub-networks percolating the problem domain. The two sub-networks may be crosslinked to each other, or many be entirely independent (although excluded volume interactions, at contacts between fibers, may take place). At small strains, the sub-networks forming the IPN are mechanically active and act in parallel leading to large stiffness. The tangent stiffness drops abruptly when the network of lower strength breaks, which leads to the emergence of an apparent yield point.46,47 This provides additional kinematic freedom to the remaining stronger network which may exhibit stiffening beyond the yield point.
Some of these mechanisms may be ruled out in specific material cases. For example, if one does not work with IPNs and the fiber diameter is rather large (e.g. d > 10 μm), inter-fiber cohesion makes a weak contribution to the overall mechanics, but friction remains a factor. These conditions apply to nonwovens, which generally exhibit a well-defined yield point, large hysteresis in loading–unloading cycles, and residual strain upon unloading. Therefore, the yield point observed in nonwovens4,37–39 may be due to either or both the plastic deformation of fibers and/or friction. A yield point and loading–unloading hysteresis are observed in a cellulose networks,28,48 particularly in conditions of elevated humidity; in this case yield is likely due to the plasticity of fibers and crosslinks. Yielding observed in cellulose nanopaper6,7 may be due to both cohesion and the plastic deformation of fibers. Collagen is known to deform plastically due to the relative sliding of micro-fibrils within collagen fibers.49 This was observed to lead to plastic deformation of collagen networks.50,51 In most of these cases it is difficult to determine experimentally which mechanism controls the yield point.
Several works have been dedicated to exploring the effect of fiber plasticity on the behavior of the network. 2D models of Mikado networks of elastic–plastic fibers have been considered in ref. 52 and 53. These models were defined in the affine range of the network. It is reported that the network yield strain is approximately equal to the fiber yield strain and the yield stress increases in proportion with the network stiffness. These models exhibit large residual strains upon unloading. Similar models were used in ref. 54 to evaluate the effect of fiber crimp on the elastic–plastic transition, but since these models are also affine, similar scaling results are obtained. Quasi-2D mats of elastic–plastic fibers with damage were modeled in ref. 28, 55 and 56, and probed both in tension and compression.56 The focus of these works was not on evaluating the elastic–plastic transition, and parameters were selected such that damage obscured the contribution of fiber plasticity. Non-affine 3D network models (diluted periodic structures) of elastic–plastic fibers were considered in ref. 57 as being representative for collagen-based extracellular matrix. This study indicates that only a small fraction of fibers become plastic and residual strains upon unloading are small. The non-linear response was strongly influenced by the stiffening rate of the fiber material, which makes the interpretation of the response difficult, but these aspects were not analyzed in detail. The respective study focuses on the extracellular matrix-mediated cell–cell interaction and not on scaling relations between network behavior and system parameters.
Although not leading to a yield point, the coupling of the fiber material non-linearity with the intrinsic geometric non-linearity of the network deformation modifies the overall, network scale non-linear behavior (relative to the case in which the fiber material is linear elastic). This has been studied in many works, including.55,58–60
In the work reported here we consider fiber plasticity in isolation from other mechanisms that may cause an apparent yield point and determine the effect of various system parameters on the yield stress, Sny, and stretch, λny, and on the non-linear deformation of the network. We distinguish between two types of network-scale elastic–plastic behaviors, applicable to affine and non-affine networks, respectively. We explain the sharp distinction between the typical response of dense and densely crosslinked networks, such as nanopapers and some nonwovens,38,52,61 and that of lower density networks composed of thin fibers, such as collagen gels and connective tissue.22,23,62,63 The network yield strain, εny, is identical to the yield strain of the fibers, εfy, if the network is affine, εny = λny − 1 = εfy, and it is larger than εfy if the network is non-affine. As the degree of non-affinity increases (w decreases, i.e. the network density decreases and/or fibers are rendered softer in bending), λny increases and yielding may never happen within the range of stretches experienced by real network materials. Further, we characterize the complex non-linear response, which combines features of the networks of linear elastic fibers with aspects associated with fiber plasticity and compute the energy dissipation during loading–unloading cycles in terms of network parameters. These results provide a unifying interpretation of phenomenological observations made with different network materials and facilitate the identification of the mechanism causing a yield point-like phenomenon in specific experimental situations.
2. Model definition and parametric space
We consider 3D athermal networks of initially straight cylindrical fibers having identical diameter, d. The crosslinks transmit forces and moments between fibers and are of ‘welded’ type, i.e. the angles formed by pairs of fibers connected at a crosslink are maintained fixed. No crosslink failure and dissociation/association behaviors are considered. Fibers may deform in the axial, bending, torsion and shear modes. The crosslinks store no strain energy. There is no embedding matrix to restrict the bending deformation of fibers. Contacts between fibers occur infrequently when loading in tension structures of low fiber volume fraction (the volume fraction of the fibers is φ = ρAf = ρπd2/4), as in the models considered here.35 Therefore, in this work we do not account for contact formation during loading.A Voronoi tessellation procedure is used to generate the network. Points are generated at random in a cubic domain of edge length 2L and are used as seeds for the tessellation. The resulting edges are considered fibers and the nodes are crosslinks. Hence, each fiber has two crosslinks, one at each end. The model thus generated is then trimmed to a cubic box of edge length, L to reduce boundary effects associated with the tessellation procedure. The fiber orientation distribution is uniform over the unit sphere. The density, ρ, is defined as the total length of fibers divided by L3. The nominal connectivity number for this network is z = 4, i.e. four fibers merge into each crosslink. Fiber length distribution is Poisson and the mean of this distribution, i.e. the mean segment length, lc, is related to the density as ρlc2 ≈ 1.64
The fiber material is considered elastic–plastic. The linear elastic component is characterized by Young's modulus Ef and Poisson ratio νf. Plastic deformation begins once the fiber material yield stress is reached, Sfy. The yield strain is εfy = Sfy/Ef and the corresponding fiber stretch at yield is λfy = εfy + 1. Linear hardening defines the plastic component of fiber behavior, with the tangent stiffness Efp being constant. The non-dimensional hardening modulus is Ēfp = Efp/Ef. Fig. S1 (ESI†) shows a typical stress–stretch curve of the fiber material.
Fibers are modeled as Timoshenko beams and represented by B31 elements in Abaqus. The solution is obtained with the commercial code Abaqus 2022 (ver. 6.22).65 An explicit method based on forward marching integration is used to obtain the solution. Quasi-static conditions are ensured by applying adequate damping such to keep the effect of inertia forces vanishingly small and the kinetic energy smaller than 5% of the strain energy.
The response is determined by applying uniaxial tension. Displacements are imposed in the loading direction, x1, on two opposing faces of the cubic model: the nodes on one face are held fixed in the x1 direction, while the x1 displacement of the nodes on the opposite face is prescribed. The lateral faces of normal x2 and x3 are kept traction free (no specified displacements or rotations). The degrees of freedom of the nodes on the two faces of normal x1 in directions x2 and x3 are also kept traction free. The rotation of fiber ends co-located with the model boundary is not constrained (and hence no moments are applied). We compute the nominal (first Piola–Kirchoff) stress, S, based on boundary tractions (computed forces corresponding to the degrees of freedom for which displacements are imposed) and the area of the respective model faces in the undeformed configuration. S has only one non-zero component, S11, the normal stress in the loading direction, which is denoted below by Sn, for brevity. The fiber material stiffness, Ef, is taken as the unit of stress. Hence, the stiffness and all stress-like quantities are normalized by Ef.
The values of structural parameters are varied in a broad range: the non-dimensional parameter w ranges from −0.63 to −5.03; this variation is realized by changing ρ by a factor of 3 and the fiber diameter by two orders of magnitude. d/lc varies by a factor of 40, ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = Sfy/Ef ranges from 0.0009 to 0.015, while Ēfp ranges from 0.016 to 0.5.
fy = Sfy/Ef ranges from 0.0009 to 0.015, while Ēfp ranges from 0.016 to 0.5.
This parametric space is sufficiently broad to be representative of many network materials. For example, polymer fiber nonwovens have basis weight in the range 10 to 300 g m−2 which, with a density of the polymer of approximately 0.9 g cm−3, is equivalent to w ∈ (−4.8, −3). Fiber properties vary from polymer to polymer, e.g. for polypropylene fibers the stiffness is in the range Ef ∈ (600, 2000) MPa, the yield stress is Sfy ∈ (20, 60) MPa, (![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy ∈ (0.01, 0.1)) and Ēfp ∈ (0.01, 0.5), with material parameters from ref. 66 and 67. Paper has a basis weight in the range 40 to 200 g m−2 which corresponds approximately to w ∈ (−4.5, −3.5). With the data from ref. 28 one obtains Ēfp ∈ (0.1, 0.5) and
fy ∈ (0.01, 0.1)) and Ēfp ∈ (0.01, 0.5), with material parameters from ref. 66 and 67. Paper has a basis weight in the range 40 to 200 g m−2 which corresponds approximately to w ∈ (−4.5, −3.5). With the data from ref. 28 one obtains Ēfp ∈ (0.1, 0.5) and ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy ≅ 0.005. Collagen fibers in blood vessels have diameter in the range 3 to 25 μm;68 the fibrils forming the fibers have diameters in the range 20 to 500 nm. Typical collagen concentration of 0.5 to 4 mg ml−1 corresponds to w ∈ (−3.3, −2), assuming a density of the collagen within fibers of 0.5 to 1 g cm−3. Individual fibrils have been tested and the following ranges are reported: Ef ∈ (2, 5) GPa, Efp ∈ (1, 2) GPa, Sfy ∈ (100, 200) MPa,69 which correspond to Ēfp ∈ (0.2, 1) and
fy ≅ 0.005. Collagen fibers in blood vessels have diameter in the range 3 to 25 μm;68 the fibrils forming the fibers have diameters in the range 20 to 500 nm. Typical collagen concentration of 0.5 to 4 mg ml−1 corresponds to w ∈ (−3.3, −2), assuming a density of the collagen within fibers of 0.5 to 1 g cm−3. Individual fibrils have been tested and the following ranges are reported: Ef ∈ (2, 5) GPa, Efp ∈ (1, 2) GPa, Sfy ∈ (100, 200) MPa,69 which correspond to Ēfp ∈ (0.2, 1) and ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy ∈ (0.02, 0.1).
fy ∈ (0.02, 0.1).
3. Results and discussion
3.1 Qualitative dependence of the response on network non-affinity
To qualitatively demonstrate how the network response changes with the degree of non-affinity of the network, Fig. 1 shows stress–stretch curves for networks of different w. The network leading to the response shown in Fig. 1a is approximately affine, with w = −0.63 (d/lc = 0.48) and![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = Sfy/Ef = 0.005, 0.01 and 0.015, and Ēfp = Efp/Ef = 0.01. The purely elastic response (Sfy → ∞) of the same networks is shown with dashed line. The curves exhibit well-defined yield points and concave shape. The yield stretch of the network is similar to that of the fibers, as shown by the dotted line which is shifted relative to the elastic branch (dashed line) by 0.2%. Unloading is performed from two maximum stretches of 1.22 and 1.5 for the network with
fy = Sfy/Ef = 0.005, 0.01 and 0.015, and Ēfp = Efp/Ef = 0.01. The purely elastic response (Sfy → ∞) of the same networks is shown with dashed line. The curves exhibit well-defined yield points and concave shape. The yield stretch of the network is similar to that of the fibers, as shown by the dotted line which is shifted relative to the elastic branch (dashed line) by 0.2%. Unloading is performed from two maximum stretches of 1.22 and 1.5 for the network with ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.01. Residual stretches which are a large fraction of the maximum applied stretch are observed in both cases. Similarly large residual stretches result upon unloading in the
fy = 0.01. Residual stretches which are a large fraction of the maximum applied stretch are observed in both cases. Similarly large residual stretches result upon unloading in the ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.005 and 0.015 cases. This behavior, familiar from metal plasticity, is generally observed in nonwovens38,52 and nanopapers.70
fy = 0.005 and 0.015 cases. This behavior, familiar from metal plasticity, is generally observed in nonwovens38,52 and nanopapers.70
Fig. 1b shows similar data for non-affine networks with w = −4.63 ≪ w0 and ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = Sfy/Ef equal to 0.005, 0.01 and 0.015, and Ēfp = Efp/Ef = 0.01. The purely elastic response shown with dashed line is hyperelastic and exhibits the stiffening regimes discussed in the Introduction. The shape of the elastic–plastic curves is significantly different from that of the affine networks in Fig. 1a. Unloading is performed from stretches of 1.22 and 1.5 for the network with
fy = Sfy/Ef equal to 0.005, 0.01 and 0.015, and Ēfp = Efp/Ef = 0.01. The purely elastic response shown with dashed line is hyperelastic and exhibits the stiffening regimes discussed in the Introduction. The shape of the elastic–plastic curves is significantly different from that of the affine networks in Fig. 1a. Unloading is performed from stretches of 1.22 and 1.5 for the network with ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.01. The residual stretches are shown by arrows pointing to the horizontal line and are much smaller (as a fraction of the unloading stretch) than in the approximately affine case shown of Fig. 1a. The dependence of the residual stretch on the degree of non-affinity (parameter w) is discussed further in Section 3.4. Note that the difference between the elastic–plastic and purely elastic S(λ) curves is smaller in the case of non-affine networks compared with the affine ones. This and the small residual stretch may lead in some experimental situations to the conclusion that fiber plasticity does not take place, despite its actual occurrence. Therefore, we suggest that the conclusion of whether plasticity takes place or not in a specific application (for which the purely elastic response is not available) should not be made based on the stress–stretch curve. An alternative is proposed in Section 3.3.
fy = 0.01. The residual stretches are shown by arrows pointing to the horizontal line and are much smaller (as a fraction of the unloading stretch) than in the approximately affine case shown of Fig. 1a. The dependence of the residual stretch on the degree of non-affinity (parameter w) is discussed further in Section 3.4. Note that the difference between the elastic–plastic and purely elastic S(λ) curves is smaller in the case of non-affine networks compared with the affine ones. This and the small residual stretch may lead in some experimental situations to the conclusion that fiber plasticity does not take place, despite its actual occurrence. Therefore, we suggest that the conclusion of whether plasticity takes place or not in a specific application (for which the purely elastic response is not available) should not be made based on the stress–stretch curve. An alternative is proposed in Section 3.3.
3.2 Scaling of the yield stress and strain with network parameters
To understand the relationship between fiber and network yield stresses and strains, several analytic considerations are in place. In affine networks, fibers deform axially and each fiber experiences the network-scale applied strain. This mandates that the network and fiber yield strains coincide:| εny = εfy. | (1) |
The force in a generic fiber at yield is Ffy = SfyAf. On the other hand, the force in the fiber scales with the network stress as Ff ∼ Snlc2. This relation follows from the observation that the mean area corresponding to one fiber (as well as to one crosslink) in the plane normal to the applied stress, Sn, is lc2, with lc being the mean segment length. At the yield point of the network, Sny ∼ SfyAf/lc2, which implies:
 | (2) |
The second proportionality relation follows from the relation between mean segment length and density, ρlc2 ≈ 1, mentioned in Section 2. Note that this analysis does not require the network response to be linear up to yielding. However, if this condition applies, eqn (2) follows directly from eqn (1) which can be written as εny = Sny/E0 = εfy = Sfy/Ef, and by considering that in the affine range E0/Ef ∼ ρd2 ∼ (d/lc)2, as reviewed in the Introduction.
A similar argument can be used to derive equivalent relations for non-affine networks. In such cases, fibers deform mainly in the bending mode. The stress in a bending fiber is proportional to Md/If, where M is the applied moment.71 Fibers yield in bending when Sfy = Mfyd/2If, where Mfy is the moment loading the fiber at yield. The mean fiber moment scales with the mean network stress as Mf ∼ Snlc3, and at yielding Mfy ∼ Snylc3. Combining these relations leads to:
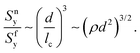 | (3) |
Inferring the ratio of the network and fiber yield strains is less straightforward since yielding of the network does not have to happen in the linear regime I. Hence, while one may write at the fiber scale εfy = Sfy/Ef, a linear relation between εny and εfy may not apply. If this restriction is nevertheless imposed, εny/εfy = (Sny/Sfy)(Ef/E0) and using the non-affine network modulus E0/Ef ∼ ρxd4 with x = 2 for Voronoi networks (see the Introduction),
 | (4) |
Eqn (1) and (4) indicate that the network yield strain is equal to the fiber yield strain in the affine limit, but it may be many times (equal to the fiber aspect ratio) larger than the fiber yield strain in non-affine cases. Since fiber segments (between successive crosslinks along given fiber) of aspect ratio 10 or larger are common in network materials, the yield strain of non-affine networks may be easily one order of magnitude larger than the yield strain of the fiber material; see Fig. 1. This indicates that low density and low crosslink density networks may never yield, within the range of stretches normally encountered in applications.
Simulations have been performed considering networks with a broad range of d/lc values to test the predictions of eqn (1)–(4). However, before proceeding, it is necessary to discuss the method used to identify the yield point. We use in this work the 0.2% offset strain criterion commonly employed to determine the yield point in (hard) engineering materials. Nevertheless, we acknowledge that this is conventional and discuss further below its applicability to soft materials.
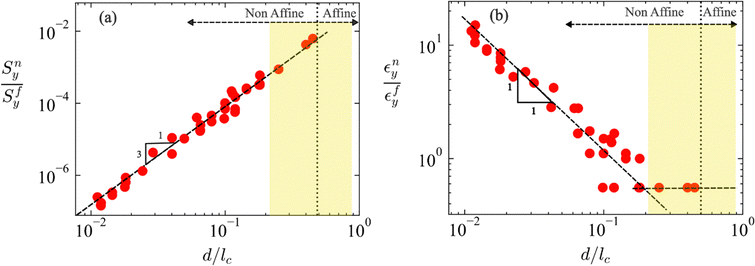
Fig. 2a shows the variation of the network yield stress, Sny, normalized by the fiber material yield stress, Sfy, with the fiber aspect ratio, d/lc. It results that Sny/Sfy ∼ (d/lc)y, with y ≈ 3 in the non-affine range, in agreement with eqn (3). The affine range is harder to reach in physical systems of athermal fibers with circular cross-section and simulations are less accurate in that range. We include several data points in the non-affine to affine transition range shown by the yellow vertical band in Fig. 2. The transition to the slope of 2 predicted by eqn (2) is not well defined since the range of close-to-affine conditions that may be accurately simulated is small.
Fig. 2b shows data equivalent to Fig. 2a, representing the ratio of the network to fiber yield strains, εny/εfy, vs. d/lc. In the non-affine range, εny/εfy ∼ (d/lc)q with q ≈ −1, in agreement with eqn (4). The curve is expected to reach a horizontal plateau in the affine range. Since the simulation and the identification of the yield point in the transition regime are progressively less accurate as d/lc increases, the numerical uncertainty increases. A plateau seems to emerge at εny/εfy ≈ 0.6, which is somewhat below the prediction of eqn (1) according to which it should occur at εny/εfy = 1.
In the context of heterogenous elastic–plastic continua, the 0.2% offset method for the identification of the yield point was associated with the percolation of plastic subdomains.72 We explore next whether the same physical consideration may be used in the context of network materials to underscore the conventional offset method. To this end, we use graph analysis tools to probe the network at each load increment to determine the presence of percolated paths of plastically deformation fibers. We introduce two dummy nodes, P and Q, connected to the nodes on the fixed and loaded faces of the network, respectively, to create a disconnected undirected graph. Fibers deforming plastically are iteratively added to this graph at each load step and the existence of a path connecting P and Q is probed on the updated graph. The load step where such path first appears is taken as the percolation point. Percolation of plastic paths takes place at strains approximately one order of magnitude larger than those identified with the 0.2% offset method. Fig. S2 (ESI†) shows the scaling of Sny/Sfy and εny/εfy with d/lc, where the yield point is associated with percolation. Using percolation as the criterion for yielding on network scale does not change the scaling of the yield stress and strain with d/lc. However, the affine plateau of εny/εfy is approximately 10 times larger than the equivalent plateau in Fig. 2b. The data in Fig. S2 (ESI†) indicates the range of variation of εny/εfy when the criterion for identification of the network yield point is varied from 0.2% offset strain to percolation of plastic paths.
A related consideration is that of the extrapolation of the uniaxial test result to multiaxial loading. While the prediction of yielding in metallic materials subjected to multiaxial loading is based on classical empirical criteria such as von Mises and Tresca, their extension to soft and compressible solids is not straightforward. Alternative criteria that account for both the strain energy of the hydrostatic and deviatoric deformation modes have been used in ref. 73 and 74 for (non-isochoric) cellular materials and applied to network materials in ref. 75. The discussion of yielding under multiaxial loading conditions is beyond the scope of the present article.
3.3 Non-linear behavior and structural evolution
The non-linear behavior of non-affine networks of elastic fibers is well described in the literature and a brief review is provided in the Introduction. Plasticity increases the complexity of this response. The optimal way to inspect the uniaxial response is by referring to the tangent stiffness–stress, Ent(Sn), version of the stress–stretch plot, Sn(λ). The tangent stiffness is computed as Ent = dSn/dλ.
Fig. 3a shows Ent(Sn) for networks with w = −3.54, Ēfp = 0.07, and several fiber yield stress values,  . The purely elastic case curve is shown for reference. The elastic curve has three visible regimes (Fig. 3): the linear elastic regime I at small stresses, where Ent = E0, and regime II where Ent is proportional to the stress, which implies exponential stiffening. A third regime of smaller strain stiffening rate is entered at large stress (and stretch). The transitions between these regimes take place gradually and are shown schematically in Fig. 3b.
. The purely elastic case curve is shown for reference. The elastic curve has three visible regimes (Fig. 3): the linear elastic regime I at small stresses, where Ent = E0, and regime II where Ent is proportional to the stress, which implies exponential stiffening. A third regime of smaller strain stiffening rate is entered at large stress (and stretch). The transitions between these regimes take place gradually and are shown schematically in Fig. 3b.
The elastic–plastic curves follow the elastic curve up to yielding. If the yield stress is sufficiently low, yielding takes place within regime I, as is the case for the curve with ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.0025. Otherwise, the network yield point is in regime II of elastic stiffening. The 0.2% offset method indicates yielding at the point where the elastic–plastic curve departs from the purely elastic curve, marked by Y in Fig. 3a, for the curve with
fy = 0.0025. Otherwise, the network yield point is in regime II of elastic stiffening. The 0.2% offset method indicates yielding at the point where the elastic–plastic curve departs from the purely elastic curve, marked by Y in Fig. 3a, for the curve with ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.0025. Yielding causes Ent of the elastic–plastic case to fall below the tangent stiffness of the elastic case at strains above the network yield strain. Percolation of the plastically deforming fibers takes place at the points marked by the open triangles (indicated as P on the
fy = 0.0025. Yielding causes Ent of the elastic–plastic case to fall below the tangent stiffness of the elastic case at strains above the network yield strain. Percolation of the plastically deforming fibers takes place at the points marked by the open triangles (indicated as P on the ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.0025 curve) for each
fy = 0.0025 curve) for each ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy. Images of the network before and after percolation are shown in Fig. S3 (ESI†). The tangent stiffness increases between Y and P since most of the network fibers are elastic, and the stiffening tendency of the purely elastic network is retained in the elastic–plastic case. However, plastic percolation may cause some reduction of the tangent stiffness if yielding takes place at small stresses and provided Ēfp is sufficiently small. Weak softening is visible in Fig. 3a for segment P–S of the
fy. Images of the network before and after percolation are shown in Fig. S3 (ESI†). The tangent stiffness increases between Y and P since most of the network fibers are elastic, and the stiffening tendency of the purely elastic network is retained in the elastic–plastic case. However, plastic percolation may cause some reduction of the tangent stiffness if yielding takes place at small stresses and provided Ēfp is sufficiently small. Weak softening is visible in Fig. 3a for segment P–S of the ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.0025 curve. Stiffening takes place again beyond S. For large enough
fy = 0.0025 curve. Stiffening takes place again beyond S. For large enough ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy, the strong stiffening of the background elastic network dominates and Ent exhibits no reduction beyond point P.
fy, the strong stiffening of the background elastic network dominates and Ent exhibits no reduction beyond point P.
As discussed in the literature on elastic networks,26,76 the response in regime II is controlled by the emergence of stress paths, i.e. of a relatively small subset of fibers that carry the largest fraction of the applied load. Fibers in the stress paths deform mostly in the axial mode, irrespective of the energy partition in the small strain regime. If fibers are elastic–plastic, the axially loaded stress paths eventually become fully plastic. This leads to a limit behavior identical to that of the purely elastic network but with a stiffness rescaled by the ratio Ēfp. This asymptote is shown in Fig. 3 by the filled circle symbols (marked SP in Fig. 3a for the case with ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.0025). Therefore, the asymptote depends only on Ēfp and is independent of
fy = 0.0025). Therefore, the asymptote depends only on Ēfp and is independent of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy.
fy.
Fig. 3b shows the tangent stiffness–stress curves for networks with w = −3.54, identical ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.0025 and various Ēfp. The regimes described in relation to Fig. 3a are visible. The network yield stress is independent of Ēfp, as expected. The same can be stated about the stress at percolation and the transition stress between the various regimes. The asymptote behavior in the large stress limit is controlled by Ēfp, as also observed in Fig. 3a. Networks with perfectly plastic fibers, Ēfp = 0, exhibit no stiffening beyond percolation, P, and their carrying capacity (maximum stress) is limited, since the only mechanism of stiffening is fiber recruitment into the stress paths. For the same reason, Ent does not vanish, even at large stretches.
fy = 0.0025 and various Ēfp. The regimes described in relation to Fig. 3a are visible. The network yield stress is independent of Ēfp, as expected. The same can be stated about the stress at percolation and the transition stress between the various regimes. The asymptote behavior in the large stress limit is controlled by Ēfp, as also observed in Fig. 3a. Networks with perfectly plastic fibers, Ēfp = 0, exhibit no stiffening beyond percolation, P, and their carrying capacity (maximum stress) is limited, since the only mechanism of stiffening is fiber recruitment into the stress paths. For the same reason, Ent does not vanish, even at large stretches.
To summarize, four regimes are observed after the network becomes plastic: two stiffening regimes, marked Y–P and S–SP in Fig. 3a, caused by the strong stiffening of the background elastic fibers, an intermediate softening regime indicated as P–S which is associated with the percolation of the plastically deforming fibers, and an asymptotic regime at large stress, SP, controlled by the fully plastic stress paths.
We remark that the yield point is better defined in the representation of Fig. 3 than in the stress–stretch curves of Fig. 1. Therefore, we recommend using the tangent stiffness–stress plot to evaluate whether the non-linear response in an experimental situation is compatible with fiber plasticity and to determine the yield point.
The network-scale observations outlined in Fig. 3 can be related to the evolution of the structure. Fig. 4 shows the evolution of the fraction of plastic fibers, fp, during deformation for all networks discussed in Fig. 3. The curves in Fig. 4a correspond to networks with different ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy and same Ēfp = 0.07, while those in Fig. 4b correspond to networks with same
fy and same Ēfp = 0.07, while those in Fig. 4b correspond to networks with same ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.0025 and different Ēfp. The evolution of the fraction of plastic fibers is essentially independent of Ēfp. The points marking the transition between the regimes of non-linear deformation shown in Fig. 3a are also indicated in Fig. 4a for the same type of network (
fy = 0.0025 and different Ēfp. The evolution of the fraction of plastic fibers is essentially independent of Ēfp. The points marking the transition between the regimes of non-linear deformation shown in Fig. 3a are also indicated in Fig. 4a for the same type of network (![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.0025 and Ēfp = 0.07). The fraction of plastic fibers increases beyond point Y. Percolation (point P) corresponds to approximately 30% plastic fibers in all systems. This should be close to the bond percolation threshold on the Voronoi network, assumption supported by the fact that plastic percolation depends neither on
fy = 0.0025 and Ēfp = 0.07). The fraction of plastic fibers increases beyond point Y. Percolation (point P) corresponds to approximately 30% plastic fibers in all systems. This should be close to the bond percolation threshold on the Voronoi network, assumption supported by the fact that plastic percolation depends neither on ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy nor on Ēfp. However, this percolation threshold is not available in literature and the cross-check is not possible at this time. The percolation point is also the inflection point of the fp(λ) curve, Fig. 4a. The plateau at large strains corresponds to the asymptote SP, i.e. to the formation of the load carrying stress path sub-network which, at this stage, is fully plastic.
fy nor on Ēfp. However, this percolation threshold is not available in literature and the cross-check is not possible at this time. The percolation point is also the inflection point of the fp(λ) curve, Fig. 4a. The plateau at large strains corresponds to the asymptote SP, i.e. to the formation of the load carrying stress path sub-network which, at this stage, is fully plastic.
 | ||
Fig. 4 Fraction of plastic fibers vs. stretch for all cases shown in Fig. 3, i.e. for networks with w = −3.54 and (a) same Ēfp = 0.07 and different fiber yield stresses, and (b) same ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.0025 and different fiber plastic stiffening rates, Ēfp. Open triangles show plastic percolation. fy = 0.0025 and different fiber plastic stiffening rates, Ēfp. Open triangles show plastic percolation. | ||
Fig. 5a shows the nematic order parameter based on the second Legendre polynomial  , where θ is the angle between the end-to-end vector of a fiber and the loading direction, and 〈
, where θ is the angle between the end-to-end vector of a fiber and the loading direction, and 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉 indicates averaging over all fibers in the model, i.e. over the distribution of θ. P2 = 0 and P2 = 1 indicate random orientation and perfect alignment of fibers in the stretch direction, respectively. This parameter is computed for a subset of the networks considered in Fig. 3 and 4. The curve corresponding to the purely elastic limit is shown for reference. The deviation from the elastic curve is modest and hence plasticity does not modify significantly the deformation-induced fiber alignment.
〉 indicates averaging over all fibers in the model, i.e. over the distribution of θ. P2 = 0 and P2 = 1 indicate random orientation and perfect alignment of fibers in the stretch direction, respectively. This parameter is computed for a subset of the networks considered in Fig. 3 and 4. The curve corresponding to the purely elastic limit is shown for reference. The deviation from the elastic curve is modest and hence plasticity does not modify significantly the deformation-induced fiber alignment.
Fig. 5b shows the dependence of the fraction of plastic fibers on the degree of orientation, fp(P2). This function is obtained at percolation of plastic paths by dividing the fiber population in groups based on their P2, with fp being computed for each group. The figure shows that, at given stretch, fp is larger for fibers preferentially oriented in the stretch direction; fibers forming the stress paths (which are approximately aligned with the tensile loading direction) have a larger probability of entering the plastic regime.
3.4 Residual stress and plastic dissipation
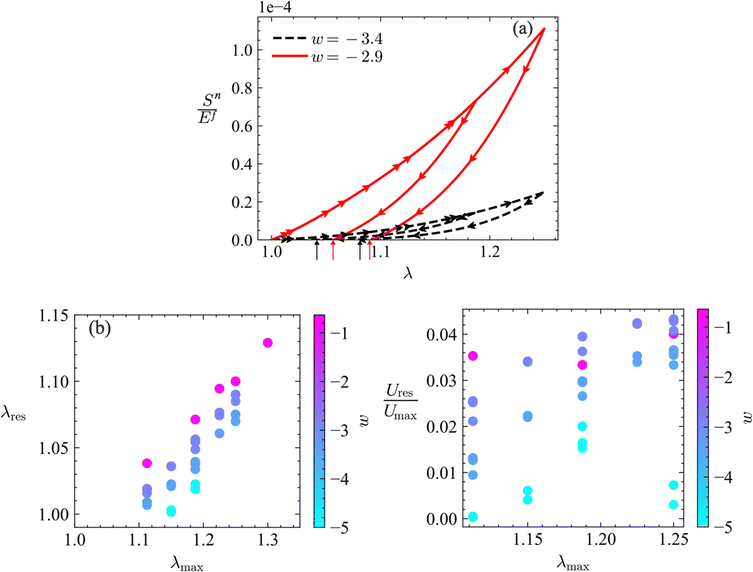
Plastic dissipation and the development of residual stresses are explored by performing unloading from stretches larger than the stretch at yielding, λny. Fig. 6a shows loading–unloading curves, Sn(λ), for networks with w = −2.9 and −3.4, and with![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.01 and Ēfp = 0.5. Two unloading branches are shown for each case. The area bounded by the loading and unloading branches of each curve is the total energy dissipated per unit volume of the network.
fy = 0.01 and Ēfp = 0.5. Two unloading branches are shown for each case. The area bounded by the loading and unloading branches of each curve is the total energy dissipated per unit volume of the network.
Residual stretches, λres, are observed in both cases. These increase with increasing the unloading stretch λmax, as expected, and increase with increasing w. Fig. 6b shows the variation of λres with λmax for networks of various w (eight w values are considered). The dependence of λres on λmax is approximately linear (goodness of fit R2 value is between 0.98 and 1 for all w values shown). The more interesting observation is the dependence of the residual stretch on the degree of non-affinity of the network characterized by w. As w decreases, the yield stretch of the network increases (Fig. 2b) and λres decreases. This implies that, for sufficiently non-affine networks, λres resulting upon unloading from realistic maximum stretches may be too small to be measured, even though the network experiences plastic deformation. Such behavior was observed in soft collagen networks in ref. 57, where it is reported that a residual stretch could not be measured despite the occurrence of plasticity. Note that this is fundamentally different from the response of approximately affine networks, Fig. 1a, for which the residual strain is a large fraction of the maximum strain.
Residual strain energy is stored in the unloaded networks. This is reported in Fig. 6c for the same range of parameters used in Fig. 6b. The figure shows the strain energy density after unloading (zero global stress), Ures, normalized by the strain energy density at the maximum stretch applied, λmax, denoted by Umax. The residual field is self-equilibrated and is due to the (structural and mechanical) heterogeneity of the network. The fraction Ures/Umax increases with λmax, and increases with increasing w. Ures/Umax appears to reach a plateau at large λmax. However, the fraction remains smaller than 5% in all cases considered. Furthermore, the residual field is a pre-stress which may cause network stiffening77 upon reloading in the direction of the initial load. However, the pre-stress is too small to lead to a detectable increase in network stiffness. This is particularly the case in more non-affine networks.
The ability of the network to dissipate energy during loading–unloading cycles is important in applications where cellular and fibrous materials are used to absorb mechanical energy, e.g. in protective gear and damping applications. The present data may be used to guide the design in such applications. Therefore, it is of importance to determine the dependence of the specific energy absorption on network parameters. To this end, dissipation in networks with different parameters may be compared based on tests in which either the maximum stress, Smax, (‘stress control’), or the maximum stretch, λmax, (‘strain control’) are imposed. For proper comparison, we keep ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy and Ēfp identical in all these cases (
fy and Ēfp identical in all these cases (![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) fy = 0.01, Ēfp = 0.5).
fy = 0.01, Ēfp = 0.5).
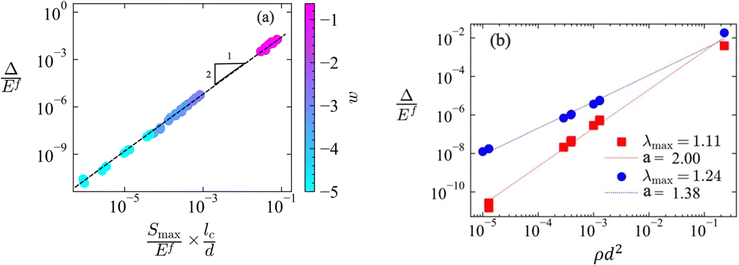
We consider first the situation in which Smax is imposed. Fig. 7a shows the scaling of the dissipation per unit volume of the network and per (first) loading–unloading cycle, Δ, with networks parameters. The dissipation per cycle, Δ, is plotted against the stress at unloading, Smax/Ef, and the nondimensional group d/lc. This normalization brings together data for various non-affine networks with a broad range of w. It results that:
 | (5) |
The specific energy dissipation, per unit mass, is ![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) = Δ/(ρfφ) = Δ/(ρfρAf) ∼ Δ/ρd2, where φ is the volume fraction of the network and ρf is the density of the network material. Hence,
= Δ/(ρfφ) = Δ/(ρfρAf) ∼ Δ/ρd2, where φ is the volume fraction of the network and ρf is the density of the network material. Hence,
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) ∼ Smax2/(ρd2)2. ∼ Smax2/(ρd2)2. | (6) |
Further, we consider the situation in which λmax is imposed, which is more often encountered in practice and more meaningful in the case of soft materials. Networks with various ρ and d are compared in Fig. 7b, where Δ/Ef is plotted versus ρd2 ∼ (d/lc)2 for two maximum stretches, λmax = 1.11 and 1.25. It is seen that:
| Δ ∼ (ρd2)a | (7) |
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) ∼ Δ/ρd2 ∼ (ρd2)a−1. ∼ Δ/ρd2 ∼ (ρd2)a−1. | (8) |
This result can be understood by observing that, at small stretches, imposing the maximum stress is equivalent to imposing the maximum strain since, in this limit, Smax = E0εmax; then, eqn (5) leads to Δ ∼ E02/ρd2 ∼ (ρd2)3 and ![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) ∼ (ρd2)2, i.e. a → 3. No such guidance is available for large stretches, where exponent a is seen to decrease.
∼ (ρd2)2, i.e. a → 3. No such guidance is available for large stretches, where exponent a is seen to decrease.
At large stretches, ![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) is essentially independent of ρd2, since a is close to 1. This is the trivial scaling expected for systems in which dissipation increases in proportion with the mass, i.e. with the increase of the number of dissipative elements.
is essentially independent of ρd2, since a is close to 1. This is the trivial scaling expected for systems in which dissipation increases in proportion with the mass, i.e. with the increase of the number of dissipative elements.
The fraction of the work performed which is dissipated due to plastic deformation under small strains increases with w. Also, this fraction increases with increasing λmax for all w in the non-affine range. Therefore, as a design recommendation for applications in which energy dissipation is desired, better performance is expected when using networks with large w.
4. Discussion
As outlined in the Introduction, the non-linear behavior of fiber networks not embedded in matrix is complex. In networks of low fiber volume fraction (i.e. most network materials, with the exception of those with densely packed fibers such as regular paper and nanopapers), the dominant contribution is the geometric non-linearity associated with the large rotations and deformations (in bending) of fibers. Formation of contacts between fibers is an important non-linear mechanism, but the number of contacts forming when the material is loaded in uniaxial tension and simple shear is relatively small and hence the contribution of this mechanism to the overall behavior is weak.The non-linear behavior of fibers has a strong effect on the overall network non-linearity. The response of thermal molecular networks is largely controlled by the non-linearity of the mechanical behavior of the constituent molecular chains. Various models have been considered for this purpose, including freely rotating78 and worm-like chain models79,80 and their effect on network response is well-known.81,82 Likewise, a variety of models have been considered for athermal fibers: bilinear models in which the fibers are loaded axially and the response in compression is much softer than that in tension,83 hyperelastic fibers that strain stiffen in tension,59 and fibers with other types of non-linearity. These models do not lead to a yield point and hence the respective mechanisms cannot be considered responsible for the yield point observed in experiments.
This work focuses on the mechanism underlying the yield point. Fig. 1 shows that the effect of fiber plasticity on the overall network response depends strongly on whether the network is affine or non-affine. As discussed in Section 3.2, in affinely-deforming networks the stress–stretch curve exhibits a clear yield point, similar to what is typically seen in metals, and the yield strain is identical or close to that of the fiber material. Consequently, the yield strain of the network is independent of the network density and hence, the yield stress scales with network parameters similarly with the scaling of the small strain stiffness, E0, with the same parameters. The residual stretch is a large fraction of the maximum stretch before unloading, Fig. 1a. Numerical studies in the literature that consider approximately affine networks demonstrate these trends.52–54 We discuss next the extent to which the present results may be used to identify fiber plasticity as the origin of the network scale yield point.
An apparent yield point may be induced by friction.41 This is seen in mats of athermal fibers, such as nonwovens. In this case too, the yield strain is independent of the density and the friction coefficient, while the yield stress increases with increasing friction and with increasing network density. The dependence on density of the yield stress is similar to that of the small strain network modulus, E0. These dependencies are similar to those introduced by fiber plasticity and hence these parameters (yield stress and yield strain) cannot be used to distinguish between the two mechanisms. The distinction can be made if the friction coefficient can be changed in the experiment, while maintaining the network density constant, case in which the yield stress would be insensitive to this modification if the controlling mechanism is fiber plasticity.
In non-affinely deforming networks, the stress–stretch curve S(λ) does not exhibit a clear yield point and fiber plasticity may not be observable based on such plot, Fig. 6a. The yield strain of the network is larger than the yield strain of the fiber material and increases with decreasing network density, Fig. 2b. The yield stress scales with the network density differently than the scaling of E0 with the same parameter, as shown in Fig. 2a and eqn (3). These observations should be sufficient to allow determining experimentally whether a network behavior is affected by fiber plasticity. In addition, inspecting the non-linear response using the tangent stiffness–stress plot is also revealing for this purpose, Fig. 3. Four non-linear regimes are described in Section 3.3. The presence of these regimes in the experimental data would be indicative of the operation of this mechanism.
Most of these features of the non-linear response are distinct from those introduced by friction.41 Also, if friction is strong enough to produce a yield point in a soft, non-affine network, it would also lead to large residual strains (as commonly seen in nonwovens37,38,52,61). This contrasts with the effect of fiber plasticity, which tends to cause small residual strains in the non-affine case, Fig. 6.
Cohesive forces between fibers may cause an apparent yield point in non-affine networks.43 We distinguish two situations: cohesive forces are weak and do not lead to bundling, and the opposite extreme case in which cohesion organizes the network into a network of fiber bundles.84 In the first case, the non-linear network response at strains larger than the yield strain is similar to the response of the network without adhesion43 and hence, the absence of the complex non-linear behavior described in Fig. 3 would indicate that fiber plasticity is not the dominant mechanism. The second case is more complex since fiber bundles may deform plastically by relative fibril sliding within bundles. This mechanism, which is expected to operate in collagen networks, should lead to a phenomenology similar to that described in this work.
5. Conclusions
A qualitative and quantitative evaluation of the effect of fiber plasticity on the mechanical behavior of network materials is presented in this article. The network yield stress and strain are evaluated in terms of fiber properties and network structural parameters. While the yield strain of affinely deforming networks is equal to the yield strain of fibers and hence is independent of network parameters, the yield strain of non-affine networks increases with increasing degree of non-affinity. This implies that network scale yielding may not happen in the most non-affine cases at experimentally-relevant stretches.In affine networks the yield stress is proportional to the small strain modulus and hence is proportional to the network density and the fiber cross-sectional area, i.e. ρd2. In non-affine networks, the network yield stress is proportional to (ρd2)3/2. Plasticity modifies the non-linear response beyond the network yield point. Four non-linear regimes are identified and are placed in relation with structural changes taking place in the network during deformation. Plasticity leads to residual strains and residual strain energy stored in the network, which both decrease with increasing degree of non-affinity. The specific (per unit mass) energy dissipated during a loading–unloading cycle increases with increasing degree of affinity.
A discussion of other mechanisms that may produce a yield point phenomenon is presented and arguments that may be used to identify the controlling mechanism in an experimental situation are provided. The data outlines the importance of the fiber plasticity mechanism in the mechanics of stochastic athermal networks.
Author contributions
S. N. Amjad: data curation, investigation, methodology, software, writing – review & editing; N. Parvez: investigation, methodology, software, writing – review & editing; R. C. Picu: conceptualization, methodology, supervision, writing original draft, funding acquisition.Data availability
The data discussed is included in the article.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supposed, in part, by the National Science Foundation through grant CMMI-2022489 and by the National Institutes of Health (NIH) through Grant No. U01 AT010326-06.References
- R. O. Hynes, The extracellular matrix: not just pretty fibrils, Science, 2009, 326(5957), 1216–1219 CAS.
- P. Fratzl, Collagen: structure and mechanics, an introduction, Collagen: structure and mechanics, Springer, 2008, pp. 1–13 Search PubMed.
- G. A. Holzapfel and H. W. Weizsäcker, Biomechanical behavior of the arterial wall and its numerical characterization, Comput. Biol. Med., 1998, 28(4), 377–392 CAS.
- S. J. Russell, Handbook of nonwovens, Woodhead Publishing, 2022 Search PubMed.
- M. A. Hubbe and J. A. Heitmann, Review of factors affecting the release of water from cellulosic fibers during paper manufacture, BioResources, 2007, 2(3), 500–533 CAS.
- A. Barhoum, P. Samyn, T. Öhlund and A. Dufresne, Review of recent research on flexible multifunctional nanopapers, Nanoscale, 2017, 9(40), 15181–15205 Search PubMed.
- A. Operamolla, Recent Advances on Renewable and Biodegradable Cellulose Nanopaper Substrates for Transparent Light-Harvesting Devices: Interaction with Humid Environment, Int. J. Photoenergy, 2019, 2019(1), 3057929 Search PubMed.
- W. Liu, K. Liu, H. Du, T. Zheng, N. Zhang and T. Xu, et al., Cellulose nanopaper: fabrication, functionalization, and applications, Nano-Micro Lett., 2022, 14(1), 104 CAS.
- W. M. Fazli Wan Nawawi, K. Y. Lee, E. Kontturi, R. J. Murphy and A. Bismarck, Chitin nanopaper from mushroom extract: natural composite of nanofibers and glucan from a single biobased source, ACS Sustainable Chem. Eng., 2019, 7(7), 6492–6496 CAS.
- N. Ezekiel Mushi, N. Butchosa, Q. Zhou and L. A. Berglund, Nanopaper membranes from chitin–protein composite nanofibers—structure and mechanical properties, J. Appl. Polym. Sci., 2014, 131(7), 40121 CrossRef.
- R. L. Whitby, T. Fukuda, T. Maekawa, S. L. James and S. V. Mikhalovsky, Geometric control and tuneable pore size distribution of buckypaper and buckydiscs, Carbon, 2008, 46(6), 949–956 Search PubMed.
- R. A. Susantyoko, F. Parveen, I. Mustafa and S. Almheiri, MWCNT/activated-carbon freestanding sheets: a different approach to fabricate flexible electrodes for supercapacitors, Ionics, 2019, 25, 265–273 Search PubMed.
- C. R. Picu, Network Materials: Structure and Properties [Internet], Cambridge University Press, 2022. Available from: https://books.google.com/books?id=A0t9EAAAQBAJ Search PubMed.
- J. Buschmann and G. M. Bürgisser, Biomechanics of tendons and ligaments: tissue reconstruction and regeneration, Woodhead Publishing, 2017 Search PubMed.
- W. Nafo and A. Al-Mayah, Mechanical investigations of biological tissues using tensile loading and indentation, Biomechanics of Soft Tissues, CRC Press, 2018, pp. 27–54 Search PubMed.
- A. Al Mayah, Biomechanics of soft tissues: principles and applications, CRC Press, 2018 Search PubMed.
- N. E. Mushi, N. Butchosa, M. Salajkova, Q. Zhou and L. A. Berglund, Nanostructured membranes based on native chitin nanofibers prepared by mild process, Carbohydr. Polym., 2014, 112, 255–263 Search PubMed.
- P. Hassanzadeh, W. Sun, J. P. de Silva, J. Jin, K. Makhnejia and G. L. Cross, et al., Mechanical properties of self-assembled chitin nanofiber networks, J. Mater. Chem. B, 2014, 2(17), 2461–2466 Search PubMed.
- N. Mittal, F. Ansari, V. K. Gowda, C. Brouzet, P. Chen and P. T. Larsson, et al., Multiscale control of nanocellulose assembly: transferring remarkable nanoscale fibril mechanics to macroscale fibers, ACS Nano, 2018, 12(7), 6378–6388 CrossRef CAS PubMed.
- A. J. Benítez and A. Walther, Cellulose nanofibril nanopapers and bioinspired nanocomposites: a review to understand the mechanical property space, J. Mater. Chem. A, 2017, 5(31), 16003–16024 RSC.
- R. Mao, N. Meng, W. Tu and T. Peijs, Toughening mechanisms in cellulose nanopaper: the contribution of amorphous regions, Cellulose, 2017, 24, 4627–4639 CrossRef CAS.
- A. J. Licup, S. Münster, A. Sharma, M. Sheinman, L. M. Jawerth and B. Fabry, et al., Stress controls the mechanics of collagen networks, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(31), 9573–9578 CrossRef CAS PubMed.
- A. Mauri, A. E. Ehret, M. Perrini, C. Maake, N. Ochsenbein-Kölble and M. Ehrbar, et al., Deformation mechanisms of human amnion: Quantitative studies based on second harmonic generation microscopy, J. Biomech., 2015, 48(9), 1606–1613 CrossRef PubMed.
- C. P. Broedersz, M. Sheinman and F. C. MacKintosh, Filament-length-controlled elasticity in 3D fiber networks, Phys. Rev. Lett., 2012, 108(7), 078102 CrossRef CAS PubMed.
- A. J. Licup, A. Sharma and F. C. MacKintosh, Elastic regimes of subisostatic athermal fiber networks, Phys. Rev. E, 2016, 93(1), 012407 CrossRef CAS PubMed.
- N. Parvez, J. Merson and R. C. Picu, Stiffening mechanisms in stochastic athermal fiber networks, Phys. Rev. E, 2023, 108(4), 044502 CrossRef CAS PubMed.
- M. Alava and K. Niskanen, The physics of paper, Rep. Prog. Phys., 2006, 69(3), 669 Search PubMed.
- S. Borodulina, A. Kulachenko, M. Nygårds and S. Galland, Stress-strain curve of paper revisited, Nord. Pulp Pap. Res. J., 2012, 27(2), 318–328 CrossRef CAS.
- J. Wilhelm and E. Frey, Elasticity of Stiff Polymer Networks, Phys. Rev. Lett., 2003, 91(10), 108103 CrossRef PubMed.
- D. A. Head, A. J. Levine and F. C. MacKintosh, Distinct regimes of elastic response and deformation modes of cross-linked cytoskeletal and semiflexible polymer networks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68(6), 061907 CrossRef CAS PubMed.
- A. S. Shahsavari and R. C. Picu, Elasticity of sparsely cross-linked random fibre networks, Philos. Mag. Lett., 2013, 93(6), 356–361 CrossRef CAS.
- S. Deogekar and R. C. Picu, On the strength of random fiber networks, J. Mech. Phys. Solids, 2018, 116, 1–16 CrossRef.
- S. Deogekar, M. Islam and R. Picu, Parameters controlling the strength of stochastic fibrous materials, Int. J. Solids Struct., 2019, 168, 194–202 CrossRef CAS PubMed.
- C. Heussinger, B. Schaefer and E. Frey, Nonaffine rubber elasticity for stiff polymer networks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76(3), 031906 CrossRef PubMed.
- M. Islam and R. Picu, Effect of network architecture on the mechanical behavior of random fiber networks, J. Appl. Mech., 2018, 85(8), 081011 CrossRef.
- R. Inai, M. Kotaki and S. Ramakrishna, Deformation behavior of electrospun poly(L-lactide-co-ε-caprolactone) nonwoven membranes under uniaxial tensile loading, J. Polym. Sci., Part B: Polym. Phys., 2005, 43(22), 3205–3212 CrossRef CAS.
- R. Jubera, A. Ridruejo, C. González and J. LLorca, Mechanical behavior and deformation micromechanisms of polypropylene nonwoven fabrics as a function of temperature and strain rate, Mech. Mater., 2014, 74, 14–25 Search PubMed.
- A. Rawal, A. Priyadarshi, N. Kumar, S. V. Lomov and I. Verpoest, Tensile behaviour of nonwoven structures: comparison with experimental results, J. Mater. Sci., 2010, 45, 6643–6652 CrossRef CAS.
- A. Ridruejo, C. González and J. LLorca, Damage micromechanisms and notch sensitivity of glass-fiber non-woven felts: An experimental and numerical study, J. Mech. Phys. Solids, 2010, 58(10), 1628–1645 CrossRef CAS.
- Q. Meng and T. J. Wang, Mechanics of strong and tough cellulose nanopaper, Appl. Mech. Rev., 2019, 71(4), 040801 CrossRef.
- V. Negi and R. Picu, Mechanical behavior of nonwoven non-crosslinked fibrous mats with adhesion and friction, Soft Matter, 2019, 15(29), 5951–5964 RSC.
- R. Picu and A. Sengab, Structural evolution and stability of non-crosslinked fiber networks with inter-fiber adhesion, Soft Matter, 2018, 14(12), 2254–2266 CAS.
- S. Amjad and R. Picu, Emergence of an apparent yield phenomenon in the mechanics of stochastic networks with inter-fiber cohesion, Soft Matter, 2023, 19(47), 9215–9223 CAS.
- Y. H. Na, Y. Tanaka, Y. Kawauchi, H. Furukawa, T. Sumiyoshi and J. P. Gong, et al., Necking phenomenon of double-network gels, Macromolecules, 2006, 39(14), 4641–4645 CAS.
- G. Jiang, C. Liu, X. Liu, Q. Chen, G. Zhang and M. Yang, et al., Network structure and compositional effects on tensile mechanical properties of hydrophobic association hydrogels with high mechanical strength, Polymer, 2010, 51(6), 1507–1515 CrossRef CAS.
- J. P. Gong, Why are double network hydrogels so tough?, Soft Matter, 2010, 6(12), 2583–2590 RSC.
- T. Nakajima, T. Kurokawa, S. Ahmed, W. L. Wu and J. P. Gong, Characterization of internal fracture process of double network hydrogels under uniaxial elongation, Soft Matter, 2013, 9(6), 1955–1966 Search PubMed.
- R. Seth and D. Page, The stress-strain curve of paper, The role of fundamental research in paper making, 1981, vol. 1, pp. 421–452 Search PubMed.
- S. Münster, L. M. Jawerth, B. A. Leslie, J. I. Weitz, B. Fabry and D. A. Weitz, Strain history dependence of the nonlinear stress response of fibrin and collagen networks, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(30), 12197–12202 Search PubMed.
- S. Nam, J. Lee, D. G. Brownfield and O. Chaudhuri, Viscoplasticity enables mechanical remodeling of matrix by cells, Biophys. J., 2016, 111(10), 2296–2308 CrossRef CAS PubMed.
- D. M. Knapp, V. H. Barocas, A. G. Moon, K. Yoo, L. R. Petzold and R. T. Tranquillo, Rheology of reconstituted type I collagen gel in confined compression, J. Rheol., 1997, 41(5), 971–993 Search PubMed.
- M. Zhang, Y. Chen, F. P. Chiang, P. I. Gouma and L. Wang, Modeling the large deformation and microstructure evolution of nonwoven polymer fiber networks, J. Appl. Mech., 2019, 86(1), 011010 CrossRef.
- V. I. Räisänen, M. Alava, R. Nieminen and K. Niskanen, Elastic-plastic behaviour in fibre networks, Nord. Pulp Pap. Res. J., 1996, 11(4), 243–248 Search PubMed.
- Z. Li, Y. Qian, Q. Bao, Z. Yang and Z. Lu, The mechanical behaviors of random curved fiber networks by numerical simulations, Int. J. Solids Struct., 2023, 270, 112200 CrossRef.
- V. Tojaga, A. Kulachenko, S. Östlund and T. C. Gasser, Modeling multi-fracturing fibers in fiber networks using elastoplastic Timoshenko beam finite elements with embedded strong discontinuities—Formulation and staggered algorithm, Comput. Methods Appl. Mech. Eng., 2021, 384, 113964 CrossRef.
- A. Brandberg and A. Kulachenko, Compression failure in dense non-woven fiber networks, Cellulose, 2020, 27(10), 6065–6082 Search PubMed.
- E. Ban, J. M. Franklin, S. Nam, L. R. Smith, H. Wang and R. G. Wells, et al., Mechanisms of plastic deformation in collagen networks induced by cellular forces, Biophys. J., 2018, 114(2), 450–461 CrossRef CAS PubMed.
- E. Berthier, H. Yang, M. Guo, P. Ronceray and C. P. Broedersz, Nonlinear mechanosensation in fiber networks, Phys. Rev. Res., 2024, 6(1), 013327 Search PubMed.
- H. Hatami-Marbini and M. Rohanifar, Mechanical properties of subisostatic random networks composed of nonlinear fibers, Soft Matter, 2020, 16(30), 7156–7164 Search PubMed.
- F. C. MacKintosh, J. Käs and P. A. Janmey, Elasticity of Semiflexible Biopolymer Networks, Phys. Rev. Lett., 1995, 75(24), 4425–4428 Search PubMed.
- A. Rawal, S. K. Patel, V. Kumar, H. Saraswat and M. A. Sayeed, Damage analysis and notch sensitivity of hybrid needlepunched nonwoven materials, Text. Res. J., 2013, 83(11), 1103–1112 CrossRef CAS.
- K. M. Pryse, A. Nekouzadeh, G. M. Genin, E. L. Elson and G. I. Zahalak, Incremental mechanics of collagen gels: new experiments and a new viscoelastic model, Ann. Biomed. Eng., 2003, 31, 1287–1296 CrossRef PubMed.
- B. Özerdem and A. Tözeren, Physical Response of Collagen Gels to Tensile Strain, J. Biomech. Eng., 1995, 117(4), 397–401 CrossRef PubMed.
- S. Deogekar, Z. Yan and R. C. Picu, Random Fiber Networks With Superior Properties Through Network Topology Control, J. Appl. Mech., 2019, 86, 081010, DOI:10.1115/1.4043828.
- Abaqus. Dassault Systèmes, 2024 [Internet]. [cited 2024 Oct 22]. Available from: https://www.3ds.com/products/simulia/abaqus.
- A. R. Osta, C. R. Picu, A. King, O. Isele, R. Hamm and A. Dreher, Effect of polypropylene fiber processing conditions on fiber mechanical behavior, Polym. Int., 2014, 63(10), 1816–1823 CrossRef CAS.
- I. Dabrowska, L. Fambri, A. Pegoretti, M. Slouf, T. Vackova and J. Kolarik, Spinning, drawing and physical properties of polypropylene nanocomposite fibers with fumed nanosilica, eXPRESS Polym. Lett., 2015, 9(3), 277–290 Search PubMed.
- J. A. Niestrawska, A. Pukaluk, A. R. Babu and G. A. Holzapfel, Differences in collagen fiber diameter and waviness between healthy and aneurysmal abdominal aortas, Microsc. Microanal., 2022, 28(5), 1649–1663 CrossRef CAS PubMed.
- J. Liu, D. Das, F. Yang, A. G. Schwartz, G. M. Genin and S. Thomopoulos, et al., Energy dissipation in mammalian collagen fibrils: Cyclic strain-induced damping, toughening, and strengthening, Acta Biomater., 2018, 80, 217–227 Search PubMed.
- A. J. Benítez, J. Torres-Rendon, M. Poutanen and A. Walther, Humidity and Multiscale Structure Govern Mechanical Properties and Deformation Modes in Films of Native Cellulose Nanofibrils, Biomacromolecules, 2013, 14(12), 4497–4506 CrossRef PubMed.
- J. M. Gere and S. Timoshenko Mechanics of Materials [Internet]. PWS Publishing Company; 1997. (Mechanics of Materials). Available from: https://books.google.com/books?id=BKJRAAAAMAAJ.
- V. Negi and R. Picu, Elastic-plastic transition in stochastic heterogeneous materials: Size effect and triaxiality, Mech. Mater., 2018, 120, 26–33 Search PubMed.
- M. Alkhader and M. Vural, An energy-based anisotropic yield criterion for cellular solids and validation by biaxial FE simulations, J. Mech. Phys. Solids, 2009, 57(5), 871–890 CrossRef.
- R. S. Ayyagari and M. Vural, Multiaxial yield surface of transversely isotropic foams: Part I—Modeling, J. Mech. Phys. Solids, 2015, 74, 49–67 Search PubMed.
- Y. Ma, H. Zhu, B. Su, G. Hu and R. Perks, The elasto-plastic behaviour of three-dimensional stochastic fibre networks with cross-linkers, J. Mech. Phys. Solids, 2018, 110, 155–172 CrossRef.
- P. Onck, T. Koeman, T. Van Dillen and E. van der Giessen, Alternative explanation of stiffening in cross-linked semiflexible networks, Phys. Rev. Lett., 2005, 95(17), 178102 CAS.
- M. Sheinman, C. Broedersz and F. MacKintosh, Actively stressed marginal networks, Phys. Rev. Lett., 2012, 109(23), 238101 Search PubMed.
- J. H. Weiner, Statistical mechanics of elasticity, Courier Corporation, 2012 Search PubMed.
- O. Kratky and G. Porod, Röntgenuntersuchung gelöster fadenmoleküle, Recl. Trav. Chim. Pays-Bas, 1949, 68(12), 1106–1122 Search PubMed.
- J. F. Marko and E. D. Siggia, Stretching dna, Macromolecules, 1995, 28(26), 8759–8770 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer physics, Oxford University Press, 2003 Search PubMed.
- M. Rubinstein and S. Panyukov, Elasticity of polymer networks, Macromolecules, 2002, 35(17), 6670–6686 Search PubMed.
- S. Domaschke, A. Morel, R. Kaufmann, J. Hofmann, R. M. Rossi and E. Mazza, et al., Predicting the macroscopic response of electrospun membranes based on microstructure and single fibre properties, J. Mech. Behav. Biomed. Mater., 2020, 104, 103634 Search PubMed.
- A. Sengab and R. Picu, Filamentary structures that self-organize due to adhesion, Phys. Rev. E, 2018, 97(3), 032506 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01427h |
| This journal is © The Royal Society of Chemistry 2025 |