Repulsions and attractions between membrane-deforming spheres, Janus-particles, and opposite tube-like deformations in giant unilamellar vesicles

Abstract

Lipid membrane deformations have been predicted to lead to indirect forces between the objects that induce these deformations. Recent experimental measurements have found an attractive interaction between spherical particles that all induce a deformation towards the inside of a giant unilamellar vesicle. Here, we complement these experimental observations by investigating the interactions between deformations pointing in opposite directions with respect to the membrane normal vector. This is experimentally realized by a particle deforming the membrane towards the inside of the GUV and pulling a membrane tube towards the outside of the membrane. Particles completely wrapped by the membrane are repelled from the tube with a strength of 3 k_BT at a distance of 0.5 μm. However, particles that strongly curve the membrane by adhering only to a patch of about 50% of its surface area are attracted to the center of the tube with a strength of −5.3 k_BT at a minimum distance of about 1 μm. We find that such Janus particles also experience attractive interactions when both deforming the membrane in the same way. These quantitative experimental observations provide new insights into interactions between oppositely membrane deforming objects, important for cooperative protein assembly at or interactions of microplastics with cell membranes.

---

1. Introduction

Membrane proteins constitute one-third of all human proteins,¹ which control cellular functions such as receptor signaling and ion transport.² Errors in their organization are linked to various diseases,^3–5 making the study of the driving forces for protein arrangements in the plasma membrane crucial. Complex proteins migrate in the fluid membrane and interact through many forces, such as electrostatic,⁶ capillary,⁷ van der Waals,⁸ hydrophobic and hydrophilic forces,⁹ depending on their structure, orientation, electrical charge, and distance to other proteins.

Besides these well-known interactions, the membrane itself also can induce forces between them.^10–13 In particular, proteins that locally bend the membrane give rise to interactions driven by the minimization of membrane bending energy.^11,14 Quantifying these deformation-mediated interactions in a biological setting is challenging, as they occur alongside a variety of other forces that complicate their isolation and measurement. Therefore, simplified models that allow selective and quantitative measurements of these interactions are employed.

To make theoretical predictions for the interactions between membrane-deforming objects, membrane inclusions with a simplified shape, such as a cone or sphere, are typically considered.^11,15,16 Weakly membrane-deforming conical inclusions in a flat membrane were found to repel each other, both for equally and oppositely oriented deformations of the membrane.^11,15,16 When including additional factors such as membrane tension or stronger deformations, the interactions between opposite inclusions were found to be attractive at longer ranges,^17–22 with conical inclusions showing an additional strong repulsion at short ranges.¹⁴ For strongly membrane deforming objects a switch from repulsion to attraction was observed even when the deformations were oriented in the same direction.^23–27 These predictions were in line with recent experimental measurements on simplified model systems consisting of membrane-deforming colloidal spheres and giant unilamellar vesicles. For equally deforming particles, an attraction was consistently found,^28–31 although the strength of the attraction varied considerably, ranging from a few k_BT to hundreds of k_BT.^29,30 This variation highlights that minute differences in the induced curvature can play a crucial role in the interaction between membrane-deforming objects.

No experimental measurements exist, though, for interactions between objects that induce opposite curvature on a membrane. While theoretical and numerical predictions for interactions between opposite membrane inclusions have been put forward, the same studies did not show agreement with experiments for equal membrane deformations, suggesting that they may not be able to predict the interactions correctly.

In this paper, we therefore use a previously developed simplified model system composed of a Giant Unilamellar Vesicle (GUV), which is made of a lipid bilayer and adhesive colloidal particles that deform the membrane to study the interactions between oppositely membrane-deforming objects. We use both fully adhesive as well as partially adhesive (Janus) colloidal particles to induce deformations by (partial) wrapping of the membrane to examine the force between equal and opposite membrane deformations. Opposite membrane deformations are realized by pulling a membrane tube from a GUV and studying the interaction with a particle that deforms the GUV towards the inside. We find that fully wrapped particles are repelled from the pulled tube, whereas partially wrapped particles which create large deformations are attracted. To complete the picture, we directly measure the attraction force between two partially wrapped particles deforming a membrane and find it to be attractive in line with earlier measurements on fully-wrapped particles.

2. Materials and methods

2.1. Chemicals

Phosphate-buffered saline (PBS) tablets, chloroform (99%), sodium phosphate (99%), D-glucose (99%), 4,4′-Azobis(4-cyanovaleric acid) (98%, ACVA), N-hydroxysulfosuccinimide sodium salt (98%), Bovine serum albumin (BSA), and 1,3,5,7-tetramethyl-8-phenyl-4,4-difluoro-bora-diaza-indacene (97%, BODIPYTM FL) were purchased from Sigma-Aldrich; methoxypoly(ethylene) glycol amine (mPEG, MW = 5000) from Alfa Aesar; 1-ethyl-3-(3-dimethylaminopropyl) carbodiimid hydrochloride (99%, EDC) were obtained from Carl Roth; NeutrAvidin (avidin) from Thermo Scientific; 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[biotinyl(polyethylene glycol)-2000] (DOPE-PEG-biotin), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (DOPE-Rhodamine), from Avanti Polar Lipids were purchased from Sigma-Aldrich. Deionized water with resistivity of 18.2 MΩ cm obtained from a Millipore Filtration System (Milli-Q Gradient A10) was used in all experiments. All chemicals were used as received.

2.2. Vesicle production

Giant Unilamellar Vesicles were prepared from a mixture of 97.5 wt% DOPC, 2.0 wt% DOPE-PEG2000-Biotin, and 0.5 wt% DOPE-Rhodamine by the electroformation method as described in ref. 31 and 32.

2.3. Particle functionalization

Carboxylated polystyrene (PS) particles with diameter of 0.98 ± 0.03 μm were prepared by surfactant-free radical polymerization.³³ The fluorescent dye BODIPY was included in the synthesis for imaging. PS particles were functionalized with NeutrAvidin and mPEG 5000 following the procedure described in ref. 29 and 34.

2.4. Sample preparation

25 mm round coverslips were coated with 0.5 g L⁻¹ BSA buffer for 2 min and then washed three times with PBS buffer. The BSA-coated coverslips allowed the particles to stick to the coverslip such that GUVs could partially attach to the substrate or particles. Vesicles were gently washed in isotonic PBS, diluted to remove small lipid aggregates and then mixed with the particles in the same buffer. Finally, the mixture was injected into a home-built stainless steel microscope chamber. The chamber was kept open after approximately 30 minutes to allow the osmolality of the external solution to increase allowing particle wrapping. All experiments were performed at room temperature.

2.5. Microscopy

Images were captured with an inverted Ti–E Nikon microscope equipped with an A1-R confocal scanner. Excitation light was passed through a 60× water immersion objective (N.A. = 1.2) and the emitted light was reflected back through the same light path to the detectors. Particles containing BODIPY and GUVs labeled with Rhodamine were simultaneously excited with 488 and 561 nm laser beams, respectively. The emitted light was collected in the ranges of 500–550 nm (particles, BODIPY) and 580–630 nm (vesicles, rhodamine). Fig. 1d corresponds to channel 1 & 2 showing fluorescence from membrane and colloid, respectively. Both laser beams scanned a field of view of either 512 × 256 pixels at 59 fps or 512 × 512 pixels at 30 fps in resonant mode.

Fig. 1 Experimental setup for measuring the inverse membrane deformation-mediated interaction. (a) Detailed schematic of the pulled membrane tube creating a deformation to the outside and a wrapped particle deforming membrane towards the inside (not to scale). 1-DOPC lipid 2-DOPE lipid 3-Biotin 4-NeutrAvidin 5-rhodamine, 6-polyethylene glycol (PEG) 7-polystyrene particle. (b) Schematic of the three-dimensional setup of a GUV (magenta) with a tube pulled by an optical trap and including wrapped, partially-wrapped and non-wrapped particles (green) (not to scale). (c) Schematic of a cross-section of a GUV highlighting positive and negative curvatures (M) and the geodesic distance from the tubes. (d) Confocal images of GUV cross sections in two separated channels, from left to right: (channel 1) particle emission 500–550 nm, (channel 2) membrane emission 565–625 nm (Overlay); scale bars are 2 μm.

2.6. Optical trapping and force measurement

An optical trap was provided by a highly focused laser beam (1064 nm Nd:YAG laser, LaserQuantum) integrated into the confocal light path to simultaneously image and trap. The laser beam front was modulated by a high-speed Meadowlark spatial light modulator (SLM) with a refresh rate of 120 Hz, and holograms were generated at 100 Hz using RedTweezers software.³⁵

The optical tweezers were calibrated using the equipartition theorem and k_OT〈Δx²〉/2 = k_BT/2, where Δx is the displacement of a trapped particle from the center of the trap and k_OT is the trap stiffness. As long as the displacement of the trapped particle from the center of the trap is small, Hooke's law holds so that the force (F) can easily be calculated by F = k_OTΔx.

2.7. Image analysis and particle tracking

The open-source Python package Trackpy³⁶ was used for locating the particle center, and circletracking³⁷ was employed to find the center and radii of GUVs by fitting an ellipse to its contour. We define our coordinate system such that the origin (x, y, z) = (0, 0, 0) is located at the center of the GUV. To reconstruct the three-dimensional positions of the particles, we approximate the GUV as an ellipsoid stretched along the x-direction as this is the direction in which the tube is pulled, with major radii a and minor radii b along y and z. Under this assumption, the z-coordinate of a particle is calculated via
where x, y, and z are relative coordinates of particles with respect to the GUV. The differences between the major and minor radii a and b was found to not be more than 1 μm. By combining the particle coordinates with the vesicle geometry, the three-dimensional positions of the particles relative to the vesicle center were determined.

To extract the interaction energy, we analyzed the evolution of the particle separations. To do so, we constructed the transition probability matrix P_ij, which gives the probability for a particle to change its separation from s_i to s_j over the interval between two frames. Assuming a constant diffusion coefficient, the equilibrium, i.e. stationary probability distribution, ρ_eq(s), was obtained from the master equation governing these transitions.³⁸ The interaction energy u(s) is then calculated via the Boltzmann relation,

u(s) = −k_BT ln[ρ_eq(s)] + const.,

with the additive constant chosen such that u(∞) → 0 at large separations.

3. Results and discussion

To measure the curvature-mediated interaction between two membrane deformations we use a model system based on a Giant Unilamellar Vesicle (GUV) composed of a lipid bilayer and adhesive spherical polystyrene particles (see Methods for details). As shown in Fig. 1a, adhesion between the colloids and GUV is achieved by NeutrAvidin proteins attached to the outer surface of the colloids which exhibit strong affinity for the biotinylated lipids which are integrated in the GUV.³⁹ Each NeutrAvidin-biotin bond is 17 k_BT strong⁴⁰ and can be considered permanent on the experimental time scale.

The functionalized particles are wrapped by the GUV when the adhesion energy surpasses the energy required for bending the membrane around the particle if membrane tension is sufficiently low.^29,31,41 By controlling the NeutrAvidin concentration on the colloids, we regulate the adhesion energy and thus the wrapping.³⁴ Wrapping was induced by keeping the microscope chamber open for about 30 min such that water could evaporate from phosphate buffered saline (PBS) media. Accordingly, the membrane tension continuously decreased due to the increasing osmolarity difference until adhesion dominated and the particles were wrapped, see methods for more details.

One way to create an experimental system with two deformations with opposite curvature would be to use two wrapped particles: one particle inside the GUV that is being wrapped towards the outside, and a second particle that is wrapped from the outside towards the inside. However, while standard encapsulation methods such as inverted emulsions can create GUVs with particles on the inside,⁴² the thus prepared GUVs possess spontaneous curvature.⁴³ Our attempts to use this method therefore resulted in the spontaneous formation of tubes that extended both inward and outward from the membrane, similar to ref. 44, making measurements of interactions between oppositely wrapped particles prohibitively difficult.

For this reason, we took an alternative approach to obtain deformations with opposite curvature. In addition to using a particle wrapped from the outside to the inside as before, we created a membrane deformation with opposite curvature by pulling a particle attached to the outside of the GUV further outwards using optical tweezers, see Fig. 1. This induces the formation of a tube and in turn a positive curvature deformation in the membrane at the point where the tube is connected to the membrane. See Fig. 1b–d for the experimental setup and Methods for experimental details. We note that this setup is similar but not precisely equivalent to two equal inclusions that induce opposite curvatures. They differ in their adhesion energy and the precise deformation they induce.

From the force F that is applied to pull the tube and the bending rigidity κ, we can also extract the membrane tension σ, using .⁴⁵ See Methods section for force measurement details. We quantified the membrane tension by assuming κ = 22 k_BT for DOPC vesicles created by electroformation^46,47 and found σ to be in a range from 3.6 to 6.8 μN m⁻¹. The tube diameter then was estimated from 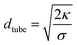to be in the range of 160 to 220 nm.⁴⁵

To image how the wrapped particle interacts with the GUV, we fluorescently labeled the membrane with 0.5 wt% Rhodamine-lipids and the particles with BODIPY dye. Fast confocal microscopy in combination with a Python-based image analysis routine³⁶ then allows both easy tracking of particles and characterization of the GUV, such as their size and the position of their center³⁷ (Fig. 1d). We monitored the colocalization of the fluorescence signal in the channels to distinguish whether the particles were wrapped or not. This can be seen in Fig. 1d, where a white color in the overlay of GUV (magenta) and colloid (green) indicates membrane-wrapped particles. To minimize many-body effects,^31,48 we worked at low particle concentrations and only considered trajectories where other wrapped particles were sufficiently far away.

The membrane tube was drawn from the equatorial plane of the GUV (Fig. 1b–d) where the focal plane of the confocal microscope was located. Taking the equator as z = 0, the z-position of the wrapped particles was extracted from knowledge of the x–y position of the particle and the constraint that it had to be confined to the membrane. To do so, we fitted the membrane with an ellipsoidal shape (see Materials and methods for details).

For symmetry reasons, the interaction energy between the two opposite inclusions is only related to their geodesic distance s, which is shown in Fig. 1c. Here s is the distance between the wrapped particle and the intersection of the tube and GUV. To quantify the interaction, various techniques have been developed to extract the free energy from the trajectory of the particles^38,49–52 Since the wrapped particles were not in the focal plane of the confocal microscope most of the time, we could not use techniques that require a long and/or continuous trajectory.^49,50 Therefore, we employed a displacement-based energy calculation relying on a master equation here.⁵³ We computed the transition probability matrix P_ij from the observed probability of a particle transitioning from s_i to s_j. By assuming a constant diffusion coefficient, we derived the stationary probability distribution ρ_eq(s) from P_ij. The interaction energy u(s) between opposite inclusions is then simply determined from the Boltzmann distribution.^29,38

3.1. Fully wrapped particles repel from a pulled tube

We first measured how a particle that was fully wrapped by the membrane interacted with the oppositely curved deformation induced by the tube. In contrast to previous work where two identical inclusions were found to attract,^29,30 the wrapped particle here was repelled from the opposite curvature induced by the tube, as can be seen in the image sequences in Fig. 2a and Video S1 (ESI†). While membrane-wrapped particles induce large deformations, previous simulations indicate that, for fully wrapped particles, the membrane-mediated interactions arise primarily from the local deformations around the tiny membrane neck rather than from the shape of the particle.³¹ These deformations around the neck are too small to be optically resolved by confocal microscopy, but their effects on the particle dynamics confirm their presence.^29,31

Fig. 2 Interaction between a positive membrane deformation induced by a tube pulled away from a GUV and a negative deformation created by a membrane-wrapped particle. (a) Confocal microscopy time series showing the motion of a particle wrapped towards the inside of the GUV and a tube being pulled by a particle towards the outside of the GUV. Scale bar is 5 μm. See also ESI† Video S1. (b) Interaction energy as a function of geodesic distance s between the tube and a fully wrapped particle (magenta circles) and an attached, non-wrapped particle (green squares). Data for fully wrapped particles were obtained from six different GUVs (diameters: 15–20 μm), analyzing trajectories of six fully wrapped particles reconstructed from a total of 26 534 frames. For non-wrapped particles, data were collected from 9 GUVs (diameters: 14–24 μm) with 14 non-wrapped colloids, and a total of 10 196 frames. Inset: A power-law fit (red line) with u/u₀ = αs^β to the interaction energy between the fully-wrapped particles and the tube yields α = 0.78 ± 0.14 and β = −0.83 ± 0.08.

We extract the interaction energy from the particle's trajectory using the transition probability matrix approach and show the result in Fig. 2b. We find that the interaction is indeed repulsive and that the energy decays strongly with distance up to about 1 μm, after which it decreases more slowly up to about 1 μm. The decay of the repulsive energy follows a power-law in the distance with an exponent of −0.83 ± 0.08, see inset of Fig. 2b. At longer distances, the potential energy reaches a plateau which we assume corresponds to the energy in the absence of any membrane deformation and therefore the average of the energy at 4 to 5 μm distance is set to zero. The k_BT order of magnitude of the interaction energy we find is in line with the observation that thermal fluctuations occasionally bring particles close to the tube despite the overall repulsion. Our observation is very different from early predictions assuming a flat and tensionless membrane as well as small membrane deformations, which did not find a different sign in the interaction between opposite and equal membrane inclusions, and a power law decay of s⁻⁴.¹¹ However, none of the underlying assumptions hold in our case.

Comparing the strength of the repulsion with earlier measurements of the interaction between two equal inclusions realized by two fully wrapped particles,²⁹ we find that although the sign of the interaction has inverted, the strength is of similar magnitude. For two equal inclusions, the minimum in the attraction was found to be −3.3 k_BT which occurred at a distance of about 1.3 μm.²⁹ In that work, it was not possible to measure distances closer than one particle diameter, equivalent to s = 0.98 μm, for steric reasons. Here, the wrapped particle can approach the tube much closer, as the tube is taking up significantly less space than another wrapped particle.

At distances below one particle diameter from the membrane neck of the pulled tube, we find a repulsion of almost 5 k_BT. A repulsion similar in strength as the attraction for two equal inclusions, i.e. 3 k_BT, is found at s = 0.5 μm, which is closer than the distance where this interaction strength occurs for two equal inclusions (Fig. 2b). The interaction decays over about 2.5 μm for the equal and 2.0 μm distance for opposite inclusions. The here observed slightly shorter interaction range and lower strength at the same distance likely arise from a higher membrane tension, which is in line with measurements on equal inclusions at higher membrane tensions.²⁹ In addition, the shape of the deformation induced by the tube as well as the adhesion energy between the particle that is being used to induce the tube and the membrane also differ from that induced by a fully but oppositely wrapped particle.

To test whether the observed interaction was solely due to the curvature imposed by the particle, we also measured the interaction of a tube and a particle that was only adhered to but did not deform the membrane. To ensure that the particles did not leave an indentation in the membrane, the control experiment was performed with particles whose surface density of NeutrAvidin was reduced by a factor of four, such that only 2.5% of their surface was covered with NeutrAvidin.²⁹ We find that there is no measurable interaction between the tube and the non-deforming particles as depicted in Fig. 2b (green squares). This implies that the deformation induced by the tube does not severely affect the geometry of the membrane surrounding it. It also demonstrates that interactions mediated by fluctuation are negligible in this system.^54,55

The repulsive interaction found in this experiment is reminiscent of the membrane-mediated interaction of two spheres on an elongated vesicle.⁵⁶ These simulations showed that the membrane-deforming particles stayed far away from the positively curved regions most of the time and were pushed away from the stretching points,⁵⁶ in agreement with our observation that wrapped particles were repelled from a tube with positive curvature.

3.2. Partially-wrapped particles attract to a pulled tube

Incidentally, partially wrapped particles were found to emerge when they were in the vicinity of the tube during the wrapping transition. Although the engulfment process regularly takes a few seconds at membrane tensions below 10 nN m⁻¹, it can take significantly longer when there is insufficient surface area available, i.e. at higher surface tensions.³² Under these conditions, we observed a particle which remained partially covered by the membrane for approximately one minute. This metastable, partially wrapped state might stem from spatially inhomogeneous Neutravidin coating on the colloids, in line with the considerable variability in Neutravidin coating across different colloids which underlies the wrapping time differences observed for each particle.²⁹

In Fig. 3a, a time sequence of a partially-wrapped particle in the vicinity of the tube is shown. These particles became fully wrapped after the tube was released likely due to the decreasing membrane tension and additional available membrane area. The attraction between a partially-wrapped particle and the outward tube manifests itself by the particle being close to the tube (Fig. 3a and Video S2, ESI†). We note that the apparent distance in the two-dimensional (2D) projection does not always correspond directly to the three-dimensional (3D) geodesic distance.

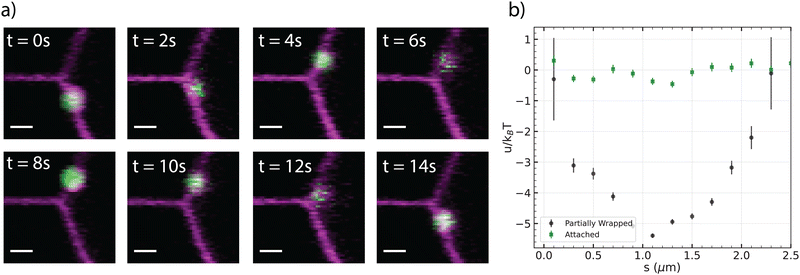Fig. 3 Interaction between a pulled tube and partially-wrapped particle. (a) Time evolution of the wrapped particle from left to right and top to bottom; the time interval between snapshots 2s (scale bar 1 μm). (b) Interaction energy as a function of geodesic distance (s) between the center of the tube and a partially wrapped particle (black crosses). Data was obtained from experiments with 3 GUVs (diameters: 21–34 μm), using three partially wrapped particles, from a total of 6326 frames. The energy values for non-wrapped particles (green squares) are replicated from Fig. 2b for comparison.

The same method as in the previous section is applied to evaluate the potential energy. As shown in Fig. 3b, the partially wrapped particle moves in an attractive potential with a depth of −5.3 k_BT, which is located about 1 μm from the center of the tube. The shape of the potential well is parabolic by approximation. The particle senses the tube from a distance of 2 μm and becomes attracted. Assuming a Hookean force and using a parabolic fit we found a potential well with a stiffness of 51.5 ± 0.5 fN μm⁻¹. Here, we directly measured the membrane tension from the force applied to the membrane tube, yielding a value of σ = 4.3 ± 1.8 μN m⁻¹.

To measure the wrapping fraction of the particle, we determined the contact perimeter from confocal cross-sections of the GUV at its equator (see Fig. S1 in the ESI†). From this perimeter, we calculated that 52 ± 1% of the particles surface is covered by the membrane.

In comparison with previous analytical and simulation studies, we find similarities and differences. Most of the predictions found attractions between two objects deforming the membrane from opposite sides.^{17,19–21,57} Within the particular range of membrane tensions used in our experiment a similar potential well has been calculated which is comparable to the interaction energy we find here in Fig. 3b.^14,58 However, that minimum of the potential well was found to be on the order of the membrane bending rigidity (κ = 22 k_BT), in contrast to the depth of our almost parabolic potential well at −5.3 k_BT.

Moreover, it is striking that we find a repulsion from the opposite deformation of the tube for fully wrapped particles and an attraction for partially wrapped particles. A similar transition from repulsion to attraction was observed by coarse-grained molecular dynamics simulations and numerical calculations for axisymmetric particles in a flat membrane.^23–27 Upon an increasing contact angle, i.e. an increasing curvature imprint, the interaction switched from a repulsion to an attraction at short distances and repulsion at longer distances. While we don't see a repulsion at larger distances, we here find a similar switch for the larger deformations induced by partially wrapped particles.

3.3. Attraction between adhesive Janus particles

To have better control over the membrane deformation, we devised a protocol in which the polystyrene spheres were intentionally only partially functionalized with NeutrAvidin, so called Janus particles. To do so, the particles were adsorbed to an interface between oil and water and were functionalized by NeutrAvidin on the surface that was exposed to the water phase, see Fig. 4a. The functionalized fraction of the particles' surface area is equal to the fraction of the particles' surfaces exposed to water. The coating fraction can then be estimated from the contact angle of the particles at the interface, which were 75° (ref. 59) for particles absorbed to a dodecane–water interface corresponding to 63% of the area, and 22° for absorption to an octanol–water interface corresponding to only 7% of the area exposed to Neutravidin.⁶⁰

Fig. 4 Interaction between two partially-wrapped particles. (a) Schematic representation of the functionalization approach used to prepare colloids partially coated with NeutrAvidin (not to scale); particles were adsorbed to an oil–water interface and selectively functionalized on the area exposed to the water phase. (b) Confocal image of a non-fluorescent polystyrene coated with NeutrAvidin conjugated with fluorescein used to validate the method clearly shows a fluorescent cap, indicating the Janus character of the particle; (c) confocal image and (d) schematic representation showing that a partially wrapped colloid (green) strongly deforms the membrane (magenta); the yellow dashed line indicates the contact between particle and membrane; scale bar is 2 μm; (e) 3D confocal reconstruction of a GUV with two particles embedded (particle shown in green, vesicle in magenta); (f) a confocal image of a GUV (magenta) with two adhered Janus particles (green) with patch size equal to 67 ± 7% of its surface area; (g) confocal microscopy image of a GUV (magenta) with two adhered Janus particles (green) with patch size equal to 5 ± 3% of its surface area; scale bars in (f) and (g) are 5 μm; (h) interaction force as a function of particle center-to-center distance (s). Blue hexagons represent data from particles with 67% wrapping fraction, obtained from experiments involving four GUVs (diameters: 21–34 μm) and analyzed from a total of 7467 frames. Green plus symbols indicate data for particles with 5% wrapping fraction, collected from five GUVs (diameters: 14–25 μm) and analyzed from a total of 7151 frames.

It is assumed that the functionalized fraction is equal to the adhered area due to the strong adhesion energy of 17 k_BT between NeutrAvidin and biotin.⁴⁰ We validated our coating mechanism using a non-fluorescent particle which we coated with NeutrAvidin conjugated with a fluorescein dye and observed by confocal microscopy, shown in Fig. 4b. To quantify the precise adhesion area, we determined the wrapping fraction between the Janus particle and the vesicle with the confocal microscope, see Fig. 4c, using the contact between the membrane and particle as indicated by the yellow dashed line indicated in the schematic of Fig. 4d. In the cases where the membrane has been strongly deformed, the particle overshoots when moving into the vesicle during wrapping^{32,41,54,61,62} and the distance of the particle from the undisturbed membrane is more than one particle diameter, which can thus not be used to measure the wrapping fraction area. These strong deformations are clearly visible in the 3D reconstruction of the membrane, as shown in Fig. 4e, and different from earlier work on penetration depth of Janus particles.⁶² We find an adhesive fraction of particles area of 67% ± 7% for particles (Fig. 4f) functionalized at the dodecane–water interface and 5% ± 3% for particles at the octanol–water interface (Fig. 4g).

We furthermore observed how two Janus particles which strongly deform the membrane aggregate and find that the attraction is so strong that the pair once formed cannot be broken by thermal fluctuation during the experimental time framework, see Video S3 (ESI†). The strong attraction precludes the use of statistical methods such as the Boltzmann weighing or the transition probability matrix that has been used in the first two sections, as we cannot obtain sufficient statistics for all canonical microstates in our experimental time frame. Therefore, we employed a dual optical trap setup to directly measure the interaction force between the particles⁴⁸ and low particle concentrations to ensure interactions between pairs of membrane-deforming particles only.

In our experiment, both particles were trapped at the top of the vesicle. One particle was confined in a strong optical trap, while the other was held in a weak trap that served as a force sensor, corresponding to the right and left particles in Video S4 (ESI†). By moving the strong trap to different positions relative to the weak trap, we varied the center-to-center distance (s) between the two particles. At each separation, we recorded the force (F) acting on the particle in the weak trap from its displacement of the center of the trap. The resulting force-distance relationship is shown in Fig. 4h. The attractive force increases the closer the particles are to each other and has a maximum of 0.4 pN when the particles are almost touching. Interestingly, there is a small repulsive force between the Janus particles at 1.7 μm distance. An important factor in membrane deformations is the bendocapillary length where the bending rigidity κ = 22 k_BT for DOPC vesicles.⁴⁷ The membrane tension σ was measured from the fluctuation spectrum of the vesicles in the equatorial contour and was found to be in the range of less than 10 nN m⁻¹.⁶³ In this regime, the membrane exhibits large fluctuations, often referred to as “floppy”. Such a low membrane tension increases the bendocapillary length λ_bc ≥ 3 μm, implying that length scales smaller than λ_bc are dominated by bending energy.⁶⁴ To verify that the measured interaction is due only to the deformation and that the employed optical traps do not perturb the vesicle, we quantify the interaction between two Janus particles with small wrapping fraction and find that they do not interact significantly, see Fig. 4g and h.

Our force measurement between two Janus particles, which deform the membrane on the same side, reveals a clear attractive interaction. In contrast to previous experiments on fully wrapped particles that exhibited a reversible attraction of approximately 0.1 pN,²⁹ the interaction observed here is significantly stronger and cannot be reversed by thermal fluctuations (see Fig. S2, ESI†). We attribute this enhancement to the much longer ranged membrane deformations induced by the partially adhesive Janus particles compared to the local deformations induced by the neck of fully membrane wrapped spheres,^24,25 which is also in line with a study using larger adhesive colloids with corrugated contact line and hence stronger deformation which reported an attractive force of about 1 pN at close contact³⁰ and work on particles inducing large deformations when confined between a membrane and a substrate.⁴⁸

Our results for two Janus particles are also very similar to Monte Carlo and molecular dynamics simulations.^25,26 In these simulations a strong attraction at close distances and a local repulsion minimum around 3R_p was found as well as a small repulsion peak at larger distances. However, in our experiments, two Janus particles do not measurably interact with each other at distances larger than 2 μm, while in the simulations the repulsive force continued to increase slightly, probably due to the larger relative size of the colloids to the vesicles.

4. Conclusion

In summary, we quantified the membrane-mediated interaction stemming from the deformation of two inclusions with opposite curvature, where one was experimentally realized by a membrane-wrapped sphere and the other by a pulled membrane tube. We find repulsions between these opposite inclusions when small deformations as created by fully membrane-wrapped particles were employed. However, for stronger deformations of the membrane which were achieved by employing partially wrapped particles, we find attractions to the opposite deformation of the membrane tube in line with predictions by Reynwar and Deserno.²⁴ Control experiment with non-wrapped particles proved that the interaction was solely due to the curvature. To better understand the effects of membrane deformation induced by partially wrapped particles, we created Janus colloidal spheres which only possessed a membrane-adhesive patch. In agreement with earlier simulations, we measured an attractive force between two spheres, which had 67% of their surface area adhered to the membrane. We quantified this interaction force using two optical traps and found it to be about 0.4 pN at near touching contact distance.

Our current model system holds the potential to advance our understanding of biological cell membranes. As biological membranes encompass multiple components and distinct liquid phases,⁶⁵ each with its own mechanical properties,⁶⁶ our model provides a platform to quantitatively explore the interaction energy between two membrane deforming objects on such membranes further. Moreover, the controlled local manipulation of the curvature, whether positive or negative, could potentially initiate dynamic rearrangements, prompting interesting avenues for future investigation.

Author contributions

A. A. and D. J. K. designed, performed the research, analyzed the data and wrote the paper.

Data availability

The data supporting this study, including an Excel file with separate sheets containing the data required to generate Fig. 1b, 2b, and 3h, is available at the following link: https://zenodo.org/records/15035402.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge useful discussions with Thomas Weikl and Markus Deserno. We would like to thank Yogesh Shelke for demonstrating the technique for placing particles at the interface of oil and water.

References

1. J. P. Overington, B. Al-Lazikani and A. L. Hopkins, Nat. Rev. Drug Discovery, 2006, 5, 993–996.
2. M. S. Almén, K. J. Nordström, R. Fredriksson and H. B. Schiöth, BMC Biol., 2009, 7, 50.
3. X. Meng, J. Clews, V. Kargas, X. Wang and R. C. Ford, Cell. Mol. Life Sci., 2017, 74, 23–38.
4. T. Suzuki, Y. Araki, T. Yamamoto and T. Nakaya, J. Biochem., 2006, 139, 949–955.
5. S. H. Lee, D. H. Kim, U. Kuzmanov and A. O. Gramolini, Am. J. Physiol.: Heart Circ. Physiol., 2021, 320, H417–H423.
6. Z. Zhang, S. Witham and E. Alexov, Phys. Biol., 2011, 8, 35001.
7. P. A. Kralchevsky and K. Nagayama, Langmuir, 1994, 10, 23–36.
8. C. M. Roth, B. L. Neal and A. M. Lenhoff, Biophys. J., 1996, 70, 977–987.
9. J. A. Killian, Biochim. Biophys. Acta, Rev. Biomembr., 1998, 1376, 401–416.
10. N. Dan, P. Pincus and S. A. Safran, Langmuir, 1993, 9, 2768–2771.
11. M. Goulian, R. Bruinsma and P. Pincus, Europhys. Lett., 1993, 23, 155.
12. R. Golestanian, M. Goulian and M. Kardar, Europhys. Lett., 1996, 33, 241–245.
13. B. J. Reynwar and M. Deserno, Biointerphases, 2008, 3, FA117–FA124.
14. T. R. Weikl, M. M. Kozlov and W. Helfrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 6988–6995.
15. J. B. Fournier and P. G. Dommersnes, Europhys. Lett., 1997, 39, 681–682.
16. K. S. Kim, J. Neu and G. Oster, Biophys. J., 1998, 75, 2274–2291.
17. T. R. Weikl, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 265–273.
18. M. M. Müller, M. Deserno and J. Guven, Europhys. Lett., 2005, 69, 482–488.
19. M. M. Müller, M. Deserno and J. Guven, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 1–16.
20. M. M. Müller and M. Deserno, Prog. Theor. Phys. Suppl., 2010, 184, 351–363.
21. S. Mkrtchyan, C. Ing and J. Z. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 1–9.
22. C. Yolcu and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 1–12.
23. B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Müller, K. Kremer and M. Deserno, Nature, 2007, 447, 461–464.
24. B. J. Reynwar and M. Deserno, Soft Matter, 2011, 7, 8567–8575.
25. A. H. Bahrami and T. R. Weikl, Nano Lett., 2018, 18, 1259–1263.
26. Y. Zhu, A. Sharma, E. J. Spangler and M. Laradji, Soft Matter, 2022, 18, 4689–4698.
27. Y. Zhu, A. Sharma, E. J. Spangler and M. Laradji, Soft Matter, 2023, 19, 7591–7601.
28. I. Koltover, J. O. Rädler and C. R. Safinya, Phys. Rev. Lett., 1999, 82, 1991–1994.
29. C. van der Wel, A. Vahid, A. Šarić, T. Idema, D. Heinrich and D. J. Kraft, Sci. Rep., 2016, 6, 1–10.
30. R. Sarfati and E. R. Dufresne, Phys. Rev. E, 2016, 94, 2–7.
31. A. Azadbakht, B. Meadowcroft, J. Májek, A. Šarić and D. J. Kraft, Biophys. J., 2024, 123, 307–316.
32. A. Azadbakht, B. Meadowcroft, T. Varkevisser, A. Šarić and D. J. Kraft, Nano Lett., 2023, 23, 4267–4273.
33. J. Appel, S. Akerboom, R. G. Fokkink and J. Sprakel, Macromol. Rapid Commun., 2013, 34, 1284–1288.
34. C. van der Wel, N. Bossert, Q. J. Mank, M. G. Winter, D. Heinrich and D. J. Kraft, Langmuir, 2017, 33, 9803–9810.
35. R. W. Bowman, G. M. Gibson, A. Linnenberger, D. B. Phillips, J. A. Grieve, D. M. Carberry, S. Serati, M. J. Miles and M. J. Padgett, Comput. Phys. Commun., 2014, 185, 268–273.
36. D. B. Allan, T. Caswell, N. C. Keim, C. M. van der Wel and R. W. Verweij, Soft-matter/trackpy: Trackpy v0.5.0, 2021 DOI:10.5281/zenodo.4682814.
37. C. van der Wel, circletracking v1.0, 2016 DOI:10.5281/zenodo.47216.
38. J. C. Crocker and D. G. Grier, Phys. Rev. Lett., 1994, 73, 352–355.
39. C. van der Wel, D. Heinrich and D. J. Kraft, Biophys. J., 2017, 113, 1037–1046.
40. V. T. Moy, E. L. Florin and H. E. Gaub, Science, 1994, 266, 257–259.
41. H. T. Spanke, R. W. Style, C. François-Martin, M. Feofilova, M. Eisentraut, H. Kress, J. Agudo-Canalejo and E. R. Dufresne, Phys. Rev. Lett., 2020, 125, 1–9.
42. A. Moga, N. Yandrapalli, R. Dimova and T. Robinson, ChemBioChem, 2019, 20, 2674–2682.
43. M. Morita and N. Noda, Langmuir, 2021, 37, 2268–2275.
44. R. Dasgupta, M. S. Miettinen, N. Fricke, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5756–5761.
45. M. Simunovic, C. Prévost, C. J. Andrew and P. Bassereau, Philos. Trans. R. Soc., A, 2016, 374, 0034.
46. W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. A. Evans, Biophys. J., 2000, 79, 328–339.
47. H. A. Faizi, C. J. Reeves, V. N. Georgiev, P. M. Vlahovska and R. Dimova, Soft Matter, 2020, 16, 8996–9001.
48. A. Azadbakht, T. R. Weikl and D. J. Kraft, ACS Nano, 2024, 18, 23067–23076.
49. F. S. Gnesotto, G. Gradziuk, P. Ronceray and C. P. Broedersz, Nat. Commun., 2020, 11, 1–9.
50. A. Frishman and P. Ronceray, Phys. Rev. X, 2020, 10, 21009.
51. J. W. Merrill, S. K. Sainis and E. R. Dufresne, Phys. Rev. Lett., 2009, 103, 1–4.
52. R. Sarfati, J. Bławzdziewicz and E. R. Dufresne, Soft Matter, 2017, 13, 2174–2180.
53. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
54. J. Agudo-Canalejo and R. Lipowsky, Soft Matter, 2017, 13, 2155–2173.
55. N. Li, N. Sharifi-Mood, F. Tu, D. Lee, R. Radhakrishnan, T. Baumgart and K. J. Stebe, Langmuir, 2017, 33, 600–610.
56. A. Vahid, A. Šaric and T. Idema, Soft Matter, 2017, 13, 4924–4930.
57. Z. Yan, Z. Wu, S. Li, X. Zhang, X. Yi and T. Yue, Nanoscale, 2019, 11, 19751–19762.
58. S. Weitz and N. Destainville, Soft Matter, 2013, 9, 7804–7816.
59. H. Al-Shehri, T. S. Horozov and V. N. Paunov, Soft Matter, 2014, 10, 6433–6441.
60. M. Sabapathy, V. Kollabattula, M. G. Basavaraj and E. Mani, Nanoscale, 2015, 7, 13868–13876.
61. C. Dietrich, M. Angelova and B. Pouligny, J. Phys. II, 1997, 7, 1651–1682.
62. E. J. Ewins, K. Han, B. Bharti, T. Robinson, O. D. Velev and R. Dimova, Chem. Commun., 2022, 58, 3055–3058.
63. J. Pécréaux, H. G. Döbereiner, J. Prost, J. F. Joanny and P. Bassereau, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 277–290.
64. M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031903.
65. S. L. Veatch and S. L. Keller, Biophys. J., 2003, 85, 3074–3083.
66. D. Needham and E. Evans, Biochemistry, 1988, 27, 8261–8269.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01415d

---