Open Access Article
Open Access ArticleDesigning optimal elastic filaments for viscous propulsion
Mariia
Dvoriashyna
 *ab and
Eric
Lauga
*ab and
Eric
Lauga
 *a
*a
aDepartment of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Rd, Cambridge CB3 0WA, UK. E-mail: m.dvoriashyna@ed.ac.uk; e.lauga@damtp.cam.ac.uk
bSchool of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, Peter Guthrie Tait Rd, Edinburgh EH9 3FD, UK
First published on 8th April 2025
Abstract
The propulsion of many eukaryotic cells is generated by flagella, flexible slender filaments that are actively oscillating in space and time. The dynamics of these biological appendages have inspired the design of many types of artificial microswimmers. The magnitude of the filament's viscous propulsion depends on the time-varying shape of the filament, and that shape depends in turn on the spatial distribution of the bending rigidity of the filament. In this work, we rigorously determine the relationship between the mechanical (bending) properties of the filament and the viscous thrust it produces using mathematical optimisation. Specifically, by considering a model system (a slender elastic filament with an oscillating slope at its base), we derive the optimal bending rigidity function along the filament that maximises the time-averaged thrust produced by the actuated filament. Instead of prescribing a specific functional form, we use functional optimisation and adjoint-based variational calculus to formally establish the link between the distribution of bending rigidity and propulsion. The optimal rigidities are found to be stiff near the base, and soft near the distal end, with a spatial distribution that depends critically on the constraints used in the optimisation procedure. These findings may guide the optimal design of future artificial swimmers.
1 Introduction
The physics of motile microorganisms, such as bacteria, microalgae and spermatozoa has recently been a subject of active research at the intersection between physics, mathematics and biology.1–5 Studying cell motility is important not only for our general understanding of biological and biophysical phenomena,6,7 but also for the development of biomimetic, synthetic microrobots in a myriad of potential applications, including drug delivery, smart surgery, sensing and detoxification.8–11Inspired by the actuation and geometry of motile microorganisms, different designs of swimming microrobots have been developed,12,13 coming in a variety of shapes (e.g. rigid helical filaments, straight or helical elastic filaments, collection of beads), actuation mechanisms (e.g. rotation of a helical shape, planar or circular oscillation of an elastic tail, prescribed shape changes) and materials (cobalt composite on helical lipids, nickel or iron-filled carbon nanotubes, magnetic beads linked with DNA strands).10,14–18 For example, recently developed undulatory multilink nano-swimmers are controlled by a planar oscillating magnetic field, which sets elastic tails into oscillatory motion and creates forward propulsion, similar to the swimming of spermatozoa.17 Another example includes artificial bacterial flagella, in which a rigid helical shape attached to a thin soft-magnetic head rotated by an external rotating magnetic field, resulting in a corkscrew-type propulsion similar to that of flagellated bacteria.18
Biological microorganisms swim on small scales, with relevant Reynolds numbers ranging between ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−5) and
(10−5) and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−1).19 In this regime, inertia of both the swimmer and the surrounding fluid are negligible, and swimming strategies have to rely on viscous (Stokesian) forces to generate propulsion. One of the simplest swimming modes capable of creating propulsive forces at zero Reynolds number is the classical ‘flexible oar’, initially proposed by Purcell in his famous lecture on ‘life at low Reynolds numbers’.20 In this setup, a flexible tail is made to passively oscillate in a viscous fluid, generating travelling waves along the filament (whose amplitude tends to decay exponentially if the forcing is localised along the filament) and resulting in propulsion in the direction opposite to that of the wave propagation.21,22
(10−1).19 In this regime, inertia of both the swimmer and the surrounding fluid are negligible, and swimming strategies have to rely on viscous (Stokesian) forces to generate propulsion. One of the simplest swimming modes capable of creating propulsive forces at zero Reynolds number is the classical ‘flexible oar’, initially proposed by Purcell in his famous lecture on ‘life at low Reynolds numbers’.20 In this setup, a flexible tail is made to passively oscillate in a viscous fluid, generating travelling waves along the filament (whose amplitude tends to decay exponentially if the forcing is localised along the filament) and resulting in propulsion in the direction opposite to that of the wave propagation.21,22
This mode of swimming has been used experimentally in multiple artificial swimmers. For instance, Guo et al.23 developed a (cm)-scale fish-like microbot, with a main body made of wooden and styrol materials placed on a permanent magnet, and the fin made of a polyimide film sheet. Directly inspired by spermatozoa, Williams et al.24 developed a (mm)-scale biohydrid swimmer made of PDMS and actuated by contractile cardiomyocyte cells lining the base of the filament. Magdanz et al.25,26 developed IRONSperm, which comprised of bovine sperm cells (≈60 μm long) coated with a suspension of 100-nm rice grain-shaped maghemite nanoparticles and controlled by a magnetic field. A related device was designed by Celi et al.,27 composed of a superparamagnetic head and a flexible gold/polypyrrole (Au/PPy) flagellum, and actuated by a magnetic field. Mushtaq et al.28 developed a nano-eel, a multifunctional piezoelectric tailed nanorobot, which consisted of a smart flexible tail made of a polyvinylidene fluoride-based copolymer linked to a PPy nanowire head, decorated with nickel (Ni) rings for magnetic actuation. Theoretical modelling can help understanding physics underlying propulsion of these artificial microswimmers and propose ways of enhancing it.
From a theoretical standpoint, and following the pioneering contributions of Machin,21 the dynamics and propulsion of an elastic filament with constant thickness oscillating in a viscous fluid were modelled physically and mathematically in classical studies.22,29 These original models relied on a small-amplitude approximation, which allows linearisation of the equations of motion for the shape of the elastic filament. The propulsion is generated as a result of the quasi-steady balance of viscous and elastic forces. These linear models have been validated experimentally, using a (cm)-scale robot with an elastic tail actuated at its base, immersed in high viscosity silicone oil.30 Beyond the small-amplitude approach, the full elastohydrodynamic problem of an oscillating filament was studied numerically using the lattice-Boltzmann method,31 asymptotic coarse-grained elastohydrodynamics,32 and regularised Stokeslets,33 while further work also addressed the non-linear dynamics of biological filaments resulting from their molecular structure.34,35
With a view on applications in micro-scale robotics, designing a hydrodynamically optimal synthetic swimmer, i.e. one that can self-propel with the highest swimming velocity for a given energy expenditure, is a problem of fundamental interest. Biologically, this optimisation problem has received a lot of attention in the context of motile eukaryotic cells. It was shown that spermatozoa have an optimal flagellum-to-head length ratio, with the most efficient swimming mode involving symmetrical travelling waves in the flagellum.36 The travelling waves were shown to lead to the optimal motion in an active filament,37–39 while the mathematically optimal shape of the wave was shown to be sawtooth-like,40 with shape singularities that may be regularised by additional biophysical constraints.41,42 Recently, by making use of the new BOSO-Micro database,43 which includes a comprehensive collection of experimental data from the literature on the swimming speed and morphological characteristics of unicellular organisms, it was shown that amplitude-to-wavelength aspect ratios of flagellar eukaryotes are very close to the hydrodynamic optimum.44 Additionally, optimal head-to-tail ratios were studied for a model swimmer equipped with elastic filament actuated at the base,45 and the optimal shape of the head was investigated for a synthetic swimmer with magnetic head and an elastic tail.46
Focusing on the specific case of actuated elastic filaments, past work demonstrated that tapering an elastic filament may lead to an increase in viscous propulsion.47 For a filament with a circular cross-section of radius r(s), which depends on the arc-length s along the filament (see e.g.Fig. 1), the bending rigidity of the filament, A, scales as A ∼ r4. Thus, the tapered filaments are more rigid near the actuation point than the free end. Further studies considered specific functional forms for the filament radius r or the bending rigidity A, such as linear, quadratic, and exponential functions of s.47–50 In most cases, the propulsive force was shown to increase if the filament is stiffer at the base and softer at the distal end. A recent experimental investigation suggested that a microrobot equipped with DNA-based filament wrapped in a tapered bundle swims faster than the one with a bundle of constant thickness.51 These studies reveal a nontrivial relationship between the bending rigidity of the filament (in particular, how it cross-section varies) and the magnitude of the propulsion generated.
In this work, we propose to rigorously determine the relationship between the mechanical properties of the filament and the produced thrust. By considering a specific model system consisting of a beating elastic filament with an oscillating slope at its base, we determine the optimal bending rigidity function that maximises the time-averaged thrust produced by the actuated filament. Instead of prescribing a specific functional shape, we use functional optimisation and variational calculus to establish formally the link between the bending rigidity function and propulsion for different sets of constraints. We find that the optimal bending rigidity for this model swimmer is invariably stiff at the base of the filament and soft at the distal end.
This paper is structured as follows. We first formulate the model problem of a beating elastic filament with an oscillating slope at its base in Section 2.1, and simplify it in Section 2.2. We then pose in Section 2.3 the optimisation problem consisting in finding the cross-sectional shape that maximises the propulsive force generated by the filament. It is solved using an adjoint approach, which is implemented numerically in a steepest ascent algorithm in Section 2.4. We present the results of the optimisation procedure in Sections 3 and 4 and conclude with a discussion in Section 5.
2 Model, methods and optimisation
2.1 Model system: oscillating slender elastic filament
We study in this paper a well-defined model system, which will allow us to solve the optimisation problem rigorously.![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) axis and its base is located at
axis and its base is located at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0. With
= 0. With ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) denoting the arclength along the filament, oscillations of the slope of the filament at
denoting the arclength along the filament, oscillations of the slope of the filament at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) =
= ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) = 0 result in a planar wave propagating between the filament base and its free end located at
= 0 result in a planar wave propagating between the filament base and its free end located at ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) = L. We denote the position of the centreline of the filament at time
= L. We denote the position of the centreline of the filament at time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) by ȳ(
by ȳ(![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), while the circular cross-section of the filament has radius
), while the circular cross-section of the filament has radius ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (
(![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ). The filament is assumed to be slender, so
). The filament is assumed to be slender, so ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (
(![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) ≪ L everywhere. The goal of the paper is to determine the function
) ≪ L everywhere. The goal of the paper is to determine the function ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (
(![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) which maximises the propulsion generated by the filament.
) which maximises the propulsion generated by the filament.
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ≈
≈ ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) . This approach captures the physics of the problem, and is known to remaining quantitatively accurate even beyond the strict small-amplitude regime of validity.30
. This approach captures the physics of the problem, and is known to remaining quantitatively accurate even beyond the strict small-amplitude regime of validity.30
In the absence of inertia, the shape of the filament is determined by a quasi-steady balance between hydrodynamic and elastic forces. To compute the viscous forces, we exploit the slenderness of the filament and use resistive force theory (RFT), which relates the hydrodynamic force density at any point along the filament to its local velocity via drag coefficients in the directions orthogonal and parallel to the local tangent to the filament, ζ⊥ = 4πμ/(ln(L/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) + 1/2), ζ‖ = 2πμ/(ln(L/
) + 1/2), ζ‖ = 2πμ/(ln(L/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) − 1/2),52 where μ denotes the dynamic viscosity of the fluid. Within the assumptions of RFT, the viscous force density per unit length of the filament at each point can be written as
) − 1/2),52 where μ denotes the dynamic viscosity of the fluid. Within the assumptions of RFT, the viscous force density per unit length of the filament at each point can be written as
![[f with combining macron]](https://www.rsc.org/images/entities/b_char_0066_0304.gif) vis = −ζ⊥ vis = −ζ⊥![[v with combining macron]](https://www.rsc.org/images/entities/b_char_0076_0304.gif) − (ζ‖ − ζ⊥)t(t· − (ζ‖ − ζ⊥)t(t·![[v with combining macron]](https://www.rsc.org/images/entities/b_char_0076_0304.gif) ), ), | (1) |
![[v with combining macron]](https://www.rsc.org/images/entities/b_char_0076_0304.gif) is the local velocity distribution along the swimmer.19 For small-amplitude beating, the viscous force occurs primarily in the direction orthogonal to the flagellum axis (i.e. the ȳ direction), with density
is the local velocity distribution along the swimmer.19 For small-amplitude beating, the viscous force occurs primarily in the direction orthogonal to the flagellum axis (i.e. the ȳ direction), with density![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) vis = −ζ⊥ vis = −ζ⊥![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , , | (2) |
 is the instantaneous velocity in ȳ direction.
is the instantaneous velocity in ȳ direction.
To compute the elastic force density, ![[f with combining macron]](https://www.rsc.org/images/entities/b_char_0066_0304.gif) elastic, we make use of classical elastic beam theory.22,53 For displacement of the filament written as ȳ(
elastic, we make use of classical elastic beam theory.22,53 For displacement of the filament written as ȳ(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ), the leading-order elastic force in the ȳ direction is given by
), the leading-order elastic force in the ȳ direction is given by
 | (3) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) = EĪ(
) = EĪ(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) is the bending stiffness, a product of the material's Young's modulus, E, (assumed to be constant) and the second moment of cross-sectional area, Ī(
) is the bending stiffness, a product of the material's Young's modulus, E, (assumed to be constant) and the second moment of cross-sectional area, Ī(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) = π
) = π![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (
(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) )4.
)4.
Imposing a quasi-steady balance between the viscous and elastic forces, eqn (2) and (3), we obtain the governing (classical) hyper-diffusion equation that describes the position of the centreline of the filament in time, in the linearised limit, as
 | (4) |
Note that the inextensibility of the filament comes in at higher order in the oscillation amplitude and, hence, does not appear in the linearised version above.
ȳ(0,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = 0 fixed base, ) = 0 fixed base, | (5a) |
 | (5b) |
 | (5c) |
 | (5d) |
Therefore, in the linearised limit ε ≪ 1, the leading-order position of the filament centreline satisfies eqn (4) along with the BCs in eqn (5).
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) direction, i.e. perpendicular to the beating direction. Although the drag coefficients ζ⊥ and ζ‖ appearing in eqn (1) depend on the local cross section of the filament, their dependence is logarithmic; we may thus treat them as constant in the slender limit.
direction, i.e. perpendicular to the beating direction. Although the drag coefficients ζ⊥ and ζ‖ appearing in eqn (1) depend on the local cross section of the filament, their dependence is logarithmic; we may thus treat them as constant in the slender limit.
Within the small-amplitude approximation we can write t ≈ (1,∂ȳ/∂![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) and
) and ![[v with combining macron]](https://www.rsc.org/images/entities/b_char_0076_0304.gif) = (0,∂ȳ/∂
= (0,∂ȳ/∂![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). The local force in the
). The local force in the ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) direction is then classically given by
direction is then classically given by  (please see ref. 19 and 54 for detailed derivation). Since waves are expected to propagate in the positive
(please see ref. 19 and 54 for detailed derivation). Since waves are expected to propagate in the positive ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) direction, and propulsion to occur in the opposite direction, the magnitude of the time-averaged propulsive force experienced by the filament,
direction, and propulsion to occur in the opposite direction, the magnitude of the time-averaged propulsive force experienced by the filament, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) , is obtained by taking a double integral in time and space of −
, is obtained by taking a double integral in time and space of −![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) x, so that
x, so that
 | (6) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) direction).
direction).
2.2 Model simplification
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) direction, and the small-amplitude motion of magnitude εL along ȳ. A relevant scale A0 for the rigidity can be defined using the length of the filament, A0 = L4ωζ⊥, so that Ā = A0A. This choice corresponds to a relevant dimensionless Sperm number, defined as Sp = L(ζ⊥ω/A0A)1/4, of one when A = 1.19
direction, and the small-amplitude motion of magnitude εL along ȳ. A relevant scale A0 for the rigidity can be defined using the length of the filament, A0 = L4ωζ⊥, so that Ā = A0A. This choice corresponds to a relevant dimensionless Sperm number, defined as Sp = L(ζ⊥ω/A0A)1/4, of one when A = 1.19
We thus define the dimensionless variables
y = ȳ/εL, t = ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ω, x = ω, x = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) /L, A = Ā/A0, /L, A = Ā/A0, | (7) |
 | (8) |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) in eqn (6) now scales with relevant magnitude (ζ⊥ − ζ‖)ε2L2ω and the dimensionless force, F, is given by
in eqn (6) now scales with relevant magnitude (ζ⊥ − ζ‖)ε2L2ω and the dimensionless force, F, is given by | (9) |
y(x,t) = f(x)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t + g(x)sin t + g(x)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t. t. | (10) |
| −f + (A(x)g′′)′′ = 0, | (11a) |
| g + (A(x)f′′)′′ = 0. | (11b) |
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 1 and
1 and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2 the left hand sides of eqn (11a) and (11b), respectively.
2 the left hand sides of eqn (11a) and (11b), respectively.
Using eqn (10), the propulsive force from eqn (9) can be then simplified as
 | (12) |
Finally, the non-dimensional boundary conditions (5) transform into
| f(0) = f′(0) = f′′(1) = f′′′(1) = 0, | (13a) |
| g′(0) = 1, g(0) = g′′(1) = g′′′(1) = 0. | (13b) |
2.3 Optimisation of bending rigidity
In this section we outline the mathematical formalism used to determine the bending rigidity of the filament leading to maximal propulsion.![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) (which is positive) over all possible distributions of bending rigidities, Ā, subject to the equations for the filament dynamics, i.e.
(which is positive) over all possible distributions of bending rigidities, Ā, subject to the equations for the filament dynamics, i.e. | (14) |
 | (15) |
The functional optimisation problem in eqn (15) in general needs to be solved numerically.
To derive the adjoint problem we consider small perturbations, A → A + δA, f → f + δf and g → g + δg, of both ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 1(11a) and
1(11a) and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2(11b). Keeping only the first-order terms we obtain
2(11b). Keeping only the first-order terms we obtain
| δf − (δAg′′)′′ − (Aδg′′)′′ = 0, | (16a) |
| δg + (δAf′′)′′ + (Aδf′′)′′ = 0. | (16b) |
 | (17) |
 | (18) |
We will specify the boundary terms later.
Following a similar calculation, the weak form of eqn (16b) with a test function j can be written as
 | (19) |
Taking the difference between eqn (18) and (19) we obtain
 | (20) |
The variation of the propulsive force F → F + δF in eqn (12) at linear order reads
 | (21) |
 | (22) |
In order to compute the functional derivative, we need to make an explicit link between δA and δF. To do this, we equate the left-hand side of (20) with the right-hand side of (22), by choosing the adjoint functions h and j to satisfy the field equations
| h − (Aj′′)′′ = g′, | (23a) |
| j + (Ah′′)′′ = f′, | (23b) |
| h(0) = h′(0) = h′′(1) = 0, (Ah′′)′(1) = f(1)/2, | (24a) |
| j(0) = j′(0) = j′′(1) = 0, (Aj′′)′(1) = −g(1)/2. | (24b) |
 | (25) |
| dF/dA := f′′j′′ + g′′h′′, | (26) |
2.4 Constraints on bending and numerical algorithm
In the second constraint C2, A is bounded below (by a) and the filament has a fixed volume. Recalling that Ā = Eπ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 4, we can rewrite it in dimensionless form as A = Ẽr4 with
4, we can rewrite it in dimensionless form as A = Ẽr4 with 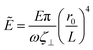 , where r0 is a characteristic thickness of the filament. The dimensionless volume of the filament is
, where r0 is a characteristic thickness of the filament. The dimensionless volume of the filament is  . The constraint for fixed volume, V, can thus be written as
. The constraint for fixed volume, V, can thus be written as  .
.
The two sets of constraints we consider are therefore
• (C1) a ≤ A(x) ≤ b; or
3 Optimal shapes with constraint C1 (bounded bending rigidity)
In this section, we use numerical simulations and theoretical analysis to determine the filament shapes that lead to optimal propulsion. Here we consider the shapes that follow the constraint C1 and thus whose bending rigidity must remain within a prescribed interval.3.1 Optimal shapes have piece-wise constant rigidity
We first run numerical simulations for several chosen values of [a,b] and for an initial smooth profile satisfying the boundary conditions A1(0) = b, A1(1) = a with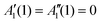 . An example where the shape is initially chosen to have a cubic profile is shown in Fig. 3 as dashed line in the case [a,b] = [0.01,0.1], an interval that contains the optimal constant value from Fig. 2.
. An example where the shape is initially chosen to have a cubic profile is shown in Fig. 3 as dashed line in the case [a,b] = [0.01,0.1], an interval that contains the optimal constant value from Fig. 2.
We applied the algorithm described in Section A.1 setting the tolerances to δ1 = δ2 = 10−5. Independently of the shape taken for the initial condition, we systematically find that the final solution for the optimisation problem is a step-like function, illustrated with solid line in Fig. 3, that takes value A = b at the proximal end, the value of A = a at the distal end and undergoes a sudden jump between a and b at a dimensionless point x0; for example, we have x0 ≈ 0.47 for [a,b] = [0.01,0.1]. When the filament is built of the same material throughout, a step-like function for the bending rigidity corresponds to a piecewise-constant radius for the filament. The corresponding spatial positions of the filament y(x,t) at different time points are shown in the inset of the Fig. 3. The resulting propulsive force is F ≈ 0.116, which is almost twice higher than the optimal force in the case of uniform rigidity (Fig. 2).
To test whether it is the only optimal solution for given [a,b], we run the algorithm for 20 random initial conditions (represented as a truncated Fourier series with random modes) and always obtain the same final step-like solution. For different choices of a and b, the optimal solutions are also invariably step functions, and the values of the jump points x0 depend on the values of both a and b.
 | ||
| Fig. 4 Normalised functional derivative dF/dA in the case of a constant dimensionless bending rigidity A (three different values, see inset). | ||
Physically, our solution indicates that the front of the optimal filament tends to be stiff, which creates a finite amplitude for the beat (akin to a filament with clamped end). The distal part, in turn, is much softer, which leads to an asymmetry in the stroke and generates propulsion.
3.2 Analytical solution for piece-wise constant A
The numerical results suggest that the optimal bending profile takes the form of a piece-wise constant value. For this type of profile, we can in fact compute a fully analytical solution for the filament shape y(x,t).Assuming that A takes form A = b + (a − b)H(x − x0), where H is a Heaviside function (i.e. H(x) = 0 for x ≤ 0 and 1 for x > 0), we can split the problem in eqn (8) into two separate equations on the left and right of the jump point x0
 | (27a) |
 | (27b) |
The boundary conditions at the point of discontinuity of A are continuity of function y and its derivative, i.e.
 | (28) |
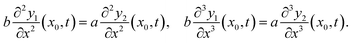 | (29) |
Looking for solutions of the form y = Re(ỹeit), these equations are simplified to
| iỹ1 = −bỹ(iv)1, x ≤ x0, | (30a) |
| iỹ2 = −aỹ(iv)2, x > x0. | (30b) |
The general solution to eqn (30) is
| ỹ1 = C1eαx + C2e−αx + C3eiαx + C4e−iαx, | (31a) |
| ỹ2 = D1eβx + D2e−βx + D3eiβx + D4e−iβx, | (31b) |
 and
and 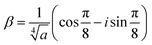 . Applying the boundary conditions from eqn (28) and (29), we obtain a linear system for the values of Ci and Di, which is easily inverted numerically.
. Applying the boundary conditions from eqn (28) and (29), we obtain a linear system for the values of Ci and Di, which is easily inverted numerically.
The propulsive force (9) can then be computed analytically using the dynamics in eqn (27), boundary conditions (28) and (29) and integration by parts,
 | (32) |
3.3 Maximum propulsive force for different bounds [a,b]
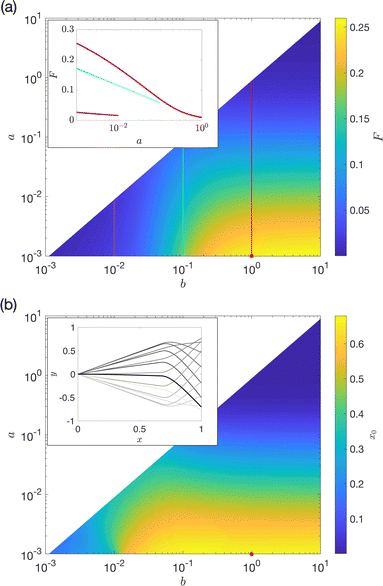
The existence of this analytical solution makes it straightforward to mathematically study the impact of varying the values of the bounding constraints a and b on the propulsive force. In Fig. 5a we show the dependence of the maximum propulsive force F on different dimensionless values of a and b, both varying from 10−3 to 10. The corresponding value for the jump point x0 is displayed in Fig. 5b.We first observe from Fig. 5a that F grows systematically when b is increasing and a is decreasing. Increasing the value of b further than 1, however, results in a very slow growth of F. Indeed, for a = 10−3, increasing b from b = 1 to b = 10, results in increasing F by only about 2%. Our results show that F reaches a maximum of ≈0.26, which is over four times higher than the maximum value of 0.06 obtained with a spatially uniform rigidity (see Fig. 2).
The contribution of the distal end of the filament to the propulsion (x > x0) is captured by the term
 | (33) |
To understand physically why the optimal value of x0 is set by the flexible end, let us consider a simplified setup and focus solely on the distal end portion, x ∈ [x0,1], in the limit where it is set into motion by an oscillating proximal end that is straight and rigid; in that case, by reversibility, the proximal end does not contribute to any propulsion. The problem in eqn (27) then reduces to,
 | (34) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t and the slope will coincide with the actuation at the base of the rigid filament yx(x0,t) = sin
t and the slope will coincide with the actuation at the base of the rigid filament yx(x0,t) = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t; the actuation of the flexible portion of the filament is therefore a combination of oscillating position and slope.
t; the actuation of the flexible portion of the filament is therefore a combination of oscillating position and slope.
The solution to eqn (34) can be found analytically, as it is a problem for a filament with constant bending rigidity.22 The resulting propulsive force, termed Fend, is shown in Fig. 6 as a function of x0 for the values a = 0.001 and b = 1. The optimal value for x0 is seen to be the same for this simplified problem as for the full optimisation, demonstrating that the propulsion is indeed governed by the distal portion of the filament. In this simplified problem, the location of x0 determines both the length of the soft distal part of the filament (1 − x0) and the displacement at its base. The intermediate value of x0 is set by a balance between the requirement of having a finite-sized length for the oscillating distal part (so x0 not too close to 1) and the requirement of having a finite oscillating amplitude (so x0 not too close to 0).
4 Optimal shapes with constraint C2 (fixed filament volume)
The previous section demonstrated that, in the case of filaments whose bending rigidities are constrained to remain within a prescribed interval (constraint C1), the optimal filament shape was always piece-wise constant. We now consider the optimisation problem with the fixed-volume constraint (C2).4.1 Optimal shapes have smoothly-decreasing bending rigidity, followed by a constant value
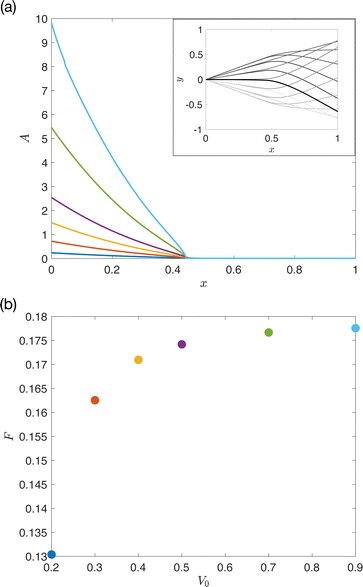
We use the algorithm in Appendix A.2 to solve the optimisation problem for given values of a and V0 starting with a random initial condition. The resulting optimal bending functions A for different values of V0 and fixed a = 0.01 are shown in Fig. 7a; the inset shows the time-varying shape of the filament for the optimal profile in the specific case where V0 = 0.5 (purple curve in main figure).Similarly in the bounded case, the value of A is seen to be constant and equal to the lower boundary a beyond a certain location x0. However, in contrast with the previous case, closer to the base (i.e. for x < x0) the bending rigidity A is no longer constant but is always a continuously decreasing function of x.
In Fig. 7b we show the resulting propulsive force. We find that larger prescribed volumes V0 lead to systematically higher propulsive force. However, as seen in the figure, the increase slows down; from V0 = 0.4 to V0 = 0.9, the value F increases only by about 4%, while from V0 = 0.7 to V0 = 0.9 only by 0.5%.
In the case where the material has a constant Young's modulus, our result for the optimal bending rigidity means we have a solution for optimal radius of the filament, given by r = (A/Ẽ)1/4. An example of the optimal r for V = 0.5 and a = 0.01 is shown with solid red line in the inset of Fig. 8.
 | ||
Fig. 8 Maximum propulsive force (colours) for A given by the empirical ansatz in eqn (35) as a function of the parameters V0 and a. Inset: The spatially variable thickness of the filament 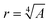 for V0 = 0.5 and a = 0.01 (i.e. we assumed Ẽ = 1). The solid curve is the optimal shape obtained numerically, while the dashed curve is the approximated optimal shape from eqn (35). for V0 = 0.5 and a = 0.01 (i.e. we assumed Ẽ = 1). The solid curve is the optimal shape obtained numerically, while the dashed curve is the approximated optimal shape from eqn (35). | ||
4.2 Approximated optimal A
In order to further study the dependency of F on values of a and V0, we introduce the empirical approximation for the optimal A as | (35) |
Using this model, we may vary the values of both a and V0 and compute the maximum value for F over possible values of x0, as shown in Fig. 8. The results are very similar to those obtained with the optimisation under the constraint C1. Indeed, the propulsive force is systematically larger if a is small and if V0 is large, as was seen in Fig. 5a, while the values of the optimal transition point x0, after which the function A, is a constant are very similar to Fig. 5b (not shown).
The physical interpretation of the results in this section is very similar to the one we proposed in the previous section and for both constraints A is stiff at the base and soft at the distal end with x0 governing the length of the soft distal end.
5 Discussion
5.1 Summary
Enhancing the propulsion of elastic filaments through optimised design is a significant challenge within the realm of micro-robotics.8 One promising approach involves the optimisation of the bending rigidity along the length of the filament, here denoted by A in its dimensionless version. In this study, we focus on the optimisation of A with the aim of maximising the propulsive force generated by a model system: an elastic slender filament with an oscillating slope at its base. To accomplish this, we employ techniques of functional optimisation, first by computing the functional derivative of A using an adjoint problem, and then by using this derivative within a steepest ascent algorithm operating in the functional space. Our optimisation process considers two sets of additional constraints: ensuring that A remains within defined bounds, or maintaining a fixed volume for the filament.Our main finding demonstrates that, in all tested cases, the optimal filament must be stiff at the base and soft at the distal end for optimal propulsion, which we were able to interpret physically. In the case where A is constrained to remain bounded between prescribed values a and b, the optimal solution is invariably piecewise constant: A assumes the upper bound near the filament's base and the lower bound at the distal end. When b is substantially larger than a the propulsive force increases by more than a factor of 4 above the optimal value for a spatially uniform A. The transition point, x0, where the rigidity abruptly goes from the upper bound to the lower bound is located about 2/3 along the filament's length, which we demonstrated is governed by the propulsive physics at the distal end. For the fixed volume constraint, the optimal filament continues to have higher stiffness at the base and becomes softer towards its distal end, but in this case the shape decreases smoothly near the base.
5.2 Practical considerations
The two constraints we considered indicate possible practical ways of designing an optimal elastic filament. The bending rigidity of a filament, A, is determined by the product of the Young's modulus of the material and the moment area of inertia, proportional to r4, where r is the filament's radius. Changes in A may thus be obtained either by changing the Young's modulus or by modifying the filament radius. In the case of bounded A, the optimal piecewise-constant rigidity could be achieved by merging two segments with different Young's moduli. For the fixed volume case, on the other hand, the Young's modulus is fixed and spatially variable radius of the filament is given by r = (A/Ẽ)1/4, shown for example in the inset of Fig. 8.To further illustrate the advantage of using a filament with varying bending rigidity, consider the (mm)-scale PDMS filament from Williams et al.24 with length L = 1.5 mm, radius r = 5 μm and Young's modulus of 3.86 MPa. Using the viscosity μ = 1.15 mPa s24 and frequency ω/2π = 3.6 Hz, we obtain the estimate A ≈ 0.03. Small oscillations with angle ε = 0.4 rad of this filament yields a propulsive force of ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ≈ 0.3 nN. If instead the distal part of the bending rigidity is reduced by one order of magnitude compared to the proximal part, the force increases by almost one order of magnitude to about
≈ 0.3 nN. If instead the distal part of the bending rigidity is reduced by one order of magnitude compared to the proximal part, the force increases by almost one order of magnitude to about ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ≈ 1.7 nN. Similarly, for a PPy filament with L = 9 μm, r = 100 nm,17 a Young's modulus of 100 MPa56 and oscillating with frequency ω/2π = 20 Hz,17 we estimate A ≈ 1 in 65% glycerol solution (μ = 15 mPa s57). Under an oscillation slope of ε = 0.4 rad, we obtained a small propulsive force of
≈ 1.7 nN. Similarly, for a PPy filament with L = 9 μm, r = 100 nm,17 a Young's modulus of 100 MPa56 and oscillating with frequency ω/2π = 20 Hz,17 we estimate A ≈ 1 in 65% glycerol solution (μ = 15 mPa s57). Under an oscillation slope of ε = 0.4 rad, we obtained a small propulsive force of ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ≈ 0.22 pN; however, lowering the bending rigidity of the distal part by two orders of magnitude increases the force by a factor of about 18, to
≈ 0.22 pN; however, lowering the bending rigidity of the distal part by two orders of magnitude increases the force by a factor of about 18, to ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ≈ 4 pN.
≈ 4 pN.
5.3 Comparison with past work
Our results demonstrate rigorously the advantages of having a stiff base and a soft distal end for enhancing propulsion, compared to a uniform filament with optimal constant rigidity, which is consistent with past work.47–50 Singh and Yadava48 reported a 22% increase in propulsion for a linearly tapered elastic filament whose slope at the base was oscillating, while Peng et al.50 found up to 12.5% increase in propulsion using an exponential taper for a clamped oscillating filament. In contrast, the optimal bending rigidity reported in our work (also for imposed oscillating slope at the base) results in a more substantial (four-fold) increase in propulsion.In Peng et al.50 the authors studied the optimal propulsion of a filament with two segments: one rigid and one soft. They showed that for the case of a clamped oscillating filament, the maximum thrust is achieved when the base is rigid and the distal end is soft, with a transition point of 0.82 of the total length. In contrast, for a hinged filament, the propulsion is maximised if the base of the filament is soft and the distal end is stiff, highlighting the importance of the actuation mechanism in determining the optimal bending rigidity.
5.4 Biological relevance
We can draw parallels between our findings and the structure of a human spermatozoon. The flagellum of a spermatozoon cell is tapered,6 with an estimated proximal-to-distal ratio in bending rigidity of 35,58 and after about 0.65 of the length of the filament, the distal end maintains a constant level of stiffness. Moreover, a sperm flagellum is forced by a continuous internal actuation via molecular motors distributed along the whole flagellum54 except for the passive soft region at the distal end (the so-called ‘end piece’). In the study by Neal et al.58 the authors noted that this passive end piece can result in a remarkable increase in swimming speed, up to 72%, and a substantial boost in hydrodynamic efficiency, up to 438%. This result is consistent with our findings, where the presence of a soft distal end is crucial for enhancing the propulsion of the filament. We note, however, that the comparison with biological cells is limited, owing to the qualitatively different actuation mechanisms.5.5 Outlook
The methodology used in this study could be extended to tackle optimisation under other actuation mechanisms. This could allow comparison with existing artificial swimmers employing rotating51 or oscillating magnetic heads.17 When applied to the case of a clamped filament with an oscillating base, we found much more complex optimal shapes than for a hinged filament, hinting at a very rich optimal landscape.Additionally, our study focused on maximising solely the propulsive force, and it will be valuable to explore other objectives such as maximising swimming speed or hydrodynamic efficiency. In our simplified model, maximising swimming speed for a swimmer with a passive filament would lead to the same optimal solution. Indeed, in that case the steady horizontal constant velocity V of the swimmer is obtained by balancing drag and propulsion as  , where Dh is drag coefficient for the head.48,54 Since, at small amplitude, only the propulsive force depends on filament dynamics, the optimisation for V is identical to that of
, where Dh is drag coefficient for the head.48,54 Since, at small amplitude, only the propulsive force depends on filament dynamics, the optimisation for V is identical to that of ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) .
.
Our study exhibits certain limitations that could be subject to future research. Firstly, our assumption of linearised elastohydrodynamics means that our model is not suitable for describing large displacements of the filament. Secondly, we rely on resistive-force theory, which simplifies our analysis by neglecting hydrodynamic interactions between different parts of the filament. While this is a reasonable approximation for small amplitude deformations, it may not hold true when the filament undergoes significant curvature. Furthermore, the model does not account for the change in drag coefficients with r, which appear in the force balance eqn (4) and in the expression of the propulsive force (6). In the present work, we looked at changes in bending stiffness up to 3–4 orders of magnitude, which would correspond to changes in r by about one order of magnitude. This will result in changing drag coefficients by about a factor of 2, which may alter the precise quantitative nature of the optimal solution.
Data availability
All results and figures in the article were generated using Matlab R2024a. The Matlab codes can be found at the following DOI: 10.5281/zenodo.15111675.Conflicts of interest
There are no conflicts to declare.Appendix
A.1 Algorithm for constraint C1 (bounded A)
For a bounded A(x), we have to make sure that at each optimisation step, it remains within the chosen domain [a,b]. To ensure this, we introduce a projection operator P(A) = max(a,min(A,b)) and we adapt the projected gradient method, which consists of the following steps:55• Choose the initial condition A1, a ≤ A1 ≤ b.
• For k = 1,2,3,…, repeat the following steps until convergence criteria are achieved
(1) Solve for filament dynamics, eqn (11)–(13), and the adjoint problem, eqn (23) and (24), with given Ak. We use Matlab solver bvp4c to solve the ODE system;
(2) Set sk = dF/dA|Ak, where the functional derivative is computed using eqn (26);
(3) Choose step σk by projected Armijo rule (see below) such that F(P(Ak + σksk)) > F(Ak);
(4) Set Ak+1 := P(Ak + σksk).
Defining the errors
| err1 = |F(Ak) − F(Ak−1)|/F(Ak−1), err2 = max|Ak − Ak−1|, | (36) |
To choose the optimisation step σk, we use the projected Armijo rule and choose maximum σk ∈ {1,1/2,1/4,…} for which
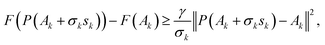 | (37) |
A.2 Algorithm for constraint C2 (fixed volume)
In the case of constraint (C2), we use a similar algorithm to the one reported in Section 2.4 but modify the objective function to account for constant volume constraint,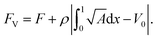 | (38) |
 . The optimisation algorithm is then similar to the one in Section A.1, replacing F with FV and considering the projection function only for lower boundary, P(A) = max(a,A). Since we do not want the final solution to depend on the value of ρ, we set the penalty parameter ρ to be an increasing sequence ρm = ρ02m, where ρ0 is an initial choice. For each value of ρm we solve the minimisation problem reported in Section A.1 until convergence is reached for given tolerances δm1 and δm2. For convenience, we work in terms of the radius r instead of A, and thus the errors at each step k are err1 = |F(Ak) − F(Ak−1)|/F(Ak−1) and err2 = max|rk − rk−1|. We then consider the next value of ρm and follow the procedure again, until the error err3 = |F(Am) − F(Am−1)|/F(Am−1) + max|rm − rm−1| gets smaller than a set tolerance δ3 or a maximum number of iterations is reached. In our solution we set min
. The optimisation algorithm is then similar to the one in Section A.1, replacing F with FV and considering the projection function only for lower boundary, P(A) = max(a,A). Since we do not want the final solution to depend on the value of ρ, we set the penalty parameter ρ to be an increasing sequence ρm = ρ02m, where ρ0 is an initial choice. For each value of ρm we solve the minimisation problem reported in Section A.1 until convergence is reached for given tolerances δm1 and δm2. For convenience, we work in terms of the radius r instead of A, and thus the errors at each step k are err1 = |F(Ak) − F(Ak−1)|/F(Ak−1) and err2 = max|rk − rk−1|. We then consider the next value of ρm and follow the procedure again, until the error err3 = |F(Am) − F(Am−1)|/F(Am−1) + max|rm − rm−1| gets smaller than a set tolerance δ3 or a maximum number of iterations is reached. In our solution we set min![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δm1 = 10−4, min
δm1 = 10−4, min![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δm2 = 10−4 and δ3 = 5 × 10−5.
δm2 = 10−4 and δ3 = 5 × 10−5.
Acknowledgements
The authors would also like to thank M. Tătulea-Codrean for useful discussions and feedback. This project has received funding from the European Research Council under the European Union's Horizon 2020 Research and Innovation Programme (Grant No. 682754 to E. L.).References
- L. J. Fauci and R. Dillon, Annu. Rev. Fluid Mech., 2006, 38, 371–394 CrossRef.
- D. L. Koch and G. Subramanian, Annu. Rev. Fluid Mech., 2011, 43, 637–659 CrossRef.
- R. E. Goldstein, Annu. Rev. Fluid Mech., 2015, 47, 343 CrossRef PubMed.
- N. Wadhwa and H. C. Berg, Nat. Rev. Microbiol., 2022, 20, 161–173 CrossRef CAS PubMed.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- E. A. Gaffney, H. Gadêlha, D. J. Smith, J. R. Blake and J. C. Kirkman-Brown, Annu. Rev. Fluid Mech., 2011, 43, 501–528 CrossRef.
- E. Lauga, Annu. Rev. Fluid Mech., 2016, 48, 105–130 CrossRef.
- B. J. Nelson, I. K. Kaliakatsos and J. J. Abbott, Annu. Rev. Biomed. Eng., 2010, 12, 55–85 CrossRef CAS PubMed.
- K. E. Peyer, A. W. Mahoney, L. Zhang, J. J. Abbott and B. J. Nelson, Microbiorobotics, 2012, 165–199 Search PubMed.
- K. E. Peyer, L. Zhang and B. J. Nelson, Nanoscale, 2013, 5, 1259–1272 Search PubMed.
- J. Li, B. E.-F. de Ávila, W. Gao, L. Zhang and J. Wang, Sci. Rob., 2017, 2, eaam6431 CrossRef PubMed.
- X.-Z. Chen, M. Hoop, F. Mushtaq, E. Siringil, C. Hu, B. J. Nelson and S. Pané, Appl. Mater. Today, 2017, 9, 37–48 CrossRef.
- H. Zhou, C. C. Mayorga-Martinez, S. Pané, L. Zhang and M. Pumera, Chem. Rev., 2021, 121, 4999–5041 Search PubMed.
- S. Schuerle, S. Pané, E. Pellicer, J. Sort, M. D. Baró and B. J. Nelson, Small, 2012, 8, 1498–1502 Search PubMed.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862–865 CrossRef CAS PubMed.
- H. C. M. Sun, P. Liao, T. Wei, L. Zhang and D. Sun, Micromachines, 2020, 11, 404 CrossRef PubMed.
- B. Jang, E. Gutman, N. Stucki, B. F. Seitz, P. D. Wendel-Garca, T. Newton, J. Pokki, O. Ergeneman, S. Pané and Y. Or, et al. , Nano Lett., 2015, 15, 4829–4833 CrossRef CAS PubMed.
- L. Zhang, J. J. Abbott, L. Dong, B. E. Kratochvil, D. Bell and B. J. Nelson, Appl. Phys. Lett., 2009, 94, 064107 CrossRef.
- E. Lauga, The fluid dynamics of cell motility, Cambridge University Press, 2020, vol. 62 Search PubMed.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- K. Machin, J. Exp. Biol., 1958, 35, 796–806 CrossRef.
- C. H. Wiggins and R. E. Goldstein, Phys. Rev. Lett., 1998, 80, 3879 CrossRef CAS.
- S. Guo, Q. Pan and M. B. Khamesee, Microsyst. Technol., 2008, 14, 307–314 CrossRef.
- B. J. Williams, S. V. Anand, J. Rajagopalan and M. T. A. Saif, Nat. Commun., 2014, 5, 3081 CrossRef PubMed.
- V. Magdanz, I. S. Khalil, J. Simmchen, G. P. Furtado, S. Mohanty, J. Gebauer, H. Xu, A. Klingner, A. Aziz and M. Medina-Sánchez, et al. , Sci. Adv., 2020, 6, eaba5855 CrossRef CAS PubMed.
- V. Magdanz, A. Klingner, L. Abelmann and I. S. Khalil, J. Micro Bio Rob., 2022, 18, 49–60 CrossRef.
- N. Celi, D. Gong and J. Cai, Sci. Rep., 2021, 11, 21728 CrossRef CAS PubMed.
- F. Mushtaq, H. Torlakcik, M. Hoop, B. Jang, F. Carlson, T. Grunow, N. Läubli, A. Ferreira, X.-Z. Chen and B. J. Nelson, et al. , Adv. Funct. Mater., 2019, 29, 1808135 CrossRef.
- C. H. Wiggins, D. Riveline, A. Ott and R. E. Goldstein, Biophys. J., 1998, 74, 1043–1060 CrossRef CAS PubMed.
- T. S. Yu, E. Lauga and A. Hosoi, Phys. Fluids, 2006, 18, 091701 CrossRef.
- T.-H. Wu, R.-S. Guo, G.-W. He, Y.-M. Liu and D. Qi, J. Theor. Biol., 2014, 349, 1–11 CrossRef PubMed.
- C. Moreau, L. Giraldi and H. Gadêlha, J. R.Soc., Interface, 2018, 15, 20180235 Search PubMed.
- M. Jabbarzadeh and H. C. Fu, J. Comput. Phys., 2020, 418, 109643 CrossRef.
- A. Hilfinger, A. K. Chattopadhyay and F. Jülicher, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 79, 051918 CrossRef PubMed.
- D. Oriola, H. Gadêlha and J. Casademunt, R. Soc. Open Sci., 2017, 4, 160698 CrossRef PubMed.
- D. Tam and A. Hosoi, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2011, 83, 045303 CrossRef PubMed.
- O. Pironneau and D. Katz, J. Fluid Mech., 1974, 66, 391–415 Search PubMed.
- O. Pironneau, D. Katz, T. Wu, C. Brokaw and C. Brennen, Swimming and Flying in Nature, 1975, vol. 1, pp. 161–172 Search PubMed.
- E. Lauga, Phys. Rev. Fluids, 2020, 5, 123101 CrossRef.
- S. J. Lighthill, Mathematical biofluiddynamics, SIAM, 1975 Search PubMed.
- S. E. Spagnolie and E. Lauga, Phys. Fluids, 2010, 22, 455 Search PubMed.
- E. Lauga and C. Eloy, J. Fluid Mech., 2013, 730, R1 CrossRef.
- M. F. Velho Rodrigues, M. Lisicki and E. Lauga, PLoS One, 2021, 16, e0252291 CrossRef CAS PubMed.
- M. Lisicki, M. F. V. Rodrigues and E. Lauga, J. Fluid Mech., 2024, 978, R1 CrossRef.
- E. Lauga, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2007, 75, 041916 CrossRef PubMed.
- H. Gadêlha, Regul. Chaotic Dyn., 2013, 18, 75–84 CrossRef.
- J. S. Rathore, R. Majumdar and N. N. Sharma, IEEE Trans. Nanotechnol., 2012, 11, 1117–1121 Search PubMed.
- T. S. Singh and R. Yadava, Biomed. Phys. Eng. Express, 2017, 4, 015019 CrossRef.
- R. Kotesa, J. Rathore and N. Sharma, Bionanoscience, 2013, 3, 343–347 CrossRef.
- Z. Peng, G. J. Elfring and O. S. Pak, Soft Matter, 2017, 13, 2339–2347 RSC.
- A. M. Maier, C. Weig, P. Oswald, E. Frey, P. Fischer and T. Liedl, Nano Lett., 2016, 16, 906–910 CrossRef CAS PubMed.
- R. Cox, J. Fluid Mech., 1970, 44, 791–810 CrossRef.
- A. Öchsner, Classical beam theories of structural mechanics, Springer, 2021, vol. 42 Search PubMed.
- O. S. Pak and E. Lauga, Fluid–Structure Interactions in Low-Reynolds-Number Flows, The Royal Society of Chemistry, 2015, pp. 100–167 Search PubMed.
- M. Hinze, R. Pinnau, M. Ulbrich and S. Ulbrich, Optimization with PDE constraints, Springer Science & Business Media, 2008, vol. 23 Search PubMed.
- J. D. Madden, Electroactive Polymers for Robotic Applications: Artificial Muscles and Sensors, Springer, 2007, ch. 5, pp. 121–152 Search PubMed.
- J. B. Segur and H. E. Oberstar, Ind. Eng. Chem., 1951, 43, 2117–2120 CrossRef CAS.
- C. V. Neal, A. L. Hall-McNair, J. Kirkman-Brown, D. J. Smith and M. T. Gallagher, Phys. Rev. Fluids, 2020, 5, 073101 CrossRef.
| This journal is © The Royal Society of Chemistry 2025 |