 Open Access Article
Open Access ArticleEffects of ligand vs. linker on phase behavior and mechanical properties of nanoparticle gels†
Qizan
Chen
 a,
Dinesh
Sundaravadivelu Devarajan
a,
Dinesh
Sundaravadivelu Devarajan
 a,
Arash
Nikoubashman
a,
Arash
Nikoubashman
 bc,
Michael P.
Howard
bc,
Michael P.
Howard
 *d and
Jeetain
Mittal
*d and
Jeetain
Mittal
 *aef
*aef
aArtie McFerrin Department of Chemical Engineering, Texas A&M University, College Station, TX 77843, USA. E-mail: jeetain@tamu.edu
bLeibniz-Institut für Polymerforschung Dresden e.V., Hohe Straße 6, 01069 Dresden, Germany
cInstitut für Theoretische Physik, Technische Universität Dresden, 01069 Dresden, Germany
dDepartment of Chemical Engineering, Auburn University, Auburn, Alabama 36849, USA. E-mail: mphoward@auburn.edu
eDepartment of Chemistry, Texas A&M University, College Station, TX 77843, USA
fInterdisciplinary Graduate Program in Genetics and Genomics, Texas A&M University, College Station, TX 77843, USA
First published on 23rd April 2025
Abstract
Nanoparticle gels have attracted considerable attention due to their highly tunable properties. One strategy for producing nanoparticle gels involves using strong local attractions between polymeric molecules, such as DNA hybridization or dynamic covalent chemistry, to form percolated nanoparticle networks. These molecules can be used in two distinct roles: as “ligands” with one end grafted to a nanoparticle or as “linkers” with both ends free. Here, we explore how these roles shape the phase behavior and mechanical properties of gel-like nanoparticle assemblies using coarse-grained simulations. We systematically vary the interaction strength and bending stiffness of both ligands and linkers. We find that phase separation can be limited to low nanoparticle volume fractions by making the ligands rigid, consistent with previous studies on linked nanoparticle gels. At fixed interaction strength and volume fraction, both ligand- and linker-mediated nanoparticle assemblies show similar mechanical responses as bending stiffness is varied. However, a comparison between the two association schemes reveals that the linked nanoparticles form rigid percolated networks that are less stretchable than the ligand-grafted gels, despite exhibiting similar tensile strength. We attribute these differences between ligands and linkers to the distinct structural arrangement of nanoparticles within the gel. Our findings highlight the potential to use different association schemes to tune specific mechanical properties.
1 Introduction
Nanoparticle gels are promising functional materials because their properties can be modulated through their mesoscopic structure, which is determined by the physical or chemical interactions between the nanoparticles.1–8 For example, the solid-like network structure of gels can give rise to distinct mechanical properties9 as well as optical properties facilitated by coupling effects such as local surface plasmon resonance.10 Compared to nanoparticle superlattices,11–13 nanoparticle gels provide a potentially more robust, processable alternative. Previous experimental and simulation studies have also shown that modulating the mesostructure within nanoparticle gels provides ample opportunities to tune their properties.14–16Nanoparticle gels are typically made by inducing a short-range attraction between the nanoparticles.17 Various strategies can be used to create attraction, including solvent-mediated van der Waals attraction and polymer-induced depletion attraction.1,18 The attraction between nanoparticles causes the fluid-like nanoparticle dispersion to become thermodynamically unstable, then the nanoparticles kinetically arrest as a gel during their spinodal decomposition into dilute and condensed phases.19 This mechanism produces a “nonequilibrium” gel that is susceptible to aging because the arrested phase separation can slowly continue over time.20–22
Alternatively, nanoparticles with a limited number of highly localized attractive sites (so-called “patchy particles”) can form long-lived networks without phase separation, resulting in an “equilibrium” gel.23–28 Because such networks are thermodynamically stable, equilibrium gels tend to be less susceptible to aging than nonequilibrium gels. Equilibrium gels have been formed in simulations of patchy nanoparticles by directly limiting the number of attractive patches29–31 and in experiments using trivalent and tetravalent DNA nanostars.32–34 However, these types of valence limitation require careful nanoscopic control that presents challenges for large-scale fabrication and tunability. One way to overcome these challenges is by introducing a secondary “linking” species, such as polymers,35–37 DNA,38,39 and ionic molecules,3,40,41 whose concentration can be used to restrict valence macroscopically.14,24 For example, recent simulations indicated that adjusting the number ratio of linkers to nanoparticles and modifying the flexibility of oligomeric linkers both significantly affected the phase behavior and structure of the resulting gels.12,27,42
For the strategies described above, both ends of the linking molecules are not permanently attached to the nanoparticle. Alternatively, one end of a molecule can be grafted to a nanoparticle to act as a surface-bound ligand that facilitates attraction. For example, reversible gel assemblies have been created using ligands with dynamic covalent chemistry strategies,14,43,44 and there is growing interest in reversible assemblies involving DNA-grafted nanoparticles.2,45–48 While strategies for using linker design to control gelation have been relatively well-studied,7,8,24,27,42 less is known about how ligand design modulates the phase behavior and mechanical properties of gels and to what extent ligand-mediated and linker-mediated gelation differ.
In this work, we employ coarse-grained molecular dynamics simulations of generic nanoparticles and linear polymers to investigate how the association mechanism, where the polymers act either as ligands or linkers, influences the phase behavior and mechanical properties of nanoparticle gels. Furthermore, we systematically vary the polymer stiffness, finding that the range of volume fractions over which phase separation occurs gradually narrows with increasing stiffness, bearing similarities to linked nanoparticle gels. Under uniaxial tensile deformation, equilibrium gels formed through both ligands and linkers showed noticeable changes in mechanical properties such as their shear modulus, tensile strength, and network stretchability as the ligand stiffness varied. Notably, a comparison between ligand-grafted nanoparticle gels and linked nanoparticle gels revealed distinct differences in certain mechanical properties, highlighting the ability to tune the mechanical response of equilibrium nanoparticle gels solely through the association scheme.
2 Model and simulation methods
Similarly to previous work on DNA-functionalized nanoparticles,49 we used a coarse-grained model of a spherical nanoparticle with surface-grafted ligands. The bare nanoparticle had diameter dc = 6σ, where σ is the unit of length in our simulations. We created grafting sites for the ligands by subdividing the faces of an icosahedron once and scaling the resulting 42 vertices to lie on the surface of the bare nanoparticle [Fig. 1(a)]. These vertices were explicitly represented as particles with mass m and diameter σ, where m is the unit of mass in our simulations. We then iteratively grafted 14 linear polymers onto the vertex sites, starting from an initial randomly chosen site that was the same for all nanoparticles, followed by a site that is farthest from the previous site(s) [Fig. 1(b)]. Each polymer consisted of 10 beads with mass m and diameter dl = σ. In total, the nanoparticle was represented by one central particle used to compute the bare nanoparticle interactions that also had mass m, 42 grafting sites, and 140 polymer beads, so the total mass of a ligand-grafted nanoparticle was 183m. We used Nc = 1000 nanoparticles and varied the nanoparticle volume fraction η = Ncπdc3/(6V) between 0.01 and 0.13 in steps of 0.02 by adjusting the volume V of the simulation box. All simulations were performed at constant temperature T.We modeled the excluded–volume interactions between the bare nanoparticles and between the bare nanoparticles and polymer beads using the purely repulsive Weeks–Chandler–Andersen (WCA) potential,50
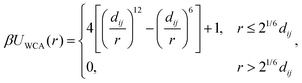 | (1) |
 | (2) |
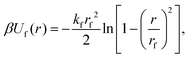 | (3) |
The polymer flexibility was controlled using a harmonic bending potential, applied between three consecutively bonded polymer beads,
 | (4) |
Attraction between the terminal beads of the ligands on different nanoparticles was modeled using the Lennard-Jones (LJ) potential,
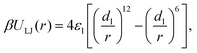 | (5) |
To compare ligand-mediated gelation with linker-mediated gelation, we created two complementary linker models based on our ligand model [Fig. 1(d)]. Linker I had the same degree of polymerization as the ligands (10 beads), but featured a terminal bead attracted to the grafting sites on the bare nanoparticle. Linker II contained twice as many monomers as linker I (20 beads) and had only terminal beads capable of connecting to the grafting sites on the nanoparticles. Hence, linker I can be regarded as a ligand without a permanent graft to the nanoparticle, while linker II effectively behaves as two linker I molecules that are permanently and exclusively paired. The number of linker molecules was chosen to keep the total number of monomers the same in all simulations. All three association schemes (ligand, linker I & II) can produce a comparable chain-like connection between two nanoparticles; however, different bonding motifs are possible for each model, and the mechanical properties associated with the connections may also differ. The attraction between the linker end(s) and a grafting site was modeled using the LJ potential [eqn (5)] with attraction strength εc; the rest of the linker interactions were the same as for the ligands.
We performed molecular dynamics simulations using HOOMD-blue (version 2.9.3)56 with features extended using azplugins (version 0.10.1).57 The integration time step was 0.005 τ, and we maintained the temperature T using a Langevin thermostat with friction coefficient 0.01 m/τ, where  is the unit of time in the simulations. Following previous studies,7,27 we prepared configurations under different conditions by slow annealing: first, we created three different initial configurations by dispersing the Nc = 1000 nanoparticles randomly in a large cubic simulation box with edge length L = 1781σ and periodic boundary conditions. Initially, there were no attractions between ligands [i.e., only purely repulsive interactions through eqn (1)], and the box was compressed to the desired volume fraction η by reducing the edge length at a constant rate over a 5 × 103τ time period, followed by an equilibration period of 5 × 104τ at the required volume fraction. We then gradually introduced attraction between the ligands by increasing εl to 5.0 in steps of 0.5, with each εl value being simulated for a duration of 105τ. We confirmed that for the initial purely repulsive interactions, both nanoparticles and polymers were able to diffuse at least the nanoparticle radius within 100τ,58 allowing the system to relax and explore new configurations (Fig. S1 and S2, ESI†).
is the unit of time in the simulations. Following previous studies,7,27 we prepared configurations under different conditions by slow annealing: first, we created three different initial configurations by dispersing the Nc = 1000 nanoparticles randomly in a large cubic simulation box with edge length L = 1781σ and periodic boundary conditions. Initially, there were no attractions between ligands [i.e., only purely repulsive interactions through eqn (1)], and the box was compressed to the desired volume fraction η by reducing the edge length at a constant rate over a 5 × 103τ time period, followed by an equilibration period of 5 × 104τ at the required volume fraction. We then gradually introduced attraction between the ligands by increasing εl to 5.0 in steps of 0.5, with each εl value being simulated for a duration of 105τ. We confirmed that for the initial purely repulsive interactions, both nanoparticles and polymers were able to diffuse at least the nanoparticle radius within 100τ,58 allowing the system to relax and explore new configurations (Fig. S1 and S2, ESI†).
An example of the evolution of the attractive potential energy per nanoparticle βULJ/Nc during the annealing process is shown in Fig. 2(a) for η = 0.01 and ks = 0. The final configurations obtained at each εl value were then used to perform an additional simulation for 104τ at each value of εl, from which 1000 configurations were collected at uniform time intervals for characterizing the structure and phase behavior. A similar procedure was used for preparing the linker-mediated assemblies, in which we incrementally increased εc simultaneously with εl from 0 to 5. We then additionally increased εc to 10, with a time period of 105τ after the increase. We note that all reported averages are computed over multiple independent simulations and the configurations collected from each.
3 Results and discussion
3.1 Ligand-grafted nanoparticle assemblies
Following previous studies,27,42 we first investigated the mesostructure of the ligand-grafted nanoparticle assemblies. To characterize whether the nanoparticles formed a single phase or tended toward phase separation, we computed their partial static structure factor, | (6) |
We additionally evaluated the percolation of the nanoparticles into a space-spanning network. Specifically, we considered two nanoparticles to be connected if the distance between any attractive particles in their ligands was less than 1.4σ, which corresponds to the approximate location of the first minimum in the radial distribution function between attractive particles of ligands on different nanoparticles (Fig. S3, ESI†). We considered a nanoparticle assembly to be percolated if a continuous path could be traced between any nanoparticle in the central simulation box and its periodic images in all three Cartesian directions [Fig. 2(c)]. These calculations were performed using NetworkX.59 We then defined a percolation boundary that demarcated the conditions under which more than 90% of sampled configurations were percolated.
The extrapolated S(0) and percolation lines are shown in Fig. 2(d)–(f) for flexible, semiflexible, and rigid ligands. Similar diagrams for other bending stiffnesses are available in Fig. S4 (ESI†). We found that S(0) < 10, indicating that the nanoparticles remained in a single phase, when εl ≲ 3 regardless of η, although percolated networks still formed for sufficiently large η. For εl ≳ 3, we found S(0) > 10 over a limited range of η, indicating phase separation of the nanoparticles. This phase-separated region narrowed with increasing bending stiffness, extending until η ≈ 0.13, 0.07, and 0.05 for the flexible, semiflexible, and rigid ligands, respectively. This behavior contrasts with previous observations for linker-mediated nanoparticle assemblies,42 where both flexible and rigid linkers led to phase separation, whereas semiflexible linkers maintained a stable fluid phase due to their tendency to bind both ends to the same nanoparticle in “loop”' motifs. Our model explicitly prohibits loop formation, supporting the hypothesis of prior works that loop formation may suppress phase separation.27,42
We selected η = 0.13 and 3 ≤ εl ≤ 5 for further investigation of the mechanical properties of the nanoparticle assemblies because these conditions produced percolated nanoparticle assemblies that were not phase separated for all bending stiffnesses investigated. For each of our three independent simulations, we subjected the final assemblies from the annealing to uniaxial tensile deformation along each of the three Cartesian directions, giving a total of 9 measurements for each ligand. We extended the length of the simulation box in the chosen direction by a factor λ that increased at a constant rate of ![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) = 5 × 10−4τ−1. To conserve the system volume, the lengths of the simulation box in the other two directions were simultaneously compressed by a factor of λ1/2, consistent with a Poisson's ratio of 0.5 typical for soft materials.60 We then computed the engineering stress from the diagonal elements of the measured stress tensor. As an example, for deformation in the x direction, we extended the box as λ = Lx/Lx,0 = 1 +
= 5 × 10−4τ−1. To conserve the system volume, the lengths of the simulation box in the other two directions were simultaneously compressed by a factor of λ1/2, consistent with a Poisson's ratio of 0.5 typical for soft materials.60 We then computed the engineering stress from the diagonal elements of the measured stress tensor. As an example, for deformation in the x direction, we extended the box as λ = Lx/Lx,0 = 1 + ![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) t, where Lx,0 and Lx are the initial and extended box lengths in the x direction, respectively. We calculated the engineering stress as σE = [σxx − (σyy + σzz)/2]/λ, where σαα is the diagonal element for direction α in the stress tensor. Typically, we simulated λ in the range of 1.0 to 3.5 (time period 5 × 103τ). Since the extension rate can affect the tensile behavior of viscoelastic media, we repeated the uniaxial deformation simulations for the semiflexible system at half the extension rate (Fig. S5, ESI†). We found that a lower extension rate leads to a decrease in σE, consistent with previous studies,61,62 but does not significantly alter the overall trend of the stress curve or the corresponding mechanical properties. Moreover, in most cases, we found consistent initial behavior between independent simulations and extension directions (Fig. S6, ESI†), so we averaged them together to improve statistics.
t, where Lx,0 and Lx are the initial and extended box lengths in the x direction, respectively. We calculated the engineering stress as σE = [σxx − (σyy + σzz)/2]/λ, where σαα is the diagonal element for direction α in the stress tensor. Typically, we simulated λ in the range of 1.0 to 3.5 (time period 5 × 103τ). Since the extension rate can affect the tensile behavior of viscoelastic media, we repeated the uniaxial deformation simulations for the semiflexible system at half the extension rate (Fig. S5, ESI†). We found that a lower extension rate leads to a decrease in σE, consistent with previous studies,61,62 but does not significantly alter the overall trend of the stress curve or the corresponding mechanical properties. Moreover, in most cases, we found consistent initial behavior between independent simulations and extension directions (Fig. S6, ESI†), so we averaged them together to improve statistics.
We found that σE gradually increased for small deformations for ligand stiffnesses ks ≲ 6, corresponding to flexible and semiflexible ligands [Fig. 3(a), (b) and Fig. S7, ESI†]. For rigid ligands, σE increased more rapidly with small changes in λ for all εl values, and also exhibited a narrower peak at smaller λ values compared to the flexible and semiflexible ligands [Fig. 3(c) and Fig. S7, ESI†]. This behavior is most apparent when σE is compared for different bending stiffnesses ks at the strongest ligand–ligand attraction simulated [εl = 5, Fig. 3(d)]. To further compare mechanical properties as a function of ligand flexibility, we extracted the maximum value of σE as the ultimate tensile strength σUTS, and its corresponding ultimate tensile extension factor λUTE as an indicator of network stretchability from Fig. 3(d). Following a recent study,7 we also determined the shear modulus G, which quantifies the rigidity of the network, by fitting σE = G(λ − 1/λ2) in the limit of small deformations [fitted regions shown in Fig. 3(d)]. We found that G and σUTS increased moderately with increasing ks up to ks = 6 (i.e., for flexible and semiflexible ligands), and then significantly increased for more rigid ligands [Fig. 3(e)]. In contrast, λUTE showed a distinct transition: it remained around λUTE = 1.4 for ks ≤ 6, but sharply decreased to approximately λUTE = 1.2 for more rigid ligands. We attribute this reduction to the more limited internal molecular degrees of freedom of rigid ligands [Fig. 3(e)]. These observations highlight that flexible and semiflexible ligands produced soft, weak nanoparticle gels that were more stretchable than those produced using rigid ligands.
3.2 Comparison to linker-mediated nanoparticle assemblies
After characterizing how the mesostructure and mechanical properties of the ligand-grafted nanoparticle assemblies varied with ligand–ligand attraction and ligand bending stiffness, we proceeded to investigate how this behavior was similar or different from that in linker-mediated nanoparticle assemblies. As described in Section 2, we studied two different types of linkers: linker I, having one end that facilitates linker–linker attraction and one end that facilitates linker-nanoparticle attraction, and linker II, which is twice as long as linker I and whose ends facilitate only linker-nanoparticle attraction. For linker I, we fixed the linker–linker attraction strength to εl = 5 to compare with the most attractive ligand-grafted nanoparticles. Linker II does not have this parameter because it is effectively two linker I molecules that are permanently associated together. We used these linkers to create nanoparticle assemblies and compute their mechanical properties for different linker-nanoparticle attraction strengths εc at the same volume fraction (η = 0.13) that was used for the ligand-grafted nanoparticles.We computed the average engineering stress σE by applying uniaxial tensile deformation on the assemblies formed with linker I and linker II for varying linker stiffness at two attraction strengths εc = 5 and 10 [Fig. 4(a)–(c) and Fig. S8, ESI†]. We found that the rate of change in σE at small deformations increased monotonically with increasing linker stiffness for both linker I and linker II. In contrast, ligand-mediated nanoparticle assemblies only exhibited prominent differences in the stress response at small deformations when the ligands became rigid, as shown by comparing the stress response for the ligand- and linker-mediated assemblies at εc = 10 [Fig. 4(a)–(c) and Fig. S8, ESI†]. Further, whether a maximum in σE was attained using linker I or linker II depended on the chain stiffness.
One direct cause of these differences in mechanical properties could be variation in association resulting from attraction or bond formation between beads. To clarify the association of terminal beads, we computed various local coordination metrics for the nanoparticles and polymers in the different models. Fig. S9(a) (ESI†) shows that when εc = 5, a significant number of linkers are not attached to the particle surface, but as εc increases to 10, such free linkers are almost absent. This is also reflected in the weak σE observed for εc = 5, whereas at εc = 10, the tensile behavior becomes comparable to that of ligand-mediated nanoparticle assemblies [Fig. 4(a)–(c) and Fig. S8, ESI†]. We further examined the specificity of the attraction between linker terminals and surface sites. Fig. S9(b) (ESI†) shows that the average number of linkers surrounding a nanoparticle exceeds 14, which is the number of ligands per nanoparticle, indicating that the distribution of linkers and ligands onto nanoparticles also differs.
We also visually noted that the linker-attaching terminal beads of linker I tended to cluster (Fig. 4), so we quantified this aggregation and compared the binding of the terminal beads in the linker I and ligand models (Fig. S10, ESI†). At εl = 5, the linker-attaching terminal beads of both models were mostly bound to each other [Fig. S10(a), ESI†], and their average coordination number was around 7 [Fig. S10(b), ESI†]. Notably, in the semiflexible regime, the difference in terminal bead aggregation between the ligand and linkers [Fig. S9(b), ESI†] or between the two types of linkers [Fig. S10(b), ESI†] is minimal; however, their σE responses differ significantly [Fig. 4(b)], suggesting that the mechanical behavior of the gels is likely influenced by the overall network structure rather than just the aggregation of the terminal beads.
Meanwhile, we also noticed significant variability in the stress curves of rigid linker II, which we attribute to the formation of lamellar-like structures [Fig. 4(c)]. Once the lamellae form, the mechanical properties become highly directional (Fig. S11, ESI†). In the direction perpendicular to the lamellae, the σUTS increases significantly. Because the orientation of the lamellae is random, isolating the effects of anisotropy in these structures is challenging. Therefore, in the subsequent analysis, we continue to average across all extension directions, which might be regarded as an orientational average.
To better quantify the impact of chain stiffness and association scheme on mechanical properties, we computed σUTS, λUTE, and G for the linker-mediated nanoparticle assemblies. To compare between the different models, we focused on εc = 10, which yielded similar magnitudes of stress for various bending stiffnesses [Fig. 5(a)–(c)]. We found that linker I, despite having the same length and self-interactions as the ligands, produced nanoparticle assemblies with distinct mechanical properties: the assemblies were more rigid (i.e., higher G) and less stretchable (i.e., lower λUTE) compared to the ligand-mediated nanoparticle assemblies, while exhibiting similar ultimate tensile strength σUTS at all ks values. As we have shown above, the aggregation behavior of their linker-attaching beads is similar [Fig. S9(b), ESI†]. Therefore, we attribute the differences in G and λUTE to the tendency of the nanoparticles to form clusters in the linker-mediated nanoparticle assemblies7 (Fig. S12 and Movies S1–S6, ESI†), as well as the disruption of attractions between surface sites and nanoparticle-attaching beads (Fig. S13, ESI†). When flexible and semiflexible linker II (i.e., ks ≲ 6) were used, the resulting assemblies were softer (lower G) and weaker (lower σUTS) compared to both the linker I and ligand-mediated assemblies, but the extent to which they could be stretched, as indicated by λUTE, fell in between that of linker I and the ligands, most likely because of the longer chain length of linker II. This variation in extension capability may also be related to the dispersion of the nanoparticles. Visualization showed that the nanoparticles with linkers tended to locally aggregate (Movies S1–S9, ESI†), reducing the uniformity of the percolated network, which we hypothesize may make it more susceptible to deformation than ligand-mediated networks. For ks > 10, both σUTS and G of the linker II systems increased rapidly due to the emergence of lamellar-like structural ordering, which was also highlighted by the presence of sharp peaks in S(q) (Fig. S14 and S15, ESI†). This lamellar structure formed when there was sufficient attraction (εc ≥ 4) between the rigid linker II chains and the nanoparticles (Fig. S16, ESI†). Such ordered structures can exhibit high resistance to tensile deformation before rupturing,63 which is consistent with the high values of σUTS and G for rigid linker II (also see Movies S1–S9, ESI†).
 | ||
| Fig. 5 (a) Shear modulus G, (b) ultimate tensile strength σUTS, and (c) its corresponding strain λUTE of gels as functions of bending stiffness ks for ligand-grafted (red), linker I mediated (blue), and linker II mediated (green) nanoparticle assemblies. These mechanical properties are extracted from the strain–stress curves shown in Fig. 3 and 4, respectively. For the linked nanoparticle assemblies, the properties are shown for linker-nanoparticle attraction strength of εc = 10. Error bars represent the standard error of the mean across independent simulations and extension directions. | ||
4 Conclusions
In this computational study, we investigated the phase behavior and mechanical properties of gel-like nanoparticle assemblies produced using associative polymers as either grafted ligands or free linkers. In the ligand-mediated nanoparticle assemblies, we found that sufficiently strong ligand–ligand attractions produced percolated networks over a broad range of nanoparticle volume fractions that gradually narrowed with increasing ligand stiffness. Under uniaxial tensile deformation, the strength and rigidity of these networks increased with increasing ligand stiffness, while the network stretchability decreased. When we replaced the ligands with comparable free linkers, the resulting nanoparticle assemblies displayed distinctly different mechanical properties. The linker-mediated nanoparticle assemblies were more rigid and less stretchable, irrespective of the bending stiffness, owing to the closely packed arrangement of nanoparticles. Nevertheless, both linker- and ligand-mediated nanoparticle assemblies exhibited comparable tensile strength. When the linker length was doubled and association occurred only through linker-nanoparticle attractions, the assemblies became considerably softer, weaker, and less stretchable compared to the ligand-mediated assemblies. Our findings provide molecular-level insights into how different polymer association schemes regulate, and hence may be used to tune, the thermodynamics and mechanical response of nanoparticle gels.Data availability
The data that supports the findings of this study are available from the authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Research was sponsored by the Army Research Office and was accomplished under Grant Number W911NF-24-1-0245 (to JM). The conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. JM also acknowledges the support provided by the Welch Foundation under the grant A-2113-20220331. MPH acknowledges support from the National Science Foundation under award no. 2223084 and the International Fine Particle Research Institute. AN acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through projects 451785257 and 470113688. We are grateful to the Texas A&M High Performance Research Computing (HPRC) for providing the computational resources required to complete this work.References
- C. A. Saez Cabezas, G. K. Ong, R. B. Jadrich, B. A. Lindquist, A. Agrawal and T. M. Truskett, et al., Gelation of plasmonic metal oxide nanocrystals by polymer-induced depletion attractions, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(36), 8925–8930 Search PubMed.
- C. Knorowski and A. Travesset, Materials design by DNA programmed self-assembly, Curr. Opin. Solid State Mater. Sci., 2011, 15(6), 262–270 Search PubMed.
- V. Lesnyak, S. V. Voitekhovich, P. N. Gaponik, N. Gaponik and A. Eychmüller, CdTe Nanocrystals Capped with a Tetrazolyl Analogue of Thioglycolic Acid: Aqueous Synthesis, Characterization, and Metal-Assisted Assembly, ACS Nano, 2010, 4(7), 4090–4096 Search PubMed.
- Y. Sun, N. C. Harris and C. H. Kiang, The reversible phase transition of DNA-linked colloidal gold assemblies, Phys. A, 2005, 354, 1–9 Search PubMed.
- R. J. Macfarlane, B. Lee, H. D. Hill, A. J. Senesi, S. Seifert and C. A. Mirkin, Assembly and organization processes in DNA-directed colloidal crystallization, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(26), 10493–10498 Search PubMed.
- A. M. Green, C. K. Ofosu, J. Kang, E. V. Anslyn, T. M. Truskett and D. J. Milliron, Assembling Inorganic Nanocrystal Gels, Nano Lett., 2022, 22(4), 1457–1466 Search PubMed.
- M. Singh, Z. M. Sherman, D. J. Milliron and T. M. Truskett, Linker-Templated Structure Tuning of Optical Response in Plasmonic Nanoparticle Gels, J. Phys. Chem. C, 2022, 126(39), 16885–16893 Search PubMed.
- C. L. Bassani, G. van Anders, U. Banin, D. Baranov, Q. Chen and M. Dijkstra, et al., Nanocrystal Assemblies: Current Advances and Open Problems, ACS Nano, 2024, 18, 14791–14840 Search PubMed.
- J. Song, M. H. Rizvi, B. B. Lynch, J. Ilavsky, D. Mankus and J. B. Tracy, et al., Programmable Anisotropy and Percolation in Supramolecular Patchy Particle Gels, ACS Nano, 2020, 14(12), 17018–17027 Search PubMed.
- N. J. Halas, S. Lal, W. S. Chang, S. Link and P. Nordlander, Plasmons in Strongly Coupled Metallic Nanostructures, Chem. Rev., 2011, 111(6), 3913–3961 Search PubMed.
- M. A. Boles, M. Engel and D. V. Talapin, Self-Assembly of Colloidal Nanocrystals: From Intricate Structures to Functional Materials, Chem. Rev., 2016, 116(18), 11220–11289 Search PubMed.
- Z. M. Sherman, A. M. Green, M. P. Howard, E. V. Anslyn, T. M. Truskett and D. J. Milliron, Colloidal Nanocrystal Gels from Thermodynamic Principles, Acc. Chem. Res., 2021, 54(4), 798–807 Search PubMed.
- M. B. Ross, J. C. Ku, M. G. Blaber, C. A. Mirkin and G. C. Schatz, Defect tolerance and the effect of structural inhomogeneity in plasmonic DNA-nanoparticle superlattices, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(33), 10292–10297 Search PubMed.
- M. N. Dominguez, M. P. Howard, J. M. Maier, S. A. Valenzuela, Z. M. Sherman and J. F. Reuther, et al., Assembly of Linked Nanocrystal Colloids by Reversible Covalent Bonds, Chem. Mater., 2020, 32(23), 10235–10245 Search PubMed.
- I. U. Arachchige and S. L. Brock, Sol–Gel Methods for the Assembly of Metal Chalcogenide Quantum Dots, Acc. Chem. Res., 2007, 40(9), 801–809 Search PubMed.
- C. Ziegler, A. Wolf, W. Liu, A. K. Herrmann, N. Gaponik and A. Eychmüller, Modern Inorganic Aerogels, Angew. Chem., Int. Ed., 2017, 56(43), 13200–13221 Search PubMed.
- F. Matter, A. L. Luna and M. Niederberger, From colloidal dispersions to aerogels: How to master nanoparticle gelation, Nano Today, 2020, 30, 100827 Search PubMed.
- M. Anyfantakis, A. Bourlinos, D. Vlassopoulos, G. Fytas, E. Giannelis and S. K. Kumar, Solvent-mediated pathways to gelation and phase separation in suspensions of grafted nanoparticles, Soft Matter, 2009, 5, 4256–4265 Search PubMed.
- A. P. R. Eberle, N. J. Wagner and R. Castañeda Priego, Dynamical Arrest Transition in Nanoparticle Dispersions with Short-Range Interactions, Phys. Rev. Lett., 2011, 106, 105704 Search PubMed.
- P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Gelation of particles with short-range attraction, Nature, 2008, 453(7194), 499–503 Search PubMed.
- E. Zaccarelli, Colloidal gels: equilibrium and non-equilibrium routes, J. Phys.: Condens. Matter, 2007, 19(32), 323101 Search PubMed.
- J. Rouwhorst, C. Ness, S. Stoyanov, A. Zaccone and P. Schall, Nonequilibrium continuous phase transition in colloidal gelation with short-range attraction, Nat. Commun., 2020, 11(1), 3558 Search PubMed.
- Ddl Heras, J. M. Tavares and M. M. T. da Gama, Phase diagrams of binary mixtures of patchy colloids with distinct numbers and types of patches: The empty fluid regime. The, J. Chem. Phys., 2011, 134(10), 104904 Search PubMed.
- B. A. Lindquist, R. B. Jadrich, D. J. Milliron and T. M. Truskett, On the formation of equilibrium gels via a macroscopic bond limitation, J. Chem. Phys., 2016, 145(7), 074906 Search PubMed.
- P. I. C. Teixeira and J. M. Tavares, Phase behaviour of pure and mixed patchy colloids—Theory and simulation, Curr. Opin. Colloid Interface Sci., 2017, 30, 16–24 Search PubMed.
- F. Sciortino and E. Zaccarelli, Equilibrium gels of limited valence colloids, Curr. Opin. Colloid Interface Sci., 2017, 30, 90–96 Search PubMed.
- M. P. Howard, R. B. Jadrich, B. A. Lindquist, F. Khabaz, R. T. Bonnecaze and D. J. Milliron, et al., Structure and phase behavior of polymer-linked colloidal gels, J. Chem. Phys., 2019, 151(12), 124901 Search PubMed.
- J. M. Ilnytskyi, A. Slyusarchuk and S. Sokołowski, Gelation of patchy ligand shell nanoparticles decorated by liquid-crystalline ligands: computer simulation study, Soft Matter, 2018, 14, 3799–3810 Search PubMed.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phase Diagram of Patchy Colloids: Towards Empty Liquids, Phys. Rev. Lett., 2006, 97, 168301 Search PubMed.
- J. Russo, P. Tartaglia and F. Sciortino, Reversible gels of patchy particles: Role of the valence, J. Chem. Phys., 2009, 131(1), 014504 Search PubMed.
- N. C. Bigall, A. K. Herrmann, M. Vogel, M. Rose, P. Simon and W. Carrillo-Cabrera, et al., Hydrogels and Aerogels from Noble Metal Nanoparticles, Angew. Chem., Int. Ed., 2009, 48(51), 9731–9734 Search PubMed.
- S. Biffi, R. Cerbino, F. Bomboi, E. M. Paraboschi, R. Asselta and F. Sciortino, et al., Phase behavior and critical activated dynamics of limited-valence DNA nanostars, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(39), 15633–15637 Search PubMed.
- L. Rovigatti, F. Smallenburg, F. Romano and F. Sciortino, Gels of DNA Nanostars Never Crystallize, ACS Nano, 2014, 8(4), 3567–3574 Search PubMed.
- J. Fernandez-Castanon, F. Bomboi and F. Sciortino, Binding branched and linear DNA structures: From isolated clusters to fully bonded gels, J. Chem. Phys., 2018, 148(2), 025103 Search PubMed.
- J. Chen, S. R. Kline and Y. Liu, From the depletion attraction to the bridging attraction: The effect of solvent molecules on the effective colloidal interactions, J. Chem. Phys., 2015, 142(8), 084904 Search PubMed.
- J. Luo, G. Yuan, C. Zhao, C. C. Han, J. Chen and Y. Liu, Gelation of large hard particles with short-range attraction induced by bridging of small soft microgels, Soft Matter, 2015, 11, 2494–2503 Search PubMed.
- C. Zhao, G. Yuan, D. Jia and C. C. Han, Macrogel induced by microgel: bridging and depletion mechanisms, Soft Matter, 2012, 8, 7036–7043 Search PubMed.
- Y. Zhang, F. Lu, K. G. Yager, D. Van Der Lelie and O. Gang, A general strategy for the DNA-mediated self-assembly of functional nanoparticles into heterogeneous systems, Nat. Nanotechnol., 2013, 8(11), 865–872 Search PubMed.
- H. Xiong, D. van der Lelie and O. Gang, DNA Linker-Mediated Crystallization of Nanocolloids, J. Am. Chem. Soc., 2008, 130(8), 2442–2443 Search PubMed.
- A. Singh, B. A. Lindquist, G. K. Ong, R. B. Jadrich, A. Singh and H. Ha, et al., Linking Semiconductor Nanocrystals into Gel Networks through All-Inorganic Bridges, Angew. Chem., Int. Ed., 2015, 54(49), 14840–14844 Search PubMed.
- V. Sayevich, B. Cai, A. Benad, D. Haubold, L. Sonntag and N. Gaponik, et al., 3D Assembly of All-Inorganic Colloidal Nanocrystals into Gels and Aerogels, Angew. Chem., Int. Ed., 2016, 55(21), 6334–6338 Search PubMed.
- M. P. Howard, Z. M. Sherman, A. N. Sreenivasan, S. A. Valenzuela, E. V. Anslyn and D. J. Milliron, et al., Effects of linker flexibility on phase behavior and structure of linked colloidal gels, J. Chem. Phys., 2021, 154(7), 074901 Search PubMed.
- S. J. Rowan, S. J. Cantrill, G. R. L. Cousins, J. K. M. Sanders and J. F. Stoddart, Dynamic Covalent Chemistry, Angew. Chem., Int. Ed., 2002, 41(6), 898–952 Search PubMed.
- Y. Jin, C. Yu, R. J. Denman and W. Zhang, Recent advances in dynamic covalent chemistry, Chem. Soc. Rev., 2013, 42, 6634–6654 Search PubMed.
- C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, A DNA-based method for rationally assembling nanoparticles into macroscopic materials, Nature, 1996, 382, 607–609 Search PubMed.
- W. B. Rogers, W. M. Shih and V. N. Manoharan, Using DNA to program the self-assembly of colloidal nanoparticles and microparticles, Nat. Rev. Mater., 2016, 1(3), 1–14 Search PubMed.
- Z. Li, R. Yu and B. Guo, Shape-Memory and Self-Healing Polymers Based on Dynamic Covalent Bonds and Dynamic Noncovalent Interactions: Synthesis, Mechanism, and Application, ACS Appl. Bio Mater., 2021, 4(8), 5926–5943 Search PubMed.
- Q. An, I. D. Wessely, Y. Matt, Z. Hassan, S. Bräse and M. Tsotsalas, Recycling and self-healing of dynamic covalent polymer networks with a precisely tuneable crosslinking degree, Polym. Chem., 2019, 10, 672–678 Search PubMed.
- Y. Ding and J. Mittal, Insights into DNA-mediated interparticle interactions from a coarse-grained model, J. Chem. Phys., 2014, 141(18), 184901 Search PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids, J. Chem. Phys., 1971, 54(12), 5237–5247 Search PubMed.
- H. R. J. Warner, Kinetic Theory and Rheology of Dilute Suspensions of Finitely Extendible Dumbbells, Ind. Eng. Chem. Fundam., 1972, 11(3), 379–387 Search PubMed.
- M. Bishop, M. H. Kalos and H. L. Frisch, Molecular dynamics of polymeric systems, J. Chem. Phys., 1979, 70(3), 1299–1304 Search PubMed.
- A. Nikoubashman, A. Milchev and K. Binder, Dynamics of single semiflexible polymers in dilute solution, J. Chem. Phys., 2016, 145, 234903 Search PubMed.
- S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, DNA-programmable nanoparticle crystallization, Nature, 2008, 451(7178), 553–556 Search PubMed.
- R. Mao, B. Minevich, D. McKeen, Q. Chen, F. Lu and O. Gang, et al., Regulating phase behavior of nanoparticle assemblies through engineering of DNA-mediated isotropic interactions, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(52), e2302037120 Search PubMed.
- J. A. Anderson, J. Glaser and S. C. Glotzer, HOOMD-blue: A Python package for high-performance molecular dynamics and hard particle Monte Carlo simulations, Comput. Mater. Sci., 2020, 173, 109363 Search PubMed.
- Available from: https://github.com/mphowardlab/azplugins.
- V. Ramasubramani, B. D. Dice, E. S. Harper, M. P. Spellings, J. A. Anderson and S. C. Glotzer, freud: A Software Suite for High Throughput Analysis of Particle Simulation Data, Comput. Phys. Commun., 2020, 254, 107275 Search PubMed.
- A. A. Hagberg, D. A. Schult and P. J. Swart, in Exploring Network Structure, Dynamics, and Function using NetworkX, ed. G. Varoquaux, T. Vaught and J. Millman, Proceedings of the 7th Python in Science Conference, Pasadena, CA USA, 2008, pp. 11–15 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, NY, 2003 Search PubMed.
- D. Hossain, M. A. Tschopp, D. K. Ward, J. L. Bouvard, P. Wang and M. F. Horstemeyer, Molecular Dynamics Simulations of Deformation Mechanisms of Amorphous Polyethylene, Polymer, 2010, 51(25), 6071–6083 Search PubMed.
- L. Lv, M. Yang, Y. Long and J. Chen, Molecular Dynamics Simulation of Structural and Mechanical Features of a Polymer-bonded Explosive Interface under Tensile Deformation, Appl. Surf. Sci., 2021, 557, 149823 Search PubMed.
- J. Choi, H. Dong, K. Matyjaszewski and M. R. Bockstaller, Flexible Particle Array Structures by Controlling Polymer Graft Architecture, J. Am. Chem. Soc., 2010, 132(36), 12537–12539 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01301h |
| This journal is © The Royal Society of Chemistry 2025 |





