Nonaffine motion and network reorganization in entangled polymer networks

Abstract

This paper presents a computational model designed to capture the mechanical behavior of entangled polymer networks, described by dynamic and slideable cross-linking junctions. The model adopts a network-level approach, where the polymer chains between junctions are represented by segments exhibiting entropic elasticity, and the sliding of chains through entanglements is governed by a frictional law. Additionally, the model incorporates stochastic processes for the creation and depletion of entanglement junctions, dynamically coupled with sliding mechanics. This framework enables the exploration of the time-dependent mechanical response of entangled polymers with and without covalent cross-links. We apply this model to study the nonlinear rheology of such networks, linking macroscopic stress–strain behavior to the underlying microscopic events within the network. The approach is computationally efficient, making it a useful tool for understanding how network design influences polymer performance in elasticity, rheology, and general mechanical features. This work provides valuable insights into the relationship between molecular-level interactions and the macroscopic properties of entangled polymer systems, with potential applications in the design and optimization of advanced polymer materials.

---

1 Introduction

It is now well established that the viscoelastic behavior of polymers depends not only on the response of its constitutive chains but also on the collective intermolecular interactions between them. In particular, above the glass transition temperature, entanglements between chains dominate molecular deformation mechanisms over long timescales.¹ Although they can exhibit complex topologies, entanglements are often conceptualized as transient (or sliding) cross-links, which strongly constrain chain movement at fast loading rates but allow their relaxation and flow over long time scales. The second half of the 20th century has seen major developments in understanding the relation between structure, entanglement, and rheology, notably with the seminal works of Green and Tobolsky,² Edwards³ and de Gennes.⁴ The effect of entanglements on viscoelasticity and extensive ductility, however, is less understood. Yet, their role is widely acknowledged in industrial applications, a notable example of which is pressure-sensitive adhesives (PSAs) whose design relies on using high molecular weight polymers with low cross-link density for their superior bond strength. These materials display a maximum fracture energy slightly above the glass transition temperature in a regime where entanglements dominate the deformation.⁵ Furthermore, recent evidence shows that a proper ratio of entanglement to covalent cross-links can yield soft materials with the ability to be highly stretched without being ruptured or damaged⁶ since they can redistribute the applied energy and dissipate it.

The critical role of entanglements on macroscopic response is due to their role in mediating the complex, non-affine, and time-dependent motion of polymer chains within a network. In this context, the term “network” does not denote the presence of covalent bonds but rather refers to an assembly of polymer chains (the segments) that are entangled at discrete junctions (the nodes). At the molecular scale, this phenomenon is characterized by the snake-like sliding of chains through a transient tube formed by surrounding chains,⁴ which leads to a nonlinear and dynamic response to external forces. As chains reptate, the local load-sharing mechanisms within the network evolve, causing a shift from initial, relatively homogeneous load distribution to a more complex, temporally variable pattern. Thus, a chain in a fully entangled network may initially deform with the surrounding medium but will eventually relax by reptation.¹ Collectively, this not only yields network-level stress relaxation but also dissipates the localized tension in chains over time, such that chain rupture events may completely disappear at low strain rates.⁷ In addition to reptation, localized events such as entanglements and disentanglements can introduce further local stress concentrations but also play a crucial role in the permanent reorganization of the network structure. As this reorganization is the source of permanent (plastic) strains⁸ that are undesirable in most structural applications (for instance in PSAs), a small number of covalent cross-links are often added to the network.⁹ In this case, cross-linking points can preserve the long-term elasticity of the polymer⁶ while relaxation from reptation dynamics can delay damage initiation.¹⁰ It is therefore not surprising that materials with a high concentration of entanglements benefit from fracture resistance and rate-dependent energy dissipation.^11,12 The interactions between entanglement dynamics and the force transfer at covalent junctions is however poorly understood⁶ and constitutes a motivation for this work.

Although the mechanisms behind reptative relaxation and delocalization may be intuitive, developing theoretical models to describe their effects on stress re-distribution and molecular structure is a challenging task. Perhaps one main reason for this is that these mechanisms of structural re-organization are inherently non-affine deformation modes.^13–15 In other words, classical models that assume microstructural motion is governed by macroscopic motion do not apply.^16,17 Instead, network conformation is highly sensitive to local load transfer between interacting chains. This calls for modeling strategies based on an accurate representation of network topology and architecture.¹⁸ The most direct way to introduce the details of these effects is by performing molecular dynamics simulations.^19–22 For instance, the work of ref. 20 aimed to study the relaxation and chain retraction of an entangled network after a large step uni-axial deformation by using the bead-spring model pioneered by Kremer and Grest.²¹ Coarse-grained molecular dynamics, such as the theoretically informed coarse-grained approach of Ramírez-Hernández et al.,²³ have also been used to explore the relaxation spectrum of entangled networks. However, it should be noted that these simulations generally suffer from prohibitive computational costs, limiting their use to small physical domains (1–100 nanometers).

More efficient models, following theoretical concepts such as the tube model and primitive path analysis, were developed with even further coarse-grained descriptions to follow the respective motion of chains and their tubes with Langevin-type stochastic equations.^23,24 This was quickly followed by full network models in the early 2000s, particularly with the primitive chain network of Masubuchi et al.^25–29 and the slip-link model by Doi and Takimoto.³⁰ In these models, entanglement points are seen as temporally cross-linked junctions (slip-links) about which chains can reptate over time. The creation and deletion of entanglement at the start and end of the tube may then be handled using a Langevin equation. These approaches were mainly used to explore the nonlinear rheology³¹ of various types of polymers (linear and star-shaped), with various molecular weights such as the works of de Pablo et al.^32,33 In a more recent work,³⁴ a slip-spring-based mesoscopic simulation was developed in which entanglements are modeled as slip-springs that can hop between Kuhn segments of two chains. These developments on modern mesoscale network models reflect their promising usage for bridging small-scale physics and network motion to better understand the mechanical behavior of polymer materials.³⁵

To further extend mesoscale simulations on entangled systems and more accurately capture strain-induced local topological changes, we propose a discretized framework that reflects physical mechanisms controlled at the individual chain level. Our approach begins with a theoretical description of an idealized network composed of entangled chains (without crosslinks). We then construct a free energy functional and employ energy minimization techniques to derive the governing equations for chain motion and reptation. Subsequently, we establish a diffusion-based model for the creation of entanglements and disentanglements, where the local topology of each chain dictates these events, as opposed to a globally applied rule controlling the number of entanglements per chain.²⁵ In more detail, we have used the diffusion dynamics of free dangling polymer chains to derive a governing timescale for the hooking processes of dangling ends which are assumed as Poisson processes. Finally, we implement the discretized governing equations within a molecular dynamics framework (using LAMMPS) and conduct a detailed analysis of stress redistribution and network reorganization in entangled networks during a uniaxial stress relaxation test. We illustrate our model to capture non-uniform motion and modes of reptation, resulting in network-scale defects that serve as initiation points for fracture or cavitation.

2 Discrete model of entangled networks

As depicted in Fig. 1A, entangled polymer networks are made of long flexible chains whose motion is restricted by entanglement junctions. Near these junctions, the steric hindrance created by the densely packed polymer chains restricts their ability to move freely, as bulky segments of one chain physically block the movement of adjacent chains, limiting the conformational freedom of the polymer segments. This is conceptually illustrated by the tube model,^4,36 in which chains can only slide through the tube-like regions formed by neighboring chains. The crowded environment then makes it more difficult for chains to disentangle or to move past each other, leading to increased frictional interactions and an overall time-dependent mechanical response of the material. This generally includes stress relaxation and a pronounced visco-elastic behavior whose characteristic timescale reflects the difficulty of chain motion in the entangled state. In addition to chain reptation, new entanglements may be formed while existing ones might be lost. These events, denoted here as re-entanglement and dis-entanglement, respectively, are discussed in more detail below. These events induce topological changes in the network which can create network defects that abruptly change network's mechanical properties.

Fig. 1 Physical depiction of an entangled polymeric network. (A) Schematic illustrating the topology of an entangled chain that can reptate in the entanglement tube constrained by mechanical interlock of entanglements. It must be noted that only one chain is highlighted here, and each chain can reptate through its entanglement tube. (B) Discretized depiction of an entangled network where the long chain is discretized to N_subchain = 4 subchains (dangling ends are not visualized) and 5 entanglements.

To capture these coupled phenomena, we here propose a meso-scale approach to model entangled polymer networks. The network exists in a two-dimensional region Ω ⊂ [Doublestruck R]² whose dimensions are much greater than the characteristic length-scale of the polymer chains. We consider that each ‘branch’ of an entangled chain (i.e., the portion spanning between two entanglements or cross-links) acts as a constrained entropic spring. The constraining network junctions are modeled by two nodes connected by a rigid spring whose centerpoint is located inside the region Ω ∈ [Doublestruck R]² (Fig. 1B). We note that these springs are significantly stiffer than polymer chains and thus exhibit very little deformation. Each node belongs to only one chain, which facilitates tracking chain sliding as pertaining to a unique polymer chain. We may, therefore, divide a single chain into N_subchain internal load carrying subchains constrained by N_subchain + 1 entanglements with two additional (dangling) end subchains which are only constrained at one end. Within a divided chain, we consider only the internal subchains as storing elastic energy and do not explicitly model the location of the dangling ends. We may then define a numbering scheme that assigns an index i ∈ {1, 2, …, N_subchain} to each internal subchain, which is, in turn, constrained by two entanglements with indices i and i + 1, respectively. We may then refer to the dangling ends as subchains 0 and N_subchain + 1, respectively, noting that their existence is accounted for to describe stochastic dis-entanglement and re-entanglement events. The details regarding chain elasticity, sliding dynamics, and stochastic re-entanglement and dis-entanglement are discussed next.

2.1 Elasticity in entangled polymer tubes and resultant junction motion

A network's constitutive properties are inherently tied to the force–extension behavior of its constitutive elements (i.e., the subchains). We here assume that subchains can be modeled as flexible Gaussian chains with a linear force–extension relationship (Fig. 2A). A more realistic model, such as the Langevin chain model,³⁷ may also be considered to account for the finite extensibility of polymer chains. Moreover, the enthalpic stiffness of the polymer backbone may be incorporated when an energetic damage criterion is desired,^7,38,39 but at the expense of increasing the model complexity. For this reason, we limit our model to moderate chain deformations such that each subchain remains in the linear elastic range (i.e. the end-to-end distance of each subchain is much shorter than its contour length). With the flexible chain model,⁴⁰ the entropic elastic free energy [scr F, script letter F]^el_i of subchain “i” with n_i Kuhn segments and end-to-end vector r_i takes the formwhere r_i = |r_i|, k is Boltzmann constant, T is the absolute temperature, and b is the Kuhn length. Furthermore, the end-to-end vector is written in terms of the position vectors x_i+1 and x_i of the adjacent junctions by r_i = x_i+1 − x_i. To further account for volume exclusion forces in the network that originate from the inherent volume of Kuhn segments, the above potential is enriched with a short-range repulsive potential preventing chains from contracting to a single point.⁴¹ This contributes the following volumetric elastic free energy [scr F, script letter F]^vol_i for subchain i:Note that while volume exclusion forces classically behave isotropically (similar to pressure), they are here modeled as an effective force between nodes that are connected by a subchain (in a pairwise manner). Consequently, the force ∂[scr F, script letter F]^vol_i/∂r_i is always in line with the end-to-end vector r_i of the subchain. The total elastic free energy [scr F, script letter F]_i of subchain i with n_i Kuhn segments can be written by combining (eqn (1) and (2)):Fig. 2 plots both free energies versus the normalized end-to-end length r* = r/bn of the chain (where bn is the contour length). In this work, we present all numerical results in normalized non-dimensional units to promote generality. Furthermore, we consider lengths in units of the Kuhn length b and energies in units of the thermal energy-scale kT. In practice, this equates to setting kT = b = 1 for obtaining numerical results.

Fig. 2 Normalized free energy [scr F, script letter F]* = [scr F, script letter F]/kT plotted for a subchain with n = 100 Kuhn segments. Energy is plotted versus normalized end-to-end length r* = r/bn, where r* = 1 is the contour length of the subchain. (A) Normalized elastic and volumetric energy contributions plotted versus normalized end-to-end length. (B) Normalized total free energy and normalized tension f* = fb/kT are plotted, and the resting length r₀ is shown on both plots.

As depicted in Fig. 2A, the chosen energy potential creates a force that repels the two ends of a subchain at a distance that is determined by the chain length (or n_i) (Fig. 2B). To calculate this equilibrium point, we minimize [scr F, script letter F] with respect to r_i, yielding r_i⁰ = bn_i^0.6, which confirms the dependency of the equilibrium segment end-to-end distance with n_i. The definition of the free energy further enables us to calculate the tension force f_i in each subchain by taking the derivative of [scr F, script letter F]_i with respect to the end-to-end vector r_i as:

By setting f_i = 0, we indeed confirm that subchains are tension-free when r₀ = bn_i^0.6 (Fig. 2B). The equation of motion for node i can then be derived using a Langevin equation, previously used by Masubuchi in ref. 25, and omitting the thermal noise term, assumed here to be small. This gives for node with index i

∑f_i − μẋ_i = m_iẍ_i, (5)

where m_i is the mass of node i, ∑f_i is the sum of the elastic forces acting from connected subchains on the entangled node pair, and μ is the viscosity imposed by medium, which resists the motion of an entanglement junction (Fig. 3B). At this molecular length-scale, inertial forces m_iẍ_i are typically much smaller than elastic and viscous forces such that the equation of motion can be simplified to

μẋ_i = ∑f_i = f_i + f_i+1 + f_j + f_j+1, (6)

where ∑f_i is the sum of the tensions applied by subchains connected to that entanglement, composed of the four subchains depicted in Fig. 3B.

Fig. 3 (A) Schematic representing a chain diffusing through it's entanglement tube from a subchain with higher pressure of Kuhn segments to the neighboring subchain with lower pressure. (B) Discretized representation of an entanglement formed between two chains at junction i − j. The free body diagram shows the forces acting on entanglement pair by the subchains which are attached to them.

2.2 Viscous chain reptation through entangled junctions

Chain reptation describes the constrained motion of polymer chains within a complex network of entanglements. The reptation model was first introduced by Pierre-Gilles de Gennes⁴ based on the snake-like movement of the chains as they navigate through this network, sliding along their length rather than moving freely in three dimensions. In this model, a polymer chain is effectively trapped within an imaginary tube formed by the surrounding entanglements, thereby confining its motion to one dimension. Importantly, the diffusion-like motion of the polymer chain within its confining tube can be described using the same diffusion coefficient as that of a free, unentangled chain predicted by the Rouse model.¹ In the present model, this diffusion describes the transfer of monomers from one side of an entanglement junction to the other (Fig. 3A). For this, we introduce the variable that measures the rate at which monomers slide through junction i. This variable is related to the rate of change ṅ_i in subchain i by the conservation relation .⁴²

To calculate the flow of Kuhn segments through each entanglement, we consider minimizing the total free energy of the chain. We first define the volume V^tube_i of the i’th segment, which can be estimated by multiplying its area by its length r_i. Using previous results showing that the diameter of a tube with n_i Kuhn segments scales with ,¹ we can write:

Next, we consider that each Kuhn segment occupies the same volume [scr V, script letter V]_i within a chain. We may then express this volume as

[scr V, script letter V]_i = V^tube_i/n_i = πb²r_i/4. (8)

We therefore find that the volume of a Kuhn segment is directly proportional to the end-to-end vector of a subchain and is independent of the number n_i of monomers in this segment. Considering reptation as a first-order thermodynamic process, we may then describe the motion of monomers across a junction using the relationIn this equation, Π_i can be interpreted as the pressure exerted by the volume [scr V, script letter V]_i of the Kuhn segment along subchain i, while ζ is the sliding friction coefficient at the sliding junction. Thus, the above equation describes a process where monomers slide along a cross-linking junction from high to low pressure. Equilibrium is reached when all Kuhn segments of each subchain have the same volume [scr V, script letter V]_i. This result can finally be used to calculate driving potential Π_i for the flow of Kuhn segments through entanglement viaeqn (9):We note that this pressure quantity is exactly equal to the magnitude of tension (eqn (4)) divided by πb²/4 in each subchain. In other words, the motion of monomers through entanglement junctions is driven by the tension difference between adjacent segments. Interestingly, a similar rule was previously empirically postulated by Masubuchi et al. in ref. 25. However, here we can see that reptation rate of monomers will be slowed down by having larger Kuhn segments.

2.3 Disentanglement and re-entanglement

In contrast to reptation, which describes the motion of chains within an existing network, entanglement/disentanglement dynamics involve changes in the network topology itself. We here describe how each of these mechanisms is accounted for in the network model. A simple study exemplifies each case to illustrate the conditions and implementation of the dynamic entanglement process.

2.3.1 Disentanglement. When a polymer chain is stretched, different segments experience varying degrees of elongation, creating a force imbalance across entanglement points. This variation in tension causes the chain to slide through the entanglement until it is completely disentangled. A disentanglement event therefore occurs when a sliding junction is removed, allowing the chains to move more freely. To illustrate how the proposed model captures this mechanism, let us consider a subchain fixed at one end and entangled with another fixed point at its other end (see Fig. 4A). The chain is assumed to initially possess n₀ Kuhn segments. On the other side of the entanglement, the chain possesses a dangling end characterized by n_res Kuhn segments in its initial state. Let us then take the system out of equilibrium by subjecting the inner subchain to a prescribed level of stretch λ = r/r₀ at stretch rate [small lambda, Greek, dot above], up to a maximum value λ_max. Deformation is ceased afterward (i.e., [small lambda, Greek, dot above] = 0) to allow for relaxation. It can easily be shown (see Appendix A) that the dangling chain will eventually slip out of its entanglement point when the maximum stretch is above the critical value λ_crit given by:The model predicts that if the maximum stretch remains below the critical stretch λ_crit, the subchain is expected to gradually relax its tension by reptation and stop sliding before a disentanglement occurs (Fig. 4). Conversely, if the stretch exceeds λ_crit, disentanglement will occur. With this said, we note that reptation is a rate-dependent process imposed by the friction parameter ζ. Thus, the subchain might exceed critical stretch before occurrence of disentanglement or it might disentangle exactly as it is stretched to critical stretch.

Fig. 4 (A) Schematic displaying a subchain initially at rest with n₀ = 100 Kuhn segments, which is entangled at one end and attached to a reciprocal link at the other end. The neighboring dangling end also has n_res = 100 Kuhn segments. (B) Normalized tension f* = fb/kT plotted versus normalized time t* = tkT/ζb³ for loading at a fast strain rate with respect to sliding [small lambda, Greek, dot above] = (kT/ζb³). (C) Normalized tension f* plotted versus normalized time t* for loading at a slow strain rate with respect to sliding [small lambda, Greek, dot above] = 0.01(kT/ζb³). In both cases critical stretch is equal to λ_crit = 1.52.

To illustrate this point, we consider stretching a chain at a rate [small lambda, Greek, dot above]_fast faster than sliding and at a rate [small lambda, Greek, dot above]_slow slower than sliding. Noting that the sliding coefficient ζ has units of viscosity (pressure × time), we may set the sliding timescale, τ = ζb³/kT in units of our characteristic length- and energy-scales. Then, ‘fast’ loading rates correspond to [small lambda, Greek, dot above] ≥ 1/τ and ‘slow’ loading rates correspond to [small lambda, Greek, dot above] < 1/τ. With this in mind, we may choose instead to characterize the loading rate by the non-dimensional strain rate number, Θ, which is defined as:

With this definition, Θ ≥ 1 corresponds to a fast deformation relative to reptation, and elastic energy will be stored in subchains. In contrast, Θ < 1 implies a relatively slow deformation such that the system remains close to equilibrium as it is deformed. One might notice that here the size of Kuhn length is also affecting this competition. As is also shown in eqn (10), the larger the Kuhn segments, the slower the rate of sliding. This can be explained by the fact that reptation is fueled by monomer diffusion through entanglement junctions, which occurs at a slower rate for larger Kuhn segments.

In Fig. 4, we consider stretch rates of [small lambda, Greek, dot above]_fast = 1/τ and [small lambda, Greek, dot above]_slow = 0.01/τ, corresponding to Θ = 1 and Θ = 0.01, respectively. We then consider three maximum stretch values of λ_max = 1.2, λ_max = 1.5, and λ_max = 1.8. By looking at tension over time curves (Fig. 4B and C), we see that disentanglement can occur both during or after deformation phase which depends on stretch rate. When the subchain is stretched slowly (Fig. 4C), there is enough time for reptation such that the subchain remains close to equilibrium during deformation. In this condition, disentanglement occurs immediately as the stretch reaches λ_crit (sub-plot in Fig. 4C). By contrast, if deformation is imposed rapidly (Fig. 4B), reptation does not have enough time to equilibrate the tension between segments, allowing the chain to temporarily reach a stretch λ > λ_crit during the deformation phase. The model therefore predicts that disentanglement takes place during relaxation phase under this condition.

2.3.2 Re-entanglement. The creation of new entanglement can arise randomly from the diffusion of chains through space, where they can become intertwined with neighboring chains.²⁵ This process can be assisted by network deformation, wherein the forced motion of chains causes them to slide past one another and become entangled. Therefore, unlike disentanglement, the creation of new entanglements is a stochastic process that is highly dependent on the local configuration and motion of the chains with respect to their neighbors. In the proposed model, entanglements can only occur between a dangling end and a neighboring subchain (Fig. 5A). An entanglement event is then modeled as an independent stochastic Poisson process with an average rate of k_ent.⁴³ We can, therefore, compute the probability of entanglement creation during each discrete timestep of simulation (Δt) as

P_ent = 1 − e^−k_entΔt. (13)

This exponential probability density function is originally expressed in differential form as dP_ent = k_ente^−k_enttdt. By integrating this probability density over the time-span of one discrete timestep Δt, we will find eqn (13). This equation, describes the cumulative probability for creation of an entanglement after one discrete timestep Δt. Let us now seek an equation to relate the number of Kuhn segments n_res in the dangling ends to the rate k_ent of stochastic re-entanglement. For this, we consider two contributions to the characteristic timescale τ_ent = 1/k_ent of entanglement: (i) the diffusive timescale τ_diff and (ii) the ‘hooking’ timescale τ_hook. The ‘hooking’ timescale is interpreted as the finite amount of time required for segments within the entanglement distance to become intertwined. In this study, we consider τ_hook to be a constant model parameter that does not depend on the distance between the dangling end and the proposed entanglement section.

Fig. 5 (A) Schematic representing a section of a network where a dangling end with n_res Kuhn segments is diffusing in space around it. The grey rings show the probability of finding the chain at each radius, and no dangling end subchain can diffuse to a distance larger than bn_res. (B) The probability distribution of entanglement creation P_ent is plotted over normalized time t* = tkT/ζb³ for a dangling end with n_res = 100 and a potential subchain at distance d. Dashed curves are the theoretical distribution given in eqn (16).

The diffusive timescale can be expressed using the Einstein relation,⁴⁰ wherein the characteristic timescale of diffusion τ_diff(d) over a distance d may be approximated as τ_diff(d) ≈ d²/D_chain, where D_chain = kT/μn_res is the diffusion coefficient for the dangling end subchain.¹ Since dangling ends are tension-free, they most likely reside at their rest length r₀ = bn_res^0.6 and are unlikely to diverge from this length due to strong volumetric exclusion. We can, therefore, assume that dangling ends need to diffuse a distance of d − bn_res^0.6 to reach their target subchain. With this said, when d − bn_res^0.6 approaches the contour length of the polymer chain, its diffusion is greatly hindered by nonlinear entropic elasticity.¹ We, therefore, normalize the diffusion time by the quantity (bn_res − d)⁻¹, making it impossible to diffuse over a total distance greater than its contour length. The timescale of diffusion can then be expressed as

Finally, we may express the entanglement rate k_ent as a function of the distance d between the dangling end and the proposed entanglement junction and the number n_res of monomers in the dangling end to beTo illustrate this stochastic event, let us consider the situation depicted in Fig. 5A, where a dangling end with n_res = 100 Kuhn segments originates from a fixed location at a distance d from a potential target subchain. We then assess the model prediction regarding the time t for an entanglement event to take place between those subchains. Due to the stochasticity of this mechanism, the results are expressed as the probability density P_ent of occurring at a specific time. The data shown in Fig. 5B is the result of 10⁴ simulations used to record the time at which re-entanglement happens. Results confirm that the probability P_ent follows a Poisson distribution consistent with eqn (13). To assess the dependency of this distribution with distance d, this exercise was repeated for three values of d. Results show, as expected, that smaller distances (d = 0.1bn_res) are associated with shorter mean entanglement times while larger distances (d = 0.9bn_res) increase this time until the entanglement event may even no longer take place. The resulting probability densities can be verified by the theoretical curve explaining the Poisson process, which is the exponential distribution expressed as

P_ent = k_ente^−k_entt. (16)

By plotting the exponential distribution curves it can be seen that results from the stochastically implemented model, match well with the exponential distribution of each case of simulation.

3 Modeling polymer networks

In this section, the previously introduced physical laws are incorporated into a discrete meso-scale model. We consider finite two-dimensional periodic domains, wherein the motion of entanglement junctions is governed by eqn (6), and sliding dynamics are described by eqn (9). The network is generated using a random walk method to capture the stochastic behavior of polymer chain configurations, following the approach outlined by Doi.⁴⁰ Implementation details are provided, along with a simulation that visualizes the evolution of the network and the resulting mechanical response.

3.1 Network generation

In this study, we focus on the generation of two-dimensional (2D) networks through a series of computational steps to achieve an equilibrium state. The process begins with the creation of an initial network using a discrete random walk method⁴⁴ on an N_cell × N_cell grid, where each cell has dimensions of l_cell × l_cell. The total number of chains, N_chains, is defined byand each chain is represented by a random walk consisting of N_subchain steps, as illustrated in Fig. 6A. The random walk is initiated from a randomly selected cell, and subsequent steps are taken randomly to neighboring Moore cells⁴⁵ until the subchains for that chain are fully generated. During this process, the random walk is constrained such that it cannot intersect it's previous cell. This operation is repeated for all chains, with the total number of chains (or chain density) determining the number of separate random walks generated on the grid. Following the initial network generation, entanglement junctions are identified at points where two chains intersect, involving exactly two nodes. To prevent overlapping entanglements, the random walk is restricted from selecting Moore neighbor cells that are already occupied by two nodes (i.e., where an entanglement is already present). For simplicity, this study focuses on mono-disperse networks, where all subchains have an equal number of Kuhn segments, N_Kuhn. After constructing the network, energy minimization is performed to bring the system to a global equilibrium state before conducting stress relaxation simulations.

Fig. 6 (A) Random walk procedure for the red subchain where it has chosen a random start point as the initial entanglement. As it can be seen it takes a step to one of the Moore neighbor cells randomly and this continues for each chain until full walking of the network. A chain cannot walk to previous cell or the cells that are already occupied by two nodes. (B) Snapshots of generated networks immediately after generation and during equilibration, where color map shows the magnitude of tension in subchains. The generated network initially exhibits numerous black subchains, indicating regions of tension. Upon reaching equilibrium, these subchains transition to a light grey color, signifying their relaxation into a rest state. Also the radial force density plots and end-to-end vector distributions are shown for each stage. These plots can help to capture local stresses and strains in addition to the total virial stress.

3.2 Numerical scheme and energy minimization

To perform energy minimization during discrete time steps, both for the initial network equilibration and throughout the simulations, it is necessary to numerically integrate the displacement of nodes and the reptation of chains through each entanglement node pair. Defining equilibrium requires quantifying the stress at the network scale, which is determined using the virial formulation given by:⁴⁶Where V is the volume of the domain, and the sum is taken over all the bonded interactions per node. Here, the inertial term of the virial stress is not considered since the overdamped assumption implies that the nodes’ inertia is negligible. Now we can define the equilibrium as σ_ij < χ_TOL, where χ_TOL is a numerical tolerance. In this work, we use χ_TOL = 1 × 10⁻⁶(kT/b³). Finally, to perform the energy minimization, we integrate the position of nodes (eqn (6)) and flow of Kuhn segments (eqn (9)) using the discrete forward Euler method whose details are found in Appendix B.

In Fig. 6B, we illustrate three snapshots of a network as generated, during minimization, and at equilibrium. The network includes N_chains = 800 chains, each having N_subchain = 4 internal subchains and two dangling ends. Regarding Kuhn segments, we have set N_Kuhn = 150 for internal subchains and N_Kuhn = 100 for dangling ends. The network is generated on a two-dimensional periodic square domain with length 800b with an area equal to the combined area of all Kuhn segments. In each snapshot, subchains under high tension are illustrated in black and they are shown thicker. To assess the topology of the network, we present two-dimensional histograms (Fig. 6B) of the normalized components of the end-to-end vector, and , at each phase. To capture the local stresses in an average manner, we have also plotted radial force density plots in which the normalized average force components, and , of the subchains oriented in each radial plane section is calculated and plotted. The gray-scale color map is based on the normalized population of each radial section (i.e., the number of subchains oriented in the range of the section divided by a maximum number of subchains between all planar sections). The progression of each of these quantities illustrates the path from a randomly generated initially out-of-equilibrium network to one that is in internal equilibrium. In the network snapshots, we see that chains have faded from black (high tension) to light grey (no tension), and the entanglement junctions have become more randomly distributed in space. From the histograms, we see that each end-to-end vector has approached its resting length r₀ = bN_Kuhn^0.6 and is uniformly distributed in all directions. Finally, we see that the forces vanish in the radial plots, indicating that all subchains are force-free. In subsequent network illustrations, we omit the scale bars and legends from the histogram and force density plots to prevent overcrowding. Note that, in all presented results, the scale bars are kept constant for comparison. We next present the basic mechanical response of an entangled network undergoing stress relaxation.

3.3 Basic mechanical response during stress relaxation test

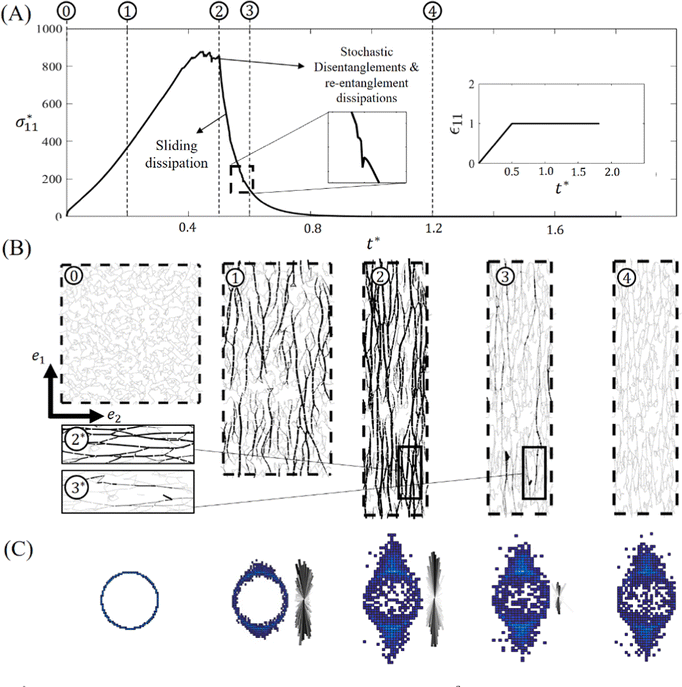
The discrete numerical schemes presented in the previous section were implemented as a custom ‘fix’ in the LAMMPS molecular dynamics codebase.⁴⁷ In this section, we illustrate its basic modeling capabilities by considering a fully entangled network subject to stress relaxation conditions. The custom-developed numerical scheme is capable of modeling both three- and two-dimensional networks (Fig. 7). However, due to computational cost of three-dimensional simulations and because similar trends are effectively captured regardless of dimensionality, the remainder of this work exclusively focuses on two-dimensional networks. The two dimensional entangled network is generated with N_chains = 800 where each chain consists of N_subchain = 4 subchains (divided by 5 entanglements) and each subchain has N_Kuhn = 150 Kuhn segments. The network is generated on a periodic square domain with initial length of 800b. The coefficient for medium viscosity is set equal to μ = 10⁻²ζb, and it must be noted that medium viscosity here is chosen so that characteristic timescale of viscous motion of entanglements is much smaller than simulation timestep. The discrete timestep is set equal to Δt = 10⁻⁶(ζb³/kT). After equilibrating the network, we stretch the domain uni-axially with non-dimensional strain rate value of Θ = 1 up to twice its initial length (ε₁₁ = (L_Ω − L_Ω0)/L_Ω0 = 1) in an isochoric manner (Fig. 8). In the second phase, a relaxation regime ensues, during which stretch is held constant until a new equilibrium state is achieved. In Fig. 8A, we plot the normalized tensile stress versus normalized time t* = tkT/ζb³ during the experiment. Five representative moments during the simulation are chosen (labeled 1–5) as indicated, and snapshots of the network configuration at these times are illustrated in Fig. 8B. Histograms of the end-to-end vectors and force density plots, as defined in Fig. 6, are plotted at these times in Fig. 8C. During loading, we see an initial rise in stress as chains begin storing elastic energy in response to the deformation. The plateau just before point (2) indicates that a significant number of disentanglements occur as the reserve of many dangling ends is depleted. As indicated in the histograms and force distribution plots, we observe a high degree of alignment of chains with the loading direction, as would be expected in a flexible polymer network.

Fig. 7 Stress relaxation test is performed on a three dimensional network. The greyscale color map of the chains is representative of tension in each chain where white chains are tension free and black ones are mostly tensioned.

Fig. 8 (A) Normalized uni-axial component of stress is plotted versus normalized time t* = tkT/ζb³ for the stress relaxation test performed on a network of fully entangled chains. (B) Network snapshots at specified time frames are shown. The sub-figures are comparing the topology of a local section after a few disentanglements and re-entanglements occurred. (C) The end-to-end vector histograms and force density plots are plotted at the same time frames to capture local forces and stretches applied to subchains. As it can be seen in force density plots all the chains have relaxed completely by time frame (4).

During the relaxation phase, two mechanisms work together to dissipate energy: (i) the reptation of segments from the dangling ends into the elastic subchains and (ii) disentanglement events. In the first process, segments flowing out of the dangling ends and into the elastic subchains leads to a larger contour length of the elastic subchains, which, in turn, leads to a softer response. Thus, the reptation of segments releases elastic energy by effectively softening the entropic springs of chains that are in tension. In contrast, disentanglement events completely dissipate all elastic energy that was stored in chains connected to the disentangled node. The insets of Fig. 8B highlight a disentanglement event occurring between time 2 and time 3. As each node in our network represents an entanglement junction, the network eventually releases all stored elastic energy as t* → ∞ as indicated by the vanishing stress and chain tension. In a network with covalent cross-links, some long-term elasticity would be maintained, as explored in the next section. Interestingly, we observe in panel 4 that the final resting configuration of the network is anisotropic, as indicated by the histogram. While this may reflect the alignment of polymer chains during the deformation, we acknowledge that the periodic e₁ dimension has increased during the deformation with respect to the periodic e₂ dimension, which could induce sampling bias in our calculation. Nonetheless, we do observe the existence of aligned ‘pockets’ even in the long-term equilibrium state. The observed anisotropy in the final equilibrium state, and the inability to capture chains retracting to their initial configuration, arises from the inclusion of volume exclusion effects of Kuhn segments within the chain energy expression (eqn (3)). This approach is not the most accurate representation of volumetric forces, as such forces are inherently many-body interactions. Specifically, volumetric interactions occur between all Kuhn segments across all subchains, rather than being limited to a single subchain. Consequently, the chains relax to a non-zero end-to-end distance determined by the number of Kuhn segments in each chain. While it is theoretically possible to introduce thermal fluctuations into the simulations, doing so would not resolve the anisotropy in the final configuration. This limitation stems from the combination of a volumetric force, which inherently acts isotropically in all directions, with a chain force modeled as a one-dimensional interaction. To overcome this limitation, we are actively developing a multi-body potential framework that can more accurately capture volumetric interactions. This approach would enable interactions between Kuhn segments to be modeled in a more realistic manner, leading to chain retraction and a uniform final configuration.

4 Results

With the foundational framework now implemented, we can investigate the influence of network architectural parameters on the macroscopic mechanical response and network reorganization. As described in Section 3.1, the number of subchains per chain, N_subchain, serves as an input parameter for the network generator, effectively representing chain length. Furthermore, we examine entangled networks in which a fraction of the entanglements, p_covalent, are covalently locked. The proportion of covalent cross-links ranges from p_covalent = 0%, representing a fully entangled network, to p_covalent = 100%, which corresponds to a fully cross-linked network. This framework allows us to study the effects of chain length and covalent cross-linking on macroscopic stress, local strains, and forces by conducting stress relaxation tests across various networks, systematically varying each parameter.

4.1 Network re-organization and stress relaxation

As observed in Fig. 8C, the length and orientation distributions of subchains change throughout the stress relaxation test, as demonstrated by the histograms of end-to-end vectors. During deformation, subchains aligned approximately in the direction of the applied strain experience the greatest elongation. Force density plots indicate that these subchains bear the majority of the load, while subchains oriented perpendicularly to the deformation carry minimal force. However, during the relaxation phase, the stretched subchains pull additional Kuhn segments from less stretched neighboring subchains, eventually relaxing to a new equilibrium state. This behavior is confirmed by the force density plots, where all energy is dissipated (force is fully relaxed), leaving no subchains under tension. The reorganization observed during relaxation is primarily driven by reptation, disentanglements, and re-entanglements. Reptation continues until tension is eliminated in all subchains, allowing fully entangled networks to redistribute stress and dissipate the stored elastic energy. In the following, we first examine the effect of strain rate, demonstrating that entangled networks can exhibit a range of stress responses, from elastic solid-like behavior to viscous fluid-like behavior, depending on the rate of deformation. Subsequently, we will investigate the influence of the two architectural parameters introduced earlier on the network's mechanical response.

4.1.1 Effect of strain rate. As shown in Fig. 9, three stress relaxation simulations were conducted at different strain rates: Θ = 1.00, Θ = 0.25, and Θ = 0.1 on the same fully entangled network discussed in Section 3.3. In each simulation, the network domain is deformed up to twice its initial length (ε₁₁ = 1) under isochoric conditions. The normalized uni-axial component of the resulting virial stress, , is plotted against normalized time, t* = tkT/ζb³, for each simulation (Fig. 9A). The results reveal that the stress response is highly dependent on the applied strain rate. When deformation is applied relatively quickly (black curve), the network exhibits behavior resembling that of an elastic solid. As the strain rate decreases (gray curve), the network's stress response becomes more characteristic of a polymer melt. The observed rate dependency arises from the time-dependent nature of reptation, which operates on a specific timescale τ = ζb³/kT determined by the friction coefficient. When the network chains are stretched slowly relative to this timescale, reptation has sufficient time to dissipate the stored elastic energy concurrently with deformation, resulting in a lower stress. Conversely, when the network is deformed rapidly, reptation cannot keep pace with the deformation, leading to higher stress at the end of the deformation phase. To analyze network reorganization, local strains and forces were examined through end-to-end vector histograms and force density plots at the end of the deformation phase for each simulation. Our results indicate that, under fast deformation, slightly larger local strains are imposed on subchains, particularly those oriented in the direction of deformation. As the strain rate decreases, the magnitude of local strains slightly diminishes, but the distortion of the sub-chain distribution intensifies. Additionally, force density plots reveal that subchains oriented in the direction of stretch are primarily responsible for carrying the load in all experiments, although the intensity of the imposed forces is significantly lower when the strain rate is reduced. We have additionally plotted the relaxation section of the stress response for each simulation on a logarithmic scale (Fig. 9B). Similar relaxation behaviors have previously been observed in molecular dynamics simulations, as reported by O’Connor et al.⁴⁸ This qualitative agreement suggests that our network model may serve as a valuable tool for bridging molecular dynamics with continuum-scale modeling in future studies.

Fig. 9 (A) Normalized uni-axial stress is plotted versus normalized time t* for the stress relaxation tests with three different strain rates of [small epsi, Greek, dot above]₁₁ = 1.00, [small epsi, Greek, dot above]₁₁ = 0.25 and [small epsi, Greek, dot above]₁₁ = 0.1. End-to-end vector histograms and force density plots are shown at the end of deformation phase for each simulation. (B) The relaxation section of normalized uni-axial stress is plotted versus normalized time in logarithmic scale.

4.1.2 Effect of chain length. To investigate the effect of chain length, networks with varying numbers of subchains (per chain) were generated and subjected to identical stress relaxation tests. The domain size and network parameters were kept consistent with those used in previous simulations (Section 3.3). To maintain constant chain concentration, as per eqn (17), networks with longer chains contained fewer total chains compared to those with shorter chains. Fig. 10A illustrates the deformation of networks with different chain lengths (N_subchain = 4, N_subchain = 8, N_subchain = 16, and N_subchain = 32) up to twice their initial length under a true strain rate of [small epsi, Greek, dot above]₁₁ = 1. The normalized tensile stress, , is plotted against normalized time, t* = tkT/ζb³, during the stress relaxation tests. The model predicts that networks with longer chains exhibit higher stress at the end of the deformation phase and longer relaxation timescales. In the subplots of Fig. 10A, the relaxation timescale of the network, τ_relax, is normalized and plotted versus N_chain to demonstrate that an increased chain length inherently extends the relaxation timescale of the network. These relaxation timescales were estimated by fitting exponential decay functions to the stress versus time data during the relaxation phase. This increase in relaxation time can be attributed to the fact that relaxation of stressed subchains primarily occurs through reptation of Kuhn segments from less stressed neighboring subchains or stress-free dangling ends. For a chain with a larger number of subchains, Kuhn segments must traverse a longer distance to relieve stress in the middle subchains. Conversely, for shorter chains, Kuhn segments travel shorter distances. This mechanism also explains the higher stress observed at the end of the deformation phase in networks with longer chains, as the lower relaxation rate allows these networks to store more elastic energy during deformation. It must be noted that the similar dependency of relaxation timescale on the number of subchains per chain was previously captured by Masubuchi et al.²⁹ A power-law fit of the relaxation timescale versus the number of subchains plot yields the relation τ_relax ∝ N_subchain^1.67, indicating that the relaxation timescale scales non-linearly with the number of subchains per chain. We note that the observed power law relation differs from that predicted by reptation theory,⁴ which suggests τ_relax ∝ N_subchain³. However, the relaxation time dependence on the number of subchains is modified by two mechanisms: tube length fluctuations and constraint release (disentanglements), both of which serve to reduce the relaxation time.¹ Given that our model incorporates both the spatial fluctuations of dangling ends and the effects of disentanglements, it is expected to observe a smaller power law dependence on N_subchain.

Fig. 10 (A) Normalized uni-axial component of stress is plotted against normalized time t* for a stress relaxation test on four networks each with different chain sizes. One subplots shows the uni-axial strain ε₁₁versus normalized time t* which is identical for all four simulation. Also one other subplot is showing the relaxation timescale versus number of subchains per chain N_subchain. (B) Force density plots and end-to-end vector histograms are plotted at three different time frames of simulation for different chain lengths of N_subchain = 4, N_subchain = 16 and N_subchain = 32.

Additionally, end-to-end vector histograms and force density plots were analyzed at three different time points (labeled 0–2) to capture network distortion. Fig. 10B shows that histograms for networks with longer chains are both more stretched and distorted, indicating greater local strains on the subchains. Force density plots confirm this observation, revealing that networks with longer chains experience larger forces and stretch compared to those with shorter chains, since reptation takes longer to relieve stress in these networks.

4.1.3 Effect of cross-link ratio. We previously introduced the concept of mixed networks, in which a fraction of entanglements are covalently locked, thereby preventing chain reptation through these junctions. To examine the impact of such covalent cross-links on macroscopic mechanical response, we generated five networks with varying covalent cross-link ratios: p_covalent = 0%, p_covalent = 40%, p_covalent = 60%, p_covalent = 80%, and p_covalent = 100%. We note that cross-links are introduced in the network after the initial energy minimization. This ensures that the generated network can reach a homogeneous mono-disperse distribution. The networks under investigation consist of N_chain = 800 chains, each composed of N_subchain = 4 subchains, with each subchain containing N_Kuhn = 150 Kuhn segments. These networks are generated on a square domain with an initial length of 800b. The medium viscosity coefficient is set to μ = 10⁻²ζb, and the discrete time step is Δt = 10⁻⁶(ζb³/kT). Following initial equilibration, the networks are deformed isochorically with a strain rate of [small epsi, Greek, dot above]₁₁ = 1 up to twice their initial length (ε₁₁ = 1) and subsequently held at the deformed state. Analysis of the stress relaxation curves presented in Fig. 11A reveals that the introduction of covalent cross-links into the entangled networks significantly alters their viscoelastic behavior. Initially, it is observed, in normalized stress versus normalized time t* plots, that networks with a higher ratio of covalent cross-links exhibit greater stress at the end of the deformation phase (see Fig. 11A). Furthermore, the inclusion of these cross-links prolongs the relaxation timescale. When the covalent cross-link ratio exceeds a critical threshold of p_covalent ≈ 41%, the network is unable to fully relax the applied stress. This indicates a transition from a viscoelastic fluid-like response to a viscoelastic solid-like behavior. The underlying reason for this transition is that covalent cross-links act as barriers to the reptation mechanism. When a sufficient number of cross-links are present, they can obstruct the reptation pathways for some chains, thereby impeding their ability to relax stress (see Fig. 11A). Consequently, deformation applied to the network may result in some chains retaining residual stress even after the system reaches equilibrium.

Fig. 11 (A) Normalized uni-axial component of stress is plotted as a function of time t* during stress relaxation tests on five networks with different covalent cross-link ratios. (B) End-to-end vector histograms and force density plots are shown for each experiment at the end of deformation phase and after reaching equilibrium.

End-to-end vector histograms and force density plots (Fig. 11B) were generated for each network at the end of the deformation phase and after reaching equilibrium to illustrate the impact of covalent cross-links on local strains and forces. The data show that the introduction of cross-links leads to slightly higher localized strains on subchains. Force density plots confirm that, beyond a certain ratio of covalent cross-links, the network fails to relax all subchains, with some remaining stretched even after equilibrium is achieved. Notably, end-to-end vector histograms indicate that adding covalent cross-links results in less distortion of the network distribution. This observation may be attributed to the absence of reptation, disentanglements, and re-entanglements in a fully cross-linked network, which significantly affects the dispersity of subchain lengths and the network's topological organization.

To elucidate the impact of covalent cross-links on stress relaxation, we present the normalized relaxed stress, σ^∞₁₁/σ^max₁₁, where σ^∞₁₁ represents the stress after sufficient time has passed for network to equilibrate and σ^max₁₁ is the maximum attained stress (Fig. 12). This normalized stress is plotted as a function of the covalent cross-link fraction, p_covalent, with each data point corresponding to a separate stress relaxation test. Additionally, snapshots of equilibrated networks at the end of the stress relaxation tests are provided at four times labeled 1 to 4. In these snapshots, stress-free subchains are depicted as thin grey lines, while highly tensioned subchains are represented by thick black lines.

Fig. 12 Normalized stress σ^∞₁₁/σ^max₁₁ is plotted against covalent cross-link ratio p_covalent. Also network snapshots are provided at four different covalent ratios p_covalent = 20%, p_covalent = 41%, p_covalent = 80% and p_covalent = 100% after the network is equilibrated in deformed form.

The results demonstrate that at low or zero covalent cross-link fractions, the network relaxes all the applied stress, resulting in stress-free subchains at the end of the stress relaxation test, as shown in subplot 1 of Fig. 12. However, beyond a critical cross-link density p_covalent ≈ 41%, the network's ability to fully relax the stress is hindered, with some subchains remaining in tension at the end of the test (subplot 2, Fig. 12). This occurs because the covalent cross-links restrict the reptation pathways for these subchains. As the covalent cross-link fraction increases more, the network retains a larger portion of the imposed stress. At p_covalent = 100%, the network conserves all the imposed stress, as evidenced by the presence of numerous highly stretched subchains in subplot 4 of Fig. 12.

5 Concluding remarks

In conclusion, we introduced a discrete network model designed to capture the time-dependent mechanical response of entangled polymer networks and its relationship with the underlying local physics, including chain stretch, reptation, entanglements, and disentanglement. This approach is driven by the need to understand how the architecture of polymer networks and their dynamic changes during deformation – such as topological shifts and chain rupture – affect the complex mechanical behavior observed in experiments. Our network model aims to improve the current understanding while maintaining a relatively simplified form leading to lower computational cost compared to traditional molecular dynamics simulations. We have demonstrated the utility of this model through a series of elementary examples and extended its application to investigate the response of networks containing a mixture of covalent bonds and entanglements, which are representative of many synthetic polymers.

In summary, we have reproduced a similar stress relaxation trend as previously reported by Masubuchi et al.^25,49 Additionally, we demonstrated that the relaxation timescale of the network exhibits a power-law dependency on the number of subchains per chain (i.e., chain length), characterized as τ_relax ∝ N_subchain^1.67. This dependency was also observed in the work of Masubuchi,²⁹ where the molecular mass of the chains—effectively their length—was varied and longer relaxation times were observed for networks with longer chains. As discussed in Section 4.1.2, the divergence of this power law from that predicted by reptation theory⁴ arises due to the latter's exclusion of tube length fluctuations and constraint release mechanisms, both of which reduce the relaxation time.

Furthermore, we conducted stress relaxation experiments using the model on mixed networks comprising both entangled junctions and covalently cross-linked junctions. These experiments revealed that the incorporation of cross-linking points significantly influences the viscoelastic properties of entangled networks. Specifically, beyond a critical proportion of covalently cross-linked junctions (41%), the network's mechanical response transitions from that of a viscoelastic fluid—capable of dissipating all imposed energy through stretching—to that of a viscoelastic solid, which can only dissipate a part of the imposed energy. The mechanics and failure mechanisms of such networks have been extensively studied in prior experimental⁶ and theoretical investigations.⁵⁰

While our discrete network model provides a powerful framework for understanding the time-dependent mechanical response of entangled polymer networks, there are several limitations that highlight areas for future improvement. First, the model currently assumes a Gaussian response for the polymer chains, which is a reasonable approximation for small deformations but becomes less accurate as the deformation increases, especially near fracture. For large deformations, more realistic models, such as the Langevin chain model, should be considered. The Langevin model accounts for the finite extensibility of polymer chains, providing a more accurate description of the material's behavior under extreme conditions. Second, the current implementation of chain sliding at entanglement points does not account for the force dependence of the friction law.⁶ Introducing a force-dependent friction law in future versions of the model would allow for a more accurate capture of the nonlinearity observed in polymer rheology.⁵¹ This enhancement would better represent how the resistance to chain motion varies with the applied force, leading to a more realistic description of the material's mechanical response.

It is important to note that this model is also capable of studying the viscoplastic behavior of entangled polymer networks. Viscoplasticity, which describes the time-dependent irreversible deformation of materials under applied stress, is a key characteristic of entangled networks.⁵² By capturing the complex interplay between molecular chains, entanglements, and external forces, this model provides valuable insights into how these networks respond under prolonged loading conditions, making it a versatile tool for investigating both elastic and plastic deformation behaviors.

Looking ahead, integrating our network approach with molecular dynamics simulations has the potential to enhance the model's realism. By performing molecular dynamics simulations on small domains, we can extract key physical parameters, such as chain friction and initial network topology, which can then be fed into the network model. This hybrid approach will allow us to model larger domains (up to several microns) while maintaining computational efficiency. Ultimately, this may enable a deeper understanding of how network design influences complex phenomena such as fracture, cavitation, and nonlinear rheology in a wide variety of polymers, including pressure-sensitive adhesives.

Data availability

The data and code supporting the findings of this study on “Nonaffine Motion and Network Reorganization in Entangled Polymer Networks” are not publicly available due to confidentiality agreements with 3M, the funding organization for this research. Access to the data and code is restricted as they contain proprietary information.

Conflicts of interest

There are no conflicts to declare.

Appendices

Appendix A: proof of critical stretch equation for disentanglement

As it can be seen in (Fig. 4A), the subchain initially at equilibrium with n₀ Kuhn segments is stretched by factor λ. It is shown that initial subchain at equilibrium has length of r₀ = bn₀^0.6 and after the deformation it will have new length of λr₀. Due to tension difference Kuhn segments will flow from dangling end to stretched subchain until new equilibrium point. We can calculate that a subchain with length λr₀ requires (λr₀/b)^5/3 or n₀λ^5/3 Kuhn segments to be at relaxed state. The disentanglement always happens if the difference between required number of Kuhn segments and initial one is greater than number Kuhn segments in the dangling end n_res:

n₀λ^5/3 − n₀ > n_res (19)

Based on this, the critical stretch above which disentanglement always happens for the system shown in (Fig. 4A) can be calculated as:

Appendix B: forward Euler integration scheme

By minimizing free energy and using a Langevin equation, we found the equation of motion for each node (eqn (6)). We can numerically solve this ordinary differential equation for each node by writing it in discrete forward Euler form asThe other side of energy minimization is related to reptation, where we integrate the flow of Kuhn segments through each node by discretizing (eqn (9)) asUsing the equations above, nodal positions and monomer flows are numerically integrated after each discrete timestep Δt.

Acknowledgements

F. J. V. gratefully acknowledges the support of the 3M Company and National Science Foundation under Award No. 2023179. This content is solely the responsibility of the authors and does not necessarily represent the official views of the University of Colorado Boulder, 3M Company and National Science Foundation.

References

1. M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003, ISBN: 9780198520597.
2. M. S. Green and A. V. Tobolsky, A new approach to the theory of relaxing polymeric media, J. Chem. Phys., 1946, 14(2), 80–92.
3. S. F. Edwards, The statistical mechanics of polymerized material, Proc. Phys. Soc., 1967, 92(1), 9.
4. P.-G. De Gennes, Reptation of a polymer chain in the presence of fixed obstacles, J. Chem. Phys., 1971, 55(2), 572–579.
5. A. Zosel, Adhesive failure and deformation behaviour of polymers, J. Adhes., 1989, 30(1–4), 135–149.
6. J. Kim, et al., Fracture, fatigue, and friction of polymers in which entanglements greatly outnumber cross-links, Science, 2021, 374(6564), 212–216.
7. S. C. Lamont, et al., Rate-dependent damage mechanics of polymer networks with reversible bonds, Macromolecules, 2021, 54(23), 10801–10813.
8. F. J. Vernerey, B. Rezaei and S. C. Lamont, A kinetic theory for the mechanics and remodeling of transient anisotropic networks, J. Mech. Phys. Solids, 2024, 190, 105713,  DOI:10.1016/j.jmps.2024.105713 , ISSN: 0022-5096, https://www.sciencedirect.com/science/article/pii/S0022509624001790.
9. J. Chen, et al., Synthesis and Characterization of Pressure-Sensitive Adhesives Based on a Naphthyl Curing Agent, Polymers, 2023, 15(23), 4516,  DOI:10.3390/polym15234516 , ISSN: 2073-4360, https://www.mdpi.com/2073-4360/15/23/4516.
10. L. Xu, et al., Nonlinear Viscoelasticity and Toughening Mechanisms in Nanoclay-PNIPAAm Double Network Hydrogels, ACS Macro Lett., 2023, 12(5), 549–554,  DOI:10.1021/acsmacrolett.3c00083.
11. W. Wang and S. Chen, Hyperelasticity, Viscoelasticity, and Nonlocal Elasticity Govern Dynamic Fracture in Rubber, Phys. Rev. Lett., 2005, 95(14), 144301.
12. J. Tauber, et al., Sharing the Load: Stress Redistribution Governs Fracture of Polymer Double Networks, Macromolecules, 2021, 54(18), 8563–8574,  DOI:10.1021/acs.macromol.1c01275 , ISSN: 0024-9297, 1520-5835, (Visited on 02/11/2022).
13. J. D. Davidson and N. C. Goulbourne, Nonaffine chain and primitive path deformation in crosslinked polymers, Modell. Simul. Mater. Sci. Eng., 2016, 24(6), 065002,  DOI:10.1088/0965-0393/24/6/065002.
14. A. Basu, et al., Nonaffine Displacements in Flexible Polymer Networks, Macromolecules, 2011, 44(6), 1671–1679,  DOI:10.1021/ma1026803.
15. S. C. Lamont and F. J. Vernerey, Generalized continuum theory for nematic elastomers:Non-affine motion and characteristic behavior, J. Mech. Phys. Solids, 2024, 190, 105718,  DOI:10.1016/j.jmps.2024.105718.
16. M. Rubinstein and S. Panyukov, Nonaffine Deformation and Elasticity of Polymer Networks, Macromolecules, 1997, 30(25), 8036–8044,  DOI:10.1021/ma970364k.
17. M. Rubinstein and S. Panyukov, Elasticity of Polymer Networks, Macromolecules, 2002, 35(17), 6670–6686,  DOI:10.1021/ma0203849 , (Visited on 01/07/2020).
18. C. Tzoumanekas and D. N. Theodorou, From atomistic simulations to sliplink models of entangled polymer melts: Hierarchical strategies for the prediction of rheological properties, Curr. Opin. Solid State Mater. Sci., 2006, 10(2), 61–72,  DOI:10.1016/j.cossms.2006.11.003 , ISSN: 1359-0286, https://www.sciencedirect.com/science/article/pii/S1359028606001100.
19. Y. Li, et al., Molecular simulation guided constitutive modeling on finite strain viscoelasticity of elastomers, J. Mech. Phys. Solids, 2016, 88, 204–226,  DOI:10.1016/j.jmps.2015.12.007.
20. W.-S. Xu, et al., Molecular dynamics investigation of the relaxation mechanisms of entangled polymers after a large step deformation, ACS Macro Lett., 2018, 7(2), 190–195.
21. K. Kremer and G. S. Grest, Dynamics of entangled linear polymer melts: A molecular-dynamics simulation, J. Chem. Phys., 1990, 92(8), 5057–5086.
22. V. A. Harmandaris, et al., Crossover from the Rouse to the Entangled Polymer Melt Regime: Signals from Long, Detailed Atomistic Molecular Dynamics Simulations, Supported by Rheological Experiments, Macromolecules, 2003, 36(4), 1376–1387,  DOI:10.1021/ma020009g.
23. A. Ramírez-Hernández, et al., Dynamical Simulations of Coarse Grain Polymeric Systems: Rouse and Entangled Dynamics, Macromolecules, 2013, 46(15), 6287–6299,  DOI:10.1021/ma400526v.
24. C. C. Hua and J. D. Schieber, Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. I. Theory and single-step strain predictions, J. Chem. Phys., 1998, 109(22), 10018–10027.
25. Y. Masubuchi, et al., Brownian simulations of a network of reptating primitive chains, J. Chem. Phys., 2001, 115(9), 4387–4394.
26. Y. Masubuchi, H. Watanabe, G. Ianniruberto, F. Greco and G. Marrucci, Primitive Chain Network Simulations of Conformational Relaxation for Individual Molecules in the Entangled State, Nihon Reoroji Gakkaishi, 2008, 36, 181–185,  DOI:10.1678/rheology.36.181.
27. T. Uneyama and Y. Masubuchi, Multi-chain slip-spring model for entangled polymer dynamics, J. Chem. Phys., 2012, 137(15), 154902,  DOI:10.1063/1.4758320.
28. Y. Masubuchi, et al., Molecular simulations of the long-time behaviour of entangled polymeric liquids by the primitive chain network model, Modell. Simul. Mater. Sci. Eng., 2004, 12(3), S91,  DOI:10.1088/0965-0393/12/3/S03.
29. Y. Masubuchi, et al., Entanglement molecular weight and frequency response of sliplink networks, J. Chem. Phys., 2003, 119(13), 6925–6930,  DOI:10.1063/1.1605382 , ISSN: 0021-9606.
30. M. Doi and J.-I. Takimoto, Molecular modelling of entanglement, Philos. Trans. R. Soc. London, Ser. A, 2003, 361(1805), 641–652.
31. A. Ramírez-Hernández, et al., A multi-chain polymer slip-spring model with fluctuating number of entanglements: Density fluctuations, confinement, and phase separation, J. Chem. Phys., 2017, 146(1), 014903,  DOI:10.1063/1.4972582 , ISSN: 0021-9606.
32. L. Schneider and J. J. de Pablo, Entanglements via Slip Springs with Soft, Coarse-Grained Models for Systems Having Explicit Liquid–Vapor Interfaces, Macromolecules, 2023, 56(18), 7445–7453,  DOI:10.1021/acs.macromol.3c00960.
33. A. Ramírez-Hernández, M. Müller and J. J. de Pablo, Theoretically informed entangled polymer simulations: linear and non-linear rheology of melts, Soft Matter, 2013, 9(6), 2030–2036,  10.1039/C2SM26674A.
34. G. Megariotis, et al., Slip spring-based mesoscopic simulations of polymer networks: Methodology and the corresponding computational code, Polymers, 2018, 10(10), 1156.
35. J. Tauber, J. van der Gucht and S. Dussi, Stretchy and disordered: Toward understanding fracture in soft network materials via mesoscopic computer simulations, J. Chem. Phys., 2022, 156(16), 160901,  DOI:10.1063/5.0081316.
36. S. F. Edwards, The statistical mechanics of polymerized material, Proc. Phys. Soc., 1967, 92(1), 9–16,  DOI:10.1088/0370-1328/92/1/303 , (Visited on 01/07/2020).
37. W. Kuhn, Beziehungen zwischen Molekülgröße, statistischer Molekülgestalt und elastischen Eigenschaften hochpolymerer Stoffe, Kolloid-Z., 1936, 76, 258–271 , https://api.semanticscholar.org/CorpusID:98292222.
38. Y. Mao, B. Talamini and L. Anand, Rupture of polymers by chain scission, Extreme Mech. Lett., 2017, 13, 17–24,  DOI:10.1016/j.eml.2017.01.003 , ISSN: 2352-4316.
39. S. C. Lamont, K. Weishaar, C. J. Bruns and F. J. Vernerey, Micromechanics and damage in slide-ring networks, Phys. Rev. E, 2023, 107(4), 044501,  DOI:10.1103/PhysRevE.107.044501.
40. M. Doi, Soft Matter Physics, OUP, Oxford, 2013, ISBN: 9780199652952, https://books.google.com/books?id=ccUaBj73PZsC.
41. R. A. L. Jones, Soft Condensed Matter, 2002, https://api.semanticscholar.org/CorpusID:121604663.
42. F. J. Vernerey and S. Lamont, Transient mechanics of slide-ring networks: A continuum model, J. Mech. Phys. Solids, 2021, 146, 104212,  DOI:10.1016/j.jmps.2020.104212 , ISSN: 0022-5096, https://www.sciencedirect.com/science/article/pii/S0022509620304294.
43. R. J. Wagner, E. Hobbs and F. J. Vernerey, A network model of transient polymers: exploring the micromechanics of nonlinear viscoelasticity, Soft Matter, 2021, 17(38), 8742–8757,  10.1039/D1SM00753J.
44. P. Révész, Random Walk in Random and Non-random Environments, World Scientific, 2013, ISBN: 9789814447515, https://books.google.com/books?id=ZpC6CgAAQBAJ.
45. D. A. Zaitsev, A generalized neighborhood for cellular automata, Theor. Comput. Sci., 2017, 666, 21–35,  DOI:10.1016/j.tcs.2016.11.002 , ISSN: 0304-3975, https://www.sciencedirect.com/science/article/pii/S0304397516305916.
46. A. K. Subramaniyan and C. T. Sun, Continuum interpretation of virial stress in molecular simulations, Int. J. Solids Struct., 2008, 45(14), 4340–4346,  DOI:10.1016/j.ijsolstr.2008.03.016 , ISSN: 0020-7683, https://www.sciencedirect.com/science/article/pii/S0020768308001248.
47. A. P. Thompson, et al., LAMMPS – a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171,  DOI:10.1016/j.cpc.2021.108171.
48. T. C. O’Connor, A. Hopkins and M. O. Robbins, Stress Relaxation in Highly Oriented Melts of Entangled Polymers, Macromolecules, 2019, 52(22), 8540–8550,  DOI:10.1021/acs.macromol.9b01161.
49. K. Furuichi, C. Nonomura, Y. Masubuchi, H. Watanabe, G. Ianniruberto, F. Greco and G. Marrucci, Entangled polymer orientation and stretch under large step shear deformations in primitive chain network simulations, Rheol. Acta, 2008, 47(5), 591–599,  DOI:10.1007/s00397-008-0258-3.
50. J. He, Y. Liu, W. Xian and Y. Li, Interplay between entanglement and crosslinking in determining mechanical behaviors of polymer networks, Int. J. Smart Nano Mater., 2023, 14(4), 474–495,  DOI:10.1080/19475411.2023.2261777.
51. D. Parisi, et al., Nonlinear Shear Rheology of Entangled Polymer Rings, Macromolecules, 2021, 54(6), 2811–2827,  DOI:10.1021/acs.macromol.0c02839.
52. R. S. Hoy and C. S. O’Hern, Viscoplasticity and large-scale chain relaxation in glassy-polymeric strain hardening, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82(4), 041803,  DOI:10.1103/PhysRevE.82.041803 , https://link.aps.org/doi/10.1103/PhysRevE.82.041803.

---