Diffusive evaporation dynamics in polymer solutions is ubiquitous

Abstract

Recent theory and experiments have shown how the buildup of a high-concentration polymer layer at a one-dimensional solvent–air interface can lead to an evaporation rate that scales with time as t^−1/2 and that is insensitive to the ambient humidity. Using phase field modelling we show that this scaling law constitutes a naturally emerging robust regime, diffusion-limited evaporation (DLE). This regime dominates the dynamical state diagram of the system, which also contains regions of constant and arrested evaporation, confirming and extending understanding of recent experimental observations and theoretical predictions. We provide a theoretical argument to show that the scaling observed in the DLE regime occurs for a wide range of parameters, and our simulations predict that it can occur in two-dimensional geometries as well. Finally, we discuss possible extensions to more complex systems.

---

1 Introduction

Solvent evaporation from concentrated solutions or suspensions is an omnipresent phenomenon. The apparent simplicity of this process is deceptive: it is in fact ridden with complications due to the interaction between multiple components and the environment, leading to complex and fascinating dynamics. Such dynamics can in turn fundamentally alter the evaporative behaviour. Its understanding is therefore important for designing or controlling any process that involves drying. For instance, evaporative dynamics controls the application of paints and inks, where the formation of a defect-free skin upon drying is desired.¹ It is also important in food preservation, where moisture content reduction increases shelf-life, but may also adversely affect flavour or texture.² Due to such practical applications and fundamental interest in the dynamics of multi-component complex systems, the physics of evaporating polymer solutions and colloidal suspensions has inspired numerous investigations.^3–7

A number of these pertain to quasi-one-dimensional evaporation from the open end of a long capillary. In this geometry, the phase behaviour of aqueous lipid solutions can respond to varying ambient water activity a_e (equivalently, relative humidity) in such a way as to render the evaporation rate practically independent of a_e.⁵ It is suggested that in this regime, the mass flux is diffusion-controlled, J_evap ∼ t^−1/2. A similar regime was predicted theoretically by Salmon et al.⁶ They argue that the evaporation-induced advective flux causes the growth of a concentrated ‘polarization layer’ at the interface, leading to mass loss increasing with the square root of time, hereafter referred to as diffusion-limited evaporation (DLE). However, the stability range of this DLE regime in parameter space was not explored because current calculations assume diffusional dynamics.

We have recently tested the predictions of Salmon et al., and observed a regime of a_e -independent evaporation in which the rate decreases as t^−1/2.⁸ We also found a transition from constant evaporation rate at early times to this t^−1/2 regime, consistent with the building up of a polymeric ‘polarisation layer’. The inclusion of elastic effects from the formation of a very thin ‘gelled skin’ right at the air–solution interface^9,10 improves the agreement between theory and experiments.

On general grounds, we expect that J_evap ∼ t^−1/2 should only be one of at least three dynamical regimes of mass loss in an evaporating polymer solution. At very low polymer concentration, we should approach pure solvent evaporation, where the mass loss m(t) ∼ t, giving a constant evaporation rate. In the absence of any evaporative driving force, for instance when the air is saturated with solvent, we expect m(t) ∼ t⁰. So, we expect that DLE, where J_evap ∼ t^−1/2 or m(t) ∼ t^1/2, represents an intermediate regime. Surprisingly, however, this is the only behaviour observed experimentally to date at long times.^5,8,11 Why this is so is currently a puzzle.

Here we set up and investigate a one-dimensional continuum phase-field model for evaporation of a polymer solution, where the evaporation is hindered by the polymer. We indeed find three main evaporative regimes that transition into one another, with predictions for the diffusive regime that agree with other studies to date. Importantly, the DLE regime dominates the predicted state diagram of the system. We characterise the generic nature of this regime and propose an argument to explain why it is so pervasive. The physical picture that emerges is a simple one. A polymer layer grows from the interface into the bulk solution. When this layer becomes concentrated enough to act as a ‘porous plug’, Darcy solvent flow through this layer is the rate limiting step, so that the evaporative dynamics becomes diffusive. Finally, we show how the model can be extended to higher dimensions, or to study more complex systems such as aerosol droplets, important in respiratory virus transmission, or multilayered paints and coatings.

2 Methods

2.1 A phase field model for evaporation

Our phenomenological model consists of two phases, inside the drop and outside (= the atmosphere), connected through a continuous interface, with periodic boundary conditions (see ESI† for details). Two continuum fields are considered. The first of these is the order parameter ϕ. In phase field modelling, the field ϕ is used to distinguish between two phases, for instance indicating a change in orientational order.¹² In our model ϕ represents the total volume density of the droplet, that differentiates the droplet phase with a higher value of ϕ, from the surrounding air, with a lower value of ϕ. The second field, c, represents the concentration of polymer, and is in practice non-zero only in the droplet phase. Note that ϕ and c have dimensionless units. Inside the droplet ϕ ≃ ϕ₁, and c has some finite value, with c = c₀ < ϕ₁ initially. We follow the phase field convention that ϕ₁ = 1 inside the drop, and note that therefore our model is fundamentally different from a two-fluid model, as ϕ + c ≠ 1. Outside the drop, there is no polymer (c ≃ 0), and the droplet phase field has some finite value ϕ ≃ ϕ₀ < ϕ₁: this phase represents ambient air, with ϕ₀ the equivalent of the relative humidity.

The dynamic evolution of these fields is governed by chemical potential gradients around the interfaces, stemming from a coupled free energy density f(ϕ,c). The two fields themselves are coupled through a convective term v(ϕ,c). Each phase field is described by a modified Cahn–Hilliard equation with an additional evaporative term:¹³

where note that ϕ is not conserved, whereas c is conserved globally. This model requires that the total volume density inside the droplet, where ϕ = ϕ₁, and outside the droplet, where ϕ = ϕ₀, are essentially constant, such that ϕ is only lost around the interface where ∇ϕ ≠ 0, Fig. 1b. A nearly constant value for ϕ in the bulk of different phases is common to phase field modelling,¹² and we suggest that this is also a reasonable assumption to describe the physics in our model, as dissolved polymers in solution have a comparable density to pure water, while the volume density of the water in the (well-mixed) ambient air is approximately constant and should only vary in a small region right next to the interface of the evaporating solution. The constant volume density inside the droplet ϕ₁ also means that the internal droplet dynamics are conserved. Furthermore, in eqn (1)M_ϕ is the mobility of the phase field ϕ, which we take as a constant, while the polymer mobility is concentration dependent, . We note that using a constant polymer mobility leads to qualitatively similar evaporation dynamics, which was also observed in ref. 6.

Fig. 1 Dynamic evolution of a unidirectional drying polymer-solvent system in 1D. (a) Time evolution of polymer concentration profiles c in a 1D polymer-solvent slab during evaporation. The colorbar indicates the time corresponding to the concentration profiles. The x-coordinates are shifted from the simulation coordinates such that the middle of the droplet is located at x = 0. Inset: Schematic of the initial concentration c₀, gelation concentration c_g, width of the polymer layer L(t) (taken as the Full Width Half Maximum) and the peak height of the polymer layer H(t). (b) Snapshot of a typical simulation profile for ϕ and c, at time t = 1800, which corresponds to the red profile of c in panel (a). The x-coordinates are shifted so that the middle of the droplet is located at x = 0. (c) Evolution of the interface Δx_i plotted over time, comparing a system with added polymer to a system of pure solvent. A log–log scaling is applied to highlight the different long time power-law behaviour. Simulation units (S.U.) for space Δx_i and time t can be converted to physical units by applying the scalings L = 2.5 × 10⁻¹⁰ m and T = 6.3 × 10⁻⁹ s, respectively, as presented in the main manuscript.

The quantity v_i is the interfacial velocity of the evaporating droplet. Physically, the driving force for evaporation is the interfacial water activity difference.¹⁴ In the absence of polymer, it was suggested that this can be represented by a gradient in ϕ,¹³ leading to v_i ∼ ∇ϕ. In our model, as the water activity inside the droplet reduces with increasing presence of polymer, an increasing polymer concentration c should reduce evaporation. Therefore we take the phenomenological expression v_i = γ∇(ϕ − (γ′/γ)c), with the parameters γ determining the relative importance of evaporation to the phase fields and γ′ the contribution of c to reducing evaporation. In the droplet with binary composition, ∇(ϕ − (γ′/γ)c) is the effective solvent gradient leading to evaporation. We note that this expression is only valid for evaporation if ϕ ≥ (γ′/γ)c, and that the expression is similar to those used in other models in terms of water activity⁶ or partial pressure.¹⁵ Using an alternative expression, where the interface velocity also depends on the local phase field as v_i = ϕ × γ∇(ϕ − (γ′/γ)c), gives similar results in the same parameter range, with a slight renormalization, as we show in the ESI.† Finally, v = −v_i in eqn (1b) is the water velocity which advects the polymer towards the interface. Inside the droplet ∇c ≠ 0, so in eqn (1b) there exists a convective flux of polymer towards the interface, which is the evaporating solvent flux to the interface, compressing the polymer.¹⁶ This is not the case in eqn (1a), as inside the droplet ∇ϕ = 0, hence the dynamics there is purely diffusive.

The term driving droplet evaporation is therefore v_i·∇ϕ at the droplet–air interface, which leads to droplet shrinking. Interestingly, in the absence of c, this has the form of a square gradient term, similar to the key nonlinearity in the Kardar–Parisi–Zhang (KPZ)¹⁷ equation, but with the opposite sign with respect to the one normally considered for growing interfaces.

The local chemical potential μ is derived from the free energy density f as for the solvent and for the polymer. We note that in phase field modelling, it is common practice to use a free energy landscape f(ϕ,c) of the phase fields ϕ and c to generate physically appropriate chemical potential terms that describe the evolution of the phase fields in eqn (1a) and (1b).¹² This definition of ϕ and c as phase fields is different compared to theoretical treatments such as Landau–Ginzburg theory, that use thermodynamic density fields. We use a Landau-like free energy density for the phase fields ϕ and c as

The first term ensures that the system separates into a solvent-rich droplet ϕ₁ with polymer (c > 0) and a surrounding vapor phase ϕ₀ that contains no polymer (c = 0), so that ϕ₀ represents the solvent concentration. κ_ϕ and κ_c determines the bare surface tension of the droplet and polymer. The phenomenological term is necessary to confine the polymer into the droplet interior, and its form is chosen in analogy to other types of phase field modelling;¹⁸ similar to those types of models, we expect that different forms favouring polymer confinement should lead to qualitatively similar results. The term penalises the transfer of polymer across the interface, where 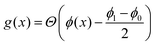is an indicator function defined in terms of the Heaviside Θ such that g = 0 if and g = 1 otherwise. When c is high enough to induce gelation, a permanent elastic stress develops, increasing the osmotic pressure and thereby the chemical potential.¹⁹ We approximate the bulk osmotic modulus contribution with 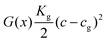,¹⁰ where K_g is a (constant) bulk osmotic modulus, c_g is the gelation concentration of the polymer, and G(x) = Θ(c(x) − c_g) is another indicator function defined again in terms of the Heaviside Θ. The remaining terms represent the virial coefficient for polymer diffusion (b₀) and excluded volume effects of the polymer (b₁). We note that eqn (2) should be accordingly adjusted to be used for modelling other systems than evaporating polymer–water droplets.

From eqn (2), the system spontaneously phase-separates into a droplet phase and an environment phase, independent of initial conditions. We tested this by initializing the system with a sinusoidal variation of ϕ and c with x, see ESI,† and found that this system quickly phase-separates and stabilizes into the general profiles seen in Fig. 1b.

Finally, we note that another way to approach the evaporation problem could be to have a two-field (or Landau–Ginzburg) model, with one field for the interior of the droplet and another for the exterior, which are joined by a moving boundary condition. However, the implementation of such a model is non-trivial. In our implementation of the single phase-field model the moving boundary, i.e. the interface, is an emergent feature from the underlying physics. A numerical drawback of our implementation is that a fine-grained grid is required to resolve the interface structure. For one-dimensional and radially symmetric problems this is not an issue, but such limitations might become more relevant for systems with increased spatial heterogeneity. Another numerical cost is the need to construct a sufficiently elaborate phase-field model that captures all the relevant physics, which leads to a relatively large amount of numerical parameters in the governing equations. This is, however, expected to be similar compared to moving boundary problems, where multiple numerical parameters are also likely to be required to correctly describe the physics in the system. For our phase-field model, we have thoroughly explored the relevant parameter spaces, for which our findings are robust.

3 Results and discussion

3.1 Unidirectional drying in 1D

We solve a 1D version of our model with periodic boundary conditions using the computational procedure provided in the ESI,† and defining the origin of the x coordinate to be in the middle of the droplet. For the case of ϕ₁ = 1, c₀ = 0.1, ϕ₀ = 0.2 and γ′/γ = 1.50, Fig. 1a shows the polymer c(x,t) in the right half (x > 0) of the droplet at a series of time points, while Fig. 1b plots the profiles of ϕ and c in the full droplet at time t = 1800. These results agree qualitatively with previous work.⁹ As the drop shrinks, a peak in c(x,t) develops just within the interface – a ‘polarisation layer’. When the peak height, H(t), reaches c_g, the peak stops growing and flattens into a plateau of increasing width, L(t) (Fig. 1a inset), until the concentration in the droplet is homogeneous and the droplet continues to shrink slowly. We note that outside the droplet the polymer concentration is not exactly c = 0, indicating minor leakage of polymer into the environment. Such minor leakage does not significantly affect the overall evaporation dynamics.

To quantify evaporative dynamics, consider the position of the interface x_i, taken to be the position of the peak in c(x,t). Fig. 1c shows a log–log plot of Δx_i(t) = x_i(t) − x_i(0) = m(t) by mass conservation if only solvent leaves the interface. For pure solvent (c₀ = 0), Δx_i ∼ t, so that J ∼ d(Δx_i)/dt is constant, which is a well-known result.¹⁴ A solvent-polymer mixture (c₀ = 0.5, with ϕ₀ = 0.35 and γ′/γ = 1.50) behaves differently. After an initial linear regime, the evaporation slows down and approaches a steady state where Δx_i ∼ t^1/2 and J ∼ t^−1/2, as found by experiments^5,8 and theory.⁶

3.2 Stability of the DLE regime

To assess the relative stability of the Δx_i ∼ t and ∼t^1/2 regimes and explore the possibility of other forms of scaling, we scan two parameters. The first, γ′/γ, regulates the extent to which c reduces the convective evaporation speed – recall v_i = γ∇(ϕ − (γ′/γ)c). The second is the phase field value outside the droplet, ϕ₀, which is equivalent to relative humidity and governs the evaporative driving force.

For the exponent α in m(t) ∼ t^α, the state diagram in Fig. 2a displays three dynamical regimes separated by relatively sharp boundaries, as indicated by the white contour lines. We identify the pure solvent-like regime (α → 1) in the bottom left corner of the state diagram and the arrested evaporation regime (α → 0) in the top right corner of the state diagram. The DLE regime where α ≈ 0.5 occupies the largest region in the state diagram, and is therefore the most robust. This is consistent with the fact that diffusive dynamics is the behaviour typically reported in experiments to date.

Fig. 2 State diagrams of the α exponent in m(t) ∼ t^α with varying ϕ₀ and γ′/γ, in a system with c₀ = 0.5, using (a) a Landau expansion for the polymer free energy and (b) a Flory–Huggins free energy f_FH(c) = b₀(1 − c)ln(1 − c) +χc(1 − c). Countour lines (white) are added to highlight the transition between the different evaporation regimes.

To understand the stability of the Δx_i ∼ t^1/2 regime, note that eqn (1) become diffusion equations in the limit v_i → 0.⁶ The system cannot start in this regime, but can only approach it asymptotically: having γ′/γ ∼ ∇_iϕ/∇_ic to give v_i → 0 (where ∇_i ≡ gradient at the interface) means no evaporation in the first place. We therefore need γ′/γ ≲ ∇_iϕ/∇_ic to confer a finite initial evaporation rate, which then decreases with time as interfacial polymer accumulates and the system approaches the diffusive regime (α = 0.5) asymptotically, Fig. 3a. How fast this happens depends on the effectiveness of interfacial polymer in reducing evaporation, which is controlled by γ′.

Fig. 3 Diffusion-limited evaporation (DLE) after long times that is independent of the external driving force. (a) Evolution of the exponent α in m(t) ∼ t^α over time steps τ in a system with ϕ₀ = 0.35 and γ′/γ = 1.5, settling on a time exponent α = 0.5. α is found through power law fitting of m(t) = Bt^α using α = d ln m(t)/d ln t. (b) Evolution of Δx_i over the square root of time τ^1/2, showing independence of the external driving force ϕ₀. Systems shown are ϕ₀ = 0.7 with γ′/γ = 0.415, ϕ₀ = 0.5 with γ′/γ = 1.00, ϕ₀ = 0.3 with γ′/γ = 1.85 and ϕ₀ = 0.1 with γ′/γ = 2.75. In (a) and (b) simulation units (S.U.) for space and time are L = 2.5 × 10⁻¹⁰ m and T = 6.3 × 10⁻⁹ s, respectively. (c). Evolution of the interface in dimensional units, scaled to experimental data as ΔX_i = [X]Δx_i, with [X] = 4.5 × 10⁻⁵ m, and T = [T]t, with [T] = 9 × 10⁻⁴ s. Simulation dataset is from a system with ϕ₀ = 0.5 with γ′/γ = 1.00. Experimental dataset at 50% relative humidity is reproduced from ref. 8.

As γ′/γ drops, this effectiveness decreases, requiring a larger polarisation layer that takes longer to establish to approach the diffusive regime. So, for finite system size and observation time, there exists a (γ′/γ)_min = ε below which the system will not cross over to Δx_i ∼ t^1/2 behaviour. We expect ε to increase with the polymer mobility, M_c: more mobile polymers require a longer time to build up a large enough polarisation layer to slow evaporation. On the other hand, a stronger driving force for evaporation due to lower external solvent concentration, ϕ₀, requires the polymer to be more effective in reducing evaporation for diffusive behaviour to emerge; so, ε should decrease with increasing ϕ₀, as observed, Fig. 2.

We establish that the scaling results from our modelling approach are insensitive to the exact implementation of the polymer free energy, by replacing the polymeric contribution from a Landau expansion to the free energy density (eqn (2)) with the Flory–Huggins mean field expression f_FH(c) = b₀(1 − c)ln(1 − c) + χc(1 − c), assuming a large degree of polymerization N ≫ 1, see ESI† for more details. The resulting state diagram for varying γ′/γ and ϕ₀ in Fig. 2b is dominated by a large region where m(t) ∼ t^0.5, indicating DLE, and the transition of long-times exponents from α = 1 to α = 0.5 and α = 0 in m(t) ∼ t^α is qualitatively similar between Fig. 2a and b upon increasing γ′/γ and ϕ₀. We note that the boundaries between the evaporation regimes in Fig. 2b are less well-defined, which is shown by comparing a line in the state diagrams in the ESI.† We attribute this effect to the divergence of the term ∼ln(1 − c) in f_FH(c) for c → 1, which leads to increased spreading and therewith slight variations in the settling interface concentration c_i < 1, that are likely to depend on the evaporation driving force, set by ϕ₀.

To understand the physics underpinning the late-stage, diffusive regime, note that by this stage, the chemical potential of the solvent (at partial pressure p) just inside the interface (where the polarisation layer is at its most concentrated), μ(p)|_xi, has nearly equilibrated with that of the solvent vapour outside, and so is nearly constant. At the same time, the solvent chemical potential in the middle of the droplet, μ(p)|_x=0, is also constant. So, there is a constant osmotic pressure difference driving solvent flow through the polarisation layer towards the interface, Δp = p|_xi−p_x=0 < 0 (because μ(p)|_xi < μ(p)|_x=0). Treating the growing polarisation of thickness L(t) as a porous medium of Darcy permeability k implies the solvent flux , with η the solvent viscosity. In the DLE regime in steady state, this flux is exactly balanced by the evaporative flux, which mass conservation requires to be dL/dt, so that we have dL/dt ∼ L⁻¹, or L(t) ∼ t^1/2, as also found in a recent theory²⁰ as well in our numerics (see ESI†). Darcy's law then implies J ∼ t^−1/2, consistent with our finding that Δx_i ∼ t^1/2 at long times (recall that J ∼ d(Δx_i)/dt), Fig. 1c.

For this physical argument to hold, we require that the rate of advective polymer accumulation, giving rise to the (growing) polarisation layer, dominates polymer diffusion which counteracts this buildup, i.e. the Péclet number . Equivalently, this means that the diffusion is slow compared to the evaporation rate. While this is true at short times, it seems at least at first sight that this condition will be broken as late times where navely one might expect Pe → 0 as v_i → 0. However, in the DLE regime, our argument suggests v_i ∼ ṁ(t) ∼ t^−1/2, L(t) ∼ t^1/2. So in fact at late times Pe ∼ t⁰, provided that 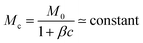. The latter is a fair approximation for systems with β ∼ 0.1–1.0 and c ∼ 0.1–1.0. Our physical argument for the diffusive regime at long times is therefore self consistent, because the balance between advection and diffusion remains constant even as v_i → 0. For a final check, we find Pe ≈ 10² ≫ 1 for a typical system in the DLE regime (γ′/γ = 1.50, ϕ₀ = 0.30), so that, indeed, advection near the interface dominates over diffusion.

Considering the concentration dependence of our results, we identify the limiting evaporation regimes of m(t) ∼ t^α for a varying initial concentration c₀. For a system where c₀ → 0, we expect that DLE never occurs and the system evaporates at a constant rate (α → 1). On the other hand, if c₀ is sufficiently high that the system is already at thermodynamic equilibrium with the environment, evaporation never occurs (α → 0). For any other value of c₀, we expect to observe the behaviour where 0 < α < 1, which approaches α → 0.5 as long as Pe ≫ 1 and the system is sufficiently large that a polarization layer can form at the solution–air interface.

In the diffusive regime, it was previously predicted⁶ that the mass loss rate should be independent of the external driving force. For water evaporation into air, the driving force is the relative humidity a_e,¹⁴ which for us is ‘tuned’ by ϕ₀. Plotting m vs. t^1/2 whilst varying ϕ₀ and γ′/γ, Fig. 3b, shows that this is indeed the case in our model.

This is a direct consequence of the fact that interfacial polymer concentration has reached a constant value, c_g, so that it is the polymer concentration gradient in the polarisation layer rather than the external humidity that drives water transport. In the theory of Salmon et al.,⁶ the same physics emerges due to the sharp fall in water activity at high polymer concentrations, so that the late stage interfacial polymer concentration varies very little over a broad range of external water activities. In both cases, the humidity independence is necessarily correlated with the emergence of DLE. However, such correlation is not logically necessary. In our earlier experiments, the formation of a thin polymer skin at the solution–air interface due to rapid adsorption also gives rise to humidity-independent evaporation, but without a porous polarisation layer, the dynamics is not diffusive.⁸

3.3 Simulation units and comparison to experimental systems

We find the simulation units in time (T) and space (L) of our system, by comparing the simulation parameters in eqn (2) to measured physical quantities of a water-PVA solution, for which measurements have been performed in experiments where a solution evaporates unidirectionally.⁸ Using the units of the simulation parameters from Table S1 in the ESI,† we obtain a set of equations for (1) the surface tension ,²¹ (2) the diffusion coefficient [D] = M₀b₀ × L²/T and (3) the osmotic pressure [π] = b₀ × E/L³, where E is the unit of energy. Using [γ] ≈ 0.07, [D] ≈ 10⁻¹¹ (ref. 15) and [π] ≈ 10⁷ Pa,²² we find L ≈ 2.5 × 10⁻¹⁰ m, T ≈ 6.3 × 10⁻⁹ s and energy unit E ≈ 1.56 × 10⁻²⁰ J. Finally, we calculate a dimensional evaporation rate from the slope of a simulation without polymer (ϕ₀ = 0.5, c₀ = 0) as V_ev ≈ 2 × 10⁻⁵L/T ≈ 0.8 μm s⁻¹, which is comparable to measurements in ref. 8.

To establish that our simulations are representative of experimental data, we map our results to the data from ref. 8 in Fig. 3c. We find excellent agreement between these two systems by scaling our simulation data to dimensional units as ΔX_i = [X]Δx_i in meters [m], where [X] = 4.5 × 10⁻⁵ m, and T = [T]t in seconds [s], where [T] = 9 × 10⁻⁴ s. It should be noted that these scalings are much higher than the simulation units in the system, which can be attributed to the experimental system being much larger than we can reasonably simulate, but that the ratios L/T ≈ 0.05 and [X]/[T] ≈ 0.043 are consistent.

3.4 Extensions of the model to more complex systems

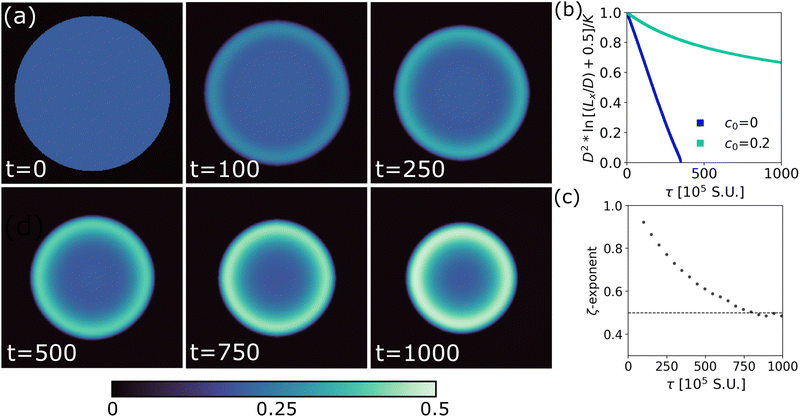
One of the major advantages of our phase field model is the ease with which it can be adapted to more complex systems and used to explore higher dimensions. Fig. 4a shows the evolution of a 2D evaporating drop geometry for a system with c₀ = 0.2, ϕ₀ = 0.35 and γ′/γ = 3.0. As in 1D, a concentrated polymer layer forms at the droplet–air interface over time.

Fig. 4 Dynamic evolution of evaporating droplets in 2D. (a) Snapshots of the time evolution of polymer concentration c in a 2D evaporating droplet, with c₀ = 0.2, ϕ₀ = 0.35 and γ′/γ = 3.0. (b) Evolution of the log-corrected area D² ln[(L_x/D) + 0.5]/G of the system in (a) plotted over time, comparing a system with added polymer to a system of pure solvent. (c) Evolution of the exponent ζ in D² ln[(L_x/D) + 0.5] ∼ t^ζ over timesteps τ in a system with ϕ₀ = 0.35 and γ′/γ = 3.0, settling on a time exponent ζ = 0.5. ζ is found through power law fitting using ζ = d ln[1 − (D²)ln[(L_x/D) + 0.5]/G]/d ln t. In (b) and (c) simulation units (S.U.) for space and time are L = 2.5 × 10⁻¹⁰ m and T = 6.3 × 10⁻⁹ s, respectively.

For 2D or 3D droplets of diameter D evaporating in an unconfined environment, D² ∼ t, so that the evaporation rate is constant.²³ However, solving the same problem in a confined system with a constant solvent chemical potential imposed at the system's boundary leads to deviations from this ‘D² law’. If viscous and buoyancy effects can be neglected, theory²³ predicts that in a 2D finite system of this kind,

D² ln[(L_x/D) + 0.5]/G = 1 − Ct, (3)

where L_x is the size of one axis of the system, C is a constant and G = D²₀ ln[(L_x/D₀) + 0.5]. Over the course of the simulations that give the results shown in Fig. 4, the value of ϕ at the (periodic) boundaries increases by ≲ 2%, so that we may expect eqn (3) to hold to a good approximation.

Our data for the evaporation of a pure solvent droplet, Fig. 4b, (blue; c₀ = 0) indeed agree with eqn (3), as apparent from the approximately linear evolution of D² ln[(L_x/D) + 0.5]/G with t. However, in a system with added polymer, deviations are observed, Fig. 4b (green, c₀ = 0.2), which recall Fig. 1c. We therefore fit these data to a power law with a running exponent ζ, D² ln[(L_x/D) + 0.5] ∼ t^ζ. The resulting ζ, Fig. 4c, clearly recalls Fig. 3a for the 1D case.

So, while a full study of the 2D case is beyond our scope, it seems reasonable to surmise that the state diagram in this case should also display a robust diffusive regime, provided that Pe is high enough. Previous experiments have demonstrated ambient humidity independent evaporation of droplets containing large glycoproteins,²⁴ which is consistent with our surmise.

4 Conclusions and outlook

In summary, we have applied a phase field modelling approach to study the evaporative dynamics of a polymer–solvent mixture. Whilst our approach is phenomenological, rather than being derived from rigorously coarse-graining a microscopic theory, we expect it to describe the system in a qualitatively accurate way, in line with previous work on phase fields. Our key result is that the DLE regime, where evaporation rate decays with time as t^−1/2, is a robust dynamical regime found over a range of parameter values. We rationalise this scaling with a simple mathematical and physical argument, according to which the −1/2 exponent is due to a diffusive growth of the polymer layer, and a Darcy flow of the solvent due to the ensuing pressure difference close to the droplet–air interface. For this argument to be self-consistent, the Péclet number Pe should remain high and nearly constant, to achieve a non-equilibrium steady state where advection dominates over diffusion at all times. We show that this requirement is, perhaps surprisingly, indeed met.

Our model is in quantitative agreement with previous theoretical and experimental results, including a near-independence of evaporation rates on relative humidity in the DLE regime. Such agreement gives confidence for applying this phase field model to study solvent and solute transfer in more complex systems and geometries. We have shown preliminary results for the evaporation of a 2D droplet to demonstrate this potential. Possible future applications include dissolution processes (e.g., making instant coffee) and the drying of multilayers involving multiple solvents and solutes (e.g., oil paintings²⁵). In the latter case, our approach has the added advantage that no assumptions need to be made on the phase of layers and/or the location of the interface over time.

Data availability

All data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funding was provided by the University of Edinburgh. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.

Notes and references

1. B. J. D. Gans and U. S. Schubert, Langmuir, 2004, 20, 7789–7793.
2. Z. Erbay and F. Icier, CRC Crit. Rev. Food Sci. Nutr., 2010, 50, 441–464.
3. M. G. Hennessy, G. L. Ferretti, J. T. Cabral and O. K. Matar, J. Colloid Interface Sci., 2017, 488, 61–71.
4. P. G. de Gennes, Eur. Phys. J. E, 2002, 7, 31–34.
5. K. Roger, M. Liebi, J. Heimdal, Q. D. Pham and E. Sparr, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10275–10280.
6. J. B. Salmon, F. Doumenc and B. Guerrier, Phys. Rev. E, 2017, 96, 032612.
7. M. Rezaei and R. R. Netz, Phys. Fluids, 2021, 33, 091901.
8. M. Huisman, P. Digard, W. C. Poon and S. Titmuss, Phys. Rev. Lett., 2023, 131, 248102.
9. K. Ozawa, T. Okuzono and M. Doi, Japan. J. Appl. Phys., 2006, 45, 8817–8822.
10. T. Okuzono and M. Doi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 030501(R).
11. K. Roger and J. J. Crassous, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2105530118.
12. N. Provatas and K. Elder, Phase-field methods in materials science and engineering, John Wiley & Sons, 2011.
13. H. G. Lee, J. Yang, S. Kim and J. Kim, Appl. Math. Comput., 2021, 390, 125591.
14. E. L. Cussler, Diffusion: Mass Transfer in Fluid Systems, CUP, Cambridge, UK, 1997.
15. M. Okazaki, K. Shioda, K. Masuda and R. Toei, J. Chem. Eng. Jpn., 1974, 7, 99–105.
16. F. Meng, L. Luo, M. Doi and Z. Ouyang, Eur. Phys. J. E, 2016, 39, 1–10.
17. M. Kardar, G. Parisi and Y.-C. Zhang, Phys. Rev. Lett., 1986, 56, 889–892.
18. R. Mueller, J. M. Yeomans and A. Doostmohammadi, Phys. Rev. Lett., 2019, 122, 048004.
19. L. Leibler and K. Sekimoto, Macromolecules, 1993, 26, 6937–6939.
20. L. Talini and F. Lequeux, Soft Matter, 2023, 19, 5835–5845.
21. M. E. Cates and E. Tjhung, J. Fluid Mech., 2018, 836, P1.
22. P. Bacchin, J. Leng and J.-B. Salmon, Chem. Rev., 2021, 122, 6938–6985.
23. L. Fei, F. Qin, G. Wang, K. H. Luo, D. Derome and J. Carmeliet, Phys. Rev. E, 2022, 105, 025101.
24. E. P. Vejerano and L. C. Marr, J. R. Soc. Interface, 2018, 15, 20170939.
25. J. R. Duivenvoorden, R. P. Kramer, M. H. van Eikema Hommes, P. D. Iedema, J. J. Hermans and K. Keune, Int. J. Heat Mass Tran., 2023, 202, 123682.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01215a

---