Open Access Article
Open Access ArticleRole of data-driven regional growth model in shaping brain folding patterns†
Jixin
Hou
a,
Zhengwang
Wu
b,
Xianyan
Chen
c,
Li
Wang
b,
Dajiang
Zhu
d,
Tianming
Liu
e,
Gang
Li
*b and
Xianqiao
Wang
 *a
*a
aSchool of Environmental, Civil, Agricultural and Mechanical Engineering, College of Engineering, University of Georgia, Athens, GA 30602, USA. E-mail: xqwang@uga.edu
bDepartment of Radiology and Biomedical Research Imaging Center, The University of North Carolina at Chapel Hill, NC 27599, USA. E-mail: gang_li@med.unc.edu
cDepartment of Epidemiology and Biostatistics, College of Public Health, University of Georgia, Athens, GA 30602, USA
dDepartment of Computer Science and Engineering, The University of Texas at Arlington, Arlington, TX 76019, USA
eSchool of Computing, The University of Georgia, Athens, GA 30602, USA
First published on 2nd January 2025
Abstract
The surface morphology of the developing mammalian brain is crucial for understanding brain function and dysfunction. Computational modeling offers valuable insights into the underlying mechanisms for early brain folding. Recent findings indicate significant regional variations in brain tissue growth, while the role of these variations in cortical development remains unclear. In this study, we explored how regional cortical growth affects brain folding patterns using computational simulation. We first developed growth models for typical cortical regions using machine learning (ML)-assisted symbolic regression, based on longitudinal real surface expansion and cortical thickness data from prenatal and infant brains derived from over 1000 MRI scans of 735 pediatric subjects with ages ranging from 29 postmenstrual weeks to 2 years of age. These models were subsequently integrated into computational software to simulate cortical development with anatomically realistic geometric models. We comprehensively quantified the resulting folding patterns using multiple metrics such as mean curvature, sulcal depth, and gyrification index. Our results demonstrate that regional growth models generate complex brain folding patterns that more closely match actual brains structures, both quantitatively and qualitatively, compared to conventional uniform growth models. Growth magnitude plays a dominant role in shaping folding patterns, while growth trajectory has a minor influence. Moreover, multi-region models better capture the intricacies of brain folding than single-region models. Our results underscore the necessity and importance of incorporating regional growth heterogeneity into brain folding simulations, which could enhance early diagnosis and treatment of cortical malformations and neurodevelopmental disorders such as cerebral palsy and autism.
1. Introduction
As the central regulator of physiological activities, the human brain exhibits an intricate tissue structure marked by pronounced heterogeneity. During early development (16–40 postmenstrual weeks), the brain undergoes considerable expansion in its volume and cortical surface area, accompanied by the noticeable observation of cortical folds, with the convex peak known as gyri and the concave valley as sulci. Typically, cortical folding begins with primary folds, which are highly conserved across individuals,1 and gradually progresses to more complex secondary and tertiary folds that exhibit significant individual variability.2 Emerging evidence links abnormal cortical folding patterns to various neurodevelopmental disorders such as autism,3 epilepsy,4 and schizophrenia,5 as well as cortical malformations like lissencephaly, pachygyria, and polymicrogyria.6 Consequently, a comprehensive understanding of the development of cortical folding is crucial for early detection and treatment of cognitive impairments and neurodevelopmental disorders.The development of cortical folding involves highly complex spatiotemporal patterns influenced by multiple physiological factors,7 such as cranial constraints,8 axon maturation,9 cerebrospinal fluid,10 genetic expression,11etc. Though the precise mechanisms underlying cortical fold formation remains elusive, increasing studies suggest that mechanics play a crucial role in modulating this process.12 Brain tissue development occurs within a complex physical environment comprising the skull, meninges, and cerebrospinal fluid. While external forces such as constraints from the skull and cerebrospinal fluid pressure are expected to affect cortical folding patterns, experimental observations indicate that the internal forces exerted within brain tissue are more dominate at the onset of folding.13 In line with these findings, Essen14 firstly proposed the “axon tension” theory, which suggests that axonal tension pulls gyral walls together, leading to formation of cortical folds. In contrast, Nie et al.15 proposed that pushing force from axonal growth could generate folding shapes similar to those observed in real cortical surface. However, despite experimental evidence of forces acting on axons, their magnitude and direction appear insufficient to pull or push brain tissues into folds.16 Conversely, the differential growth theory, which has garnered more experimental support,17,18 posits that the mismatch in growth ratios between two-layered brain structure triggers the bulking of cortical surface.19 Specifically, the fast-growing outer layer (gray matter), under connectivity constraint of slow-growing inner layer (white matter), generates excessive compressive forces that initiate cortical folding. Therefore, it is essential to investigate how varying tissue growth influences the initiation and regulation of cortical folding patterns.
Computational simulation, such as finite element method (FEM), have emerged as a powerful tool for modeling the spatiotemporally complex development of cortical folding patterns, due to its superiority in reproducibility and cost-effectiveness compared to experimental and longitudinal imaging methods.20 To replicate folding patterns, most studies have assumed uniform growth patterns such as isotropic growth and purely tangential growth across growing tissues.21–25 While these approaches have greatly advanced our understanding of cortical folding mechanisms, their effectiveness diminishes when comparing the simulated patterns to actual brain structures, particularly in brain-wide simulations.26,27 This discrepancy arises because uniform growth assumptions conflict with the heterogeneous nature of growth as observed in experimental and imaging investigations.28,29 Recent studies, including our own study,30 have shown that the cortical surface can be parcellated into 18 distinct regions, each exhibiting significantly different area expansion ratios from the third trimester of pregnancy to the first two years post-birth, as illustrated in Fig. 1. Similar parcellation based on heterogenous development of cortical thickness have also been reported.31 These observations underscore the pronounced spatiotemporal heterogeneity in cortical tissue growth.
Despite its significance, the effect of growth heterogeneity on cortical folding patterns has been largely overlooked in computational studies. Budday and Steinmann32 were among the first to investigate this effect by incorporating manually designed sinusoidal variations in growth distributions during folding simulations based on idealized models. Their findings revealed that regional variations in cortical growth primarily influence secondary instabilities, contributing to the irregularity of folding patterns. Wang et al.33 further explored this by simulating cortical folding evolution on theoretical brain models with regionally heterogeneous growth, linking the growth ratio to local curvature. Their results demonstrate the role of regional growth in shaping complex cortical folding patterns, characterized by fast-growing gyri and slow-growing sulci. Similar conclusions were drawn by Zhang et al.,34 who reported that gyral convex patterns consistently emerge in cortical regions with faster growth speed. While these studies have enhanced our understanding of the critical role of heterogeneous growth in cortical folding development, they have primarily focused on spatial heterogeneity and relied on idealized geometric models with manually defined growth patterns. These approaches deviate significantly from real brain scenarios. A comprehensive study examining the effects of realistic heterogeneous growth on cortical folding patterns in models that closely resemble real brains is still lacking.
In this study, we aim to explore how anatomically realistic regional growth affects the simulated cortical folding patterns on geometric models derived from real brains. We first employed ML-assisted symbolic regression to generate regional growth models using longitudinal surface area and cortical thickness data, including over 1000 infant magnetic resonance imaging (MRI) scans from developing prenatal and neonatal human brains. These predicted growth models were then integrated into ABAQUS to simulate mechanical folding development using tangential differential growth theory, applied to regional geometric models constructed from initial brain surfaces. The spatiotemporal folding patterns were analyzed and compared with those observed in real brains, both qualitatively and quantitatively. Additionally, we conducted an in-depth analysis by decomposing the growth's value and trajectory to assess their individual impacts on cortical folding patterns. Our results highlight the importance of considering growth heterogeneity in simulations of brain folding development. This approach could potentially contribute to early diagnosis of cortical malformations such as lissencephaly and polymicrogyria and improve treatments for neurodevelopmental disorders like epilepsy and autism.
2. Methods
2.1. Biomechanics in modeling brain folding
Differential growth theory indicates that cortical folding during brain development arises due to disparities in growth ratio between the faster-growing cortical layer and the slower-growing white matter layer. To investigate the effect of regional growth on folding evolution in the developing brain, we conducted nonlinear finite element simulations grounded in continuum mechanics theory and the finite growth assumption. In describing deformation kinematics, we introduce a one-to-one mapping denoted as x = φ(X), which carries a material particle initially positioned at X in the reference configuration to its new position x in the current configuration
to its new position x in the current configuration  . Leveraging the theory of multiplicative decomposition proposed by Rodriguez et al.,35 we decompose the deformation gradient F and the Jacobian J into elastic and growth components:
. Leveraging the theory of multiplicative decomposition proposed by Rodriguez et al.,35 we decompose the deformation gradient F and the Jacobian J into elastic and growth components:F = ∇Xφ = Fe·Fg and J = det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F = Je·Jg. F = Je·Jg. | (1) |
Fg = gtI + (gr − gt)![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ⊗ ⊗![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) and Jg = det and Jg = det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fg, Fg, | (2) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) is the local surface normal, oriented positively in the out-of-plane direction. Growth kinematics alone generate a stress-free state, which must be balanced by the elastic deformation gradient introduced by material confinement to avoid incompatible deformation.36
is the local surface normal, oriented positively in the out-of-plane direction. Growth kinematics alone generate a stress-free state, which must be balanced by the elastic deformation gradient introduced by material confinement to avoid incompatible deformation.36
We characterized the constitutive behavior of the brain tissue through the following neo-Hookean strain energy function, parameterized exclusively in terms of the elastic components of deformation gradient Fe and its Jacobian Je,
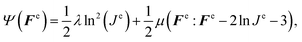 | (3) |
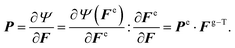 | (4) |
Div![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_i_char_2009.gif) P = 0 P = 0 | (5) |
2.2. Symbolic regression for discovering growth models
Inspired by Darwinian principles of natural selection, symbolic regression autonomously uncovers mathematical relationships exclusively from provided data without requiring prior knowledge, thereby significantly enhancing the interpretability and flexibility of the model discovery process.37 It has demonstrated promising applications in model characterization38–40 and parameter calibration.41 Symbolic regression operates through a process known as genetic programming (GP). During GP execution, functional expressions are efficiently formatted using a binary-tree structure, which consists of nodes and branches.A complete tree structure, as illustrated in Fig. 2a, involves variables, mathematical operators (either unary or binary), and constants. The evolution process experiences the genetic operations of evaluation, selection, mutation, and crossover, while the latter two are essential for updating the tree structure. Specifically, the mutation operation amplifies population's genetic diversity by randomly altering some nodes in an expression tree, as exemplified in Fig. 2b, where a new offspring is generated by substituting the exponential operator (exp) with the hyperbolic tangent (tanh). Conversely, the crossover operation allows the algorithm to create new offspring by combining building blocks from different parent candidates, as demonstrated in Fig. 2c. This iterative process of evaluation, selection, mutation, and crossover continues until the optimal expression is obtained or the maximum number of generations is reached, whichever is reached first.37
In this study, we employed symbolic regression to discover appropriate growth models for the human brain cortex. The raw data includes the measured surface area of each parcellated region in the developing brain cortex along with the corresponding gestational ages, as shown in Fig. 3a.
To facilitate computational implementation, we first converted the data into unitless growth ratio g(t) and virtual time t using the following formulas:
 | (6) |
All symbolic regression analyses were performed using PYSR,42 a powerful open-source package developed alongside the Julia library SymbolicRegression.jl. During the training of symbolic regression, the binary operators are restricted to addition (+), multiplication (*), and polynomial (tn), while the unary operators are limited to the exponential (exp), hyperbolic tangent (tanh), square (t2), cube (t3), and natural logarithmic (ln) functions. Given the balance between computational cost and model performance, the training time is limited to 30 minutes or a maximum of 1000 iterations, whichever is reached first, as our observations indicate that most qualified models could be identified within this timeframe. The maximum depth of the expression tree is set to 10, and the maximum complexity is constrained to 100. Notably, the nested behavior of the exponential, hyperbolic tangent, and logarithmic functions is forbidden, while the square and cube operators are restricted to occur, if desired, only once inside the exponential, hyperbolic tangent, and logarithmic functions. We adopt the default criterion (“best”) to guide the model selection process. For each algorithm, the training is repeated at least three times, and favorable candidates are selected as the target models. All training was performed on a Legion PC equipped with a six-core Intel Core I7-8750H 2.2 GHz CPU, 4 GB NVIDIA GTX 1050Ti GPU, and 24 GB of memory.
2.3. Computational modeling of a developing brain
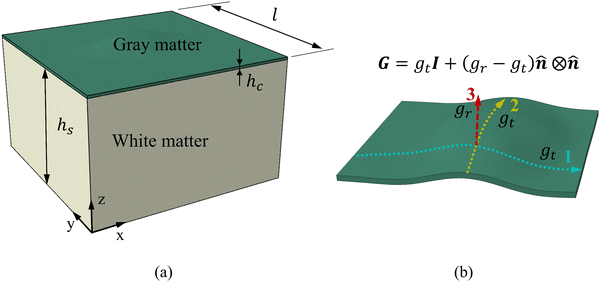
The identified regional growth models (both tangential and radial) were used to construct the growth tensor Fg, which can be applied to simulate folding evolution using the FEM, as shown in Fig. 3b. The simulation results were then compared with the brain imaging data for model validation, as illustrated in Fig. 3c. To simulate the folding evolution of the developing brain, we constructed a three-dimensional double-layer patch model based on the geometries of a human brain at 29 postmenstrual weeks, as depicted in Fig. 3b. Initially, the regional brain inner surface (the interface between the gray matter and white matter) was extracted using the parcellation map provided by Huang et al.30 The extracted surface was first extended by 2–5 mm along the boundary's local curvature. Laplacian smoothing was then applied to the boundary area using a smoothing parameter of 0.2, with the number of iterations ranging from 15 to 22 across all extracted surfaces. During smoothing, the intermediate area remains fixed to preserve the integrity of the initial geometry (see Fig. S1 in the ESI†). Subsequently, we interpolated the extended surface with a flat plane of 80 mm × 80 mm and merged these two surfaces using Boolean operations. The connecting areas were further smoothed to ensure a natural transition of the curvature. This extension and interpolation ensured that the model's dimensions were large enough compared to the wavelength of folded patterns observed in experiments, thereby preventing boundary effects.25 Additionally, the squared boundaries significantly simplified the prescription of boundary conditions during modeling. We then shifted the interpolated surface upwards by 2 mm to form the initial cortical layer and extended the squared boundary downwards by 50 mm to generate the initial white matter layer. This design was based on experimental observations in neonatal human brains, which indicate that the cerebral cortex is a thin layer with a thickness of 2–3.5 mm, while the core has a much greater thickness of around 50 mm.43 Consequently, the base model's dimensions were approximately 80 mm × 80 mm × 50 mm (excluding cortical thickness), as illustrated in Fig. 4a, where l = 80 mm, hs = 50 mm, and hc = 2 mm.All simulations were performed using the commercial software ABAQUS (Dassault Systems, Paris, France).44 Dynamic-explicit solver was employed due to its superior performance in solving nonlinear, dynamic, and larger deformation problems.45,46 Both the gray and white matters were modeled as incompressible neo-Hookean materials, with elastic stiffness values of 0.31 kPa for the cortical and 0.45 kPa for the white matter layer.47 For detailed material parameter settings, please refer to the Table S1 in the ESI.† Orthotropic growth was defined for the cortical layer, while isotropic growth was applied to the white matter layer. In our modeling approach, growth was simulated using thermal expansion, considering the analogy between the volumetric growth and the thermal expansion.48 The expansion ratio α(t) correlates to the growth ratio as α(t) = g(t) − 1. Specifically, for the white matter layer, the expansion ratio was defined as α(t) = 0, while for the cortical layer, α(t) = gr(t) − 1 was applied to out-of-plane growth and α(t) = gt(t) − 1 to in-plane growth, as shown in Fig. 4b. The customized growth models (gr(t) and gt(t)), derived from symbolic regression, were implemented into the finite element algorithm through a user-defined subroutine VUEXPAN. Symmetric boundary conditions were prescribed on the four sides of the model and the bottom surface of the white matter layer was fixed. Free boundary conditions were applied to the top surface of the cortical layer, accompanied by a self-contact constraint to prevent self-penetration. The total simulation time was set to 1 s. To avoid computational instabilities, the maximum time step was determined as  where a is the average mesh size, ρ is the mass density, K is bulk modulus.49 Temperature variation was applied using a sigmoidal smooth step function.
where a is the average mesh size, ρ is the mass density, K is bulk modulus.49 Temperature variation was applied using a sigmoidal smooth step function.
Structural meshing with the element type C3D8R was conducted for both the cortical and white matter layer. To determine the appropriate mesh size, we conducted a mesh sensitivity analysis with mesh size ranging from 0.3 mm to 0.8 mm (ESI,† Fig. S2 and S3). Based on the mesh convergence analysis—where simulation results with the coarsest mesh closely matched those of the finest mesh—we selected a mesh size of 0.5 mm for all models. This results in 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 elements for the cortical layer and 278
700 elements for the cortical layer and 278![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 elements for the white matter layer. During the simulations, we recorded the coordinates and displacements of the region of interest (ROI) for each frame. The ROI was defined as the smallest square area encompassing the extracted brain surface region. Although this definition introduces some redundant areas, which potentially biases the quantitative measurements, it serves our primary goal: to compare the effectiveness of the regional growth model with the widely used isotropic growth theory. The inclusion of these redundant areas does not significantly impact this comparative analysis. Additionally, defining the ROI in this manner simplifies the partitioning process in ABAQUS and facilitates area reconstructions during postprocessing. All simulations were performed on a Dell workstation equipped with a 16-core Intel(R) Xeon(R) CPU E5-2687 W@3.1 GHz, and 64 GB of memory.
300 elements for the white matter layer. During the simulations, we recorded the coordinates and displacements of the region of interest (ROI) for each frame. The ROI was defined as the smallest square area encompassing the extracted brain surface region. Although this definition introduces some redundant areas, which potentially biases the quantitative measurements, it serves our primary goal: to compare the effectiveness of the regional growth model with the widely used isotropic growth theory. The inclusion of these redundant areas does not significantly impact this comparative analysis. Additionally, defining the ROI in this manner simplifies the partitioning process in ABAQUS and facilitates area reconstructions during postprocessing. All simulations were performed on a Dell workstation equipped with a 16-core Intel(R) Xeon(R) CPU E5-2687 W@3.1 GHz, and 64 GB of memory.
2.4. Postprocessing and quantitative metrics
After the simulations, the recorded coordinates and displacements were first extracted from the result file using Python and subsequently imported into MATLAB to reconstruct the deformed surface. During reconstruction, the surface was interpolated five times to generate a sufficiently smooth surface, and the original quadrilateral surface mesh was transformed into a triangular mesh, facilitating the calculation of quantitative features such as curvatures, gyrification index, and sulcal depth in MATLAB.The curvatures of the triangular mesh were calculated using the method introduced by Meyer et al.,52 where finite volume discretization was employed to estimate the local integral of mean curvature over the normal areas of triangular faces associated with each point. If the surrounding faces are obtuse triangles, the barycentric area was calculated; otherwise, the Voronoi area was used. However, the calculated mean curvature is dependent on the geometry's shape or size, meaning its magnitude varies with brain scales. To address this, we further introduced a non-dimensional measure of mean curvature using the method provided by Balouchzadeh et al.,53 where the mean curvature is multiplied by a characteristic length lc,
 | (7) |
 | (8) |
 where N denotes the number of data points, yi represents the actual feature values measured from real brain data, ȳ is the mean of actual values, and ŷi is the predicted value from the simulation. An R2 value close to 1 indicates a strong agreement between the simulation results and real brain imaging data. MAPE, expressed as a percentage, quantifies the average absolute error between predicted (ŷi) and actual values (yi). It is calculated using the formula:
where N denotes the number of data points, yi represents the actual feature values measured from real brain data, ȳ is the mean of actual values, and ŷi is the predicted value from the simulation. An R2 value close to 1 indicates a strong agreement between the simulation results and real brain imaging data. MAPE, expressed as a percentage, quantifies the average absolute error between predicted (ŷi) and actual values (yi). It is calculated using the formula: | (9) |
 | (10) |
 is the mean of actual values. All these evaluation metrics were calculated in Python using the sklearn and scipy libraries. Noted, due to the discrepancy in the number of data points between the simulation results and the actual data, we applied an interpolation method to resample the extracted simulation data, ensuring a consistent data size before computing the evaluation metrics.
is the mean of actual values. All these evaluation metrics were calculated in Python using the sklearn and scipy libraries. Noted, due to the discrepancy in the number of data points between the simulation results and the actual data, we applied an interpolation method to resample the extracted simulation data, ensuring a consistent data size before computing the evaluation metrics.
2.5. Brain imaging data
In this study, we aimed to conduct symbolic regression to identify tangential growth models by measuring brain surface area data from two high-quality, publicly available imaging datasets focused on early brain development: the developing Human Connectome Project (dHCP) and the Baby Connectome Project (BCP). The dHCP dataset includes 549 MRI scans from 500 healthy neonates (279 males, 221 females) aged between 29 and 45 postmenstrual weeks.55 These MR images were obtained using a Philips 3T scanner with a 32-channel neonate-dedicated head coil at St. Thomas Hospital, London, UK.56 The BCP dataset comprises 488 longitudinal MRI scans from 235 healthy, term-born infants (108 males, 127 females) scanned between 41 and 144 postmenstrual weeks. These images were collected using 3T Siemens Prisma MRI scanners equipped with Siemens 32-channel head coils at The University of North Carolina at Chapel Hill and University of Minnesota. To investigate the developmental regionalization of cortical surface area expansion during pregnancy and infancy, a data-driven method known as nonnegative matrix factorization (NMF) was utilized to partition the cortical surface into distinct regions by clustering cortical vertices with similar developmental patterns. For more details, please refer to our recent work.30The radial growth model was characterized using thickness data measured in the developing neonatal brain.31 It is important to note that the radial growth dataset consisted exclusively of postnatal measurement. Consequently, we could not perform symbolic regression on a continuous dataset spanning from 29 to 136 postmenstrual weeks, as we did for the tangential growth model. To address this limitation, we assumed a linear increase in cortical thickness during the perinatal period (29–40 postmenstrual weeks) based on brain imaging analyses57,58 and applied linear extrapolation to ensure a smooth transition. However, it should be mentioned that there is no clear consensus on the exact developmental trajectory of cortical thickness during the perinatal stage. For example, Demirci and Holland59 recently reported a weak linear correlation between cortical thickness and scan ages during 29–43 postmenstrual weeks. For simplicity, we extended the linear growth trend observed in early postnatal measurements to the perinatal period. Additionally, we introduced several constraints to the symbolic regression algorithm: no growth occurs at the initial stage (gr(GA = 29) = 1), and the derivatives at the connection stage were required to be smooth  .
.
We constructed all computational models using publicly available 4D infant cortical surface atlases.60,61 These atlases also served as the base model for measuring quantities such as curvature, GI, and SulcDepth, providing a baseline for quantitative comparison. In our previous study, the cortical surface was parcellated into 18 distinct regions based on the NMF method.30 For this study, however, the primary objective was to compare the effectiveness of the regional growth model with classic growth theories. Therefore, we selected five representative regions that exhibit significant distinctions in surface area and cortical thickness. These regions are slow-growing region 1, medium-growing regions 4, 9, and 11, and fast-growing Region 16, corresponding to the cortical areas of “Dorsal Precentral, Paracentral and Posterior Cingulate”, “Lateral Precentral and Postcentral”, “Supra Marginal”, “Caudal Middle Frontal”, and “Dorsal Prefrontal”, respectively. As illustrated in Fig. 5, the development of the surface area and cortical thickness from 29 postmenstrual weeks to 2 years of age exhibits significant differences among these regions, with the p-values all smaller than 0.001. Here, we conducted paired Student's t-test to compute the significance of these differences, with the null hypothesis being no difference in surface area or cortical thickness between the two regions.
3. Results
In this study, we first employed a symbolic regression algorithm to identify suitable growth models using longitudinal surface area and cortical thickness data from developing human brains, with ages ranging from 29 postmenstrual weeks to 2 years of age. These growth models were then integrated into ABAQUS via a user-defined subroutine to simulate mechanical folding evolutions caused by differential growth in double-layer structures. The dynamic folding patterns were analyzed and compared with anatomically realistic brain imaging models both in qualitative and quantitative manner. Subsequently, we substituted the regional growth model with classical growth models commonly used in previous studies, such as isotropic growth and purely tangential growth. We evaluated and compared the effectiveness of each model in modeling cortical folding development using quantitative metrics introduced in Section 2.4. We further investigated whether the accuracy of modeling is more influenced by the value of growth ratio or the trajectory of the growth model. Finally, we built a multi-regional model incorporating three regions with distinct growth patterns predicted by symbolic regression.3.1. Regional growth models identified from symbolic regression
We investigated suitable tangential growth models through symbolic regression using the in-plane growth ratio data, normalized by the initial growth ratio as shown in eqn (6). This normalization ensures that the growth ratio starts from an initial value of 1. Moreover, given that the cortical surface area continues to increase beyond 24 postnatal months,62,63 the derivative of the growth ratio at this point must remain positive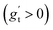 . These constraints were incorporated into the symbolic regression algorithm by customizing the loss function to impose a significant penalty for any violation. Fig. 6 illustrates the tangential growth model identified for each representative region using symbolic regression. All models exhibit satisfactory accuracies, with R2 values exceeding 0.85, effectively capturing the growth patterns characterized by an initial linear increasing phase transitioning into a gradually steady phase, forming an upper-sigmoid shape. Intriguingly, among the predefined operators such as “exp”, “tanh”, “ln”, and polynomials, as introduced in Section 2.2, the symbolic regression consistently selected a combination of tanh and polynomials. Moreover, a consistent model format, gt(t) = (a × t + b) × tanh(c × t) + 1, where a, b, and c are constants, was discovered for almost all regions except for region 1. This finding suggests a promising model choice for characterizing brain in-plane growth patterns.
. These constraints were incorporated into the symbolic regression algorithm by customizing the loss function to impose a significant penalty for any violation. Fig. 6 illustrates the tangential growth model identified for each representative region using symbolic regression. All models exhibit satisfactory accuracies, with R2 values exceeding 0.85, effectively capturing the growth patterns characterized by an initial linear increasing phase transitioning into a gradually steady phase, forming an upper-sigmoid shape. Intriguingly, among the predefined operators such as “exp”, “tanh”, “ln”, and polynomials, as introduced in Section 2.2, the symbolic regression consistently selected a combination of tanh and polynomials. Moreover, a consistent model format, gt(t) = (a × t + b) × tanh(c × t) + 1, where a, b, and c are constants, was discovered for almost all regions except for region 1. This finding suggests a promising model choice for characterizing brain in-plane growth patterns.
For out-of-plane growth models, we applied distinct conditions to constrain growth behaviors. In addition to the initial value constraint (gr|t=0 = 1), we incorporated an additional constraint to ensure the derivative is smooth at the connection stage  due to the use of linear extrapolation to address data scarcity during the perinatal period. Moreover, as the cortical thickness development tends to be stabilized within the first two years after birth,64,65 the derivative at the phase end must be zero
due to the use of linear extrapolation to address data scarcity during the perinatal period. Moreover, as the cortical thickness development tends to be stabilized within the first two years after birth,64,65 the derivative at the phase end must be zero  . Fig. 7 shows the radial growth models identified for each representative region through symbolic regression. Despite significant variance, the predicted growth model can still decipher the mathematical relationship from the provided data points. All growth models exhibit an inverted U-shape, peaking during the intermediate period. This phenomenon is consistent with imaging observations by Gilmore et al.66 For growth in the out-of-plane directions, symbolic regression exclusively selected the polynomial operators to construct the base models. The general model format can be summarized as a combination of up to fourth order polynomials: gr(t) = a × t4 + b × t3 + c × t2 + d × t + e, where a, b, c, d, e are constants. This result suggests a potential model choice for characterizing brain out-of-plane growth patterns. Though the accuracy was degraded by data variance, symbolic regression still proves robust in identifying suitable regional growth models for the human brain cortex, as validated in our recent paper.39 These predicted models will be integrated into ABAQUS via user-defined subroutines to simulate brain folding evolution.
. Fig. 7 shows the radial growth models identified for each representative region through symbolic regression. Despite significant variance, the predicted growth model can still decipher the mathematical relationship from the provided data points. All growth models exhibit an inverted U-shape, peaking during the intermediate period. This phenomenon is consistent with imaging observations by Gilmore et al.66 For growth in the out-of-plane directions, symbolic regression exclusively selected the polynomial operators to construct the base models. The general model format can be summarized as a combination of up to fourth order polynomials: gr(t) = a × t4 + b × t3 + c × t2 + d × t + e, where a, b, c, d, e are constants. This result suggests a potential model choice for characterizing brain out-of-plane growth patterns. Though the accuracy was degraded by data variance, symbolic regression still proves robust in identifying suitable regional growth models for the human brain cortex, as validated in our recent paper.39 These predicted models will be integrated into ABAQUS via user-defined subroutines to simulate brain folding evolution.
3.2. Regional growth models accurately simulate folding evolutions patterns
Fig. 8 illustrates the evolution of cortical folding on simulated brain surface, incorporating the regional growth model. The folding patterns at six key simulation moments are displayed and rendered with the displacement magnitude. As displayed, the non-uniform curvature inherent on initial brain surface (29 postmenstrual weeks) was sufficient to initiate bulking at around 0.2 s and generate intrinsic folding modes, which evolved to form distinct gyri and sulci over time. The resulting folding patterns of regional models are visually different. Specifically, regions 4, 11, and 16 exhibited denser folds compared to regions 1 and 9, indicating shorter folding wavelengths in these regions. This disparity is primarily attributed to differences in initial geometry and potentially the effects of growth. Additionally, for each model, areas with higher initial altitude (characterized in the out-of-plane direction) tend to experience greater displacements, as depicted in dark red areas. Since we applied consistent growth ratios both in tangential and radial directions across each model, the non-uniform displacements likely stem from the in-plane compressions caused by tangential growth under boundary confinements. This suggests that tangential growth has a more significant influence on folding evolutions than radial growth, which is also evident in the larger values observed in tangential growth models compared to radial growth model in Fig. 6 and 7. | ||
| Fig. 8 Longitudinal brain developing patterns for five regions. Cortical folding patterns of six moments ranging from t = 0 to t = 1.0 were recorded and rendered with displacement magnitude. | ||
The nonuniform distribution of displacement remains prominent at the interface between the gray matter and white matter. As shown in Fig. 9a and b, greater displacements occur in areas with higher initial altitude. Additionally, the simulated folding surfaces exhibit characteristic pattern of cusped sulci and smooth gyri, consistent with the morphology observed in real human brain structures.67 To validate our simulation results, we focused on the folding patterns at the interface where the initial locations approximately cover the extracted brain regions, as illustrated in Fig. 9c. We then compared these patterns with those of a 24-postnatal-month brain, as highlighted in Fig. 9d.61 As shown, our simulated brain folding closely replicates the realistic brain pattern, particularly in regions 1 and 4. For the other three regional models, certain characteristic morphologies are comparable to those in real brains, such as the ladder-shaped concaves in region 16 and the sharp ridge along with a narrow valley in region 9. To quantitatively compare these folding patterns, we further computed the curvature (MC), sulcal depth (SulcDepth), and gyrification index (GI) using the methods described in Section 2.4. The distributions of MC and SulcDepth are shown in the contour plot of Fig. 10. As depicted, positive curvatures tend to appear on the gyri, while negative on the sulci. This distinction suggests that mean curvature can serve as a metric to deliberately extract gyri and sulci for further investigations.45,50,68
 | ||
| Fig. 10 Mean curvature and sulcal depth. Distribution of dimensionless mean curvature and sulcal depth of the five selected regions at the final state. | ||
Fig. 11 shows the comparisons of those quantitative metrics measured in the simulated brain (circular dots and line) with those from a realistic human brain (square dots), with the dots representing the mean values of each metric averaged across the entire ROI surface. As shown in the figure, most of simulation results align well with the realistic brain data in both trend and values. The simulation trajectories exhibit sigmoid-like shapes, starting with flat initial phases, then increasing dramatically after the onset of geometry instabilities (around 0.2 s, as seen in Fig. 8), and finally stabilizing once the folding patterns mature. This trend aligns with the identified regional growth models depicted in Fig. 6 and 7. Among the three metrics, mean curvature was poorly predicted compared to the other two metrics, as reflected in the insignificantly correlated trends and poor alignments, represented by low R2 values equal to 0. It is important to note that the initial curvatures in the simulation are not zero because the simulation models were constructed based on brain regional surfaces, which already display curvatures at the initial state (29 postmenstrual weeks). The discrepancy between the two trajectories can potentially be explained by the following factors: (1) absence of external constraints: the simulation does not incorporate the influence of external constraints from the brain skull, meninges, or cerebrospinal fluid. While these factors do not initiate cortical folding, they play an important role in regulating the brain's local geometry. For instance, contact with the skull and meninges may flatten the gyrus upon contact, resulting in wider and smoother gyral peeks.20 (2) Inaccurate sampling of the region of interest (ROI): for simplicity in postprocessing, we defined the ROI as the smallest rectangular area enclosing the extracted brain regions. This approach inevitably introduces redundant areas, thereby reducing the precision of quantitative metrics, such as mean curvature, compared to measurements taken directly on the exact brain regions. The sulcal depth and gyrification index correlate well across all regions except for region 16, where a significant deviation occurs after t = 0.4 s. This discrepancy mainly arises from the geometric model being constructed based on a single region. Since region 16 exhibits the highest growth ratio among all selected models, it undergoes the largest deformations during simulation, which, under boundary confinement, would generate the most convoluted folding structures, resulting in the highest GI and sulcal depth. However, in real brain, the compression caused by rapid expansion of region 16 would be relaxed by the surrounding regions, which yields less complex folding patterns such as shallower sulci, as observed in Fig. 9. In summary, both qualitative and quantitative comparisons affirm the effectiveness of regional growth models in simulating the brain folding evolution process.
3.3. Regional growth models outperform classic unified growth models
To compare the effectiveness of regional growth models with classic models such as isotropic growth and purely tangential growth, we performed simulations on three regional models with varying growth speeds: the slow-growing region 1, medium-growing region 9, and fast-growing region 16. In both isotropic growth and tangential growth cases, the growth ratio was defined as a constant which is commonly adopted in previous studies.25,53,67 The performances of different growth theories were compared in Fig. 12 (ESI,† Fig. S4), where folding patterns at t = 1 s were presented and rendered with displacement, mean curvature, and sulcal depth, respectively, to facilitate qualitative comparisons. Quantitative comparisons were also provided by averaging each metric across the entire ROI surface.
which is commonly adopted in previous studies.25,53,67 The performances of different growth theories were compared in Fig. 12 (ESI,† Fig. S4), where folding patterns at t = 1 s were presented and rendered with displacement, mean curvature, and sulcal depth, respectively, to facilitate qualitative comparisons. Quantitative comparisons were also provided by averaging each metric across the entire ROI surface.
As shown in Fig. 12a–c, the regional growth model generates more sulcal and gyral folds compared to the isotropic growth model, especially evident in the intermediate areas corresponding to the initial brain surface. The increased number of folds indicates that regional growth model yields more convoluted folding patterns with shorter wavelengths. This phenomenon concurs with the findings of Budday and Steinmann,32 which demonstrates that variation in cortical growth modulates secondary instabilities, culminating in highly irregular folding patterns. However, the difference in wavelength between the regional growth model and the tangential growth model is not evident, even though the regional growth model tends to produce more cusped and deep sulci, as well as curled gyri. This suggests that tangential growth theory generates more convoluted patterns than isotropic growth, consistent with previous findings.69,70 Furthermore, this proves that tangential (in-plane) growth plays a more dominant role in affecting folding patterns than radial (out-of-plane) growth.
The quantitative comparison illustrated in Fig. 12d shows that the regional growth model provides more accurate folding measures compared to the other two growth theories. This is evidenced by the closer alignment of the resulting curvature, sulcal depth, and GI with real brain data, as reflected by lower MAPE values. Additionally, the regional growth model initiates the folding earlier and reaches the stabilization stage sooner than the other two models. This suggests that the regional growth model can significantly reduce computational costs in simulating brain folding evolution by supplementing a stopping criterion based on stabilization.
3.4. Growth ratio values influence folding evolution more than growth trajectory
The regional growth model and purely tangential growth model exhibit similar primary folding patterns, with the regional growth model producing more cusped and deep sulci and curled gyri in secondary details. Both models adopt a similar format of tangential growth, but their values and growth trajectories differ. Noted, the effect of radial growth is ignored due to its minor impact on modulating folding. To figure out whether the value or growth trajectory dominates the folding patterns, we performed simulations on geometric model of region 9 using three growth models with the same resulting growth ratio but different growing trajectories. In addition to the regional growth model, we introduced two additional growth models following linear and Gompertz distributions, respectively, as shown in Fig. 13. The Gompertz distribution has been proven successful in modeling tissue growth,71 such as the growth mode of myelinated brain white matter72 and tumor growth with necrosis.73 The Gompertz distribution is expressed as follows:| gt(t) = a × exp(−exp(−b × (t − c))) + 1, | (11) |
 | ||
| Fig. 13 Three distinct growth models for region 9. Initial and final values keep the same for all three models, respectively, while the developing trajectories are different. | ||
Fig. 14 illustrates the qualitative comparison of folding patterns rendered with displacement, curvature, and sulcal depth, as well as the quantitative comparison by averaging each metric across the entire ROI surface. As seen in Fig. 14a–c, despite the difference in growing trajectories, the resulting folding demonstrates nearly identical patterns, especially in the linear and Gompertz models. This is also evident in quantitative measurements shown in Fig. 14d. Though the regional growth model initiates instabilities earlier due to its rapid growth within the first 0.2 s, the resulting measures of GI and curvature are almost the same across all models. Additionally, the regional growth model generates deeper sulci compared to the other two models. When compared to the findings in Section 3, it becomes apparent that the growth trajectories have a less significant impact on folding patterns than the magnitude of growth itself. This observation remains consistent with the findings of Wang et al.,49 who report that the cortical growth mode has a limited influence on surface morphology complexity. Interestingly, this result appears to be an intrinsic feature of brain folding, as it persists across various simulation approaches. Our simulations were based on anatomically realistic brain models, incorporating a physical accurate growth pattern. In contrast, Wang et al.49 employed idealized spherical models with manually defined growth patterns to represent brain structure. Despite these differences in methodology, the core finding—minor impact of growth trajectories on folding patterns—remains consistent.
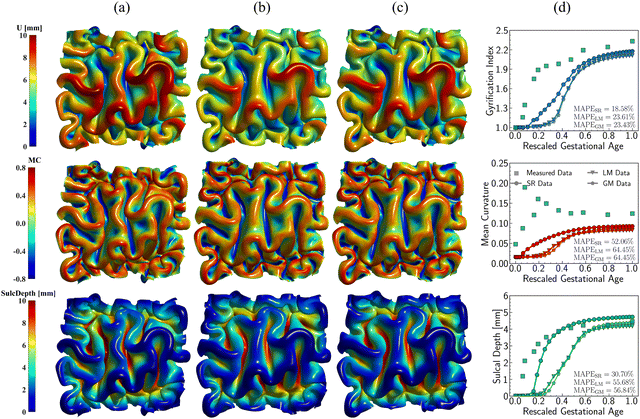 | ||
| Fig. 14 Impact of growth trajectory on the folding patterns. Three growth models with distinct developing patterns for region 9, including symbolic regression model (SR) (a), linear growth model (LM) (b), and Gompertz growth model (GM) (c). Distribution of displacement (U), mean curvature (MC), and sulcal depth (SulcDepth) are present with their quantitative measure present at the right (d). The simulation errors relative to real brain imaging data are quantified using MAPE. In simulations, the above growth models are exclusively functioned in the tangential direction, while the growth in thickness remains consistent, and the radial growth model predicted from symbolic regression is employed, as shown in Fig. 6. | ||
3.5. Multi-region model provides more realistic folding results than single-regional model
All simulations discussed above were conducted on a single brain region, where we applied symmetric confinements to their boundaries to prevent out-of-boundary growth. Despite our efforts to minimize the boundary effects by sufficiently extending the ROI boundaries, this condition may still be overly restrictive in generating compression, which is pivotal for triggering instabilities, resulting in unrealistic folding patterns as observed in region 16 (see Fig. 8 and 11). Additionally, in real brains, no region functions or deforms independently without affecting or being affected by surrounding regions. To address these limitations, we constructed a new computational model using the initial geometries of three adjacent regions: regions 1, 4, and 11. The constructed model is shown in Fig. 15a. After proper smoothing and extension, the model uniformly partitions a squared area into three parts, following an approximate proportion of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for regions 1, 11, and 4, respectively.
2 for regions 1, 11, and 4, respectively.
The simulated patterns are illustrated in Fig. 15b–d. Compared to the single-region model (see Fig. 8), the multi-region model generates more uniform folds across each region. For example, in the single-region modeling, the folding patterns are fairly condensed in the ROI of region 11 but sparse in region 1. Conversely, these patterns are uniformly distributed in the multi-region model, which is consistent with the anatomical morphology of the real human brain. However, certain characteristic features like the central sulcus were missed, which could be improved by incorporating more regions into the model construction process.
The quantitative comparison in Fig. 16 indicates that the multi-region model produces more realistic results compared to the single-region model. This is demonstrated by the closer alignment of quantitative measures for GI, mean curvature, and sulcal depth with real brain data, as evidenced by lower MAPE values and higher correlation coefficient in most cases. These results highlight the superiority of the multi-region model in simulating brain folding evolutions over the single-region model. Looking ahead, it is expected that a brain-wide model incorporating all 18 regions could yield more promising brain folding predictions, both in terms of qualitative patterns and quantitative measures.
4. Discussion
Computational simulations, such as finite element methods, have emerged as promising tools to elucidate the mechanical influence on cortical development, providing valuable insights into the underlying mechanisms22,67,74 and enabling predictive modeling of brain tissue behaviors under various conditions.75–77 Herein, we show that integrating simulations with regional growth models, derived through symbolic regression using brain developmental data, produces more realistic brain folding patterns. These region-based developing cortical patterns further exhibit accurate alignment with quantitative measures of real brain development. Our findings challenge the conventional views that isotropic, unified growth is sufficient to mimic cortical folding evolutions with modeling results more consistent with the imaging analyses.21,23 Instead, our results suggest that heterogenous growth patterns play an indispensable role in modulating brain cortical development, as suggested in the works of Holland et al.78 and Budday and Steinmann.32The longitudinal brain data encompass surface area expansion measured from 29 postmenstrual weeks to 2 years of age30 and cortical thickness recorded within the first two years after birth.31 We employed symbolic regression to derive explicit mathematical expressions for growth models across various brain regions, spanning from slow-growing areas to fast-growing areas. The models identified exhibit consistent patterns in describing both in-plane and out-of-plane growth for nearly all regions. This uniformity in regional growth reflects a characteristic growth mode of neural tissues79 and has also been observed in tumor development.71,80 Symbolic regression was chosen over conventional methods, such as multiple regression or neural networks, due to its ability to predict interpretable models from data without requiring prior knowledge of the model structure, which must be predefined in multiple regression.81,82 Moreover, symbolic regression explores an infinite functional space to identify candidate models, even with constraints applied to expedite the search process, highlighting its superior performance over other machine-learning-based methods,83,84 which are restricted to a limited functional space. The explicit mathematical expression of the growth model greatly facilitates the implementation of these models in ABAQUS simulations using user-defined subroutines. Though directly incorporating data into simulation can ensure closer alignments with the provided data, this approach is highly sensitive to noises, particular outliers, and may fail in scenarios requiring further operations, such as differentiation or integration.
Uniform growth theories such as isotropic growth have been extensively employed to model brain development.21–25 While these methods have significantly advanced our understanding of cortical folding mechanisms, their effectiveness degrades when comparing the resulting cortical folding patterns with imaging observations, particularly in brain-wide simulations.26,27 To address this limitation, additional physiological effects such as axonal fibers23,78 and cells migrations85,86 have been incorporated to more accurately simulate brain folding anatomy. However, these additions inevitably complicate modeling endeavors. Herein, we found that exclusively implementing regional growth into simulations can produce more realistic cortical folding patterns that closely match quantitative measurements of the real brain. This outcome aligns with the principle of Occam's Razor: the fewer deviations from real conditions, the better the simulation's alignment with the observed data. This finding underscores the superiority of heterogeneous growth over homogeneous growth in brain modeling.20 As presented in Section 3.3, even purely tangential growth can yield more complex folding patterns, similar to those observed in regional growth scenarios, compared to isotropic growth. Introducing such heterogeneity decreases the system's stability by triggering earlier bulking and more convoluted folding patterns. In addition to the regional growth, heterogeneity also exists in other brain properties like stiffness,32 surface curvature,87 and cortical thickness.88 These factors collectively contribute to the complex evolution of brain folding patterns.
While the brain surface bulking is predominantly driven by intrinsic properties such as initial surface curvature, relative stiffness or thickness ratio between gray matter and white matter, the growth does influence the cortical folding, especially in terms of cortical depth and folding complexity, as revealed by quantitative measures. Moreover, the value of growth ratio plays a more crucial role in modulating folding evolutions compared to the growth trajectory. Intuitively, the external forces, such as the thermal expansion introduced here, do not dictate the bulking modes but rather influence the timing of bulking initialization and the extent of bulking development. However, brain folding is a dynamic process, with numerous complex factors interacting in a coupled manner. Heterogenous growth can alter these intrinsic features. For example, differential growth in the in-plane and out-of-plane directions can change the thickness ratios between the gray matter and white matter. Similarly, axonal maturation, influenced by cell migration, can affect tissues stiffness.89 These features evolve dynamically, introducing variability into the cortical folding process.
Conducting simulations on a single brain region allows for comparative analysis of distinct growth theories and their effects on brain folding. However, this approach may lead to unrealistic folding patterns due to the artificially imposed boundary conditions. Our findings indicate that a multi-region computational model, which considers three adjacent regions simultaneously, offers a more reliable result by producing more uniformly distributed folding patterns. In the future, a brain-wide model encompassing all 18 parcellated regions is expected to yield more realistic folding predictions, by integrating regional growth models derived through symbolic regression. Moreover, our study can be improved by addressing the following issues: first, we assumed uniform cortical thickness across each brain region. Incorporating anatomically accurate cortical thickness, accounting for both gray and white matter in the model construction process, would provide a more convincing geometric model. Second, the tangential growth within the cortical layer was assumed to be uniform. In reality, this growth varies spatially, as evident in differential growth within the six-layered cortex.90 Future studies should consider adopting a spatially dependent growth profile, as proposed by Tallinen et al.8 Third, in current study, the tangential and radial growth models were characterized based on different datasets, as shown in Fig. 6 and 7. Future studies that integrate surface area and cortical thickness measurements from the same dataset would significantly enhance the integrity and rigor of the predicted growth model. Last but not least, the brain tissue in our model was treated as an incompressible hyperelastic material described by the neo-Hookean strain energy function. Incorporating a regional hyperelastic model with a degree of compressibility, characterized though symbolic regression, could account for the heterogeneity in stiffness and further enhance the reliability of our simulation results.
5. Conclusion
In this study, we investigated the impact of regional growth on the computational simulation of brain cortical folding. Using symbolic regression, we derived explicit mathematical growth models using the longitudinal data of cortical surface area expansion and cortical thickness measured on real human brains. These regressed models were then integrated into ABAQUS to simulate the evolution process of cortical folding. The resulting folding patterns were recorded and quantified using several mechanical descriptors, including mean curvature, sulcal depth, and gyrification index. Our findings demonstrate that regional growth models can generate complex folding patterns that closely resemble the anatomical structure of the brain in both quantitative and qualitative aspects. These models outperformed conventional uniform growth models such as isotropic growth and purely tangential growth in accurately modeling brain folding developments. We observed that the magnitude of growth, rather than its trajectory, plays a more predominate role in shaping folding patterns. Moreover, multi-region modeling produces more uniform folding patterns similar to imaging observations compared to single-region models. Our results underscore the importance of implementing regional growth in brain folding simulations. This approach holds promise for advancing early diagnostics of cortical malformations like pachygyria, lissencephaly, and polymicrogyria and improves treatment for neurodevelopmental disorders such as autism and epilepsy.Author contributions
JH: methodology, software, validation, investigation, writing – original draft; ZW: data curation, writing – review and editing; XC: formal analysis, writing – review and editing; LW: validation, writing – review and editing; DZ: validation, writing – review and editing; TL: validation, writing – review and editing; GL: conceptualization, validation, writing – review and editing; XW: conceptualization, validation, supervision, funding acquisition, writing – original draft, writing – review and editing.Data availability
The original contributions presented in the study are included in the article/ESI.† Further inquiries can be directed to the corresponding authors. The dHCP dataset is publicly available at the Developing Human Connectome Project repository: https://www.developingconnectome.org.91 The BCP dataset is publicly available in NIMH Data Archive: https://nda.nih.gov/edit_collection.html?id=2848.92Conflicts of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.Acknowledgements
JH and XW acknowledge the support from National Science Foundation (IIS-2011369) and National Institutes of Health (1R01NS135574-01). GL is supported in part by National Institutes of Health (MH123202, ES033518, AG075582, NS128534, and NS135574). This work also utilizes approaches developed by an NIH grant (1U01MH110274) and the efforts of the UNC/UMN Baby Connectome Project Consortium. Some of the data was provided by the developing Human Connectome Project, KCL-Imperial-Oxford Consortium funded by the European Research Council under the European Union Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. [319456]. We are grateful to the families who generously supported this research.References
- G. Lohmann, D. Y. von Cramon and A. C. F. Colchester, Cereb. Cortex, 2007, 18, 1415–1420 CrossRef PubMed.
- J. E. Schmitt, A. Raznahan, S. Liu and M. C. Neale, Cereb. Cortex, 2021, 31, 702–715 CrossRef PubMed.
- J. Zeidan, E. Fombonne, J. Scorah, A. Ibrahim, M. S. Durkin, S. Saxena, A. Yusuf, A. Shih and M. Elsabbagh, Autism Res., 2022, 15, 778–790 CrossRef PubMed.
- E. Beghi, Neuroepidemiology, 2020, 54, 185–191 Search PubMed.
- R. A. McCutcheon, T. R. Marques and O. D. Howes, JAMA Psychiatry, 2020, 77, 201–210 CrossRef PubMed.
- L. Subramanian, M. E. Calcagnotto and M. F. Paredes, Front. Cell. Neurosci., 2020, 13, 576 CrossRef PubMed.
- D. C. Van Essen, Semin. Cell Dev. Biol., 2023, 140, 90–104 CrossRef CAS PubMed.
- T. Tallinen, J. Y. Chung, J. S. Biggins and L. Mahadevan, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12667–12672 CrossRef CAS PubMed.
- E. Takahashi, R. D. Folkerth, A. M. Galaburda and P. E. Grant, Cereb. Cortex, 2011, 22, 455–464 CrossRef PubMed.
- R. M. Fame and M. K. Lehtinen, Dev. Cell, 2020, 52, 261–275 CrossRef CAS PubMed.
- L. F. Franchini, Front. Cell Dev. Biol., 2021, 9, 591017 CrossRef PubMed.
- P. V. Bayly, L. A. Taber and C. D. Kroenke, J. Mech. Behav. Biomed. Mater., 2014, 29, 568–581 CrossRef CAS PubMed.
- C. D. Kroenke and P. V. Bayly, J. Neurosci., 2018, 38, 767–775 CrossRef CAS PubMed.
- D. C. V. Essen, Nature, 1997, 385, 313–318 CrossRef PubMed.
- J. Nie, L. Guo, K. Li, Y. Wang, G. Chen, L. Li, H. Chen, F. Deng, X. Jiang, T. Zhang, L. Huang, C. Faraco, D. Zhang, C. Guo, P.-T. Yap, X. Hu, G. Li, J. Lv, Y. Yuan, D. Zhu, J. Han, D. Sabatinelli, Q. Zhao, L. S. Miller, B. Xu, P. Shen, S. Platt, D. Shen, X. Hu and T. Liu, Cereb. Cortex, 2011, 22, 2831–2839 CrossRef PubMed.
- G. Xu, A. K. Knutsen, K. Dikranian, C. D. Kroenke, P. V. Bayly and L. A. Taber, J. Biomech. Eng., 2010, 132, 071013 CrossRef PubMed.
- L. Ronan, N. Voets, C. Rua, A. Alexander-Bloch, M. Hough, C. Mackay, T. J. Crow, A. James, J. N. Giedd and P. C. Fletcher, Cereb. Cortex, 2014, 24, 2219–2228 CrossRef PubMed.
- M. R. Rosenzweig, Dev. Neuropsychol., 2003, 24, 523–540 CrossRef PubMed.
- D. P. Richman, R. M. Stewart, J. Hutchinson and V. S. Caviness Jr, Science, 1975, 189, 18–21 CrossRef CAS PubMed.
- M. Darayi, M. E. Hoffman, J. Sayut, S. Wang, N. Demirci, J. Consolini and M. A. Holland, J. Biomech., 2022, 139, 110851 CrossRef PubMed.
- P. V. Bayly, R. J. Okamoto, G. Xu, Y. Shi and L. A. Taber, Phys. Biol., 2013, 10, 016005 CrossRef CAS PubMed.
- S. Budday, P. Steinmann and E. Kuhl, J. Mech. Phys. Solids, 2014, 72, 75–94 CrossRef PubMed.
- P. Chavoshnejad, X. Li, S. Zhang, W. Dai, L. Vasung, T. Liu, T. Zhang, X. Wang and M. J. Razavi, Brain Multiphys., 2021, 2, 100029 CrossRef.
- M. Holland, S. Budday, A. Goriely and E. Kuhl, Phys. Rev. Lett., 2018, 121, 228002 CrossRef CAS PubMed.
- M. J. Razavi, T. Liu and X. Wang, Cerebral Cortex Commun., 2021, 2, tgab044 CrossRef PubMed.
- J. Nie, L. Guo, G. Li, C. Faraco, L. Stephen Miller and T. Liu, J. Theor. Biol., 2010, 264, 467–478 CrossRef PubMed.
- S. N. Verner and K. Garikipati, Extreme Mech. Lett., 2018, 18, 58–69 CrossRef.
- K. E. Garcia, X. Wang, S. E. Santiago, S. Bakshi, A. P. Barnes and C. D. Kroenke, Cereb. Cortex, 2024, 34, bhae172 CrossRef PubMed.
- C. D. Kroenke, E. N. Taber, L. A. Leigland, A. K. Knutsen and P. V. Bayly, Cereb. Cortex, 2009, 19, 2916–2929 CrossRef PubMed.
- Y. Huang, Z. Wu, F. Wang, D. Hu, T. Li, L. Guo, L. Wang, W. Lin and G. Li, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2121748119 CrossRef CAS PubMed.
- F. Wang, C. Lian, Z. Wu, H. Zhang, T. Li, Y. Meng, L. Wang, W. Lin, D. Shen and G. Li, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 15855–15860 CrossRef CAS PubMed.
- S. Budday and P. Steinmann, Int. J. Solids Struct., 2018, 132, 31–41 CrossRef.
- S. Wang, N. Demirci and M. A. Holland, Biomech. Model. Mechanobiol., 2021, 20, 555–567 CrossRef PubMed.
- T. Zhang, M. J. Razavi, X. Li, H. B. Chen, T. M. Liu and X. Q. Wang, Sci. Rep., 2016, 6, 37272 CrossRef CAS PubMed.
- E. K. Rodriguez, A. Hoger and A. D. McCulloch, J. Biomech., 1994, 27, 455–467 CrossRef CAS PubMed.
- G. A. Holzapfel, Nonlinear solid mechanics: a continuum approach for engineering science, Kluwer Academic Publishers, Dordrecht, 2002 Search PubMed.
- D. Angelis, F. Sofos and T. E. Karakasidis, Arch. Comput. Methods Eng., 2023, 30, 3845–3865 CrossRef PubMed.
- B. Bahmani and W. Sun, Int. J. Numer. Meth. Eng., 2024, 125, e7473 CrossRef.
- J. Hou, X. Chen, T. Wu, E. Kuhl and X. Wang, Acta Biomater., 2024, 188, 276–296 CrossRef PubMed.
- Z. Zhang, Z. Zou, E. Kuhl and G. E. Karniadakis, Comput. Methods Appl. Mech. Eng., 2024, 419, 116647 CrossRef.
- W. Ben Chaabene and M. L. Nehdi, Constr. Build. Mater., 2021, 280, 122523 CrossRef.
- M. Cranmer, arXiv, 2023, preprint, arXiv:2305.01582 DOI:10.48550/arXiv.2305.01582.
- J. Dubois, M. Alison, S. J. Counsell, L. Hertz-Pannier, P. S. Hüppi and M. J. Benders, J. Magn. Reson. Imaging, 2021, 53, 1318–1343 CrossRef PubMed.
- G. Abaqus, Dassault Systemes Simulia Corporation, Providence, RI, USA, 2011, vol. 3 Search PubMed.
- P. Chavoshnejad, L. Chen, X. Yu, J. Hou, N. Filla, D. Zhu, T. Liu, G. Li, M. J. Razavi and X. Wang, Cereb. Cortex, 2023, 33, 9354–9366 CrossRef PubMed.
- M. Jalil Razavi, M. Reeves and X. Wang, Comput. Methods Biomech. Biomed. Eng., 2017, 20, 1212–1222 CrossRef PubMed.
- J. Weickenmeier, R. de Rooij, S. Budday, T. C. Ovaert and E. Kuhl, J. Mech. Behav. Biomed. Mater., 2017, 76, 119–124 CrossRef PubMed.
- Y. Cao, Y. Jiang, B. Li and X. Feng, Acta Mech. Solida Sin., 2012, 25, 483–492 CrossRef.
- X. Wang, J. Lefèvre, A. Bohi, M. A. Harrach, M. Dinomais and F. Rousseau, Sci. Rep., 2021, 11, 7686 CrossRef CAS PubMed.
- S. Zhang, P. Chavoshnejad, X. Li, L. Guo, X. Jiang, J. Han, L. Wang, G. Li, X. Wang, T. Liu, M. J. Razavi, S. Zhang and T. Zhang, Hum. Brain Mapp., 2022, 43, 4540–4555 CrossRef PubMed.
- D. Duan, S. Xia, I. Rekik, Z. Wu, L. Wang, W. Lin, J. H. Gilmore, D. Shen and G. Li, Hum. Brain Mapp., 2020, 41, 1985–2003 CrossRef PubMed.
- M. Meyer, M. Desbrun, P. Schröder and A. H. Barr, Discrete Differential-Geometry Operators for Triangulated 2-Manifolds, Berlin, Heidelberg, 2003 Search PubMed.
- R. Balouchzadeh, P. V. Bayly and K. E. Garcia, Brain Multiphys., 2023, 4, 100065 CrossRef PubMed.
- H. J. Yun, K. Im, J.-J. Yang, U. Yoon and J.-M. Lee, PLoS One, 2013, 8, e55977 CrossRef CAS PubMed.
- A. Makropoulos, E. C. Robinson, A. Schuh, R. Wright, S. Fitzgibbon, J. Bozek, S. J. Counsell, J. Steinweg, K. Vecchiato and J. Passerat-Palmbach, NeuroImage, 2018, 173, 88–112 CrossRef PubMed.
- E. J. Hughes, T. Winchman, F. Padormo, R. Teixeira, J. Wurie, M. Sharma, M. Fox, J. Hutter, L. Cordero-Grande and A. N. Price, Magn. Reson. Med., 2017, 78, 794–804 CrossRef CAS PubMed.
- J. De Asis-Cruz, J.-H. Kim, D. Krishnamurthy, C. Lopez, K. Kapse, N. Andescavage, G. Vezina and C. Limperopoulos, Dev. Cognit. Neurosci., 2023, 63, 101282 CrossRef PubMed.
- L. Zubiaurre-Elorza, S. Soria-Pastor, C. Junque, R. Sala-Llonch, D. Segarra, N. Bargallo and A. Macaya, PLoS One, 2012, 7, e42148 CrossRef CAS PubMed.
- N. Demirci and M. A. Holland, Cereb. Cortex, 2024, 34, bhad462 CrossRef PubMed.
- G. Li, L. Wang, F. Shi, J. H. Gilmore, W. Lin and D. Shen, Med. Image Anal., 2015, 25, 22–36 CrossRef PubMed.
- Z. Wu, L. Wang, W. Lin, J. H. Gilmore, G. Li and D. Shen, Hum. Brain Mapp., 2019, 40, 3860–3880 CrossRef PubMed.
- A. E. Lyall, F. Shi, X. Geng, S. Woolson, G. Li, L. Wang, R. M. Hamer, D. Shen and J. H. Gilmore, Cereb. Cortex, 2014, 25, 2204–2212 CrossRef PubMed.
- H. Kalantar-Hormozi, R. Patel, A. Dai, J. Ziolkowski, H.-M. Dong, A. Holmes, A. Raznahan, G. A. Devenyi and M. M. Chakravarty, NeuroImage, 2023, 268, 119885 CrossRef PubMed.
- H. Huang, R. Xue, J. Zhang, T. Ren, L. J. Richards, P. Yarowsky, M. I. Miller and S. Mori, J. Neurosci., 2009, 29, 4263–4273 CrossRef CAS PubMed.
- M. Ouyang, T. Jeon, A. Sotiras, Q. Peng, V. Mishra, C. Halovanic, M. Chen, L. Chalak, N. Rollins, T. P. L. Roberts, C. Davatzikos and H. Huang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4681–4688 CrossRef CAS PubMed.
- J. H. Gilmore, R. C. Knickmeyer and W. Gao, Nat. Rev. Neurosci., 2018, 19, 123–137 CrossRef CAS PubMed.
- T. Tallinen, J. Y. Chung, F. Rousseau, N. Girard, J. Lefèvre and L. Mahadevan, Nat. Phys., 2016, 12, 588–593 Search PubMed.
- T. Zhang, H. Chen, M. J. Razavi, Y. Li, F. Ge, L. Guo, X. Wang and T. Liu, Hum. Brain Mapp., 2018, 39, 4134–4149 CrossRef PubMed.
- P. Chavoshnejad, L. Vallejo, S. Zhang, Y. Guo, W. Dai, T. Zhang and M. J. Razavi, Sci. Rep., 2023, 13, 13177 CrossRef CAS PubMed.
- K. E. Garcia, C. D. Kroenke and P. V. Bayly, Philos. Trans. R. Soc., B, 2018, 373, 30249772 CrossRef PubMed.
- M. Peterson, B. C. Warf and S. J. Schiff, J. Neurosurg. Pediatr., 2018, 21, 478–485 Search PubMed.
- N. Sadeghi, M. Prastawa, P. T. Fletcher, J. Wolff, J. H. Gilmore and G. Gerig, NeuroImage, 2013, 68, 236–247 CrossRef PubMed.
- C. Vaghi, A. Rodallec, R. Fanciullino, J. Ciccolini, J. P. Mochel, M. Mastri, C. Poignard, J. M. Ebos and S. Benzekry, PLoS Comput. Biol., 2020, 16, e1007178 CrossRef CAS PubMed.
- M. Jalil Razavi, T. Zhang, T. Liu and X. Wang, Sci. Rep., 2015, 5, 14477 CrossRef CAS PubMed.
- M. Alenyà, X. Wang, J. Lefèvre, G. Auzias, B. Fouquet, E. Eixarch, F. Rousseau and O. Camara, Brain Multiphys., 2022, 3, 100045 CrossRef.
- K. E. Garcia, X. Wang and C. D. Kroenke, Nat. Commun., 2021, 12, 6681 CrossRef CAS PubMed.
- M. A. Holland, S. Budday, G. Li, D. Shen, A. Goriely and E. Kuhl, Eur. Phys. J.: Spec. Top., 2020, 229, 2757–2778 Search PubMed.
- M. A. Holland, K. E. Miller and E. Kuhl, Ann. Biomed. Eng., 2015, 43, 1640–1653 CrossRef PubMed.
- E. M. W. Billig, W. P. O'Meara, E. M. Riley and F. E. McKenzie, Malar. J., 2012, 11, 64 CrossRef PubMed.
- K. R. Swanson, C. Bridge, J. Murray and E. C. Alvord Jr, J. Neurol. Sci., 2003, 216, 1–10 CrossRef PubMed.
- N. Filla, J. Hou, T. Liu, S. Budday and X. Wang, J. Mech. Behav. Biomed. Mater., 2024, 150, 106271 CrossRef CAS PubMed.
- J. Hou, N. Filla, X. Chen, M. J. Razavi, T. Liu and X. Wang, arXiv, 2023, preprint, arXiv:2310.10762 DOI:10.48550/arXiv.2310.10762.
- M. Flaschel, S. Kumar and L. De Lorenzis, Comput. Methods Appl. Mech. Eng., 2023, 405, 115867 CrossRef.
- K. Linka, S. R. S. Pierre and E. Kuhl, Acta Biomater., 2023, 160, 134–151 CrossRef PubMed.
- R. d Rooij and E. Kuhl, J. Mech. Phys. Solids, 2018, 112, 563–576 CrossRef.
- M. S. Zarzor, S. Kaessmair, P. Steinmann, I. Blümcke and S. Budday, Brain Multiphys., 2021, 2, 100025 CrossRef.
- S. Budday, P. Steinmann, A. Goriely and E. Kuhl, Extreme Mech. Lett., 2015, 4, 193–198 CrossRef.
- N. Demirci and M. A. Holland, Hum. Brain Mapp., 2022, 43, 2064–2084 CrossRef.
- J. Guo, G. Bertalan, D. Meierhofer, C. Klein, S. Schreyer, B. Steiner, S. Wang, R. V. da Silva, C. Infante-Duarte and S. Koch, Acta Biomater., 2019, 99, 433–442 CrossRef CAS PubMed.
- S. Wang, K. Saito, H. Kawasaki and M. A. Holland, PLoS Comput. Biol., 2022, 18, e1010190 CrossRef CAS PubMed.
- D. H. C. Project, Accessed 2024.
- B. R. Howell, M. A. Styner, W. Gao, P.-T. Yap, L. Wang, K. Baluyot, E. Yacoub, G. Chen, T. Potts and A. Salzwedel, NeuroImage, 2019, 185, 891–905 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01194e |
| This journal is © The Royal Society of Chemistry 2025 |