Liquid crystalline self-assembly of mixtures of rod- and wedge-shaped MIDA boronates

Abstract

Rod-like MIDA boronates form smectic mesophases, while wedge-shaped MIDA boronates self-assemble into columnar mesophases. However, the phase behavior of mixtures is less understood. In order to obtain further insight on the molecular self-assembly of MIDA boronate mixtures two series of binary mixtures of rod-like and wedge-shaped mesogens were prepared. The phase behavior was studied using differential scanning calorimetry (DSC), polarizing optical microscopy (POM) and X-ray diffraction (XRD). The study revealed a strong dependency of the mesophase structure on the mesogen composition. Usage of a less bulky columnar mesogen suppressed the formation of columnar mesophases in the mixture and led to a decrease in melting and clearing temperatures. The phase behavior is discussed in terms of the packing parameter model typically applied for lyotropic liquid crystals.

---

Introduction

Liquid crystalline mixtures of rod-like mesogens are very important for applications such as liquid crystal displays (LCDs). This is due to the fact that the temperature range and phase stability of the mixture is significantly expanded as compared to the single components. Moreover, in such mixtures physical properties such as viscosity, optical refractive indices, elastic constants, electric permittivities etc. can be efficiently tailored in a desired fashion.¹ Mixtures of rod-like mesogens can also lead to new mesophase types, which were not observed in the pure compounds as was recently reported by Mandle for the splay nematic phase N_S.²

Also for other functional liquid crystals the importance of mixtures to obtain new properties has been highlighted.^3–7 On the one hand, mixtures of discotic liquid crystals have been examined in several theoretical studies.^8–36 Most recently Sambritzki investigated binary mixtures of discotic liquid crystals differing in their molecular thickness by molecular dynamics (MD) simulations.³⁷ Various experimental studies on discotic mixtures have been performed, dealing for example with bent-core mesogens^38–41 forming columnar banana phases, chiral dopants forming chiral nematic discotic phases in discotic host materials,^42–45 donor–acceptor systems consisting of electron-rich discotic molecules and non-mesogenic electron acceptors such as trinitrofluorenone (TNF).^46–49 In addition, mixtures of structurally closely related discotic compounds were also studied with respect to phase behaviour, electric conductivity or magnetic properties.^50–60 On the other hand, mixtures of rod- and disk-shaped molecules,⁶¹ rod- and rod-shaped molecules⁶² and ILC compounds⁶³ were much less explored.

Previous work by us has shown that the N-methyl-iminodiacetic acid (MIDA) boronate unit is a strongly beneficial mesophase promoter both from a fundamental point of view^64–66 but also for applications such as electrooptical birefringence (Kerr effect).⁶⁷ This is due to the high polarity of the MIDA unit (μ = 7.6 D) as compared to boronic acids (μ = 2.8 D) and borolanes (μ = 1.4 D), resulting in a pronounced tendency to form polar subdomains within the mesophase.^64,68–70 Depending on the structure of the (hetero)aryl core and the number of alkoxy side chains, the phase type and stability of the corresponding rod-like or wedge-shaped MIDA boronates was controlled,^64–66i.e., rod-like MIDA boronates formed lamellar smectic A (SmA) phases while wedge-shaped derivatives formed columnar hexagonal (Col_h) phases (Scheme 1). With respect to mixtures between these components we were curious whether the rod-like or the wedge-shaped MIDA boronate would control the self-assembly of the mixture. The results towards this goal are reported below.

Scheme 1 Overview of preliminary work on rod-like and wedge-shaped MIDA boronates.⁶⁴

Results and discussion

For a better overview and sake of clarity the following nomenclature will be used for the mixtures: the first series of mixtures consisting of MIDA boronates 1 and 2 carrying 1 and 2 dodecyloxy side chains respectively will be abbreviated 1/2 [X₁] with the molar fraction X₁ of 1. The second series of mixtures consisting of MIDA boronates 1 and 3 carrying 1 and 3 dodecyloxy side chains respectively will be abbreviated 1/3 [X₁] with the molar fraction X₁ of 1.

Mixtures with molar fractions of X₁ = 0.2, 0.4, 0.5, 0.6, 0.8 were prepared initially and studied by polarizing optical microscopy (POM), differential scanning calorimetry (DSC) regarding their phase behaviour. Selected mixtures were investigated by X-ray diffraction (XRD) to assign the phase structure. The results were compared with the known behaviour of the pure MIDA compounds 1, 2 and 3 respectively.⁶⁴

First the series 1/2 [X₁] with the molar fraction X₁ of 1 was examined by POM. The pure mono-substituted boronate 1 (1/2 [1.0]), displayed at 180 °C upon cooling from the isotropic phase large areas of homeotropic alignment with a few Maltese cross defects, which are characteristic for a SmA phase (Fig. 1a) as reported earlier.⁶⁴ For the pure disubstituted MIDA boronate 2 (1/2 [0.0]), fan-shaped textures were observed (Fig. 1g) in agreement with the previously assigned Col_h phase for this MIDA boronate 2. Upon increasing the amount of bis-dodecyloxy MIDA boronate 2 the tendency towards homeotropic alignment decreased with decreasing molar fraction of the mono-dodecyloxy MIDA boronate 1. Textures changed from Maltese crosses and fan textures (e.g.Fig. 1b for X₁ = 0.8) to uncharacteristic textures for X₁ = 0.2 (Fig. 1f). For all studied mixtures 1/2 [X₁] with X₁ = 0.8–0.2 textures were easily shearable and highly fluid, suggesting smectic phases with low order were favoured as compared to columnar phase.⁷¹

Fig. 1 POM textures of mixture series 1/2 [X₁] with molar fractions X₁ = (a) 1.0 (180 °C), (b) 0.8 (125 °C), (c) 0.6 (128 °C), (d) 0.5 (124 °C), (e) 0.4 (120 °C), (f) 0.2 (123 °C), (g) 0.0 (160 °C). Taken during cooling from the isotropic liquid (cooling rate 5 K min⁻¹).

Next the series 1/3 [X₁] with the molar fraction X₁ of 1 was examined by POM (Fig. 2). For the pure tri-substituted MIDA boronate 3 (1/3 [0.0]), large fan-shaped textures were visible under the POM (Fig. 2g), which are characteristic for columnar phases in agreement with recent work.⁶⁴ The mixtures 1/3 [X₁] with X₁ = 0.8 and X₁ = 0.6 were easily shearable and possessed a high fluidity in analogy to the 1/2 [X₁] mixtures of the other series. In contrast, 1/3 [X₁] mixtures with X₁ = 0.5–0.2 displayed a much higher viscosity as compared to the mixtures with higher molar fractions (X₁ = 0.6–0.8). In comparison with the pure trisubstituted MIDA compound 3 (1/3 [0.0]), mixtures 1/3 [X₁] with X₁ = 0.5–0.2 showed a lower viscosity and better shearability.

Fig. 2 POM textures of mixture series 1/3 [X₁] with molar fractions X₁ = (a) 1.0 (180 °C), (b) 0.8 (121 °C), (c) 0.6 (82 °C), (d) 0.5 (119 °C), (e) 0.4 (120 °C), (f) 0.2 (125 °C), (g) 0.0 (82 °C). Taken during cooling from the isotropic liquid (cooling rate 5 K min⁻¹).

In order to assign the phase transition temperatures and enthalpies differential scanning calorimetry (DSC) experiments were performed. All DSC data of mixtures 1/2 [X₁] are shown in Fig. S3 (ESI†) and are summarized in Table S3 (ESI†). The DSC curves of exemplary mixtures 1/2 [0.15], 1/2 [0.4] and 1/2 [0.5] are shown in Fig. 3. In the DSC curve of 1/2 [0.5] weak endothermal melting and clearing transitions at 55 °C and 145 °C, respectively, are visible (Fig. 3a). In the cooling cycle the isotropic to mesophase transition appeared at 146 °C, while no crystallization could be observed. Instead, slow vitrification of the sample occurred upon cooling in agreement with the DSC results reported for the MIDA boronates 1, 2 and 3⁶⁴ and Pyr(n)MIDA⁶⁶ (for details of the molecular structure, see Fig. S1, ESI†). The DSC curves of 1/2 [0.4] (Fig. 3b) displayed endothermal melting and clearing at 57 °C and 134 °C upon heating, and in the cooling cycle the exothermal phase transitions appeared at 136 °C and 72 °C. In comparison with the pure mono- and bis-substituted MIDA boronates 1 (1/2 [1.0]), and 2 (1/2 [0.0]), melting and clearing transitions decreased considerably for the mixtures 1/2 [X₁] with X₁ = 0.5, 0.4. A phase diagram summarizes the results of the various mixtures 1/2 [X₁] (Fig. 4a). When comparing the whole series of mixtures 1/2 [X₁] with X₁ = 0.8–0.2 with the pure compounds 1 (1/2 [1.0]), and 2 (1/2 [0.0]), clearing transitions decreased with decreasing X₁, i.e., decreasing amount of 1 from 194 °C (X₁ = 1.0) until the minimum value 137 °C for X₁ = 0.4 and then increased again up to 169 °C for X₁ = 0.0. On the other hand, melting transitions of the mixtures (X₁ = 0.8–0.2) were significantly lower as compared to the values for the pure compounds 1 (1/2 [1.0]) and 2 (1/2 [0.0]), but for all mixtures (X₁ = 0.8–0.2) the melting transitions remained relatively constant around 54–62 °C irrespective of the molar fraction.

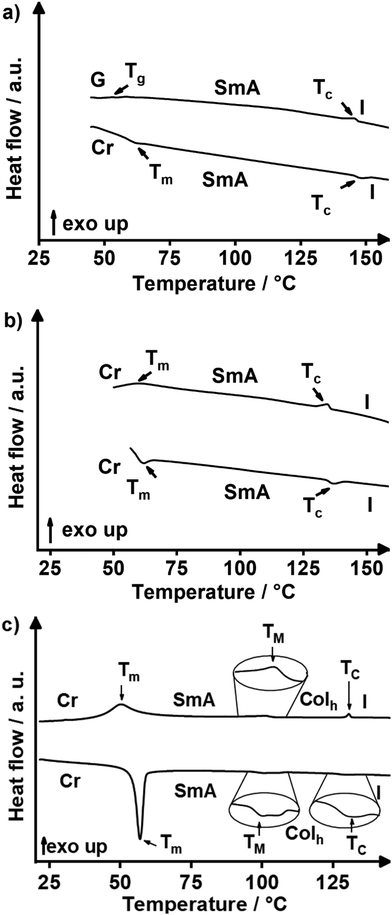Fig. 3 DSC traces of 1/2 [X₁] mixture series: (a) 1/2 [0.5], (b) 1/2 [0.4] and (c) 1/2 [0.15] (2nd heating (bottom) and 2nd cooling (top) cycle, heating/cooling rate 10 K min⁻¹).

Fig. 4 Phase diagram of the binary systems (a) 1/2 [X₁] and (b) 1/3 [X₁] from DSC measurements (2nd heating cycle; rate 10 K min⁻¹; red: SmA phase; blue: Col_h phase; grey: crystalline; crosshatched grey: not investigated, but added for enhanced comparability; note that the SmA to Col_h transition temperatures of X₁ = 0.2 in (a) and X₁ = 0.5 and 0.45 in (b) were determined from the 2nd cooling cycle).

While initial POM investigation of the 1/2 [X₁] mixtures suggested solely the presence of a SmA phase based on homeotropic alignment, bâtonnets and focal-conic fan texture (Fig. 2b–f), we were curious about the transition between the SmA and the Col_h phases which has to occur somewhere between X₁ = 0 and 0.2. Due to the symmetry change from D_∞h symmetry with only one-dimensional long-range translational order in the SmA phase to the p6/mmm symmetry in the Col_h phase, the phase transition has to be of first order according to Landau theory.⁷² Thus, a biphasic region is necessary to occur between the two phases. Therefore, the mixtures 1/2 [X₁] with X₁ = 0.15, 0.2 and 0.25 were examined more closely by DSC and POM. The DSC curve of mixture 1/2 [0.15] displayed an endothermal melting transition at 54 °C, a very weak mesophase to mesophase transition at 96 °C and a weak clearing transition at 125 °C in the heating cycle (Fig. 3c). In the cooling cycle the isotropic to mesophase transition occurred at 131 °C, the mesophase to mesophase transition at 104 °C and the crystallization at 60 °C, respectively. The change of the texture was also visible by POM upon cooling (Fig. S6a–c, ESI†) supporting the presence of Col_h and SmA phases at higher and lower temperatures, respectively. At high temperatures the typical fan texture⁷³ of the Col_h phase prevails (Fig. S6a, ESI†) which turns into a less distinct, grainy texture at lower temperatures (Fig. S6c, ESI†). The latter uncharacteristic texture is associated with the uncommon rearrangement of the mesogens from the columnar to the lamellar structure of the SmA phase. Indeed, a biphasic region is observed in between the two phases, as predicted by symmetry arguments, in which the fan texture is spotted with darker patches (Fig. S6b, ESI†). DSC curves of 1/2 [0.20] (Fig. S3b, ESI†) again suggested the presence of both SmA and Col_h phases. However, the transition was too weak to be analysed from the heating cycle, and thus could only be determined from the cooling cycle, which leaves some doubts whether or not the Col_h phase at this composition is enantiotropic or only monotropic. In contrast, in the mixture 1/2 [0.25] the higher temperature mesophase totally disappeared (Fig. S6d, ESI†). Complementary POM studies showed Maltese crosses and homeotropic alignment (Fig. S6d, ESI†) suggesting that in this mixture only an enantiotropic SmA phase prevails. The phase diagram constructed from this data is shown in Fig. 4a. The presence of biphasic regions was neglected in the diagram due to their narrow temperature ranges and the associated difficulties in determining them.

Next, the mixtures 1/3 [X₁] were investigated. All DSC data of 1/3 [X₁] are shown in Fig. S4 (ESI†) and summarized in Table S4 (ESI†). The DSC curve of mixture of 1/3 [0.6] displayed an endothermal melting transition at 45 °C and an endothermal clearing transition at 96 °C upon heating, while the corresponding exothermal transition appeared at 102 °C and 55 °C in the cooling cycle (Fig. 5a). As the POM texture showed Maltese crosses with homeotropic alignment (Fig. 2a–c), an enantiotropic SmA phase was assigned. On the other hand, for the mixture 1/3 [0.4] melting and clearing transitions at 39 °C and 142 °C were both visible in the heating and cooling cycle (47 °C, 143 °C) (Fig. 5b). For this mixture the POM fan-like textures (Fig. 2e) strongly suggested a Col_h phase. In order to characterise the SmA to Col_h transition of the phase diagram shown in Fig. 4b, 1/3 [X₁] mixtures with X₁ = 0.55, 0.5 and 0.45 were examined additionally. For 1/3 [0.55] a single enantiotropic mesophase was detected (Fig. S6f, ESI†), which was assigned as a SmA phase based on the Maltese cross textures and homeotropic alignment observed by POM. In the DSC curve of 1/3 [0.45] a weak endothermal melting at 37 °C and a clearing transition at 126 °C were detected together with an extremely small hump which hints at the existence of two enantiotropic mesophases, but is too small to evaluate (Fig. 5c).

Fig. 5 Exemplary DSC traces of 1/3 [X₁] mixture series: (a) 1/3 [0.6], (b) 1/3 [0.4] (c) 1/3 [0.45] and (2nd heating (bottom) and 2nd cooling (top) cycle, heating/cooling rate 10 K min⁻¹).

Upon subsequent cooling a small isotropic to mesophase transition at 130 °C, a weak exothermal mesophase to mesophase transition at 61 °C and a weak exothermal crystallization peak at 53 °C were detected. By POM fan-shaped textures at 100 °C indicated the presence of the Col_h phase as a higher temperature phase (Fig. S6e, ESI†) and the SmA phase as lower temperature phase. Likewise, the DSC curve of the mixture 1/3 [0.5] displayed a lower temperature SmA phase and a higher temperature Col_h phase (Fig. S4d, ESI†). Whether or not the Col_h phase in these two mixtures is monotropic or if the transition enthalpy is just extremely small could not be fully elucidated at this point.

While Fig. 4a demonstrated the strong influence of the rod-like mesogen 1 on the phase type and the temperature-modulating effect of 2 in the 1/2 [X₁] series, Fig. 4b revealed a much more pronounced effect of the wedge-shaped mesogen 3 on both phase type and transition temperatures in the 1/3 [X₁] mixtures. Upon increasing the amount of trisubstituted MIDA boronate 3 a decrease of melting and particularly clearing temperatures were observed for 1/3 [0.8] and 1/3 [0.6] resulting in a decrease of the stability and temperature range of the SmA phase from 75 K (X₁ = 1.0) to 31 K (X₁ = 0.55) phase widths (Fig. S5, ESI†). Upon further increasing the amount of wedge-shaped mesogen 3 in the mixture, the SmA phase was disfavoured against the Col_h phase. Both mesophases were present for X₁ = 0.5, 0.45 until X₁ = 0.4, where the SmA phase completely disappeared and only the Col_h phase remained. Regarding clearing transitions of the Col_h phase, increasing the relative amount of 3 (i.e., decrease of X₁) resulted in increasing clearing temperatures with a maximum at X₁ = 0.4 and then decrease until X₁ = 0 (pure wedge-shaped mesogen 3). Similarly, to the 1/2 [X₁] series, melting points were relatively little affected by the change of X₁.

It appears that the additional side chain of 3 in comparison with 2 introduces a stronger effect on the molecular self-assembly. Whereas in the 1/2 [X₁] system a high amount of 2 of up to X₁ = 0.25 only resulted in the formation of a smectic layer structure rather than the formation of a columnar structure, while the 1/3 [X₁] system showed a columnar phase at molar X₁ fractions as high as X₁ = 0.5. This may be rationalized by the increasing steric demand of 3 in comparison to 2 resulting in larger effective wedge size and increased space filling favouring columnar over layered phase structures.

For selected mixtures of both series X-ray diffraction experiments (WAXS, SAXS) were carried out. The equimolar mixture 1/2 [0.5] displayed a sharp small angle reflection at 36.0 Å, which was assigned as the (001) layer reflection of the SmA phase and a broad halo in the wide angle region around 4.8 Å caused by the liquid-like order of the flexible side chains (Fig. 6a, b and Table S5, ESI†). Temperature-dependent XRD measurements of the layer reflection showed a decrease of the d values with increasing temperature, which is characteristic for the SmA phase.⁷⁴

Fig. 6 (a) XRD results of 1/2 [X₁] mixtures; (a) WAXS profile of X₁ = 0.5 at 108 °C and corresponding 2D patterns of the SAXS (left image, at 91 °C) and WAXS measurement (left image, at 108 °C); (b) temperature dependent layer spacing of X₁ = 0.5; (c) comparison of temperature dependent layer spacing of the mixture of X₁ = 0.5 with X₁ = 1.0, i.e., the neat 1.

Upon comparison of temperature-dependent layer distances of the mixture 1/2 [0.5] and the pure mono-substituted MIDA boronate 1 surprisingly the d values of 1/2 [0.5] increased much stronger with decreasing temperature as compared to the pure compound 1, i.e., the slope was 4 times larger as compared to the former case (Fig. 6c). This result might be rationalized by the different layer structures in the mixture vs. pure MIDA boronate. The smectic layer of pure 1 already possesses a high degree of order, which increases only slightly upon cooling and thus the d value also increases only slightly. In contrast, the mixture 1/2 [0.5] presumably possesses a lower order parameter close to the clearing temperature, resulting in a strong increase of the d value due to the strong increase of the order parameter upon cooling. Due to the observed thermal decomposition for all kind of different MIDA boronates,^64–66 the temperature dependent XRD measurements of 1/2 [0.5] were only conducted at temperatures closer to the melting point, since the set of data points was considered sufficient to determine the phase order of the lamellar phase, i.e., SmA or SmC.

Presumably within the smectic layers a statistic distribution of both components 1 and 2 seems to be reasonable. From the temperature-dependent layer distance the reduced layer distance d_red = 32.5 Å was obtained by extrapolation at the reduced temperature T_red.⁷⁴ For MIDA boronates 1 and 2 the molecular lengths were calculated to 24.3 Å and 24.4 Å respectively via the Avogadro software (Version Avogadro 1.2.0) using an Universal Force Drive (OFF) for geometry optimization.⁷⁵ In analogy to the known pyridine and pyrimidine MIDA boronates Pyr(n)MIDA, Pym(n)MIDA⁶⁶ and phenylester MIDA derivatives Ph(n)EsterMIDA⁶⁵ (for details, see Scheme S1, ESI†) the reduced layer distance d_red is larger than the molecular length L_calc and much smaller than the twofold molecular lengths 2 L_calc, i.e., 2 L_calc < d_red > L_calc, which can be explained by a smectic bilayer arrangement with interdigitated side chains (Fig. 7).

Fig. 7 Proposed packing model of the mixture series 1/2 [X₁] with calculated reduced layer spacing d_red and molecular lengths.

To confirm the correct assignment of both phases in the 1/2 phase diagram, the mixture 1/2 [0.15] was studied by SAXS and WAXS at 120 °C in the Col_h phase and at 85 °C in the SmA phase (Fig. S7, ESI†). Both diffraction patterns look rather similar, again featuring one sharp scattering maximum in the small-angle region and a broad halo in the wide-angle region. Unfortunately, elongating the measurement time did not lead to the appearance of further reflexes. However, by plotting the small-angle scattering maxima vs. the azimuthal angle χ (Fig. S8, ESI†), several individual maxima turn up in the scattering experiment obtained at 120 °C. Measuring the angle between these maxima reveals that they originate from two differently aligned domains with hexagonal symmetry, since the angle between maxima belonging together amounts to approximately 60° (Table S6, ESI†). Cooling down to 85 °C leads to the emergence of two strong scattering peaks at χ = 0 and 180 °C as typically found for aligned layered structures, with the other maxima present at higher temperature dwindling down to soft undulations. These findings strongly suggest that the assignment of phases in the 1/2 system, i.e., the Col_h phase at high temperatures and the SmA phase at low temperatures, is correct.

XRD experiments at 117 °C of the equimolar mixture 1/3 [0.5] showed a sharp reflection at 32.4 Å in the SAXS and a broad halo around 4.8 Å in the wide-angle section (Fig. 8 and Table 1). Further scattering patterns of the mixtures 1/3 [X₁] with X₁ = 0.45, 0.55 are shown in Fig. S10 and S12 (ESI†). Extensive efforts were conducted to obtain aligned samples in order to clarify the phase geometry. However, attempts to prepare aligned samples by fiber extrusion, alignment in a magnetic field and slow cooling from the isotopic phase failed to result in monodomain samples. Nevertheless, when plotting the small-angle diffraction pattern of X₁ = 0.45 at 100 °C vs. the azimuthal angle χ (Fig. S11, ESI†), a multitude of clear-cut scattering maxima emerges, some of which may be attributed to individual hexagonal domains (Table S7, ESI†). By cooling down to 57 °C the peaks become less distinct and even vanish in some cases, but still reflect a multi-domain alignment. In total, evidence from XRD experiments for the correct assignment of the Col_h phase at high temperatures and the SmA phase at low temperatures is weaker for the 1/3 mixtures than the 1/2 mixtures, but considering the structural similarities of the molecules, characteristic textures observed by POM, the high viscosity and low shearability which hints at the presence of a more ordered phase, as compared to the rather fluid SmA phase, the assignment seems more than likely. Thus, the distinct reflection at higher temperatures was assigned as (001) reflection of a Col_h phase.

Fig. 8 (a) SAXS profile of 1/3 [0.5] at 107 °C and corresponding 2D pattern; (b) WAXS profile of 1/3 [0.5] at 117 °C and corresponding 2D pattern.

Table 1 X-ray diffraction data for neat MIDA boronates 2, 3 and binary mixture 1/3 [0.5]. The measurements were performed during cooling from the isotropic liquid phase. The halo was determined from WAXS. Data for 2 and 3 was taken from ref. 64

Compound	Mesophase	a/Å	d exp/Å	Miller indices	Z
1/3 [0.5]	Colh at 117 °C	a = 37.3	32.4	(001)	6
			4.8	Halo
2	Colh at 120 °C	a = 37.7	32.6	(001)	5
			16.3	(002)
			4.1	Halo
3	Colh at 70 °C	a = 36.3	31.5	(001)	4
			4.7	Halo

---

For the molecular mass the median of the masses from 1 and 3 were taken and the number Z of molecules per unit cell was calculated according to the procedure described in ref. 76 Thus, a Col_h (p6mm) phase with lattice parameter a = 37.3 Å and Z = 6 was calculated (Table 1) for the equimolar mixture 1/3 [0.5]. When comparing these values with the known lattice parameters of 3⁶⁴ (Col_h (p6mm) at 70 °C, a = 36.3 Å, halo 4.7 Å, Z = 4), the optimum space filling can be obtained for the mixture 1/3 [0.5] if 3 rod-like MIDA boronates 1 and 3 wedge-shaped MIDA boronates 3 co-assemble in a supramolecular disc, i.e., a slice through the columnar aggregate, which has a slightly larger diameter (i.e., a value) than the corresponding disk consisting of only 4 wedge-shaped molecules 3 (Table 1). These results correlate well with a recent study by Williams on the coexistence of folded and unfolded shape-incompatible, conformers of discotic dimers resulting in modest perturbations of the phase behaviour.^77–79 Moreover, Shimizu reported for triphenylens with attached peripheral alkoxyazobenzenes calamitic discotic mesomorphism and a dynamic change of molecular conformation generating a variation of the liquid crystalline phases.⁸⁰

By studying the phase behaviour of two different series of binary mixtures containing mono-dodecyloxy-substituted MIDA boronates 1 and either bis-dodecyloxy-substituted MIDA boronates 2, i.e., 1/2 [X₁] or tri-dodecyloxy-substituted MIDA boronates 3, i.e., 1/3 [X₁], we obtained new insights into the liquid crystalline self-assembly of mixtures of rod-like and wedge-shaped mesogens. The results revealed that contrary to the common observation that shape incompatible mesogens often phase separate quite readily unless they are covalently linked (e.g. in dendritic molecules ternary block-copolymers, rod-coil molecules, polyphilic low molecular weight block molecules, amphiphiles^81,82 and disc-rod mesogens^83,84) rods and wedges were fully miscible at all concentrations. Presumably, the highly polar boronate groups interact strongly via dipole–dipole interactions, which overcomes the tendency to separate.⁸⁵ This would be in good agreement with our previous experimental oberservation that related mesogens with less polar “head goups”, such as boronates, pinacol borolanes, or iminoboronates, do not self-assemble into mesophases regardless of the number and lengths of the alkoxy side chains at the aryl units.⁶⁴ Thus, most likely due to the polar MIDA head groups the boronates tend to aggregate in layers or columns, forming a polar sublayer or polar core, in order to avoid charge separation.

A second important finding of our study is that in 1/2 [X₁] mixtures the monosubsituted boronate 1 drives the phase behaviour leading to the SmA phase dominating the phase diagram, while in 1/3 [X₁] mixtures both boronates 1 and 3 contribute, which results in a well-balanced proportion of the SmA and the Col_h phase. This finding agrees well with studies by Tschierske et al.⁸⁶ who investigated mixtures of amphiphilic N-benzoyl-1-amino-1-deoxy-D-glucitol derivatives with one, two or three aliphatic chains as well as by Finkelmann et al.^87–89 who studied lyotropic liquid crystals composed of amphiphile mixtures with one or two hydrophobic or hydrophilic chains. Both groups discuss their results in terms of the average molecular geometry and the packing parameter model by Israelachvili.⁹⁰ Thus, it seems reasonable to apply the same approach and draw analogies with mixed lyotropic systems. The model, which we adjusted to our thermotropic case, defines the packing parameter P as

with V_c the volume of the apolar hydrocarbon chain, l_c the length of the apolar hydrocarbon chain and a₀ the cross-section of the boronate “head group”. It predicts that spherical aggregates are formed for P ≤ 1/3, cylindrical aggregates evolve for 1/3 < P < 1/2, bilayers predominate for P ≈ 1/2 and inverse aggregates, i.e., with the boronate moiety in the centre of the aggregate, occur for P > 1/2 with reversed order of aggregates. Considering that both a₀ and l_c are untouched by changing the number of dodecyloxy chains of the investigated mesogens, the only decisive factor is the increase of V_c with increasing number of chains. Consequently, the packing parameter P should be the smallest for the mesogen 1, intermediate for 2 and largest for 3, which reveals that the boronate moieties point to the centre of the columnar aggregates in the Col_h phase. Combining the experimental results with the packing parameter model gives P ≈ 1/2 for the rod-shaped 1 and 1/2 < P < 2/3 for the wedge-shaped 2 and 3, with P being closer to 1/2 for 2 and closer to 2/3 for 3. Thus, even a small perturbation of the Col_h phase of 2 by diluting with the rod shaped 1 in it should push the system towards the SmA phase. In contrast, 3 favors the Col_h phase due to optimal space filling and reaches the cross over point to the SmA phase only at higher loading of the rod-shaped mesogen 1.

In addition, these considerations may explain the rather uncommon phase sequence of the Col_h phase at high temperatures and the SmA phase at lower temperatures, which is typically observed in reversed order due to the dimensionality of long-range order in the two mesophases. Increasing the temperature will lead to more thermal fluctuations of the dodecyloxy chains, which results in an increase of its volume V_c. Hence, the packing parameter is shifted to larger values at higher temperature, favouring the formation of inverse columnar aggregates over bilayers.

Conclusion

In order to understand the phase behaviour of mixtures of rod- and wedge-shaped MIDA boronates two binary series were prepared, which differed in the number and relative amount of dodecyloxy side chains. According to POM, DSC and XRD studies of the mixtures, rods and wedges were fully miscible at all concentrations due to the strong dipole–dipole interactions of the MIDA headgroups. The observed preference of either SmA or Col_h phase could be rationalized by the chain volume V_c in agreement with the packing parameter model adapted from lyotropic liquid crystals. Future work needs to demonstrate, whether the design principle to control liquid crystalline self-assembly presented in this study can be transferred to other mixtures of rod- and wedge-shaped mesogens forming supramolecular liquid crystals as well and if the analogies to the formation of lyotropic liquid crystal phases hold true.

Data availability

The data supporting this article have been included in the main manuscript and as part of the ESI.†

Conflicts of interest

The authors declare no competing interest.

Acknowledgements

Generous financial support by the Ministerium für Wissenschaft, Forschung und Kunst des Landes Baden-Württemberg, the Fonds der Chemischen Industrie, the Deutsche Forschungsgemeinschaft and the Carl-Schneider-Stiftung Aalen (shared instrumentation grant) is gratefully acknowledged. We would like to thank the referees for valuable suggestions and comments.

Notes and references

1. M. Klasen-Memmer and H. Hirschmann, in Handbook of liquid crystals, ed. T. Kato, H. Gleeson, P. Raynes, J. W. Goodby, P. J. Collings and C. Tschierske, Wiley-VCH, Weinheim, 2nd edn, 2014, pp. 1–25.
2. P. L. M. Connor and R. J. Mandle, Soft Matter, 2020, 16, 324–329.
3. T. Kato, J. Uchida, T. Ichikawa and T. Sakamoto, Angew. Chem., Int. Ed., 2018, 57, 4355–4371.
4. H. Shimura, M. Yoshio, K. Hoshino, T. Mukai, H. Ohno and T. Kato, J. Am. Chem. Soc., 2008, 130, 1759–1765.
5. T. Kato, M. Yoshio, T. Ichikawa, B. Soberats, H. Ohno and M. Funahashi, Nat. Rev. Mater., 2017, 2, 17001.
6. M. K. Sonali, P. Bhagavath, M. Srinivasulu, R. K. Sinha and K. Swamynathan, J. Fluorine Chem., 2022, 259–260, 110002.
7. F. S. Alamro, H. A. Ahmed, M. S. Khushaim, N. S. Bedowr and N. S. Al-Kadhi, Crystals, 2023, 13, 899.
8. T. Coussaert and M. Baus, J. Chem. Phys., 2002, 116, 7744–7751.
9. D. De Las Heras and M. Schmidt, Philos. Trans. R. Soc., A, 2013, 371, 20120259.
10. A. Galindo, G. Jackson and D. J. Photinos, Chem. Phys. Lett., 2000, 325, 631–638.
11. A. Galindo, A. J. Haslam, S. Varga, G. Jackson, A. G. Vanakaras, D. J. Photinos and D. A. Dunmur, J. Chem. Phys., 2003, 119, 5216–5225.
12. F. Gámez, R. D. Acemel and A. Cuetos, Mol. Phys., 2013, 111, 3136–3146.
13. J. Landman, E. Paineau, P. Davidson, I. Bihannic, L. J. Michot, A.-M. Philippe, A. V. Petukhov and H. N. W. Lekkerkerker, J. Phys. Chem. B, 2014, 118, 4913–4919.
14. M. Chen, H. Li, Y. Chen, A. F. Mejia, X. Wang and Z. Cheng, Soft Matter, 2015, 11, 5775–5779.
15. N. Doshi, G. Cinacchi, J. S. Van Duijneveldt, T. Cosgrove, S. W. Prescott, I. Grillo, J. Phipps and D. I. Gittins, J. Phys.: Condens. Matter, 2011, 23, 194109.
16. J. Phillips and M. Schmidt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041401.
17. H. N. W. Lekkerkerker, R. Tuinier and H. H. Wensink, Mol. Phys., 2015, 113, 2666–2673.
18. T. Nakato, Y. Yamashita, E. Mouri and K. Kuroda, Soft Matter, 2014, 10, 3161.
19. M. Golmohammadi and A. D. Rey, Entropy, 2008, 10, 183–199.
20. M. Golmohammadi and A. D. Rey, Liq. Cryst., 2009, 36, 75–92.
21. G. Cinacchi and A. Tani, J. Chem. Phys., 2002, 117, 11388–11395.
22. M. A. Bates and G. R. Luckhurst, Liq. Cryst., 1998, 24, 229–241.
23. M. A. Bates, Liq. Cryst., 2003, 30, 181–190.
24. J. Idé, R. Méreau, L. Ducasse, F. Castet, H. Bock, Y. Olivier, J. Cornil, D. Beljonne, G. D’Avino, O. M. Roscioni, L. Muccioli and C. Zannoni, J. Am. Chem. Soc., 2014, 136, 2911–2920.
25. O. Cienega-Cacerez, J. A. Moreno-Razo, E. Díaz-Herrera and E. J. Sambriski, Soft Matter, 2014, 10, 3171.
26. R. Berardi and C. Zannoni, Soft Matter, 2012, 8, 2017.
27. S. Belli, A. Patti, R. Van Roij and M. Dijkstra, J. Chem. Phys., 2010, 133, 154514.
28. S. Varga, E. Velasco, L. Mederos and F. J. Vesely, Mol. Phys., 2009, 107, 2481–2492.
29. A. A. Verhoeff, H. H. Wensink, M. Vis, G. Jackson and H. N. W. Lekkerkerker, J. Phys. Chem. B, 2009, 113, 13476–13484.
30. Y. Martínez-Ratón, E. Velasco and L. Mederos, J. Chem. Phys., 2005, 123, 104906.
31. T. Koda, A. Nishioka and S. Ikeda, J. Phys.: Condens. Matter, 2005, 17, S2875–S2878.
32. S. Lago, A. Cuetos, B. Martínez-Haya and L. F. Rull, J. Mol. Recognit., 2004, 17, 417–425.
33. G. Cinacchi, L. Mederos and E. Velasco, J. Chem. Phys., 2004, 121, 3854–3863.
34. Y. Martínez-Ratón and J. A. Cuesta, J. Chem. Phys., 2003, 118, 10164–10173.
35. S.-M. Cui and Z. Y. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 3747–3754.
36. R. A. Wheeler and G. R. Van Hecke, in Liquid Crystals and Ordered Fluids, ed. A. C. Griffin and J. F. Johnson, Springer US, Boston, MA, 1984, pp. 283–297.
37. O. Cienega-Cacerez, C. García-Alcántara, J. A. Moreno-Razo, E. Díaz-Herrera and E. J. Sambriski, Soft Matter, 2016, 12, 1295–1312.
38. A. Juríková, K. Csach, J. Miškuf, N. Tomašovičová, Z. Mitróová, P. Kopčanský, N. Éber, K. Fodor-Csorba and A. Vajda, Mol. Cryst. Liq. Cryst., 2015, 610, 187–192.
39. D. S. S. Rao, M. V. Kumar, S. K. Prasad, U. S. Hiremath, M. Sarvamangala and S. Basavaraja, J. Mater. Chem. C, 2013, 1, 7488.
40. M. Kohout, J. Tůma, J. Svoboda, V. Novotná, E. Gorecka and D. Pociecha, J. Mater. Chem. C, 2013, 1, 4962.
41. Y. Yamazaki, Y. Takanishi and J. Yamamoto, EPL, 2009, 88, 56004.
42. H. Taing, J. G. Rothera, J. F. Binder, C. L. B. Macdonald and S. H. Eichhorn, Liq. Cryst., 2018, 45, 1147–1154.
43. A. Hauser, M. Thieme, A. Saupe, G. Heppke and D. Krüerke, J. Mater. Chem., 1997, 7, 2223–2229.
44. C. J. Booth, D. Krüerke and G. Heppke, J. Mater. Chem., 1996, 6, 927–934.
45. P. Le Barny, J. Billard and J.-C. Dubois, in Liquid Crystals and Ordered Fluids, ed. A. C. Griffin and J. F. Johnson, Springer US, Boston, MA, 1984, pp. 57–74.
46. L. An, M. Jing, B. Xiao, X.-Y. Bai, Q.-D. Zeng and K.-Q. Zhao, Chin. Phys. B, 2016, 25, 096402.
47. A. Grafe, D. Janietz, T. Frese and J. H. Wendorff, Chem. Mater., 2005, 17, 4979–4984.
48. J. R. Hughes, G. R. Luckhurst, K. Praefcke, D. Singer and W. M. Tearle, Mol. Cryst. Liq. Cryst., 2003, 396, 187–225.
49. N. Usoltseva, V. Bykova, E. Kudrik, G. Shaposhnikov, A. Smirnova, G. Ananjeva and I. Nikolaev, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 2001, 367, 509–516.
50. S.-H. Wu and H.-H. Chen, Tetrahedron, 2019, 75, 220–229.
51. S. Iqbal and A. A. Khan, RSC Adv., 2019, 9, 6335–6345.
52. M. Jasiński, K. Szymańska, A. Gardias, D. Pociecha, H. Monobe, J. Szczytko and P. Kaszyński, ChemPhysChem, 2019, 20, 636–644.
53. A. A. Khan, G. Rughoobur, M. A. Kamarudin, A. Sepe, J. A. Dolan, A. J. Flewitt, M. M. Qasim and T. D. Wilkinson, Org. Electron., 2016, 36, 35–44.
54. Y. Shimizu, Y. Matsuda, F. Nekelson, Y. Miyake, H. Yoshida, A. Fujii and M. Ozaki, in Emerging Liquid Crystal Technologies VII, ed. L.-C. Chien, SPIE, 2012, 82790G.
55. S. Sergeyev, O. Debever, E. Pouzet and Y. H. Geerts, J. Mater. Chem., 2007, 17, 3002.
56. A. Pecchia, O. R. Lozman, B. Movaghar, N. Boden, R. J. Bushby, K. J. Donovan and T. Kreouzis, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104204.
57. T. Kreouzis, K. Scott, K. J. Donovan, N. Boden, R. J. Bushby, O. R. Lozman and Q. Liu, Chem. Phys., 2000, 262, 489–497.
58. W. K. Lee, B. A. Wintner, E. Fontes, P. A. Heiney, M. Ohba, J. N. Haseltine and A. B. Smith, Liq. Cryst., 1989, 4, 87–102.
59. C. Destrade, P. Foucher, J. Malthete and N. Huu Tinh, Phys. Lett. A, 1982, 88, 187–190.
60. C. Vauchier, A. Zann, P. L. Barny, J. C. Dubois and J. Billard, Mol. Cryst. Liq. Cryst., 1981, 66, 103–114.
61. W.-R. Chen, C.-M. Chen, J.-C. Hwang and B.-R. Liaw, Jpn. J. Appl. Phys., 2005, 44, 3126.
62. N. Lindner, M. Kölbel, C. Sauer, S. Diele, J. Jokiranta and C. Tschierske, J. Phys. Chem. B, 1998, 102, 5261–5273.
63. M. Inb-Elhaj, D. Guillon, A. Skoulios, P. Maldivi, A. M. Giroud-Godquin and J.-C. Marchon, J. Phys. II, 1992, 2, 2237–2253.
64. T. Wöhrle, R. Gündemir, W. Frey, F. Knecht, A. Köhn and S. Laschat, Chem. – Eur. J., 2017, 23, 4149–4159.
65. C. Schilling, F. Schulz, A. Köhn and S. Laschat, Org. Mater., 2020, 02, 288–299.
66. C. Schilling, A. Bauer, J. A. Knöller, F. Schulz, A. Zens and S. Laschat, J. Mol. Liq., 2022, 367, 120519.
67. M. C. Schlick, N. Kapernaum, M. M. Neidhardt, T. Wöhrle, Y. Stöckl, S. Laschat and F. Giesselmann, ChemPhysChem, 2018, 19, 2305–2312.
68. For other polar boron containing liquid crystals see ref. 69 and 70.
69. L. Jacob, E. Rzeszotarska, M. Koyioni, R. Jakubowski, D. Pociecha, A. Pietrzak and P. Kaszynski, Chem. Mater., 2022, 34, 6476–6491.
70. A. Jankowiak, A. Baliński, J. E. Harvey, K. Mason, A. Januszko, P. Kaszyński, V. G. Young and A. Persoons, J. Mater. Chem. C, 2013, 1, 1144–1159.
71. Y. Shimizu, H. Monobe, M. Heya and K. Awazu, Mol. Cryst. Liq. Cryst., 2005, 441, 287–295.
72. L. D. Landau, Zh. Eksp. Teor. Fiz., 1937, 7, 926.
73. S. J. Cowling, in Handbook of liquid crystals, ed. J. W. G. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. F. Gleeson and E. P. Raynes, Wiley-VCH, Weinheim, 2014, pp. 1–38.
74. P. H. J. Kouwer and T. M. Swager, J. Am. Chem. Soc., 2007, 129, 14042–14052.
75. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
76. M. Lehmann, C. Köhn, H. Meier, S. Renker and A. Oehlhof, J. Mater. Chem., 2006, 16, 441–451.
77. C. O. Zellman and V. E. Williams, J. Org. Chem., 2021, 86, 15076–15084.
78. C. O. Zellman and V. E. Williams, Phys. Chem. Chem. Phys., 2023, 25, 1363–1371.
79. C. O. Zellmann-Parrotta and V. E. Williams, Soft Matter, 2024, 20, 4504–4514.
80. Y. Shimizu, H. Sanada, K. Kitagawa, A. Oka, N. Ohta, T. Kawai and K. Uchida, Liq. Cryst., 2024, 1–8.
81. C. Tschierske, J. Mater. Chem., 2001, 11, 2647–2671.
82. C. Tschierske, Curr. Opin. Colloid Interface Sci., 2002, 7, 355–370.
83. P. H. Kouwer, C. J. Welch, G. McRobbie, B. J. Dodds, L. Priest and G. H. Mehl, J. Mater. Chem., 2004, 14, 1798–1803.
84. P. H. Kouwer and G. H. Mehl, J. Mater. Chem., 2009, 19, 1564–1575.
85. We would like to thank one of the referees for suggesting this rationalization.
86. K. Borisch, S. Diele, P. Goring, H. Muller and C. Tschierske, Liq. Cryst., 1997, 22, 427–443.
87. K. Kratzat, F. Guittard, E. Taffin de Givenchy and A. Cambon, Langmuir, 1996, 12, 6346–6350.
88. K. Kratzat, C. Stubenrauch and H. Finkelmann, Colloid Polym. Sci., 1995, 273, 257–262.
89. J. M. Walsh and G. J. Tiddy, Langmuir, 2003, 19, 5586–5594.
90. J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01132e

---