Optimizing gelation time for cell shape control through active learning

Abstract

Hydrogels are popular platforms for cell encapsulation in biomedicine and tissue engineering due to their soft, porous structures, high water content, and excellent tunability. Recent studies highlight that the timing of network formation can be just as important as mechanical properties in influencing cell morphologies. Conventionally, time-dependent properties can be achieved through multi-step processes. In contrast, one-pot synthesis can improve both the efficiency and uniformity of cell encapsulation. Reaction kinetics are sensitive to temperatures and pH conditions, thus, monitoring gelation time across different conditions is essential for formulation. In this work, we choose tetra-poly(ethylene glycol) (TPEG) macromers as a model system to examine the relationship between the rate of polymer network formation and cell morphology. Previous studies of this system focused on reactions at neutral pH and room temperature, leaving much of the formulation space underexplored. We use Gaussian process regression (GPR) to minimize response surface errors by strategically selecting additional investigation points based on prior knowledge. Then we extend the knowledge from pre-trained data at neutral pH to a new surface at physiological pH. We find that the gelation time surface can effectively predict the aspect ratio of the encapsulated cells. Additionally, through focal adhesion kinase inhibition, we show that cell shape is influenced by the properties of the forming network in the initial hours as cells develop connections with the matrix. We demonstrate the utility of a high-throughput microrheology approach in enhancing fabrications of synthetic extracellular matrix and cell assemblies.

---

1 Introduction

Hydrogels are 3D, hydrophilic polymer networks with mechanical properties resembling the extracellular matrix.^1,2 Hence, they are commonly used as reduced model systems to emulate various aspects of cellular microenvironments. Cells are highly responsive to the viscoelastic characteristics of their surroundings.^3,4 For instance, matrix stiffness can impact cell spreading,⁵ migration,⁶ proliferation,⁷ differentiation,⁸ and phenotype.⁹ Nonetheless, the majority of the studies to date focus on static networks, even though dynamic tissue mechanics underlie many physiological and pathological processes, including morphogenesis,¹⁰ fibrosis,¹¹ and tumor progression.¹² Thus, there is a growing interest in developing networks with time-dependent mechanical properties.^13,14 Among these, double networks, comprised of a collagen primary network and a synthetic secondary network, are a popular choice because they combine the biocompatibility of collagen with enhanced mechanical properties from the secondary network,^15,16 which can be independently tuned.

In addition to mechanical properties, the timing of network formation can significantly impact cell morphologies.^14,17,18 Typically, cells are first encapsulated in collagen, which is subsequently infiltrated with either alginate¹⁷ or photoactive precursors,^18,19 and then crosslinked with calcium ions or ultraviolet (UV) illumination. This process forms secondary networks that stiffen the collagen. Cells in networks that are stiffened immediately tend to adopt a more rounded shape compared to those in networks where stiffening is delayed, in which case cells are first allowed to spread in the collagen network.^17,18 Cells with different spreading states show distinct responses to biochemical cues, even when they are encapsulated in networks with the same final properties.¹⁷ These observations highlight that cells are sensitive to mechanical properties during the first few hours of cell encapsulation, when they must develop focal adhesions and degrade the matrix to effectively spread and migrate. However, most studies to date require additional steps to infiltrate and crosslink the secondary network, after the primary collagen network has formed. Thus, it is desirable to understand how to formulate the hydrogel in a “one-pot synthesis” to achieve various cell shapes.

A wide array of biocompatible systems undergo gelation.^20–22 In principle, these gelling formulations may serve as a natural testbed for how cells respond to continuously transforming viscoelasticity. In practice, a significant challenge is the high cost of accurately mapping the gelation time across various temperatures and concentration conditions. Gelation kinetics are often characterized at neutral pH,^23–25 in an ion-free environment. However, such hypotonic conditions are unsuitable for encapsulation, as they can cause cells to swell from the fluid influx. Recent studies note the effect of pH on hydrogel crosslinking,^26–30 further complicating the picture for predicting the gelation time. Hence, there is a considerable need for tools to rapidly screen formulation conditions, and bridge the gap between gelation studies under neutral conditions and those optimized for cell encapsulation.

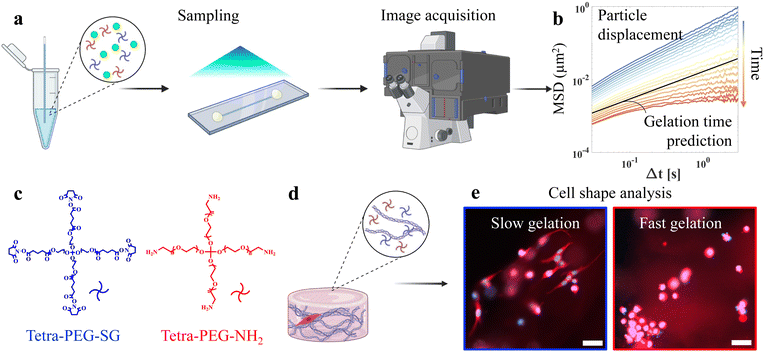
In this regard, microrheology is an attractive alternative to bulk rheometry in characterizing evolving soft matter systems^22,30 due to its minimal sample volume, non-destructive nature, and high-throughput capabilities.³¹ In passive microrheology, one analyzes the thermally-driven motion of particles embedded in a material to infer its mechanical properties^32,33 (Fig. 1a). As gelation occurs, the particle motion slows down, as quantified by the mean-squared displacement (MSD, Fig. 1b), which can be obtained either by multiple particle tracking (MPT)^34,35 or differential dynamic microscopy (DDM).³⁶ Afterward, by manually shifting each time-dependent MSD to collapse them onto master curves, one may determine gelation time and critical scaling exponents.²⁰ More recently, we have developed a framework to extract gelation time that does not require user intervention for manually superposing MSD curves or specifying a suitable range of Fourier basis,³⁷ which further automates the analysis.

Fig. 1 Process flow diagram of our active learning approach. (a) The solution is mixed with particles, drawn up in a capillary, and imaged to quantify the mean-squared displacement. (b) An example of the mean-squared displacement as gelation occurs. (c) The chemical structures of the two TPEGs used in this study. They are mixed in a 1 : 1 stoichiometric ratio. (d) Schematics of the cell encapsulation experiments where the matrix is composed of collagen and TPEGs. (e) Representative micrographs of encapsulated cells at two reaction conditions. The scale bars are 50 μm.

To illustrate the need for in situ, high-throughput methods to assess gelation times affected by formulation conditions, we choose two complementary tetra-poly(ethylene glycol) (TPEG, Fig. 1c) as our model system. TPEGs are four-armed PEG precursors that form highly regular networks.^38,39 We explore the gelation between TPEG-SG, which has reactive succinimidyl glutarate groups that can bind to the nucleophilic primary amine groups on the TPEG-NH₂. The two undergo a highly specific, spontaneous, sol–gel reaction without UV light, eliminating issues related to phototoxicity and variation in UV dosage. Prior work^23,37 indicates that the gelation time of this system is highly sensitive to small changes in concentration. Additionally, the hydrolysis of the NHS ester group in TPEG-SG accelerates with increasing pH,⁴⁰ and can lead to network heterogeneity.⁴¹ Excessive hydrolysis can prevent gelation and result in failed encapsulation. For this system and many others, the complexity of multicomponent systems and potential side reactions complicate efficient phase space sampling. To address these concerns, we adopt an active learning approach, which adaptively selects the most informative data point as the next testing point.

In this work, we integrate active learning with high-throughput microrheology screening to explore how predicted gelation response surface can be used to control cell shapes. Using Gaussian process regression (GPR), we sample gelation time at neutral pH = 7, and then apply this knowledge to improve the phase diagram prediction at pH = 7.4, which is necessary for cell encapsulation but is not available in the literature. GPR provides an accurate map from formulation conditions to gelation time based on a small number of data. Furthermore, the assessed uncertainty from the GPR model, expressed as predictive intervals, can inform whether additional experiments are needed at a particular input region, and thereby reduce the total number of experiments required to achieve a satisfying level of accuracy in prediction. We begin by examining cell morphologies on 2D substrates. Afterward, we synthesize the collagen-TPEG double networks in a single step and use them for cell encapsulation (Fig. 1d). We find that the predicted gelation time surface has high predictive power for the cell shape, with a Pearson correlation coefficient of around 0.8, thus explaining most of the variability in the shape of encapsulated cells (Fig. 1e) by the controlled formulation and experimental reaction condition. Finally, we verify that the timing of the mechanical stimuli plays a crucial role in the cell spreading state. This work has broad implications for biofabrication, and the design of dynamic extracellular matrix mimics.

2 Materials and methods

2.1 Materials

TPEGs (MW = 20k g mol⁻¹), terminated with primary amide (NH₂) and succinimidyl glutarate (SG) groups were purchased from JenKem Technology USA (Plano, TX). Ultra-pure water (resistance = 18.2 MΩ cm) was used to disperse the polymers. Dimethylsulfoxide (DMSO) and phosphate-buffered saline (PBS) tablets were sourced from Sigma-Aldrich (St. Louis, MO). Green fluorescent beads (diameter 2a = 1 μm) were purchased from Fisher Scientific (Hampton, NH). Sterilized PBS (1×), 0.25 wt% Trpsin–EDTA (1×), Dulbecco's modified Eagle medium (DMEM, 1×), Pen Strep (100×), phosphate-buffered saline (PBS), paraformaldehyde (PFA, 16% w/v), trypan blue, CellTracker DeepRed (C34565), Hoechst 33342 was purchased from Thermo Fisher Scientific (Waltham, MA). High-concentration rat tail type I collagen was purchased from Corning, Inc. (Corning, NY). Calf serum (CS) was purchased from the American Type Culture Collection (Manassas, VA). Complete media was made with 90 vol% DMEM, 10 vol% CS, and 1× Pen Strep, and used within one week. FAK inhibitor 14 (item no. 14485) was purchased from Cayman Chemical (Ann Arbor, MI). NIH3T3 cells were acquired from the Yale Cancer Center cell line repository in a frozen aliquot at an early passage (P < 5). Passages P5–20 were used in this study. No significant difference in cell behaviors between passages was noted.

2.2 Experimental methods

2.2.1 TPEG hydrogel preparation. Stock solutions of TPEG-SG and TPEG-NH₂ were prepared on the day of the experiment at a concentration of 100 mg mL⁻¹ in DMSO and water, respectively. TPEG-SG stock solution was prepared in DMSO to minimize hydrolysis. Afterward, the two were mixed together where the molar ratio of the SG group and NH₂ group was 1 : 1, and additional water was added to reach the desired final concentration. The total concentration is reported as the final concentration of both TPEGs, ranging from 20 to 40 mg mL⁻¹. Microrheology was also carried out at pH = 7.4 by dispersing the TPEGs in 1× PBS, immediately before the experiments.

2.2.2 Microrheology. Trace amount (ϕ = 0.02 vol%) of fluorescent beads were homogeneously dispersed into the solution, either in water or PBS, acting as probes. Each sample was prepared to have a final volume of 10 μL. The temperature during gelation (25 °C to 40 °C) was controlled by a ZEISS incubation system, which was equilibrated before experiments. After TPEGs were mixed in an Eppendorf vial, the solution was introduced into a square capillary (0.10 mm × 1.0 mm × 0.09 mm, Friedrich & Dimmock Inc, Millville, NJ), sealed on two ends, and secured onto a glass slide with UV curable glue (Norland Optical Adhesive, Jamesburg, NJ), to minimize convection due to leaking and evaporation. The samples were imaged with an inverted Zeiss Axio Observer 7 microscope in fluorescence mode, standard GFP filter sets, and a 20× objective. Each image has a resolution of 512 × 512 pixels, with a pixel size of 0.29 μm per pixel. Each video includes 500 time steps with a step size of 0.0309 seconds. For each reaction conditions, a typical set of video is taken at a time interval of 6 minutes, 3 minutes, or 1.5 minutes using an automated, preprogrammed acquisition flow. We tracked the time elapsed between mixing the two components and the start of image acquisition, to ensure the reported time points represent the time since mixing, and were consistent across all experiments. The acquisition time (15 seconds) was short compared to the time interval between measurements, so particle displacements were averaged during this window to represent a specific time point t since the reaction began.

2.2.3 Cell culturing and encapsulation. NIH3T3 cells were maintained in complete media, at 37 °C and 5% CO₂, and subcultured every 2–3 days at around 70–80% confluency. A total of 50 μL solution consisting of 1 part 10× PBS, 4 parts DI water mixed with PEGs, and 5 parts collagen (concentration = 10.35 mg mL⁻¹) were mixed thoroughly on ice, and then pipetted into a 4-chamber glass bottom dish (D35C4-20-1.5-N, Cellvis, Mountain View, CA). TPEG-SG and TPEG-NH₂ were first dispersed in DI water, resulting in a final concentration of TPEGs at 0 (control), 20, 25, 30, 35, and 40 mg mL⁻¹. Cells were resuspended in complete media at a density of ∼2 × 10⁶ cells per mL. 5 μL of the cell suspension were added to the neutralized collagen, resulting in a seeding density of ∼2 × 10⁵ cells per mL. The sample was allowed to gel spontaneously at the desired temperatures (25, 30, and 37 °C). Upon the completion of gelation of all samples (∼3 hours), more complete media was added to the dish and the samples were incubated at 37 °C and 5% CO₂.

2.2.4 Cell treatments, fixing and staining. To understand cell spreading in the presence of focal adhesion kinase inhibitor (FAKi). FAKi stock solution was prepared in DI water at 250 μM, diluted 100 times to 2.5 μM, and combined with collagen and 10× PBS to result in a final FAKi concentration of 1 μM. After gelation, the hydrogel was rinsed three times with complete media to remove FAKi, and then more media was added.

Twenty-four hours after initial encapsulation, cells were fixed using 4 wt% PFA in 1× PBS for 15 minutes at room temperature, and then rinsed three times with 1× PBS. Cells were stained with Hoechst 33342 (nuclei, blue, 1 μg mL⁻¹) and CellTracker (cytoplasm, red, 1 μM) in 1× PBS for subsequent visualization by microscopy and cell shape analysis.

2.2.5 Bulk rheometry. The moduli of both collagen-TPEG double networks and TPEG-only networks were characterized using bulk rheometry as gelation occurs. Double-networks: the samples were prepared using the same procedure and composition as in the cell encapsulation experiments, with total TPEG concentrations of 0, 25, 30, and 40 mg mL⁻¹. Neutralized collagen solutions, with or without TPEGs, were thoroughly mixed on ice just before measurements. Samples were loaded at 25 °C. Prior to measurements, the solution was pre-conditioned 30 °C for 3 minutes. TPEG-only networks: the two TPEGs were mixed at room temperature, and measured as soon as the stage temperature was equilibrated. In both cases, the solutions were loaded onto a TA Discovery HR 30 rheometer (New Castle, DE), and measured using a 20 mm parallel plate geometry and a 20 mm sand-blasted bottom plate, on a temperature-controlled Peltier system. Oscillatory time sweeps were carried out at 30 °C, at a fixed frequency of 1 Hz, a fixed strain rate of 0.1%, and a fixed gap size of 650 μm. A solvent trap was used to prevent evaporation.

2.3 Computational methods

2.3.1 Multiple particle tracking. Particles were tracked using an open-source multiple particle tracking (MPT) algorithm^32,34,42 that identifies the centroid position of each particle in every frame. Thereafter, particle positions were linked across frames to generate trajectories of individual particles as a function of time. The mean squared displacement (MSD) for each lag time Δt is calculated as the average of the squared 2D displacements for all particles i and time t:

〈Δr²(Δt)〉 = 〈(x₁(t + Δt)) − x₁(t))² + (x₂(t + Δt)) − x₂(t))²〉 (1)

where x₁ and x₂ are the coordinates of the image. The time and length scales accessible by passive microrheology are limited by microscope acquisition frame rate and resolution limits. In general, stiff materials (>1 Pa) are challenging to characterize due to small probe displacements, using μm-sized probe particles. In addition, towards the end of gelation, local concentration fluctuations can lead to convective probe displacement. These are difficult to avoid. Instead, we carry out a procedure to mitigate the effect of the convective term on MSD as outlined in Note S1 in the ESI.†

2.3.2 Automated determination of gelation time. To validate the accuracy of MSD curve shifting for determining the gelation time, we also analyzed these videos based on the ab initio uncertainty quantification (AIUQ) framework, an automated, Fourier-based analysis tool,³⁷ using the open-sourced software package.⁴³ A main advantage lies in its ability to optimally average the information at each Fourier basis, or wavevector. Therefore, the analysis removes the need for selecting a range of Fourier bases to fit the image structure function in differential dynamic microscopy.³⁶ More details can be found in Note S2 in ESI.† The algorithm is implemented by calling the AIUQ package in R Software using the SAM function for scattering analysis of microscopy, with the intensity matrix, lag time Δt, and pixel size as inputs. We follow ref. 37 and set the model to be an Ornstein–Uhlenbeck (O–U) process due to its capacity to separate MSD curves into two master branches. The O–U process has MSD of the form:

〈Δr²(Δt)〉 = σ_s²(1 − ρ^Δt) (2)

consists of two parameters σ_s and ρ. The MSD can be related to the intermediate scattering function in scattering analysis of microscopy,^44,45 and these parameters are estimated by maximum marginal likelihood estimator in AIUQ that weighs all wavevectors, for each t corresponding to a certain time point after mixing the two TPEGs. In particular, ρ quantifies the curvature of the mean squared displacement (MSD) transitioning from Brownian diffusion to the Ornstein–Uhlenbeck process, a smaller ρ means the system deviates more from the diffusive process. Thereafter, the estimated parameter ρ from the AIUQ package at any time t is fit to a generalized logistic curve:where β is a fitting constant, t_gel is the gelation time. Compared to MPT, which requires manual shifting, obtaining gelation time by AIUQ is free from subjectivity.

2.3.3 Gaussian process regression. Gaussian process regression (GPR),⁴⁶ is a non-parametric approach, well-suited for predicting a nonlinear map by a small number of data points, on the order of 10 s of input dimensions, to predict gelation time and cell aspect ratio (AR) in this case, which can be challenging for other machine learning models. GPR provides a flexible way for capturing nonlinear maps by modeling the distance between any inputs, here the formulations and experimental conditions, through a covariance function. The outcome gelation time between two inputs will be more similar if these two inputs are close to each other. Compared to conventional spatial interpolation techniques, GPR provides a posterior credible interval at any input for assessing the uncertainty of the prediction. We use the RobustGaSP package in R Software to implement GPR.⁴⁷ The pH, reaction temperature, and concentration are set to be the input vectors, while gelation time and cell AR are the outputs. We predict around 10⁴ data points on equally spaced inputs for temperature from 25 to 40 °C and concentration from 20 to 32 mg mL⁻¹. The GPR model is invoked with a command, rgasp, to call the robust marginal posterior mode estimation⁴⁸ for estimating the parameters, appropriate for a small number of data points; and another command, predict, to compute the predictive mean, variance and posterior credible interval at any given input vector or matrix.

3 Results and discussion

3.1 Defining the constraints

We first define the formulation space for this problem. The gelation temperature is varied between 25 to 40 °C. It has been reported that TPEG-SG, TPEG-NH₂ binary system gels at 4 wt% (40 mg mL⁻¹) at room temperature in less than 2 minutes.²³ For samples gelling faster than 5 minutes, it is difficult to mix all components uniformly. Beyond 90 minutes, TPEG-SG undergoes significant hydrolysis. Hence, we focus on gelation time between 5–90 minutes. The temperature and concentration vary in increments of 0.5 °C and 0.5 mg mL⁻¹, respectively, which determine the precision of the probed gelation conditions.

3.2 Tracking the evolution of probe displacement and extracting gelation times

We present the color-coded plots of MSD to show how particle dynamics evolve with reaction time since mixing the two TPEGs (Fig. 2). At earlier times, particles exhibit diffusive behavior where 〈Δr²(Δt)〉 ∼ Δt (Fig. 2a and b). Gradually, the overall magnitude of 〈Δr²(Δt)〉 decreases. The gelling solution begins to show more solid-like characteristics, accompanied by a decrease of the log slope , and the motion becomes more subdiffusive.⁴⁹ Then we determine gelation time by time-cure superposition of the MSD curves, introduced by Larsen and Furst.²⁰ Using this method, gelation kinetics are analyzed by empirically shifting the 〈Δr²(Δt)〉 curves at various time points to superimpose onto a master pregel curve and a master postgel curve (Fig. 2c and d). The shifting was carried out by multiplying the MSD and Δt by coefficients a and b, so that each dataset exhibits some overlap with the subsequent one. The shift factors a and b diverge as they approach gelation (Fig. 2e and f).

Fig. 2 Illustration of MSD shifting procedure at different temperature and concentration conditions. (a) and (b) Families of MSD curves, each representing a different time point during gelation for (a) 23 mg mL⁻¹ TPEG at 28 °C, and (b) 32 mg mL⁻¹ TPEG at 30 °C. The shifted MSD is shown in (c) and (d), and the shifting constant plotted against time is shown in (e) and (f). (g) and (h) Shift factors a (red open and filled circles) and b (blue open and filled triangles) are plotted versus the distance from the gel point, ε, y and z denote the scaling exponents, a ∼ ε^y, b ∼ ε^z, pregel and postgel. (i) and (j) The same sets of experiments were analyzed by AIUQ, which estimates ρ, error bars denote the 95% confidence interval of the estimated ρ from the AIUQ package. AIUQ produces similar gelation times. Solid lines denote fits to the logistical curve in eqn (3).

Using the above procedures, we determine the gelation time to be 40.5 minutes for 23 mg mL⁻¹ TPEG at 28 °C (Fig. 2e), and 13.8 minutes for 32 mg mL⁻¹ TPEG at 30 °C (Fig. 2f), consistent with more rapid development of the gel network at higher concentrations and temperatures, and in line with earlier study of this system.²³ Upon identifying the gelation time, we collapse the shift factors based on their distance to the gelation point , as shown in Fig. 2g and h where a ∼ ε^y and b ∼ ε^z. At the gelation point, the MSD exhibits critical, power-law dependence,^50,51 with an exponent of . For the two cases investigated in Fig. 2, we obtain n = 0.74 and 0.77. Similarly, we apply this procedure to MSD curves for each condition to determine the gelation time and power-law exponents, which are tabulated in Table S1 (ESI†). All cases appear to yield a n of around 0.75, independent of temperature and concentration. This suggests that the microstructure of the critical gel appears to be similar within the concentration range and reaction conditions tested. In summary, MPT provides a detailed analysis of kinetics around crucial gelation points³⁰ and can reveal gel heterogeneity by tracking individual probe particle movements.

On the other hand, Fourier-based analysis offers a user-friendly approach to high-throughput material characterization, as it minimizes the need for user intervention.^52–54 This class of methods calculates image differences and connects image decorrelation to system dynamics, which reflect the contribution of all particles in the field of view, without particle-level information. Thus, this approach is especially useful when processing large amounts of data to identify average quantities, such as the MSD. Previously, we have also demonstrated AIUQ's ability to obtain gelation time automatically for a system of curves.³⁷ This is achieved by fitting the model parameter ρ(t) to time t (eqn (3)). Here, we apply AIUQ to this extensive dataset of curves (>100 total MSDs, >50 GB video microscopy data). We confirm that AIUQ yields gelation times that agree with those obtained by shifting the MPT curves manually, as shown in Fig. 2i and j. Additional results are presented in Table S1 (ESI†).

3.3 Deriving the response surface using sequential design

Collecting data at fine resolution across the entire formulation space remains largely infeasible, even with AIUQ's automated analysis. To address this challenge, we use Gaussian process regression (GPR) to model the response surface based on input conditions for unsampled data. This approach is especially effective for small sample sizes, as it provides not only an estimate but also a predictive interval for quantifying the uncertainty of the prediction at any given input.

To efficiently sample the parameter space in constructing this surface, we adopt an active learning approach, by placing the next test point at the condition with the highest uncertainty interval prior to its placement. We illustrate this first with the gelation time obtained through microrheology at pH = 7, as this condition is commonly tested in literature.²³ As more data points are incorporated into training the model, the average 95% predictive interval length, which are calculated from the difference between the upper and lower bounds of the estimated parameters, gradually decreases. This is illustrated graphically in Fig. S2 (ESI†). Upon increasing observation from 4 points to 10 points, the confidence interval for the entire map is reduced by 85%.

Next, we use the same microrheology procedure to obtain 16 gelation time data points at pH = 7.4. We compare the performance by fitting the gelation response surface using both linear regression and GPR (Fig. 3a and b). Both models generate gelation surfaces that align with expectations, that higher concentrations and temperatures will lead to shorter gelation times (Fig. 3a and c). Intuitively, increasing TPEG concentration leads to more collisions between reactive groups, while higher temperatures accelerate reaction kinetics.

Fig. 3 (a) and (b) Predicted gelation time surface at pH = 7.4 based on compositions and temperatures using 16 observed points using (a) linear regression and (b) Gaussian process regression fit. Filled circles represent experimentally measured gelation time, and their colors denote observed values. (c) and (d) Comparison of 95% predictive interval length for these same input data points using (c) linear regression and (d) Gaussian process regression fit. (e) and (f) Comparison of (e) average 95% predictive interval length across the entire response surface and (f) out-of-sample RMSE between linear (blue circles) and Gaussian process (magenta triangles) regressions, by leaving one out and using the rest to predict.

Using linear regression, the gelation time response surface and uncertainty map predicted from these observations are presented in Fig. 3a. This approach produces a linearly varying response surface across all temperatures and concentrations. However, based on the filled circles, which are color-coded with the same color map to represent the observed gelation time, the predicted surface obtained by linear regression deviates from the observation at multiple points (Fig. 3a).

For comparison, we use the same set of observed data to predict the surface and uncertainty interval using GPR, which can capture non-linear responses, as shown in Fig. 3b. First, we confirm that the GPR-predicted surface captures the variability of observed values more accurately than linear regression. Furthermore, both methods also yield an uncertainty map based on 95% confidence intervals (Fig. 3c and d) which decrease with more data points. We find that the average interval length across all grid points is reduced significantly using GPR, with the same 16 data points. The average interval length associated with GPR predictions is significantly smaller than that of the linear regression model (Fig. 3e), by 71%.

To assess the accuracy of the GPR model's predictions, we also perform leave-one-out, out-of-sample validation, which is briefly described here. We start with the first five observations. Among those, we randomly designate four points as training data and withhold one as test data. The model is trained on these four points to learn the relationships between the input variables (temperatures and compositions) and the output variable (gelation time). After training, the model predicts gelation time for the test point, which is not used in training. We then compare these predictions to the observed gelation time to assess the model's performance on unsampled data. This process is repeated for all five points, and prediction accuracy is quantified using root mean squared error (RMSE). We sequentially repeat the above process with more data points, from 6 to 16 points. As more data points are added, the out-of-sample RMSE decreases, indicating that the GPR model's ability to predict new data improves with additional training points (Fig. 3f). In contrast, the RMSE decreased much more slowly for the linear model. Overall, GPR consistently outperforms linear regression in this scenario. Ultimately, the RMSE can be reduced to around 10 minutes using GPR, which is around 47% lower than the RMSE using linear regression with the same data. The remaining uncertainty may be inherent to the system and arises due to sample preparation, time resolution of the acquisition, estimates of the MSDs, and variation in shifting the MSDs.

The same comparison between linear and GPR is also performed for pH = 7 (Fig. S3, ESI†). Even though GPR also produces a smaller confidence interval (Fig. S3c, ESI†), we find that in this case, GPR does not offer a similar reduction of RMSE compared to linear regression (Fig. S3d, ESI†). High-throughput microrheology measurements produce gelation time datasets that facilitate testing statistically meaningful scaling relationships. To understand the difference between two pHs, we fit a linear regression model for gelation time against both temperature and concentration as variables (Table 1). For pH = 7, the linear coefficients of both concentration and temperature significantly differ from zero. The analysis therefore indicates that the relationship of response surface of gelation time is close to linear for both temperature and concentration at neutral pH conditions. However, at pH = 7.4, the coefficient of concentration is not significant, indicating that the relation between concentration and gelation time may not be linear. In summary, under neutral pH conditions, the variability of both variables is effectively captured by the linear model, resulting in a similar out-of-sample RMSE compared to GPR.

Table 1 Linear regression model for gelation time. t_gel ∼ A₁C + A₂T where t_gel represents the gelation time, T represents temperature, C represents concentration. The t-statistics for testing whether the linear regression coefficients A₁, A₂ are zero, their p-value and significance levels are given in columns 5–7. A small p-value indicates the corresponding linear coefficient is significantly different from zero

	Parameter	Coefficient	Std. error	t-Value	p-Value	Sig. level
Sig. codes: ‘***’ = 0–0.001, ‘**’ = 0.001–0.01, ‘*’ = 0.01–0.05, no symbol = 0.1–1.0.
pH = 7	(Intercept)	134	23.4	5.73	7.14 × 10^−4	***
	C (conc.)	−1.88	0.970	0.485	6.08 × 10^−3	**
	T (temp.)	−2.14	0.456	0.500	3.67 × 10^−3	**
pH = 7.4	(Intercept)	130	30.2	4.29	8.76 × 10^−4	***
	C (conc.)	−1.36	0.485	0.970	0.185
	T (temp.)	−1.77	0.500	0.456	1.94 × 10^−3	**

---

3.4 Improving gelation time prediction at cell encapsulation pH with prior knowledge at neutral pH

As the gelation time is typically reported at neutral pH conditions, we test whether this information can be used to extrapolate gelation time and boost the performance of GPR. To do so, pH is treated as the third independent variable to generate the prediction. The out-of-sample RMSE calculated using only pH = 7.4 data is replotted here for comparison.

We find that, initially, with fewer than 11 data points at pH = 7.4, the out-of-sample RMSE is much smaller when the surface is learned jointly, indicating that including the data points at pH = 7 helps reduce the predictive error when pH = 7.4. After the 12^th point, adding data from pH = 7 does not improve the predictions at pH = 7.4, as shown in Fig. 4a. This is attributed to variations in the kinetics of the secondary reaction at these two pHs, where TPEG hydrolysis occurs much faster at pH above 7 than at neutral pH, as confirmed by UV-vis measurement (Fig. S4, ESI†). These differences limit the accuracy of predictions at pH = 7.4 using the prior knowledge from pH = 7 when more instances of gelation time are observed at pH = 7.4. In both cases, the RMSEs approach a similar value after all 16 data points at pH = 7.4 are used. The response surfaces are displayed as 3D plots in Fig. 4b and c, with the training data points shown as black filled circles. There is a good agreement between the observed values and the learned 3D response surface in both cases. Due to increased hydrolysis, gelation time tends to be longer at pH = 7.4. Taken together, these results suggest that prior knowledge of the response surface at pH = 7 can significantly reduce uncertainty and error in predicting the response surface at pH = 7.4, facilitating experimental design, when additional data at pH = 7.4 is unavailable or inaccessible.

Fig. 4 (a) Out-of-sample RMSE computed for surfaces learned from observations at pH = 7.4 (blue cirlces) and from observations at pH = 7 and pH = 7.4 jointly (magenta triangles). (b) and (c) The response surfaces are plotted in 3D for (b) pH = 7 and (c) pH = 7.4. Observed data are plotted as filled circles.

3.5 Characterizing cell morphologies on 2D substrates

To explore the TPEG-collagen double network as a potential material for cell scaffolds, we first prepare 2D substrates made with different TPEG concentrations (25, 30, and 40 mg mL⁻¹). Prior to seeding the cells, we ensure that the networks are completely crosslinked. After seeding and culturing them on the 2D substrates for 24 hours, the cells are fixed and stained, as illustrated in the representative images (Fig. 5a–c). While networks prepared with a higher concentration of TPEG (40 mg mL⁻¹, Fig. 5a) are slightly stiffer (Fig. S5, ESI†), cells cultured on these substrates exhibit more rounded morphologies than those cultured on softer substrates, prepared with lower TPEG concentrations (25 mg mL⁻¹, Fig. 5c). As demonstrated by ref. 55 and 56, cell spreading on 2D depends on not only the stiffness of the substrate but also the density and the type of the adhesion ligands. The gelation rate of both collagen and TPEG appears to affect the density of adhesive ligands on the surface of the double networks, thereby influencing cell morphology in 2D. Given these observations, we pose the question: could we similarly expect different cell morphologies in 3D? In 3D, network formation takes place simultaneously with the development of cell focal adhesions, so gelation kinetics could have a greater impact on cell morphologies. Furthermore, cells must also break down the surrounding matrix to spread and migrate. Therefore, we next investigate the relationship between gelation time and cell shape in 3D.

Fig. 5 Cells cultured on double-network hydrogels with TPEG concentration of (a) 25 mg mL⁻¹, (b) 30 mg mL⁻¹, and (c) 40 mg mL⁻¹. The scale bars are 50 μm.

3.6 Characterizing cell morphologies in 3D double networks

We synthesize double networks in a one-pot reaction to examine the morphology of encapsulated cells. Cells, neutralized collagen, and TPEGs are mixed together in PBS and incubated at 25, 30, and 37 °C, allowing the formulation to gel. After 24 hours, cells are fixed and stained for imaging. Representative snapshots are shown in Fig. 6a. As in the 2D case, we find that cells encapsulated in hydrogel formed at higher TPEG concentration and temperature tend to have a more rounded morphology, compared to those in slow-gelling formulations that have a more elongated morphology. Cell encapsulation in pure collagen (0 mg mL⁻¹ TPEG) serves as a control at all three temperatures to rule out temperature as a factor affecting cell morphologies. These results suggest that the fast development of the secondary TPEG network also inhibits cell spreading.

Fig. 6 (a) Cell shape characterization by fluorescent microscopy. Red and blue channels denote the cytoplasm and nucleus, respectively. An example of the best-fit ellipse is shown as an inset, where l, w are the major and minor axes of the ellipse, as shown. The scale bar is 20 μm. (b) The hydrogel is crosslinked at different temperatures, resulting in different rates of crosslinking and cell morphologies. (c) Time-dependent bulk rheometry measurements for gels crosslinked at 30 °C are measured from pure collagen plus TPEG at concentrations 0, 25, 30, and 40 mg mL⁻¹.

Introducing non-degradable TPEG into the matrix strengthens the matrix, but also creates regions within the matrix that cells cannot access or modify. Previously, such a network was found to resist collagen contraction.¹⁵ We hypothesize that when the TPEG networks gel rapidly (for instance, at higher temperature or higher PEG concentration), cells are trapped before they have time to develop focal adhesion, and thus exhibit rounded morphology (Fig. 6b). Using microrheology, we find that the reaction rate between the SG and NH₂ groups is highly sensitive to temperature and concentrations (Fig. 4c). Likewise, the trend of microrheology is echoed by bulk rheology measurements of the double networks (Fig. 6c). At 30 °C, the network forms much faster at 40 mg mL⁻¹ TPEG than at 25 or 30 mg mL⁻¹ TPEG. Our findings are consistent with earlier studies showing that cell shapes are influenced by the timing of mechanical stimuli.^14,17,18 While bulk rheology reveals that the secondary network formation accelerates with increasing TPEG addition, its rate is obscured by the dominating mechanical property of the collagen network, which gels shortly after mixing, where storage modulus is always greater than the loss modulus (Fig. S6, ESI†). Thus, it is challenging to establish a metric for the rate of secondary network formation to understand cell shape.

As an additional verification, we perform bulk rheometry for the TPEG-only formulation (Fig. S7, ESI†), and determine the gelation time by the crossover between G′ and G′′. We find that, using this criterion, most of the formulation gels in a matter of minutes, compares to 10 s of minutes using time-cure superposition. The different gelation times observed with these methods likely stem from the distinct length scales of macroscopic rheometer geometry (D = 20 mm) compared to the size of the probe (2a = 1 μm). Similar to ref. 23, we conclude that the solid-like network initially detected by the rheometer may be relatively open, allowing the probe particles to move freely within those open spaces. For 2D substrates and 3D encapsulation, microrheology seems to probe structure formation at a length scale more relevant to the evolving cell morphology. As shown in Fig. S7 and Table S2 (ESI†), all formulations examined at 30 °C gel immediately. However, when cells are seeded on these networks (Fig. 5) or encapsulated within them (Fig. 6a), we observe distinct cell morphologies.

Our work establishes microrheology as a valuable tool for probing secondary network formation whereas bulk rheology can be painstaking. During bulk rheology measurements, care is taken to avoid shear break-up, and minimize loading history, evaporation, and slipping. Each experiment uses about 0.5 mL of sample, but reloading is often necessary, meaning preparation, loading, measurement, and cleanup can take several hours for each condition. In contrast, microrheology offers advantages that include automated analysis, rapid temperature equilibration, and small sample volumes (∼10 μL). Crucially, microrheology yields a key differentiating metric, the gelation time, that highly correlates with the rate of network formation of the secondary network on the length scale of cells. Overall, microrheology is well-suited for mapping various input conditions to construct a response surface for gelation time. Here, such mapping aids in optimizing formulation and processing conditions to promote cell spreading while enhancing the mechanical properties of pure collagen networks. This study offers additional insights into the behavior of cells encapsulated in a continuously varying matrix and presents a method for formulation control of cell shapes without UV activation.

3.7 Predicting cell shapes by gelation time

To demonstrate that gelation time can predict average final cell morphologies, we first extract cell shapes by thresholding and binarizing the images. Next, we fit an ellipse to the cytoplasm channel (Fig. S8, ESI†) through an automated batch process using a custom FIJI plug-in developed in our previous work.⁵⁷ We find the average AR of the projection of the encapsulated cells. It is approximated by fitting an ellipse to the cytoplasm channel of the image, where l and w are the major and minor axis of the cell, respectively, and aspect ratio , averaged for all cells. The histograms of AR distribution for all conditions are shown in Fig. S9 (ESI†). Approximately 100–200 cells are analyzed for each temperature and concentration condition. In addition, we have compared (AR) by fitting an ellipse to several other metrics to quantify the cell shape: by computing the eigenvalues of the gyration tensor, whose square roots represent the radii that characterize the major axes of the ellipsoid describing the cell shape, or by computing the cell area. As shown in Fig. S10 in ESI,† all three metrics are highly correlated with each other. Therefore, we will report the aspect ratio based on the ellipse fitting to the cytoplasm channel in subsequent analyses. In both 2D and 3D scenarios, we find that cell aspect ratio follows similar trends with varying concentrations of TPEG (Fig. S11, ESI†). To create a phase diagram, we generate a surface similar to gelation time to predict cell aspect ratios under various preparation conditions (Fig. 7a).

Fig. 7 Measuring the strength of the correlation between gelation time and cell shape. Panels (a) and (e) show the predicted phase diagrams of AR and gelation time, respectively. Panel (b) and (d) show the color-coded, observed gelation time and AR. Panels (c) and (f) show the correlation analysis between the predicted and observed quantities. The 95% predictive intervals from GPR data are plotted as grey error bars. Solid red lines denote the least squared linear fit between the observed and predicted quantities.

From the phase diagram in Fig. 7a, we predict the cell shape based on the input conditions used to generate the gelation plot (open circles), where the gelation time is observed (Fig. 7b). The predicted cell shape is plotted against the observed gelation time in Fig. 7c. Then we compute the Pearson correlation coefficient, which is a common way of measuring linear correlation:

where Cov(·,·) denotes the covariance between the two inputs, and σ stands for the standard deviation of that input. There is intrinsic variation in cell shapes (Fig. S12, ESI†). Hence, we compute both the Pearson correlation coefficient and its weighted version (Note S3, ESI†). Their differences are small, and the unweighted results are reported here. We found a correlation coefficient r = 0.797 when predicting cell shape based on known gelation time. Generally, r > 0.5 indicates a moderately positive correlation. Due to a high correlation between the two surfaces, the predicted gelation time can similarly explain the observed cell shape. We carry out a similar test with the observed cell shape (colored circles, Fig. 7d), with the corresponding gelation time precited from the gelation time plot, learned jointly with data from pH = 7 and pH = 7.4 (open circles, Fig. 7e). A correlation coefficient r = 0.845 is obtained (Fig. 7f) when the observed cell aspect ratio is accounted for by a known gelation time phase diagram.

Cell shape regulates transcriptional signals and gene expressions.⁵⁸ Here, we demonstrate a method for controlling cell shape through the gelation time. These results indicate that fibroblast morphology is responsive to dynamic matrix viscoelasticity, echoing earlier results that cell shape depends most critically on the total time spent in fast-relaxing (more liquid-like) conditions.¹⁴ For the first time, we use a combination of experimental techniques and machine learning to quantitatively assess how gelation time impacts cell morphology.

3.8 Examining the timing of matrix formation and focal adhesion development on cell spreading

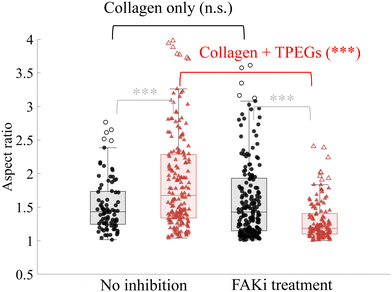
The primary factor influencing differences in cell spreading state appears to be the mechanical history, particularly the gelation time, rather than the final mechanical properties of the matrix. As the matrix gels over time, cells can sense and respond to these changes through focal adhesions, which connect them to the extracellular matrix. Focal adhesions convey information such as matrix moduli and degradability, allowing cells to adjust the stiffness of their actin cytoskeleton accordingly. These actions are mediated through focal adhesion kinase (FAK), which plays a central role in cell adhesion⁵⁹ and cell morphology.⁶⁰

To determine if a difference in response of cell spreading is due to focal adhesion formation, we perform control encapsulation experiments in the presence of FAK inhibitor (FAKi),⁶¹ during the initial stage of network formation of the hydrogels. We encapsulate cells in a slow-gelling double network (TPEGs = 30 mg mL⁻¹, crosslinked at 30 °C, t_gel ≈ 45 minutes) containing 1 μM of FAKi. After gelation, the hydrogel is washed and replenished with complete media. Twenty-four hours after initial encapsulation, cells are fixed and stained for imaging. Altogether, cells are exposed to FAKi for the first 3 hours. They are compared to cells that have never been exposed to FAKi (Fig. 8). As a control, we perform the same experiments with cells encapsulated in a collagen matrix without TPEGs. We observe no statistical difference in aspect ratios of the cells, with or without the FAKi treatment, when they are encapsulated in pure collagen (Fig. 8), based on pairwise comparison using one-way analysis of variance (ANOVA). This indicates that NIH3T3 cells can recover and elongate in a collagen matrix once the FAKi is removed. In contrast, cells in the double network cannot elongate if the TPEG network forms before FAKi is removed. In this case, we find that the aspect ratio of cells in the double network differs significantly depending on whether or not they are exposed to FAKi during the formation of the network. In the presence or absence of FAKi, the double network undergoes the same preparation and therefore has similar nanoscale mesh structures and mechanical properties. These results indicate that the timing of mechanical stimuli plays a crucial role in cell spreading, and the process is FAK-dependent. Furthermore, we note that within each group – whether untreated or treated with FAKi – the cell aspect ratios are also different, illustrating cells' sensitivity to both the magnitude and timing of the mechanical stimuli.

Fig. 8 Aspect ratios are depicted for collagen-only matrix (black circles) and collagen + TPEGs double networks (red triangles). Statistical quantities are shown in a box plot, where the open symbols denote outliers, outside of 1.5 standard deviations. All data are used in the one-way ANOVA analysis. Significance levels are denoted as: ‘***’ = 0–0.001, ‘**’ = 0.001–0.01, ‘*’ = 0.01–0.05, n.s. = 0.1–1.0.

4 Conclusion

Double networks are frequently employed to impart desirable responses to collagen-based hydrogels.^15,16 By infiltrating a collagen network with synthetic polymers and then crosslinking these polymers using external stimuli, it is possible to achieve time-dependent network properties.¹⁴ One-pot synthesis largely simplifies these multi-step procedures, but requires an understanding of how gelation time affects cell morphology, which can, in turn, profoundly influence their collective forces. Therefore, phase diagrams mapping input conditions to cell shape and matrix properties can guide the design of cell assemblies, but constructing them often requires significant human and material costs.

We combine high-throughput microrheology and data-driven analysis to address this problem. Data-driven methods optimize soft matter formulations, while microrheology probes evolving systems in situ. We achieve an efficient sampling of the formulation space by combining automated microscopy acquisition and streamlining image analysis. The large data set yields gelation times at different conditions, which serve as inputs to learn the gelation response surface. Using Gaussian process regression, we construct the gelation response surface, which proves more flexible and accurate than linear regression. Additionally, we introduce an active learning procedure that uses intervals computed by Gaussian process regression to systematically reduce the uncertainty of the response surface.

Our study highlights that a fast-relaxing environment is critical for cell spreading within the first few hours after encapsulation, and for achieving elongated cell shapes, even when controlling for the final mechanical properties of the hydrogel. For spreading to occur, cells must first establish focal adhesions before the formation of non-degradable networks. Thus, we show that managing gelation time is a powerful method for altering cell morphology. Our findings could also improve techniques such as 3D printing,⁶² which depend on precise control of the viscoelastic properties of bio-inks. The experimental and analytical capabilities described here could also enhance the design of time-dependent synthetic extracellular matrix mimics,⁶³ facilitate the creation of anisotropic cell assemblies,⁶⁴ and improve the study of cell–extracellular matrix interactions⁶⁵ at both microscopic and macroscopic scales.

Author contributions

Yimin L designed the project. Yuxin L and JC performed experiments. Yuxin L, Yimin L and MG performed numerical modeling and analysis. All authors have contributed to the writing of the manuscript and given approval to the final version of the manuscript.

Data availability

The data collected and the analysis codes generated for this study is available through a permanent DOI on Dryad: https://doi.org/10.5061/dryad.8w9ghx3xn.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank the Yale Cancer Center for providing the NIH3T3 cell line, Juliet Gottfried for assistance with subculturing and maintenance of the cell line, and Xinyi Fang for discussion on the cell shape analysis code. We acknowledge the use of UV-vis spectrophotometer at the Yale Chemical and Biophysical Instrumentation Center, and rheometer at the Yale Mechanical and Thermal Analysis Instrumentation Core. This work is partially supported by the National Science Foundation under Grants OAC-2411043 and OAC-2411044.

References

1. N. A. Peppas and A. S. Hoffman, Biomaterials science, Elsevier, 2020, pp. 153–166.
2. S. R. Caliari and J. A. Burdick, Nat. Methods, 2016, 13, 405–414.
3. C.-M. Lo, H.-B. Wang, M. Dembo and Y.-L. Wang, Biophys. J., 2000, 79, 144–152.
4. P. Chaudhuri, L. Berthier and W. Kob, Phys. Rev. Lett., 2007, 99, 060604.
5. A. S. Rowlands, P. A. George and J. J. Cooper-White, Am. J. Physiol.: Cell Physiol., 2008, 295, C1037–C1044.
6. R. Sunyer, V. Conte, J. Escribano, A. Elosegui-Artola, A. Labernadie, L. Valon, D. Navajas, J. M. Garca-Aznar, J. J. Muñoz and P. Roca-Cusachs, et al. , Science, 2016, 353, 1157–1161.
7. R. A. Marklein and J. A. Burdick, Soft Matter, 2010, 6, 136–143.
8. J. Swift, I. L. Ivanovska, A. Buxboim, T. Harada, P. D. P. Dingal, J. Pinter, J. D. Pajerowski, K. R. Spinler, J.-W. Shin and M. Tewari, et al. , Science, 2013, 341, 1240104.
9. J. L. Balestrini, S. Chaudhry, V. Sarrazy, A. Koehler and B. Hinz, Integr. Biol., 2012, 4, 410–421.
10. F. Serwane, A. Mongera, P. Rowghanian, D. A. Kealhofer, A. A. Lucio, Z. M. Hockenbery and O. Campas, Nat. Methods, 2017, 14, 181–186.
11. B. Hinz, Curr. Rheumatol. Rep., 2009, 11, 120–126.
12. O. Maller, A. P. Drain, A. S. Barrett, S. Borgquist, B. Ruffell, I. Zakharevich, T. T. Pham, T. Gruosso, H. Kuasne and J. N. Lakins, et al. , Nat. Mater., 2021, 20, 548–559.
13. M. Guvendiren and J. A. Burdick, Nat. Commun., 2012, 3, 792.
14. P. Crandell and R. Stowers, ACS Biomater. Sci. Eng., 2023, 9, 6860–6869.
15. C. Lotz, F. F. Schmid, E. Oechsle, M. G. Monaghan, H. Walles and F. Groeber-Becker, ACS Appl. Mater. Interfaces, 2017, 9, 20417–20425.
16. G. M. Fernandes-Cunha, K. M. Chen, F. Chen, P. Le, J. H. Han, L. A. Mahajan, H. J. Lee, K. S. Na and D. Myung, Sci. Rep., 2020, 10, 16671.
17. H. Liu, M. Wu, Y. Jia, L. Niu, G. Huang and F. Xu, NPG Asia Mater., 2020, 12, 45.
18. D. J. Munoz-Pinto, A. C. Jimenez-Vergara, T. P. Gharat and M. S. Hahn, Biomaterials, 2015, 40, 32–42.
19. I. G. Mercer, K. Yu, A. J. Devanny, M. B. Gordon and L. J. Kaufman, Acta Biomater., 2024, 187, 242–252.
20. T. H. Larsen and E. M. Furst, Phys. Rev. Lett., 2008, 100, 146001.
21. M. Shayegan and N. R. Forde, PLoS One, 2013, 8, e70590.
22. R. L. Martineau, A. V. Bayles, C.-S. Hung, K. G. Reyes, M. E. Helgeson and M. K. Gupta, Adv. Biol., 2022, 6, 2101070.
23. E. Parrish, K. A. Rose, M. Cargnello, C. B. Murray, D. Lee and R. J. Composto, Soft Matter, 2020, 16, 2256–2265.
24. S. T. Lust, D. Hoogland, M. D. Norman, C. Kerins, J. Omar, G. M. Jowett, T. T. Yu, Z. Yan, J. Z. Xu and D. Marciano, et al. , ACS Biomater. Sci. Eng., 2021, 7, 4293–4304.
25. J. Yang, J. Steck and Z. Suo, Extreme Mech. Lett., 2020, 40, 100898.
26. T. H. Larsen, M. C. Branco, K. Rajagopal, J. P. Schneider and E. M. Furst, Macromolecules, 2009, 42, 8443–8450.
27. Z. Ji, H. Liu, L. Yu, Q. Duan, Y. Chen and L. Chen, Food Hydrocolloids, 2020, 104, 105733.
28. T. M. FitzSimons, E. V. Anslyn and A. M. Rosales, ACS Polym. Au, 2021, 2, 129–136.
29. C. Tanger, M. Müller, D. Andlinger and U. Kulozik, Food Hydrocolloids, 2022, 123, 106903.
30. M. Meleties, D. Britton, P. Katyal, B. Lin, R. L. Martineau, M. K. Gupta and J. K. Montclare, Macromolecules, 2022, 55, 1239–1247.
31. Y. Luo, M. Gu, C. E. Edwards, M. T. Valentine and M. E. Helgeson, Soft Matter, 2022, 18, 3063–3075.
32. E. M. Furst and T. M. Squires, Microrheology, Oxford University Press, 2017.
33. P. Liu and P. J. Beltramo, Soft Matter, 2023, 19, 7708–7716.
34. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
35. J. C. Crocker, M. T. Valentine, E. R. Weeks, T. Gisler, P. D. Kaplan, A. G. Yodh and D. A. Weitz, Phys. Rev. Lett., 2000, 85, 888.
36. R. Cerbino and V. Trappe, Phys. Rev. Lett., 2008, 100, 188102.
37. M. Gu, Y. He, X. Liu and Y. Luo, Phys. Rev. E, 2024, 110, 034601.
38. T. Sakai, T. Matsunaga, Y. Yamamoto, C. Ito, R. Yoshida, S. Suzuki, N. Sasaki, M. Shibayama and U.-I. Chung, Macromolecules, 2008, 41, 5379–5384.
39. T. Sakai, React. Funct. Polym., 2013, 73, 898–903.
40. M. Kurakazu, T. Katashima, M. Chijiishi, K. Nishi, Y. Akagi, T. Matsunaga, M. Shibayama, U.-I. Chung and T. Sakai, Macromolecules, 2010, 43, 3935–3940.
41. K. A. Rose, E. Marino, C. S. O'Bryan, C. B. Murray, D. Lee and R. J. Composto, Soft Matter, 2022, 18, 9045–9056.
42. Y. Gao and M. L. Kilfoil, Opt. Express, 2009, 17, 4685–4704.
43. Y. He, X. Liu and M. Gu, AIUQ: Ab Initio Uncertainty Quantification, 2024, R package version 0.5.2., code available at https://cran.r-project.org/web/packages/AIUQ/index.html.
44. A. V. Bayles, T. M. Squires and M. E. Helgeson, Soft Matter, 2016, 12, 2440–2452.
45. M. Gu, Y. Luo, Y. He, M. E. Helgeson and M. T. Valentine, Phys. Rev. E, 2021, 104, 034610.
46. C. E. Rasmussen, Gaussian processes for machine learning, MIT Press, 2006.
47. M. Gu, J. Palomo and J. O. Berger, R J., 2019, 11, 112–136.
48. M. Gu, Bayesian Anal., 2018, 14, 857–885.
49. R. Poling-Skutvik, R. Krishnamoorti and J. C. Conrad, ACS Macro Lett., 2015, 4, 1169–1173.
50. H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382.
51. F. Chambon and H. H. Winter, J. Rheol., 1987, 31, 683–697.
52. A. V. Bayles, T. M. Squires and M. E. Helgeson, Rheol. Acta, 2017, 56, 863–869.
53. R. You and R. McGorty, Rev. Sci. Instrum., 2021, 92, 023702.
54. V. A. Martinez, R. Besseling, O. A. Croze, J. Tailleur, M. Reufer, J. Schwarz-Linek, L. G. Wilson, M. A. Bees and W. C. Poon, Biophys. J., 2012, 103, 1637–1647.
55. A. Engler, L. Bacakova, C. Newman, A. Hategan, M. Griffin and D. Discher, Biophys. J., 2004, 86, 617–628.
56. A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689.
57. Y. Luo, M. Gu, M. Park, X. Fang, Y. Kwon, J. M. Urueña, J. Read de Alaniz, M. E. Helgeson, C. M. Marchetti and M. T. Valentine, J. R. Soc., Interface, 2023, 20, 20230160.
58. P. Haftbaradaran Esfahani and R. Knöll, Biophys. Rev., 2020, 12, 895–901.
59. K. E. Michael, D. W. Dumbauld, K. L. Burns, S. K. Hanks and A. J. Garca, Mol. Biol. Cell, 2009, 20, 2508–2519.
60. B. Xu, Y. Ju and G. Song, J. Biosci. Bioeng., 2014, 117, 624–631.
61. A. Krouwels, F. P. Melchels, M. H. Van Rijen, C. B. Ten Brink, W. J. Dhert, F. C. Öner, M. A. Tryfonidou and L. B. Creemers, Acta Biomater., 2018, 66, 238–247.
62. S. Nöbel, B. Seifert, K. Daffner, J. Schäfer and J. Hinrichs, Food Hydrocolloids, 2021, 113, 106450.
63. M. Sarkar, B. M. Burkel, S. M. Ponik and J. Notbohm, Acta Biomater., 2024, 177, 253–264.
64. J. Chen and Y. Luo, ACS Appl. Mater. Interfaces, 2024, 16, 33223–33234.
65. K. M. Schultz, K. A. Kyburz and K. S. Anseth, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E3757–E3764.

---

Footnote

† Electronic supplementary information (ESI) available: Notes S1–S3, Tables S1, S2 and Fig. S1–S12. See DOI: https://doi.org/10.1039/d4sm01130a

---