 Open Access Article
Open Access ArticleThe effect of selective surface interaction on polymer phase separation with explicit polydispersity during polymerization
Hyeonmin
Jeong
a,
Junsi
Gu
b,
Paul
Mwasame
b,
Kshitish
Patankar
 b,
Decai
Yu
b and
Charles E.
Sing
b,
Decai
Yu
b and
Charles E.
Sing
 *a
*a
aDepartment of Chemical and Biomolecular Engineering, University of Illinois Urbana-Champaign, Urbana, IL 61801, USA. E-mail: cesing@illinois.edu
bDow Chemical Company, Midland, MI 48667, USA
First published on 13th January 2025
Abstract
In polymerization-induced phase separation, the impact of polymer–substrate interaction on the dynamics of phase separation for polymer blends is important in determining the final morphology and properties of polymer materials as the surface can act as another driving force for phase separation other than polymerization. We modify the previously-developed polymerizing Cahn–Hilliard (pCH) method by adding a surface potential to model the phase separation behavior of a mixture of two species independently undergoing linear step-growth polymerization in the presence of a surface. In our approach, we explicitly model polydispersity by separately considering different molecular-weight components with their own respective diffusion constants, and with the surface potential preferentially acting on only one species. We first show that the surface potential induces faster phase separation of smaller molecules at early stages before the degree of polymerization becomes large enough to drive bulk phase separation. This model is then used to investigate the degree of anisotropic ordering in a direction perpendicular to the surface over various polymerization rates ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and strengths of the potential Ṽ. We find that at low
and strengths of the potential Ṽ. We find that at low ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , smaller molecules have sufficient time to diffuse and accumulate at the potential surface, resulting in richer production of heavier polymers at the surface without the need for larger polymers to diffuse on their own toward the surface. Conversely, at high
, smaller molecules have sufficient time to diffuse and accumulate at the potential surface, resulting in richer production of heavier polymers at the surface without the need for larger polymers to diffuse on their own toward the surface. Conversely, at high ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , larger polymers first evenly accumulate throughout the system before undergoing phase separation; the concentration wave initiated from the potential surface then propagates into the bulk, resulting in anisotropic phase separation.
, larger polymers first evenly accumulate throughout the system before undergoing phase separation; the concentration wave initiated from the potential surface then propagates into the bulk, resulting in anisotropic phase separation.
1. Introduction
Surface-directed phase separation (SDPS) describes a phenomenon where a surface exhibits preferential attraction to one component over others in a mixture, thereby inducing phase separation. Consequently, SDPS results in the formation of a wetting layer of the favored component proximal to the surface, accompanied by the propagation of anisotropic concentration waves perpendicular to the surface, extending into the bulk.1–7 SDPS and the effect of surfaces have been extensively studied in experiments1,2,8–10 as well as in theoretical and computational research,4–7,10–20 due not only to the important role of surfaces in inducing unique phase separation behaviors and morphologies but also to their diverse range of applications spanning from food,21 surface-responsive materials,22 to photovoltaic devices.23 The presence of a surface can significantly influence the phase separation behavior in polymeric systems, playing a crucial role in determining the morphology and properties of the resulting material. First, surfaces introduce different energetic interactions compared to the bulk polymer. The nature of these interactions, whether attractive or repulsive, can affect how polymers adsorb, arrange, and move on the surface. The compatibility between the polymer and the surface material can lead to preferential wetting of one component over another, influencing the phase morphology.1–7,24 Second, the surface can confine the polymer blend to a limited dimension. This confinement can alter the kinetics and thermodynamics of phase separation, often leading to faster phase separation compared to bulk behavior.25–27 In addition, while polymers in the bulk phase separate isotropically, the symmetry near a surface is broken, leading to anisotropic domain shapes and orientations.5,6,28 Hence, it is important to understand molecular-level details of the SDPS process as it provides a means to precisely control phase separation pathways, final properties and structures of materials for targeted specific functions.In comparison to SDPS, polymerization-induced phase separation (PIPS) describes the phenomenon where initially homogeneous components of a polymer blend or solution spontaneously segregate into separate regions or phases due to chemical disparities as molecular weight increases.29,30 PIPS presents numerous advantages over conventional phase separation methodologies, notably in its capacity to meticulously regulate the morphology of resultant materials. This includes the attainment of cylindrical,31,32 lamellar,33–35 and globular structures,36–38 each achievable through the evolving morphological processes. Such outcomes are dictated by the intricate interplay between polymerization kinetics and phase separation dynamics, thereby determining the final morphology of the system. PIPS manifests across diverse systems, encompassing polymeric blends, solutions, or colloidal suspensions, typically initiated through thermal39–42 or photochemical means.43–46 It finds widespread application in the fabrication of polymer-based materials, notably membranes,47–49 functional coatings,50,51 and composites (or adhesives).52–55 In this sense, comprehending the underlying physics of PIPS and exercising control over this phenomenon are pivotal, given their significant implications across a broad spectrum of industrial and technological applications. Furthermore, combining PIPS and SDPS presents two different time scales of phase separation driven by two competing factors, polymerization and surface potential, for more sophisticated control of phase separating systems.
The classical model of phase separation dynamics in polymer blends integrates two key components: the thermodynamic driving force described by the Flory–Huggins56 theory of polymer mixing, and the macromolecular transport described by the Cahn–Hilliard57 formalism. The Flory–Huggins theory considers mean-field pairwise interactions between species, characterized by the Flory–Huggins χ parameter, which increases with the degree of immiscibility among different components.56 In symmetric, binary polymer blends with a degree of polymerization N, the Flory–Huggins theory predicts phase separation above a critical point at χN = 2, resulting in the formation of two phases; it delineates the thermodynamic state and driving force underlying this phase separation phenomenon.56 In contrast, the Cahn–Hilliard formalism captures the dynamics of phase separation in polymer systems at continuum length scales, offering insight into the non-equilibrium process leading to the phase-separated state. It is frequently applied to investigate phenomena like spinodal decomposition, material diffusion, and microstructure formation in a range of materials; alloys,58–60 polymers,61–66 and others.67,68
The Cahn–Hilliard formalism is a form of the diffusion equation integrated with a free energy functional, such as the Flory–Huggins mixing free energy, to simulate the temporal evolution of component densities. In polymer systems, the combination of Flory–Huggins and Cahn–Hilliard models has been extensively utilized for modeling both binary62–64 and ternary65,66,69 melt blends, in addition to polymer solutions.70–76 The Cahn–Hilliard approach offers a notable advantage in its ability to explore larger time and length scales compared to particle-based simulations. Moreover, it has been adapted and widely used to accommodate more complex systems, incorporating features such as reactions64,74,75,77–82 or coupling with other equations such as the Stokes equation.62,83,84 The Cahn–Hilliard formalism has provided key insights into the phase separation dynamics of polymer blends such as quantifying the evolution of concentration fluctuations into larger inhomogeneities during the early stages of phase separation in initially homogeneous and isotropic systems.85–88 It can also capture the late stage of phase separation driven by interfacial interactions including surface tension,85,89 where its characteristic scaling of size growth of phase separated domains corresponds to t1/3 (t is time).85,86,89–91
The Cahn–Hilliard equation is a robust tool for modeling and comprehending phase separation phenomena, and remains an active research field given its broad applicability and adaptability to accommodate complex physical scenarios.92,93 This versatility renders it particularly promising for modeling surface-directed phase separation (SDPS) and polymerization-induced phase separation (PIPS). In this study, we elucidate our approach of coupling a multicomponent Cahn–Hilliard model with surface potential which decays away from the surface during the process of linear step-growth polymerization involving two partially immiscible polymer species. By modeling the complete molecular weight distribution of both species, we explore the interplay among polymerization kinetics, surface potential and phase separation dynamics across all polymer lengths. This comprehensive approach explicitly accounts for the varying molecular mobilities and contributions to the mixing free energy inherent in different polymer lengths.
2. Methods
In this study, we modify our previously-developed polymerizing Cahn–Hilliard (pCH) model94 so that it incorporates the effect of surface and the preferential adsorption of one of the polymer species. We investigate a binary system with two different types of species α = A,B, with a volume fraction ϕα(r,t) that is a function of space r and time t. For a given species α, this volume fraction can be further divided into components of different molecular weight ϕα,Nα(r,t) such that and there is a molecular weight distribution wα(Nα,r,t) =ϕα,Nα(r,t)/ϕα(r,t). We assume that the monomers of both species α are bi-functional and polymerize in linear step-growth fashion with a constant reaction rate kα independent of molecular-weight.95 Our numerical simulation scheme evolves ϕα,Nα(r,t) over time and space through diffusion and polymerization from an initial state featuring a homogeneous mixture of monomers A and B(ϕA,1(r,0) = ϕB,1(r,0) = 0.5). All simulations are performed on a two-dimensional grid.
and there is a molecular weight distribution wα(Nα,r,t) =ϕα,Nα(r,t)/ϕα(r,t). We assume that the monomers of both species α are bi-functional and polymerize in linear step-growth fashion with a constant reaction rate kα independent of molecular-weight.95 Our numerical simulation scheme evolves ϕα,Nα(r,t) over time and space through diffusion and polymerization from an initial state featuring a homogeneous mixture of monomers A and B(ϕA,1(r,0) = ϕB,1(r,0) = 0.5). All simulations are performed on a two-dimensional grid.
2.1. Multi-component Cahn–Hilliard equation
The Cahn–Hilliard equation is used to predict the time-evolution of the component concentration fields, ϕα,Nα(r,t) = ϕi(r,t), in the context of phase separation for immiscible material blends.57 Based on the previously-developed model,94 we write the Cahn–Hilliard equation in a non-dimensional form: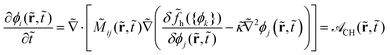 | (1) |
This equation is rendered non-dimensional via a reference mobility M0, a reference molecular weight N0, a reference distance L0, and a reference timescale t0 = L02/M0. In eqn (1), the indices i, j and k refer to both the species α and the specific degree of polymerization Nα for explicitly treating the polydispersity of each species. The Onsager coefficient ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ij is non-dimensionalized by the reference mobility M0 = kBT/6πaN0ζ; kBT, a and ζ represent thermal energy, effective hydrodynamic radius, and monomer friction coefficient, respectively. We treat as simply
ij is non-dimensionalized by the reference mobility M0 = kBT/6πaN0ζ; kBT, a and ζ represent thermal energy, effective hydrodynamic radius, and monomer friction coefficient, respectively. We treat as simply ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ij(
ij(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) = ϕi(
) = ϕi(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )Miδij/M0 = ϕi
)Miδij/M0 = ϕi![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) iδij under the Rouse dynamics assumption that mobility is inversely proportional to molecular weight (i.e. ∼ 1/Ni). Finally, we introduce a shorthand denoting the entire right-hand side of the first equation as
iδij under the Rouse dynamics assumption that mobility is inversely proportional to molecular weight (i.e. ∼ 1/Ni). Finally, we introduce a shorthand denoting the entire right-hand side of the first equation as ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) CH(
CH(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), which we later use in describing our numerical procedure combining the Cahn–Hilliard formalism with reaction kinetics.
), which we later use in describing our numerical procedure combining the Cahn–Hilliard formalism with reaction kinetics.
In our approach to modeling the thermodynamics of polymers, in addition to a surface potential Ṽ(r) we will discuss later, we consider a Flory–Huggins contribution to the homogeneous free energy density ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) h(
h(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) ) =
) = ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) FH(
FH(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) ) + Ṽ(
) + Ṽ(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) ) at position
) at position ![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) :94
:94
 | (2) |
This expression is normalized by the thermal energy kBT. NA,max and NB,max represent the maximum degrees of polymerization that are chosen for practical considerations, and beyond which polymers are assumed to diffuse similarly slowly, χ is the Flory–Huggins interaction parameter, and ξ is a compressibility parameter. We choose ξ = 100 as a suitably high value to ensure that  , while permitting small local fluctuations in concentration to enhance the numerical stability of our methodology. This deviation from traditional methods of solving the Cahn–Hilliard equation, which typically maintain strict mass conservation by evaluating n − 1 transport equations against a reference component,71–73,80,88,96 renders our approach more numerically manageable. This adaptation of
, while permitting small local fluctuations in concentration to enhance the numerical stability of our methodology. This deviation from traditional methods of solving the Cahn–Hilliard equation, which typically maintain strict mass conservation by evaluating n − 1 transport equations against a reference component,71–73,80,88,96 renders our approach more numerically manageable. This adaptation of ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) FH incorporates different degrees of polymerization NA or NB, treating them as distinct species characterized by their respective density fields, ϕA,NA and ϕB,NB, which independently contribute to the mixing entropy. Concurrently, the sum over fields A and B (i.e.
FH incorporates different degrees of polymerization NA or NB, treating them as distinct species characterized by their respective density fields, ϕA,NA and ϕB,NB, which independently contribute to the mixing entropy. Concurrently, the sum over fields A and B (i.e. ) impacts both the enthalpic χ term, and the incompressibility constraint.97
) impacts both the enthalpic χ term, and the incompressibility constraint.97
The gradient energy coefficient ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) is treated as a constant based on the Random Phase Approximation98–101 such that κ = b2/(36〈ϕA〉〈ϕB〉) where b denotes the Kuhn length, and we use the overall volume fractions of the species 〈ϕA〉 and 〈ϕB〉 for simplicity. This form of the square gradient term is notably approximate and independent of chain length; however, more sophisticated treatments would account for NA and NB that may be non-negligible for short chains and of interest for future studies.102 We do not expect those to be important for this compressible scheme, where gradients in one species do not directly imply gradients in the other species, but this may also be of interest for future studies. To keep the length scale consistent with the previous work,94 we keep
is treated as a constant based on the Random Phase Approximation98–101 such that κ = b2/(36〈ϕA〉〈ϕB〉) where b denotes the Kuhn length, and we use the overall volume fractions of the species 〈ϕA〉 and 〈ϕB〉 for simplicity. This form of the square gradient term is notably approximate and independent of chain length; however, more sophisticated treatments would account for NA and NB that may be non-negligible for short chains and of interest for future studies.102 We do not expect those to be important for this compressible scheme, where gradients in one species do not directly imply gradients in the other species, but this may also be of interest for future studies. To keep the length scale consistent with the previous work,94 we keep ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10 and a reference molecular weight of N0 = 10 to define the length scale L0 = C × RG,0 as a fraction C of the radius of gyration of the reference chain. Therefore, the use a reference chain length to render our equations dimensionless only sets the interfacial length scale versus the grid discretization, and not the relationship between chains of different lengths. Similarly, off-diagonal contributions to the square gradient term (i.e. relating the gradient of species A to species B) have been shown to be important for incompressible models.103 Thus, C depends on the choice of the reference chain length N0 such that the relationship C = [6〈ϕA〉〈ϕB〉
= 10 and a reference molecular weight of N0 = 10 to define the length scale L0 = C × RG,0 as a fraction C of the radius of gyration of the reference chain. Therefore, the use a reference chain length to render our equations dimensionless only sets the interfacial length scale versus the grid discretization, and not the relationship between chains of different lengths. Similarly, off-diagonal contributions to the square gradient term (i.e. relating the gradient of species A to species B) have been shown to be important for incompressible models.103 Thus, C depends on the choice of the reference chain length N0 such that the relationship C = [6〈ϕA〉〈ϕB〉![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) N0]−1/2 holds. The temporal and spatial dimensions of our model are constrained by the requirement for an adequately large κ to ensure numerical stability. Considering the typical length scales (i.e. a ∼ 0.5 nm) and based on prior definitions, we observe that phase separation occurs on the order of ca. 10 μs in our system.
N0]−1/2 holds. The temporal and spatial dimensions of our model are constrained by the requirement for an adequately large κ to ensure numerical stability. Considering the typical length scales (i.e. a ∼ 0.5 nm) and based on prior definitions, we observe that phase separation occurs on the order of ca. 10 μs in our system.
For real systems with longer polymers, the relevant time scales would naturally be extended, but our reaction rate constant ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) is considerably faster than those typically observed in experimental settings.95 We anticipate that the physical arguments presented in this paper should scale directly to experimentally relevant time scales.
is considerably faster than those typically observed in experimental settings.95 We anticipate that the physical arguments presented in this paper should scale directly to experimentally relevant time scales.
2.2. Surface
The presence of a surface significantly impacts the behavior of phase separation in polymer systems, playing a vital role in shaping the morphology and characteristics of the final material.1,2,4–20 In our scheme, we implement the Neumann boundary condition at![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1 and
= 1 and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = Z, where
= Z, where ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) denotes the x-coordinate of
denotes the x-coordinate of ![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) , and Z represents the number of discretized grids along both x- and y-directions, and is set to 64. This approach ensures no flux of polymers across the boundaries, effectively creating impenetrable surfaces at both ends of the x-axis. Conversely, we employ periodic boundary conditions along the y-direction.
, and Z represents the number of discretized grids along both x- and y-directions, and is set to 64. This approach ensures no flux of polymers across the boundaries, effectively creating impenetrable surfaces at both ends of the x-axis. Conversely, we employ periodic boundary conditions along the y-direction.
The Neumann condition at the x-boundaries can be expressed as:
 | (3) |
This combination of boundary conditions allows for the simulation of a confined system in the x-direction while maintaining periodicity in the y-direction, providing a robust framework for studying polymer dynamics under the presence of a surface.
2.3. Surface potential
Surfaces that exhibit energetically favorable interactions with only one species, polymer A, can induce different phase behaviors compared to those observed in the bulk. The characteristics of these interactions, whether attractive or repulsive, influence the adsorption, arrangement, and mobility of polymers on the surface, which may result in the preferential wetting of one component over another, thereby impacting the overall phase separation dynamics.1–7,24 For our simulation, we apply the surface potential Ṽ for only one surface at![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = θs = 1, and it exponentially decays away from the surface in the x-direction as follows:
= θs = 1, and it exponentially decays away from the surface in the x-direction as follows:Ṽ(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = Ṽ0exp(−γ( ) = Ṽ0exp(−γ(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) − θs)) − θs)) | (4) |
Here, the surface potential Ṽ is normalized by the thermal energy kBT. Ṽ0 is the initial surface potential at the surface (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = θs), and γ is the decaying strength of the potential. In this method, we choose γ = 0.2, for which Ṽ0 decays to less than 1 percent of its original value at
= θs), and γ is the decaying strength of the potential. In this method, we choose γ = 0.2, for which Ṽ0 decays to less than 1 percent of its original value at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 25. In other words, the decaying potential spans roughly two-fifths of the simulation box along the x-direction.
= 25. In other words, the decaying potential spans roughly two-fifths of the simulation box along the x-direction.
2.4. Polymerization kinetics
In our framework, polymers grow through linear step-growth polymerization, adhering to the rate laws for each chemical species α: | (5) |
The terms depicted on the right-hand side of the equation denote generation and consumption, respectively. We again introduce the shorthand ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) P for this term, to be used to describe our numerical calculation. In eqn (5),
P for this term, to be used to describe our numerical calculation. In eqn (5), ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = kt0/(ṽ0L03) represents the reaction rate, which is normalized using the reference timescale and length scales, and encompasses the dimensionless monomer volume ṽ0. The conversion from volume fraction to number densities is achieved by dividing volume fractions of corresponding polymers by Nα and N′α. In our scheme, we impose a restriction on the upper limit of the molecular weight distribution, Nα,max, which has only minor quantitative effects on our results. For the linear step-growth polymerization, we adhere to the standard assumption that
= kt0/(ṽ0L03) represents the reaction rate, which is normalized using the reference timescale and length scales, and encompasses the dimensionless monomer volume ṽ0. The conversion from volume fraction to number densities is achieved by dividing volume fractions of corresponding polymers by Nα and N′α. In our scheme, we impose a restriction on the upper limit of the molecular weight distribution, Nα,max, which has only minor quantitative effects on our results. For the linear step-growth polymerization, we adhere to the standard assumption that ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) remains constant throughout the simulation, independent of molecular weight.95
remains constant throughout the simulation, independent of molecular weight.95
The polymer concentration field evolves over time via both diffusion and local extent of polymerization. To account for both of these process, we consider a straightforward combination of both eqn (1) and (5), that sequentially evaluates the change in polymer density at each time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) and location
and location ![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) . We write our time-evolution scheme as:
. We write our time-evolution scheme as:
ϕα,Nα(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) + Δ + Δ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) = ϕα,Nα( ) = ϕα,Nα(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) + Δ ) + Δ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) [ [![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) CH( CH(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) + ) + ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) P( P(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )] )] | (6) |
In this case, the change in density fields based on the Cahn–Hilliard equation and the polymerization rate laws are independently added to give the overall change in field densities.
In this work, we comprehensively examine the full range of molecular weights, enabling us to explore the entire mass distribution function wA(NA,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) as a function of
) as a function of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) . Furthermore, our model incorporates an assessment of the reaction kinetics associated with step-growth polymerization by monitoring various metrics, including both the number-averaged 〈NA〉n and weight-averaged 〈NA〉w degree of polymerization of the A-component, as well as the entire distribution function wA(NA,r,t). Finally, we utilize equal reaction rates for both species (i.e.
. Furthermore, our model incorporates an assessment of the reaction kinetics associated with step-growth polymerization by monitoring various metrics, including both the number-averaged 〈NA〉n and weight-averaged 〈NA〉w degree of polymerization of the A-component, as well as the entire distribution function wA(NA,r,t). Finally, we utilize equal reaction rates for both species (i.e. ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) A =
A = ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) B, such that the system is symmetric) and data for each set of parameters reported represents an average over 30 independent trajectories.
B, such that the system is symmetric) and data for each set of parameters reported represents an average over 30 independent trajectories.
3 Results
With our pCH model, we study polymerization-induced phase separation under the effect of surface potential which decays away from the surface. We consider symmetric blends where both A and B species exhibit the same polymerization rate constant![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , and the only difference is how they are affected by the surface potential Ṽ. This complex process is quantified and characterized by using the degree of phase separation ψ(
, and the only difference is how they are affected by the surface potential Ṽ. This complex process is quantified and characterized by using the degree of phase separation ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), degree of anisotropy E(
), degree of anisotropy E(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), overarching order parameter ω(
), overarching order parameter ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), and ordering transition point
), and ordering transition point ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). First, ψ(
). First, ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is defined as:
) is defined as: | (7) |
The angle brackets indicate a spatial average. This expression reflects the difference in local volume fractions between two different components, averaging and normalizing over the entire space to yield a number between ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) = 0 and 1. A fully homogeneous system holds the relationship 〈ϕA(
) = 0 and 1. A fully homogeneous system holds the relationship 〈ϕA(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )ϕB(
)ϕB(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )〉 = 〈ϕA(
)〉 = 〈ϕA(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )〉〈ϕB(
)〉〈ϕB(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )〉 such that ψ(
)〉 such that ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) = 0. In a fully phase-separated system, the values of ψ(
) = 0. In a fully phase-separated system, the values of ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is nearly 1 since ϕA(
) is nearly 1 since ϕA(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) or ϕB(
) or ϕB(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is close to zero, making the second term vanish in eqn (7). Thus, a phase separation process will proceed from the ψ(
) is close to zero, making the second term vanish in eqn (7). Thus, a phase separation process will proceed from the ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) value of 0 toward 1 over time; the endpoint is determined by the phase separation intensity and the interface width between the two bulk phases. In addition, we similarly define ψx(
) value of 0 toward 1 over time; the endpoint is determined by the phase separation intensity and the interface width between the two bulk phases. In addition, we similarly define ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ):
):
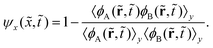 | (8) |
ψ
x
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is averaged over only the y-direction to measure the degree of phase separation in one slice at each fixed
) is averaged over only the y-direction to measure the degree of phase separation in one slice at each fixed ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) value, unlike the overall degree of phase separation ψ(
value, unlike the overall degree of phase separation ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) which is averaged over all space. Fig. 1a exhibits phase separation behavior along the x-direction from one surface (
) which is averaged over all space. Fig. 1a exhibits phase separation behavior along the x-direction from one surface (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1) to the other (
= 1) to the other (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 60); the time advances from red (
= 60); the time advances from red (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0) to purple (
= 0) to purple (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp), where τp is the phase separation time for the system to reach ψ(τp) = 0.4. This arbitrary choice for the definition of τp is a heuristic that we find useful for quantifying the overall kinetics of phase separation, though is not specific to the surface-driven processes that we will consider in more detail later in this article. Fig. 1a plots ψx(
= τp), where τp is the phase separation time for the system to reach ψ(τp) = 0.4. This arbitrary choice for the definition of τp is a heuristic that we find useful for quantifying the overall kinetics of phase separation, though is not specific to the surface-driven processes that we will consider in more detail later in this article. Fig. 1a plots ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) versus
) versus ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) for several time points
for several time points ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , and shows how the phase separation evolves. To be more specific, near
, and shows how the phase separation evolves. To be more specific, near ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1, ψx(
= 1, ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) rises quickly because the surface potential attracts the preferred species type A and induces phase separation, whereas in the “bulk” (
) rises quickly because the surface potential attracts the preferred species type A and induces phase separation, whereas in the “bulk” (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40), it phase separates based on polymerization rather than surface potential due to its exponential decay. The strength of phase separation ψx(
= 40), it phase separates based on polymerization rather than surface potential due to its exponential decay. The strength of phase separation ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is weaker at
) is weaker at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40 than
= 40 than ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1, which we attribute to the decay of the surface potential. At
= 1, which we attribute to the decay of the surface potential. At ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40, the system effectively reproduces the bulk phase separation behavior unaffected by the surface potential. The smooth fluctuation in ψx(
= 40, the system effectively reproduces the bulk phase separation behavior unaffected by the surface potential. The smooth fluctuation in ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp) near the surface potential (
= τp) near the surface potential (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) < 20) is due to the presence of alternating interfaces between lamellar-like stripes, where eqn (8) outputs quantities close to 0 for ψx(
< 20) is due to the presence of alternating interfaces between lamellar-like stripes, where eqn (8) outputs quantities close to 0 for ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at interfaces (e.g. 〈ϕA(
) at interfaces (e.g. 〈ϕA(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )〉y = 0.5) and are not considered “phase separated” with this metric. Eqn (8) thus does not distinguish a locally well-mixed regime from the interface between phase separated domains, because their 〈ϕA(
)〉y = 0.5) and are not considered “phase separated” with this metric. Eqn (8) thus does not distinguish a locally well-mixed regime from the interface between phase separated domains, because their 〈ϕA(![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )〉 values are the same. Although ψx(
)〉 values are the same. Although ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is a useful parameter to measure the degree of phase separation, it does not quantify the anisotropic ordering behavior arising from the surface potential.
) is a useful parameter to measure the degree of phase separation, it does not quantify the anisotropic ordering behavior arising from the surface potential.
To measure the extent to which phase separation driven by the surface potential produces an anisotropic concentration wave perpendicular to the surface and quantify this anisotropic ordering behavior, we introduce a value that quantifies the degree of anisotropy Ex(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ):104
):104
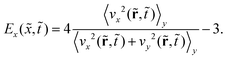 | (9) |
Here,  and
and  where ux and uy are the unit vectors in the x- and y-direction, respectively. Ex(
where ux and uy are the unit vectors in the x- and y-direction, respectively. Ex(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) ranges from −1 to 1 for isotropic and anisotropic ordering structures, respectively, along the direction perpendicular to the potential surface; it is averaged over y-direction similar to ψx(
) ranges from −1 to 1 for isotropic and anisotropic ordering structures, respectively, along the direction perpendicular to the potential surface; it is averaged over y-direction similar to ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). Fig. 1b illustrates Ex(
). Fig. 1b illustrates Ex(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) for multiple representative simulation times
) for multiple representative simulation times ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , depicting the progressive ordering behavior extending from the surface potential (
, depicting the progressive ordering behavior extending from the surface potential (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1) into the bulk towards the other surface (
= 1) into the bulk towards the other surface (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1) over time. We find that there is a big jump from the initial time in Fig. 1b reflecting the weak initial ordering behavior induced by the surface potential at
= 1) over time. We find that there is a big jump from the initial time in Fig. 1b reflecting the weak initial ordering behavior induced by the surface potential at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1 whereas the regime near the surface on the other side (
= 1 whereas the regime near the surface on the other side (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 60) does not show anisotropic ordering behavior. However, Fig. 1b alone does not provide any information about the intensity of phase separation. In order to convey the details of both order parameters ψx(
= 60) does not show anisotropic ordering behavior. However, Fig. 1b alone does not provide any information about the intensity of phase separation. In order to convey the details of both order parameters ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) and Ex(
) and Ex(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), and quantify directional phase separation caused by the surface potential, we introduce an overarching order parameter ω(
), and quantify directional phase separation caused by the surface potential, we introduce an overarching order parameter ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) as follows:
) as follows:
ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) =Ex( ) =Ex(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) ×ψx( ) ×ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). ). | (10) |
ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is introduced to capture both the phase separation and the anisotropic structure; ω(
) is introduced to capture both the phase separation and the anisotropic structure; ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at −1, 0 and 1 indicates isotropic full phase separation, no phase separation, and anisotropic full phase separation, respectively. Fig. 1c shows significant anisotropic phase separation near the surface potential at
) at −1, 0 and 1 indicates isotropic full phase separation, no phase separation, and anisotropic full phase separation, respectively. Fig. 1c shows significant anisotropic phase separation near the surface potential at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≈ 5 as indicated by an increasing ω(
≈ 5 as indicated by an increasing ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), while isotropic phase separation in the bulk is found near
), while isotropic phase separation in the bulk is found near ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40 as indicated by the negative growth of ω(
= 40 as indicated by the negative growth of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). This is consistent with the corresponding concentration profiles exhibiting the behavior of surface-directed spinodal decomposition near the surface potential (
). This is consistent with the corresponding concentration profiles exhibiting the behavior of surface-directed spinodal decomposition near the surface potential (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1) shown in Fig. 1d. We note that a surface excess of A could also lead to a positive value of ω(
= 1) shown in Fig. 1d. We note that a surface excess of A could also lead to a positive value of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), though all χ ≠ 0 cases considered in this manuscript are at values of χN that quickly exceed the critical (χN)crit = 2.0 where symmetric binary blends will spontaneously phase separate. This approach allows us to consider the interplay between surface potential and polymerization, which gets more complex as phase separation is competitively driven by both the surface potential and polymerization. ω(
), though all χ ≠ 0 cases considered in this manuscript are at values of χN that quickly exceed the critical (χN)crit = 2.0 where symmetric binary blends will spontaneously phase separate. This approach allows us to consider the interplay between surface potential and polymerization, which gets more complex as phase separation is competitively driven by both the surface potential and polymerization. ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) = 0 near the potential surface also allows us to characterize the ordering transition point,
) = 0 near the potential surface also allows us to characterize the ordering transition point, ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), at which bulk (isotropic) and lamellar-like (anisotropic) phase separation regimes intersect (
), at which bulk (isotropic) and lamellar-like (anisotropic) phase separation regimes intersect (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≈ 15) as shown in Fig. 1c and d. Measuring
≈ 15) as shown in Fig. 1c and d. Measuring ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) provides insight into the effective potential range at which the concentration wave, induced by the potential surface, predominantly decays. This measurement also offers information about the isotropic–anisotropic transition in the system as shown in Fig. 1d.
) provides insight into the effective potential range at which the concentration wave, induced by the potential surface, predominantly decays. This measurement also offers information about the isotropic–anisotropic transition in the system as shown in Fig. 1d.
The consideration of quantities ψx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), Ex(
), Ex(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), ω(
), ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), and
), and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) enables us to elucidate the interconnected roles of the Flory–Huggins interaction parameter, the reaction rate, and the surface potential in determining their impacts on the phase separation behavior under polymerization and selective surface.
) enables us to elucidate the interconnected roles of the Flory–Huggins interaction parameter, the reaction rate, and the surface potential in determining their impacts on the phase separation behavior under polymerization and selective surface.
3.1. Effect of surface potential strength Ṽ0
We first consider how the surface potential strength affects the degree of phase separation ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), and the effective potential range
), and the effective potential range ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) over time. Here, we keep other parameters such as χ and
) over time. Here, we keep other parameters such as χ and ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) the same to isolate the effect of the potential strength.
the same to isolate the effect of the potential strength.
Starting with the effect of the potential strength on phase separation time, we plot the time-evolution of ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) for various Ṽ0 values including no potential case (Ṽ0 = 0) in Fig. 2a. In the case of Ṽ0 = 0, the phase separation is purely driven by the polymerization which increases the free energetic penalty for longer polymers to remain mixed. For sufficiently long polymer chains, a large value of χN leads to spontaneous phase separation. However, in a system with surface potential, not only the polymerization but also the surface potential plays a role as the driving force for phase separation, suggesting a competition between the two driving forces. In Fig. 2a, as Ṽ0 increases, phase separation occurs at earlier times
) for various Ṽ0 values including no potential case (Ṽ0 = 0) in Fig. 2a. In the case of Ṽ0 = 0, the phase separation is purely driven by the polymerization which increases the free energetic penalty for longer polymers to remain mixed. For sufficiently long polymer chains, a large value of χN leads to spontaneous phase separation. However, in a system with surface potential, not only the polymerization but also the surface potential plays a role as the driving force for phase separation, suggesting a competition between the two driving forces. In Fig. 2a, as Ṽ0 increases, phase separation occurs at earlier times ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , indicating the higher potential strength drives enhanced molecular transport towards the surface by preferentially attracting one species and prompting an earlier rise of ψ(
, indicating the higher potential strength drives enhanced molecular transport towards the surface by preferentially attracting one species and prompting an earlier rise of ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). We note that, in the absence of a driving force for phase separation (i.e. χN = 0.0), ψ ∼
). We note that, in the absence of a driving force for phase separation (i.e. χN = 0.0), ψ ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−3) remains very small and there is only a slight increase in the A species at the surface.
(10−3) remains very small and there is only a slight increase in the A species at the surface.
 | ||
Fig. 2 (a) ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) over different Ṽ0 at constant χ = 0.8 and ) over different Ṽ0 at constant χ = 0.8 and ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−3. Phase separation starts earlier as Ṽ0 increases. (b) ω( = 10−3. Phase separation starts earlier as Ṽ0 increases. (b) ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at a specific time ) at a specific time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 10 × 105 from Fig. 2a. For Ṽ0 = 0, only isotropic phase separation occurs whereas systems with surface potential produces anisotropic phase separation closer to surface potential ( = 10 × 105 from Fig. 2a. For Ṽ0 = 0, only isotropic phase separation occurs whereas systems with surface potential produces anisotropic phase separation closer to surface potential (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1). (c) Higher Ṽ0 increases the anisotropic–isotropic transition front = 1). (c) Higher Ṽ0 increases the anisotropic–isotropic transition front ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0( ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) (i.e. larger anisotropic regime near the surface potential), which gradually increases over time as the concentration wave propagates further into the bulk. ) (i.e. larger anisotropic regime near the surface potential), which gradually increases over time as the concentration wave propagates further into the bulk. | ||
Then, we further investigate how anisotropic phase separation emerges in the x-direction at a specific time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 10 × 105 denoted by the black dashed line in Fig. 2a. At
= 10 × 105 denoted by the black dashed line in Fig. 2a. At ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 10 × 105, we plot ω(
= 10 × 105, we plot ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) in Fig. 2b; ω(
) in Fig. 2b; ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) > 0 represents anisotropic lamellar-like phase separation in the direction perpendicular to the potential surface, and ω(
) > 0 represents anisotropic lamellar-like phase separation in the direction perpendicular to the potential surface, and ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) < 0 indicates isotropic phase separation with no specific directionality. For the zero-potential case (Ṽ0 = 0) in Fig. 2b, the system exhibits purely isotropic phase separation (ω(
) < 0 indicates isotropic phase separation with no specific directionality. For the zero-potential case (Ṽ0 = 0) in Fig. 2b, the system exhibits purely isotropic phase separation (ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) < 0), whereas systems with the potential Ṽ0 > 0 show strong alignment (ω(
) < 0), whereas systems with the potential Ṽ0 > 0 show strong alignment (ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) > 0) near the potential surface (
) > 0) near the potential surface (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1). In this case, ω(
= 1). In this case, ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) gradually decreases below zero away from the potential surface, entering the “bulk” regime where the system phase separates isotropically. Moreover, the strength of the potential does not affect the intensity of ω(
) gradually decreases below zero away from the potential surface, entering the “bulk” regime where the system phase separates isotropically. Moreover, the strength of the potential does not affect the intensity of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) in the bulk regime (
) in the bulk regime (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ∼ 40) as shown in Fig. 2b.
∼ 40) as shown in Fig. 2b.
Lastly, we characterize the thickness of the anisotropic regime by the quantity ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) for different Ṽ0 values to examine the extent of surface-guided phase separation over time;
) for different Ṽ0 values to examine the extent of surface-guided phase separation over time; ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) describes when ω(
) describes when ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = 0 (i.e. intersects with the black dashed line in Fig. 2b). Fig. 2c shows the time-evolution of
) = 0 (i.e. intersects with the black dashed line in Fig. 2b). Fig. 2c shows the time-evolution of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), demonstrating that stronger Ṽ0 initially produces a thicker anisotropic regime, and the subsequent growth with time is similar such that this initial offset persists regardless of the Ṽ0 values.
), demonstrating that stronger Ṽ0 initially produces a thicker anisotropic regime, and the subsequent growth with time is similar such that this initial offset persists regardless of the Ṽ0 values.
3.2. Effect of polymer incompatibility χ
We now consider how the Flory–Huggins parameter χ governing the polymer incompatibility changes the degree of phase separation ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), and possibly competes with surface potential as the driving force for phase separation.
), and possibly competes with surface potential as the driving force for phase separation.
To investigate the effect of polymer incompatibility on phase separation under the surface potential, we plot the time evolution of ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) for three representative values of χ in Fig. 3. First, we show that larger χ values promote faster phase separation regardless of surface potential Ṽ0 at a constant reaction rate
) for three representative values of χ in Fig. 3. First, we show that larger χ values promote faster phase separation regardless of surface potential Ṽ0 at a constant reaction rate ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) . In terms of Ṽ0 at each χ, we observe a similar trend of ψ(
. In terms of Ṽ0 at each χ, we observe a similar trend of ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) with increasing Ṽ0 relative to its corresponding zero-potential system (Ṽ0 = 0). For a surface potential of Ṽ0 = 10−3, the phase separation begins slightly earlier, as indicated by the earlier rise in ψ(
) with increasing Ṽ0 relative to its corresponding zero-potential system (Ṽ0 = 0). For a surface potential of Ṽ0 = 10−3, the phase separation begins slightly earlier, as indicated by the earlier rise in ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). As Ṽ0 increases gradually from 0 to 10−1, the influence of the surface potential becomes more pronounced. This enhances anisotropic phase separation (or wetting) behavior, leading to faster phase separation. Interestingly, the impact of Ṽ0 is more significant for systems with lower χ. In these systems, weaker polymer incompatibility delays the phase separation because sufficient polymerization and the formation of larger chains are required to drive phase separation. This extended timescale allows the surface potential to attract more components, amplifying its effect on phase separation.
). As Ṽ0 increases gradually from 0 to 10−1, the influence of the surface potential becomes more pronounced. This enhances anisotropic phase separation (or wetting) behavior, leading to faster phase separation. Interestingly, the impact of Ṽ0 is more significant for systems with lower χ. In these systems, weaker polymer incompatibility delays the phase separation because sufficient polymerization and the formation of larger chains are required to drive phase separation. This extended timescale allows the surface potential to attract more components, amplifying its effect on phase separation.
3.3. Effect of reaction rate ![[k with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_006b_0303.gif)
Fig. 4 is the compilation of the order parameter ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) for wide ranges of
) for wide ranges of ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and Ṽ0 values at fixed χ of 1.0. In Fig. 4, each row and column shares the same Ṽ0 and
and Ṽ0 values at fixed χ of 1.0. In Fig. 4, each row and column shares the same Ṽ0 and ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , respectively. The rainbow color gradient represents the progression of time, transitioning from red (
, respectively. The rainbow color gradient represents the progression of time, transitioning from red (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0) to purple (
= 0) to purple (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp), where τp is defined to characterize the phase separation time at ψ(
= τp), where τp is defined to characterize the phase separation time at ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) = 0.4.
) = 0.4.
 | ||
Fig. 4 The compilation of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) under different conditions of Ṽ0 and ) under different conditions of Ṽ0 and ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) at constant χ = 1.0. Each row and column shares the same Ṽ0 and at constant χ = 1.0. Each row and column shares the same Ṽ0 and ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , respectively. For all 16 sub-Fig. 4a–p, the rainbow color gradient represents the progression of time, transitioning from red ( , respectively. For all 16 sub-Fig. 4a–p, the rainbow color gradient represents the progression of time, transitioning from red (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0) to purple ( = 0) to purple (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp) denoted with an arrow in Fig. 4m. For the zero-potential systems shown in (a) to (d), systems only isotopically phase separate (ω( = τp) denoted with an arrow in Fig. 4m. For the zero-potential systems shown in (a) to (d), systems only isotopically phase separate (ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) < 0) due to the absence of surface potential. With the surface potential shown in (e) to (p), systems develop positive values of ω( ) < 0) due to the absence of surface potential. With the surface potential shown in (e) to (p), systems develop positive values of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) near the surface potential ( ) near the surface potential (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1). For Ṽ0 > 0, higher Ṽ0 induces faster phase separation near the surface potential ( = 1). For Ṽ0 > 0, higher Ṽ0 induces faster phase separation near the surface potential (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1); the spatiotemporal evolution of ω( = 1); the spatiotemporal evolution of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) from red ( ) from red (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0) to next lighter red appears more clearly regardless of = 0) to next lighter red appears more clearly regardless of ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) . At a reaction rate of . At a reaction rate of ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−5 in (e), (i) and (m), anisotropic phase separation dominantly propagates and induces ordering behavior (ω( = 10−5 in (e), (i) and (m), anisotropic phase separation dominantly propagates and induces ordering behavior (ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) > 0) throughout the system. Such enhanced penetration is attributed to the prevalent smaller molecules with higher mobility at lower reaction rate ) > 0) throughout the system. Such enhanced penetration is attributed to the prevalent smaller molecules with higher mobility at lower reaction rate ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−5. Furthermore, the difference in timescales between surface-directed and polymerization-induced phase separation plays a pivotal role; the system rapidly reaches τp due to surface-driven phase separation before polymerization-induced phase separation occurs. When increasing = 10−5. Furthermore, the difference in timescales between surface-directed and polymerization-induced phase separation plays a pivotal role; the system rapidly reaches τp due to surface-driven phase separation before polymerization-induced phase separation occurs. When increasing ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , a weaker “wetting” behavior occurs near the surface potential. This phenomena is due to rapid emergence of larger chains with low mobility and rapid consumption of smaller molecules at higher , a weaker “wetting” behavior occurs near the surface potential. This phenomena is due to rapid emergence of larger chains with low mobility and rapid consumption of smaller molecules at higher ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) . In this regard, at lower . In this regard, at lower ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) values, the extended lifetime of smaller chains enhances polymer diffusion under the influence of surface potential. values, the extended lifetime of smaller chains enhances polymer diffusion under the influence of surface potential. | ||
First, in Fig. 4, we find that the evolution from the initial profile (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0) to the subsequent one is higher for larger Ṽ0. In other words, larger Ṽ0 initially induces stronger accumulation of the preferred species, ϕA, at the potential surface
= 0) to the subsequent one is higher for larger Ṽ0. In other words, larger Ṽ0 initially induces stronger accumulation of the preferred species, ϕA, at the potential surface ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1 (i.e. faster growth of ω(
= 1 (i.e. faster growth of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) near
) near ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1) regardless of the reaction rate. This stronger attraction of ϕA from a higher surface potential Ṽ0 leads to faster transport and phase separation, and thus smaller τp as shown in Fig. 2a and 5, respectively.
= 1) regardless of the reaction rate. This stronger attraction of ϕA from a higher surface potential Ṽ0 leads to faster transport and phase separation, and thus smaller τp as shown in Fig. 2a and 5, respectively.
The analysis of varying reaction rates ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) in Fig. 4 reveals several key trends. As
in Fig. 4 reveals several key trends. As ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) decreases, the generation of larger chains capable of driving phase separation slows down. This results in reduced intensity for ω(
decreases, the generation of larger chains capable of driving phase separation slows down. This results in reduced intensity for ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) < 0 near
) < 0 near ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40 at
= 40 at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp. At sufficiently low
= τp. At sufficiently low ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) values, surface potential-driven phase separation becomes the dominant mechanism before
values, surface potential-driven phase separation becomes the dominant mechanism before ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp, as evidenced in Fig. 4e, i and m. Notably, systems with surface potential (Ṽ0 > 0) at
= τp, as evidenced in Fig. 4e, i and m. Notably, systems with surface potential (Ṽ0 > 0) at ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−5 predominantly display ω(
= 10−5 predominantly display ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) ≥ 0 for all
) ≥ 0 for all ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) and
and ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , indicating no isotropic phase separation prior to τp. In contrast, increasing
, indicating no isotropic phase separation prior to τp. In contrast, increasing ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) leads to rapid formation of larger polymers, resulting in a decrease in mobility and reduced polymer attraction to the surface potential as shown in Fig. 4. Moreover, Fig. 4k shows a unique behavior; the system at
leads to rapid formation of larger polymers, resulting in a decrease in mobility and reduced polymer attraction to the surface potential as shown in Fig. 4. Moreover, Fig. 4k shows a unique behavior; the system at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp (purple) shows contraction near the surface potential instead of further expansion toward the bulk (i.e. reduction of
= τp (purple) shows contraction near the surface potential instead of further expansion toward the bulk (i.e. reduction of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )). This indicates merging of two thin layers of the lamellar-like domain into one thicker layer.
)). This indicates merging of two thin layers of the lamellar-like domain into one thicker layer.
In Fig. 5, to compare each τp which corresponds to the last purple curve of each sub-figure in Fig. 4, we plot τp for various combinations of ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and Ṽ0 along with the zero-potential case (Ṽ0 = 0). The observed trends across the parameter space are consistent for both diffusion-limited and reaction-limited regimes. For
and Ṽ0 along with the zero-potential case (Ṽ0 = 0). The observed trends across the parameter space are consistent for both diffusion-limited and reaction-limited regimes. For ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) > 10−4, the system exhibits diffusion-limited behavior, as shown in Fig. 5. In this regime, increasing the reaction rate
> 10−4, the system exhibits diffusion-limited behavior, as shown in Fig. 5. In this regime, increasing the reaction rate ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) leads to a longer characteristic phase separation time, τp. We attribute this phenomena to the rapid accumulation of larger polymer chains with higher NA, which significantly slows down molecular diffusion (∝ 1/N). Here, the influence of the surface potential Ṽ0 remains consistent across different
leads to a longer characteristic phase separation time, τp. We attribute this phenomena to the rapid accumulation of larger polymer chains with higher NA, which significantly slows down molecular diffusion (∝ 1/N). Here, the influence of the surface potential Ṽ0 remains consistent across different ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) values, but the changes in τp are minimal. This is expected because, in a diffusion-limited regime, molecular diffusion driven by the surface potential is also restricted and cannot effectively attract long, less-mobile polymers. Conversely, in a reaction-limited regime (
values, but the changes in τp are minimal. This is expected because, in a diffusion-limited regime, molecular diffusion driven by the surface potential is also restricted and cannot effectively attract long, less-mobile polymers. Conversely, in a reaction-limited regime (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ⪅ 10−4), the phase separation time τp decreases with increasing
⪅ 10−4), the phase separation time τp decreases with increasing ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) . In this scenario, the driving force from polymer incompatibility rapidly intensifies with higher
. In this scenario, the driving force from polymer incompatibility rapidly intensifies with higher ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , enhancing the rate of phase separation. Unlike in the diffusion-limited regime, the surface potential Ṽ0 significantly impacts the phase separation time τp in a reaction-limited regime, as illustrated in Fig. 5. This is because lower
, enhancing the rate of phase separation. Unlike in the diffusion-limited regime, the surface potential Ṽ0 significantly impacts the phase separation time τp in a reaction-limited regime, as illustrated in Fig. 5. This is because lower ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) values extend the lifetime of smaller chains, making the surface potential more effective due to both the higher mobility and the prolonged lifetime of these smaller molecules. To be more specific, this is attributed to the potential-induced, selective attraction of ϕA to the surface, which allows for faster diffusive transport when the molecular weight is low (i.e. at the early stages of phase separation) and leads to an earlier onset of phase separation. As a result, the initial phase separation, driven by the surface potential, intensifies and grows away from the surface in layers. This continues until the average degree of polymerization increases sufficiently through polymerization to further drive phase separation. In essence, the surface potential compensates for the times over which phase separation does not occur due to slower polymerization, resulting in a more pronounced phase separation at smaller
values extend the lifetime of smaller chains, making the surface potential more effective due to both the higher mobility and the prolonged lifetime of these smaller molecules. To be more specific, this is attributed to the potential-induced, selective attraction of ϕA to the surface, which allows for faster diffusive transport when the molecular weight is low (i.e. at the early stages of phase separation) and leads to an earlier onset of phase separation. As a result, the initial phase separation, driven by the surface potential, intensifies and grows away from the surface in layers. This continues until the average degree of polymerization increases sufficiently through polymerization to further drive phase separation. In essence, the surface potential compensates for the times over which phase separation does not occur due to slower polymerization, resulting in a more pronounced phase separation at smaller ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) .
.
To characterize the timescales between diffusion and reaction, the Damköhler number Da is defined:
 | (11) |
Here, ζ0 is the friction coefficient. At ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−4, Da = 0.15, which denotes a reaction-limited regime where polymerization occurs slowly with respect to diffusion and phase separation. In the absence of the surface potential, this leads to longer τp as the rate
= 10−4, Da = 0.15, which denotes a reaction-limited regime where polymerization occurs slowly with respect to diffusion and phase separation. In the absence of the surface potential, this leads to longer τp as the rate ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) decreases due to the slow polymerization of chains that must be sufficiently long before phase separation can occur. In Fig. 5, the surface potential drives phase separation for
decreases due to the slow polymerization of chains that must be sufficiently long before phase separation can occur. In Fig. 5, the surface potential drives phase separation for ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ≤ 10−4, thus the phase separation process is not limited by the extent of reaction; rather lower
≤ 10−4, thus the phase separation process is not limited by the extent of reaction; rather lower ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) indirectly helps the process by not rapidly producing heavier polymers which will hinder the phase separation. Conversely, at
indirectly helps the process by not rapidly producing heavier polymers which will hinder the phase separation. Conversely, at ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−3 or Da = 1.5, the system is in a diffusion-limited regime (
= 10−3 or Da = 1.5, the system is in a diffusion-limited regime (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) > 10−4) as shown in Fig. 5. In this scenario, the surface potential slightly enhances the phase separation by preferentially attracting molecules but does not make a significant difference due to rapid accumulation of heavier chains from faster polymerization, leading to overall slower dynamics.
> 10−4) as shown in Fig. 5. In this scenario, the surface potential slightly enhances the phase separation by preferentially attracting molecules but does not make a significant difference due to rapid accumulation of heavier chains from faster polymerization, leading to overall slower dynamics.
We also provide ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) over different rates of reaction at Ṽ0 = 10−3 in Fig. 6a with the corresponding molecular weight distribution wA at
) over different rates of reaction at Ṽ0 = 10−3 in Fig. 6a with the corresponding molecular weight distribution wA at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 2 × 105 in Fig. 6b to examine the most abundant species with length NA and its behavior at the onset of phase separation. Fig. 6a illustrates how the phase separation parameter ψ(
= 2 × 105 in Fig. 6b to examine the most abundant species with length NA and its behavior at the onset of phase separation. Fig. 6a illustrates how the phase separation parameter ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) varies with the reaction rate
) varies with the reaction rate ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , contrasting with the dependency on the Flory–Huggins parameter χ shown in Fig. 3. At a fixed surface potential Ṽ0, two distinct trends emerge as previously identified in Fig. 5. Notably, for the system with
, contrasting with the dependency on the Flory–Huggins parameter χ shown in Fig. 3. At a fixed surface potential Ṽ0, two distinct trends emerge as previously identified in Fig. 5. Notably, for the system with ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−5, indicated by the red color in Fig. 6a, phase separation is significantly delayed despite the presence of a surface potential. This delay is attributed to the competition between surface potential and the free energy of polymer mixing, where the surface potential strength (Ṽ0 = 10−3) is insufficient to overcome the mixing free energy. Additionally, at this low reaction rate, polymer chains grow very slowly, maintaining miscibility for an extended period. This observation aligns with findings that systems with Ṽ0 = 10−3 behave similarly to zero-potential systems regarding phase separation onset, as depicted in Fig. 3. It is further supported by the slow evolution of molecular weight distribution shown in Fig. 6b. Consistent with our observation, the molecular weight distribution wA in Fig. 6b indicates that the smaller chains are abundant for lower
= 10−5, indicated by the red color in Fig. 6a, phase separation is significantly delayed despite the presence of a surface potential. This delay is attributed to the competition between surface potential and the free energy of polymer mixing, where the surface potential strength (Ṽ0 = 10−3) is insufficient to overcome the mixing free energy. Additionally, at this low reaction rate, polymer chains grow very slowly, maintaining miscibility for an extended period. This observation aligns with findings that systems with Ṽ0 = 10−3 behave similarly to zero-potential systems regarding phase separation onset, as depicted in Fig. 3. It is further supported by the slow evolution of molecular weight distribution shown in Fig. 6b. Consistent with our observation, the molecular weight distribution wA in Fig. 6b indicates that the smaller chains are abundant for lower ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and the systems accumulate larger chains more as
and the systems accumulate larger chains more as ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) increases; wA shows which length of polymer is the primary participant in the phase separation process at early time (
increases; wA shows which length of polymer is the primary participant in the phase separation process at early time (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 2 × 105). Thus, we attribute an earlier rise of ψ(
= 2 × 105). Thus, we attribute an earlier rise of ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) for lower
) for lower ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) to the surface potential which drives the diffusion of unreacted smaller molecules as shown in Fig. 6b, which results in enhanced phase separation as depicted in Fig. 2a, 3 and 5.
to the surface potential which drives the diffusion of unreacted smaller molecules as shown in Fig. 6b, which results in enhanced phase separation as depicted in Fig. 2a, 3 and 5.
 | ||
Fig. 6 (a) The effect of reaction rate ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) on ψ( on ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at constant Ṽ0 = 10−3 and χ= 1.0. (a) shows consistency with previous observations in Fig. 5 that the initial increase in ) at constant Ṽ0 = 10−3 and χ= 1.0. (a) shows consistency with previous observations in Fig. 5 that the initial increase in ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) leads to faster phase separation but further increase slows down phase separation. (b) shows molecular weight distribution wA at leads to faster phase separation but further increase slows down phase separation. (b) shows molecular weight distribution wA at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 2 × 105 in Fig. 6a. It describes the distribution of chain lengths participating in a phase separation process at the moment. This supports the findings that higher = 2 × 105 in Fig. 6a. It describes the distribution of chain lengths participating in a phase separation process at the moment. This supports the findings that higher ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) in a diffusion-hindered regime leads to a longer phase separation time because rapid accumulation of larger chains hinder diffusion and phase separation, and higher in a diffusion-hindered regime leads to a longer phase separation time because rapid accumulation of larger chains hinder diffusion and phase separation, and higher ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) in a reaction-limited region leads to faster phase separation with increasing polymer incompatibility. in a reaction-limited region leads to faster phase separation with increasing polymer incompatibility. | ||
We analyze the phase separating regimes away from the surface potential to characterize the “bulk” phase separation regime at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40, where isotropic phase separation (i.e. ω(
= 40, where isotropic phase separation (i.e. ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) < 0) occurs as shown in Fig. 4. First, we keep track of ω(
) < 0) occurs as shown in Fig. 4. First, we keep track of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) values over time at
) values over time at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40 as shown in Fig. 7 to represent the isotropic phase separation behaviors for the “bulk” regime. In Fig. 7a, we observe that ω(
= 40 as shown in Fig. 7 to represent the isotropic phase separation behaviors for the “bulk” regime. In Fig. 7a, we observe that ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40,
= 40,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) curves exhibit a near-collapse for identical
) curves exhibit a near-collapse for identical ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) > 10−4 (diffusion-limited regime), irrespective of Ṽ0 values. This behavior is anticipated, given the sufficient distance from the anisotropic concentration wave induced by the surface potential in a diffusion-limited system. The trend closely resembles a system devoid of surface potential, where higher
> 10−4 (diffusion-limited regime), irrespective of Ṽ0 values. This behavior is anticipated, given the sufficient distance from the anisotropic concentration wave induced by the surface potential in a diffusion-limited system. The trend closely resembles a system devoid of surface potential, where higher ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) values necessitate extended time for phase separation due to the accelerated generation of slower-diffusing, heavier polymers.94 Consistently, Fig. 7a demonstrates that increasing the reaction rate
values necessitate extended time for phase separation due to the accelerated generation of slower-diffusing, heavier polymers.94 Consistently, Fig. 7a demonstrates that increasing the reaction rate ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) decelerates isotropic bulk phase separation at
decelerates isotropic bulk phase separation at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40, as illustrated in Fig. 5. Fig. 7b depicts ω(
= 40, as illustrated in Fig. 5. Fig. 7b depicts ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40,
= 40,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) for lower reaction rates (
) for lower reaction rates (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ≤ 10−4) in the reaction-limited regime, revealing distinct behaviors compared to Fig. 7a. At
≤ 10−4) in the reaction-limited regime, revealing distinct behaviors compared to Fig. 7a. At ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−4, the intensity diminishes significantly, except for Ṽ0 = 0, relative to Fig. 7a. This reduction signifies the system's transition from a diffusion-limited to reaction-limited regime, where the surface potential exerts a more pronounced influence on phase separation, as evidenced in Fig. 5. Further reduction of
= 10−4, the intensity diminishes significantly, except for Ṽ0 = 0, relative to Fig. 7a. This reduction signifies the system's transition from a diffusion-limited to reaction-limited regime, where the surface potential exerts a more pronounced influence on phase separation, as evidenced in Fig. 5. Further reduction of ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) to 10−5 yields positive values of ω(
to 10−5 yields positive values of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40,
= 40,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), excluding the zero-potential system. This indicates a deeper penetration of the concentration wave from the surface potential and the development of anisotropic phase separation beyond the point (
), excluding the zero-potential system. This indicates a deeper penetration of the concentration wave from the surface potential and the development of anisotropic phase separation beyond the point (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40) previously considered as “bulk”. In this scenario, surface-driven phase separation is sufficient and allows ample time for further propagation, expanding the anisotropic regime while suppressing isotropic phase separation, as demonstrated in Fig. 4e, i, and m.
= 40) previously considered as “bulk”. In this scenario, surface-driven phase separation is sufficient and allows ample time for further propagation, expanding the anisotropic regime while suppressing isotropic phase separation, as demonstrated in Fig. 4e, i, and m.
 | ||
Fig. 7 The bulk phase separation intensity ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40, = 40,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) over ) over ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and Ṽ0 at constant χ = 1.0. (a) For varying Ṽ0, the curves nearly collapse onto one another for the same and Ṽ0 at constant χ = 1.0. (a) For varying Ṽ0, the curves nearly collapse onto one another for the same ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) . This is expected for a diffusion-limited regime because the anisotropic concentration wave induced by the surface potential propagates less effectively, meaning that phase separation in the “bulk” depends on . This is expected for a diffusion-limited regime because the anisotropic concentration wave induced by the surface potential propagates less effectively, meaning that phase separation in the “bulk” depends on ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) . As the reaction rate . As the reaction rate ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) increases, more time is required for isotropic phase separation in the bulk regime due to the rapid accumulation of longer chains. (b) In a reaction-limited regime, surface potential becomes more dominant due to the prevalent smaller molecules with faster diffusion, effectively altering the bulk phase separation behaviors. At increases, more time is required for isotropic phase separation in the bulk regime due to the rapid accumulation of longer chains. (b) In a reaction-limited regime, surface potential becomes more dominant due to the prevalent smaller molecules with faster diffusion, effectively altering the bulk phase separation behaviors. At ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−5, ω( = 10−5, ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40, = 40,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) shows positive growth for Ṽ0 > 0, indicating a deeper penetration of anisotropic concentration wave towards the bulk regime as shown in Fig. 4e, i and m. ) shows positive growth for Ṽ0 > 0, indicating a deeper penetration of anisotropic concentration wave towards the bulk regime as shown in Fig. 4e, i and m. | ||
To more thoroughly understand how different ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) values affect the competition between surface-driven and bulk phase separation, we examine volume fractions of each individual chains with different degrees of polymerization NA for species A. We do not plot species B, which shares the same large-
values affect the competition between surface-driven and bulk phase separation, we examine volume fractions of each individual chains with different degrees of polymerization NA for species A. We do not plot species B, which shares the same large-![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) behavior but exhibits oscillations that are opposite of those in A, and does not provide additional physical insight. We consider both slow (
behavior but exhibits oscillations that are opposite of those in A, and does not provide additional physical insight. We consider both slow (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−5) and fast (
= 10−5) and fast (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−2) polymerization kinetics in Fig. 8 and 9, respectively. Fig. 8a provides the overall behavior of ω(
= 10−2) polymerization kinetics in Fig. 8 and 9, respectively. Fig. 8a provides the overall behavior of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at a smaller reaction rate (
) at a smaller reaction rate (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−5) for a reaction-limited regime, which is the same as Fig. 4m. All of the same color in both Fig. 8a and c denotes the same time over the course of phase separation from red (
= 10−5) for a reaction-limited regime, which is the same as Fig. 4m. All of the same color in both Fig. 8a and c denotes the same time over the course of phase separation from red (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0) to purple (
= 0) to purple (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp) as visualized in Fig. 8b.
= τp) as visualized in Fig. 8b.
 | ||
Fig. 8 Plots demonstrating the dynamic evolution of the full molecular weight distribution for slow polymerization kinetics (i.e. ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) of 10−5, reaction-limited regime). All figures share the same x-axis for a normalized simulation box, and color scale from red ( of 10−5, reaction-limited regime). All figures share the same x-axis for a normalized simulation box, and color scale from red (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0) to purple ( = 0) to purple (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp). (a) replicates ω( = τp). (a) replicates ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) shown in Fig. 4m. (b) The visualization of one of the simulation trajectories at ) shown in Fig. 4m. (b) The visualization of one of the simulation trajectories at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0 and τp. (c) The time-evolution of polymer concentration profiles along = 0 and τp. (c) The time-evolution of polymer concentration profiles along ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) . Phase separation near the surface potential gets more profound for short- or medium-sized NA. Consumption and polymerization are shown with NA = 1, 2 and 4 while generation and polymerization are found with NA = 8, 16 and 32. In this slower reacting system, smaller molecules diffuse to the surface, accumulate, and polymerize locally, leading to local generation of heavier polymers at the concentrated regions such as near the surface potential. . Phase separation near the surface potential gets more profound for short- or medium-sized NA. Consumption and polymerization are shown with NA = 1, 2 and 4 while generation and polymerization are found with NA = 8, 16 and 32. In this slower reacting system, smaller molecules diffuse to the surface, accumulate, and polymerize locally, leading to local generation of heavier polymers at the concentrated regions such as near the surface potential. | ||
 | ||
Fig. 9 Plots demonstrating the dynamic evolution of the full molecular weight distribution for slow polymerization kinetics (i.e. ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) of 10−2, diffusion-limited regime). All figures share the same x-axis for the normalized simulation box, and color scale from red ( of 10−2, diffusion-limited regime). All figures share the same x-axis for the normalized simulation box, and color scale from red (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0) to purple ( = 0) to purple (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = τp). (a) Replicated ω( = τp). (a) Replicated ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) shown in Fig. 4p. (b) Visualization of one of the simulation trajectories at ) shown in Fig. 4p. (b) Visualization of one of the simulation trajectories at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0 and τp. (c) The time-evolution of polymer concentration profiles along = 0 and τp. (c) The time-evolution of polymer concentration profiles along ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) . Phase separation near the surface potential gets more profound for NA = 16 or 32. No meaningful differences are found but to be completely consumed in NA = 1,2,4 and 8 due to large . Phase separation near the surface potential gets more profound for NA = 16 or 32. No meaningful differences are found but to be completely consumed in NA = 1,2,4 and 8 due to large ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) of 10−2. For NA = 16, mostly consumption takes place while phase separating with small fluctuation near the surface. In NA = 32, we observe that it accumulates first before it phase separates. This fast reacting system shows that polymerization is too fast for smaller molecules to diffuse, leading to accumulation of heavier polymers evenly throughout the space first, and then these larger molecules drive the phase separation. of 10−2. For NA = 16, mostly consumption takes place while phase separating with small fluctuation near the surface. In NA = 32, we observe that it accumulates first before it phase separates. This fast reacting system shows that polymerization is too fast for smaller molecules to diffuse, leading to accumulation of heavier polymers evenly throughout the space first, and then these larger molecules drive the phase separation. | ||
In Fig. 8c, the concentration profiles of individual polymer chains with specific chain lengths (NA) along the x-direction are presented for NA = 1, 2, 4, 8, 16, and 32. This analysis examines the role of reaction rate under the influence of surface potential in relation to polydispersity. In the case of a slow reaction rate, monomers (NA = 1) are weakly attracted to the surface potential over time and are continuously consumed through polymerization. For polymers with NA = 2 and 4, an initial single peak (representing a polymer-rich or concentrated region) forms near the surface potential (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1), followed by fluctuating concentrations extending toward
= 1), followed by fluctuating concentrations extending toward ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 60 as they are progressively consumed. This behavior persists for larger polymers (NA = 8), with an additional observation of polymer generation during phase separation as the system evolves toward τp. The trend becomes more pronounced with increasing chain length. Heavier polymers (NA = 16 and 32) exhibit simultaneous phase separation and generation, suggesting that larger molecules are formed based on the pre-established concentration fields of smaller chains. This eliminates the need for these larger molecules to diffuse and phase separate independently, as smaller molecules have already undergone phase separation over sufficient time at low reaction rates (
= 60 as they are progressively consumed. This behavior persists for larger polymers (NA = 8), with an additional observation of polymer generation during phase separation as the system evolves toward τp. The trend becomes more pronounced with increasing chain length. Heavier polymers (NA = 16 and 32) exhibit simultaneous phase separation and generation, suggesting that larger molecules are formed based on the pre-established concentration fields of smaller chains. This eliminates the need for these larger molecules to diffuse and phase separate independently, as smaller molecules have already undergone phase separation over sufficient time at low reaction rates (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−5). Fig. 9 instead illustrates a diffusion-limited system with a relatively high polymerization rate constant
= 10−5). Fig. 9 instead illustrates a diffusion-limited system with a relatively high polymerization rate constant ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−2, such that short chains are almost immediately consumed by the reaction. All other variables are kept constant as in Fig. 8 to specifically isolate the effect of the polymerization rate. Fig. 9a (which is also shown in Fig. 4p) shows two major differences in terms of ω(
= 10−2, such that short chains are almost immediately consumed by the reaction. All other variables are kept constant as in Fig. 8 to specifically isolate the effect of the polymerization rate. Fig. 9a (which is also shown in Fig. 4p) shows two major differences in terms of ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). First, Fig. 9a exhibits ω(
). First, Fig. 9a exhibits ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) values below 0 (i.e. isotropic phase separation), which is not observed in Fig. 8a. This is attributed to the comparable timescales between surface-directed phase separation and polymerization-induced phase separation; for
) values below 0 (i.e. isotropic phase separation), which is not observed in Fig. 8a. This is attributed to the comparable timescales between surface-directed phase separation and polymerization-induced phase separation; for ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−2, the system quickly builds up sufficient incompatibility to initiate polymerization-induced phase separation before the surface-driven phase separation becomes dominant. Second, the system exhibits significantly less propagation of anisotropic concentration waves into the bulk, even under the same surface potential strength (Ṽ0 = 10−1). This is because smaller molecules are rapidly consumed, limiting their diffusive transport. This rapid consumption turns into the generation of larger molecules with reduced mobility, which hinders overall diffusion in the system even under the surface potential at
= 10−2, the system quickly builds up sufficient incompatibility to initiate polymerization-induced phase separation before the surface-driven phase separation becomes dominant. Second, the system exhibits significantly less propagation of anisotropic concentration waves into the bulk, even under the same surface potential strength (Ṽ0 = 10−1). This is because smaller molecules are rapidly consumed, limiting their diffusive transport. This rapid consumption turns into the generation of larger molecules with reduced mobility, which hinders overall diffusion in the system even under the surface potential at ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 10−2.
= 10−2.
Fig. 9c illustrates that for NA = 1, 2, 4, and 8, the reaction (or consumption) rate is so high that molecules have insufficient time to diffuse near the potential surface. Only for larger chain lengths (NA = 16) do we observe subtle simultaneous consumption and phase separation over time. At early times (indicated by red colors), the system exhibits minimal compositional variation and lacks evident phase separation. Gradual phase separation becomes apparent as the system approaches τp. For the largest chains considered (NA = 32), the system initially shows a nearly uniform accumulation of polymers throughout space due to the rapid reaction rate. This is evident at early times when ϕA,32 averages around 0.07 for NA = 32, as shown in Fig. 9c. A concentration wave emerges from the surface potential, propagating into the bulk and driving anisotropic phase separation. Additionally, bulk phase separation occurs at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40 over longer timescales near τp, as depicted in Fig. 9a and b. However, this bulk phase separation does not result in significant changes in ϕA,32 at
= 40 over longer timescales near τp, as depicted in Fig. 9a and b. However, this bulk phase separation does not result in significant changes in ϕA,32 at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 40 due to spatial averaging along the y-direction.
= 40 due to spatial averaging along the y-direction.
4 Conclusions
We have modified and developed a pCH model to study how phase separation in a polymerizing binary blend is affected by the presence of a preferential surface, and show that there is a complex interplay between polymer incompatibility, strength of the preferential surface interactions and polymerization kinetics on the dynamics and structure of the phase separating polymer.We first demonstrate how the strength Ṽ0 of an applied preferential surface potential affects phase separation (Fig. 2a), and use an order parameter ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) (Fig. 2b) and related phase ordering transition quantity
) (Fig. 2b) and related phase ordering transition quantity ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) (Fig. 2c) to track the phase separation process over time. We found that phase separation at a preferential surface occurs before phase separation in the bulk, because larger values of Ṽ0 locally concentrate one of the species near the surface potential; this increases both the local rate of polymerization and promotes the formation of the phase enriched in the preferred species. This leads to a layered, anisotropic structure at the surface, and we show that this structure grows monotonically with time by monitoring the anisotropic–isotropic transition point
) (Fig. 2c) to track the phase separation process over time. We found that phase separation at a preferential surface occurs before phase separation in the bulk, because larger values of Ṽ0 locally concentrate one of the species near the surface potential; this increases both the local rate of polymerization and promotes the formation of the phase enriched in the preferred species. This leads to a layered, anisotropic structure at the surface, and we show that this structure grows monotonically with time by monitoring the anisotropic–isotropic transition point ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ω=0(
ω=0(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). This quantity reveals that stronger Ṽ0 initially results in a thicker anisotropic regime, which repeats contraction upon merging of anisotropic domains and expansion upon further penetration of concentration wave over time.
). This quantity reveals that stronger Ṽ0 initially results in a thicker anisotropic regime, which repeats contraction upon merging of anisotropic domains and expansion upon further penetration of concentration wave over time.
We further investigate the influence of polymer incompatibility, characterized by χ, on the phase separation dynamics in the presence of a surface potential, Ṽ0. As illustrated in Fig. 3, the behavior of ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) aligns with expectations as χ varies; specifically, higher χ values result in accelerated phase separation. For each χ value, the system exhibits a monotonic dependence on Ṽ0, where larger Ṽ0 values lead to an earlier onset of the rise in ψ(
) aligns with expectations as χ varies; specifically, higher χ values result in accelerated phase separation. For each χ value, the system exhibits a monotonic dependence on Ṽ0, where larger Ṽ0 values lead to an earlier onset of the rise in ψ(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ).
).
We define and employ the order parameter for directional phase separation, ω(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), across various combinations of the surface potential Ṽ0 and reaction rate
), across various combinations of the surface potential Ṽ0 and reaction rate ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , as illustrated in Fig. 4. Together with Fig. 5 and the Damköhler number Da analysis, we identify diffusion-limited and reaction-limited regimes. This framework enables us to systematically explore how phase behavior evolves as a function of
, as illustrated in Fig. 4. Together with Fig. 5 and the Damköhler number Da analysis, we identify diffusion-limited and reaction-limited regimes. This framework enables us to systematically explore how phase behavior evolves as a function of ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and Ṽ0 within each regime.
and Ṽ0 within each regime.
By explicitly accounting for polydispersity in our framework, we investigate the intricate interplay between surface potential and reaction rate, as illustrated by the molecular weight distribution wA in Fig. 6b. This analysis provides a clear physical understanding of the dominant factors driving phase separation in both polymerization-limited and diffusion-limited regimes. Furthermore, we explore the spatiotemporal evolution of molecular weight under the influence of surface potential. Our findings reveal distinct phase separation pathways that arise from the competition between the timescales of surface-driven and polymerization-driven phase separation, governed by the polydispersity and molecular weight-dependent mobility.
Overall, we have demonstrated that phase separation under a preferential surface is governed by two distinct processes; surface-driven polymerization and bulk polymerization. The behavior of these two processes is governed by a competition between the polymerization rate and molecular diffusion, which has implications for practical materials systems such as surface-directed105–108 or self-stratifying108–110 coatings. This approach could also be further modified to account for other types of systems, such as coatings involving higher-functionality monomers that can undergo gelation,111–113 or other types of polymerization reaction kinetics.113–115 Similarly, it would be possible to modify this approach to account for other polymer dynamic behaviors, in particular directly including entangled polymer dynamics64,113 through changes to the molecular-weight dependence of the diffusion constant.
Author contributions
Charles Sing and Hyeonmin Jeong designed the computational model and the theoretical framework, analyzed the data, carried out the implementation, and performed the calculations. Hyeonmin Jeong wrote the manuscript and designed the figures with the supervision of Charles Sing. Junsi Gu, Paul Mwasame, Kshitish Patankar, and Decai Yu provided guidance on the direction of the study. Paul Mwasame and Decai Yu helped connect Dows internal modeling resources. All authors provided critical feedback and helped shape the research and manuscript.Data availability
Data for this article, including raw data (*.xlsx) for all figures and computational code (*.c) for running the polymerizing Cahn–Hilliard program, are available at https://github.com/Sing-group-ChBE-UIUC.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the Dow University Partnership Initiative (UPI Program) for financial support, and also the helpful discussions with Fabio Aguirre-Vargas (Dow), Michaeleen Pacholski (Dow), Harshad Shah (Dow), Guarav Singhal (UIUC), Lihong Lao (UIUC), Piyush Singh (UIUC), Paul Braun (UIUC), Charles Schroeder (UIUC), and Simon Rogers (UIUC). The authors also acknowledge helpful comments from the anonymous reviewers, who found a non-trivial error in our original method.References
- R. A. Jones, L. J. Norton, E. J. Kramer, F. S. Bates and P. Wiltzius, Phys. Rev. Lett., 1991, 66, 1326 CrossRef CAS PubMed.
- M. Geoghegan, R. Jones and A. Clough, J. Chem. Phys., 1995, 103, 2719–2724 CrossRef CAS.
- S. Puri, K. Binder and H. L. Frisch, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 6991 CrossRef CAS.
- S. Puri and K. Binder, Phys. Rev. A:At., Mol., Opt. Phys., 1992, 46, R4487 CrossRef CAS.
- M. Tabatabaieyazdi, P. K. Chan and J. Wu, Modell. Simul. Mater. Sci. Eng., 2015, 23, 075004 CrossRef.
- S. Ghaffari, P. K. Chan and M. Mehrvar, Polymers, 2021, 13, 256 CrossRef CAS.
- I. C. Henderson and N. Clarke, Macromol. Theory Simul., 2005, 14, 435–443 CrossRef CAS.
- E. Kim, G. Krausch, E. J. Kramer and J. O. Osby, Macromolecules, 1994, 27, 5927–5929 CrossRef CAS.
- M. Geoghegan, H. Ermer, G. Jüngst, G. Krausch and R. Brenn, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 940 CrossRef CAS.
- G. Krausch, E. J. Kramer, F. S. Bates, J. Marko, G. Brown and A. Chakrabarti, Macromolecules, 1994, 27, 6768–6776 CrossRef CAS.
- G. Brown and A. Chakrabarti, Phys. Rev. A:At., Mol., Opt. Phys., 1992, 46, 4829 CrossRef CAS.
- S. Puri and K. Binder, J. Stat. Phys., 1994, 77, 145–172 CrossRef.
- S. Puri and K. Binder, Phys. Rev. Lett., 2001, 86, 1797 CrossRef CAS PubMed.
- S. Puri, J. Phys.: Condens. Matter, 2005, 17, R101 CrossRef CAS.
- S. Puri, Phys. A, 2007, 384, 100–107 CrossRef CAS.
- K. Binder, S. K. Das and J. Horbach, Mod. Phys. Lett. B, 2009, 23, 549–565 CrossRef CAS.
- K. Binder, S. Puri, S. K. Das and J. Horbach, J. Stat. Phys., 2010, 138, 51–84 CrossRef CAS.
- S. Puri, P. Jaiswal and S. K. Das, Eur. Phys. J.:Spec. Top., 2013, 222, 961–974 Search PubMed.
- L.-T. Yan and X.-M. Xie, Macromol. Theory Simul., 2006, 15, 226–237 CrossRef CAS.
- L.-T. Yan and X.-M. Xie, Polymer, 2006, 47, 6472–6480 CrossRef CAS.
- E. Dickinson and P. Walstra, Food colloids and polymers: stability and mechanical properties, Elsevier, 1993 Search PubMed.
- T. Russell, Science, 2002, 297, 964–967 CrossRef CAS PubMed.
- Y. Vaynzof, D. Kabra, L. Zhao, L. L. Chua, U. Steiner and R. H. Friend, ACS Nano, 2011, 5, 329–336 CrossRef CAS PubMed.
- R. A. Jones and R. W. Richards, Polymers at surfaces and interfaces, 1999 Search PubMed.
- M. Müller and K. Binder, J. Phys.: Condens. Matter, 2005, 17, S333 CrossRef.
- K. Binder, J. Horbach, R. Vink and A. De Virgiliis, Soft Matter, 2008, 4, 1555–1568 RSC.
- P.-G. De Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- G. Reiter, Phys. Rev. Lett., 1992, 68, 75 CrossRef CAS PubMed.
- J. Doane, N. Vaz, B.-G. Wu and S. Žumer, Appl. Phys. Lett., 1986, 48, 269–271 CrossRef CAS.
- R. J. Williams, B. A. Rozenberg and J.-P. Pascault, Polymer analysis polymer physics, 2005, pp. 95–156 Search PubMed.
- M. A. Hillmyer, P. M. Lipic, D. A. Hajduk, K. Almdal and F. S. Bates, J. Am. Chem. Soc., 1997, 119, 2749–2750 CrossRef CAS.
- R. Motokawa, Y. Iida, Y. Zhao, T. Hashimoto and S. Koizumi, Polym. J., 2007, 39, 1312–1318 CrossRef CAS.
- J. Oh and A. Rey, Comput. Theor. Polym. Sci., 2001, 11, 205–217 CrossRef CAS.
- R. Yu, S. Zheng, X. Li and J. Wang, Macromolecules, 2012, 45, 9155–9168 CrossRef CAS.
- E. S. Zofchak, J. A. LaNasa, V. M. Torres and R. J. Hickey, Macromolecules, 2020, 53, 835–843 CrossRef CAS.
- T. Inoue, Prog. Polym. Sci., 1995, 20, 119–153 CrossRef CAS.
- F. Meng, S. Zheng, W. Zhang, H. Li and Q. Liang, Macromolecules, 2006, 39, 711–719 CrossRef CAS.
- Z. Dong, H. Cui, H. Zhang, F. Wang, X. Zhan, F. Mayer, B. Nestler, M. Wegener and P. A. Levkin, Nat. Commun., 2021, 12, 247 CrossRef CAS.
- K. Yamanaka, Y. Takagi and T. Inoue, Polymer, 1989, 30, 1839–1844 CrossRef CAS.
- J. Kim, C. Cho, P. Palffy-Muhoray and T. Kyu, Phys. Rev. Lett., 1993, 71, 2232 CrossRef CAS.
- L. Peng, J. Cui and S. Li, Macromol. Chem. Phys., 2000, 201, 699–704 CrossRef CAS.
- J. Zhang, H. Zhang and Y. Yang, J. Appl. Polym. Sci., 1999, 72, 59–67 CrossRef CAS.
- C. R. Szczepanski, C. S. Pfeifer and J. W. Stansbury, Polymer, 2012, 53, 4694–4701 CrossRef CAS PubMed.
- C. R. Szczepanski and J. W. Stansbury, Polymer, 2015, 70, 8–18 CrossRef CAS.
- E. Kemiklioglu and L.-C. Chien, Eur. Phys. J. E:Soft Matter Biol. Phys., 2017, 40, 1–6 CrossRef CAS.
- G. Liang, S. Yu, Z. Huang, K. Wu, T. Fu, Y. Tang and Z. Li, Adv. Photonics Res., 2021, 2, 2100185 CrossRef CAS.
- M. W. Schulze, L. D. McIntosh, M. A. Hillmyer and T. P. Lodge, Nano Lett., 2014, 14, 122–126 CrossRef CAS.
- L. Chen, D. T. Hallinan Jr, Y. A. Elabd and M. A. Hillmyer, Macromolecules, 2009, 42, 6075–6085 CrossRef CAS.
- S. C. Price, X. Ren, A. C. Jackson, Y. Ye, Y. A. Elabd and F. L. Beyer, Macromolecules, 2013, 46, 7332–7340 CrossRef CAS.
- Y. Tang, K. Wu, S. Yu, J. Chen, X. Ding, L. Rao and Z. Li, Opt. Lett., 2020, 45, 2918–2921 CrossRef.
- D. C. Hoekstra, B. P. van der Lubbe, T. Bus, L. Yang, N. Grossiord, M. G. Debije and A. P. Schenning, Angew. Chem., 2021, 133, 11030–11036 CrossRef.
- K. Yamanaka and T. Inoue, Polymer, 1989, 30, 662–667 CrossRef CAS.
- C. B. Bucknall and A. H. Gilbert, Polymer, 1989, 30, 213–217 CrossRef CAS.
- M. Kimoto and K. Mizutani, J. Mater. Sci., 1997, 32, 2479–2483 CrossRef CAS.
- N. G. Yun, Y. G. Won and S. C. Kim, Polymer, 2004, 45, 6953–6958 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- L. Löchte, A. Gitt, G. Gottstein and I. Hurtado, Acta Mater., 2000, 48, 2969–2984 CrossRef.
- M. Honjo and Y. Saito, ISIJ Int., 2000, 40, 914–919 CrossRef CAS.
- R. Abazari, H. Rezazadeh, L. Akinyemi and M. Inc, Comput. Appl. Math., 2022, 41, 389 CrossRef.
- J.-C. Lin and P. Taylor, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1993, 237, 25–31 CrossRef CAS.
- N. Vasishtha and E. Nauman, Chem. Eng. Commun., 1994, 129, 29–39 CrossRef CAS.
- D. Q. He and E. Nauman, J. Polym. Sci., Part B: Polym. Phys., 1997, 35, 897–907 CrossRef CAS.
- J. Oh and A. D. Rey, Macromol. Theory Simul., 2000, 9, 641–660 CrossRef CAS.
- A. A. Alfarraj and E. B. Nauman, Macromol. Theory Simul., 2007, 16, 627–631 CrossRef CAS.
- P. Inguva, L. R. Mason, I. Pan, M. Hengardi and O. K. Matar, Data-Centric Eng., 2020, 1, e13 CrossRef.
- S. Dargaville and T. W. Farrell, Electrochim. Acta, 2013, 94, 143–158 CrossRef CAS.
- Y. Zeng and M. Z. Bazant, MRS Online Proc. Libr., 2013, 1542, 1–15 CrossRef.
- E. B. Nauman and D. Q. He, Polymer, 1994, 35, 2243–2255 CrossRef CAS.
- C. Huang, M. O. de La Cruz and B. Swift, Macromolecules, 1995, 28, 7996–8005 CrossRef CAS.
- B. Barton and A. McHugh, J. Polym. Sci., Part B: Polym. Phys., 1999, 37, 1449–1460 CrossRef CAS.
- P. Graham, B. Barton and A. McHugh, J. Polym. Sci., Part B: Polym. Phys., 1999, 37, 1461–1467 CrossRef CAS.
- D. R. Tree, L. F. Dos Santos, C. B. Wilson, T. R. Scott, J. U. Garcia and G. H. Fredrickson, Soft Matter, 2019, 15, 4614–4628 RSC.
- K. Luo, Eur. Polym. J., 2006, 42, 1499–1505 CrossRef CAS.
- K.-W. D. Lee, P. K. Chan and X. Feng, Macromol. Theory Simul., 2003, 12, 413–424 CrossRef CAS.
- P. K. Inguva, P. J. Walker, H. W. Yew, K. Zhu, A. J. Haslam and O. K. Matar, Soft Matter, 2021, 17, 5645–5665 RSC.
- T. Ohnaga, W. Chen and T. Inoue, Polymer, 1994, 35, 3774–3781 CrossRef CAS.
- H. Tanaka, T. Suzuki, T. Hayashi and T. Nishi, Macromolecules, 1992, 25, 4453–4456 CrossRef CAS.
- S. C. Glotzer, E. A. Di Marzio and M. Muthukumar, Phys. Rev. Lett., 1995, 74, 2034 CrossRef CAS PubMed.
- M. D. Tikekar, K. T. Delaney, M. C. Villet, D. R. Tree and G. H. Fredrickson, Soft Matter, 2022, 18, 877–893 RSC.
- P. K. Chan and A. D. Rey, Macromolecules, 1996, 29, 8934–8941 CrossRef CAS.
- P. K. Chan and A. D. Rey, Macromolecules, 1997, 30, 2135–2143 CrossRef CAS.
- B. Zhou and A. C. Powell, J. Membr. Sci., 2006, 268, 150–164 CrossRef CAS.
- F. Boyer, C. Lapuerta, S. Minjeaud, B. Piar and M. Quintard, Transp. Porous Media, 2010, 82, 463–483 CrossRef.
- T. Rogers and R. C. Desai, Phys. Rev. B:Condens. Matter Mater. Phys., 1989, 39, 11956 CrossRef.
- P.-G. de Gennes, J. Chem. Phys., 1980, 72, 4756–4763 CrossRef CAS.
- K. Binder, J. Chem. Phys., 1983, 79, 6387–6409 CrossRef CAS.
- C. Huang and M. Olvera de La Cruz, Macromolecules, 1994, 27, 4231–4241 CrossRef CAS.
- E. D. Siggia, Phys. Rev. A:At., Mol., Opt. Phys., 1979, 20, 595 CrossRef CAS.
- A. J. Bray, Adv. Phys., 2002, 51, 481–587 CrossRef.
- P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys., 1977, 49, 435 CrossRef CAS.
- W. Chen, C. Wang, X. Wang and S. M. Wise, J. Comput. Phys.:X, 2019, 3, 100031 Search PubMed.
- P.-H. Chiu, J. Comput. Phys., 2019, 392, 115–140 CrossRef.
- H. Jeong, J. Gu, P. Mwasame, K. Patankar, D. Yu and C. E. Sing, Soft Matter, 2024, 20, 681–692 RSC.
- G. Odian, Principles of polymerization, John Wiley & Sons, 2004 Search PubMed.
- P. K. Inguva, P. J. Walker, H. W. Yew, K. Zhu, A. J. Haslam and O. K. Matar, Soft Matter, 2021, 17, 5645–5665 RSC.
- H. Tang and K. F. Freed, Macromolecules, 1991, 24, 958–966 CrossRef CAS.
- D. Prusty, V. Pryamitsyn and M. Olvera de la Cruz, Macromolecules, 2018, 51, 5918–5932 CrossRef CAS.
- A. Z. Akcasu, Macromolecules, 1989, 22, 3682–3689 CrossRef CAS.
- J. T. Cabral and J. S. Higgins, Prog. Polym. Sci., 2018, 81, 1–21 CrossRef CAS.
- G. R. Strobl, Macromolecules, 1985, 18, 558–563 CrossRef CAS.
- H. Tang and K. F. Freed, J. Chem. Phys., 1991, 94, 6307–6322 CrossRef CAS.
- R. Alhasan and D. R. Tree, Macromolecules, 2022, 55, 759–765 CrossRef CAS.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B:Condens. Matter Mater. Phys., 1983, 28, 784 CrossRef CAS.
- H.-G. Braun and E. Meyer, Thin Solid Films, 1999, 345, 222–228 CrossRef CAS.
- I. Povstugar, P.-P. Choi, D. Tytko, J.-P. Ahn and D. Raabe, Acta Mater., 2013, 61, 7534–7542 CrossRef CAS.
- J. Rysz, H. Ermer, A. Budkowski, M. Lekka, A. Bernasik, S. Wrobel, R. Brenn, J. Lekki and J. Jedlinski, Vacuum, 1999, 54, 303–307 CrossRef CAS.
- A. Budkowski, A. Bernasik, P. Cyganik, J. Rysz and R. Brenn, e-Polymers, 2002, 2, 005 Search PubMed.
- J. Baghdachi, H. Perez, P. Talapatcharoenkit and B. Wang, Prog. Org. Coat., 2015, 78, 464–473 CrossRef CAS.
- S. Zahedi and S. Ghaffarian, Trans. IMF, 2021, 99, 133–140 CrossRef CAS.
- Z. Mester, A. Mohan and G. H. Fredrickson, Macromolecules, 2011, 44, 9411–9423 CrossRef CAS.
- J. Ambati and S. E. Rankin, J. Colloid Interface Sci., 2011, 362, 345–353 CrossRef CAS PubMed.
- S. P. Danielsen, A. N. Semenov and M. Rubinstein, Macromolecules, 2023, 56, 5661–5677 CrossRef CAS.
- Q. Tran-Cong-Miyata and H. Nakanishi, Polym. Int., 2017, 66, 213–222 CrossRef CAS.
- H. Nakanishi, M. Satoh, T. Norisuye and Q. Tran-Cong-Miyata, Macromolecules, 2006, 39, 9456–9466 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |



