Pinch-off dynamics of emulsion filaments before and after polymerization of the internal phase

Abstract

The capillary break-up of complex fluid filaments occurs in many scientific and industrial applications, particularly in bio-printing where both liquid and polymerized droplets exist in the fluid. The simultaneous presence of fluid and solid particles within a carrier fluid and their interactions lead to deviations in the filament break-up from the well-established capillary breakup dynamics of single-phase liquids. To examine the significance of the dispersed phase and the internal interactions between liquid droplets and solid particles, we prepare emulsions through photopolymerization and conduct experimental investigations into the pinch-off dynamics of fluid filaments, focusing on the impact of varying concentrations of liquid droplets (before polymerization) and polymerized droplets. Despite the increase in bulk viscosity due to the presence of polymerized droplets in the fluid and their aggregation, the results show that polymerization significantly reduces the length of the fluid filament before breakup, thus shortening the duration of pinch-off. We investigate two categories of complex fluids, characterized by their droplet sizes: (i) sub-micrometer droplets and (ii) droplets with an average diameter of 50 micrometers. In emulsions containing sub-micrometer droplets, the individual droplet contributions remain undetectable during capillary breakup, and the measured pinch-off dynamics predominantly reflect the bulk shear viscosity or viscoelasticity of the system. This is due to the droplet sizes falling below our imaging resolution. In contrast, emulsions with larger polymerized droplets exhibit behavior analogous to single-phase carrier fluids: once the filament's length equals the droplet diameter, the droplets are expelled. Concurrently, larger liquid droplets are deformed and elongated along the flow direction. Our study highlights the effect of mixing liquid and polymerized droplets on the capillary breakup dynamics of fluid filaments, providing insights to formulate 3D printing inks.

---

Introduction

Colloidal dispersions are commonly used as inks in droplet-on-demand 3D printing systems, with applications across food,^1–3 pharmaceuticals,^4,5 and environmental industries.^6,7 Biofluid printing, in particular,^8–10 facilitates the fabrication of biological or colloidal structures that mimic the architecture and functionality of natural tissues.^11,12 Bio-inks are predominantly composed of hydrogel-based materials containing colloidal particles and living cells.^13,14 During printing, a bio-ink filament undergoes breaks up due to the capillary instability, forming droplets that are often deposited on a solid surface.^15,16 The printability of these materials depends on the carrier fluid properties and the characteristics of the hard colloidal particles and soft living cells. To improve resolution and quality in 3D bioprinting, it is essential to understand how a filament's rheology influences its extensional flow and capillary-driven pinch-off dynamics. This understanding allows targeted adjustments to both the bio-ink formulation (e.g., viscosity, elasticity) and process parameters (e.g., extrusion rate, nozzle geometry), ensuring consistent filament formation, reduced droplet generation, and improved structural fidelity of the printed constructs.

The pinch-off dynamics of droplets have been extensively studied across a wide range of materials, from simple Newtonian fluids^17,18 to complex, non-Newtonian (yield stress, shear thinning, and viscoelastic) liquids.^15,19–22 For Newtonian liquids, the thinning dynamics often display self-similarity, with a progression through various stages with distinct time dependencies. Specifically, these phases are identified by how the minimum neck radius (h_min) relates to the time approaching pinch-off (τ = t_p − t), expressed as h_min ≈ τ^α, where, t_p signifies the time of pinch-off and t represents the observation time.^{17,18,23–28} Although extensive research has been conducted on the breakup dynamics of Newtonian and non-Newtonian single-phase liquids, the dynamics of multiphase systems, such as emulsions and particle dispersions, still require further investigation.

Emulsions are mixtures of two immiscible liquids where one liquid is dispersed in the form of droplets in a continuous liquid phase, with the droplets stabilized using surfactants, particles, and/or polymers. Due to their properties, such as shear-rate-dependent viscosity, viscoelasticity, and the ability to encapsulate different materials, emulsions have attracted attention in 3D printing applications.^29–31 The pinch-off of an emulsion filament is influenced by droplet size and concentration^32–34 and the types of surface-active agents.^35,36 In emulsions where droplets are significantly smaller than the diameter of the thinning liquid filament, the pinch-off dynamics closely mirror those observed in single-phase liquids, where the emulsion bulk viscosity dominates the process.^35,36 For example, the pinch-off dynamics of emulsions composed of castor oil droplets dispersed in water, stabilized by 1 wt% sodium dodecyl sulfate, with an average droplet diameter of ≈3 μm, exhibited no significant inhomogeneity during the pinch-off process. In yield stress emulsions where the volumetric concentration of dispersed phase is below 70%, the minimum neck radius of the thinning filament followed a power-law exponent of α ≈ 0.67. For emulsions with the volumetric concentration of dispersed phase above 72%, the exponent shifted to unity, indicating more viscous behavior.³⁷ When the emulsion droplet size is comparable to the fluid filament, it can introduce heterogeneities in the thinning filament and influence the capillary break-up dynamics.

In contrast to emulsions, where the dispersed phase is liquid and deformable, in colloidal particle dispersions the dispersed phase can be solid and rigid. Recent studies indicate that the presence of particles in the filament introduces a characteristic length scale to the system, which is influenced by the particle diameter.³⁸ In particular, a filament of a particle dispersion with a Newtonian continuous phase thins like a single-phase Newtonian liquid until a critical point, after which thinning speeds up, culminating in a particle-free breakage similar to a Newtonian viscous liquid.^39–41 Aside from studies on emulsion filaments (liquid droplets) and dispersions of hard particles, the pinch-off dynamics of microgel particle dispersions have also been investigated in the context of their interfacial assemblies. It has been shown that these solid but deformable particles, such as microgels, induce elastic effects driven by particle interactions at the interface.⁴² While the pinch-off dynamics of emulsions and particle dispersions have been studied, how filaments behave when composed of both rigid and deformable droplets is still not well understood. The unique rheology of mixtures containing both rigid particles and deformable cells⁴³ initiated our interest in exploring whether breakup dynamics, such as neck thinning during drop pinch-off, differ under extensional flow conditions.

In this study, we utilize emulsion photopolymerization to create colloidal dispersions containing both liquid and polymerized droplets. In particular, we make mixtures with various volume fraction of liquid droplets before polymerization and after polymerization and study the pinch-off dynamics of these colloidal dispersions. We focus on characterizing, and, where possible, understanding how the polymerization of the dispersed phase and having a mixture of both liquid and polymerized dispersed phases influence the filament pinch-off behavior in these complex fluids. Such understanding is important in many 3D printing systems, for example, as it directly impacts the response of bio-ink formulations.

Experiments

Materials

Trimethylolpropane triacrylate (TMPTA, ρ = 1.10 g cm⁻³) serves as the oil-based polymer solution. The UV-sensitive photoinitiator (PI) used in this study is 2-hydroxy-2-methylpropiophenone (ρ = 1.07 g cm⁻³). A 40 wt% silica nanoparticle dispersion (HS 40, ρ = 1.29 g cm⁻³) is the source for the nanoparticle dispersions and acts as the stabilizer agent for the emulsions. Glycerol (ρ = 1.26 g cm⁻³) is used as a density modifier, ensuring compatibility in density between the oil and aqueous phases, which helps to reduce droplet sedimentation during the experiments. All chemicals were purchased from Sigma. Syringe filters (VWR) with a membrane pore size of 10 μm were used for filtration of the emulsions.

Shear rheology

Shear viscosity and viscoelasticity measurements were conducted using a stress-controlled rheometer (Anton Paar Physica MCR 301) set at 21 °C. The apparatus utilized a roughened parallel-plate design with a diameter of 50 mm. The use of roughened plates was chosen to reduce wall slip. The plate gap was set to 1 mm. During shear rate ramp tests, we maintained a constant shear rate for a minimum of 30 seconds before making any adjustments and all experiments were conducted at shear rates smaller than 100 s⁻¹. Additionally, we assessed the elastic and viscous moduli of the suspensions through small amplitude oscillatory shear rheology (SAOS) with a fixed strain rate of 1%.

Pinch-off

An emulsion sample was injected vertically with a fixed flow rate of 0.1 μl s⁻¹ (equivalent to an injection speed of ≈40 μm s⁻¹), using a needle with inner diameter (D) of 1.8 mm, into a glass cuvette. A drop was formed and was approximately at rest for 10 seconds before thinning starts. We recorded the thinning of the emulsion thread with a high-speed camera (Phantom v7.3) at 4000 frames per second (fps) and a resolution of 6.5 μm per pixel (10× magnification, Nikon). The measurements yielded the time history of the minimum thread radius h_min(τ), with τ = t_p − t, where t_p is the time instant of pinch-off and t is the time of the experiment.

Interfacial tension

To measure the interfacial tension between the emulsion/dispersion droplets and the surrounding medium (air), we employed a pendant drop method. Images of the droplet profiles were captured using a camera (Phantom v7.3) and processed with the DropSnake plugin in the ImageJ software package. This plugin allows for precise detection of droplet contours and extraction of geometric parameters necessary for the interfacial tension calculation. The interfacial tension was determined by fitting the droplet profiles to the Young–Laplace equation.

Microscopy

The emulsion droplet size distribution was measured using an inverted fluorescent microscope (Leica DFC 300 FX, Wetzlar, Germany) at a resolution of 1 μm per pixel.

Emulsion preparation and polymerization

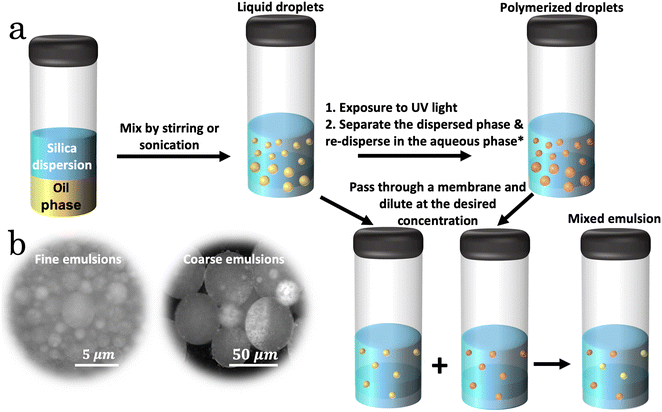
Emulsions were formulated with equal volumes of oil and a 4.0 wt% silica nanoparticle dispersion. Silica nanoparticles (d_avg ∼ 9 nm) act as stabilizing agents, ensuring the emulsions remain stable. These nanoparticles provide effective steric stabilization to the droplets, preventing coalescence and phase separation by creating a physical barrier between droplets. The oil phase is a mixture of the monomer (TMPTA) and photoinitiator (PI) in a 10 : 1 volume ratio. We prepared and analyzed oil-in-water emulsions using two distinct methods, ultra-sonication and filtration, which we refer to as fine and coarse emulsions, respectively.

The ultra-sonication of the mixture employs a sonic probe for one minute at an amplitude of 100 W, producing emulsions with sub-micrometer droplet sizes (characterized by dynamic light scattering, Fig. S1a, ESI†). In the filtration method, initially oil-in-water emulsions are produced using magnetic stirring for 1 hour at 1000 rpm. Given the oil phase's higher density, oil droplets settle to the bottom of the container. These droplets are subsequently collected with a 1 ml syringe and passed through a syringe filter with a 10-micrometer pore size. This filtration process is repeated three times to ensure a narrow drop size distribution. The filtration method generates coarse emulsions with an average droplet diameter of 50 micrometers (Fig. S1b, ESI†).

After preparation, the emulsions are exposed to UV light for 100 seconds at an intensity of 95 mW cm⁻², which results in a phase change of liquid droplets to solid particles. Post-polymerization particles from ultra-sonicated emulsions are separated using centrifuges operating at 25 000 rpm for 10 minutes. Coarse emulsion droplets separate within 30 minutes without requiring centrifugation. The settled particles are then redispersed in a mixture of 4.0 wt% silica dispersion and glycerol in a 7 : 3 volume ratio, maintaining the same density as the polymerized droplets (ρ = 1.10 g ml⁻¹). Throughout this study, the combined volumetric concentration of the dispersed phase (both liquid and polymerized droplets) is consistently maintained at 25% volume fraction relative to the continuous aqueous phase. Fig. 1 illustrates the emulsion formation, droplet separation, and formation of the colloidal dispersion containing both liquid and polymerized droplets.

Fig. 1 Emulsion formation and polymerization. (a) Equal volumes of oil and aqueous phases before emulsification. Samples are emulsified by mixing two phases, where yellow droplets represent the liquid droplets. Emulsions are UV polymerized (orange droplets) and centrifuged, and droplets are collected and re-dispersed in the mixture of a silica dispersion and glycerol at the desired concentration. (b) Microscopic images of fine and coarse emulsions.

Results and discussions

1. Shear rheology

We investigate the shear rheology of fine emulsions, generated through ultra-sonication, and coarse emulsions, generated via filtration. The experimental results focus on the effective viscosity of emulsions containing both liquid droplets and polymerized droplets. Fig. 2a and b documents the variation of emulsion viscosity with shear rate during shear rate ramps ranging from 1 to 1000 s⁻¹. Each sequential ramp was conducted with a 30-second interval for both fine (Fig. 2a) and coarse (Fig. 2b) emulsions.

Fig. 2 Shear rheology of fine and coarse emulsions containing 25.0% volume fraction droplets. The measurements were conducted using a parallel plate geometry with a fixed gap size of 1 mm. Green triangles: 25.0% volume fraction liquid droplets and no polymerized droplets, blue circles: 16.5% volume fraction liquid droplets and 8.5% volume fraction polymerized droplet, orange squares: 12.5% volume fraction liquid droplets and 12.5% volume fraction polymerized droplet, red inverted triangles: 8.5% volume fraction liquid droplets and 16.5% volume fraction polymerized droplet, and black diamonds: no liquid droplets and 25.0% volume fraction polymerized droplet. Viscosity as a function of shear rate of (a) fine and (b) coarse emulsions. Frequency sweep test of (c) fine and (d) coarse emulsions. Elastic modulus (G′) and loss modulus (G′′) are plotted as a function of frequency.

When a fraction of the liquid droplets is replaced by polymerized droplets, the viscosity of both fine and coarse emulsions increases, as demonstrated by the results in Fig. 2a and b. In fine emulsions (Fig. 2a), the dispersion with 25% liquid droplets shows a Newtonian-like behavior, where the viscosity remains constant at approximately 70 mPa s as the shear rate increases. However, when 8.5% of the liquid droplets are replaced by polymerized droplets, bringing the concentration of liquid droplets to 16.5%, the viscosity increases to about 250 mPa s at low shear rates and exhibits shear-thinning behavior below a shear rate of 10 s⁻¹, above which the viscosity remains constant at ≈90 mPa s. As the concentration of polymerized droplets increases to 12.5%, the viscosity further rises to around 700 mPa s, and the shear-thinning behavior extends over a broader shear rate range, especially below 100 s⁻¹, after which the viscosity stabilizes at ≈135 mPa s. When the polymerized droplet concentration reaches 16.5%, the viscosity exceeds 1000 mPa s at low shear rates and becomes constant at ≈150 mPa s. Finally, the polymerized droplet dispersion exhibits shear-thinning behavior over an extended shear rate range, where it becomes nearly constant at shear rates above 200 s⁻¹, reaching a value of ≈180 mPa s.

For coarse emulsions (Fig. 2b), at the same volume fractions, the viscosity is consistently lower than in fine emulsions. At 25% liquid droplets, the viscosity starts at around 100 mPa s at low shear rates and decreases to 18 mPa s as the shear rate increases to 1000 s⁻¹, showing shear-thinning behavior. As polymerized droplets are added, the viscosity slightly increases when the liquid droplet concentration is 16.5%, and the shear-thinning behavior becomes more pronounced at shear rates below 100 s⁻¹. When the polymerized droplet concentration reaches 12.5%, the viscosity increases further to around 100 mPa s at 1000 s⁻¹, and at 25% polymerized droplets, the viscosity exceeds 200 mPa s, maintaining shear-thinning behavior across all shear rates.

Emulsions often exhibit shear-thinning behavior. As shear is applied, the droplets align in the flow direction, reducing their effective cross-sectional area.^44,45 This alignment leads to a decrease in viscosity, so that the fluid flows with less resistance as the shear rate increases, which is especially relevant to highly concentrated emulsions.^46,47 The emulsion droplet size also plays a crucial role in determining the effective viscosity and shear thinning behavior of the emulsion.⁴⁸ Specifically, when two emulsion samples have the same volume fractions, the sample with smaller droplets tends to exhibit higher viscosity, which is consistent with our measurement (green data points in Fig. 2a and b). It is essential to recognize that the interpretation of droplet size should be considered in conjunction with volume fraction, as this interplay significantly impacts the emulsion's rheological characteristics. In hard particle dispersions, as the particle size decreases, the surface area to volume ratio increases, often leading to higher viscosities due to increased interactions among the particles.^49,50

As is well known, particle concentration also plays a significant role in determining viscosity. As the concentration of particles in the suspension increases, the viscosity rises due to more frequent interactions between particles, which can lead to the formation of particle clusters that create additional resistance to flow.⁵¹ Moreover, suspensions exhibit non-linear increases in viscosity, especially when the particles nearly or actually touch or form structured networks.⁵²

Our results demonstrate a substantial difference in viscosity between samples with liquid droplets and samples with polymerized droplets, deviating significantly from the Einstein relation, which assumes non-interacting spherical particles and is valid at low volume fractions. According to this classical model, the viscosity of the suspension should increase linearly with particle volume fraction, with nonlinear effects setting in already beyond a few volume percent particles, but our findings, particularly with the polymerized droplets, suggest an additional contribution due to interparticle forces that are not captured in the model. Several studies have addressed similar deviations in complex systems. For instance, investigations into particle-laden interfaces have shown that when particles interact through attractive forces, such as van der Waals or depletion interactions, they can form gels or networks, resulting in a marked increase in the viscosity and yield stress of the suspension.^53,54 This behavior is consistent with our observation that the slope of viscosity versus shear rate for the polymerized droplets is approximately −1, which suggests a yield stress typical of particle gels or networks.⁵⁵

To investigate the potential interactions between polymerized droplets, we conducted a series of flow experiments inside a capillary tube (see Section 2 of the ESI†). The results show that as the dispersion of polymerized droplets flows through the channel, particle clusters form and move together (Fig. S2 and S3, ESI†), suggesting particle–particle interactions that contribute to the increase in viscosity. These findings highlight the importance of considering interparticle interactions and potential network formation when analyzing the rheological behavior of colloidal suspensions.

The viscosity of colloidal dispersions is greatly influenced by the nature of the particles within the suspension. When a colloidal dispersion contains a mixture of both liquid and polymerized droplets, the resulting viscosity is a complex interplay of the individual characteristics of each particle type and their interactions with each other and the surrounding medium. For example, Perazzo et al. (2021) studied, through experiments and simulations, a mixture of healthy blood cells, resembling soft particles, and rigid particles. The results showed that the addition of a small amount (5% volume fraction) of rigid particles to the blood cells, in a solution 25% volume fraction particles, significantly increases the shear viscosity of the suspension.⁴³ The mixtures of liquid and polymerized droplets in Fig. 2a and b with the same volume fraction as samples in Perazzo et al. (2021) indicates the same trend while our particles/droplets are different in size.

The outcomes of the frequency sweep test in Fig. 2c (fine emulsion) and Fig. 2d (coarse emulsion) reveal that in the absence of polymerized droplets the emulsion samples exhibited an elastic behavior, where in all cases the elastic modulus surpassed the viscous modulus. At 25% droplet concentration, although the emulsion droplets do not form a percolated network, they still significantly influence the system's elasticity through droplet deformation and interfacial effects. Liquid droplets store elastic energy as they deform under stress, which contributes to the elastic response of the emulsion.⁵⁶ When liquid droplets are replaced with polymerized droplets, the system loses this ability to store elastic energy, as polymerized droplet do not deform under flow.⁵⁶ The interfacial tension between liquid droplets and the continuous phase also resists deformation, acting like an elastic spring. This interfacial elasticity plays a crucial role in the overall elastic modulus. However, polymerized droplet, being rigid, do not contribute to interfacial elasticity in the same way, leading to a decrease in elasticity as their concentration increases.⁵⁷

In summary, at a constant dispersed phase concentration of 25%, increasing the proportion of polymerized droplets while decreasing liquid droplets alters the emulsion's rheological properties: viscosity increases while the elastic modulus decreases. The higher viscosity arises from stronger hydrodynamic interactions and crowding, as rigid polymerized droplets resist deformation and amplify the effective volume fraction.^58,59 Additionally, polymerized droplets may form aggregates or transient networks due to interparticle forces, further hindering flow.⁶⁰ In contrast, liquid droplets deform under flow, reducing hydrodynamic drag and lowering viscosities in emulsions with higher liquid droplet concentrations.⁴⁸ These findings align with studies linking viscosity to hydrodynamic interactions,⁵⁸ crowding effects,⁵⁹ and droplet deformability,⁵⁶ while highlighting interfacial tension's role in enhancing elasticity.⁶¹

2. Pinch-off: fine emulsions

We now consider the shape evolution of filaments of fine emulsions. A series of time-lapse images provides a qualitative comparison of the thinning behavior between threads of fine emulsions (droplet size ∼1 μm) containing liquid droplets (Fig. 3a), polymerized droplets (Fig. 3c), and both (Fig. 3b). These samples have an equilibrium interfacial tension γ_eq = 32.3 ± 3 mN m⁻¹. Ohnesorge number (ratio of viscous to inertial forces and surface tension forces), ; the Reynolds number of these interfacial driven flows, with typical speed γ_eq/μ, corresponds to 1/Oh². The Oh value increases with an increase in the concentration of polymerized droplets inside the emulsion thread.

Fig. 3 Shape evolution of fine emulsion filaments containing 25.0% volume fraction droplets. (a) and (a′) 25.0% volume fraction liquid droplets and no polymerized droplets, (b) and (b′) 12.5% volume fraction liquid droplets and 12.5% volume fraction polymerized droplets, (c) and (c′) no liquid droplets and 25.0% volume fraction polymerized droplets. The instant of pinch-off is denoted as t_p and the time difference between pinch-off and the given time is indicated by τ = t_p − t. (a)–(c) A time series of images from the neck formation until the break-up for each emulsion sample. (a′)–(c′) The overlapped boundaries of the extracted drops, emphasizing the visual distinctions among emulsion samples with varying concentrations of liquid and polymerized droplets.

We first observe that the emulsion system with a lower concentration of polymerized droplets exhibits a longer and more gradual thinning process (Fig. 3a). As we progress to a mixture of liquid and polymerized droplets, Fig. 3b, the neck thins more rapidly and the length of the thread at the moment of pinch-off is reduced. This intermediate system shows how the addition of polymerized droplets begins to influence the pinch-off dynamics, leading to a faster detachment and a shorter thread length. In Fig. 3c, the emulsion thread with the highest concentration of polymerized droplets exhibits a more abrupt thinning behavior. The increased viscosity and reduced elastic properties of the thread, due to the higher polymerized droplet content, result in a shorter and more rapid pinch-off process. We interpret this rapid thinning to indicate that the polymerized droplets form some clusters, which resist deformation and facilitates faster breakup.

To identify the filament length scale below which the thinning velocity becomes constant, we calculate −dh_min/dt and plot it as a function of h_min. This helps us determine when the system transitions to a power-law regime.¹⁷ For the emulsion with 25% liquid droplets, the thinning velocity remains relatively constant at ∼50 μm ms⁻¹ for length scales below 200 μm. As the proportion of polymerized droplets increases, the rate of thinning becomes faster, particularly at smaller h_min. The system with 25% polymerized droplets exhibits the most abrupt thinning behavior, ∼110 μm ms⁻¹, increasing sharply as h_min decreases. The water system shows a faster thinning rate compared to the emulsions, while the glycerol system demonstrates a slower thinning (Fig. 4a). The corresponding timescale at which the thinning velocity remains unchanged upon decreasing neck radius is selected for pinch-off exponent analysis in Fig. 4b.

Fig. 4 Dynamic of fine emulsions filament pinch-off. (a) The relationship between the rate of change of the minimum filament thickness, , and the minimum filament thickness, h_min, for different emulsion systems with varying ratios of liquid and polymerized droplets. The x-axis represents h_min in micrometers on a logarithmic scale, while the y-axis represents in micrometers per millisecond, also on a logarithmic scale. (b) The minimum neck radius as a function of time to pinch-off. Green triangles: 25.0% volume fraction liquid droplets and no polymerized droplets, blue circles: 16.5% volume fraction liquid droplets and 8.5% volume fraction polymerized droplets, orange squares: 12.5% volume fraction liquid droplets and 12.5% volume fraction polymerized droplets, red inverted triangles: 8.5% volume fraction liquid droplets and 16.5% volume fraction polymerized droplets, black diamonds: no liquid droplets and 25.0% volume fraction polymerized droplets, gray stars: water, and brown stars: glycerol. (c) Images of water, glycerol, and emulsion filaments 0.25 ms before pinch-off.

To understand the effect of particle rigidity on the pinch-off of colloidal dispersions containing both liquid and polymerized droplets, we first discuss the pinch-off dynamics of single-phase liquids with a three magnitude difference in viscosity, specifically water (Oh = 0.004) and glycerol (Oh = 4.4). In the case of water (gray stars in Fig. 4b), the neck radius decreases proportional to τ^2/3, known as the capillary-inertia regime. In contrast, for glycerol (brown stars in Fig. 4b), the neck radius decreases proportional to τ, referred to as the capillary-viscous regime. Additionally, the images of water and glycerol drops taken 0.25 ms before pinch-off (Fig. 4c) reveal a significant sixfold increase in the length of the liquid filament as the viscosity increases from 1 to 1250 mPa s. Higher viscosity typically leads to slower droplet detachment due to increased internal resistance to flow. Therefore, we expect longer filaments as the droplet stretches before eventually pinching off.

Next, we consider two-phase liquid samples, i.e., emulsions, and observe in Fig. 4b that the neck radius decreases with τ, regardless of the concentration of liquid and polymerized droplets. In contrast to single-phase liquids, an increase in emulsion viscosity from 72 to 185 mPa s leads to a reduction in the length of the liquid filament by 40%, as shown in Fig. 4c.

The dynamics of droplet pinch-off in two-phase colloidal dispersions present a contrast to those observed in single-phase liquids like water and glycerol, e.g., interfacial tension and rheological properties can play significant roles in dictating the pinch-off behavior. The colloidal dispersion used in this study have similar values of interfacial tension. Emulsions containing liquid droplets that have higher elastic moduli exhibited longer liquid filaments before pinch-off (Fig. 3b), indicating the dominance of elastic forces in stretching the liquid filament. However, an inverse relationship is observed between the viscoelastic properties and the concentration of polymerized droplets (Fig. 2c, d and 3b, c). The competition between the fluid's viscosity and elasticity, which characterizes its ability to regain shape post-deformation, could be a key factor in determining the behavior of multiphase liquid filaments at pinch-off. Here, we observe that samples containing polymerized droplets have lower elastic moduli and exhibit faster pinch-off and shorter filament lengths (Fig. 3b–d). The rigidity of these particles resists the typical elongation and deformation seen in particle-free viscous fluids, thus reducing the filament length.

In our study, both viscosity and elasticity play critical roles in determining the deformation and length of the emulsion filaments during pinch-off. Higher viscosity increases the resistance to flow, meaning the filament stretches for a longer time before breaking because the viscous forces resist the capillary forces driving the thinning. As a result, a more viscous fluid tends to form longer filaments. Elasticity, on the other hand, refers to the ability of the fluid to store and recover energy when deformed. In viscoelastic emulsions, elastic forces act like a restoring mechanism during filament thinning. As the filament is stretched, elastic energy is stored, which resists further deformation. This stored energy also helps extend the filament length before pinch-off.¹⁹ Thus, both viscosity and elasticity act to prolong the filament length, but through different mechanisms. Viscosity dissipates energy, slowing down the flow, while elasticity stores energy, resisting further deformation. In our observations, however, the balance between these two factors shows that reduced elasticity (due to fewer deformable liquid droplets) tends to shorten the filament more than the increased viscosity extends it. Even though higher viscosity slows down neck thinning, the loss of elasticity plays a more significant role in leading to faster pinch-off and shorter filaments, as the system can no longer store as much elastic energy to resist deformation.

For fine emulsions, the droplet and particle sizes are below the resolution limit of 10 micrometers. Therefore, the pinch-off dynamics observed at scales larger than this limit are primarily influenced by the bulk emulsion, rather than the individual droplets. As a result, we do not capture the effects of single droplets on the pinch-off process, but instead observe and report their collective impact on the overall dynamics. Additionally, while the crossover from viscous to inertial regimes has been discussed in previous theoretical works,²⁸ capturing this transition experimentally requires higher spatio-temporal resolution, which is beyond the capabilities of our current setup.

3. Pinch-off: coarse emulsions

Next, we present the results for coarse emulsions. Fig. 5 presents a time series of coarse emulsion pinch-off processes, comparing the behavior of liquid, polymerized, and mixed droplet emulsions. Panels a–c depict the evolution of the liquid thread as the neck thins and eventually breaks, while panels a′–c′ show the corresponding neck profiles at various time intervals before pinch-off. In Fig. 5a, the emulsion composed entirely of liquid droplets exhibits a relatively long liquid thread before the pinch-off. There are multiple pinch-off points, as the filament thins unevenly at several locations. In Fig. 5b, a mixed emulsion (12.5% liquid and 12.5% polymerized droplets) shows a reduced thread length and fewer pinch-off points compared to the emulsion with liquid droplets. The presence of polymerized droplets limits the filament's deformability, reducing the number of heterogeneities along length and resulting in fewer pinch-off points. In Fig. 5c, the polymerized droplet emulsion shows the shortest thread length before pinch-off, with a single, well-defined pinch-off point. Overall, the images show that increasing the concentration of polymerized droplets shortens the filament and accelerates the pinch-off process, with fewer and more uniform breakage points.

Fig. 5 Shape evolution of coarse emulsion filaments containing 25.0% volume fraction droplets. (a) and (a′) 25.0% volume fraction liquid droplets and no polymerized droplets, (b) and (b′) 12.5% volume fraction liquid droplets and 12.5% volume fraction polymerized droplets, (c) and (c′) no liquid droplets and 25.0% volume fraction polymerized droplets. The instant of pinch-off is denoted as t_p and the time difference between pinch-off and given time is indicated by τ = t_p − t. (a)–(c) Time series of images from the neck formation until the break-up for each emulsion sample. (a′)–(c′) Overlapped boundaries of the extracted drops, emphasizing the visual distinctions among emulsion samples with varying concentrations of liquid and polymerized droplets.

Fig. 6a shows the pinch-off velocity versus minimum neck radius. Similar to the fine emulsions, emulsions with higher concentrations of polymerized droplets have higher speeds, which is 2.5 higher for 25% polymerized droplet compared to 25% liquid particles. For the emulsion with liquid droplets, the neck radius decreases with τ (Fig. 6b), similar to the behavior observed in the fine emulsion samples with liquid droplets. However, in emulsions containing both liquid and polymerized droplets, the neck radius decreases with τ^0.74±0.03, indicating a slightly smaller exponent compared to the fine emulsion samples. Furthermore, the pinch-off dynamics in coarse emulsions with polymerized droplets follow h_min ∼ τ^2/3, which closely resembles the pinch-off behavior observed in water droplets. This suggests the expulsion of polymerized droplets from the neck region during pinch-off (Fig. 6c and Movies S3 and S4, ESI†), so that the final stages are dominated by the properties of the continuous phase.

Fig. 6 Dynamic of coarse emulsions filament pinch-off. (a) The relationship between the rate of change of the minimum filament thickness, , and the minimum filament thickness, h_min, for different emulsion systems with varying ratios of liquid and polymerized droplets. (b) The minimum neck radius as a function of time. Green triangles: 25.0% volume fraction liquid droplets and no polymerized droplets, blue circles: 16.5% volume fraction liquid droplets and 8.5% volume fraction polymerized droplets, orange squares: 12.5% volume fraction liquid droplets and 12.5% volume fraction polymerized droplets, red inverted triangles: 8.5% volume fraction liquid droplets and 16.5% volume fraction polymerized droplets, black diamonds: no liquid droplets and 25.0% volume fraction polymerized droplets. (c) Images of emulsion filaments 0.25 ms before the pinch-off.

The expulsion of polymerized particles from the neck region during the pinch-off of the filament is controlled by a combination of capillary forces and hydrodynamic stresses, which become increasingly significant as the filament thins. Capillary forces, which aim to minimize the surface area of the fluid filament, dominate the thinning process and result in rapid narrowing of the neck.²⁶ As the neck radius decreases, the velocity of the fluid within the neck region increases, leading to enhanced hydrodynamic forces—particularly pressure gradients. These forces carry particles along with the accelerating fluid flow, which becomes more pronounced as the neck continues to thin.^41,62 When the neck diameter approaches the size of the polymerized particles, steric hindrance becomes significant. At this critical point, the polymerized particles can no longer be accommodated within the thinning filament due to their inability to deform, resulting in their expulsion from the neck region. The increased capillary pressure in the narrowing neck, combined with the rigidity of the particles, forces them out of the filament. Additionally, repulsive interactions between particles, such as electrostatic or steric forces, may contribute to this expulsion by promoting particle displacement away from the neck region.

Thievenaz and Suaret (2022) reported that during the pinch-off of suspensions, the dynamics shift from a homogeneous regime (where the suspension behaves like a viscous liquid) to a heterogeneous regime (where particle size and concentration become significant). Initially, the filament thins down uniformly, but once the thickness approaches a critical value related to the particle size, the dynamics change.⁴¹ The presence of particles disrupts the thinning process, leading to localized fluctuations in particle concentration. The critical filament thickness depends both on the particle diameter and the volume fraction of the suspension. Specifically, the transition to the heterogeneous regime occurs at a critical thickness, which is much larger than the particle diameter, particularly at high volume fractions. At a particle volume fraction of 25%, the critical filament thickness is estimated to range between 2 to 5 times the particle diameter. Once the filament thins below this critical thickness, the particles begin to separate, marking the end of the dislocation regime. As the thinning continues, the dynamics accelerate as the suspension shifts from being governed by particle–particle interactions to being dominated by the behavior of the interstitial fluid.

The introduction of polymerized droplets into emulsion systems significantly reduces the pinch-off time compared to systems consisting solely of liquid droplets. In fine emulsions (Fig. 4), for example, a filament containing 25% liquid droplets requires approximately 300 milliseconds to reach pinch-off (Fig. 4a). When the emulsion composition is adjusted to 16.5% liquid droplets and 8.5% polymerized droplets, the pinch-off time decreases to about 200 milliseconds. This decreasing trend continues with higher concentrations of polymerized droplets; an emulsion with 12.5% polymerized droplets exhibits a pinch-off time of around 120 milliseconds. The most pronounced reduction is observed in the system with 25% polymerized droplets, which reaches pinch-off in approximately 70 milliseconds.

A similar behavior is observed in coarse emulsions (Fig. 6). The system with 25% liquid droplets has a pinch-off time of approximately 320 milliseconds. Incorporating 12.5% liquid droplets and 12.5% polymerized droplets reduces the pinch-off time to about 150 milliseconds. The system containing 25% polymerized droplets shows a substantial reduction, reaching pinch-off in approximately 80 milliseconds. Coarse emulsions, characterized by larger droplet sizes, generally exhibit longer pinch-off times than fine emulsions due to the greater deformability of the liquid droplets. However, increasing the concentration of polymerized droplets leads to a more pronounced decrease in pinch-off time in both fine and coarse emulsion systems. Similar to the findings for fine emulsions shown in Fig. 4c, an increase in emulsion viscosity from 22 to 105 mPa s leads to a reduction in the length of the liquid filament before break-up. The presence of heterogeneities in the emulsion samples with liquid droplets highlights the entrapment of liquid droplets within the filament.

Conclusion

In summary, we conducted a comprehensive investigation into the pinch-off dynamics of filaments formed by complex colloidal dispersions. Our study primarily focused on emulsions containing varying concentrations of liquid and polymerized droplets while maintaining a constant overall volumetric concentration. The findings demonstrated that the existence of polymerized droplets in the emulsion reduces the length of the liquid thread before it breaks and speeds up the entire neck thinning process. We interpret this phenomenon as a result of the enhanced stiffness of the droplets, correspondingly, the decreased elastic modulus of the emulsion, and the increased aggregation tendencies among the droplets after polymerization. The trials with small and large emulsion droplets additionally highlight the impact of droplet size on the dynamics of filament pinch-off. When emulsions are made up of submicrometer droplets, these droplets often remain trapped in the filaments. On the other hand, when emulsions have larger droplets, these droplets are more likely to be pushed out, particularly when the filaments are similar in length to the droplet size, which then leads to dynamics of a thread of solvent. This difference emphasizes the importance of droplet size in influencing the filament behavior and how long the thread remains stable during the pinch-off process.

In this study, the total droplet concentration was fixed at 25% volume fraction. An increase in overall concentration would result in an enhance droplet–droplet interactions, leading to an increase in effective viscosity and significantly influencing the filament thinning dynamics. In systems with higher concentrations of liquid droplets, this could result in multiple pinch-off points due to the entrapment of liquid deformable droplets along the filament. In contrast, systems with higher concentrations of polymerized droplets may experience more pronounced particle aggregation, and in extreme cases, jamming may occur, potentially inhibiting the droplet pinch-off process. At lower total particle concentrations, the influence of particle–particle interactions diminishes, causing the system's behavior to more closely resemble that of a Newtonian fluid. In systems with liquid droplets at these reduced concentrations, the limited interactions between deformable droplets lead to more uniform filament thinning and delayed pinch-off, as the effects of droplet deformability become less significant. In polymerized droplet-dominated systems, the reduction in particle interactions allows the filament to elongate more freely, resulting in a more gradual pinch-off with less pronounced effects from individual particles on the thinning dynamics. These findings suggest that variations in total particle concentration could have a significant impact on the pinch-off dynamics, and this remains a subject for future research.

Data availability

All data generated or analyzed during this study are included in this manuscript and its ESI.† The raw data that support the findings of this study are available from the corresponding author Parisa Bazazi, pbazazi@mines.edu upon request.

Conflicts of interest

The authors declare no conflict of interest regarding the publication of this article. All research was conducted impartially, without any financial or personal relationships that could influence the work. Any funding sources or affiliations relevant to this study are disclosed in the acknowledgment section to ensure transparency.

Acknowledgements

We are grateful to the National Heart, Lung, and Blood Institute (Grant No. R01HL132906) for partial support when we started to investigate mixtures of hard and soft particles. We also think three anonymous reviewers whose feedback improved the paper.

References

1. Z. Liu, M. Zhang, B. Bhandari and Y. Wang, 3D printing: Printing precision and application in food sector, Trends Food Sci. Technol., 2017, 69, 83–94.
2. Q. Jiang, M. Zhang and A. S. Mujumdar, Novel evaluation technology for the demand characteristics of 3D food printing materials: A review, Crit. Rev. Food Sci. Nutr., 2022, 62(17), 4669–4683.
3. L. Qiu, M. Zhang, B. Bhandari, B. Chitrakar and L. Chang, Investigation of 3D printing of apple and edible rose blends as a dysphagia food, Food Hydrocolloids, 2023, 135, 108184.
4. G. Chen, Y. Xu, P. C. L. Kwok and L. Kang, Pharmaceutical applications of 3D printing, Addit. Manuf., 2020, 34, 101209.
5. V. M. Vaz and L. Kumar, 3D printing as a promising tool in personalized medicine, AAPS PharmSciTech, 2021, 22, 1–20.
6. S. Zhao, C. Guo, A. Kumarasena, F. G. Omenetto and D. L. Kaplan, 3D printing of functional microalgal silk structures for environmental applications, ACS Biomater. Sci. Eng., 2019, 5(9), 4808–4816.
7. P. S. Matharu, Z. Wang, J. H. Costello, S. P. Colin, R. H. Baughman and Y. T. Tadesse, Sojel-A 3D printed jellyfish-like robot using soft materials for underwater applications, Ocean Eng., 2023, 279, 114427.
8. R. M. Cardoso, P. R. Silva, A. P. Lima, D. P. Rocha, T. C. Oliveira and T. M. do Prado, et al., 3D-printed graphene/polylactic acid electrode for bioanalysis: Biosensing of glucose and simultaneous determination of uric acid and nitrite in biological fluids, Sens. Actuators, B, 2020, 307, 127621.
9. K. R. Hossain, J. Wu, X. Xu, K. Cobra, M. M. Jami and M. B. Ahmed, et al., Tribological bioinspired interfaces for 3D printing, Tribol. Int., 2023, 108904.
10. H. Cheng, L. Yi, J. Wu, G. Li, G. Zhao and Z. Xiao, et al., Drug preconcentration and direct quantification in biofluids using 3D-printed paper cartridge, Biosens. Bioelectron., 2021, 189, 113266.
11. B. Mahendiran, S. Muthusamy, S. Sampath, S. Jaisankar, K. C. Popat and R. Selvakumar, et al., Recent trends in natural polysaccharide based bioinks for multiscale 3D printing in tissue regeneration: A review, Int. J. Biol. Macromol., 2021, 183, 564–588.
12. A. Fatimi, O. V. Okoro, D. Podstawczyk, J. Siminska-Stanny and A. Shavandi, Natural hydrogel-based bio-inks for 3D bioprinting in tissue engineering: A review, Gels, 2022, 8(3), 179.
13. A. Chakraborty, A. Roy, S. P. Ravi and A. Paul, Exploiting the role of nanoparticles for use in hydrogel-based bioprinting applications: Concept, design, and recent advances, Biomater. Sci., 2021, 9(19), 6337–6354.
14. H. Taneja, S. M. Salodkar, A. S. Parmar and S. Chaudhary, Hydrogel based 3D printing: Bio ink for tissue engineering, J. Mol. Liq., 2022, 120390.
15. C. Xu, Z. Zhang, J. Fu and Y. Huang, Study of pinch-off locations during drop-on-demand inkjet printing of viscoelastic alginate solutions, Langmuir, 2017, 33(20), 5037–5045.
16. Z. Zhang, Y. Jin, J. Yin, C. Xu, R. Xiong and K. Christensen, et al., Evaluation of bioink printability for bioprinting applications, Appl. Phys. Rev., 2018, 5(4), 041304.
17. J. R. Lister and H. A. Stone, Capillary breakup of a viscous thread surrounded by another viscous fluid, Phys. Fluids, 1998, 10(11), 2758–2764.
18. J. R. Castrejón-Pita, A. A. Castrejón-Pita, S. S. Thete, K. Sambath, I. M. Hutchings and J. Hinch, et al., Plethora of transitions during breakup of liquid filaments, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(15), 4582–4587.
19. S. L. Anna and G. H. McKinley, Elasto-capillary thinning and breakup of model elastic liquids, J. Rheol., 2001, 45(1), 115–138.
20. Y. Amarouchene, D. Bonn, J. Meunier and H. Kellay, Inhibition of the finite-time singularity during droplet fission of a polymeric fluid, Phys. Rev. Lett., 2001, 86(16), 3558.
21. C. Wagner, Y. Amarouchene, D. Bonn and J. Eggers, Droplet detachment and satellite bead formation in viscoelastic fluids, Phys. Rev. Lett., 2005, 95(16), 164504.
22. R. Sattler, S. Gier, J. Eggers and C. Wagner, The final stages of capillary break-up of polymer solutions, Phys. Fluids, 2012, 24(2), 023101.
23. J. B. Keller and M. J. Miksis, Surface tension driven flows, SIAM J. Appl. Math., 1983, 43(2), 268–277.
24. Y.-J. Chen and P. H. Steen, Dynamics of inviscid capillary breakup: collapse and pinchoff of a film bridge, J. Fluid Mech., 1997, 341, 245–267.
25. R. F. Day, E. J. Hinch and J. R. Lister, Self-similar capillary pinchoff of an inviscid fluid, Phys. Rev. Lett., 1998, 80(4), 704.
26. J. Eggers, Nonlinear dynamics and breakup of free-surface flows, Rev. Mod. Phys., 1997, 69(3), 865.
27. D. Leppinen and J. R. Lister, Capillary pinch-off in inviscid fluids, Phys. Fluids, 2003, 15(2), 568–578.
28. J. Eggers and E. Villermaux, Physics of liquid jets, Rep. Prog. Phys., 2008, 71(3), 036601.
29. B. M. Rauzan, A. Z. Nelson, S. E. Lehman, R. H. Ewoldt and R. G. Nuzzo, Particle-free emulsions for 3D printing elastomers, Adv. Funct. Mater., 2018, 28(21), 1707032.
30. M. R. Sommer, L. Alison, C. Minas, E. Tervoort, P. A. Rühs and A. R. Studart, 3D printing of concentrated emulsions into multiphase biocompatible soft materials, Soft Matter, 2017, 13(9), 1794–1803.
31. T. Ma, R. Cui, S. Lu, X. Hu, B. Xu and Y. Song, et al., High internal phase pickering emulsions stabilized by cellulose nanocrystals for 3D printing, Food Hydrocolloids, 2022, 125, 107418.
32. F. Huisman, S. Friedman and P. Taborek, Pinch-off dynamics in foams, emulsions and suspensions, Soft Matter, 2012, 8(25), 6767–6774.
33. N. Louvet, D. Bonn and H. Kellay, Nonuniversality in the pinch-off of yield stress fluids: Role of nonlocal rheology, Phys. Rev. Lett., 2014, 113(21), 218302.
34. D. Lohse, Fundamental fluid dynamics challenges in inkjet printing, Annu. Rev. Fluid Mech., 2022, 54, 349–382.
35. J. Dinic, L. N. Jimenez and V. Sharma, Pinch-off dynamics and dripping-onto-substrate (dos) rheometry of complex fluids, Lab Chip, 2017, 17(3), 460–473.
36. D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Yield stress materials in soft condensed matter, Rev. Mod. Phys., 2017, 89(3), 035005.
37. M. Aytouna, J. Paredes, N. Shahidzadeh-Bonn, S. Moulinet, C. Wagner and Y. Amarouchene, et al., Drop formation in non-newtonian fluids, Phys. Rev. Lett., 2013, 110(3), 034501.
38. V. Thiévenaz and A. Sauret, Pinch-off of viscoelastic particulate suspensions, Phys. Rev. Fluids, 2021, 6(6), L062301.
39. J. Château, É. Guazzelli and H. Lhuissier, Pinch-off of a viscous suspension thread, J. Fluid Mech., 2018, 852, 178–198.
40. V. Thiévenaz, S. Rajesh and A. Sauret, Droplet detachment and pinch-off of bidisperse particulate suspensions, Soft Matter, 2021, 17(25), 6202–6211.
41. V. Thiévenaz and A. Sauret, The onset of heterogeneity in the pinch-off of suspension drops, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(13), e2120893119.
42. L. Chagot, S. Migliozzi and P. Angeli, Microfluidic droplet pinch-off modified by hard and soft colloids: A scaling transition, Phys. Rev. Fluids, 2024, 9(5), L052201.
43. A. Perazzo, Z. Peng, Y.-N. Young, Z. Feng, D. K. Wood and J. M. Higgins, et al., The effect of rigid cells on blood viscosity: linking rheology and sickle cell anemia, Soft Matter, 2022, 18(3), 554–565.
44. H. A. Barnes, Rheology of emulsions—a review, Colloids Surf., A, 1994, 91, 89–95.
45. S. R. Derkach, Rheology of emulsions, Adv. Colloid Interface Sci., 2009, 151(1–2), 1–23.
46. R. Pons, C. Solans and T. F. Tadros, Rheological behavior of highly concentrated oil-in-water (o/w) emulsions, Langmuir, 1995, 11(6), 1966–1971.
47. Y. Zhu, H. Gao, W. Liu, L. Zou and D. J. McClements, A review of the rheological properties of dilute and concentrated food emulsions, J. Texture Stud., 2020, 51(1), 45–55.
48. R. Pal, Effect of droplet size on the rheology of emulsions, AIChE J., 1996, 42(11), 3181–3190.
49. R. Andersson, G. Hernández, K. Edström and J. Mindemark, Micro versus nano: impact of particle size on the flow characteristics of silicon anode slurries, Energy Technol., 2020, 8(7), 2000056.
50. Y. Liu, Q. Zhang and R. Liu, Effect of particle size distribution and shear rate on relative viscosity of concentrated suspensions, Rheol. Acta, 2021, 60, 763–774.
51. B. Konijn, O. Sanderink and N. P. Kruyt, Experimental study of the viscosity of suspensions: Effect of solid fraction, particle size and suspending liquid, Powder Technol., 2014, 266, 61–69.
52. A. Y. Malkin, Non-newtonian viscosity in steady-state shear flows, J. Non-Newtonian Fluid Mech., 2013, 192, 48–65.
53. A. J. Banchio and J. F. Brady, Accelerated stokesian dynamics: Brownian motion, J. Chem. Phys., 2003, 118(22), 10323–10332.
54. J. Wang, H. Jing and Y. Wang, Possible effects of complex internal structures on the apparent viscosity of multiple emulsions, Chem. Eng. Sci., 2015, 135, 381–392.
55. M. Fuchs and M. E. Cates, Theory of nonlinear rheology and yielding of dense colloidal suspensions, Phys. Rev. Lett., 2002, 89(24), 248304.
56. T. Mason, J. Bibette and D. Weitz, Elasticity of compressed emulsions, Phys. Rev. Lett., 1995, 75(10), 2051.
57. H. Katepalli, V. T. John, A. Tripathi and A. Bose, Microstructure and rheology of particle stabilized emulsions: Effects of particle shape and inter-particle interactions, J. Colloid Interface Sci., 2017, 485, 11–17.
58. J. J. Stickel and R. L. Powell, Fluid mechanics and rheology of dense suspensions, Annu. Rev. Fluid Mech., 2005, 37(1), 129–149.
59. J. Mewis and N. J. Wagner, Colloidal suspension rheology, Cambridge University Press, Cambridge, 2012, vol. 10.
60. H. Barnes, Shear-thickening (“Dilatancy”) in suspensions of nonaggregating solid particles dispersed in Newtonian liquids, J. Rheol., 1989, 33(2), 329–366.
61. H. Princen, Rheology of foams and highly concentrated emulsions: I. elastic properties and yield stress of a cylindrical model system, J. Colloid Interface Sci., 1983, 91(1), 160–175.
62. R. J. Furbank and J. F. Morris, An experimental study of particle effects on drop formation, Phys. Fluids, 2004, 16(5), 1777–1790.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00618f

---