A multi-body finite element model for hydrogel packings: linear response to shear

Abstract

We study a multi-body finite element model of a packing of hydrogel particles using the Flory–Rehner constitutive law to model the deformation of the swollen polymer network. We show that while the dependence of the pressure, Π, on the effective volume fraction, ϕ, is virtually identical to a monolithic Flory material, the shear modulus, μ, behaves in a non-trivial way. μ increases monotonically with Π from zero and remains below about 80% of the monolithic Flory value at the largest Π we study here. The local shear strain in the particles has a large spatial variation. Local strains near the centers of the particles are all roughly equal to the applied shear strain, but the local strains near the contact facets are much smaller and depend on the orientation of the facet. We show that the slip between particles at the facets depends strongly on the orientation of the facet and is, on average, proportional to the component of the applied shear strain resolved onto the facet orientation. This slip screens the stress transmission and results in a reduction of the shear modulus relative to what one would obtain if the particles were welded together at the facet. Surprisingly, given the reduction in the shear modulus arising from the facet slip, and the spatial variations in the local shear strain inside the particles themselves, the deformation of the particle centroids is rather homogeneous with the strains of the Delaunay triangles having fluctuations of only order ±5%. These results should open the way to construction of quantitative estimates of the shear modulus in highly compressed packings via mean-field, effective-medium type approaches.

---

I. Introduction

Particles made of hydrogels – chemically cross-linked polymeric materials which swell when they absorb water – are important in industries such as pharmaceuticals, bioengineering, agriculture, food science, and cosmetics.^1–4 Owing to their softness and the in situ tunability of their size via controlled swelling, they have also been used more recently as a test bed for basic ideas in the physics of jamming and the glass transition.^5–11 The basic statistical mechanical description of the mechanical properties of macroscopic, monolithic pieces of hydrogel material goes back to Flory and Rehner,^12–15 however, the properties of suspensions or packings of particles made out of the hydrogel are much more subtle and have been the subject of active research only over the past couple of decades.

Typically, in experiments, the particles in a suspension are initially allowed to freely swell at low number density, then, once fully swollen, are subjected to osmotic confinement with a membrane^11,16,17 or to centrifugation,¹⁸ forcing the swollen particles into persistent contact and making a jammed solid where the particles are no longer free to diffuse and pass each other without incurring an energetic penalty associated with deformation of the polymer network. At low degrees of confinement, the particles remain essentially spherical, and contacts between them are only slightly deformed. The mechanics and energetics of the interactions in this regime should be reasonably well described by standard Hertzian contact mechanics¹⁹ treating one contact at a time resulting in a pairwise description of the energy of the whole system. However, as the confinement increases, the inter-particle contacts will develop into curved facets,^20,21 and, at large enough confinement, the void space with pure solvent will completely disappear altogether. In foams and emulsions at such large particle volume fractions, it is known that not only does linear contact mechanics fail to describe the interactions at a given contact, but even worse, pairwise descriptions of any kind become qualitatively inaccurate in this regime,^22–24 and there is no reason to think that the micro gel packings of interest here will be any different. One must consider in detail the deformation inside the particles. It is this strongly confined, fully-faceted, regime which is of primary interest to us here.

Several groups^11,16,17 have measured the elastic modulus, G, of highly compressed microgel packings under osmotic confining pressure, Π, at increasing nominal volume fraction, ϕ. In all cases, one observes a rapid increase of Π and G from, essentially, zero as the particles are first forced into contact at the jamming transition when ϕ reaches the random close packing point ϕ_J. The observed behavior of Π and G is qualitatively consistent with the jamming picture²⁵ where Π and G are both zero below the jamming point, ϕ_J, and, near jamming, scale as non-trivial power of δϕ = ϕ − ϕ_J. Precise scaling laws for Π and G are difficult to obtain in experiments, but in all experiments, there is an obvious and dramatic onset of both Π and G near a critical ϕ value. At higher ϕ, away from jamming on approach to the fully faceted regime, the situation becomes more complicated. Cloitre et al.,¹¹ have shown that there is a transition from a more pronounced to a less pronounced dependence of G on ϕ and argued that it occurs at the point at which the assembly becomes fully faceted with no void regions of pure solvent remaining. Liétor-Santos et al.¹⁷ showed that G, Π, and, the compression modulus, K, all scaled with K_p, the compression modulus of an isolated particle osmotically confined to the same average particle size as in the packing, so that G/K_p, K/K_p, and Π/K_p were all universal constants in the compressed packing independent of the degree of compression of the packing or the degree of crosslinking of the particles. Menut et al.¹⁶ have studied a variety of particles with different cross-linking densities and sizes. They argued that sufficiently far above the jamming point, the density dependence of the modulus followed the trend that would be expected for a monolithic Flory material.^12,13 Here, we find, what is perhaps the simplest non-trivial outcome one could have expected: a pressure vs. ϕ behavior almost precisely the same as the monolithic Flory material and a universal shear modulus vs. pressure curve for systems with different cross-linking density when the modulus and pressure are both scaled by the Flory pressure, NkT, where N is the density of cross-links in the dry reference state.

II. Model

Previous modeling work has proceeded along many fronts. Many groups assume pair-wise additive interactions between particles even in a very high-density regime far from jamming,^20,26–29 sometimes modified to attempt to account for ϕ dependent effective interactions,^24,30–35 which are, however, still pair-wise contact interactions. As we mention above, this approach is known to fail in foams and emulsions due to strong many-body effects in the particle–particle forces,²⁴ and we would expect it to fail as well here for the microgel packings in the high ϕ, fully faceted, regime. More realistic and appropriate models take into account the nature of the deformation of the polymer network itself.^{21,27,36–39} Nikolova et al.³⁹ studied a bead-spring coarse-grained model with dissipative particle dynamics (DPD) to model both the elasticity of the gel network and the dynamics of solvent expulsion out of the network as the packing is confined. They allowed their particles to swell and subjected them to isotropic osmotic confinement. They found that, above ϕ = 1, K/K_p approached a constant value of about 0.8, in agreement with the experiments of Liétor-Santos et al.,¹⁷ but they did not study the shear modulus.

Here, we take a different approach. Rather than using a bead-spring model to explicitly represent the gel network, we represent the gel network as a homogenized continuum using the Flory–Rehner constitutive law. This approach is standard in the solid mechanic's community where various non-linear elastic properties of macroscopic swollen gels are of interest,^40–43 however, perhaps surprisingly, it has not been applied to particle packings. The model can easily incorporate spatial variations in local cross-linking densities within a particle which may arise in various particle synthesis procedures (e.g. a hard, moderately swollen, core with high cross-link density enclosed by a soft, highly swollen, corona with low cross-link density), but in this preliminary work, we assume a homogeneous cross-linking density across the particle, and we assume the same cross-linking density for large and small particles. The main disadvantage of our approach is that we cannot realistically study the fluid dynamics of solvent uptake/expulsion from the network and are restricted to compression and shear rates which are slow enough that we can assume the hydrodynamic forces generated by solvent flows are negligible. However, as we are primarily interested in the quasi-static regime in this work where the packing is sheared slowly enough to allow the fluid to be fully expelled/absorbed before further shearing, we are not adversely affected by this limitation. Another potential disadvantage is that we are not able to capture inter-digitation of polymer segments across inter-particle facets.^21,39,44,45 However, the effects of inter-digitation are largely uncontrolled in bead-spring models; this will give rise to tangential forces at the facets in a way that is not particularly well controlled or calibrated. In our opinion, it is best to study and characterize a model which at first excludes these effects explicitly and only later introduces them in a controlled way. Furthermore, in ref. 39, the authors tune the properties of their bead-spring network to make sure that it behaves mechanically as a Flory solid, whereas here, we simply start with a Flory solid by construction.

Flory's constitutive law is governed by a total free energy density, W_tot, which gives the free energy per unit (unswollen reference) volume where W_tot = W_e + W_m receives independent contributions from non-linear elastic deformation of the polymer network, W_e, and from the free energy of mixing of the polymer and solvent, W_m. We have, for W_e and W_m,^12–15,40

where N is the number of cross-links per unit volume in the dry reference state, k is Boltzmann's constant, T is the temperature, F_αβ = δ_αβ − ∂_αu_β is the deformation gradient where u is the displacement of the polymer network away from its unswollen reference configuration, d is the dimension of the system, J is the determinant of F_αβ (so that J gives the volumetric expansion at a given point relative to the dry reference and J^1/d = λ gives the linear stretch ratio), Ω is the volume of a solvent particle (which is taken to be constant) and χ gives the energetic contribution to the free energy of mixing. In this preliminary work, we consider entropic swelling only and set χ = 0, so there is one and only one dimensionless parameter in the model: NΩ, the number of cross-links in the dry reference configuration per unit solvent particle volume. In the case of strongly hydrophobic energetics (large χ), the interplay between stretching of the network and demixing of the polymer from the solvent can lead to a non-monotonic pressure vs. volume fraction dependence which could, in principle, affect the mechanics of the assembly. However, this non-monotonic pressure dependence occurs in the tensile regime of stresses and would not qualitatively affect the main results in our study. For large NΩ the particles will be stiffer and undergo less free swelling, while for small NΩ, the particles will undergo more free swelling and be softer. If we consider the isotropic swelling case with a linear stretch factor, λ, we have, F_αβ = λδ_αβ and J = λ^d so F_αβF_αβ = dλ² = dJ^2/d. The osmotic pressure, Π, is simply the derivative of the free energy with respect to the logarithm of the volume, , so

The degree of free swelling is determined by setting Π = 0 and solving for the equilibrium, J₀. J₀ will depend on NΩ, with larger NΩ (more cross-linking) giving less unconstrained swelling.^12–15,40 We study three different NΩ values: 1/20, 1/133, and 1/754, and solving for Π = 0 gives: J₀ = 4.00762, 8.99301, 20.2519 respectively. That is: our least densely cross-linked (softest) particles freely swell to roughly 20 times their dry area, while our most densely cross-linked (hardest) particles freely swell to roughly 4 times their dry area.

We simulate the system using standard finite element method (FEM) techniques using constant strain triangle (CST) elements to mesh the particles⁴⁶ and use a simple gradient descent to re-equilibrate the system. We use a 50 : 50 mixture of two species of circular particles with the ratio between the radii equal to 1.4.²⁵ The disks are initialized on a square grid, allowed to swell freely, and then slowly compressed.

To enforce impenetrability constraints, we simply introduce a strong power-law repulsion between surface nodes of opposing particle FEM meshes: V_ij = V₀(r_ij/R)^−a where r_ij is the distance between the surface nodes on opposing particle meshes, R is the length-scale of the repulsion, V₀ is the energy scale of the repulsion, taken here to simply be NkT, and a = 12 is an exponent which is chosen to be large enough that it prevents inter-penetration and does not otherwise affect the results. To avoid artificial interlocking of surface nodes and the resulting tangential forces, we choose a lengthscale for the power-law repulsion which is roughly 6 times the surface node spacing in the dry reference mesh, and we find that this sufficiently suppresses tangential traction forces at the facets. Because of the stiffness of the surface repulsion, the surface interactions do not contribute significantly to the overall energy or stress, so we neglect them when reporting stresses and moduli. However, the numerical scheme results in a skin at the facets between the surface nodes which has a constant size which does not change as the packing is subjected to contraction of the space. This results in a larger and larger fraction of the space being taken up by the spurious skin as the system is compressed. To compensate for this artifact, we define the Cauchy stress, whose trace is the pressure, as the derivative with respect to an infinitesimal strain increment of the total energy of the deformed elastic network divided by the area occupied by the gel excluding the area of the skin region. We have checked that the contribution of the power-law repulsion to the total energy is negligible as long as the exponent is chosen to be sufficiently large. We similarly define ϕ = J₀/〈J〉 as the ratio of the total freely-swollen particle area to the current total particle area occupied excluding the skin. This definition of ϕ – which is, by construction, greater than or equal to 1 for compressed particles – is somewhat un-natural near the jamming onset where one would want to divide the freely swollen particle volume by the area of the simulation cell rather than just the area occupied by the polymer network. To measure ϕ = J₀/〈J〉 in an experiment, one would need to have an independent measurement of the pore volume in the sample to infer the current total particle volume, but, nevertheless, it is the natural quantity to use in the model to make a direct connection between the mechanical response of the packing and the mechanical response of the equivalent monolithic continuum.

III. Results

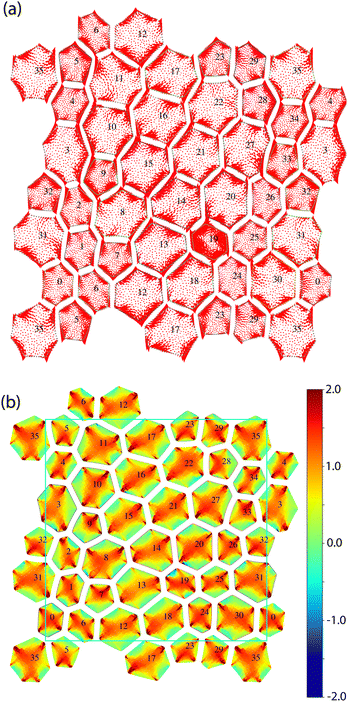
In Fig. 1, we show an image of the local pressure in units of NkT for a typical system of 16 particles with NΩ = 1/133 at a nominal ϕ = 1.73 which is in the fully faceted regime with no remaining voids of pure solvent. Each triangular element in the FEM mesh is colored according to its pressure (with the standard solid mechanics convention that compressive stresses are negative). We observe some high-frequency oscillations from element to element, but we have checked that these are suppressed using higher-order finite element schemes and do not affect any of the main results of this work. Some general trends can be seen here which are observed in other members of the ensemble and at various other NΩ and various other ϕ. (i) Small particles tend to have higher pressure than large particles. (ii) Pressure tends to be larger near the centers of facets than near the facet junctions. (iii) Facets between large and small particles tend to be convex on the small-particle side and concave on the large-particle side: that is, the small particles tend to protrude into the large ones. (iv) Particles with fewer facets tend to be at larger pressure and vice versa. For instance, particle 14, a small particle which has four neighbors, is at a larger pressure than the other small particles which have 5 or 6 neighbors, while particle 10, a large particle which has eight neighbors, is at a smaller pressure than the other large particles which have 7 or 6 neighbors.

Fig. 1 Local pressure, Π, in units of NkT for a typical system of 16 particles with NΩ = 1/133 at a nominal ϕ = 1.73. Particles are labeled with a unique identification number for discussion in the text.

In the inset of Fig. 2, we show the pressure, Π, vs. ϕ (recall the definition of ϕ = J₀/J excludes regions of pure solvent). The results are for an ensemble of 36-particle systems. The symbols represent the pressure computed in the actual packing, and the curves simply represent the pressure for an isotropic monolith of Flory material as computed from eqn (3) at the given J = J₀/ϕ. The agreement is striking! The pressure field inside the particles is inhomogeneous: it is large near the facets and smaller near the vertices in the facet network with overall fluctuations of order tens of percent. Yet despite this inhomogeneity, the spatial average of the pressure is very close to that of the isotropically confined Flory monolith at the same density as the average density of the packing. There is no fundamental reason why this relation must be an exact identity, and we do see deviations from the monolithic result of the order of a few percent. It is a manifestation of the fact that the distribution of local J values has a width that is small relative to its average and that the Π(J) function from eqn (3) varies relatively slowly on that scale so that 〈Π(J)〉 ≈ Π(〈J〉).

Fig. 2 Main: Shear modulus vs. osmotic pressure, Π, for various cross-link densities. The red line is the shear modulus of a two-dimensional monolithic Flory material. Inset: Π/NkT vs. ϕ. Dots are data from the FEM simulation. Solid lines are for a monolithic Flory solid.

The pressure diverges locally as J → 1 from above, and this sets an upper bound on ϕ at ϕ_max = J₀ as the solvent is completely expelled from the system. Accordingly, we see Π begin to diverge first for the system with the highest NΩ and last for the system with the lowest NΩ. Our numerical scheme becomes unstable at a pressure of about Π = 10NkT for all systems, so we are able to reach slightly higher ϕ for the systems with lower NΩ.

To measure the shear modulus, we make a small axial deformation to all FEM nodes and the periodic boundaries with extension along the horizontal, x, and contraction along the vertical, y: x → e^εx ≈ (1 + ε)x,y → e^−εy ≈ (1 − ε)y, re-equilibrate, and then measure the tangent modulus as μ = Δσ/ε where Δσ is the change in the shear component of the Cauchy stress. Since we hold the cell in a square shape during the initial swelling of the circular particles, there will be a random residual shear stress which is distributed normally about zero in our ensemble. It is very small compared to μ and does not affect the results.

In the main plot of Fig. 2, we show the shear modulus, μ, vs. the osmotic pressure, Π. For a monolithic Flory material in 2D, μ = NkT regardless of NΩ and completely independent of Π (and/or ϕ). For our particle packing, the curves all start at zero near the jamming point at Π = 0 and increase monotonically remaining below the monolithic Flory value. Strikingly, the curves collapse, indicating that the shear modulus of the packing is a function of the pressure alone and is independent of the cross-linking density (after scaling by NkT). This observation for the shear modulus is in a similar spirit to the observation of Liétor-Santos et al.¹⁷ that the pressure and shear modulus scale like the single-particle compression modulus, but must differ in detail as we argue below.

In Fig. 3(a), we show a typical NΩ = 1/20 system with 36 particles at ϕ = 2.09 subjected to a small strain step as described above. We show only the non-affine component of the nodal displacements. In Fig. 3(b), we show the combination of the components of the gradient of the displacement corresponding to the applied strain: (∂_xu_x − ∂_yu_y)/2 normalized by the applied strain so that a value of 1 indicates that the material is locally shearing precisely according to the globally imposed shear strain. The strain is quite inhomogeneous across the particles. In the centers of all the particles, the shear strain is approximately equal to the globally imposed shear strain, while the deformation near facets and vertices depends on the orientation. Facets that are roughly vertical or horizontal have essentially no relative displacement, while facets that are roughly diagonal across the cell have a significant amount of relative tangential motion indicating sliding along those facets.

Fig. 3 (a) Non-affine displacement field normalized by the imposed shear strain. The imposed shear strain is axial with vertical contraction (horizontal extension) and area-preserving at ϕ = 2.1 for a system with cross-linking density NΩ = 1/20. Arrows are drawn to scale to precisely give the non-affine displacement per unit applied strain. (b) Local shear strain, (∂_xu_x − ∂_yu_y)/2, scaled by the imposed shear strain.

In Fig. 4, to illustrate this point, we zoom in on the facet between particles 25 and 31, since this facet is nearly vertical. For ease of discussion, we label the triple junction with particle 26 on top and with particle 30 on the bottom as T and B respectively. Since the facet is a contact between a large and small particle, it has a slight curvature toward the small particle, but this should not significantly affect the response. The facet is nearly vertical, and there is essentially no non-affine displacement on either side. However, the displacement on particle 26 at the T vertex is downward, and the displacement on particle 30 at the B vertex is upward, so the facet is shortening. As particles 26 and 30 are advancing into the facet, the strain near their vertices at the triple junctions is nearly zero: green in the color scheme of the image. On the other hand, the material near the four vertices on particles 25 and 31 at the T and B triple junctions is very strongly sheared – with local shear strains greater than the applied shear strain – to accommodate the shortening of the facet. The two other facets connected to T and the two other facets connected to B are all oriented approximately 30 degrees from horizontal and have a significant amount of slipping. Since the tangential traction forces at the slipping interface are zero, and the shear stress must be zero along the facet, the slip results in a screened region where the strains in the particles are quite small and nearly zero at the facet.

Fig. 4 Closeup on the facet between particles 25 and 31 from Fig. 3. The triple junction with particle 26 on the top and 30 on the bottom are labeled T and B respectively for ease of discussion in the text.

The same scenario plays out in reverse for facets which are oriented horizontally. The result is that all particle vertices in the packing whose opposing facet is nearly horizontal or vertical should have a very low strain in their neighborhood, and a quick scan of the packing shows this to be true. For example, the facet between particles 34 and 35 is nearly horizontal, so it is lengthening, and the corresponding vertices on particles 28 and 4 have a very low shear strain on them: the fact that particle 28 has 5 neighbors and is compressed into a pentagon is incidental and has little impact on this result.

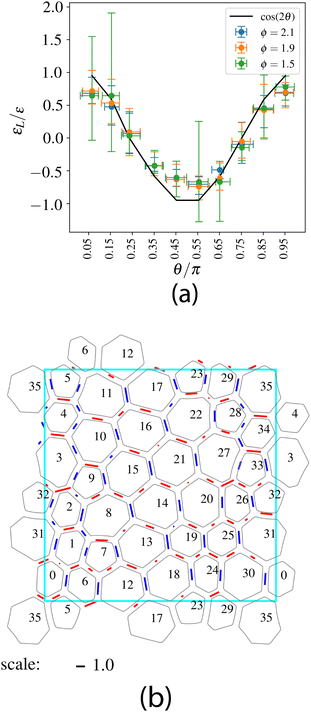
In Fig. 5 and 6, we show the slip and strain on the facets as a function of the facet angle. We approximate the facet network as polygonal and identify the vertices of the polygonal network with the surface nodes of the mesh located at the triple junctions. Then, to define the facet slip, ω, we simply take the difference in the average tangential component of displacement on either side of the facet. Similarly, to define the facet strain, ε_L, we take the difference in the component of the end-to-end displacement along the end-to-end separation and divide by the current facet length. What we see agrees remarkably well with the anecdotal description of the displacement fields in Fig. 3 where facets along the box diagonals slip significantly but neither shorten nor lengthen while facets along the axes do not slip but shorten (the vertical ones) or lengthen (the horizontal ones). In fact, we can make some simple assumptions about the deformation kinematics. If we assume the slip on a facet is equal to the locally resolved transverse component of the applied displacement gradient: ω = n̂_αt̂_β∂_αu_β where ∂_αu_β is the imposed deformation and n̂ and t̂ are the unit normal and tangent to the facet, then we would get: ω = ε sin(2θ) where θ is the angle of the tangent. For the strain, if one imagines that the triple junctions in the facet network deform affinely with the imposed shear, one would expect that ε_L = t̂_αt̂_β∂_αu_β = ε cos(2θ). We see that the data follow that trend remarkably well regardless of ϕ with no discernible trend with ϕ. Our argument seems to slightly overestimate the slip and underestimate the strain, but all things considered, this prediction with no adjustable parameters seems to work out well: the deformation of the facet network is essentially affine and equal to the homogeneously imposed deformation.

Fig. 5 (a) Facet slip, ω (defined in text) scaled by applied strain ε vs. facet angle θ for three different NΩ systems at ϕ = 1.5, 1.9 and 2.1. (b) Facet slip in real space with arrow length indicating the amount of slip with red and blue indicating counter-clockwise and clockwise vorticity respectively.

Fig. 6 (a) Facet strain, ε_L (defined in text) scaled by applied strain ε vs. facet angle θ for three different NΩ systems at ϕ = 1.5, 1.9 and 2.1. (b) Facet strain in real space with bar length indicating the amount of relative lengthening (red) or shortening (blue).

In Fig. 7, we show the strains associated with the motion of the particle centroids. We define the strain as piecewise constant on the Delaunay triangulation⁴⁷ of the contact network using linear interpolation of the three centroid displacements. What we see is that the resulting deformation of the particle centroids is quite homogeneous despite the large inhomogeneities within any given particle. It is hard to draw any statistical trends or make correlations between the Delaunay strain and any obvious geometrical or topological properties of the packing.

Fig. 7 Shear strain of the particle centroids scaled by the applied strain. The strain is computed for each Delaunay triangle in the contact network by linear interpolation. Slip vectors are reproduced from the figure for convenience 5.

IV. Discussion and summary

We have shown here that the microgel packings behave in one of the simplest ways one could have imagined: the pressure has a density dependence as if it were a monolithic Flory material, while the shear modulus, although it has a non-trivial ϕ dependence and starts from zero at the jamming point, is a universal function of the dimensionless pressure, Π/NkT, independent of cross-linking densities. The μ/NkT vs. Π/NkT curve shows a transition from a more strongly pressure-dependent regime at low pressure near jamming onset to a much weaker pressure dependence in the fully-faceted regime and is consistent with the conjecture in Cloitre et al.¹¹ that the transition to the weaker concentration dependence of G occurred at the onset of full-faceting where solvent-pure void space completely disappeared. This is also completely consistent with the arguments of Menut et al.¹⁶ who claimed that their systems showed monolithic Flory behavior at high density (although we point out that the scaling behavior for a Flory monolith in 3D is μ ∼ ϕ^1/3 rather than the μ ∼ ϕ¹ suggested in that work).^14,15

We note that our definitions for ϕ and Π are based on the notion of excluding the artificial skin region which results as an artifact from our algorithm that enforces the impenetrability constraints, and it was necessary for us to make these corrections to get precise agreement with the monolithic Flory curve at all ϕ. In order to make a closer comparison with experiments to see whether the Π vs. ϕ behavior is a also described by a monolithic Flory material, one would want to independently measure the volume of pure solvent in a packed sample (which would vanish in the fully-faceted regime) and remove this volume when calculating Π and ϕ as we did here in the model. However, in experiments, there is an extra complication arising due to the uncertainty in defining a particle volume even in the case of freely swollen, highly dilute systems where the edges of the network consist of a corona of dangling segments. Despite this complication, one might still hope to recover the monolithic Flory behavior in the fully faceted regime where the current total particle volume is simply equal to the system volume and there is no pure-solvent region to correct for. In fact, we now discuss how the Π/K_pvs. ϕ results in ref. 17, may be in agreement with monolithic Flory behavior. At face value, our results would seem to be inconsistent with Liétor-Santos et al.¹⁷ where Π became independent of ϕ when scaled by the particle compression modulus, K_p, rather than the Flory modulus, NkT. However, in Fig. 8, we plot the compression modulus, K, vs. the pressure, Π, for our three NΩ values for a homogeneously compressed Flory solid where 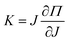. The compression modulus for the zero pressure freely swollen state is around K_eq ≈ 2NkT and has only a weak dependence on cross-linking density NΩ. We see that Π/K does not vary dramatically over the pressure range, and for the two more weakly cross-linked systems, Π/K ≈ 0.4 above about Π = 4NkT. Since our Π vs. ϕ curves for the packing are virtually identical to the monolith, this means that our results are roughly consistent with ref. 17 where Π/K was roughly constant above ϕ = 1. Our results for the shear modulus, in distinction with the pressure and compression modulus, are not as easy to reconcile with ref. 17. If we were to scale the shear modulus by K rather than NkT, because of the NΩ dependence of K illustrated in Fig. 8, we would break the good collapse obtained in Fig. 2. Furthermore, the ϕ-independent values of G/K_p obtained in ref. 17 are of the order of a few percent, whereas here, our values of μ/NkT are around 0.8 for most of the pressure range of interest; our values for μ/K would vary much more strongly with pressure than our μ/NkT do.

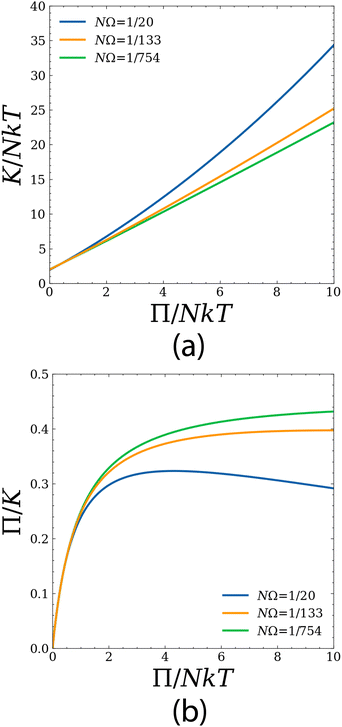Fig. 8 (a) Compression modulus, K/NkT, vs. osmotic pressure, Π/NkT, for a monolithic Flory material in the range of pressures of interest in this work 0 < Π/NkT < 10. (b) Their ratio, Π/K, vs. Π/NkT.

What we've shown here is that, once the system is in the fully faceted regime, the kinematics of shear deformation becomes largely insensitive to the compression. The vertices in the facet network, on average, follow the imposed homogeneous deformation. The resulting slip at the facets results in a reduction of the modulus of the packing away from the monolithic Flory value by some tens of percent but remains of the order of the monolithic value. In the future, it would be important to use the kinematic information about the affine motion of the facet-vertex network to try to construct quantitative estimates for the modulus reduction away from the Flory value. Since each particle is assumed to be homogeneous, the result of imposing a homogeneous deformation on the particle's boundary would be a homogeneous deformation of the particle interior, and the result would be a recovery of the full Flory shear modulus as if the particles were welded together at the facets. So it seems, going beyond considering the average kinematic behavior of the facet network would be necessary to obtain any corrections to the Flory shear modulus.

In this work, we made many simplifying assumptions. We assumed that: (i) the particles were homogeneous disks, (ii) the free energy of mixing was completely entropic with χ = 0, (iii) the facets were free of friction and neglected any possible effects of inter-digitation of the polymer networks across the facets, (iv) the deformation was slow enough that kinetics and viscous flow effects were negligible and that the solvent was able to freely flow into and out of the polymer network with no resistance (v) the particles were large enough that Brownian effects were negligible, (vi) the system was 2D. It will be useful to go beyond these assumptions in future models. In particular, interdigitation and/or roughness across the facets – which could be accounted for, in a model like ours, through a Coulomb friction term – might suppress the slipping we see at the facets and bring the shear modulus up toward the monolithic Flory value. It would be interesting to account for this quantitatively. It would also be important to know how the many-body interactions studied here at large volume fraction affect the plastic yielding behavior at large strains and the glass transition for the Brownian case, and, more generally, the overall rheological response at arbitrary strains and strain rates. Despite these interesting future directions for study, our explanation for the corrections to the monolithic Flory behavior induced by the affine facet slip provides a starting point for future quantitative models of the mechanical response of these packings.

Data availability

The Multibody FEA code used in this article can be found in the repository at https://github.com/aelgailani/MBFEA. The repository also includes input data for 4 × 4 and 6 × 6 lattice systems. Unfortunately, the original data used in the article was permanently lost due to a technical incident that damaged the cloud storage our group utilized. However, the results can be reproduced using the FEA code and input data available in the repository.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank Alberto Fernandez-Nieves, Emanuela Zaccarelli, Lorenzo Rovigatti, Michel Cloitre, Robin Selinger, and especially Massimo Pica Ciamarra, Max Bi, and Jeffrey Sokoloff for useful discussions in the early stages of this work. We thank Manuel Valera for their help with code development and optimization. We thank MGHPCC for computing support. This material is based upon work supported by the National Science Foundation under Grant No. CMMI-1822020.

References

1. E. Pashkovski, Applications of Biopolymer Microgels, John Wiley and Sons, Ltd, 2011, pp. 423–450. Available from: https://onlinelibrary.wiley.om/doi/abs/10.1002/9783527632992.ch17.
2. L. A. Lyon, G. R. Hendrickson, Z. Meng and A. N. St John Iyer, Exploiting the Optical Properties of Microgels and Hydrogels as Microlenses and Photonic Crystals in Sensing Applications, John Wiley and Sons, Ltd, 2011, pp. 355–374. Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/9783527632992.ch14.
3. Y. Ben, I. Robb, P. Tonmukayakul and Q. Wang, Microgels for Oil Recovery, John Wiley and Sons, Ltd, 2011, pp. 407–422. Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/9783527632992.ch16.
4. M. Malmsten, Microgels in Drug Delivery, John Wiley and Sons, Ltd, 2011, pp. 375–405. Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/9783527632992.ch15.
5. P. Agarwal and L. A. Archer, Strain-accelerated dynamics of oft colloidal glasses, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2011, 83(4), 041402.
6. J. Mattsson, H. M. Wyss, A. Fernandez-Nieves, K. Miyazaki, Z. Hu and D. R. Reichman, et al., Soft colloids make strong glasses, Nature, 2009, 462(7269), 83–86,  DOI:10.1038/nature08457.
7. A. Basu, Y. Xu, T. Still, P. E. Arratia, Z. Zhang and K. N. Nordstrom, et al., Rheology of soft colloids across the onset of rigidity: scaling behavior, thermal, and non-thermal responses, Soft Matter, 2014, 10(17), 3027–3035.
8. L. Berthier, E. Flenner, H. Jacquin and G. Szamel, Scaling of the glassy dynamics of soft repulsive particles: A mode-coupling approach, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 81(3), 031505.
9. M. Cloitre, R. Borrega, F. Monti and L. Leibler, Glassy dynamics and flow properties of soft colloidal pastes, Phys. Rev. Lett., 2003, 90(6), 068303.
10. M. Cloitre, R. Borrega and L. Leibler, Rheological aging and rejuvenation in microgel pastes, Phys. Rev. Lett., 2000, 85(22), 4819–4822.
11. M. Cloitre, R. Borrega, F. Monti and L. Leibler, Structure and flow of polyelectrolyte microgels: from suspensions to glasses, C. R. Phys., 2003, 4(2), 221–230.
12. P. J. Flory and J. Rehner, Statistical Mechanics of Cross-Linked Polymer Networks I. Rubberlike Elasticity, J. Chem. Phys., 1943, 11(11), 512–520,  DOI:10.1063/1.1723791.
13. P. J. Flory and J. Rehner, Statistical Mechanics of Cross-Linked Polymer Networks II. Swelling, J. Chem. Phys., 1943, 11(11), 521–526,  DOI:10.1063/1.1723792.
14. M. Doi, Soft Matter Physics, Oxford, 2013.
15. M. Rubinstein and R. H. Colby, Polymer Physics, Oxford, 2003.
16. P. Menut, S. Seiffert, J. Sprakel and D. A. Weitz, Does size matter? Elasticity of compressed suspensions of colloidaland granular-scale microgels, Soft Matter, 2012, 8(1), 156–164.
17. J. J. Lietor-Santos, B. Sierra-Martin and A. Fernandez-Nieves, Bulk and shear moduli of compressed microgel suspensions, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2011, 84(6), 060402(R).
18. K. N. Nordstrom, E. Verneuil, W. G. Ellenbroek, T. C. Lubensky, J. P. Gollub and D. J. Durian, Centrifugal compression of soft particle packings: Theory and experiment, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 82(4), 041403.
19. K. L. Johnson, Contact Mechanics, Cambridge University Press, Cambridge, 1985. Available from: https://www.cambridge.org/core/books/contact-mechanics/E3707F77C2EBCE727C3911AFBD2E4AC2.
20. F. Scheffold, Pathways and challenges towards a complete haracterization of microgels, Nat. Commun., 2020, 11(1), 4315,  DOI:10.1038/s41467-020-17774-5.
21. A. Scotti, M. Brugnoni, A. A. Rudov, J. E. Houston, I. I. Potemkin and W. Richtering, Hollow microgels squeezed in overcrowded environments, J. Chem. Phys., 2018, 148(17), 174903,  DOI:10.1063/1.5026100.
22. R. Hoehler and S. Cohen-Addad, Many-body interactions in soft jammed materials, Soft Matter, 2017, 13(7), 1371–1383.
23. D. Weaire, R. Höhler and S. Hutzler, Bubble-bubble interactions in a 2d foam, close to the wet limit, Adv. Colloid Interface Sci., 2017, 247, 491–495 . Dominique Langevin Festschrift: Four Decades Opening Gates in Colloid and Interface Science. Available from: https://www.sciencedirect.com/science/article/pii/S000186861730204X.
24. R. Höhler and D. Weaire, Can liquid foams and emulsions be modeled as packings of soft elastic particles?, Adv. Colloid Interface Sci., 2019, 263, 19–37 . Available from: https://www.sciencedirect.com/science/article/pii/S0001868618302744.
25. C. O’Hern, L. Silbert, A. Liu and S. Nagel, Jamming at zero temperature and zero applied stress: The epitome of disorder, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2003, 68(1), 011306.
26. M. J. Bergman, N. Gnan, M. Obiols-Rabasa, J. M. Meijer, L. Rovigatti and E. Zaccarelli, et al., A new look at effective interactions between microgel particles, Nat. Commun., 2018, 9(1), 5039.
27. I. B. de Aguiar, T. van de Laar, M. Meireles, A. Bouchoux, J. Sprakel and K. Schroen, Deswelling and deformation of microgels in concentrated packings, Sci. Rep., 2017, 7, 10223.
28. G. M. Conley, C. Zhang, P. Aebischer, J. L. Harden and F. Scheffold, Relationship between rheology and structure of interpenetrating, deforming and compressing microgels, Nat. Commun., 2019, 10(1), 2436,  DOI:10.1038/s41467-019-10181-5.
29. L. Berthier, A. J. Moreno and G. Szamel, Increasing the density melts ultrasoft colloidal glasses, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 82(6), 060501(R).
30. M. Urich and A. R. Denton, Swelling, structure, and phase stability of compressible microgels, Soft Matter, 2016, 12(44), 9086–9094.
31. T. Liu, F. Khabaz, R. T. Bonnecaze and M. Cloitre, On the universality of the flow properties of soft-particle glasses, Soft Matter, 2018, 14, 7064–7074,  10.1039/C8SM01153B.
32. R. Higler and J. Sprakel, Apparent strength versus universality in glasses of soft compressible colloids, Sci. Rep., 2018, 8(1), 16817,  DOI:10.1038/s41598-018-35187-9.
33. M. D. Lacasse, G. S. Grest, D. Levine, T. G. Mason and D. A. Weitz, Model for the Elasticity of Compressed Emulsions, Phys. Rev. Lett., 1996, 76, 3448–3451 . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.76.3448.
34. T. G. Mason, M. D. Lacasse, G. S. Grest, D. Levine, J. Bibette and D. A. Weitz, Osmotic pressure and viscoelastic shear moduli of concentrated emulsions, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 3150–3166 . Available from: https://link.aps.org/doi/10.1103/PhysRevE.56.3150.
35. R. Höhler and S. Cohen-Addad, Many-body interactions in soft jammed materials, Soft Matter, 2017, 13, 1371–1383,  10.1039/C6SM01567K.
36. G. Romeo and M. P. Ciamarra, Elasticity of compressed microgel suspensions, Soft Matter, 2013, 9(22), 5401–5406.
37. L. Rovigatti, N. Gnan, L. Tavagnacco, A. J. Moreno and E. Zaccarelli, Numerical modelling of non-ionic microgels: an overview, Soft Matter, 2019, 15(6), 1108–1119.
38. L. Rovigatti, N. Gnan and E. Zaccarelli, Internal structure and swelling behaviour of in silico microgel particles, J. Phys.:Condens. Matter, 2018, 30(4), 044001.
39. S. V. Nikolov, A. Fernandez-Nieves and A. Alexeev, Behavior and mechanics of dense microgel suspensions, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(44), 27096–27103 . Available from: https://www.pnas.org/doi/abs/10.1073/pnas.2008076117.
40. S. Cai and Z. Suo, Equations of state for ideal elastomeric gels, EPL, 2012, 97(3), 34009.
41. Z. Liu, W. Hong, Z. Suo, S. Swaddiwudhipong and Y. Zhang, Modeling and simulation of buckling of polymeric membrane thin film gel [Article; Proceedings Paper], Comput. Mater. Sci., 2010, 49(1), S60–S64 . Symposium Q: Computational Materials Design at All Scales: From Theory to Application International Conference on Materials for Advanced Technologies (ICMAT), undefined, Singapore, JUN 28-JUL 03, 2009.
42. S. Cai and Z. Suo, Mechanics and chemical thermodynamics of phase transition in temperature-sensitive hydrogels, J. Mech. Phys. Solids, 2011, 59(11), 2259–2278.
43. W. Hong, Z. Liu and Z. Suo, Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load, Int. J. Solids Struct., 2009, 46(17), 3282–3289.
44. P. S. Mohanty, S. Nöjd, K. van Gruijthuijsen, J. J. Crassous, M. Obiols-Rabasa and R. Schweins, et al., Interpenetration of polymeric microgels at ultrahigh densities, Sci. Rep., 2017, 7(1), 1487,  DOI:10.1038/s41598-017-01471-3.
45. A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, How Softness Matters in Soft Nanogels and Nanogel Assemblies [doi: 10.1021/acs.chemrev.2c00035], Chem. Rev., 2022, 122(13), 11675–11700,  DOI:10.1021/acs.chemrev.2c00035.
46. D. V. Hutton Fundamentals of Finite Element Analysis, 2003.
47. F. P. Preparata and M. I. Shamos, Computational Geometry: An Introduction, Springer, 1985.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00916a

---