Open Access Article
Open Access ArticleCollective motion of energy depot active disks†
Juan Pablo
Miranda
 *ab,
Demian
Levis
*ab,
Demian
Levis
 *cd and
Chantal
Valeriani
*cd and
Chantal
Valeriani
 ab
ab
aDepartamento de Estructura de la Materia, Física Térmica y Electrónica, Universidad Complutense de Madrid, Madrid 28040, Spain. E-mail: juanpami@ucm.es
bGISC - Grupo Interdisciplinar de Sistemas Complejos, Madrid 28040, Spain
cComputing and Understanding Collective Action (CUCA) Lab, Condensed Matter Physics Department, Universitat de Barcelona, Marti i Franquès 1, Barcelona 08028, Spain. E-mail: levis@ub.edu
dUniversity of Barcelona Institute of Complex Systems (UBICS), Martí i Franquès 1, Barcelona E08028, Spain
First published on 18th November 2024
Abstract
In the present work we have studied collectives of active disks with an energy depot, moving in the two-dimensional plane and interacting via an excluded volume. The energy depot accounts for the extraction of energy taking place at the level of each particle in order to perform self-propulsion, included in an underdamped Langevin dynamics. We show that this model undergoes a flocking transition, exhibiting some of the key features of the Vicsek model, namely, band formation and giant number fluctuations. These bands, either single or multiple, are dense and very strongly polarised propagating structures. Large density bands disappear as the activity is further increased, eventually reaching a homogeneous polar state. We unravel an effective alignment interaction at the level of two-particle collisions that can be controlled by activity and gives rise to flocking at large scales.
1 Introduction
Active matter systems, composed of a collection of interacting self-propelled units, have been the focus of a great deal of research efforts over the last decades.1–3 Given that they are not in equilibrium, these systems exhibit a number of large-scale phenomena, not detected in equilibrium systems. A salient example is the emergence of collective motion, widely observed both in the living world and in synthetic realizations of active particles designed in the laboratory.4,5 Collective motion has been reported in a broad range of time and length scales, ranging from systems made of 10−7–10−6 m objects (e.g. actomyosin networks,6 bacteria7–9 and colloidal suspensions10,11) up to systems composed of agents of the order of ∼1 m in size (e.g. animal groups12).To gain a theoretical insight into this seemingly common feature displayed by a large variety of active systems of self-propelled units, simple models have been proposed, such as active Brownian particles,13 the Vicsek model14 together with their continuum hydrodynamic descriptions.14–17 Spherical active Brownian particles have been shown to exhibit phase separation even when interacting only repulsively. This phase separation is induced by self-propulsion and appears in dense enough situations.17 Whereas the Vicsek model describes the behaviour of self-propelled aligning particles, propelled at a constant speed and solely interacting via velocity-alignment interactions, being ferromagnetic/polar or nematic.5 In two dimensions, a collection of polarly aligning self-propelled particles exhibits a flocking transition towards a collectively moving state, the emergence of which is typically accompanied by large density heterogeneities in the form of traveling bands.18,19 Beyond the ideal case in which particles are just point-like, aligning particles have also been demonstrated to undergo a flocking transition, with the emergence of band-like patterns, even when repulsive interactions are taken into account.20–23 These works suggest that neither excluded-volume interactions nor collision rules are enough to change the phenomenology of the order–disorder transition in the Vicsek model. Flocking can also arise from particles’ shape (e.g. self-propelled rod-like particles aligning upon collision24,25) or from collisions between spherical particles which are not momentum conserving, such as vibrated polar grains26–28 (the latter are typically modeled as particles ‘self’ re-orienting their direction of self-propulsion with the one of their instantaneous velocity29–32).
Although self-propulsion needs an energy intake from the environment (or from an internal fuel) to convert it into motion in the presence of dissipation, Vicsek-type models and other simple active particle descriptions do not consider it explicitly. These models describe a system of active particles at a larger mesoscopic scale, somehow coarse-graining the microscopic details of the self-propulsion mechanism. One of the earliest models of active particles33 explicitly considering an internal energy intake leading to self-propulsion is the so-called energy depot model.34 The dynamics of such an energy depot active particle (EDAP) model has been thoroughly studied in the past, mostly considering medium-mediated inter-particle interactions35 or their dynamics in an external potential.36–38 This model has proven useful for a stochastic thermodynamic description of active matter,39,40 even though most authors have used active Brownian particles41,42 and active Ornstein–Uhlenbeck particles43,44 for this purpose.
As far as we know, the collective behavior of dense suspensions of EDAP with excluded volume interactions has not been explored so far. Other works have focused on modifying the model considering different assumptions, leading to substantial differences in diffusivity and transport properties, such as the effect of cross-correlated noise,45,46 a braking mechanism,47,48 the coupling of a load to an energy depot particle49 and even their motion in disordered media where their propulsion is coupled to the properties of the latter.50
In the present work, we consider repulsive spherical EDAP (disks) in two dimensions. We show that the mere competition between crowding effects and self-propulsion is enough to trigger a flocking transition, exhibiting some of the key features of Vicsek model's phenomenology, namely band formation and giant number fluctuations. As compared to suspensions of active Brownian particles, where motility-induced phase separation is observed,17 our system of repulsive spherical EDAP does not show evidence of such a phenomenon. Moreover, ABP suspensions undergo fluid–hexatic and hexatic–solid transitions at higher densities.51 Here we focus instead on the emergence of collective motion in a system of repulsive, non-polar, spherical EDAP, putting aside the investigation of the phase transitions associated with 2d melting at larger densities.
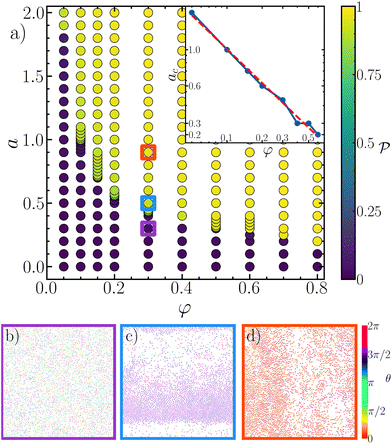
In the ‘density-activity’ plane plotted in Fig. 1, we report the value of the global polar order parameter for different state points, using a color code ranging from yellow (high polarity) to blue (low polarity). Each state point (represented by a circle) corresponds to an independent numerical simulation of a system with N = 2000 disks. Beyond a given threshold in density and/or activity, the system sets in a collectively moving state. The transition towards such a state is accompanied by the formation of large density bands that disappear as the activity is further increased, eventually reaching a homogeneous polar state. To understand this behaviour, we extract an effective interaction via the radial distribution function and find that pair-collisions lead to an effective alignment that can be controlled by activity and is responsible for the flocking transition to occur.
The paper is structured as follows: in Section 2 we define the model and its different regimes; in Section 3 we focus on the identification and characterisation of collective motion; in Section 4 we shed light on the origins of the reported flocking behaviour in the absence of explicit alignment, showing that an effective alignment interaction emerges from two-particle collisions.
2 Model for self-propelled particles with an energy depot
We consider a two dimensional suspension of N particles whose position and velocities are ri and vi, respectively. Each particle carries an internal energy depot εi, describing the conversion of energy extracted from the environment into kinetic energy at the level of individual particles. The dynamics of εi is over-damped and given by33,34![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) i(t) = q − cεi(t) − dvi2εi(t) i(t) = q − cεi(t) − dvi2εi(t) | (1) |
 | (2) |
 | (3) |
 | (4) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) i(t) = 0 in eqn (1) and then injecting its solution in Eqn (2). In Fig. 2(b) we represent the different dynamic regimes in terms of the behaviour of γ(v). We denote
i(t) = 0 in eqn (1) and then injecting its solution in Eqn (2). In Fig. 2(b) we represent the different dynamic regimes in terms of the behaviour of γ(v). We denote  , the velocity for which γ(v0) = 0, being a > b (orange line). We can then identify two different situations depending on the value of the velocity with respect to this reference. For v > v0 the motion is damped with 0 < γ(v) < γ0, approaching the passive limit as v increases. Meanwhile, for v < v0, γ(v) < 0, meaning that the energy depot accelerates the motion in the direction of v. Eventually, as the particle accelerates, it reaches a velocity close to v0, above which its motion is damped. All in all, the average velocity of a single EDAP is v0.34 For a < b, particles always exhibit damped Brownian motion as γ(v) remains positive (blue and green lines in Fig. 2). The passive limit is recovered when a → 0, allowing for a smooth connection with a well-known equilibrium system. We shall thus identify a as our activity parameter, and consider the other energy depot parameters as fixed. For a single particle the mean-square displacement reads, in the weak noise (strong pumping) approximation34,52
, the velocity for which γ(v0) = 0, being a > b (orange line). We can then identify two different situations depending on the value of the velocity with respect to this reference. For v > v0 the motion is damped with 0 < γ(v) < γ0, approaching the passive limit as v increases. Meanwhile, for v < v0, γ(v) < 0, meaning that the energy depot accelerates the motion in the direction of v. Eventually, as the particle accelerates, it reaches a velocity close to v0, above which its motion is damped. All in all, the average velocity of a single EDAP is v0.34 For a < b, particles always exhibit damped Brownian motion as γ(v) remains positive (blue and green lines in Fig. 2). The passive limit is recovered when a → 0, allowing for a smooth connection with a well-known equilibrium system. We shall thus identify a as our activity parameter, and consider the other energy depot parameters as fixed. For a single particle the mean-square displacement reads, in the weak noise (strong pumping) approximation34,52 | (5) |
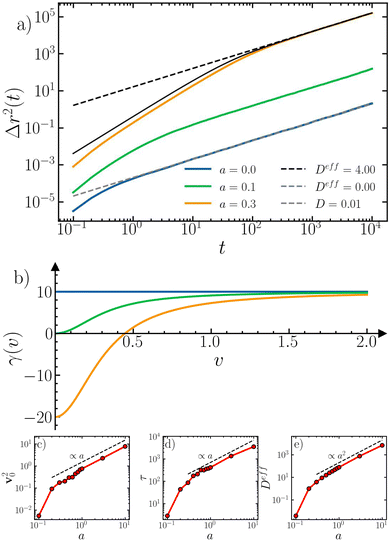 | ||
| Fig. 2 (a) MSD of non-interacting energy depot particles for different degrees of activity at fixed γ0 = 10, kBT = 5.10−4 and b = 1/10. The black solid line represents the analytical expression (5) for a system with a = 0.3. Discontinuous lines represent the long time diffusive behavior with the effective diffusivity given in the key. The blue line represents a system with a = 0, i.e., in the Brownian case. The green line corresponds to the limit case a = b. The orange line represents a system in the regime a > b with a = 3. (b) Different values of γ(v) depending on their velocity for the corresponding colors of panel a. We extract, by fitting our data to eqn (5), v02 (panel c), τ (panel d) and Deff (panel e), and compare them to the expected scaling with a. | ||
The interactions between particles derive from a pairwise potential U(rij = |ri − rj|), that here we choose to be purely repulsive and short-range. In practice, we use the following WCA form:53
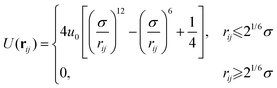 | (6) |
We simulate a system of N active particles in an L × L box with periodic boundary conditions and area fraction 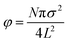 . The Langevin dynamics has been implemented by means of the LAMMPS54 open source package, making use of the Velocity Verlet integrator. In order to perform these simulations we have used different initial configurations. At intermediate densities, we have started from random positions and velocities (uniformly distributed); whereas at higher densities we have located particles in an ordered square lattice, with again random velocities.
. The Langevin dynamics has been implemented by means of the LAMMPS54 open source package, making use of the Velocity Verlet integrator. In order to perform these simulations we have used different initial configurations. At intermediate densities, we have started from random positions and velocities (uniformly distributed); whereas at higher densities we have located particles in an ordered square lattice, with again random velocities.
All physical quantities are expressed in Lennard–Jones reduced units, with lengths, times and energies given in terms of σ = τLJ = u0 = 1, where  and m = 1. We have run simulations of systems with N = 2000 up to 30
and m = 1. We have run simulations of systems with N = 2000 up to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles at different area fractions φ, in the range φ = 0.05, …, 0.8. In our simulations, we set γ0 = 10, the time step to Δt/τLJ = 10−3 and the reduced temperature kBT/u0 = 5 × 10−4. We explore the collective behavior of the model at fixed b = 1/10 as a function of both a and φ. In practice, due to the extent of the parameter space in the model, we choose to fix c, d and γ0, while the activity a is varied changing the values of q. As we group the parameters, this choice is equivalent to varying the parameter a while fixing b. The values of the original parameters were c = 1, d = 10 and q varying between 0 and 30. This is equivalent to vary a from 0 to 3. The chosen parameters allow us to set an energy scale (being c directly proportional to the depot internal energy) and to explore different dynamical regimes by only varying a (having chosen a small value for b). It has to be taken into account the fact that systems with a < b cannot be considered motile, even though we have also studied them.
000 particles at different area fractions φ, in the range φ = 0.05, …, 0.8. In our simulations, we set γ0 = 10, the time step to Δt/τLJ = 10−3 and the reduced temperature kBT/u0 = 5 × 10−4. We explore the collective behavior of the model at fixed b = 1/10 as a function of both a and φ. In practice, due to the extent of the parameter space in the model, we choose to fix c, d and γ0, while the activity a is varied changing the values of q. As we group the parameters, this choice is equivalent to varying the parameter a while fixing b. The values of the original parameters were c = 1, d = 10 and q varying between 0 and 30. This is equivalent to vary a from 0 to 3. The chosen parameters allow us to set an energy scale (being c directly proportional to the depot internal energy) and to explore different dynamical regimes by only varying a (having chosen a small value for b). It has to be taken into account the fact that systems with a < b cannot be considered motile, even though we have also studied them.
3 Transition to a flocking state
To quantify collective motion, we employ the global polar order parameter![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) , or polarisation, given by the modulus of the average direction of the instantaneous velocity vector of each particle
, or polarisation, given by the modulus of the average direction of the instantaneous velocity vector of each particle | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi,sin
θi,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi), and 〈·〉 denotes a steady-state average. Values of
θi), and 〈·〉 denotes a steady-state average. Values of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) > 0 indicate that a fraction of the particles is aligned, thus moving coherently, whereas
> 0 indicate that a fraction of the particles is aligned, thus moving coherently, whereas ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) = 0 corresponds to particles moving in random directions.
= 0 corresponds to particles moving in random directions.
Fig. 3(a) represents the values of polarisation obtained for a range of activities and area fractions φ (as indicated in the legend). Increasing activity, at a fixed φ, we observe a disorder (low polar order) to order (high polar order) transition. Interestingly, the value of a beyond which the transition takes place depends on the system area fraction, decreasing when the area fraction increases. To establish the robustness of this transition and the relevance of finite-size effects, we have performed simulations at the same φ = 0.3 and for different system sizes. As shown in Fig. 3(b), the disorder-to-order transition is always present and the value of activity needed for the transition to take place is not significantly affected by the system size (in the chosen parameter range).
Polar order appears in a suspension of EDAP repulsive particles, in the absence of a prescribed orientation and an explicit alignment rule akin to Vicsek-like models.14 Particle activity (as a self-propulsion) is controlled by a velocity dependent friction γ(v), which changes its modulus in the under-damped regime. Thus when a particle's self propulsion strength overcomes the particle's rotational noise, the persistence length of the particle increases resulting in a local alignment of colliding particles. The emergence of flocking, typical of polar systems, is caused by particle interactions controlled by activity when self propulsion overcomes rotational noise. More examples of particles with polar order without an explicit alignment have been earlier reported.10,26,55 In ref. 26 the authors describe experiments on a two dimensional system of disks with a “built-in polar asymmetry” (due to an asymmetric mass distribution). These studies and more recent ones underlined the existence of particles’ alignment through collisional arguments using kinetic theory.56,57 Unlike these works, our system is made of isotropically interacting particles whose activity is encoded in a velocity-dependent friction, resulting in the velocity to change its modulus in an under-damped regime. To explain the observed flocking, we quantify two-body effective interactions,23,58,59 showing how it develops a tendency to align particle's velocity as activity is increased. A heuristic argument based on particle collisions is presented in Section 4.
Briefly, we have found that collisions favour alignment via the combined effect of self-propulsion in the direction of the particles’ velocities and steric repulsion. When two particles collide, repulsive forces accelerate them longitudinally. Their speed is thus reduced and activity thus pushes them along a direction that will typically reduce the angle between their velocities. As the rate of collisions increases with density, the onset of flocking decays with φ.
Fig. 1(a) shows the region in parameter space where flocking occurs (in yellow). To detect the onset of collective motion we measure the parameter ac. First, we calculate the susceptibility as the variance of the order parameter: Δ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) = 〈
= 〈![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 2〉 − 〈
2〉 − 〈![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 〉2, and denote ac the activity corresponding to the maximum of the susceptibility. The inset represents the activity threshold ac(φ) above which we detect collective motion: ac decays with the area fraction (in a way that phenomenologically suggests ac ∼ φ−0.77).
〉2, and denote ac the activity corresponding to the maximum of the susceptibility. The inset represents the activity threshold ac(φ) above which we detect collective motion: ac decays with the area fraction (in a way that phenomenologically suggests ac ∼ φ−0.77).
As shown in Fig. 1(b)–(d) the system in steady state displays different structures. To better understand the nature of the transition towards collective motion, we characterize the structural properties of the different states by computing the probability density of the local order parameter F(![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) l) and the local area fraction G(φi). The local polar order parameter
l) and the local area fraction G(φi). The local polar order parameter ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) l is obtained from dividing the system into 100 square cells and computing the average polarisation of the particles inside each one. The local area fraction G(φi) is obtained from a Voronoi tessellation. Based on the results of local density and polarisation, presented in Fig. 4, we identify three states, reported in Fig. 1(b)–(d). The first one (Fig. 1(b)) is the disordered state, which corresponds to a homogeneous density distribution centered around the mean density (orange and green curves in Fig. 4(a)), and a homogeneous local polarisation distribution (orange and green curves in Fig. 2(b)) corresponding to the absence of polar ordering. With increasing activity we detect a transition to an ordered phase. Beyond the onset of flocking one can identify two different states based on their local density and polarisation. A heterogeneous state (Fig. 1(c)) is observed close to the transition, for which G(φi) is no longer uni-modal, but displays two maximum values (one at low and one at high densities), indicating a dense region coexisting with a dilute disordered background (see a = 0.45, Fig. 4(a)). Interestingly, heterogeneity in the distribution of polarisation coincides with this density heterogeneity. As shown in Fig. 4(b), F(P) exhibits a sharp peak close to 1 with a very broad tail at smaller values, signaling large fluctuations. Such states, as illustrated in Fig. 1(c) correspond to traveling bands, as typically observed in models of flocking. Bands are dense and very strongly polarized propagating structures. A dynamical state of single and multiple band structures is observed at very long times, see ref. 60. The band profile is again reminiscent to the one found in the Vicsek system.19 As expected, particles in the band accumulate at the front and are better oriented than particles located at the dilute part of the band.
l is obtained from dividing the system into 100 square cells and computing the average polarisation of the particles inside each one. The local area fraction G(φi) is obtained from a Voronoi tessellation. Based on the results of local density and polarisation, presented in Fig. 4, we identify three states, reported in Fig. 1(b)–(d). The first one (Fig. 1(b)) is the disordered state, which corresponds to a homogeneous density distribution centered around the mean density (orange and green curves in Fig. 4(a)), and a homogeneous local polarisation distribution (orange and green curves in Fig. 2(b)) corresponding to the absence of polar ordering. With increasing activity we detect a transition to an ordered phase. Beyond the onset of flocking one can identify two different states based on their local density and polarisation. A heterogeneous state (Fig. 1(c)) is observed close to the transition, for which G(φi) is no longer uni-modal, but displays two maximum values (one at low and one at high densities), indicating a dense region coexisting with a dilute disordered background (see a = 0.45, Fig. 4(a)). Interestingly, heterogeneity in the distribution of polarisation coincides with this density heterogeneity. As shown in Fig. 4(b), F(P) exhibits a sharp peak close to 1 with a very broad tail at smaller values, signaling large fluctuations. Such states, as illustrated in Fig. 1(c) correspond to traveling bands, as typically observed in models of flocking. Bands are dense and very strongly polarized propagating structures. A dynamical state of single and multiple band structures is observed at very long times, see ref. 60. The band profile is again reminiscent to the one found in the Vicsek system.19 As expected, particles in the band accumulate at the front and are better oriented than particles located at the dilute part of the band.
Increasing activity even further, density heterogeneities disappear, and G(φi) presents a uniform distribution again, although broader than in the small activity limit (see Fig. 4(a)). This regime corresponds to the emergence of a homogeneous polar state (Fig. 1(d)). The polarisation distribution now exhibits a sharp peak close to 1, whose width decreases with increasing activity. So far, we have only detected band formation for intermediate densities close to the transition, quickly disappearing upon increasing activity.
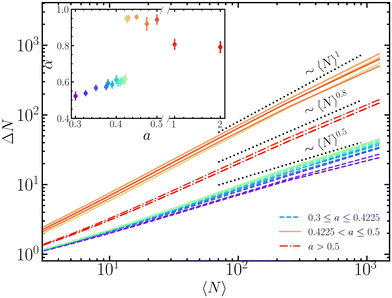
As known from the literature of polar fluids,61 giant number fluctuations typically appear in the flocking phase. We measure the number density fluctuations to unravel possible connections between orientational order and giant number fluctuations. To do so, we divide the system into 2k cells and count the number of particles in each cell, considering a large number of configurations, to estimate the mean number of particles 〈N〉 and its variance ΔN. We repeat the procedure over boxes with different sizes (ranging from k = 2, …, 8) and obtain a value of 〈N〉 for each box size. We then extract a power-law relation ΔN ∼ Nα where a value α > 1/2 signals giant number fluctuations.
Fig. 5 shows the variance of the number of particles ΔN as a function of the mean number of particles for systems at fixed density (ϕ = 0.3) but varying the value of the activity parameter. In all cases, ΔN ∼ Nα. However, as clearly shown in the inset, depending on the activity, the exponent α noticeably varies, jumping from values around 1/2 to almost 1 when a ≈ ac. When α > 0.5 the system exhibits giant number fluctuations. As shown in Fig. 5, this occurs beyond the onset of flocking. When α ≈ 0.5, number fluctuations follow what one expects from the central limit theorem. The variation on the value of α with the activity parameter thus provides a complementary way of locating the onset of flocking. When the system sets into the homogeneously dense polar state, at large values of a, we find a value α ≈ 0.8, still exhibiting large number fluctuations, although with a smaller exponent than the one in the band regime. This value of α ≈ 0.8 is close to the value of 0.725 reported by Deseigne et al.26 for vibrated polar disks, and coincides with the exponent of 0.8 in the Vicsek system reported by Chaté et al.19
4 Understanding the effective alignment
Even though many body interactions might be relevant to understand collective phenomena in active particle systems,62 one might start with unraveling the emergence of collective motion from the analysis of two body interactions.To understand whether the emergent behavior is due to pair interactions, we compute the two-particle pair correlation function, depending on both the inter-particle distances and the relative orientation of their velocities. This function can be defined as (ref. 63 and 64)
 | (8) |
To further quantify such alignment, we extract an effective potential from the radial distribution and study its behavior in terms of the different parameters (such as the activity). This procedure has been conducted earlier to estimate effective interactions between Active Brownian Particles.23,58,59 Assuming that g(r,θ) = exp(−βUeff(r,θ)), one can map the radial distribution function to an effective potential. Fig. 7 shows the effective potential as a function of the angle (panel a) and the effective potential as a function of the inter-particle distance, for varying values of the activity parameter a (panel b). On the one hand, as reported in Fig. 7(a), activity lowers the minima of the potential, favoring an effective alignment: Ueff is lowered as a increases for relative angles close to 0, thus increasing the effective alignment as self propulsion is increased. On the other hand, as shown in Fig. 7(b), the minimum of the effective potential corresponds to the cutoff of the WCA potential r = 21/6σ ≃ 1.12σ. This reveals that the alignment arises from the interplay between the excluded volume interactions and activity.
Since the only interactions are given through excluded volume, the mechanism for alignment has to be mediated by contact interactions (collisions), explaining why the minima of the effective potential occurs at the contact distance between two particles. This also has to do with the fact that the other part of the mechanism is the active force, as the effective potential develops a deeper minimum as activity is increased.
In our model, self-propulsion is controlled by a velocity dependent friction. Particles velocity changes in modulus and direction when particles interact. When two particles collide, their velocity is reduced along the longitudinal, center-to-center direction, while the transverse component remains roughly unchanged at short time scales. Large enough persistence thus generates long collision times, where the longitudinal component of the velocity drops, resulting in a velocity with a larger transversal component, as illustrated in Fig. 8. In this way velocity alignment is induced at the two particle level and this effect is amplified when considering the entire system, thus leading to a polar order at large length scales. Large activity thus induces a velocity alignment in this model, where, as compared to active Brownian particles, rotational noise is absent. We show in Fig. 8 a sequence of snapshots during a collision event. The top-right particle hits the other one from behind and it is slowed down by the interaction potential. This makes the collision lasting longer than if the two particles were passive, since the active force is pushing the particle to collide again.
 | ||
| Fig. 8 Successive snapshots during a collision between two particles, where their velocities are represented as orange arrows. The snapshots are ordered from left to right, as time goes on. | ||
So far, the model defined by eqn (1) and (2) was only considered in the limit in which the internal energy depot relaxes much faster than any other degrees of freedom in the system, i.e. the depot is fully over damped. When this assumption is relaxed, we talk about the time dependent energy deport model. We implement the full dynamics of the internal depot by integrating eqn (1) with an Euler scheme. To compare the time dependent model with its adiabatic limit, we have performed a set of simulations for N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles, φ = 0.3 and a ranging from 0.3 to 2. In this parameter regime, the over-damped model exhibits the characteristic states described above, namely, a is the disordered state, followed by a polar state featuring dense bands and moderate valued of a > ac. Once the full evolution of the energy depot is considered, polar order is lost in this parameter regime, as Fig. 3 shows. The time scale of the energy relaxation, 1/c = 1, is typically smaller than the persistence time, τ in the regime where flocking is observed. However, in the time-dependent case, the
000 particles, φ = 0.3 and a ranging from 0.3 to 2. In this parameter regime, the over-damped model exhibits the characteristic states described above, namely, a is the disordered state, followed by a polar state featuring dense bands and moderate valued of a > ac. Once the full evolution of the energy depot is considered, polar order is lost in this parameter regime, as Fig. 3 shows. The time scale of the energy relaxation, 1/c = 1, is typically smaller than the persistence time, τ in the regime where flocking is observed. However, in the time-dependent case, the ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) term has a faster relaxation that cannot be ignored. As these results are only validated for b = 0.1, further parameter exploration could provide a more accurate description on how the polarisation is lost when this time dependence is introduced. The loss of polar order raises the question of whether there is a way to restore it in a different parameter regime, or, eventually, the emergence of other collective states. We leave such an investigation for future work.
term has a faster relaxation that cannot be ignored. As these results are only validated for b = 0.1, further parameter exploration could provide a more accurate description on how the polarisation is lost when this time dependence is introduced. The loss of polar order raises the question of whether there is a way to restore it in a different parameter regime, or, eventually, the emergence of other collective states. We leave such an investigation for future work.
5 Conclusions
The present work studied a system of active disks that are self-propelled by an internal energy depot, characterized by a velocity dependent friction and an isotropic repulsive (hard) potential. The novelty of this version of the EDAP model with respect to others is that it presents polar alignment, despite repulsive interactions and not an explicit alignment mechanism. A Vicsek-like transition from a non-polar isotropic state to a polar and ordered state is identified and characterized in terms of the polar order parameter and the giant number fluctuations. The structural analysis reveals the presence of different phases, such as a non-polar homogeneous density phase, and two polar phases. The polar phases are divided into a homogeneously dense and a band phase.Even though the flocking behavior exhibited by this model resembles the one of the Vicsek model,19 here the alignment arises from steric collisions in the presence of activity (encapsulated in an internal depot) with no need of an explicit interaction of this kind. Once alignment, controlled by activity, becomes strong enough, flocking occurs, with strong similarities to the well-known phenomenology of Vicsek-type models. As increasing activity increases the tendency of particles to align, the emergence of large-scale polar order is controlled by competition between noise and alignment. Given that the alignment mechanism is not explicit, an explanation is provided in terms of an effective potential originated by collisions between particles. The effective potential reveals a connection between the potential and the activity, which is translated as the torque acting on particles.
From our results, we conclude that this model is a good candidate for more realistic systems of active engines65 at the micro-scale, since it allows a theoretical approach that could complement numerical simulations (as in ref. 66–68).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. V. acknowledges funding IHRC22/00002 and PID2022-140407NB-C21 from AEI/MICINN. D. L. acknowledges AEI/MICINN for funding under Project PID2022-140407NB-C22. J. P. M. thanks Miguel Barriuso and José Martín-Roca for helpful scientific discussions.References
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Nat. Rev. Phys., 2020, 2, 181–199 CrossRef.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- T. Vicsek and A. Zafeiris, Phys. Rep., 2012, 517, 71–140 CrossRef.
- H. Chaté, Annu. Rev. Condens. Matter Phys., 2020, 11, 189–212 CrossRef.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73–77 CrossRef CAS.
- F. Peruani, J. Starruß, V. Jakovljevic, L. Søgaard-Andersen, A. Deutsch and M. Bär, Phys. Rev. Lett., 2012, 108, 098102 CrossRef PubMed.
- A. Sokolov and I. S. Aranson, Phys. Rev. Lett., 2012, 109, 248109 CrossRef PubMed.
- H. Li, X.-q Shi, M. Huang, X. Chen, M. Xiao, C. Liu, H. Chaté and H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 777–785 CrossRef CAS PubMed.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- A. Kaiser, A. Snezhko and I. S. Aranson, Sci. Adv., 2017, 3, e1601469 CrossRef.
- W. Bialek, A. Cavagna, I. Giardina, T. Mora, E. Silvestri, M. Viale and A. M. Walczak, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4786–4791 CrossRef CAS.
- P. Romanczuk, M. Bär, W. Ebeling, B. Lindner and L. Schimansky-Geier, Eur. Phys. J.: Spec. Top., 2012, 202, 1–162 CAS.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226–1229 CrossRef CAS.
- J. Toner and Y. Tu, Phys. Rev. Lett., 1995, 75, 4326–4329 CrossRef CAS PubMed.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- A. P. Solon, H. Chaté and J. Tailleur, Phys. Rev. Lett., 2015, 114, 068101 CrossRef PubMed.
- H. Chaté, F. Ginelli, G. Grégoire and F. Raynaud, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77(4 Pt 2), 046113 CrossRef.
- R. Martinez, F. Alarcon, D. Rogel Rodriguez, J. L. Aragones and C. Valeriani, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 91 CrossRef PubMed.
- J. Barré, R. Chétrite, M. Muratori and F. Peruani, J. Stat. Phys., 2015, 158, 589–600 CrossRef.
- E. Sese-Sansa, I. Pagonabarraga and D. Levis, Europhys. Lett., 2018, 124, 30004 CrossRef.
- E. Sesé-Sansa, D. Levis and I. Pagonabarraga, Phys. Rev. E, 2021, 104, 054611 CrossRef.
- M. Bär, R. Großmann, S. Heidenreich and F. Peruani, Annu. Rev. Condens. Matter Phys., 2020, 11, 441–466 CrossRef.
- R. Großmann, I. S. Aranson and F. Peruani, Nat. Commun., 2020, 11, 5365 CrossRef PubMed.
- J. Deseigne, O. Dauchot and H. Chaté, Phys. Rev. Lett., 2010, 105, 098001 CrossRef.
- A. Kudrolli, G. Lumay, D. Volfson and L. S. Tsimring, Phys. Rev. Lett., 2008, 100, 058001 CrossRef.
- V. Narayan, S. Ramaswamy and N. Menon, Science, 2007, 317, 105–108 CrossRef CAS PubMed.
- B. Szabo, G. Szöllösi, B. Gönci, Z. Jurányi, D. Selmeczi and T. Vicsek, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061908 CrossRef CAS PubMed.
- O. Dauchot and V. Démery, Phys. Rev. Lett., 2019, 122, 068002 CrossRef CAS PubMed.
- O. Dauchot, Active Matter and Nonequilibrium Statistical Physics: Lecture Notes of the Les Houches Summer School: Volume 112, September 2018, 2022, vol. 112, p. 102 Search PubMed.
- M. Paoluzzi, D. Levis and I. Pagonabarraga, Commun. Phys., 2024, 7, 57 CrossRef.
- F. Schweitzer, W. Ebeling and B. Tilch, Phys. Rev. Lett., 1998, 80, 5044–5047 CrossRef CAS.
- F. Schweitzer and J. D. Farmer, Brownian agents and active particles: collective dynamics in the natural and social sciences, Springer, 2003, vol. 1 Search PubMed.
- V. Lobaskin and M. Romenskyy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052135 CrossRef PubMed.
- F. Schweitzer, W. Ebeling and B. Tilch, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021110 CrossRef CAS.
- R. Mach and F. Schweitzer, Bull. Math. Biol., 2007, 69, 539–562 CrossRef PubMed.
- W. Ebeling, F. Schweitzer and B. Tilch, BioSystems, 1999, 49, 17–29 CrossRef CAS PubMed.
- D. Chaudhuri, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022131 CrossRef PubMed.
- U. Seifert, Annu. Rev. Condens. Matter Phys., 2019, 10, 171–192 CrossRef CAS.
- G. Szamel, Phys. Rev. E, 2019, 100, 050603 CrossRef CAS.
- S. Shankar and M. C. Marchetti, Phys. Rev. E, 2018, 98, 020604 CrossRef CAS PubMed.
- É. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. Van Wijland, Phys. Rev. Lett., 2016, 117, 038103 CrossRef.
- L. Caprini, U. M. B. Marconi, A. Puglisi and A. Vulpiani, J. Stat. Mech.: Theory Exp., 2019, 2019, 053203 CrossRef.
- Y. Fang, Y. Luo, Z. Ma and C. Zeng, Phys. A, 2021, 564, 125503 CrossRef.
- L. Guan, Y. Fang, K. Li, C. Zeng and F. Yang, Phys. A, 2018, 505, 716–728 CrossRef.
- Y. Zhang and C. K. Kim, et al. , New J. Phys., 2008, 10, 103018 CrossRef.
- Y. Zhang, C. K. Kim, K.-J.-B. Lee and Y. Park, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 29, 345–349 CrossRef CAS PubMed.
- M. Ann and P. J. Park, et al. , Phys. A, 2015, 436, 126–134 CrossRef.
- K. S. Olsen, L. Angheluta and E. G. Flekkøy, Soft Matter, 2021, 17, 2151–2157 RSC.
- P. Digregorio, D. Levis, A. Suma, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Phys. Rev. Lett., 2018, 121, 098003 CrossRef CAS PubMed.
- A. Mikhailov and D. Meinköhn, Stochastic Dynamics, Heidelberg, Berlin, 1997, pp. 334–345 Search PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ‘t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- C. A. Weber, T. Hanke, J. Deseigne, S. Léonard, O. Dauchot, E. Frey and H. Chaté, Phys. Rev. Lett., 2013, 110, 208001 CrossRef CAS.
- T. Hanke, C. A. Weber and E. Frey, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052309 CrossRef.
- K.-D. N. T. Lam, M. Schindler and O. Dauchot, New J. Phys., 2015, 17, 113056 CrossRef.
- T. F. Farage, P. Krinninger and J. M. Brader, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 042310 CrossRef CAS PubMed.
- U. M. B. Marconi, M. Paoluzzi and C. Maggi, Mol. Phys., 2016, 114, 2400–2410 CrossRef CAS.
- See ESI†.
- K.-D. N. T. Lam, M. Schindler and O. Dauchot, J. Stat. Mech.: Theory Exp., 2015, 2015, P10017 CrossRef.
- F. Turci and N. B. Wilding, Phys. Rev. Lett., 2021, 126, 038002 CrossRef CAS PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of simple liquids: with applications to soft matter, Academic press, 2013 Search PubMed.
- J. Bialké, H. Löwen and T. Speck, Europhys. Lett., 2013, 103, 30008 CrossRef.
- É. Fodor and M. E. Cates, Europhys. Lett., 2021, 134, 10003 CrossRef.
- K. Sekimoto, Stochastic Energetics, 2010 Search PubMed.
- K. Sekimoto, Prog. Theor. Phys. Suppl., 1998, 130, 17–27 CrossRef CAS.
- C. Ganguly and D. Chaudhuri, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 032102 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00785a |
| This journal is © The Royal Society of Chemistry 2025 |