Nitrate sensing with molecular cage ionophores: a potentiometric approach

Abstract

Nitrate ions are widespread environmental pollutants in water and soil, posing critical risks to both human health and ecosystems. This study introduces a molecular cage as a novel ionophore for potentiometric nitrate-selective ion-selective electrodes (ISEs) designed for enhanced specificity and sensitivity. Among six synthetic candidates, the electrode incorporating a 1,3,5-tri(p-hydroxyphenyl)benzene-based chlorotriazine pillared cage molecule (CAGE-1) exhibited superior performance, characterized by a linear response in the nitrate concentration range of 1.0 × 10⁻⁵ to 1.0 × 10⁻¹ M, with a high coefficient of determination (R² = 0.9971) and a slope of −53.1 ± 1.4 mV dec⁻¹. The electrode also achieved a limit of detection of 7.5 × 10⁻⁶ M. These findings highlight the potential of molecular cages as ionophores for nitrate sensing in environmental applications.

---

1. Introduction

Nitrogen is a fundamental element vital for the growth and reproduction of all living organisms and one of the most important mineral nutrients for crops.^1–3 To pursue high grain yields, nitrogen supplementation is required in the soil to support the production of food, feed, and fiber.^4,5 In order to sustain agricultural productivity, it is imperative to apply fertilizers at the appropriate time, location, amount, and methods.⁶ Excessive nitrate levels can lead to extensive environmental pollution, including groundwater pollution,⁷ soil acidification,⁸ and water eutrophication.¹ Hence, there is a growing desire for swift, cost-effective, and real-time nitrate measurement in both water and soil samples.

Techniques for the analysis of nitrate ions, including ion exchange chromatography (diode-array detection)⁹ and liquid chromatography (UV light absorption¹⁰ and fluorescence detection),¹¹ are costly and intricate due to the necessity of expensive instrumentation for precise measurements. Furthermore, they entail using chemical reagents, generating significant chemical waste, and demand specialized expertise to perform the measurements.¹² Additionally, these methods are not suitable for in situ measurement. Compared to spectroscopic methods, electrochemical techniques offer advantages such as ease of operation, high sensitivity, convenient miniaturization, real-time measurement capabilities, and cost-effectiveness. The electrochemical detection of nitrate can be categorized into various groups based on their sensing methods which are amperometry,¹³ conductometry,¹⁴ cyclic voltammetry¹⁵ and potentiometry.¹⁶ Nonetheless, NO₃⁻ poses a notable challenge for voltammetric methods due to its demand for substantial overpotentials and sample preparation.¹⁷ On the other hand, the growing need for swift on-site analysis highlights potentiometric methods as a viable choice due to their precision, ease of use, and cost-effectiveness. Potentiometric ion-selective electrodes find extensive utility in quantifying ion concentrations across diverse samples, offering a broad measurement range encompassing both positively and negatively charged ions. One crucial element of this technology is the ionophore, which enables the selective and accurate quantification of specific ions in a solution. Ionophores are organic molecules adept at selectively binding to specific ions and facilitating their passage through the electrode membrane. The ionophores typically employed in the fabrication of solid-contact ion-selective electrodes for nitrate determination include tridodecylmethylammonium nitrate (TDMAN),^17–19 polypyrrole (PPy) doped with NO₃⁻ ions,^20,21 nitrate ionophore VI,^22–24 cobalt(II) complexes with 4,7-diphenyl-1,10-phenanthroline,²⁵ and tetradecylammonium nitrate (TDANO₃).²⁶ In particular, the commercial nitrate ionophore VI exhibits exceptional selectivity and reproducibility for nitrate measurement. Unfortunately, the majority of ionophores can be sourced from natural origins, including specific plants or microorganisms. These methods entail lengthy and costly extraction, purification, and characterization procedures. During the past few decades, organic molecular cages have gained considerable interest due to their distinctive structural features, such as intrinsic voids that can be customized in both size and functionality. This tunability makes them suitable candidates for a variety of applications, including gas sorption,^27,28 separation,²⁹ sensing,³⁰ and catalysis.³¹ Such fine-tuning of their internal cavities enabled these molecules to be utilized as hosts for recognizing specific molecules and ions.^32–35 A recent study demonstrated the use of oxatub[4]arenes as ionophores in potentiometric sensors for acetylcholine. These macrocycles exhibited strong host–guest interactions through cation–π interactions and hydrogen bonding, resulting in enhanced selectivity, low detection limits, and high stability.³⁶

The research on anion recognition through host–guest interactions has been a hot spot for an extended period in supramolecular chemistry due to their importance in environmental and biological applications.^37–39 In this regard, organic cage compounds have revealed promising results due to their high association constants (K_a) and selectivity, marking notable progress in the recognition of anions. For example, in 2021, Badjić et al. reported the synthesis of a hexapodal cage compound and investigated its complexation behavior with anions.⁴⁰ Their findings demonstrated that the hexapodal cage compound exhibited a distinct affinity for sulfate (SO₄²⁻) and hydrogen phosphate (HPO₄²⁻) anions compared to halides and carbonate (CO₃²⁻) ions. In the following year, Mastalerz et al.⁴¹ presented a cage compound that has structural similarity to the one that Anslyn and co-workers previously published.⁴² Precise adjustments of the cage structure for nitrate encapsulation enhanced the strengths of hydrogen bonding and π-stacking interactions between the host and guest, resulting in a significant improvement in nitrate selectivity compared to chloride (Cl⁻) and hydrogen sulfate (HSO₄⁻) anions. The recognition studies with cage structures mainly involve secondary interactions such as hydrogen bonding and/or π-stacking interactions. On the other hand, recent studies have also recognized anion–π interactions as a potential non-covalent attractive force between neutral electron-deficient aromatic units and negatively charged ions.^43,44 Wang et al.⁴⁵ examined interactions between halides and a structurally stable D_3h symmetric cage molecule known as “bis(tetraoxacalix[2]arene[2]triazine)”, which has three V-shaped clefts with electron-deficient triazine rings. The study notably revealed the easily observed anion–π interactions between sulfonates and the electron-deficient triazine rings. Several other studies have used the same cage molecule as a platform for anion–π interactions in specific applications such as anion–π catalysts,^46,47 perrhenate removal from an aqueous medium,⁴⁸ and formation of anion–π directed self-assemblies,⁴⁹ illustrating the versatility of the cage in anion–π motifs. Although significant progress has been made in understanding cage-based ion capture and recognition, examples of organic cage molecules in potentiometric ion sensing are limited in the literature.⁵⁰ To our knowledge, such cage compounds have not been used previously as ionophores in potentiometric sensor applications for the selective detection of nitrate in an aqueous environment. In this study, we comprehensively investigate molecular cages as selective ionophores for nitrates in potentiometric ion-selective electrodes. Fine-tuning of the size and electronic structure of the cage molecules enabled us to boost nitrate selectivity over other anions in aqueous analytes. The electrode prepared using the 1,3,5-tri(p-hydroxyphenyl)benzene-based chlorotriazine pillared ether-linked cage molecule (CAGE-1) showed a linear response for NO₃⁻ ions within the concentration range of 1.0 × 10⁻⁵ to 1.0 × 10⁻¹ M, with a high coefficient of determination (R² = 0.9971) and a slope of −53.1 ± 1.4 mV dec⁻¹. The calculated limit of detection for the NO₃⁻ selective electrode was found to be 7.5 × 10⁻⁶ M. This study presents the potential of the cage molecules as ionophores for detecting nitrate ions in aqueous environments and provides new insights into the development of potentiometric ion-selective electrodes.

2. Materials and methods

2.1 Potentiometric measurements

Potentiometric measurements were performed using a Metrohm Potentiostat/Galvanostat μStat-i 400s instrument. An Ag/AgCl reference electrode (filled with saturated potassium chloride (36% w/w)) (Gamry) was used for all measurements. The indicator and reference electrodes were submerged at the same depth in a 30 mL tested solution, with continuous stirring maintained at a constant rate to obtain steady-state measurements. Before each measurement sequence, the reference and indicator electrodes were thoroughly rinsed with distilled deionized water and delicately dried using a gentle adsorbent tissue.

2.2 Fabrication of electrodes

First, a 1 : 1 ratio graphite–epoxy slurry (50 mg : 50 mg) was dispersed in the appropriate amount of tetrahydrofuran (100 mL) to prepare solid contact electrodes. It was mixed until it reached a thick consistency. The open end of the isolated copper wire (10 cm length and 0.5 mm radius) was dipped into this mixture a few times to obtain a solid-state contact with a coating thickness of about 0.2 mm and dried in an oven at 50 °C for 24 hours. Scheme 1 illustrates the structure of the cage molecules used, and the synthesis is detailed in the ESI.† The solutions of cage molecules were prepared by dissolving 10 mg of each cage molecule (E1–E6) into 400 μL of tetrahydrofuran. This mixture was then sonicated for 10 minutes to ensure complete dissolution and homogenization of the cage molecules within the solvent. For the preparation of the ion-selective electrodes, the homogeneous cage solutions were carefully drop-cast onto the surface of the electrodes. This process involved depositing small, controlled amounts of the solution to form a uniform coating. Once the cage solutions were applied, the electrodes were placed in an oven at 50 °C. They were left to dry under these conditions for 24 hours, allowing the solvent to evaporate completely and leaving behind a well-adhered film of the cage molecules on the electrode surface. This procedure was repeated for all cage molecules from E1 to E6. The detailed fabrication steps of the ion-selective electrodes, including the preparation and application of the cage solutions, are illustrated and described in Scheme 2.

Scheme 1 Electrode codes, cage type, and structure.

Scheme 2 The fabrication steps of ISEs.

3. Results and discussion

3.1 Synthesis and characterization of cage-based ionophores

The synthetic pathways of preparing cage compounds are summarized in Scheme 3. The synthesis and exterior surface functionalization of compounds were accomplished by the controlled reactivity of cyanuric chloride. First, CLEFT-0 was synthesized by reacting phloroglucinol with cyanuric chloride in the presence of Hünig's base (N,N-diisopropylethylamine) at 0 °C. The formation of CAGE-0 was accomplished by the closure of CLEFT-0 with the addition of an equimolar amount of phloroglucinol in the presence of Hünig's base at room temperature.⁴⁵ CAGE-1 was also synthesized by following a similar two-step procedure applied to synthesize CAGE-0. The reaction of 1,3,5-tri(p-hydroxyphenyl)benzene with cyanuric chloride in the presence of Hünig's base afforded the intermediate product, CLEFT-1, in a high yield. Then, treating CLEFT-1 with equal moles of 1,3,5-tri(p-hydroxyphenyl) benzene gave the desired product, CAGE-1.⁵¹ Simply switching the phloroglucinol units with 1,3,5-tri(4-hydroxyphenyl)benzene provides not only a larger void size to CAGE-1 compared to CAGE-0 but also larger V-shaped clefts between three triazine group units (Scheme 3). The high electron-deficient nature of the aromatic triazine ring and the high reactivity of chlorine units located at the periphery of CAGE-0 and CAGE-1 enabled the functionalization of cage units with dialkylamines through a nucleophilic substitution reaction under mild reaction conditions (Scheme 3). In this way, the electronic structure of the cage compounds was altered by replacing the electron-withdrawing chlorine groups with the electron-donating dimethylamine groups to provide CAGE-2 and CAGE-3. The variation of the size and the electronic structure can endow cage molecules with the potential for optimizing host–guest interactions.

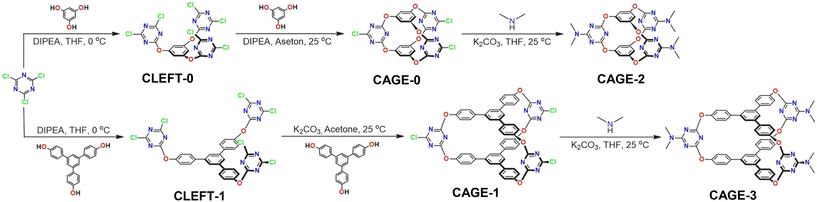Scheme 3 Synthesis pathways of cage compounds, namely CLEFT-0, CAGE-0, CAGE-2, CLEFT-1, CAGE-1, and CAGE-3.

The cage compounds were characterized using Fourier transform infrared spectroscopy (FT-IR), nuclear magnetic resonance spectroscopy (NMR), and mass spectroscopy (MS). The chemical structure of cage compounds was initially confirmed using FT-IR (Fig. 1A). The presence of characteristic C=N and C–N stretching bands located at 1500 and 1350 cm⁻¹, respectively, indicates the structural preservation of cage units. Furthermore, the disappearance of the stretching band of chlorine groups (C–Cl) at 750 cm⁻¹, coupled with the appearance of distinct aliphatic stretching (C–H) bands stemming from dimethylamine moieties, indicates the transformation of CAGE-0 and CAGE-1 to CAGE-2 and CAGE-3, respectively. ¹H NMR spectroscopy was conducted to verify the formation of the cage structures (Fig. 1B and C). The proton signals associated with the central benzene ring of the 1,3,5-tri(p-hydroxyphenyl)benzene moiety experienced a chemical shift towards the upfield region after reacting with CLEFT-1 with an equimolar amount of 1,3,5-tri(p-hydroxyphenyl)benzene. This spectral change supports the formation of CAGE-1. ¹H NMR spectra of other cages, as well as their corresponding ¹³C spectra, are provided in the ESI.† Also, nucleophilic substitution reactions on CAGE-0 and CAGE-1 with the dimethyl amine caused a significant shift for all the protons to the upfield region, along with the appearance of the distinct C–H signal (Fig. S2 and S4†). The collected mass spectra of cage molecules further prove the proposed chemical structures of cage compounds (ESI†).

Fig. 1 (A) FT-IR spectra of cage molecules, (B) ¹H NMR spectrum of CLEFT-1, and (C) ¹H NMR spectrum of CAGE-1.

3.2 Morphological characterization of electrodes

Impregnation of ion-selective CAGE molecules onto the electrodes was conducted using the dip coating technique. Scanning electron microscopy (SEM) was employed to assess the morphological properties of the electrodes. SEM images of the electrodes are depicted in Fig. 2. Fig. 2A presents the CAGE ionophore-free electrode, and Fig. 2B reveals the electrode with incorporated CAGE ionophores after one step of dip-coating. The closer examination of the SEM images at higher magnification reveals that graphite flakes are observable before the impregnation of CAGE molecules (Fig. 2A). However, after the impregnation of CAGE molecules, the visibility of surface features of graphite flakes becomes less pronounced (highlighted in the red ellipse in Fig. 2), verifying the successful inclusion of the CAGE molecules as a uniform layer. The SEM imaging assures that the surface of graphite was readily modified by the CAGE ionophore slurry.

Fig. 2 SEM images of electrodes before (A) and after (B) CAGE impregnation.

3.3 Potentiometric and computational validation of CAGE incorporated electrodes

Table 2 illustrates the impact of varying CAGE structures on the electrodes in the presence of NO₃⁻ ions within a concentration range of 1.0 × 10⁻¹ to 1.0 × 10⁻⁵ M. From the data presented in Table 2, it is evident that electrode E4 (CAGE-1) displayed the most pronounced slope and highest R² value within the linear range of 1.0 × 10⁻¹ to 1.0 × 10⁻⁵ M for NO₃⁻ ions. Notably, systematic variations in the structure and size of cage molecules play a crucial role in the interaction with NO₃⁻ ions. To investigate the effect of cage structure on the detection of NO₃⁻ ions, electrodes E1 and E3 are intentionally designed with an open geometry, referred to as CLEFTs, which are expected to interact less with NO₃⁻ ions compared to electrodes E2 and E4, which feature a CAGE geometry conducive to hosting NO₃⁻ ions. The electrodes E1 and E3, which were prepared using CLEFT-0 and CLEFT-1, respectively, exhibited similar slopes (dV/dC) across the concentration range of 1.0 × 10⁻¹ to 1.0 × 10⁻⁵ M. Nonetheless, they did not reveal a fully reversible exchange of NO₃⁻ ions between the electrodes and the solution. This finding suggests that CLEFTs do not provide reversible NO₃⁻ ion binding as ionophores under the tested conditions. Then, the CAGE structures of electrodes E2 and E4 were evaluated under identical conditions, resulting in slopes (dV/dC) of −42.5 and −50.3 mV, respectively. Although both cage structures have the same symmetry and functionality, only the response of electrode E4 with a larger cage size revealed an enhanced level of reversible interaction compared to E2 with a smaller cage size. The reversible response of electrode E4 compared to the non-reversible response of electrode E2 is attributed to the size of the CAGE structures incorporated into each electrode. In the E4 electrode, synthetic ionophore CAGE-1 provides effective hosting for NO₃⁻ ions, allowing a more stable and reversible interaction between the electrode and the ions in solution.⁴⁴ As a result, electrode E4 demonstrates a more pronounced and consistent response over the tested concentration range, indicating its ability to effectively capture and release NO₃⁻ ions in a reversible manner. On the other hand, electrode E2 exhibited a non-reversible response, suggesting that the CAGE structure incorporated into this electrode may not be as well-suited for facilitating reversible ion binding.⁴⁵ The BSSE (the basis set superposition error)-corrected binding energies (E_bind) are listed in Table 1. A negative value of E_bind suggests that the complexation is energetically favorable and occurs spontaneously. The highest binding energy, −24.4 kJ mol⁻¹, is observed for E2* NO₃⁻, while the lowest binding energy, −8.36 kJ mol⁻¹, is found for E4* NO₃⁻. The stability hierarchy is as follows: E2* NO₃⁻ > E5* NO₃⁻ > E6* NO₃⁻ > E4* NO₃⁻. The binding energy between CAGE molecules (E5–E6) substituted with a dimethylamine group and the nitrate ion was calculated in a similar manner. The main difference between the E2 and E4 molecules lies in the groups attached to the triazine. The electronegative chlorine (Cl) group on the smaller CAGE (E2) molecule reduces the binding energy with NO₃⁻. However, this trend is not observed for the relatively larger CAGE molecules (E4 and E6), where the binding energy of the Cl-substituted CAGE molecule (E4) is higher than that of E6. The Nernstian behavior of E4 may be attributed to the reversible binding of NO₃⁻ as compared to other CAGE molecules. These results are in accordance with our design principles because increasing the electron density of the cage molecules with electron-donating units such as amine groups decreases the anion–pi interactions between the NO₃⁻ ions and the host molecules, leading to weak interactions between the NO₃⁻ ions and cage ionophores. On the other hand, electron-withdrawing groups boost the NO₃⁻ binding by decreasing the electron density of the cages and increasing the anion–pi interactions. Overall, these results underscore the importance of carefully designing and optimizing cage ionophores for achieving reliable and reversible ion-sensing performance in electrochemical applications.

Table 1 The counterpoise binding energies of nitrate ions using B3LYP-D3/def2-TZVP functional

Complex	E bind binding energy (in kJ mol^−1)
E2* NO3^−	−24.4
E4* NO3^−	−8.36
E5* NO3^−	−11.9
E6* NO3^−	−11.5

---

The impact of the coating cycle on the potentiometric response of E4 was examined, and the findings are presented in Table 2. The potentiometric performance decreases as the number of CAGE-1 (E4) coating cycles increases. This trend suggests that an excessive coating cycle may lead to uneven or discontinuous layers, which increases the resistance and reduces the efficiency of ion diffusion and electron transfer at the electrode interface. Consequently, the E4.1 coded CAGE-1 incorporated NO₃⁻ selective electrode (cNSE), with its optimal cage structure and coating cycle, exhibited the steepest slope and highest R² value for NO₃⁻ ions within the linear range of 1.0 × 10⁻¹ to 1.0 × 10⁻⁵ M.

Table 2 Potentiometric parameters of CAGE-incorporated electrodes

Electrode code	LRR (M)	LOD (M)	Slope, mV dec^−1	R ^2 value
LRR: linear response range. LOD: limit of detection * B1 represents a baseline electrode without the incorporation of cage ionophores, serving as a control for comparison.
B1	1.0 × 10^−4–1.0 × 10^−1	1.0 × 10^−4	−10.9	0.7347
E1	1.0 × 10^−5–1.0 × 10^−1	9.0 × 10^−6	−46.7	0.9613
E2	1.0 × 10^−5–1.0 × 10^−1	9.0 × 10^−6	−42.5	0.9635
E3	1.0 × 10^−5–1.0 × 10^−1	9.0 × 10^−6	−45.5	0.9798
E4	1.0 × 10^−5–1.0 × 10^−1	7.5 × 10^−6	−50.3	0.9956
E5	1.0 × 10^−4–1.0 × 10^−1	1.0 × 10^−4	−29.8	0.9418
E6	1.0 × 10^−4–1.0 × 10^−1	1.0 × 10^−4	−31.2	0.9069

---

Electrode code	Coating cycle		Slope, mV dec^−1	R ^2 value
E4.1	5 μL		−53.1	0.9971
E4.2	5 μL + 5 μL		−50.3	0.9956
E4.3	5 μL + 5 μL + 5 μL		−45.5	0.9935
E4.4	5 μL + 5 μL + 5 μL + 5 μL		−42.5	0.974

---

3.4 Linear range, slope, and LOD of cNSE

The cNSE's potentiometric behavior towards NO₃⁻ ions, within a concentration range of 1.0 × 10⁻⁶ to 1.0 × 10⁻¹ M at pH 7.0, is illustrated in Fig. 3. Notably, the cNSE demonstrates a linear response between 1.0 × 10⁻⁵ and 1.0 × 10⁻¹ M, with a high degree of linearity (R² = 0.9971) and a consistent slope of −53.1 ± 1.4 mV dec⁻¹. This linear response zone highlights the electrode's reliability and accuracy across a substantial concentration range. Moreover, employing the methodology endorsed by IUPAC,⁵² the limit of detection for cNSE was determined to be 7.5 × 10⁻⁶ M. CAGE-1 based cNSE was compared with previously reported nitrate selective electrodes based on validation parameters such as slope, LRR and LOD in the ESI† (Table S1). The slope of cNSE is within the range observed for other ionophores, though slightly below the Nernstian theoretical value. Ionophores such as TDMAN and Co(Bphen)₂(NO₃)₂(H₂O)₂ exhibit similar or higher slopes, indicating strong potentiometric responses. cNSE has a linear response range of 1.0 × 10⁻⁵–1.0 × 10⁻¹ M, comparable to other nitrate-selective ionophores like TDANO₃ and Nitrate Ionophore VI, which also operate effectively over wide concentration ranges. The detection limit of 7.5 × 10⁻⁶ M for cNSE is in the mid-range among the ionophores compared.

Fig. 3 Potentiometric responses depend on the NO₃⁻ concentrations (A), linear calibration plot for NO₃⁻ concentration change (1.0 × 10⁻⁵–1.0 × 10⁻¹ M, pH = 7) of cNSE (B).

3.5 Repeatability, response time, and effects of pH of cNSE

To assess the repeatability of cNSE, real-time potentials were recorded for solutions at concentrations of 1.0 × 10⁻³, 1.0 × 10⁻², and 1.0 × 10⁻¹ M (pH = 7.0), as depicted in Fig. 4A. The potentiometric measurements were conducted both from low to high concentrations and vice versa. The resulting average potential values, accompanied by their respective standard deviations, were determined as follows: −138.3 ± 2.3 mV for 1.0 × 10⁻³ M, −80.6 ± 1.3 mV for 1.0 × 10⁻² M, and −23.1 ± 1.0 mV for 1.0 × 10⁻¹ M. These negligible standard deviation values highlight the remarkable reproducibility of cNSE. Such consistency in the recorded potential underscores the electrode's reliability and its ability to provide consistent measurements across varying concentrations. This robust performance makes it a dependable tool for analytical tasks where precision and repeatability are paramount. The lifetime of cNSE was estimated to be ∼14 days (Fig. S1†).

Fig. 4 Repeatability and reversibility of cNSE (a: 1.0 × 10⁻³ M; b: 1.0 × 10⁻² M; c: 1.0 × 10⁻¹ M NO₃⁻ (pH: 7.0)) (A). Response time of cNSE (1.0 × 10⁻³–1.0 × 10⁻² concentration change) (B). pH dependence of the potentiometric response of cNSE (a: 1.0 × 10⁻³ M; b: 1.0 × 10⁻² M NO₃⁻) (C).

The determination of an ion-selective electrode's response time is facilitated by various methods developed by the International Union of Pure and Applied Chemistry (IUPAC). One such method, outlined by Buck and Lindner in 1994,⁵³ quantifies response time as the duration (t₉₅) required for 95% of the potential change to reach an equilibrium state. As per IUPAC guidelines, the response time denotes the duration for the potential to stabilize after the ion-selective working electrode and reference electrode are introduced into a solution containing the analyte. In Fig. 4B, the response time of cNSE was evaluated using NO₃⁻ solutions at different standard concentrations. According to the prescribed method, the average response time was determined to be approximately 10 seconds. This metric signifies the electrode's efficiency in promptly achieving a stable potential upon immersion, thus facilitating swift and accurate measurements in analytical settings. The influence of pH on the potentiometric response of cNSE was explored by varying the pH levels of solutions containing 1.0 × 10⁻² and 1.0 × 10⁻³ M NO₃⁻. pH adjustments were achieved using NaOH and HCl solutions, spanning pH values from 2.5 to 12. The alterations in the cNSE's potential response corresponding to these pH changes are illustrated in Fig. 4C. As depicted in Fig. 4C (a: 1.0 × 10⁻³ M), a notable OH⁻ ion interference was observed at low NO₃⁻ concentrations, becoming prominent beyond pH 9. Conversely, under acidic conditions, the potential stabilizes notably after pH 4. At low pH, the ionophore or electrode material may undergo protonation, altering the electrochemical environment at the interface. This modification affects the electrode's response, leading to an increase in potential. Additionally, the relative activity of anions such as NO₃⁻ decreases due to stronger interactions with counter ions like H⁺ in the solution, further contributing to the observed potential shift. Conversely, the abundance of hydroxide ions in alkaline solutions can interfere with the ion-selective electrode's response. These OH⁻ ions compete with nitrate ions for binding to the ionophore or the electrode surface, resulting in changes to the electrode potential. Therefore, it suggests a pH range for optimal cNSE performance, approximately from pH 4 to 9. These observations shed light on the electrode's sensitivity to pH variations and potential applications across different pH regimes.

3.6 Selectivity of cNSE

The relative response of the electrode to the primary ion in the presence of the interfering ions is commonly expressed by the selectivity of an electrode, which is of major significance. Traditionally, the IUPAC recommendation's procedures are used to determine the selectivity coefficients in detail. For the purpose of simplicity and efficiency, we chose to use the separate solution method in the current investigation to compute the selectivity coefficients for a variety of interfering ions.⁵² In this approach, a calibration curve was constructed using nitrate ion (NO₃⁻, denoted as “a_A”) solutions with concentrations ranging from 1.0 × 10⁻⁵ to 1.0 × 10⁻¹ M (pH = 7.0). The cNSE was then tested in individual solutions of interfering ions, each at a single concentration of 1.0 × 10⁻² M (denoted as “a_B”). The corresponding potential values for each interfering ion were recorded (n = 3). Using the calibration curve for the primary ion, the associated primary ion activity (a_A) was calculated based on the measured potentials for the interfering ions. Lastly, based on the calibration plot and the measured potential values, the associated primary ion activity (a_A) was calculated. The values of the selectivity coefficient were determined for each of the interferents investigated and are shown in Table 3 by substituting the calculated primary ion activity (a_A) and respective interfering ion activity (a_B) into the equation below:⁵²

K^pot_A,B = a_A/(a_B)^Z_A/Z_B

where Z_A and Z_B are the net charges of primary and interfering ions.

The utilization of molecular CAGE-1 (E4) as an ionophore significantly improves the diffusion and reversible binding of NO₃⁻, as evidenced by the superior potentiometric performance characteristics for cNSE as compared to the cage-free electrode (Fig. 5A and B). This observation ascertains that molecular CAGE-1 (E4) has a more pronounced and consistent response at the tested concentration of NO₃⁻, indicating its ability to effectively capture and release NO₃⁻ ions in a reversible manner.

Table 3 Logarithmic selectivity coefficient values for cNSE calculated by the separate solution method

Interferents	log K^potA,B	Interferents	log K^potA,B
Cl^−	−1.65	HPO4^2−	−3.11
F^−	−3.24	S2O3^2−	−3.57
HCO3^−	−3.02	CO3^2−	−3.55
ClO3^−	−2.53	SO4^2−	−3.82

---

Fig. 5 Potentiometric responses of cNSE (A) and cage-free electrode (B) for varying concentrations of anions.

ClO₄⁻, SCN⁻, Br⁻, and I⁻, which are at the top of the Hofmeister series, exhibit significant interference but do not provide a reversible response. Specifically, the potentials of SCN⁻ and I⁻ solutions do not change consistently when transitioning from low to high concentrations. Instead, they display differences only when moving from dilute to concentrated solutions, causing severe interference at concentrations above 1.0 × 10⁻² M. Due to their non-reversible response and erratic potential changes at higher concentrations, these anions have not been included in the selectivity table. The selectivity coefficients of the proposed electrode were compared with those reported for other nitrate-selective electrodes in the ESI† (Table S2).

3.7 Determination of nitrate ion concentration in real samples

To evaluate the suitability of the cNSE for nitrate determination in real samples, measurements were conducted using tap water and mineral water. The procedure was modified by adding 0.5 mL of a 1.0 M Na₂SO₄ solution to 50 mL of each sample to ensure constant ionic activity, with Na₂SO₄ acting as an ionic strength buffer. Recovery rates were also assessed. The results, summarized in Table 4, demonstrate acceptable recovery rates for samples, confirming that the proposed cNSE is an affordable and straightforward analytical tool for monitoring nitrates in various water samples.

Table 4 Determination of nitrates in unspiked and spiked water samples

Sample	Nitrate,^a [mg L^−1] found by cNSE	Recovery, %
a Number of measurements (N = 5).
Tap water	11.2 ± 0.21	—
Tap water + 500 μL, 0.1 M NO3^−	71.0 ± 0.25	97.0
Mineral water	7.4 ± 0.32	—
Mineral water + 500 μL, 0.1 M NO3^−	68.2 ± 0.20	98.3

---

4. Conclusions

In conclusion, the prevalence of nitrate ions as pollutants in water and soil highlights the urgent need for robust monitoring methods to safeguard human health and the environment. Electrochemical analysis, particularly employing potentiometric ion-selective electrodes, emerges as a powerful tool for accurate and sensitive detection of nitrate levels. While traditional ionophores derived from natural sources have limitations in selectivity and modifiability, synthetic ionophores offer greater flexibility and specificity for targeted ions. Our study demonstrates the successful utilization of a molecular cage as an ionophore for nitrate ions, showcasing its ability to provide a linear response within a wide concentration range and a low detection limit. Achieving this effectiveness relied on optimizing the interaction between the cage molecules and nitrate ions. We achieved this optimization by modifying the cage molecule's internal dimensions and electron density to create a competitive environment conducive to selective binding with nitrate ions. The resulting nitrate-selective cage-electrode exhibited potentiometric characteristics of ∼53.1 ± 1.4 mV dec⁻¹ for slope, a limit of detection of 7.5 × 10⁻⁶ M, and a linear response range of 1.0 × 10⁻⁵ to 1.0 × 10⁻¹ M. This innovation represents a significant advancement in the field of electrochemical analysis, offering a practical solution for effectively monitoring nitrate pollution. This study may be extended to other ions such as SO₄²⁻ and PO₄³⁻ by careful design of CAGE molecules, and it may assist in utilizing synthetic ionophore-based ion selective electrodes.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Scientific and Technological Research Council of Turkey (TUBITAK Project Grant No: 117F243 and BIDEB 2247 D Project Grant No: 120C132). The authors thank the Nuclear Magnetic Resonance Application and Research Center (NMRM-IZTECH).

Notes and references

1. M. Cui, L. Zeng, W. Qin and J. Feng, Environ. Pollut., 2020, 263, 114553.
2. M. Karimi and K. Moradi, J. Plant Nutr., 2018, 41, 1695–1704.
3. C.-W. Liu, Y. Sung, B.-C. Chen and H.-Y. Lai, Int. J. Environ. Res. Public Health, 2014, 11, 4427–4440.
4. A. F. Colaço and J. P. Molin, Precis. Agric., 2017, 18, 169–191.
5. C. Hyusein and V. Tsakova, J. Electroanal. Chem., 2023, 930, 117172.
6. D. L. Dinnes, D. L. Karlen, D. B. Jaynes, T. C. Kaspar, J. L. Hatfield, T. S. Colvin and C. A. Cambardella, Agron. J., 2002, 94, 153–171.
7. Y. Li, J. Li, L. Gao and Y. Tian, PLoS One, 2018, 13, e0204570.
8. P. Borrelli, P. Panagos, C. Ballabio, E. Lugato, M. Weynants and L. Montanarella, Land Degrad. Dev., 2016, 27, 1093–1105.
9. P. Niedzielski, I. Kurzyca and J. Siepak, Anal. Chim. Acta, 2006, 577, 220–224.
10. Y. Zuo, C. Wang and T. Van, Talanta, 2006, 70, 281–285.
11. M. Akyüz and Ş. Ata, Talanta, 2009, 79, 900–904.
12. M. E. E. Alahi and S. C. Mukhopadhyay, Sens. Actuators, A, 2018, 280, 210–221.
13. F. Can, S. Korkut Ozoner, P. Ergenekon and E. Erhan, Mater. Sci. Eng., C, 2012, 32, 18–23.
14. W. Xuejiang, S. Dzyadevych, J. Chovelon, N. Renault, C. Ling, X. Siqing and Z. Jianfu, Talanta, 2006, 69, 450–455.
15. T. Madasamy, M. Pandiaraj, M. Balamurugan, K. Bhargava, N. K. Sethy and C. Karunakaran, Biosens. Bioelectron., 2014, 52, 209–215.
16. S. S. M. Hassan, H. E. M. Sayour and S. S. Al-Mehrezi, Anal. Chim. Acta, 2007, 581, 13–18.
17. F. Paré, A. Visús, G. Gabriel and M. Baeza, Chemosensors, 2023, 11, 174.
18. R. G. Hjort, R. R. A. Soares, J. Li, D. Jing, L. Hartfiel, B. Chen, B. Van Belle, M. Soupir, E. Smith, E. McLamore, J. C. Claussen and C. L. Gomes, Microchim. Acta, 2022, 189, 122.
19. N. T. D. Thuy, X. Wang, G. Zhao, T. Liang and Z. Zou, Sensors, 2022, 22, 9730.
20. L. Fozia, G. Zhao, Y. Nie, J. Jiang, Q. Chen, C. Wang, X. Xu, M. Ying, Z. Hu and H. Xu, Electrocatalysis, 2023, 14, 534–545.
21. L. Zhang, Z. Wei and P. Liu, PLoS One, 2020, 15, e0240173.
22. C. L. Baumbauer, P. J. Goodrich, M. E. Payne, T. Anthony, C. Beckstoffer, A. Toor, W. Silver and A. C. Arias, Sensors, 2022, 22, 4095.
23. Y. Liu, Y. Liu, Z. Meng, Y. Qin, D. Jiang, K. Xi and P. Wang, Talanta, 2020, 208, 120374.
24. Y. Fan, Y. Huang, W. Linthicum, F. Liu, A. O. Beringhs, Y. Dang, Z. Xu, S.-Y. Chang, J. Ling, B. D. Huey, S. L. Suib, A. W. K. Ma, P.-X. Gao, X. Lu, Y. Lei, M. T. Shaw and B. Li, ACS Sens., 2020, 5, 3182–3193.
25. K. Pietrzak, C. Wardak and R. Łyszczek, Electroanalysis, 2020, 32, 724–731.
26. M.-Y. Kim, J.-W. Lee, D. J. Park, J.-Y. Lee, N. V. Myung, S. H. Kwon and K. H. Lee, J. Electroanal. Chem., 2021, 897, 115553.
27. O. Buyukcakir, Y. Seo and A. Coskun, Chem. Mater., 2015, 27, 4149–4155.
28. K. Tian, S. M. Elbert, X. Hu, T. Kirschbaum, W. Zhang, F. Rominger, R. R. Schröder and M. Mastalerz, Adv. Mater., 2022, 34, 2202290.
29. M. Liu, L. Zhang, M. A. Little, V. Kapil, M. Ceriotti, S. Yang, L. Ding, D. L. Holden, R. Balderas-Xicohténcatl, D. He, R. Clowes, S. Y. Chong, G. Schütz, L. Chen, M. Hirscher and A. I. Cooper, Science, 1979, 2019(366), 613–620.
30. Q. Song, S. Jiang, T. Hasell, M. Liu, S. Sun, A. K. Cheetham, E. Sivaniah and A. I. Cooper, Adv. Mater., 2016, 28, 2629–2637.
31. P. Bhandari and P. S. Mukherjee, ACS Catal., 2023, 13, 6126–6143.
32. T. Hasell, M. Miklitz, A. Stephenson, M. A. Little, S. Y. Chong, R. Clowes, L. Chen, D. Holden, G. A. Tribello, K. E. Jelfs and A. I. Cooper, J. Am. Chem. Soc., 2016, 138, 1653–1659.
33. T. Jiao, L. Chen, D. Yang, X. Li, G. Wu, P. Zeng, A. Zhou, Q. Yin, Y. Pan, B. Wu, X. Hong, X. Kong, V. M. Lynch, J. L. Sessler and H. Li, Angew. Chem., Int. Ed., 2017, 56, 14545–14550.
34. S. O. Kang, J. M. Llinares, V. W. Day and K. Bowman-James, Chem. Soc. Rev., 2010, 39, 3980.
35. Y. Liu, W. Zhao, C.-H. Chen and A. H. Flood, Science, 1979, 2019(365), 159–161.
36. Q. Chen, L.-P. Yang, D.-H. Li, J. Zhai, W. Jiang and X. Xie, Sens. Actuators, B, 2021, 326, 128836.
37. M. J. Langton, C. J. Serpell and P. D. Beer, Angew. Chem., Int. Ed., 2016, 55, 1974–1987.
38. L. Chen, S. N. Berry, X. Wu, E. N. W. Howe and P. A. Gale, Chem, 2020, 6, 61–141.
39. N. H. Evans and P. D. Beer, Angew. Chem., Int. Ed., 2014, 53, 11716–11754.
40. H. Xie, T. J. Finnegan, V. W. L. Gunawardana, R. Z. Pavlović, C. E. Moore and J. D. Badjić, J. Am. Chem. Soc., 2021, 143, 3874–3880.
41. J. C. Lauer, A. S. Bhat, C. Barwig, N. Fritz, T. Kirschbaum, F. Rominger and M. Mastalerz, Chem. – Eur. J., 2022, 28, e202201527.
42. A. P. Bisson, V. M. Lynch, M. C. Monahan and E. V. Anslyn, Angew. Chem., Int. Ed. Engl., 1997, 36, 2340–2342.
43. A. P. Bisson, V. M. Lynch, M. C. Monahan and E. V. Anslyn, Angew. Chem., Int. Ed. Engl., 1997, 36, 2340–2342.
44. D.-X. Wang and M.-X. Wang, Acc. Chem. Res., 2020, 53, 1364–1380.
45. D. Wang, Q. Wang, Y. Han, Y. Wang, Z. Huang and M. Wang, Chem. – Eur. J., 2010, 16, 13053–13057.
46. N. Luo, Y. Ao, D. Wang and Q. Wang, Angew. Chem., Int. Ed, 2021, 60, 20650–20655.
47. N. Luo, Y. Ao, D. Wang and Q. Wang, Chem. – Asian J., 2021, 16, 3599–3603.
48. H. Qin, J. Jiang, X. Sun, N. Lin, P. Yang and Y. Chen, Inorg. Chem., 2023, 62, 6458–6466.
49. X.-Y. Wang, J. Zhu, Q.-Q. Wang, Y.-F. Ao and D.-X. Wang, Inorg. Chem., 2019, 58, 5980–5987.
50. L. Li, H. Liu, J. Tang, P. Zhang and Y. Qian, Anal. Chem., 2022, 94, 13762–13769.
51. M. M. Naseer, D.-X. Wang, L. Zhao, Z.-T. Huang and M.-X. Wang, J. Org. Chem., 2011, 76, 1804–1813.
52. Y. Umezawa, P. Bühlmann, K. Umezawa, K. Tohda and S. Amemiya, Pure Appl. Chem., 2000, 72, 1851–2082.
53. R. P. Buck and E. Lindner, Pure Appl. Chem., 1994, 66, 2527–2536.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sd00359d

---